Experimental Investigation on the Influence of a Double-Walled Confined Width on the Velocity Field of a Submerged Waterjet
Abstract
:1. Introduction
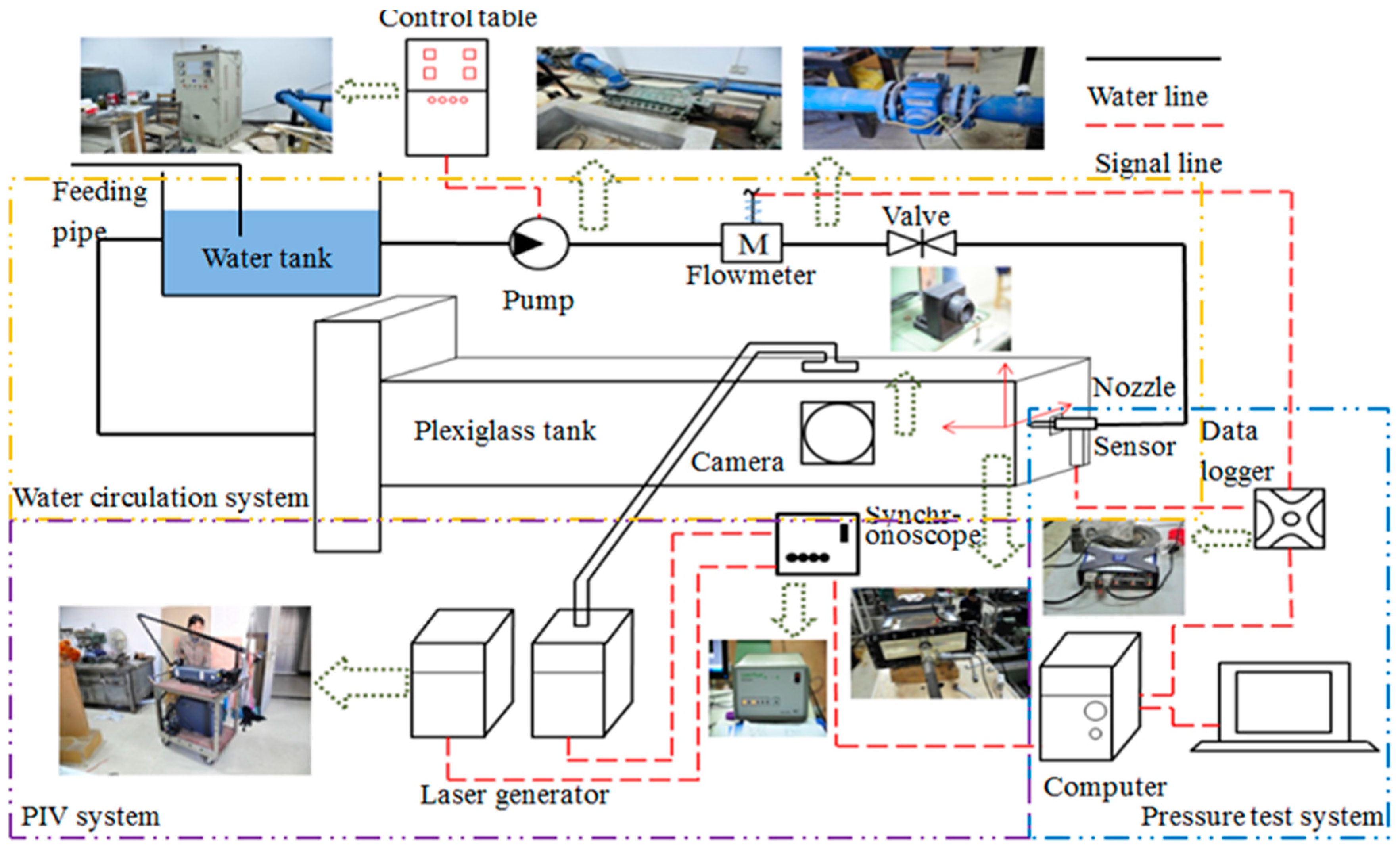
2. Experimental Setup and Procedures
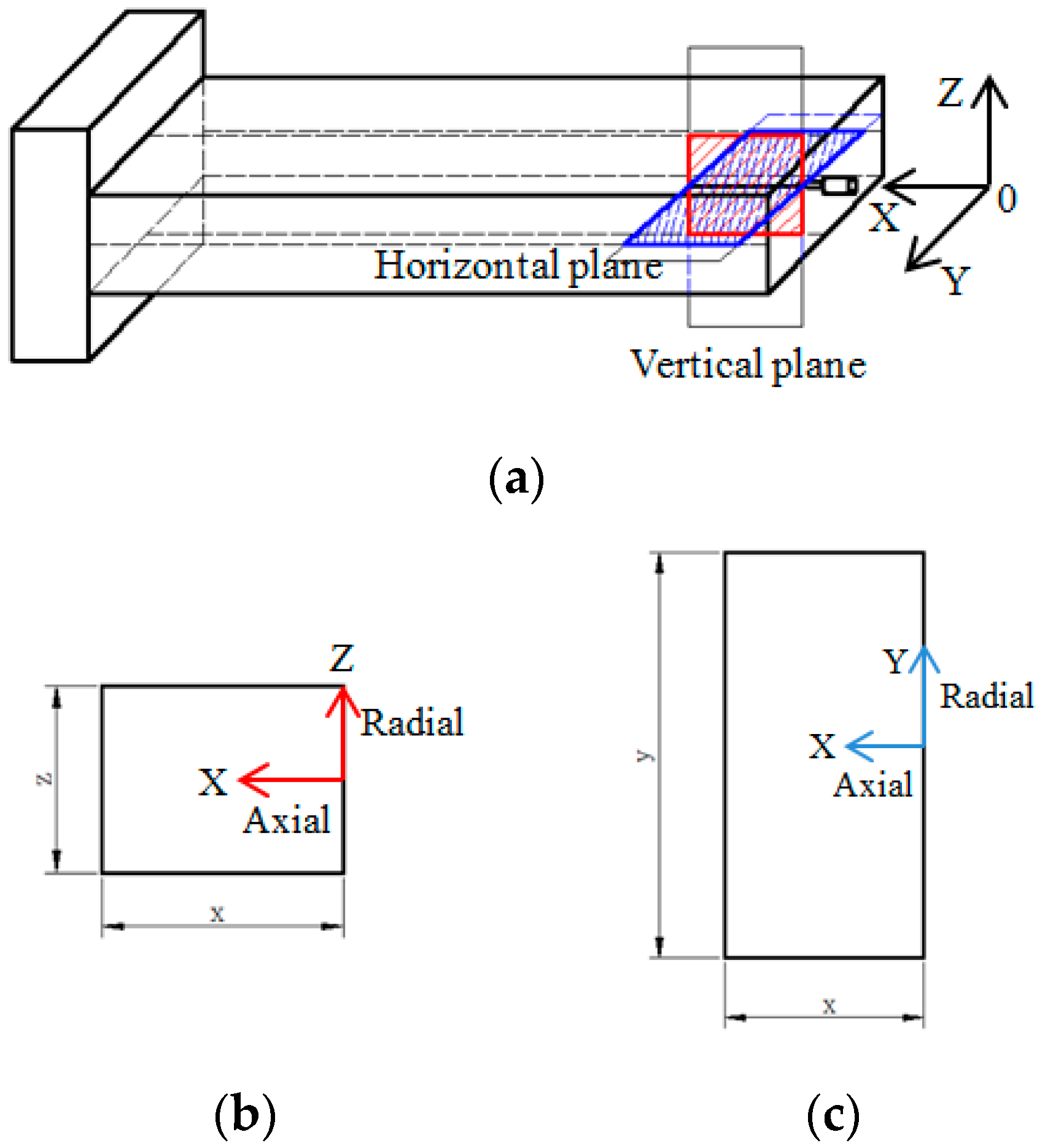
2.1. Facilities and Setup
2.2. Nozzles and Flow Conditions
2.3. Analysis of the Experimental Uncertainty
3. Results and Discussion
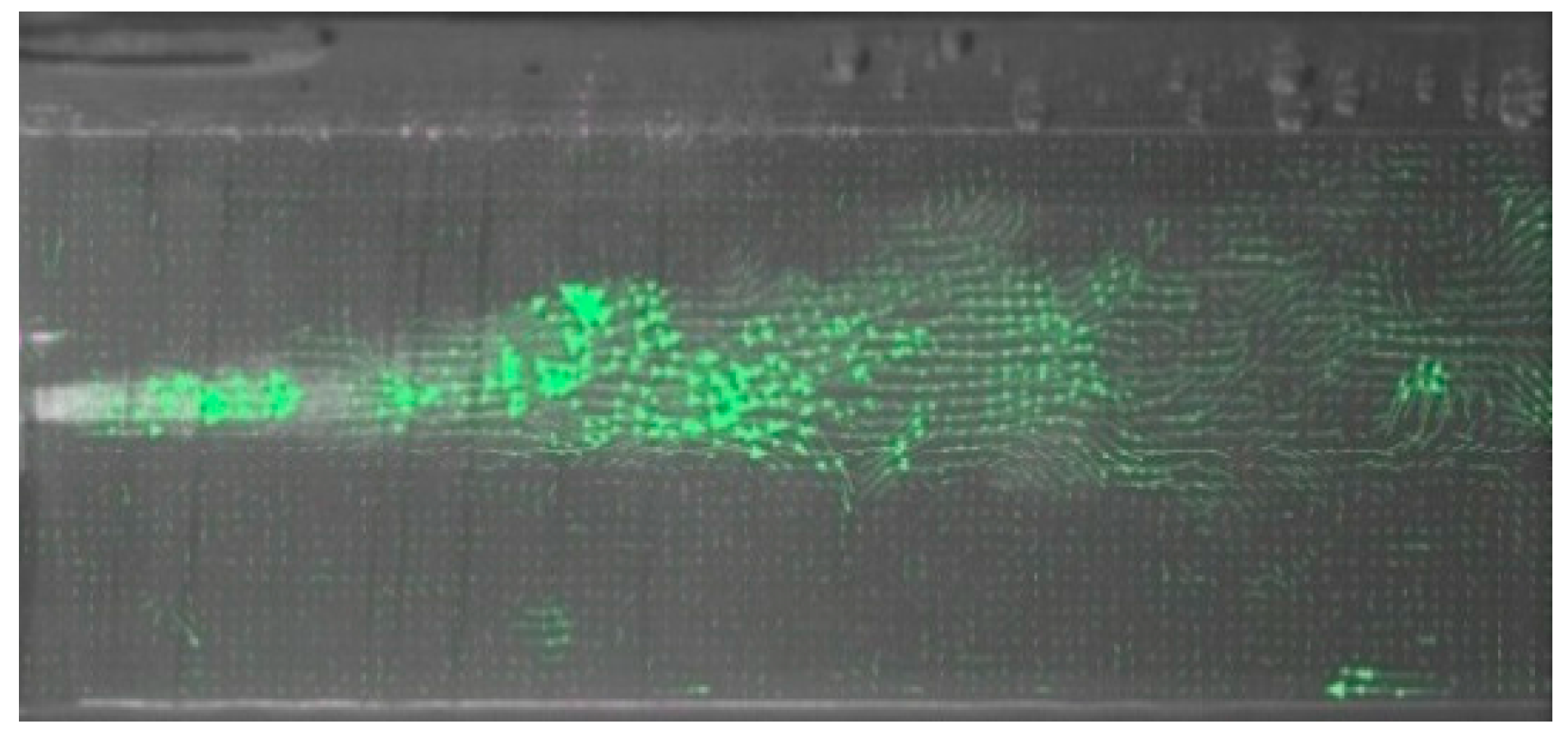
3.1. The Flow Field Characteristics of the Double-Walled Confined Waterjet
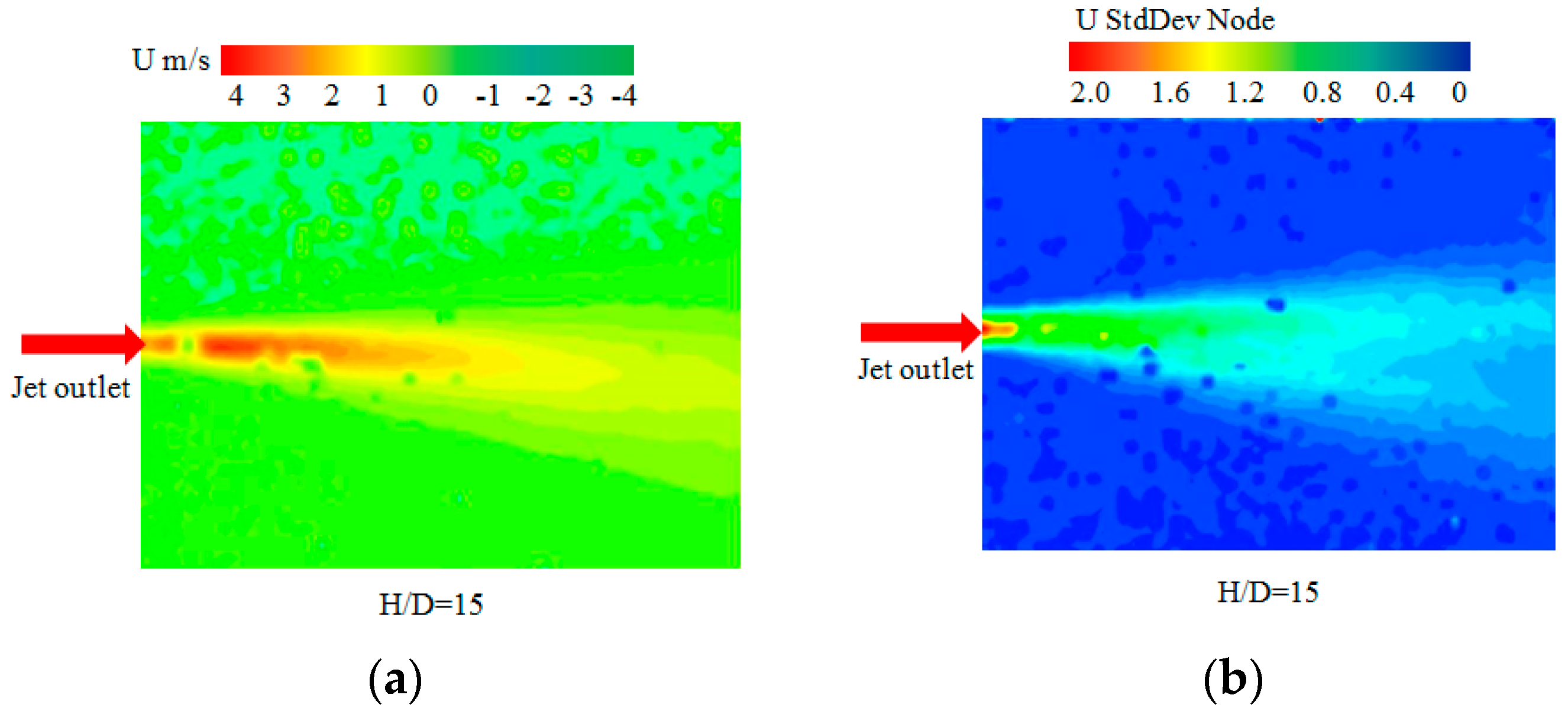
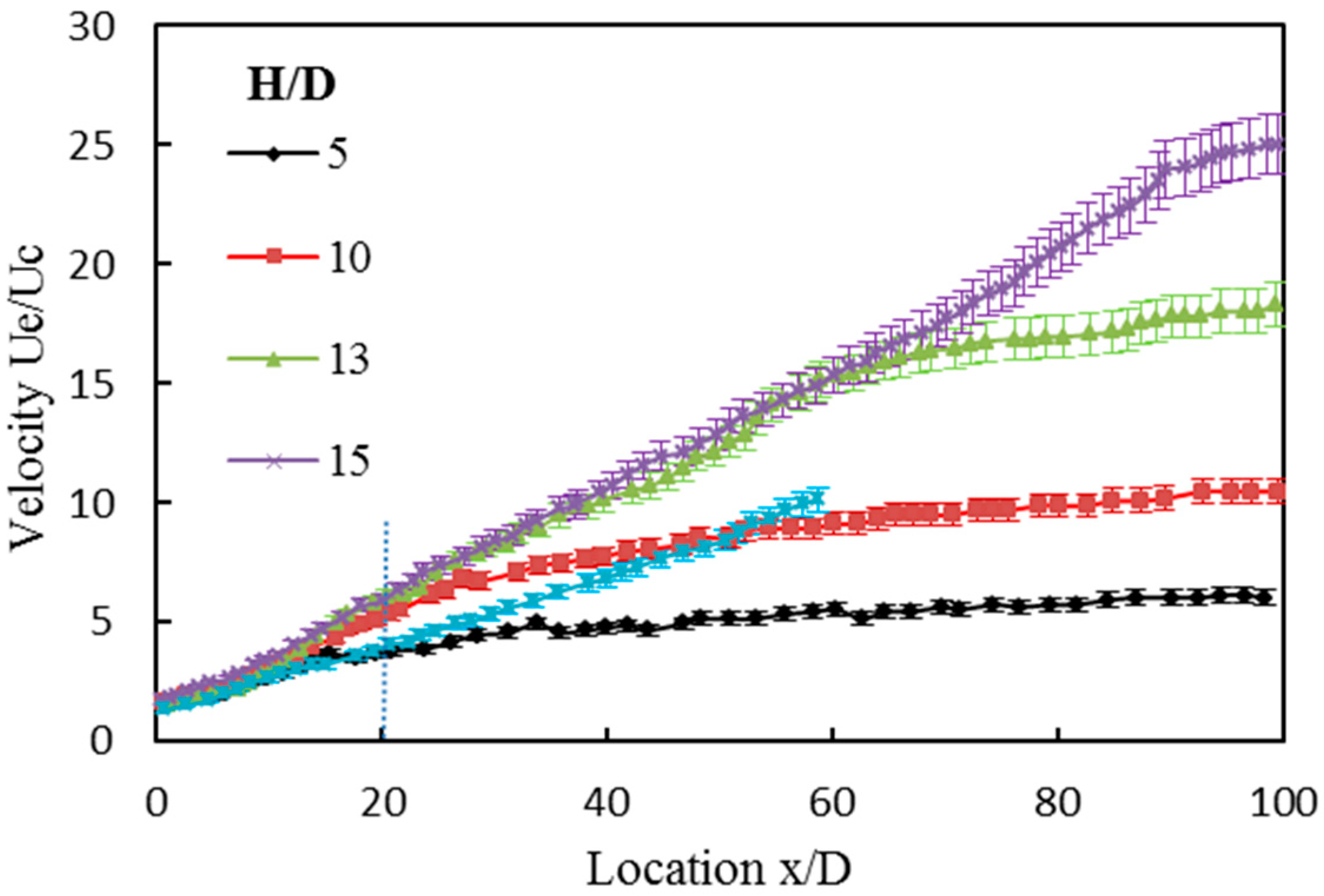
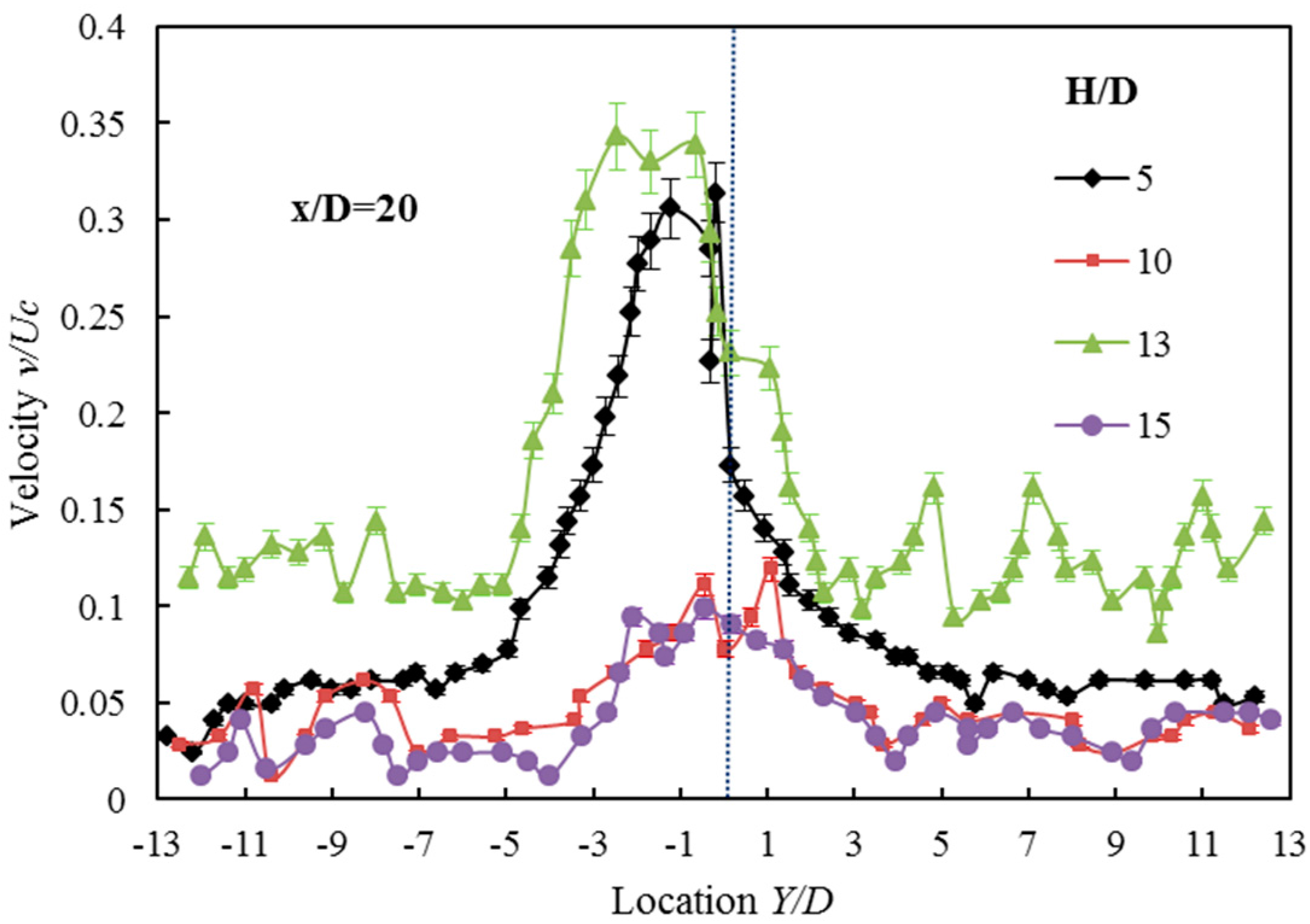
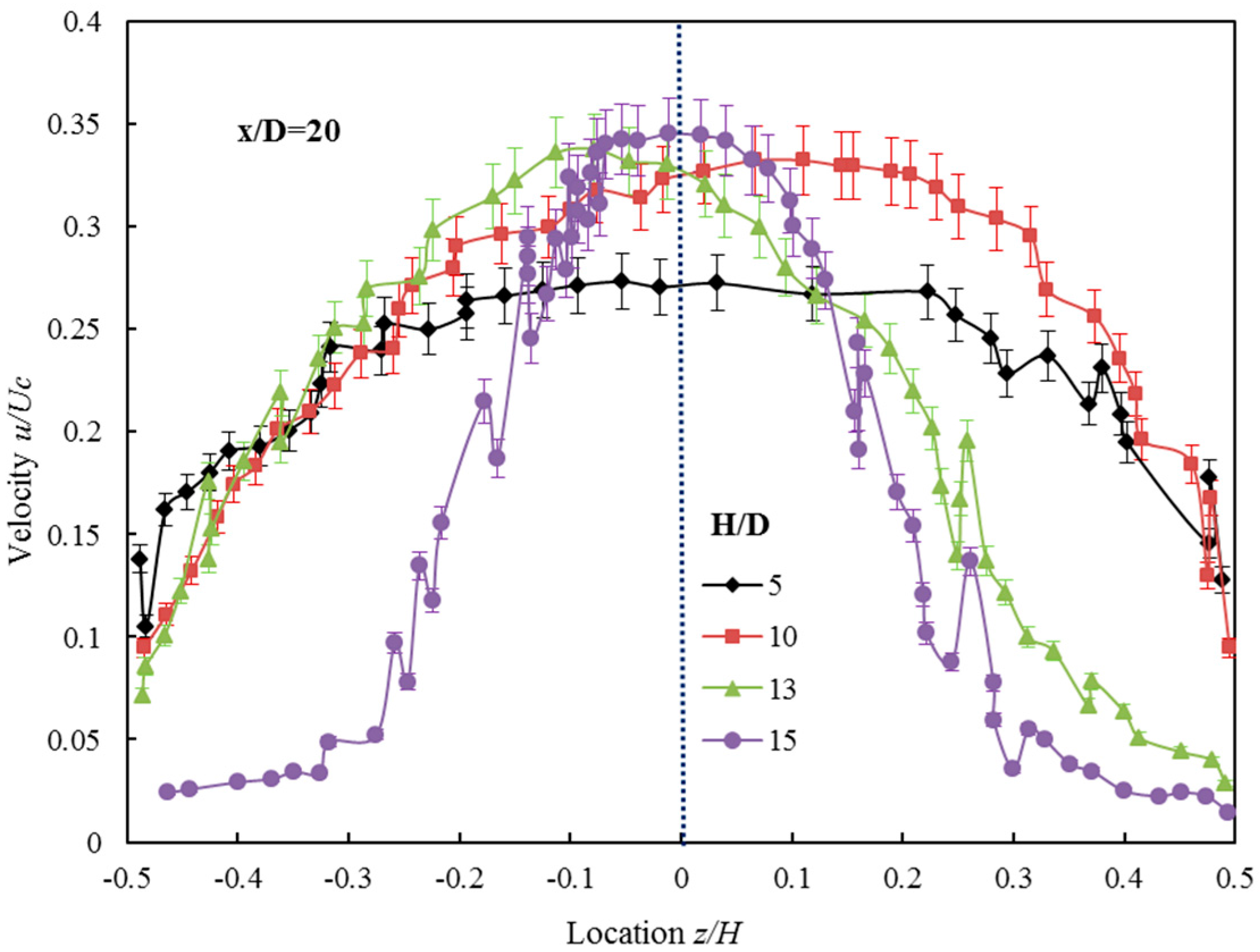
3.2. The Axial Velocity of the Double-Walled Confined Waterjet
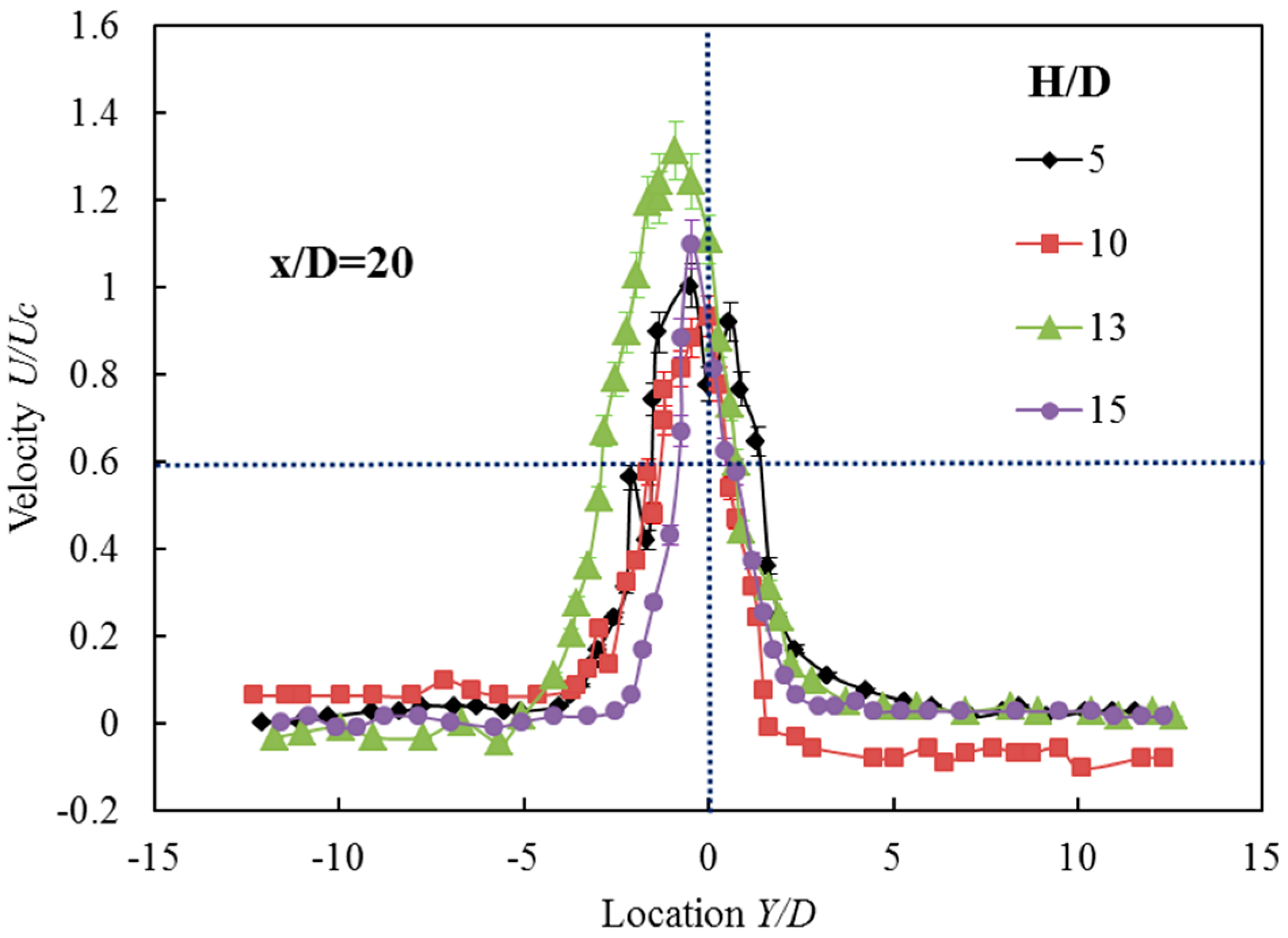
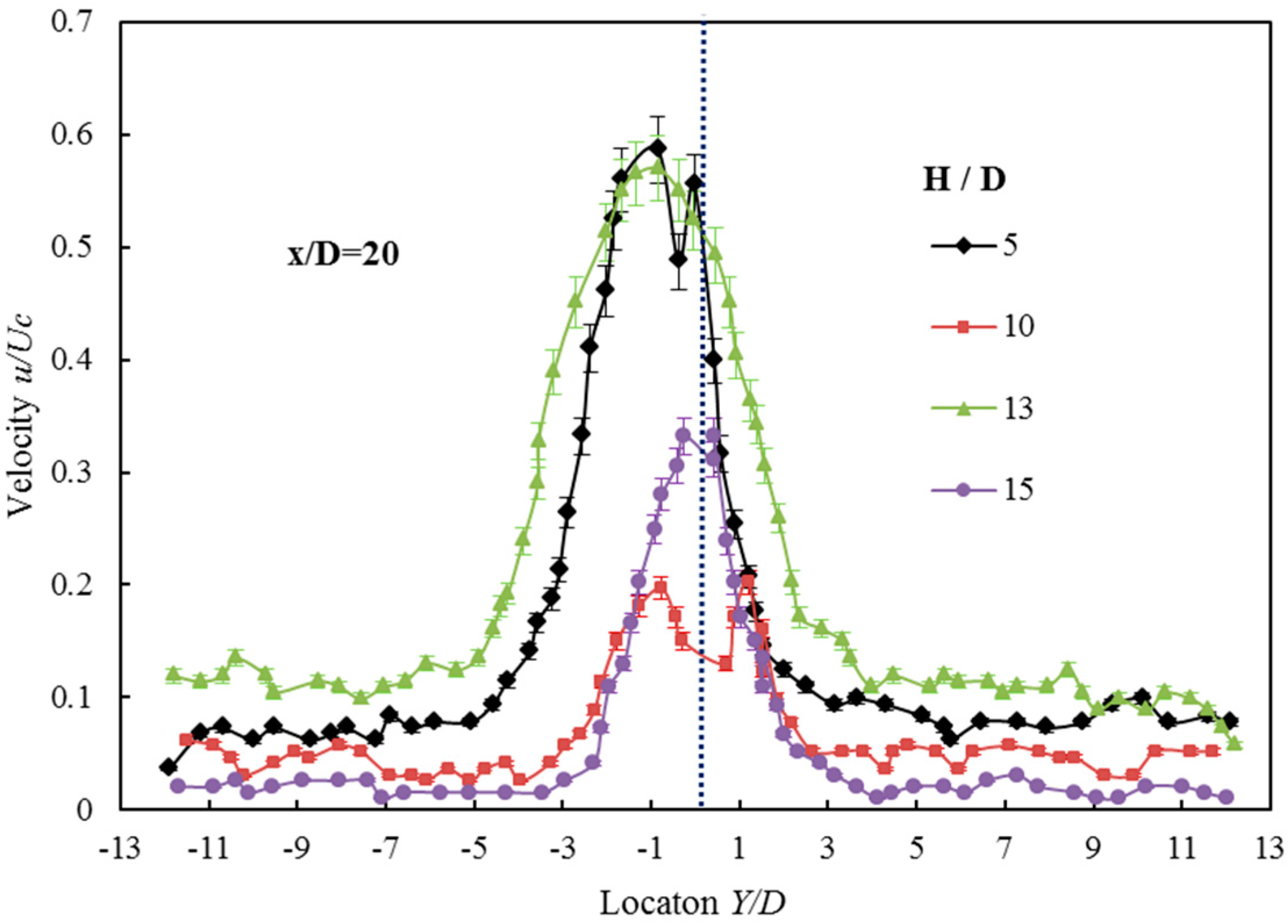
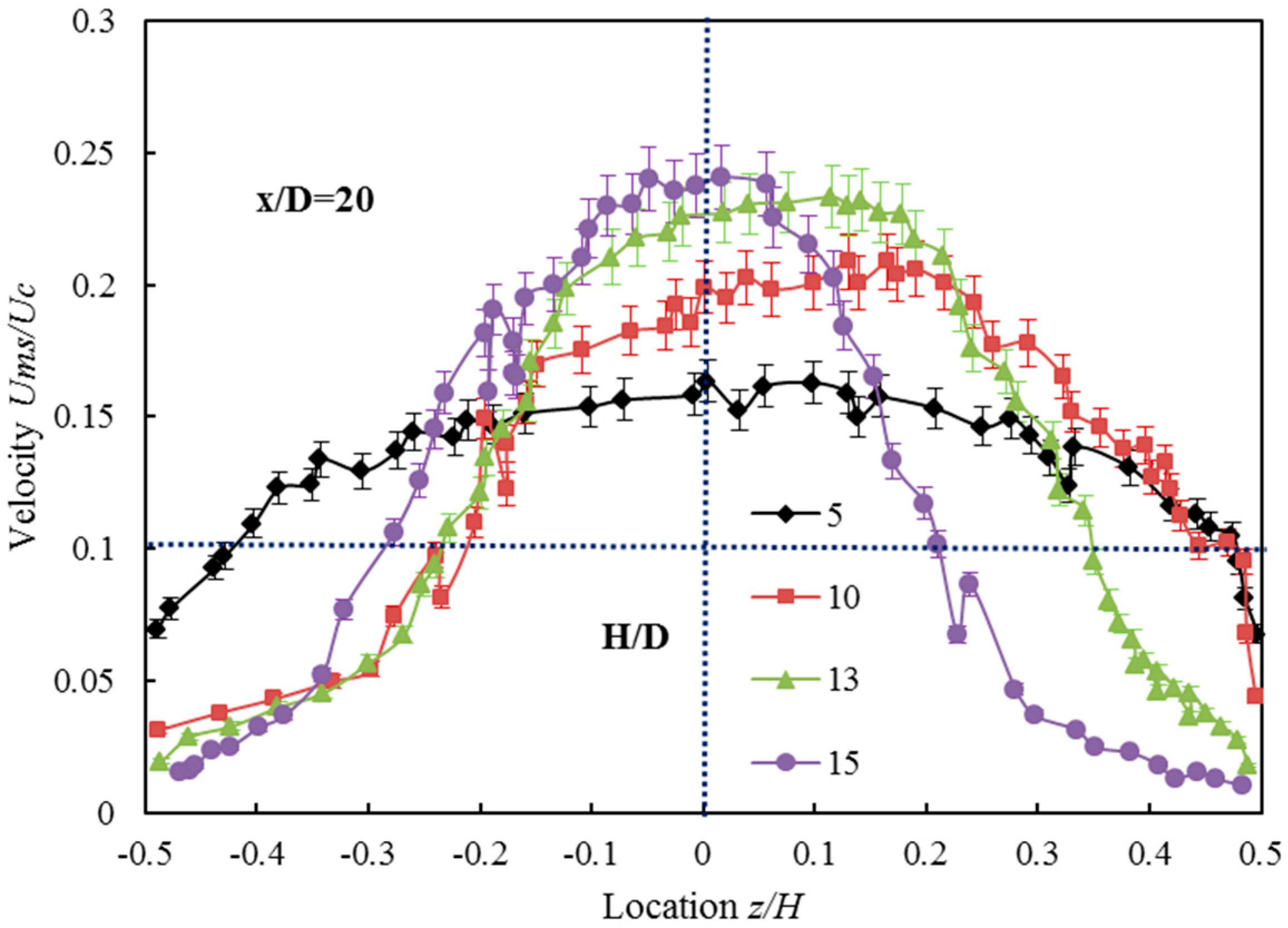
3.3. The Mean Velocity of the Double-Walled Confined Waterjet
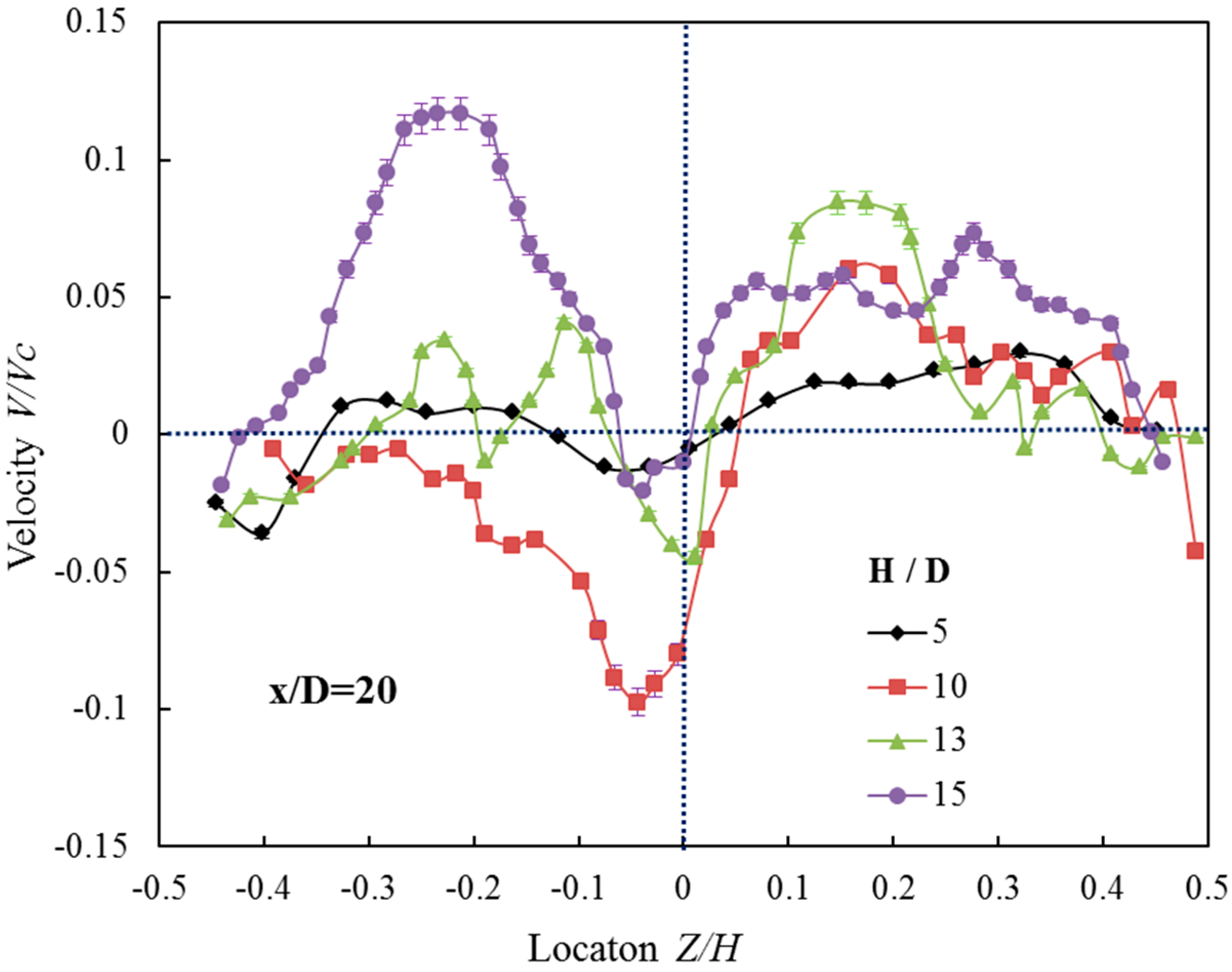
3.4. The Turbulent Intensity of the Double-Walled Confined Waterjet
4. Conclusions
- The vertical confinement has an obvious effect on the decay rate of the mean centerline velocity. When the confined width changes from 15 to 5, the speed is reduced by 20%. The slower decay rate can be explained by the conservation of mass which demands an increase in the jet velocity compared to the free jet because the cross-sectional area of the jet becomes constrained by the boundaries.
- The vertical confinement has a significant effect on the jet spread. With the decrease of the confined width, the jet has a tendency to spread horizontally. The confinement has a profound effect on the axial velocity profiles in the vertical plane. As the flow goes downstream, the jet spreads to the boundaries and the axial velocity above and below the jet centerline increases rapidly.
- The vertical confined region induces a space hysteresis effect which changes the location of the transition region moving downstream. With the enlarging of the confined width, the position moves back.
- The fluid could form a negative pressure region near the confined wall, and negative pressure will lead to the trend of inward movement of the wall, rather than outward expansion.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hong, Y.K.; Moon, K.H. Experimental research on a waterjet to simulate erosion by impact of a water drop. Wear 2016, 368–369, 116–123. [Google Scholar] [CrossRef]
- Caydas, U.; Hascahk, A. A study on surface roughness in abrasive waterjet machining process using artificial neural networks and regression analysis method. J. Mater. Process. Technol. 2008, 202, 574–582. [Google Scholar] [CrossRef]
- Zain, A.M.; Haron, H.; Sharif, S. Estimation of the minimum machining performance in the abrasive waterjet machining using integrated ANN-SA. Expert Syst. Appl. 2011, 38, 8316–8326. [Google Scholar] [CrossRef]
- Azhari, A.; Schindier, C.; Hilbert, K.; Godard, C.; Kerscher, E. Influence of waterjet peening and smoothing on the material surface and properties of stainless steel 304. Surf. Coat. Technol. 2014, 258, 1176–1182. [Google Scholar] [CrossRef]
- Liu, S.Y.; Liu, X.H.; Chen, J.F.; Lin, M.X. Rock breaking performance of a pick assisted by high-pressure water jet under different configuration models. Chin. J. Mech. Eng. 2015, 28, 607–617. [Google Scholar] [CrossRef]
- Glover, H.W.; Brass, T.; Bhagat, R.K.; Davidson, J.F.; Pratt, L.; Wilson, D.L. Cleaning of complex soil layers on vertical walls by fixed and moving impinging liquid jets. J. Food Eng. 2016, 178, 95–109. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Wang, X.C.; Ding, X.L.; Fang, Z.L. Effects of nozzle inner surface roughness on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2016, 74, 444–452. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Ding, X.L.; Wang, X.C.; Fang, Z.L. Effects of area discontinuity at nozzle inlet on the characteristics of self-resonating cavitating waterjet. Chin. J. Mech. Eng. 2016, 29, 813–824. [Google Scholar] [CrossRef]
- Guha, A.; Barron, R.M.; Balachander, R. An experimental and numerical study of water jet cleaning process. Mater. Process. Technol. 2011, 211, 610–617. [Google Scholar] [CrossRef]
- Hu, Y.; Kang, Y.; Wang, X.C.; Li, X.H.; Long, X.P.; Zhai, G.Y.; Huang, M. Mechanism and experimental investigation of ultrahigh pressure water jet on rubber cutting. Int. J. Precis. Manuf. 2014, 15, 1937–1978. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, H.L.; Lee, J.P.; Rajagopalan, S. Jet flow characteristics of sinusoidal wavy nozzles. J. Mech. Sci. Technol. 2012, 26, 4007–4016. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Ding, X.L.; Liu, W.C. Experimental study on the effects of feeding pipe diameter on the cavitation erosion performance of self-resonating cavitating waterjet. Exp. Therm. Fluid Sci. 2017, 82, 314–325. [Google Scholar] [CrossRef]
- Azimi, A.H.; Qian, Y.; Zhu, D.Z.; Rajaratnam, N. An experimental study of circular sand-water wall jets. Int. J. Multiph. Flow 2015, 74, 34–44. [Google Scholar] [CrossRef]
- Johnson, B.K.; Prud’homme, R.K. Chemical processing and micromixing in confined impinging jets. AiChE J. 2003, 49, 2264–2282. [Google Scholar] [CrossRef]
- Kaffel, A.; Moureh, J.; Harion, J.L.; Russeil, S. TR-PIV measurement and POD analysis of the plane wall jet subjected to lateral perturbation. Exp. Therm. Fluid Sci. 2016, 77, 71–90. [Google Scholar] [CrossRef]
- Donaldsion, C.D.; Snedeker, R.S. A study of free jet impingement. J. Fluid Mech. 1971, 45, 281–319. [Google Scholar] [CrossRef]
- Wang, X.N.; Zheng, X.J.; Wang, P. Direct numerical simulation of particle-laden plane turbulent wall jet and the influence of Stokes number. Int. J. Multiph. Flow 2017, 92, 82–92. [Google Scholar] [CrossRef]
- Rafferty, L.; Kaminski, D. Non-dimensionalization and mixing quantification of laminar twin semi-confined jets. Int. J. Heat Fluid Flow 2014, 48, 15–23. [Google Scholar] [CrossRef]
- Hadziabdic, M.; Hanjalic, K. Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 2008, 596, 221–260. [Google Scholar] [CrossRef]
- Tani, I.; Komatsu, Y. Impingement of a round jet on a flat surface. In Applied Mechanics, Proceedings of the 11th International Congress of Applied Mechanics Munich; Springer: Heidelberg, Germany, 1964; pp. 672–676. [Google Scholar]
- Choo, K.; Kim, S.J. The influence of nozzle diameter on the circular hydraulic jump of liquid jet impingement. Exp. Therm. Fluid Sci. 2016, 72, 12–17. [Google Scholar] [CrossRef]
- Icardi, M.; Gavi, E.; Marchisio, D.; Barresi, A.A.; Olsen, M.G.; Fox, R.O.; Lakehal, D. Investigation of the flow field in a three dimensional confined impinging jets reactor by means of microPIV and DNS. Chem. Eng. J. 2011, 166, 294–305. [Google Scholar] [CrossRef]
- Rothenfluh, T.; Schuler, M.J.; von Rohr, P.R. Experimental heat transfer study on impinging, turbulent, near-critical water jets confined by an annular wall. J. Supercrit. Fluids 2013, 77, 79–90. [Google Scholar] [CrossRef]
- Fan, J.Y.; Zhang, Y.; Wang, D.Z. Experimental study on the vortex and entrainment characteristics for a round transverse jet in shallow water. J. Hydrodyn. 2009, 21, 386–393. [Google Scholar] [CrossRef]
- Adane, K.F.K.; Tachie, M.F. Experimental and numerical study of laminar round jet flows along a wall. J. Fluids Eng.-Trans. ASME 2010, 132. [Google Scholar] [CrossRef]
- Craft, T.J.; Launder, B.E. On the spreading mechanism of the three-dimensional turbulent wall jet. J. Fluid Mech. 2000, 435, 305–326. [Google Scholar] [CrossRef]
- Shinneeb, M. Confinement Effects in Shallow Water Jets. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2006. [Google Scholar]
- Shinneeb, M.; Bugg, J.D.; Balachander, R. Coherent structures in shallow water jets. J. Fluids Eng. 2011, 133, 011203. [Google Scholar]
- Shinneeb, A.M.; Balachander, R.; Bugg, J.D. Confinement effects in shallow water jets. J. Hydraul. Eng. 2011, 137, 300–314. [Google Scholar] [CrossRef]
- Ghidelli, M.; Sebastiani, M.; Johanns, K.E.; Pharr, G.M. Effects of indenter angle on micro-scale fracture toughness measurement by pillar splitting. J. Am. Ceram. Soc. 2017, 100, 5713–5738. [Google Scholar] [CrossRef]
- Ghidelli, M.; Sebastiani, M.; Collet, C.; Guillemet, R. Determination of the elastic moduli and residual stresses of freestanding Au-TiW bilayer thin films by nanoindentation. Mater. Des. 2016, 106, 436–445. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, C. Heat transfer and flow characteristics of a rectangular channel with a small circular cylinder having slit-vent vortex generator. Int. J. Therm. Sci. 2016, 104, 158–171. [Google Scholar] [CrossRef]
- Vinze, R.; Chandel, S.; Limaye, M.D.; Prabhu, S.V. Heat transfer distribution and shadowgraph study for impinging underexpanded jets. Appl. Therm. Eng. 2017, 115, 41–52. [Google Scholar] [CrossRef]
- Fang, Z.L.; Kang, Y.; Yuan, B.; Yang, X.F.; Wang, X.C. Slotting radius prediction model of soft coal seams with high-pressure pulse water jet. Disaster Adv. 2013, 6, 431–437. [Google Scholar]
- Gent, M.; Menendez, M.; Torno, S.; Torano, J.; Schenk, A. Experimental evaluation of the physical properties required of abrasives for optimizing waterjet cutting of ductile materials. Wear 2012, 25, 284–285. [Google Scholar] [CrossRef]
- Huang, L.; Folkes, J.; Kinnell, P.; Shipway, P.H. Mechanisms of damage initiation in a titanium alloy subjected to water droplet impact during ultra-high pressure plain waterjet erosion. J. Mater. Process. Technol. 2012, 212, 1906–1915. [Google Scholar] [CrossRef]
- Wang, J.; Shanmugan, D.K. Cutting meat with bone using an ultrahigh pressure abrasive waterjet. Meat Sci. 2009, 81, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Jegaraj, J.J.R.; Babu, N.R. A strategy for efficient and quality cutting of materials with abrasive waterjets considering the variation in orifice and focusing nozzle diameter. Int. J. Mach. Tools Manuf. 2005, 45, 12–13. [Google Scholar] [CrossRef]
- Bugg, J.D.; Rezkallah, K.S. An analysis of noise in PIV images. J. Vis. 1988, 1, 217–226. [Google Scholar] [CrossRef]


| Item | Power | Impulse Frequency | Scanning Speed | Wavelength | Width |
|---|---|---|---|---|---|
| Value | 120 mJ/Pulse | 30 HZ | 3.75/s | 532 nm | 1 mm |
| Item | Resolution | Image Acquisition Frequency | Region of View |
|---|---|---|---|
| Value | 1600 × 1200 pixels | 32 fps | 600 × 600 mm |
| The Actual Width | 20 mm | 40 mm | 52 mm | 60 mm |
|---|---|---|---|---|
| The dimensionless width | 5 | 10 | 13 | 15 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Kang, Y.; Li, D.; Yuan, B.; Wang, X. Experimental Investigation on the Influence of a Double-Walled Confined Width on the Velocity Field of a Submerged Waterjet. Appl. Sci. 2017, 7, 1281. https://doi.org/10.3390/app7121281
Ding X, Kang Y, Li D, Yuan B, Wang X. Experimental Investigation on the Influence of a Double-Walled Confined Width on the Velocity Field of a Submerged Waterjet. Applied Sciences. 2017; 7(12):1281. https://doi.org/10.3390/app7121281
Chicago/Turabian StyleDing, Xiaolong, Yong Kang, Deng Li, Bo Yuan, and Xiaochuan Wang. 2017. "Experimental Investigation on the Influence of a Double-Walled Confined Width on the Velocity Field of a Submerged Waterjet" Applied Sciences 7, no. 12: 1281. https://doi.org/10.3390/app7121281
APA StyleDing, X., Kang, Y., Li, D., Yuan, B., & Wang, X. (2017). Experimental Investigation on the Influence of a Double-Walled Confined Width on the Velocity Field of a Submerged Waterjet. Applied Sciences, 7(12), 1281. https://doi.org/10.3390/app7121281







