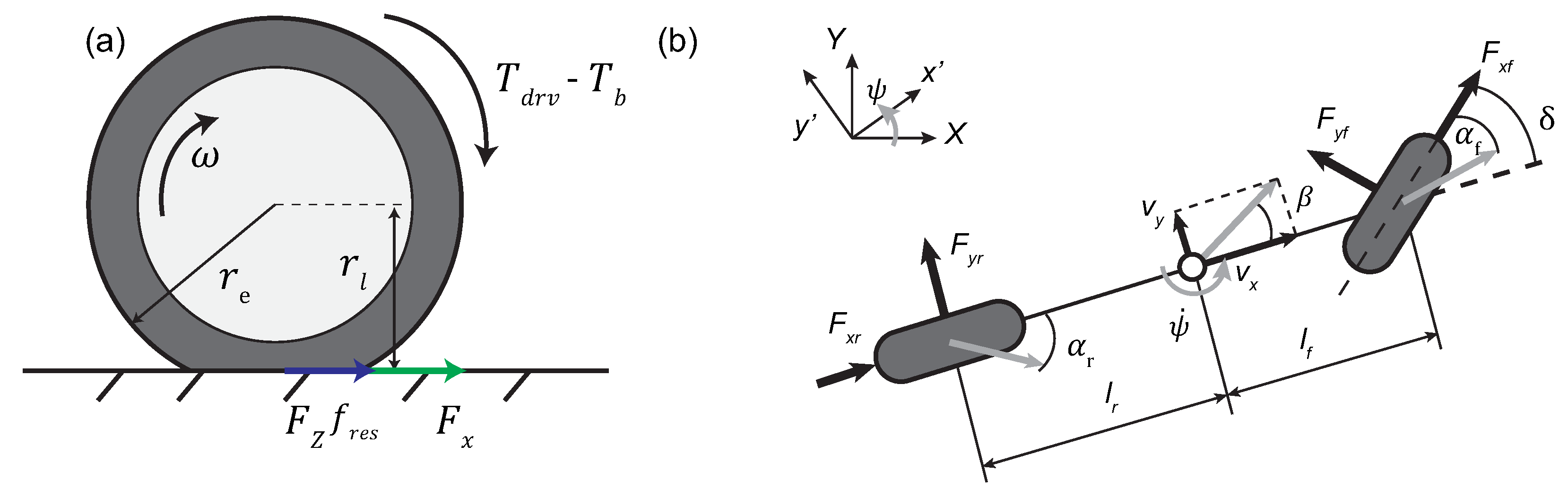
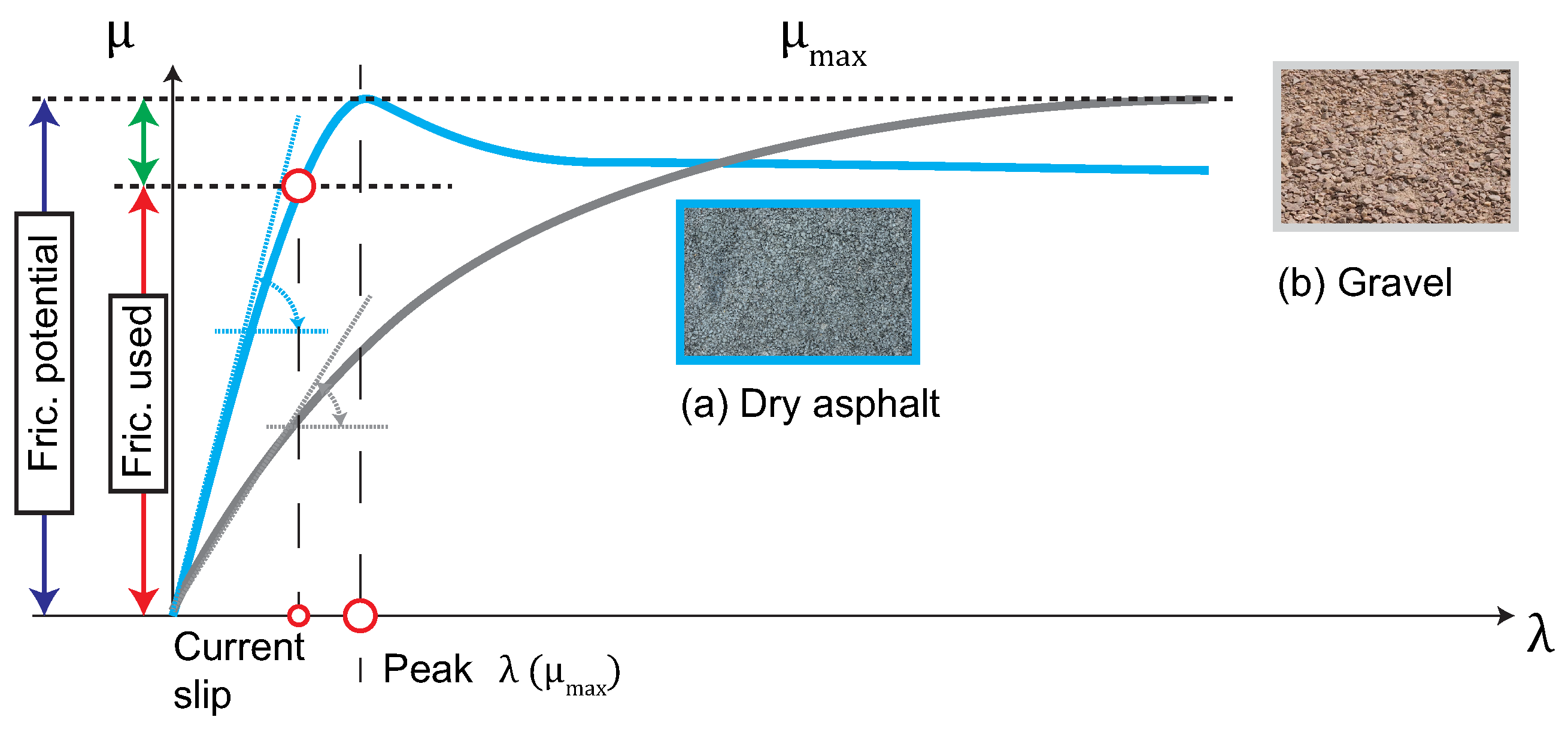
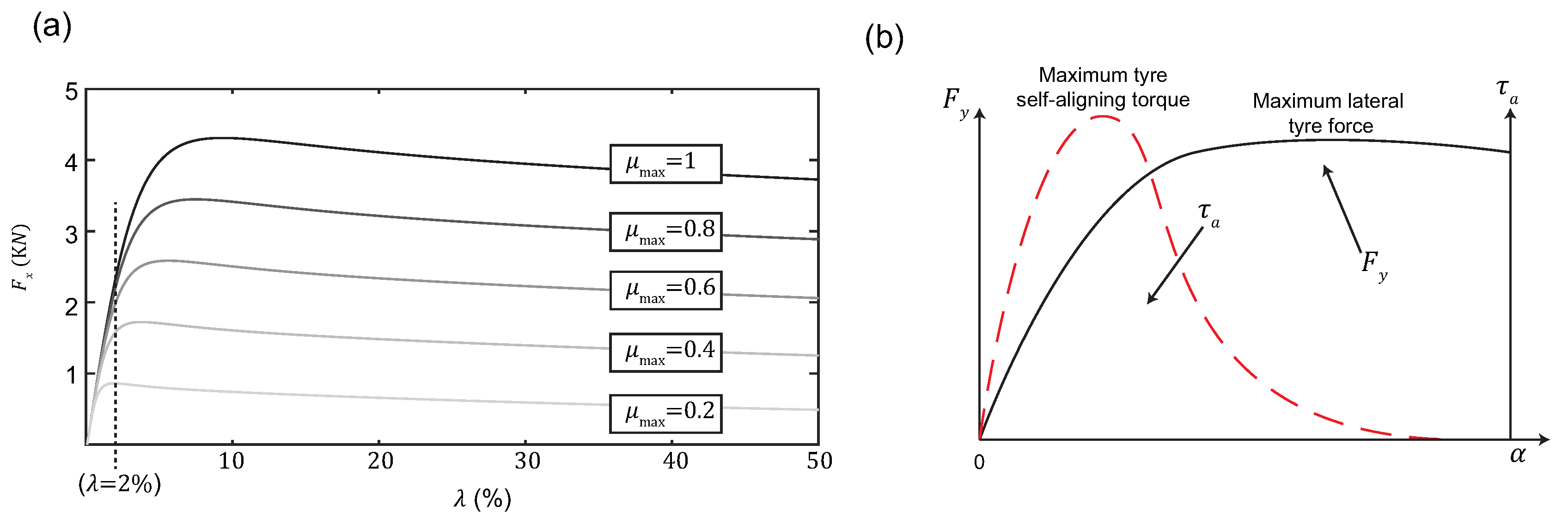
In
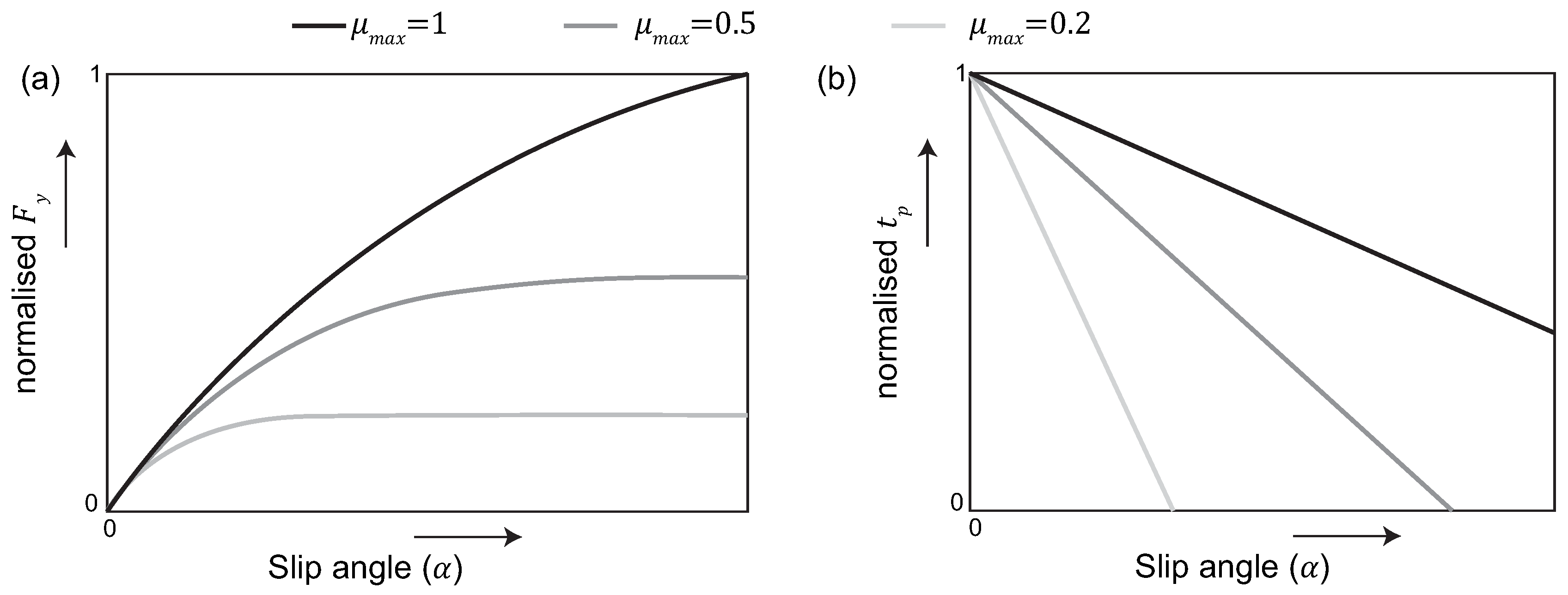
Figure 11a the tyre longitudinal forces obtained from a parameterised
Magic Formula 6.1 tyre model [
3] are depicted. As can be noticed, the slope of these forces does not change significantly between high and low adherence rigid road surfaces (e.g., dry asphalt, wet asphalt) when the longitudinal excitation is kept low (i.e., negligible
difference is observed between
and
for
<
). This behaviour is derived from the infinitely rigid road assumption employed to formulate the
Brush and
Magic Formula tyre models [
67]. As a consequence, the slope of the tyre forces is considered only a function of the tyre tread stiffness in these models, and is not affected by the
coefficient. This has been evidenced experimentally under well-controlled braking tests performed in a wide range of rigid surfaces by Andrieux et al. [
45]. Nevertheless, in a large number of works the previous statement is refuted and the so-called “slip slope” concept is presented. In particular, the slip slope idea states that the tyre longitudinal stiffness (slope on
Figure 11a) presents significant variations between high and low adherence surfaces. In these works it is claimed that the slip slope tyre phenomena facilitate the estimation of the friction potential under minimum excitation levels using traditional slip-based approaches. As this approach is often tested on rigid as well as loose surfaces (e.g., snow, dry asphalt, ice, and gravel) the change in the slip slope might be induced by the soft material (e.g., sand) deposited between the tyre and the rigid road [
17]. Moreover, the slip slope presents significant variations depending on external tyre parameters, such as the tyre pressure or the tyre wear [
6,
7]. As a certain degree of controversy exists around the slip slope idea, these results are considered in more detail in the following sections.
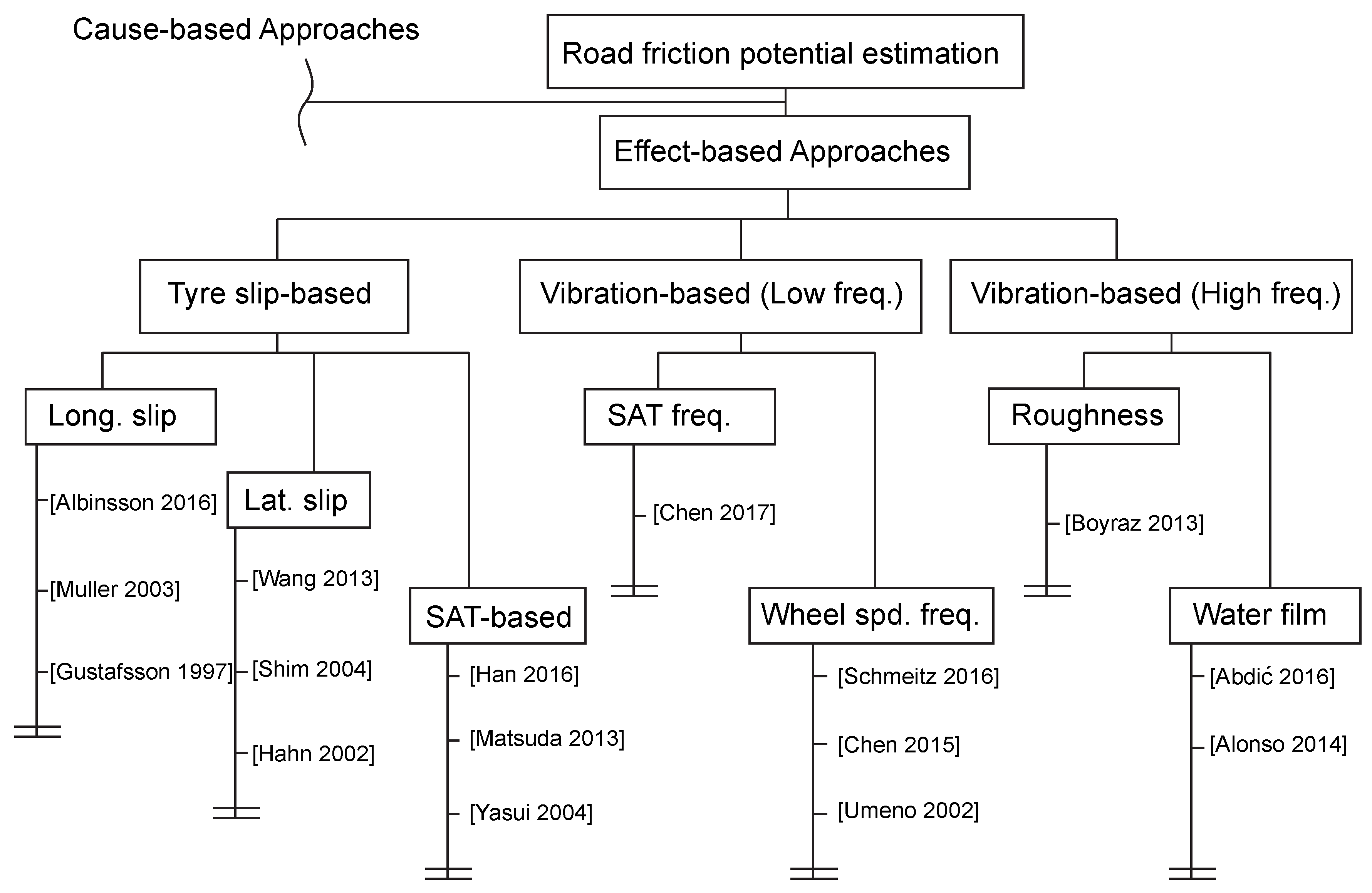
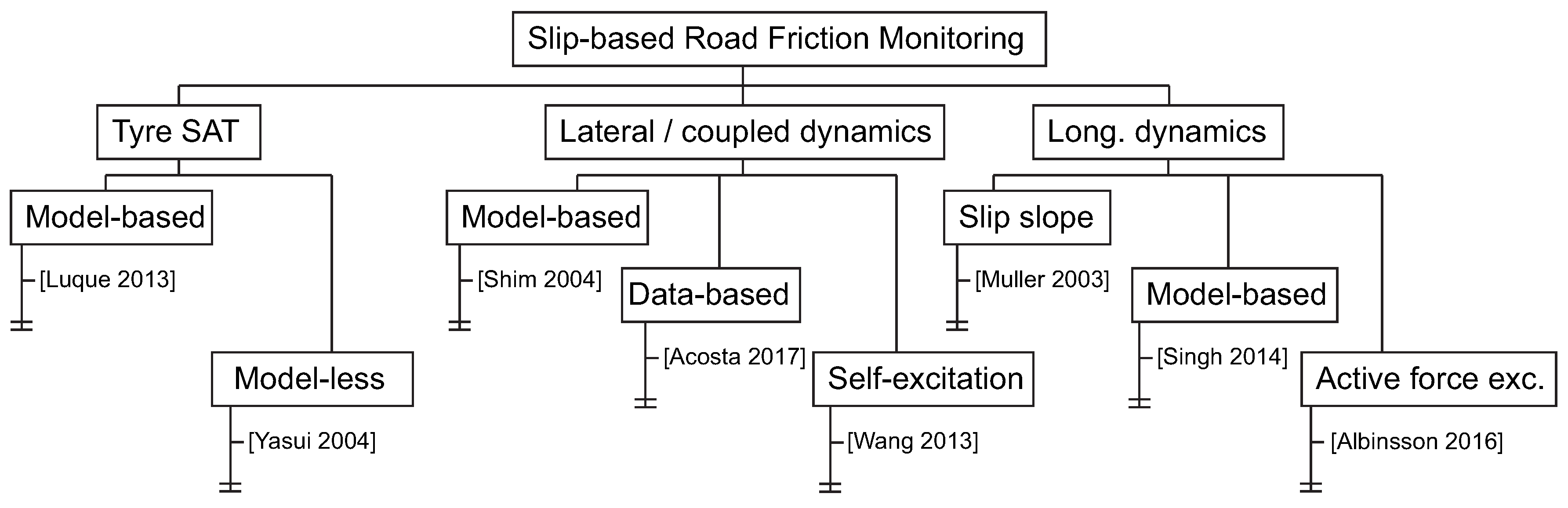
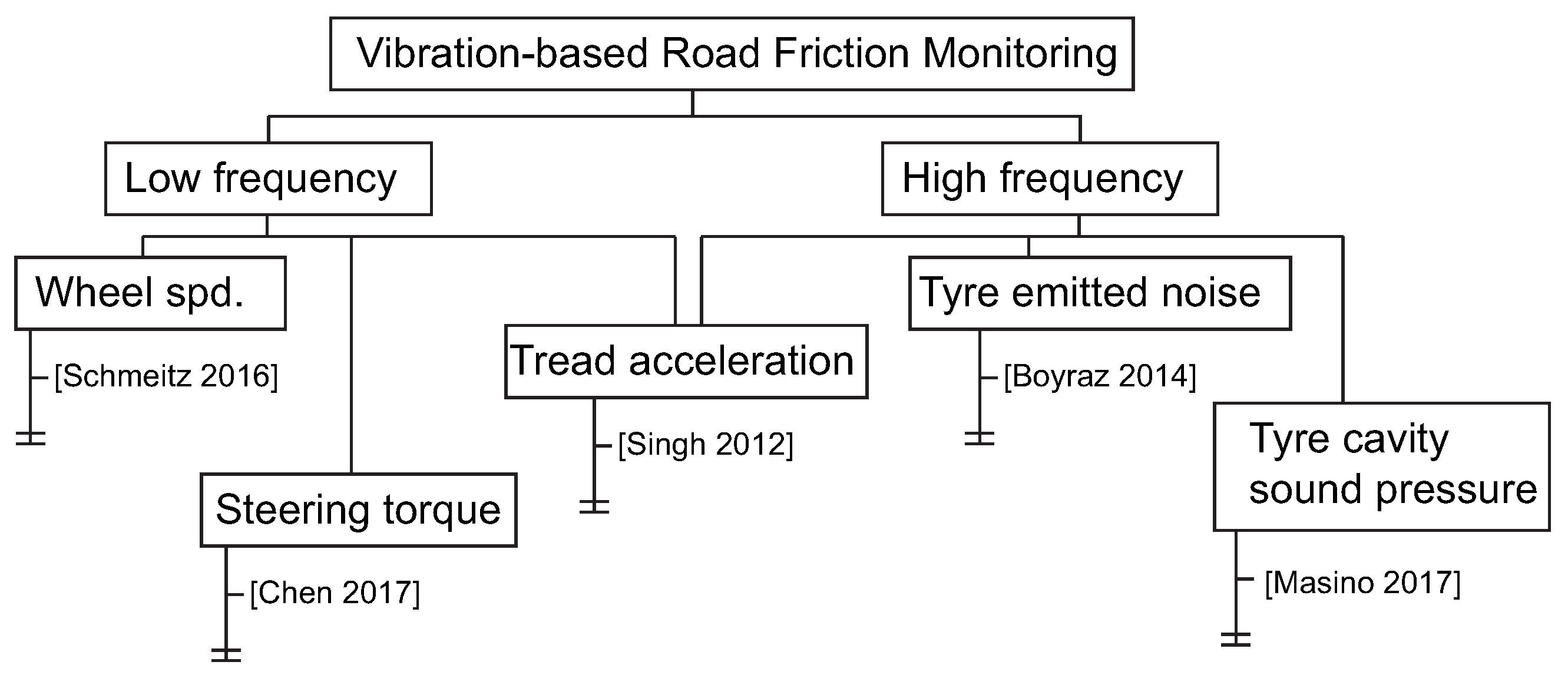
3.1. Longitudinal Dynamics
A large number of works have been presented to estimate the friction potential from the vehicle longitudinal dynamics (e.g., braking manoeuvres). These can be classified into longitudinal stiffness or slip slope-based approaches [
6,
7,
17,
44,
91,
92], friction model-based approaches [
12,
13,
16,
18,
19,
21,
93,
94,
95] and active force excitation approaches [
71,
96]. Despite slip slope approaches belong to the friction model-based group (i.e., linear longitudinal stiffness tyre model), a distinction has been made to treat them in greater detail. Furthermore, a new promising approach recently developed by Albinsson et al. (active force excitation) has been added to the discussion.
Slip slope approaches are based on the assumption that the tyre longitudinal stiffness depends on the maximum road friction coefficient [
6]. Therefore, provided that a suitable function
is found, the friction estimation problem can be solved by monitoring the tyre longitudinal stiffness. In Gustafsson [
6] a linearised friction model is presented to estimate the slip slope
and the friction bias
from the tyre longitudinal slip
and the normalised longitudinal force (
),
where the force
is obtained from the measured engine torque and
is calculated using the difference between the driven and non-driven wheel speeds. Different roads (asphalt, wet asphalt, gravel, snow and ice) and tyres (MXT, MXV2 (almost worn out), NCT2 and Eurofrost (winter tyres)) were tested, and a rule-based classifier was proposed based on the empirical results. Slip slope coefficients varied significantly depending on the tyre considered, and well-clustered surfaces were obtained only for the Eurofrost tyre. In addition, authors remarked that the values obtained in these tests were very sensitive to variations in tyre parameters such as the tyre pressure or the tyre tread depth (tyre wear). In Muller et al. [
7] several braking manoeuvres were performed on dry (
) and soapy roads (
). The tyre forces were measured from a strain-based torque sensor and the braking action was performed only at the front wheels. The slip slope was calculated using recursive least squares (RLS) on the model given by expression (
43) and significant differences between the tested surfaces were obtained for grip consumption levels of
. These tests were repeated employing a cost-effective experimental setup and the following slip slope ranges were found,
Table 2:
Once again, the high variability of the slip slope coefficient was highlighted by the authors. Moreover, Muller et al. indicated that the
relation that works at the present time might not work during the next month, thus remarking the strong dependence of this coefficient on tyre parameters such as inflation pressure or tyre wear. In Ahn [
17] longitudinal stiffness values of a Pirelli 255/50R-17 installed in a Jaguar S-type are provided,
Table 3. Additional details regarding the temperature at which the tests on ice were performed are not given. As will be seen in
Section 4.1, some authors argue that the ice temperature can have a significant impact on the tyre longitudinal stiffness or slip slope factor.
A linear regression was performed to obtain these values setting the maximum longitudinal slip to
. Ahn presents the “equivalent tyre-road stiffness” theory [
42,
53] to explain the differences seen on
. Specifically, this theory attributes the variations in slip slope to the presence of soft material (e.g., gravel, snow or wet ice) in the road-rubber interface. Under these conditions, the surface can no longer be considered infinitely rigid with respect to the tyre carcass, as states the accepted tyre modelling theory [
67].
In Rajamani et al. [
44] the slip slope
is estimated using RLS from the linear relationship
In addition, the authors proposed a linear expression to relate the slip slope to the road friction potential,
, where
A and
C are constant parameters determined empirically. In particular, the authors found the previous coefficients from the slip slope estimates obtained in dry asphalt and gravel surfaces. In this case, the “equivalent tyre-road stiffness” theory holds, and the abrupt reduction of
in gravel conditions correlates well with the experimental tyre model parameterisations on gravel performed by other authors [
71]. Unfortunately, the previous expression has not been reproduced experimentally in a wider range of rigid road surfaces. The same expression was adopted by Li et al. [
91]. The authors mention that the coefficients
A and
C were obtained experimentally, but additional details are not provided. In Wang et al. [
92] more details are provided regarding the linear
-
relationship. Specifically, the slip slope is estimated from gentle braking inputs performed with a winter maintenance vehicle on dry concrete and concrete with light loose snow covering, and the slip slope values
and
are obtained for each test case.
An attempt to clarify whether the slip slope can be related to the road friction potential has been performed by Andrieux et al. [
45]. The authors performed field trials on five different rigid pavements of different micro and macro-textures (with friction potential coefficients ranging from 0.1 to 1.2). In addition, manoeuvres were repeated with summer and winter tyres, two tyre manufacturers, new and worn tyres, and a wet road surface with a water film thickness of 0.4 mm.
The combination of the above conditions provided 40 cases for each one where braking at different levels of deceleration and slip were conducted. Andrieux et al. found that the longitudinal stiffness of summer tyres is greater than that of winter tyres and the longitudinal stiffness of worn tyres is greater than that of new tyres. They also concluded that the longitudinal stiffness does not allow discrimination between the pavements, while their maximum friction coefficients varied almost three times and presented very different textures. In conclusion, they stated that a clear relationship - was not verified, and therefore it may be impossible to estimate the maximum available grip from the longitudinal stiffness .
Due to the fuzziness associated to slip slope methods, other authors have opted for using more sophisticated friction modelisations (e.g.,
Dugoff model) to estimate the road grip potential [
13,
16,
18,
19,
21,
93,
94]. These are designated here as model-based approaches. In brief, in these works linear and nonlinear regression algorithms are employed to infer the parameter
from a friction model updated with suitable force and slip estimates. In Singh [
16] nonlinear least squares (NLLS) are applied to the analytical
Brush tyre model. The authors provide different minimum grip consumption thresholds based on the results obtained in high and low mu conditions (
and
). Specifically, it is highlighted that a grip utilisation between
and
is required to estimate
with an accuracy within the
band. The
Brush model was also employed by Zhao et al. [
13]. In this case, the tyre longitudinal stiffness is assigned a fixed value (under the assumption of invariability during a short period of time) and only the
coefficient is estimated. The nonlinear
Brush model is linearised to apply an RLS identification routine and several braking manoeuvres are simulated under the actuation of a threshold-based ABS and a Sliding Mode control (SMC) based ABS. Moreover, the estimator was verified experimentally under the actuation of the former ABS. In this case, the analysis is reduced to limit braking manoeuvres, and further details regarding the estimation accuracy on lower consumption thresholds are not provided. Han et al. [
19] proposed a third-order force model of the form,
where
and
are model parameters estimated using linearised recursive least squares (LRLS) and the friction potential is defined as
. Several simulations and experimental tests are conducted and authors state that this estimation approach requires around 60–70% of the total friction consumption to achieve accurate estimates. In Johansson [
94] a tyre model designated as BW and developed by Ola Nockhammar at
BorgWarner TorqTransfer Systems AB was employed. Instead of assuming a constant
, the author used the linear slip slope relationship [
44] described in the previous paragraphs. The
A and
C parameters were obtained from field tests performed in dry asphalt and ice/snow surfaces. Once again, the nonlinear tyre model was linearised in order to apply the RLS routine and a predefined friction consumption threshold was set to carry out the estimation only during dynamic excitation exceeding this value. A combined linear-nonlinear identification routine was employed in Svendenius [
18]. Specifically, the author employed the least squares method in a linearised version of the
Brush model during low excitation levels and a
Gauss-Newton optimisation routine during high longitudinal excitation levels. Experimental tests (acceleration ramp) were executed with winter tyres on asphalt, snow and ice surfaces. The maximum friction consumption level during the execution of these tests was maintained below the
band in snow and asphalt surfaces, and below the
band in icy conditions. Svendenius [
18] remarked that good results were obtained in snow conditions (converging the friction estimate to the true value at a
grip consumption level) and ice conditions (at a full tyre saturation level), but accurate results were not achieved on asphalt due to the reduced friction potential utilisation.
Li et al. [
21] proposed an algorithm to classify the slipperiness of the road surface. A rule-based classifier is proposed to identify the slipperiness grade (ranging from 1-asphalt to 3-oil or icy patches) based on the slip estimated at each wheel and the vehicle longitudinal acceleration. Moreover, the algorithm includes a
Magic Formula curve fitting step executed when enough data points spread along the
-
curve are available. Experimental tests at reduced acceleration (
<
G) are performed on a path composed of sand and gravel segments. Despite accurate results are obtained on the sandy segment (detected as a grade 3 segment), the algorithm misclassified the gravel terrain. The authors remark that a classifier relying on the wheel slip might not be accurate enough to distinguish rough road segments from rigid ones, and propose a second classifier based on the wheel speed fluctuations. Other works employing different friction models have been found in the literature. A dynamic
Lugre model was employed in Alvarez et al. [
93]. A fast-convergence observer was developed based on a parameter adaption law employing wheel angular velocity and longitudinal acceleration measurements. The observer was simulated under emergency braking manoeuvres. Finally, Zhang et al. [
95] and Zhao et al. [
97] employed the
Burckhardt [
15] tyre model to estimate the friction potential during braking manoeuvres.
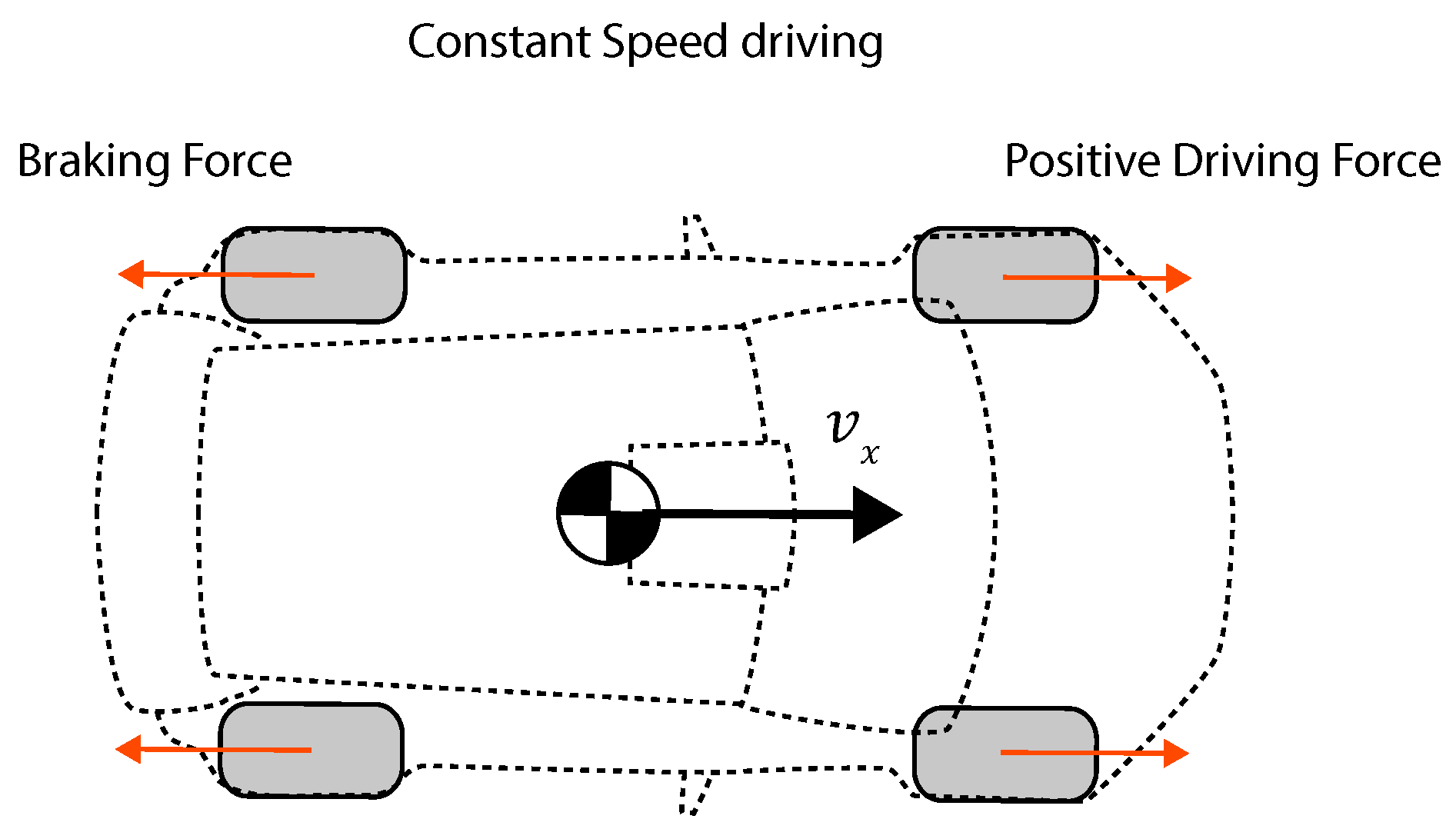
The solutions discussed up to now were proposed based on the assumption that a certain longitudinal excitation can be generated (e.g., some braking or acceleration events during a regular driving journey). In order to eliminate this requirement and facilitate the estimation of the friction potential during constant speed conditions Albinsson et al. introduced recently the “active force excitation” concept [
71,
96]. In [
96] a method to generate wheel torques of opposite sign on the front and rear axles (front driving—rear braking in a front-wheel-drive FWD configuration) was investigated. Such approach depicted schematically in
Figure 13, facilitates the generation of high excitation levels with minimum longitudinal speed variations. A torque input is applied at the front axle and a proportional-integral-derivative (PID) controller is employed to adjust the rear braking torque based on the error between the angular velocities of the driven wheels and the longitudinal velocity at the start of the intervention.
An algorithm is proposed to avoid the direct measurement of the longitudinal velocity. Instead, an estimate of this signal is obtained from wheel speed measurements using a vertical load proportionality principle [
67]. Several ramp acceleration tests were executed on dry asphalt and wet basalt and the road friction was calculated offline fitting the
Brush model to a cloud of experimental data with nonlinear least squares. Authors remarked that this solution presented a high sensitivity to the noise present on the wheel speed signals. In addition, high grip consumption levels were reported to achieve the model fitting, especially during the basalt tests (≈
). This research has been continued in [
71], where it is investigated how the tyre force should be applied in order to minimise the friction estimate error. Authors conclude that a suitable force ramp has the benefit of being easily implementable. Moreover, it is highlighted that if realistic noise levels are considered, at least a
of friction utilisation for a given tyre-road combination (the analysis is focused on wet asphalt and gravel surfaces) is required in order to have a grip potential estimate with a
normalised force accuracy when the
Magic Formula is employed. The friction utilisation is increased to
when the
Brush model is adopted.
3.2. Lateral Dynamics
A large number of solutions have been presented in the literature in order to extend the operating range of the friction potential estimation to manoeuvres in which the vehicle lateral dynamics are excited (e.g., lane change). Such approaches present a higher flexibility and can perform an accurate grip estimation during acceleration, braking and cornering events. In other cases, the friction potential estimation is limited to cornering manoeuvres and the longitudinal dynamics are disregarded. A comprehensive discussion on pure lateral and combined (lateral and longitudinal) dynamics is presented in this subsection. The majority of the solutions proposed in the literature are predominantly model-based approaches [
8,
23,
34,
43,
98,
99,
100,
101,
102,
103,
104,
105,
106,
107,
108,
109,
110,
111], and differ depending on the technical solution adopted to infer the friction potential from the parameterised friction or tyre force model (e.g., Unscented Kalman filter (UKF) [
8] or Bayesian Hypothesis selection [
43,
111]). Apart from this dominant group, additional solutions have been proposed using data-based [
3,
112], rule-based [
20], self-excitation [
113], or wheel acceleration-based approaches [
114]. These will be briefly discussed in the following.
To start with, Antonov et al. [
8] proposed a UKF based on a two-track vehicle model to estimate the vehicle states and augmented the vector of states with the road friction potential, modelled as a random walk variable. A simplified
Magic Formula tyre model was embedded into the UKF and the vehicle states and friction potential were calculated from lateral acceleration, yaw rate, and wheel speed measurements. The UKF was tested experimentally on ABS braking manoeuvres and lane change tests performed on dry asphalt and ice surfaces. In this case, the analysis was focused on limit handling manoeuvres, and additional details regarding the grip utilisation thresholds to infer the road grip were not provided. The same concept was applied in Gao and Yu [
98]. A simplified single-track modelisation was proposed this time, and an
arctangent tyre model was implemented in an Extended Kalman Filter (EKF). The observer is simulated on high and low mu surfaces using IPG-CarMaker under limit steering inputs but grip utilisation levels are not provided. An EKF was also employed in Li et al. [
102], and a
Dugoff tyre model was adopted to estimate the road friction potential. Contrary to the approached adopted by Antonov et al. [
8], Li et al. estimated the longitudinal forces in a separated block (using a wheel rotating dynamics-based approach [
53]), and limited the friction potential estimation to pure lateral dynamics events. The vehicle responses were simulated using veDYNA software and different limit double lane change manoeuvres were performed in surfaces of
and
. Additional discussion on grip utilisation thresholds is not provided.
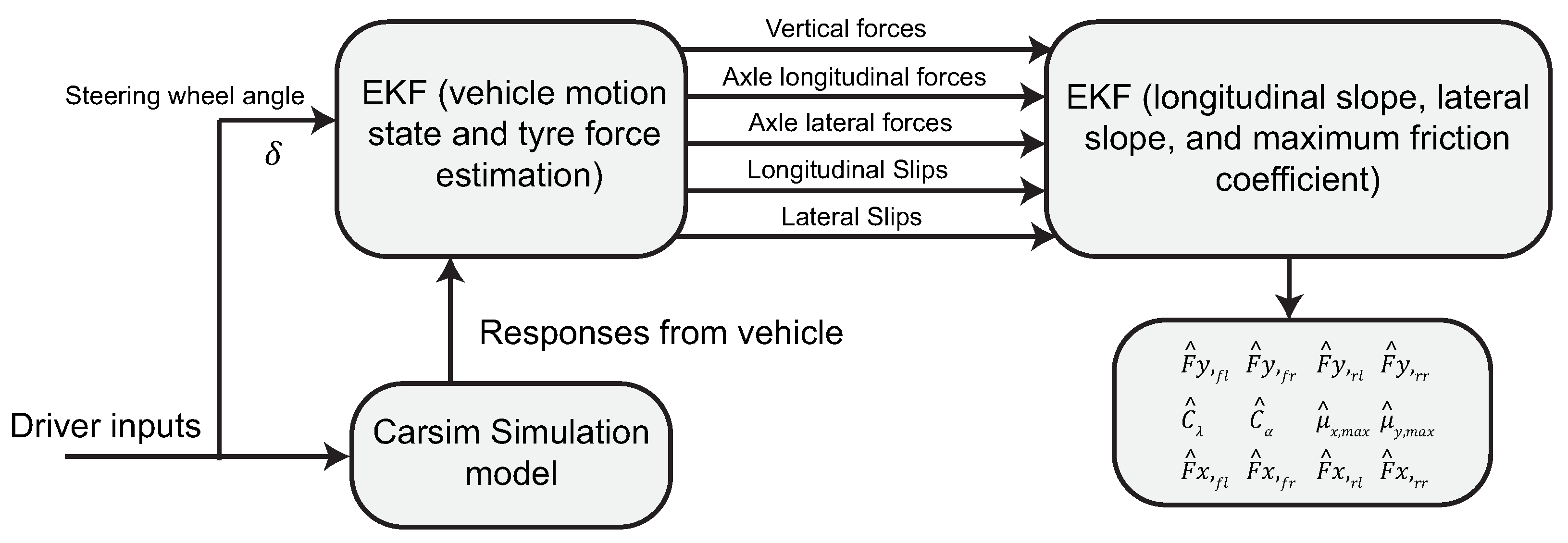
Qi et al. [
101] performed the estimation of the friction potential and the tyre forces using a two-step approach,
Figure 14. In first place, the tyre forces are modelled as random walk variables and estimated in addition to the vehicle planar motion states in a EKF structure using readily available CAN measurements. These estimates are then used in a second EKF structure to calculate the lateral and longitudinal tyre stiffness (
), and the friction potential coefficients in the longitudinal and lateral directions
. In addition, a novel tyre model of reduced complexity is proposed. Simulations are carried out on high and low mu surfaces under pure braking, pure steering, and combined limit inputs. Additional braking tests were simulated under lower excitation levels and the observer experienced some difficulties to converge to the true maximum friction potential values. The same two-step approach was followed in Chen et al. [
108], where the one-directional friction potential coefficients
were estimated using a UKF structure and a modified
Dugoff tyre model. The tyre forces were obtained from a discrete EKF using chassis acceleration and yaw acceleration measurements. A Mean Square Error (MSE) weighted fusion method is proposed to obtain the resultant friction potential estimate depending on the uncertainty associated with each one-directional estimate. Such uncertainties are computed from second-order surfaces that depend on the lateral and longitudinal tyre slips. Despite this simulation results are presented on surfaces of different grip potentials, a discussion on grip utilisation levels is omitted.
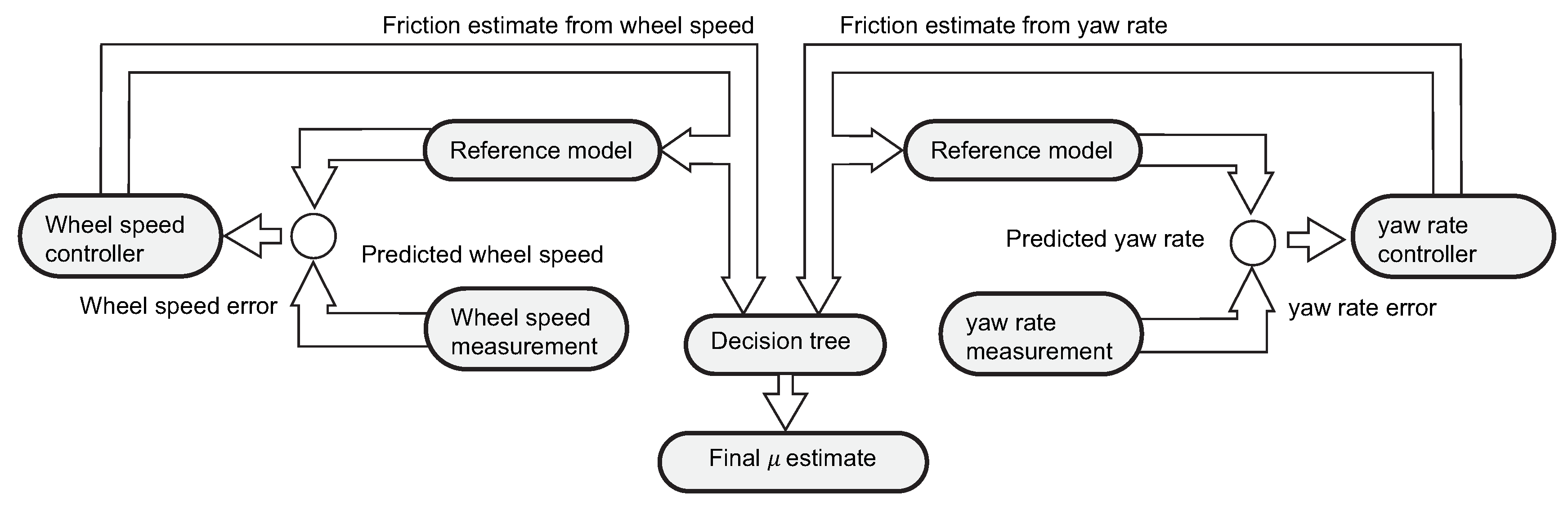
Shim et al. [
103] proposed a proportional-integral-derivative (PID) controller to estimate the road friction potential. Specifically, the responses obtained from a two-track vehicle model equipped with an analytical model developed by the authors in [
115] are compared to wheel speed and yaw rate measurements, following the structure depicted in
Figure 15. The model was validated experimentally in dry asphalt and gravel terrains and friction potential estimates were obtained from the wheel speed and yaw rate signal errors. Finally, a weighting strategy was proposed to fuse these estimates based on the steering wheel angle and the longitudinal velocity signals. A similar reference vehicle model-based approach has been reported in the Europen project “Friction” [
104] and in Koskinen [
23]. This algorithm was developed by VDO Automotive AG and compares yaw rate sensor measurements with the responses obtained from a reference vehicle model. Additional details regarding the tyre parameterisation employed in the reference vehicle model were not found in these works. The friction estimator was integrated with a steering wheel torque-based friction observer (provided by Centro Ricerche Fiat S.C.p.A.) and a Vehicle Feature Fusion (VFF) block was formed. After performing a detailed experimental assessment of the proposed solutions on dry asphalt, snow, and ice surfaces, Koskinen remarks that acceleration levels higher than 3 m/s
are required by both structures to achieve an accurate estimation.
In Wang et al. [
106] an observer is proposed to estimate the lateral velocity and the road friction potential. The authors used separated strategies for the linear and nonlinear lateral dynamics. In the linear dynamics case, it is assumed that the friction potential does not affect the vehicle response, and the tyre cornering stiffness (
) is considered unaltered. The estimation of the Tyre Road Friction Coefficient (TRFC) is therefore limited to the nonlinear lateral dynamics and is carried out using an observation law based on the resultant lateral force error obtained from lateral acceleration measurements and a
Magic Formula tyre model. A kinematic-based observer is used to estimate the lateral velocity required by the
Magic Formula tyre model during the operation in the nonlinear region. The authors proposed a similar approach in [
109]. In this case, the vehicle body slip is assumed to be measured, and the one-directional friction potential coefficients
are estimated using the adaptation laws
with
and
being suitable gains.
is the measured longitudinal force (inferred from the current of an electric motor) and
is the tyre lateral force (assumed to be measured by a sensor). Finally, the authors proposed a weighting function based on the tyre longitudinal and lateral slips to fuse the one-directional grip potential estimates. As occurred in the previous cases, a detail discussion regarding grip utilisation levels is not provided. Such discussion is also missing in the solution proposed by Peng et al. [
105], where an observer to estimate simultaneously the vehicle longitudinal and lateral velocities and the road friction potential from wheel speed and chassis acceleration measurements is proposed. Despite an observer convergence analysis is provided, details regarding the lateral acceleration levels at which the observer converges are not provided.
To continue with this model-based discussion, Han et al. [
100] proposed a feedforward approach to estimate the friction potential during pure lateral dynamics conditions from a
Dugoff tyre model. Using this model the friction potential was expressed as a function of the lateral force, vertical force, cornering stiffness and tyre lateral slip angles. The cornering stiffness was assumed a known constant parameter, the tyre forces were obtained from the measurements provided by a 6-dof inertial motion unit, and the vehicle body slip necessary to compute the tyre lateral slips from a Luenberger yaw-sideslip observer. Simulation results were presented and accurate friction estimates were obtained for
and
at the expenses of normalised lateral force levels of
0.30–0.4 and
0.20–0.25 respectively. Choi et al. [
99] proposed an estimation structure to calculate the road friction potential and the tyre longitudinal and lateral stiffnesses (
),
Figure 16. In this structure, the tyre forces and lateral and longitudinal slips are estimated in separated blocks, and fed through a linearised recursive least squares block (LRLS) based on a linearised
Brush tyre model. An adaptive multiple forgetting factor strategy is adopted to compensate the variation rate of the tyre properties (
, which vary slowly) and the friction potential (
, which can vary quickly during mu-jump situations). Moreover, the structure is enhanced to estimate left and right friction potentials in case of transversal mu-split conditions. Simulation results are presented in Carsim, and an accurate tracking of the friction potential and tyre parameters is achieved in a road formed by
under a continuous lateral excitation level of approximately 4 m/s
. The
Brush tyre model has been also employed by Hahn et al. [
34,
43]. In this case, the authors proposed an adaptive law to estimate the tyre cornering stiffness and friction potential using a differential Global Positioning System (DGPS) setup. Several experiments were performed on high
and low mu
roads and accurate results were obtained by the proposed algorithms. The author remarked that the results obtained evidenced a good performance even under small lateral slip values, but the lack of lateral acceleration or grip utilisation results complicates extracting further conclusions.
Ray [
111] presented a Bayesian Hypothesis selection process to infer the friction potential from a parameterised tyre model. The same approach is also reported in Rajamani et al. [
43]. In brief, this method provides a most likely friction potential value
for a given set of tyre forces and tyre slips. Following a similar approach than the works presented previously, the tyre forces and tyre slips are estimated in an external Extended Kalman-Bucy filter (EKBF). The estimation routine is validated experimentally under J-turn and braking manoeuvres performed on a dry asphalt (
) segment. The authors remark that for low longitudinal or lateral slip levels (e.g.,
G,
G) the algorithm does not perform well due to the proximity of the tyre force curves in the low slip regions,
Figure 11a. Zhang and Göhlich [
110] employed a Bayes-based estimator in combination to a General Regression Neural Network (GRNN) estimator. Specifically, the GRNN is employed during low excitation levels (
), while the Bayes-based estimator is employed at high slip values. Finally, acceleration-braking and lane change simulations performed in Carsim are presented. Further conclusions regarding grip utilisation levels are difficult to extract.
Alternative approaches have been proposed in the literature apart from the model-based solutions described previously. To start with, a data-based approach was proposed by Song et al. [
112]. This time authors presented a back-propagation (BP) Neural Networks structure to estimate the road friction potential from wheel speed, tyre longitudinal slip, yaw rate, longitudinal and lateral acceleration, and steering wheel angle values. A two-hidden-layer structure composed of ten neurons each is trained from simulation data obtained with veDYNA vehicle dynamics simulation software. Authors highlight that the approach still presents significant drawbacks (e.g., estimation may become inaccurate if the simulation model employed during the NN training does not match the real vehicle) and further improvements are to be performed. In the paper by Acosta and Kanarachos [
3] an observer composed of three Neural Network structures is proposed to estimate the friction potential. In particular, RLS is applied to extract the maximum road grip from a linear interpolation model. In order to avoid large errors during reduced excitation levels (e.g., straight-line driving) the estimation is carried when a certain lateral acceleration level is present (
m/s
). Overall, grip utilisation levels ranging from 40 to
are required to estimate the road friction potential.
In Kim et al. [
114] a novel approach based on the three-axis wheel accelerations is provided. A parametric model of the form
is proposed to estimate the friction utilised by each tyre. Individual wheel accelerations are obtained from the vehicle body accelerations, which are measured using a six-degree-of-freedom (6-DoF) inertial motion unit, and RLS and Gradient Estimator (GE) are applied to estimate the vector of parameters
. The authors validated the proposed grip utilisation observer under emergency braking manoeuvres on dry asphalt. Despite the fact that it is indicated that the friction potential can be calculated from the friction consumption level additional results in this line are not provided. A tyre model-less approach was presented by Li et al. in [
20]. In this case, the grip utilisation levels during braking
, driving
, and cornering
manoeuvres are employed in a signal fusion fashion to obtain a “comprehensive” road friction estimate (
), defined as
where
are certainty factors computed from the tyre slips and the chassis accelerations. A rule-based approach is presented in order to update the friction estimates during braking and cornering manoeuvres only when the utilised friction is closed to the maximum road friction level. A Fuzzy logic controller is adopted to achieve the previous task during driving events. Experimental results were reported on dry asphalt, packed-snow, and icy roads for emergency braking manoeuvres, lane change, hard acceleration, slalom, and steady-state cornering driving. Overall, the validation of the algorithms focuses on limit handling manoeuvres, and additional conclusions on low excitation levels cannot be extracted.
Finally, in a similar manner to the active force excitation approach described in the longitudinal dynamics section [
71,
96], Wang et al. [
113] introduced a yaw-excitation solution to estimate the road friction potential and tyre cornering stiffness. Such yaw-excitation strategy is based on a four-wheel independently-actuated (FWIA) electric vehicle, and pursues the estimation of these parameters during regular driving conditions without affecting the desired vehicle motion. Specifically, during straight line or slow turns an additional yaw moment is generated by differential traction inputs, and the cornering stiffness
is estimated using an update law based on the
Brush tyre model and the lateral force error. Such estimation is performed assuming a negligible effect of the road friction potential on the lateral force at reduced lateral slip values. During corners at which the lateral excitation is higher the same update law is employed, the cornering stiffness estimated in the previous step is kept constant in the
Brush tyre model, and the friction potential is estimated from the lateral force error. The estimation of
is verified experimentally in a dry asphalt road by means of an additional yaw moment applied by the rear wheels of a prototype vehicle. A corrective steering action is applied manually due to the lack of steering actuator in the test vehicle. After that, cornering manoeuvres are performed on high and low mu road segments and the friction potential is estimated without the use of an additional yaw moment. Despite the cornering stiffness is estimated at low excitation levels additional investigations on the friction potential estimation at such excitation levels would be of interest.
3.3. Tyre Self-Alignment Torque
The discussion on slip-based methods is completed with the revision of road friction potential estimation approaches which rely on the tyre self-alignment torque (SAT) signal. Among the papers consulted, the vast majority employ an analytical friction modelisation to estimate the coefficient
[
9,
11,
17,
35,
37,
39,
40,
87,
88,
107,
116,
117,
118,
119,
120,
121,
122,
123]. In particular, the
Brush tyre model has received greater attention on the works reviewed. On the other hand, a reduced number of approaches avoiding the use of any particular friction model have been found in this survey [
10,
68,
124]. Both, tyre model-less and tyre model-based approaches are treated briefly in the following.
Regarding the tyre model-based works, an extensive research has been performed by different authors with the aim to extract the road friction potential from the variations of the tyre pneumatic trail. As was mentioned at the beginning of this section, the tyre SAT peaks at lower lateral slip levels than the tyre forces. As the tyre SAT
is directly related to the tyre lateral force
by the pneumatic trail
,
some authors argue that by monitoring the evolution of the tyre pneumatic trail, changes on the friction potential could be identified at significantly lower excitation levels compared to the longitudinal and lateral dynamics-based works described previously. In Hsu et al. [
88] the road friction potential and the front axle cornering stiffness
are estimated from body slip, yaw rate, longitudinal velocity, steering wheel angle, and steer-by-wire motor current measurements. The total steering torque is obtained from the steer-by-wire current using a second-order steering system model. A nonlinear least square (NLS) optimisation routine is run continuously to estimate the cornering stiffness assuming a constant
. In parallel, the least squares (LS) algorithm is run and the residuals are compared to those obtained with the NLS. When a large difference is obtained, enough information of the nonlinear tyre characteristics is available and
is estimated and updated in the
Brush model. A ramp experimental test is performed on dry asphalt and steady-state road potential estimates are obtained when the lateral acceleration exceeds
G.
The previous work was continued in [
87]. In this case, nonlinear adaptation laws are presented to estimate the friction potential and the front axle lateral slip (
) from vehicle speed, yaw rate, steering wheel angle, lateral acceleration and the total aligning torque seen at the steering system. Regarding the latter, a linear disturbance observer is employed and the steering system is modelled as a second-order system. The nonlinear update laws are based on the error between the measured lateral tyre forces and front total aligning torque, and the estimates of these signals, which are obtained from a
Brush tyre model. The additional torque components derived from the vertical loads are compensated using suspension and steering kinematic models. The friction estimation algorithm is tested experimentally in ramp and slalom tests performed on a dry road. In order to avoid issues during moments of low lateral excitation, the algorithm only provides
estimates once the lateral acceleration is above the
G threshold. In Hsu et al. [
41] the authors employed a
Brush tyre model for the lateral forces and a linearised model for the pneumatic trail,
where
and it is assumed that the tyre is not fully sliding. An adaptation law is proposed to estimate the front axle lateral slip based on the error between the measured and estimated tyre lateral force. In this case,
is estimated rather than
with the aim to identify the tyre friction characteristics without requiring a normal force state estimator. Ramp and slalom tests are performed on a dry surface and the discussion of the results is limited to the axle lateral slip estimates accuracy. This estimation structure is also addressed in [
122]. In [
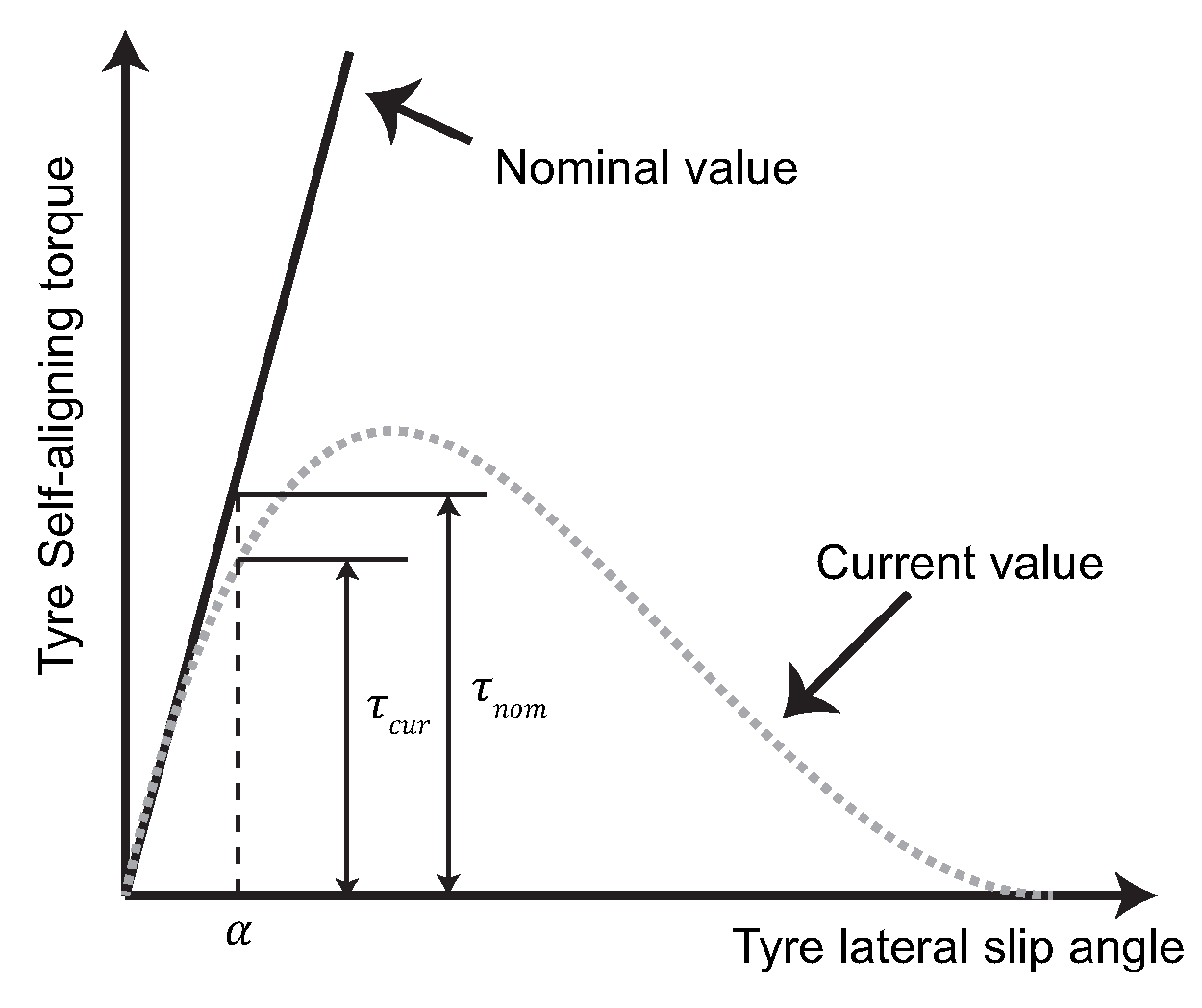
40] the authors revisit the linearised pneumatic trail model (51). In this work Hsu et al. provide a comprehensive explanation regarding the selection of the linearised pneumatic trail model. Specifically, it is argued that while the lateral force remains invariant for low lateral slip values the pneumatic trail slope changes drastically with the friction potential,
Figure 17.
Therefore, by monitoring the factor
the friction potential can be detected at lower lateral excitation levels. A nonlinear observer based on the tyre lateral force error and similar to [
41] is described and a proof of stability is provided. Field tests were executed on dry asphalt and gravel surfaces. Ramp steer and slalom tests are performed in the former surface, and convergence to the true friction values is observed for excitation levels above
grip utilisation. Sharp transient turns are executed on gravel and authors remark that the proposed observer provides accurate estimates of the friction potential for grip consumption levels around
. Additional details regarding these publications can be found in [
120].
The linear pneumatic trail model (51) was also employed by Han et al. in [
39]. In this case, the authors referred to this model as the pneumatic trail stiffness. An open loop observer is presented to estimate the axle lateral slips from lateral acceleration and yaw acceleration measurements, using a simplified single-track planar dynamics model. Moreover, the cornering stiffness is considered constant along the lateral dynamics linear region and RLS is employed to estimate the pneumatic trail stiffness from the axle lateral slip and the measured pneumatic trail. Despite further details regarding the estimation of
are not provided, authors highlight that the tyre SAT was directly acquired by wheel force transducers (WFT). Frequency response tests were performed on a high mu road (
[0.8–0.9]) and convergence of the friction potential estimates was observed for grip consumption levels between
and
.
In Ahn et al. [
118] two approaches are proposed to estimate the friction potential. Firstly, the authors introduce a maximum torque method to derive
from the peak value of the tyre SAT versus axle lateral slip curve. As this approach can only provide accurate results once the maximum tyre SAT is identified (significant lateral excitation is required), Ahn et al. proposed a nonlinear least squares method to estimate the friction potential and the front axle lateral slip from a blended function composed of the lateral force and tyre SAT estimated form readily-available measurements and the same signals obtained from a reference
Brush tyre model,
Figure 18. Sinusoidal constant speed manoeuvres were simulated in
Carsim on different grips (
,
and
). Overall, results evidence a good performance of the nonlinear least squares observer, and a limited accuracy of the maximum tyre SAT approach. Nevertheless, authors indicate that the latter method can be employed to identify the lower bound of the friction potential, using this on the nonlinear least square optimisation. Additional discussion regarding grip utilisation levels is not provided. This work is completed later in [
107], where Ahn et al. proposed a robust friction potential observer for lateral and longitudinal dynamics. In this case a division is made between medium and high lateral excitation and small and large longitudinal excitation. Update laws for the axle lateral slip and friction potential are provided. Moreover, the observer gains are optimised using Sequential Quadratic Programming (SQP) to guarantee the observer robustness to tyre friction uncertainties. This observer is integrated with the maximum tyre SAT approach described previously, which is used only during high lateral excitation. The authors proposed a rule-based integration scheme to estimate
and
based on vehicle dynamics measurements such as the lateral acceleration or the yaw rate. The observer was tested experimentally in a mu-jump scenario composed of concrete, ice, packed snow and concrete with ice paths segments. Accurate results were obtained subjecting the test vehicle to sinusoidal-like inputs with
2 m/s
. Additional details can be found on the Ph.D. of the author [
17].
In Matilainen and Tuononen [
11] an open loop observer is proposed to estimate the friction potential on the front left and front right wheels using the
Brush tyre model. The tyre self-alignment torque is obtained from the axial forces measured by strain-gauge sensors attached to the tie rods. A simplified steering and suspension kinematics model is employed to translate the previous forces from the tie rods to the wheel-ground contact. The observer is validated experimentally under steady-state mu-split and ramp mu-transition manoeuvres. The observer exhibits a good performance and is able to infer the friction potential of high and low mu surfaces (
,
) for tyre friction levels ranging from
to
. The
Brush tyre model has been also employed by Liu et al. in [
123]. In particular, authors proposed a modified version of the previous model based on test data. The friction potential is obtained using an iterative method that requires the axle lateral slip, and tyre SAT. The former is obtained from a combined auxiliary particle filter and iterated extended kalman filter (APF-IEKF) observer, while the latter is calculated using a linear disturbance observer, as in [
17]. The observer is verified under steering inputs below 0.3 G performed at a constant speed on a surface covered by snow (
). Further conclusions regarding grip utilisation levels cannot be extracted.
Relevant approaches employing a tyre modelisation different from the
Brush model have been also found in the literature [
9,
35,
116,
117,
121]. Specifically, in [
116] Shao et al. employed two different models for the tyre lateral forces and the tyre SAT respectively:
TMsimple and
TMeasy. The authors grouped the front axle wheel slip and the road friction potential in the term
with the aim to detect if the steering excitation is large enough to estimate
in spite of the current surface grip potential. An input-state-stable (ISS) observer is proposed to estimate
x from lateral acceleration, yaw acceleration, steering wheel angle measurements and an estimate of the total front axle aligning torque obtained from a linear disturbance observer. The road friction potential is obtained from the previous estimate (
x) using recursive total least squares (RTLS). The estimation algorithms are simulated in IPG-CarMaker under sinusoidal and lane change steering inputs on different road conditions. A threshold on the variable
x is defined (1.3 degrees) in order to update
only when enough lateral excitation is present. As this threshold is not directly related to the grip utilisation level extracting further conclusions is complicated. In [
117] the same authors proposed a nonlinear adaptive observer and provided a stability analysis of the same. Nevertheless, the validation of the observer is performed on a single-track planar dynamics model, and therefore additional conclusions regarding the observer performance on a high-fidelity vehicle model cannot be extracted. A tyre-SAT-based friction estimator developed by Centro Ricerche Fiat (CRF) is also reported in the European project Friction [
104] and in Koskinen [
23]. The observer is described as a model-based algorithm in which tyre SAT and “standard” vehicle signals are employed to compute
. Additional technical details are not provided. Authors remark that a certain lateral excitation is required to perform the estimation. Specifically, a friction utilisation threshold
is reported in these works as necessary to estimate the friction potential on a high mu road. This excitation threshold is also found in the Intelligent Vehicle Safety System (IVSS) project [
36,
37]. In this case, it is argued that a correlation between the tyre SAT stiffness and the road grip potential can be established, following an analogy with the slip slope approach presented in the longitudinal dynamics section. Different experimental tests are performed on dry asphalt, snow, and ice. Overall, a 0.3 G excitation level is reported as necessary to guarantee an accurate friction potential estimation.
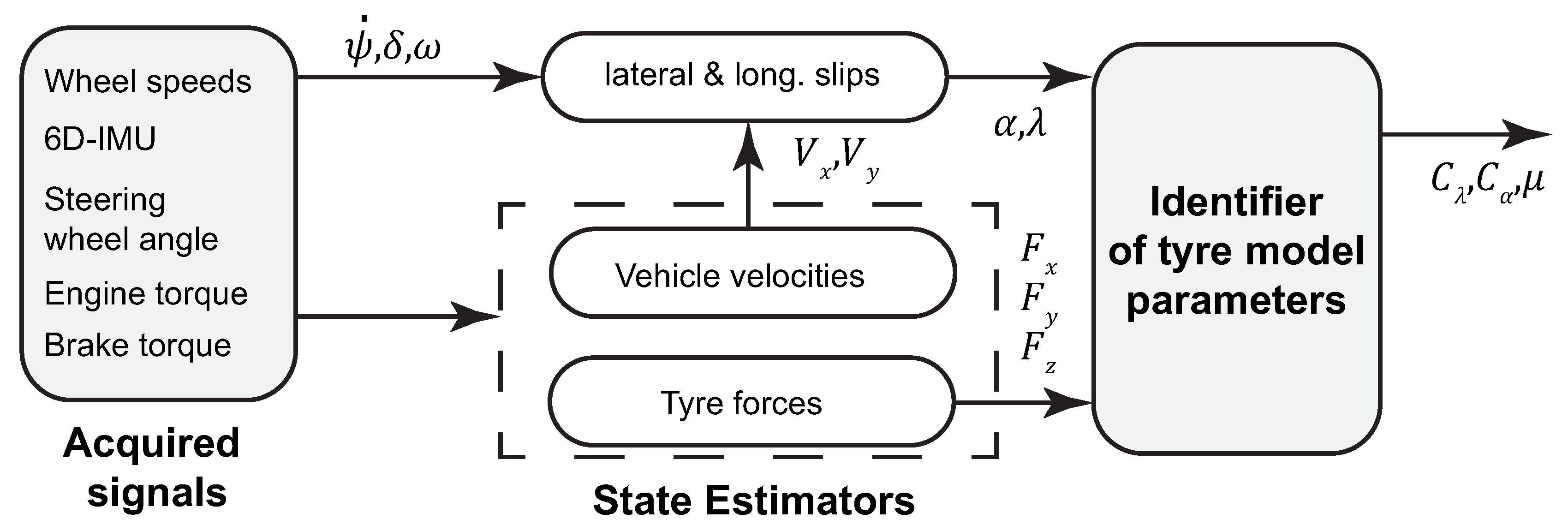
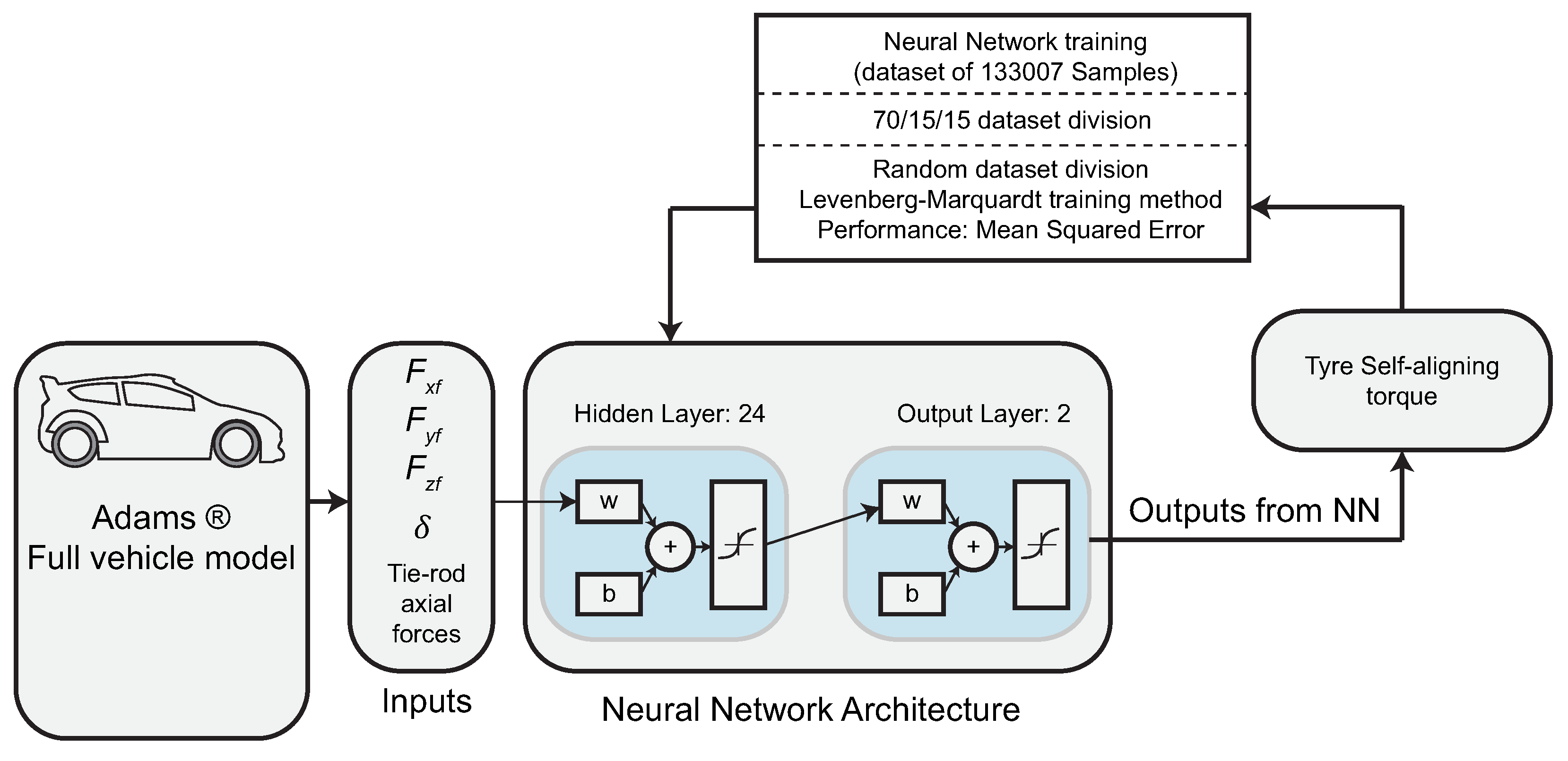
In Luque et al. [
9] the
Magic Formula tyre model was employed to infer the road friction potential from the tyre SAT and the axle lateral slip. Specifically, the authors employed a random-walk EKF to estimate the axle lateral, longitudinal and vertical forces and vehicle planar motion states from signals readily available on the CAN bus of modern vehicles. The front axle lateral forces, in addition to the angle steered by the front wheels and the steering tie rod forces, were employed to estimate the individual tyre SATs from a Neural Network structure,
Figure 19. The NN training was carried out using simulation data from a multi-body simulation model. Finally, the road friction potential
was obtained from a
Magic Formula tyre model using an interpolation algorithm and the pair (
,
). Despite the fact that several simulation results are presented in the multi-body simulation software MSC ADAMS the analysis is focused on the observer accuracy, and further conclusions on grip utilisation levels could not be extracted.
To conclude with the model-based approaches, solutions employing the friction similarity method presented in [
67] have been found in [
35,
121]. Ren et al. [
121] integrated an UKF to estimate the vehicle planar motion states and a tyre-road friction estimator in a hybrid fashion. In this case, the maximum tyre SAT approach introduced in [
118] is employed to estimate the road grip potential during medium lateral slip levels. For higher excitations, a full sliding model is considered. Fishhook manoeuvres are simulated in Carsim at three different road friction levels: high mu, low mu, and mixed mu. As additional manoeuvres at lower excitation levels (e.g., slalom) are not provided it is not possible to establish a fair comparison with the results described in [
118]. Matsuda et al. [
35] presented an EKF observer to estimate the road friction potential from yaw rate, speed, steering wheel angle and EPS current measurements. Specifically, a simplified single-track yaw-sideslip vehicle model was employed in the EKF to estimate the vehicle planar motion states and the road friction potential, modelled as a random-walk variable. A simplified suspension and steering kinematics model was employed to translate the total axle alignment torque to the tyre SAT, neglecting the jacking torques at each wheel, assuming that cancel each other. The authors proposed a sigma-modification method in order to keep the road friction potential estimates within realistic limits. The proposed estimator was validated experimentally in a mu-jump transition (asphalt
to basalt tile
). The results evidenced an accurate detection of the mu transition under a reduced lateral excitation level (
m/s
).
Regarding tyre model-less approaches, relevant works have been presented in [
10,
38,
68,
119,
124,
125,
126]. To start with, Pasterkamp and Pacejka [
10] presented a data-based approach using Neural Networks to estimate the road friction potential. Specifically, two NN were concatenated to recognise the road grip potential: the first to estimate the tyre forces in the three axes and tyre SAT when fed by the steering wheel angle, forces on the king pin, force on the steering link and suspension inclination angle. The second NN was aimed at estimating the wheel slip and friction potential from the outputs of the preceding structure. A grip utilisation threshold (
) was set to limit the friction potential estimation to situations in which a certain excitation is present. The NN was trained with data from surfaces of
and
. In a second step, data not included on the training dataset were employed to validate the estimation structure. Despite accurate results are obtained, only a reduced number of test cases are presented, and therefore a more comprehensive analysis regarding the extrapolation ability of the proposed NN cannot be assessed. In addition to this work, the authors provided further details regarding the NN structures on [
68].
An alternative tyre model-less approach was proposed by Lee et al. in [
124] to detect slippery road segments. In this case, steering torque thresholds corresponding to a high mu asphalt road are defined for different vehicle speeds. At each time step, the current steering wheel torque measured by the EPS system is compared to the dynamic thresholds representative of high-mu situations. If significant differences are appreciated, the low mu road flag is triggered, and the EPS steering friction is augmented slightly with the aim to maintain a constant steering effort. Moreover, the authors proposed an additional algorithm to detect off-road segments from the wheel speed fluctuations. In this case, it is pursued to have more robustness against kick forces induced by the irregularities rather than the detection of the road grip potential. As the detection of
is not the main aim of this work, additional results or discussion on this topic is not provided. Other tyre model-less works have focused on providing a relative measurement of the remaining road friction, known as the lateral grip margin (LGM), and defined as
, rather than trying to estimate the real value of
[
38,
119,
125,
126]. Yasui et al. [
38] defined the LGM as:
where
is the current tyre SAT and
is the tyre SAT stiffness. In brief, the LGM is defined as the ratio between the tyre SAT measured on high mu conditions and the current tyre SAT (assuming that the tyre lateral slip remains within the tyre SAT linear limits),
Figure 20.
In [
38] a modular structure is presented to estimate the tyre SAT from the EPS signals, and the tyre lateral slip required to compute the LGM is calculated with a single-track yaw-body slip observer. The authors provided an interesting analysis regarding the sensitivity of the LGM to the grip utilisation level. Specifically, the authors evidence that the LGM presents an earlier sensitivity to low-mu surfaces compared to other metrics such as the yaw rate deviation. Ono et al. [
119,
125] continued with this research line. The authors enhanced the previous approach to account for the influence of the longitudinal forces. In this case, the solution adopted is not purely tyre model-less, as the
Brush model is employed to derive a relationship between the tyre SAT, the longitudinal force, the utilised tyre SAT, and the tyre grip margin TGM (the previous nomenclature is modified in this work). Following this model, Ono et al. proposed a three-dimensional surface to extract the TGM from the current
and the tyre SAT utilisation level (
). The TGM estimation algorithm is embedded into an integrated four-wheel-distributed steering and four-wheel-distributed traction/braking control system. Simulations are performed and the discussion is oriented towards the controller closed-loop behaviour enhancement. Finally, Minaki and Hori [
126] employed a TGM observer in a steering torque control and in-wheel motor control architecture. This time, authors suggested calculating TGM directly by monitoring the pneumatic trail. This way, the TGM is defined as the state variation of the pneumatic trail, being zero when the tyre slides laterally and the pneumatic trail is null or negative. Authors proposed to compute
directly from tyre SAT estimation and lateral force measurements provided by Load Sensing Bearings (LSB). For further details regarding LSB [
53] can be consulted. Finally, simulation results are provided to evidence the controller actuation, but a comprehensive discussion on the TGM observer is not provided.