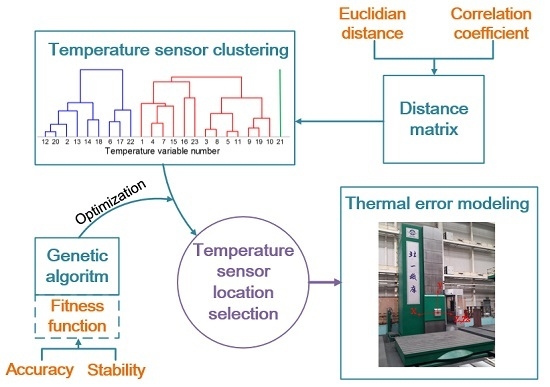
A Temperature Sensor Clustering Method for Thermal Error Modeling of Heavy Milling Machine Tools
Abstract
:1. Introduction
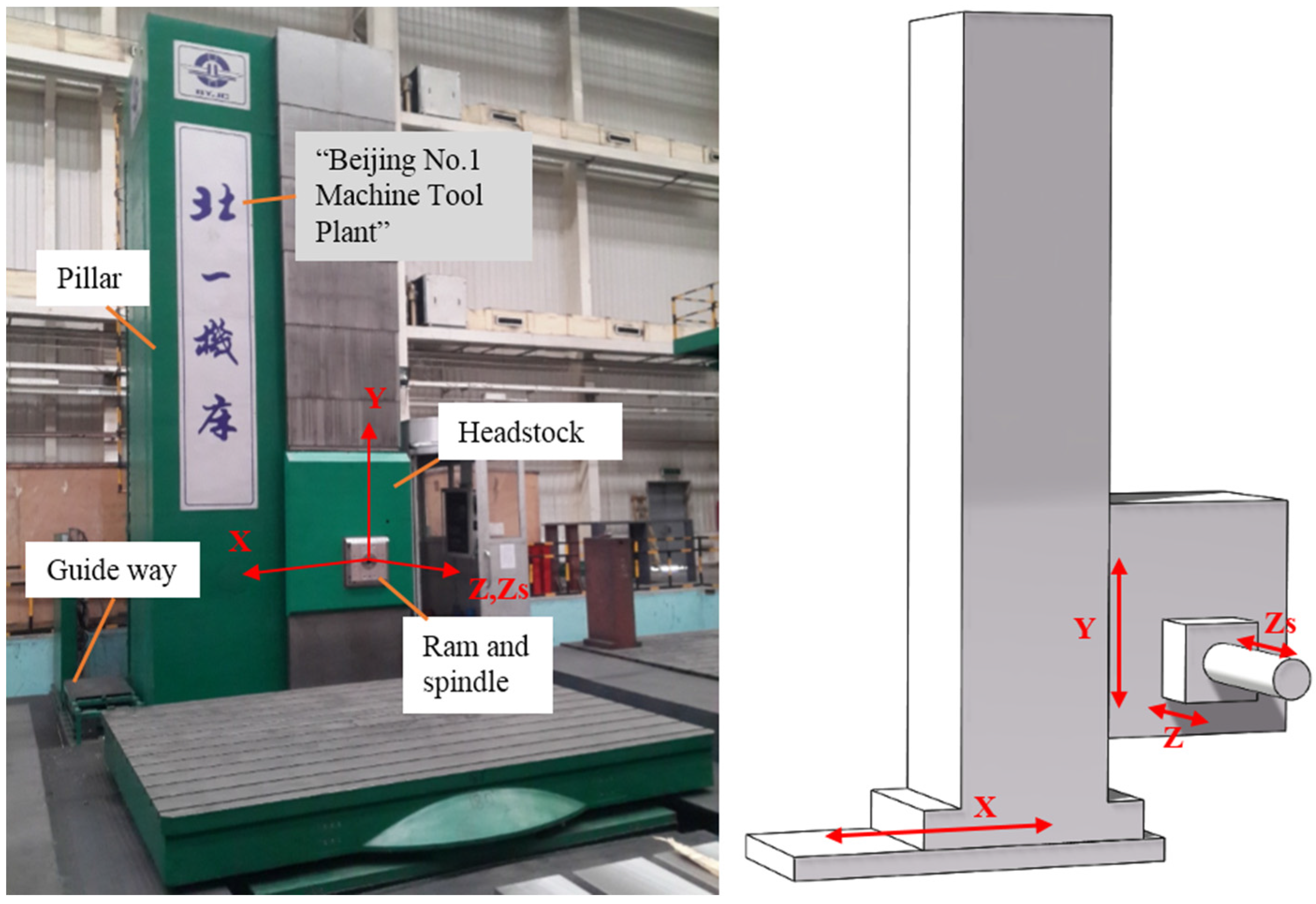
2. Structure of the Investigated Machine Tool
3. Temperature Sensor Clustering Method
3.1. Indicator Construction
3.2. Establishment of the Distance Matrix
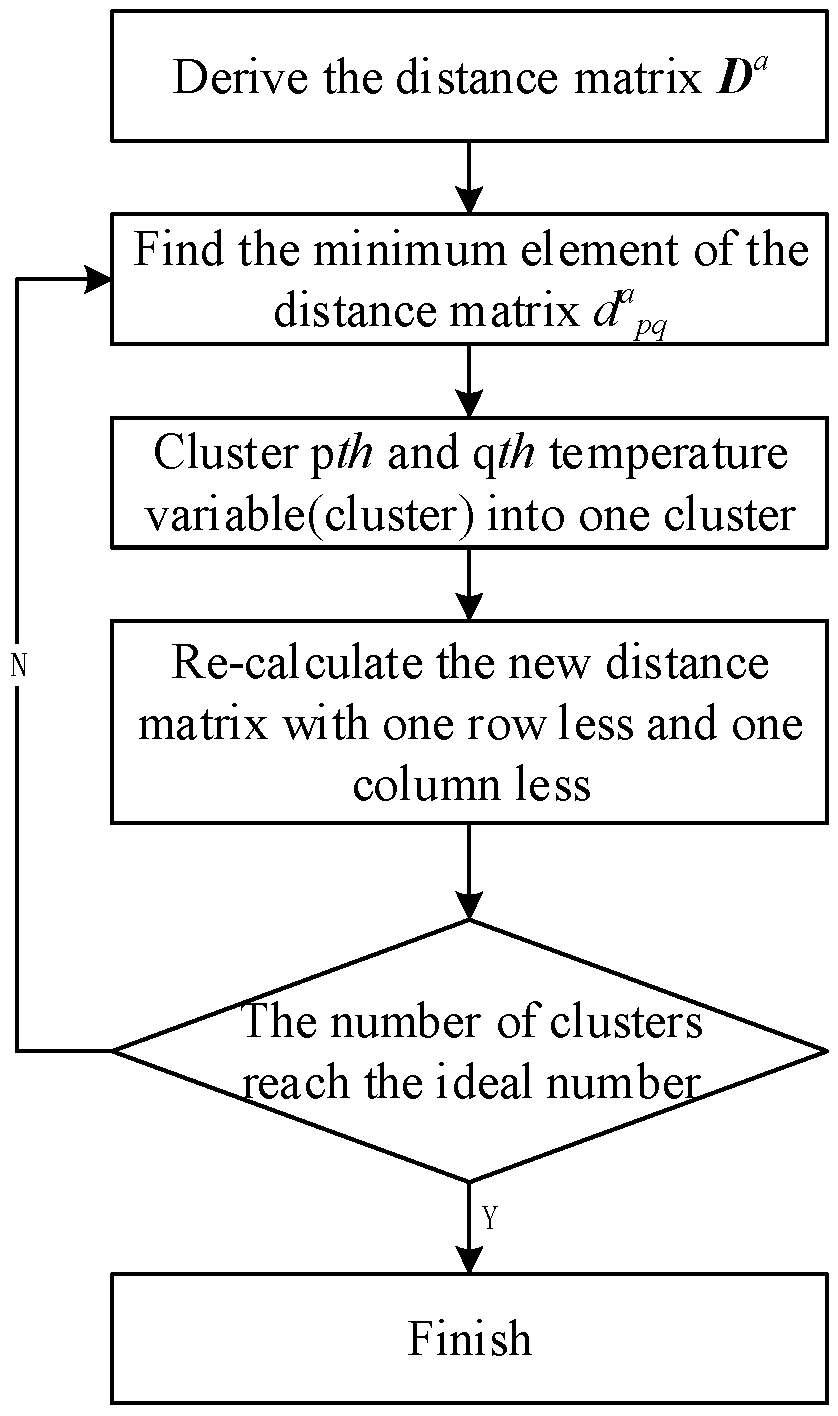
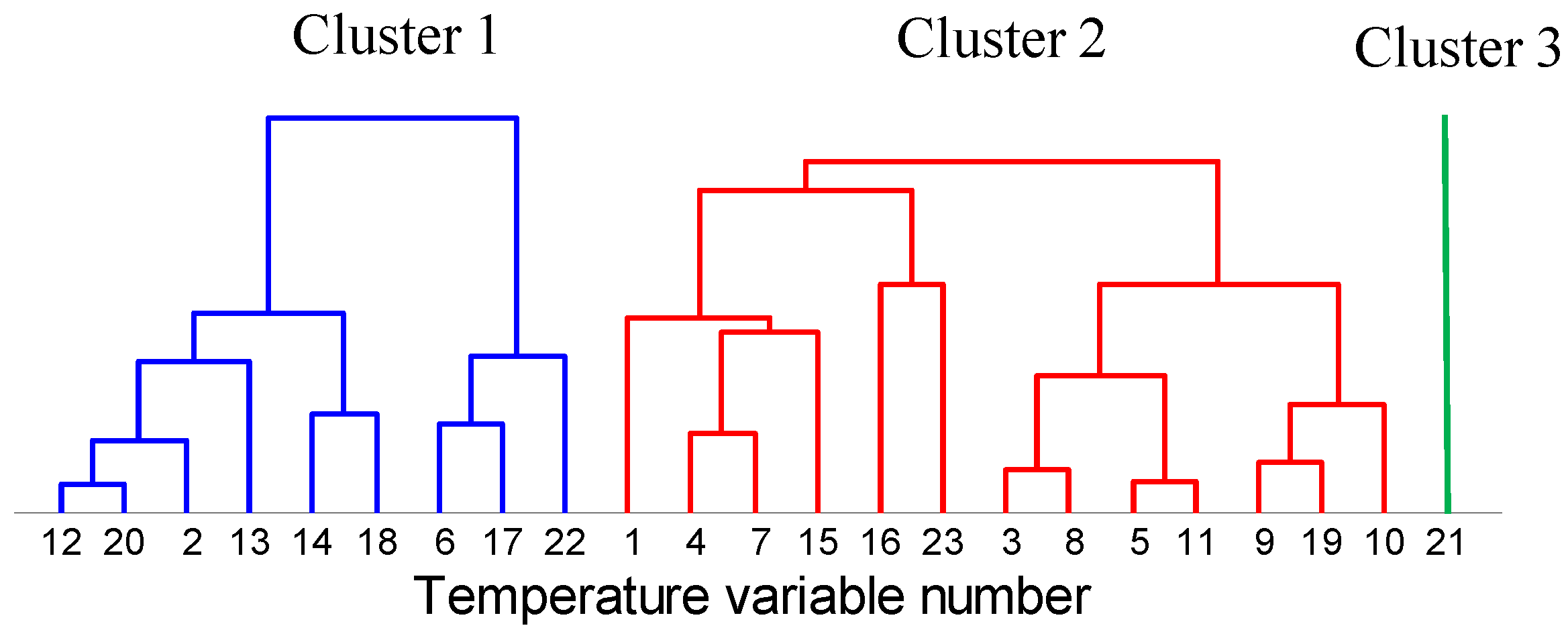
3.3. Hierarchical Clustering Method
- Find the minimum element of the upper triangular part of the distance matrix , named as , which means temperature sensors and have the smallest distance, and clustering and into one cluster, named as ;
- Since and are clusterd, the distance matrix is re-calculated:
- 2.1
- Delete the row and the column of the original distance matrix ;
- 2.2
- Calculate the average temperature of by rows, named as ;
- 2.3
- Calculate the new and between and other temperature sensors (clusters) according to Equations (4), (5), (7), and (10);
- 2.4
- Derive the new based on new and according to Equation (13);
- 2.5
- There is one new between and every other temperature sensor (cluster). Thus, different can be obtained. Arrange them into the corresponding place of the row and the column of the distance matrix to derive a new distance matrix with rows and columns;
- Loop step 1 and step 2 until , which is the size of the distance matrix , reduced to an ideal number . is the number of the clusters we would like to cluster to. The temperature sensors in each cluster can also be derived according to step 1.
3.4. Optimization of the Parameters
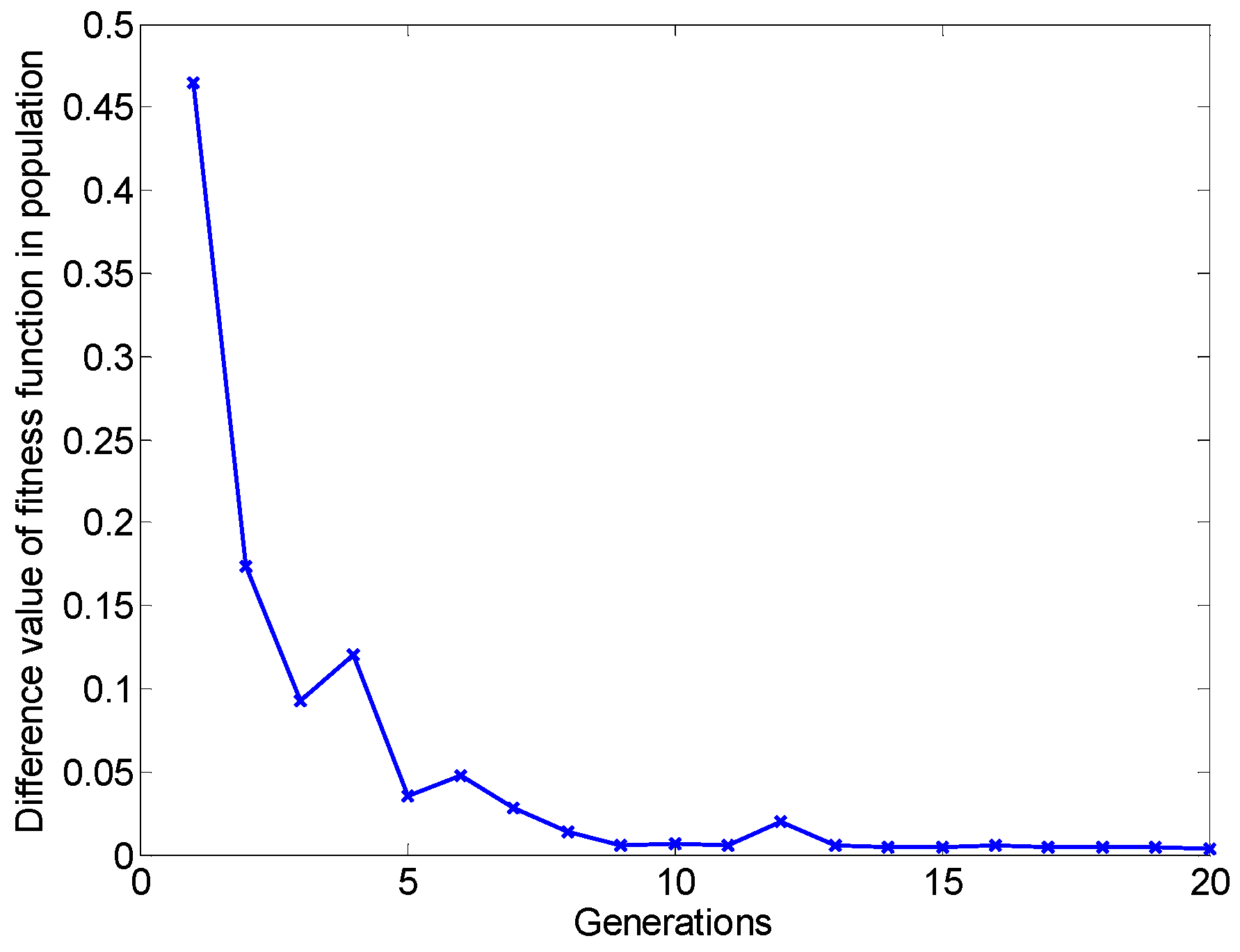
Genetic Algorithm (GA)
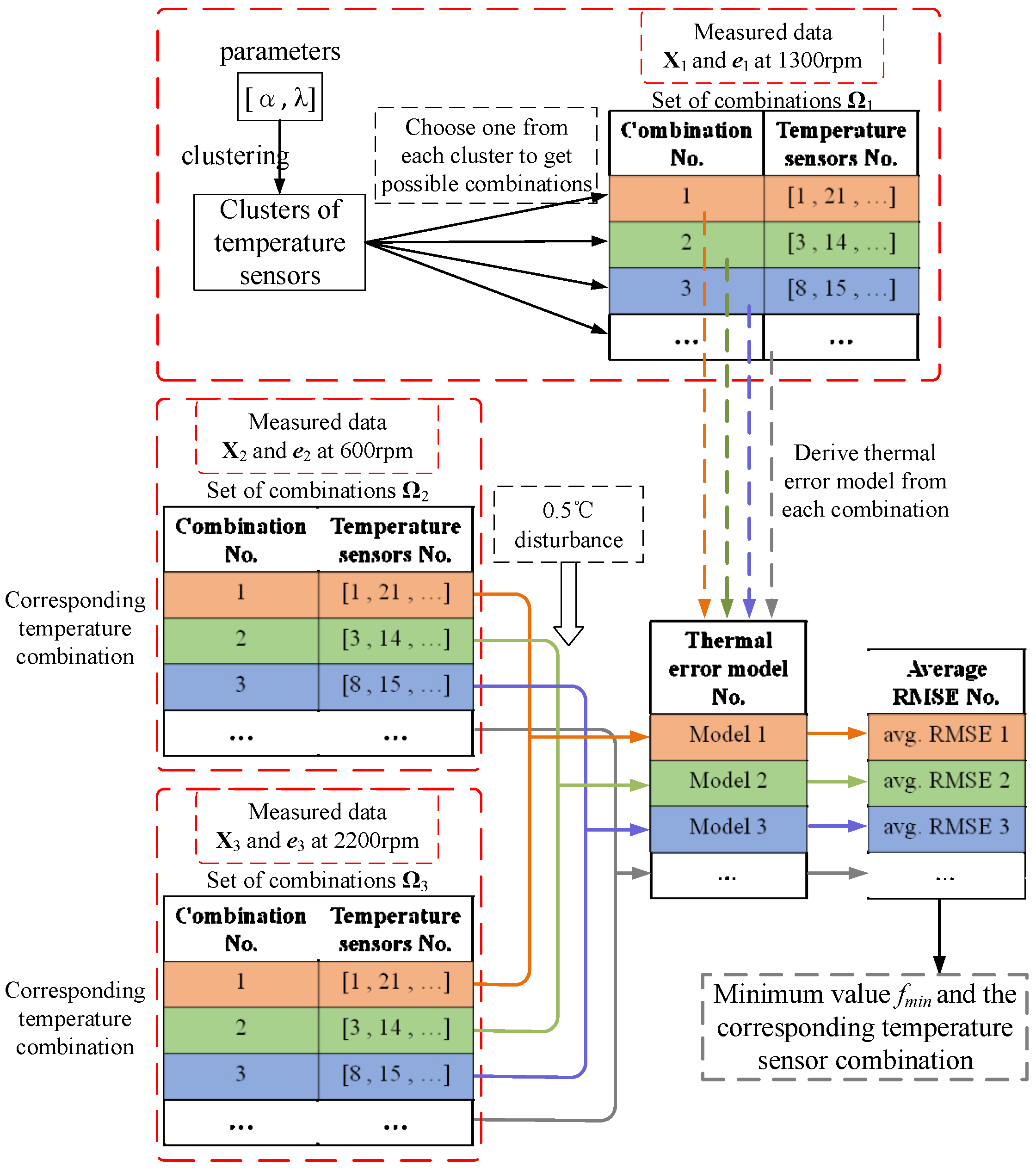
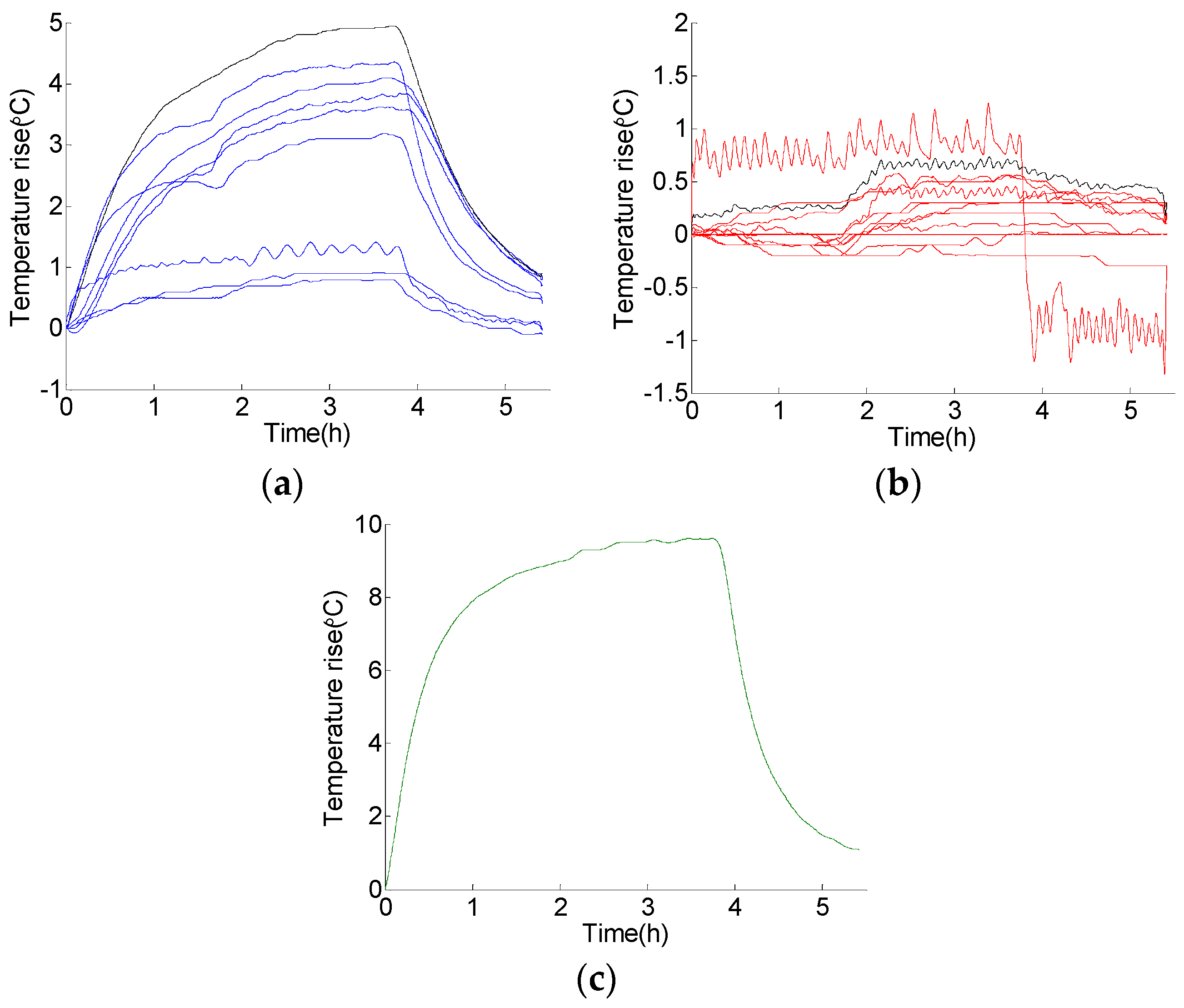
- The machine tool was firstly operated at the rotation speed of 1300 rpm, obtaining the temperature of the sensors , and the thermal error ;
- According to the clustering method in Section 3.2 and Section 3.3 and the two parameters , all temperature sensors are clustered into clusters: , ,…,;
- Choose one temperature sensor from each cluster to form a combination. Thus, we derive a set of all possible combinations, denoted as . For each combination of temperature sensors, a thermal error model can be derived;
- The machine tool was operated at two different rotation speeds, 600 rpm and 2200 rpm, respectively, obtaining , and , ;
- Corresponding to , combinations of the temperature sensors in and were obtained. For each combination of temperature sensors, a 0.5 °C of disturbance was added to simulate the disturbance, then they were used to derive the predicted thermal error and according to the corresponding thermal error model obtained in step 3. Thus, a set of average root mean square errors (RMSE) were derived, each of them is expressed as:where and are the number of the elements in and , respectively;
- Among the set of the average RMSEs, find the minimum one, , which is considered as the value of the fitness function. Meanwhile, the best combination of temperature sensors corresponding to can also be derived.
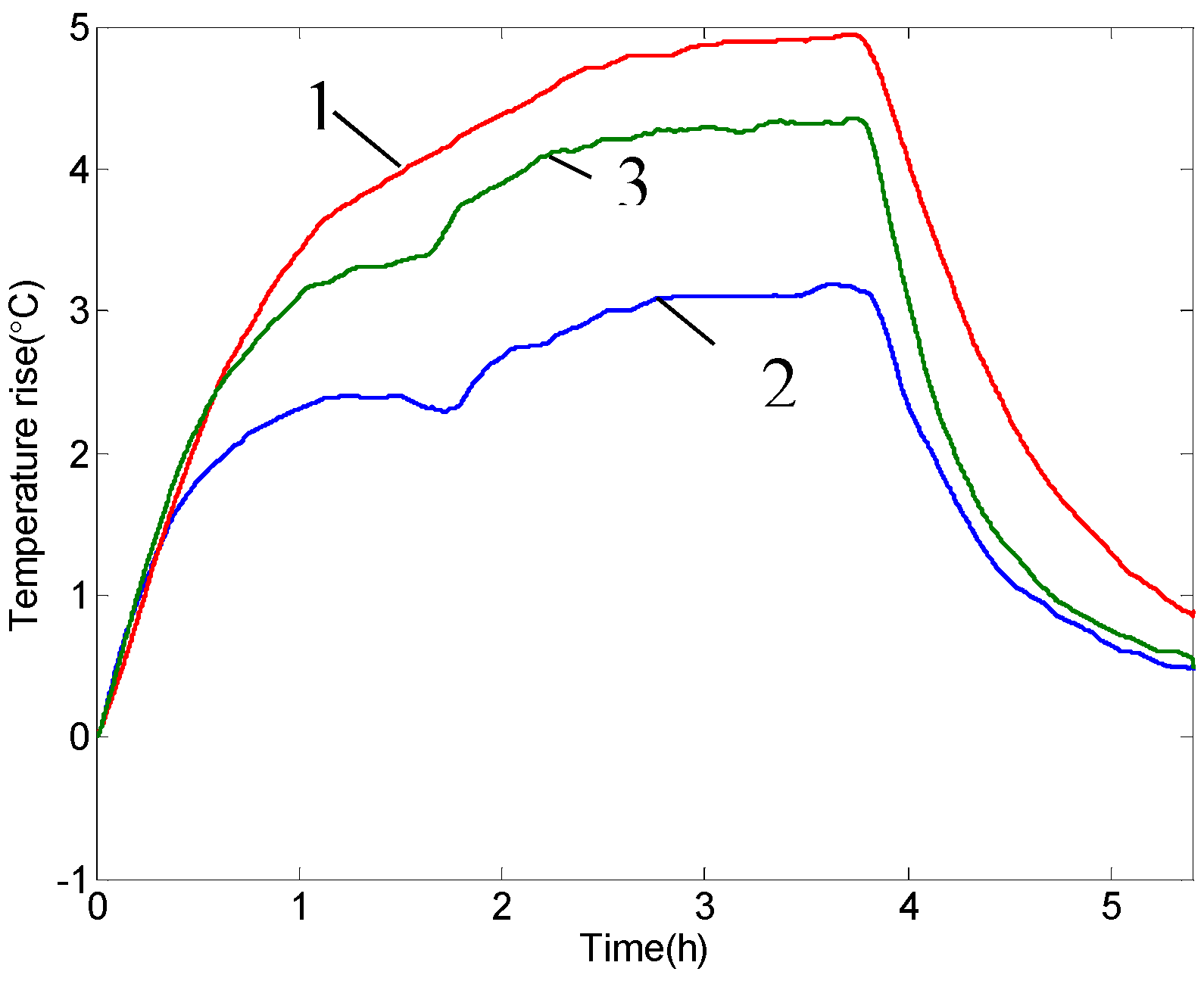
4. Verification of the Method
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Slocum, A.H. Precision Machine Design; Society of Manufacturing Engineers: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Diaz-Tena, E.; Ugalde, U.; de Lacalle, L.N.L.; de la Iglesia, A.; Calleja, A.; Campa, F.J. Propagation of assembly errors in multitasking machines by the homogenous matrix method. Int. J. Adv. Manuf. Techchnol. 2013, 68, 149–164. [Google Scholar] [CrossRef]
- Olvera, D.; Lopez de Lacalle, L.N.; Compean, F.I.; Fz-Valdivielso, A.; Lamikiz, A.; Campa, F.J. Analysis of the tool tip radial stiffness of turn-milling centers. Int. J. Adv. Manuf. Techchnol. 2012, 60, 883–891. [Google Scholar] [CrossRef]
- Mayr, J.; Jedrzejewski, J.; Uhlmann, E.; Alkan Donmez, M.; Knapp, W.; Härtig, F.; Wendt, K.; Moriwaki, T.; Shore, P.; Schmitt, R.; et al. Thermal issues in machine tools. CIRP Ann. Manuf. Technol. 2012, 61, 771–791. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, M.A.; Poo, A.N. Error compensation in machine tools—A review Part II: Thermal errors. Int. J. Mach. Tool Manuf. 2000, 40, 1257–1284. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Li, T.; Li, F. A hybrid thermal error modeling method of heavy machine tools in z-axis. Int. J. Adv. Manuf. Technol. 2015, 80, 389–400. [Google Scholar] [CrossRef]
- Wang, K.; Tseng, P. Thermal Error Modeling of a Machine Tool Using Data Mining Scheme. J. Adv. Mech. Des. Syst. 2010, 4, 516–530. [Google Scholar] [CrossRef]
- Li, J.W.; Zhang, W.J.; Yang, G.S.; Tu, S.D.; Chen, X.B. Thermal-error modeling for complex physical systems: The-state-of-arts review. Int. J. Adv. Manuf. Technol. 2009, 42, 168–179. [Google Scholar] [CrossRef]
- Wu, C.W.; Tang, C.H.; Chang, C.F.; Shiao, Y.S. Thermal error compensation method for machine center. Int. J. Adv. Manuf. Technol. 2012, 59, 681–689. [Google Scholar] [CrossRef]
- Gomez-Acedo, E.; Olarra, A.; de la Calle, L.N.L. A method for thermal characterization and modeling of large gantry-type machine tools. Int. J. Adv. Manuf. Technol. 2012, 62, 875–886. [Google Scholar] [CrossRef]
- Gomez-Acedo, E.; Olarra, A.; Orive, J.; de la Calle, L.N.L. Methodology for the design of a thermal distortion compensation for large machine tools based in state-space representation with Kalman filter. Int. J. Mach. Tool Manuf. 2013, 75, 100–108. [Google Scholar] [CrossRef]
- Zhu, X.; Xiang, S.; Yang, J. Novel thermal error modeling method for machining centers. Proc. Inst. Mech. Eng. C 2015, 229, 1500–1508. [Google Scholar] [CrossRef]
- Dargie, W.; Poellabauer, C. Fundamentals of Wireless Sensor Networks: Theory and Practice; John Wiley & Sons Ltd.: New York, NY, USA, 2010. [Google Scholar]
- Lin, F.; Chiu, P.L. A near-optimal sensor placement alaorithm to achieve complete coverage/discrimination in sensor networks. IEEE Commun. Lett. 2005, 9, 43–45. [Google Scholar]
- Sagara, S.; Nakano, K.; Soji, K. Optimal sensor allocation strategies considering observability in linear distributed-parameter systems. Electr. Eng. Jpn. 1980, 100, 135–142. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, F.; Meng, Z.; Zhao, B.; Li, Y. A novel linear virtual temperature constructing method for thermal error modeling of machine tools. Int. J. Adv. Manuf. Technol. 2015, 80, 1965–1973. [Google Scholar] [CrossRef]
- Yang, J.; Shi, H.; Feng, B.; Zhao, L.; Ma, C.; Mei, X. Thermal error modeling and compensation for a high-speed motorized spindle. Int. J. Adv. Manuf. Tech. 2015, 77, 1005–1017. [Google Scholar] [CrossRef]
- Wang, Y.D.; Zhang, G.X.; Moon, K.S.; Sutherland, J.W. Compensation for the thermal error of a multi-axis machining center. J. Mater. Process. Technol. 1998, 75, 45–53. [Google Scholar] [CrossRef]
- Herzog, R.; Riedel, I. Sequentially optimal sensor placement in thermoelastic models for real time applications. Optim. Eng. 2015, 16, 737–766. [Google Scholar] [CrossRef]
- Koevoets, A.H.; Eggink, H.J.; van der Sanden, J.; Dekkers, J.; Ruijl, T.A.M. Optimal Sensor Configuring Techniques for the Compensation of Thermo-Elastic Deformations in High-Precision Systems. In Proceedings of the Thermal Investigation of ICs and Systems (THERMINIC), Budapest, Hungary, 17–19 September 2007; pp. 208–213.
- Lo, C.H.; Yuan, J.X.; Ni, J. Optimal temperature variable selection by grouping approach for thermal error modeling and compensation. Int. J. Mach. Tool Manuf. 1999, 39, 1383–1396. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, J.G.; Gelvis, T.; Li, Y.Y. Optimization of measuring points for machine tool thermal error based on grey system theory. Int. J. Adv. Manuf. Technol. 2008, 35, 745–750. [Google Scholar] [CrossRef]
- Yan, J.Y.; Yang, J.G. Application of synthetic grey correlation theory on thermal point optimization for machine tool thermal error compensation. Int. J. Adv. Manuf. Technol. 2009, 43, 1124–1132. [Google Scholar] [CrossRef]
- Lee, D.S.; Choi, J.Y.; Choi, D.H. ICA based thermal source extraction and thermal distortion compensation method for a machine tool. Int. J. Mach. Tool Manuf. 2003, 43, 589–597. [Google Scholar] [CrossRef]
- Han, J.; Wang, L.P.; Wang, H.T.; Cheng, N.B. A new thermal error modeling method for CNC machine tools. Int. J. Adv. Manuf. Technol. 2012, 62, 205–212. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. The application of ANFIS prediction models for thermal error compensation on CNC machine tools. Appl. Soft Comput. 2015, 27, 158–168. [Google Scholar] [CrossRef]
- Jian, H.; Liping, W.; Ningbo, C.; Haitong, W. Thermal error modeling of machine tool based on fuzzy c-means cluster analysis and minimal-resource allocating networks. Int. J. Adv. Manuf. Technol. 2012, 60, 463–472. [Google Scholar]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S.; Myers, A. Thermal error modelling of machine tools based on ANFIS with fuzzy c-means clustering using a thermal imaging camera. Appl. Math. Model. 2015, 39, 1837–1852. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Li, T.; Han, J. Thermal sensor selection for the thermal error modeling of machine tool based on the fuzzy clustering method. Int. J. Adv. Manuf. Technol. 2013, 69, 121–126. [Google Scholar] [CrossRef]
- Yanqun, H.; Jie, Z.; Xu, L.; Liangjv, T. Thermal error modeling by integrating GA and BP algorithms for the high-speed spindle. Int. J. Adv. Manuf. Technol. 2014, 71, 1669–1675. [Google Scholar]
- Soori, M.; Arezoo, B.; Habibi, M. Tool Deflection Error of Three-Axis Computer Numerical Control Milling Machines, Monitoring and Minimizing by a Virtual Machining System. J. Manuf. Sci. Eng. 2016, 138, 081005. [Google Scholar] [CrossRef]
- Chen, T.; Chang, C.; Hung, J.; Lee, R.; Wang, C. Real-Time Compensation for Thermal Errors of the Milling Machine. Appl. Sci. 2016, 6. [Google Scholar] [CrossRef]
- Chen, J.S.; Yuan, J.; Ni, J. Thermal error modelling for real-time error compensation. Int. J. Adv. Manuf. Technol. 1996, 12, 266–275. [Google Scholar] [CrossRef]
- Chen, J.S.; Yuan, J.; Ni, J.; Wu, S.M. Real-Time Compensation for Time-Variant Volumetric Errors on a Machining Center. J. Eng. Ind. 1993, 115, 472–479. [Google Scholar] [CrossRef]

| Sensor No. | Sensor Location | Sensor No. | Sensor Location |
|---|---|---|---|
| 1 | Oil of the guide way of the -axis | 13 | Hydrostatic oil of the guide way of the -axis |
| 2 | surface of the oil box for gearbox lubrication | 14 | Hydrostatic oil of the spindle |
| 3 | Foundation of the machine tool | 15 | Surface of the worktable |
| 4 | Upper surface on the rear of the ram | 16 | Inlet of the cooling box |
| 5 | Cooling water of -axis feed motor | 17 | Front surface of the ram |
| 6 | Upper surface of the pillar | 18 | Cooling water of the spindle motor |
| 7 | Air near the head stock | 19 | Upper surface on the front of the ram |
| 8 | Middle surface of the pillar | 20 | Cooling oil of the gearbox |
| 9 | Side surface in the front of the ram | 21 | Near the spindle motor |
| 10 | Oil of the gearbox | 22 | Near the hydrostatic oil in the ram |
| 11 | Lower surface of the pillar | 23 | Environment temperature near the pillar |
| 12 | Surface of the cooling oil tube in the rear of the ram | - | - |
| Main Parameters | Value |
|---|---|
| Initial population size | 20 |
| Crossover possibility | 0.8 |
| Mutation rate | 0.005 |
| Maximum generations | 20 |
| Temperature Sensor 1 | Temperature Sensor 2 | Temperature Sensor 3 |
|---|---|---|
| No. 14 (hydrostatic oil of the spindle) | No. 10 (oil of gear box) | No. 21 (near the spindle motor) |
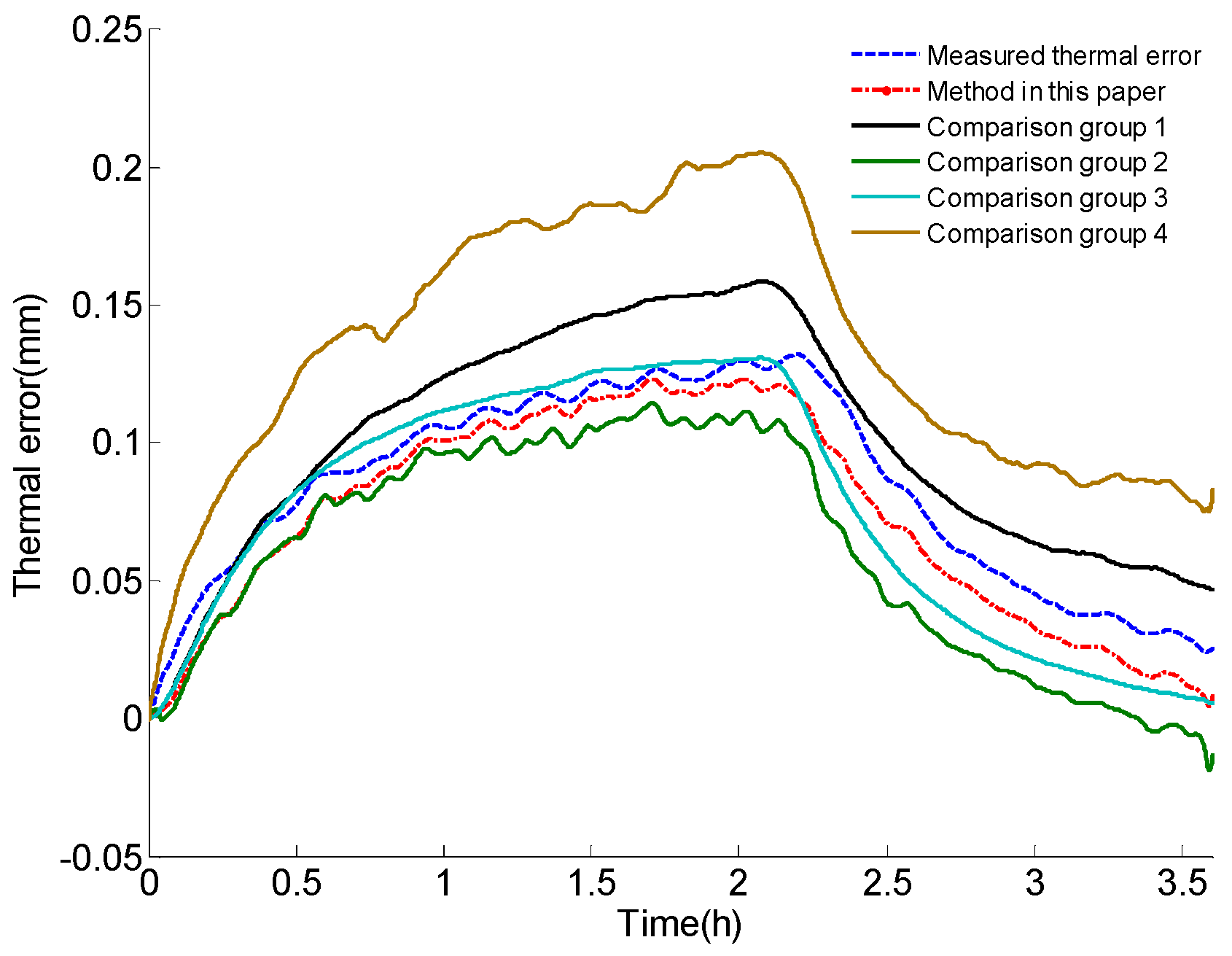
| New Method | Comparison Group 1 | Comparison Group 2 | Comparison Group 3 | Comparison Group 4 | |
|---|---|---|---|---|---|
| RMSE | 0.0118 mm | 0.0192 mm | 0.0261 mm | 0.0164 mm | 0.0528 mm |
| Maximum deviation | 0.0227 mm | 0.0318 mm | 0.0498 mm | 0.0329 mm | 0.0785 mm |
| Rotation Speed | 300 rpm | 500 rpm | 100 rpm | 1500 rpm | Pause | 500 rpm | Stop |
|---|---|---|---|---|---|---|---|
| Duration | 0.5 h | 0.64 h | 0.47 h | 0.47 h | 0.5 h | 0.56 h | 2.41 h |
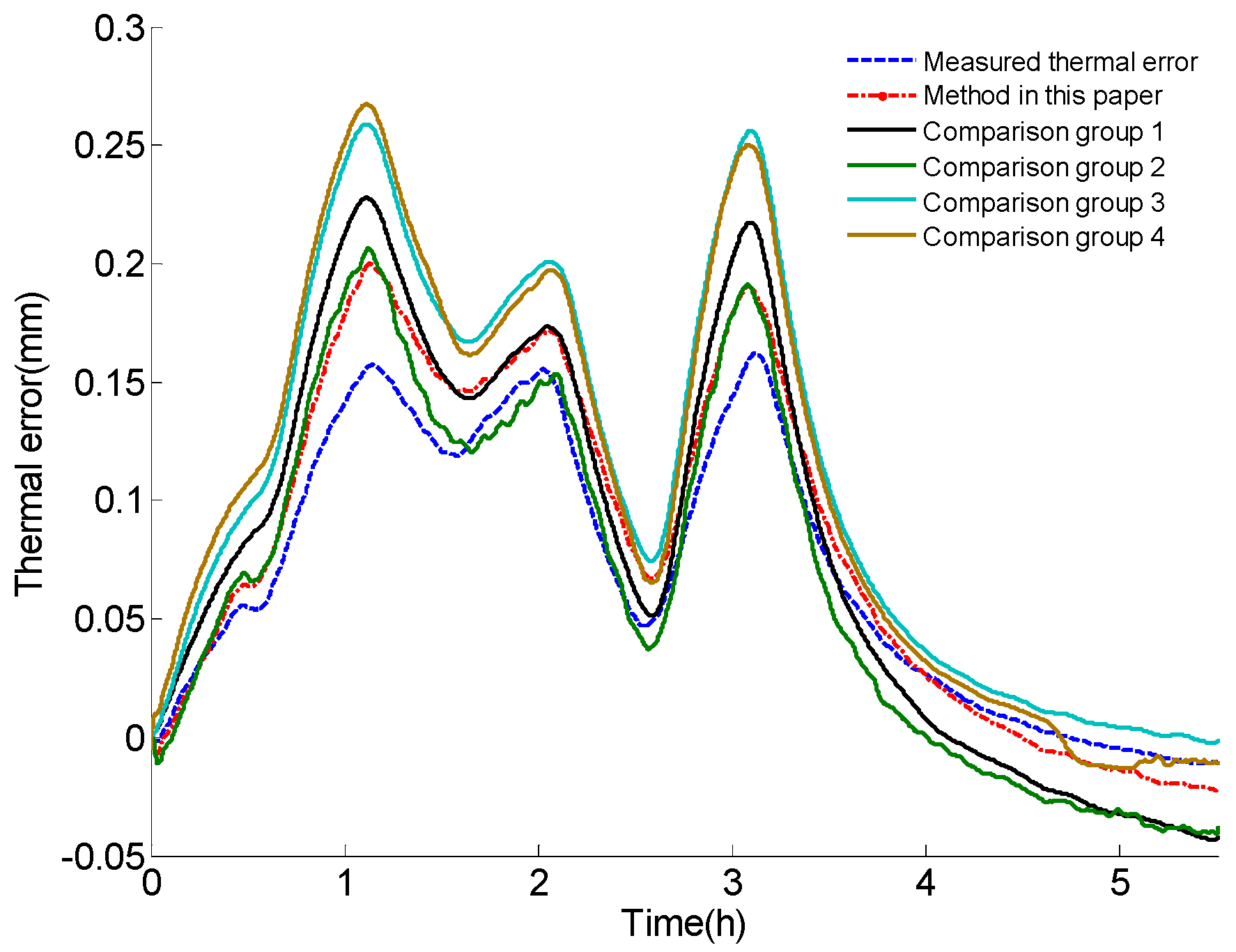
| New Method | Comparison Group 1 | Comparison Group 2 | Comparison Group 3 | Comparison Group 4 | |
|---|---|---|---|---|---|
| RMSE | 0.0200 mm | 0.0320 mm | 0.0228 mm | 0.0491 mm | 0.0501 mm |
| Maximum deviation | 0.0434 mm | 0.0742 mm | 0.0500 mm | 0.1052 mm | 0.1136 mm |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Li, T.; Wang, H.; Jiang, Y. A Temperature Sensor Clustering Method for Thermal Error Modeling of Heavy Milling Machine Tools. Appl. Sci. 2017, 7, 82. https://doi.org/10.3390/app7010082
Li F, Li T, Wang H, Jiang Y. A Temperature Sensor Clustering Method for Thermal Error Modeling of Heavy Milling Machine Tools. Applied Sciences. 2017; 7(1):82. https://doi.org/10.3390/app7010082
Chicago/Turabian StyleLi, Fengchun, Tiemin Li, Haitong Wang, and Yao Jiang. 2017. "A Temperature Sensor Clustering Method for Thermal Error Modeling of Heavy Milling Machine Tools" Applied Sciences 7, no. 1: 82. https://doi.org/10.3390/app7010082
APA StyleLi, F., Li, T., Wang, H., & Jiang, Y. (2017). A Temperature Sensor Clustering Method for Thermal Error Modeling of Heavy Milling Machine Tools. Applied Sciences, 7(1), 82. https://doi.org/10.3390/app7010082