Experimental and Numerical Investigation on Non-Newtonian Nanofluids Flowing in Shell Side of Helical Baffled Heat Exchanger Combined with Elliptic Tubes
Abstract
:1. Introduction
2. Experimental Method
2.1. Sample Preparation and Measurements
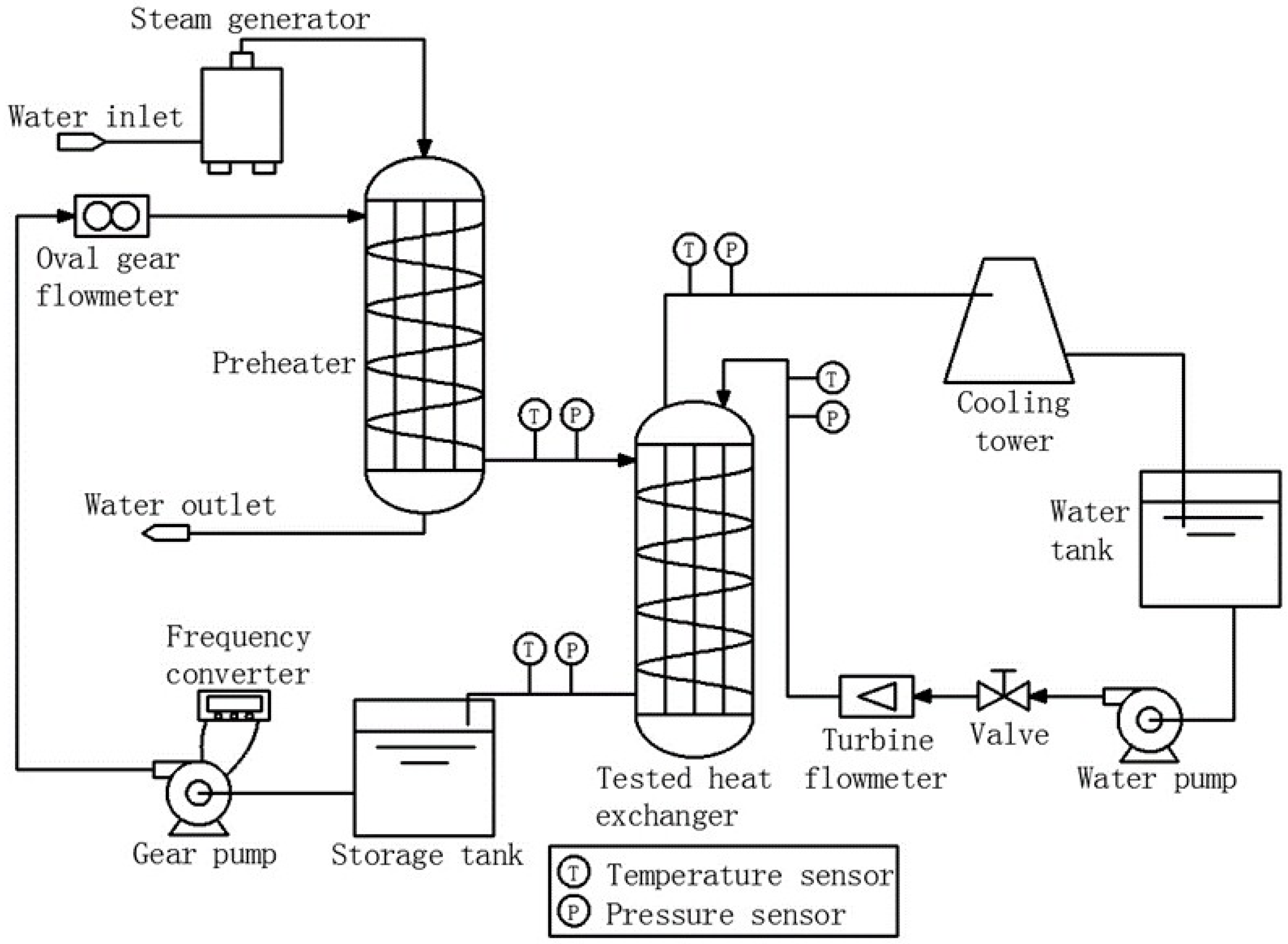
2.2. Experimental System
2.3. Data Reduction
3. Mathematical Modeling
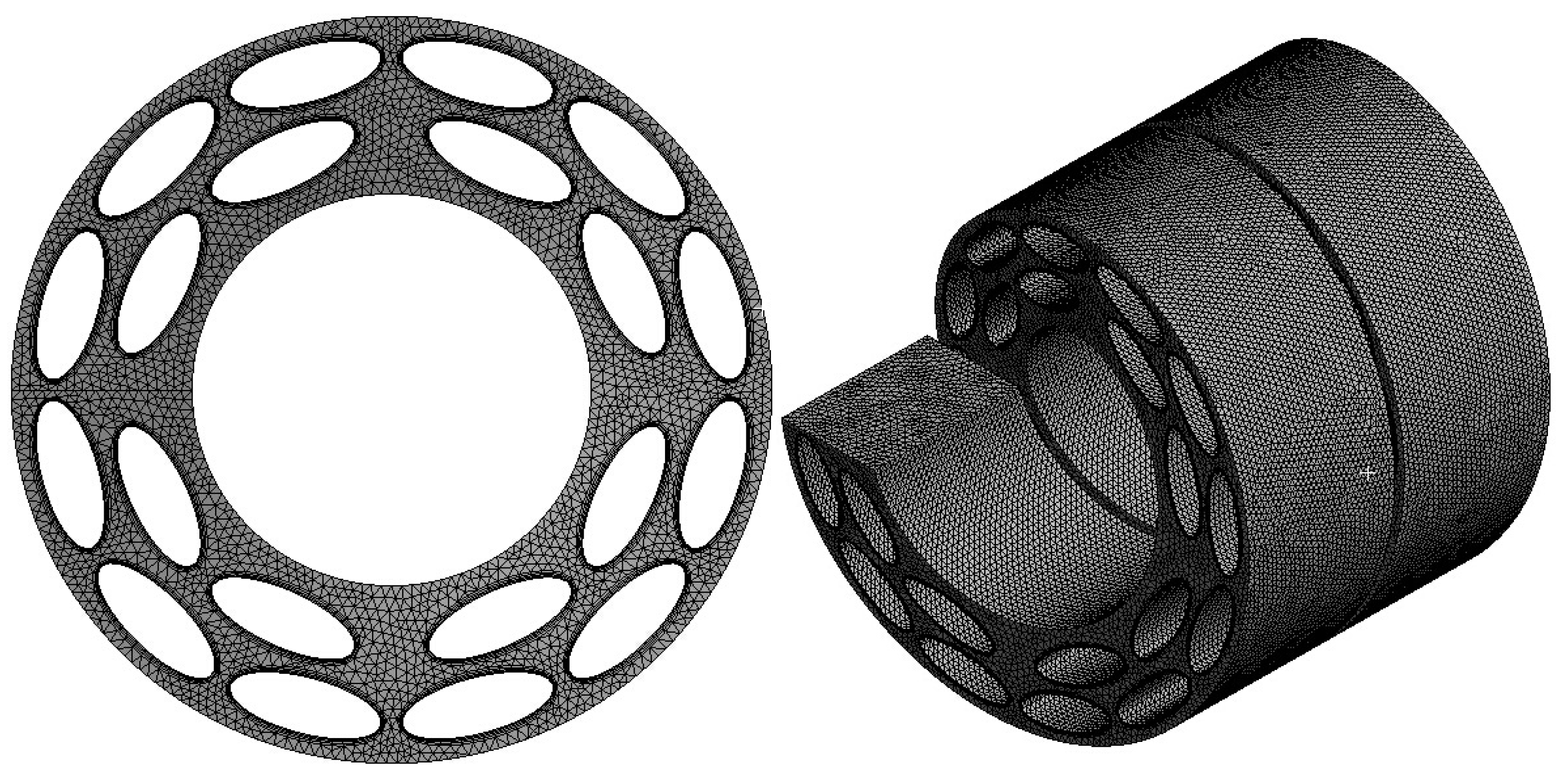
3.1. Physical Model
3.2. Governing Equations and Numerical Method
3.3. Boundary Conditions
- (1)
- The inlet of shell side used the mass flow inlet boundary condition as follow:
- (2)
- The outlet shell side used the pressure outlet boundary condition as follow:where n is the normal vector of outlet. The outlet temperature and pressure results of calculation were obtained from this plane.
- (3)
- The adiabatic wall boundary conditions were adopted for the shell walls and baffle walls:
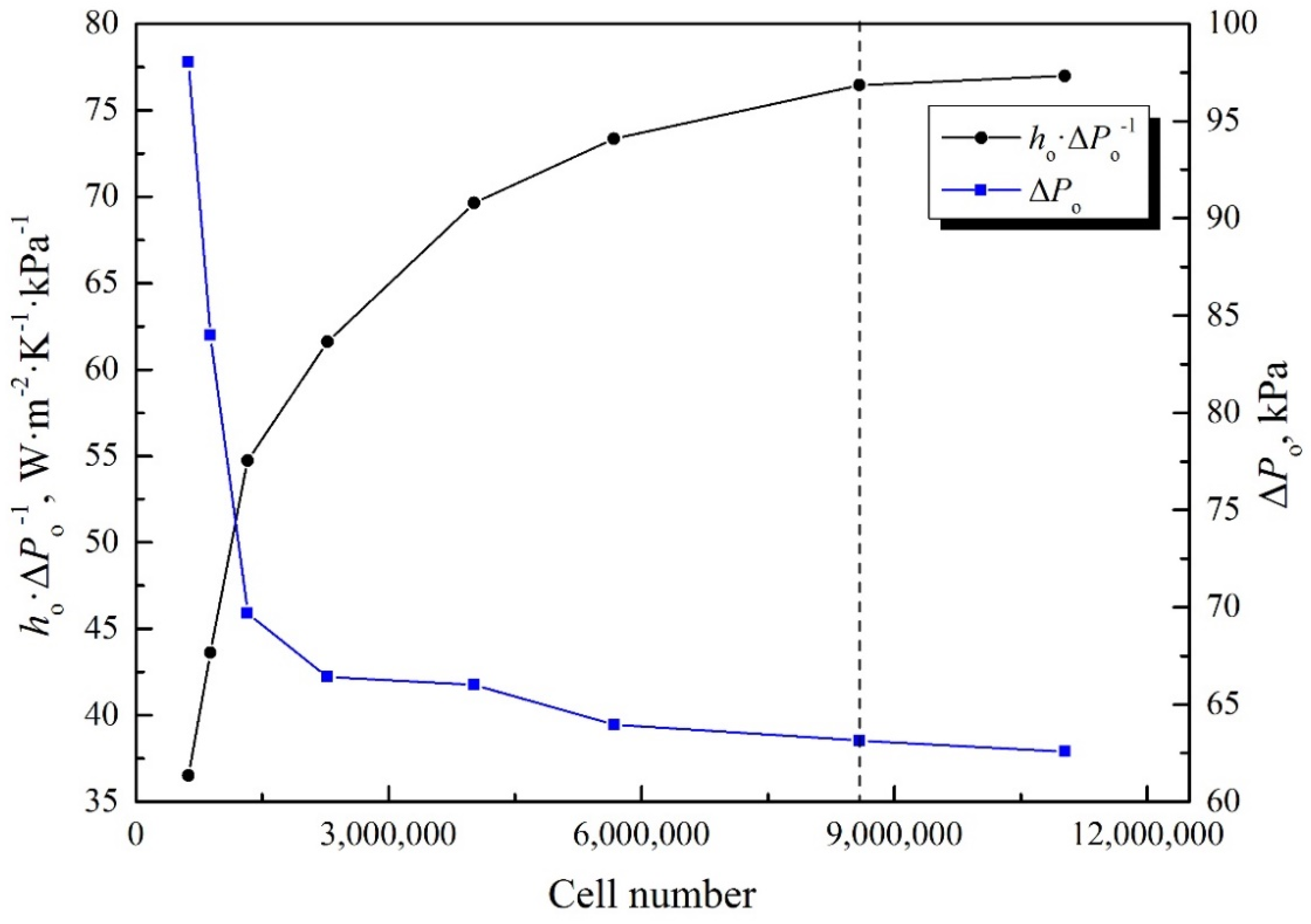
3.4. Grid Generation and Independence
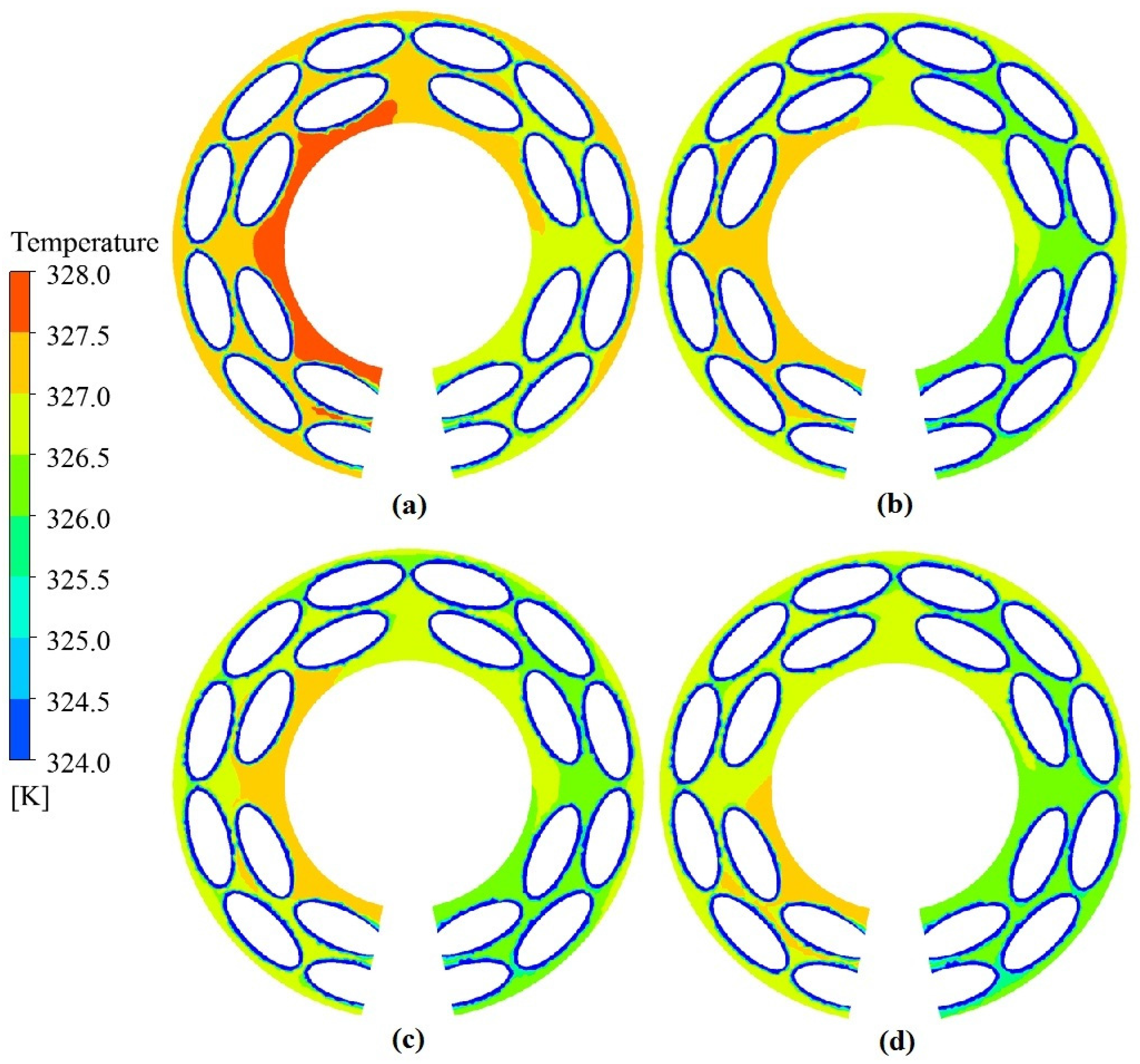
4. Results and Discussion
4.1. Thermal-Physical Properties of Non-Newtonian Nanofluids
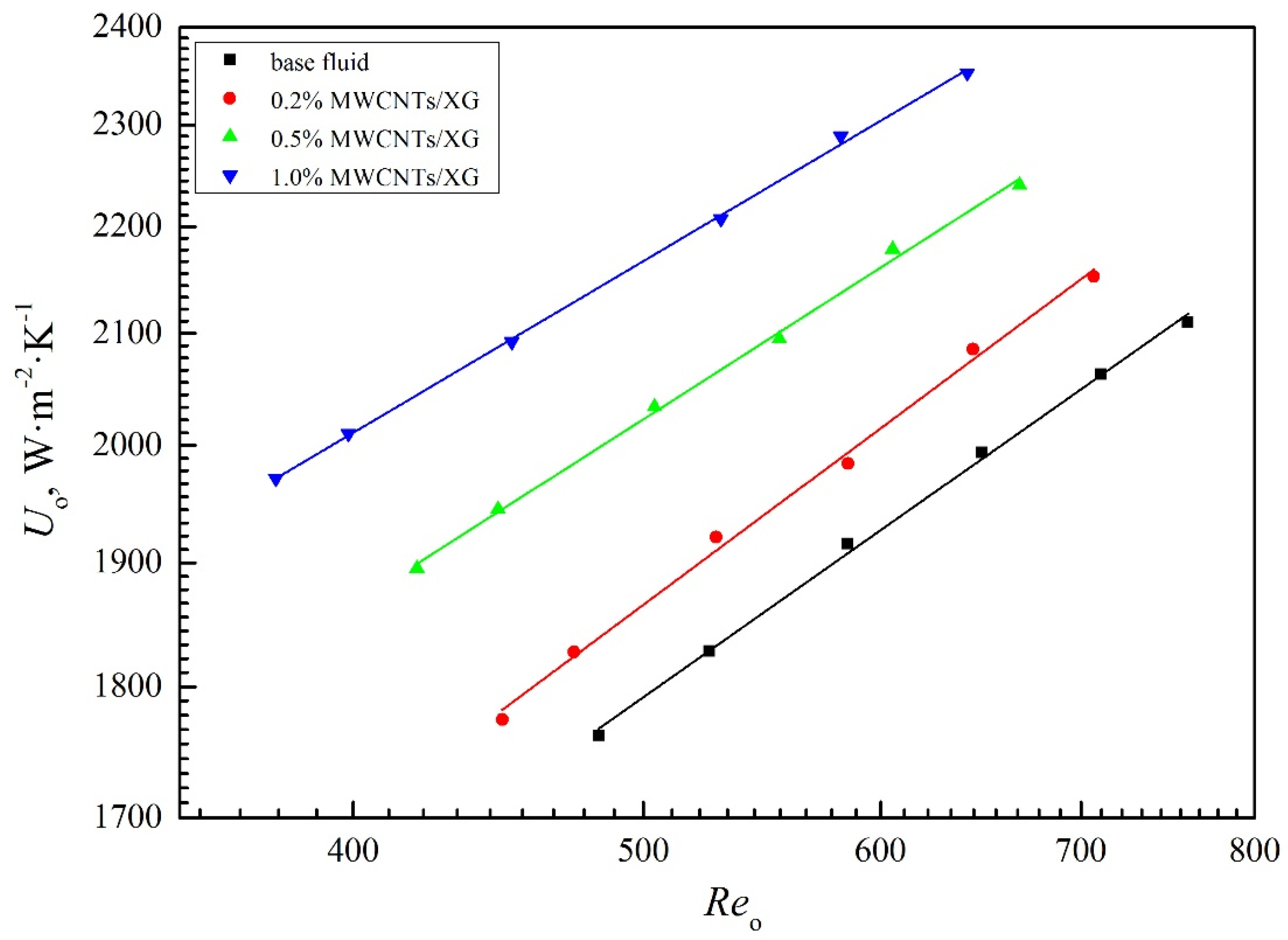
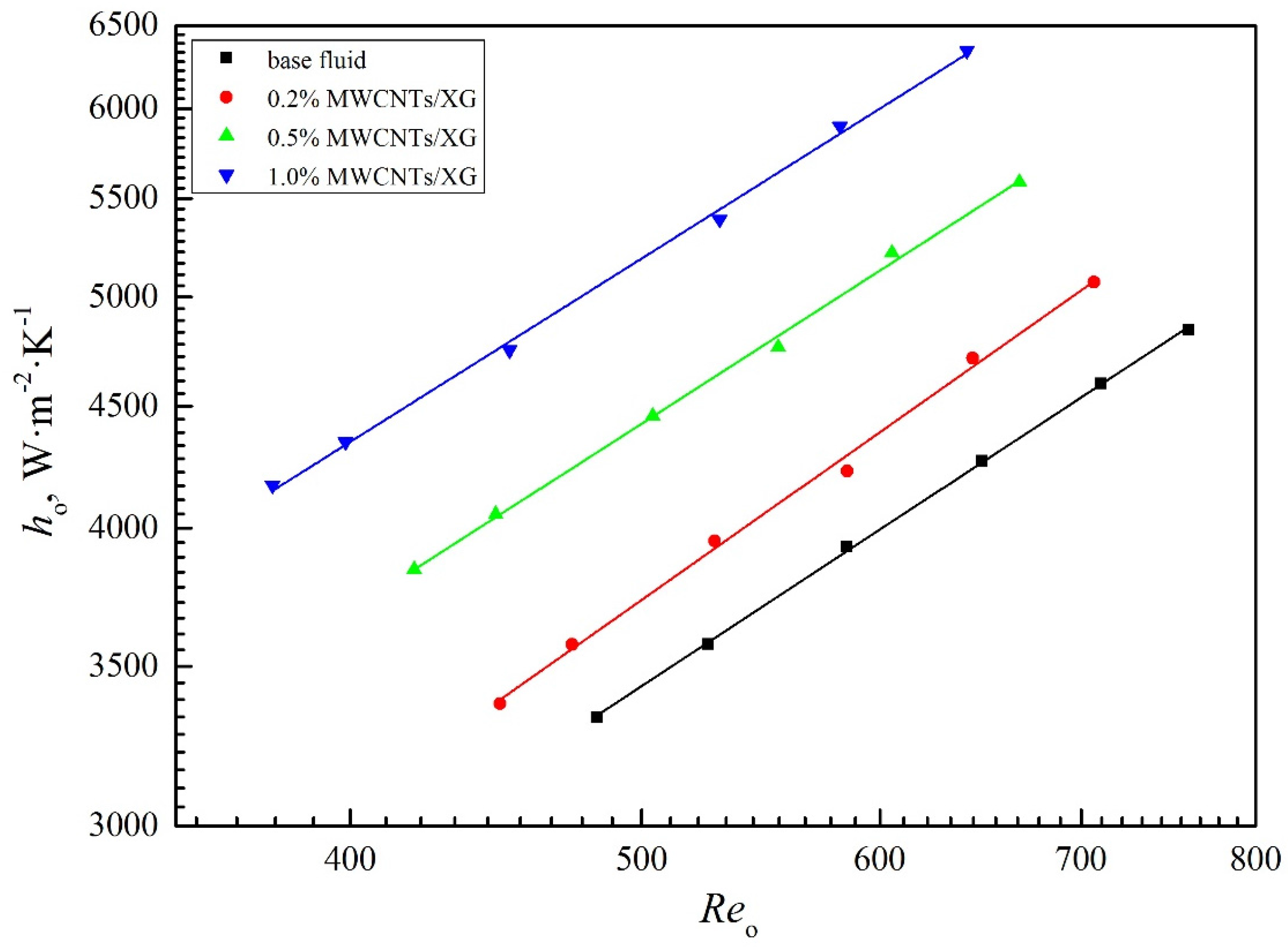
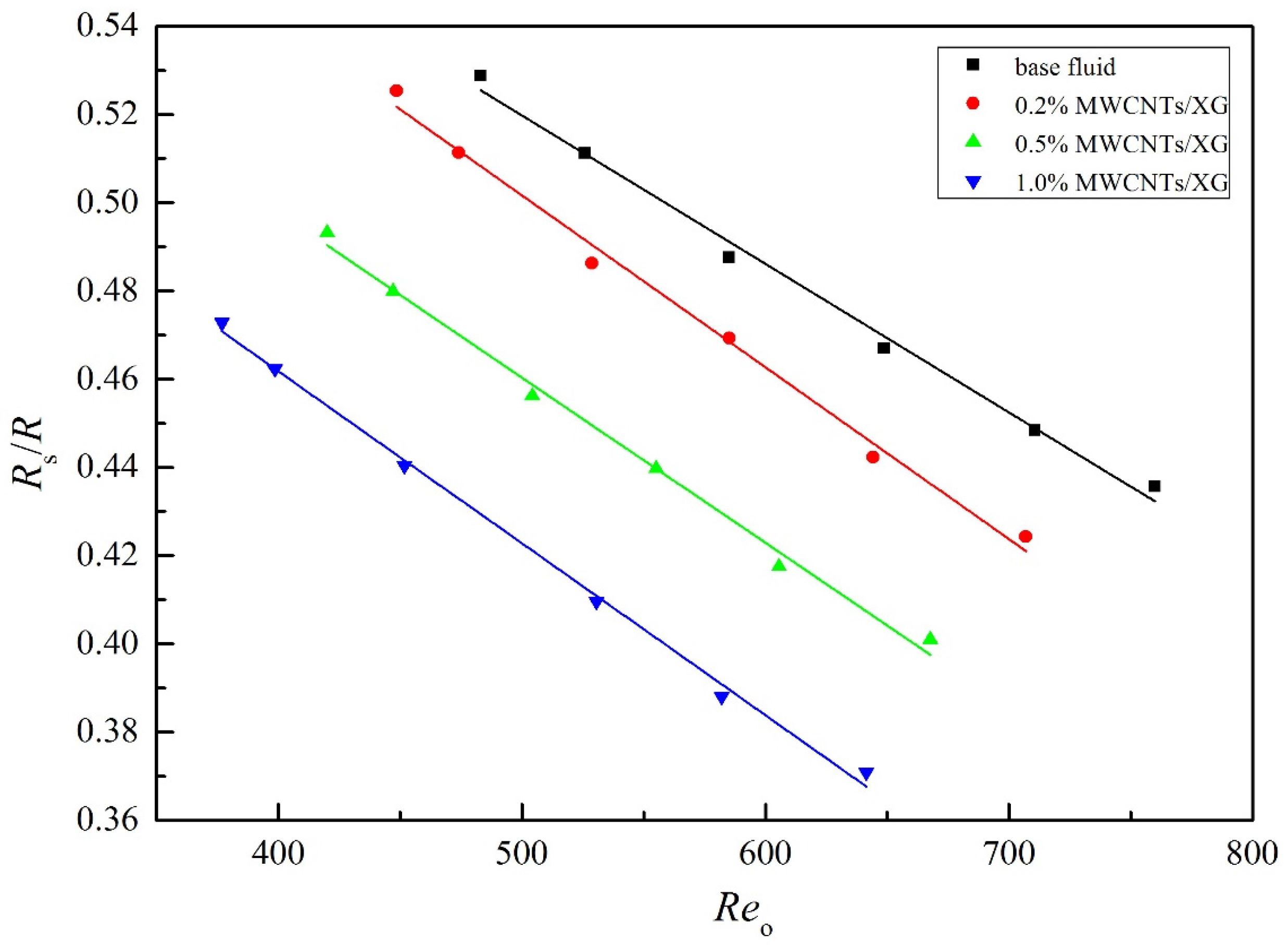
4.2. Overall and Shell-Side Heat Transfer Coefficient
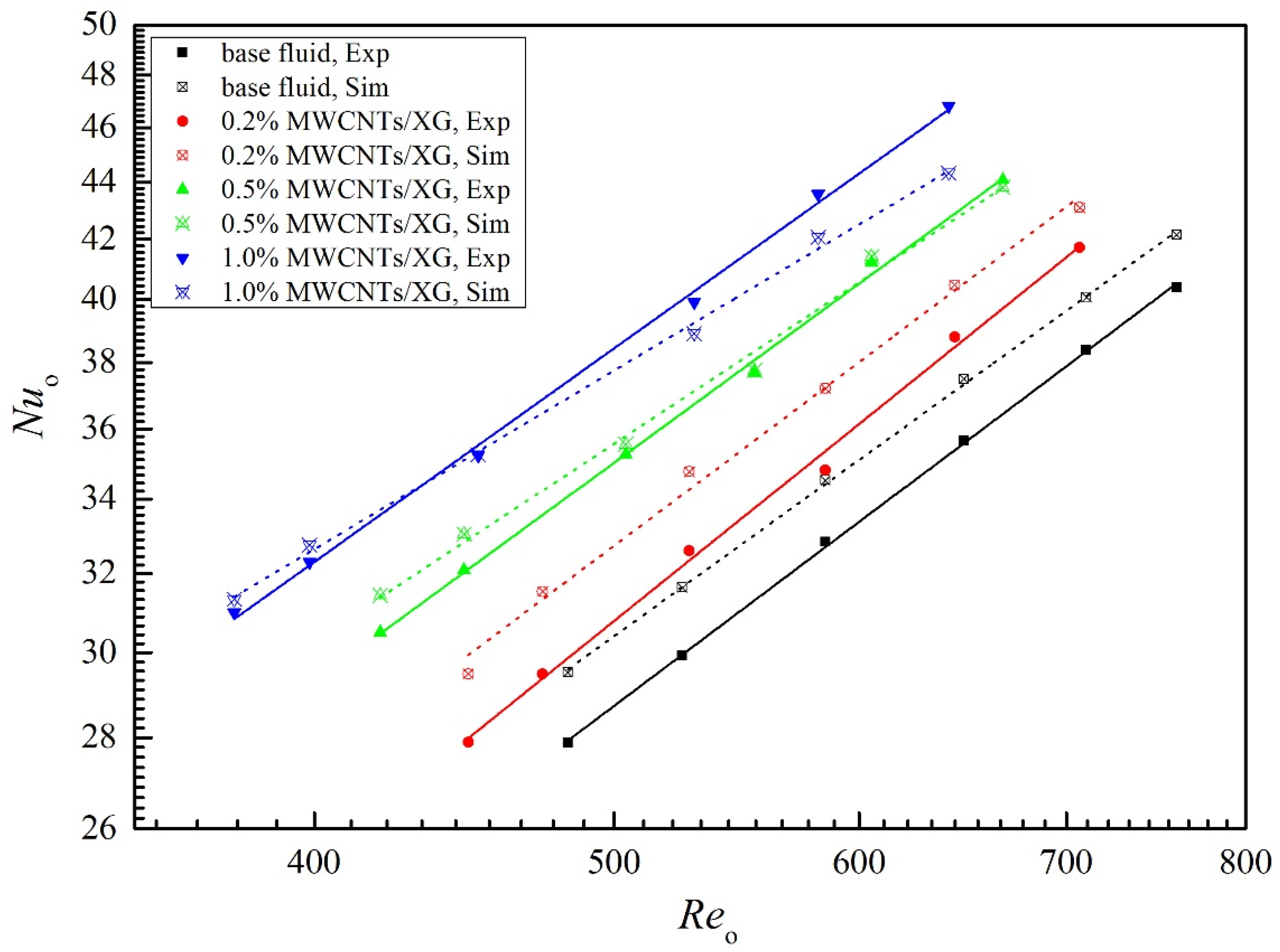
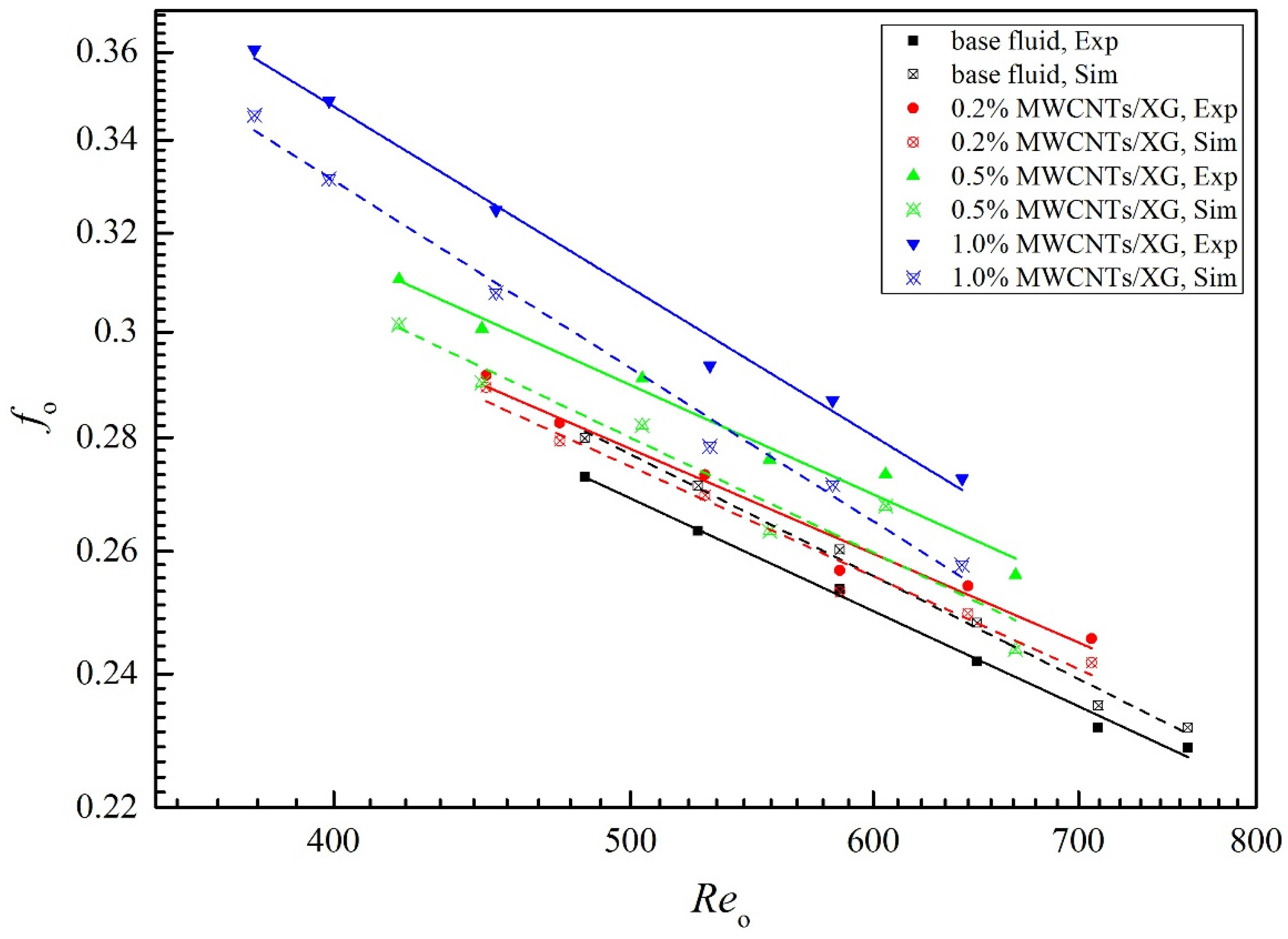
4.3. Nusselt Number and Friction Factor
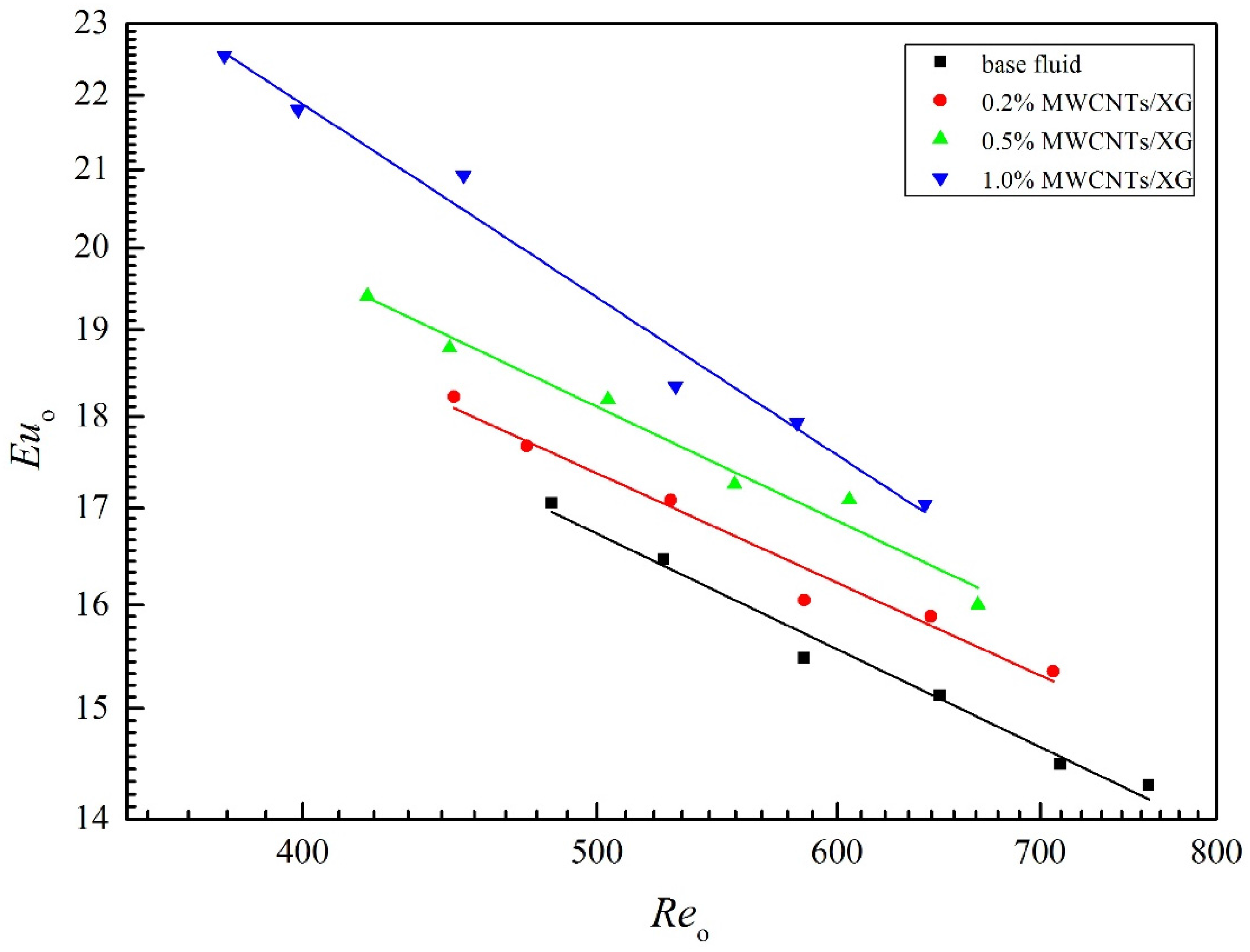
4.4. Euler Number
4.5. Correlations
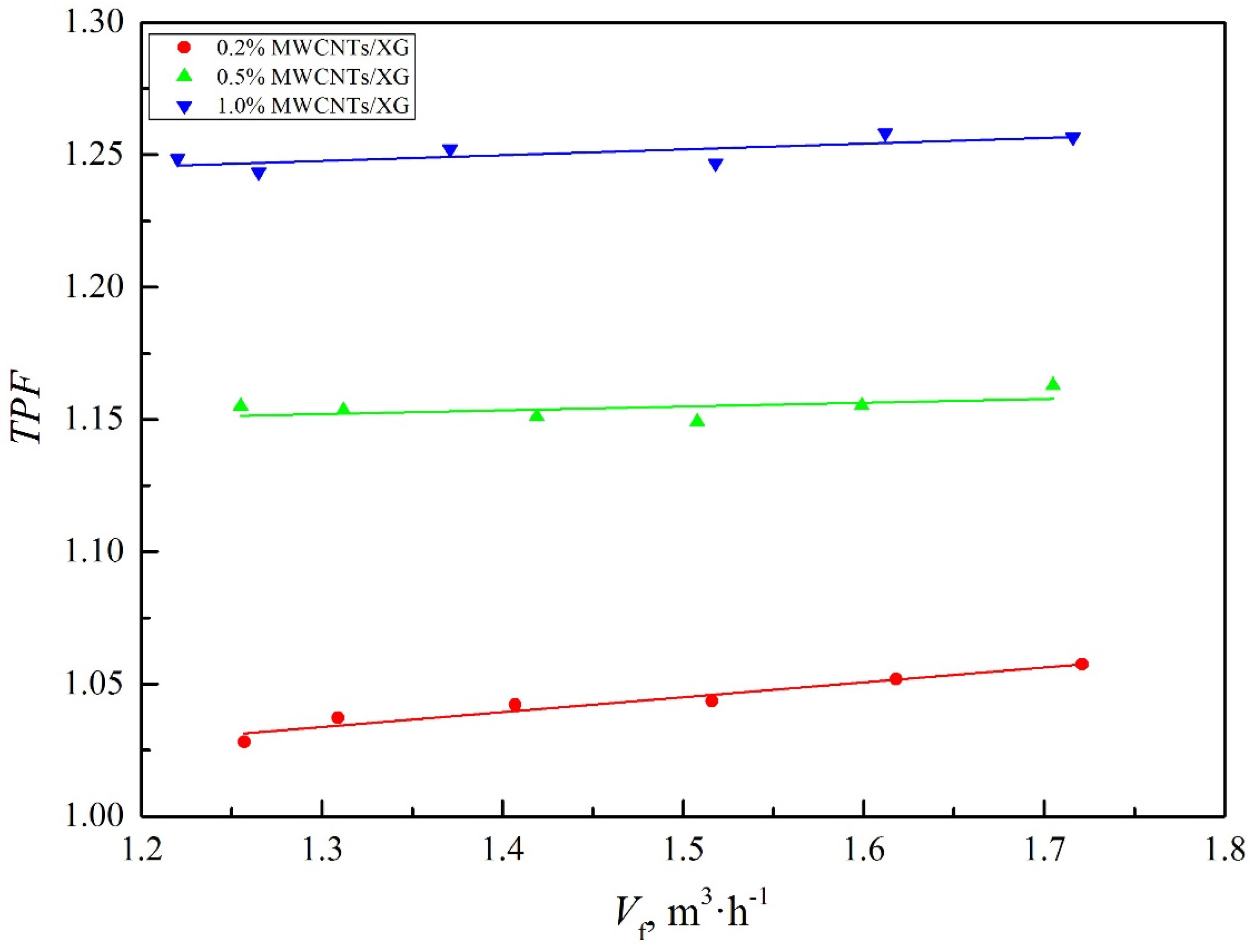
4.6. Comprehensive Performance
5. Conclusions
- (1)
- Experiment results have proven that the accuracy of numerical simulation model is satisfactory. Good agreements exist between experimental and numerical data. The single-phase flow model can simulate the flow and heat transfer characteristic of non-Newtonian nanofluids at low concentration.
- (2)
- The heat transfer is significantly enhanced by adding nanoparticle compared to base fluid. The overall and shell-side heat transfer coefficients of nanofluids are higher than those of base fluid at the same Reynolds number. The enhancement in heat transfer coefficient increases with the increasing in the weight fraction of MWCNTs.
- (3)
- The Nuo, fo, Euo increase with the increasing in the weight fraction of nanoparticle at the same Reynolds number. In the whole range of volume flow rate, the TPF of nanofluids are all higher than 1.0. The changes in flow and heat characteristic of nanofluids can be attributed to the enhanced thermal conductivities and viscosities.
- (4)
- Correlations for predicting the shell-side Nusselt number, friction factor and Euler number of non-Newtonian nanofluids in the helically baffled heat exchanger with elliptic tubes were obtained based on experimental results, and fitted the data very well.
Acknowledgments
Author Contributions
Conflicts of Interest
| Nomenclature | |
| a, b, c | coefficients in corrections |
| A | surface area (m2) |
| B | baffle spacing (m) |
| C1, C2 | coefficients in k-ε turbulence model |
| Eu | Euler number |
| f | friction factor |
| FT | correction factor |
| j | j-factor |
| k | turbulent fluctuation kinetic energy (m2·s−2) |
| K | consistency index (Pa·sn) |
| l | length of tube (m) |
| M | mass flow rate (kg·s−1) |
| n | power law index |
| Nu | Nusselt number |
| P | pressure (Pa) |
| Pr | Prandtl number |
| r | effect variable |
| R | thermal resistance (m2·K−1·W−1) |
| Re | Reynolds number |
| T | temperature (K) |
| TPF | thermal performance factor |
| u, v, w | velocity (m·s−1) |
| Uo | overall heat transfer coefficient based on Ao (W·m−2·K−1) |
| V | volume flow rate (m3·s−1) |
| xn | effect variable |
| x, y, z | coordinate (mm) |
| y+ | dimensionless distance from the wall |
| Greek Symbol | |
| ρ | density (kg·m−3) |
| η | dynamic viscosity (Pa·s) |
| ν | kinematic viscosity (m2·s−1) |
| λ | thermal conductivity (W·m−1·K−1) |
| τ | turbulent kinematic viscosity (m2·s−1) |
| ε | turbulent kinetic energy dissipation rate (m2·s−3) |
| δ | wall thickness (mm) |
| σk | Prandtl number for k |
| σε | Prandtl number for ε |
| γ | shear rate (s−1) |
| ζ | heat balance deviation |
| ϕ | weight fraction of nanoparticle |
| Δ | difference |
| Subscripts | |
| bf | base fluid |
| f | non-Newtonian fluid |
| i | inside |
| in | inlet |
| max | maximum |
| nf | nanofluid |
| o | outside |
| wall | tube wall |
References
- Kasaeian, A.; Eshghi, A.T.; Sameti, M. A review on the applications of nanofluids in solar energy systems. Int. J. Heat Mass Transf. 2015, 43, 584–598. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; Seyf, H.R.; Zhang, Y. Performance augmentation and optimization of aluminum oxide-water nanofluid flow in a two-fluid microchannel heat exchanger. J. Heat Transf. Trans. ASME 2014, 136, 228–240. [Google Scholar] [CrossRef]
- Ghanbarpour, M.; Haghigi, E.B.; Khodabandeh, R. Thermal properties and rheological behavior of water based Al2O3 nanofluid as a heat transfer fluid. Exp. Therm. Fluid Sci. 2014, 53, 227–235. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Al-Nimr, M.A.; Pop, I.; Sahin, A.Z. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Hussein, A.M.; Sharma, K.V.; Bakar, R.A.; Kadirgama, K. A review of forced convection heat transfer enhancement and hydrodynamic characteristics of a nanofluid. Renew. Sustain. Energy Rev. 2014, 29, 734–743. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles, International mechanical engineering congress and exhibition. ASME 1995, 231, 12–17. [Google Scholar]
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with snusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zia, Q.M.Z.; Ellahi, R. Influence of induced magnetic field on free convection of nanofluid considering Koo-Kleinstreuer-Li (KKL) correlation. Appl. Sci. 2016, 6, 324. [Google Scholar] [CrossRef]
- Rahman, S.U. Simultaneous effects of nanoparticles and slip on Jeffrey fluid through tapered artery with mild stenosis. J. Mol. Liq. 2016, 218, 484–493. [Google Scholar] [CrossRef]
- Akbarzadeh, M. A sensitivity analysis on thermal and pumping power for the flow of nanofluid inside a wavy channel. J. Mol. Liq. 2016, 220, 1–13. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu–H2O mathContainer loading mathjax, nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Rashidi, S. Study of stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium. J. Magn. Magn. Mater. 2015, 378, 128–137. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Kandelousi, M.S.; Ellahi, R. Simulation of ferrofluid flow for magnetic drug targeting using the lattice boltzmann method. Z. Neuropsychol. A 2015, 70, 115–124. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel. J. Magn. Magn. Mater. 2015, 381, 405–415. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Aggregation effects on water base Al2O3 nanofluid over permeable wedge in mixed convection. Asia Pac. J. Chem. Eng. 2016, 76, 3825–3835. [Google Scholar] [CrossRef]
- Mamourian, M. Optimization of mixed convection heat transfer with entropy generation in a wavy surface square lid-driven cavity by means of Taguchi approach. Int. J. Heat Mass Transf. 2016, 102, 544–554. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hassan, M. Particle shape effects on Marangoni convection boundary layer flow of a nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2160–2174. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: London, UK, 2008. [Google Scholar]
- Tian, J.; He, Z.B.; Xu, T.; Fang, X.M.; Zhang, Z.G. Rheological Property and Thermal Conductivity of Multi-walled Carbon Nanotubes-dispersed Non-Newtonian Nanofluids Based on an Aqueous Solution of Carboxymethyl Cellulose. Exp. Heat Transf. 2015. [Google Scholar] [CrossRef]
- Hojjat, M.; Etemad, S.G.; Bagheri, R.; Thibault, J. Turbulent forced convection heat transfer of non-newtonian nanofluids. Exp. Therm. Fluid Sci. 2011, 35, 1351–1356. [Google Scholar] [CrossRef]
- Kral, D.; Stehlik, P.; Van Der Ploeg, H.; Master, B.I. Helical baffles in shell-and-tube heat exchangers, Part I: Experimental verification. Heat Transf. Eng. 1996, 17, 93–101. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Li, Q.X.; Xu, T.; Fang, X.M.; Gao, X.N. Condensation heat transfer characteristics of zeotropic refrigerant mixture R407C on single, three-row petal-shaped finned tubes and helically baffled condenser. Appl. Therm. Eng. 2012, 39, 63–69. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Ma, D.B.; Fang, X.M.; Gao, X.N. Experimental and numerical heat transfer in a helically baffled heat exchanger combined with one three-dimensional finned tube. Chem. Eng. Process. 2008, 47, 1738–1743. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Wu, C.S.; Fang, X.M.; Gao, X.N.; Wang, Z.Y. Experimental study of shell-side heat transfer coefficient and pressure drop for an integrally helical baffled heat exchanger combined with different enhanced tubes. Ind. Eng. Chem. Res. 2009, 48, 4040–4044. [Google Scholar] [CrossRef]
- He, Z.B.; Fang, X.M.; Zhang, Z.G.; Gao, X.N. Numerical investigation on performance comparison of non-Newtonian fluid flow in vertical heat exchangers combined helical baffle with elliptic and circular tubes. Appl. Therm. Eng. 2016, 100, 84–97. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing uncertainties in single-sample experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- F. Inc. FLUENT 6.3 User’s Guide; F. Inc.: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Dong, C.; Chen, Y.P.; Wu, J.F. Flow and heat transfer performances of helical baffle heat exchangers with different baffle configurations. Appl. Therm. Eng. 2015, 80, 328–338. [Google Scholar] [CrossRef]
- Tao, W.Q. Numerical Heat Transfer; Xi’an Jiaotong University Press: Xi’an, China, 2001. [Google Scholar]
- Xu, K.; Bo, R.; Meng, H. A thermal performance factor for evaluation of active engine cooling with asymmetric heating. Appl. Therm. Eng. 2014, 73, 351–356. [Google Scholar] [CrossRef]


| Fluid | Correlations (298.15 K < T < 338.15 K) | ||||
|---|---|---|---|---|---|
| K (m2·sn) | n | λ (W·m−1·K−1) | ρ (kg·m−3) | cp (kJ·kg−1·K−1) | |
| Base fluid | −0.0131T + 4.6322 (R2 = 0.999) | 0.0043T − 0.9469 (R2 = 0.988) | 0.0043T − 0.6265 (R2 = 0.979) | −0.0073T2 + 4.2840T + 382.8 (R2 = 0.991) | −2.7149 × 10 − 5T2 − 0.01189T + 4.8763 (R2 = 0.996) |
| 0.2 wt % MWCNTs/XG | −0.0124T + 4.4211 (R2 = 0.999) | 0.0040T − 0.8517 (R2 = 0.989) | 0.0035T − 0.4168 (R2 = 0.987) | −0.0067T2 + 3.8902T + 451.2 (R2 = 0.991) | −5.4948 × 10 − 5T2 + 0.04071T − 3.5919 (R2 = 0.991) |
| 0.5 wt % MWCNTs/XG | −0.0111T + 4.1513 (R2 = 0.992) | 0.0025T − 0.3962 (R2 = 0.982) | 0.0026T − 0.1468 (R2 = 0.995) | −0.0052T2 + 2.9004T + 611.5 (R2 = 0.990) | −3.9137 × 10 − 5T2 + 0.03135T − 2.3183 (R2 = 0.998) |
| 1.0 wt % MWCNTs/XG | −0.0130T + 4.8356 (R2 = 0.996) | 0.0021T − 0.3016 (R2= 0.998) | 0.0025T − 0.1473 (R2 = 0.988) | −0.0016T2 + 0.6362T + 965.2 (R2 = 0.987) | 6.9542 × 10 − 5T2 − 0.04154T + 9.6727 (R2 = 0.972) |
| Non-Dimensional Number | Fluid | Average Deviation |
|---|---|---|
| Nuo | Base fluid | 5.11% |
| 0.2 wt % MWCNTs/XG | 5.63% | |
| 0.5 wt % MWCNTs/XG | 1.17% | |
| 1.0 wt % MWCNTs/XG | −1.14% | |
| fo | Base fluid | 0.25% |
| 0.2 wt % MWCNTs/XG | 0.60% | |
| 0.5 wt % MWCNTs/XG | −0.62% | |
| 1.0 wt % MWCNTs/XG | −5.06% |
| Correlation | a | b | c | Maximum Deviation |
|---|---|---|---|---|
| Equation (15) | 0.0284 | 0.8692 | 0.3081 | 9.62% |
| Equation (16) | 4.8456 | −0.4650 | 0.4484 | 4.04% |
| Equation (17) | 310.17 | −0.4694 | 0.4364 | 4.66% |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, Z.; He, Z.; Xu, T.; Fang, X.; Gao, X.; Zhang, Z. Experimental and Numerical Investigation on Non-Newtonian Nanofluids Flowing in Shell Side of Helical Baffled Heat Exchanger Combined with Elliptic Tubes. Appl. Sci. 2017, 7, 48. https://doi.org/10.3390/app7010048
Ling Z, He Z, Xu T, Fang X, Gao X, Zhang Z. Experimental and Numerical Investigation on Non-Newtonian Nanofluids Flowing in Shell Side of Helical Baffled Heat Exchanger Combined with Elliptic Tubes. Applied Sciences. 2017; 7(1):48. https://doi.org/10.3390/app7010048
Chicago/Turabian StyleLing, Ziye, Zhenbin He, Tao Xu, Xiaoming Fang, Xuenong Gao, and Zhengguo Zhang. 2017. "Experimental and Numerical Investigation on Non-Newtonian Nanofluids Flowing in Shell Side of Helical Baffled Heat Exchanger Combined with Elliptic Tubes" Applied Sciences 7, no. 1: 48. https://doi.org/10.3390/app7010048
APA StyleLing, Z., He, Z., Xu, T., Fang, X., Gao, X., & Zhang, Z. (2017). Experimental and Numerical Investigation on Non-Newtonian Nanofluids Flowing in Shell Side of Helical Baffled Heat Exchanger Combined with Elliptic Tubes. Applied Sciences, 7(1), 48. https://doi.org/10.3390/app7010048







