All About Audio Equalization: Solutions and Frontiers
Abstract
:1. Introduction
2. History of Audio Equalization
3. Parametric Equalizers
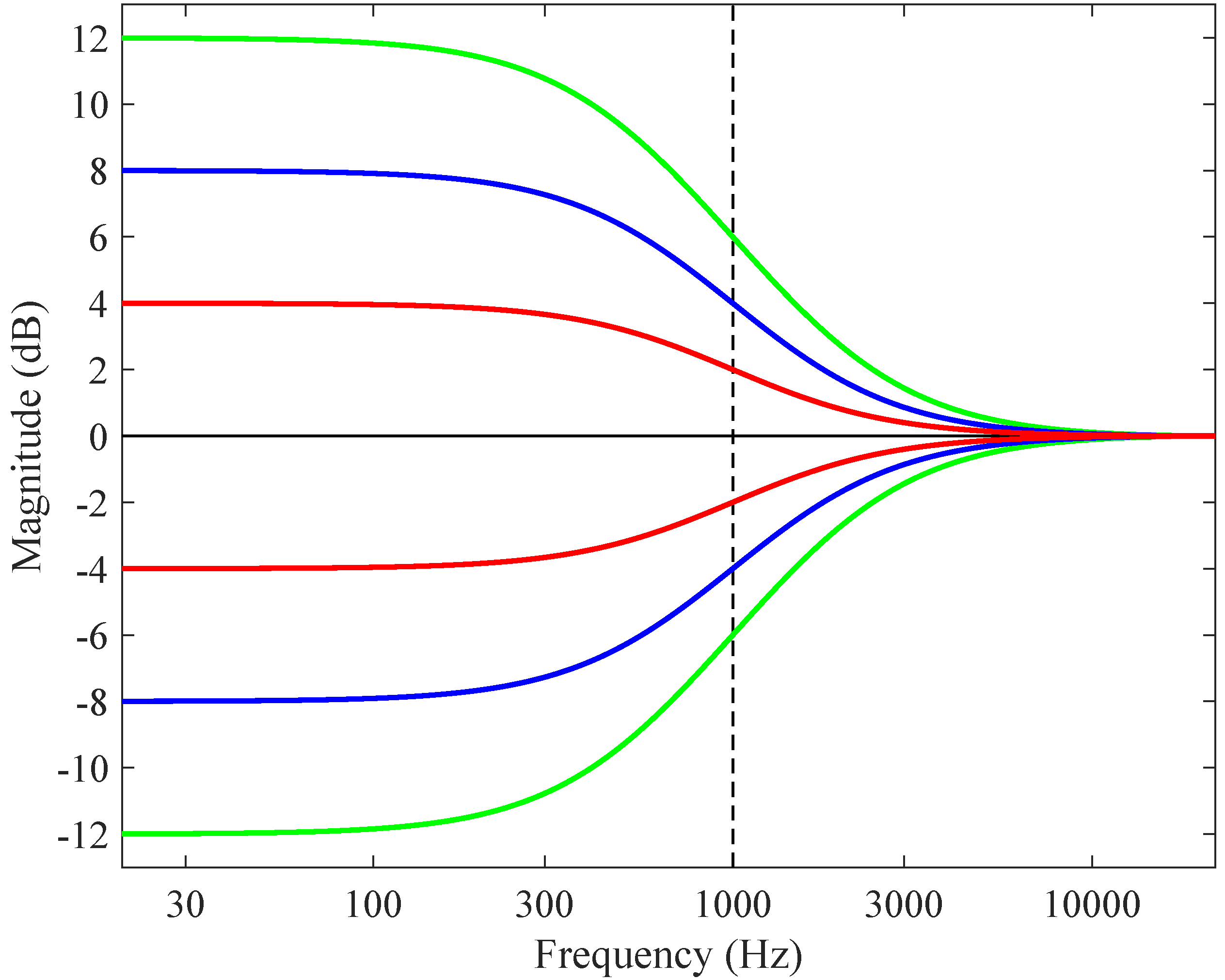
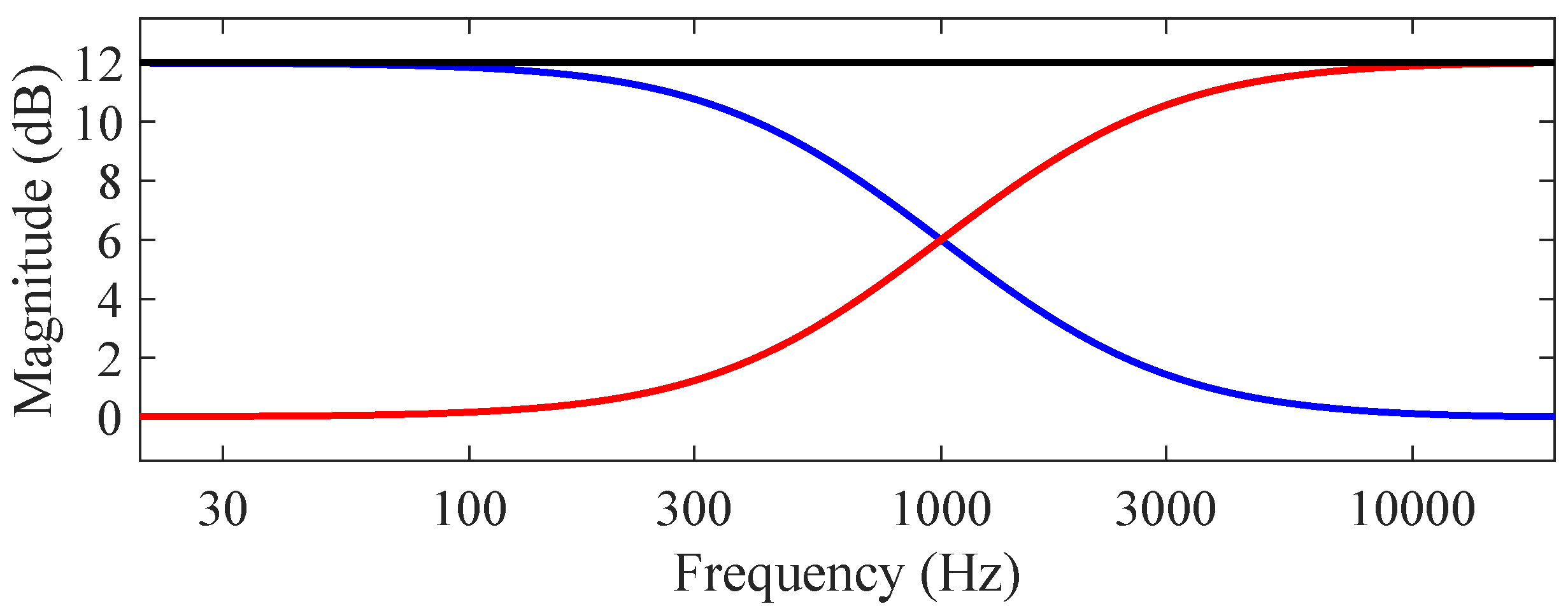
3.1. First Order Shelving Filters
3.2. Second Order Shelving Filters
3.3. Second Order Peaking and Notch Filters
3.4. High Order Filter Designs
3.5. FIR Shelving Filter Designs
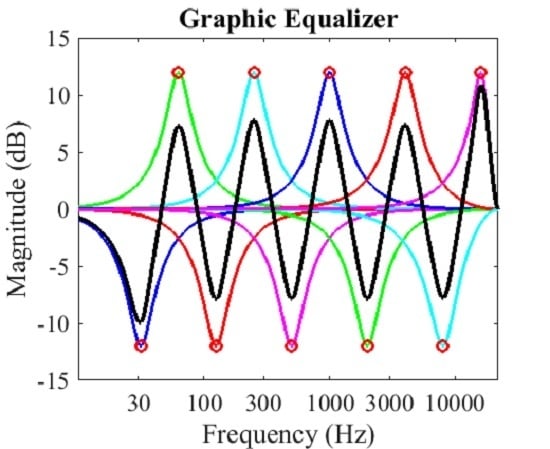
4. Graphic Equalizers
4.1. Bands in Graphic Equalizers
4.2. Cascade Graphic Equalizers
4.3. Parallel Graphic Equalizers
4.4. FIR Graphic Equalizers
4.4.1. Graphic Equalization Using Fast Convolution
4.4.2. Parallel and Multirate FIR Graphic Equalizers
5. Other Equalization Filter Designs
5.1. Matched EQ and Optimal Design Techniques
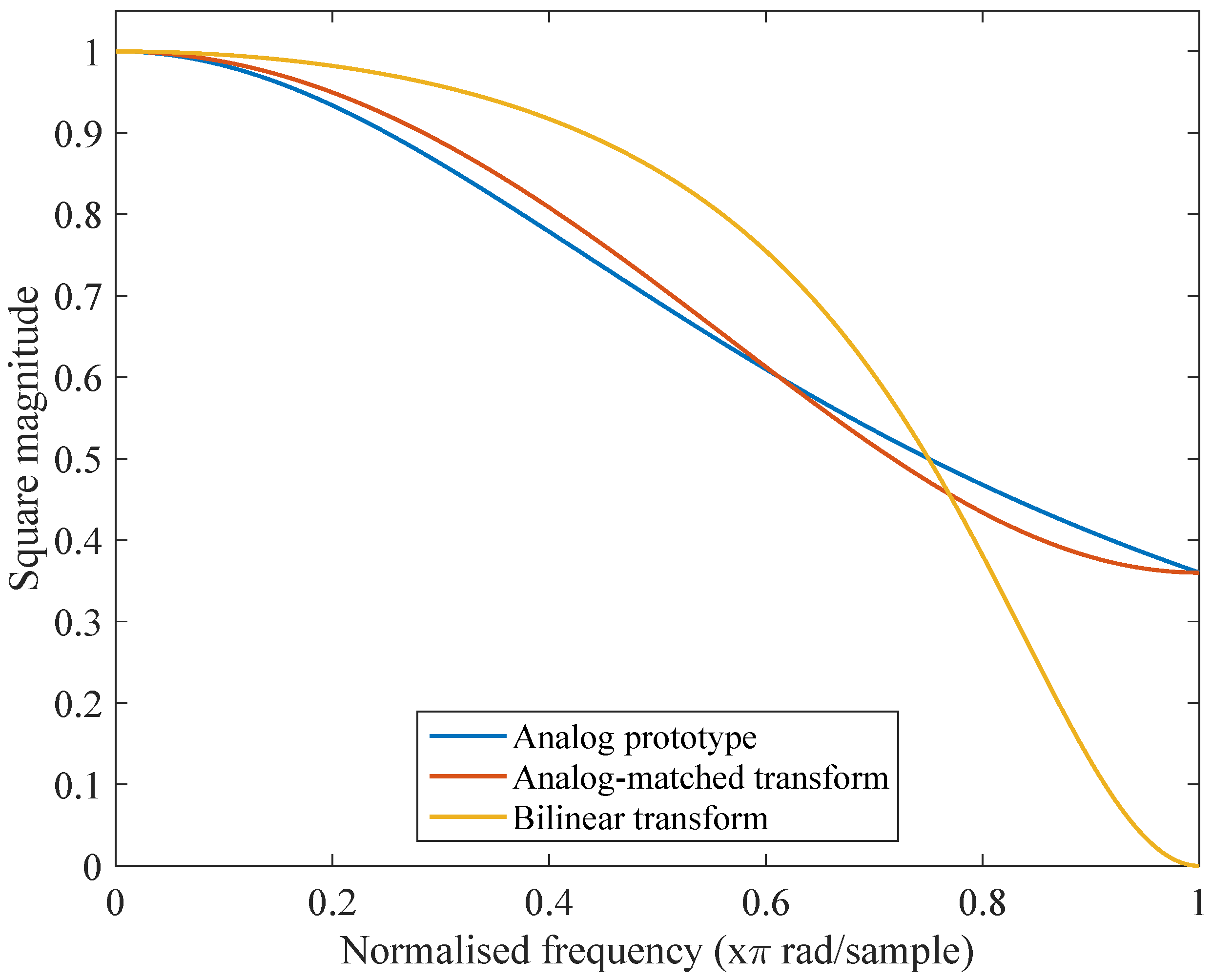
5.2. Digital Equalizer Design Matching Analog Prototypes
5.3. Linear Phase IIR Filters
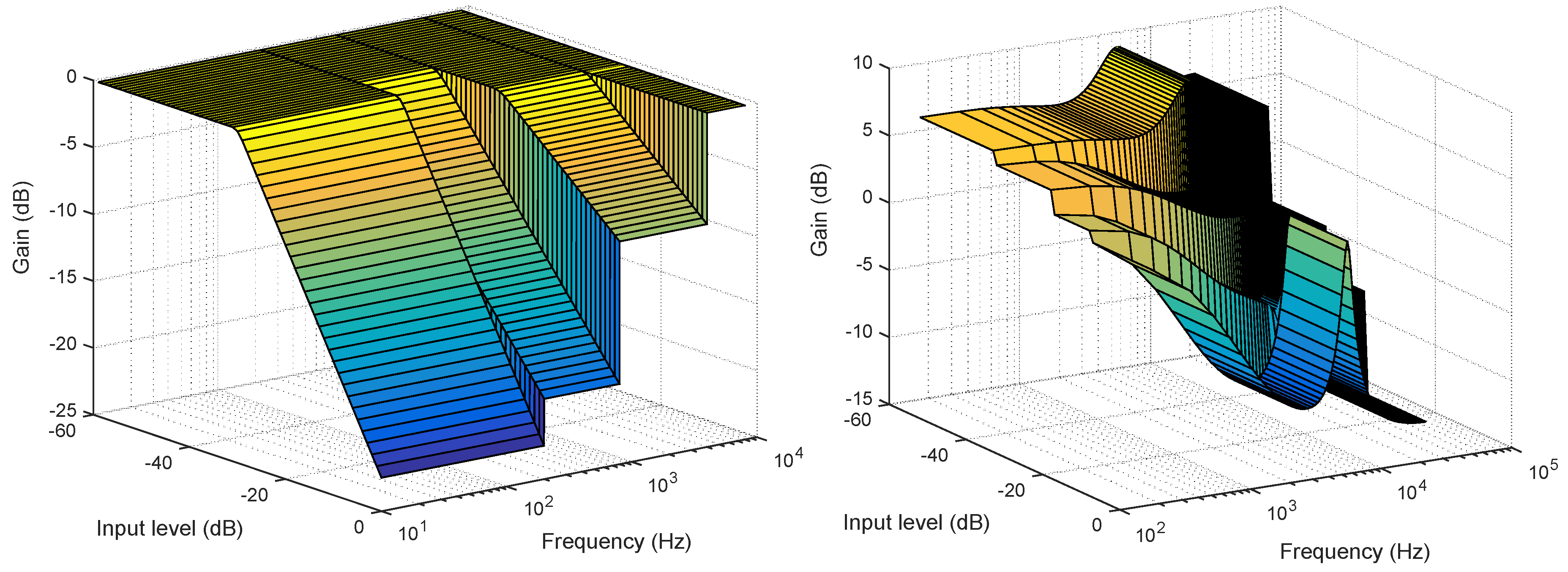
5.4. Dynamic Equalization
6. Sound Reproduction Applications
6.1. Tone Control
6.2. Loudspeaker Equalization
6.3. Room Equalization
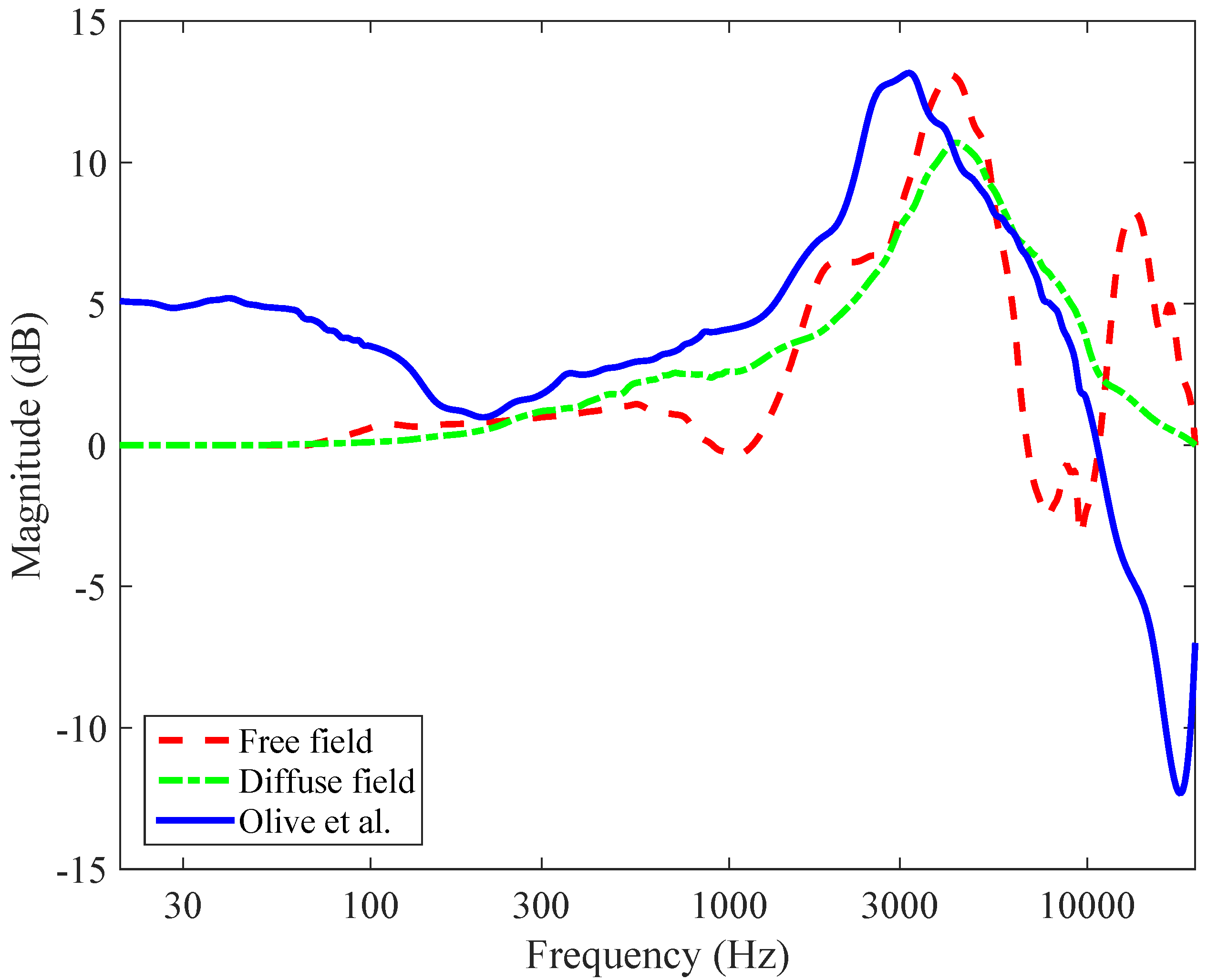
6.4. Headphone Equalization
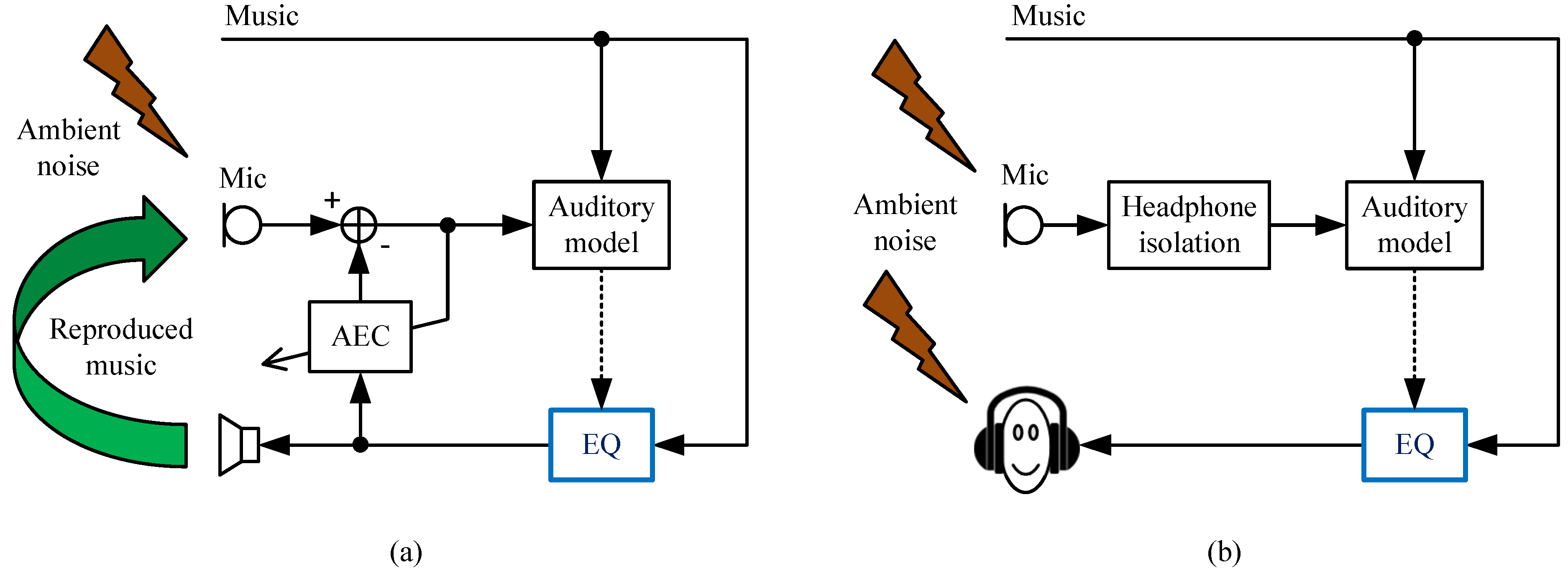
6.5. Equalization to Combat Ambient Noise
7. Audio Content Creation
7.1. Adaptive and Intuitive Interfaces
7.2. Autonomous and Intelligent Systems for Equalization
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
- Matlab code demonstrating a parametric equalizer comprised of a first order low shelving filter, second order peaking/notch filter and first order high shelving filter, see Section 3, especially Section 3.1 and Section 3.3;
- Matlab code for second order low and high shelving filter, see Section 3.2.
- Matlab code for generating a wide variety of high order filter designs of arbitrary order and for differing definitions of the gain at crossover frequencies, see Section 3.4;
- Matlab code for cascade and parallel graphic equalizer design, see Section 4;
- Matlab code for a lowpass filter matching the analog frequency response, see Section 5.2;
- Matlab code for illustrating dynamic equalization and multiband dynamic range compression, see Section 5.4;
- A Powerpoint file containing original versions of many of the figures; and
- Any additions or errata since initial publication.
References
- Bohn, D.A. Operator adjustable equalizers: An overview. In Proceedings of the Audio Engineering Society 6th International Conference on Sound Reinforcement, Nashville, Tennessee, 5–8 May 1988; pp. 369–381.
- Orfanidis, S.J. IIR digital filter design (Chapter 11). In Introduction to Signal Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1996; pp. 573–643. [Google Scholar]
- Zölzer, U. Equalizers (Chapter 5). In Digital Audio Signal Processing, 2nd ed.; Wiley: Chichester, UK, 2008; pp. 115–190. [Google Scholar]
- Reiss, J.D.; McPherson, A. Filter effects (Chapter 4). In Audio Effects: Theory, Implementation and Application; CRC Press: Boca Raton, FL, USA, 2015; pp. 89–124. [Google Scholar]
- Lundheim, L. On Shannon and Shannon’s formula. Telektronikk 2002, 98, 20–29. [Google Scholar]
- Campbell, G.A. Physical theory of the electric wave-filter. Bell Syst. Tech. J. 1922, 1, 1–32. [Google Scholar] [CrossRef]
- Zobel, O.J. Theory and design of uniform and composite electric wave-filters. Bell Syst. Tech. J. 1923, 2, 1–46. [Google Scholar] [CrossRef]
- Bauer, B. A century of microphones. Proc. IRE 1962, 50, 719–729. [Google Scholar] [CrossRef]
- Williamson, D.T.N. Design of tone controls and auxiliary gramophone circuits. Wireless World 1949, 55, 20–29. [Google Scholar]
- Baxandall, P.J. Negative-feedback tone control. Wireless World 1952, 58, 402–405. [Google Scholar]
- Stanton, W.O. Magnetic pickups and proper playback equalization. J. Audio. Eng. Soc. 1955, 3, 202–205. [Google Scholar]
- Hoff, P. Tape (NAB) equalization. In Consumer Electronics for Engineers; Cambridge University Press: Cambridge, UK, 2008; pp. 131–135. [Google Scholar]
- Rudmose, W. Equalization of sound systems. Noise Control 1958, 24, 82–85. [Google Scholar] [CrossRef]
- Boner, C.P.; Boner, C.R. Minimizing feedback in sound systems and room-ring modes with passive networks. J. Acoust. Soc. Am. 1965, 37, 131–135. [Google Scholar] [CrossRef]
- Boner, C.P.; Boner, C.R. Behavior of sound system response immediately below feedback. J. Audio. Eng. Soc. 1966, 14, 200–203. [Google Scholar]
- Conner, W.K. Theoretical and practical considerations in the equalization of sound systems. J. Audio Eng. Soc. 1967, 15, 194–198. [Google Scholar]
- Flickinger, D. Amplifier System Utilizing Regenerative and Degenerative Feedback to Shape the Frequency Response. U.S. Patent #3,752,928, 14 August 1973. [Google Scholar]
- Massenburg, G. Parametric equalization. In Proceedings of the 42nd Convention of the Audio Engineering Society, Los Angeles, CA, USA, 2–5 May 1972.
- McNally, G.W. Microprocessor mixing and processing of digital audio signals. J. Audio Eng. Soc. 1979, 27, 793–803. [Google Scholar]
- Guarino, C.R. Audio equalization using digital signal processing. In Proceedings of the 63rd Convention of the Audio Engineering Society, Los Angeles, CA, USA, 15–18 May 1979.
- Hirata, Y. Digitalization of conventional analog filters for recording use. J. Audio Eng. Soc. 1981, 29, 333–337. [Google Scholar]
- Berkovitz, R. Digital equalization of audio signals. In Proceedings of the Audio Engineering Society 1st International Conference on Digital Audio, Rye, NY, USA, 3–6 June 1982.
- White, S.A. Design of a digital biquadratic peaking or notch filter for digital audio equalization. J. Audio Eng. Soc. 1986, 34, 479–483. [Google Scholar]
- Regalia, P.; Mitra, S. Tunable digital frequency response equalization filters. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 118–120. [Google Scholar] [CrossRef]
- Brandt, M.; Bitzer, J. Hum removal filters: Overview and analysis. In Proceedings of the 132nd Convention of the Audio Engineering Society, Budapest, Hungary, 26–29 April 2012.
- Van Waterschoot, T.; Moonen, M. Fifty years of acoustic feedback control: State of the art and future challenges. Proc. IEEE 2011, 99, 288–327. [Google Scholar] [CrossRef]
- Harris, f.; Brooking, E. A versatile parametric filter using an imbedded all-pass sub-filter to independently adjust bandwidth, center frequency, and boost or cut. In Proceedings of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–28 October 1992; pp. 269–273.
- Moorer, J.A. The manifold joys of conformal mapping: Applications to digital filtering in the studio. J. Audio Eng. Soc. 1983, 31, 826–841. [Google Scholar]
- Constantinides, A. Spectral transformations for digital filters. Proc. IEE 1970, 117, 1585–1590. [Google Scholar] [CrossRef]
- Fontana, F.; Karjalainen, M. A digital bandpass/bandstop complementary equalization filter with independent tuning characteristics. IEEE Signal Process. Lett. 2003, 10, 119–122. [Google Scholar] [CrossRef]
- Berners, D.P.; Abel, J.S. Discrete-time shelf filter design for analog modeling. In Proceedings of the 115th Convention of the Audio Engineering Society, New York, NY, USA, 10–13 October 2003.
- Keiler, F.; Zölzer, U. Parametric second- and fourth-order shelving filters for audio applications. In Proceedings of the IEEE Workshop on Multimedia Signal Processing, Siena, Italy, 29 September–1 October 2004; pp. 231–234.
- Christensen, K.B. A generalization of the biquadratic parametric equalizer. In Proceedings of the 115th Convention of the Audio Engineering Society, New York, NY, USA, 10–13 October 2003.
- Jot, J.M. Proportional parametric equalizers—Application to digital reverberation and environmental audio processing. In Proceedings of the 139th Convention of the Audio Engineering Society, New York, NY, USA, 29 September–1 October 2015.
- Clark, R.J.; Ifeachor, E.C.; Rogers, G.M.; Van Eetvelt, P.W. Techniques for generating digital equalizer coefficients. J. Audio Eng. Soc. 2000, 48, 281–298. [Google Scholar]
- Orfanidis, S.J. Digital parametric equalizer design with prescribed Nyquist-frequency gain. J. Audio Eng. Soc. 1997, 45, 444–455. [Google Scholar]
- Bristow-Johnson, R. The equivalence of various methods of computing biquad coefficients for audio parametric equalizers. In Proceedings of the 97th Convention of the Audio Engineering Society, San Francisco, CA, USA, 10–13 November 1994.
- Reiss, J.D. Design of audio parametric equalizer filters directly in the digital domain. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 1843–1848. [Google Scholar] [CrossRef]
- Orfanidis, S.J. High-order digital parametric equalizer design. J. Audio Eng. Soc. 2005, 53, 1026–1046. [Google Scholar]
- Holters, M.; Zölzer, U. Parametric higher-order shelving filters. In Proceedings of the European Signal Process. Conference (EUSIPCO), Florence, Italy, 4–8 September 2006; pp. 1–4.
- Fernandez-Vazquez, A.; Rosas-Romero, R.; Rodriguez-Asomoza, J. A new method for designing flat shelving and peaking filters based on allpass filters. In Proceedings of the International Conference on Electronics, Communications and Computers (CONIELECOMP-07), Cholula, Puebla, Mexico, 26–28 February 2007.
- Särkkä, S.; Huovilainen, A. Accurate discretization of analog audio filters with application to parametric equalizer design. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2486–2493. [Google Scholar] [CrossRef]
- Lim, Y.C. Linear-phase digital audio tone control. J. Audio Eng. Soc. 1987, 35, 38–40. [Google Scholar]
- Lian, Y.; Lim, Y.C. Linear-phase digital audio tone control using multiplication-free FIR filter. J. Audio Eng. Soc. 1993, 41, 791–794. [Google Scholar]
- Yang, R.H. Linear-phase digital audio tone control using dual RRS structures. Electron. Lett. 1989, 25, 360–362. [Google Scholar] [CrossRef]
- Vieira, J.M.N.; Ferreira, A.J.S. Digital tone control. In Proceedings of the 98th Convention of the Audio Engineering Society, Paris, France, 25–28 February 1995.
- Greiner, R.A.; Schoessow, M. Design aspects of graphic equalizers. J. Audio Eng. Soc. 1983, 31, 394–407. [Google Scholar]
- Takahashi, S.; Kameda, H.; Tanaka, Y.; Miyazaki, H.; Chikashige, T.; Furukawa, M. Graphic equalizer with microprocessor. J. Audio Eng. Soc. 1983, 31, 25–28. [Google Scholar]
- Kontro, J.; Koski, A.; Sjöberg, J.; Väänänen, M. Digital car audio system. IEEE Trans. Consum. Electron. 1993, 35, 514–521. [Google Scholar] [CrossRef]
- Kim, H.G.; Cho, J.M. Car audio equalizer system using music classification and loudness compensation. In Proceedings of the International Conference on ICT Convergence (ICTC), Seoul, Korea, 28–30 September 2011; pp. 553–558.
- Abel, J.S.; Berners, D.P. Filter design using second-order peaking and shelving sections. In Proceedings of the International Computer Music Conference, Coral Gables, FL, USA, 1–6 November 2004.
- Holters, M.; Zölzer, U. Graphic equalizer design using higher-order recursive filters. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Montreal, QC, Canada, 18–20 September 2006; pp. 37–40.
- Rämö, J.; Välimäki, V. Optimizing a high-order graphic equalizer for audio processing. IEEE Signal Process. Lett. 2014, 21, 301–305. [Google Scholar] [CrossRef]
- Motorola Inc. Digital stereo 10-band graphic equalizer using the DSP56001. Appl. Note 1988, APR2/D. [Google Scholar]
- Tassart, S. Graphical equalization using interpolated filter banks. J. Audio Eng. Soc. 2013, 61, 263–279. [Google Scholar]
- Rämö, J.; Välimäki, V.; Bank, B. High-precision parallel graphic equalizer. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1894–1904. [Google Scholar] [CrossRef]
- Adams, R.W. An automatic equalizer/analyzer. In Proceedings of the 67th Convention of the Audio Engineering Society, New York, NY, USA, 31 October–3 November 1980.
- Erne, M.; Heidelberger, C. Design of a DSP-based 27 band digital equalizer. In Proceedings of the 90th Convention of the Audio Engineering Society, Paris, France, 19–22 February 1991.
- Azizi, S.A. A new concept of interference compensation for parametric and graphic equalizer banks. In Proceedings of the 111th Convention of the Audio Engineering Society, New York, NY, USA, 30 November–3 December 2001.
- Miller, R. Equalization methods with true response using discrete filters. In Proceedings of the 116th Convention of the Audio Engineering Society, Berlin, Germany, 8–11 May 2004.
- ISO. ISO 266, Acoustics—Preferred frequencies for measurements. 1975. [Google Scholar]
- Bohn, D.A. Constant-Q graphic equalizers. J. Audio Eng. Soc. 1986, 34, 611–626. [Google Scholar]
- Oliver, R.J.; Jot, J.M. Efficient multi-band digital audio graphic equalizer with accurate frequency response control. In Proceedings of the 139th Convention of the Audio Engineering Society, New York, NY, USA, 29 September–1 October 2015.
- Lee, Y.; Kim, R.; Cho, G.; Choi, S.J. An adjusted-Q digital graphic equalizer employing opposite filters. In Lect. Notes Comput. Sci.; Springer-Verlag: London, UK, 2005; Volume 3768, pp. 981–992. [Google Scholar]
- McGrath, D.; Baird, J.; Jackson, B. Raised cosine equalization utilizing log scale filter synthesis. In Proceedings of the 117th Convention of the Audio Engineering Society, San Francisco, CA, USA, 28–31 October 2004.
- Chen, Z.; Lin, Y.; Geng, G.; Yin, J. Optimal design of digital audio parametric equalizer. J. Inform. Comput. Sci. 2014, 11, 57–66. [Google Scholar] [CrossRef]
- Belloch, J.A.; Bank, B.; Savioja, L.; Gonzalez, A.; Välimäki, V. Multi-channel IIR filtering of audio signals using a GPU. In Proceedings of the IEEE International Conference Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6692–6696.
- Bank, B. Perceptually motivated audio equalization using fixed-pole parallel second-order filters. IEEE Signal Process. Lett. 2008, 15, 477–480. [Google Scholar] [CrossRef]
- Bank, B. Audio equalization with fixed-pole parallel filters: An efficient alternative to complex smoothing. J. Audio Eng. Soc. 2013, 61, 39–49. [Google Scholar]
- Belloch, J.A.; Välimäki, V. Efficient target response interpolation for a graphic equalizer. In Proceedings of the IEEE International Conference Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 564–568.
- Virgulti, M.; Cecchi, S.; Piazza, F. IIR filter approximation of an innovative digital audio equalizer. In Proceedings of the International Symposium on Image and Signal Processing and Analysis (ISPA), Trieste, Italy, 4–6 September 2013; pp. 410–415.
- Jensen, J.A. A new principle for an all-digital preamplifier and equalizer. J. Audio Eng. Soc. 1987, 35, 994–1003. [Google Scholar]
- Henriquez, J.A.; Riemer, T.E.; Trahan, R.E., Jr. A phase-linear audio equalizer: Design and implementation. J. Audio Eng. Soc. 1990, 38, 653–666. [Google Scholar]
- Principe, J.; Gugel, K.; Adkins, A.; Eatemadi, S. Multi-rate sampling digital audio equalizer. In Proceedings of the IEEE Southeastcon-91, Williamsburg, VA, USA, 7–10 April 1991; pp. 499–502.
- Waters, M.; Sandler, M.; Davies, A.C. Low-order FIR filters for audio equalization. In Proceedings of the 91st Convention of the Audio Engineering Society, New York, NY, USA, 4–8 October 1991.
- Slump, C.H.; van Asma, C.G.M.; Barels, J.K.P.; Brunink, W.J.A.; Drenth, F.B.; Pol, J.V.; Schouten, D.; Samsom, M.M.; Herrmann, O.E. Design and implementation of a linear-phase equalizer in digital audio signal processing. In Proceedings of the Workshop on VLSI Signal Processing, Napa Valley, CA, USA, 28–30 October 1992; pp. 297–306.
- Väänänen, R.; Hiipakka, J. Efficient audio equalization using multirate processing. J. Audio Eng. Soc. 2008, 56, 255–266. [Google Scholar]
- Mäkivirta, A.V. Loudspeaker design and performance evaluation. In Handbook of Signal Processing in Acoustics; Springer: New York, NY, USA, 2008; pp. 649–667. [Google Scholar]
- McGrath, D.S. A new approach to digital audio equalization. In Proceedings of the 97th Convention of the Audio Engineering Society, San Francisco, CA, USA, 10–13 November 1994.
- Kraght, P.H. A linear-phase digital equalizer with cubic-spline frequency response. J. Audio Eng. Soc. 1992, 40, 403–414. [Google Scholar]
- Oliver, R.J. Frequency-Warped Audio Equalizer. U.S. Patent #7,764,802 B2, 27 July 2010. [Google Scholar]
- Stockham, T.G., Jr. High-speed convolution and correlation. In Proceedings of the Spring Joint Computer Conference, New York, NY, USA, 26–28 April 1966; pp. 229–233.
- Schöpp, H.; Hetze, H. A linear-phase 512-band graphic equalizer using the fast-Fourier transform. In Proceedings of the 96th Convention of the Audio Engineering Society, Amsterdam, The Netherlands, 26 February–1 March 1994.
- Fernandes, G.F.P.; Martins, L.G.P.M.; Sousa, M.F.M.; Pinto, F.S.; Ferreira, A.J.S. Implementation of a new method to digital audio equalization. In Proceedings of the 106th Convention of the Audio Engineering Society, Munich, Germany, 8–11 May 1999.
- Ries, S.; Frieling, G. PC-based equalizer with variable gain and delay in 31 frequency bands. In Proceedings of the 108th Convention of the Audio Engineering Society, Paris, France, 19–22 February 2000.
- Kulp, B.D. Digital equalization using Fourier transform techniques. In Proceedings of the 85th Convention of the Audio Engineering Society, Los Angeles, CA, USA, 3–6 November 1988.
- Gardner, W.G. Efficient convolution without input-output delay. J. Audio Eng. Soc. 1995, 43, 127–136. [Google Scholar]
- Garcia, G. Optimal filter partition for efficient convolution with short input/output delay. In Proceedings of the 113th Convention of the Audio Engineering Society, Los Angeles, CA, USA, 5–8 October 2002.
- Välimäki, V.; Parker, J.D.; Savioja, L.; Smith, J.O.; Abel, J.S. Fifty years of artificial reverberation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1421–1448. [Google Scholar] [CrossRef]
- Wefers, F. Partitioned Convolution Algorithms for Real-Time Auralization. Ph.D. Thesis, RWTH Aachen University, Institute of Technical Acoustics, Aachen, Germany, 2014. [Google Scholar]
- Primavera, A.; Cecchi, S.; Romoli, L.; Peretti, P.; Piazza, F. A low latency implementation of a non-uniform partitioned convolution algorithm for room acoustic simulation. Signal, Image Video Process. 2014, 8, 985–994. [Google Scholar] [CrossRef]
- McGrath, D.S. An efficient 30-band graphic equalizer implementation for a low-cost DSP processor. In Proceedings of the 95th Convention of the Audio Engineering Society, New York, NY, USA, 7–10 October 1993.
- Vieira, J.M.N. Digital five-band equalizer with linear phase. In Proceedings of the 100th Convention of the Audio Engineering Society, Copenhagen, Denmark, 11–14 May 1996.
- Cecchi, S.; Palestini, L.; Moretti, E.; Piazza, F. A new approach to digital audio equalization. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 21–24 October 2007; pp. 62–65.
- Soewito, A.W. Least Square Digital Filter Design in the Frequency Domain. Ph.D. Thesis, Rice University, Houston, TX, USA, 1991. [Google Scholar]
- Smith, J.O. Recursive digital filter design (Appendix I). In Introduction to Digital Filters with Audio Applications, Second Printing; W3K Publishing: Palo Alto, CA, USA, 2008. [Google Scholar]
- Levi, E.C. Complex-curve fitting. IRE Trans. Automatic Control 1959, 4, 37–44. [Google Scholar] [CrossRef]
- Lee, R. Simple arbitrary IIRs. In Proceedings of the 125th Convention of the Audio Engineering Society, San Francisco, CA, USA, 2–5 October 2008.
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Friedlander, B.; Porat, B. The modified Yule-Walker method of ARMA spectral estimation. IEEE Trans. Aerospace Electron. Syst. 1984, 20, 158–173. [Google Scholar] [CrossRef]
- Jackson, L.B. Frequency-domain Steiglitz-McBride method for least-squares IIR filter design, ARMA modeling, and periodogram smoothing. IEEE Signal Process. Lett. 2008, 15, 49–52. [Google Scholar] [CrossRef]
- Vargas, R.; Burrus, C. The direct design of recursive or IIR digital filters. In Proceedings of the Third International Symposium on Communications, Control and Signal Processing, St. Julian’s, Malta, 12–14 March 2008; pp. 188–192.
- Oppenheim, A.V.; Johnson, D.H. Discrete representation of signals. Proc. IEEE 1972, 60, 681–691. [Google Scholar] [CrossRef]
- Härmä, A.; Karjalainen, M.; Savioja, L.; Välimäki, V.; Laine, U.K.; Huopaniemi, J. Frequency-warped signal processing for audio applications. J. Audio Eng. Soc. 2000, 48, 1011–1031. [Google Scholar]
- Strube, H.W. Linear prediction on a warped frequency scale. J. Acoust. Soc. Am. 1980, 68, 1071–1076. [Google Scholar] [CrossRef]
- Asavathiratham, C.; Beckmann, P.E.; Oppenheim, A.V. Frequency warping in the design and implementation of fixed-point audio equalizers. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 17–20 October 1999; pp. 55–58.
- Kautz, W. Transient synthesis in the time domain. Trans. IRE Prof. Group Circuit Theory 1954, 1, 29–39. [Google Scholar] [CrossRef]
- Karjalainen, M.; Paatero, T. Equalization of loudspeaker and room responses using Kautz filters: Direct least squares design. EURASIP J. Adv. Signal Process. 2007. [Google Scholar] [CrossRef]
- Backman, J. Digital realisation of phono (RIAA) equalisers. IEEE Trans. Consum. Electron. 1991, 37, 659–662. [Google Scholar] [CrossRef]
- Xia, J. A digital implementation of tape equalizers. IEEE Trans. Consum. Electron. 1994, 40, 114–118. [Google Scholar] [CrossRef]
- Massberg, M. Digital low-pass filter design with analog-matched magnitude response. In Proceedings of the 131st Convention of the Audio Engineering Society, New York, NY, USA, 20–23 October 2011.
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Al-Alaoui, M.A. Novel approach to analog-to-digital transforms. IEEE Trans. Circ. Syst. I: Regular Papers 2007, 54, 338–350. [Google Scholar] [CrossRef]
- Al-Alaoui, M.A. Improving the magnitude responses of digital filters for loudspeaker equalization. J. Audio Eng. Soc. 2010, 58, 1064–1082. [Google Scholar]
- Powell, S.R.; Chau, P.M. A technique for realizing linear phase IIR filters. IEEE Trans. Signal Process. 1991, 39, 2425–2435. [Google Scholar] [CrossRef]
- Willson, A.N.; Orchard, H.J. An improvement to the Powell and Chau linear phase IIR filters. IEEE Trans. Signal Process. 1994, 42, 2842–2848. [Google Scholar] [CrossRef]
- Kurosu, A.; Miyase, S.; Tomiyama, S.; Takebe, T. A technique to truncate IIR filter impulse response and its application to real-time implementation of linear-phase IIR filters. IEEE Trans. Signal Process. 2003, 51, 1284–1292. [Google Scholar] [CrossRef]
- Azizi, S.A. Efficient arbitrary sample rate conversion using zero phase IIR filters. In Proceedings of the 116th Convention of the Audio Engineering Society, Berlin, Germany, 8–11 May 2004.
- Mouffak, A.; Belbachir, M.F. Noncausal forward/backward two-pass IIR digital filters in real time. Turkish J. Electr. Eng. Comp. Sci. 2012, 20, 769–789. [Google Scholar]
- Laakso, T.I.; Välimäki, V. Energy-based effective length of the impulse response of a recursive filter. IEEE Trans. Instr. Meas. 1999, 48, 7–17. [Google Scholar] [CrossRef]
- Giannoulis, D.; Massberg, M.; Reiss, J.D. Digital dynamic range compressor design—A tutorial and analysis. J. Audio Eng. Soc. 2012, 60, 399–408. [Google Scholar]
- Pestana, P.D.; Reiss, J.D. Intelligent audio production strategies informed by best practices. In Proceedings of the Audio Engineering Society 53rd International Conference on Semantic Audio, London, UK, 27–29 January 2014.
- Ma, Z.; De Man, B.; Pestana, P.D.L.; Black, D.A.A.; Reiss, J.D. Intelligent multitrack dynamic range compression. J. Audio Eng. Soc. 2015, 63, 412–426. [Google Scholar] [CrossRef]
- Godsill, S.; Rayner, P.; Cappé, O. Digital audio restoration. In Applications of Digital Signal Processing to Audio and Acoustics; Kahrs, M., Brandenburg, K., Eds.; Kluwer: New York, NY, USA, 2002; pp. 133–194. [Google Scholar]
- Lindemann, E. The continuous frequency dynamic range compressor. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 21–24 October 1997.
- Zölzer, U. (Ed.) DAFX: Digital Audio Effects, 2nd ed.; Wiley: Chichester, UK, 2011.
- Wise, D.K. Concept, design, and implementation of a general dynamic parametric equalizer. J. Audio Eng. Soc. 2009, 57, 16–28. [Google Scholar]
- Newcomb, A.L., Jr.; Young, R.N. Practical loudness: An active circuit design approach. J. Audio Eng. Soc. 1976, 24, 32–35. [Google Scholar]
- Holman, T.; Kampmann, F. Loudness compensation: Use and abuse. J. Audio Eng. Soc. 1978, 26, 526–536. [Google Scholar]
- Grimes, J.; Doran, S. Equal loudness contour circuit using an operational amplifier. IEEE Trans. Audio Electroacoust. 1970, 18, 313–315. [Google Scholar] [CrossRef]
- Seefeldt, A. Loudness domain signal processing. In Proceedings of the 123rd Convention of the Audio Engineering Society, New York, NY, USA, 5–8 October 2007.
- Hawker, O.; Wang, Y. A method of equal loudness compensation for uncalibrated listening systems. In Proceedings of the 139th Convention of the Audio Engineering Society, New York, NY, USA, 29 September–1 October 2015.
- Yeh, D.T.; Smith, J.O. Discretization of the ’59 Fender Bassman tone stack. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Montreal, QC, Canada, 18–20 September 2006; pp. 1–5.
- Gabrielli, L.; Välimäki, V.; Penttinen, H.; Squartini, S.; Bilbao, S. A digital waveguide based approach for Clavinet modeling and synthesis. EURASIP J. Appl. Signal Process. 2013, 2013, 1–14. [Google Scholar] [CrossRef]
- Clarkson, P.M.; Mourjopoulos, J.; Hammond, J.K. Spectral, phase, and transient equalization for audio systems. J. Audio Eng. Soc. 1985, 33, 127–132. [Google Scholar]
- Wilson, R.; Adams, G.; Scott, J. Application of digital filters to loudspeaker crossover networks. J. Audio Eng. Soc. 1989, 37, 455–464. [Google Scholar]
- Greenfield, R.; Hawksford, M.J. Efficient filter design for loudspeaker equalization. J. Audio Eng. Soc. 1991, 39, 739–751. [Google Scholar]
- Karjalainen, M.; Piirilä, E.; Järvinen, A.; Huopaniemi, J. Comparison of loudspeaker equalization methods based on DSP techniques. J. Audio Eng. Soc. 1999, 47, 15–31. [Google Scholar]
- MacDonald, J.A.; Tran, P.K. Loudspeaker equalization for auditory research. Behav. Res. Methods 2007, 39, 133–136. [Google Scholar] [CrossRef] [PubMed]
- Berndtsson, G. Acoustical properties of wooden loudspeakers used in an artificial reverberation system. Appl. Acoust. 1995, 44, 7–23. [Google Scholar] [CrossRef]
- Pueo, B.; López, J.J.; Ramos, G.; Escolano, J. Efficient equalization of multi-exciter distributed mode loudspeakers. Appl. Acoust. 2009, 70, 737–746. [Google Scholar] [CrossRef]
- Höchens, L.; de Vries, D. Comparison of measurement methods for the equalization of loudspeaker panels based on bending wave radiation. In Proceedings of the 130th Convention of the Audio Engineering Society, London, UK, 13–16 May 2011.
- Lähdeoja, O.; Haapaniemi, A.; Välimäki, V. Sonic scenography—Equalized structure-borne sound for aurally active set design. In Proceedings of the International Computer Music Conference Joint with the Sound Music Computing Conference, Athens, Greece, 14–20 September 2014.
- Ho, J.H.; Berkhoff, A.P. Flat acoustic sources with frequency response correction based on feedback and feed-forward distributed control. J. Acoust. Soc. Am. 2015, 137, 2080–2088. [Google Scholar] [CrossRef] [PubMed]
- Kitson, A.B. Equalisation of sound systems by ear and instruments: Similarities and differences. In Proceedings of the 5th Australian Regional Convention of the Audio Engineering Society, Sydney, Australia, 26–28 April 1995.
- Terrell, M.; Sandler, M. Optimizing the controls of homogeneous loudspeaker arrays. In Proceedings of the 129th Convention of the Audio Engineering Society, San Francisco, CA, USA, 4–7 November 2010.
- Vidal Wagner, F.; Välimäki, V. Automatic calibration and equalization of a line array system. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Trondheim, Norway, 30 November–3 December 2015; pp. 123–130.
- Cecchi, S.; Virgulti, M.; Primavera, A.; Piazza, F.; Bettarelli, F.; Li, J. Investigation on audio algorithms architecture for stereo portable devices. J. Audio Eng. Soc. 2016, 64, 175–188. [Google Scholar] [CrossRef]
- Wilson, R. Equalization of loudspeaker drive units considering both on- and off-axis responses. J. Audio Eng. Soc. 1991, 39, 127–139. [Google Scholar]
- Hatziantoniou, P.D.; Mourjopoulos, J.N. Generalized fractional-octave smoothing of audio and acoustic responses. J. Audio Eng. Soc. 2000, 48, 259–280. [Google Scholar]
- Toole, F.E. Loudspeaker measurements and their relationship to listener preferences: Part 1. J. Audio Eng. Soc. 1986, 34, 227–235. [Google Scholar]
- Linkwitz, S.H. Active crossover networks for noncoincident drivers. J. Audio Eng. Soc. 1976, 24, 2–8. [Google Scholar]
- Ramos, G.; López, J.J. Filter design method for loudspeaker equalization based on IIR parametric filters. J. Audio Eng. Soc. 2006, 54, 1162–1178. [Google Scholar]
- Ramos, G.; Tomas, P. Improvements on automatic parametric equalization and cross-over alignment of audio systems. In Proceedings of the 126th Convention of the Audio Engineering Society, Munich, Germany, 7–10 May 2009.
- Behrends, H.; von dem Knesebeck, A.; Bradinal, W.; Neumann, P.; Zölzer, U. Automatic equalization using parametric IIR filters. J. Audio Eng. Soc. 2011, 59, 102–109. [Google Scholar]
- Karjalainen, M.; Piirilä, E.; Järvinen, A. Loudspeaker response equalization using warped digital filters. In Proceedings of the Nordic Signal Processing Conference (NORSIG), Espoo, Finland, 24–27 September 1996; pp. 367–370.
- Wang, P.; Ser, W.; Zhang, M. A dual-band equalizer for loudspeakers. J. Audio Eng. Soc. 2000, 48, 917–921. [Google Scholar]
- Wang, P.; Ser, W.; Zhang, M. Bark scale equalizer design using warped filter. In Proceedings of the IEEE International Conference Acoustics, Speech and Signal Processing (ICASSP), Salt Lake City, UT, USA, 7–11 May 2001; Volume 5, pp. 3317–3320.
- Tyril, M.; Pedersen, J.A.; Rubak, P. Digital filters for low-frequency equalization. J. Audio Eng. Soc. 2001, 49, 36–43. [Google Scholar]
- Ramos, G.; López, J.J.; Pueo, B. Cascaded warped-FIR and FIR filter structure for loudspeaker equalization with low computational cost requirements. Digital Signal Process. 2009, 19, 393–409. [Google Scholar] [CrossRef]
- Li, X.; Cai, Z.; Zheng, C.; Li, X. Equalization of loudspeaker response using balanced model truncation. J. Acoust. Soc. Am. 2015, 137, EL241–EL247. [Google Scholar] [CrossRef] [PubMed]
- Herzog, S.; Hilsamer, M. Low frequency group delay equalization of vented boxes using digital correction filters. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Erlangen, Germany, 1–5 September 2014.
- Abel, J.; Smith, J.O. Robust design of very high-order allpass dispersion filters. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Montreal, QC, Canada, 18–20 September 2006.
- Elliott, S.J.; Nelson, P.A. Multiple-point equalization in a room using adaptive digital filters. J. Audio Eng. Soc. 1989, 37, 899–907. [Google Scholar]
- Bellini, A.; Cibelli, G.; Armelloni, E.; Ugolotti, E.; Farina, A. Car cockpit equalization by warping filters. IEEE Trans. Consum. Electron. 2001, 47, 108–116. [Google Scholar] [CrossRef]
- Kim, L.H.; Lim, J.S.; Choi, C.; Sung, K.M. Equalization of low frequency response in automobile. IEEE Trans. Consum. Electron. 2003, 49, 243–252. [Google Scholar]
- Cecchi, S.; Palestini, L.; Peretti, P.; Piazza, F.; Bettarelli, F.; Toppi, R. Automotive audio equalization. In Proceedings of the Audio Engineering Society 36th International Conference on Automotive Audio, Dearborn, MI, USA, 2–4 June 2009.
- Bahne, A.; Ahlén, A. Optimizing the similarity of loudspeaker-room responses in multiple listening positions. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 340–353. [Google Scholar] [CrossRef]
- Craven, P.G.; Gerzon, M.A. Practical adaptive room and loudspeaker equalizer for hi-fi use. In Proceedings of the 92nd Convention of the Audio Engineering Society, Vienna, Austria, 24–27 March 1992.
- Bank, B. Combined quasi-anechoic and in-room equalization of loudspeaker responses. In Proceedings of the 134th Convention of the Audio Engineering Society, Rome, Italy, 4–7 May 2013.
- Bank, B.; Ramos, G. Improved pole positioning for parallel filters based on spectral smoothing and multiband warping. IEEE Signal Process. Lett. 2011, 18, 299–302. [Google Scholar]
- Mourjopoulos, J. On the variation and invertibility of room impulse response functions. J. Sound Vibr. 1985, 102, 217–228. [Google Scholar] [CrossRef]
- Mourjopoulos, J.N. Digital equalization of room acoustics. J. Audio Eng. Soc. 1994, 42, 884–900. [Google Scholar]
- Haneda, Y.; Makino, S.; Kaneda, Y. Multiple-point equalization of room transfer functions by using common acoustical poles. IEEE Trans. Speech Audio Process. 1997, 5, 325–333. [Google Scholar] [CrossRef]
- Fontana, F.; Gibin, L.; Rocchesso, D.; Ballan, O. Common pole equalization of small rooms using a two-step real-time digital equalizer. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 17–20 October 1999; pp. 195–198.
- Bharitkar, S.; Hilmes, P.; Kyriakakis, C. Robustness of spatial average equalization: A statistical reverberation model approach. J. Acoust. Soc. Am. 2004, 116, 3491–3497. [Google Scholar] [CrossRef] [PubMed]
- Stefanakis, N.; Sarris, J.; Jacobsen, F. Regularization in global sound equalization based on effort variation. J. Acoust. Soc. Am. 2009, 126, 666–675. [Google Scholar] [CrossRef] [PubMed]
- Karjalainen, M.; Paatero, T.; Mourjopoulos, J.N.; Hatziantoniou, P.D. About room response equalization and dereverberation. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 16–19 October 2005; pp. 183–186.
- Mäkivirta, A.; Antsalo, P.; Karjalainen, M.; Välimäki, V. Modal equalization of loudspeaker-room responses at low frequencies. J. Audio Eng. Soc. 2003, 51, 324–343. [Google Scholar]
- Karjalainen, M.; Esquef, P.A.A.; Antsalo, P.; Mäkivirta, A.; Välimäki, V. Frequency-zooming ARMA modeling of resonant and reverberant systems. J. Audio Eng. Soc. 2002, 50, 1012–1029. [Google Scholar]
- Fazenda, B.M.; Stephenson, M.; Goldberg, A. Perceptual thresholds for the effects of room modes as a function of modal decay. J. Acoust. Soc. Am. 2015, 137, 1088–1098. [Google Scholar] [CrossRef] [PubMed]
- Mertins, A.; Mei, T.; Kallinger, M. Room impulse response shortening/reshaping with infinity- and p-norm optimization. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 249–259. [Google Scholar] [CrossRef]
- Krishnan, L.; Teal, P.D.; Betlehem, T. A robust sparse approach to acoustic impulse response shaping. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 738–742.
- Jungmann, J.O.; Mazur, R.; Kallinger, M.; Mei, T.; Mertins, A. Combined acoustic MIMO channel crosstalk cancellation and room impulse response reshaping. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1829–1842. [Google Scholar] [CrossRef]
- Kodrasi, I.; Goetze, S.; Doclo, S. Regularization for partial multichannel equalization for speech dereverberation. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 1879–1890. [Google Scholar] [CrossRef]
- Lim, F.; Zhang, W.; Habets, E.A.P.; Naylor, P.A. Robust multichannel dereverberation using relaxed multichannel least squares. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1379–1390. [Google Scholar] [CrossRef]
- Liem, H.M.; Gan, W.S. Headphone equalization using DSP approaches. In Proceedings of the 107th Convention of the Audio Engineering Society, New York, NY, USA, 24–27 September 1999.
- Rämö, J. Equalization Techniques for Headphone Listening. Ph.D. Thesis, Aalto University, Espoo, Finland, 2014. [Google Scholar]
- Hiipakka, M.; Tikander, M.; Karjalainen, M. Modeling the external ear acoustics for insert headphone usage. J. Audio Eng. Soc. 2010, 58, 269–281. [Google Scholar]
- Gómez Bolaños, J.; Pulkki, V. Estimation of pressure at the eardrum in magnitude and phase for headphone equalization using pressure-velocity measurements at the ear canal entrance. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 18–21 October 2015.
- Olive, S.; Welti, T.; McMullin, E. Listener preferences for in-room loudspeaker and headphone target responses. In Proceedings of the 135th Convention of the Audio Engineering Society, New York, NY, USA, 17–20 October 2013.
- Rämö, J.; Välimäki, V. Signal processing framework for virtual headphone listening tests in a noisy environment. In Proceedings of the 132nd Convention of the Audio Engineering Society, Budapest, Hungary, 26–29 April 2012.
- Gómez Bolaños, J.; Mäkivirta, A.; Pulkki, V. Automatic regularization parameter for headphone transfer function inversion. J. Audio Eng. Soc. 2016, unpublished work. [Google Scholar]
- Briolle, F.; Voinier, T. Transfer function and subjective quality of headphones: Part 2, subjective quality evaluations. In Proceedings of the Audio Engineering Society 11th International Conference on Test and Measurement, Portland, OR, USA, 29–31 May 1992.
- Olive, S.E.; Welti, T.; McMullin, E. A virtual headphone listening test methodology. In Proceedings of the Audio Engineering Society 51st International Conference on Loudspeakers and Headphones, Helsinki, Finland, 21–24 August 2013.
- Blauert, J. Spatial Hearing: The Psychophysics of Human Sound Localization; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Sunder, K.; He, J.; Tan, E.L.; Gan, W.S. Natural sound rendering for headphones: Integration of signal processing techniques. IEEE Signal Process. Mag. 2015, 32, 100–113. [Google Scholar] [CrossRef]
- Mackenzie, J.; Huopaniemi, J.; Välimäki, V.; Kale, I. Low-order modeling of head-related transfer functions using balanced model truncation. IEEE Signal Process. Lett. 1997, 4, 39–41. [Google Scholar] [CrossRef]
- Ramos, G.; Cobos, M. Parametric head-related transfer function modeling and interpolation for cost-efficient binaural sound applications. J. Acoust. Soc. Am. 2013, 134, 1735–1738. [Google Scholar] [CrossRef] [PubMed]
- Huopaniemi, J.; Zacharov, N.; Karjalainen, M. Objective and subjective evaluation of head-related transfer function filter design. J. Audio Eng. Soc. 1999, 47, 218–239. [Google Scholar]
- Kulkarni, A.; Colburn, H.S. Role of spectral detail in sound-source localization. Nature 1998, 396, 747–749. [Google Scholar] [CrossRef] [PubMed]
- Hiekkanen, T.; Mäkivirta, A.; Karjalainen, M. Virtualized listening tests for loudspeakers. J. Audio Eng. Soc. 2009, 57, 237–251. [Google Scholar]
- Härmä, A.; Jakka, J.; Tikander, M.; Karjalainen, M.; Lokki, T.; Hiipakka, J.; Lorho, G. Augmented reality audio for mobile and wearable appliances. J. Audio Eng. Soc. 2004, 52, 618–639. [Google Scholar]
- Lindeman, R.W.; Noma, H.; De Barros, P.G. Hear-through and mic-through augmented reality: Using bone conduction to display spatialized audio. In Proceedings of the IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 173–176.
- Tikander, M.; Karjalainen, M.; Riikonen, V. An augmented reality audio headset. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Espoo, Finland, 1–4 September 2008.
- Välimäki, V.; Franck, A.; Rämö, J.; Gamper, H.; Savioja, L. Assisted listening using a headset: Enhancing audio perception in real, augmented, and virtual environments. IEEE Signal Process. Mag. 2015, 32, 92–99. [Google Scholar] [CrossRef]
- Hoffmann, P.F.; Christensen, F.; Hammershøi, D. Insert earphone calibration for hear-through options. In Proceedings of the Audio Engineering Society 51st International Conference on Loudspeakers and Headphones, Helsinki, Finland, 21–24 August 2013.
- Riikonen, V.; Tikander, M.; Karjalainen, M. An augmented reality audio mixer and equalizer. In Proceedings of the 124th Convention of the Audio Engineering Society, Amsterdam, The Netherlands, 17–20 May 2008.
- Rämö, J.; Välimäki, V. Digital augmented reality audio headset. J. Electr. Comput. Eng. 2012. [Google Scholar] [CrossRef]
- Rämö, J.; Välimäki, V.; Tikander, M. Live sound equalization and attenuation with a headset. In Proceedings of the Audio Engineering Society 51st International Conference on Loudspeakers and Headphones, Helsinki, Finland, 21–24 August 2013.
- Goldin, A.A.; Budkin, A.; Kib, S. Automatic volume and equalization control in mobile devices. In Proceedings of the 121st Convention of the Audio Engineering Society, San Francisco, CA, USA, 5–8 October 2006.
- Kitzen, W.J.W.; Kemna, J.W.; Druyvesteyn, W.F.; Knibbeler, C.L.C.M.; van de Voort, A.T.A.M. Noise-dependent sound reproduction in a car: Application of a digital audio signal processor. J. Audio Eng. Soc. 1988, 36, 18–26. [Google Scholar]
- Al-Jarrah, O.; Shaout, A. Automotive volume control using fuzzy logic. J. Intell. Fuzzy Syst. 2007, 18, 329–343. [Google Scholar]
- Christoph, M. Noise dependent equalization control. In Proceedings of the Audio Engineering Society 48th International Conference on Automotive Audio, Munich, Germany, 21–23 September 2012.
- Sack, M.C.; Buchinger, S.; Robitza, W.; Hummelbrunner, P.; Nezveda, M.; Hlavacs, H. Loudness and auditory masking compensation for mobile TV. In Proceedings of the IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Shanghai, China, 24–26 March 2010; pp. 1–6.
- Rämö, J.; Välimäki, V.; Alanko, M.; Tikander, M. Perceptual frequency response simulator for music in noisy environments. In Proceedings of the Audio Engineering Society 45th Conference on Applications of Time-Frequency Processing in Audio, Helsinki, Finland, 1–4 March 2012; pp. 269–278.
- Miller, T.E.; Barish, J. Optimizing sound for listening in the presence of road noise. In Proceedings of the 95th Convention of the Audio Engineering Society, New York, NY, USA, 7–10 October 1993.
- Sondhi, M.M.; Berkley, D.A. Silencing echoes on the telephone network. Proc. IEEE 1980, 68, 948–963. [Google Scholar] [CrossRef]
- Tzur (Zibulski), M.; Goldin, A. Sound equalization in a noisy environment. In Proceedings of the 110th Convention of the Audio Engineering Society, Amsterdam, The Netherlands, 12–15 May 2001.
- Rämö, J.; Välimäki, V.; Tikander, M. Perceptual headphone equalization for mitigation of ambient noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 724–728.
- Hodgson, J. A field guide to equalisation and dynamics processing on rock and electronica records. Pop. Music 2010, 29, 283–297. [Google Scholar] [CrossRef]
- Neuman, A.C.; Levitt, H.; Mills, R.; Schwander, T. An evaluation of three adaptive hearing aid selection strategies. J. Acoust. Soc. Am. 1987, 82, 1967–1976. [Google Scholar] [CrossRef] [PubMed]
- Durant, E.A.; Wakefield, G.H.; Van Tasell, D.J.; Rickert, M.E. Efficient perceptual tuning of hearing aids with genetic algorithms. IEEE Trans. Speech Audio Process. 2004, 12, 144–155. [Google Scholar] [CrossRef]
- Wakefield, G.H.; van den Honert, C.; Parkinson, W.; Lineaweaver, S. Genetic algorithms for adaptive psychophysical procedures: Recipient-directed design of speech-processor MAPs. Ear Hear. 2005, 26, 57S–72S. [Google Scholar] [CrossRef] [PubMed]
- Kuk, F.K.; Pape, N.M. The reliability of a modified simplex procedure in hearing aid frequency response selection. J. Speech Hear. Res. 1992, 35, 418–429. [Google Scholar] [CrossRef] [PubMed]
- Stelmachowicz, P.G.; Lewis, D.E.; Carney, E. Preferred hearing-aid frequency responses in simulated listening environments. J. Speech Hear. Res. 1994, 37, 712–719. [Google Scholar] [CrossRef] [PubMed]
- Dewey, C.; Wakefield, J. Novel designs for the parametric peaking EQ user interface. In Proceedings of the 134th Convention of the Audio Engineering Society, Rome, Italy, 4–7 May 2013.
- Loviscach, J. Graphical control of a parametric equalizer. In Proceedings of the 124th Convention of the Audio Engineering Society, Amsterdam, the Netherlands, 17–20 May 2008.
- Heise, S.; Hlatky, M.; Loviscach, J. A computer-aided audio effect setup procedure for untrained users. In Proceedings of the 128th Convention of the Audio Engineering Society, London, UK, 22–25 May 2010.
- Reed, D. A perceptual assistant to do sound equalization. In Proceedings of the 5th International Conference on Intelligent User Interfaces, New Orleans, LA, USA, 9–12 January 2000; pp. 212–218.
- Mecklenburg, S.; Loviscach, J. SubjEQt: Controlling an equalizer through subjective terms. In Proceedings of the Human Factors in Computing Systems (CHI-06), Montreal, QC, Canada, 22–27 April 2006.
- Sabin, A.; Pardo, B. Rapid learning of subjective preference in equalization. In Proceedings of the 125th Convention of the Audio Engineering Society, San Francisco, CA, USA, 2–5 October 2008.
- Sabin, A.; Pardo, B. 2DEQ: An intuitive audio equalizer. In Proceedings of the ACM Conference on Creativity and Cognition, Berkeley, CA, USA, 27–30 October 2009; pp. 435–436.
- Sabin, A.; Pardo, B. A method for rapid personalization of audio equalization parameters. In Proceedings of the ACM Multimedia Conference, Beijing, China, 19–24 October 2009.
- Sabin, A.T.; Rafii, Z.; Pardo, B. Weighted-function-based rapid mapping of descriptors to audio processing parameters. J. Audio Eng. Soc. 2011, 59, 419–430. [Google Scholar]
- Pardo, B.; Little, D.; Gergle, D. Towards speeding audio EQ interface building with transfer learning. In Proceedings of the International Conference on New Interfaces for Musical Expression (NIME), Ann Arbor, MI, USA, 21–23 May 2012.
- Cartwright, M.; Pardo, B. Social-EQ: Crowdsourcing an equalization descriptor map. In Proceedings of the International Conference Music Information Retrieval (ISMIR), Curitiba, Brazil, 4–8 November 2013.
- Cartwright, M.; Pardo, B.; Reiss, J.D. Mixploration: Rethinking the audio mixer interface. In Proceedings of the International Conference on Intelligent User Interfaces, Haifa, Israel, 24–27 February 2014.
- Stasis, S.; Stables, R.; Hockman, J. A model for adaptive reduced-dimensionality equalisation. In Proceedings of the International Conference on Digital Audio Effects (DAFX), Trondheim, Norway, 30 November–3 December 2015; pp. 315–320.
- Stasis, S.; Stables, R.; Hockman, J. Semantically controlled adaptive equalization in reduced dimensionality parameter space. Appl. Sci. 2016, 6, 116. [Google Scholar] [CrossRef]
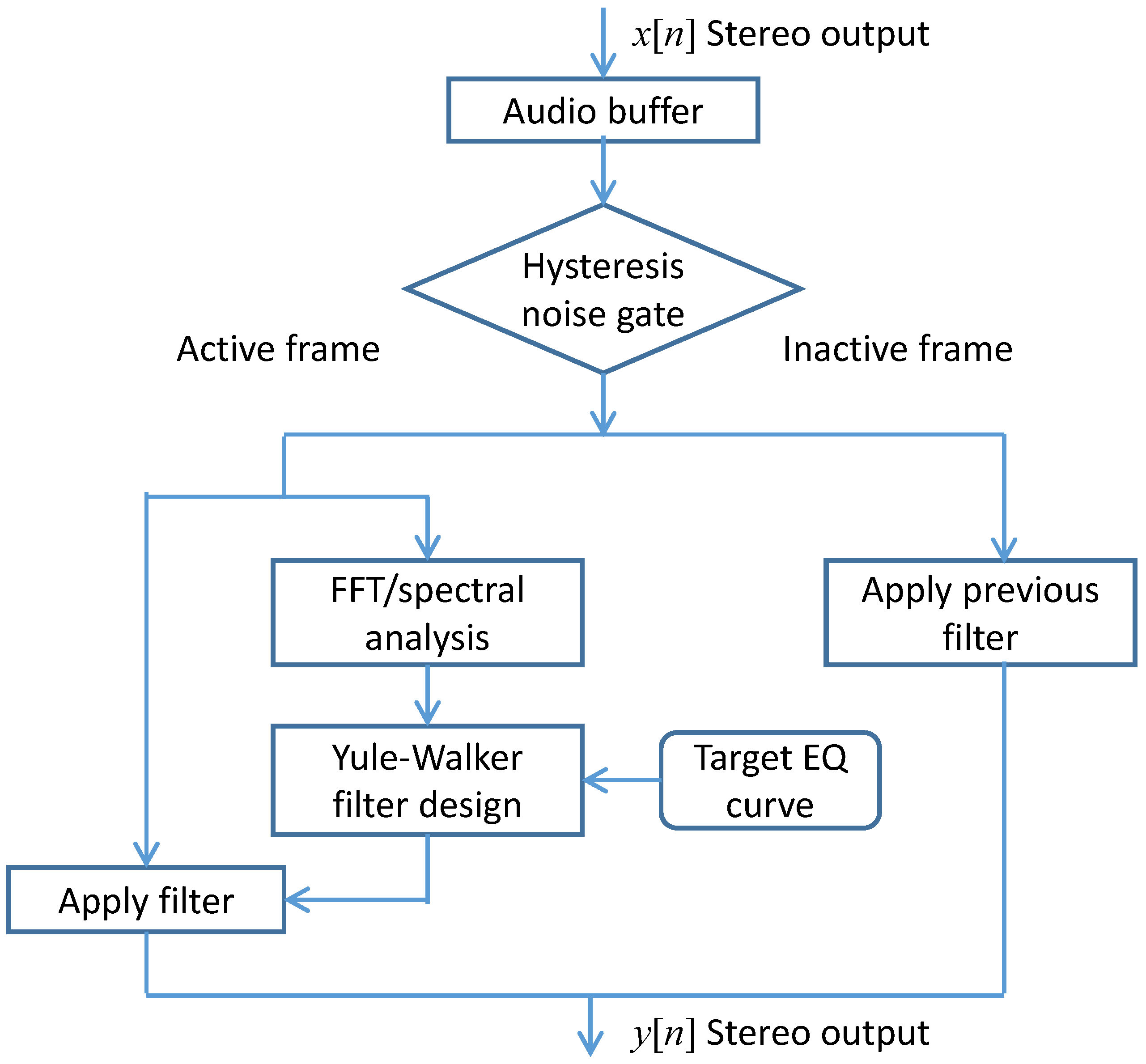
- Ma, Z.; Reiss, J.D.; Black, D. Implementation of an intelligent equalization tool using Yule-Walker for music mixing and mastering. In Proceedings of the 134th Convention of the Audio Engineering Society, Rome, Italy, 4–7 May 2013.
- Pestana, P.D.; Ma, Z.; Reiss, J.D.; Barbosa, A.; Black, D. Spectral characteristics of popular commercial recordings 1950-2010. In Proceedings of the 135th Convention of the Audio Engineering Society, New York, NY, USA, 17–20 October 2013.
- Perez Gonzalez, E.; Reiss, J.D. Automatic equalization of multi-channel audio using cross-adaptive methods. In Proceedings of the 127th Convention of the Audio Engineering Society, New York, NY, USA, 9–12 October 2009.
- Hafezi, S.; Reiss, J.D. Autonomous multitrack equalization based on masking reduction. J. Audio Eng. Soc. 2015, 63, 312–323. [Google Scholar] [CrossRef]
- Barchiesi, D.; Reiss, J.D. Reverse engineering the mix. J. Audio. Eng. Soc. 2010, 58, 563–576. [Google Scholar]
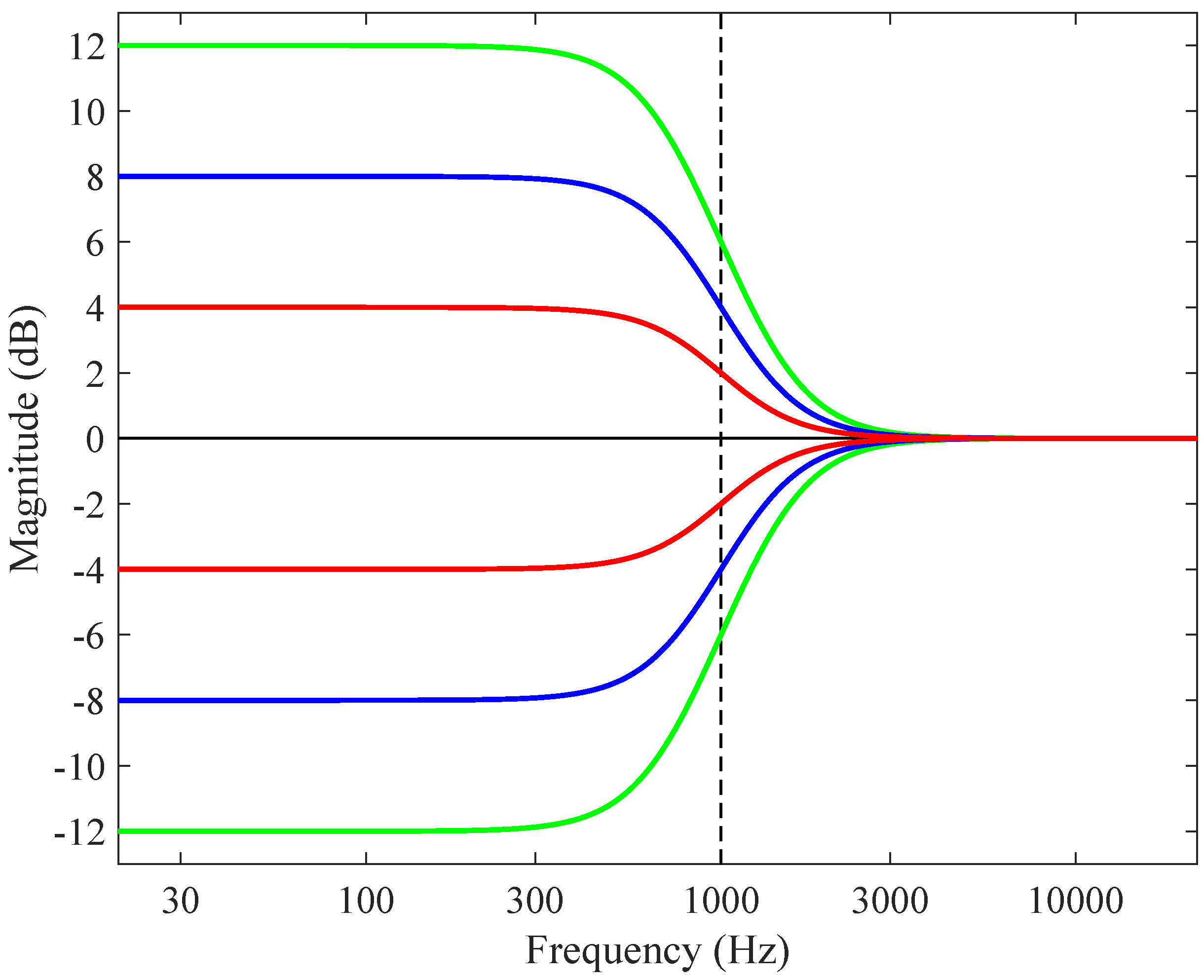
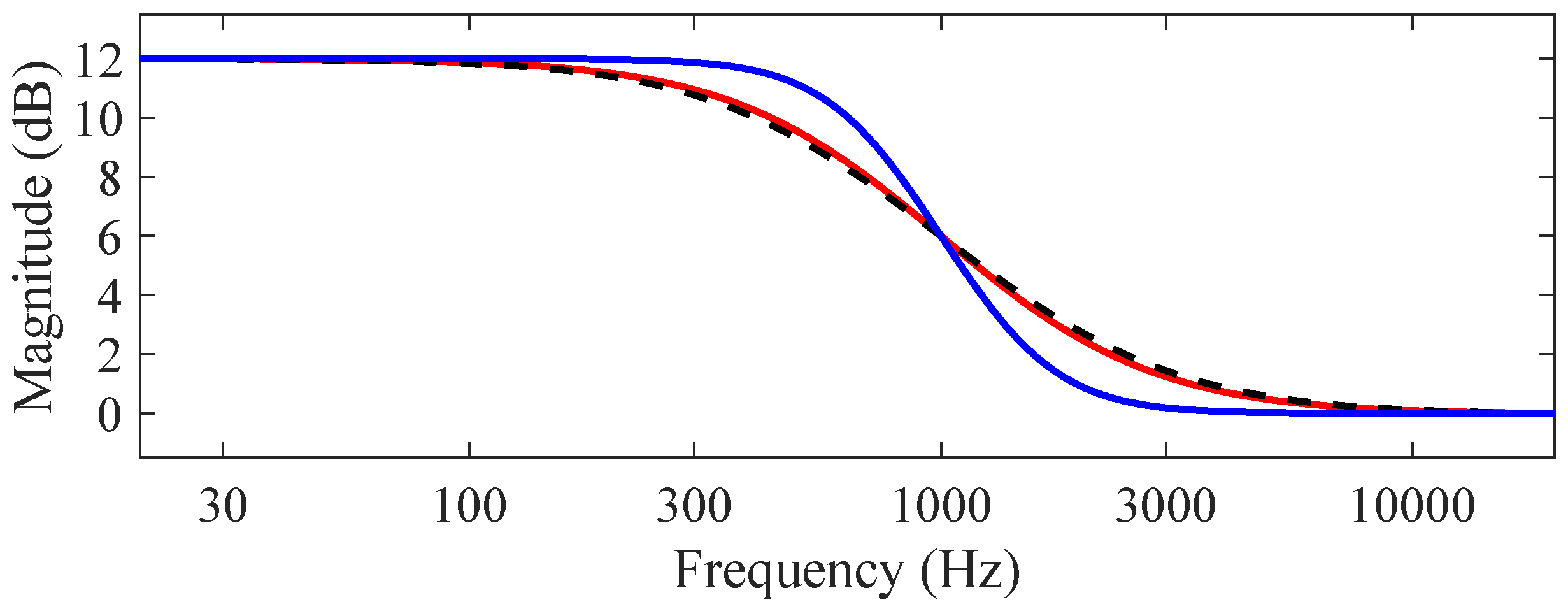
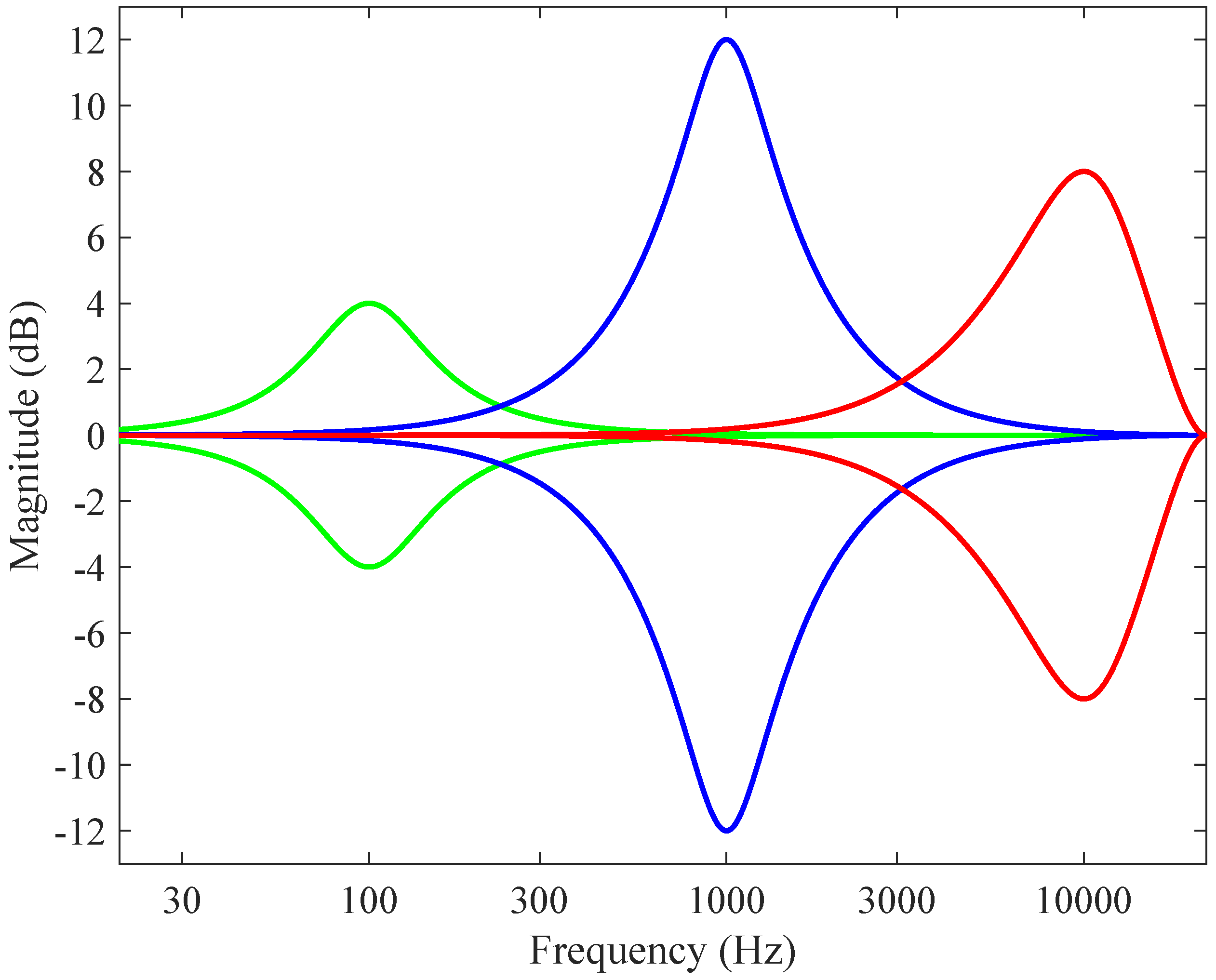


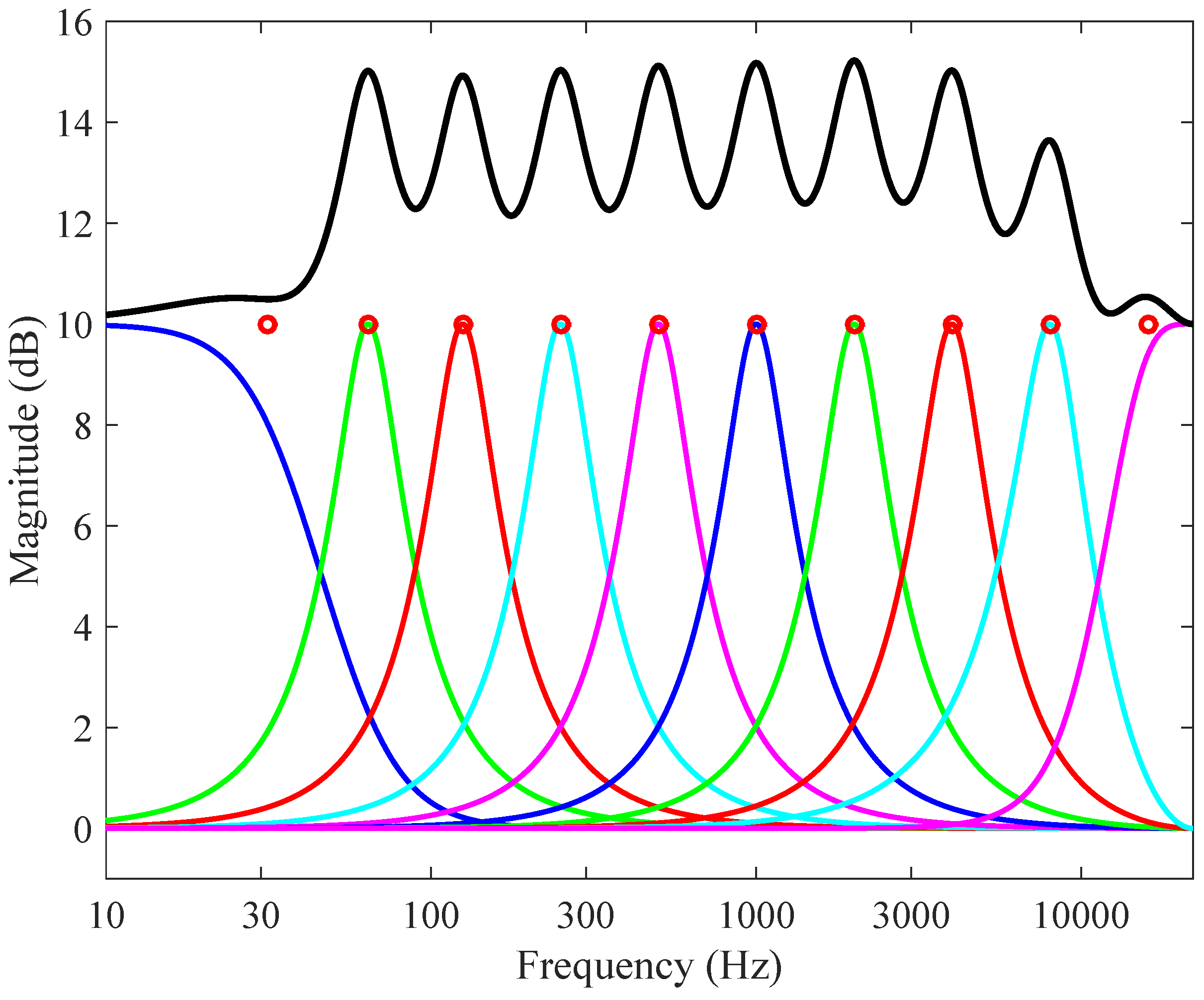
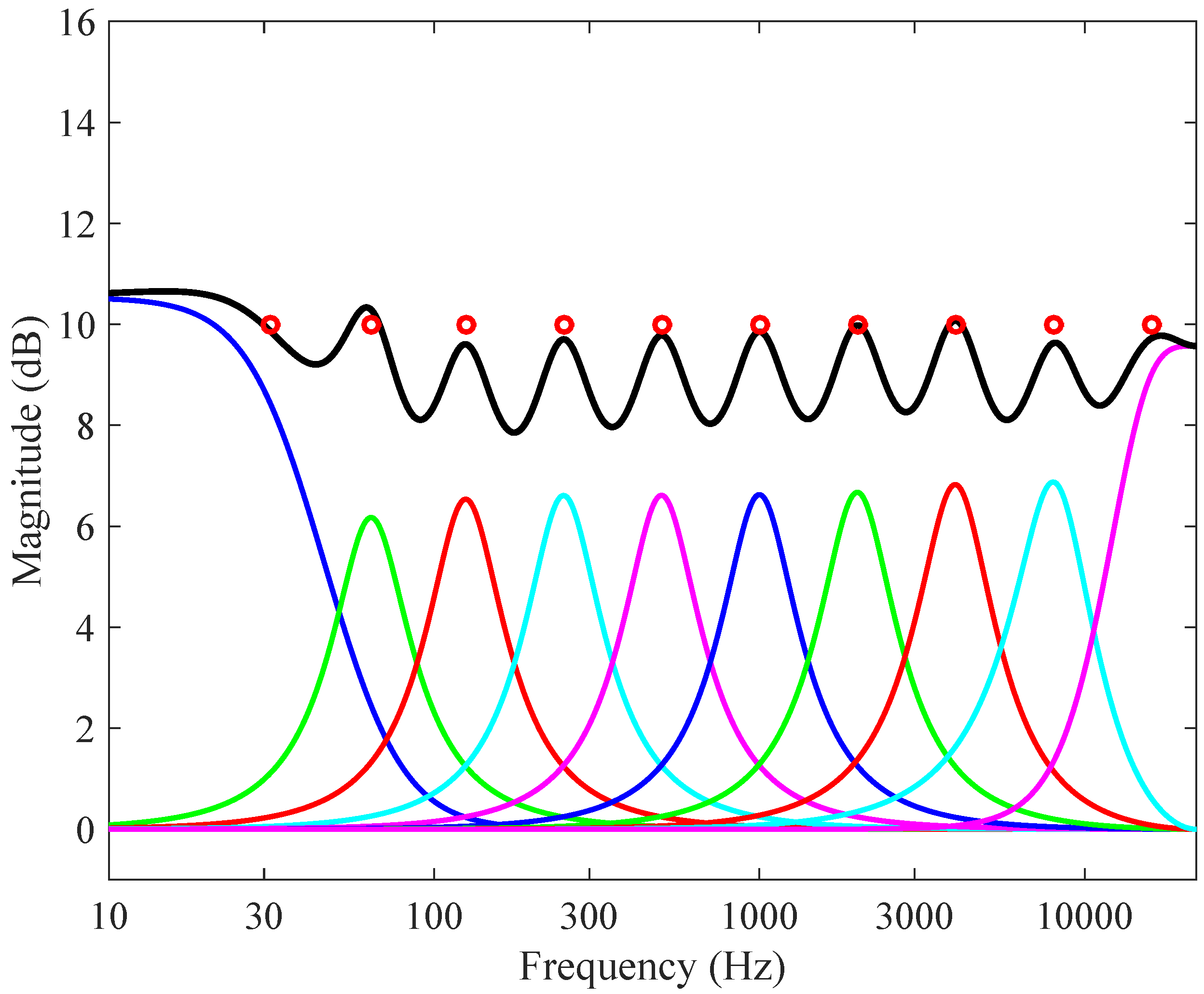
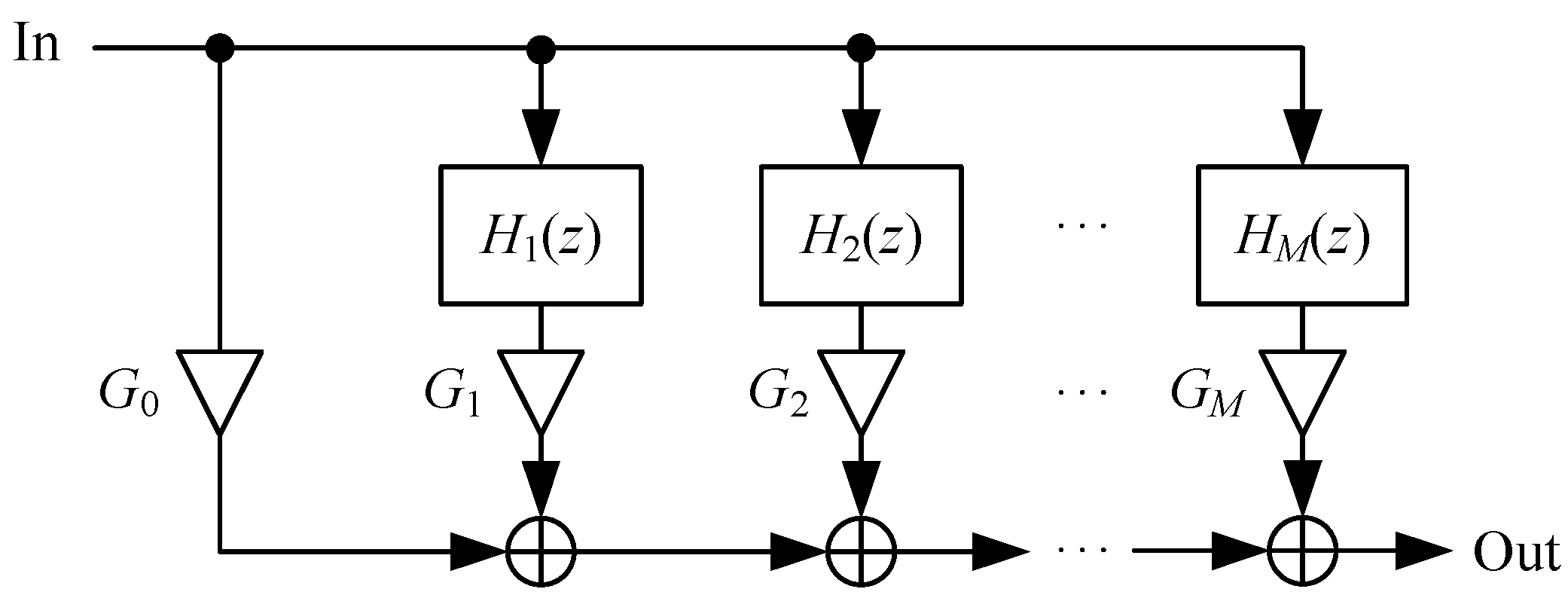
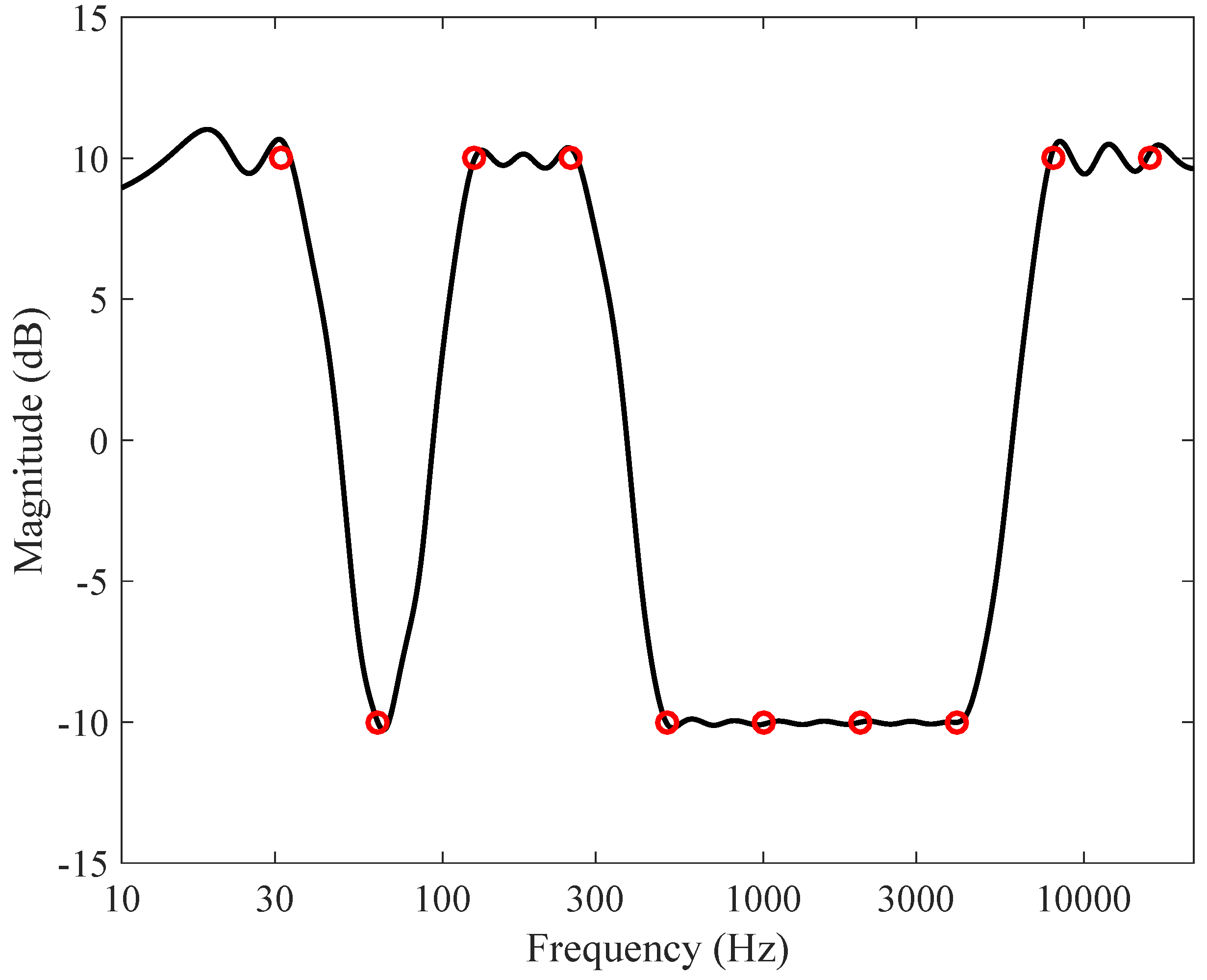
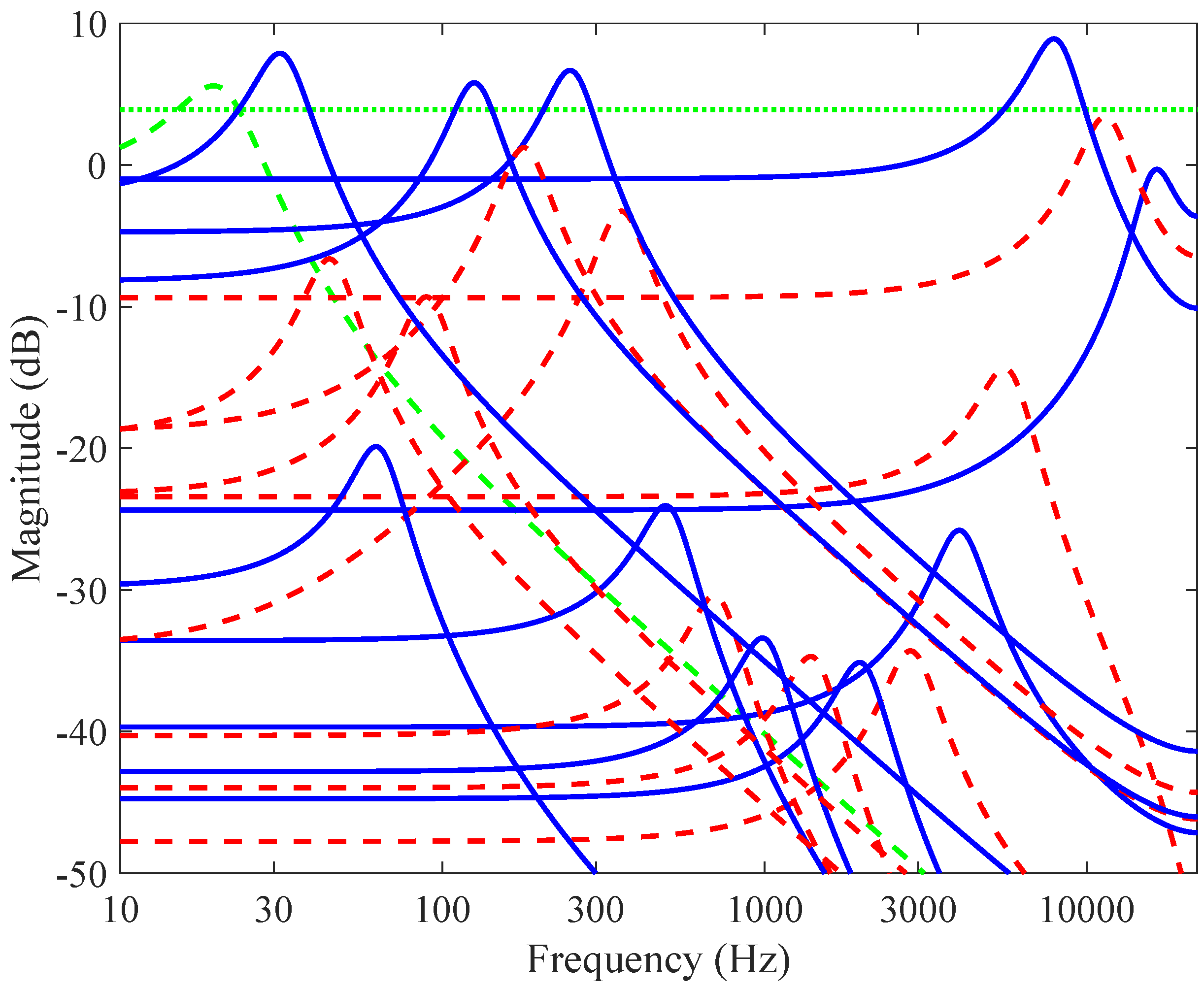
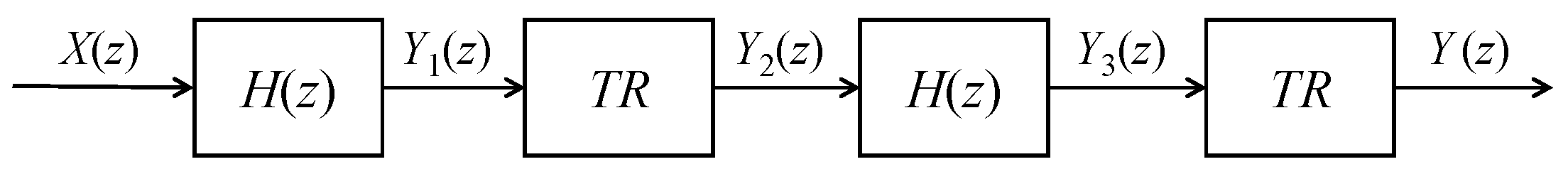
| Lower frequency (Hz) | Geometric mean frequency (Hz) | Upper frequency (Hz) |
|---|---|---|
| 22 | 31.5 | 44 |
| 44 | 63 | 88 |
| 88 | 125 | 177 |
| 177 | 250 | 355 |
| 355 | 500 | 710 |
| 710 | 1,000 | 1,420 |
| 1,420 | 2,000 | 2,840 |
| 2,840 | 4,000 | 5,680 |
| 5,680 | 8,000 | 11,360 |
| 11,360 | 16,000 | 22,720 |
| (Hz) | (Hz) | (Hz) | (Hz) | (Hz) | (Hz) |
|---|---|---|---|---|---|
| 22.4 | 25 | 28.2 | 708 | 800 | 891 |
| 28.2 | 31.5 | 35.5 | 891 | 1,000 | 1,122 |
| 35.5 | 40 | 44.7 | 1,122 | 1,250 | 1,413 |
| 44.7 | 50 | 56.2 | 1,413 | 1,600 | 1,778 |
| 56.2 | 63 | 70.8 | 1,778 | 2,000 | 2,239 |
| 70.8 | 80 | 89.1 | 2,239 | 2,500 | 2,818 |
| 89.1 | 100 | 112 | 2,818 | 3,150 | 3,548 |
| 112 | 125 | 141 | 3,548 | 4,000 | 4,467 |
| 141 | 160 | 178 | 4,467 | 5,000 | 5,623 |
| 178 | 200 | 224 | 5,623 | 6,300 | 7,079 |
| 224 | 250 | 282 | 7,079 | 8,000 | 8,913 |
| 282 | 315 | 355 | 8,913 | 10,000 | 11,220 |
| 355 | 400 | 447 | 11,220 | 12,500 | 14,130 |
| 447 | 500 | 562 | 14,130 | 16,000 | 17,780 |
| 562 | 630 | 708 | 17,780 | 20,000 | 22,390 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Välimäki, V.; Reiss, J.D. All About Audio Equalization: Solutions and Frontiers. Appl. Sci. 2016, 6, 129. https://doi.org/10.3390/app6050129
Välimäki V, Reiss JD. All About Audio Equalization: Solutions and Frontiers. Applied Sciences. 2016; 6(5):129. https://doi.org/10.3390/app6050129
Chicago/Turabian StyleVälimäki, Vesa, and Joshua D. Reiss. 2016. "All About Audio Equalization: Solutions and Frontiers" Applied Sciences 6, no. 5: 129. https://doi.org/10.3390/app6050129
APA StyleVälimäki, V., & Reiss, J. D. (2016). All About Audio Equalization: Solutions and Frontiers. Applied Sciences, 6(5), 129. https://doi.org/10.3390/app6050129