1. Introduction
In recent years, the usage and improvement of mobile techniques have been growing for a variety of real-life applications. For instance, many intelligent transportation systems (ITSs) and services have been designed and developed by several enterprises [
1,
2,
3,
4]. For the development of ITSs, studying how to collect the traffic information efficiently is a really important topic. The case studies of cooperative intelligent transportation systems (C-ITS) [
2,
3] and connected-vehicle technology [
4] developed real-time traffic information collection methods and evaluated traffic status. Furthermore, Gao
et al. [
1] considered traffic status to predict travel time for the design of a navigation system and the avoidance of traffic jams.
ITSs have three kinds of popular position collection approaches, which are the vehicle detector (VD), the reports of global positioning system (GPS)-equipped probe cars and cellular floating vehicle data (CFVD). VD is a sensor based on the techniques of active infrared/laser, magnetic, radar or video to regularly detect vehicles on a road for the analysis of time mean speed and traffic flow [
5,
6] GPS-equipped probe cars can periodically report their location information to a server for computing the space mean speed [
7]. CFVD, which is obtained by tracking the network signals of the mobile station (MS) in the car, can be analyzed to estimate the traffic information (e.g., traffic flow, vehicle speed and traffic density) [
5]. The advantages and limitations of these three methods are illustrated in the following paragraphs.
The establishment cost and maintenance fees of VDs were discussed and analyzed in some studies from different countries [
8]. For instance, the Texas Transportation Institute spent 43,500 U.S. dollars to install video image vehicle detection systems (VIVD) for the detection of real-time traffic information in 2002. The Ministry of Transportation and Communications in Taiwan spent 75,873 U.S. dollars to establish one VD per each kilometer on Taiwan Highway No. 1 for the collection of real-time road information [
9]. However, the maintenance fees of VD solutions are really high because the damage of VD usually result by the environmental factors.
Some studies discussed traffic collection and estimation methods based on the reports of GPS-equipped probe cars, which were compared to the traffic information from VDs for the evaluation of traffic estimation accuracies. For instance, Cheu
et al. [
10] showed that the lower error rate of space mean speed estimation (less than 3%) can be obtained with enough active probe vehicles. Herrera
et al. [
10] showed that GPS-equipped probe vehicles periodically recorded their speeds and locations in practical environments for traffic information estimation. Furthermore, their study suggested that a 2%–3% penetration of GPS-equipped probe vehicles is enough to provide accurate measurements of space mean speed. However, the cost of deployment of GPS-equipped probe cars is very expensive for reaching a penetration rate of 2%–3% [
10,
11].
CFVD can be obtained by tracking MS signals (call arrival (CA), handover (HO), double handover (DHO), normal location update (NLU) and period location update (PLU)), and it can be used for the analysis of traffic status [
12,
13]. Furthermore, the International Telecommunication Union (ITU) indicated that the handphone penetration rate is more than 100% in many countries [
14], and the penetration rate is high enough to assume that everyone has a handphone. Therefore, some studies assumed one handphone in one vehicle. For instance, Lin
et al. [
9] analyzed two HO locations based on the location service (LCS) as CFVD to estimate the real-time travel time and real-time vehicle speed between HO locations. Their experimental results indicated that the accuracy of the proposed traffic information estimation method was high. However, due to tracing the routes of each MS, a higher computation power is required, and privacy threats may exist. Moreover, future traffic information forecasting based on CFVD has not been investigated.
Therefore, this study proposes analytic models and traffic information estimation methods based on CFVD to obtain a low-cost solution for ITS. The proposed analytic models are used to analyze the relationship between traffic information (e.g., traffic flow, traffic density and vehicle speed) and the amount of cellular network signals (e.g., HO, NLU, CA and PLU). Then, traffic information can be estimated based on the proposed analytic models and CFVD. Furthermore, a vehicle speed forecasting method based on a back-propagation neural network (BPNN) algorithm is proposed to analyze the estimated vehicle speeds from CFVD and to predict the future vehicle speed for road users.
The rest of this study is organized as follows.
Section 2 discusses the related studies and techniques of traffic information estimation and forecasting methods.
Section 3 purposes vehicle speed estimation and forecasting methods based on CFVD. A case study of a highway in Taiwan and experimental results are illustrated and analyzed in
Section 4. Finally,
Section 5 summarizes the contributions of this study and presents future work.
3. Traffic Information Estimation and Forecasting Methods
The traffic information estimation methods based on CFVD are proposed and analyzed in
Section 3.1, and the estimated traffic information is adopted as the input parameters for the proposed traffic forecasting method in
Section 3.2. The details of traffic information estimation and forecasting methods are described as follows.
3.1. Traffic Information Estimation Methods
This study proposes some analytic models to estimate traffic flow based on the amount of HOs and NLUs and to estimate traffic density based on the amount of CAs and PLUs. The traffic information estimation method of CFVD is applied to estimate the traffic flow and traffic density. The estimated traffic flow and traffic density are then used for vehicle speed estimation. The notation used in this paper is summarized in
Table 1. The vehicle speed can be estimated in accordance with traffic flow and traffic density by Equation (1) [
19].
Table 1.
The definition of notation. PLU, periodic location update; HO, handover; CA, all arrival; NLU, normal location update.
Table 1.
The definition of notation. PLU, periodic location update; HO, handover; CA, all arrival; NLU, normal location update.
| Parameter | Description |
|---|
| Q (car/h) | The practical traffic flow |
| K (car/km) | The practical traffic density |
| U (km/h) | The practical vehicle speed |
| τ (h/call) | The call inter-arrival time |
| λ (call/h) | The call arrival rate |
| t (h/call) | The call holding time |
| 1/μ (h/call) | The mean call holding time |
| x (km) | The time x is between the preceding call arrival and entering the target road |
| li (km) | The length of road segment covered by Celli |
| b (h) | The cycle time of PLU |
| (event/h) | The amount of HOs of road segment covered by Celli |
| (event/h) | The amount of CAs of road segment covered by Celli |
| (event/h) | The amount of PLUs of road segment covered by Celli |
| (car/h) | The estimated traffic flow by using |
| (car/h) | The estimated traffic flow by using NLU events |
| (car/km) | The estimated traffic density by using |
| (car/km) | The estimated traffic density by using |
| (km/h) | The estimated vehicle speed by using and |
| (km/h) | The estimated vehicle speed by using and |
| (km/h) | The estimated vehicle speed by using and |
| (km/h) | The estimated vehicle speed by using and |
| (km/h) | The practical vehicle speed of road segment i at cycle |
| (km/h) | The practical vehicle speed of road segment i at cycle |
| (km/h) | The predicted vehicle speed of road segment i at cycle |
| (km/h) | The estimated vehicle speed of at cycle |
| (km/h) | The estimated vehicle speed of at cycle |
| (km/h) | The estimated vehicle speed of at cycle |
| (km/h) | The estimated vehicle speed of at cycle |
3.1.1. Traffic Flow Estimation
This study considers the amount of HOs (hi) and the amount of NLUs (qi,n) to estimate traffic flow (Qi) on the road segment covered by Celli.
Traffic Flow Estimation by Using HO Events
When a call arrives within the coverage area of a cell, the destination (or the originating) MS will be connected if a channel is available. While a communicating MS moves from the coverage area of one cell to the coverage area of another cell, the channel in the old cell is released, and the new cell will provide a channel to the MS if there is a free channel. This process is called a handover.
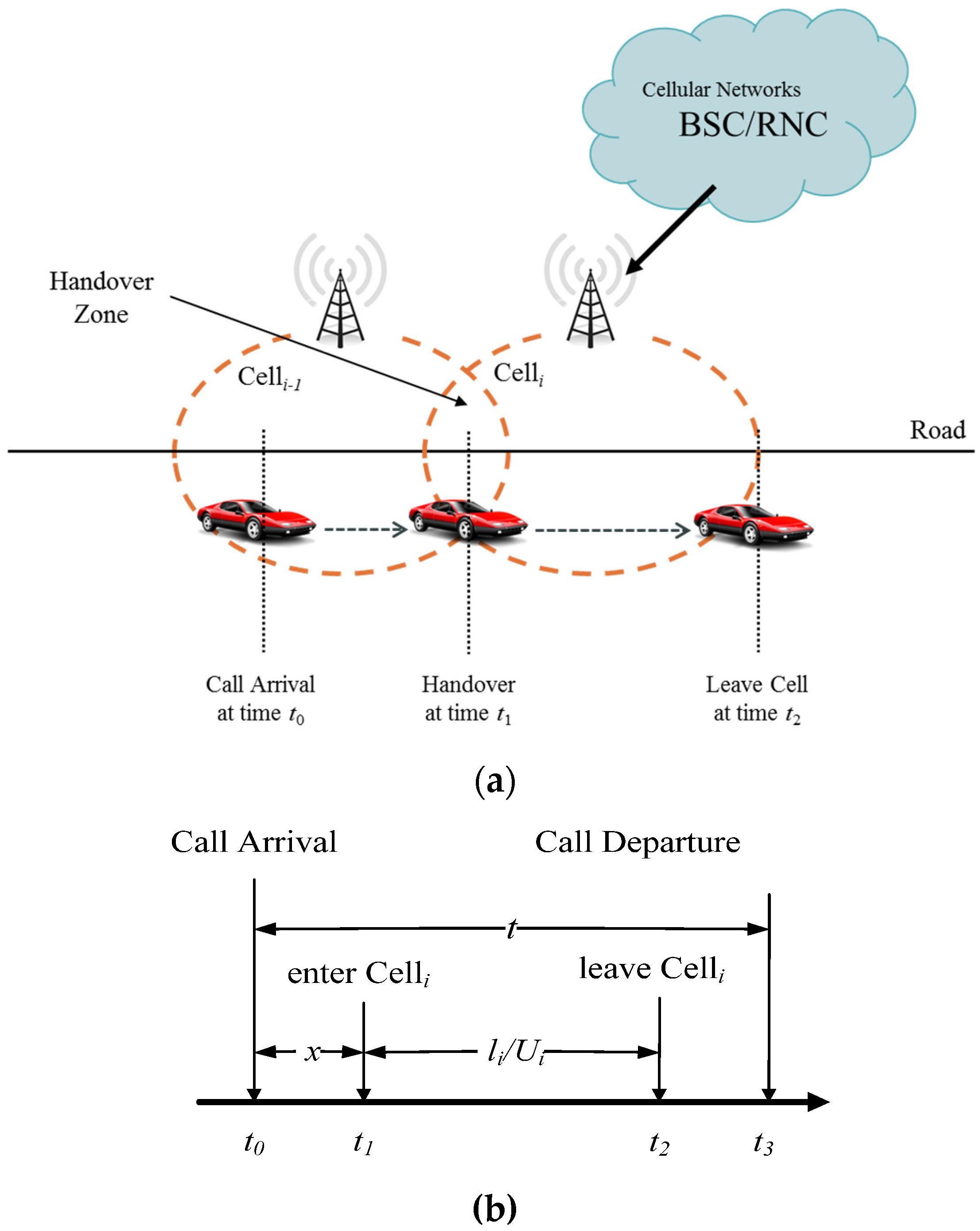
Figure 1a illustrates the space diagram for vehicle movement and the handover on a road.
Figure 1b depicts the timing diagram for the handover on the road segment covered by Cell
i. The MS in a car performs the call set-up at time
t0 (in
Figure 1a,b); then, the MS goes into the handover area of the coverage of Cell
i−1 and Cell
i at time
t1 (in
Figure 1a,b), and the base station controller (BSC) or radio network controller (RNC) will allocate an available channel for the communicating MS. At this moment, if Cell
i has a free channel, the connection between the MS and Cell
i will be established successfully. The process is called a handover from Cell
i−1 to Cell
i.
Figure 1.
(a) The scenario diagram for vehicle movement and the handover on the road; (b) the timing diagram for the handover on the road segment covered by Celli. BSC, base station controller; RNC, radio network controller.
Figure 1.
(a) The scenario diagram for vehicle movement and the handover on the road; (b) the timing diagram for the handover on the road segment covered by Celli. BSC, base station controller; RNC, radio network controller.
This study assumes that the call holding time (
t) is exponentially distributed with the mean
to generate handovers [
25]. The average speed of cars is
Ui, and the traffic flow is
Qi. Furthermore, the length of road segment covered by Cell
i is
li. Let the variable
x be the time difference between
t0 and
t1, and
li/
Ui denotes the time difference between
t1 and
t2. The handover procedure will be performed when the call holding time (
t) is larger than
x. Thereby, the amount of handover (
hi) on the road segment covered by Cell
i can be expressed as Equation (2), and this study can estimate traffic flow (
) by using Equation (3), which is the traffic flow multiplied by the number of HO events.
Traffic Flow Estimation by Using NLU Events
In cellular networks, the NLU event is generated when an MS moves from a location area (LA) to another LA. Therefore, traffic flow can be estimated by using the number of NLU events. This study assumes that the actual traffic flow on the road segment covered by Cell
i is
and one MS is in each car (shown in
Figure 2) [
24]. Therefore, the estimated traffic flow
(
i.e., the number of NLU events) on the road segment covered by Cell
i can be calculated as Equation (4), which is the traffic flow multiplied by the number of NLU events.
Figure 2.
The scenario diagram of location update events. LA, location area.
Figure 2.
The scenario diagram of location update events. LA, location area.
3.1.2. Traffic Density Estimation
For traffic density estimation, this study considers the amount of CAs (ai) and the amount of periodic location updates (PLUs) (pi) to estimate traffic density (Ki) on the road segment covered by Celli.
Traffic Density Estimation by Using CA events
In cellular networks, a cell is supplied with radio service by vicinal BTSs or Node Bs. The BSC in GSM and RNC in UMTS are responsible for the network control. When a call arrives within the coverage area of a cell, the BSC or the RNC provides a free channel to the MS, and the MS will be connected with the corresponding base station if there is a free channel.
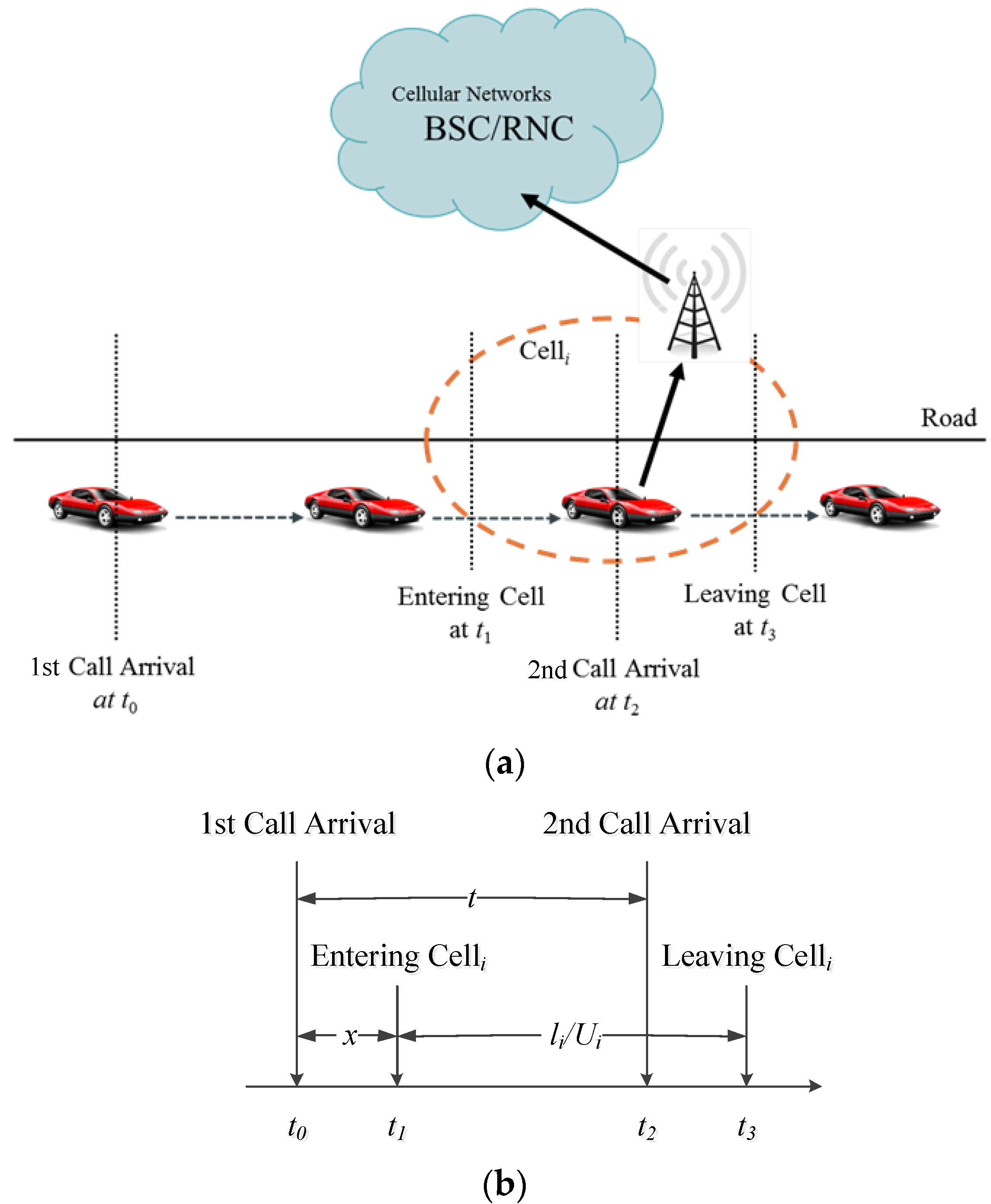
Figure 3a depicts the scenario diagram for vehicle movement and call arrivals on the road.
Figure 4b shows the timing diagram for call arrivals on the road segment covered by a specific Cell
i. The MS in a car moving along the road performs the first call at time
t0 (in
Figure 3a,b) and enters the coverage area of Cell
i at time
t1 (in
Figure 3a,b). The MS performs another call at time
t2 (in
Figure 3a,b) before leaving Cell
i (time
t3 in
Figure 3a,b), and the call performed by the MS is called a call arrival in Cell
i.
Figure 3.
(a) The scenario diagram for vehicle movement and call arrivals on the road; (b) the timing diagram for call arrivals on the road segment covered by Celli.
Figure 3.
(a) The scenario diagram for vehicle movement and call arrivals on the road; (b) the timing diagram for call arrivals on the road segment covered by Celli.
This study assumes that the call inter-arrival time (
) is exponentially distributed with the mean
to generate call arrivals [
25]. The length of road segment covered by Cell
i is
li, and the average speed of cars is
Ui. Therefore,
li/
Ui denotes the time difference between
t1 and
t3. This study analyzes the amount of call arrivals (
ai) that occur between
t1 and
t3 on the road segment covered by Cell
i. The amount of call arrivals can be expressed as Equation (5), and Equation (6) indicates that this study can derive estimated traffic density (
) from the amount of call arrivals.
Traffic Density Estimation by Using PLU Events
For mobility management, the MS periodically performs the PLU event for the core network in cellular networks. Some MSs may perform the PLU event across the cell in
Figure 2. Therefore, the probability models shown in Equations (7) and (8) are proposed to provide estimated vehicle density
(
i.e., the number of MS) on the road segment covered by Cell
i according to the number of PLU events. This model had been proven in [
24,
38], and this study summarizes the assumptions in this model as follows.
- •
The actual vehicle density and traffic speed can be obtained from VD on the road. Furthermore, the length of a road segment covered by the cell is .
- •
The call arrival rate to a cell is , and the call arrival process is assumed to be a Poisson process.
- •
The cycle time of PLU is , and the number of PLU events is .
3.1.3. Vehicle Speed Estimation
In this paper, the vehicle speed is obtained by the estimated traffic flow by using HO events (
qi,h), the estimated traffic flow by using NLU events (
qi,n), the estimated traffic density by using CA events (
ki,a) and the estimated traffic density by using PLU events (
ki,p). Based on
Section 3.1.1 and
Section 3.1.2, the estimated vehicle speeds
,
,
and
can be expressed as Equations (9)–(12). For instance, the estimated vehicle speed
can be obtained by using
qi,h and
ki,a; the estimated vehicle speed
can be obtained by using
qi,n and
ki,a; the estimated vehicle speed
can be obtained by using
qi,h and
ki,p; the estimated vehicle speed
can be obtained by using
qi,n and
ki,p.
3.2. Vehicle Speed Forecasting Method
For vehicle speed prediction, a BPNN algorithm is considered to predict the future vehicle speed in accordance with the current traffic information (
i.e., the estimated vehicle speeds from CFVD in
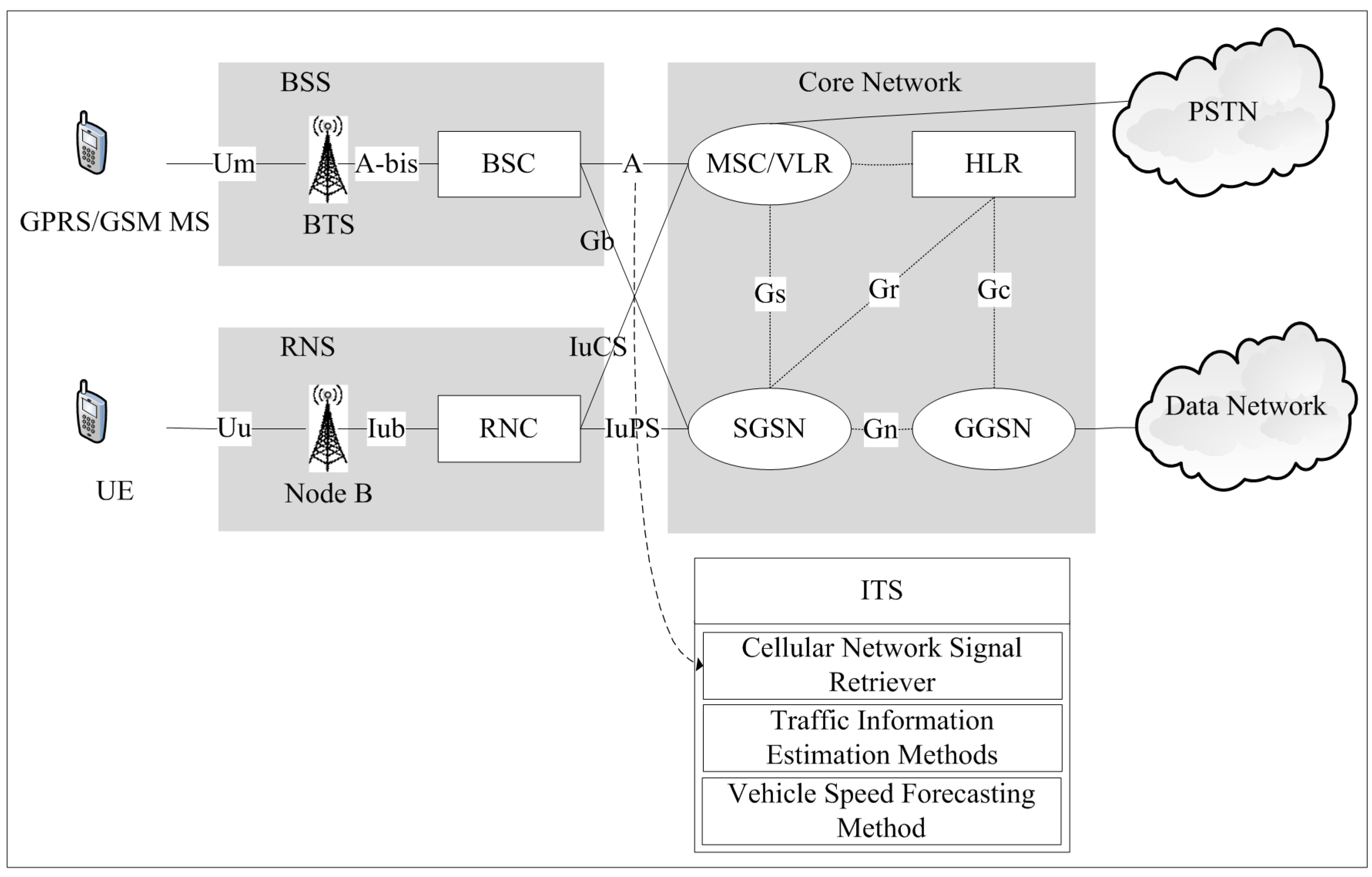
Section 3.1). An intelligent transportation system, which includes a cellular network signal retriever (CNSR), traffic information estimation methods and a vehicle speed forecasting method, has been designed and implemented for traffic information estimation and prediction (shown in
Figure 4). The ITS can retrieve cellular network signals (e.g., NLU, PLU, HO and CA) via the A interface and the IuCS interface and analyze these signals to estimate traffic information (e.g., traffic flow, traffic density and vehicle speed). Then, the estimated vehicle speed can be adopted as input characteristics into the proposed vehicle speed forecasting method to predict short-term vehicle speed for road user decision.
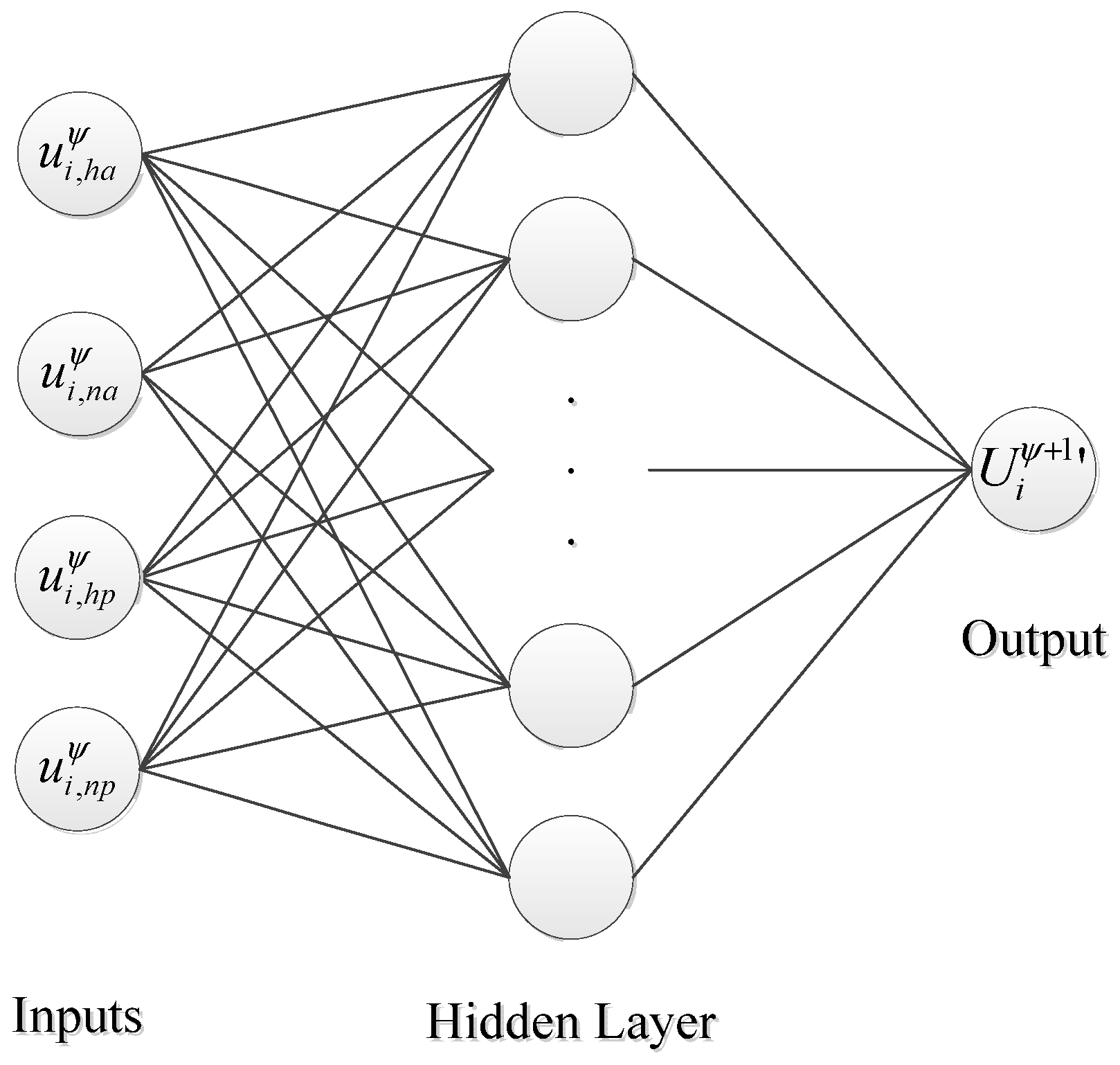
In this subsection, the average vehicle speed of road segment
i at cycle
is expressed as
, and the estimated vehicle speed at cycle
in accordance with Equations (9)–(12) can be expressed as
,
,
and
, respectively. This study collects the values of the current traffic information (
i.e.,
,
,
and
) as the input characteristics of the neurons in the BPNN to predict the future vehicle speed (
i.e.,
) (see
Figure 5). Therefore, the number of neurons in the input layer is four. There is one hidden layer, and the output value of the predicted vehicle speed
can be obtained by BPNN.
Figure 4.
Intelligent transportation system based on the proposed methods.
Figure 4.
Intelligent transportation system based on the proposed methods.
Figure 5.
Vehicle speed estimation based on the back-propagation neural network algorithm.
Figure 5.
Vehicle speed estimation based on the back-propagation neural network algorithm.
In the training stage, the historical datasets of cellular network signals from CNSR and traffic information from VDs are collected and calculated the amount of NLU, PLU, HO and CA events. Then vehicle speed can be estimated in accordance with the estimated traffic flows by using NLU and HO events and the estimated traffic densities by using PLU and CA events to obtain the values of , , and at cycle . Moreover, the average vehicle speed of road segment i at next cycle ( + 1) can be collected by VD. The proposed vehicle speed forecasting method based on BPNN adopts , , and as input characteristics and as the output characteristic to train a neural network.
In the runtime stage, the real-time estimated vehicle speeds can be obtained by the proposed traffic information estimation methods based on using CFVD. Then, the estimated vehicle speeds (, , and ) of road segment i can be adopted into the trained neural network in the training stage to forecast the short-term vehicle speed at the next cycle.
4. Experimental Results and Analyses
This section adopts the practical traffic information (
i.e., traffic flow and vehicle speed) from Taiwan Area National Freeway Bureau as the input characteristics of the traffic simulation program and refers to the MS communication behaviors from Chunghwa Telecom to simulate the traffic information and communication records. The details of the experimental environments are presented in
Section 4.1. The traffic information estimation and forecasting methods are illustrated in
Section 4.2 and
Section 4.3.
4.1. Experimental Environments
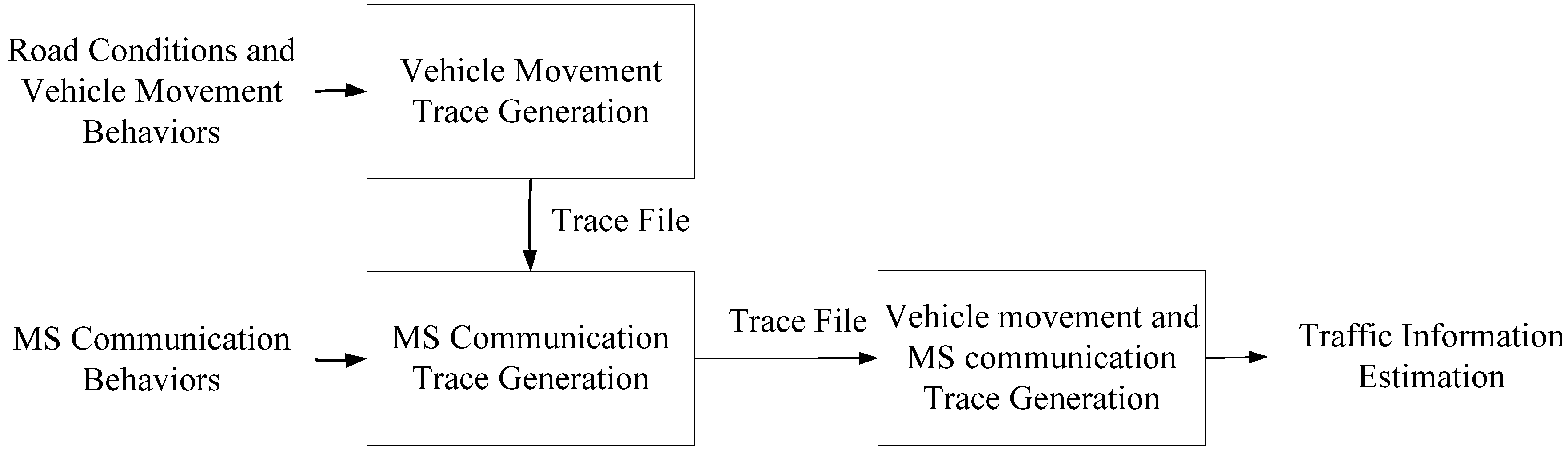
In this study, trace-driven experiments, which consider vehicle movement traces and MS communication traces, are designed to evaluate the traffic information estimation and forecasting methods based on CFVD (shown in
Figure 6). The inputs of the trace generator include the road conditions (e.g., the length of the road, the number of lanes, the locations of handover points and traffic flows), the vehicle movement behaviors (e.g., vehicles speeds, car following model and lane-changing model) and MS communication behaviors (e.g., call inter-arrival time and call holding time). The output is a trace file, which records the vehicle’s ID, vehicle speed, its CAs, its HOs, its NLUs and its PLUs. For the generation of vehicle movement traces, the practical traffic information, which included traffic flows and vehicle speeds from VDs on National Highway No. 3 in Taiwan during October in 2010, was collected and expressed as the characteristics of road conditions (
i.e., traffic flows) and vehicle movement behaviors (
i.e., vehicle speeds) for traffic simulation. Furthermore, call holding time is exponentially distributed with the mean
, and the call inter-arrival time is exponentially distributed with the mean
in accordance with the mobile communication records from Chunghwa Telecom for the generation of MS communication traces [
13]. Then, vehicle movement and MS communication traces can be generated by a traffic simulation program, VISSIM.
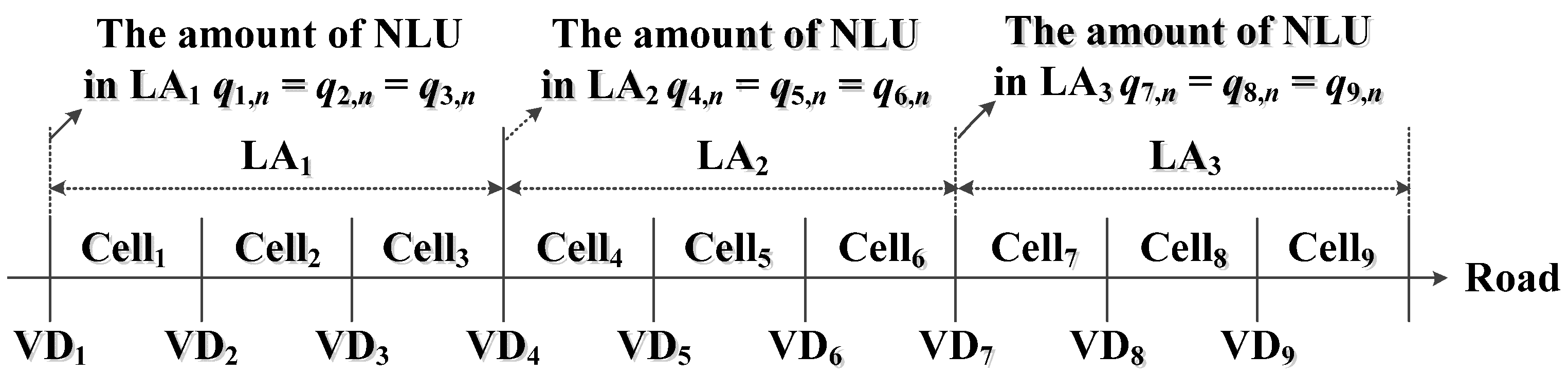
Figure 7 shows nine handover points and nine cells distributed in three location areas on the road from 0–9 km, and the coverage of a cell is 1 km. Moreover, this study assumes that there are nine VDs, which are built in the same locations with handover points for evaluating the traffic information of each road segment covered by a cell.
Figure 6.
Trace-driven simulation for the traffic information estimations.
Figure 6.
Trace-driven simulation for the traffic information estimations.
Figure 7.
The distribution of cells, location areas and vehicle detectors (VDs) in the simulation experiments.
Figure 7.
The distribution of cells, location areas and vehicle detectors (VDs) in the simulation experiments.
4.2. The Evaluation of Traffic Information Estimation Methods
The proposed analytic models were evaluated for the evaluation of traffic flow estimation based on the amount of HOs and NLUs and the evaluation of traffic density estimation based on the amount of CAs and PLUs in
Section 4.2.1 and
Section 4.2.2. Finally, the vehicle speed estimation methods based on the estimated traffic flow and the estimated traffic density were evaluated in
Section 4.2.3.
4.2.1. The Evaluation of Traffic Flow Estimation
For the evaluation of traffic flow estimation, the simulated amounts of HOs and NLUs from Cell
i are collected as CFVD to generate
and
. NLU is only performed with MS entering new LA, so the estimated traffic flows are consistence in the same LA in the proposed approach. For instance, the amount of HOs in Cell
1 (
) was 126 at 8 a.m. and 9 a.m., so the traffic flow of the first road segment (
) could be estimated as 7560 car/h by utilizing Equation (3) and MS communication behaviors (e.g., the expected value (
) of call holding time is 1 min/call). Furthermore, because 6672 NLUs in Cell
1 were performed at 8 a.m. and 9 a.m., the traffic flow of the first road segment (
) could be estimated as 6672 car/h according to Equation (4). This study calculated the accuracies of traffic flow estimation as
and
.
Table 2 shows that the average accuracies of traffic flow estimation of the first road segment between 8 a.m. and 22 p.m. are 89% for the amount of HOs and 100% for the amount of NLUs. As shown in
Table 3, the comparison of the traffic flow estimation comparisons between
and
indicates that the amount of NLUs is more suitable for traffic flow estimation than the amount of HOs.
Table 2.
The accuracies of traffic flow estimation of the road segment covered by Cell1.
Table 2.
The accuracies of traffic flow estimation of the road segment covered by Cell1.
| Time | Q1 | The Amount of HOs | The Amount of NLUs | | | | |
|---|
| 8 | 6672 | 126 | 6672 | 7560 | 6672 | 87% | 100% |
| 9 | 6200 | 112 | 6200 | 6720 | 6200 | 92% | 100% |
| 10 | 5435 | 92 | 5435 | 5520 | 5435 | 98% | 100% |
| 11 | 5663 | 80 | 5663 | 4800 | 5663 | 85% | 100% |
| 12 | 5532 | 90 | 5532 | 5400 | 5532 | 98% | 100% |
| 13 | 5265 | 90 | 5265 | 5400 | 5265 | 97% | 100% |
| 14 | 5546 | 90 | 5546 | 5400 | 5546 | 97% | 100% |
| 15 | 6368 | 88 | 6368 | 5280 | 6368 | 83% | 100% |
| 16 | 5762 | 78 | 5762 | 4680 | 5762 | 81% | 100% |
| 17 | 6101 | 124 | 6101 | 7440 | 6101 | 78% | 100% |
| 18 | 6122 | 104 | 6122 | 6240 | 6122 | 98% | 100% |
| 19 | 5378 | 74 | 5378 | 4440 | 5378 | 83% | 100% |
| 20 | 4667 | 72 | 4667 | 4320 | 4667 | 93% | 100% |
| 21 | 4625 | 64 | 4625 | 3840 | 4625 | 83% | 100% |
| 22 | 4312 | 60 | 4312 | 3600 | 4312 | 83% | 100% |
| Mean | | | | | | 89% | 100% |
Table 3.
The accuracies of traffic flow estimation of each road segment.
Table 3.
The accuracies of traffic flow estimation of each road segment.
| Cell | | |
|---|
| Cell1 | 89% | 100% |
| Cell2 | 76% | 100% |
| Cell3 | 77% | 100% |
| Cell4 | 78% | 100% |
| Cell5 | 70% | 100% |
| Cell6 | 67% | 99% |
| Cell7 | 68% | 100% |
| Cell8 | 70% | 100% |
| Cell9 | 72% | 100% |
| Mean | 74% | 100% |
4.2.2. The Evaluation of Traffic Density Estimation
For the evaluation of traffic density estimation, the simulated amounts of CAs and PLUs from Cell
i are collected as CFVD to generate
and
. For instance, the amount of CAs in Cell
1 (
) was 97 at 8 a.m., so the traffic density of the first road segment (
) could be estimated as 97 car/km by Equation (6) and MS communication behaviors (e.g., the expected value (
) of the call inter-arrival time is 1 h/call). Furthermore, because 126 PLUs were performed in Cell
1 at 8 a.m., the traffic density of the first road segment (
) could be estimated as 128 car/h in accordance with Equation (8) and MS communication behaviors (e.g., call inter-arrival time). This study calculated the accuracies of traffic density estimation as
and
.
Table 4 shows that the average accuracies of traffic density estimation of the first road segment between 8 a.m. and 22 p.m. are 91% for the amount of CAs and 81% for the amount of PLUs. As shown in
Table 5, the results of the traffic density estimation between
and
indicate that the amount of CAs is more suitable for traffic density estimation than the amount of PLUs.
Table 4.
The accuracies of traffic density estimation of the road segment covered by Cell1.
Table 4.
The accuracies of traffic density estimation of the road segment covered by Cell1.
| Time | K1 | The Amount of CAs | The Amount of PLUs | | | | |
|---|
| 8 | 97 | 97 | 126 | 97 | 128 | 99% | 67% |
| 9 | 88 | 86 | 112 | 86 | 103 | 97% | 83% |
| 10 | 77 | 71 | 92 | 71 | 81 | 93% | 95% |
| 11 | 69 | 62 | 80 | 62 | 74 | 90% | 92% |
| 12 | 67 | 69 | 90 | 69 | 58 | 96% | 87% |
| 13 | 63 | 69 | 90 | 69 | 70 | 91% | 89% |
| 14 | 67 | 69 | 90 | 69 | 74 | 97% | 89% |
| 15 | 78 | 68 | 88 | 68 | 99 | 87% | 72% |
| 16 | 70 | 60 | 78 | 60 | 85 | 86% | 78% |
| 17 | 87 | 96 | 124 | 96 | 105 | 89% | 78% |
| 18 | 87 | 80 | 104 | 80 | 105 | 92% | 79% |
| 19 | 76 | 57 | 74 | 57 | 97 | 75% | 72% |
| 20 | 56 | 55 | 72 | 55 | 60 | 99% | 92% |
| 21 | 55 | 49 | 64 | 49 | 70 | 89% | 73% |
| 22 | 51 | 46 | 60 | 46 | 64 | 90% | 75% |
| Mean | | | | | | 91% | 81% |
Table 5.
The accuracies of traffic density estimation of each road segment.
Table 5.
The accuracies of traffic density estimation of each road segment.
| Cell | | |
|---|
| Cell1 | 91% | 81% |
| Cell2 | 88% | 75% |
| Cell3 | 90% | 70% |
| Cell4 | 86% | 86% |
| Cell5 | 84% | 75% |
| Cell6 | 88% | 73% |
| Cell7 | 86% | 76% |
| Cell8 | 87% | 84% |
| Cell9 | 84% | 73% |
| Mean | 87% | 77% |
4.2.3. The Evaluation of Vehicle Speed Estimation
For the evaluation of vehicle speed estimation, the estimated vehicle speeds
,
,
and
can be generated via the estimated traffic flow from HO events (
qi,h) Equation (3), the estimated traffic flow by using NLU events (
qi,n) Equation (4), the estimated traffic density by using CA events (
ki,a) and the estimated traffic density by using PLU events (
ki,p) by Equations (9)–(12). For instance, the average vehicle speed of the first road segment
can be estimated as 78 km/h (
i.e.,
) at 8 a.m. in accordance with the estimated traffic flow by using HO events (
i.e.,
q1,h = 7560 car/h) and the estimated traffic density by using CA events (
i.e.,
k1,a = 97 car/km). This study calculated the accuracies of traffic density estimation as
,
,
and
. In accordance with the results in
Section 4.2.1 and
Section 4.2.2,
Table 6 shows that the average accuracies of vehicle speed estimation of the first road segment between 8 a.m. and 22 p.m. are 92%, 90%, 81% and 85% for the estimated vehicle speeds
,
,
and
, respectively. As shown in
Table 7, the results of the vehicle speed estimation show that the estimated traffic flow based on the amount of NLUs and estimated traffic density based on the amount of CAs can obtain the highest accuracy of vehicle speed estimation.
Table 6.
The accuracies of vehicle speed estimation of the road segment covered by Cell1.
Table 6.
The accuracies of vehicle speed estimation of the road segment covered by Cell1.
| Time | U1 | | | | | | | | |
|---|
| 8 | 69 | 78 | 69 | 59 | 52 | 87% | 99% | 85% | 75% |
| 9 | 70 | 78 | 72 | 65 | 60 | 89% | 97% | 93% | 86% |
| 10 | 71 | 78 | 77 | 69 | 67 | 90% | 92% | 97% | 95% |
| 11 | 83 | 77 | 91 | 65 | 76 | 94% | 89% | 78% | 92% |
| 12 | 83 | 78 | 80 | 93 | 96 | 94% | 96% | 88% | 85% |
| 13 | 83 | 78 | 76 | 77 | 75 | 94% | 92% | 92% | 90% |
| 14 | 83 | 78 | 80 | 73 | 75 | 94% | 97% | 88% | 90% |
| 15 | 82 | 78 | 94 | 53 | 64 | 95% | 86% | 65% | 78% |
| 16 | 83 | 78 | 96 | 55 | 68 | 94% | 84% | 67% | 82% |
| 17 | 70 | 78 | 64 | 71 | 58 | 90% | 90% | 100% | 82% |
| 18 | 70 | 78 | 77 | 59 | 58 | 89% | 91% | 84% | 83% |
| 19 | 71 | 78 | 94 | 46 | 55 | 90% | 67% | 65% | 78% |
| 20 | 84 | 79 | 85 | 72 | 78 | 94% | 99% | 86% | 93% |
| 21 | 84 | 78 | 94 | 55 | 66 | 93% | 87% | 65% | 79% |
| 22 | 84 | 78 | 94 | 56 | 67 | 93% | 89% | 67% | 80% |
| Mean | | | | | | 92% | 90% | 81% | 85% |
Table 7.
The accuracies of vehicle speed estimation of each road segment.
Table 7.
The accuracies of vehicle speed estimation of each road segment.
| Cell | | | | |
|---|
| Cell1 | 92% | 90% | 81% | 85% |
| Cell2 | 80% | 86% | 62% | 81% |
| Cell3 | 75% | 90% | 62% | 79% |
| Cell4 | 86% | 83% | 72% | 88% |
| Cell5 | 76% | 81% | 59% | 80% |
| Cell6 | 73% | 85% | 55% | 80% |
| Cell7 | 76% | 84% | 57% | 82% |
| Cell8 | 72% | 85% | 64% | 86% |
| Cell9 | 78% | 80% | 56% | 78% |
| Mean | 79% | 85% | 63% | 82% |
4.3. The Evaluation of Vehicle Speed Forecasting Method
In this subsection, an LR algorithm and a BPNN algorithm were implemented for the evaluation and comparison of the vehicle speed forecasting method. The estimated vehicle speeds , , and from CFVD at cycle were used to predict the future vehicle speed at the next cycle in experiments. For instance, the estimated vehicle speeds of the first road segment , , and from CFVD at 8 a.m., which were 78 km/h, 69 km/h, 59 km/h and 52 km/h, were adopted as input characteristics in the LR and BPNN algorithms. The predicted vehicle speed could be calculated as 69 km/h by the BPNN algorithm, and the practical vehicle speed was 70 km/h. Therefore, the accuracy of vehicle speed forecasting could be measured as 98.90% (i.e., ).
Table 8 shows that the average accuracies of vehicle speed forecasting based on the LR and BPNN algorithms between 8 a.m. and 22 p.m. are 94.82% and 96.01%. As shown in
Table 9, the results of the vehicle speed forecasting comparisons indicate that the BPNN algorithm is more suitable for predicting the future vehicle speed for ITS.
Table 8.
The accuracies of vehicle speed forecasting of the road segment covered by Cell1. LR, logistic regression.
Table 8.
The accuracies of vehicle speed forecasting of the road segment covered by Cell1. LR, logistic regression.
| Time | | Forecasted Vehicle Speed of LR | Forecasted Vehicle Speed of BPNN | The Accuracy of LR | The Accuracy of BPNN |
|---|
| 8 | 70 | 76 | 69 | 92.32% | 98.90% |
| 9 | 71 | 78 | 73 | 90.05% | 96.32% |
| 10 | 83 | 79 | 77 | 95.95% | 93.26% |
| 11 | 83 | 83 | 81 | 99.78% | 97.30% |
| 12 | 83 | 85 | 86 | 98.40% | 96.86% |
| 13 | 83 | 80 | 80 | 96.60% | 96.74% |
| 14 | 82 | 80 | 80 | 97.89% | 98.18% |
| 15 | 83 | 81 | 78 | 97.89% | 93.95% |
| 16 | 70 | 82 | 79 | 83.16% | 87.91% |
| 17 | 70 | 72 | 73 | 97.73% | 96.19% |
| 18 | 71 | 74 | 75 | 95.30% | 93.91% |
| 19 | 84 | 79 | 81 | 94.50% | 96.52% |
| 20 | 84 | 79 | 80 | 94.54% | 95.47% |
| 21 | 84 | 80 | 84 | 94.75% | 99.93% |
| 22 | 85 | 79 | 86 | 93.47% | 98.76% |
| Mean | | | | 94.82% | 96.01% |
Table 9.
The accuracies of vehicle speed forecasting of each road segment.
Table 9.
The accuracies of vehicle speed forecasting of each road segment.
| Cell | The Accuracy of LR | The Accuracy of BPNN |
|---|
| Cell1 | 94.82% | 96.01% |
| Cell2 | 93.76% | 96.29% |
| Cell3 | 93.42% | 95.24% |
| Cell4 | 92.39% | 94.03% |
| Cell5 | 93.25% | 94.72% |
| Cell6 | 93.59% | 97.35% |
| Cell7 | 92.26% | 95.74% |
| Cell8 | 93.73% | 95.19% |
| Cell9 | 93.84% | 96.88% |
| Mean | 93.45% | 95.72% |
5. Conclusions and Future Work
Several studies have reviewed and analyzed how to obtain the traffic information from CFVD. However, they cannot be applied directly to predict the future traffic information in dynamical environments. Therefore, this study proposes analytic models to estimate the traffic flow in accordance with the amounts of HOs and NLUs and to estimate the traffic density in accordance with the amounts of CAs and PLUs. Furthermore, the vehicle speeds can be estimated according to the estimated traffic flows and estimated traffic densities. For vehicle speed forecasting, a back-propagation neural network algorithm is considered to predict the future vehicle speed via the current traffic information. In an experimental environment, this study adopted the practical traffic information from Taiwan Area National Freeway Bureau as the input characteristics of the traffic simulation program and referred to the MS communication behaviors from Chunghwa Telecom to simulate the traffic information and communication records. The experimental results illustrated that the average accuracies of vehicle speed estimation of road segments are 79%, 85%, 63% and 82% for the estimated vehicle speeds , , and , respectively. Moreover, the average accuracy of the vehicle speed forecasting method based on BPNN is 95.72%. Therefore, the proposed methods can be used to estimate and predict vehicle speed from CFVD for ITS.
However, this study assumes that each MS in the car can be filtered and tracked for the collection of cellular network signals (e.g., CAs, HOs, NLUs and PLUs). In the future, filtering out non-vehicle terminals and correctly predicting the routes of vehicle terminals can be investigated in the next study. Furthermore, this study focuses on analyzing the signals from GSM and UMTS networks to estimate the traffic information of the highway for the evaluation of the proposed methods. As the demand for real-time traffic information increases, the next goal is to estimate and analyze the traffic congestion and transportation delays of urban road segments.