1. Introduction
In the well-known acoustic text book [
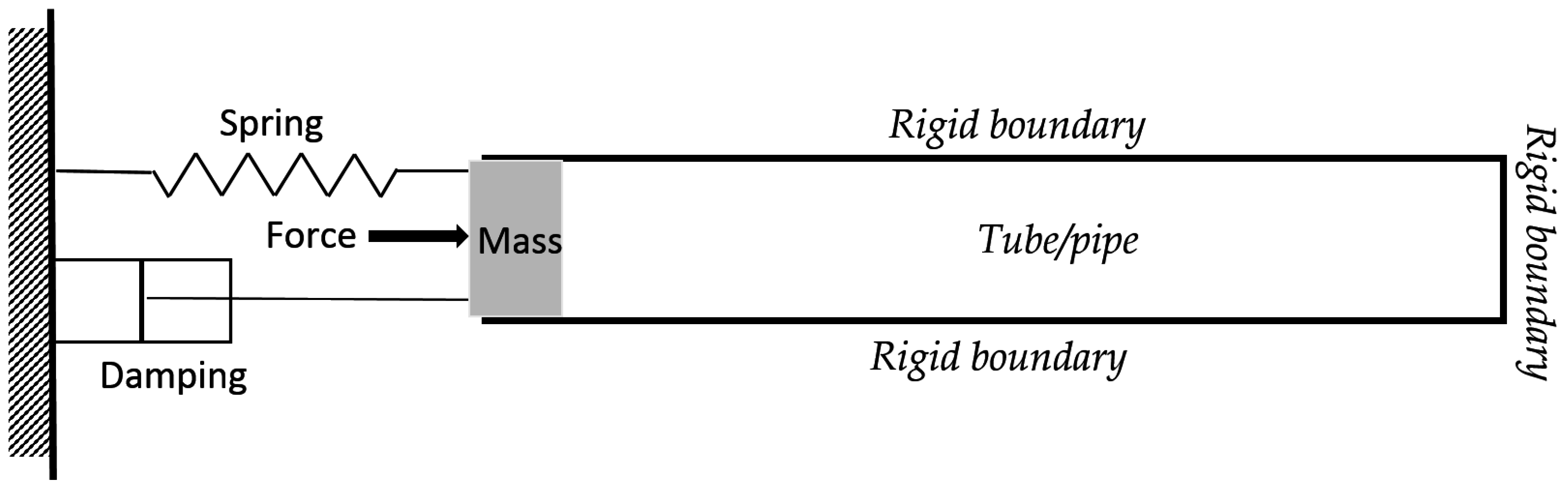
1], an investigation of resonating tube/pipe accounts for the properties of a mechanical driver, which is driven by external excitation (see
Figure 1). The driver has its own mechanical impedance. Thus, the system considers the coupling between a linear spring-mass and an internal cavity with rigid acoustic boundaries. Similar to other structural–acoustic problems, the aforementioned problem does not include the structural nonlinearity and non-rigid acoustic boundary.
In practice, there are many engineering problems with structural acoustics, a few examples being: (1) the sound absorption of a panel absorber backed by an air cavity; (2) the vibration response of an aircraft cabin which is a “tube-like” structure enclosing a cavity; and (3) the noise within a rectangular ventilation duct that is formed by thin metal sheets. In these examples, the structures are usually made of thin metal panels and are easily excited to vibrate nonlinearly, and the boundaries of the cavities are not perfectly rigid or fully open. In fact, there have been many research works about linear structural acoustics (e.g., [
2,
3,
4]) or nonlinear vibrations (e.g., [
5,
6,
7,
8,
9,
10,
11,
12]). However, there are limited works about nonlinear structural–acoustic problems with non-rigid acoustic boundary conditions. This study is a further work of the aforementioned linear structural–acoustic problem in [
1]. Thus, this paper would focus on structural nonlinearity and non-rigid acoustic boundary. Moreover, the multi-level residue harmonic balance method, which was developed by Leung and Guo [
13] in 2011, and then modified by Hansan et al. [
14] in 2013, is employed to solve the nonlinear differential equations, which represent the large-amplitude structural vibration of a flexible panel coupled with a cavity.
Table 1 shows the numbers of algebraic equations generated in the multi-level residue harmonic balance method and the classical harmonic method for a cubic nonlinear undamped beam problem. When compared with the classical harmonic balance method, this harmonic balance method requires less computational effort because it requires solving one nonlinear algebraic equation and one set of linear algebraic equations for obtaining each higher-level solution. The solutions from the proposed method are verified by those from the classical harmonic balance method. Parametric studies are performed, and the effects of structural nonlinearity and acoustic boundary condition on the nonlinear vibration responses are investigated in detail.
2. Theory
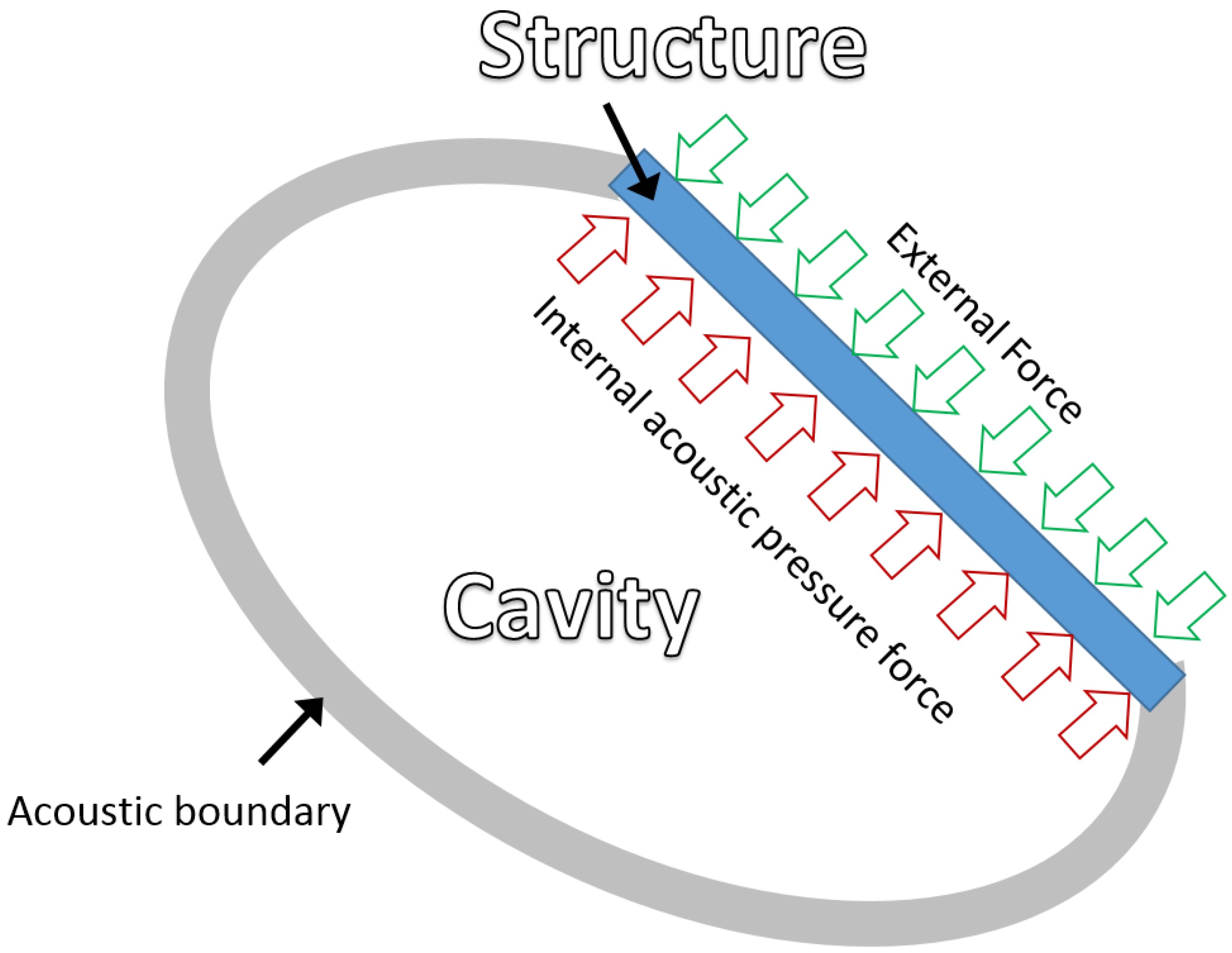
Figure 2 shows the general concept of a structural–acoustic model, in which the structural part is in contact with a finite cavity by physical boundaries. The enclosed volume would induce the acoustic resonant behavior, which is normally modeled using the well-known wave equation [
1,
2,
15,
16,
17]. This wave equation has been used in numerous applied science/engineering problems for the past few decades. The structural part in the model usually is a plate or a shell, which is subject to an external force and coupled with the internal acoustic pressure within the cavity. The structural vibration directly affects the magnitude of the acoustic pressure acting on the structure. This is so-called structural–acoustic interaction. In the past, many researchers just focused on particular linear/nonlinear plate modellings (e.g., [
5,
6,
7,
8,
9,
10,
11,
12,
18]) or linear structural–acoustic problems with perfectly rigid acoustic boundaries. In this paper, the focuses include the nonlinear structural–acoustic interaction and non-rigid acoustic boundary.
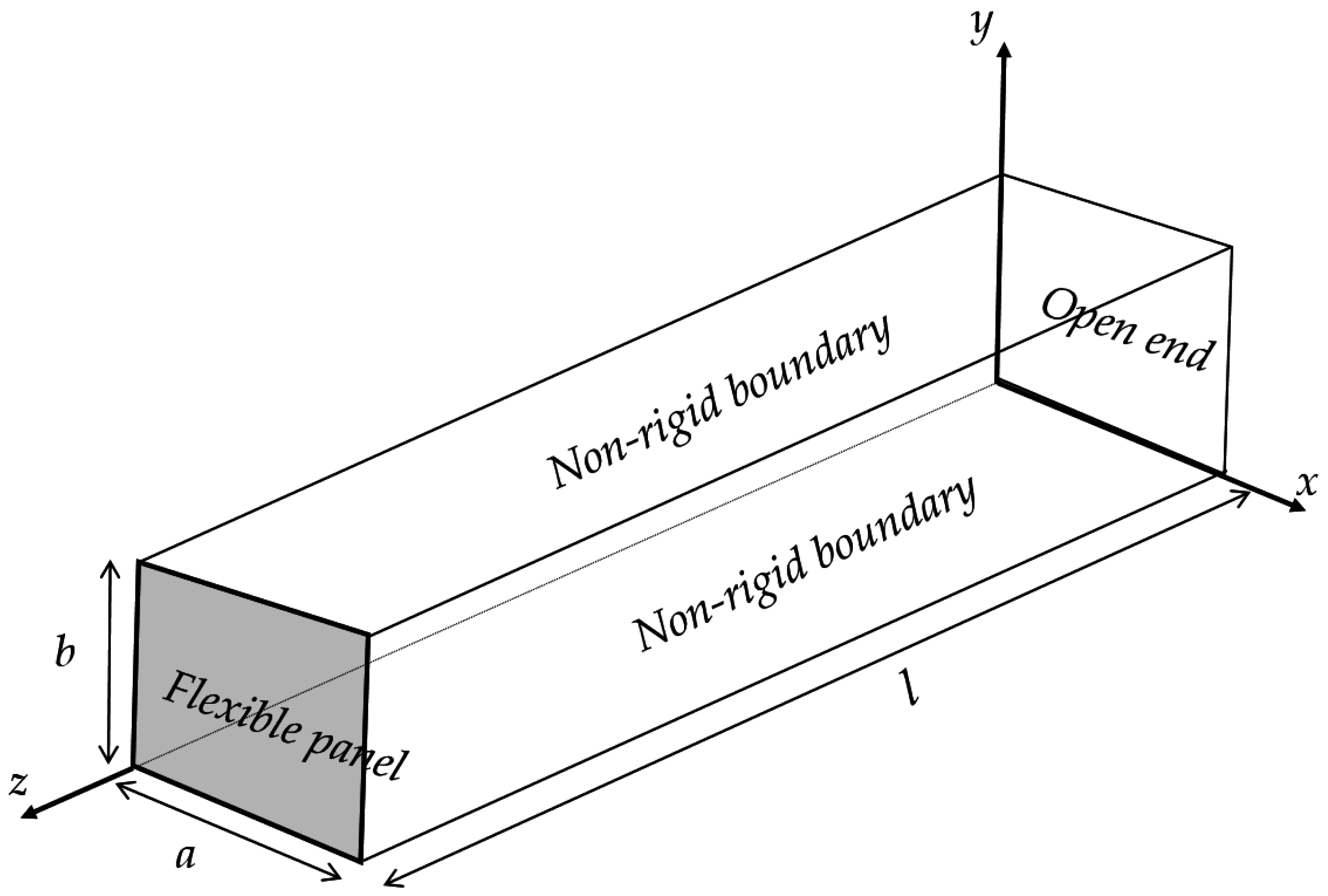
Figure 3 shows the problem considered in this study. The acoustic pressure within the rectangular tube is obtained from the homogeneous wave equation.
where
Ph is the
h-th harmonic component of the acoustic pressure within the cavity;
Ca is the speed of sound.
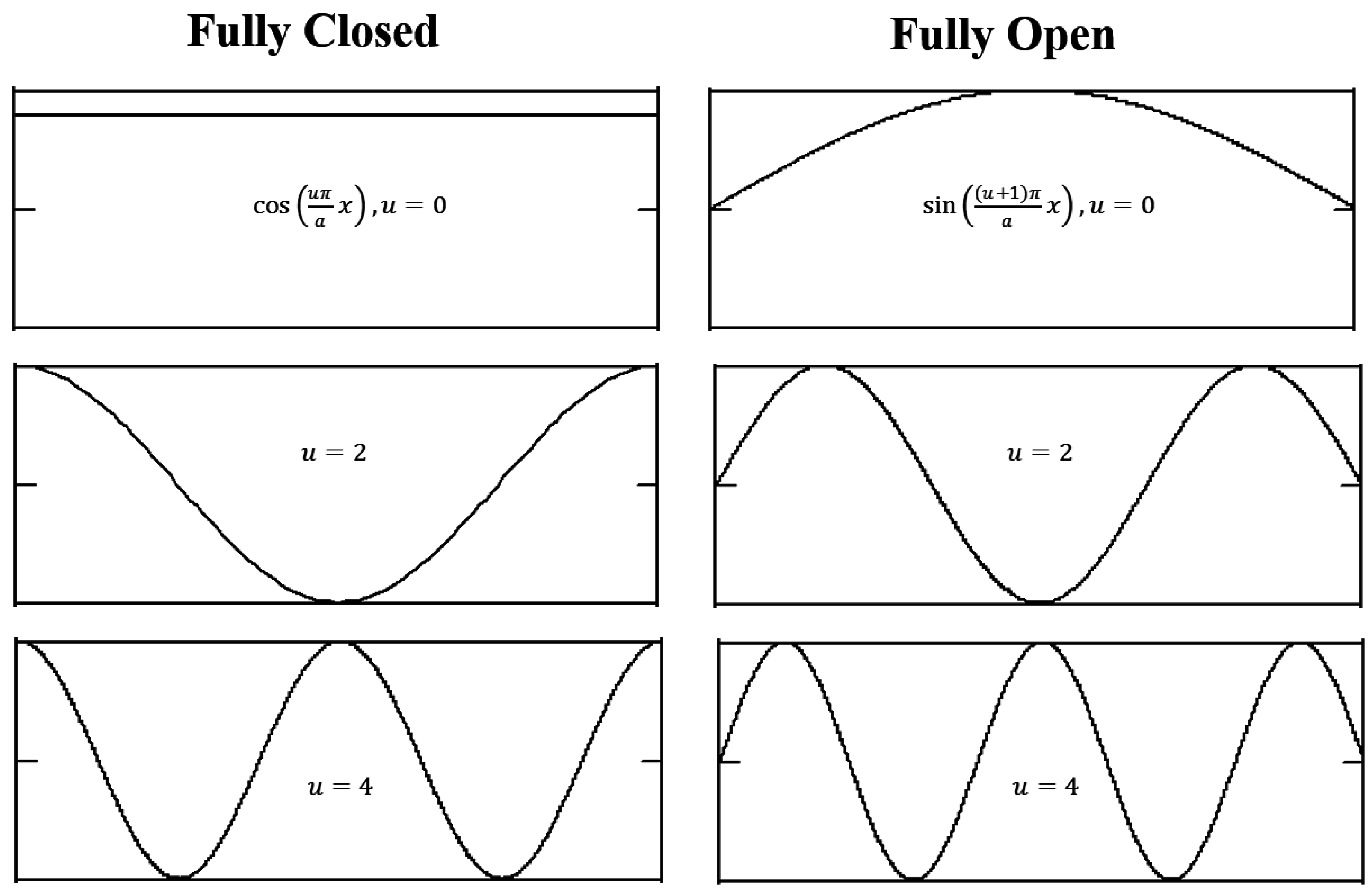
In
Figure 4, the boundary conditions of the perfectly rigid and fully open cases at
x = 0 and
a;
y = 0 and
b are given by
According to Equations (2a) and (2b), the acoustic pressure mode shapes of the perfectly rigid and fully open cases are given by
where
is the (
u,v) acoustic mode,
a and
b are the cross-sectional dimensions of the duct, and
u and
v are the acoustic mode numbers.
Hence, the acoustic pressure mode shape of non-rigid case is defined by
where
; θ is the phase shift parameter. If η is set as zero in Equation (4), then the acoustic mode shapes become those in the perfectly rigid case.
The boundary conditions at
z =
l and 0 are given by
where
l is the duct length; ρ
a = air density; ω = excitation frequency. Note that the external sound pressure at
z = 0 is simple harmonic excitation (i.e. no higher harmonic components).
P0 = excitation magnitude, γ ×
Pref; γ is the dimensionless parameter;
Pref is the reference pressure level, 10
2 N/m
2.
= the
hth harmonic component of the nonlinear panel displacement at
z = l.
where
= the (
m,n) panel mode (it is simply supported).
;
Ah is the panel vibration amplitude. The total response of the panel is equal to the summation of all harmonic components and given by
where
is the displacement response of the panel at
z =
l.
H = the number of harmonic terms. Then, the multi-level residue harmonic balance method is adopted for solving the differential equations and obtaining the unknown panel displacement responses. For simplicity, only the zero, 1st and 2nd level solution procedures (or three harmonic components are considered) are shown here. According to the multi-level residue harmonic balance solution form proposed in [
14,
19],
where ε is an embedding parameter. Any terms associated with ε
0, ε
1, ε
2 represent those terms considered in the zero, 1st and 2nd level solution procedures respectively. Then, the zero, 1st and 2nd level solutions,
,
and
, are given by
The 1st, 2nd and 3rd harmonic components of the total displacement amplitude,
,
and
, are given by
Then, the solution form of the acoustic pressure in Equation (1) is given by [
1,
2,
15,
16,
19]
where
;
and
are coefficients that depend on the boundary conditions at
z = 0 and
z = l;
U and
V are the numbers of acoustic modes used.
The unknown coefficients and can be obtained by applying the boundary condition at z = 0 and z = l in Equations (5a)–(5c) to Equation (11). They are given by for h = 1, and ; for h ≠ 1, and ; ; ; ; .
Once
and
are obtained, the modal pressure force magnitude at
z =
l can be found using Equation (11)
where
;
.
In this study, the nonlinear free vibration formulation of panel adopted in [
16] is employed.
where
ρl and ω
l are the surface density and linear resonant frequency of the panel; β
l represents the nonlinear stiffness coefficient due to the large-amplitude vibration.
where
r = a/b is the aspect ratio;
ν is the Poisson’s ratio.
E is the Young’s modulus. τ is the panel thickness.
By putting the acoustic force terms developed from Equations (12a) and (12b) into Equation (13), the governing equation for the nonlinear forced vibrations is given by
Substitute Equation (9) into Equation (15) and consider those terms associated with ε
0. Then consider the harmonic balance of
. The zero-level equation without the damping term is given by
where
; The unbalanced residual in the zero-level procedure is
.
According to Equation (16), the damped vibration amplitude is given in the following form
where
;
;
is the internal material damping coefficient;
is the nonlinear resonant peak frequency; “
” represents the radiation damping term [
1,
20].
Again, substitute Equation (9) into Equation (15) and consider those terms associated with
ε1 to obtain the following 1st level equation
where
L1 represents the summation of the 1st level terms and the unbalanced residual in the zero level.
is the residual in the zero level.
Then, consider the harmonic balances of
and
for Equation (18)
Hence, and can be found by solving Equations (19a) and (19b).
Similarly, substitute Equation (9) into Equation (15) and consider those terms associated with ε
2 to obtain the following 2nd level equation
where
L2 represents the summation of the 2nd level terms and the unbalanced residual in the 1st level.
is the residual in the zero level.
Then, consider the harmonic balances of
,
and
for Equation (20)
Hence, , and can be found by solving Equations (21a)–(21c).
3. Results and Discussion
In this section, the material properties in the numerical cases are as follows: Young’s modulus = 7.1 × 10
10 N/m
2, Poisson’s ratio = 0.3, and mass density = 2700 kg/m
3; panel dimensions = 0.4 m × 0.4 m × 2 m; damping ratio ξ = 0.02.
Table 2,
Table 3 and
Table 4 show the convergence studies of normalized panel vibration amplitude for various excitation magnitudes and frequencies. The nine acoustic mode solutions, three structural mode solutions, and 2nd level solutions are normalized as one hundred. The acoustic boundaries are rigid (i.e., θ = 0). The zero, 1st and 2nd level solutions contain 1, 2 and 3 harmonic components, respectively (i.e.,
,
, and
). It is shown that the 1st level 4 acoustic mode and two structural mode approach is good enough for convergent and accurate vibration amplitude solution.
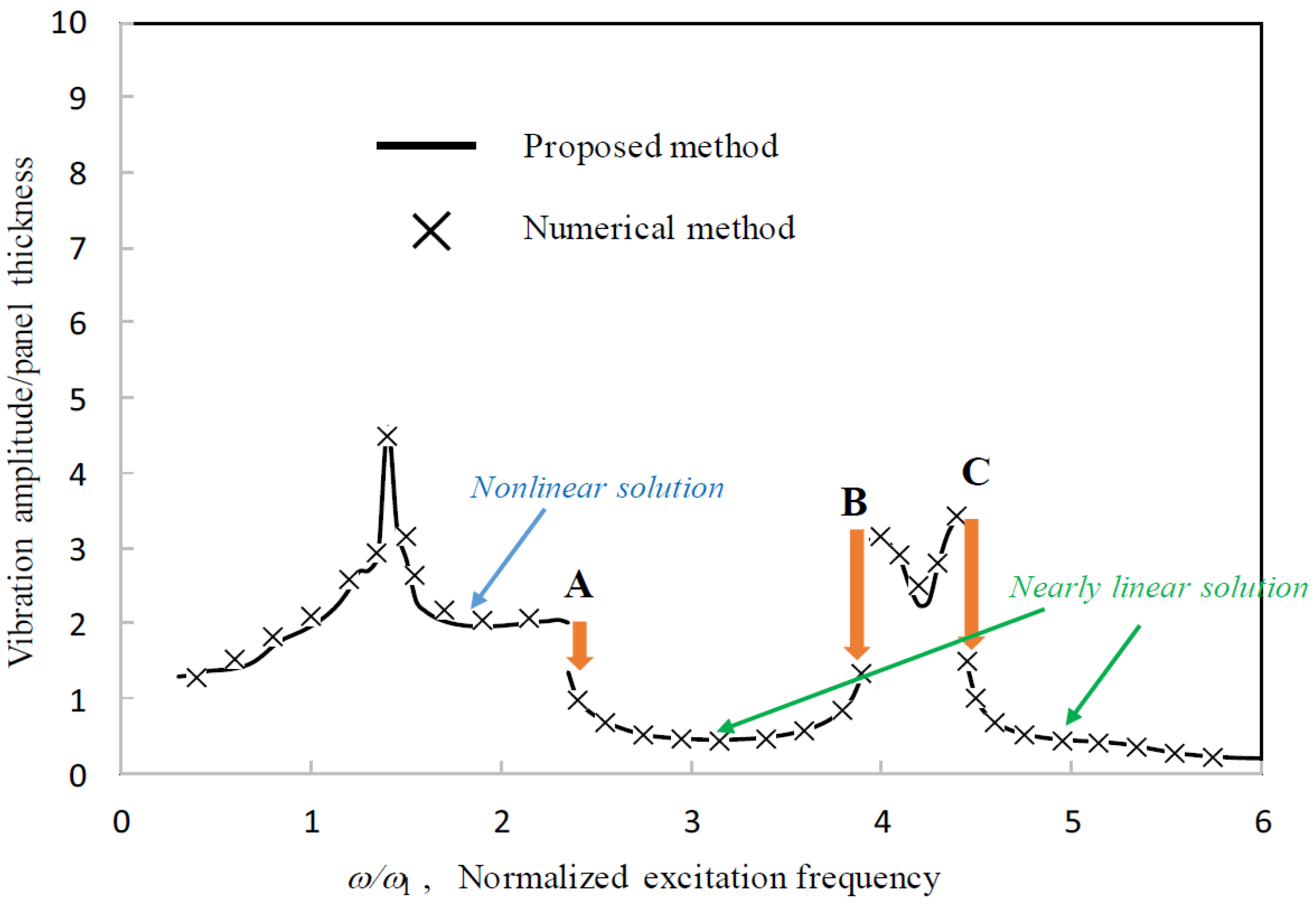
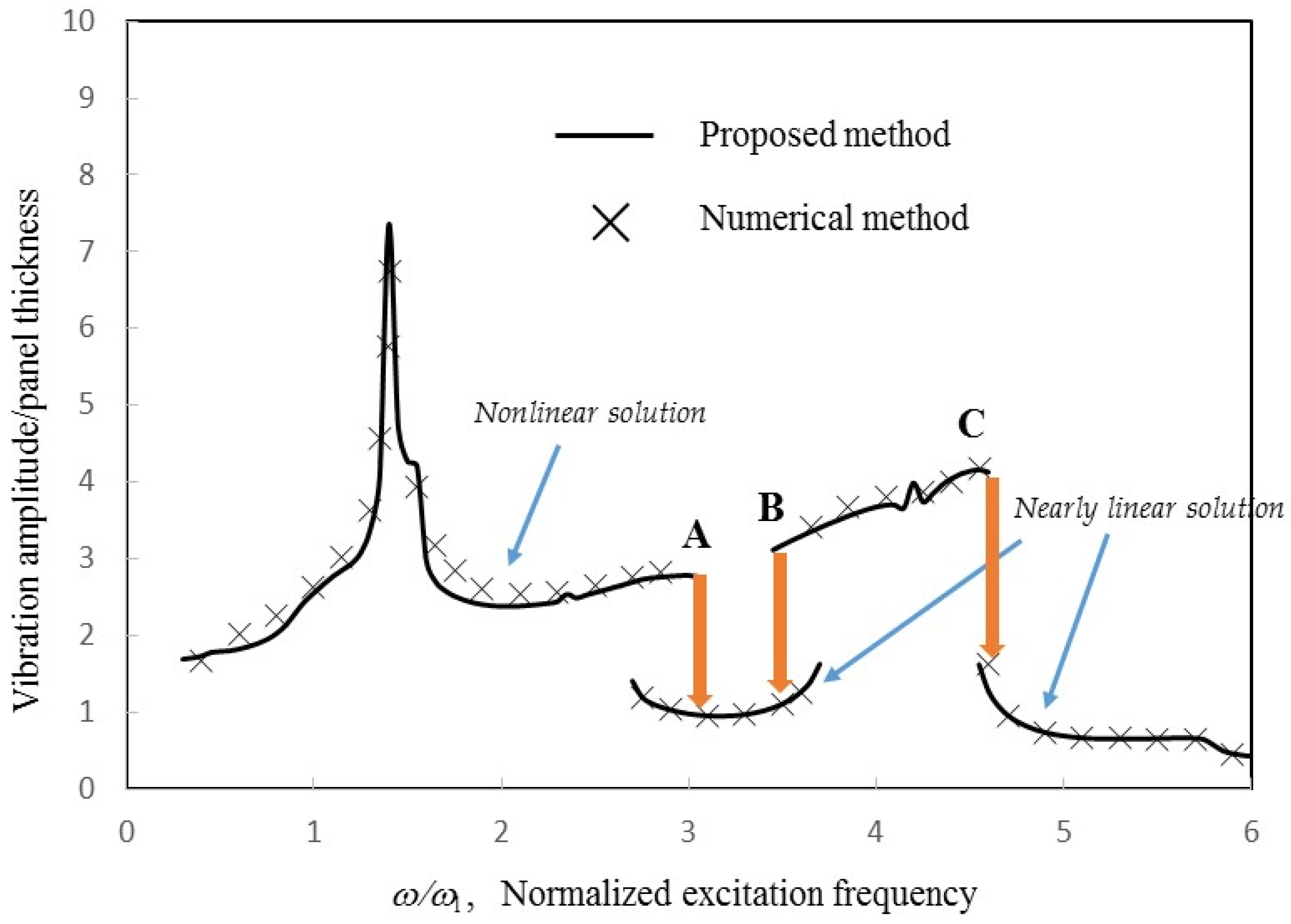
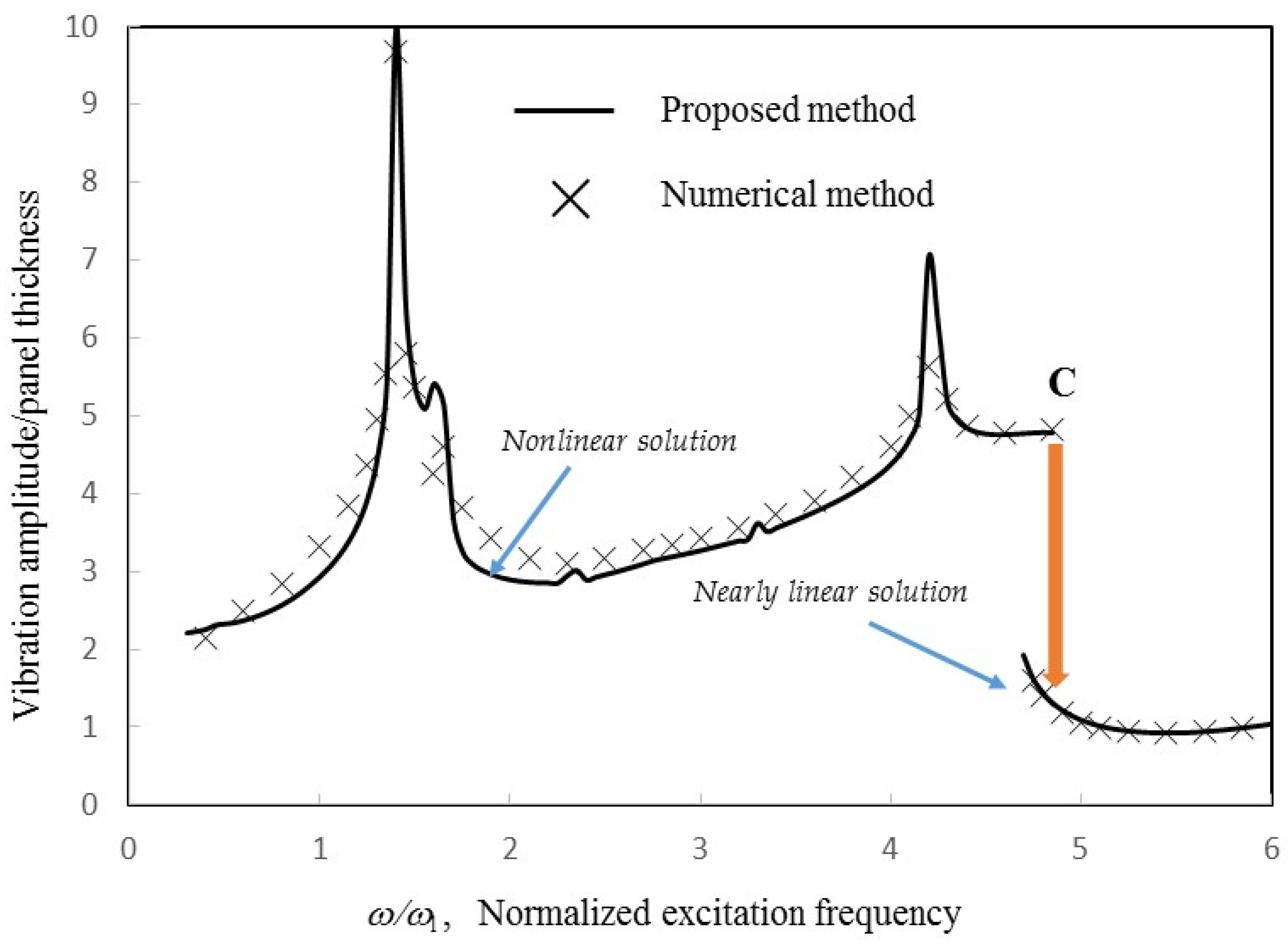
Figure 5,
Figure 6 and
Figure 7 present the comparisons between the vibration amplitudes obtained from the present harmonic balance method and numerical method used in [
6]. The results obtained from the two methods are generally in good agreement. Note that the numerical method is unable to generate the unstable solutions. For fair comparisons, the unstable solutions from the harmonic balance methods are not generated. In fact, the classical harmonic balance method can be coupled with the asymptotic numerical method, which enables the capture of unstable solutions (e.g., [
21,
22,
23]). According to [
14], the solutions from the proposed method come from the cubic algebraic equations transformed from the Duffing differential equations representing the nonlinear panel vibration. The unstable solutions occur when the cubic algebraic equations have three real solutions. Generally, the unstable solution is in between the nonlinear and nearly linear solutions. It is slightly lower than the real nonlinear solution around the peak frequency and slightly higher than the nearly linear solution when the excitation frequency is far from the peak frequency.
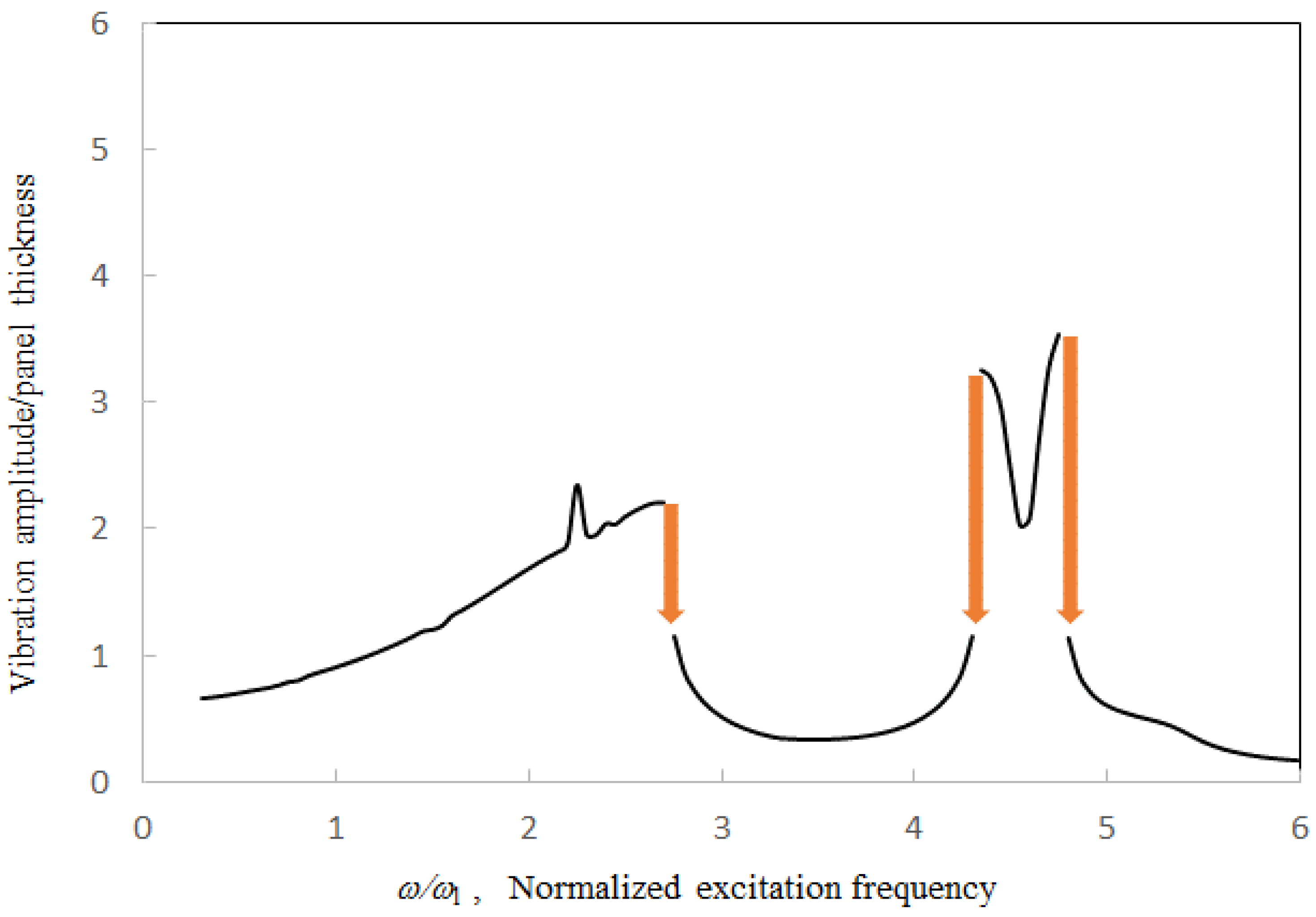
Relatively, the agreement in
Figure 5 is the best because of smaller nonlinearity. In
Figure 6 and
Figure 7, some deviations are observed around the major peak values. Note that there are some minor peaks around ω/ω
l = 2.3 and 3.4 in
Figure 7. In these three cases, the first acoustic resonances occur around ω/ω
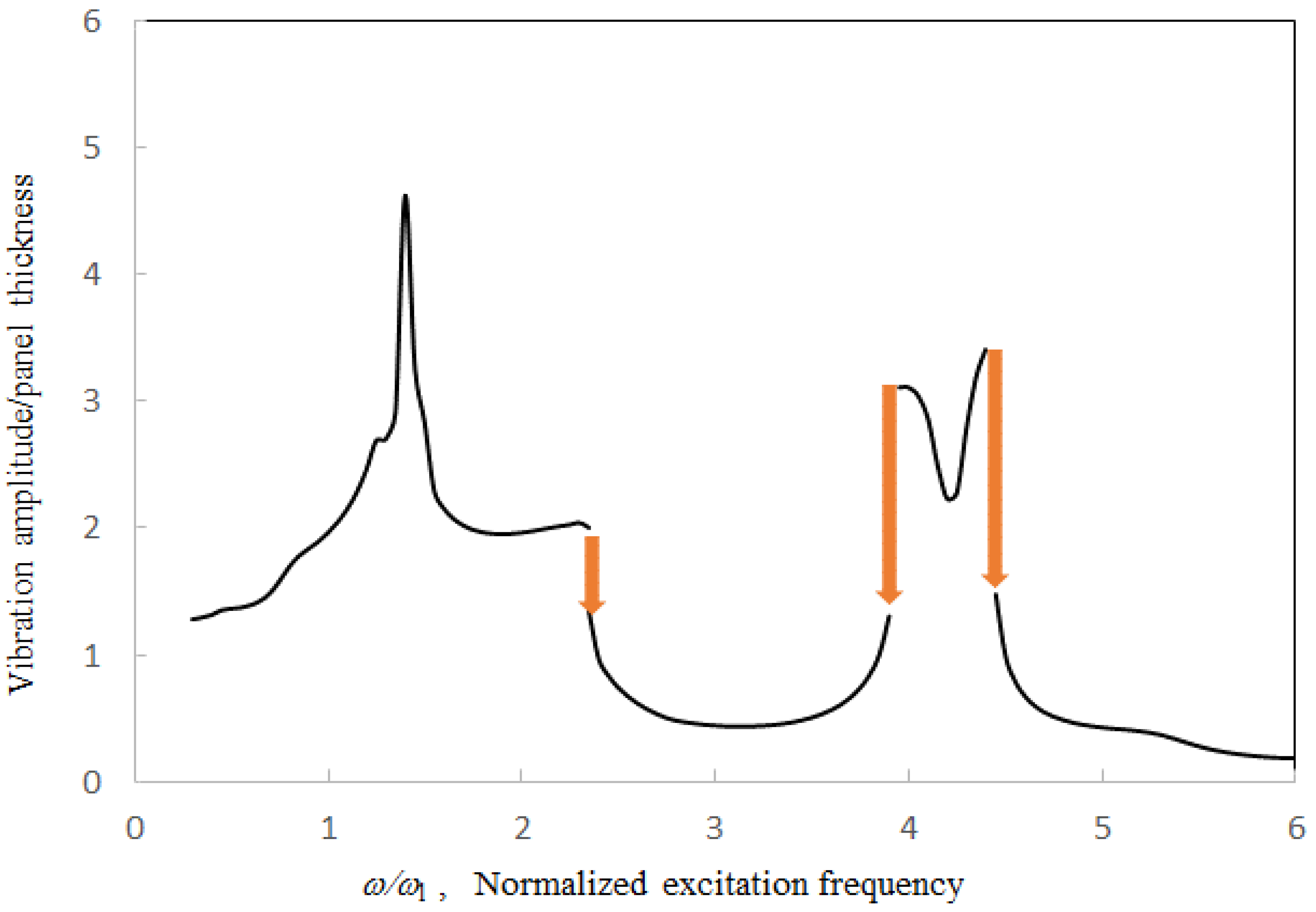
l = 1.4. In the case of γ = 2, the well-known jump phenomena, which are due to the first structural resonance and higher acoustic resonances, occurs around ω/ω
l = 2.3, 3.9 and 4.5 (see Points A, B and C). The nonlinear solution line discontinues there. Generally, the nearly linear solution lines are much lower than the nonlinear solution lines. In the cases of γ = 4 and 8, the jump phenomena due to the first structural resonance and higher acoustic resonances occur at the higher frequencies. Unlike the trough on the solution line in the case of γ = 2, a small peak and a large peak occur on the nonlinear solution lines of γ = 4 and 8 around ω/ω
l = 4.2, respectively. Besides, Points A and B in the case of γ = 4 are very close. There are no Points A and B in the case of γ = 8 (i.e., no discontinuous portion). In
Figure 7, due to the large excitation level, the vibration responses are highly nonlinear. The nonlinear solution lines further extend so that Points A and B are joined and the linear solution line disappears. In this case, there is only one real solution obtained from the cubic algebraic equation transformed from the Duffing differential equations representing the nonlinear panel vibration. In the practical structural design of a similar structural–acoustic system, the disappearance of the linear solution (or small-amplitude solution), which is replaced by the nonlinear solution (or large-amplitude solution), implies that a stronger structural design is needed to overcome the larger vibration amplitude.
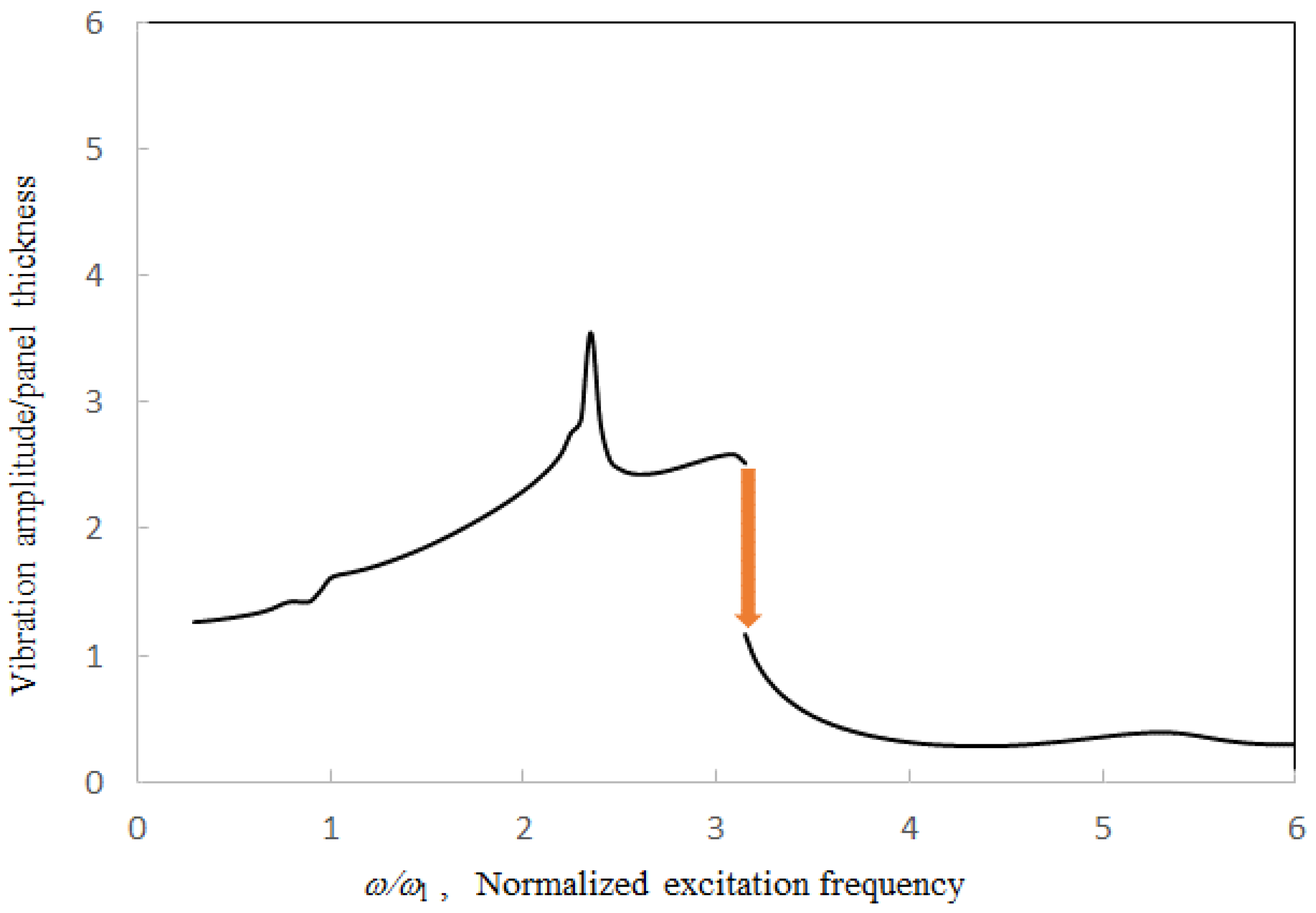
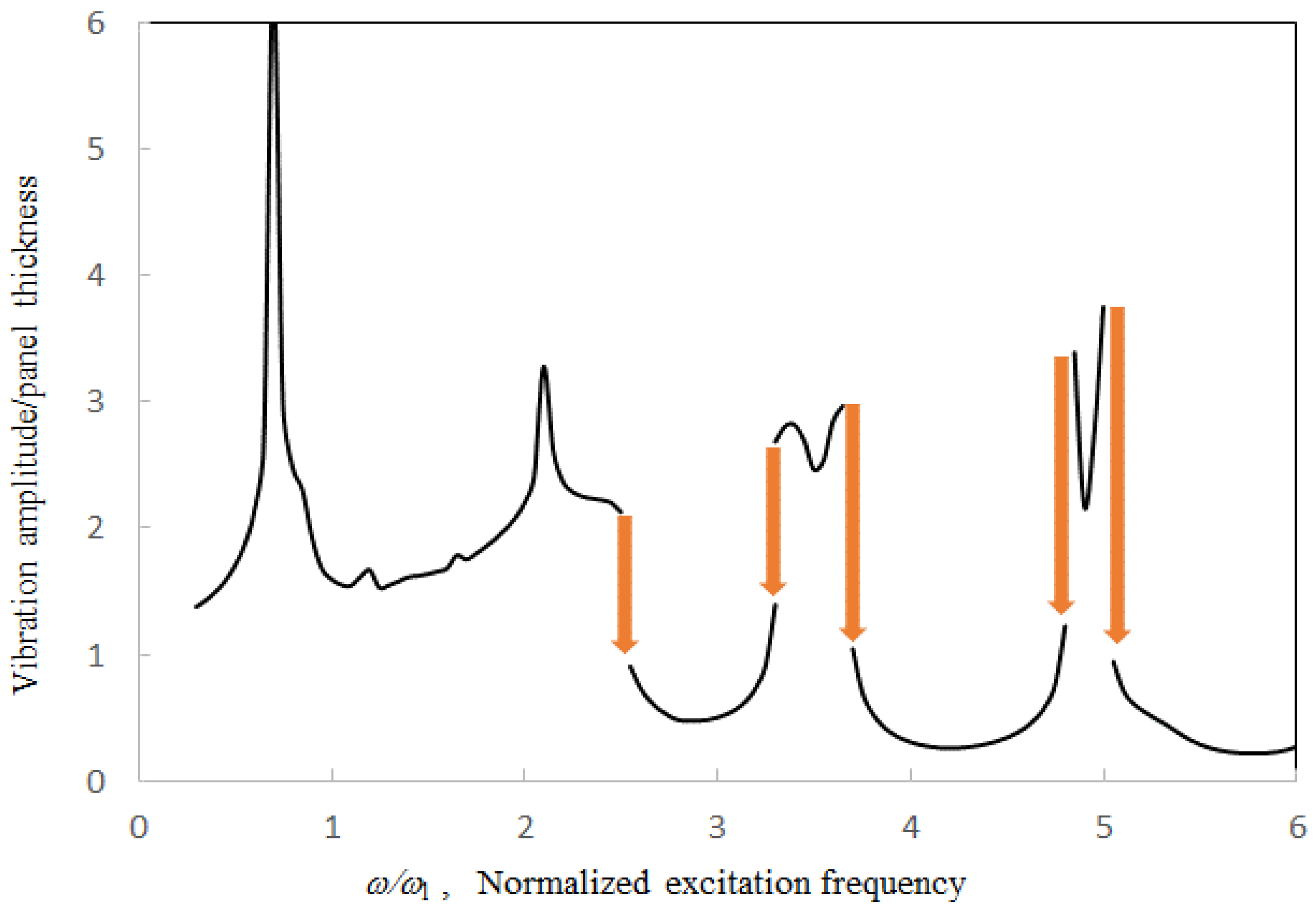
Figure 8,
Figure 9 and
Figure 10 show the vibration amplitude plotted against the excitation frequency for various tube lengths. The first peak value due to the acoustic resonance and first jump-down frequency increase with the tube length, while the first peak frequency and the first trough frequency decrease with the tube length. In the case of
l = 10
a, the tube length is the longest among the three cases. Thus, the second peak occurs around ω/ω
l = 2.1, which is lower than the first jump-down frequency, and there are more acoustic resonant peaks on the solution line. In the case of
l = 3
a, the tube length is the shortest among the three cases. The trough occurs out of the frequency range (i.e. ω/ω
l > 6).
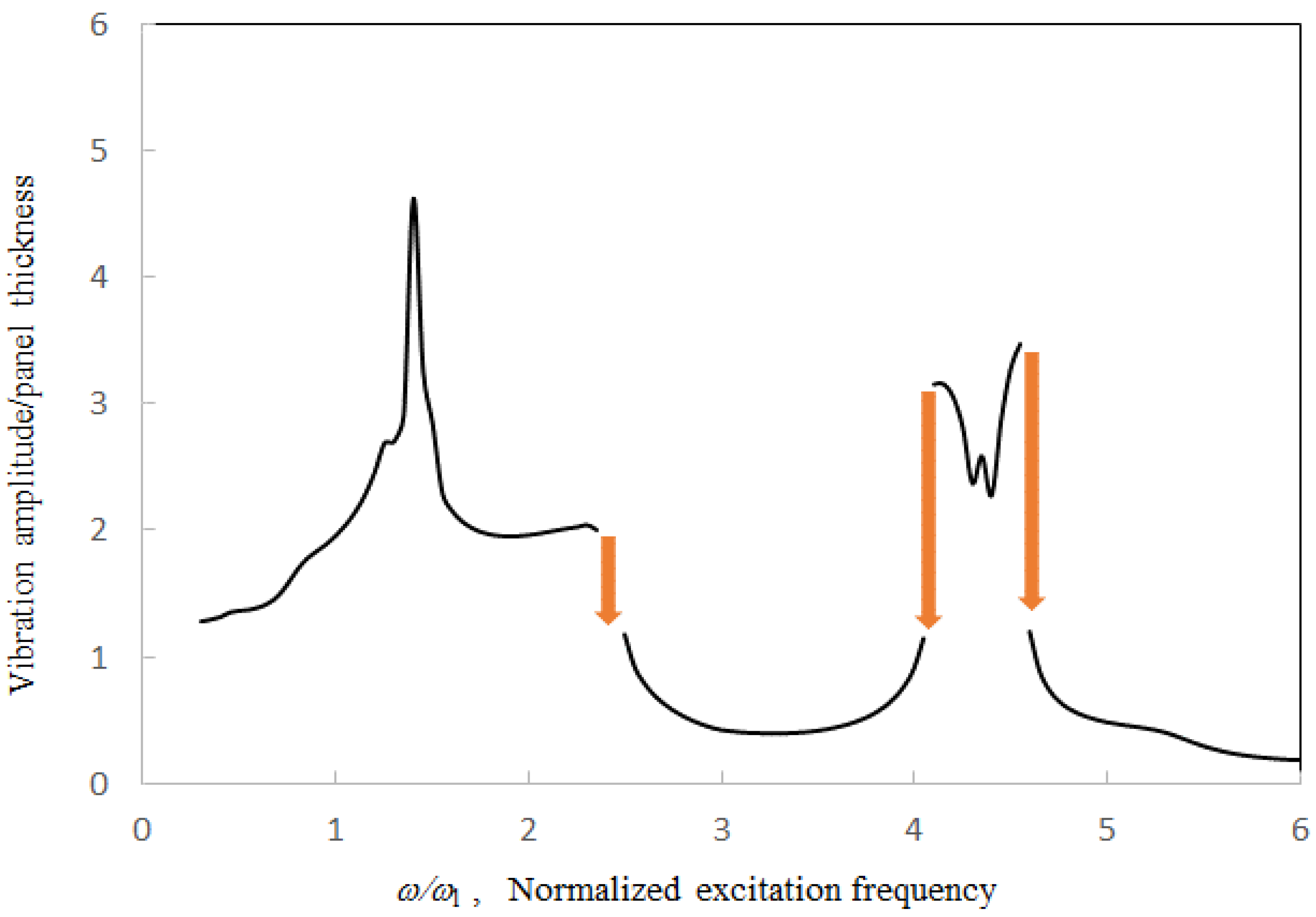
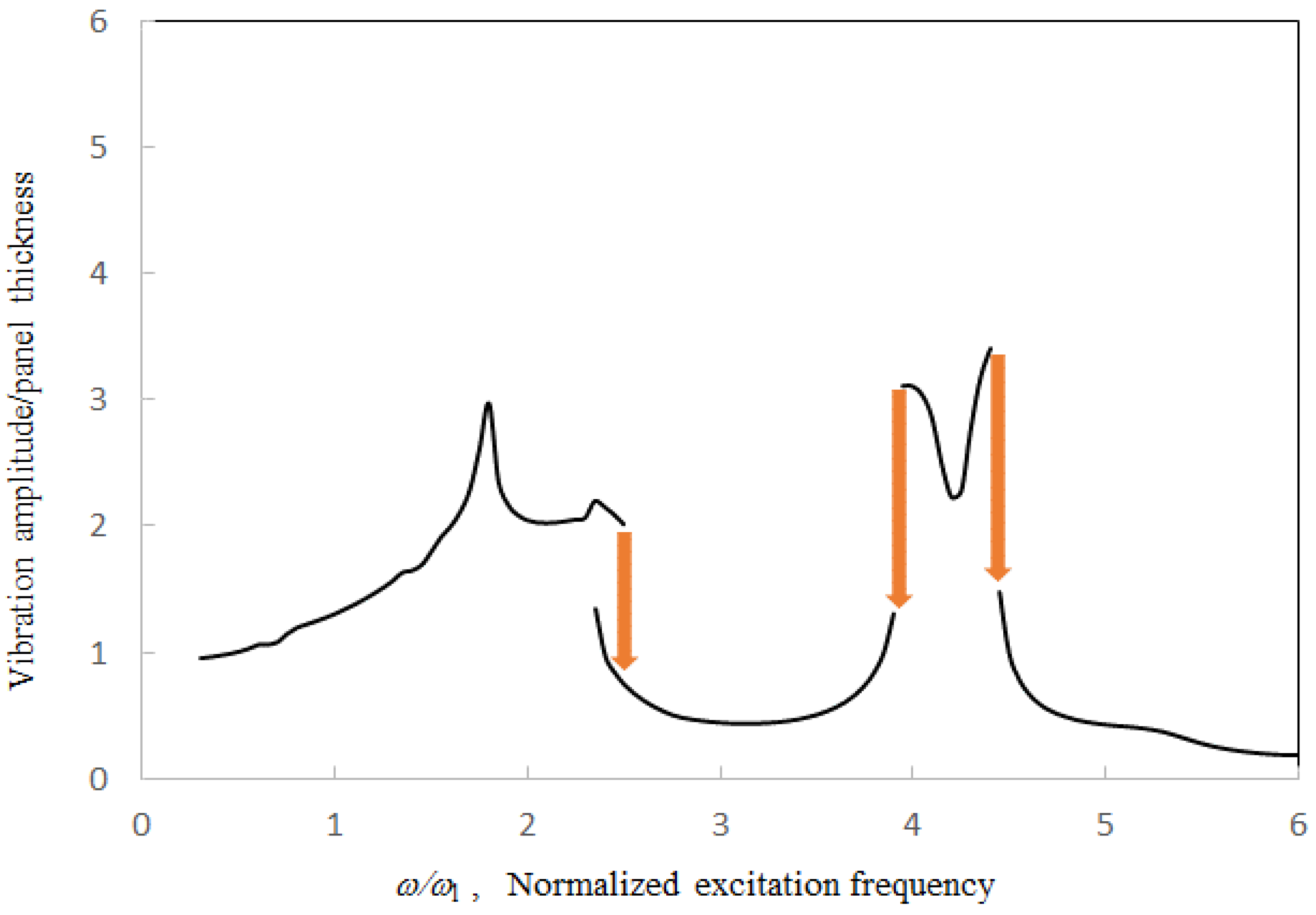
Figure 11,
Figure 12 and
Figure 13 show the vibration amplitude plotted against the excitation frequency for various phase shift parameters. The first peak frequency due to the acoustic resonance, the first jump-down frequency, and the trough frequency increase with the phase shift parameter, while the first peak value decreases with the tube length. In the cases of θ = 5 and 10, it is implied that the tube boundaries are not perfectly rigid and the corresponding air particle velocities are non-zero. It is noted that the first peak is quite small, marginally detectable when the phase shift is only 8 degrees.
Moreover, the phase shift does not significantly affect the higher acoustic resonances.
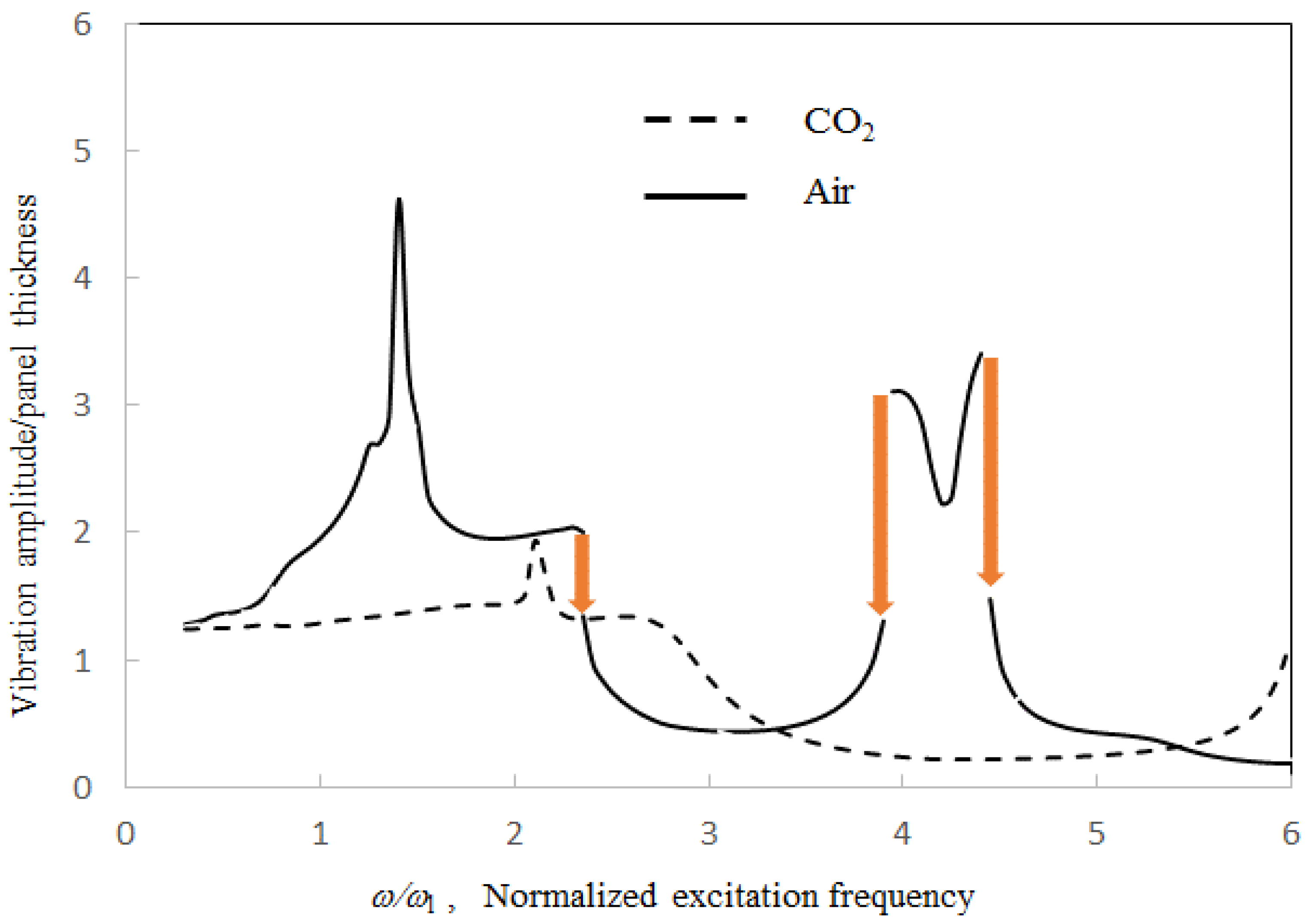
Figure 14 shows the vibration amplitudes of the tubes filled with air and CO
2 plotted against the corresponding excitation frequency. The density of CO
2 and the corresponding sound speed are about 50% higher than those in the case of air. There is a big difference between the two cases. In the case of CO
2, the first peak is much smaller and the jump phenomenon disappears. The peaks due to higher acoustic resonances are out of the frequency range. In the practical structural design of a similar structural–acoustic system, the disappearance of the nonlinear solution (or large-amplitude solution), which is replaced by the linear solution (or small-amplitude solution), implies that a smaller amount of structural material is needed.