Axial Turbine Cascade Correlation
Abstract
:1. Introduction
2. Flow Loss Model
3. Cascade Experiments
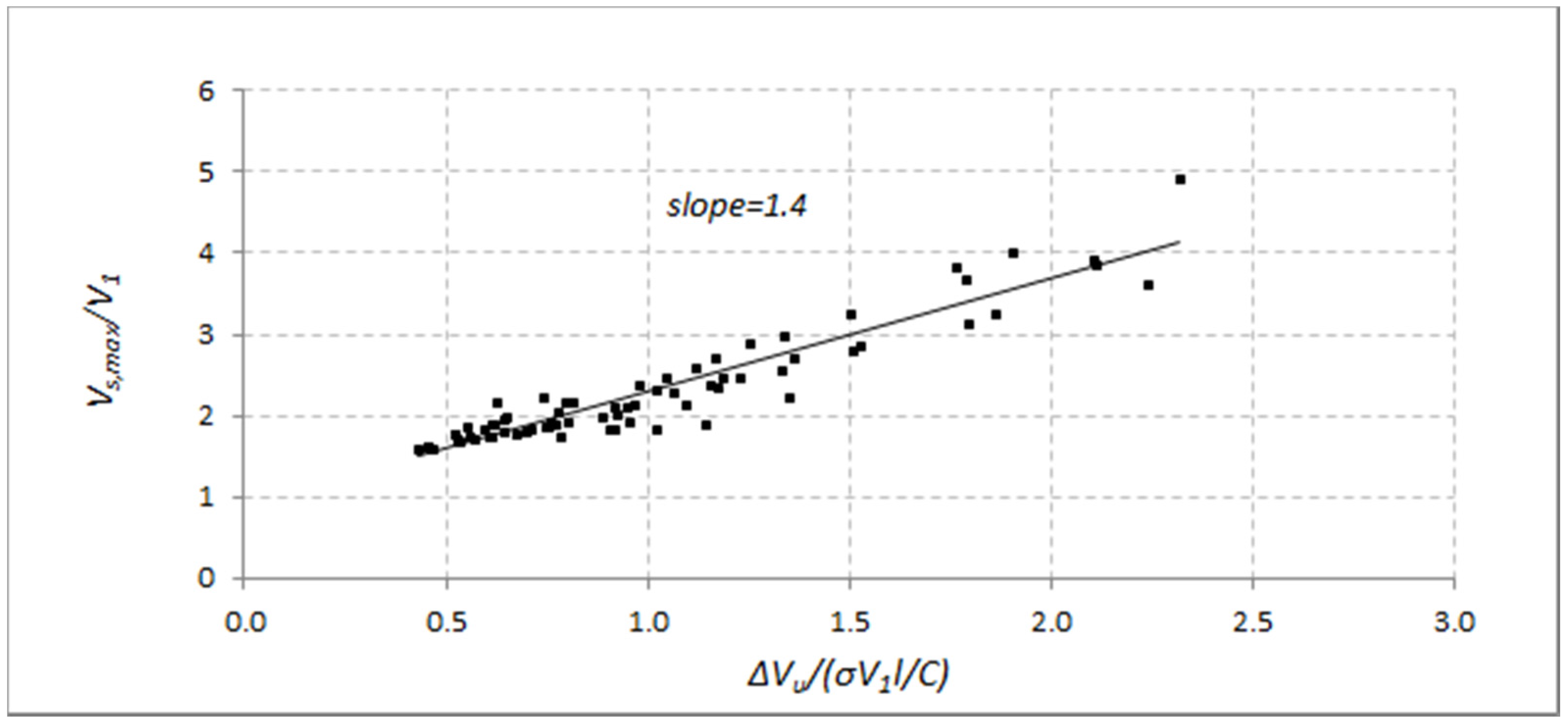
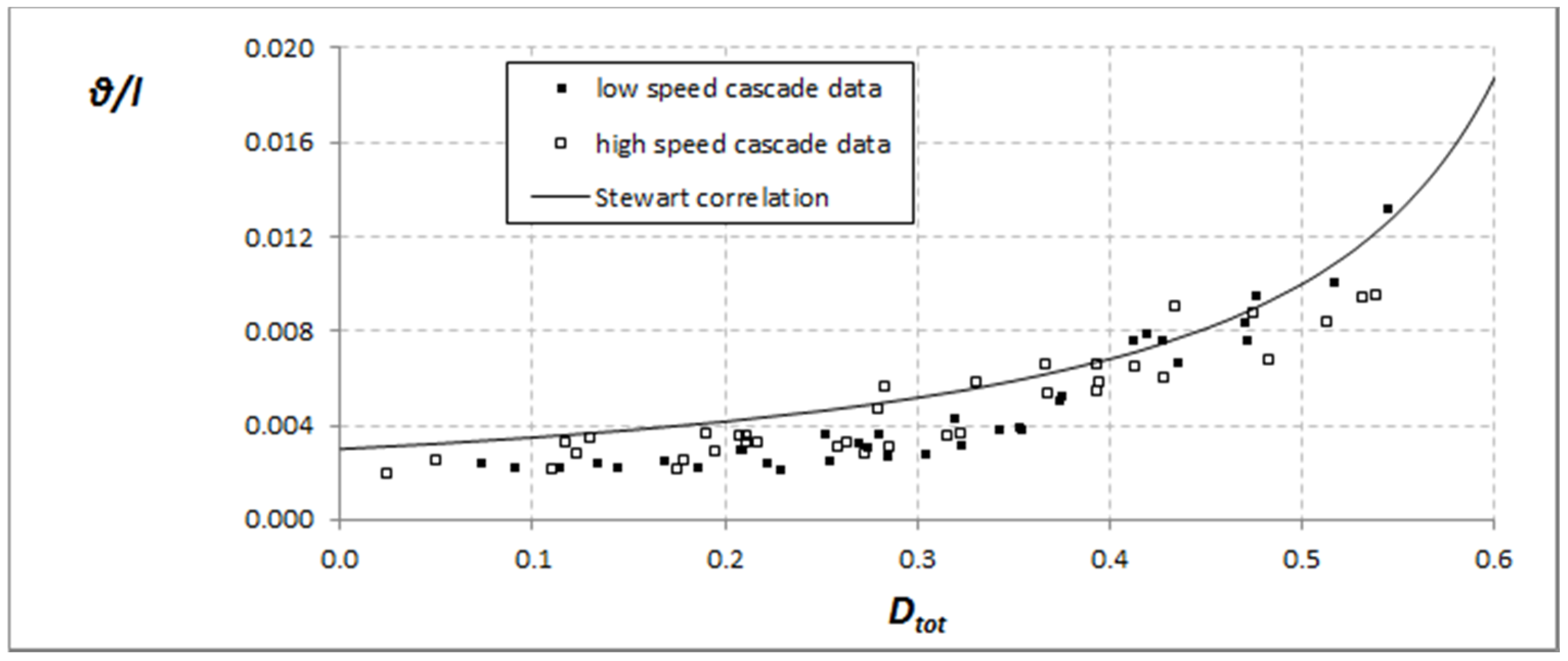
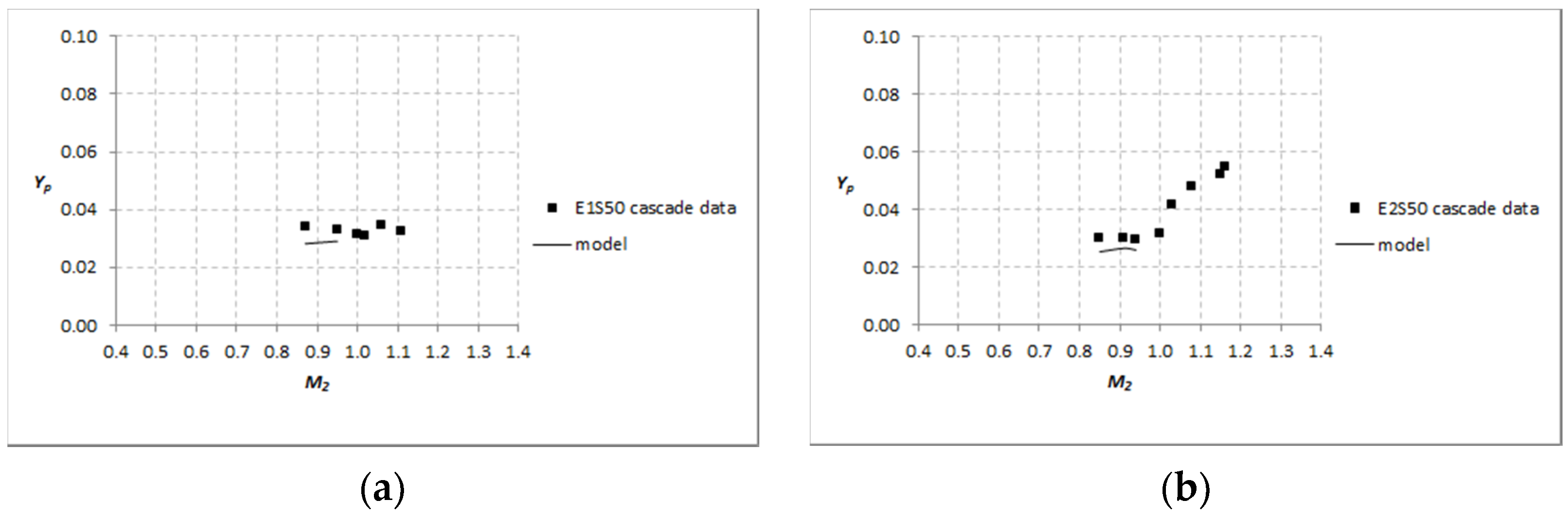
3.1. Analysis of Experimental Data
3.2. Cascade Correlation
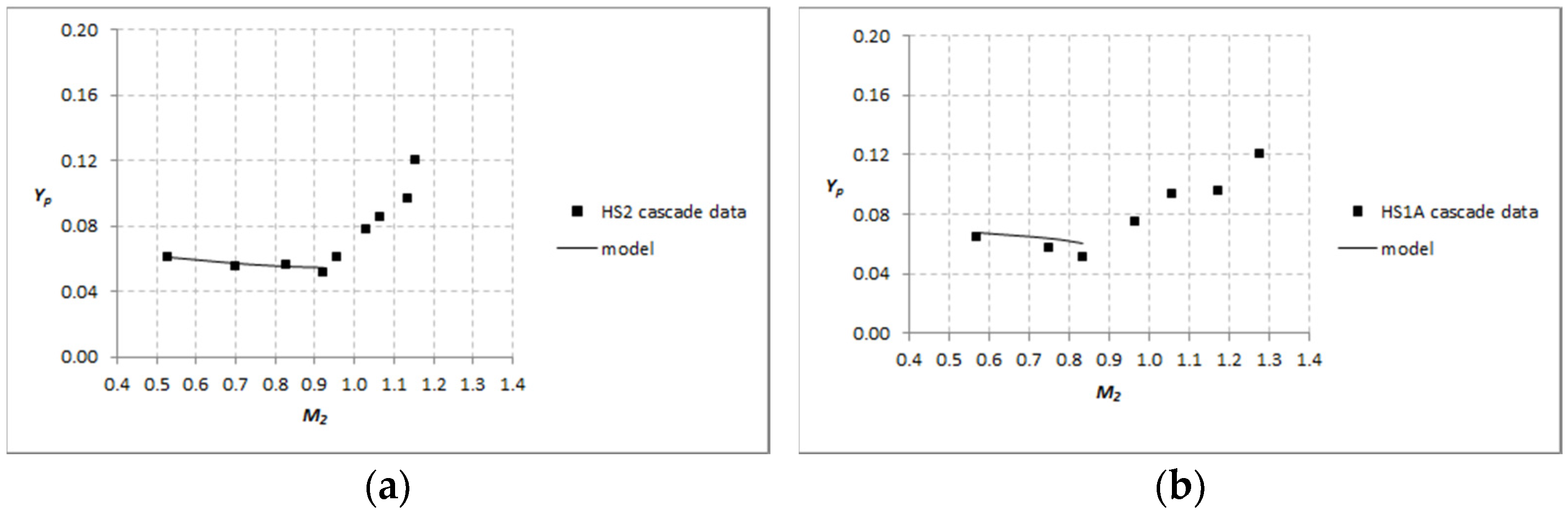
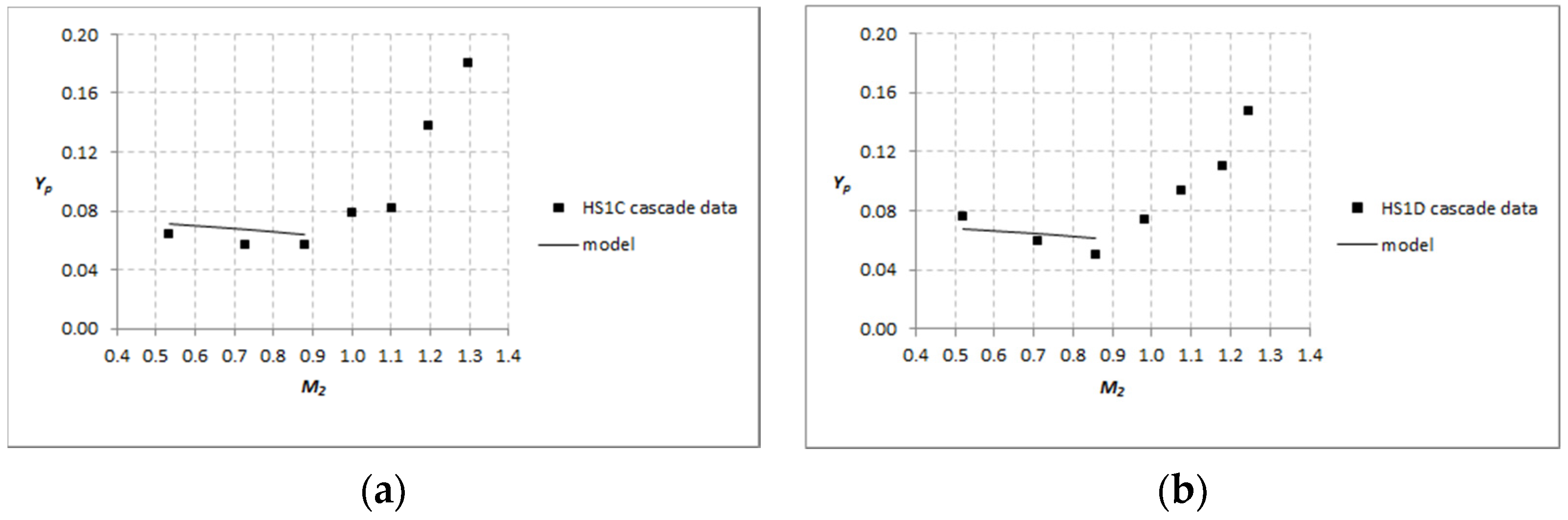
3.3. Transonic Cascade
4. Further Validation
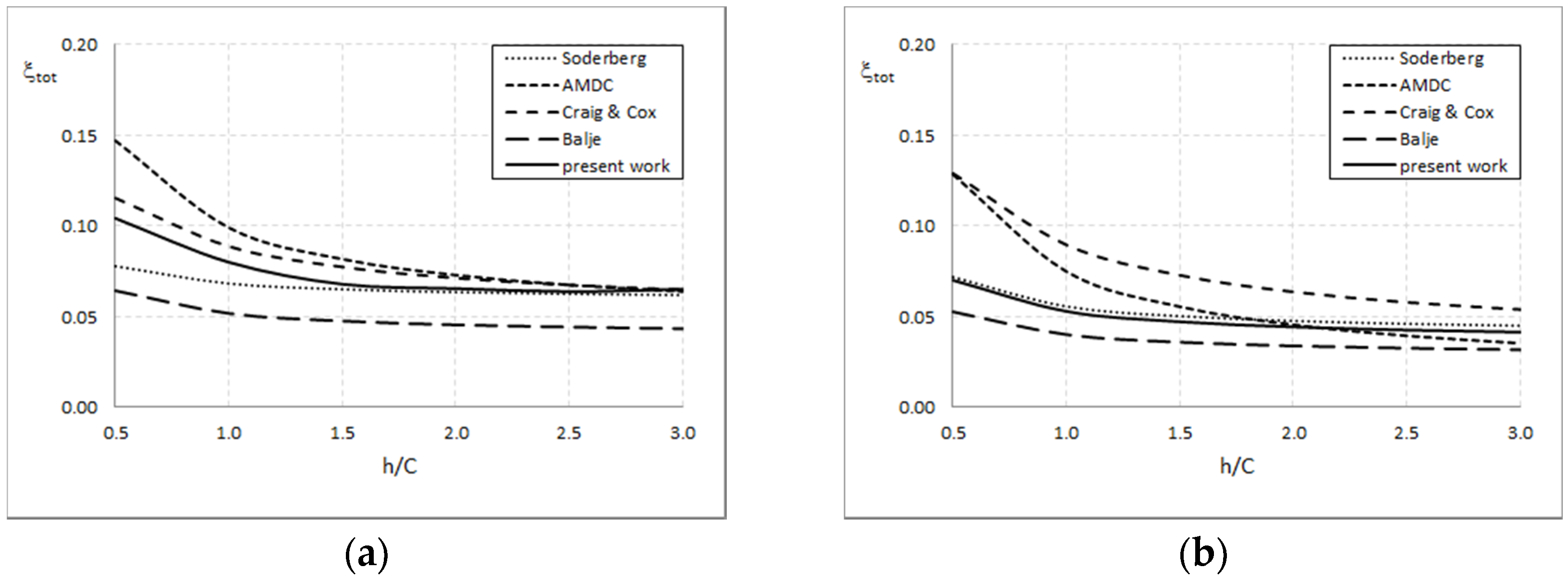
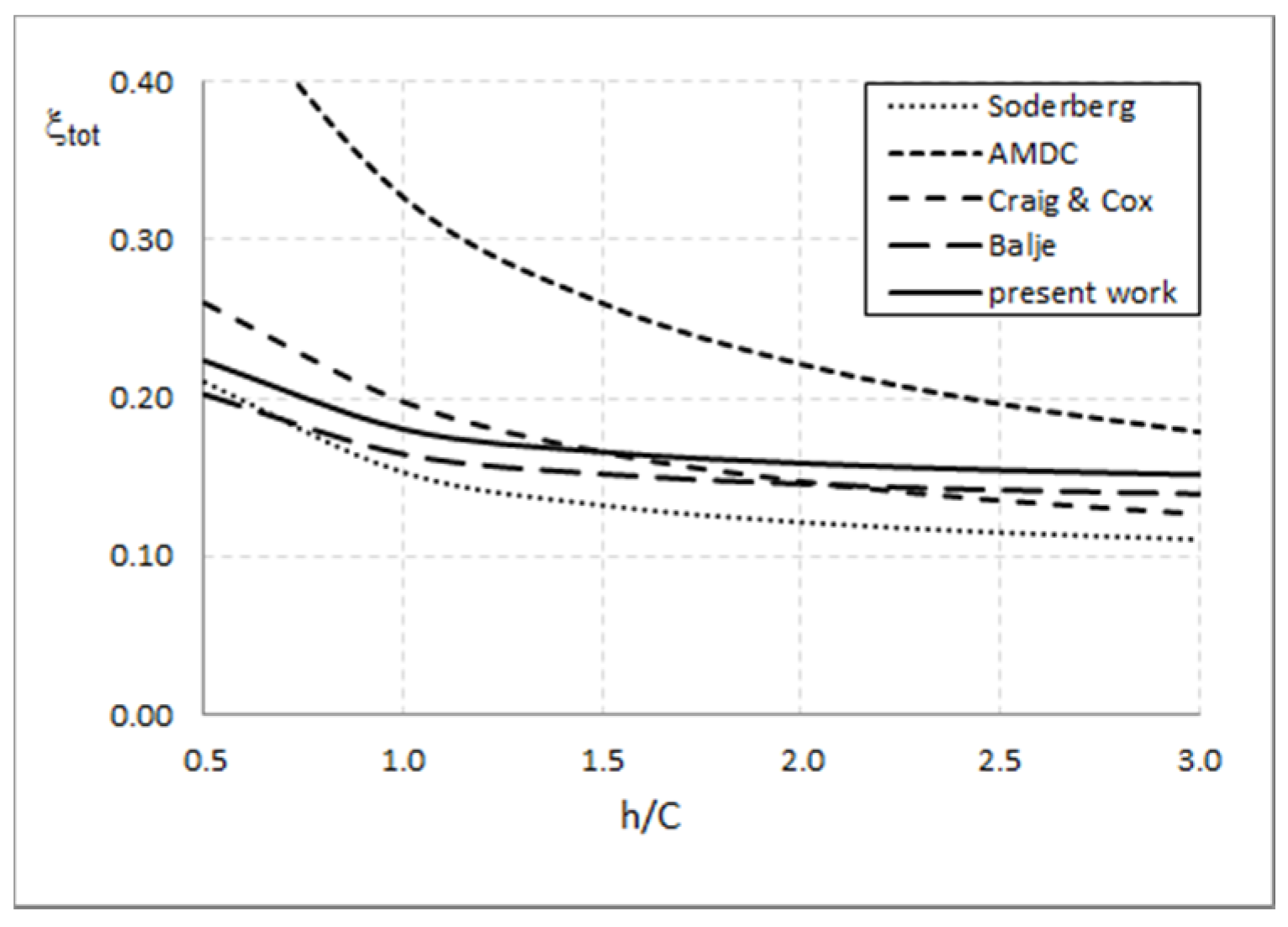
4.1. Comparison with Traditional Estimation Methods
4.2. Comparison with Stage Performance Results
4.3. Design Point Performance Simulation
5. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| C | Blade chord length |
| c0 | Spouting velocity, from converting the ideal enthalpy drop into kinetic energy |
| d | Blade thickness |
| D | Diffusion factor |
| h | Blade span |
| l | Blade meanline curvature length |
| M | Mach number |
| t | Blade pitch |
| u | Blade peripheral speed |
| V | Velocity |
| Y | Total pressure loss coefficient |
| λ | Flow angle |
| ξ | Enthalpy or kinetic energy loss coefficient, based on isentropic kinetic energy |
| θ | Boundary layer momentum thickness |
| σ | Cascade solidity, chord to pitch ratio. |
Subscipts: | |
| 1 | Upstream |
| 2 | Downstream |
| min | Minimum |
| max | Maximum |
| p | Pressure surface |
| s | Suction surface |
| u | Tangential direction |
| x | Axial direction |
| tot | Total |
References
- Horlock, J.H.; Denton, J.D. A Review of Some Early Design Practice Using Computational Fluid Dynamics and a Current Perspective. J. Turbomach. 2005, 127, 5–13. [Google Scholar] [CrossRef]
- Denton, J.D. Throughflow Calculations for Transonic Axial Flow Turbines. ASME J. Eng. Power 1978, 100, 212–218. [Google Scholar] [CrossRef]
- Denton, J.D. An Improved Time-Marching Method for Turbomachinery Flow Calculation. ASME J. Eng. Power 1983, 105, 514–521. [Google Scholar] [CrossRef]
- Baljé, O.E. A Study on Design Criteria and Matching of Turbomachines: Part A–Similarity Relations and Design Criteria of Turbines. ASME J. Eng. Power 1962, 84, 83–102. [Google Scholar] [CrossRef]
- Glassman, A.J. Turbine Design and Application; NASA SP-290; NASA: Washington, DC, USA, 1972; p. 390. [Google Scholar]
- Dixon, S.L. Fluid Mechanics and Thermodynamics of Turbomachinery, 4th ed.; Butterworth-Heinemann: Woburn, MA, USA, 1998. [Google Scholar]
- Ainley, D.G.; Mathieson, G.C.R. A Method of Performance Estimation for Axial-Flow Turbines; N.G.T.E. Report R. 111; Aeronautic Research Council: London, UK, 1952. [Google Scholar]
- Dunham, J.; Came, P.G. Improvements to the Ainley-Mathieson Method of Turbine Performance Prediction. J. Eng. Power 1970, 92, 252–256. [Google Scholar] [CrossRef]
- Kacker, S.C.; Okapuu, U. A Mean Line Prediction Method for Axial Flow Turbine Efficiency. J. Eng. Power 1981, 104, 111–119. [Google Scholar] [CrossRef]
- Craig, H.R.M.; Cox, H.J.A. Performance Estimation of Axial Flow Turbines. Proc. Inst. Mech. Eng. 1970, 185, 407–424. [Google Scholar] [CrossRef]
- Baljé, O.E. Axial Cascade Technology and Application to Flow Path Designs. ASME J. Eng. Power 1968, 90, 309–328. [Google Scholar] [CrossRef]
- Lieblein, S.; Schwenk, F.C.; Broderick, R.L. Diffusion factor for Estimating Losses and Limiting Blade Loadings in Axial Flow Compressor Blade Elements; NACA RM E53D01; National Advisory Committee for Aeoronautics: Washington, DC, USA, 1953.
- Lieblein, S. Loss and Stall Analysis of Compressor Cascades. ASME J. Basic Eng. 1959, 81, 387–400. [Google Scholar]
- Stewart, W.L.; Whitney, W.J.; Wong, R.Y. A Study of Boundary Layer Characteristics of Turbomachine Blade Rows and their Relation to Over-all Blade Losses. ASME J. Eng. Power 1960, 82, 588–592. [Google Scholar]
- Dunavant, J.C.; Erwin, J.R. Investigation of a Related Series of Turbine-Blade Profiles in Cascade; NACA TN 3802; National Advisory Committee for Aeoronautics: Washington, DC, USA, 1956.
- Stewart, L.; Whitney, W.; Miser, J. Use of Momentum Thickness in Describing Turbine Rotor-Blade Losses; NACA RM E56B29; National Advisory Committee for Aeoronautics: Washington, DC, USA, 1956.
- Baljé, O.E. A Study on Reynolds Number Effects in Turbomachines. ASME J. Eng. Power 1964, 86, 227–235. [Google Scholar] [CrossRef]
- Langston, L.S. Crossflows in a Turbine Cascade Passage. J. Eng. Power 1980, 102, 866–874. [Google Scholar] [CrossRef]
- Stewart, W.L.; Whitney, W.J.; Wong, R.Y. Use of Mean Section Boundary Layer Parameters in Predicting Three Dimensional Turbine Stator Losses; NACA RM E55L12A; National Advisory Committee for Aeoronautics: Washington, DC, USA, 1956.
- Stewart, W.L. Analysis of Two-Dimensional Compressible Flow Loss Characteristics Downstream of a Turbomachine Blade Rows in Terms of Basic Boundary Layer Characteristics; NACA TN 3515; National Advisory Committee for Aeoronautics: Washington, DC, USA, 1955.
- Monaco, L.; Vogt, D.; Fransson, T. A New Linear cascade Test Facility for Use in Engineering Education. In Proceedings of the XXI Biennial Symposium on Measuring Techniques in Turbomachinery, Valencia, Spain, 22–23 March 2012.
- Kiock, R.; Lehthaus, F.; Baines, N.C.; Sieverding, C.H. The Transonic Flow through a Plane Turbine Cascade as Measured in Four European Wind Tunnels. ASME J. Eng. Gas Turbines Power 1986, 108, 277–284. [Google Scholar] [CrossRef]
- Jeffries, M.S. Initial Investigations of the Transonic Turbine Aerodynamics Using the Carleton University High-Speed Wind Tunnel. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, October 2000. [Google Scholar]
- Corriveau, D. Influence of Loading Distribution on the Performance of High Pressure Turbine Blades. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, July 2005. [Google Scholar]
- Sooriyakumaran, C. Experimental Study of Profile Losses in Three Transonic Turbine Cascades. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2014. [Google Scholar]
- Sieverding, C.H. Axial Turbine Performance Prediction Methods. In Thermodynamics and Fluid Mechanics of Turbomachinery; Üçer, A.Ş., Stow, P., Hirsch, C.H., Eds.; Martinus Nijhoff Publishers: Dordrecht, The Netherlands, 1985; Volume II, pp. 737–784. [Google Scholar]
- Mee, D.J.; Baines, N.C.; Oldfield, M.L.G.; Dickens, T.E. An Examination of the Contributions to Loss on a Transonic Turbine Blade in Cascade. J. Turbomach. 1992, 114, 155–162. [Google Scholar] [CrossRef]
- Martelli, F.; Boretti, A. A Simple Procedure to Compute Losses in Transonic Turbine Cascades. In Proceedings of the Gas Turbine Conference and Exhibit, Houston, TX, USA, 18–21 March 1985.
- Graham, C.G.; Kost, F.H. Shock Boundary layer Interaction on High Turning Transonic Turbine Cascades. In Proceedings of the ASME 1979 International Gas Turbine Conference and Exhibit and Solar Energy Conference, San Diego, CA, USA, 12–15 March 1979.
- Berrino, M.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F. Aerodynamic Loading distribution Effects on Off-Design Performance of a Highly Loaded LP Turbine Cascades Under Steady and Unsteady Incoming Flows. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016.
- Howell, R.J.; Ramesh, O.N.; Hodson, H.P.; Harvey, N.W.; Schulte, V. High Lift and Aft Loaded Profiles for Low Pressure Turbines. J. Turbomach. 2000, 123, 181–188. [Google Scholar] [CrossRef]
- Lozza, G. A Comparison between the Craig & Cox and the Kacker-Okapuu Methods of Turbine Performance Prediction. Meccanica 1982, 17, 211–221. [Google Scholar]
- Wei, N. Significance of Loss Models in Aerothermodynamic Simulation for Axial Turbines. Ph.D. Thesis, Kungliga Tekniska högskolan, Stockholm, Sweden, 2000. [Google Scholar]
- Benini, E.; Boscolo, G.; Garavello, A. Assessment of Loss Correlations for Performance Prediction of Low Reaction Gas Turbine Stages. In Proceedings of the ASME 2008 International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008.
- Miser, J.W.; Stewart, W.L.; Whitney, W. Analysis of Turbomachine Viscous Losses Affected by Changes in Blade Geometry; NACA RM E56F21; National Advisory Committee for Aeoronautics: Washington, DC, USA, 1956.
- Martins, G.L. Performance of Single Stage Partial Admission Axial Expander Applied to a Waste Heat Recovery Rankine Organic Cycle. Ph.D. Thesis, PUC-RIO, Rio de Janeiro, Brazil, May 2015. [Google Scholar]
- Ohlsson, G.O. Low Aspect Ratio Turbines. ASME J. Eng. Power 1964, 86, 13–16. [Google Scholar] [CrossRef]
- Ohlsson, G.O. Admission, Low Aspect Ratios and Supersonic Speeds in Small Turbines. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, January 1956. [Google Scholar]
- American Petroleum Institute. Petroleum, Petrochemical and Natural Gas Industries—Steam Turbines—Special Purpose Applications, 7th ed.; API Standard 612; American Petroleum Institute: Washington, DC, USA, 2014. [Google Scholar]
- The American Sociaty of Mechanical Engineers. ASME Performance Test Code 6 on Steam Turbines; ASME PTC 6-2004; ASME: New York, NY, USA, 2004. [Google Scholar]
- Macchi, E.; Perdichizzi, A. Efficiency Prediction for Axial-Flow Turbines Operating with Nonconventional Fluids. J. Eng. Power 1981, 103/719, 718–724. [Google Scholar] [CrossRef]
- Aungier, R.H. Turbine Aerodynamics: Axial-Flow and Radial-Flow Turbines Design and Analysis; ASME: New York, NY, USA, 2006. [Google Scholar]
- Baljé, O.E. Turbo Machines, A Guide to Design, Selection and Theory; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
| Cascade | HS2 | HS1A | HS1C | HS1D | E1S50 | E2S50 |
|---|---|---|---|---|---|---|
| solidity-σ | 1.408 | 1.414 | 1.387 | 1.486 | 1.474 | 1.519 |
| inlet flow angle-λ1 | 120° | 136° | 136° | 136° | 96° | 108° |
| exit flow angle-λ2 | 22° | 31.5° | 31.5° | 31.5° | 30.3° | 40.4° |
| trailing edge blockage | 0.181 | 0.079 | 0.079 | 0.079 | 0.021 | 0.045 |
| Rotor | h/C | ξtot (Experiment) | ξtot (Simulation) |
|---|---|---|---|
| a | 0.44 | 0.253 | 0.272 |
| b | 0.79 | 0.272 | 0.243 |
| c | 0.18 | 0.554 | 0.821 |
| d | 0.11 | 0.769 | --- |
| Parameter | Turbine #1 | Turbine #2 |
|---|---|---|
| specific speed | 0.203 | 0.116 |
| specific diameter | 5.86 | 10.48 |
| velocity ratio-u/c0 | 0.395 | 0.413 |
| machine Reynolds number | 1.57 × 107 | 4.50 × 107 |
| admission fraction | 0.41 | 0.29 |
| nozzle blade axial solidity | 1.13 | 1.73 |
| nozzle blade exit metal angle | 18° | 16° |
| rotor blade aspect ratio | 1.41 | 0.49 |
| rotor blade solidity | 1.42 | 1.66 |
| rotor blade hub to tip radius ratio | 0.88 | 0.93 |
| rotor blade stagger angle | 90° | 70° |
| rotor blade flare angle | 7° | 4° |
| rotor blade exit metal angle | 30° | 25° |
| number of rotating blades | 98 | 72 |
| axial clearance between rotor and stator blades to tip diameter ratio | 0.004 | 0.012 |
| Parameter | Turbine #1 | Turbine #2 |
|---|---|---|
| nozzle enthalpy loss coefficient | 0.078 | 0.099 |
| nozzle exit Mach number | 1.28 | 1.24 |
| rotor blade diffusion factor | 0.54 | 0.51 |
| rotor enthalpy loss coefficient | 0.135 | 0.195 |
| rotor relative inlet Mach number | 0.78 | 0.70 |
| rotor relative exit Mach number | 0.83 | 0.76 |
| rotor exit to inlet density ratio | 0.88 | 0.85 |
| degree of reaction | 0.10 | 0.13 |
| total to static efficiency | 0.723 | 0.634 |
| measured isentropic efficiency | 0.724 | 0.643 |
| Parameter | Turbine #1 | Turbine #2 |
|---|---|---|
| nozzle loss | 25.1% | 23.4% |
| rotor loss | 19.2% | 19.3% |
| leakage loss | 15.0% | 27.4% |
| partial admission loss | 7.3% | 13.0% |
| wheel friction loss | 0.9% | 2.4% |
| exit kinetic energy loss | 32.5% | 14.5% |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leibsohn Martins, G. Axial Turbine Cascade Correlation. Appl. Sci. 2016, 6, 420. https://doi.org/10.3390/app6120420
Leibsohn Martins G. Axial Turbine Cascade Correlation. Applied Sciences. 2016; 6(12):420. https://doi.org/10.3390/app6120420
Chicago/Turabian StyleLeibsohn Martins, Guilherme. 2016. "Axial Turbine Cascade Correlation" Applied Sciences 6, no. 12: 420. https://doi.org/10.3390/app6120420
APA StyleLeibsohn Martins, G. (2016). Axial Turbine Cascade Correlation. Applied Sciences, 6(12), 420. https://doi.org/10.3390/app6120420





