Improved ADRC for a Maglev Planar Motor with a Concentric Winding Structure
Abstract
:1. Introduction
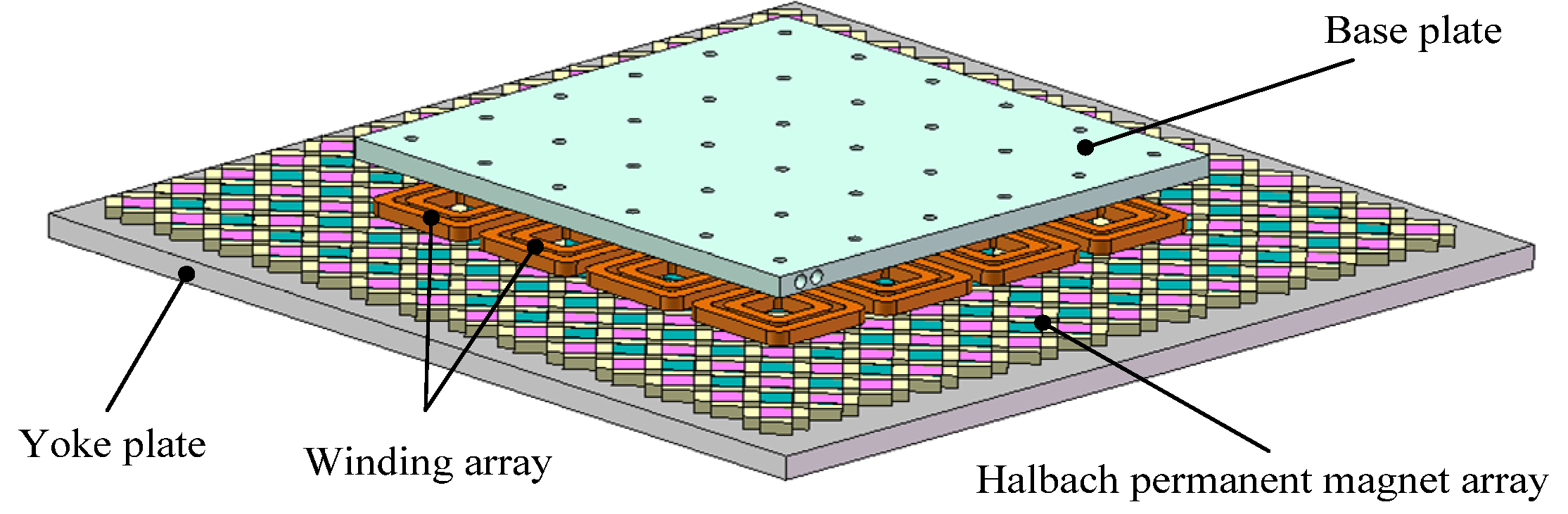
2. Motor Structure and Working Principle
2.1. Structure
2.2. Working Principle
3. Electromagnetic Model and Current Decoupling
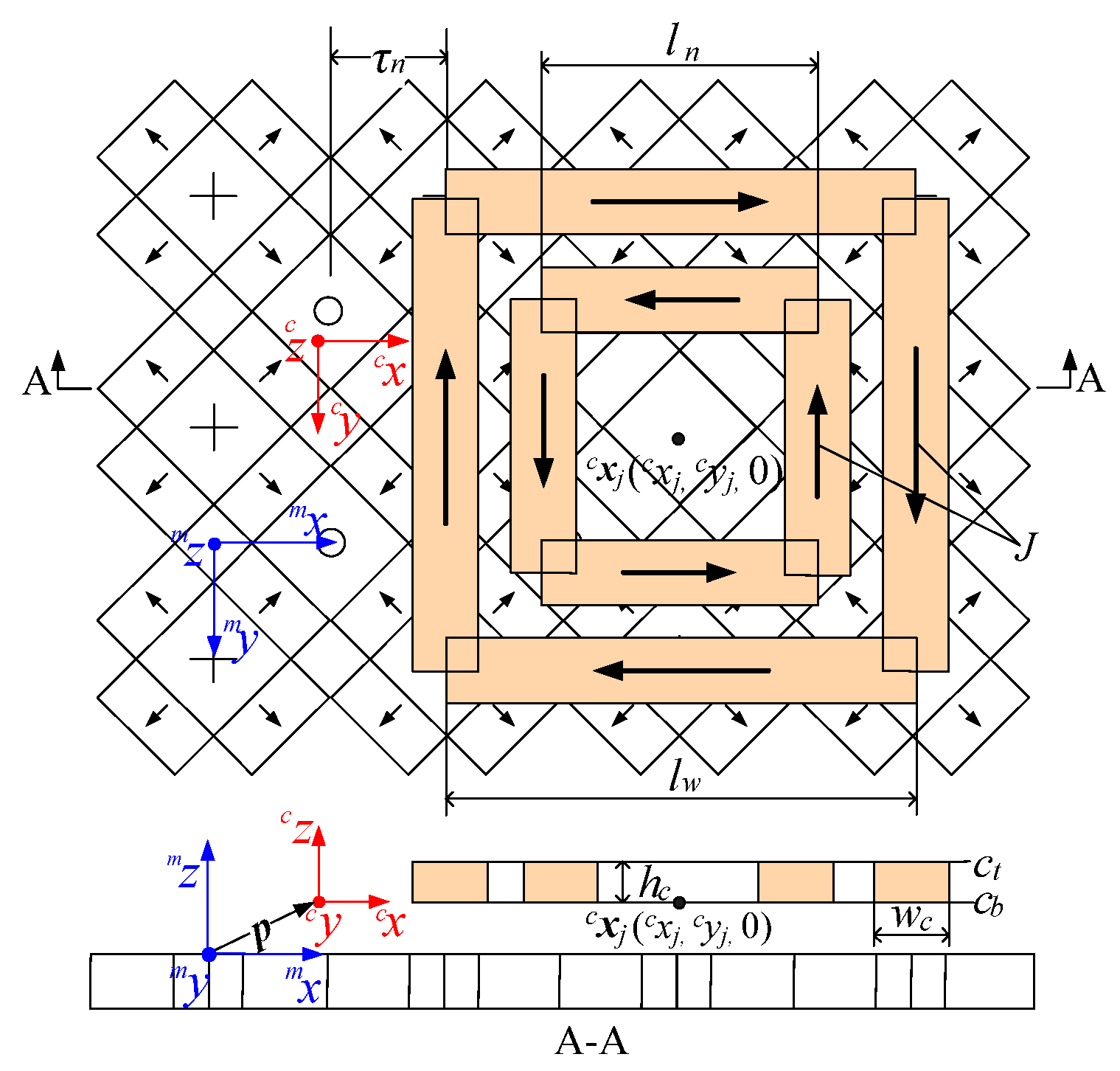
3.1. Electromagnetic Model Analysis
3.1.1. Parameter and Coordinate Definition
3.1.2. Magnetic Flux Density Distribution
3.1.3. Electromagnetic Force and Torque
3.2. Current Decoupling
3.3. Dynamics Model
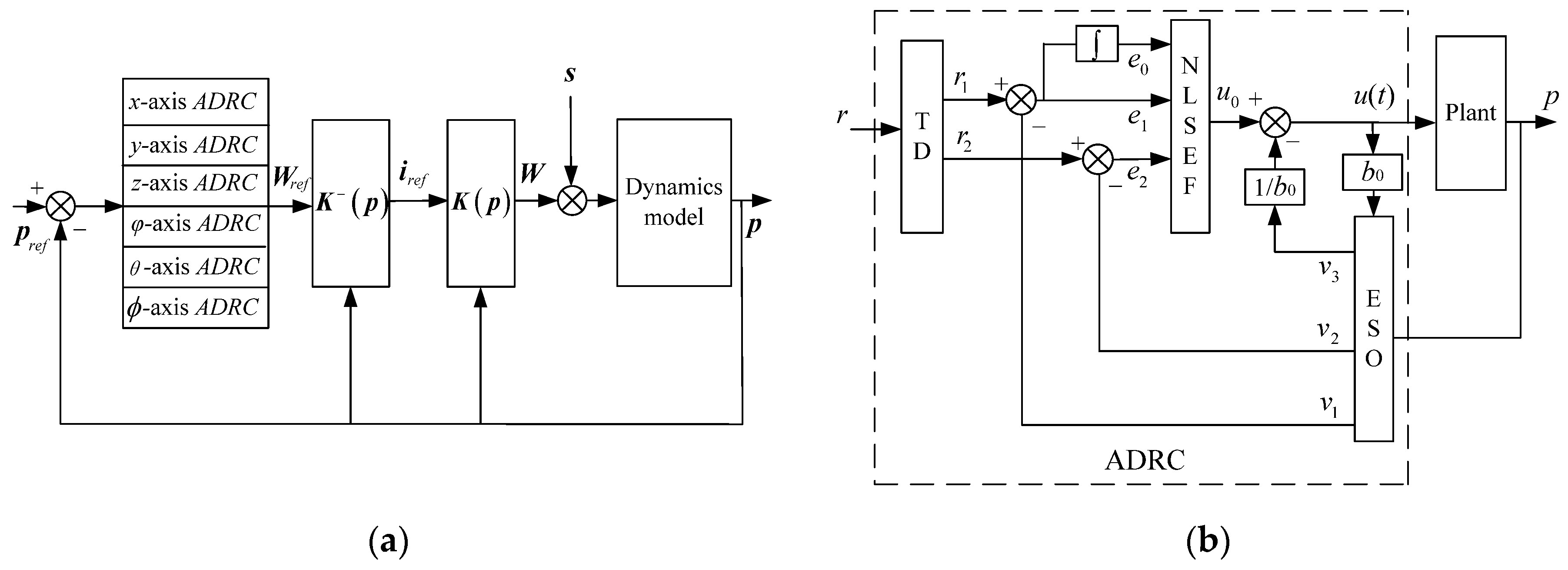
4. Control System Design
4.1. Control System Structure
4.2. ADRC Controller Design
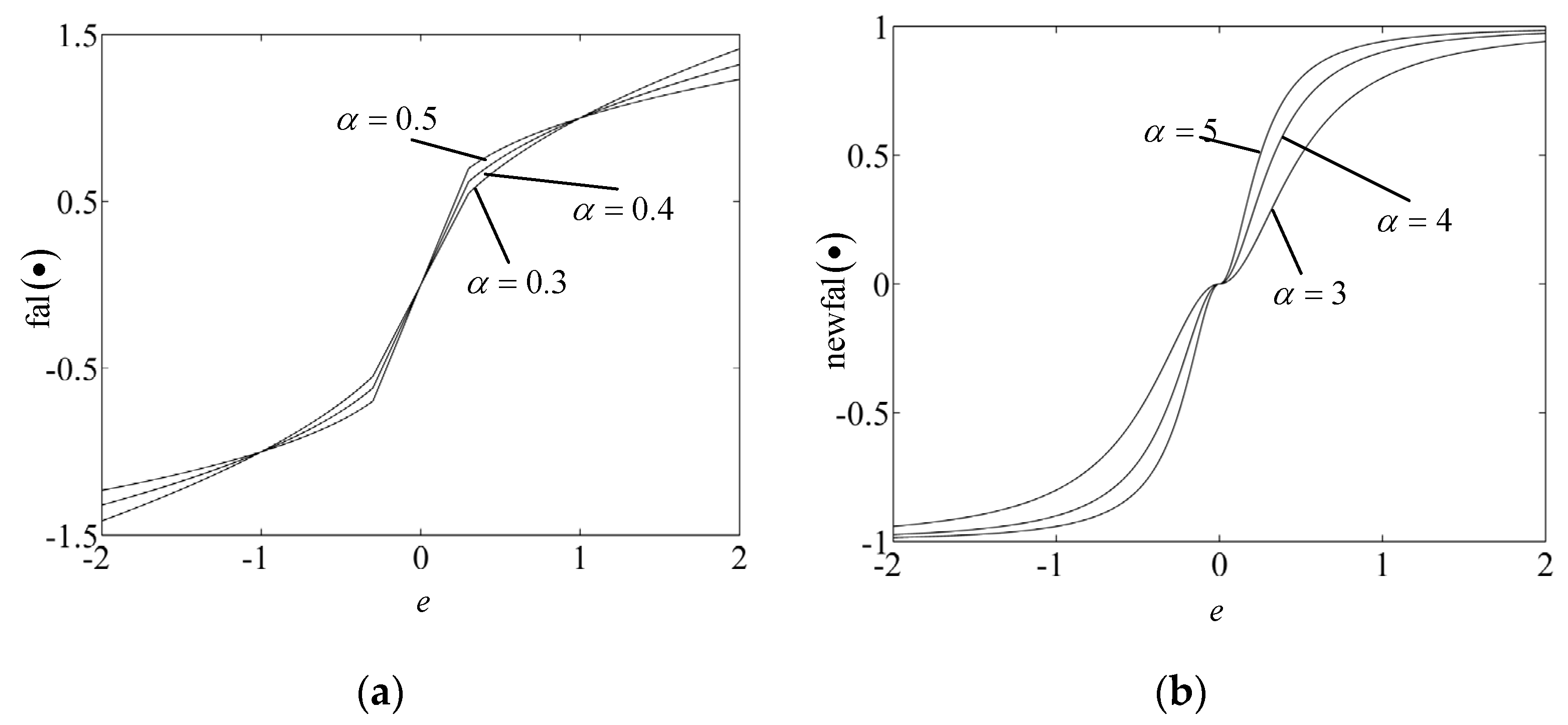
4.3. Improved ADRC Controller
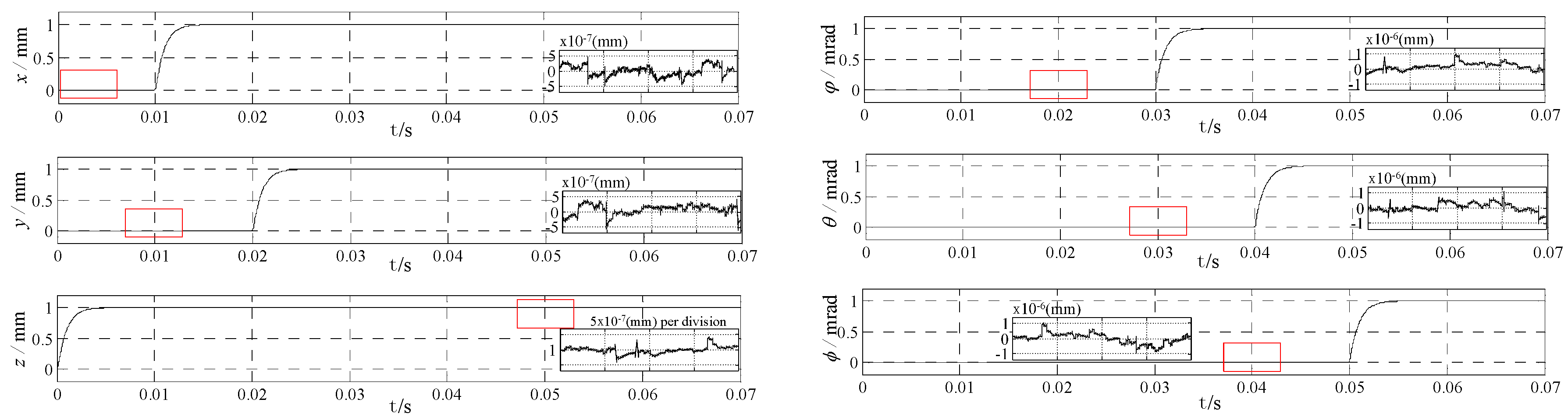
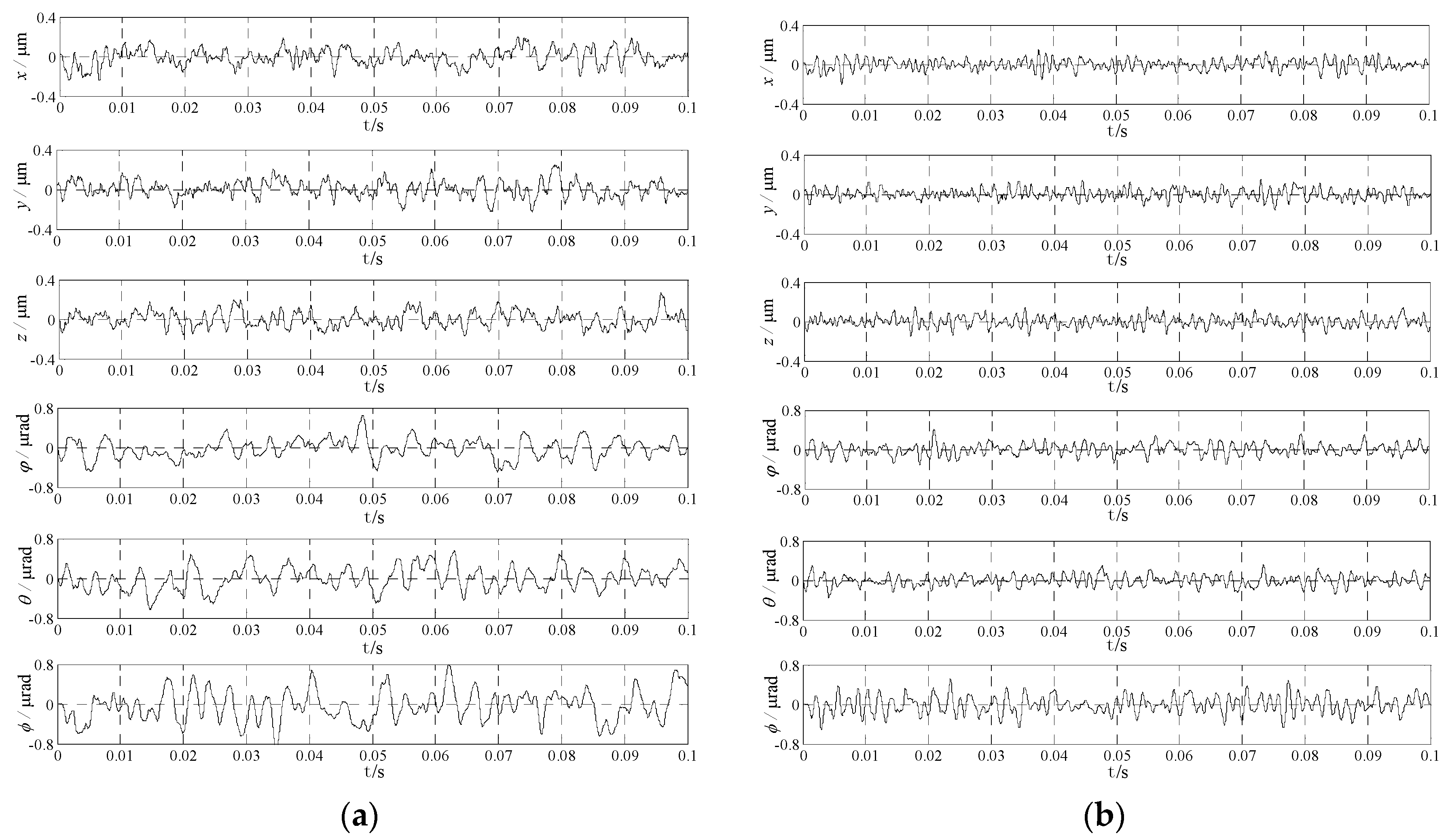
5. Validation and Analysis
5.1. Electromagnetic Model Validation
5.2. Decoupling Validation
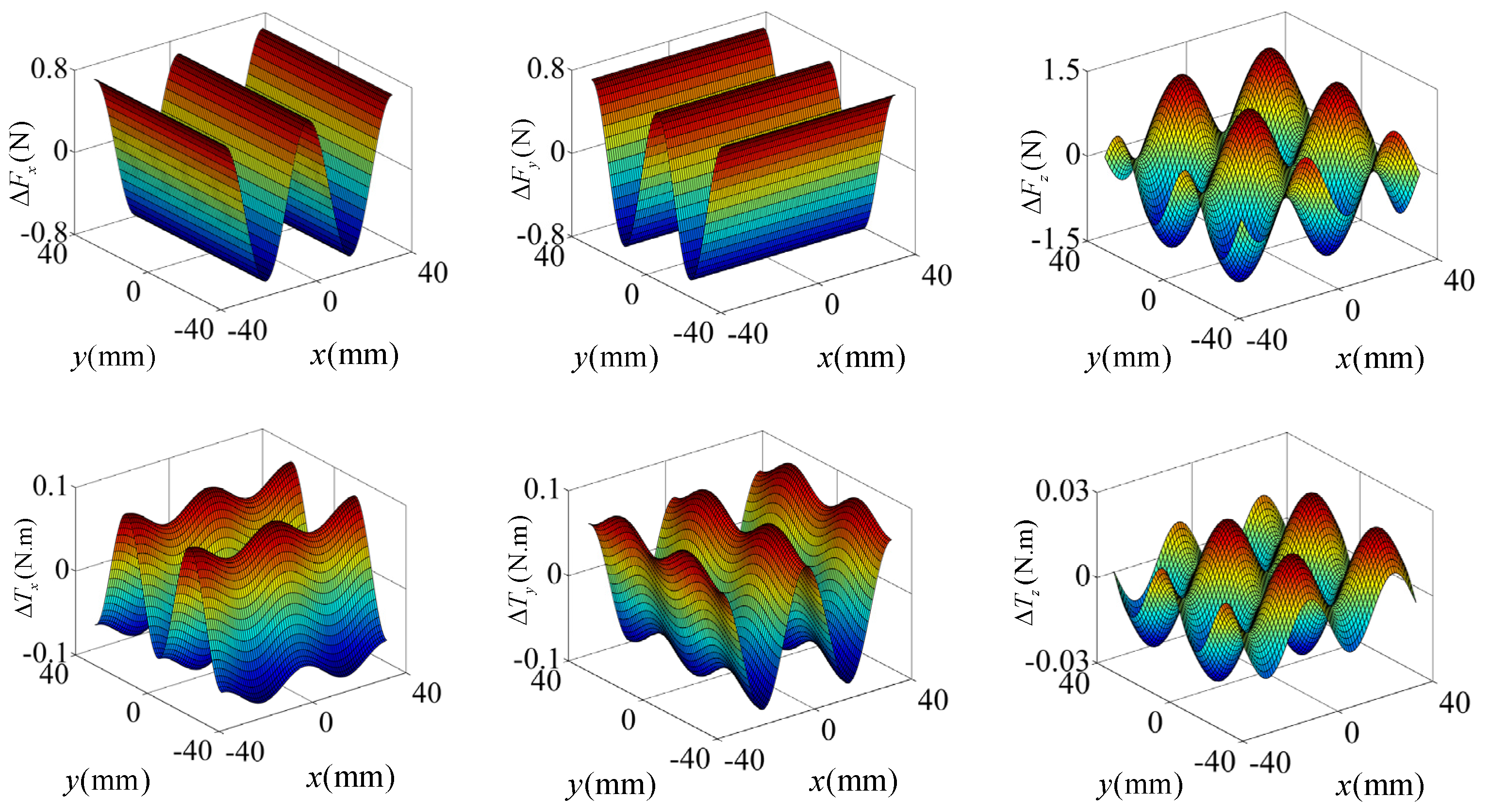
5.3. Disturbance Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rovers, J.M.M.; Jansen, J.W.; Compter, J.C.; Lomonova, E.A. Analysis Method of the Dynamic Force and Torque Distribution in the Magnet Array of a Commutated Magnetically Levitated Planar Actuator. IEEE Trans. Ind. Electron. 2012, 59, 2157–2166. [Google Scholar] [CrossRef]
- Kim, W.J.; Trumper, D.L. High-precision magnetic levitation stage for photolithography. J. Precis. Eng. 1998, 22, 66–77. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.Q.; Zhang, H.; Guo, S.L. Characteristic Analysis of a Long-Stroke Synchronous Permanent Magnet Planar Motor. IEEE Trans. Magn. 2012, 48, 4658–4661. [Google Scholar] [CrossRef]
- Achtenberg, J.; Rovers, J.M.M.; van Lierop, C.M.M.; Jansen, J.W.; van den Bosch, P.P.J.; Lomonova, E.A. Model based commutation containing edge coils for a moving magnet planar actuator. IEEE Trans. Ind. Appl. 2010, 130, 1147–1152. [Google Scholar] [CrossRef]
- Compter, J.C. Electro-dynamic planar motor. J. Precis. Eng. 2004, 28, 171–180. [Google Scholar] [CrossRef]
- Min, W.; Zhang, M.; Zhu, Y.; Chen, B.D.; Duan, G.H.; Hu, J.C.; Yin, W.S. Analysis and optimization of a new 2-D magnet array for planar motor. IEEE Trans. Magn. 2010, 46, 1167–1171. [Google Scholar] [CrossRef]
- Overboom, T.T.; Smeets, J.P.C.; Jansen, J.W.; Lomonova, E. Semianalytical calculation of the torque in a linear permanent-magnet motor with finite yoke length. IEEE Trans. Magn. 2012, 48, 3575–3578. [Google Scholar] [CrossRef]
- Choi, J.H.; Park, J.H.; Baek, Y.S. Design and Experimental Validation of Performance for a Maglev Moving-Magnet-Type Synchronous PM Planar Moto. IEEE Trans. Magn. 2006, 42, 3419–3421. [Google Scholar] [CrossRef]
- Overboom, T.T.; Smeets, J.P.C.; Jansen, J.W.; Lomonova, E. Topology comparison for a magnetically suspended ceiling actuator. In Proceedings of the IEEE International Electric Machines & Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011; pp. 296–301.
- Kou, B.Q.; Zhang, H.; Li, L.Y. Analysis and Design of a Novel 3-DOF Lorentz-Force-Driven DC Planar Motor. IEEE Trans. Magn. 2011, 47, 2118–2126. [Google Scholar]
- Nguyen, V.H.; Kim, J.W. Design and control of a compact lightweight planar position moving over a concentrated-Field Magnet Matrix. IEEE Trans. Mech. 2013, 18, 1090–1099. [Google Scholar] [CrossRef]
- Jansen, J.W.; Smeets, J.P.C.; Overboom, T.T. Overview of Analytical Models for the Design of Linear and Planar Motors. IEEE Trans. Magn. 2014, 50, 39–52. [Google Scholar] [CrossRef]
- Min, W.; Zhang, M.; Zhu, Y.; Liu, F.; Duan, G.; Hu, J.; Yin, W. Analysis and design of novel overlapping ironless windings for planar motors. IEEE Trans. Magn. 2011, 47, 4635–4642. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.Q.; Li, L.Y. Modeling and Design of an Integrated Winding Synchronous Permanent Magnet Planar Motor. IEEE Trans. Plasma Sci. 2013, 41, 1214–1219. [Google Scholar] [CrossRef]
- Van Lierop, C.M.M.; Jansen, J.W.; Damen, A.A.H.; Lomonova, E.A.; van den Bosch, P.P.J.; Vandenput, A.J.A. Model-Based Commutation of a Long-Stroke Magnetically Levitated Linear Actuator. IEEE Trans. Ind. Appl. 2009, 45, 1982–1990. [Google Scholar] [CrossRef]
- Jansen, J.W.; Van Lierop, C.M.M.; Lomonova, E.A.; Vandenput, A.J.A. Modeling of Magnetically Levitated Planar Actuators With Moving Magnets. IEEE Trans. Magn. 2007, 43, 15–25. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Contr. Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Singhal, R.; Padhee, S.; Kaur, G. Design of fractional order PID controller for speed control of DC motor. Int. J. Sci. Res. Publ. 2012, 2, 1–8. [Google Scholar]
- Han, J.Q. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Xia, Y.Q.; Pu, F.; Li, S.F.; Gao, Y. Lateral Path Tracking Control of Autonomous Land Vehicle Based on ADRC and Differential Flatness. IEEE Trans. Ind. Electron. 2016, 63, 3091–3099. [Google Scholar] [CrossRef]
- Han, J.Q. Disturbance Rejection Controller and its Application. Control Decis. 1998, 13, 19–23. [Google Scholar]
- Zhang, L.; Kou, B.Q.; Xing, F.; Luo, J. Modeling and Analysis of a Magnetically Levitated Synchronous Permanent Magnet Planar Motor with Concentric Structure Winding. In Proceedings of the Electromagnetic Launch Technology, La Jolla, CA, USA, 7–11 July 2014; pp. 1–6.
- Li, S.Q.; Li, J.; Mo, Y.P. Piezoelectric Multimode Vibration Control for Stiffened Plate Using ADRC-Based Acceleration Compensation. IEEE Trans. Ind. Electron. 2014, 61, 6892–6902. [Google Scholar] [CrossRef]
- Chen, Q.M.; Li, L.Y.; Wang, M.Y.; Pei, L. The precise modeling and active disturbance rejection control of voice coil motor in high precision motion control system. Appl. Math. Model. 2015, 39, 5936–5948. [Google Scholar] [CrossRef]
- Rahman, M.M.; Chowdhury, A.H. Comparative study of ADRC and PID based Load Frequency Control. In Proceedings of the International Conference on Electrical Engineering and Information Communication Technology, Dubai, UAE, 23–24 December 2015; pp. 1–5.
- Jansen, J.W. Magnetically Levitated Planar Actuator with Moving Magnets: Electromechanical Analysis and Design. Ph.D. Thesis, Eindhoven Univ. Technol., Eindhoven, The Netherlands, November 2007. [Google Scholar]
- Peng, J.; Zhou, Y.F.; Liu, G.D. Calculation of a New Real-Time Control Model for the Magnetically Levitated Ironless Planar Motor. IEEE Trans. Magn. 2013, 49, 1416–1422. [Google Scholar] [CrossRef]
| Parameter | Value | Unit |
|---|---|---|
| Pole pitch τn | 17.68 | mm |
| Winding width wc | 11.8 | mm |
| Winding height hc | 7 | mm |
| Outer coil equivalent length lw | 76.7 | mm |
| Inner coil equivalent length ln | 41.3 | mm |
| Air gap h | 1 | mm |
| x-axis moment of inertia Ix | 0.268 | kg·m2 |
| y-axis moment of inertia Iy | 0.268 | kg·m2 |
| z-axis moment of inertia Iz | 0.533 | kg·m2 |
| Mover mass m | 20 | kg |
| Vertical component of magnetic flux density Bz | 0.8 | T |
| Horizontal component of magnetic flux density Bxy | 0.566 | T |
| Acceleration of gravity g | 9.8 | m/s2 |
| Number of turns N | 180 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, B.; Xing, F.; Zhang, C.; Zhang, L.; Zhou, Y.; Wang, T. Improved ADRC for a Maglev Planar Motor with a Concentric Winding Structure. Appl. Sci. 2016, 6, 419. https://doi.org/10.3390/app6120419
Kou B, Xing F, Zhang C, Zhang L, Zhou Y, Wang T. Improved ADRC for a Maglev Planar Motor with a Concentric Winding Structure. Applied Sciences. 2016; 6(12):419. https://doi.org/10.3390/app6120419
Chicago/Turabian StyleKou, Baoquan, Feng Xing, Chaoning Zhang, Lu Zhang, Yiheng Zhou, and Tiecheng Wang. 2016. "Improved ADRC for a Maglev Planar Motor with a Concentric Winding Structure" Applied Sciences 6, no. 12: 419. https://doi.org/10.3390/app6120419
APA StyleKou, B., Xing, F., Zhang, C., Zhang, L., Zhou, Y., & Wang, T. (2016). Improved ADRC for a Maglev Planar Motor with a Concentric Winding Structure. Applied Sciences, 6(12), 419. https://doi.org/10.3390/app6120419







