Sizing Subsurface Defects in Metallic Plates by Square Pulse Thermography Using an Oriented Gradient Map
Abstract
:1. Introduction
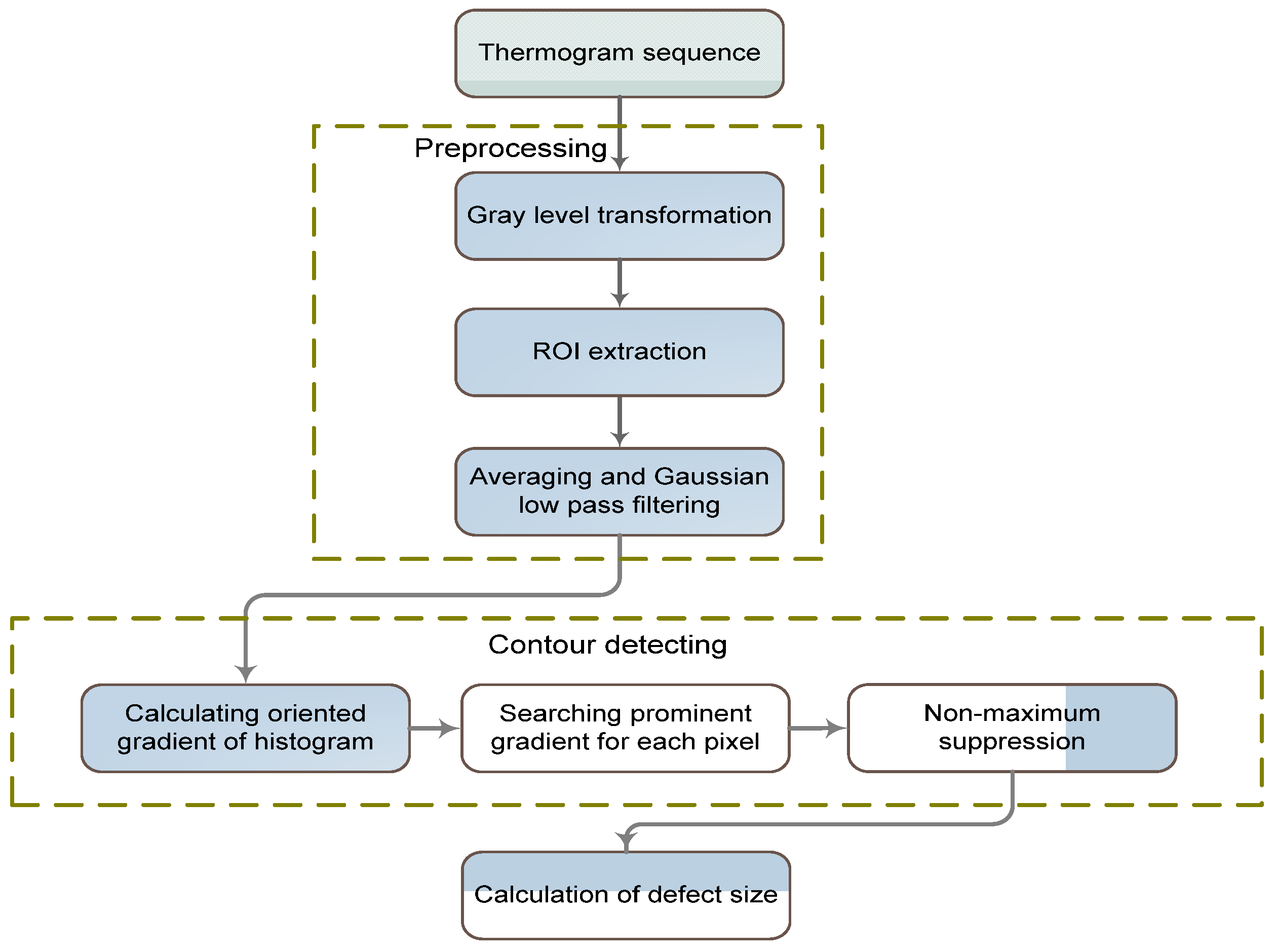
2. Details of the Proposed Approach
2.1. Preprocessing of Raw Thermograms
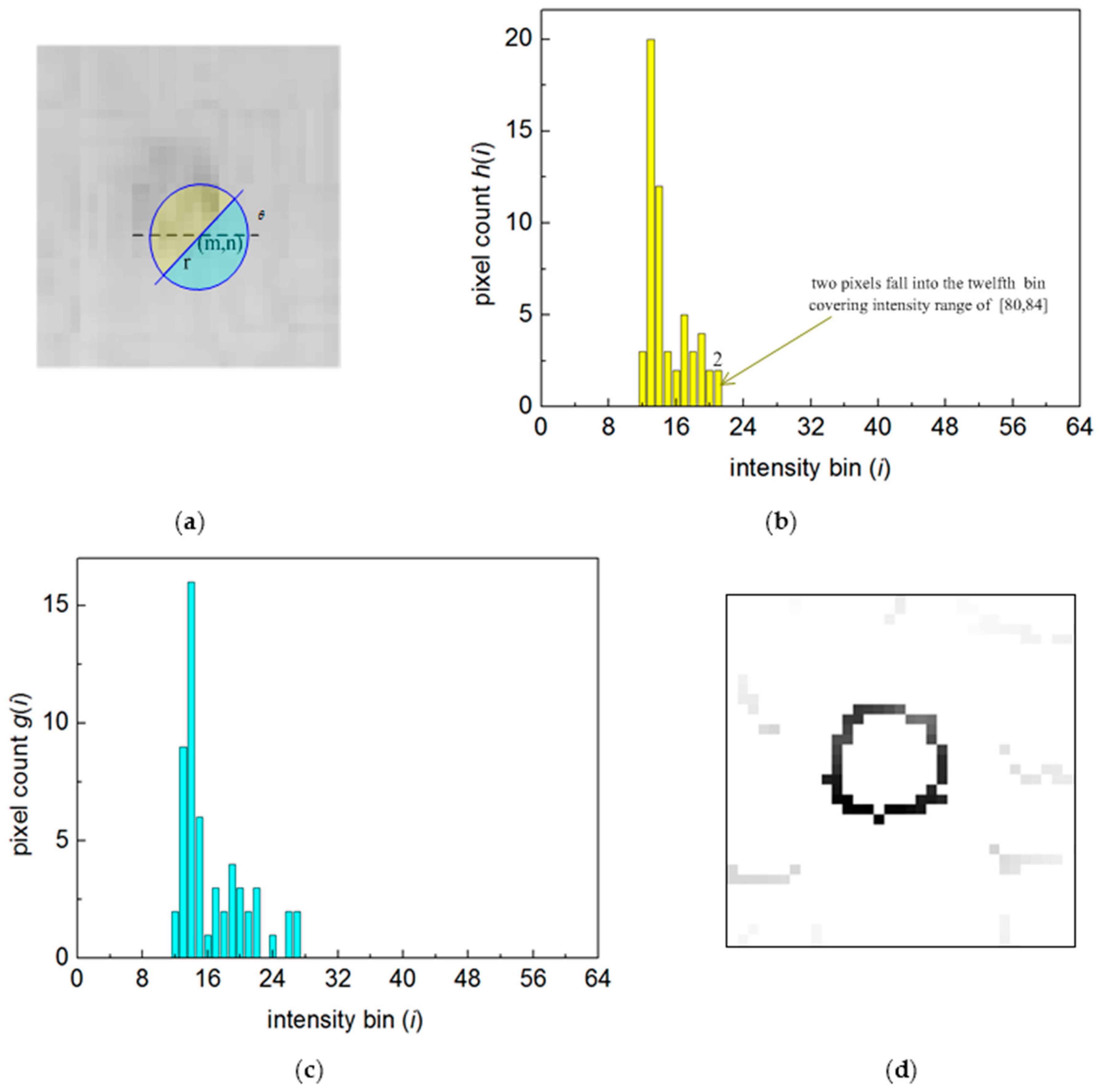
2.2. Contour Detection Using the Oriented Gradient of a Histogram
3. Experiment Result and Discussion
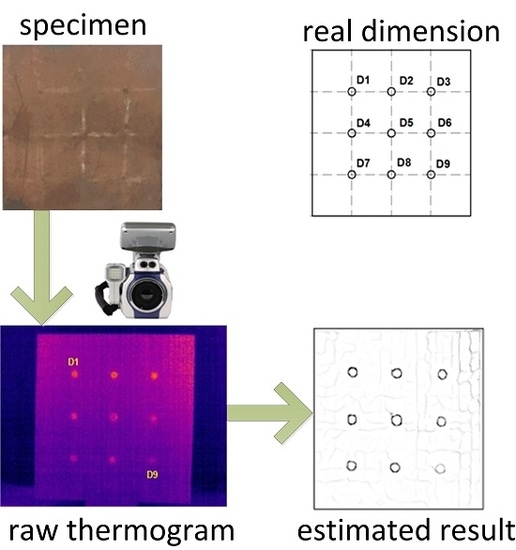
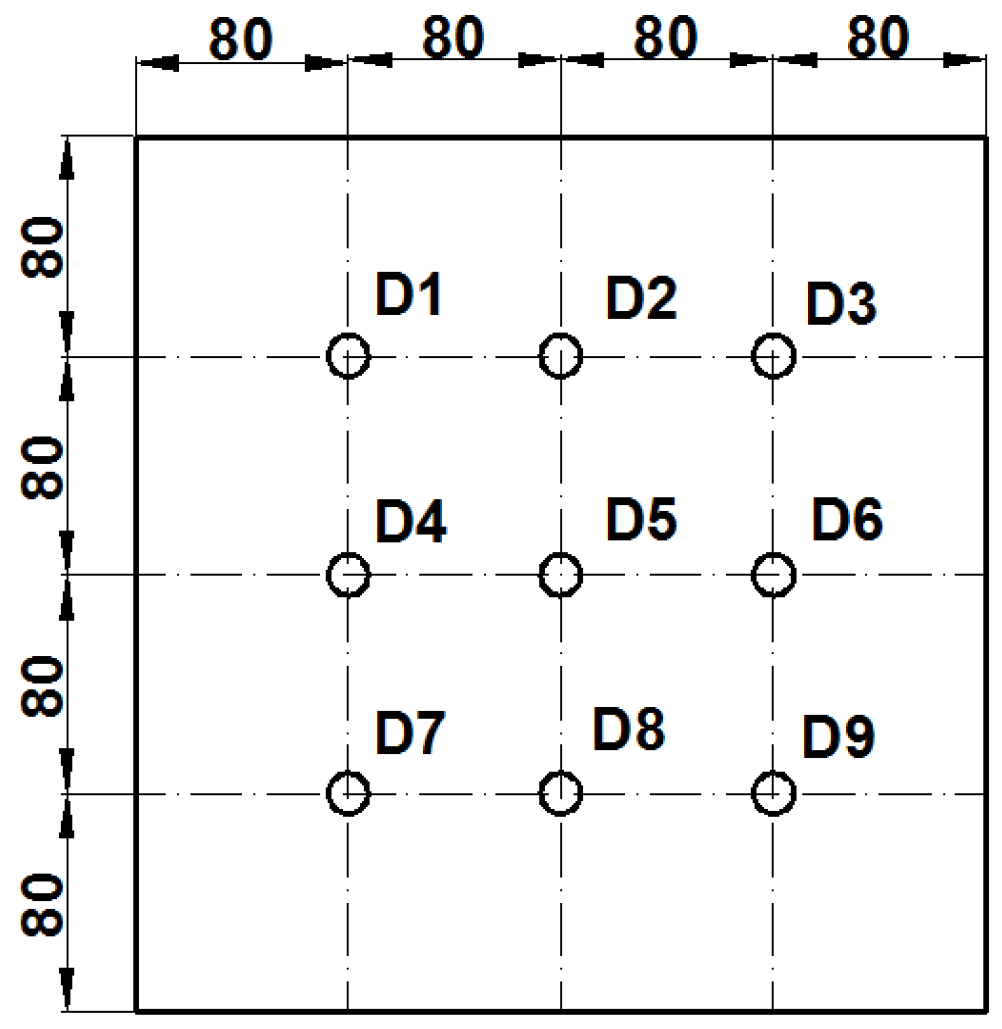
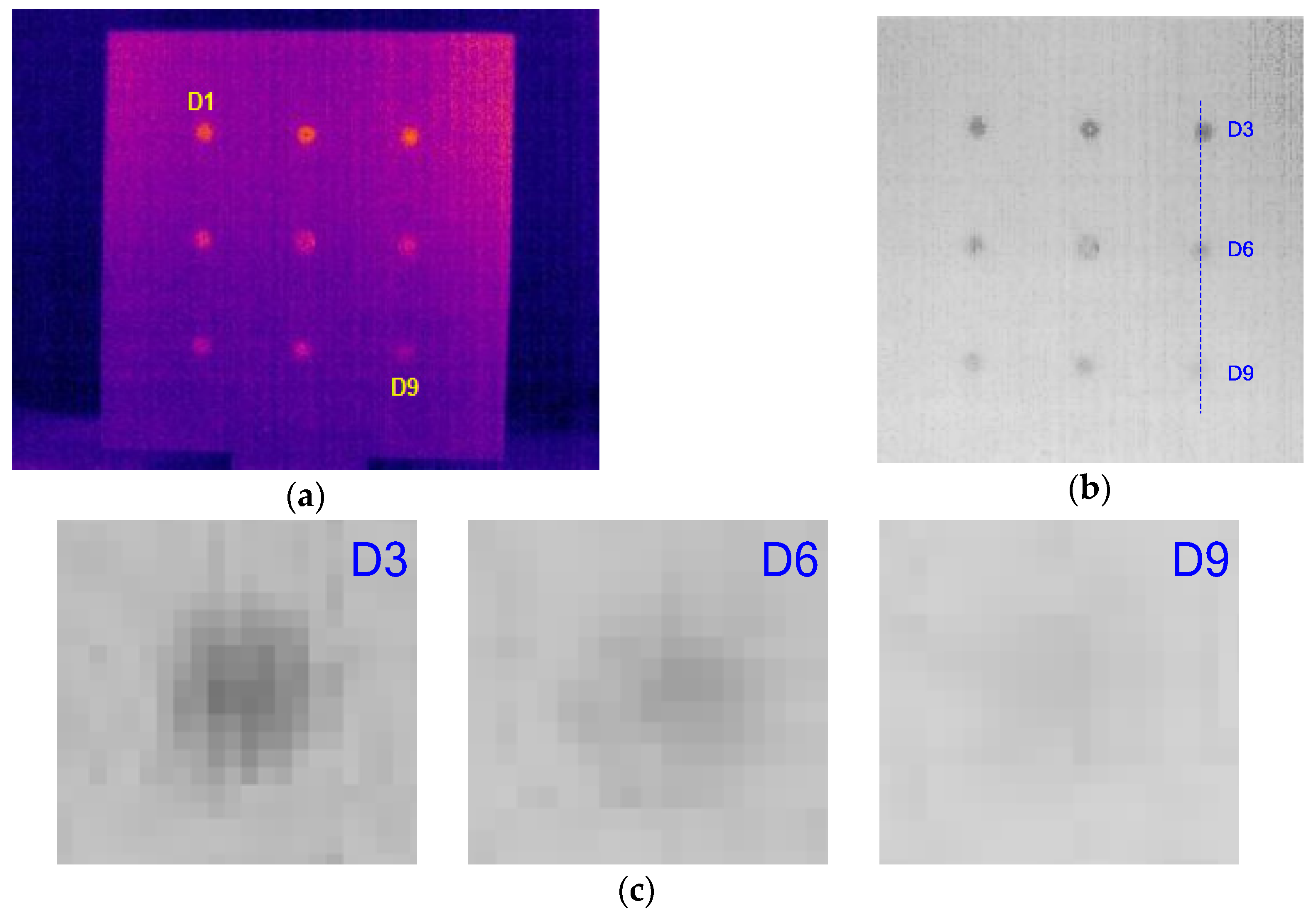
3.1. Experimental Setup
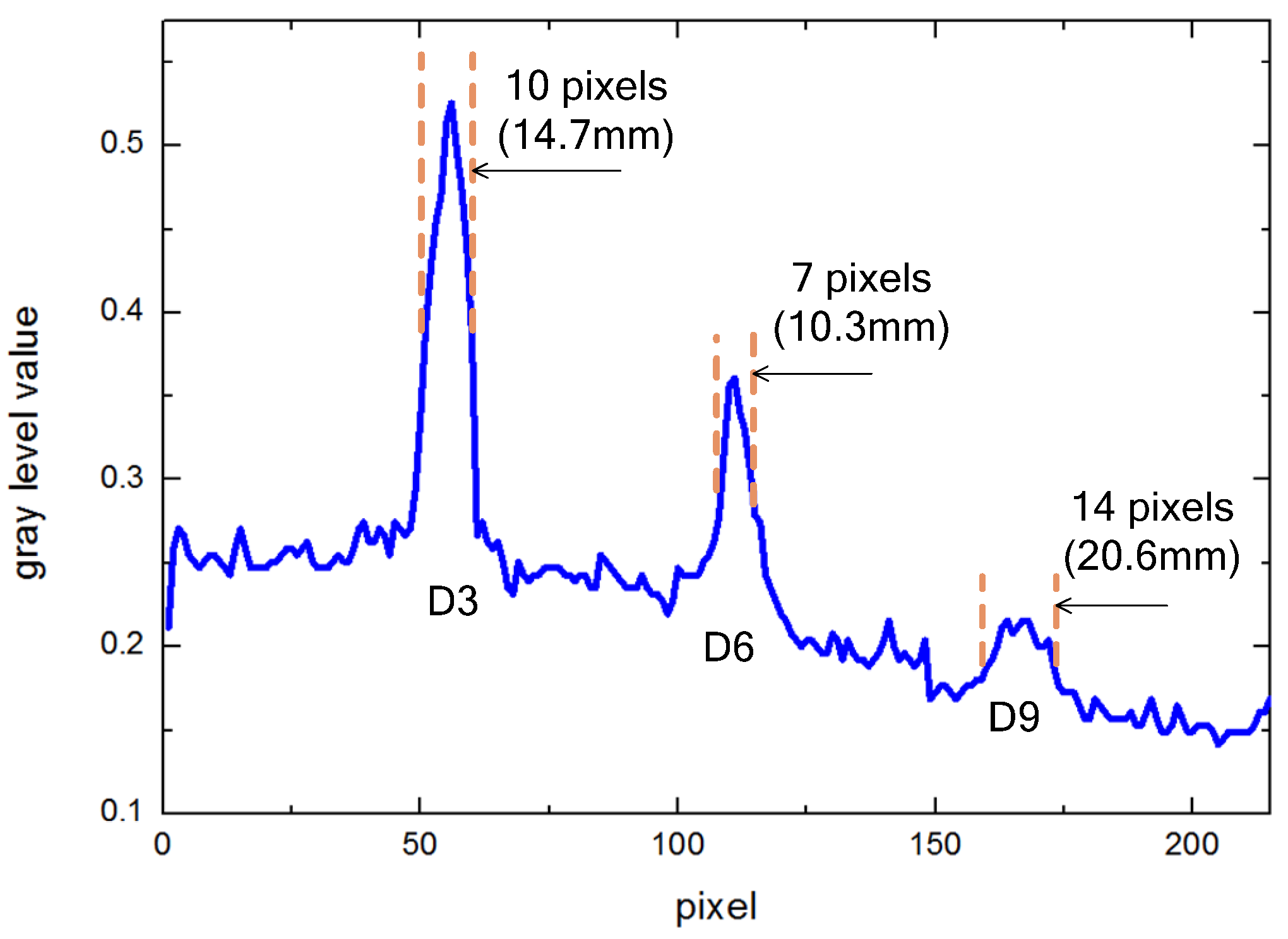
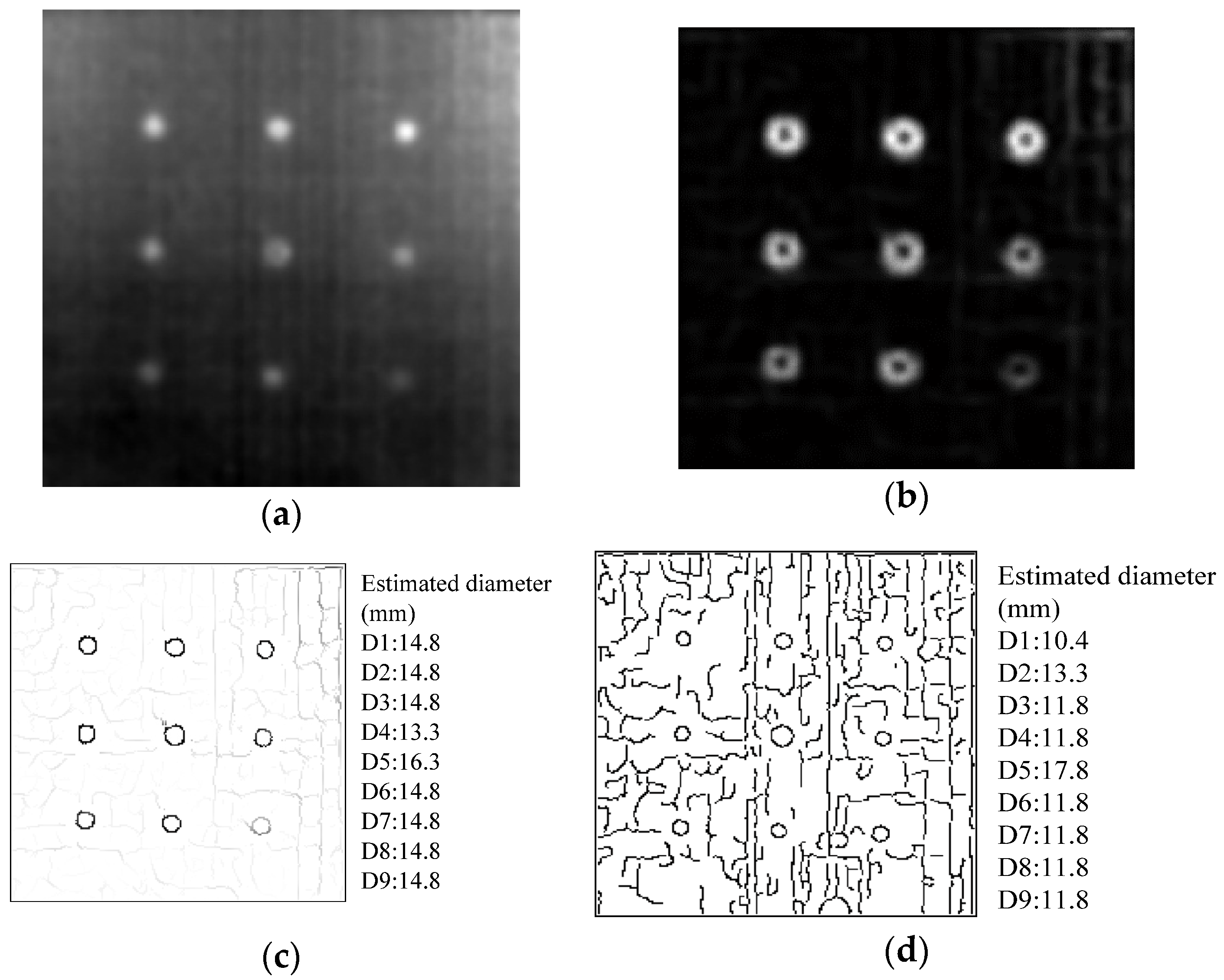
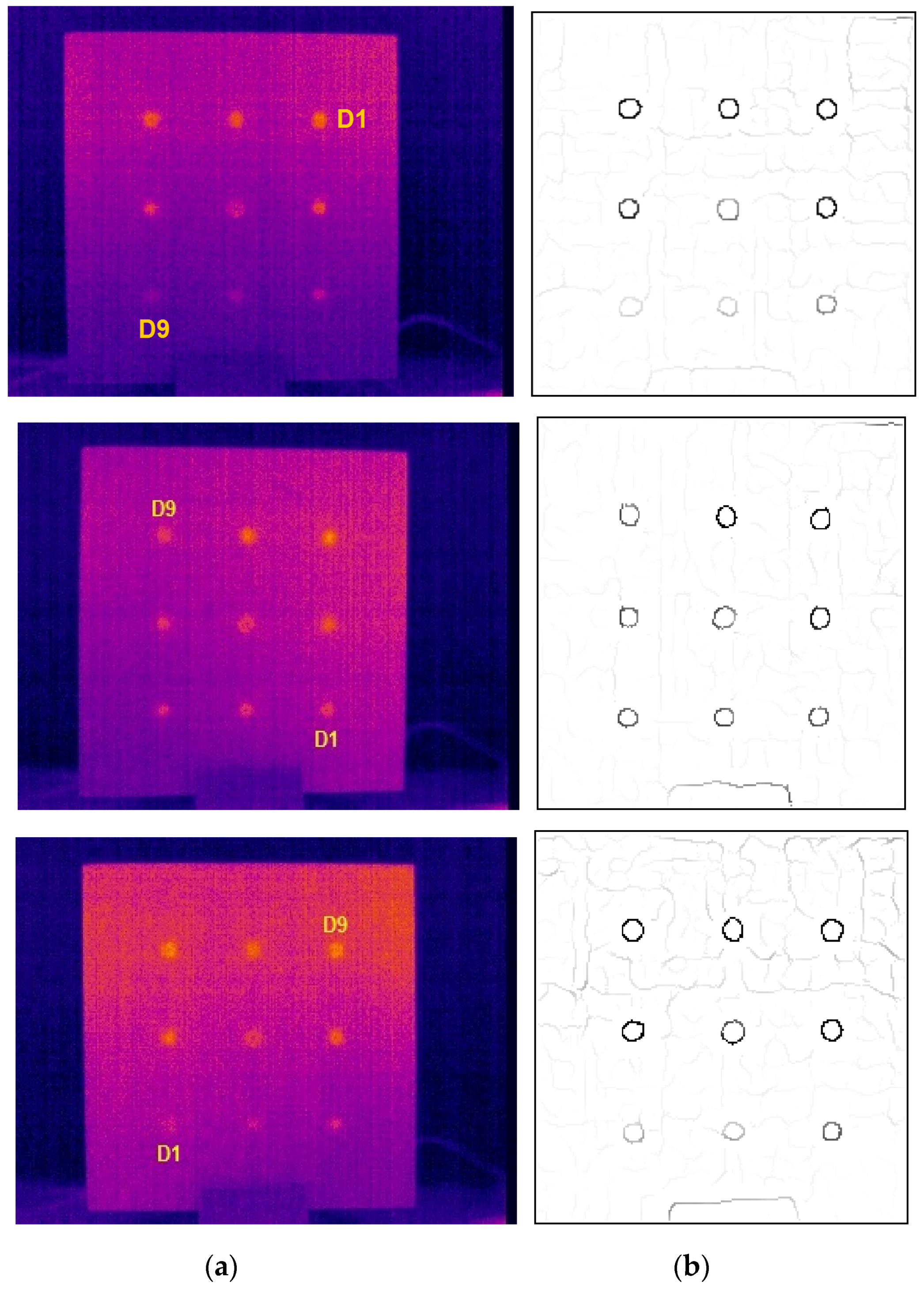
3.2. Sizing Results on Experimental Thermograms
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marks, R.; Clarke, A.; Featherston, C.; Paget, C.; Pullin, R. Lamb Wave interaction with adhesively bonded stiffeners and disbonds using 3D vibrometry. Appl. Sci. 2016, 6, 12. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.; Wang, Z.; Li, Y. Proof-of-concept study of monitoring bolt connection status using a piezoelectric based active sensing method. Smart Mater. Struct. 2013, 22, 087001. [Google Scholar] [CrossRef]
- Kersemans, M.; Martens, A.; Degrieck, J.; Van Den Abeele, K.; Delrue, S.; Pyl, L.; Zastavnik, F.; Sol, H.; Van Paepegem, W. The ultrasonic polar scan for composite characterization and damage assessment: Past, present and future. Appl. Sci. 2016, 6, 58. [Google Scholar] [CrossRef]
- De Angelis, G.; Meo, M.; Almond, D.P. A new technique to detect defect size and depth in composite structures using digital shearography and unconstrained optimization. NDT E Int. 2012, 45, 91–96. [Google Scholar] [CrossRef]
- Vavilov, V.; Burleigh, D.D. Review of pulsed thermal NDT: Physical principles, theory and data processing. NDT E Int. 2015, 73, 28–52. [Google Scholar] [CrossRef]
- Parvasi, S.M.; Xu, C.; Kong, Q.; Song, G. Detection of multiple thin surface cracks using vibrothermography with low-power piezoceramic-based ultrasonic actuator—A numerical study with experimental verification. Smart Mater. Struct. 2016, 25, 055042. [Google Scholar] [CrossRef]
- Bagavathiappan, S.; Lahiri, B.B.; Saravanan, T.; Philip, J.; Jayakumar, T. Infrared thermography for condition monitoring—A review. Infrared Phys. Technol. 2013, 60, 35–55. [Google Scholar] [CrossRef]
- Marinetti, S.; Vavilov, V. IR thermographic detection and characterization of hidden corrosion in metals: General analysis. Corros. Sci. 2010, 52, 865–872. [Google Scholar] [CrossRef]
- Maldague, X. Applications of infrared thermography in non-destructive evaluation. In Trends in Optical Nondestructive Testing; Rastogi, P., Inaudi, D., Eds.; Elsevier Science: Lausanne, Switzerland, 2000; pp. 591–609. [Google Scholar]
- Choi, M.; Kang, K.; Park, J.; Kim, W.; Kim, K. Quantitative determination of a subsurface defect of reference specimen by lock-in infrared thermography. NDT E Int. 2008, 41, 119–124. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Avdelidis, N.P.; Maldague, X.P. Quantitative pulsed phase thermography applied to steel plates. In Defense and Security; International Society for Optics and Photonics: Orlando, FL, USA, 2005; pp. 342–351. [Google Scholar]
- Sakagami, T.; Kubo, S. Applications of pulse heating thermography and lock-in thermography to quantitative nondestructive evaluations. Infrared Phys. Technol. 2002, 43, 211–218. [Google Scholar] [CrossRef]
- Maldague, X. Nondestructive Evaluation of Materials by Infrared Thermography; Springer: London, UK, 1993. [Google Scholar]
- Ludwig, N.; Teruzzi, P. Heat losses and 3D diffusion phenomena for defect sizing procedures in video pulse thermography. Infrared Phys. Technol. 2002, 43, 297–301. [Google Scholar] [CrossRef]
- Almond, D.P.; Lau, S.K. Defect sizing by transient thermography. I. An analytical treatment. J. Phys. D Appl. Phys. 1998, 27, 1063–1069. [Google Scholar] [CrossRef]
- Wysocka-Fotek, O.; Oliferuk, W.; Maj, M. Reconstruction of size and depth of simulated defects in austenitic steel plate using pulsed infrared thermography. Infrared Phys. Technol. 2012, 55, 363–367. [Google Scholar] [CrossRef]
- Lai, W.W.L.; Lee, K.K.; Poon, C.S. Validation of size estimation of debonds in external wall’s composite finishes via passive Infrared thermography and a gradient algorithm. Constr. Build. Mater. 2015, 87, 113–124. [Google Scholar] [CrossRef]
- Wysocka-Fotek, O.; Maj, M.; Oliferuk, W. Use of pulsed IR thermography for determination of size and depth of subsurface defect taking into account the shape of its cross-section area. Arch. Metall. Mater. 2015, 60, 615–620. [Google Scholar] [CrossRef]
- Breitenstein, O.; Altmann, F. Inversion of microscopic lock-in thermograms in the presence of emissivity contrast. NDT E Int. 2006, 39, 636–640. [Google Scholar] [CrossRef]
- Pickering, S.; Almond, D. Matched excitation energy comparison of the pulse and lock-in thermography NDE techniques. NDT E Int. 2008, 41, 501–509. [Google Scholar] [CrossRef]
- Tsanakas, J.A.; Chrysostomou, D.; Botsaris, P.N.; Gasteratos, A. Fault diagnosis of photovoltaic modules through image processing and Canny edge detection on field thermographic measurements. Int. J. Sustain. Energy 2015, 34, 351–372. [Google Scholar] [CrossRef]
- Dutta, T.; Sil, J.; Chottopadhyay, P. Condition monitoring of electrical equipment using thermal image processing. In Proceedings of the IEEE First International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2016; pp. 311–315.
- Gao, B.; Woo, W.L.; He, Y.; Tian, G.Y. Unsupervised sparse pattern diagnostic of defects with inductive thermography imaging system. IEEE Trans. Ind. Inform. 2016, 12, 371–383. [Google Scholar] [CrossRef]
- Sham, F.C.; Chen, N.; Long, L. Surface crack detection by flash thermography on concrete surface. Insight-Non-Destr. Test. Cond. Monit. 2008, 50, 240–243. [Google Scholar] [CrossRef]
- Patel, P.M.; Lau, S.K.; Almond, D.P. A review of image analysis techniques applied in transient thermographic nondestructive testing. Nondestruct. Test. Eval. 1992, 6, 343–364. [Google Scholar] [CrossRef]
- Grys, S.; Vokorokos, L.; Borowik, L. Size determination of subsurface defect by active thermography-Simulation research. Infrared Phys. Technol. 2014, 62, 147–153. [Google Scholar] [CrossRef]
- Grys, S. Filtered thermal contrast based technique for testing of material by infrared thermography. Opto-Electron. Rev. 2011, 19, 234–241. [Google Scholar] [CrossRef]
- Macleod, G.; Wolfond, H. Image processing for automated flaw detection in pulsed thermography. In Proceeding of the 6th International Workshop-NDT Signal Processing, London, ON, Canada, 24–27 August 2009; pp. 1–9.
- Florez-Ospina, J.F.; Benitez-Restrepo, H.D. Toward automatic evaluation of defect detectability in infrared images of composites and honeycomb structures. Infrared Phys. Technol. 2015, 71, 99–112. [Google Scholar] [CrossRef]
- Xu, C.; Xie, J.; Chen, G.; Huang, W. An infrared thermal image processing framework based on superpixel algorithm to detect cracks on metal surface. Infrared Phys. Technol. 2014, 67, 266–272. [Google Scholar] [CrossRef]
- Benmoussat, M.S.; Guillaume, M.; Caulier, Y.; Spinnler, K. Automatic metal parts inspection: Use of thermographic images and anomaly detection algorithms. Infrared Phys. Technol. 2013, 61, 8–80. [Google Scholar] [CrossRef]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using local brightness, color and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef] [PubMed]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Neubeck, A.; Van Gool, L. Efficient non-maximum suppression. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR 2006), Hong Kong, China, 20–24 August 2006; pp. 850–855.

| Methods | Sizing Error (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | |
| Canny operator | 4.6 | 1.7 | 3.2 | 3.2 | 2.8 | 3.2 | 3.2 | 3.2 | 3.2 |
| FWHM | 0.3 | 0.3 | 0.3 | 3.3 | 1.2 | 4.7 | 2.6 | 1.7 | 5.6 |
| Proposed approach | 0.2 | 0.2 | 0.2 | 1.7 | 1.3 | 0.2 | 0.2 | 0.2 | 0.2 |
| Defect | Defect Diameter (mm) | Estimated Size by the Proposed Approach (mm) | ||||
|---|---|---|---|---|---|---|
| Testing Direction | Mean Error | |||||
| 0° | 90° | 180° | 270° | |||
| D1 | 15 | 14.8 | 15.2 | 15.2 | 15.2 | 0.1 |
| D2 | 14.8 | 15.2 | 15.2 | 16.7 | 0.5 | |
| D3 | 14.8 | 15.2 | 15.2 | 16.7 | 0.5 | |
| D4 | 13.3 | 15.2 | 15.2 | 15.2 | 0.3 | |
| D5 | 16.3 | 16.7 | 16.8 | 16.7 | 1.6 | |
| D6 | 14.8 | 13.7 | 13.7 | 15.2 | 0.7 | |
| D7 | 14.8 | 16.7 | 15.2 | 13.6 | 0.1 | |
| D8 | 14.8 | 15.2 | 15.2 | 15.2 | 0.1 | |
| D9 | 14.8 | 16.7 | 15.2 | 16.7 | 0.9 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Xu, C.; Gong, X.; Huang, W.; Chen, G. Sizing Subsurface Defects in Metallic Plates by Square Pulse Thermography Using an Oriented Gradient Map. Appl. Sci. 2016, 6, 389. https://doi.org/10.3390/app6120389
Xie J, Xu C, Gong X, Huang W, Chen G. Sizing Subsurface Defects in Metallic Plates by Square Pulse Thermography Using an Oriented Gradient Map. Applied Sciences. 2016; 6(12):389. https://doi.org/10.3390/app6120389
Chicago/Turabian StyleXie, Jing, Changhang Xu, Xumei Gong, Weiping Huang, and Guoming Chen. 2016. "Sizing Subsurface Defects in Metallic Plates by Square Pulse Thermography Using an Oriented Gradient Map" Applied Sciences 6, no. 12: 389. https://doi.org/10.3390/app6120389
APA StyleXie, J., Xu, C., Gong, X., Huang, W., & Chen, G. (2016). Sizing Subsurface Defects in Metallic Plates by Square Pulse Thermography Using an Oriented Gradient Map. Applied Sciences, 6(12), 389. https://doi.org/10.3390/app6120389