Numerical Models for Exact Description of in-situ Digital In-Line Holography Experiments with Irregularly-Shaped Arbitrarily-Located Particles
Abstract
:1. Introduction
2. Numerical Simulator
2.1. Amplitude Distribution of the Beam in the Plane of the Object
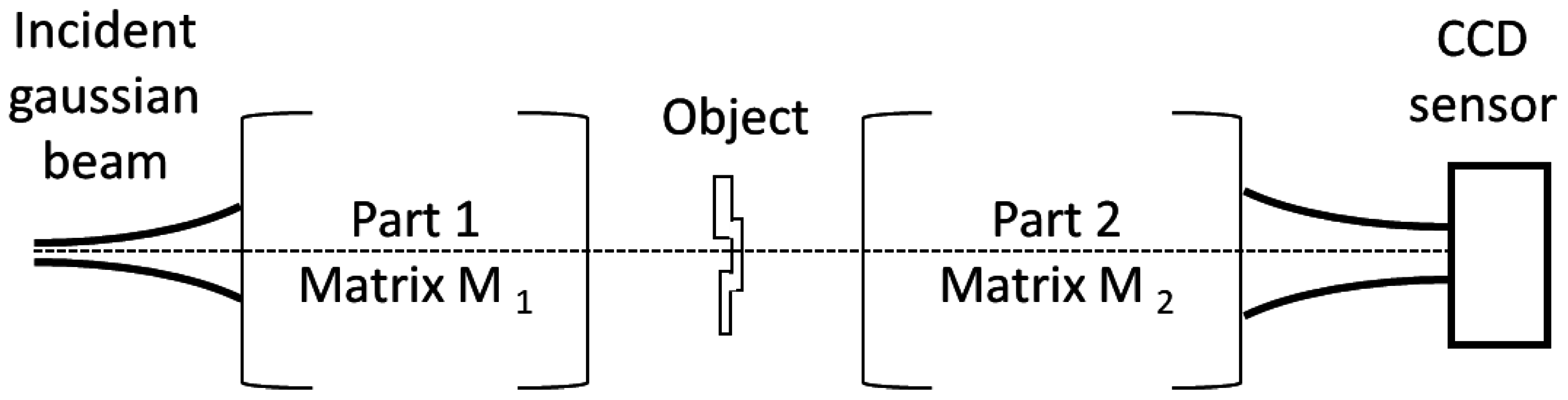
2.2. Definition of the Objects
2.3. Amplitude and Intensity Distributions in the Plane of the CCD Sensor
2.4. Hologram Analysis by Fractional Fourier Transform
3. Simulation of Two Objects in Different Longitudinal Planes: Mixing of Opaque and Phase Objects
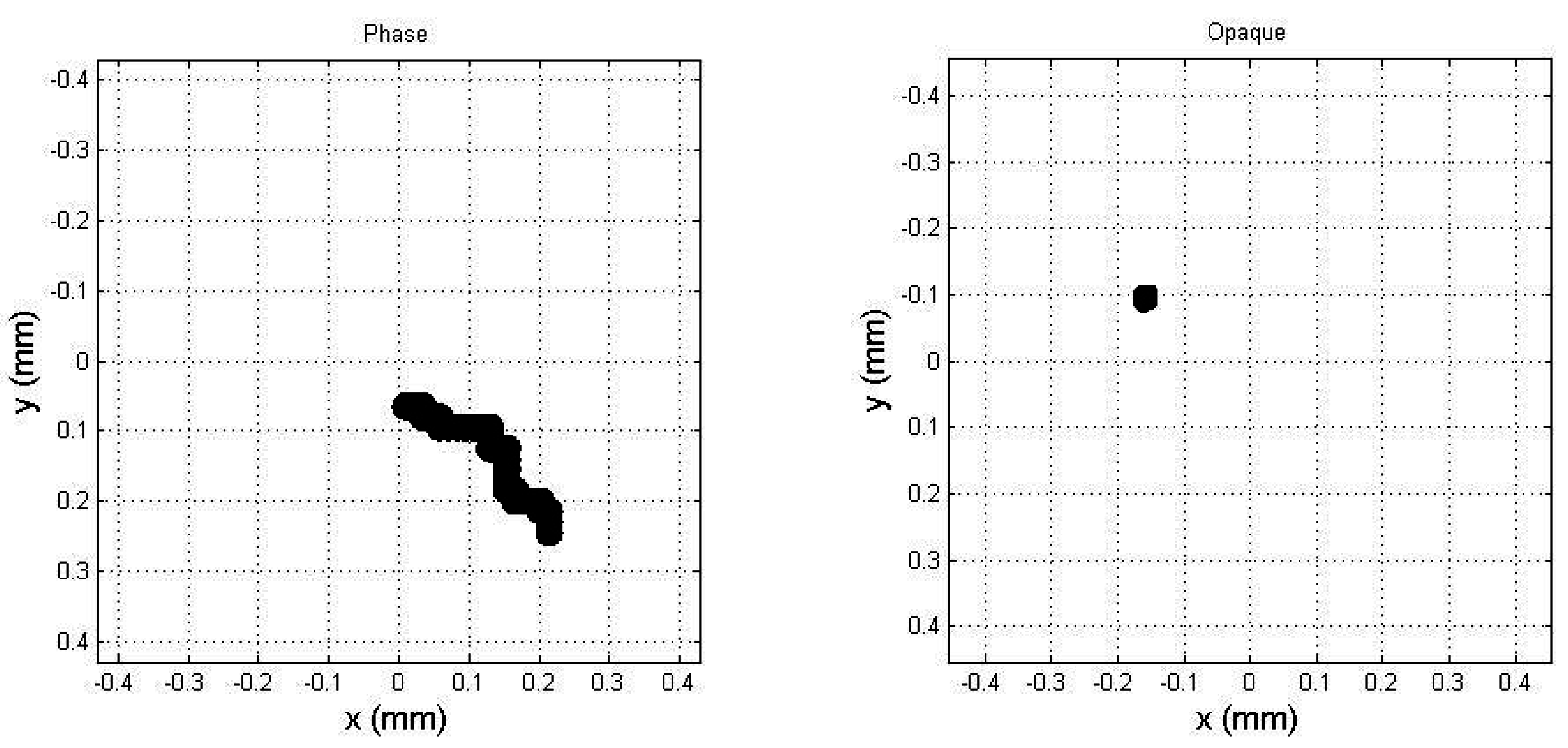
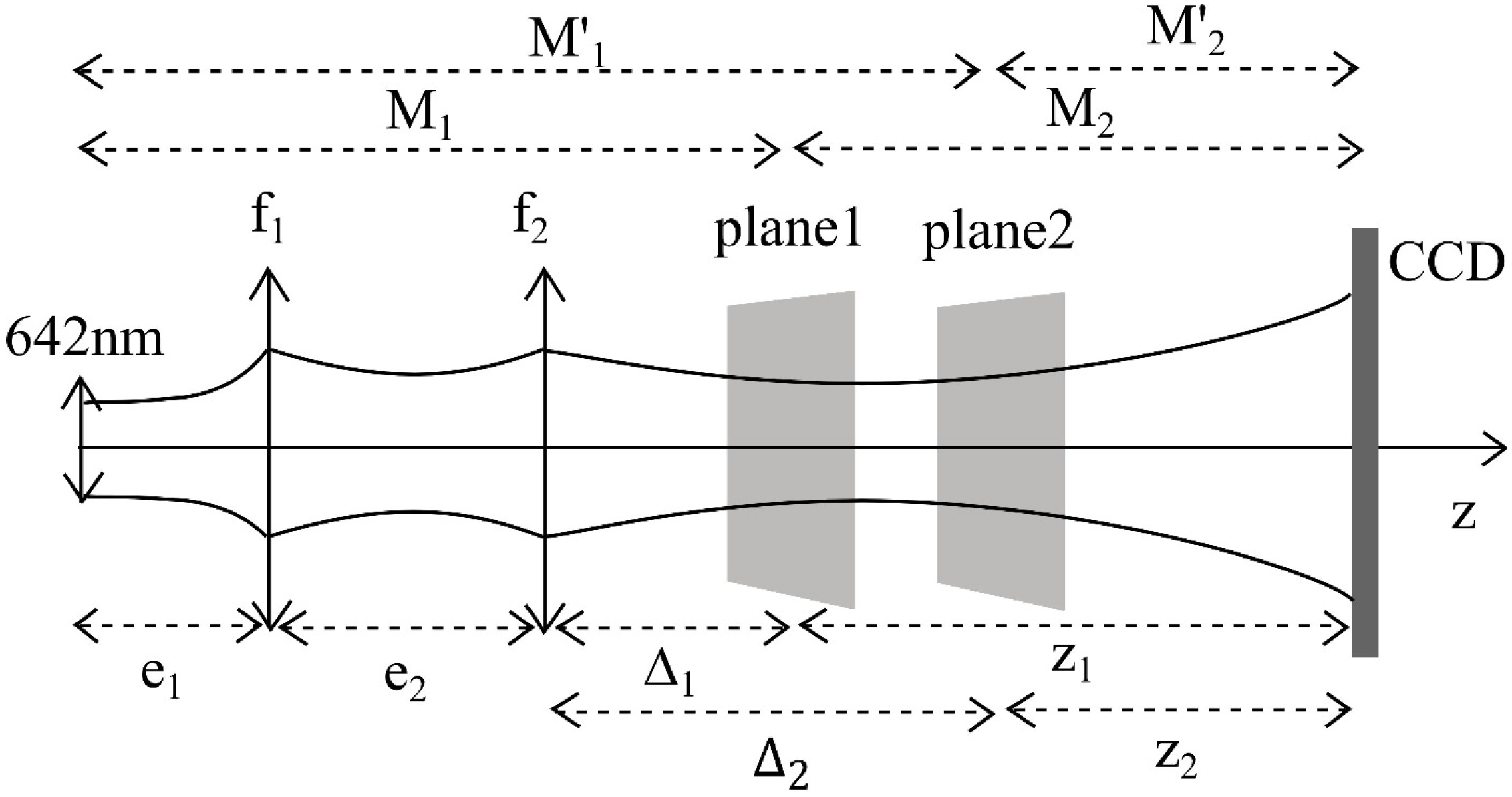
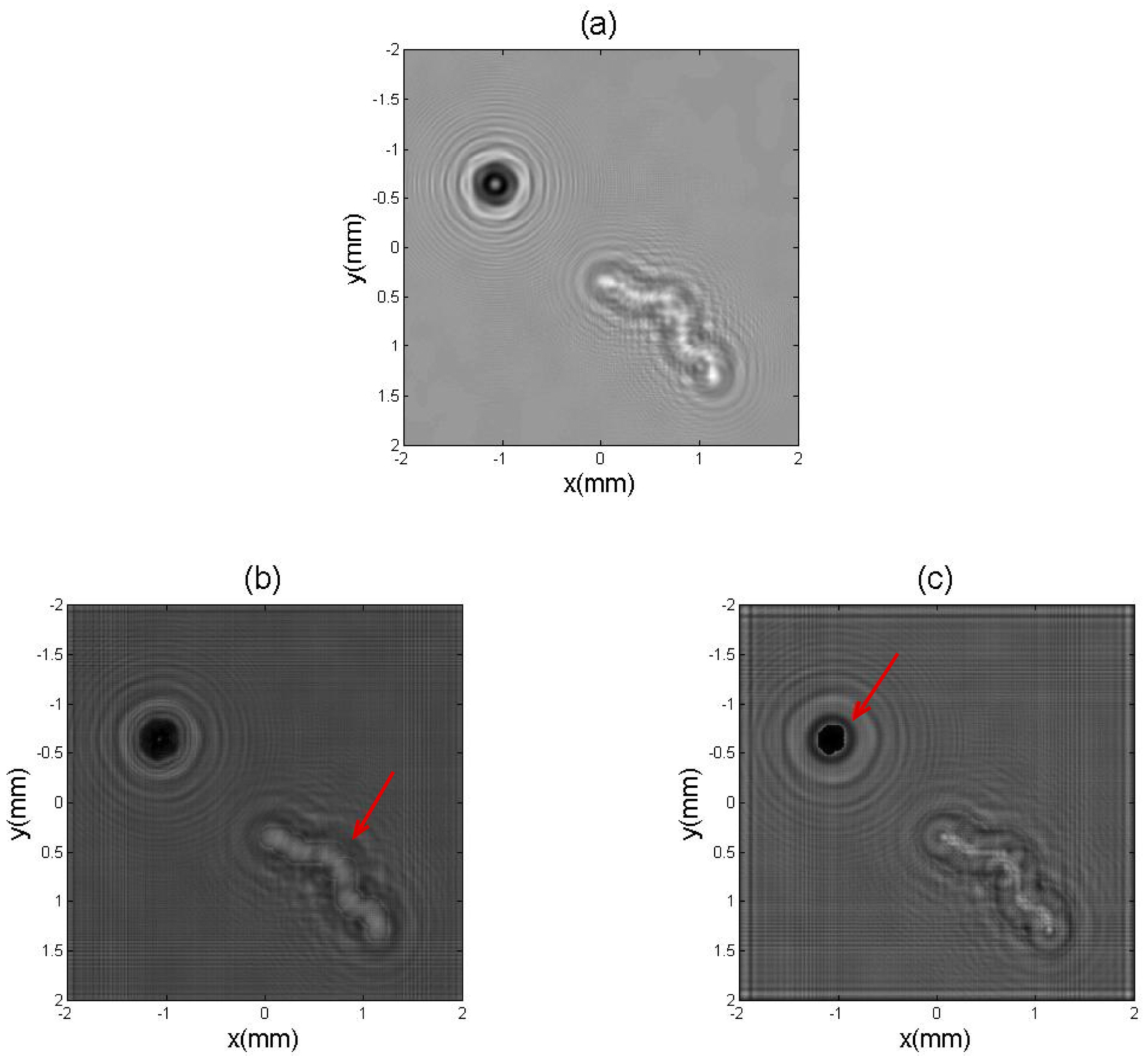
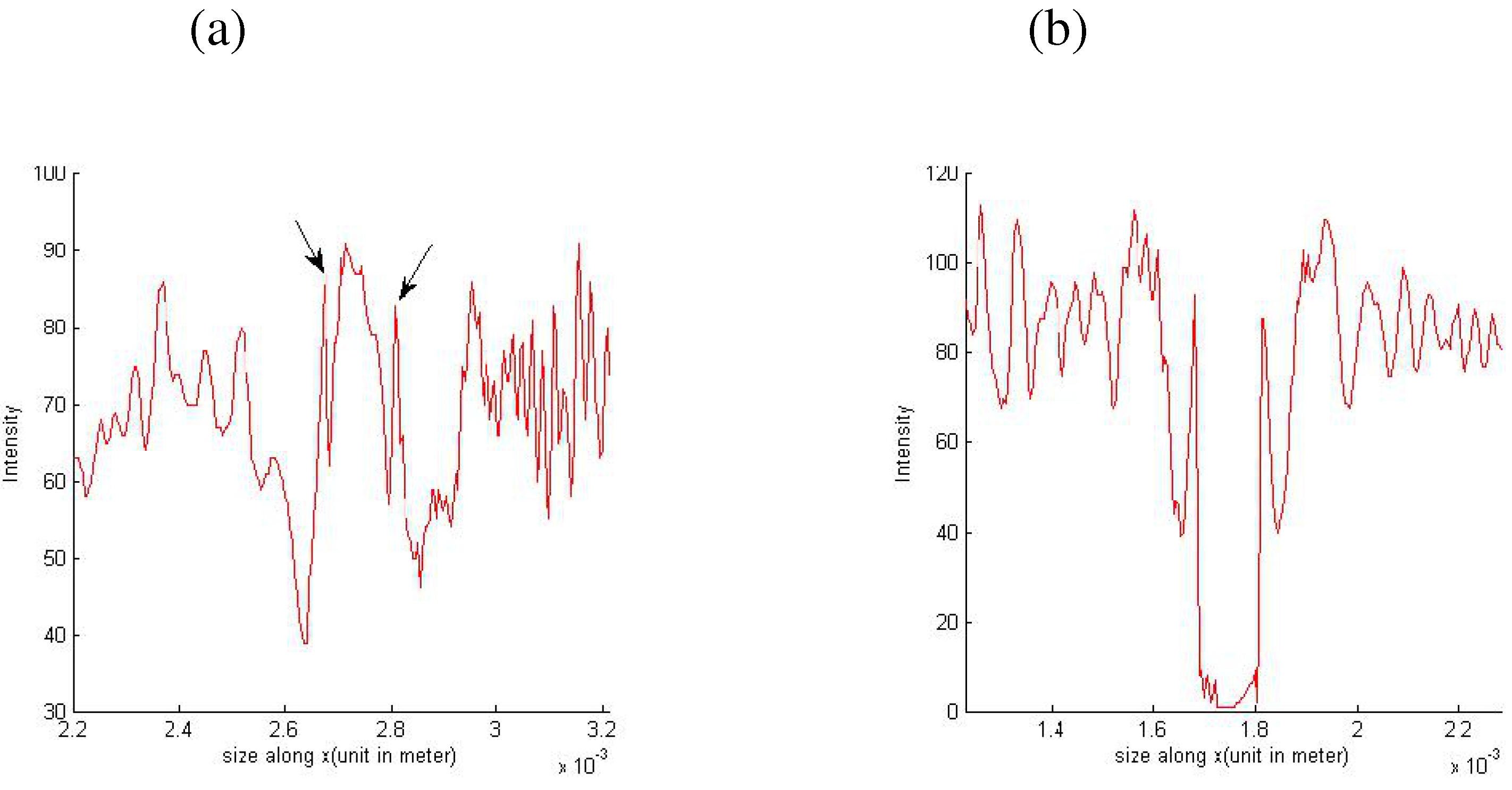
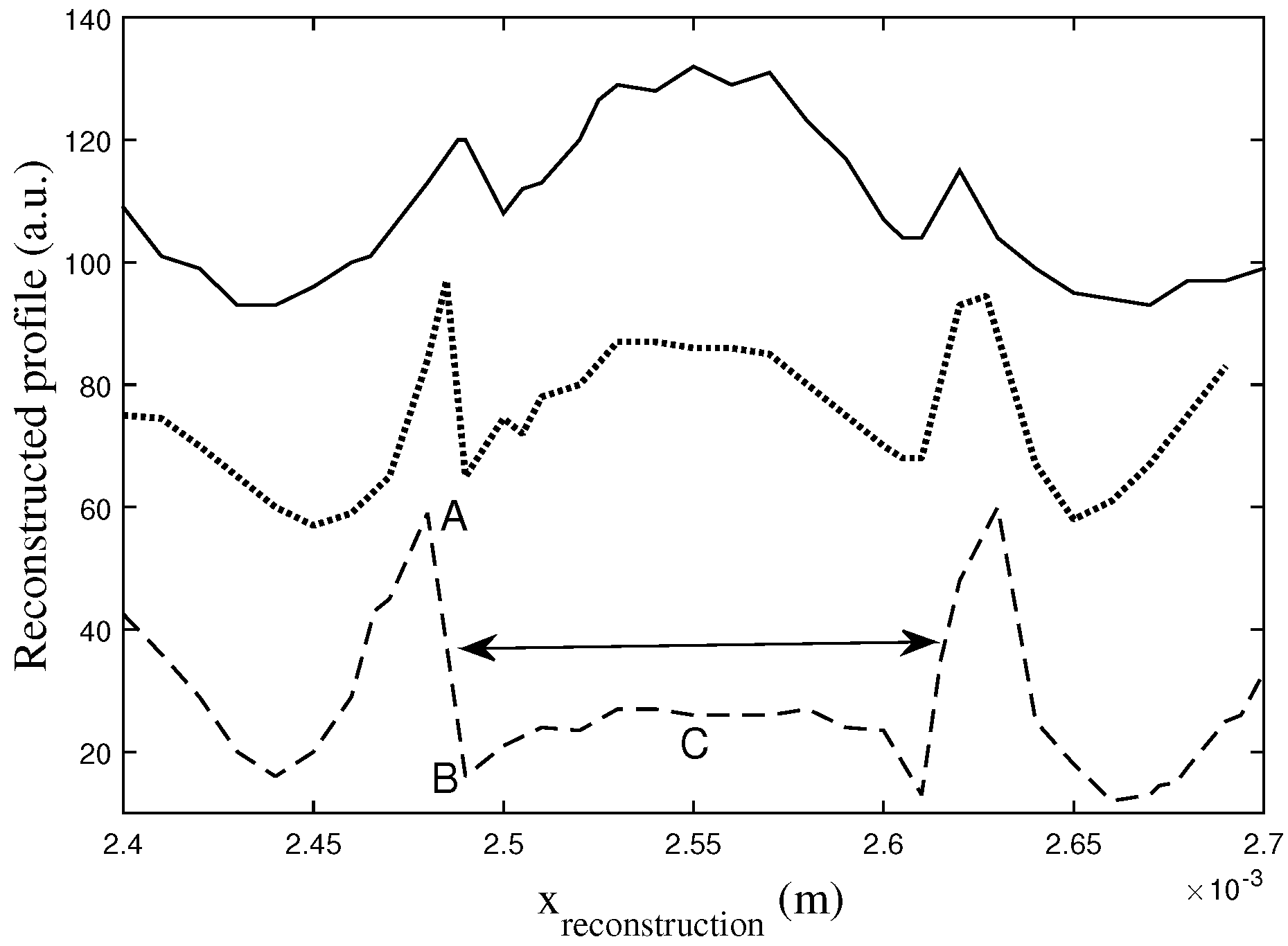
4. Two Examples of Application
4.1. Simulation of Phase Objects in a Droplet for Detection of Nanoparticles
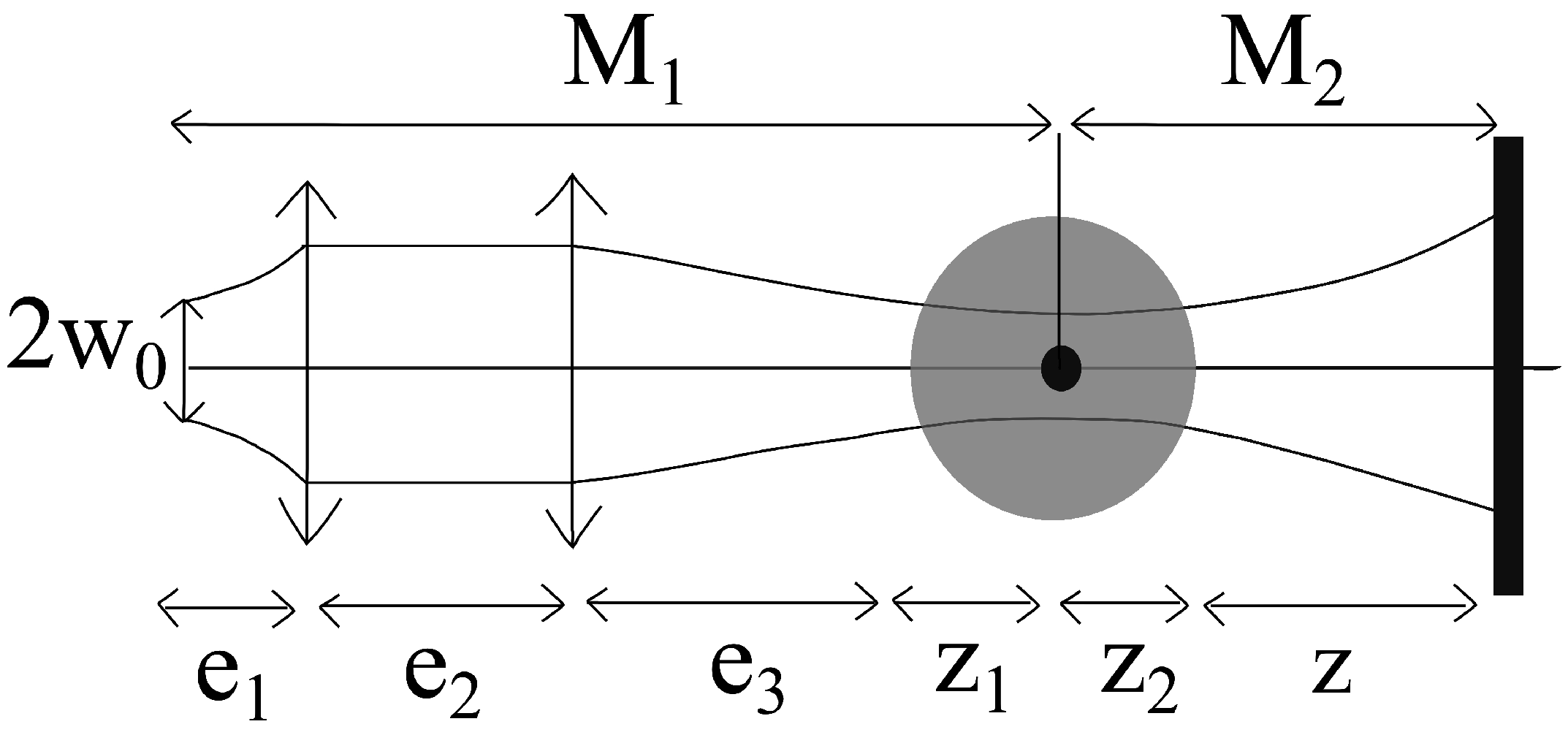
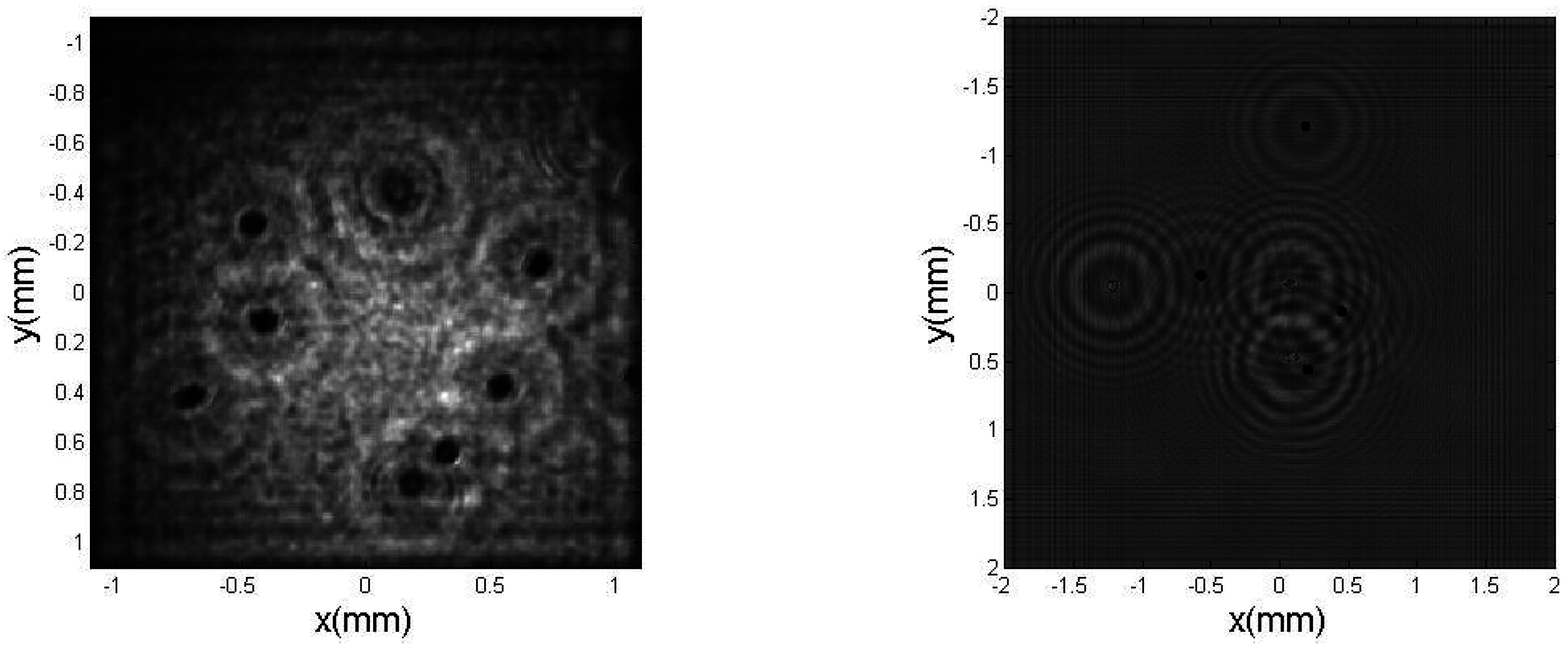
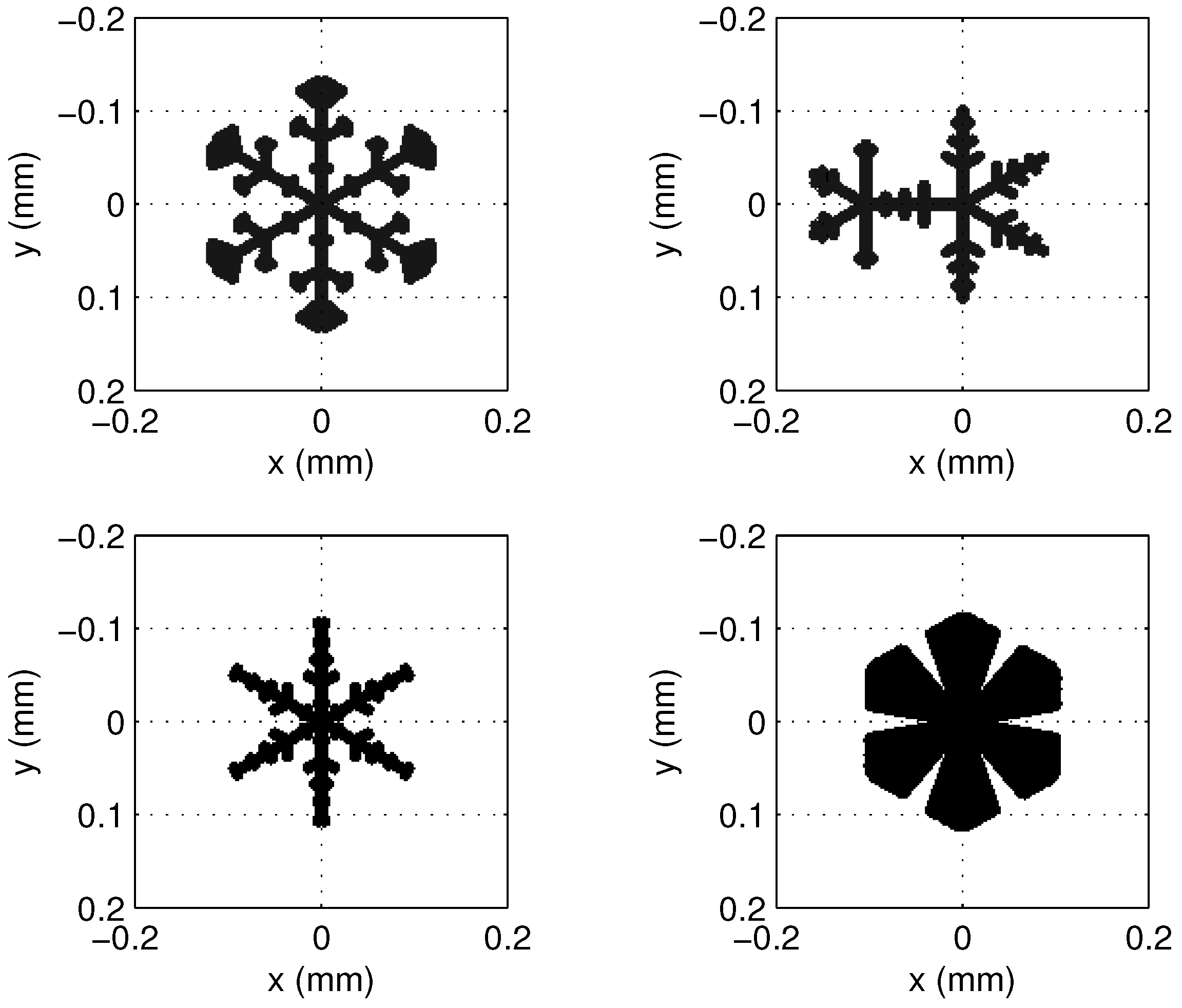
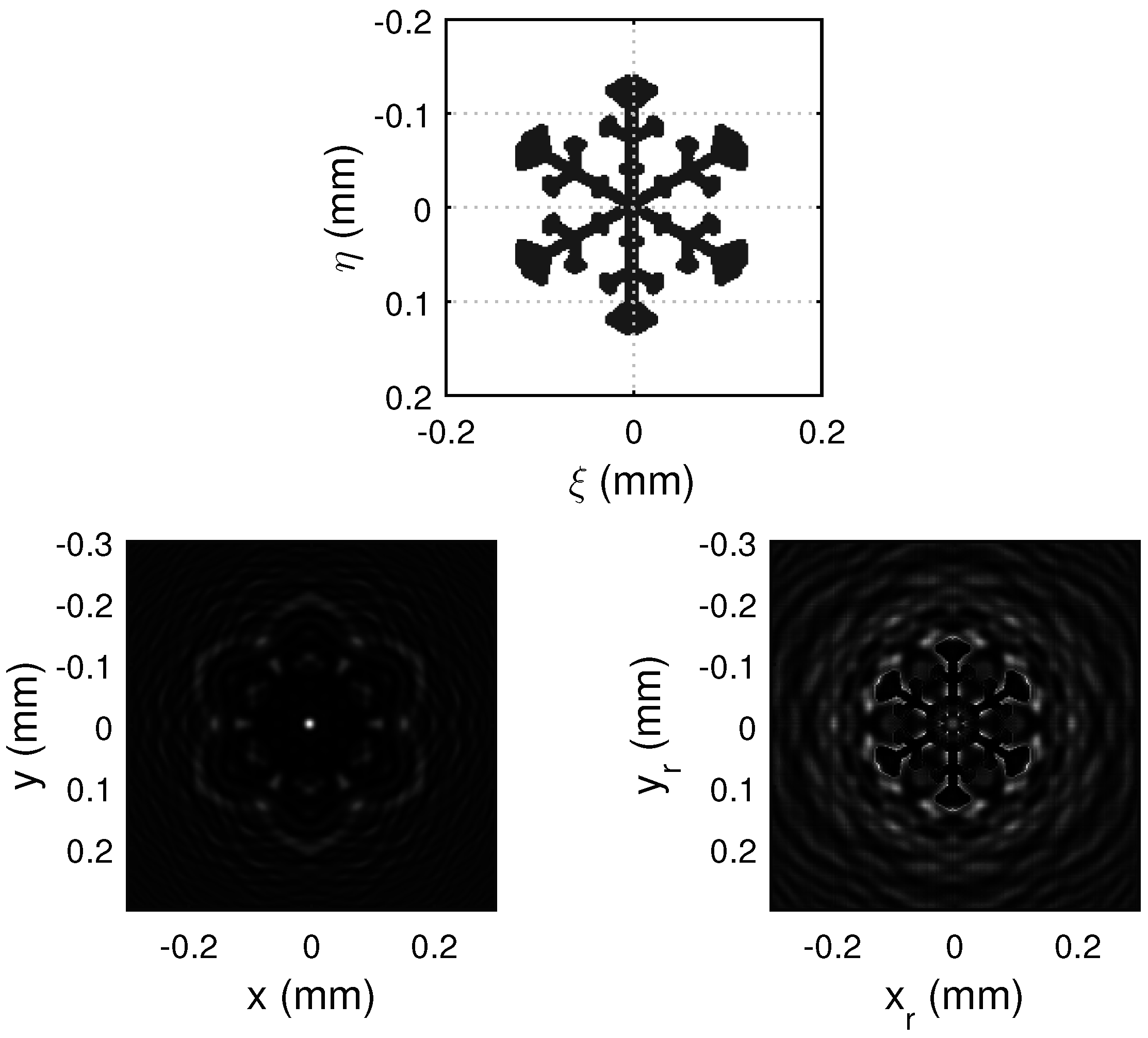
4.2. Library of Ice Crystal Objects for the Calibration of Interferometric Airborne Instruments
5. Conclusions
Acknowledgments
Author Contribution
Conflicts of Interest
References
- Schnars, U.; Jueptner, W.P. Direct recording of holograms by a CCD target and numerical reconstruction. Appl. Opt. 1994, 33, 179–181. [Google Scholar] [CrossRef] [PubMed]
- Katz, J.; Sheng, J. Applications of Holography in Fluid Mechanics and Particle Dynamics. Ann. Rev. Fluid Mech. 2010, 42, 531–555. [Google Scholar] [CrossRef]
- Buraga-Lefebvre, C.; Coetmellec, S.; Lebrun, D.; Ozkul, C. Application of wavelet transform to hologram analysis: three-dimensional location of particles. Opt. Las. Eng. 2000, 33, 409–421. [Google Scholar] [CrossRef]
- Pan, G.; Meng, H. Digital holography of particle fields: reconstruction by use of complex amplitude. Appl. Opt. 2003, 42, 827–833. [Google Scholar] [CrossRef] [PubMed]
- Denis, L.; Fournier, C.; Fournel, T.; Ducottet, C.; Jeulin, D. Direct extraction of the mean particle size from a digital hologram. Appl. Opt. 2006, 45, 944–952. [Google Scholar] [CrossRef] [PubMed]
- Desse, J.M.; Picart, P.; Tankam, P. Digital three-color holographic interferometry for flow analysis. Opt. Express 2008, 16, 5471–5480. [Google Scholar] [CrossRef] [PubMed]
- Verrier, N.; Remacha, C.; Brunel, M.; Lebrun, D.; Coetmellec, S. Micropipe flow visualization using digital in-line holographic microscopy. Opt. Express 2010, 18, 7807–7819. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K. Wavelength-scanning digital interference holography for optical section imaging. Opt. Lett. 1999, 24, 1693–1695. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K. Tomographic three-dimensional imaging of a biological specimen using wavelength-scanning digital interference holography. Opt. Exp. 2000, 7, 305–310. [Google Scholar] [CrossRef]
- Garcia-Sucerquia, J.; Xu, W.; Jericho, M.H.; Kreuzer, H.J. Immersion digital in-line holographic microscopy. Opt. Lett. 2006, 31, 1211–1213. [Google Scholar] [CrossRef] [PubMed]
- Cuche, E.; Marquet, P.; Depeursinge, C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 1999, 38, 6994–7001. [Google Scholar] [CrossRef] [PubMed]
- Cuche, E.; Bevilacqua, F.; Depeursinge, C. Digital holography for quantitative phase-contrast imaging. Opt. Lett. 1999, 24, 291–293. [Google Scholar] [CrossRef] [PubMed]
- Brunel, M.; Coetmellec, S.; Lebrun, D.; Ait Ameur, K. Digital phase contrast with the fractional Fourier transform. Appl. Opt. 2009, 48, 579–583. [Google Scholar] [CrossRef] [PubMed]
- Absil, E.; Tessier, G.; Gross, M.; Atlan, M.; Warnasooriya, N.; Suck, S.; Coppey-Moisan, M.; Fournier, D. Photothermal heterodyne holography of gold nanoparticles. Opt. Express 2010, 18, 780–786. [Google Scholar] [CrossRef] [PubMed]
- Picart, P.; Leval, J. General theoretical formulation of image formation in digital Fresnel holography. J. Opt. Soc. Am. A 2008, 25, 1744–1761. [Google Scholar] [CrossRef]
- Dubois, F.; Schockaert, C.; Callens, N.; Yourrassowsky, C. Focus plane detection criteria in digital holography microscopy by amplitude analysis. Opt. Express 2006, 14, 5895–5908. [Google Scholar] [CrossRef] [PubMed]
- Atlan, M.; Gross, M.; Absil, E. Accurate phase-shifting digital interferometry. Opt. Lett. 2007, 32, 1456–1458. [Google Scholar] [CrossRef] [PubMed]
- Gross, M.; Atlan, M. Digital holography with ultimate sensitivity. Opt. Lett. 2007, 32, 909–911. [Google Scholar] [CrossRef] [PubMed]
- Verrier, N.; Coetmellec, S.; Brunel, M.; Lebrun, D. Digital in-line holography in thick optical systems: Application to visualization in pipes. Appl. Opt. 2008, 47, 4147–4157. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Meunier-Guttin-Cluzel, S.; Wu, Y.; Saengkaew, S.; Lebrun, D.; Brunel, M.; Chen, L.; Coetmellec, S.; Cen, K.; Grehan, G. Holography and micro-holography of droplets: A numerical standard. Opt. Commun. 2012, 285, 3013–3020. [Google Scholar] [CrossRef]
- Coetmellec, S.; Wichitwong, W.; Grehan, G.; Lebrun, D.; Brunel, M.; Janssen, A.J.E.M. Digital in-line holography assessment for general phase and opaque particle. J. Eur. Opt. Soc. Rap. Publ. 2014, 9, 14021. [Google Scholar] [CrossRef]
- Coetmellec, S.; Pejchang, D.; Allano, D.; Grehan, G.; Lebrun, D.; Brunel, M.; Janssen, A.J.E.M. Digital in-line holography in a droplet with cavitation air bubbles. J. Eur. Opt. Soc. Rap. Publ. 2014, 9, 14056. [Google Scholar] [CrossRef]
- Brunel, M.; Shen, H.; Coetmellec, S.; Lebrun, D. Extended ABCD matrix formalism for the description of femtosecond diffraction patterns; application to femtosecond Digital In-line Holography with anamorphic optical systems. Appl. Opt. 2012, 51, 1137–1148. [Google Scholar] [CrossRef] [PubMed]
- Brunel, M.; Shen, H.; Coetmellec, S.; Lebrun, D.; Ait Ameur, K. Phase contrast metrology using digital in-line holography: General models and reconstruction of phase discontinuities. J. Quant. Spectrosc. Radiat. Transf. 2013, 126, 113–121. [Google Scholar] [CrossRef]
- Palma, C.; Bagini, V. Extension of the Fresnel transform to ABCD systems. J. Opt. Soc. Am. A 1997, 14, 1774–1779. [Google Scholar] [CrossRef]
- Lambert, A.J.; Fraser, D. Linear systems approach to simulation of optical diffraction. Appl. Opt. 1998, 37, 7933–7939. [Google Scholar] [CrossRef] [PubMed]
- Yura, H.T.; Hanson, S.G. Optical beam wave propagation through complex optical systems. J. Opt. Soc. Am. A 1987, 4, 1931–1948. [Google Scholar] [CrossRef]
- McBride, A.C.; Kerr, F.H. On Namias fractional Fourier transforms. IMA J. Appl. Math. 1987, 39, 159–175. [Google Scholar] [CrossRef]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. J. Inst. Math. Its Appl. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Lohmann, A.W. Image rotation, Wigner rotation, and the fractional Fourier transform. J. Opt. Soc. Am. A 1993, 10, 2180–2186. [Google Scholar] [CrossRef]
- Coetmellec, S.; Lebrun, D.; Ozkul, C. Application of the two-dimensional fractional-order Fourier transformation to particle field digital holography. J. Opt. Soc. Am. A 2002, 19, 1537–1546. [Google Scholar] [CrossRef]
- Mas, D.; Pérez, J.; Hernández, C.; Vázquez, C.; Miret, J.J.; Illueca, C. Fast numerical calculation of Fresnel patterns in convergent systems. Opt. Commun. 2003, 227, 245–258. [Google Scholar] [CrossRef]
- Brunel, M.; Coetmellec, S.; Lelek, M.; Louradour, F. Fractional-order Fourier analysis for ultrashort pulse characterization. J. Opt. Soc. Am. A 2007, 24, 1641–1646. [Google Scholar] [CrossRef]
- Wichitwong, W.; Coetmellec, S.; Lebrun, D.; Allan, D.; Grehan, G.; Brunel, M. Long exposure time Digital In-line Holography for the trajectography of micronic particles within a suspended millimetric droplet. Opt. Commun. 2014, 326, 160–165. [Google Scholar] [CrossRef]
- Chaari, A.; Grosges, T.; Giraud-Moreau, L.; Barchiesi, D. Nanobubble evolution around nanowire in liquid. Opt. Express 2013, 21, 26942–26954. [Google Scholar] [CrossRef] [PubMed]
- Querel, A.; Lemaitre, P.; Brunel, M.; Porcheron, E.; Grehan, G. Real-time global interferometric laser imaging for the droplet sizing (ILIDS) algorithm for airborne research. Meas. Sci. Technol. 2010, 21, 015306. [Google Scholar] [CrossRef]
- Glover, A.R.; Skippon, S.M.; Boyle, R.D. Interferometric laser imaging for droplet sizing: A method for droplet-size measurement in sparse spray systems. Appl. Opt. 1995, 34, 8409–8421. [Google Scholar] [CrossRef] [PubMed]
- Damaschke, N.; Nobach, H.; Tropea, C. Optical limits of particle concentration for multi-dimensional particle sizing techniques in fluid mechanics. Exp. Fluids 2002, 32, 143–152. [Google Scholar]
- Shen, H.; Coetmellec, S.; Grehan, G.; Brunel, M. ILIDS revisited: elaboration of transfer matrix models for the description of complete systems. Appl. Opt. 2012, 51, 5357–5368. [Google Scholar] [CrossRef] [PubMed]
- Brunel, M.; Coetmellec, S.; Grehan, G.; Shen, H. Interferometric out-of-focus imaging simulator for irregular rough particles. J. Eur. Opt. Soc. Rap. Publ. 2014, 9, 14008. [Google Scholar] [CrossRef]
- Brunel, M.; Gonzalez Ruiz, S.; Jacquot, J.; van Beeck, J. On the morphology of irregular rough particles from the analysis of speckle-like interferometric out-of-focus images. Opt. Commun. 2015, 338, 193–198. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brunel, M.; Wichitwong, W.; Coetmellec, S.; Masselot, A.; Lebrun, D.; Gréhan, G.; Edouard, G. Numerical Models for Exact Description of in-situ Digital In-Line Holography Experiments with Irregularly-Shaped Arbitrarily-Located Particles. Appl. Sci. 2015, 5, 62-76. https://doi.org/10.3390/app5020062
Brunel M, Wichitwong W, Coetmellec S, Masselot A, Lebrun D, Gréhan G, Edouard G. Numerical Models for Exact Description of in-situ Digital In-Line Holography Experiments with Irregularly-Shaped Arbitrarily-Located Particles. Applied Sciences. 2015; 5(2):62-76. https://doi.org/10.3390/app5020062
Chicago/Turabian StyleBrunel, Marc, Wisuttida Wichitwong, Sébastien Coetmellec, Adrien Masselot, Denis Lebrun, Gérard Gréhan, and Guillaume Edouard. 2015. "Numerical Models for Exact Description of in-situ Digital In-Line Holography Experiments with Irregularly-Shaped Arbitrarily-Located Particles" Applied Sciences 5, no. 2: 62-76. https://doi.org/10.3390/app5020062
APA StyleBrunel, M., Wichitwong, W., Coetmellec, S., Masselot, A., Lebrun, D., Gréhan, G., & Edouard, G. (2015). Numerical Models for Exact Description of in-situ Digital In-Line Holography Experiments with Irregularly-Shaped Arbitrarily-Located Particles. Applied Sciences, 5(2), 62-76. https://doi.org/10.3390/app5020062





