A Review of Cavity Design for Kerr Lens Mode-Locked Solid-State Lasers
Abstract
:1. Introduction
2. Outline
3. Basic Principles of Pulsed Operation in a Laser
3.1. Formation of Ultrashort Pulses
3.2. Active/Passive Mode-Locking
4. The Optical Kerr Effect
5. Cavity Analysis in CW Operation
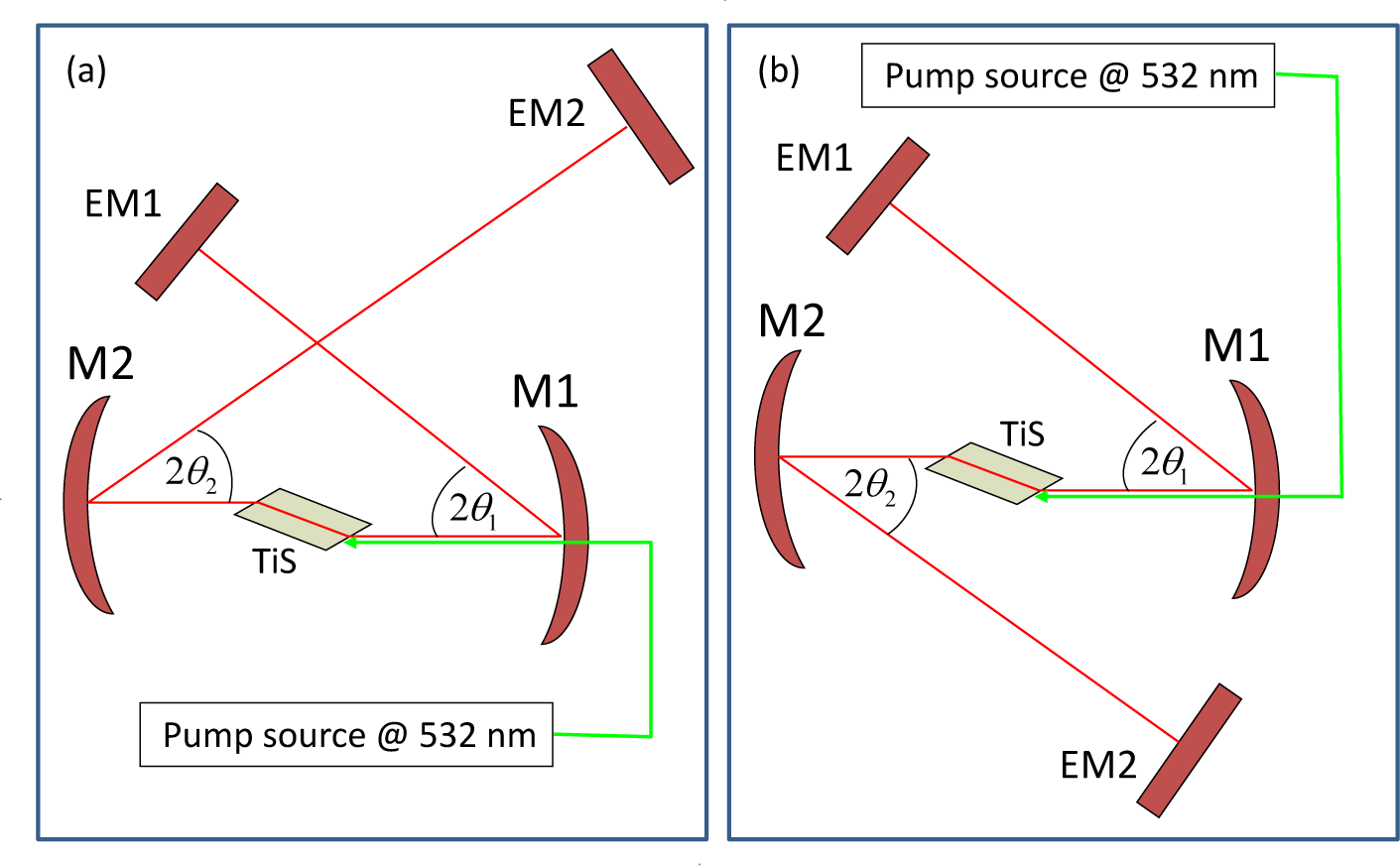
5.1. Basic Configuration of a Ti:sapphire Oscillator
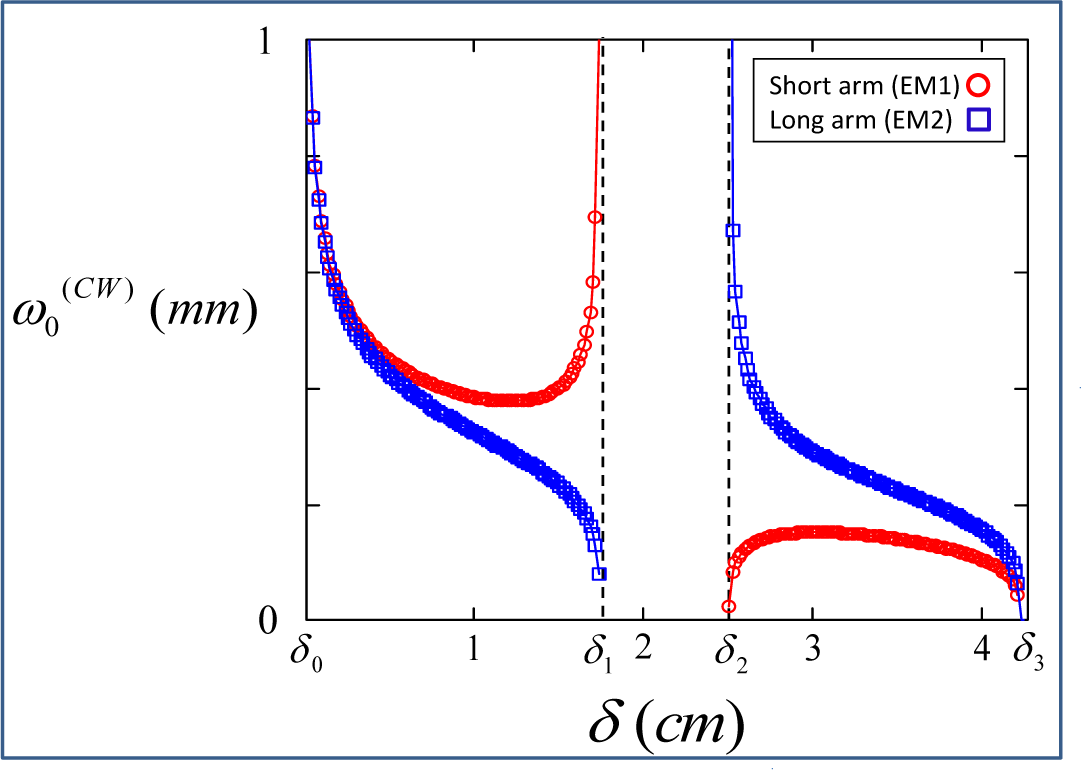
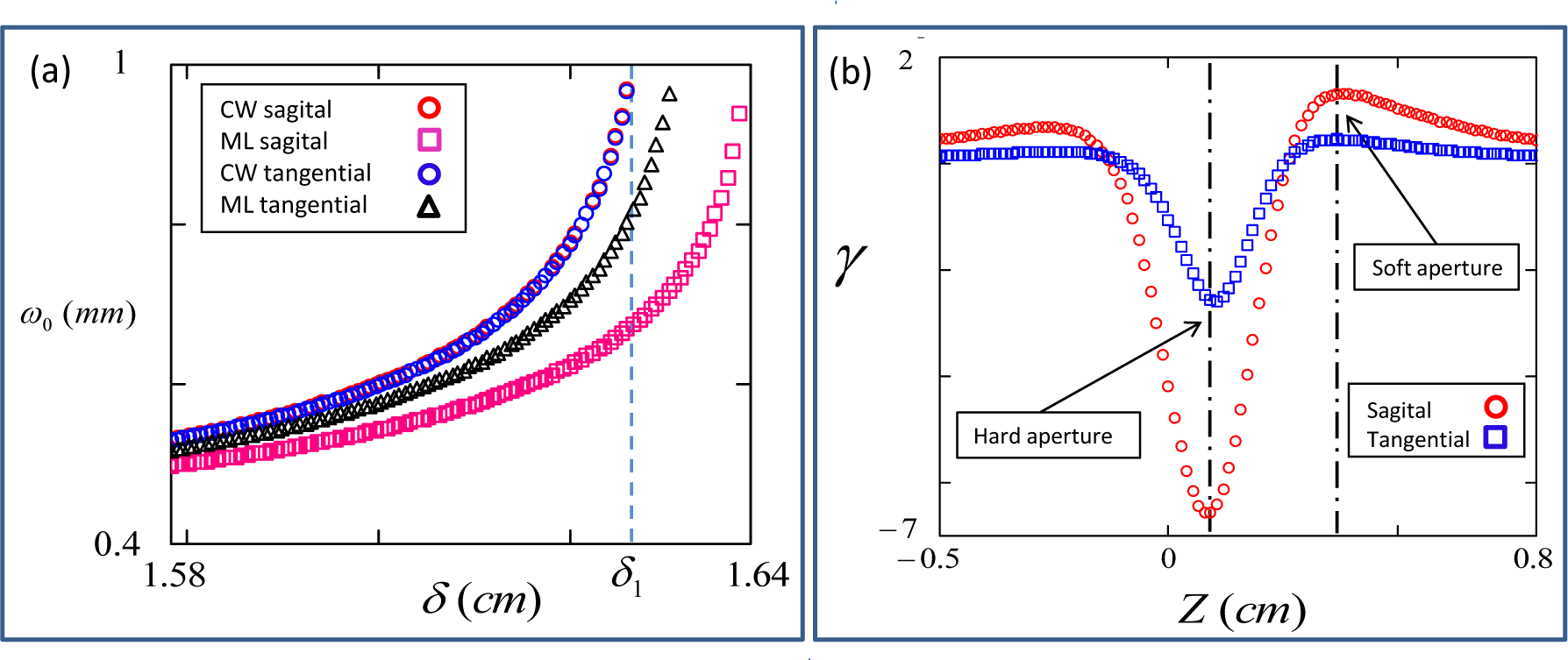
5.2. Stability Ranges and Limits
5.3. Gaussian Modes
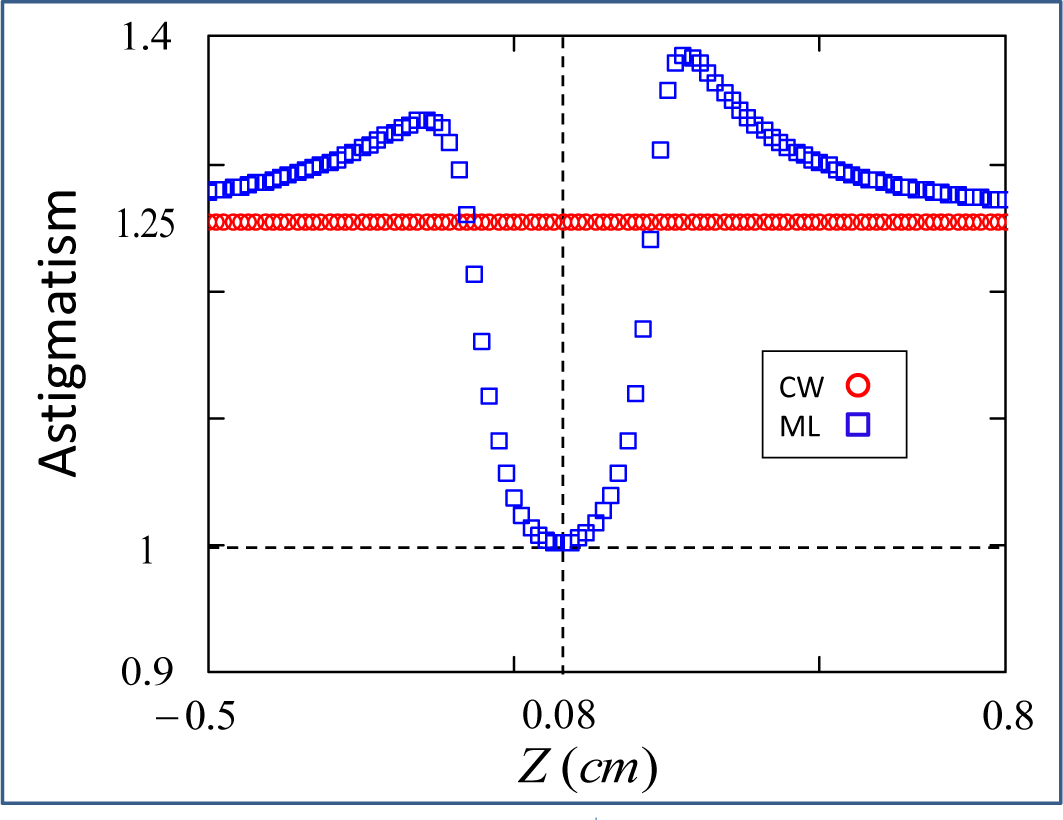
5.4. Linear Astigmatism
6. Cavity Analysis in Mode-Locked Operation
6.1. A Gaussian Beam in a Kerr Medium
7. Mode-Locking Techniques
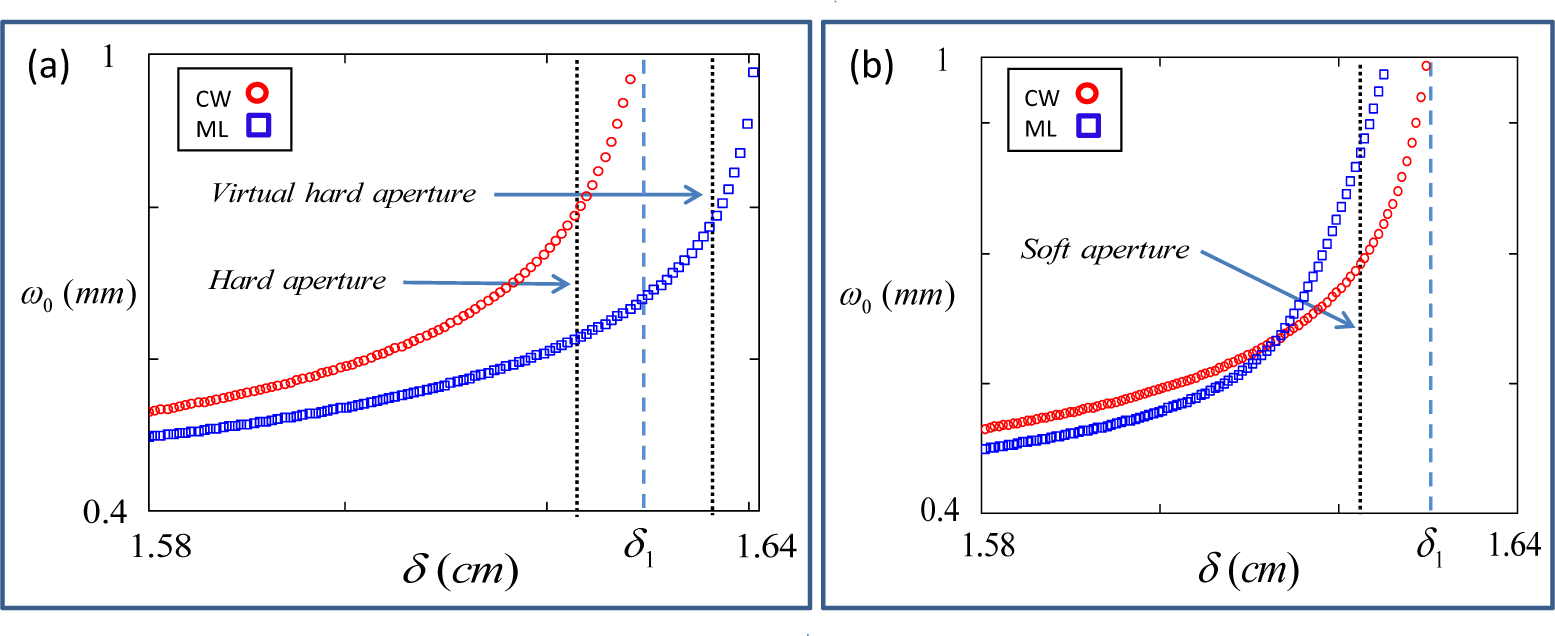
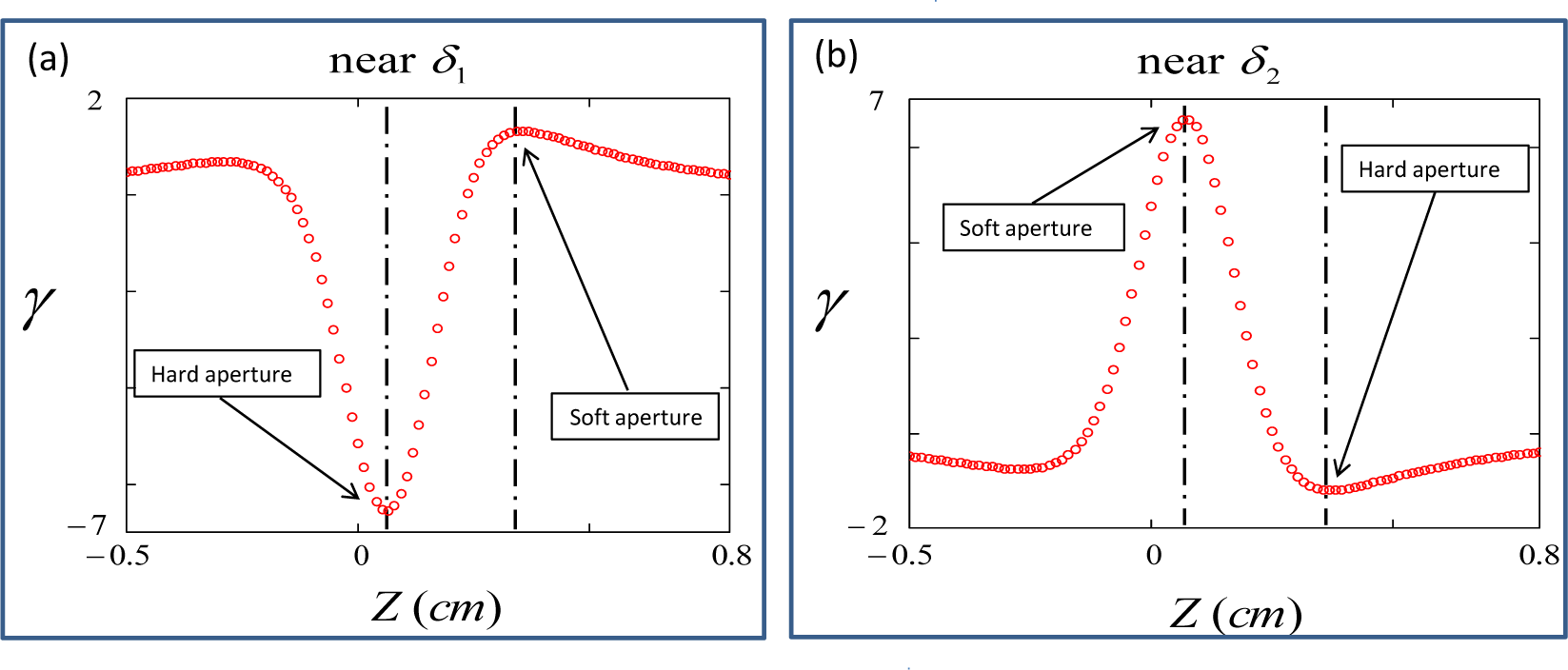
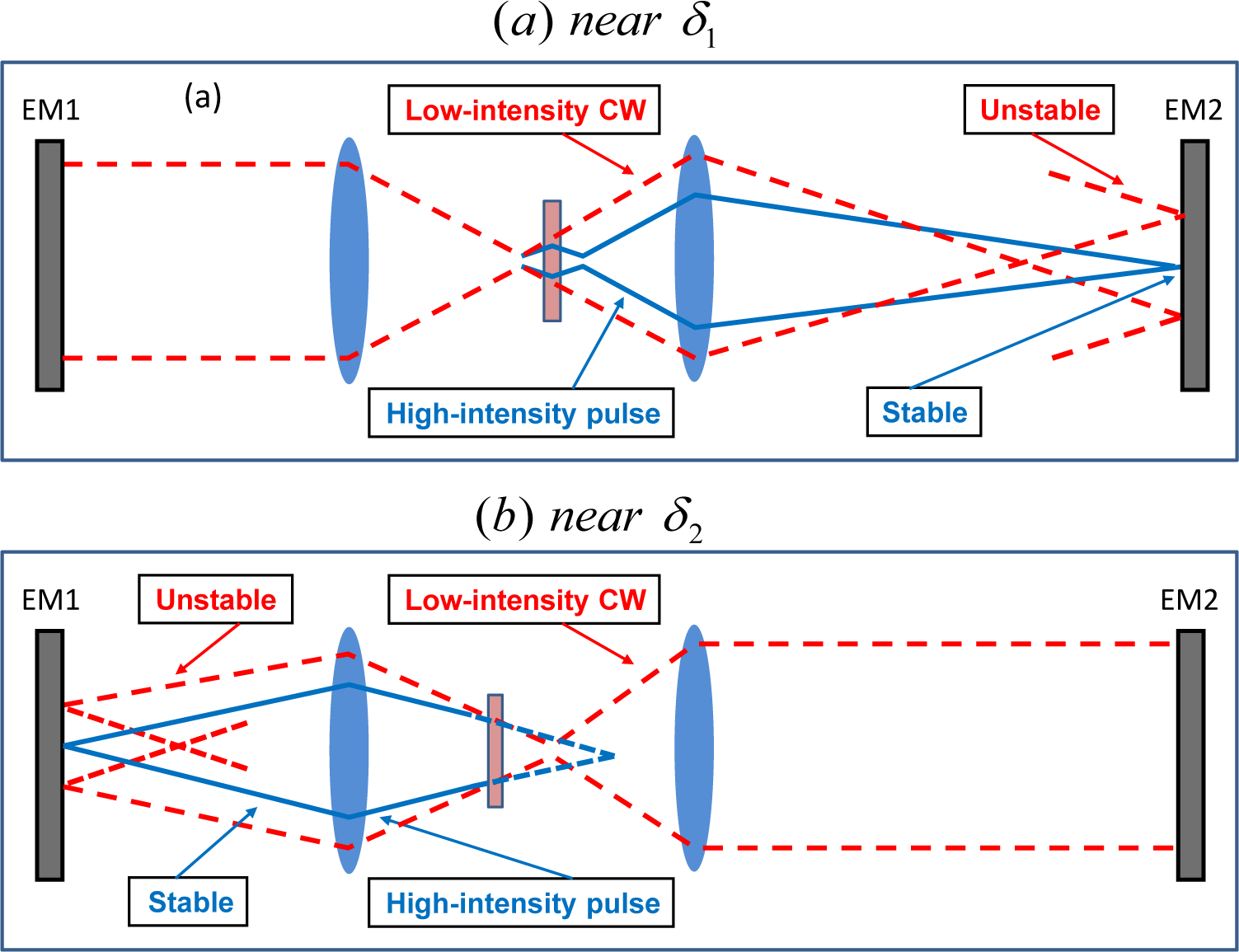
7.1. Hard/Soft Aperture Mode-Locking
7.1.1. Hard Aperture
7.1.2. Soft Aperture
7.2. Virtual Hard Aperture Mode-Locking
8. Nonlinear Kerr Lens Astigmatism
9. Dispersion Compensation
9.1. Group Delay Dispersion
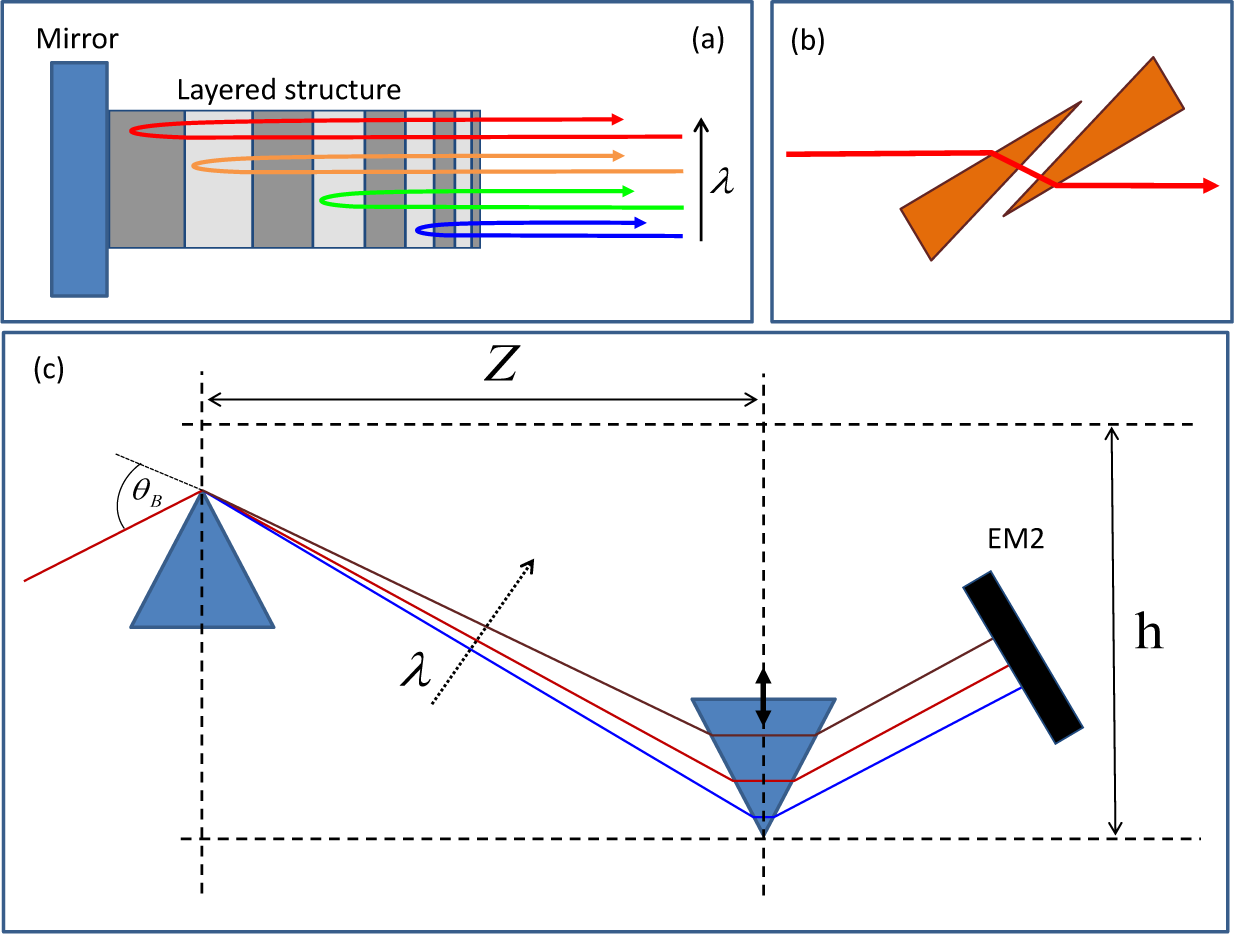
9.2. Chirped Mirrors
9.3. Prism Pair
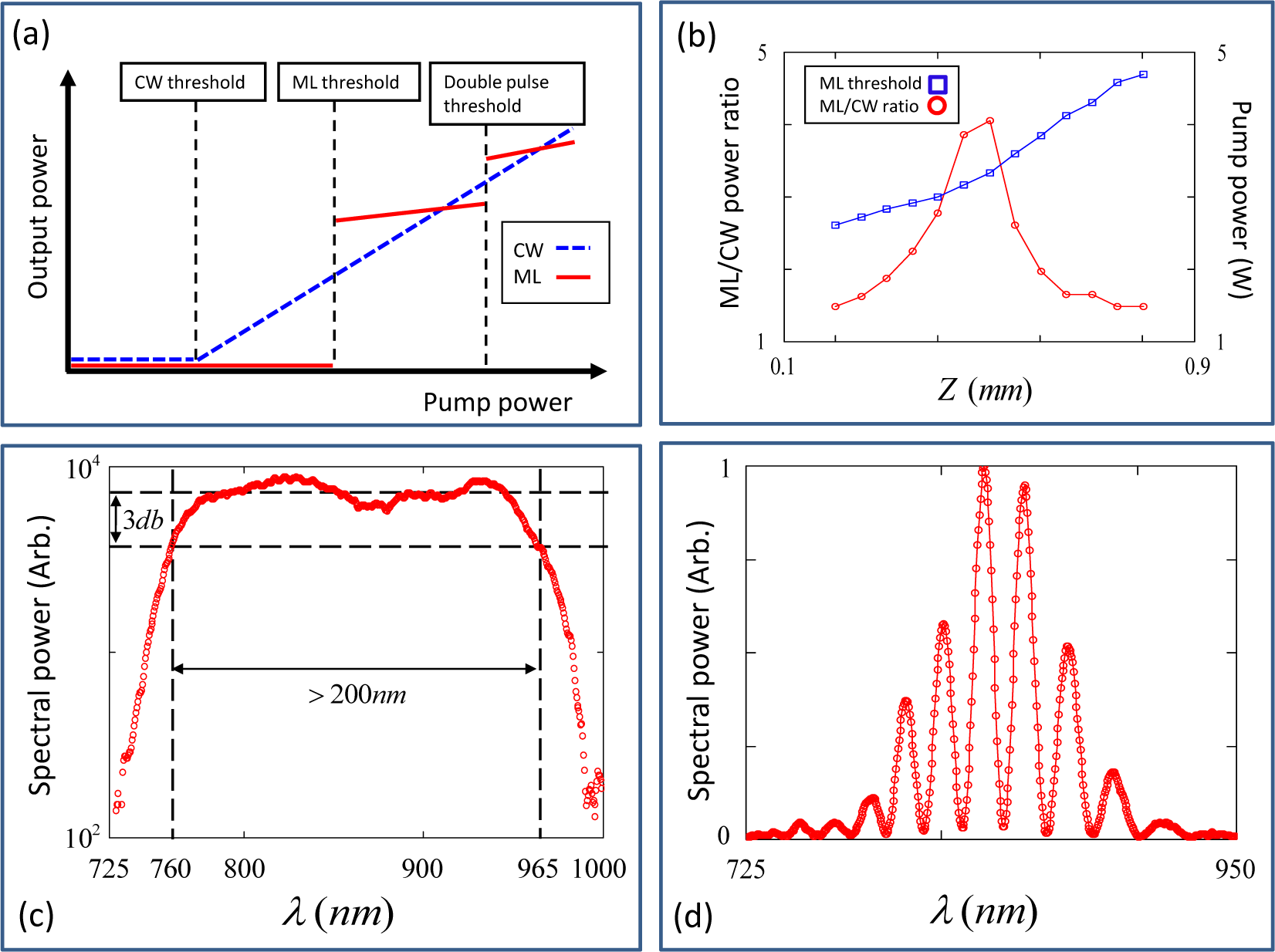
10. Typical Characteristics of Pulsed Operation
11. Beyond the Standard Cavity Design
11.1. Optimization of Laser Parameters: Compactness, Optical Elements, Stability and Pulse Duration
11.2. Elimination of Nonlinear Astigmatism
11.3. Two-Color Pulses by Intra-Cavity Gain Shaping
12. Summary
Acknowledgments
Conflicts of Interest
Appendix
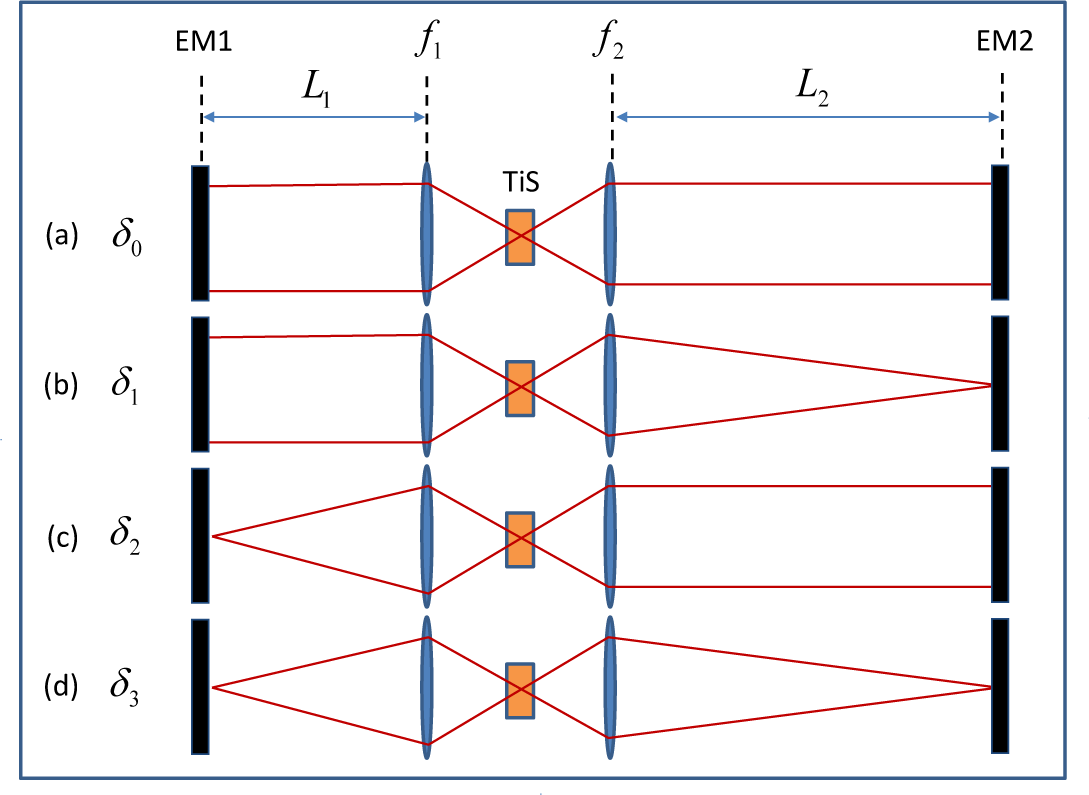
A. Generalized Linear Astigmatism Compensation
| δi | D1i | D2i |
|---|---|---|
| δ0 | ∞ | ∞ |
| δ1 | ∞ | L2 |
| δ2 | L1 | ∞ |
| δ3 | L1 | L2 |
References
- Zewail, A.H. Femtochemistry: Atomic-scale dynamics of the chemical bond. J. Phys. Chem. A. 2000, 104, 5660–5694. [Google Scholar]
- Hoover, E.E.; Squier, J.A. Advances in multiphoton microscopy technology. Nat. Photonics. 2013, 7, 93–101. [Google Scholar]
- Cundiff, S.T.; Ye, J. Colloquium: Femtosecond optical frequency combs. Rev. Mod. Phys. 2003, 75, 325–342. [Google Scholar]
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279–1295. [Google Scholar]
- Hänsch, T.W. Nobel Lecture: Passion for precision. Rev. Mod. Phys. 2006, 78, 1297–1309. [Google Scholar]
- Ultrafast Lasers: Technology and Applications; Fermann, M.E.; Galvanauskas, A.; Sucha, G. (Eds.) Marcel Dekker: Basel, Switzerland, 2001.
- Sibbett, W.; Lagatsky, A.A.; Brown, C.T.A. The development and application of femtosecond laser systems. Opt. Express. 2012, 20, 6989–7001. [Google Scholar]
- Hargrove, L.E.; Fork, R.L.; Pollack, M.A. Locking of He-Ne laser modes induced by synchronous intracavity modulation. Appl. Phys. Lett. 1964, 5, 4–5. [Google Scholar]
- Spence, D.E.; Kean, P.N.; Sibbett, W. 60-fsec pulse generation from a self-mode-locked Ti:sapphire laser. Opt. Lett. 1991, 16, 42–44. [Google Scholar]
- Salin, F.; Squier, J.; Piché, M. Mode locking of Ti:Al2O3 lasers and self-focusing: A Gaussian approximation. Opt. Lett. 1991, 16, 1674–1676. [Google Scholar]
- Chen, S.; Wang, J. Self-starting issues of passive self-focusing mode locking. Opt. Lett. 1991, 16, 1689–1691. [Google Scholar]
- Brabec, T.; Spielmann, C.; Curley, P.F.; Krausz, F. Kerr lens mode locking. Opt. Lett. 1992, 17, 1292–1294. [Google Scholar]
- Herrmann, J. Starting dynamic, self-starting condition and mode-locking threshold in passive, coupled-cavity or Kerr-lens mode-locked solid-state lasers. Opt. Commun. 1993, 98, 111–116. [Google Scholar]
- Morgner, U.; Kärtner, F.X.; Cho, S.H.; Chen, Y.; Haus, H.A.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T. Sub-two-cycle pulses from a Kerr-lens mode-locked Ti:sapphire laser. Opt. Lett. 1999, 6, 411–413. [Google Scholar]
- Sutter, D.H.; Steinmeyer, G.; Gallmann, L.; Matuschek, N.; Morier-Genoud, F.; Keller, U.; Scheuer, V.; Angelow, G.; Tschudi, T. Semiconductor saturable-absorber mirror-assisted Kerr-lens mode-locked Ti:sapphire laser producing pulses in the two-cycle regime. Opt. Lett. 1991, 24, 631–633. [Google Scholar]
- Asaki, M.T.; Huang, C.; Garvey, D.; Zhou, J.; Kapteyn, H.C.; Murnane, M.M. Generation of 11-fs pulses from a self-modelocked Ti:sapphire Laser. Opt. Lett. 1993, 18, 977–979. [Google Scholar]
- Stingl, A.; Spielmann, C.; Krausz, F. Generation of 11-fs pulses from a Ti:sapphire laser without the use of prisms. Opt. Lett. 1994, 19, 204–206. [Google Scholar]
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Kuizenga, D. FM and AM mode locking of the homogeneous laser—Part I: Theory. IEEE J. Quantum Electron 1970, 6, 694–708. [Google Scholar]
- Kuizenga, D. FM and AM mode locking of the homogeneous laser—Part II: Experimental results in a Nd:YAG laser with internal FM modulation. IEEE J. Quantum Electron 1970, 6, 709–715. [Google Scholar]
- Ippen, E.P.; Shank, C.V.; Dienes, A. Passive mode locking of the cw dye laser. Appl. Phys. Lett. 1972, 21, 348–350. [Google Scholar]
- Haus, H.A. Theory of mode locking with a fast saturable absorber. J. Appl. Phys. 1975, 46, 3049–3058. [Google Scholar]
- Becker, M.; Kuizenga, D.J.; Siegman, A. Harmonic mode locking of the Nd:YAG laser. IEEE J. Quantum Electron 1972, 8, 687–693. [Google Scholar]
- McDuff, O.; Thati, D.; Shetty, R. A study of the chirping of a single-sideband mode-locked laser. IEEE Proc. Southeastcon ’91 1991, 1, 293–297. [Google Scholar]
- Keller, U. Recent developments in compact ultrafast lasers. Nature 2003, 424, 831–838. [Google Scholar]
- Keller, U.; Weingarten, K.J.; Kärtner, F.X.; Kopf, D.; Braun, B.; Jung, I.D.; Fluck, R.; Hönninger, C.; Matuschek, N.; der Au, J.A. Semiconductor saturable absorber mirrors (SESAM’s) for femtosecond to nanosecond pulse generation in solid-state lasers. IEEE J. Sel. Top. Quantum Electron 1996, 2, 435–452. [Google Scholar]
- Kärtner, F.X.; Morgner, U.; Schibli, T.; Ell, R.; Haus, H.A.; Fujimoto, J.G.; Ippen, E.P. Few-cycle laser pulse generation and its applications. Top. Appl. Phys. 2004, 95, 73–136. [Google Scholar]
- Krausz, F.; Fermann, M.E.; Brabec, T.; Curley, P.F.; Hofer, M.; Ober, M.H.; Spielmann, C.; Wintner, E.; Schmidt, A.J. Femtosecond solid-state lasers. IEEE J. Quantum Electron 1992, 28, 2097–2122. [Google Scholar]
- Haus, H.A. Mode-Locking of Lasers. IEEE J. Sel. Topics Quantum Electron 2000, 6, 1173–1185. [Google Scholar]
- Haus, H.A.; Fujimoto, J.G.; Ippen, E.P. Structures for additive pulse mode locking. J. Opt. Soc. Am. B. 1991, 8, 2068–2076. [Google Scholar]
- Brabec, T.; Spielmann, C.; Krausz, F. Mode locking in solitary lasers. Opt. Lett. 1991, 16, 1961–1963. [Google Scholar]
- Stolen, R.H.; Ashkin, A. Optical Kerr effect in glass waveguide. Appl. Phys. Lett. 1973, 22, 294–296. [Google Scholar]
- Sheik-Bahae, M.; Hutchings, D.C.; Hagan, D.J.; Stryland, E.W.V. Dispersion of bound electron nonlinear refraction in solids. IEEE J. Quantum Electron 1991, 27, 1296–1309. [Google Scholar]
- Herrmann, J. Theory of Kerr-lens mode locking: Role of self-focusing and radially varying gain. J. Opt. Soc. Am. B. 1944, 11, 498–512. [Google Scholar]
- Major, A.; Yoshino, F.; Nikolakakos, I.; Aitchison, J.S.; Smith, P.W.E. Dispersion of the nonlinear refractive index in sapphire. Opt. Lett. 2004, 29, 602–604. [Google Scholar]
- Magni, V.; Cerullo, G.; Silvestri, S.D.; Monguzzi, A. Astigmatism in Gaussian-beam self-focusing and in resonators for Kerr-lens mode locking. J. Opt. Soc. Am. B. 1995, 12, 476–485. [Google Scholar]
- Shimizu, F. Frequency broadening in liquids by a short light pulse. Phys. Rev. Lett. 1967, 19, 1097–1100. [Google Scholar]
- Wall, K.F.; Sanchez, A. TItanium sapphire lasers. Linc. Lab. J. 1990, 3, 447–462. [Google Scholar]
- Dong, J.; Deng, P. Ti:sapphire crystal used in ultrafast lasers and amplifiers. J. Cryst. Growth. 2004, 261, 514–519. [Google Scholar]
- Kogelnik, H.; Li, T. Laser beams and resonators. Appl. Opt. 1966, 5, 1550–1567. [Google Scholar]
- Fortier, T.M.; Bartels, A.; Diddams, S.A. Octave-spanning Ti:sapphire laser with a repetition rate >1 GHz for optical frequency measurements and comparisons. Opt. Lett. 2006, 31, 1011–1013. [Google Scholar]
- Tache, J.P. Ray matrices for tilted interfaces in laser resonators. Appl. Opt. 1987, 26, 427–429. [Google Scholar]
- Kogelnik, H.; Ippen, E.P.; Dienes, A.; Shank, C.V. Astigmatically Compensated Cavities for CW Dye Lasers. IEEE J. Quantum Electron 1972, 8, 373–379. [Google Scholar]
- Magni, V. Multielement stable resonators containing a variable lens. J. Opt. Soc. Am. A. 1987, 4, 1962–1969. [Google Scholar]
- Magni, V.; Cerullo, G.; Silvestri, S.D. ABCD matrix analysis of propagation of Gaussian beams through Kerr media. Opt. Commun. 1993, 96, 348–355. [Google Scholar]
- Lin, W.Z.; Chen, Y.C.; Wen, J.H. A novel modeling for KLM solid-state laser resonator. Laser Phys 1999, 9, 324–327. [Google Scholar]
- Haus, H.A.; Fujimoto, J.G.; Ippen, E.P. Analytic Theory of Additive Pulse and Kerr Lens Mode Locking. IEEE J. Quantum Electron 1992, 28, 2086–2096. [Google Scholar]
- Fibich, G.; Gaeta, A.L. Critical power for self-focusing in bulk media and in hollow waveguides. Opt. Lett. 2000, 25, 335–337. [Google Scholar]
- Lin, K.; Lai, Y.; Hsieh, W. Simple analytical method of cavity design for astigmatism-compensated Kerr-lens mode-locked ring lasers and its applications. J. Opt. Soc. Am. B. 1995, 12, 468–475. [Google Scholar]
- Lin, K.; Hsieh, W. Analytical design of symmetrical Kerr-lens mode-locking laser cavities. J. Opt. Soc. Am. B. 1994, 11, 737–741. [Google Scholar]
- Fibich, G.; Ilan, B. Self-focusing of elliptic beams: An example of the failure of the aberrationless approximation. J. Opt. Soc. Am. B. 2000, 17, 1749–1758. [Google Scholar]
- Yefet, S.; Pe’er, A. Mode locking with enhanced nonlinearity—A detailed study. Opt. Express. 2013, 21, 19040–19046. [Google Scholar]
- Yefet, S.; Jouravsky, V.; Pe’er, A. Kerr lens mode locking without nonlinear astigmatism. J. Opt. Soc. Am. B. 2013, 30, 549–551. [Google Scholar]
- Walmsley, I.; Waxer, L.; Dorrer, C. The role of dispersion in ultrafast optics. Rev. Sci. Instrum. 2001, 72, 1–29. [Google Scholar]
- Diels, J.C.; Rudolph, W. Ultrashort Laser Pulse Phenomena; Academic Press: San Diego, CA, USA, 2006; pp. 61–143. [Google Scholar]
- Chen, L.; Zhang, M.; Zhang, Z. Frontiers in Guided Wave Optics and Optoelectronics; InTech: Vukovar, Croatia, 2010; pp. 165–182. [Google Scholar]
- De Silvestri, S.; Laporta, P.; Svelto, O. The role of cavity dispersion in CW mode-locked lasers. IEEE J. Quantum Electron 1984, 20, 533–539. [Google Scholar]
- Cojocaru, E. Analytic expressions for the fourth- and the fifth-order dispersions of crossed prisms pairs. Appl. Opt. 2003, 42, 6910–6914. [Google Scholar]
- Szipőcs, R.; Ferencz, K.; Spielmann, C.; Krausz, F. Chirped multilayer coatings for broadband dispersion control in femtosecond lasers. Opt. Lett. 1994, 19, 201–203. [Google Scholar]
- Steinmeyer, G. Femtosecond dispersion compensation with multilayer coatings : Toward the optical octave. Appl. Opt. 2006, 45, 1484–1490. [Google Scholar]
- Kärtner, F.X.; Matuschek, N.; Schibli, T.; Keller, U.; Haus, H.A.; Heine, C.; Morf, R.; Scheuer, V.; Tilsch, M.; Tschudi, T. Design and fabrication of double-chirped mirrors. Opt. Lett. 1997, 22, 831–833. [Google Scholar]
- Matuschek, N.; Kärtner, F.X.; Keller, U. Theory of double-chirped mirrors. IEEE J. Sel. Top. Quantum Electron 1998, 4, 197–208. [Google Scholar]
- Matuschek, N.; Kärtner, F.; Keller, U. Analytical design of double-chirped mirrors with custom-tailored dispersion characteristics. IEEE J. Quantum Electron 1999, 35, 129–137. [Google Scholar]
- Fork, R.L.; Martinez, E.; Gordon, J.P. Negative dispersion using pairs of prisms. Opt. Lett. 1984, 9, 150–152. [Google Scholar]
- Fork, R.L.; Cruz, C.H.B.; Becker, P.C.; Shank, C.V. Compression of optical pulses to six femtoseconds by using cubic phase compensation. Opt. Lett. 1987, 12, 483–485. [Google Scholar]
- Zhang, Z.; Yagi, T. Observation of group delay dispersion as a function of the pulse width in a mode locked Ti:sapphire laser. Appl. Phys. Lett. 1993, 63, 2993–2995. [Google Scholar]
- Arissian, L.; Diels, J.C. Carrier to envelope and dispersion control in a cavity with prism pairs. Phys. Rev. A. 2007, 75, 013814. [Google Scholar]
- Sherriff, R.E. Analytic expressions for group-delay dispersion and cubic dispersion in arbitrary prism sequences. J. Opt. Soc. Am. B. 1998, 15, 1224–1230. [Google Scholar]
- Naganuma, K.; Mogi, K. 50-fs pulse generation directly from a colliding-pulse mode-locked Ti:sapphire laser using an antiresonant ring mirror. Opt. Lett. 1991, 16, 738–740. [Google Scholar]
- Treacy, E.B. Optical pulse compression with diffraction gratings. IEEE J. Quantum Electron 1969, 5, 454–458. [Google Scholar]
- Tournois, P. New diffraction grating pair with very linear dispersion for laser pulse compression. Electron. Lett. 1993, 29, 1414–1415. [Google Scholar]
- Li, K.; Chen, M.; Wang, L.; Yang, S. Generation of negative group-velocity dispersion by a single prism and wedge mirror in femtosecond lasers. Opt. Eng. 1999, 38, 1801–1805. [Google Scholar]
- Moulton, P.F. Spectroscopic and laser characteristics of Ti:Al2O3. J. Opt. Soc. Am. B. 1986, 3, 125–133. [Google Scholar]
- Bartels, A.; Heinecke, D.; Diddams, S.A. Passively mode-locked 10 GHz femtosecond Ti:sapphire laser. Opt. Lett. 2008, 33, 1905–1907. [Google Scholar]
- Matsushima, I.; Yashiro, H.; Tomie, T. 10 kHz 40 W Ti:sapphire regenerative ring amplifier. Opt. Lett. 2006, 31, 2066–2068. [Google Scholar]
- Kowalevicz, A.M., Jr.; Schibli, T.R.; Kärtner, F.X.; Fujimoto, J.G. Ultralow-threshold Kerr-lens mode-locked Ti:Al2O3 laser. Opt. Lett. 2002, 27, 2037–2039. [Google Scholar]
- Dewald, S.; Lang, T.; Schröter, C.D.; Moshammer, R.; Ullrich, J.; Siegel, M.; Morgner, U. Ionization of noble gases with pulses directly from a laser oscillator. Opt. Lett. 2006, 31, 2072–2074. [Google Scholar]
- Gordon, A.; Fischer, B. Phase transition theory of pulse formation in passively mode-locked lasers with dispersion and Kerr nonlinearity. Opt. Commun. 2003, 223, 151–156. [Google Scholar]
- Rosen, A.; Weill, R.; Levit, B.; Smulakovsky, V.; Bekker, A.; Fischer, B. Experimental observation of critical phenomena in a laser light system. Phys. Rev. Lett. 2010, 105, 013905. [Google Scholar]
- Diels, J.C.M.; Fontaine, J.J.; McMichael, I.C.; Simoni, F. Control and measurement of ultrashort pulse shapes (in amplitude and phase) with femtosecond accuracy. Appl. Opt. 1985, 24, 1270–1282. [Google Scholar]
- Trebino, R.; DeLong, K.W.; Fittinghoff, D.N.; Sweetser, J.N.; Krumbügel, M.A.; Richman, B.A.; Kane, D.J. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 1997, 68, 3277–3295. [Google Scholar]
- Gallmann, L.; Sutter, D.H.; Matuschek, N.; Steinmeyer, G.; Keller, U.; Iaconis, C.; Walmsley, I.A. Characterization of sub-6-fs optical pulses with spectral phase interferometry for direct electric-field reconstruction. Opt. Lett. 1999, 24, 1314–1316. [Google Scholar]
- Gallmann, L.; Sutter, D.; Matuschek, N.; Steinmeyer, G.; Keller, U. Techniques for the characterization of sub-10-fs optical pulses: A comparison. Appl. Phys. B. 2000, 70, S67–S75. [Google Scholar]
- Reynaud, F.; Salin, F.; Barthelemy, A. Measurement of phase shifts introduced by nonlinear optical phenomena on subpicosecond pulses. Opt. Lett. 1989, 14, 275–277. [Google Scholar]
- Kalashnikov, V.L.; Sorokin, E.; Sorokina, I.T. Multipulse operation and limits of the Kerr-lens mode-locking stability. IEEE J. Quantum Electron 2003, 39, 323–336. [Google Scholar]
- Kalashnikov, V.L.; Kalosha, V.P.; Poloyko, I.G.; Mikhailov, V.P. Optimal resonators for self-mode locking of continuous-wave solid-state lasers. J. Opt. Soc. Am. B. 1997, 14, 964–969. [Google Scholar]
- Brabec, T.; Curley, P.F.; Spielmann, C.; Wintner, E.; Schmidt, A.J. Hard-aperture Kerr-lens mode locking. J. Opt. Soc. Am. B. 1993, 10, 1029–1034. [Google Scholar]
- Liau, Y.; Unterreiner, A.N.; Arnett, D.C.; Scherer, N.F. Femtosecond-pulse cavity-dumped solid-state oscillator design and application to ultrafast microscopy. Appl. Opt. 1999, 38, 7386–7392. [Google Scholar]
- Chen, Y.; Kärtner, F.X.; Morgner, U.; Cho, S.H.; Haus, H.A.; Ippen, E.P.; Fujimoto, J.G. Dispersion-managed mode locking. J. Opt. Soc. Am. B. 1999, 16, 1994–2004. [Google Scholar]
- Ell, R.; Morgner, U.; Kärtner, F.X.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T.; Lederer, M.J.; Boiko, A.; et al. Generation of 5-fs pulses and octave-spanning spectra directly from a Ti:sapphire laser. Opt. Lett. 2001, 26, 373–375. [Google Scholar]
- Dudovich, N.; Oron, D.; Silberberg, Y. Single-pulse coherently controlled nonlinear Raman spectroscopy and microscopy. Nature 2002, 418, 512–514. [Google Scholar]
- Saar, B.G.; Freudiger, C.W.; Reichman, J.; Stanley, C.M.; Holtom, G.R.; Xie, X.S. Video-rate molecular imaging in vivo with stimulated raman scattering. Science 2010, 330, 1368–1370. [Google Scholar]
- Freudiger, C.W.; Min, W.; Saar, B.G.; Lu, S.; Holtom, G.R.; He, C.; Tsai, J.C.; Kang, J.X.; Xie, X.S. Label-free biomedical imaging with high sensitivity by stimulated raman scattering microscopy. Science 2008, 322, 1857–1860. [Google Scholar]
- Marian, A.; Stowe, M.C.; Lawall, J.; Felinto, D.; Ye, J. United time-frequency spectroscopy for dynamics and global structure. Science 2004, 306, 2063–2067. [Google Scholar]
- Debarros, M.R.X.; Becker, P.C. 2-color synchronously mode locked femtosecond Ti-sapphire laser. Opt. Lett. 1993, 18, 631–633. [Google Scholar]
- Evans, J.M.; Spence, D.E.; Burns, D.; Sibbett, W. Dual wavelength self mode locked Ti-sapphire laser. Opt. Lett. 1993, 18, 1074–1076. [Google Scholar]
- Szipőcs, R.; Finger, E.; Euteneuer, A.; Hofmann, M.; Kohazi-Kis, A. Multicolor mode-locked Ti sapphire laser with zero pulse jitter. Laser Phys. 2000, 10, 454457. [Google Scholar]
- Ma, L.; Shelton, R.K.; Kapteyn, H.C.; Murnane, M.M.; Ye, J. Sub-10-femtosecond active synchronization of two passively mode-locked Ti:sapphire oscillators. Phys. Rev. A. 2001, 64, 021802. [Google Scholar]
- Hegenbarth, R.; Steinmann, A.; Toth, G.; Hebling, J.; Giessen, H. Two-color femtosecond optical parametric oscillator with 1.7 W output pumped by a 7.4 W Yb:KGW laser. J. Opt. Soc. Am. B. 2011, 28, 1344–1352. [Google Scholar]
- Wei, Z.; Kaboyashi, Y.; Torizuka, K. Passive synchronization between femtosecond Ti:sapphire and Cr:forsterite lasers. Appl. Phys. B. 2002, 74, 171–176. [Google Scholar]
- Dykaar, D.R.; Darack, S.B.; Knox, W.H. Cross locking dynamics in a 2-color mode locked Ti-sapphire laser. Opt. Lett. 1994, 19, 1058–1060. [Google Scholar]
- Leitenstorfer, A.; Furst, C.; Laubereau, A. Widely tunable two-color mode-locked Ti sapphire laser with pulse jitter of less than 2 fs. Opt. Lett. 1995, 20, 916–918. [Google Scholar]
- Yefet, S.; Amer, N.; Pe’er, A. Intra-cavity gain shaping of mode-locked Ti:Sapphire laser oscillations. Opt. Express. 2012, 20, 9991–9998. [Google Scholar]
- Christov, I.P.; Michailov, N.I.; Danailov, M.B. Mode locking with spatial dispersion in the gain medium. Appl. phys. B 1991, 53, 115–118. [Google Scholar]
- Christov, I.P. Intracavity shaping of mode-locked laser pulses. IEEE J. Quantum Electron 1993, 29, 2397–2404. [Google Scholar]
- Michailov, N.I. Passively mode-locked dye laser with spatial dispersion in the gain medium. J. Opt. Soc. Am. B. 1992, 9, 1369–1373. [Google Scholar]

© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yefet, S.; Pe'er, A. A Review of Cavity Design for Kerr Lens Mode-Locked Solid-State Lasers. Appl. Sci. 2013, 3, 694-724. https://doi.org/10.3390/app3040694
Yefet S, Pe'er A. A Review of Cavity Design for Kerr Lens Mode-Locked Solid-State Lasers. Applied Sciences. 2013; 3(4):694-724. https://doi.org/10.3390/app3040694
Chicago/Turabian StyleYefet, Shai, and Avi Pe'er. 2013. "A Review of Cavity Design for Kerr Lens Mode-Locked Solid-State Lasers" Applied Sciences 3, no. 4: 694-724. https://doi.org/10.3390/app3040694
APA StyleYefet, S., & Pe'er, A. (2013). A Review of Cavity Design for Kerr Lens Mode-Locked Solid-State Lasers. Applied Sciences, 3(4), 694-724. https://doi.org/10.3390/app3040694




