Scaling Law for Photon Transmission through Optically Turbid Slabs Based on Random Walk Theory
Abstract
:1. Introduction
 ), while expressing the total photon path length in terms of the mean distance traveled on each step of the walk. In this communication we consider transmittance through slabs and provide corrections to some previously-derived RWT equations [12] that contain typographical errors. Also, we correct some expressions appearing in the appendix of [12], where a factor of
), while expressing the total photon path length in terms of the mean distance traveled on each step of the walk. In this communication we consider transmittance through slabs and provide corrections to some previously-derived RWT equations [12] that contain typographical errors. Also, we correct some expressions appearing in the appendix of [12], where a factor of  was overlooked and various conversions were affected. We then derive the transmittance expression for isotropic scattering media without absorption and demonstrate an unusual scaling law for anisotropic scattering that arises by using a mixture of rms step lengths and mean path lengths within the RWT formulation [12].
was overlooked and various conversions were affected. We then derive the transmittance expression for isotropic scattering media without absorption and demonstrate an unusual scaling law for anisotropic scattering that arises by using a mixture of rms step lengths and mean path lengths within the RWT formulation [12].2. Expressions Correction and Monte Carlo Verification




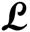 is in error by a factor of
is in error by a factor of  . For example,
. For example, 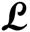 should be 10 instead of 10
should be 10 instead of 10  for the results shown in Figure 1.
for the results shown in Figure 1.

 Σs-1, where d is the physical thickness of the slab. It can be shown that the limit of Equation (A4) when Σa
Σs-1, where d is the physical thickness of the slab. It can be shown that the limit of Equation (A4) when Σa 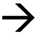 0 is:
0 is:
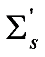 ) was calculated according to
) was calculated according to 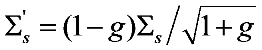 and used in Equation (6), where g is the anisotropy factor of the medium. The data shown in Figure 2 were obtained by simulating the multiple scattering process and recording the transmitted photons using a π/2 acceptance angle. The simulations were conducted for various particle concentrations assuming the following scatterers with various g: micron-sized water droplets in air (g = 0.77), polystyrene particles in water (g = 0.92), and hydrocarbon fuel droplets in air (g = 0.55). Note that the different phase functions can have the same g. We have performed simulations with different phase functions with the same g, and the results indicated that the transmission is less sensitive to the exact profile of the phase function than to g. As can be seen, Equation (6) predicts the transmittance with good accuracy across a wide range of conditions (in terms of OD and type of scatterer). We expect it to be a useful expression in the study of multiple scattering problems, especially in the design of experiments.
and used in Equation (6), where g is the anisotropy factor of the medium. The data shown in Figure 2 were obtained by simulating the multiple scattering process and recording the transmitted photons using a π/2 acceptance angle. The simulations were conducted for various particle concentrations assuming the following scatterers with various g: micron-sized water droplets in air (g = 0.77), polystyrene particles in water (g = 0.92), and hydrocarbon fuel droplets in air (g = 0.55). Note that the different phase functions can have the same g. We have performed simulations with different phase functions with the same g, and the results indicated that the transmission is less sensitive to the exact profile of the phase function than to g. As can be seen, Equation (6) predicts the transmittance with good accuracy across a wide range of conditions (in terms of OD and type of scatterer). We expect it to be a useful expression in the study of multiple scattering problems, especially in the design of experiments.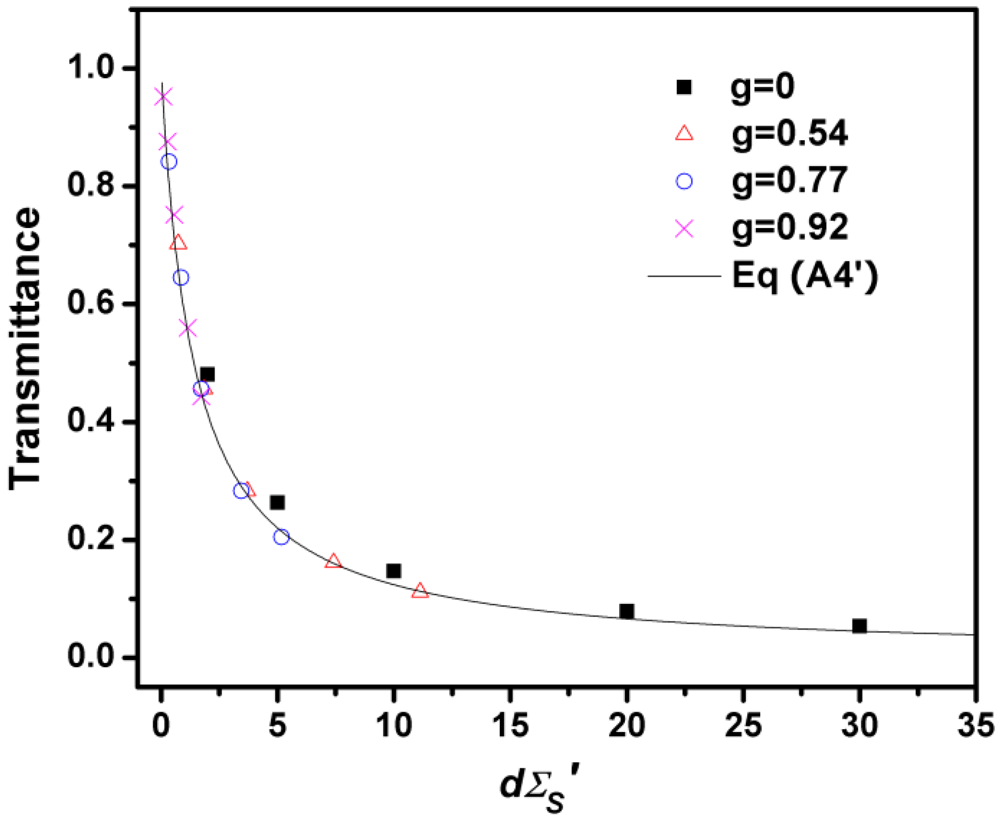
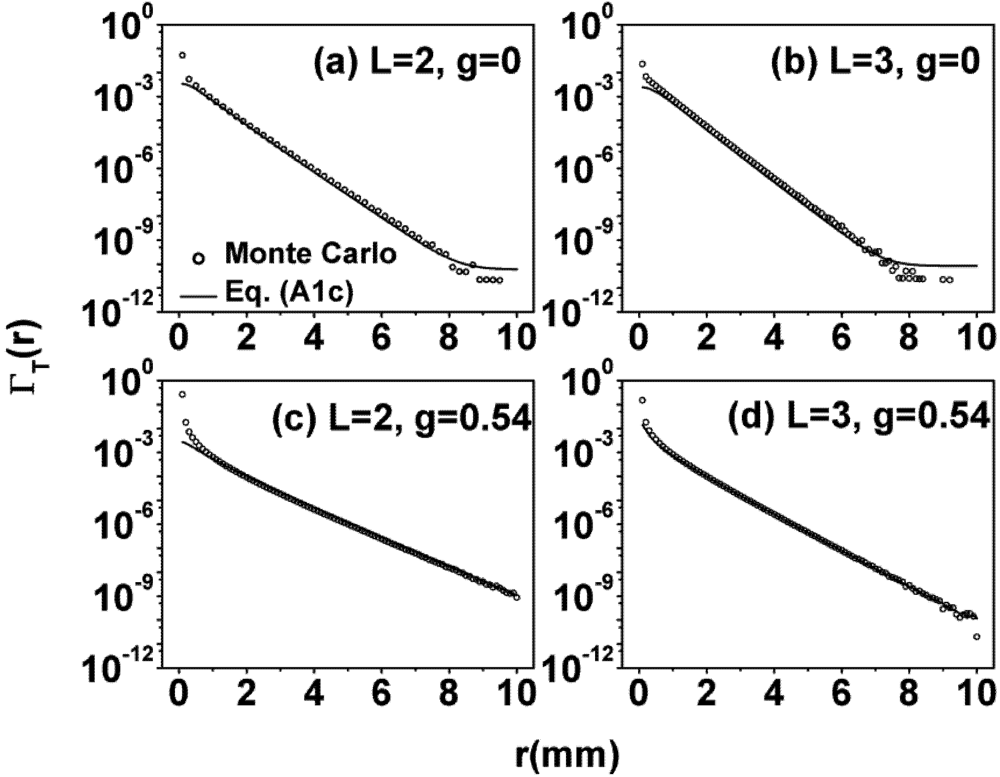
 in these figures). For the rest of the results, the scaling law
in these figures). For the rest of the results, the scaling law 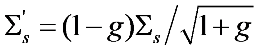 was applied. As can be seen from Panel (c) and (d) of Figure 3, at intermediate g, Equation (1) also agrees well with the Monte Carlo simulations even at relatively small OD under this scaling law. However, as shown in Figure 1, the discrepancy increases as g increases and decreases as OD increases. At g = 0.77, acceptable agreement begins at L = 7; and at g = 0.92, it begins at L = 30. These trends were observed in all our comparisons with various gs, and it suggested that the applicable range of the RWT can be quantified by an effective OD defined as OD
was applied. As can be seen from Panel (c) and (d) of Figure 3, at intermediate g, Equation (1) also agrees well with the Monte Carlo simulations even at relatively small OD under this scaling law. However, as shown in Figure 1, the discrepancy increases as g increases and decreases as OD increases. At g = 0.77, acceptable agreement begins at L = 7; and at g = 0.92, it begins at L = 30. These trends were observed in all our comparisons with various gs, and it suggested that the applicable range of the RWT can be quantified by an effective OD defined as OD 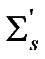 . The agreement between the RWT and Monte Carlo simulation improves with increasing effective OD.
. The agreement between the RWT and Monte Carlo simulation improves with increasing effective OD.3. Conclusion
Acknowledgments
References
- Hebden, J.C.; Hall, D.J.; Firbank, M.; Delpy, D.T. Time-resolved optical imaging of a solid tissue-equivalent phantom. Appl. Opt. 1995, 34, 8038–8047. [Google Scholar]
- Paciaroni, M.; Linne, M.; Hall, T.; Delplanque, J.P.; Parker, T. Single-shot two-dimensional ballistic imaging of the liquid core in an atomizing spray. At. Sprays 2006, 16, 51–69. [Google Scholar]
- Sobol, I.M. The Monte Carlo Method; The University of Chicago Press: Chicago, IL, USA, 1967. [Google Scholar]
- Berrocal, E.; Sedarsky, D.L.; Paciaroni, M.E.; Meglinski, I.V.; Linne, M.A. Laser light scattering in turbid media part i: Experimental and simulated results for the spatial intensity distribution. Opt. Express 2007, 15, 10649–10665. [Google Scholar]
- Boas, D.A.; Culver, J.P.; Stott, J.J.; Dunn, A.K. Three dimensional monte carlo code for photon migration through complex heterogeneous media including the adult human head. Opt. Express 2002, 10, 159–170. [Google Scholar]
- Zaccanti, G. Monte-carlo study of light-propagation in optically thick media—Point-source case. Appl. Opt. 1991, 30, 2031–2041. [Google Scholar]
- Fang, Q.Q.; Boas, D.A. Monte carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt. Express 2009, 17, 20178–20190. [Google Scholar]
- Kokhanovsky, A.A. Analytical solutions of multiple light scattering problems: A review. Meas. Sci. Technol. 2002, 13, 233–240. [Google Scholar]
- Contini, D.; Martelli, F.; Zaccanti, G. Photon migration through a turbid slab described by a model based on diffusion approximation. 2. Theory. Appl. Opt. 1997, 36, 4587–4599. [Google Scholar] [CrossRef]
- Gandjbakhche, A.H.; Bonner, R.F.; Nossal, R. Scaling relationships for anisotropic random-walks. J. Stat. Phys. 1992, 69, 35–53. [Google Scholar]
- Gandjbakhche, A.H.; Nossal, R.; Bonner, R.F. Scaling relationships for theories of anisotropic random-walks applied to tissue optics. Appl. Opt. 1993, 32, 504–516. [Google Scholar]
- Gandjbakhche, A.H.; Weiss, G.H.; Bonner, R.F.; Nossal, R. Photon path-length distributions for transmission through optically turbid slabs. Phys. Rev. E 1993, 48, 810–818. [Google Scholar]
- Sun, X.; Li, X.; Ma, L. A closed-form method for calculating the angular distribution of multiply scattered photons through isotropic turbid slabs. Opt. Express 2011, 19, 22932–23937. [Google Scholar]
- Moon, J.A.; Reintjes, J. Image-resolution by use of multiply scattered-light. Opt. Lett. 1994, 19, 521–523. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, X.; Ma, L. Scaling Law for Photon Transmission through Optically Turbid Slabs Based on Random Walk Theory. Appl. Sci. 2012, 2, 160-165. https://doi.org/10.3390/app2010160
Li X, Ma L. Scaling Law for Photon Transmission through Optically Turbid Slabs Based on Random Walk Theory. Applied Sciences. 2012; 2(1):160-165. https://doi.org/10.3390/app2010160
Chicago/Turabian StyleLi, Xuesong, and Lin Ma. 2012. "Scaling Law for Photon Transmission through Optically Turbid Slabs Based on Random Walk Theory" Applied Sciences 2, no. 1: 160-165. https://doi.org/10.3390/app2010160
APA StyleLi, X., & Ma, L. (2012). Scaling Law for Photon Transmission through Optically Turbid Slabs Based on Random Walk Theory. Applied Sciences, 2(1), 160-165. https://doi.org/10.3390/app2010160



