Abstract
Past work has demonstrated the value of a random walk theory (RWT) to solve multiple-scattering problems arising in numerous contexts. This paper’s goal is to investigate the application range of the RWT using Monte Carlo simulations and extending it to anisotropic media using scaling laws. Meanwhile, this paper also reiterates rules for converting RWT formulas to real physical dimensions, and corrects some errors which appear in an earlier publication. The RWT theory, validated by the Monte Carlo simulations and combined with the scaling law, is expected to be useful to study multiple scattering and to greatly reduce the computation cost.
1. Introduction
Multiple-scattering represents a fundamental scientific problem, with implications in a wide spectrum of practical applications ranging from biological imaging [1] to dense spray diagnostics [2]. However, multiple-scattering problems usually are complicated and have to be solved numerically, which is computationally costly and often does not provide intuitive understanding of the problem. As an example, Monte Carlo simulation [3,4,5,6], which is an extensively used numerical technique, can be prohibitively expensive when probing large optical depth. Considerable efforts have been investigated to overcome this limitation, and one notable technique demonstrated recently [7] involves the use of GPU (Graphical Processing Units) to parallelize and accelerate Monte Carlo simulations. Alternatively, theoretical approaches have been developed to derive analytical expressions for the observable quantities involved in multiple-scattering [8]. Notable examples include photon diffusion theory [9] and random walk theory (RWT) [10,11]. This report focuses on the RWT approach, which can yield analytical solutions to provide insights not easily obtained with numerical methods such as the Monte Carlo simulations.
In particular, RWT expressions have been derived for such quantities as transmittance, reflectance, and the intensity distributions of transmitted and reflected photons. These expressions not only address the computational limitation of numerical techniques, but also provide physical insights into the underlying phenomena. They have been validated by extensive comparisons against Monte Carlo simulations, and have been found to be useful for a range of practical applications such as the estimation of signal levels and the design of imaging optics. However, RWT analytical expressions are obtained in terms of lattice units and step lengths, and careful attention must be given to their conversion to expressions involving physical units, viz., the absorption and scattering coefficients (μs and μa), and the anisotropy factor, g. Furthermore, it is desirable to quantitatively understand the applicable range of the RWT expressions, and to investigate the feasibility of extending these expressions to anisotropic media.
In the case of isotropic scattering, random walk expressions can be related to real macroscopic variables by equating the RWT lattice unit to the real displacement divided by the rms (root mean square) scattering length (equivalent to dividing the macroscopic scattering coefficient by 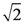 ), while expressing the total photon path length in terms of the mean distance traveled on each step of the walk. In this communication we consider transmittance through slabs and provide corrections to some previously-derived RWT equations [12] that contain typographical errors. Also, we correct some expressions appearing in the appendix of [12], where a factor of
), while expressing the total photon path length in terms of the mean distance traveled on each step of the walk. In this communication we consider transmittance through slabs and provide corrections to some previously-derived RWT equations [12] that contain typographical errors. Also, we correct some expressions appearing in the appendix of [12], where a factor of 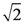 was overlooked and various conversions were affected. We then derive the transmittance expression for isotropic scattering media without absorption and demonstrate an unusual scaling law for anisotropic scattering that arises by using a mixture of rms step lengths and mean path lengths within the RWT formulation [12].
was overlooked and various conversions were affected. We then derive the transmittance expression for isotropic scattering media without absorption and demonstrate an unusual scaling law for anisotropic scattering that arises by using a mixture of rms step lengths and mean path lengths within the RWT formulation [12].
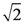 ), while expressing the total photon path length in terms of the mean distance traveled on each step of the walk. In this communication we consider transmittance through slabs and provide corrections to some previously-derived RWT equations [12] that contain typographical errors. Also, we correct some expressions appearing in the appendix of [12], where a factor of
), while expressing the total photon path length in terms of the mean distance traveled on each step of the walk. In this communication we consider transmittance through slabs and provide corrections to some previously-derived RWT equations [12] that contain typographical errors. Also, we correct some expressions appearing in the appendix of [12], where a factor of 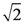 was overlooked and various conversions were affected. We then derive the transmittance expression for isotropic scattering media without absorption and demonstrate an unusual scaling law for anisotropic scattering that arises by using a mixture of rms step lengths and mean path lengths within the RWT formulation [12].
was overlooked and various conversions were affected. We then derive the transmittance expression for isotropic scattering media without absorption and demonstrate an unusual scaling law for anisotropic scattering that arises by using a mixture of rms step lengths and mean path lengths within the RWT formulation [12].2. Expressions Correction and Monte Carlo Verification
We first comment on several algebraic errors in the equations published in [12], where Equations (A1) and (A2) express the transmittance and the photon-path length of the transmitted photons, respectively, in terms of the optical properties of an isotropic scattering medium. These equations should have appeared as follows, where the corrections are underscored:
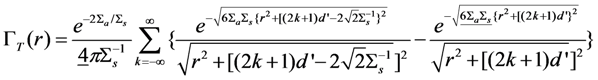
and
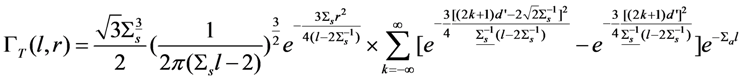
The correctness of these equations was confirmed by comparison against Monte Carlo simulations.
There also are two errors in the previously-published Equations (12b) and (23) [12]. The amended equations are shown below, again with the changes underscored:
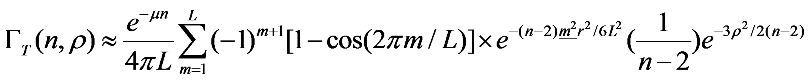
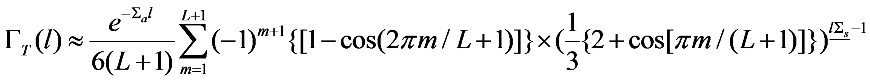
Correspondingly, there is a typo in the captions of Figure 2 and Figure 3 in [12], where the parameter 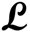 is in error by a factor of
is in error by a factor of 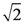 . For example,
. For example, 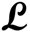 should be 10 instead of 10
should be 10 instead of 10 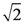 for the results shown in Figure 1.
for the results shown in Figure 1.
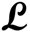 is in error by a factor of
is in error by a factor of 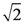 . For example,
. For example, 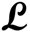 should be 10 instead of 10
should be 10 instead of 10 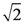 for the results shown in Figure 1.
for the results shown in Figure 1.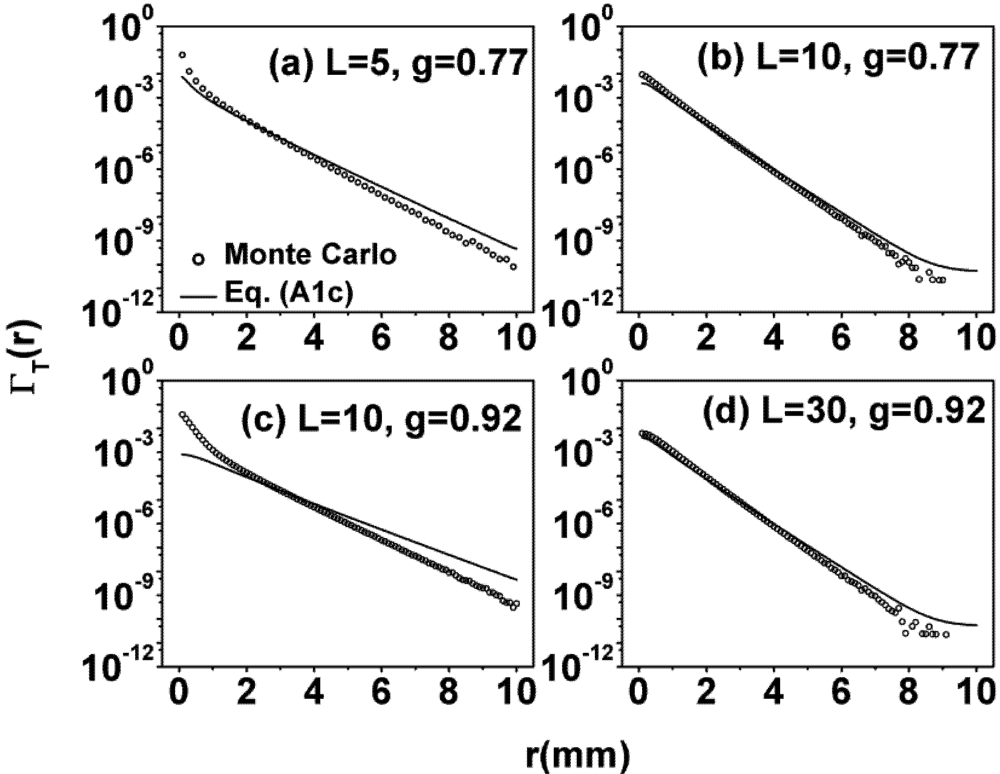
Figure 1.
Comparison of the radial distribution of transmitted photons at large g.
Second, many applications involve non-absorbing media, for which it is desirable to have a simple expression for the transmittance (and reflectance), including for the general case of anisotropic scattering. Equation (A4) in [12] provides an expression for the transmittance for an absorbing, isotropic scattering medium, viz.,
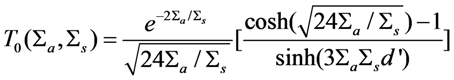
where Σs and Σa are the scattering and absorption coefficients of the slab, respectively, and d′ is the corrected sample thickness defined as d′ = d+ 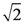 Σs-1, where d is the physical thickness of the slab. It can be shown that the limit of Equation (A4) when Σa
Σs-1, where d is the physical thickness of the slab. It can be shown that the limit of Equation (A4) when Σa 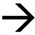 0 is:
0 is:
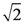 Σs-1, where d is the physical thickness of the slab. It can be shown that the limit of Equation (A4) when Σa
Σs-1, where d is the physical thickness of the slab. It can be shown that the limit of Equation (A4) when Σa 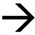 0 is:
0 is: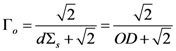
where OD is the optical depth of the media defined as the product of the slab thickness (d) and the scattering coefficient (Σs). Figure 2 shows the transmittance predicted by Equation (6) compared with Monte Carlo simulations for both isotropic and anisotropic media. Mie theory was used to calculate the phase functions in the Monte Carlo simulations. For the cases of anisotropic media, the scattering coefficients were scaled using a similarity relationship developed for RWT [10,11]. Following this similarity relationship, an effective scattering coefficient ( 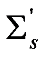 ) was calculated according to
) was calculated according to 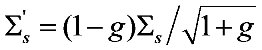 and used in Equation (6), where g is the anisotropy factor of the medium. The data shown in Figure 2 were obtained by simulating the multiple scattering process and recording the transmitted photons using a π/2 acceptance angle. The simulations were conducted for various particle concentrations assuming the following scatterers with various g: micron-sized water droplets in air (g = 0.77), polystyrene particles in water (g = 0.92), and hydrocarbon fuel droplets in air (g = 0.55). Note that the different phase functions can have the same g. We have performed simulations with different phase functions with the same g, and the results indicated that the transmission is less sensitive to the exact profile of the phase function than to g. As can be seen, Equation (6) predicts the transmittance with good accuracy across a wide range of conditions (in terms of OD and type of scatterer). We expect it to be a useful expression in the study of multiple scattering problems, especially in the design of experiments.
and used in Equation (6), where g is the anisotropy factor of the medium. The data shown in Figure 2 were obtained by simulating the multiple scattering process and recording the transmitted photons using a π/2 acceptance angle. The simulations were conducted for various particle concentrations assuming the following scatterers with various g: micron-sized water droplets in air (g = 0.77), polystyrene particles in water (g = 0.92), and hydrocarbon fuel droplets in air (g = 0.55). Note that the different phase functions can have the same g. We have performed simulations with different phase functions with the same g, and the results indicated that the transmission is less sensitive to the exact profile of the phase function than to g. As can be seen, Equation (6) predicts the transmittance with good accuracy across a wide range of conditions (in terms of OD and type of scatterer). We expect it to be a useful expression in the study of multiple scattering problems, especially in the design of experiments.
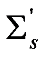 ) was calculated according to
) was calculated according to 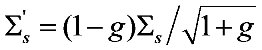 and used in Equation (6), where g is the anisotropy factor of the medium. The data shown in Figure 2 were obtained by simulating the multiple scattering process and recording the transmitted photons using a π/2 acceptance angle. The simulations were conducted for various particle concentrations assuming the following scatterers with various g: micron-sized water droplets in air (g = 0.77), polystyrene particles in water (g = 0.92), and hydrocarbon fuel droplets in air (g = 0.55). Note that the different phase functions can have the same g. We have performed simulations with different phase functions with the same g, and the results indicated that the transmission is less sensitive to the exact profile of the phase function than to g. As can be seen, Equation (6) predicts the transmittance with good accuracy across a wide range of conditions (in terms of OD and type of scatterer). We expect it to be a useful expression in the study of multiple scattering problems, especially in the design of experiments.
and used in Equation (6), where g is the anisotropy factor of the medium. The data shown in Figure 2 were obtained by simulating the multiple scattering process and recording the transmitted photons using a π/2 acceptance angle. The simulations were conducted for various particle concentrations assuming the following scatterers with various g: micron-sized water droplets in air (g = 0.77), polystyrene particles in water (g = 0.92), and hydrocarbon fuel droplets in air (g = 0.55). Note that the different phase functions can have the same g. We have performed simulations with different phase functions with the same g, and the results indicated that the transmission is less sensitive to the exact profile of the phase function than to g. As can be seen, Equation (6) predicts the transmittance with good accuracy across a wide range of conditions (in terms of OD and type of scatterer). We expect it to be a useful expression in the study of multiple scattering problems, especially in the design of experiments.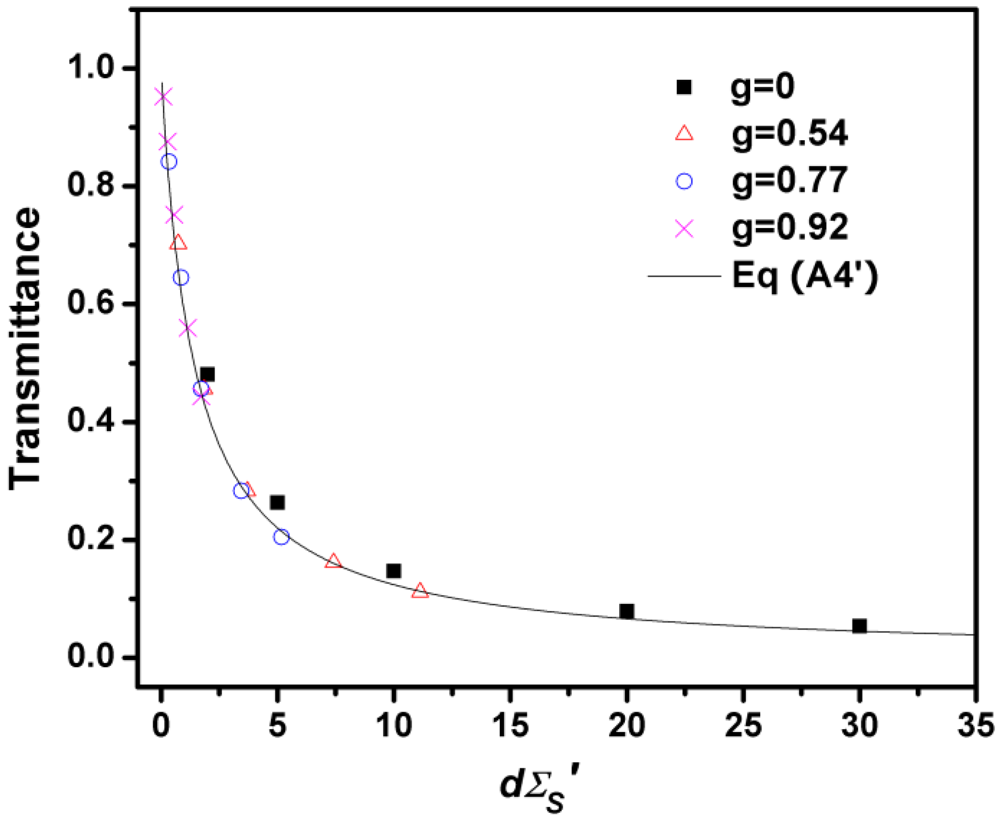
Figure 2.
Comparison of transmittance predicted by Equation (A4′) [12] with results of Monte Carlo simulations.
Lastly, in some applications, it is desirable to know the radial distribution of the transmitted photons. Example applications include the analysis of the angular distribution of the transmitted photons [13] and the analysis of the spatial resolution of the transmittance measurements [14]. Equation (1) from the RWT provides an analytical expression for the radial distribution of the transmitted photons. However, in order to apply Equation (1) in practical systems, it is necessary to understand several aspects of this equation. First, what is the application range of it in terms of the OD? Equation (1) is derived based on the assumption of large OD, and it is desirable to have a quantitative understanding of the valid range of this assumption. Second, how to extend Equation (1) to anisotropic media? Equation (1) is developed for isotropic media (i.e., g = 0), however many practical systems involve scatters which are anisotropic. Thus it is desirable to extend Equation (1) to anisotropic media. Past work has investigated the use of various scaling laws for such extension [10,11], and here we examined these scaling laws specifically for the radial distribution.
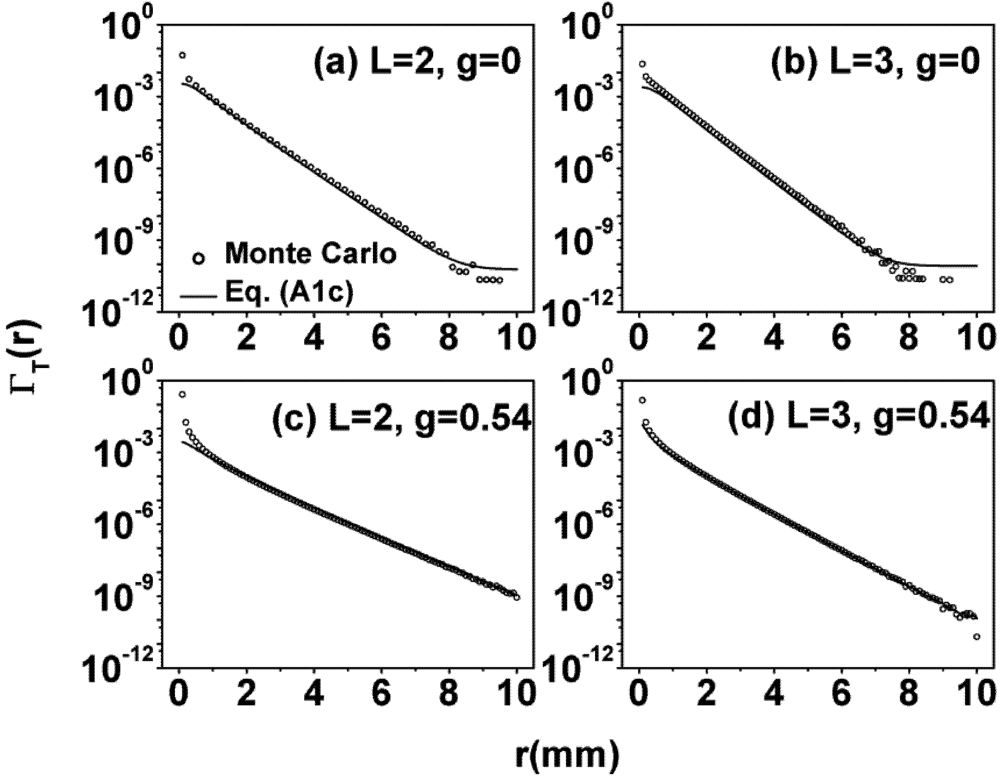
Figure 3.
Comparison of the radial distribution of transmitted photons at small g.
To understand these questions, Monte Carlo simulations were performed to obtain the radial distribution of transmitted photons and representative results were summarized and compared to Equation (1) in Figure 1 and Figure 3. Panel (a) and (b) of Figure 3 show the results obtained for isotropic media, and it can seen that Equation (1) agrees well with the Monte Carlo simulation even for relative small OD (L is defined as OD/ 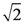 in these figures). For the rest of the results, the scaling law
in these figures). For the rest of the results, the scaling law 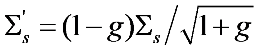 was applied. As can be seen from Panel (c) and (d) of Figure 3, at intermediate g, Equation (1) also agrees well with the Monte Carlo simulations even at relatively small OD under this scaling law. However, as shown in Figure 1, the discrepancy increases as g increases and decreases as OD increases. At g = 0.77, acceptable agreement begins at L = 7; and at g = 0.92, it begins at L = 30. These trends were observed in all our comparisons with various gs, and it suggested that the applicable range of the RWT can be quantified by an effective OD defined as OD
was applied. As can be seen from Panel (c) and (d) of Figure 3, at intermediate g, Equation (1) also agrees well with the Monte Carlo simulations even at relatively small OD under this scaling law. However, as shown in Figure 1, the discrepancy increases as g increases and decreases as OD increases. At g = 0.77, acceptable agreement begins at L = 7; and at g = 0.92, it begins at L = 30. These trends were observed in all our comparisons with various gs, and it suggested that the applicable range of the RWT can be quantified by an effective OD defined as OD 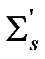 . The agreement between the RWT and Monte Carlo simulation improves with increasing effective OD.
. The agreement between the RWT and Monte Carlo simulation improves with increasing effective OD.
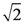 in these figures). For the rest of the results, the scaling law
in these figures). For the rest of the results, the scaling law 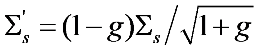 was applied. As can be seen from Panel (c) and (d) of Figure 3, at intermediate g, Equation (1) also agrees well with the Monte Carlo simulations even at relatively small OD under this scaling law. However, as shown in Figure 1, the discrepancy increases as g increases and decreases as OD increases. At g = 0.77, acceptable agreement begins at L = 7; and at g = 0.92, it begins at L = 30. These trends were observed in all our comparisons with various gs, and it suggested that the applicable range of the RWT can be quantified by an effective OD defined as OD
was applied. As can be seen from Panel (c) and (d) of Figure 3, at intermediate g, Equation (1) also agrees well with the Monte Carlo simulations even at relatively small OD under this scaling law. However, as shown in Figure 1, the discrepancy increases as g increases and decreases as OD increases. At g = 0.77, acceptable agreement begins at L = 7; and at g = 0.92, it begins at L = 30. These trends were observed in all our comparisons with various gs, and it suggested that the applicable range of the RWT can be quantified by an effective OD defined as OD 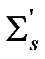 . The agreement between the RWT and Monte Carlo simulation improves with increasing effective OD.
. The agreement between the RWT and Monte Carlo simulation improves with increasing effective OD.3. Conclusion
In summary, this work examined a theory based on random walks to model multiple light scattering. The theory is attractive because it provided close-form solutions to properties of great interest to practical applications. This work corrected some errors published previously, validated the theory by comparison with Monte Carlo simulations, and also quantified the theory applicable ranges. Also, it extends the theory by demonstrating that the theory, combined with a scaling law, can be applied to anisotropic media. These findings are expected to be useful to study multiple scattering and to greatly reduce the computation cost.
Acknowledgments
The authors greatly acknowledge the many technical discussions with Amir H. Gandjbakhche, George. H. Weiss, Robert F. Bonner, and Ralph Nossal from the National Institutes of Health, Bethesda, MD, USA.
References
- Hebden, J.C.; Hall, D.J.; Firbank, M.; Delpy, D.T. Time-resolved optical imaging of a solid tissue-equivalent phantom. Appl. Opt. 1995, 34, 8038–8047. [Google Scholar]
- Paciaroni, M.; Linne, M.; Hall, T.; Delplanque, J.P.; Parker, T. Single-shot two-dimensional ballistic imaging of the liquid core in an atomizing spray. At. Sprays 2006, 16, 51–69. [Google Scholar]
- Sobol, I.M. The Monte Carlo Method; The University of Chicago Press: Chicago, IL, USA, 1967. [Google Scholar]
- Berrocal, E.; Sedarsky, D.L.; Paciaroni, M.E.; Meglinski, I.V.; Linne, M.A. Laser light scattering in turbid media part i: Experimental and simulated results for the spatial intensity distribution. Opt. Express 2007, 15, 10649–10665. [Google Scholar]
- Boas, D.A.; Culver, J.P.; Stott, J.J.; Dunn, A.K. Three dimensional monte carlo code for photon migration through complex heterogeneous media including the adult human head. Opt. Express 2002, 10, 159–170. [Google Scholar]
- Zaccanti, G. Monte-carlo study of light-propagation in optically thick media—Point-source case. Appl. Opt. 1991, 30, 2031–2041. [Google Scholar]
- Fang, Q.Q.; Boas, D.A. Monte carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt. Express 2009, 17, 20178–20190. [Google Scholar]
- Kokhanovsky, A.A. Analytical solutions of multiple light scattering problems: A review. Meas. Sci. Technol. 2002, 13, 233–240. [Google Scholar]
- Contini, D.; Martelli, F.; Zaccanti, G. Photon migration through a turbid slab described by a model based on diffusion approximation. 2. Theory. Appl. Opt. 1997, 36, 4587–4599. [Google Scholar] [CrossRef]
- Gandjbakhche, A.H.; Bonner, R.F.; Nossal, R. Scaling relationships for anisotropic random-walks. J. Stat. Phys. 1992, 69, 35–53. [Google Scholar]
- Gandjbakhche, A.H.; Nossal, R.; Bonner, R.F. Scaling relationships for theories of anisotropic random-walks applied to tissue optics. Appl. Opt. 1993, 32, 504–516. [Google Scholar]
- Gandjbakhche, A.H.; Weiss, G.H.; Bonner, R.F.; Nossal, R. Photon path-length distributions for transmission through optically turbid slabs. Phys. Rev. E 1993, 48, 810–818. [Google Scholar]
- Sun, X.; Li, X.; Ma, L. A closed-form method for calculating the angular distribution of multiply scattered photons through isotropic turbid slabs. Opt. Express 2011, 19, 22932–23937. [Google Scholar]
- Moon, J.A.; Reintjes, J. Image-resolution by use of multiply scattered-light. Opt. Lett. 1994, 19, 521–523. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).