The Application of Lite-GRU Embedding and VAE-Augmented Heterogeneous Graph Attention Network in Friend Link Prediction for LBSNs
Abstract
1. Introduction
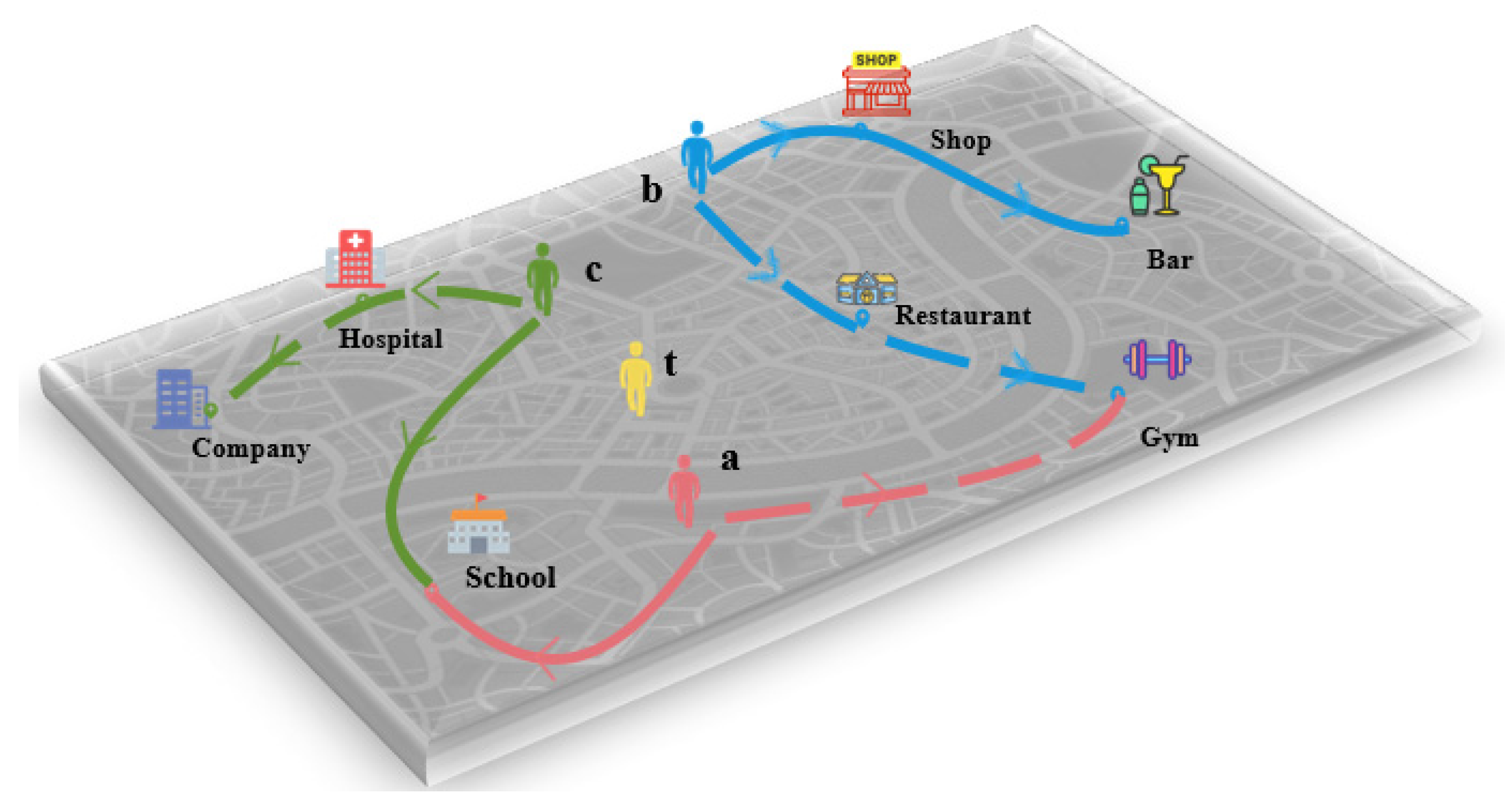
- Heterogeneous Graph Construction: In response to the difficulty of processing rich heterogeneous data in LBSNs and the challenge that traditional graph models face in balancing complexity and information extraction, this paper proposes a heterogeneous graph model consisting of two types of nodes and three types of edges. This model can extract topological and semantic information from the network, enabling a better understanding and utilization of the complex structure in LBSNs.
- Node Feature Embedding Learning Module: To address the difficulty of extracting precise and effective node features from the complex spatiotemporal data in Location-Based Social Networks (LBSNs), a strategy combining Skip-Gram and Lite-GRU is employed. Skip-Gram effectively captures the contextual relationships between POIs. In this paper, user trajectories are divided by day. Considering that sub-trajectory nodes are relatively few and contain dependencies, Lite-GRU, with its simplified gating mechanism, offers superior computational efficiency compared with LSTM and Transformer models. Unlike the bidirectional structure of BiLSTM, Lite-GRU uses unidirectional information flow, avoiding redundant information, and is more suited to the non-sequential nature of check-in behavior. While Transformer has advantages in modeling long sequences, its dense positional encoding mechanism can lead to overfitting under sparse data and cold start problems. In contrast, Lite-GRU handles temporal dependencies more effectively through a dynamic gating mechanism. Therefore, we use the Skip-Gram model to learn POI embeddings and combine it with Lite-GRU to learn user embeddings with temporal data processing capabilities, ultimately generating high-quality embedding vectors.
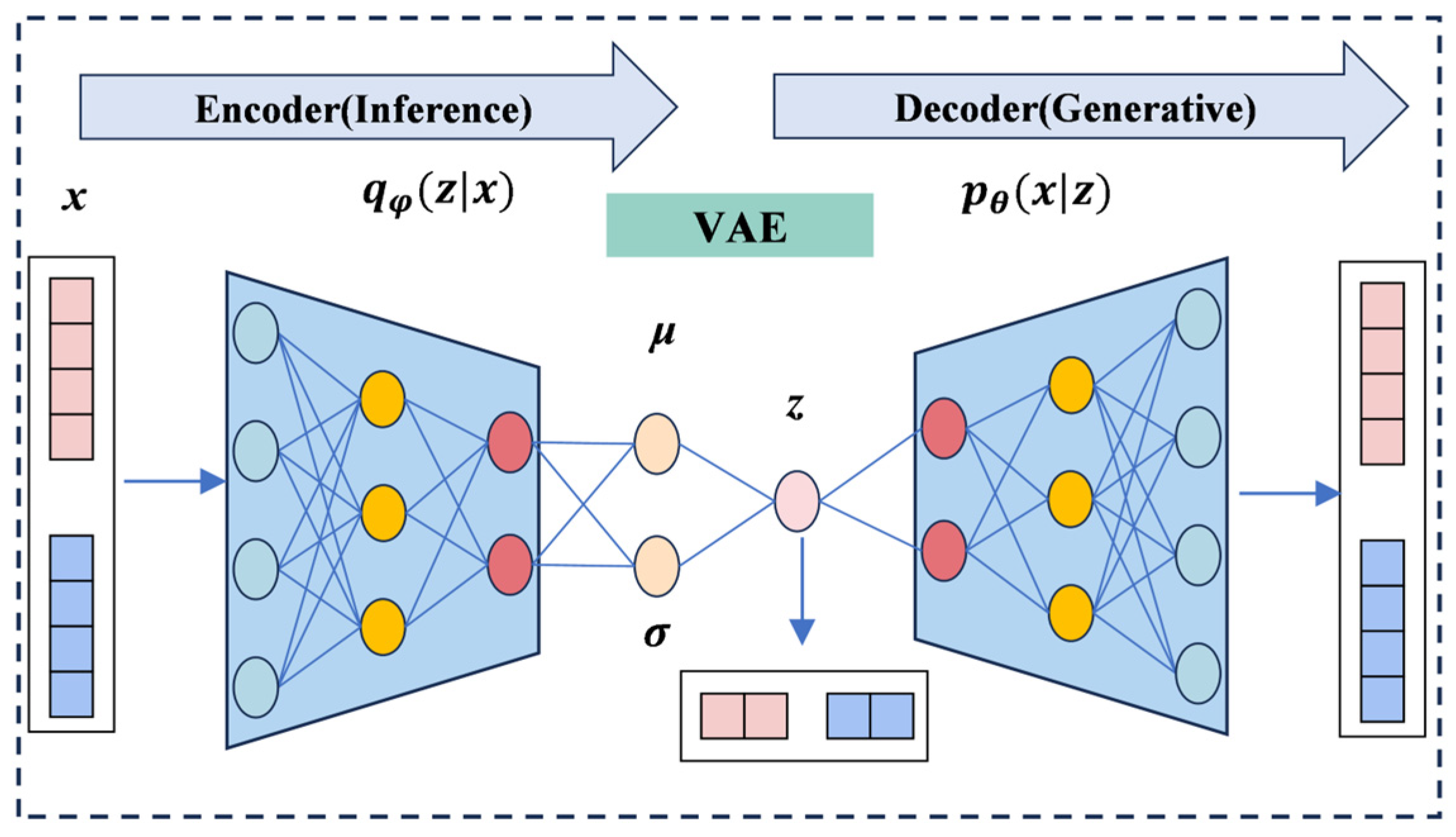
- VAE Module: To tackle the high dimensionality and noise problems of LBSN data, this paper introduces VAE, which can extract useful features from high-dimensional noisy data, reduce dimensionality, and mitigate noise interference, thereby enhancing the model’s robustness. Considering that VAE can better capture complex nonlinear relationships while maintaining global topological structures, it overcomes the linear limitations of Principal Component Analysis (PCA), avoids the overfitting issues that may arise with AutoEncoder (AE), and is more efficient than t-Distributed Stochastic Neighbor Embedding (t-SNE) when handling large-scale datasets.
- Edge-Level Attention: In response to the challenge of effectively parsing the complex network structure in LBSNs, where traditional methods fail to fully leverage edge properties and weights to accurately extract features and propagate information, this paper introduces an edge-level attention mechanism. By considering the properties and weights of edges, it learns the importance of different types of edges to enhance information propagation and feature extraction. Additionally, by combining node residual connections and multi-head attention, the node aggregation and propagation process is further optimized, effectively integrating the diverse information contained in different types of nodes and edges to obtain better node representations.
2. Related Work
2.1. Traditional Methods
2.2. Graph Neural Network Methods
2.2.1. Homogeneous Graph Methods
2.2.2. Heterogeneous Graph Methods
2.2.3. Hypergraph Methods
3. Problem and Definition
3.1. Problem Description
3.2. Relevant Definitions
4. Methods
4.1. Constructing a Heterogeneous Graph
4.2. Node Feature Learning
4.2.1. Learning POI Embeddings
4.2.2. User Embedding Learning
4.2.3. Feature Mapping
4.3. VAE Dimensionality Reduction and Denoising
4.3.1. Encoder and Latent Space
4.3.2. Decoder and Data Reconstruction
4.3.3. Variational Lower Bound
4.4. Node Aggregation and Update
4.4.1. Edge-Level Attention
4.4.2. Residual Connections
4.4.3. Multi-Head Attention
4.5. Link Prediction
4.5.1. Cosine Similarity
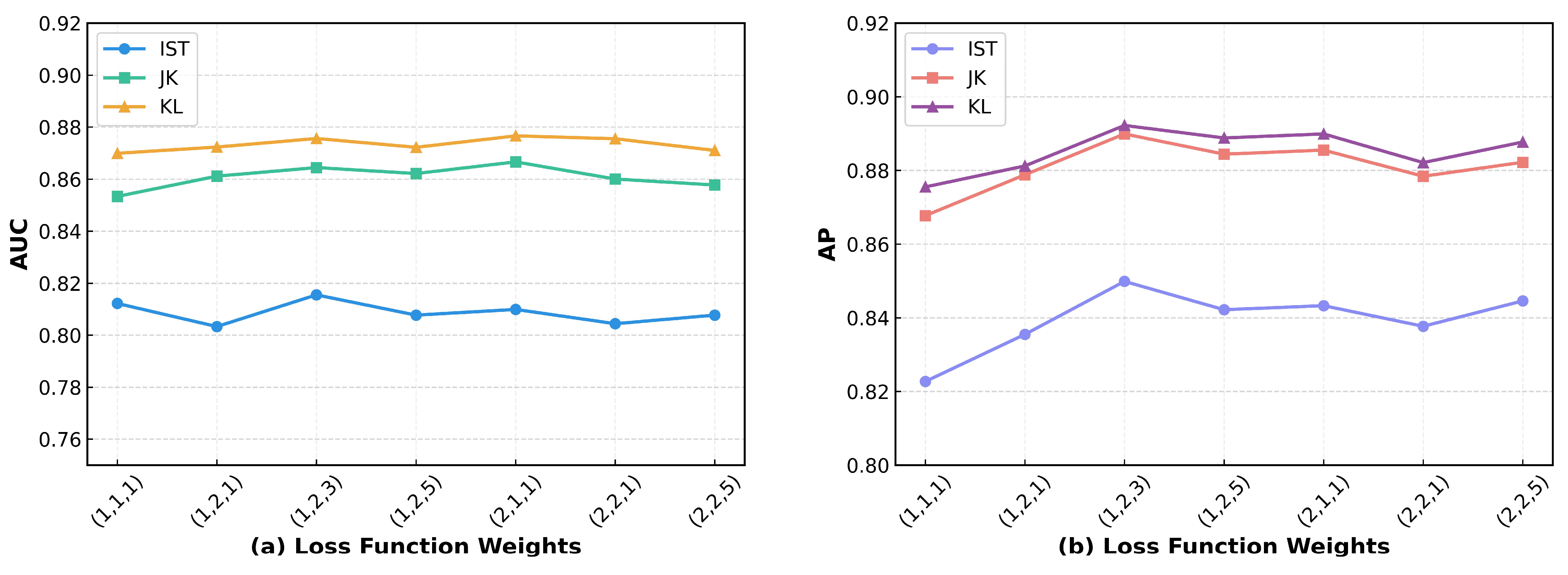
4.5.2. Joint Loss Function
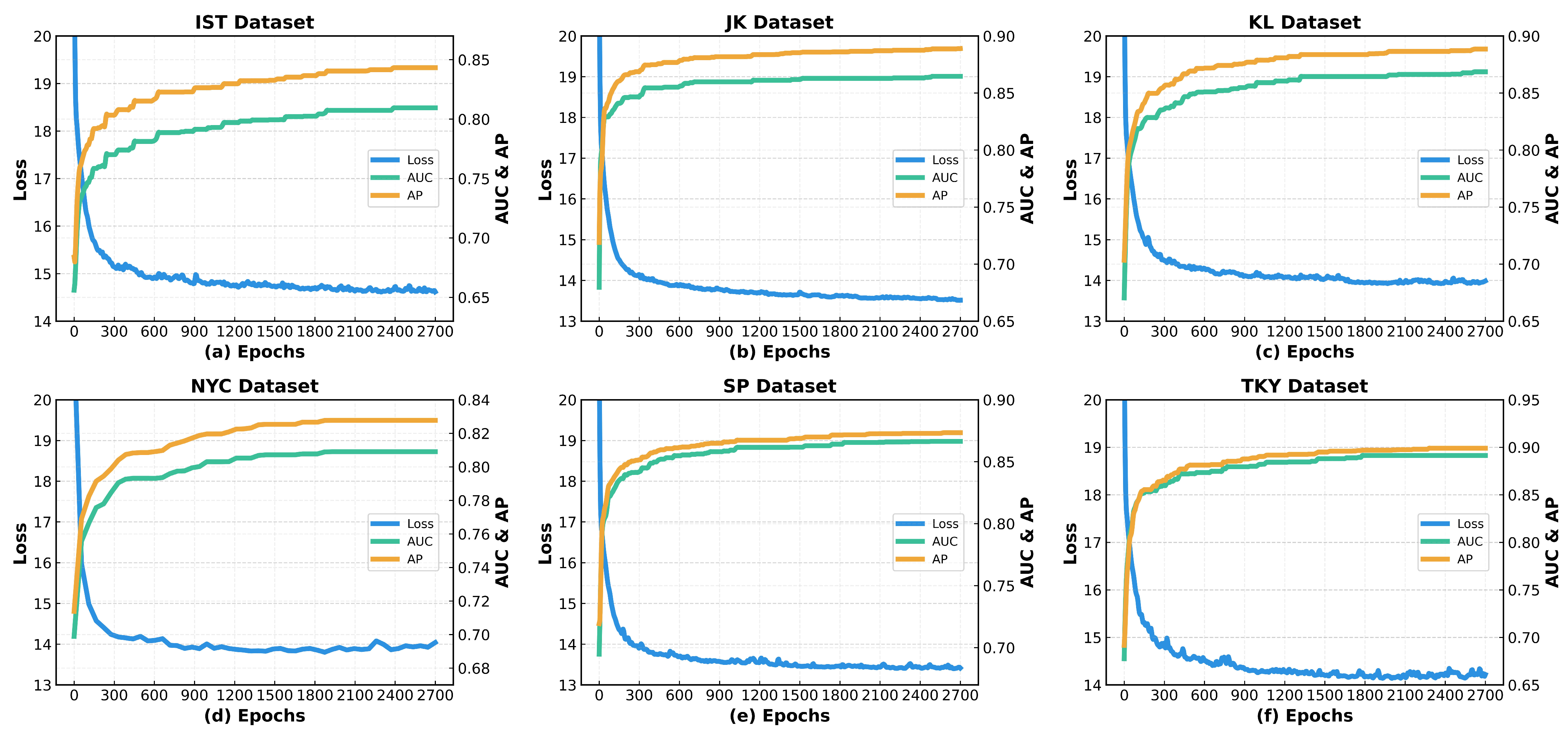
5. Experimental Setup
5.1. Dataset
5.2. Evaluation Metrics
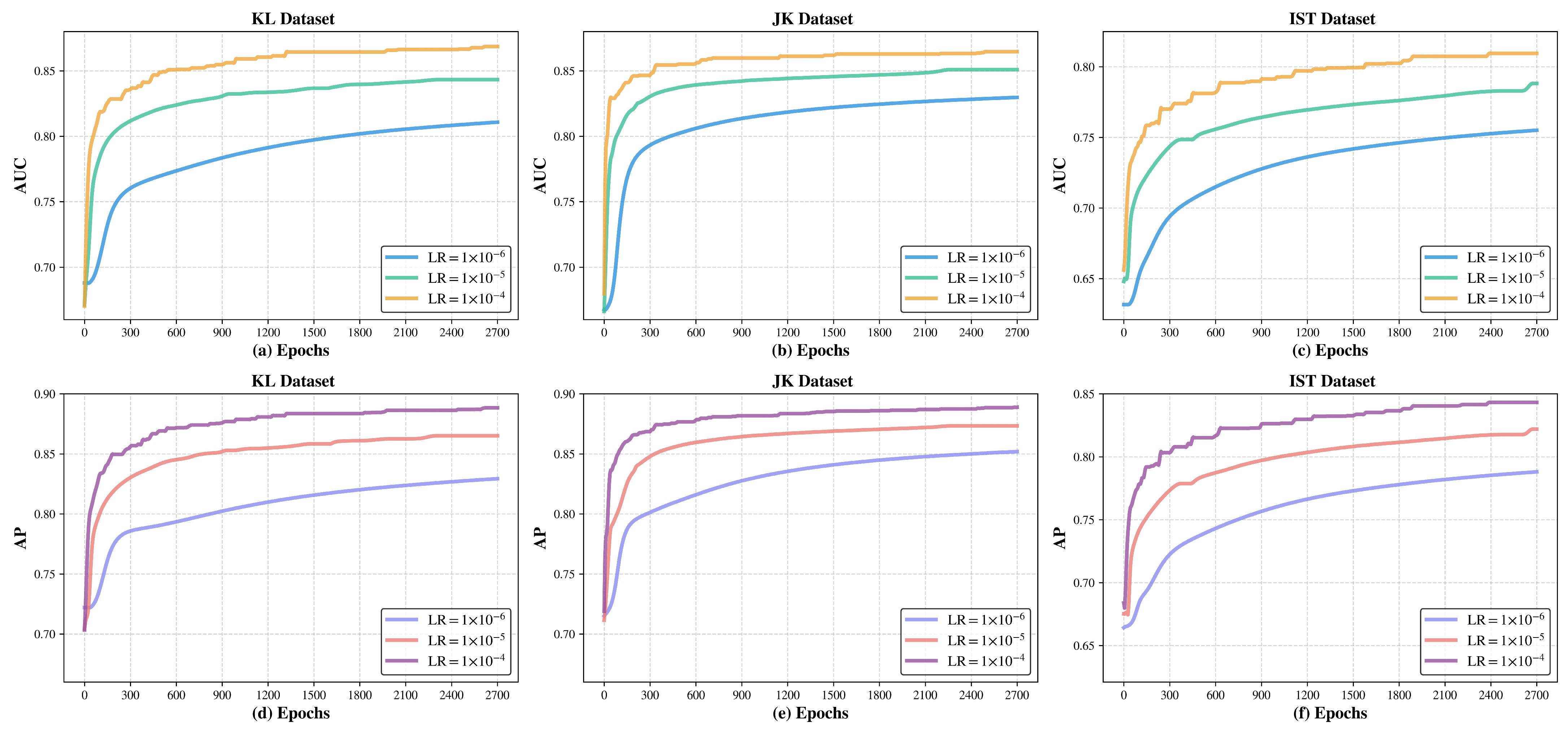
5.3. Parameter Settings
5.4. Baseline Methods
5.4.1. Experimental Methods for Homogeneous Graphs
5.4.2. Experimental Methods for Heterogeneous Graphs
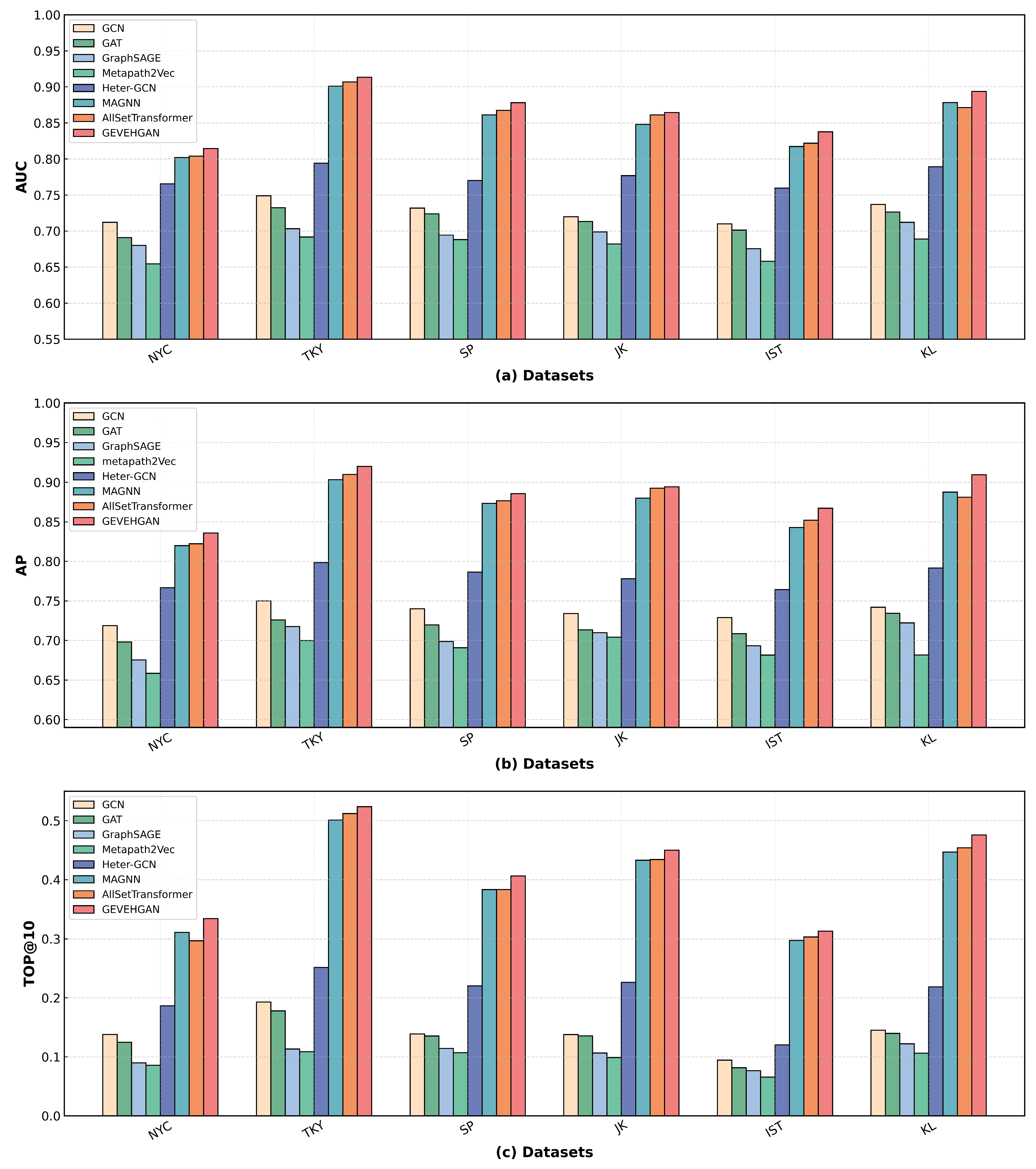
5.5. Comparative Experiments
5.6. Ablation Study
- GEVEHGAN-Init: The node feature initialization module in the input layer is removed, and the heterogeneous graph node features are randomly initialized with small values. Other parts of the model remain unchanged.
- GEVEHGAN-Vae: The Variational Autoencoder module is removed, and the initialized features are directly used. Other parts of the model remain unchanged.
- GEVEHGAN-Att: The edge-type attention mechanism in the node feature learning process is removed, and the importance of neighbor nodes remains the same. Other parts of the model remain unchanged.
- GEVEHGAN-Res: The node pre-activation residual connection mechanism is removed, and the traditional GNN node aggregation update method is used. Other parts of the model remain unchanged.
- Node Feature Embedding Module: After removing the node feature embedding module, the node’s initial features loses the semantic associations and temporal patterns obtained through pretraining, resulting in a reduction in the information available to the model when understanding user behavior and interests. The three metrics of the GEVEHGAN-Init model decrease by 4.11%, 4.51%, and 3.81%, respectively. This indicates that the features learned through Skip-Gram and Lite-GRU as the initial node features for the heterogeneous graph provide richer information for the nodes, significantly enhancing the model’s performance.
- Variational Autoencoder Module: After removing the VAE module, the model fails to perform noise reduction on high-dimensional sparse features, leading to more irrelevant data being included in the information, thus reducing the clarity and usability of the features. The three metrics of the GEVEHGAN-Vae model decrease by 2.17%, 2.47%, and 2.42%, respectively. This shows that the VAE module condenses the key information from the original node features, removes redundancy and noise, and provides the model with more refined feature representations.
- Edge-Type Attention Mechanism: After removing the edge-type attention mechanism, the model is unable to dynamically adjust the weights of the edges, resulting in an imbalance in the propagation of information across multiple relations, with key information not receiving enough attention. The three metrics of the GEVEHGAN-Att model decrease by 5.45%, 5.76%, and 4.42%, respectively. This demonstrates that the edge-type attention mechanism helps focus on key edge information, integrates multiple relationships to enhance feature representation, and improves information utilization efficiency through adaptive information selection and optimized propagation paths.
- Node Residual Connection Mechanism: After removing the node residual connection mechanism, the information gradually diminishes during propagation through the deeper layers of the network, causing the model to lose the ability to maintain differentiation between nodes, leading to gradient vanishing and learning difficulties during training. The three metrics of the GEVEHGAN-Res model decrease by 3.06%, 3.87%, and 3.51%, respectively. This suggests that the node residual connection mitigates gradient issues, improves backpropagation, facilitates parameter updates, and prevents information loss. Additionally, it further improves feature fusion, leading to better representations and enhanced model performance.
5.7. Model Performance Evaluation Experiment
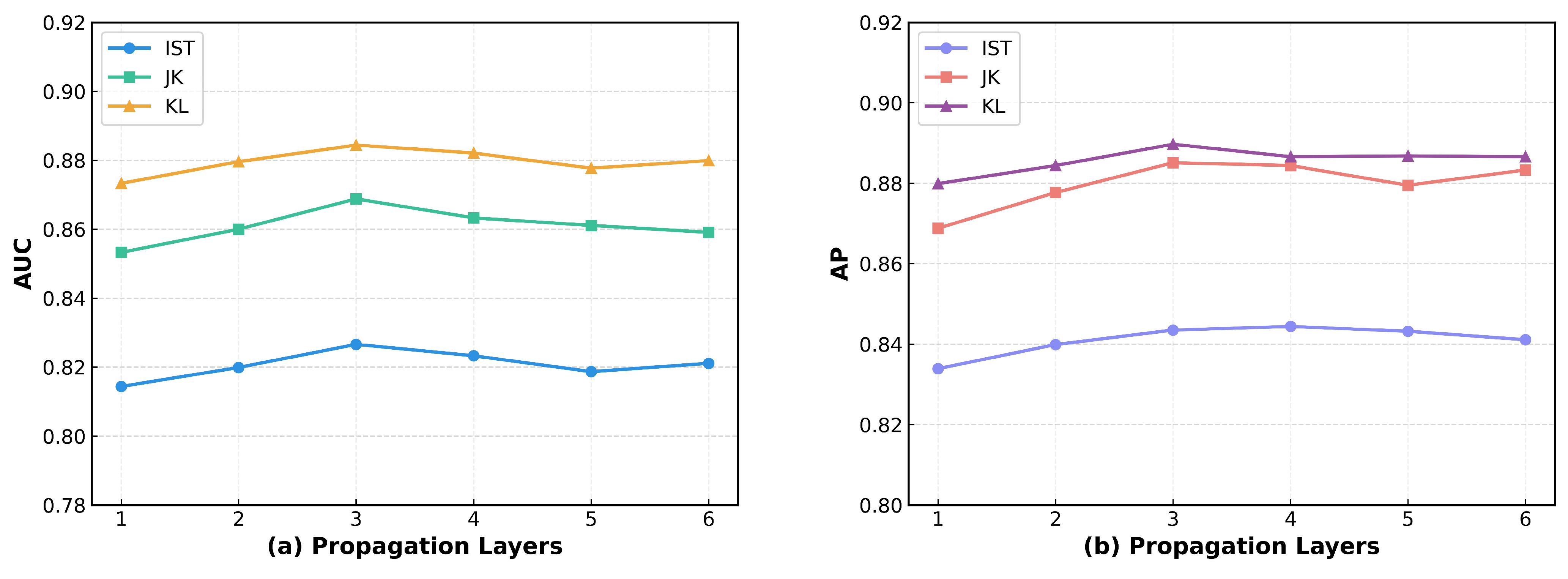
5.8. Hyperparameter Tuning Experiment
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liben-Nowell, D.; Kleinberg, J. The Link Prediction Problem for Social Networks. In Proceedings of the Twelfth International Conference on Information and Knowledge Management, New Orleans, LA, USA, 3–8 November 2003; ACM: New York, NY, USA; pp. 556–559. [Google Scholar]
- Gu, J. Research on Precision Marketing Strategy and Personalized Recommendation Method Based on Big Data Drive. Wirel. Commun. Mob. Comput. 2022, 2022, 6751413. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Huang, H.-H.; Chiu, S.-M.; Lee, C. Joint Promotion Partner Recommendation Systems Using Data from Location-Based Social Networks. ISPRS Int. J. Geo-Inf. 2021, 10, 57. [Google Scholar] [CrossRef]
- MacPhail, A.; Tannehill, D.; Ataman, R. The Role of the Critical Friend in Supporting and Enhancing Professional Learning and Development. Prof. Dev. Educ. 2024, 50, 597–610. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W. A Review of Research on Location-Based Social Network Point of Interest Recommendation Systems. J. Front. Comput. Sci. Technol. 2022, 16, 1462–1478. [Google Scholar] [CrossRef]
- Newman, M.E.J. Clustering and Preferential Attachment in Growing Networks. Phys. Rev. E 2001, 64, 025102. [Google Scholar] [CrossRef] [PubMed]
- Tong, H.; Faloutsos, C.; Pan, J. Fast Random Walk with Restart and Its Applications. In Proceedings of the Sixth International Conference on Data Mining (ICDM’06), Hong Kong, China, 18–22 December 2006; IEEE: Hong Kong, China; pp. 613–622. [Google Scholar]
- Liu, W.; Lü, L. Link Prediction Based on Local Random Walk. Europhys. Lett. 2010, 89, 58007. [Google Scholar] [CrossRef]
- Wang, C.; Satuluri, V.; Parthasarathy, S. Local Probabilistic Models for Link Prediction. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; IEEE: Los Alamitos, CA, USA; pp. 322–331. [Google Scholar]
- Neville, J. Statistical Models and Analysis Techniques for Learning in Relational Data; University of Massachusetts Amherst: Amherst, MA, USA, 2006. [Google Scholar]
- Yu, K.; Chu, W.; Yu, S.; Tresp, V.; Xu, Z. Stochastic Relational Models for Discriminative Link Prediction. Adv. Neural Inf. Process. Syst. 2006, 19, 1553–1560. [Google Scholar]
- Du, Y.; Zheng, Y.; Lee, K.; Zhe, S. Probabilistic Streaming Tensor Decomposition. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Sentosa, Singapore, 17–20 November 2018; IEEE: Los Angeles, CA, USA; pp. 99–108. [Google Scholar]
- Sarukkai, R.R. Link Prediction and Path Analysis Using Markov Chains. Comput. Netw. 2000, 33, 377–386. [Google Scholar] [CrossRef]
- Li, X.; Du, N.; Li, H.; Li, K.; Gao, J.; Zhang, A. A Deep Learning Approach to Link Prediction in Dynamic Networks. In Proceedings of the 2014 SIAM International Conference on Data Mining, Philadelphia, PA, USA, 28 April 2014; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA; pp. 289–297. [Google Scholar]
- Wang, X.-W.; Chen, Y.; Liu, Y.-Y. Link Prediction through Deep Generative Model. Iscience 2020, 23, 101626. [Google Scholar] [CrossRef]
- Wang, H.; Shi, X.; Yeung, D.-Y. Relational Deep Learning: A Deep Latent Variable Model for Link Prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 31. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling Relational Data with Graph Convolutional Networks. In The Semantic Web; Gangemi, A., Navigli, R., Vidal, M.-E., Hitzler, P., Troncy, R., Hollink, L., Tordai, A., Alam, M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 10843, pp. 593–607. ISBN 978-3-319-93416-7. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational Graph Auto-Encoders 2016. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lian, D.; Jin, S.; Chen, E. Graph Convolutional Networks on User Mobility Heterogeneous Graphs for Social Relationship Inference. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence Main Track, Macau, China, 10–16 August 2019; pp. 3898–3904. [Google Scholar]
- Backes, M.; Humbert, M.; Pang, J.; Zhang, Y. Walk2friends: Inferring Social Links from Mobility Profiles. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; ACM: New York, NY, USA; pp. 1943–1957. [Google Scholar]
- Zhang, W.; Lai, X.; Wang, J. Social Link Inference via Multiview Matching Network from Spatiotemporal Trajectories. IEEE Trans. Neural Netw. Learn. Syst. 2020, 34, 1720–1731. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. Stat 2017, 1050. [Google Scholar] [CrossRef]
- Wang, X.; Ji, H.; Shi, C.; Wang, B.; Ye, Y.; Cui, P.; Yu, P.S. Heterogeneous Graph Attention Network. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; ACM: New York, NY, USA; pp. 2022–2032. [Google Scholar]
- Hu, Q.; Lin, W.; Tang, M.; Jiang, J. Mbhan: Motif-Based Heterogeneous Graph Attention Network. Appl. Sci. 2022, 12, 5931. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Z.; Liu, X.; Liu, Y.; Sun, G. An Improved Context-Aware Weighted Matrix Factorization Algorithm for Point of Interest Recommendation in LBSN. Inf. Syst. 2024, 122, 102366. [Google Scholar] [CrossRef]
- Seo, Y.-D.; Cho, Y.-S. Point of Interest Recommendations Based on the Anchoring Effect in Location-Based Social Network Services. Expert Syst. Appl. 2021, 164, 114018. [Google Scholar] [CrossRef]
- Wang, C.; Yuan, M.; Zhang, R.; Peng, K.; Liu, L. Efficient Point-of-Interest Recommendation Services with Heterogenous Hypergraph Embedding. IEEE Trans. Serv. Comput. 2022, 16, 1132–1143. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Tran, C.L.H.; Luong, H.H. Mobility Prediction on a Location-Based Social Network Using K Latest Movements of Friends. In Intelligent Systems and Networks; Anh, N.L., Koh, S.-J., Nguyen, T.D.L., Lloret, J., Nguyen, T.T., Eds.; Lecture Notes in Networks and Systems; Springer Nature Singapore: Singapore, 2022; Volume 471, pp. 279–286. ISBN 978-981-19-3393-6. [Google Scholar]
- Li, Y.; Fan, Z.; Zhang, J.; Shi, D.; Xu, T.; Yin, D.; Deng, J.; Song, X. Heterogeneous Hypergraph Neural Network for Friend Recommendation with Human Mobility. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; ACM: New York, NY, USA; pp. 4209–4213. [Google Scholar]
- Li, Y.; Fan, Z.; Yin, D.; Jiang, R.; Deng, J.; Song, X. HMGCL: Heterogeneous Multigraph Contrastive Learning for LBSN Friend Recommendation. World Wide Web 2023, 26, 1625–1648. [Google Scholar] [CrossRef]
- Yang, L.; Marmolejo Duarte, C.R.; Martí Ciriquiá, P. Exploring the Applications and Limitations of Location-Based Social Network Data in Urban Spatiotemporal Analysis. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2021. [Google Scholar]
- Laman, H.; Eluru, N.; Yasmin, S. Using Location-Based Social Network Data for Activity Intensity Analysis. J. Transp. Land Use 2019, 12, 723–740. [Google Scholar] [CrossRef]
- Nolasco-Cirugeda, A.; García-Mayor, C. Social Dynamics in Cities: Analysis through LBSN Data. Procedia Comput. Sci. 2022, 207, 877–886. [Google Scholar] [CrossRef]
- Xu, D.; Chen, Y.; Cui, N.; Li, J. Towards Multi-Dimensional Knowledge-Aware Approach for Effective Community Detection in LBSN. World Wide Web 2023, 26, 1435–1458. [Google Scholar] [CrossRef]
- Wang, K.; Wang, X.; Lu, X. POI Recommendation Method Using LSTM-Attention in LBSN Considering Privacy Protection. Complex Intell. Syst. 2023, 9, 2801–2812. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Y.; Lu, R.; Zhu, H.; Zhang, Y. Towards Privacy-Preserving Category-Aware POI Recommendation over Encrypted LBSN Data. Inf. Sci. 2024, 662, 120253. [Google Scholar] [CrossRef]
- Sai, A.M.V.V.; Zhang, K.; Li, Y. User Motivation Based Privacy Preservation in Location Based Social Networks. In Proceedings of the 2021 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/IOP/SCI), Atlanta, GA, USA, 18–21 October 2021; IEEE: Los Alamitos, CA, USA; pp. 471–478. [Google Scholar]
- Jaccard, P. Distribution de La Flore Alpine Dans Le Bassin Des Dranses et Dans Quelques Régions Voisines. Bull Soc. Vaudoise. Sci. Nat. 1901, 37, 241–272. [Google Scholar]
- Adamic, L.A.; Adar, E. Friends and Neighbors on the Web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Barabâsi, A.-L.; Jeong, H.; Néda, Z.; Ravasz, E.; Schubert, A.; Vicsek, T. Evolution of the Social Network of Scientific Collaborations. Phys. Stat. Mech. Its Appl. 2002, 311, 590–614. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.; Zhang, Y.-C. Predicting Missing Links via Local Information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
- Salton, G. Modern Information Retrieval; McGraw-Hill Education: New York, NY, USA, 1983. [Google Scholar]
- Lü, L.; Jin, C.-H.; Zhou, T. Similarity Index Based on Local Paths for Link Prediction of Complex Networks. Phys. Rev. E 2009, 80, 046122. [Google Scholar] [CrossRef]
- Katz, L. A New Status Index Derived from Sociometric Analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Rafiee, S.; Salavati, C.; Abdollahpouri, A. CNDP: Link Prediction Based on Common Neighbors Degree Penalization. Phys. Stat. Mech. Its Appl. 2020, 539, 122950. [Google Scholar] [CrossRef]
- Yuliansyah, H.; Othman, Z.A.; Bakar, A.A. A New Link Prediction Method to Alleviate the Cold-Start Problem Based on Extending Common Neighbor and Degree Centrality. Phys. Stat. Mech. Its Appl. 2023, 616, 128546. [Google Scholar] [CrossRef]
- Aziz, F.; Gul, H.; Muhammad, I.; Uddin, I. Link Prediction Using Node Information on Local Paths. Phys. Stat. Mech. Its Appl. 2020, 557, 124980. [Google Scholar] [CrossRef]
- Ayoub, J.; Lotfi, D.; El Marraki, M.; Hammouch, A. Accurate Link Prediction Method Based on Path Length between a Pair of Unlinked Nodes and Their Degree. Soc. Netw. Anal. Min. 2020, 10, 9. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; ACM: New York, NY, USA; pp. 639–648. [Google Scholar]
- Chen, L.; Xie, Y.; Zheng, Z.; Zheng, H.; Xie, J. Friend Recommendation Based on Multi-Social Graph Convolutional Network. IEEE Access 2020, 8, 43618–43629. [Google Scholar] [CrossRef]
- van den Berg, R.; Kipf, T.N.; Welling, M. Graph Convolutional Matrix Completion 2017. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Zhang, C.; Song, D.; Huang, C.; Swami, A.; Chawla, N.V. Heterogeneous Graph Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 25 July 2019; ACM: New York, NY, USA; pp. 793–803. [Google Scholar]
- Dong, Y.; Chawla, N.V.; Swami, A. Metapath2vec: Scalable Representation Learning for Heterogeneous Networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; ACM: New York, NY, USA; pp. 135–144. [Google Scholar]
- Fu, X.; Zhang, J.; Meng, Z.; King, I. MAGNN: Metapath Aggregated Graph Neural Network for Heterogeneous Graph Embedding. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; ACM: New York, NY, USA; pp. 2331–2341. [Google Scholar]
- Fan, Y.; Ju, M.; Zhang, C.; Zhao, L.; Ye, Y. Heterogeneous Temporal Graph Neural Network 2021. arXiv 2021, arXiv:2110.13889. [Google Scholar]
- Salamat, A.; Luo, X.; Jafari, A. HeteroGraphRec: A Heterogeneous Graph-Based Neural Networks for Social Recommendations. Knowl.-Based Syst. 2021, 217, 106817. [Google Scholar] [CrossRef]
- Shao, Y.; Liu, C. H2Rec: Homogeneous and Heterogeneous Network Embedding Fusion for Social Recommendation. Int. J. Comput. Intell. Syst. 2021, 14, 1303–1314. [Google Scholar] [CrossRef]
- Yadati, N.; Nimishakavi, M.; Yadav, P.; Nitin, V.; Louis, A.; Talukdar, P. Hypergcn: A New Method for Training Graph Convolutional Networks on Hypergraphs. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Dong, Y.; Sawin, W.; Bengio, Y. HNHN: Hypergraph Networks with Hyperedge Neurons 2020. arXiv 2020, arXiv:2006.12278. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3558–3565. [Google Scholar]
- Huang, J.; Yang, J. UniGNN: A Unified Framework for Graph and Hypergraph Neural Networks 2021. arXiv 2021, arXiv:2105.00956. [Google Scholar]
- Chien, E.; Pan, C.; Peng, J.; Milenkovic, O. You Are AllSet: A Multiset Function Framework for Hypergraph Neural Networks 2022. arXiv 2022, arXiv:2106.13264. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space 2013. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Ravanelli, M.; Brakel, P.; Omologo, M.; Bengio, Y. Light Gated Recurrent Units for Speech Recognition. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 92–102. [Google Scholar] [CrossRef]
- Brody, S.; Alon, U.; Yahav, E. How Attentive Are Graph Attention Networks? arXiv 2022, arXiv:2105.14491. [Google Scholar]
- Li, G.; Muller, M.; Thabet, A.; Ghanem, B. Deepgcns: Can Gcns Go as Deep as Cnns? In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9267–9276. [Google Scholar]
- Li, G.; Xiong, C.; Thabet, A.; Ghanem, B. DeeperGCN: All You Need to Train Deeper GCNs 2020. arXiv 2020, arXiv:2006.07739. [Google Scholar]
- Lv, Q.; Ding, M.; Liu, Q.; Chen, Y.; Feng, W.; He, S.; Zhou, C.; Jiang, J.; Dong, Y.; Tang, J. Are We Really Making Much Progress?: Revisiting, Benchmarking and Refining Heterogeneous Graph Neural Networks. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, Singapore, 14–18 August 2021; ACM: New York, NY, USA; pp. 1150–1160. [Google Scholar]
- Wu, J.; Hu, R.; Li, D.; Ren, L.; Hu, W.; Xiao, Y. Where Have You Been: Dual Spatiotemporal-Aware User Mobility Modeling for Missing Check-in POI Identification. Inf. Process. Manag. 2022, 59, 103030. [Google Scholar] [CrossRef]



| Dataset | User Number | POI Number | Check-In Number | Friends Number | Average Sign-In Count |
|---|---|---|---|---|---|
| NYC | 3754 | 3626 | 104,991 | 12,098 | 27.97 |
| TKY | 7166 | 10,856 | 698,889 | 57,142 | 97.53 |
| SP | 3811 | 6255 | 247,683 | 16,363 | 64.99 |
| JK | 6184 | 8805 | 376,076 | 17,798 | 60.81 |
| IST | 9993 | 12,608 | 884,313 | 45,002 | 88.49 |
| KL | 6324 | 10,804 | 524,061 | 34,537 | 82.87 |
| Experiment Environment | Specific Configuration |
|---|---|
| Operating System | Windows 11 64-bit OS |
| CPU | 12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz |
| GPU | NVIDIA GeForce RTX 3080 |
| Memory | 64 GB |
| Programming Language | Python 3.10 |
| Deep Learning Framework | PyTorch 1.12 |
| Library Versions | numpy = 1.13.1, scikit-learn = 1.0.2, dgl = 0.7.2 |
| Parameter Name | Parameter Description | Parameter Value |
|---|---|---|
| Window size | Skip-Gram window size | 10 |
| Initial embedding dim | Initial embedding dimension size | 64 |
| Lite-GRU num layers | Lite-GRU layer number | 1 |
| Node embedding dim | Node feature mapping dimension | 128 |
| Edge embedding dim | Edge feature mapping dimension | 10 |
| (·) | Nonlinear activation function | ReLU(·) |
| Learn | Adam optimizer learning rate | 0.001 |
| Epochs | Iterations | 2700 |
| GNN num layers | GNN layer number | 3 |
| K | Multiple attention number | 4 |
| Window size | Skip-Gram window size | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, B.; Wang, Y.; Liu, A. The Application of Lite-GRU Embedding and VAE-Augmented Heterogeneous Graph Attention Network in Friend Link Prediction for LBSNs. Appl. Sci. 2025, 15, 4585. https://doi.org/10.3390/app15084585
Yang Z, Li B, Wang Y, Liu A. The Application of Lite-GRU Embedding and VAE-Augmented Heterogeneous Graph Attention Network in Friend Link Prediction for LBSNs. Applied Sciences. 2025; 15(8):4585. https://doi.org/10.3390/app15084585
Chicago/Turabian StyleYang, Ziteng, Boyu Li, Yong Wang, and Aoxue Liu. 2025. "The Application of Lite-GRU Embedding and VAE-Augmented Heterogeneous Graph Attention Network in Friend Link Prediction for LBSNs" Applied Sciences 15, no. 8: 4585. https://doi.org/10.3390/app15084585
APA StyleYang, Z., Li, B., Wang, Y., & Liu, A. (2025). The Application of Lite-GRU Embedding and VAE-Augmented Heterogeneous Graph Attention Network in Friend Link Prediction for LBSNs. Applied Sciences, 15(8), 4585. https://doi.org/10.3390/app15084585






