Trajectory Tracking Control Strategy of 20-Ton Heavy-Duty AGV Considering Load Transfer
Abstract
1. Introduction
2. Establishment of Heavy-Duty AGV Vehicle Model
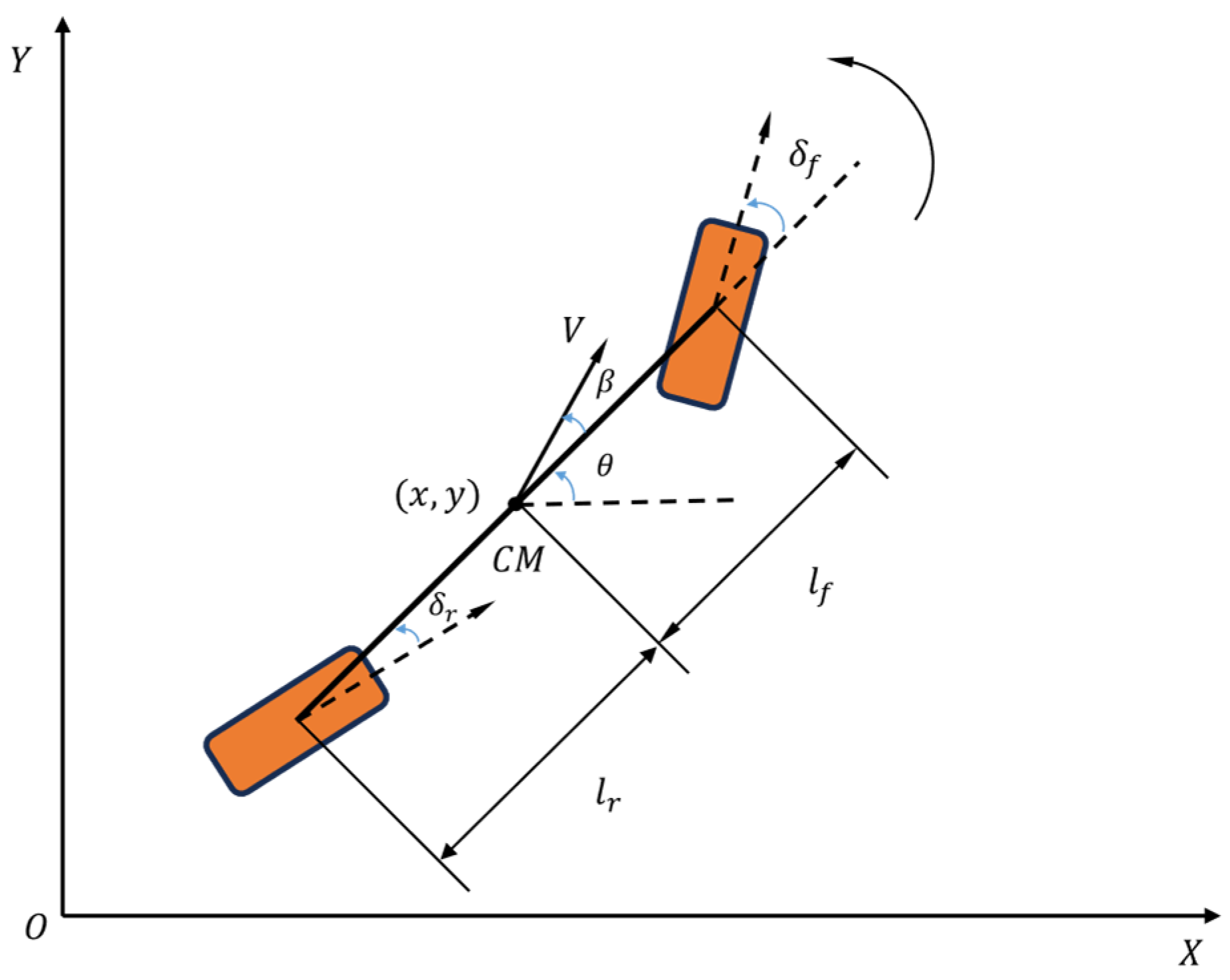
2.1. Three-Degree-of-Freedom Vehicle Kinematics Model
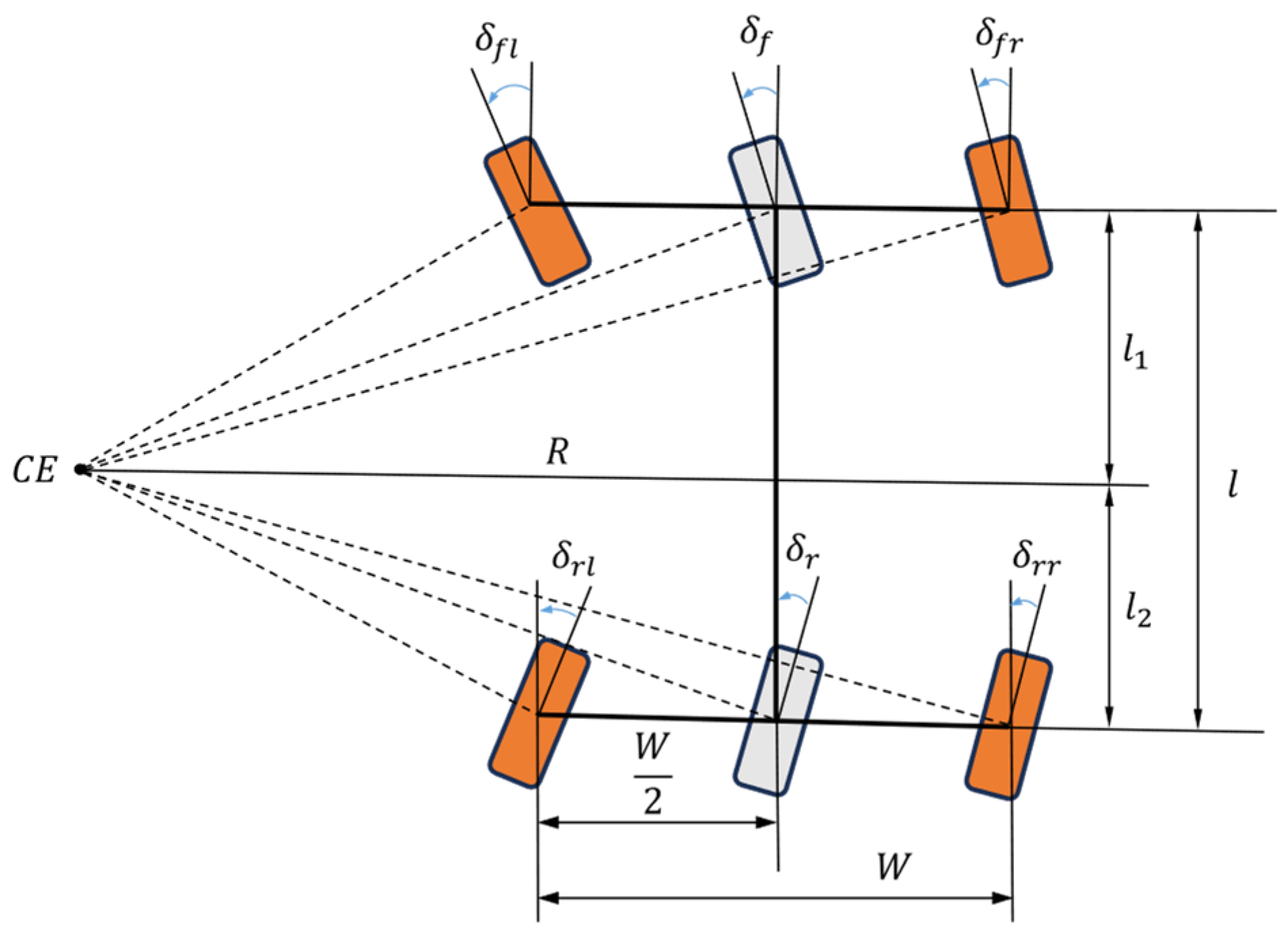
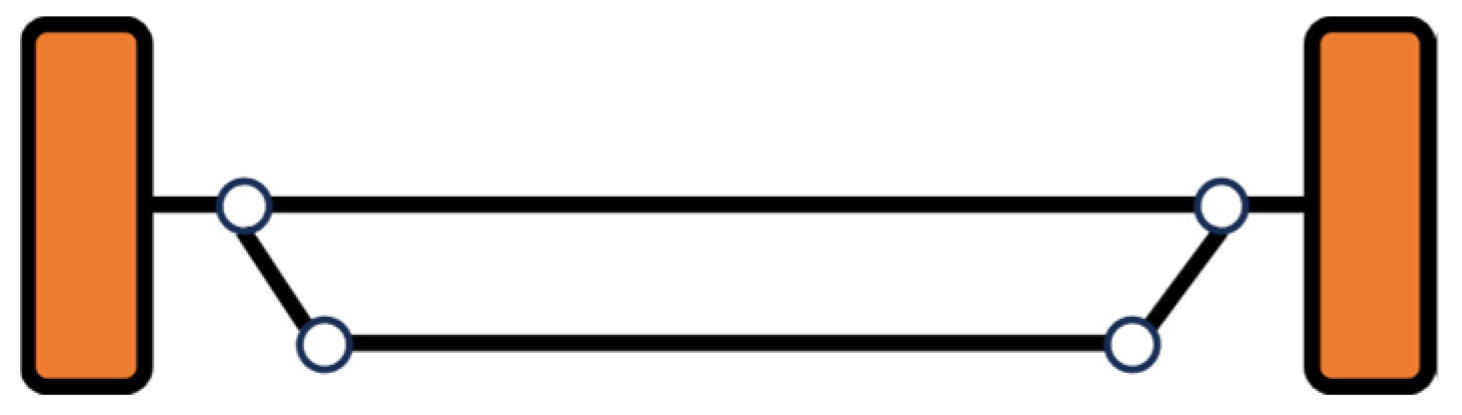
2.2. Pose Linear Error Model of Double Ackermann Steering
3. Load Transfer Analysis
3.1. Lateral Load Transfer Analysis
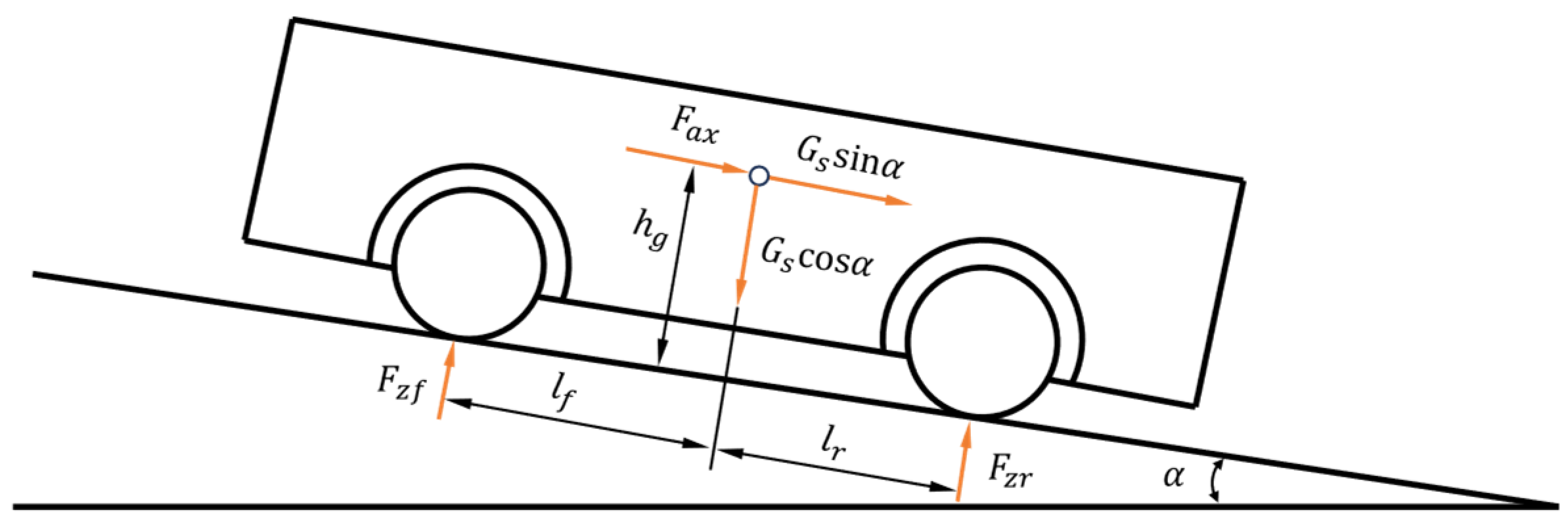
3.2. Longitudinal Load Transfer Analysis
4. Design of Trajectory Tracking Control Strategy Considering Load Transfer
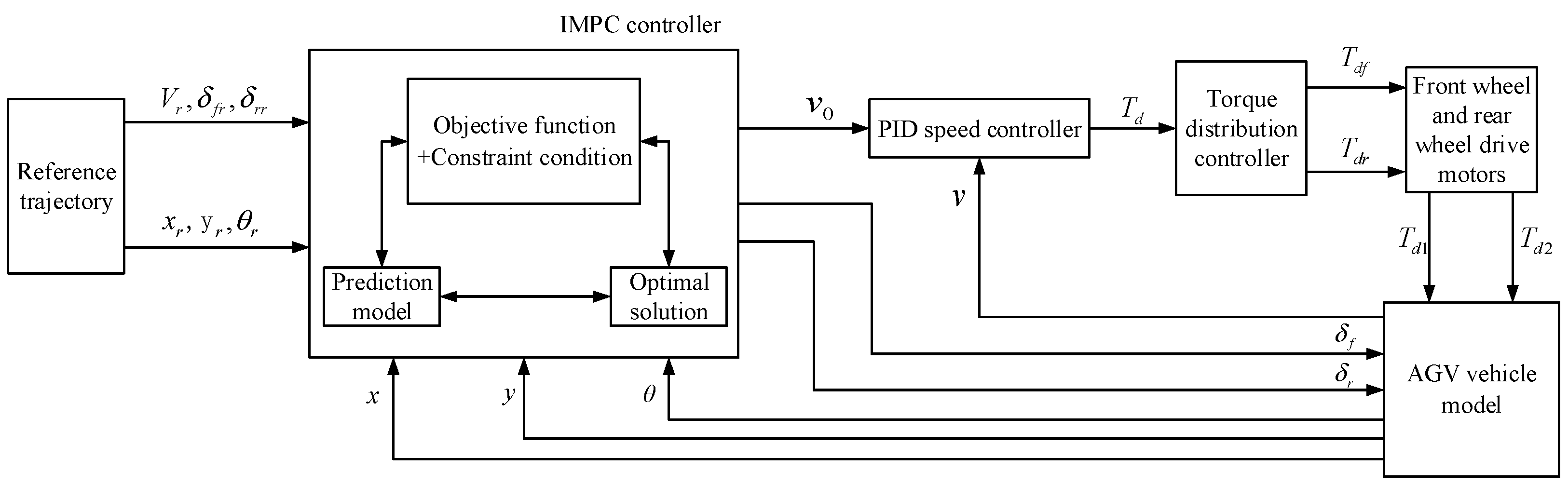
4.1. Overall Control Strategy Design
- An MPC controller for optimizing lateral acceleration based on the kinematic model. The improved MPC controller receives the state reference quantities (xr, yr, θr) output by the reference trajectory, the control reference quantities (vr, δfr, δrr), and the actual pose (x, y, θ) of the AGV. A cost function that minimizes both the lateral acceleration term and the tracking error term is designed, along with constraints on the maximum and minimum values of the control variables and their increments, as well as the equality constraint in Equation (9). A prediction model is established to output the control variables and perform feedback correction so as to achieve AGV trajectory tracking while reducing the lateral load transfer;
- A velocity controller for calculating the total driving torque. The PID velocity controller receives the desired velocity v0 output by the MPC controller and the actual velocity v of the AGV, thereby computing and outputting the total driving torque Td of the AGV;
- A torque distribution controller for allocating the total driving torque to each motor and transferring it to the vehicle model. After receiving the total driving torque calculated by the PID velocity controller, the torque distribution controller allocates the total driving torque into the input torques Tdf and Tdr of the front and rear drive motors according to the vertical load proportion allocation method, thereby driving the AGV movement.
4.2. Lateral Load Transfer IMPC Control Strategy
4.2.1. Design of Prediction Model
4.2.2. Design of Objective Function
4.2.3. Constraint Condition Design Based on Double Ackerman Angle Constraint
4.3. Torque Adaptive Distribution Longitudinal Load Transfer Control Strategy
5. Trajectory Tracking Co-Simulation Analysis Based on Simulink and CarSim
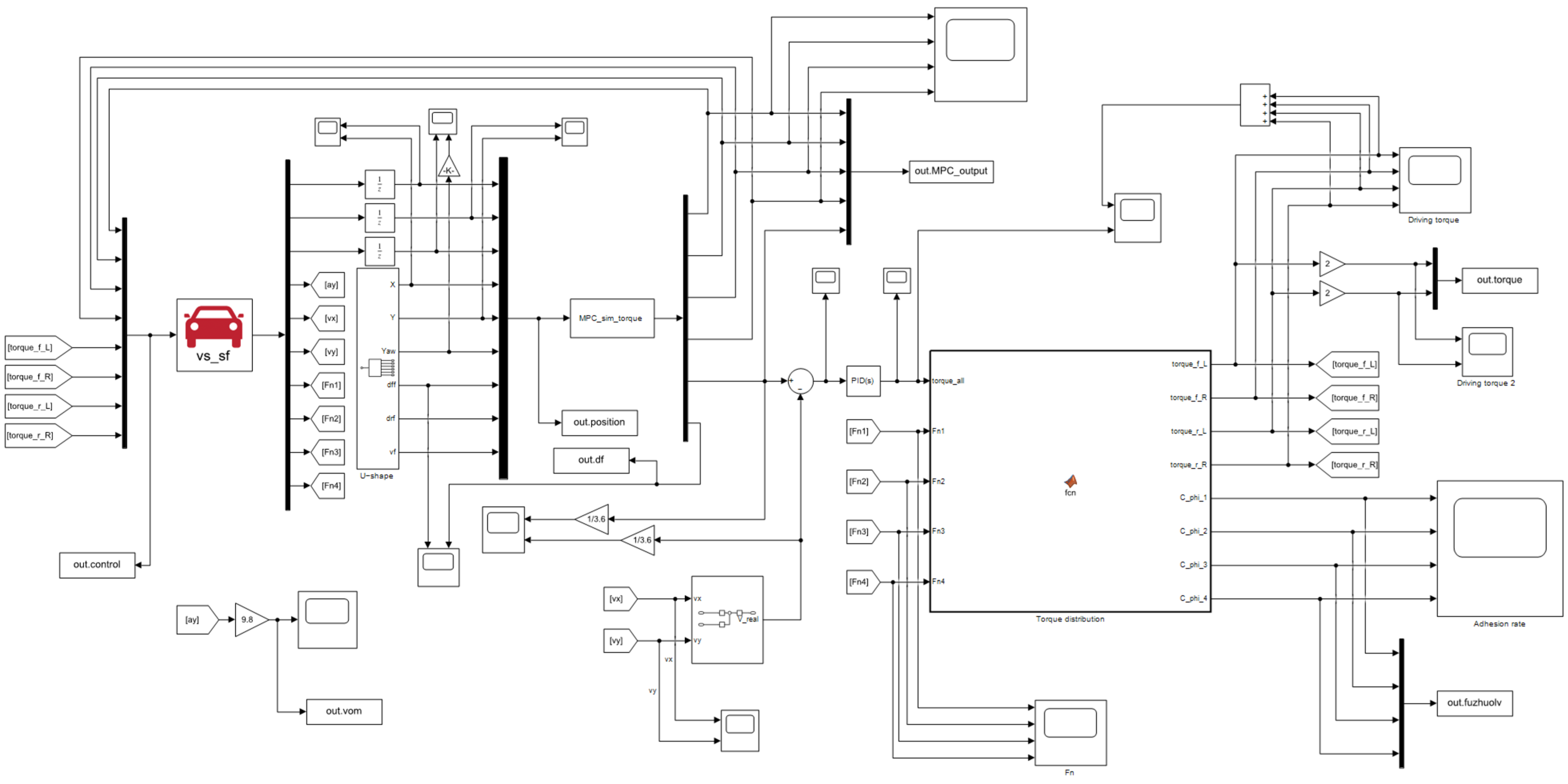
5.1. Establishment of a Simulation Model
- The IMPC controller receives the state reference quantities (xr, yr, θr) output by the reference trajectory, the control reference quantities (vr, δfr, δrr), and the actual pose (x, y, θ) of the AGV from CarSim. By solving the constrained objective function described above, the front and rear wheel angles and the desired velocity are calculated;
- The PID velocity controller computes and outputs the total driving torque Td of the AGV based on the error between the actual velocity and the desired velocity;
- The torque distribution controller receives the total driving torque Td calculated by the PID velocity controller and allocates it into the driving torques Tdf and Tdr of the front and rear drive motors according to the vertical load proportion allocation method, which is then output to the CarSim module;
- The CarSim module receives the front and rear wheel driving torques from the torque distribution controller and the front and rear wheel angles from the IMPC controller to control the vehicle’s driving and steering and feeds back the vehicle’s state information.
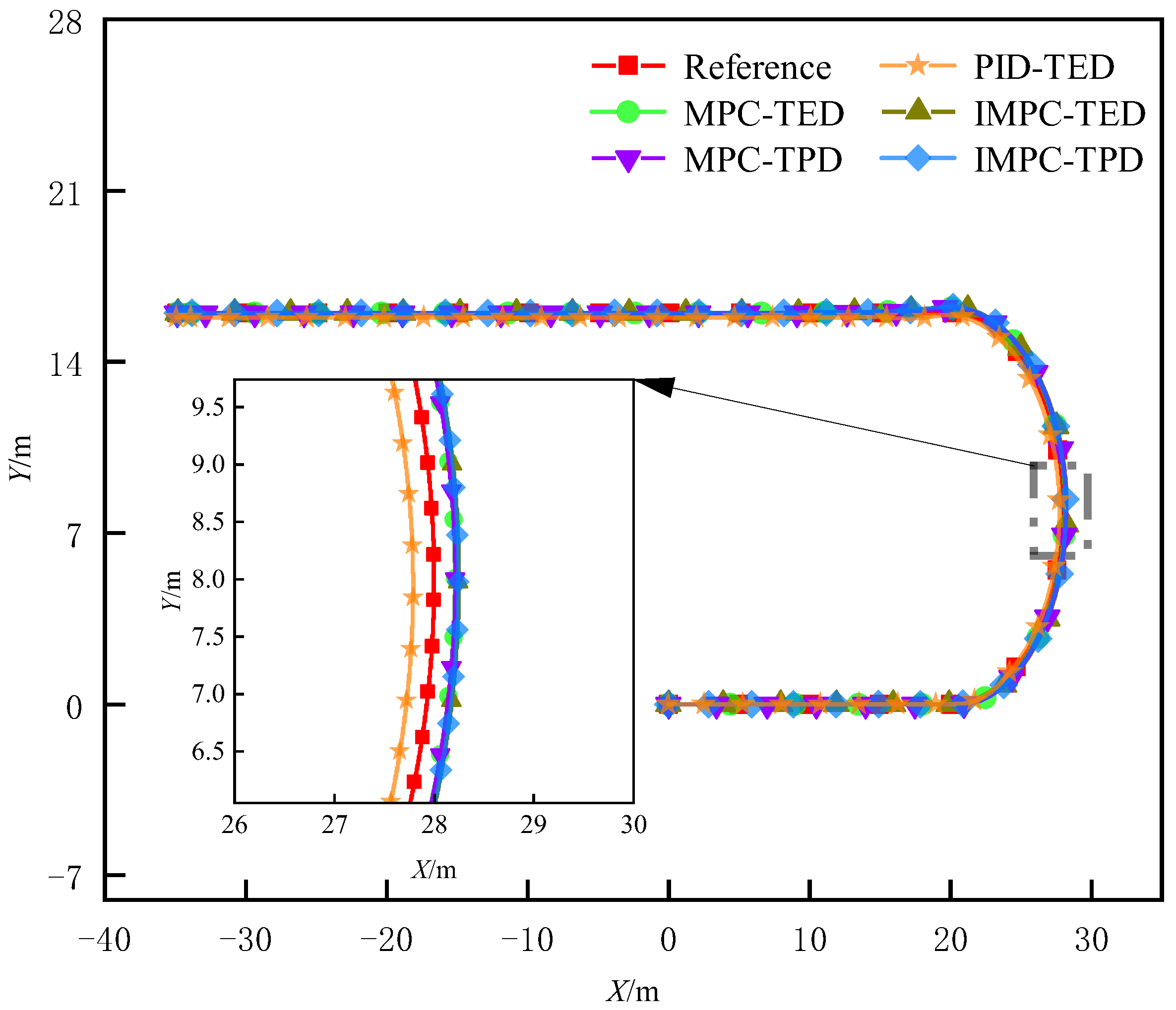
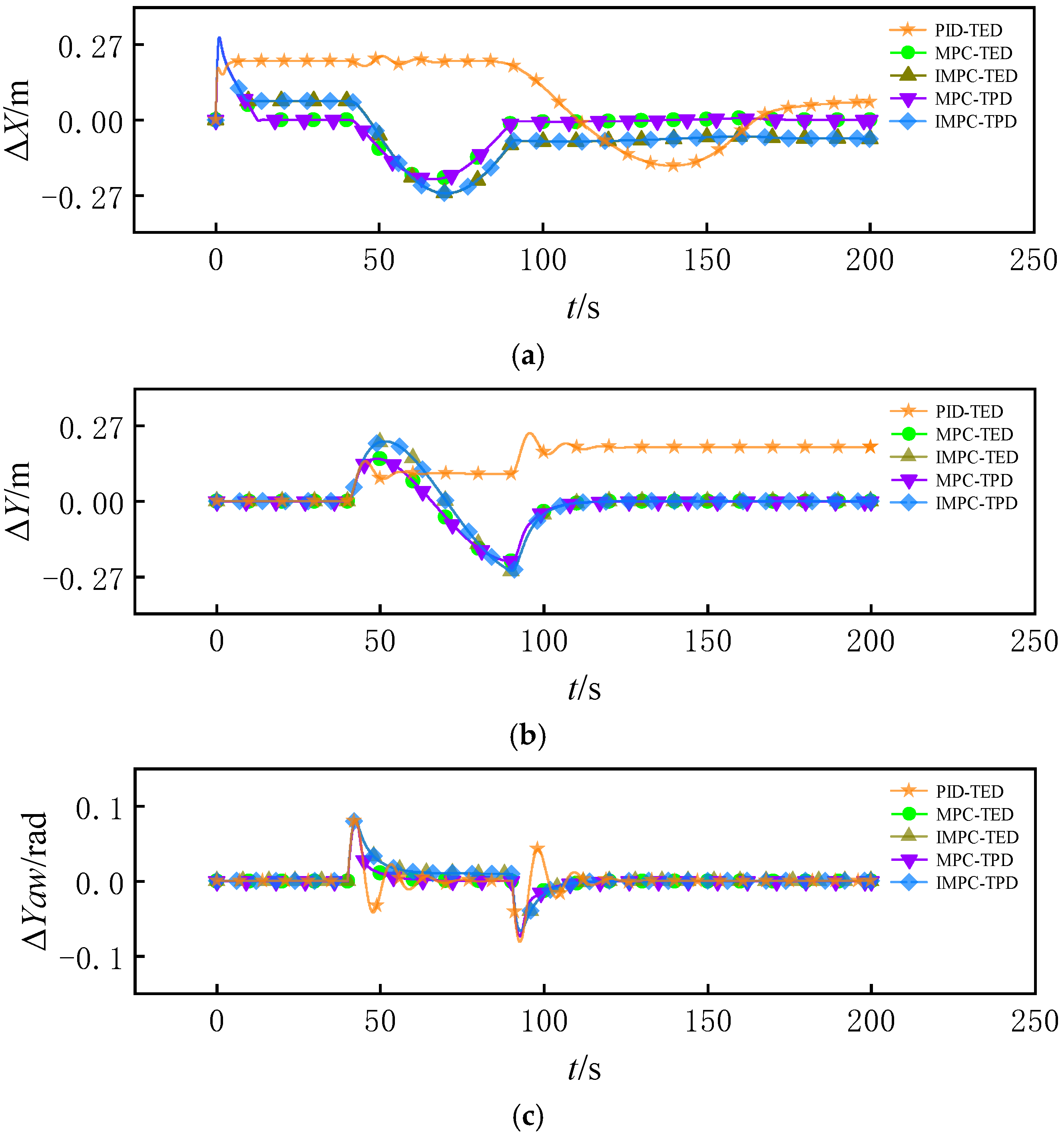
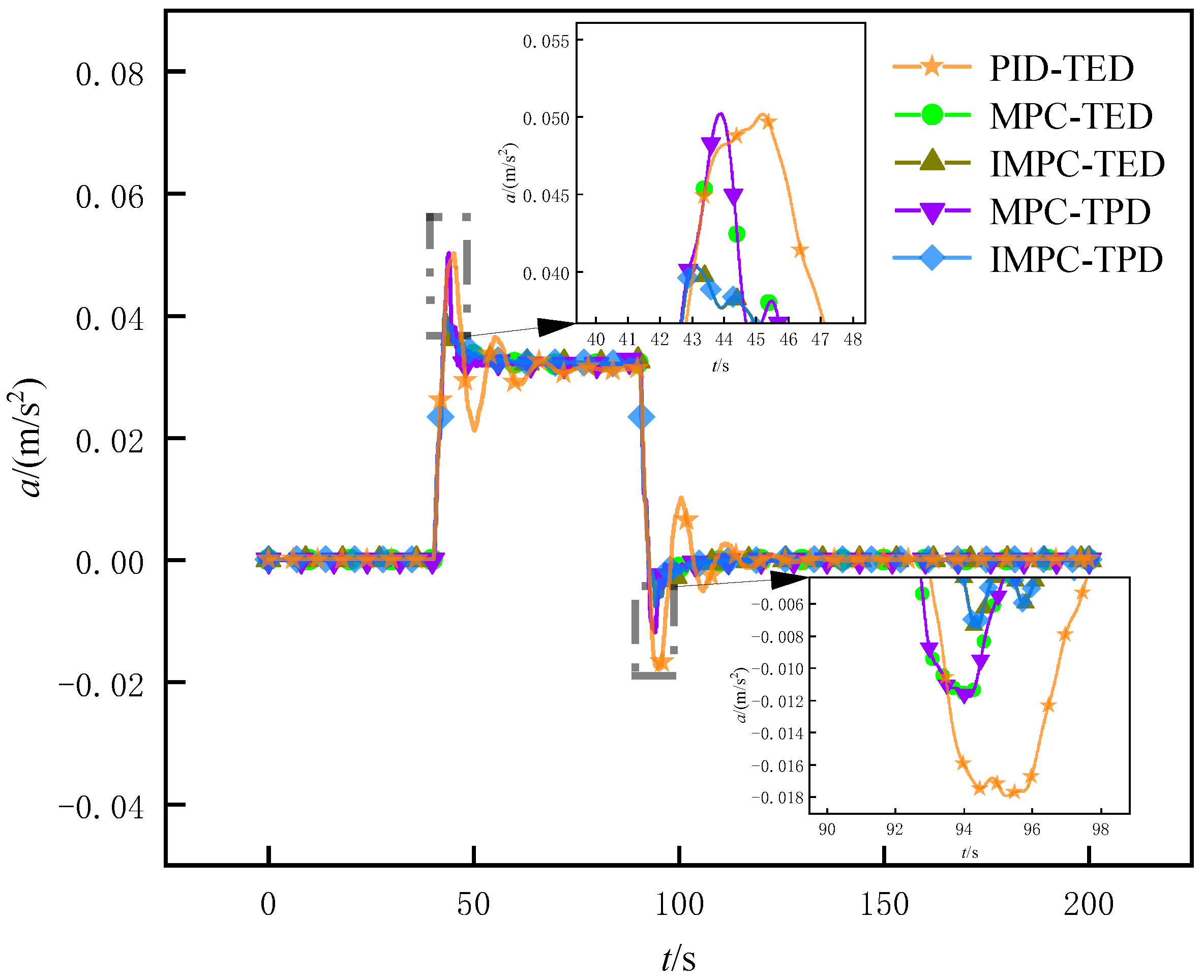
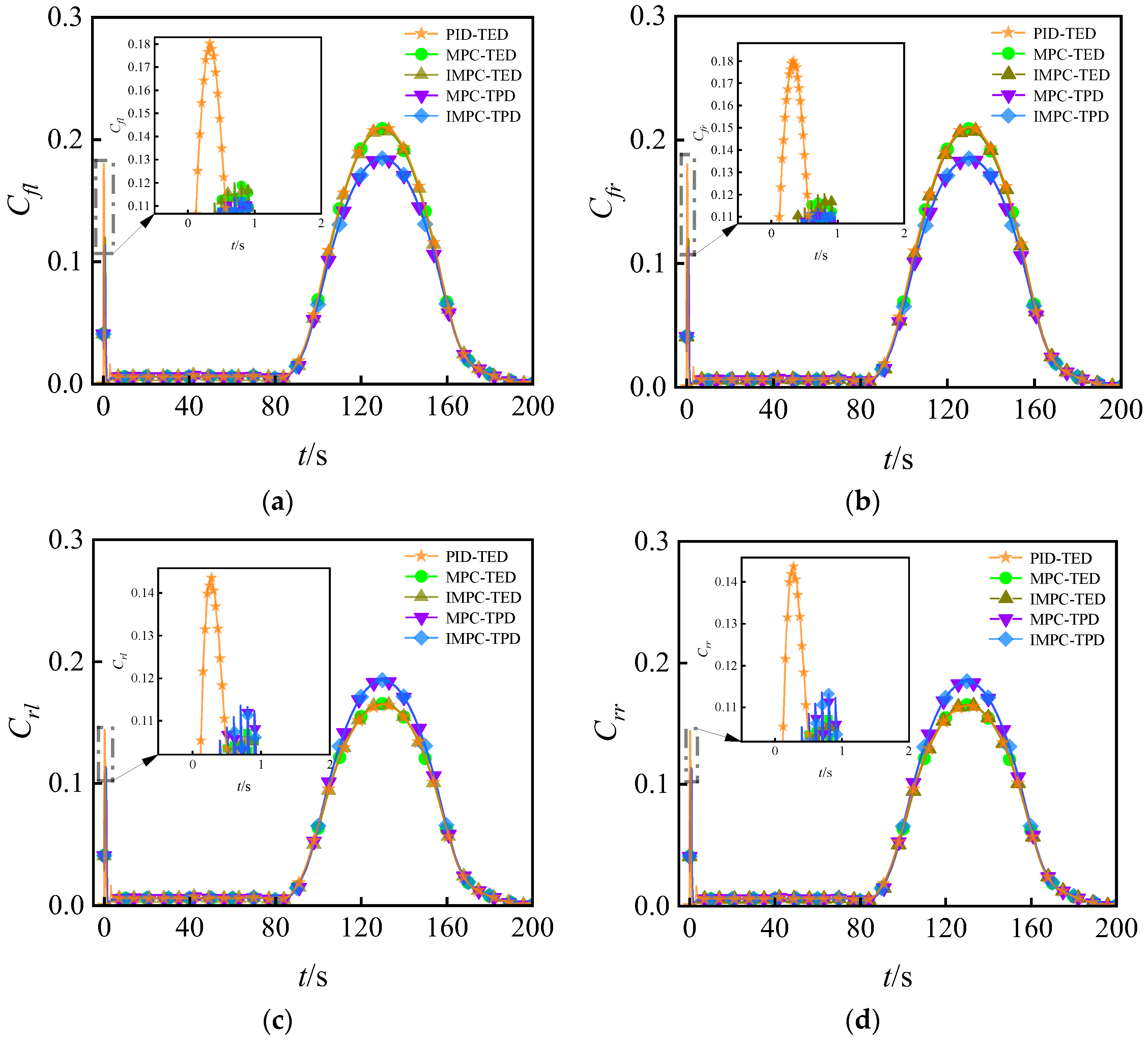
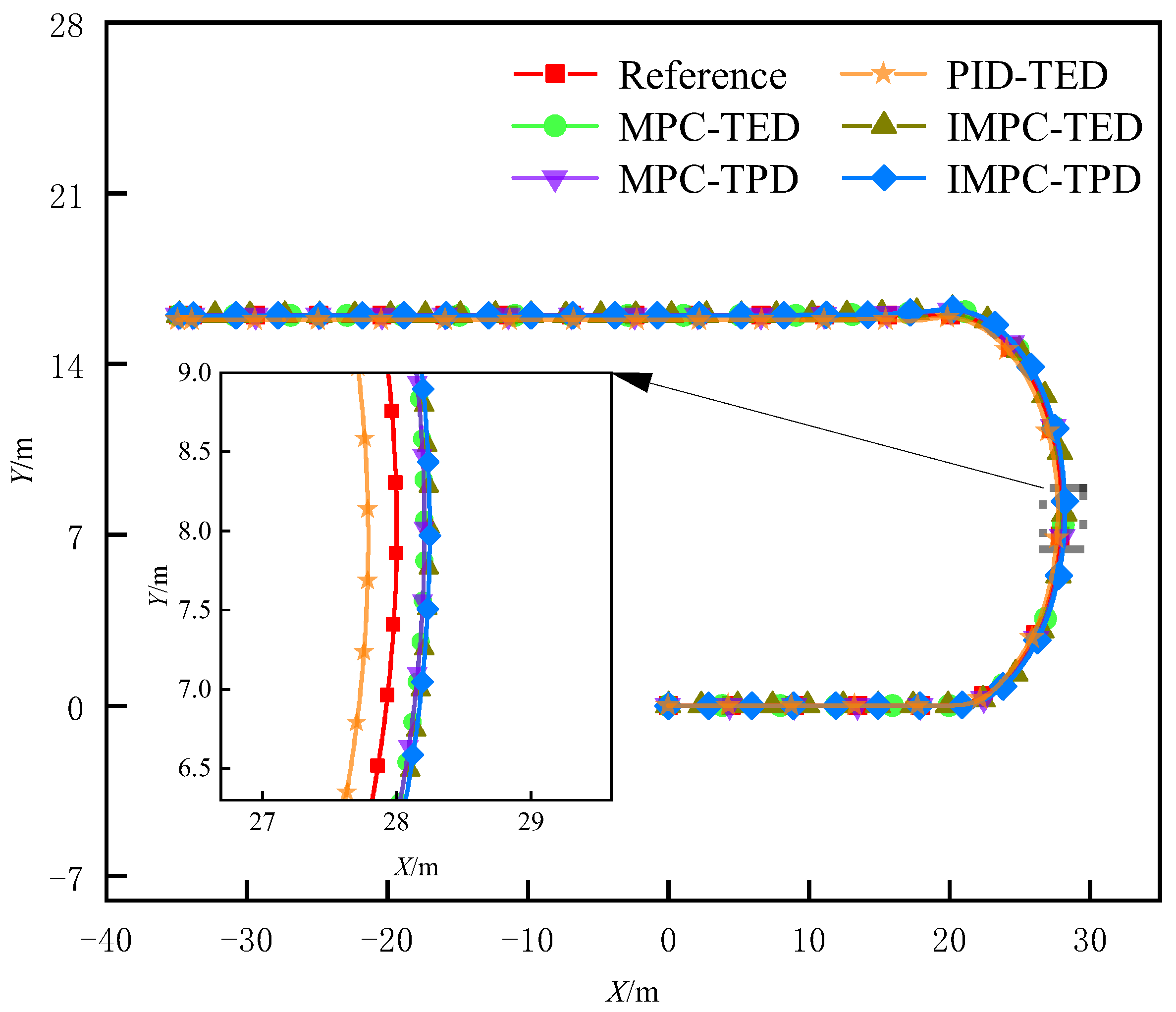
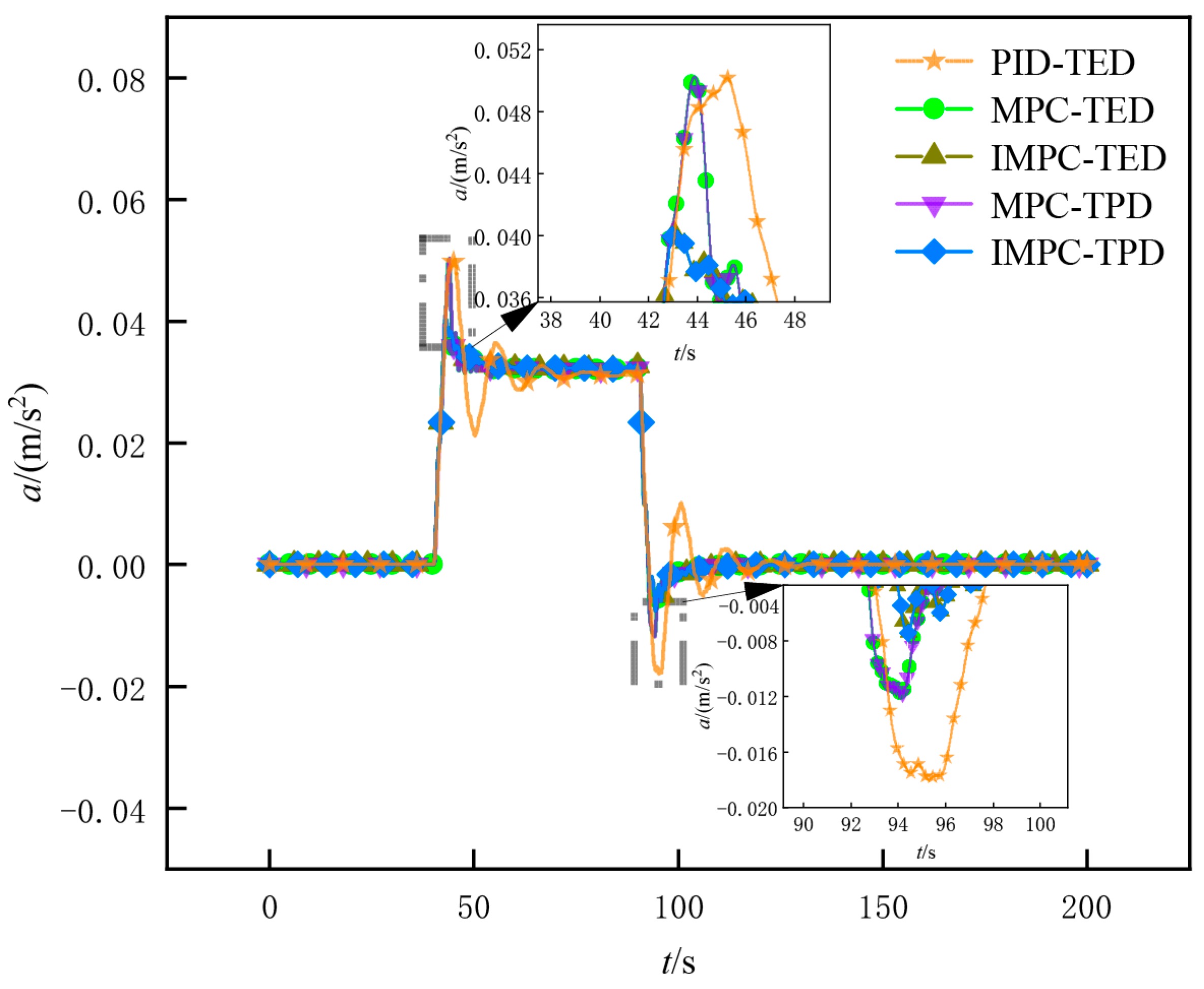
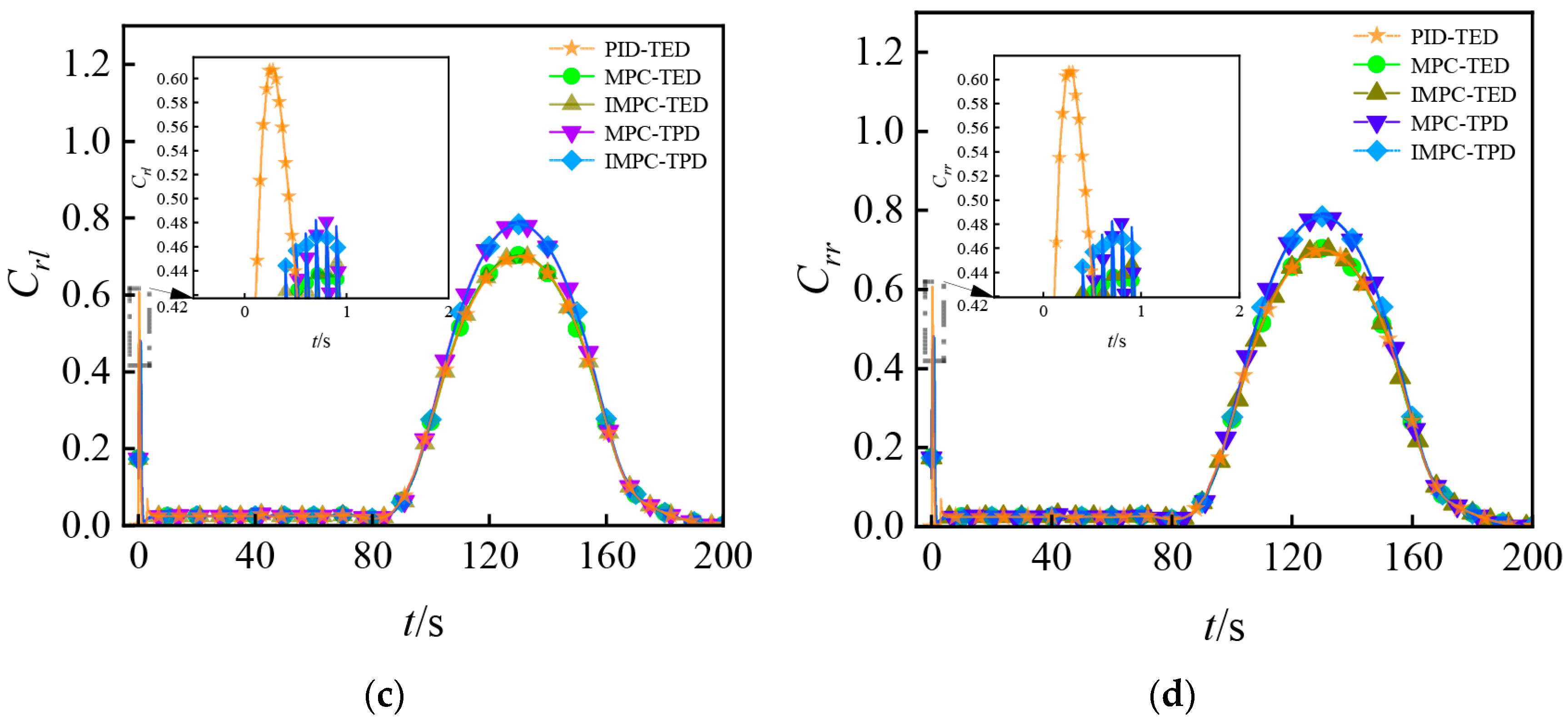
5.2. Simulation Results Extraction and Analysis
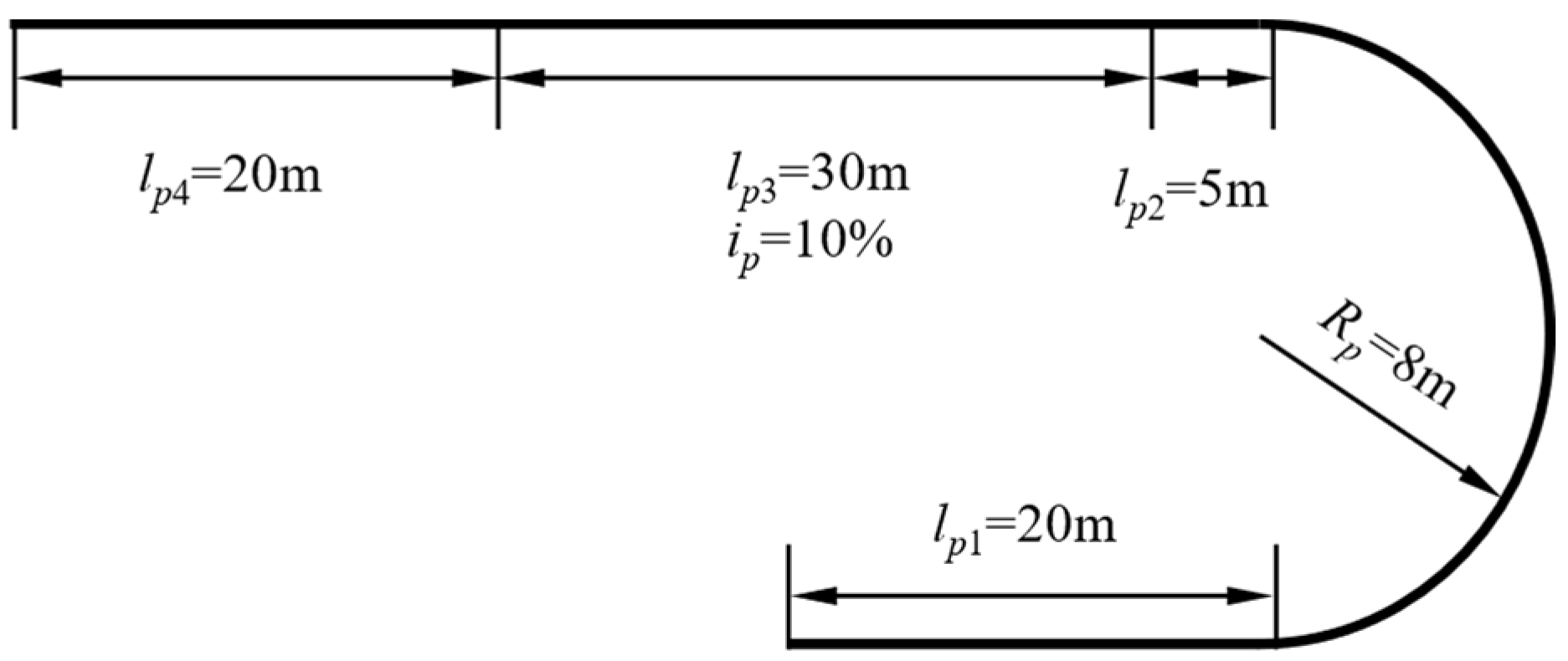
5.2.1. Trajectory Tracking Simulation Under High Pavement Adhesion Coefficient
5.2.2. Trajectory Tracking Simulation Under Low Pavement Adhesion Coefficient
6. Conclusions
- A 3-DOF kinematic model of the heavy-duty AGV is established. Through analysis of lateral and longitudinal load transfer under complex pavement conditions, the laws governing load transfer are derived;
- A control strategy considering both lateral and longitudinal load transfer is proposed. A lateral load-improved MPC controller based on lateral acceleration is designed alongside an adaptive torque distribution strategy according to longitudinal load transfer;
- Finally, a MATLAB/Simulink and CarSim co-simulation platform is built to conduct simulations on pavements with high and low adhesion coefficients. The results show that on both pavement types, the proposed control strategy effectively reduces vehicle lateral acceleration and lateral load transfer while maintaining tracking accuracy, decreases maximum tire adhesion rate, and improves driving stability, achieving ideal control performance for heavy-duty AGV.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, W.; Meng, W. An Efficient Genetic Algorithm for Multi AGV Scheduling Problem about Intelligent Warehouse. Robot. Intell. Automat. 2023, 43, 382–393. [Google Scholar] [CrossRef]
- Li, K.; Liu, T.; Kumar, P.N.R.; Han, X. A Reinforcement Learning-Based Hyper-Heuristic for AGV Task Assignment and Route Planning in Parts-to-Picker Warehouses. Transp. Res. Part E Logist. Transp. Rev. 2024, 185, 103518. [Google Scholar] [CrossRef]
- Liu, W.; Wan, Y.; Zhang, Q.; Yu, Y.; Liu, P.; Shi, Z. Trajectory Tracking Control of Four-Wheel Steering Automatic Guided Vehicle under the Working Condition of Moving Centroid. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 691–705. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q. A Branch-and-Bound Approach for AGV Dispatching and Routing Problems in Automated Container Terminals. Comput. Ind. Eng. 2022, 166, 107968. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, S.; He, Y. Wheel Design and Motion Analysis of a New Heavy-Duty AGV in Aircraft Assembly Lines. Assem. Autom. 2020, 40, 387–397. [Google Scholar] [CrossRef]
- Udengaard, M.; Iagnemma, K. Analysis, Design, and Control of an Omnidirectional Mobile Robot in Rough Terrain. J. Mech. Des. 2009, 131, 121002. [Google Scholar] [CrossRef]
- Wang, K.; Liang, W.; Shi, H.; Zhang, J.; Wang, Q. Driving Line-Based Two-Stage Path Planning in the AGV Sorting System. Robot. Auton. Syst. 2023, 169, 104505. [Google Scholar] [CrossRef]
- Yu, R.; Zhao, H.; Zhen, S.; Huang, K.; Chen, X.; Sun, H.; Shao, K. A Novel Trajectory Tracking Control of AGV Based on Udwadia-Kalaba Approach. IEEE/CAA J. Autom. Sin. 2024, 11, 1069–1071. [Google Scholar] [CrossRef]
- Li, S.; Fan, L.; Jia, S. A Hierarchical Solution Framework for Dynamic and Conflict-Free AGV Scheduling in an Automated Container Terminal. Transp. Res. Part C Emerg. Technol. 2024, 165, 104724. [Google Scholar] [CrossRef]
- Fu, W.J.; Liu, Y.; Zhang, X.M. Research on Accurate Motion Trajectory Control Method of Four-Wheel Steering AGV Based on Stanley-PID Control. Sensors 2023, 23, 7219. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Q.; Jiang, J.; Lu, X.; Yu, Z. MPC-Based Motion Control of AGV with Improved A* and Artificial Potential Field. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 239, 1035–1044. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, J.; Tu, X.-W.; Yang, A.-L.; Fei, M.-R. Real-Time Predictive Sliding Mode Control Method for AGV with Actuator Delay. Adv. Manuf. 2019, 7, 448–459. [Google Scholar] [CrossRef]
- Lee, M.-Y.; Chen, B.-S. Robust H∞ Network Observer-Based Attack-Tolerant Path Tracking Control of Autonomous Ground Vehicle. IEEE Access 2022, 10, 58332–58353. [Google Scholar] [CrossRef]
- Li, W.; Yu, S.; Tan, L.; Li, Y.; Chen, H.; Yu, J. Integrated Control of Path Tracking and Handling Stability for Autonomous Ground Vehicles with Four-Wheel Steering. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 239, 315–326. [Google Scholar] [CrossRef]
- Wang, T.T.; Dong, R.Y.; Zhang, R.; Qin, D.C. Research on Stability Design of Differential Drive Fork-Type AGV Based on PID Control. Electronics 2020, 9, 1072. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Song, Z.B. Adaptive Sliding Mode Trajectory Tracking Control for Wheeled Mobile Robots. Int. J. Control 2019, 92, 2255–2262. [Google Scholar] [CrossRef]
- Wu, X.; Jin, P.; Zou, T.; Qi, Z.Y.; Xiao, H.N.; Lou, P.H. Backstepping Trajectory Tracking Based on Fuzzy Sliding Mode Control for Differential Mobile Robots. J. Intell. Robot. Syst. 2019, 96, 109–121. [Google Scholar] [CrossRef]
- Zhang, K.W.; Sun, Q.; Shi, Y. Trajectory Tracking Control of Autonomous Ground Vehicles Using Adaptive Learning MPC. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5554–5564. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, H.; Can, N.K.; Ozguney, O.C.; Yagiz, N. Sliding Mode Control of a Line Following Robot. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 561. [Google Scholar] [CrossRef]
- Han, Y.X.; Cheng, Y.; Xu, G.W. Trajectory Tracking Control of AGV Based on Sliding Mode Control With the Improved Reaching Law. IEEE Access 2019, 7, 20748–20755. [Google Scholar] [CrossRef]
- Wang, D.; Wei, W.; Yeboah, Y.; Li, Y.; Gao, Y. A Robust Model Predictive Control Strategy for Trajectory Tracking of Omni-directional Mobile Robots. J. Intell. Robot. Syst. 2020, 98, 439–453. [Google Scholar] [CrossRef]
- Xing, B.; Xu, E.; Wei, J.; Meng, Y. Recurrent Neural Network Non-Singular Terminal Sliding Mode Control for Path Following of Autonomous Ground Vehicles with Parametric Uncertainties. IET Intell. Transp. Syst. 2022, 16, 616–629. [Google Scholar] [CrossRef]
- Liu, K.; Gao, H.; Ji, H.; Hao, Z. Adaptive Sliding Mode Based Disturbance Attenuation Tracking Control for Wheeled Mobile Robots. Int. J. Control Autom. Syst. 2020, 18, 1288–1298. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; He, W.; Qiao, H.; Ji, H. Adaptive-Neural-Network-Based Trajectory Tracking Control for a Nonholonomic Wheeled Mobile Robot With Velocity Constraints. IEEE Trans. Ind. Electron. 2021, 68, 5057–5067. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, K.; Zhang, W.; Jin, X. A Velocity-Adaptive MPC-Based Path Tracking Method for Heavy-Duty Forklift AGVs. Machines 2024, 12, 558. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G. Simulation and Test of Stability Control for Distributed Drive Electric Vehicles. Automot. Eng. 2019, 41, 792–799. [Google Scholar]
- Fu, W.; Wang, X.; Zhang, X. Rollover Stability of Heavy-Duty AGVs in Turns Considering Variation in Friction Coefficient. Lubricants 2023, 11, 119. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, W.; Liu, P. Fault-Tolerant Control of Automated Guided Vehicle Under Centroid Variation. IEEE Access 2022, 10, 68995–69009. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Q.; Wan, Y.; Liu, P.; Yu, Y.; Guo, J. Yaw Stability Control of Automated Guided Vehicle under the Condition of Centroid Variation. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 18. [Google Scholar] [CrossRef]
- Liu, X.; Wang, G.; Chen, K. Nonlinear Model Predictive Tracking Control With C/GMRES Method for Heavy-Duty AGVs. IEEE Trans. Veh. Technol. 2021, 70, 12567–12580. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yang, C.-C.; Hung, J.Y. Path Tracking of an Autonomous Ground Vehicle With Different Payloads by Hierarchical Improved Fuzzy Dynamic Sliding-Mode Control. IEEE Trans. Fuzzy Syst. 2018, 26, 899–914. [Google Scholar] [CrossRef]
- Sun, Z.; Xie, H.; Zheng, J.; Man, Z.; He, D. Path-Following Control of Mecanum-Wheels Omnidirectional Mobile Robots Using Nonsingular Terminal Sliding Mode. Mech. Syst. Signal Proc. 2021, 147, 107128. [Google Scholar] [CrossRef]
- Liu, W.; Yu, Y.; Wan, Y. Rollover Control of AGV Combined with Differential Drive, Active Steering, and Centroid Adjustment under Slope Driving Condition. Math. Probl. Eng. 2022, 2022, 9331756. [Google Scholar] [CrossRef]
- Nguyen, V.; Schultz, G.; Balachandran, B. Lateral Load Transfer Effects on Bifurcation Behavior of Four-Wheel Vehicle System. J. Comput. Nonlinear Dyn. 2009, 4, 041007. [Google Scholar] [CrossRef]
- Yue, M.; Yang, L.; Sun, X.-M.; Xia, W. Stability Control for FWID-EVs With Supervision Mechanism in Critical Cornering Situations. IEEE Trans. Veh. Technol. 2018, 67, 10387–10397. [Google Scholar] [CrossRef]
- Mutoh, N. Driving and Braking Torque Distribution Methods for Front- and Rear-Wheel-Independent Drive-Type Electric Vehicles on Roads With Low Friction Coefficient. IEEE Trans. Ind. Electron. 2012, 59, 3919–3933. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P. Wheel Torque Distribution Criteria for Electric Vehicles With Torque-Vectoring Differentials. IEEE Trans. Veh. Technol. 2014, 63, 1593–1602. [Google Scholar] [CrossRef]
- Yu, Z.; Xia, Q. Automobile Theory, 6th ed.; China Machine Press: Beijing, China, 2018; pp. 114–120. [Google Scholar]
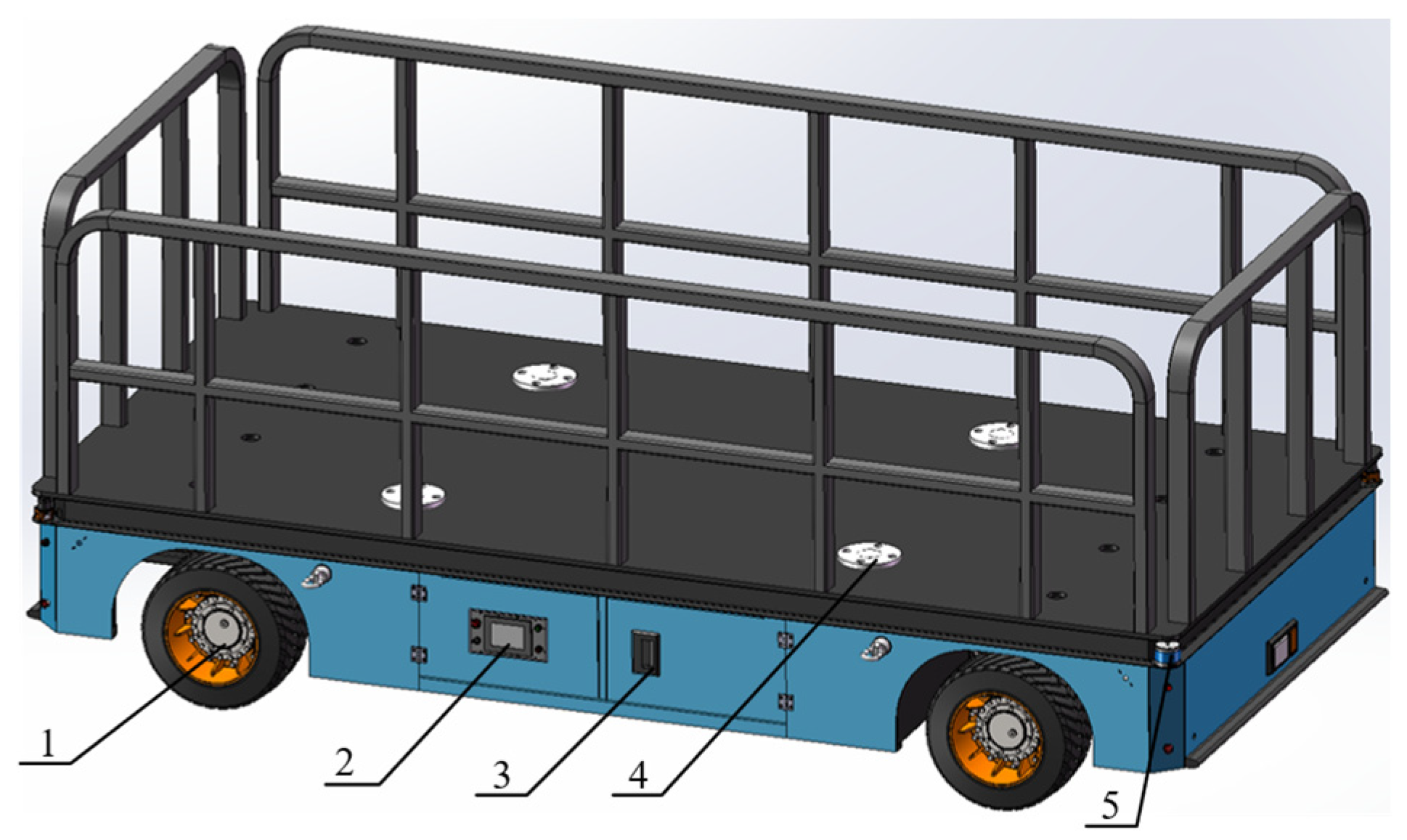




| Parameter | Unit | Value |
|---|---|---|
| Overall size (length/width/height) | m | 5/2.4/0.6 |
| wheelbase | m | 3 |
| wheel track | m | 2.1 |
| dead weight | t | 5 |
| load | t | 20 |
| reference speed | m/s | 0.5 |
| Name | Trajectory Tracking Method | Torque Distribution Method |
|---|---|---|
| PID-TED | PID | Torque Equal Distribution |
| MPC-TED | MPC | Torque Equal Distribution |
| IMPC-TED | IMPC | Torque Equal Distribution |
| MPC-TPD | MPC | Torque Proportional Distribution |
| IMPC-TPD | IMPC | Torque Proportional Distribution |
| PID-TED | PID | Torque Equal Distribution |
| Control Strategy | |eX|max/m | |eY|max/m | |eYaw|max/m | |ay|max/(m/s2) | Cmax | |
|---|---|---|---|---|---|---|
| PID | PID-TED | 0.2272 | 0.2419 | 0.0816 | 0.0502 | 0.2102 |
| MPC | MPC-TED | 0.2947 | 0.2132 | 0.0808 | 0.0502 | 0.2087 |
| MPC-TPD | 0.1846 | |||||
| IMPC | IMPC-TED | 0.2947 | 0.2492 | 0.0823 | 0.0403 | 0.2087 |
| IMPC-TPD | 0.1846 | |||||
| comparison | IMPC and PID | 29.7% | 3.0% | 0.9% | −19.7% | - |
| IMPC and MPC | 0 | 16.9% | 1.9% | −19.7% | - | |
| TPD and TED | - | - | - | - | −11.5% | |
| Control Strategy | |eX|max/m | |eY|max/m | |eYaw|max/m | |ay|max/(m/s2) | Cmax | |
|---|---|---|---|---|---|---|
| PID | PID-TED | 0.2273 | 0.2419 | 0.0816 | 0.0502 | 0.8934 |
| MPC | MPC-TED | 0.2947 | 0.2132 | 0.0808 | 0.0502 | 0.8871 |
| MPC-TPD | 0.7847 | |||||
| IMPC | IMPC-TED | 0.2947 | 0.2492 | 0.0823 | 0.0403 | 0.8871 |
| IMPC-TPD | 0.7847 | |||||
| comparison | IMPC and PID | 29.7% | 3.0% | 0.9% | −19.7% | - |
| IMPC and MPC | 0 | 16.9% | 1.9% | −19.7% | - | |
| TPD and TED | - | - | - | - | −11.5% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, S.; Chen, X.; Liu, B.; Wang, C.; Su, Y. Trajectory Tracking Control Strategy of 20-Ton Heavy-Duty AGV Considering Load Transfer. Appl. Sci. 2025, 15, 4512. https://doi.org/10.3390/app15084512
Li X, Chen S, Chen X, Liu B, Wang C, Su Y. Trajectory Tracking Control Strategy of 20-Ton Heavy-Duty AGV Considering Load Transfer. Applied Sciences. 2025; 15(8):4512. https://doi.org/10.3390/app15084512
Chicago/Turabian StyleLi, Xia, Shengzhan Chen, Xiaojie Chen, Benxue Liu, Chengming Wang, and Yufeng Su. 2025. "Trajectory Tracking Control Strategy of 20-Ton Heavy-Duty AGV Considering Load Transfer" Applied Sciences 15, no. 8: 4512. https://doi.org/10.3390/app15084512
APA StyleLi, X., Chen, S., Chen, X., Liu, B., Wang, C., & Su, Y. (2025). Trajectory Tracking Control Strategy of 20-Ton Heavy-Duty AGV Considering Load Transfer. Applied Sciences, 15(8), 4512. https://doi.org/10.3390/app15084512





