Effect of Surface Texture Depth with Various Geometric Shapes on the Steady-State Performance and Dynamic Stability of Noncircular Lobed Journal Bearings
Abstract
1. Introduction
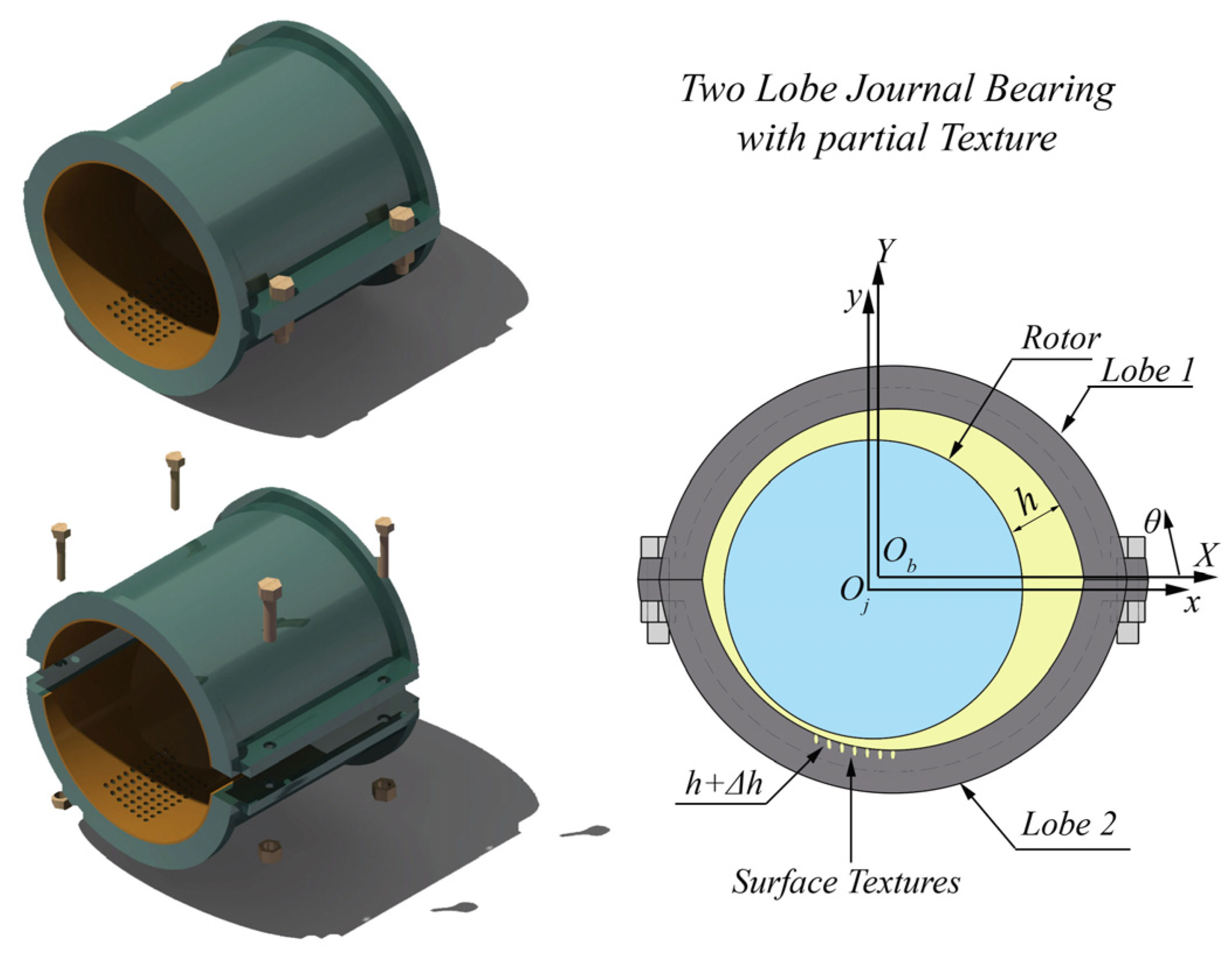
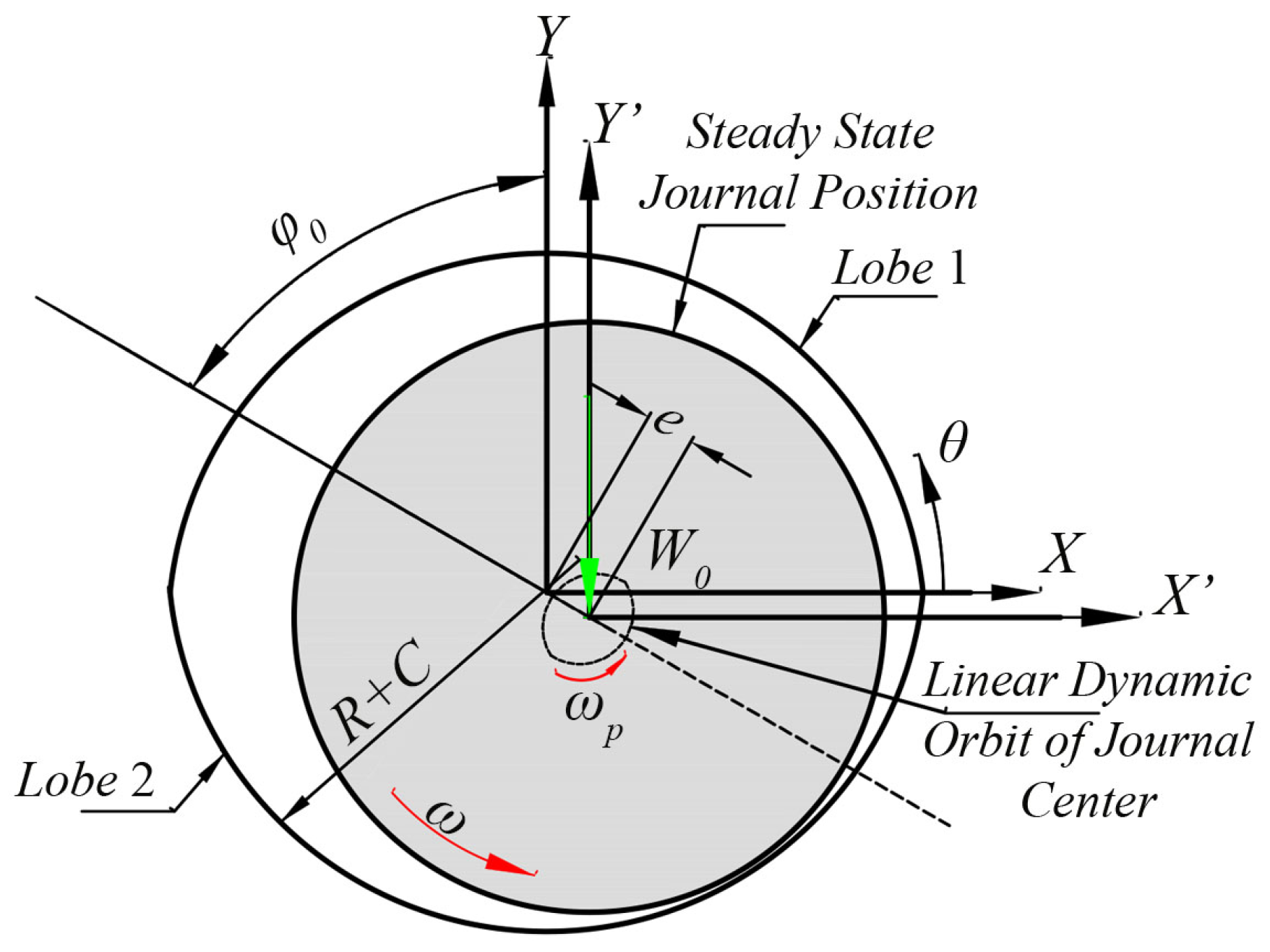
2. Theory
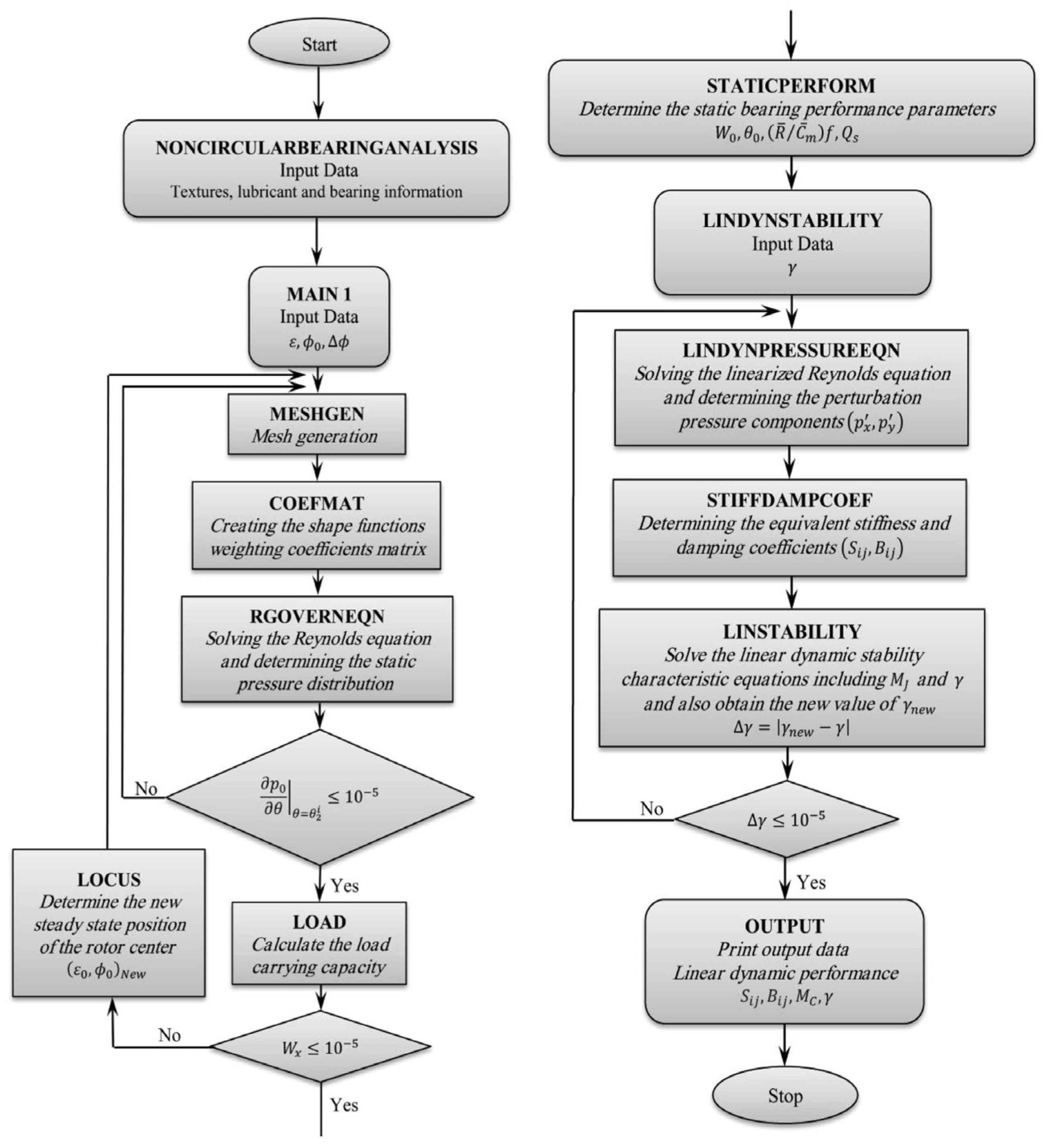
3. Governing Equations
3.1. Reynolds Equation
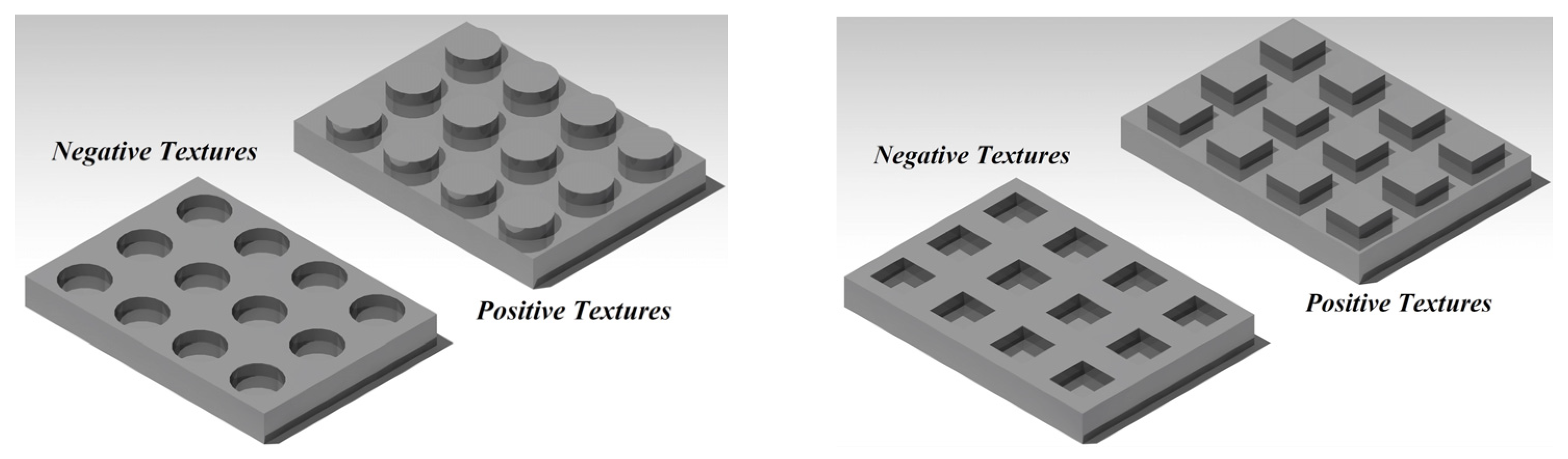
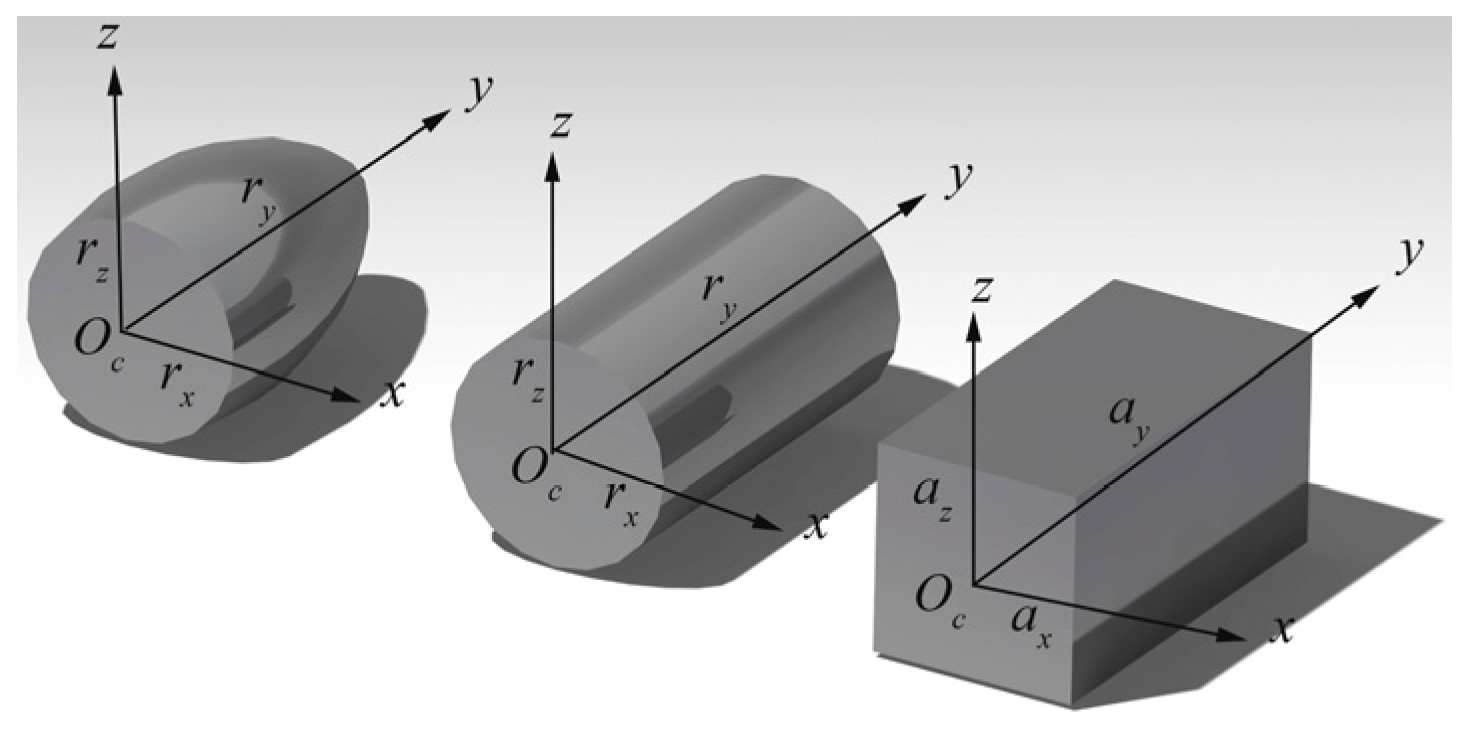
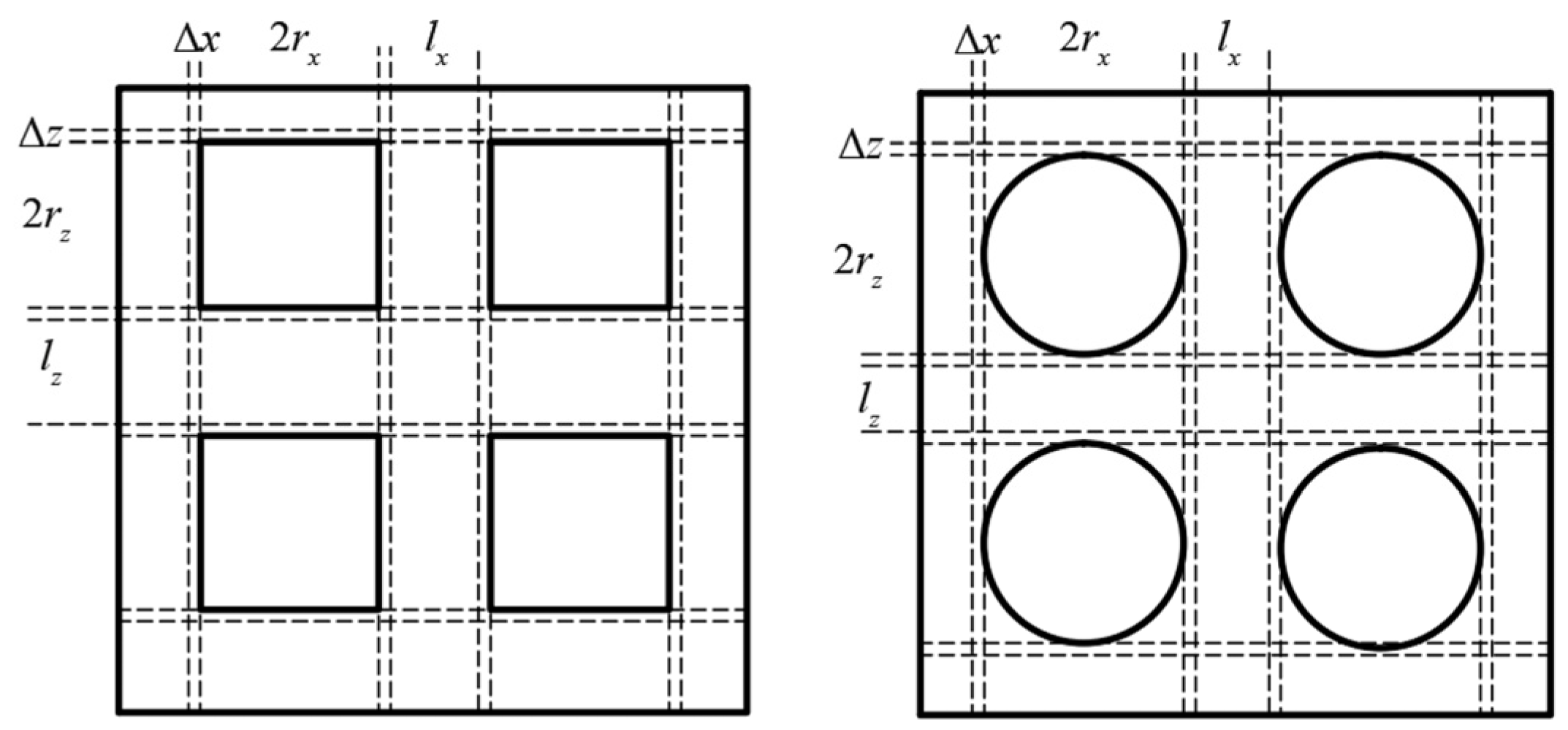
3.2. The Geometric Shape of the Utilized Textures
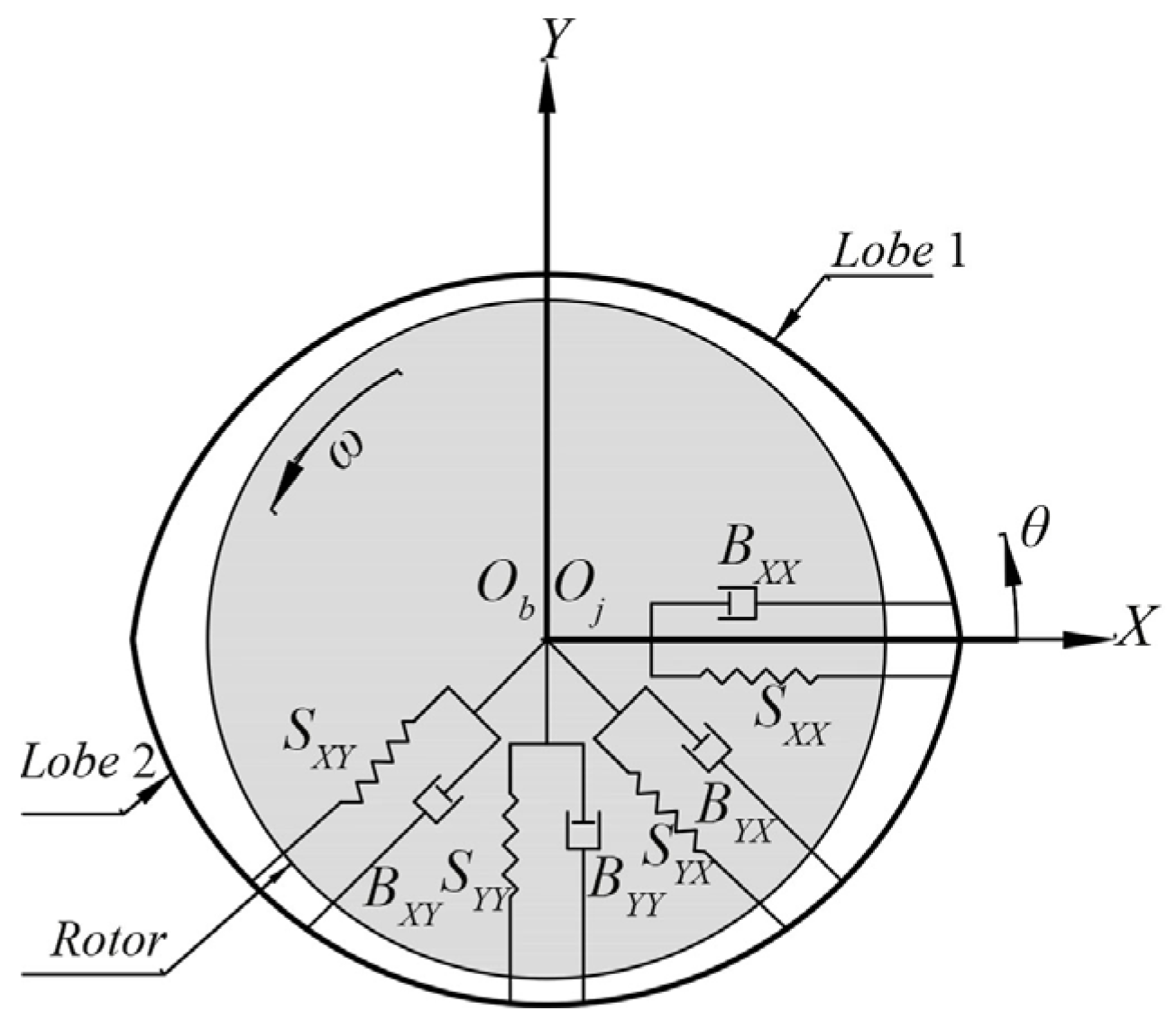
3.3. Dynamic Behavior Analysis of Rotor Using a Linear Model
3.4. Static Performance Characteristics of the Lobed Bearing
3.4.1. Load Carrying Capacity
3.4.2. Attitude Angle
3.5. Dynamic Stability of Bearings Based on the Linear Model
4. Results and Discussion
5. Conclusions
- 1.
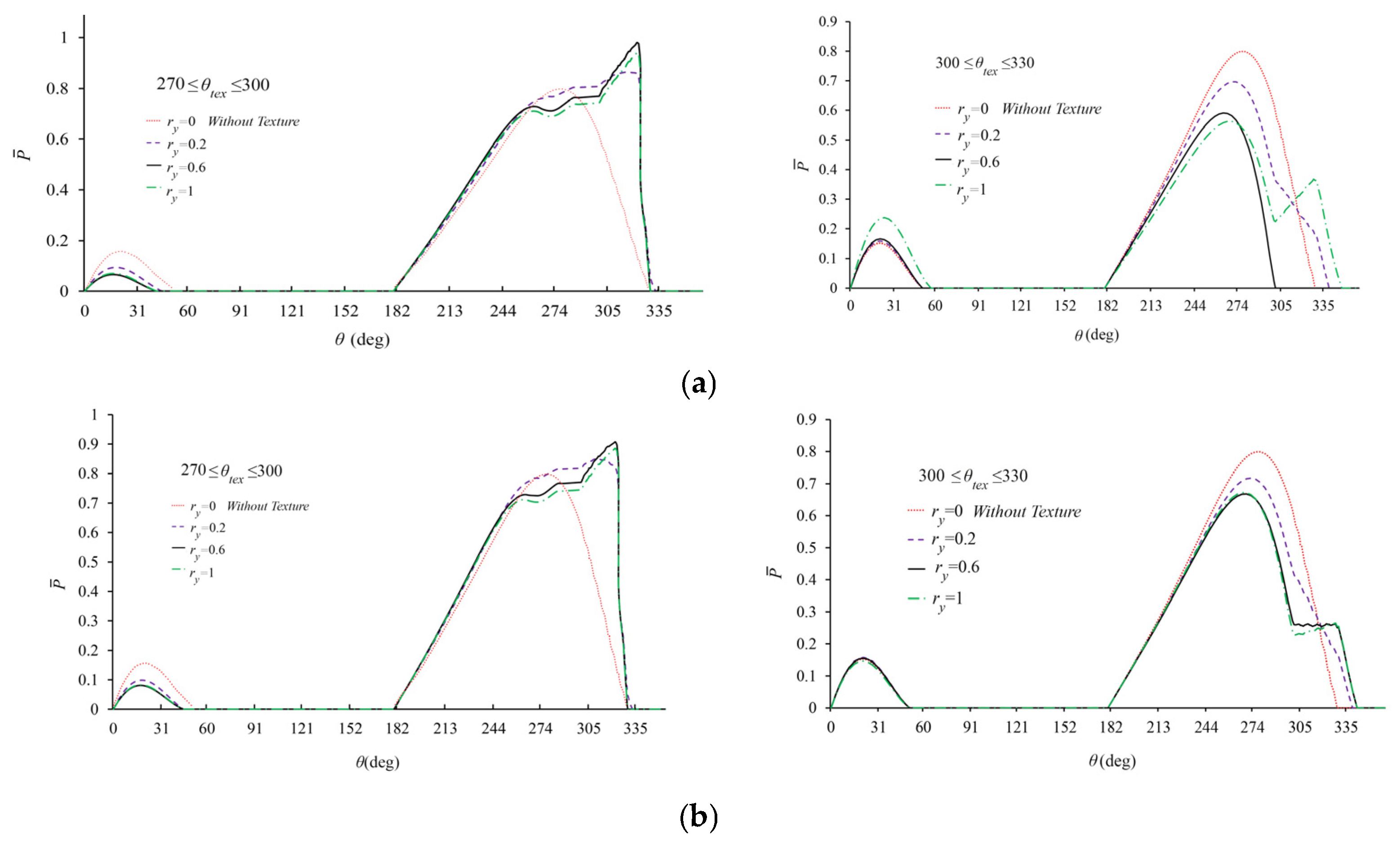
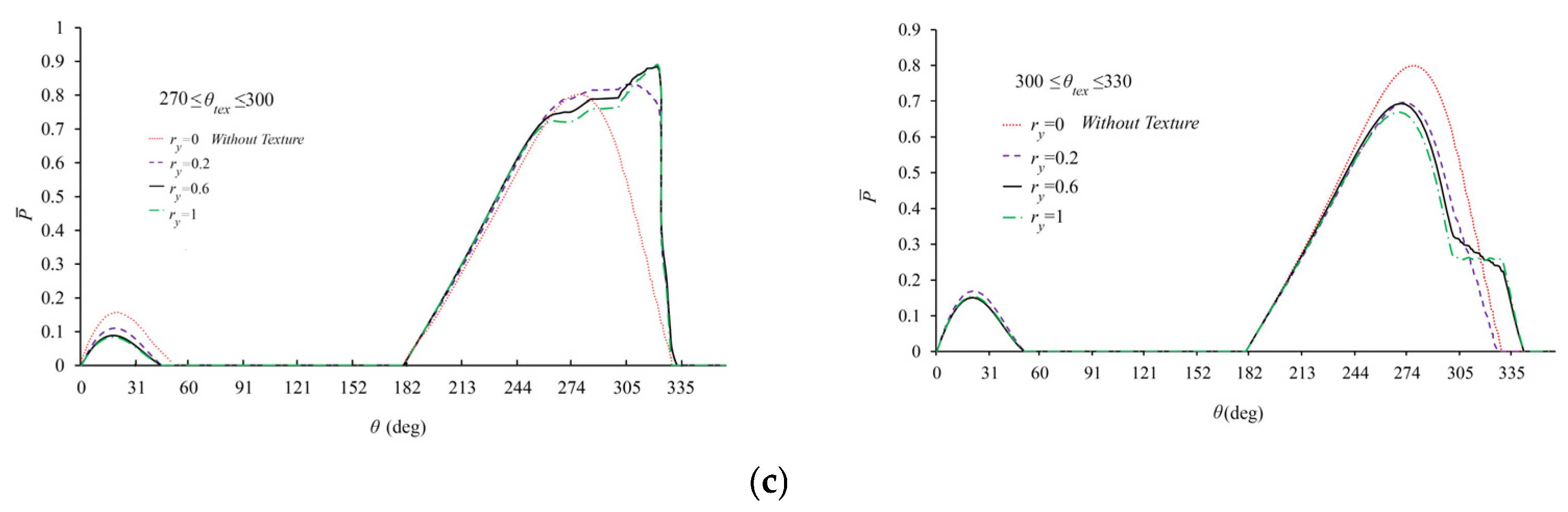
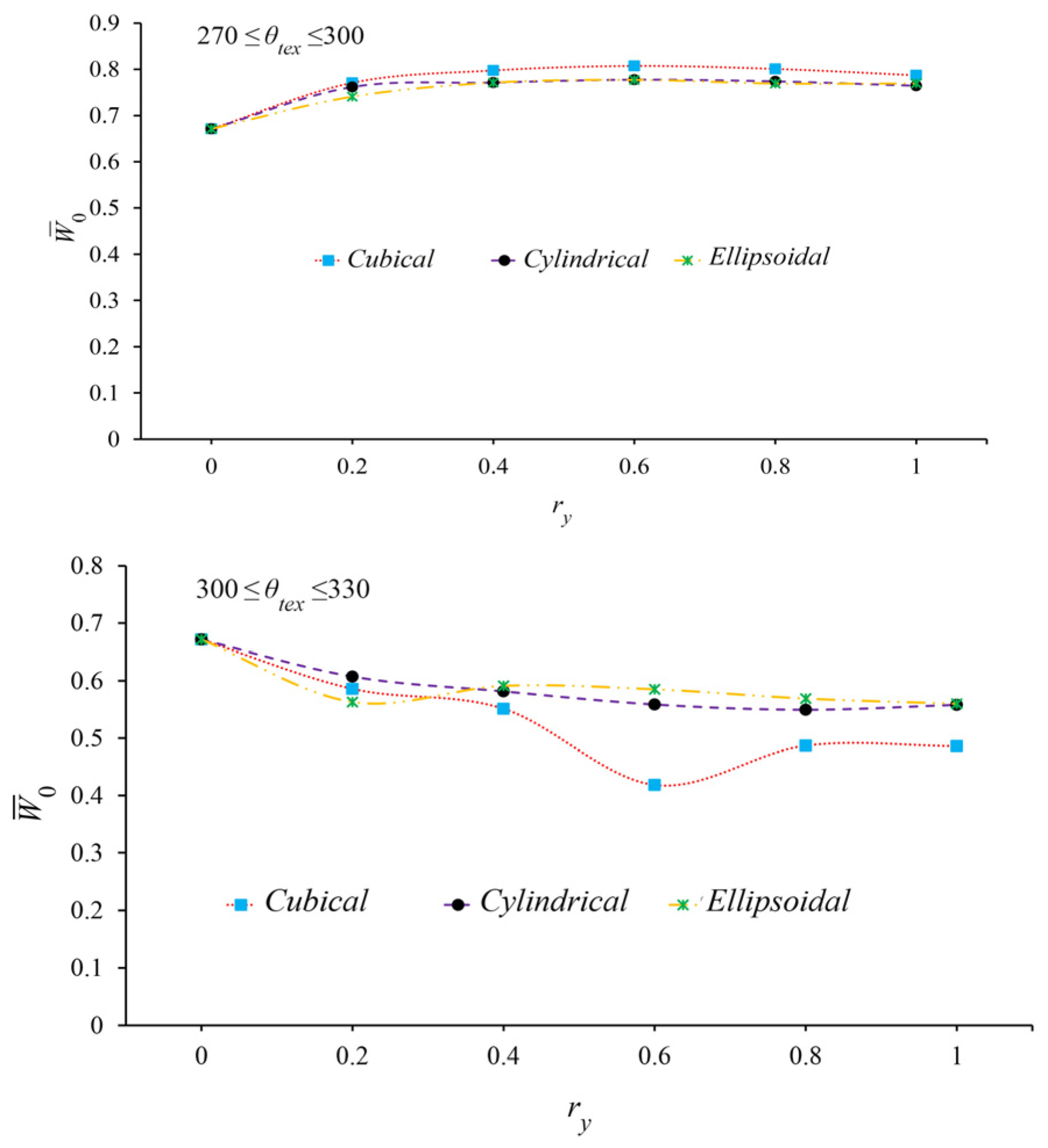
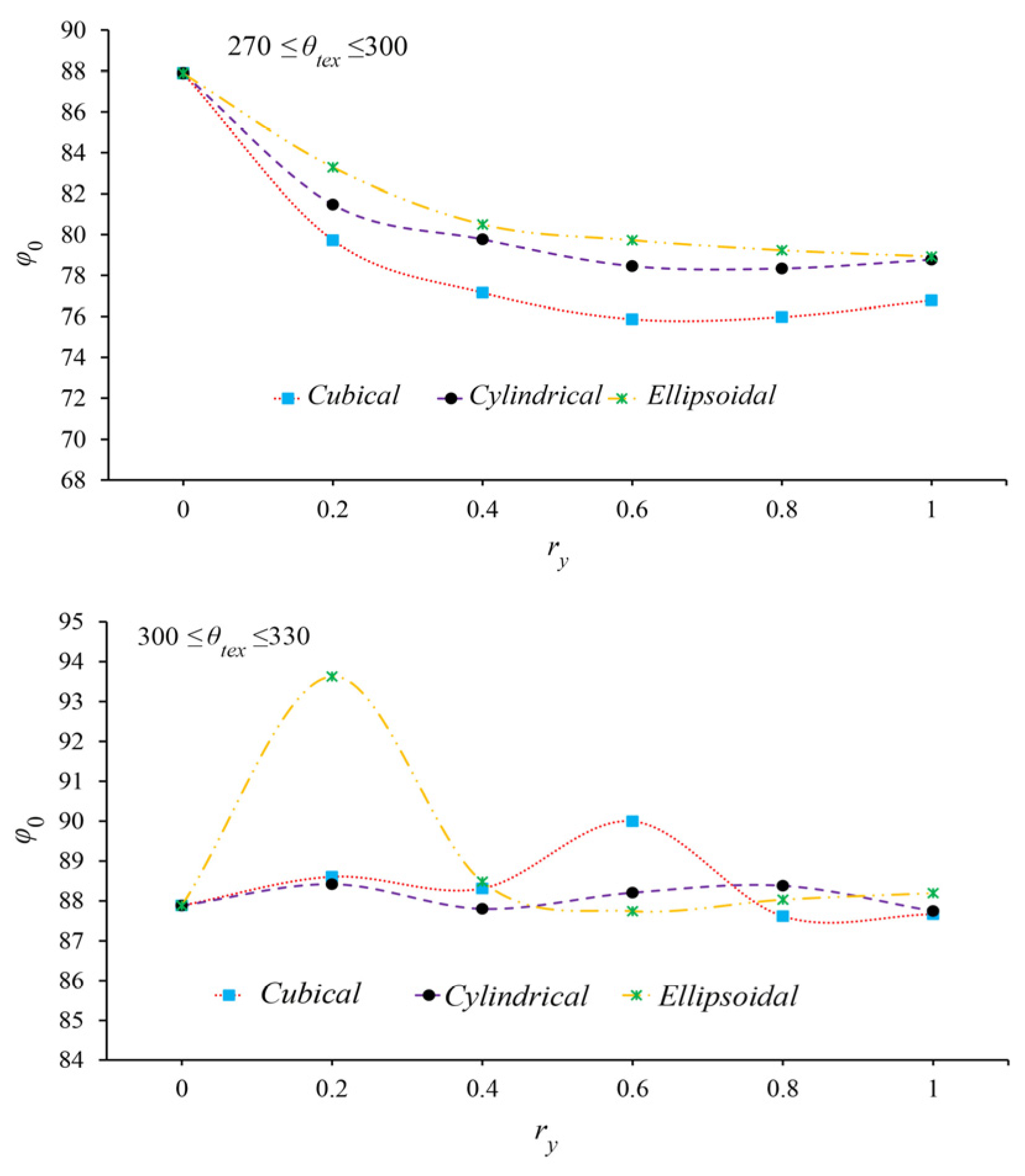
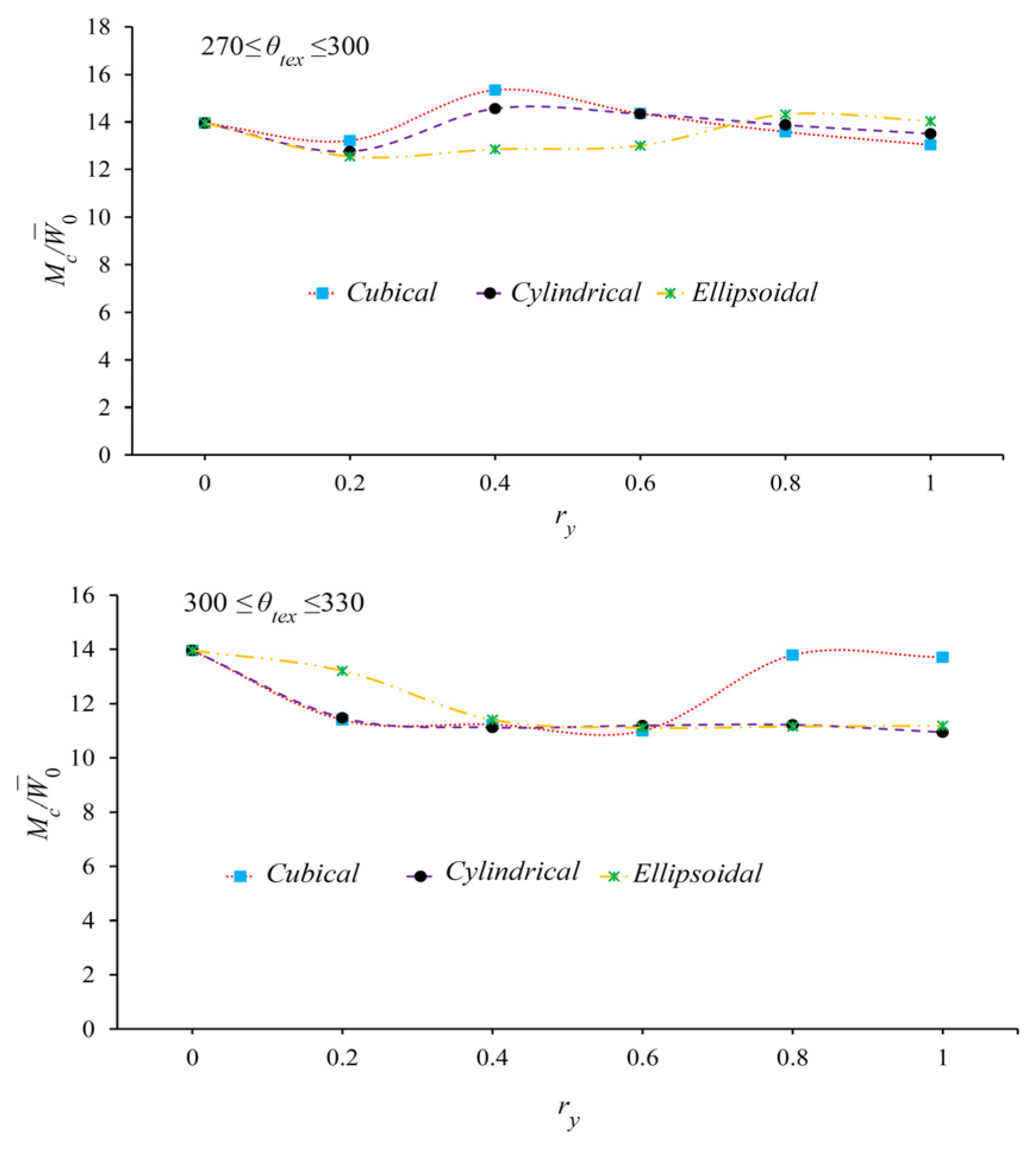
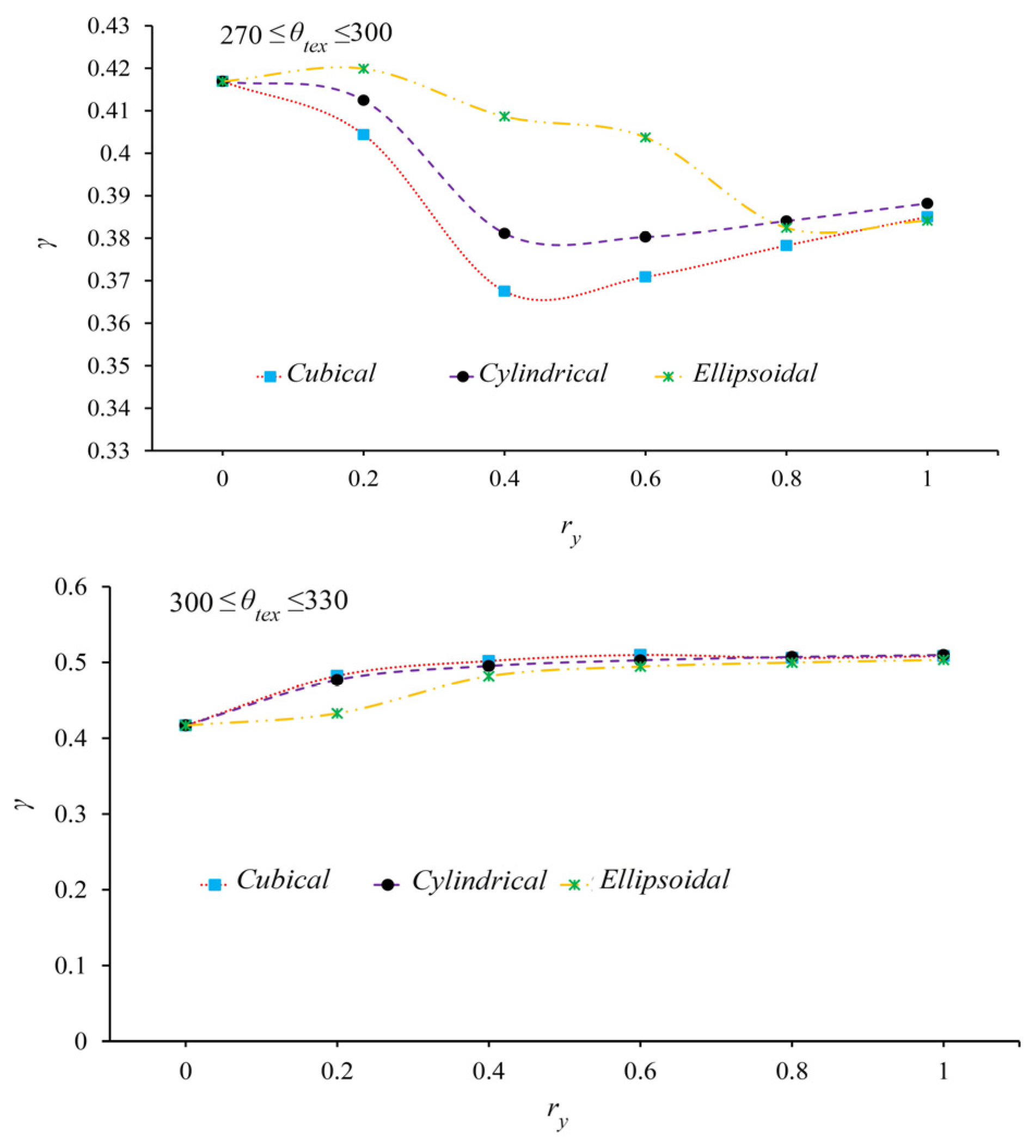
- Among the tested surface textures, cubic patterns demonstrated the most significant impact on both static and dynamic performance of two-lobe bearings, particularly when positioned at 270–300° in the high-pressure region of the lower lobe. Cylindrical and semi-ellipsoidal textures followed in effectiveness, respectively.
- 2.
- The improvement trend of two-lobe bearing performance parameters—including load capacity, critical mass, and whirling frequency reduction—with increasing texture depth is not monotonic. Beyond a geometry-dependent critical depth, the enhancement rate decreases or even reverses.
- 3.
- Cubic textures achieve maximum performance improvements in two-lobe bearings at shallower depths compared to other patterns. The optimal dimensionless depth range for cubic textures falls between 0.4 and 0.5, while cylindrical and semi-ellipsoidal textures require greater depths for peak performance.
- 4.
- The linear dynamic model demonstrates that implementing surface textures while maintaining constant bearing design parameters effectively controls rotor disturbances and reduces surface wear/collisions by enhancing the stability through increased critical mass and reduced whirling frequency. This performance enhancement is more pronounced with cubic textures compared to cylindrical and semi-ellipsoidal patterns.
- 5.
- Surface texturing in low-pressure bearing regions (such as the 300–330° zone of the lower lobe or cavitation areas of the lubricant film) demonstrates negligible performance enhancement and proves economically inefficient. However, computer-aided optimization of texture location, geometry, and depth can achieve peak operational performance of two-lobe bearings while simultaneously reducing both manufacturing and maintenance costs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Conventional radial clearance, | Local coordinate of textures | ||
| Minor clearance when journal and bearing centers are coincident, | Steady state position of rotor center with respect to Cartesian axes | ||
| Bearing diameter, | Greek symbols | ||
| Lubricant film thickness, | |||
| Bearing length, | Eccentricity ratio | ||
| Bearing center | Absolute viscosity of the Newtonian fluid, | ||
| Center of the surface textures | Bearing aspect ratio, | ||
| Journal center | Preload of the bearing, | ||
| Nondimensional critical mass parameter | Angle of journal and bearing line of centers with axis | ||
| Fluid film pressure, | angle at leading and ending edge of the ith lobe | ||
| Perturbed component of fluid film pressure, | Angular velocity of the rotor, | ||
| Journal radius, | Angular velocity of the rotor center perturbations, | ||
| The radius and depth of surface texture along the Cartesian coordinate axis, | Angular coordinate measured from axis | ||
| Time, | Whirl frequency ratio, | ||
| Journal velocity, | Subscripts and superscripts | ||
| Steady state resultant load carrying capacity, | |||
| Lubricant force components along the and axes | Subscript or superscript for lobedesignation, | ||
| Cartesian axes with respect to geometric center of bearing | Subscripts and superscript indicating the directions of Cartesian axes | ||
| Perturbed component of rotor center motion along the Cartesian axes measured from static equilibrium point | 0 | Steady state position of rotor and journal bearing | |
Appendix A
| Symbol | Variable | Value | Unit |
|---|---|---|---|
| Density of oil lubricant | 868 | ||
| Oil film viscosity | 0.065 | ||
| Bearing length | 0.1 | ||
| Journal radius | 0.05 | ||
| Minimum clearance width | |||
| Angular speed of rotor | 3000 |
| Quantity | Unit | Parametric Coefficients | Nondimensional Form | Numerical Coefficients |
|---|---|---|---|---|
| 3,545,200.043 | ||||
| 8863.000108 | ||||
| 73,858,334.23 | ||||
| 235,098.3796 | ||||
| 748.3413846 | ||||
| 314.1592654 |
References
- Etsion, I.; Burstein, L. A model for mechanical seals with regular microsurface structure. Tribol. Trans. 1996, 39, 677–683. [Google Scholar] [CrossRef]
- Ausas, R.; Ragot, P.; Leiva, J.; Jai, M.; Bayada, G.; Buscaglia, G.C. The impact of the cavitation model in the analysis of microtextured lubricated journal bearings. J. Tribol. 2007, 129, 868–875. [Google Scholar] [CrossRef]
- Sinanoglu, C. Investigation of load carriage capacity of journal bearings by surface texturing. Ind. Lubr. Tribol. 2009, 61, 261–270. [Google Scholar] [CrossRef]
- Kango, S.; Sharma, R.K. Studies on the influence of surface texture on the performance of hydrodynamic journal bearing using power law model. Int. J. Surf. Sci. Eng. 2010, 4, 505–524. [Google Scholar] [CrossRef]
- Rao, T.V.V.L.N.; Rani, A.M.A.; Nagarajan, T.; Hashim, F.M. Analysis of slider and journal bearing using partially textured slip surface. Tribol. Int. 2012, 56, 121–128. [Google Scholar] [CrossRef]
- Chan, C.W.; Han, Y.F.; Wang, Z.; Wang, J.; Shi, F.; Wang, N.; Wang, Q.J. Exploration on a fast EHL computing technology for analyzing journal bearings with engineered surface textures. Tribol. Trans. 2014, 57, 206–215. [Google Scholar] [CrossRef]
- Lin, Q.; Wei, Z.; Wang, N.; Chen, W. Effect of large-area texture/slip surface on journal bearing considering cavitation. Ind. Lubr. Tribol. 2015, 67, 216–226. [Google Scholar] [CrossRef]
- Yu, R.; Li, P.; Chen, W. Study of grease lubricated journal bearing with partial surface texture. Ind. Lubr. Tribol. 2016, 68, 149–157. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Zhang, D.; Xie, Y. Transient analysis of the textured journal bearing operating with the piezoviscous and shear-thinning fluids. J. Tribol. 2017, 139, 051708. [Google Scholar] [CrossRef]
- Senator, A.; Rao, T.V.V.L.N. Partial slip texture slider and journal bearing lubricated with Newtonian fluids: A review. J. Tribol. 2018, 140, 040810. [Google Scholar] [CrossRef]
- Sharma, S.; Jamwal, G.; Awasthi, R.K. Numerical study on steady state performance enhancement of partial textured hydrodynamic journal bearing. Ind. Lubr. Tribol. 2019, 71, 1055–1063. [Google Scholar] [CrossRef]
- Mo, F.; Shen, C.; Zhou, J.; Khonsari, M.M. Statistical Analysis of the Influence of Imperfect Texture Shape and Dimensional Uncertainty on Surface Texture Performance. IEEE Access 2017, 5, 27023–27035. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic Lubrication of Textured Surfaces: A Review of Modeling Techniques and Key Findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Mehrjardi, M.Z.; Rahmatabadi, A.D.; Meybodi, R.R. A study on the stability performance of noncircular lobed journal bearings with micropolar lubricant. J. Eng. Tribol. 2016, 230, 14–30. [Google Scholar] [CrossRef]
- Rahmani, F.; Makki, E.; Giri, J. Influence of bearing wear on the stability and modal characteristics of a flexible rotor supported on powder-lubricated journal bearings. Lubricants 2023, 11, 355. [Google Scholar] [CrossRef]
- Xie, Z.; Tian, Y.; Liu, S.; Ma, W.; Gao, W.; Du, P.; Zhao, B. Fluid-structure interaction analysis of a novel water-lubricated bearing with particle-dynamic effect: Theory and experiment. Tribol. Int. 2025, 204, 110474. [Google Scholar] [CrossRef]
- Zare Mehrjardi, M. Dynamic stability analysis of noncircular two-lobe journal bearings with couple stress lubricant regime. J. Eng. Tribol. 2020, 235, 1150–1167. [Google Scholar] [CrossRef]
- Sun, L.; Shi, J.; Jiang, T.; Li, Z.; Xie, Q.; Liu, Z.; Xu, W. Stability analysis of the rotor-journal bearing system considering shear and gaseous cavitation. Lubricants 2024, 12, 48. [Google Scholar] [CrossRef]
- Hong, S.H.; Jeon, W.J. Lubrication performance of misaligned journal bearings with flexible structure under shock load conditions. Lubricants 2023, 11, 500. [Google Scholar] [CrossRef]
- Xie, Z.; Yang, K.; Yang, M.; Zhao, B.; Du, P.; Xu, J. The anti-random impact performances of a novel propulsive bearing-shaft system: Theory and experiment. Mech. Syst. Signal Process. 2025, 225, 112309. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.; Wang, X.; Xie, F.; Wu, S. Study on fault mechanism and dynamics of spur gear pair with time-varying backlash. Nonlinear Dyn. 2024, 112, 14853–14877. [Google Scholar] [CrossRef]
- Zhou, K.; Wen, L.; Gong, D.; Zhou, J.; Chen, Y. Vibro-acoustic analysis and suppression of corrugated sandwich panel structures with general boundary conditions. Thin-Walled Struct. 2025, 212, 113196. [Google Scholar] [CrossRef]
- Babak, V.; Babak, S.; Zaporozhets, A. Stochastic Models of Diagnostic Signals Arising During the Operation of Electrical Equipment. In Statistical Diagnostics of Electric Power Equipment; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2025; Volume 573, pp. 75–122. [Google Scholar]
- Babak, V.; Zaporozhets, A.; Kuts, Y.; Fryz, M.; Scherbak, L. Identification of Vibration Noise Signals of Electric Power Facilities. In Noise Signals; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2025; Volume 567, pp. 143–170. [Google Scholar]
- Sharma, S.; Jamwal, G.; Awasthi, K.R. Dynamic and stability performance improvement of the hydrodynamic bearing by using triangular-shaped textures. J. Eng. Tribol. 2020, 234, 1436–1451. [Google Scholar] [CrossRef]
- Ramos, L.I.; Ramos, D.J.; Daniel, G.B. Evaluation of textured journal bearings under dynamic operating conditions in rotating machinery. J. Eng. Tribol. 2020, 234, 842–857. [Google Scholar] [CrossRef]
- Han, Y.; Fu, Y. Influence of micro-grooves on the lubrication performance of a misaligned bearing. J. Eng. Tribol. 2020, 234, 887–899. [Google Scholar] [CrossRef]
- Tomar, A.K.; Sharma, S.C. An investigation into surface texture effect on hole-entry hybrid spherical journal bearing performance. Tribol. Int. 2020, 151, 106417. [Google Scholar] [CrossRef]
- Rao, T.V.V.L.N.; Rani, A.M.A.; Mohamed, N.M.; Ya, H.H.; Awang, M.; Hashim, F.M. Analysis of journal bearing with partial texture lubricated using micropolar and power-law fluids. In Tribology in Materials and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 211–225. [Google Scholar]
- Manser, B.; Belaidi, I.; Khelladi, S.; Chikh, M.A.A.; Deligant, M.; Bakir, F. Computational investigation on the performance of hydrodynamic micro-textured journal bearing lubricated with micropolar fluid using mass-conserving numerical approach. J. Eng. Tribol. 2020, 234, 1310–1331. [Google Scholar] [CrossRef]
- Awasthi, R.K.; Maan, J.S. Influence of surface texture on the performance of hydrodynamic journal bearing operating under turbulent regime. Tribol. Online 2021, 16, 99–112. [Google Scholar] [CrossRef]
- Nie, T.; Yang, K.; Zhou, L.; Wu, X.; Wang, Y. CFD analysis of load capacity of journal bearing with surface texture. Energy Rep. 2022, 8, 327–334. [Google Scholar] [CrossRef]
- Mishra, S.; Aggarwal, S. A review of performance of textured journal bearing. Tribol. Online 2023, 18, 494–507. [Google Scholar] [CrossRef]
- Singh, S.; Kango, S. Effect of sliding speed on the thermohydrodynamic performance of partially slip-textured slider bearings. Lubr. Sci. 2023, 35, 574–595. [Google Scholar] [CrossRef]
- Wang, H.; Bie, W.; Zhang, S.; Liu, T. Theoretical and experimental study of friction characteristics of textured journal bearing. Micromachines 2023, 14, 577. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jacobs, G.; König, F.; Zhang, S.; von Goeldel, S. Investigation of microflow effects in textures on hydrodynamic performance of journal bearings using CFD simulations. Lubricants 2023, 11, 20. [Google Scholar] [CrossRef]
- Wang, L.; Duan, J.; He, M.; Liu, Y.A.; Bao, Y. Study on antifriction mechanism of surface textured elliptical bearings. J. Tribol. 2023, 145, 011702. [Google Scholar] [CrossRef]
- Profito, F.J.; Vladescu, S.C.; Reddyhoff, T.; Dini, D. Numerical and experimental investigation of textured journal bearings for friction reduction. Tribol. Int. 2024, 195, 109643. [Google Scholar] [CrossRef]
- Gu, C.; Cui, Y.; Zhang, D. Research on the optimal design approach of the surface texture for journal bearings. Lubricants 2024, 12, 111. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, S. Parametric study of textured hydrodynamic journal bearing for turbulent flow using CFD analysis. Int. J. Interact. Des. Manuf. 2025, 19, 2987–2997. [Google Scholar] [CrossRef]
- Jearl, W. More on boomerangs, including their connection with the dimpled golf ball. Sci. Am. 1979, 240, 180. [Google Scholar]
- Cupillard, S. Thermohydrodynamics of Sliding Contacts with Textured Surfaces. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2009. [Google Scholar]
- Rahmatabadi, A.D.; Mehrjardi, M.Z.; Fazel, M.R. Performance analysis of micropolar lubricated journal bearings using GDQ method. Tribol. Int. 2010, 43, 2000–2009. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Fillon, M.; Maspeyrot, P. Effect of textured area on the performances of a hydrodynamic journal bearing. Tribol. Int. 2011, 44, 211–219. [Google Scholar] [CrossRef]
- Lund, J.W.; Thomsen, K.K. A calculation method and data for the dynamic coefficients of oil-lubricated journal bearings. In Topics in Fluid Film Bearing and Rotor Bearing System Design and Optimization; ASME: Chicago, IL, USA, 1978; pp. 1–29. [Google Scholar]

| 0 | 90 | 0 | 0.5 | 11.75 | 11.63 | 48.5 | 47.7 |
| 0 | 45 | 0 | 0.25 | 11.96 | 11.76 | 50.4 | 51.3 |
| 175 | 220 | 0.12 | 0.5 | 12.18 | 12.25 | 49 | 49.3 |
| 180 | 225 | 0.2 | 0.5 | 12.11 | 12.21 | 49.6 | 49.5 |
| 185 | 230 | 0.12 | 0.5 | 12.19 | 12.15 | 49 | 48.7 |
| Bearings Characteristics | ||||
|---|---|---|---|---|
| Present Study | Ref. [45] | Present Study | Ref. [45] | |
| 90.41 | 90.37 | 70.93 | 69.69 | |
| 0.59 | 0.58 | 1.37 | 1.34 | |
| −4.68 | −4.79 | −0.17 | −0.16 | |
| 5.49 | 5.58 | 3.54 | 3.60 | |
| 8.78 | 8.93 | 5.22 | 5.36 | |
| 4.86 | 4.82 | 1.43 | 1.42 | |
| −4.39 | −4.5 | 1.36 | 1.34 | |
| 17.82 | 17.99 | 7.81 | 7.67 | |
| Parameter | Definition | Number and Magnitude (Dimensionless) |
|---|---|---|
| The number of textures in the circumferential direction | 5 | |
| Number of textures in the longitudinal direction | 10 | |
| Dimensionless radius of textures in the circumferential direction | 0.047619 | |
| Dimensionless radius of textures in the longitudinal direction | 0.0238095 | |
| Eccentricity ratio | 0.5 | |
| The starting point of the texture in the longitudinal direction | 0.05 | |
| Termination point of the texture in the longitudinal direction | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrjardi, M.Z.; Shooroki, A.R.; Rabani, M.; Rabani, M. Effect of Surface Texture Depth with Various Geometric Shapes on the Steady-State Performance and Dynamic Stability of Noncircular Lobed Journal Bearings. Appl. Sci. 2025, 15, 4412. https://doi.org/10.3390/app15084412
Mehrjardi MZ, Shooroki AR, Rabani M, Rabani M. Effect of Surface Texture Depth with Various Geometric Shapes on the Steady-State Performance and Dynamic Stability of Noncircular Lobed Journal Bearings. Applied Sciences. 2025; 15(8):4412. https://doi.org/10.3390/app15084412
Chicago/Turabian StyleMehrjardi, Mahdi Zare, Abolfazl Rasoolizadeh Shooroki, Mehran Rabani, and Mehrdad Rabani. 2025. "Effect of Surface Texture Depth with Various Geometric Shapes on the Steady-State Performance and Dynamic Stability of Noncircular Lobed Journal Bearings" Applied Sciences 15, no. 8: 4412. https://doi.org/10.3390/app15084412
APA StyleMehrjardi, M. Z., Shooroki, A. R., Rabani, M., & Rabani, M. (2025). Effect of Surface Texture Depth with Various Geometric Shapes on the Steady-State Performance and Dynamic Stability of Noncircular Lobed Journal Bearings. Applied Sciences, 15(8), 4412. https://doi.org/10.3390/app15084412









