Abstract
Community detection is increasingly important in social networks with the rapid growth of big data, which provides a deep understanding of the mesoscopic structure of social networks. In this article, we propose a label improvement algorithm, DegreeRank Label Propagation (DRLP), which is based on the degree centrality of nodes and adopts a PageRank optimization strategy. We present a damping factor reflecting the affinity between nodes, which can be adjusted to affect the change of affinity between nodes caused by unexpected events, aiming to simulate interpersonal communication in real networks. Next, a novel importance index is designed for nodes to solve the random problem of existing similar algorithms by globalizing the local characteristics of nodes. We also develop an update algorithm with low time complexity during the label selection process to ensure the sum of influence propagation is maximized within each community. Experimental results verify that the algorithm achieves stable and excellent community partitioning results on real network datasets and artificial synthetic networks. Especially in large and medium-sized networks, our method demonstrates higher accuracy and better performance in terms of normalized mutual information (NMI) and modularity than other methods.
1. Introduction
Social networks, as mappings of social relationships, have been widely studied within the framework of complex network theory. They encompass broad and profound interpersonal relationships and information exchange, covering the fields of social science and computer science, with far-reaching implications for business, politics, healthcare, and other fields [1,2]. In complex networks, individuals are abstracted as nodes, and the relationships between nodes are abstracted as edges [3]. Social networks are characterized by many complex network features, including the small-world phenomenon [4], scale-free [5], community structure [6], and so on. Recent research has shown that an in-depth exploration of the characteristics of the community structure of social networks is helpful to reveal the intrinsic organization and patterns of networks in community structures [7]. In this way, it provides strong theoretical support for a more comprehensive understanding of the structure and function of social networks.
In recent years, social network structure optimization methods have been classified into global optimization algorithms and local optimization algorithms based on the scope of their search space and the nature of their objectives. In the 20th century, Kernighan et al. [8] proposed the Kernighan–Lin algorithm, which partitions the network into predefined sizes and quantities, defining a function gain for network partitioning and dividing the community based on the change in gain. A large variety of global optimization algorithms evolved from this idea. Newman [9] defines edge betweenness as the importance index of edges, and they sequentially remove non-community core edges from the network to obtain the community partitioning result; in contrast, Shen et al. [10] propose a merging clustering algorithm to add edges to the network sequentially based on maximal clusters. Newman et al. [9] first proposed a modular function to measure the results of community division in 2004, and since then a lot of optimization algorithms have been proposed and improved based on modular functions. Boettcher et al. [11] optimize the modular function Q using the fitness value of genetic algorithms; Li et al. [12] present an extreme optimization semi-supervised algorithm based on pairwise constraint structure enhancement, which solved the pseudo-connection problem. However, the modularity optimization algorithm is an NP-complete problem, and it is difficult to find the optimal solution in polynomial time. Donath et al. [13] first introduced the concept of spectral clustering, and in the same year, Fielder et al. [14] extended spectral clustering to community detection technology by using the Laplace matrix. Shi et al. [15] and Ng et al. [16] use the normalized Laplacian matrix to define the spectral clustering algorithm to achieve processing of large datasets under sparse similarity graph constraints. However, each of these global optimization algorithms has obvious limitations in application by requiring information about the topology of the entire network, as well as the number and size of predefined communities. Later, Clauset et al. [17] proposed a local optimization algorithm, which led to the emergence of various local optimization algorithms such as the clique percolation method [18], the label propagation algorithm [19], and the local edge clustering optimization algorithm [20].
The traditional label propagation algorithm [19] is an efficient local optimization algorithm that does not require complete network structure information and has lower time complexity, which is close to linear complexity, but the algorithm is highly random and weakly robust and is prone to fall into local optima, which makes it difficult to obtain effective community detection. Zhang et al. [21] present a node importance label optimization algorithm based on Bayesian networks, which updates the order of nodes based on their importance to optimize the stochasticity of traditional LPA algorithms, but it requires a large amount of prior knowledge in defining the node importance. Kouni et al. [22] use the LPA strategy, allowing a node to contain multiple labels, giving a label confidence function, and updating labels according to the confidence coefficients of different labels. Yu et al. [23] propose a Deep Walk label optimization algorithm for overlapping community detection. This method utilizes the Deep Walk model to learn the network topology and obtain low-dimensional vector representations of nodes. It constructs a weight matrix by vector dot product operations and detects overlapping communities based on information exchange between nodes. Hosseini et al. [24] used the similarity index to assign weights to edges and transformed the label propagation process into the ant colony traversal process according to the ant colony optimization (ACO) algorithm, which transforms the problem of labeling influence into a problem of transfer probability. Wang et al. [25], in order to improve the robustness of the LPA algorithm, propose an importance metric that combines network locality with the node’s global position in the network, but at the expense of increasing the complexity of the algorithm itself and sacrificing the advantages of the LPA algorithm’s fast running speed and low time overhead. Similarly, Liu et al. [26] add multi-step greedy fusion [27] to optimize the LPA algorithm to improve the robustness of the algorithm and increases the complexity of the algorithm. Laassem et al. [28] extended Coulomb’s law for electrostatic attraction in physics to social networks, proposing a novel similarity matrix that quantifies node importance through pairwise attraction forces. However, this Coulomb matrix-based approach incurs significant computational overhead in both time and space complexity. In order to solve the problem of the instability and low quality of the attribute graph, Berahmand et al. [29] generate a weighted graph combining node attributes and topological structure from the attribute graph of nodes with edge connections, so that the detected community is characterized by both structural cohesion and attribute homogeneity, which maintains the original efficiency of the LPA algorithm and reduces the number of iterations. However, most label optimization algorithms tend to consider only local node information while ignoring global importance. Additionally, while some optimization algorithms improve community division results, they still suffer from instability issues.
Meanwhile, with the rapid development of deep learning techniques, community detection methods based on Graph Neural Networks (GNNs), such as GCNs [30] and GAT [31], have gradually emerged as a research hotspot. These methods overcome the limitations of traditional approaches that rely on handcrafted features or optimization functions by learning low-dimensional node representations in an end-to-end manner, automatically capturing both global topological and local neighborhood features. CPGC [32] effectively detects overlapping and non-overlapping communities by integrating representation learning with clustering, improving graph convolution operations, and introducing community perspective similarity, thereby leveraging both attribute and structural information. However, challenges remain in computational efficiency and scalability. GEAM [33], a graph-enhanced attention model designed for multiplex networks, enhances community detection accuracy by effectively integrating cross-layer semantic information via inter-layer contrastive learning, a self-attention adaptive fusion mechanism, and an edge density-driven module. Additionally, for large-scale networks, inductive learning methods such as GraphSAGE [34] achieve efficient training by sampling neighboring nodes.
Although deep learning methods have demonstrated excellent performance in community detection, their effectiveness relies heavily on high-quality training data. Moreover, their black-box nature makes community partitioning results difficult to interpret, and they often exhibit limited generalizability on sparse networks. To address the advantages and disadvantages of existing algorithms, we propose a new label propagation algorithm for network node importance, called the DegreeRank Label Propagation (DRLP) Algorithm. By explicitly defining node importance metrics and label update rules, DRLP maintains algorithmic efficiency while achieving interpretable community partitioning logic. Specifically, by defining a new update rule and fixing the order of nodes for the label update, DRLP improves both the robustness of the traditional LPA and community detection accuracy. Firstly, DRLP generates a specific metric indicator to reflect the importance of nodes in the whole network topology based on the local and global structural characteristics of each node. Secondly, DRLP repeats the process of labeling each node according to a new label updating rule until the community structure of the whole network is detected. Throughout the algorithm phase, we determine the update order of nodes in descending order of node importance to reduce the randomness of the algorithm; meanwhile, in the label update rules, we consider that the update of node labels is determined by both the authority of the neighboring nodes (node importance) and the closeness between the node and the neighboring nodes. Finally, DRLP divides all nodes with the same label into a community. The main contributions of this paper are summarized as follows:
- We propose a new method to reflect the correlation between network nodes that can efficiently find the shortest path and decrease the time complexity. We obtain a way to detect the correlation between nodes more accurately when analyzing the influence of nodes such that network topology information is kept.
- We introduce a damping factor that reflects the affinity between nodes, which can be adjusted to affect the change of affinity between nodes caused by unexpected events, which is more in line with interpersonal interactions in real social networks.
- We present a new node importance metric to solve the random problem of existing similar algorithms by globalizing the local characteristics of nodes. This metric provides a more accurate assessment of node importance, which can improve the accuracy of community partition.
- We propose a modified label propagation strategy. We emphasize the influence of neighboring nodes on the target node when selecting a label, which ensures the maximization of influence propagation within each community during the community partitioning process. This method is used to solve the problem of random selection of nodes, which enhances the efficiency and feasibility of the algorithm.
- We perform simulations to verify the stability and superiority of the DRLP algorithm on real network datasets and artificial synthetic networks. We also validate the higher accuracy and better performance in terms of NMI and modularity than other methods.
The rest of this paper is organized as follows. Section 2 summarizes related work. Then, in Section 3, we introduce the main ideas and detailed process of our algorithm, and we also analyze the complexity of the proposed algorithm. We introduce the relevant parameter settings of our algorithm and discuss the experimental results of the real-world and synthetic networks in Section 4. Finally, Section 5 provides conclusions and perspectives.
2. Related Works
2.1. Traditional Label Propagation Algorithm
The label propagation algorithm (LPA) [19] is a heuristic algorithm that follows the principle that labels propagate among network nodes according to certain rules, and the process is finished when the labels of every node are settled or stop changing; then, nodes with the same label will belong to the same community. The process can be described in discrete stages:
Initialization stage: a unique label is initially allocated to each node in the network.
Propagation stage: the label with the highest frequency among its neighbors is selected to update, executing iteratively for each node until the stop condition is reached.
Stopping Criterion: the algorithm will terminate if the labels of all the nodes in the network no longer change or the maximum number of iterations is reached.
Characteristics of the LPA include its simplicity, easily implemented fast execution, and suitability for large-scale networks. However, due to its random and local nature, it is probably unlikely to find the globally optimal community structure and may be affected by the initial label allocation and the structure of the network.
2.2. Degree Centrality
Definition 1
(Degree Centrality, DC). DC is a widely used metric for node centrality that measures the significance of individual nodes in social network analysis. It is defined based on the degree of nodes. Thus, DC can be denoted as follows:
where is the degree of node i and n is the number of nodes in the network.
Degree centrality is one of the most intuitive node centrality metrics, which measures the degree of direct connection of a node in the network. The higher the degree centrality of a node, the more connections to other nodes in the network.
2.3. The PageRank Strategy
The PageRank algorithm [35] is a classic link analysis algorithm. This algorithm allocates a numerical value to each node denoting the importance of each node by analyzing the connections between nodes in a network. Although originally designed for webpage ranking, the PageRank algorithm has been widely used in the field of network research, especially community detection. The PageRank strategy is applied to measure node importance, thus helping to identify important nodes or community structures in the network, which provides a way to better understand the structure and functionality of networks.
Although the PageRank algorithm is not similarly directly applied in community detection as it is in website ranking, it offers an effective method to elevate node importance based on the relationships between nodes. In this article, we propose a label improvement algorithm, DRLP, which is based on the degree centrality of nodes and adopts the PageRank optimization strategy in order to improve the accuracy and efficiency of community detection.
3. Solution for DRLP
We will introduce the main ideas of DRLP and show how to efficiently solve it step by step in this section. Firstly, we extract the sub-graph at each stage of the experiment, and the process is shown in Figure 1.
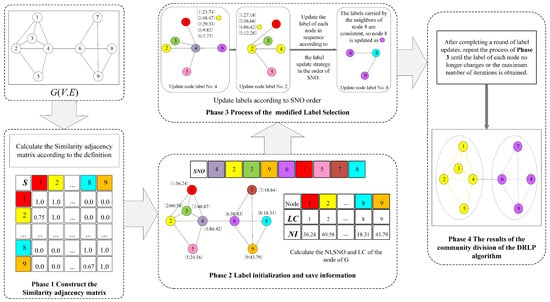
Figure 1.
Example of DRLP process.
DRLP is designed in four stages. In phase 1, a similarity adjacency matrix is constructed according to the node correlation coefficients. In phase 2, a unique label is initially assigned to each node, the node importance (NI) index is calculated, and a sorted node order (SNO) list is generated based on their importance. In phase 3, a novel label update strategy is proposed, namely utilizing a preference selection strategy for label updating. Finally, the community division is finished when the label propagation process stops. From Figure 1, it can be seen that our algorithm’s community segmentation results are evident.
The details of the DRLP model will be elaborated as follows. For better discussion, the descriptions of notations used in this paper are listed in Abbreviations section.
3.1. Construction of Similarity Adjacency Matrix
In this section, we present a weighted adjacency matrix that can reflect the correlation between network nodes.
Many network analysis techniques, such as Shortest Path Distance [36], Average Path Length [4], Diameter [4], Clustering Coefficient [4], and Jaccard Similarity [37], can be used to measure the distance or similarity between nodes in a graph or complex network. Among these metrics, the Shortest Path Distance and Diameter are usually necessary for calculating the shortest path lengths between nodes, resulting in high time complexity, which gives poor performance in large-scale networks. Although the density of connections between nodes and their neighbors is provided by the Clustering Coefficient, the distance or similarity between individual nodes is not directly reflected by the coefficient. Jaccard Similarity partially denotes the intersection of neighbor sets between two nodes, but in real-world social networks, the similarity or distance between two nodes is not always consistent. For example, if node A has only node B as its neighbor while node B has other neighbors besides A, the influence of B on A is much greater than that of A on B. Therefore, we propose a new metric to measure the distance or similarity between nodes.
Definition 2
(Similarity adjacency matrix, S). The model of a social network is an undirected complex graph , where each node u in V is a user or entity in the social network, and each edge in E is the social relationship between entities u and v. For any two nodes u and v, the similarity index of node u for node v in graph G is defined as follows:
The method for calculating the similarity adjacency matrix S is given in Algorithm 1.
| Algorithm 1 Constructing the similarity adjacency matrix |
3.2. Node Importance Index
Complex networks consist of numerous nodes [38] with diverse and intricate topological configurations. There are some drawbacks in most of the existing methods for measuring node importance, such as monolithic metrics and ignoring the global or local roles of nodes in the network topology. To address this problem, a new metric for node importance is defined by combining the characteristics of PageRank and the degree centrality index.
Definition 3
(Node importance, NI). For any node u in V, the node importance index of node u in graph G is defined as follows:
where is the node importance index of node u, is the degree of node v, and α is the damping factor. The importance of each node is initialized first based on the degree centrality and neighborhood relevance among the given importance metrics, and then the importance of each node is iteratively updated following the PageRank strategy, with the number of iterations denoted as β.
The method for calculating the node importance (NI) is given in Algorithm 2.
| Algorithm 2 Solving node importance index |
3.3. Modified Label Selection Process
In this section, we propose a modified label update rule and introduce a preference label selection strategy.
Differently from the existing algorithms, we not only analyze the frequency of labels among the neighbors of the node, but also refer to the intimacy between nodes and their neighbors and the influence of neighbor nodes. According to our strategy, the greater the proportion of shared neighbors in all the neighbors of the target node, the greater the influence over the target node. Similarly, the node with greater importance will have a greater influence on the target node. Therefore, we define the label influence as the impact of label groups among neighbors on the node.
Definition 4
(Label influence, ). For any node u in V and v in , the influence of the label on node u is defined as follows:
where is the influence of label on node u, and is the set of neighbors of node u with label .
The process of improved label selection is given in Algorithm 3.
| Algorithm 3 The modified label selection process |
3.4. DegreeRank Label Propagation (DRLP) Algorithm
After giving some core definitions of the algorithm, this section demonstrates the detailed process of the DegreeRank Label Propagation Algorithm, as shown in Algorithm 4.
3.5. Complexity Analysis
Given an undirected unweighted graph G, where is the number of nodes, is the total number of edges, and d is the average degree of nodes, the time complexity of each step of the DRLP is calculated as follows:
- Step 1:
- Initialize each node with a unique label and time complexity ;
- Step 1:
- Construct the similarity adjacency matrix with time complexity ;
- Step 1:
- Calculate the DC value of each node with time complexity ;
- Step 1:
- Calculate the list of NI with time complexity ;
- Step 1:
- Sort the nodes based on their importance with time complexity ;
- Step 1:
- Update the labels for each node with t iterations and time complexity .
Therefore, we obtain the time complexity of the DRLP algorithm, which is .
| Algorithm 4 DRLP algorithm |
4. Experimental Results and Analysis
4.1. Evaluation Metrics
4.1.1. Normalized Mutual Information (NMI)
[39] is commonly used to evaluate the degree of similarity between the results of two clustered partitions. In this article, it is used to measure the effectiveness of the network partition results. The definition of is as follows:
where is the set of partitioning results of the real community; is the set of partitioning results measured by the experiment. is the result of a community division in . M is the partition information matrix, where the rows are actual communities and the columns are communities detected by experiments; is the number of nodes that are contained by both community and community . is the sum of the row of the partition information matrix representing the community , and is the sum of the column of the community .
4.1.2. Modularity Q
Modularity [9] is a globally relevant metric of the network that could quantify the topological characteristics of communities. It is usually used to evaluate the quality of community partitioning results. The value of modularity is generally distributed in the range of [0, 1]; when , it means that there is no community structure, and means that all the nodes in the same community. And higher Q-values mean better community division results, stronger connections within communities, and sparser connections between communities. Q is defined as follows:
where is the modularity, i and j are two nodes in the graph, is the degree of node i, and is the Dirac function. if , which indicates that node i and node j are in the same community; otherwise, .
4.1.3. Modularity Density D
Modularity density is another widely used evaluation metric for measuring the effectiveness of community partitioning. In general, if nodes in the network have more connections within the same community and fewer connections between different communities, the D will be higher; this means that the network is more densely structured and can be more easily divided into independent functional modules or communities. D is defined as follows:
where is the modularity density of the community partitioning result. is the number of connections between nodes within community , is the number of connections between nodes within community and nodes in other communities, and is the number of nodes in community .
4.2. Comparative Algorithms and Test Set
To assess the effectiveness of DRLP, we compare it with various community detection algorithms on three synthetic networks and seven real-world network datasets. Since DRLP is an optimization algorithm based on label propagation, the compared algorithms include the traditional LPA [19], spectral clustering (SC), and the Louvain algorithm [40], as well as existing optimized algorithms based on label propagation, which include CNLLP [28], LPA_CL [41], and CDEP [42]. Additionally, all experiments are implemented in Python 3.9.18 and executed on a Windows 10 environment with an Intel® Core™ i5-13400@2.5GHz CPU and 32.00 GB of memory.
Seven real-world network datasets are selected from the datasets applied in most community detection algorithms. Their sizes range from 34 nodes to 23,133 nodes, covering both small-scale and large-scale networks. They are the Zachary karate club dataset [43], the dolphin dataset [44], the polbooks dataset [45], the football dataset [6], the PGP dataset [46], the CA_AstroPh dataset, and the CA_CondMat dataset [47]. By comparing the DRLP algorithm on datasets of different sizes, we comprehensively validate its effectiveness. Table 1 provides the number of node () in the network and the node relationships (). Additionally, the actual number of communities () of the real-world network datasets is given if it exits.

Table 1.
Specific information on real networks.
For synthetic networks, we consider both the Stochastic Block Model (SBM) [48] and the LFR benchmark network [49], ultimately adopting the latter due to its richer parameterization for modeling realistic community structures. The LFR network includes various adjustable parameters: the number of nodes (), the node degree distribution (the average node degree (), the max node degree ()), community size (the min community size and the max community size ), and the power distribution exponent for node degree and power distribution exponent for community size (, ). Furthermore, the fuzziness of community boundaries in the LFR network can be influenced by adjusting the mixing parameter . As increases, the community structure becomes more fuzzy, making community detection more difficult accordingly. We perform experiments on three different sizes of LFR networks (LFR1, LFR2, and LFR3). Details of parameter settings for synthetic networks are described in Table 2.

Table 2.
Specific information on synthetic networks.
4.3. Experimental Parameter Analysis
4.3.1. Parameter
In the proposed algorithm, a damping factor is introduced for the node importance to evaluate the quantity and quality of a node’s neighbors during each iteration. It also illustrates sudden changes in closeness or distance between nodes due to unexpected events. In addition, a higher damping factor means that the connections between nodes have a greater influence on their relationships, while sudden changes due to unexpected events have a lesser impact, which is more closely aligned with the interpersonal relationships observed in real social networks. To denote the importance, the value of the damping factor is set as 0.85 in the experiments.
4.3.2. Parameter
In real social networks, there is a “spillover effect” [50]; that is, interacting with influential individuals can expand personal social networks, thus broadening the sphere of one’s influence. By establishing relationships with influential individuals, a person can obtain more resources, information, and opportunities, thus enhancing personal influence. Therefore, in coordination with the above parameter , we need to set another parameter in the algorithm. It is the number of iterations performed when calculating node importance. The importance of each node is updated by iterative calculations. As a result, the importance of the neighbors or close connections of the nodes with higher importance also increases accordingly.
The modularity Q-values and the mean modularity (Q) detected by the proposed algorithm at different values on various network datasets are shown in Figure 2a,b. We show the changing of Q-values with the varying of parameter on different datasets. From Figure 2a, it can be observed that the modularity tends to decrease to some extent with an increase in the number of iterations on all datasets. And in particular, as the number of iterations exceeds 25, the modularity values of the three datasets, namely, karate, Dolphin, and football, decrease by nearly 20%. Moreover, Figure 2b shows a sharp decline in the mean modularity. This is because, as the number of iterations increases, the difference in importance between individual nodes becomes smaller and smaller, and nodes with supposedly small importance gradually increase in importance after many iterations, and may even exceed the expected importance. From Figure 2a,b, we can also find that when the number of iterations ranges from four to eight, more optimal results are achieved for all datasets. Therefore, in all experiments, the value of is set within the range of [4, 8].
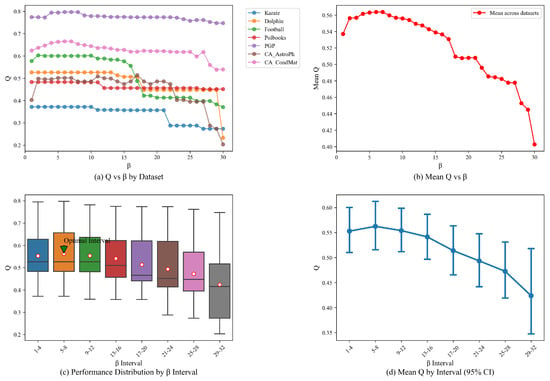
Figure 2.
Analysis and comparison of parameter results.
Furthermore, to systematically validate the effectiveness of parameter selection, we performed one-way ANOVA. The results are presented in Figure 2c,d, where Figure 2c illustrates the distribution of Q-values across different intervals, and Figure 2d displays the mean Q-values with corresponding 95% confidence intervals for each interval. The optimal performance interval is explicitly indicated by a green arrow in Figure 2c. The experimental results demonstrate that the [5, 8] interval exhibits both a concentrated and stable Q-value distribution (as shown in the boxplot of Figure 2c), with its significant superiority confirmed by 95% confidence interval analysis (Figure 2d). Therefore, based on the aforementioned experimental results and ANOVA statistical testing, we recommend configuring within the [4, 8] range to simultaneously maximize system performance (Q-value) and optimal operational stability.
4.4. Detection Result Analysis
4.4.1. Analysis of Community Detection Results in Real Networks
We compare the DRLP algorithm with six other algorithms (LPA, Louvain, SC, CNLLP, LPA_CL, and CDEP) on seven real network datasets to demonstrate the efficacy of our algorithm. The experimental analysis results of the compared algorithms are shown in Table 3, which provides the corresponding modularity Q-values.

Table 3.
The modular value Q of the community detection results of the real network datasets (bold indicates maximum values across all datasets).
Table 3 shows that the Louvain algorithm achieves a maximum Q-value of 0.4160 on the Karate dataset, and the LPA algorithm has the lowest average modularity among all algorithms. In addition, the average modularity value Q of the LPA is found to be consistent based on test results across all networks, with a significant discrepancy between the maximum modularity values and average modularity values. This is due to the high frequency of using random functions in the LPA algorithm, which leads to its low robustness. On small-scale datasets, the LPA_CL algorithm achieves stable and relatively good results. On large-scale datasets, it was unable to efficiently produce findings for community detection. As the size of the dataset increases, we can see that the time required by the LPA_CL algorithm increases significantly, and it performs poorly on large-scale datasets. The CDEP algorithm has a low time complexity and can achieve convergent community detection results on all datasets. However, its Q-values on small-scale and some large-scale networks are even lower than the LPA algorithm. The proposed DRLP algorithm achieves good community detection results on all datasets. Although it does not attain the maximum Q-value on certain datasets, its performance remains close to the maximum, even nearly identical on the football dataset. While Louvain obtains comparatively high modularity (Q) values on medium-scale networks, its effectiveness is constrained by resolution limits and randomness, and the modularity metric may obscure the loss of true community structures. On the other datasets, the DRLP algorithm consistently achieves the highest Q-values. The analysis of Q-values presented in Table 3 demonstrates the effectiveness of the DRLP algorithm. These results illustrate that the proposed DRLP algorithm performs better compared to other algorithms in this paper.
The normalized mutual information values that we recorded in experiments for our algorithm and the other compared algorithms are listed as Table 4, which provides community detection results on four real network datasets. The definition of NMI makes it clear that if the experimental results perfectly match the actual community division outcomes, then NMI = 1.

Table 4.
NMI of community detection results in real network datasets (bold indicates maximum values across all datasets).
From Table 4, the results of the experiment indicate that, when the algorithm’s partitioning result matches the actual network community structure ( value of 1), the corresponding modularity value in Table 3 is 0.3715 for the KarateClub dataset. However, for the Louvain and CNLLP algorithms, their Q-values are greater than 0.3715 in Table 3, but their corresponding values in Table 4 are both less than 1. This is because, for these two evaluation metrics, the Q-value is measured by the connections between the internal and external community structures, and the is assessed according to the real network partitioning, and there is a certain inverse relationship between and Q-values. Therefore, although the LPA_CL algorithm obtains a lower Q-value than the DRLP algorithm on the Dolphin dataset in Table 3, its value is higher than that of the DRLP algorithm in Table 4. And Table 4 indicates that with the exception of the Dolphin dataset, the DRLP algorithm achieves higher values across other datasets. These results illustrate that the proposed method performs well in detecting communities with higher values.
The modular density values that we recorded in experiments for our algorithm and the other compared algorithms are shown in Table 5, which provides community detection results on seven real network datasets. Based on the definitions of modularity and modular density, higher values indicate tighter community connections. The difference is that Q is used to measure the quality of the global community partition of the network, while D measures the closeness of the connection within the community.

Table 5.
Modularity density D of community detection results of real network datasets (bold indicates maximum values across all datasets).
Table 5 shows that the LPA algorithm achieves the highest modular density on the Karate dataset among the five algorithms. But the DRLP algorithm achieves higher modular density values than the other algorithms on other network datasets. This is because the modular density will be larger than that of the actual community due to the LPA algorithm’s randomization, which produces more community division results. The experiment results in Table 3 and Table 5 show that the DRLP algorithm demonstrates more compact community structures and better structural characteristics on both large- and small-scale networks. These results illustrate the effectiveness of the proposed DRLP algorithm.
4.4.2. Synthetic Network Community Detection Results and Analysis
The curves of NMI variation with for the DRLP algorithm and six other algorithms running 100 times on the LFR1 network are shown in Figure 3. The parameter is increased from 0.1 to 0.7 with increments of 0.05 to ensure the accuracy of the test results.
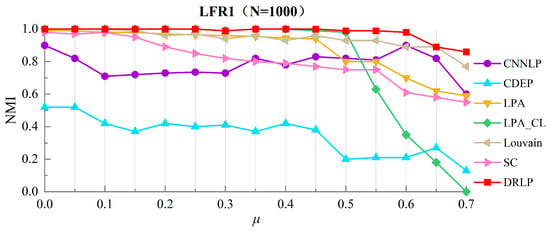
Figure 3.
Community detection results on the LFR1 network dataset.
When the mixing parameter is in the interval [0, 4.5], the community structure of the LFR network is relatively clear. In this case, the LPA, LPA_CL, Louvain, and DRLP algorithms achieve good community detection results. In particular, the DRLP and LPA_CL algorithms mostly reach the optimal NMI value of 1 within this interval. However, as increases and the network’s community structure becomes increasingly blurred, the accuracy of the LPA_CL algorithm drops significantly. In contrast, although the Louvain algorithm does not reach the optimal accuracy, its NMI value remains consistently stable above 0.9. Interestingly, the CNLLP algorithm demonstrates even stronger robustness when the community structure is ambiguous, with its NMI value surpassing its performance under clear community structures. It can be obviously observed that, in the entire range of 0 to 0.7, the DRLP algorithm consistently maintains excellent metrics, significantly surpassing those of the comparison algorithms. This indicates that our DRLP algorithm can effectively detect meaningful community structures, whether the community structure is clear or blurred.
The curves of NMI variation with for the DRLP algorithm and six other algorithms running 100 times on the LFR2 network are shown in Figure 4. The parameter is increased from 0.1 to 0.7 with increments of 0.05 to ensure the accuracy of the test results.
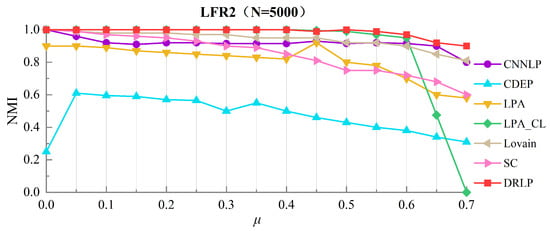
Figure 4.
Community detection results on the LFR2 network dataset.
From Figure 4, it can be observed that the community structure is relatively clear when the network size is 5000 and . The CNLLP algorithm shows a significant improvement, with metrics consistently above 0.85 compared to the LFR1 network. The DRLP, Louvain, and LPA_CL algorithms all maintain high community detection accuracy, with the first two algorithms having NMI values close to 1. However, when , the value for the LPA_CL algorithm begins to drop sharply, while the CNLLP, Louvain, and DRLP algorithms continue to detect effective community structures. Although the CNLLP and Louvain algorithms maintain stability in the entire range of [0, 0.7], the DRLP algorithm achieves values greater than 0.9 throughout the same range. This further demonstrates that the DRLP algorithm can effectively detect meaningful community structures in networks with different connection characteristics.
The curves of NMI variation with for the DRLP algorithm and six other algorithms running 100 times on the LFR3 network are shown in Figure 5. The parameter is increased from 0.1 to 0.8 with increments of 0.05 to ensure the accuracy of the test results.
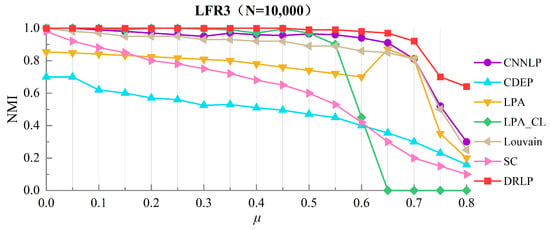
Figure 5.
Community detection results on the LFR3 network dataset.
As shown in Figure 5, in large-scale LFR networks with 10,000 nodes, when the community mixing parameter < 0.5, both the DRLP and LPA_CL algorithms demonstrate excellent performance consistent with their performance in smaller networks (LFR1 and LFR2), with their NMI metrics consistently maintained at near-optimal levels close to 1. Notably, the CNLLP algorithm shows significant improvement in the larger networks compared to its performance in smaller networks, achieving detection accuracy comparable to that of both the DRLP and LPA_CL algorithms. However, as the mixing parameter exceeds 0.5, the performance of the algorithms begins to diverge: the NMI values of the LPA_CL algorithm exhibit a cliff-like decline, completely failing at = 0.65; except for DRLP and CNLLP, the detection accuracy of all other algorithms shows significant degradation; and when rises to 0.7, the network community structure becomes highly blurred, yet the DRLP algorithm still maintains stable detection performance. This further verifies that our DRLP algorithm can detect effective community structures in networks regardless of the community size, and it is further shown that the DRLP algorithm can detect effective community structures for both large-scale and small-scale networks, regardless of having a clear or fuzzy community structure.
5. Conclusions
Addressing complex and diverse community detection tasks, this paper proposes a Degree and PageRank-based Label Propagation (DRLP) algorithm. First, we calculate the weight matrix for each node, then compute the node importance based on the weight matrix, and finally sort the nodes in descending order of importance. During the label propagation process, a novel neighbor closeness strategy is adopted, which avoids the random selection of the traditional LPA and effectively improves the accuracy of community detection. Using different evaluation indicators, DRLP was compared and analyzed with several label improvement algorithms. Simulation results on real and synthetic network datasets show that our algorithm achieves better modular density with maintaining high modularity, and it demonstrates high accuracy for both small-scale and medium-to-large-scale synthetic networks. However, the algorithm’s complexity might present scalability limitations for very large networks (e.g., ), necessitating additional optimization.
While DRLP demonstrates good performance across medium-to-large-scale networks, we recognize that its complexity may impose scalability limitations for extremely large networks. Therefore, future work could explore some optimization strategies such as parallel computing or similar techniques to reduce the algorithm’s time complexity. Furthermore, based on the existing framework, we plan to extend DRLP’s applicability to more complex network scenarios in the future, including weighted networks, dynamic networks, and optimized implementations for overlapping community detection. Additionally, we will explore potential synergies between DRLP and GNN architectures to further enhance its performance. These comprehensive optimizations will collectively expand the algorithm’s practical utility while preserving its core advantage in community detection accuracy.
Author Contributions
Conceptualization, M.L.; data curation, M.L., A.W. and B.L.; formal analysis, M.L.; funding acquisition, A.W. and B.L.; methodology, M.L. and A.W.; project administration, M.L.; resources, A.W. and B.L.; software, X.G.; supervision, A.W.; validation, M.L., X.G. and B.L.; visualization, M.L. and X.G.; writing—original draft, M.L.; writing—review and editing, A.W. and X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Collaborative Research Projects of “Chunhui Program”, Ministry of Education of China, grant number RZ2300003745, and in part by Shanxi Province Graduate Student Practice and Innovation Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| G | Complex network. |
| V | Set of nodes in the G. |
| E | Set of edges in the G. |
| u,v | nodes in the G. |
| S | Similarity adjacency matrix. |
| Set of neighbors of node u. | |
| The label of node u. | |
| NSL | Set of neighbors of node with same label. |
| LC | Set of labels for all nodes. |
| SNO | List of sorted node order. |
| LP | Set of labels for all nodes before propagation. |
| The damping factor. | |
| The number of iterations performed when calculating node importance. |
References
- Chen, X.; Li, J. Community detection in complex networks using edge-deleting with restrictions. Phys. A Stat. Mech. Its Appl. 2019, 519, 181–194. [Google Scholar] [CrossRef]
- Rezvanian, A.; Moradabadi, B.; Ghavipour, M.; Khomami, M.M.D.; Meybodi, M.R. Learning Automata Approach for Social Networks; Springer: Berlin/Heidelberg, Germany, 2019; Volume 820. [Google Scholar]
- Rajita, B.; Panda, S. Community detection techniques for evolving social networks. In Proceedings of the 2019 9th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 10–11 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 681–686. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Shang, R.; Zhang, W.; Jiao, L.; Zhang, X.; Stolkin, R. Dynamic immunization node model for complex networks based on community structure and threshold. IEEE Trans. Cybern. 2020, 52, 1539–1552. [Google Scholar] [CrossRef]
- Kernighan, B.W.; Lin, S. An efficient heuristic procedure for partitioning graphs. Bell Syst. Tech. J. 1970, 49, 291–307. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Shen, H.; Cheng, X.; Cai, K.; Hu, M.-B. Detect overlapping and hierarchical community structure in networks. Phys. A Stat. Mech. Its Appl. 2009, 388, 1706–1712. [Google Scholar] [CrossRef]
- Boettcher, S.; Percus, A.G. Extremal optimization for graph partitioning. Phys. Rev. E 2001, 64, 026114. [Google Scholar] [CrossRef]
- Li, L.; Du, M.; Liu, G.; Hu, X.; Wu, G. Extremal optimization-based semi-supervised algorithm with conflict pairwise constraints for community detection. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China, 17–20 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 180–187. [Google Scholar]
- Donath, W.E.; Hoffman, A.J. Lower bounds for the partitioning of graphs. IBM J. Res. Dev. 1973, 17, 420–425. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process. Syst. 2001, 14, 849–856. [Google Scholar]
- Clauset, A. Finding local community structure in networks. Phys. Rev. E 2005, 72, 026132. [Google Scholar] [CrossRef]
- Palla, G.; Derényi, I.; Farkas, I.; Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 2005, 435, 814–818. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef]
- Ahn, Y.-Y.; Bagrow, J.P.; Lehmann, S. Link communities reveal multiscale complexity in networks. Nature 2010, 466, 761–764. [Google Scholar] [CrossRef]
- Zhang, X.-K.; Ren, J.; Song, C.; Jia, J.; Zhang, Q. Label propagation algorithm for community detection based on node importance and label influence. Phys. Lett. A 2017, 381, 2691–2698. [Google Scholar] [CrossRef]
- Kouni, I.B.E.; Karoui, W.; Romdhane, L.B. Node importance based label propagation algorithm for overlapping community detection in networks. Expert Syst. Appl. 2020, 162, 113020. [Google Scholar] [CrossRef]
- Yu, H.; Ma, R.; Chao, J.; Zhang, F. An overlapping community detection approach based on deepwalk and improved label propagation. IEEE Trans. Comput. Soc. Syst. 2022, 10, 311–321. [Google Scholar] [CrossRef]
- Hosseini, R.; Rezvanian, A. Antlp: Ant-based label propagation algorithm for community detection in social networks. CAAI Trans. Intell. Technol. 2020, 5, 34–41. [Google Scholar] [CrossRef]
- Wang, T.; Chen, S.; Wang, X.; Wang, J. Label propagation algorithm based on node importance. Phys. A Stat. Mech. Its Appl. 2020, 551, 124137. [Google Scholar] [CrossRef]
- Liu, X.; Murata, T. Advanced modularity-specialized label propagation algorithm for detecting communities in networks. Phys. A Stat. Mech. Its Appl. 2010, 389, 1493–1500. [Google Scholar] [CrossRef]
- Schuetz, P.; Caflisch, A. Efficient modularity optimization by multistep greedy algorithm and vertex mover refinement. Phys. Rev. E 2008, 77, 046112. [Google Scholar] [CrossRef]
- Laassem, B.; Idarrou, A.; Boujlaleb, L.; Iggane, M.B. Label propagation algorithm for community detection based on coulomb’s law. Phys. A Stat. Mech. Its Appl. 2022, 593, 126881. [Google Scholar] [CrossRef]
- Berahmand, K.; Haghani, S.; Rostami, M.; Li, Y. A new attributed graph clustering by using label propagation in complex networks. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 1869–1883. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Liu, H.; Wei, J.; Xu, T. Community detection based on community perspective and graph convolutional network. Expert Syst. Appl. 2023, 231, 120748. [Google Scholar] [CrossRef]
- Wang, B.; Cai, X.; Xu, M.; Xiang, W. A graph-enhanced attention model for community detection in multiplex networks. Expert Syst. Appl. 2023, 230, 120552. [Google Scholar] [CrossRef]
- Xu, D.; Ruan, C.; Korpeoglu, E.; Kumar, S.; Achan, K. Inductive representation learning on temporal graphs. arXiv 2020, arXiv:2002.07962. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; ACM: New York, NY, USA, 2022; pp. 287–290. [Google Scholar]
- Jaccard, P. The distribution of the flora in the alpine zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Zhu, X.; Li, X.; Zhang, S.; Xu, Z.; Yu, L.; Wang, C. Graph pca hashing for similarity search. IEEE Trans. Multimed. 2017, 19, 2033–2044. [Google Scholar] [CrossRef]
- Zhang, W.; Shang, R.; Jiao, L. Large-scale community detection based on core node and layer-by-layer label propagation. Inf. Sci. 2023, 632, 1–18. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Inkpen, A.C.; Tsang, E.W. Social capital, networks, and knowledge transfer. Acad. Manag. Rev. 2005, 30, 146–165. [Google Scholar] [CrossRef]
- Zhao, X.; Liang, J.; Wang, J. A community detection algorithm based on graph compression for large-scale social networks. Inf. Sci. 2021, 551, 358–372. [Google Scholar] [CrossRef]
- Zachary, W.W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations: Can geographic isolation explain this unique trait? Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Krebs, V. Books About Us Politics. 2004. Available online: http://www.orgnet.com/ (accessed on 3 March 2023).
- Boguná, M.; Pastor-Satorras, R.; Díaz-Guilera, A.; Arenas, A. Models of social networks based on social distance attachment. Phys. Rev. E 2004, 70, 056122. [Google Scholar] [CrossRef] [PubMed]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. Data (TKDD) 2007, 1, 2-es. [Google Scholar] [CrossRef]
- Holland, P.W.; Laskey, K.B.; Leinhardt, S. Stochastic blockmodels: First steps. Soc. Netw. 1983, 5, 109–137. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Phys. Rev. E 2009, 80, 016118. [Google Scholar] [CrossRef]
- Sun, P.G. Weighting links based on edge centrality for community detection. Phys. A Stat. Mech. Its Appl. 2014, 394, 346–357. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).