Parametric Estimation and Analysis of Lifetime Models with Competing Risks Under Middle-Censored Data
Abstract
1. Introduction
1.1. Middle-Censored Data and Competing Risks
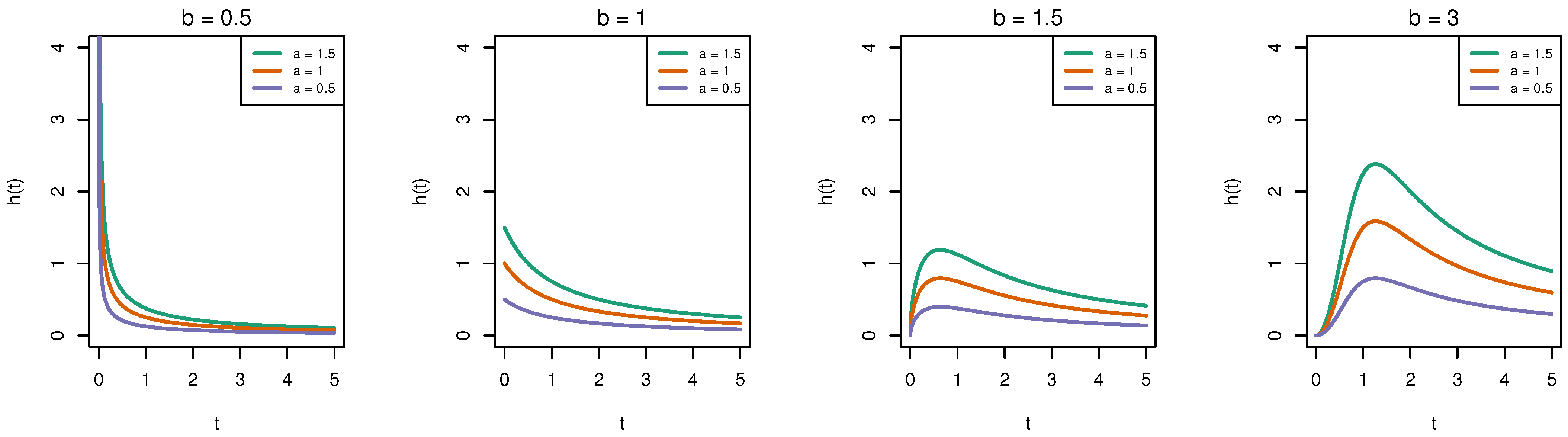
1.2. Burr-XII Distribution
2. Model Assumption and Notation
3. Frequentist Estimation
3.1. Maximum Likelihood Estimators
3.2. EM Algorithm
- ,
- ,
- ,
| Algorithm 1 The EM algorithm for obtaining MLEs under middle-censored data with competitive risks |
| 1: Input: , initial parameter , and 2: Initialization: 3: while not converged do 4: E-step (Expectation step): 5: Under the current parameter estimate , calculate the expectations: 6: M-step (Maximization step): 7: Update the parameter estimates by using Equations (25) and (26) 8: 9: end while 10: Output: Estimated parameter and |
3.3. Asymptotic Confidence Intervals
4. Bayesian Estimation
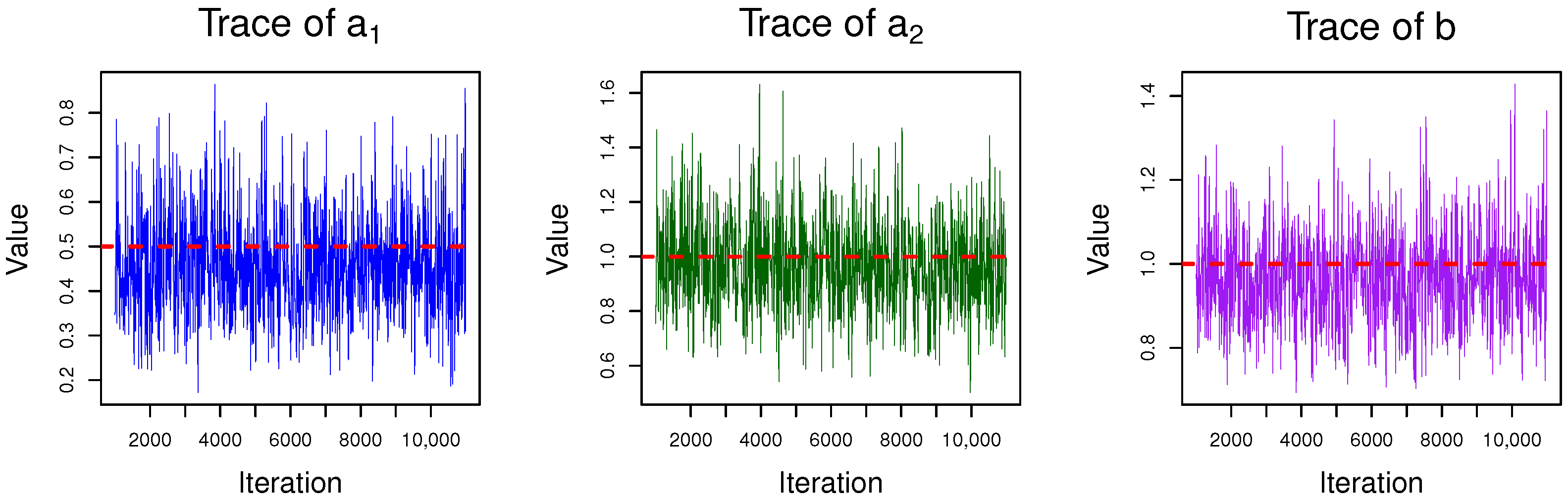
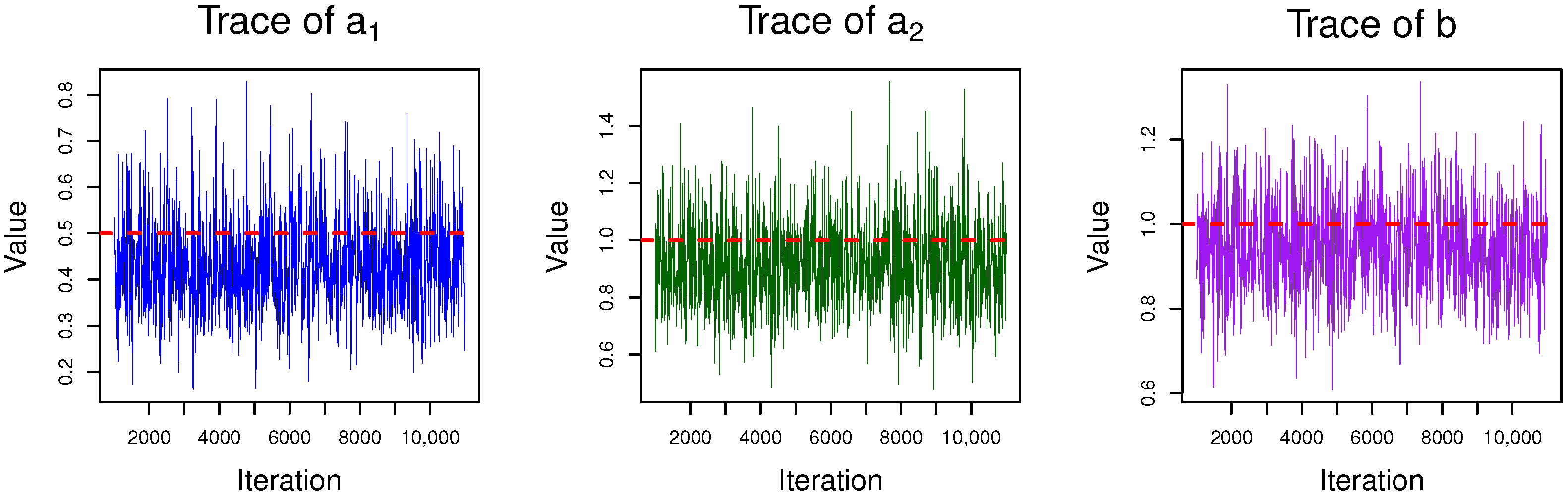
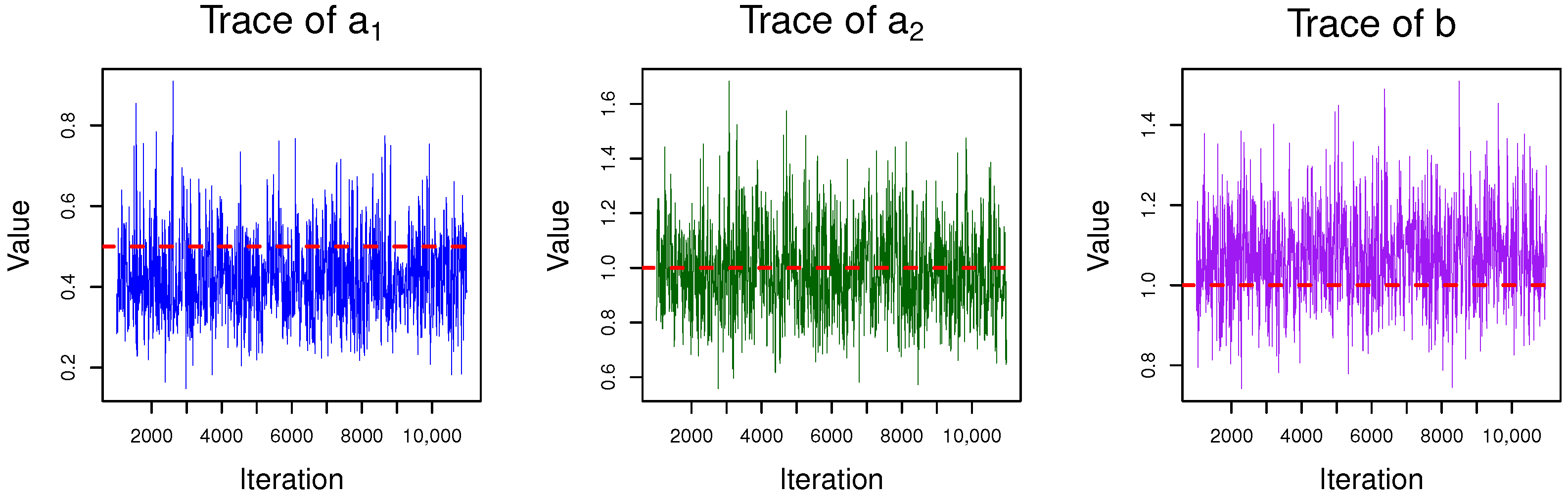
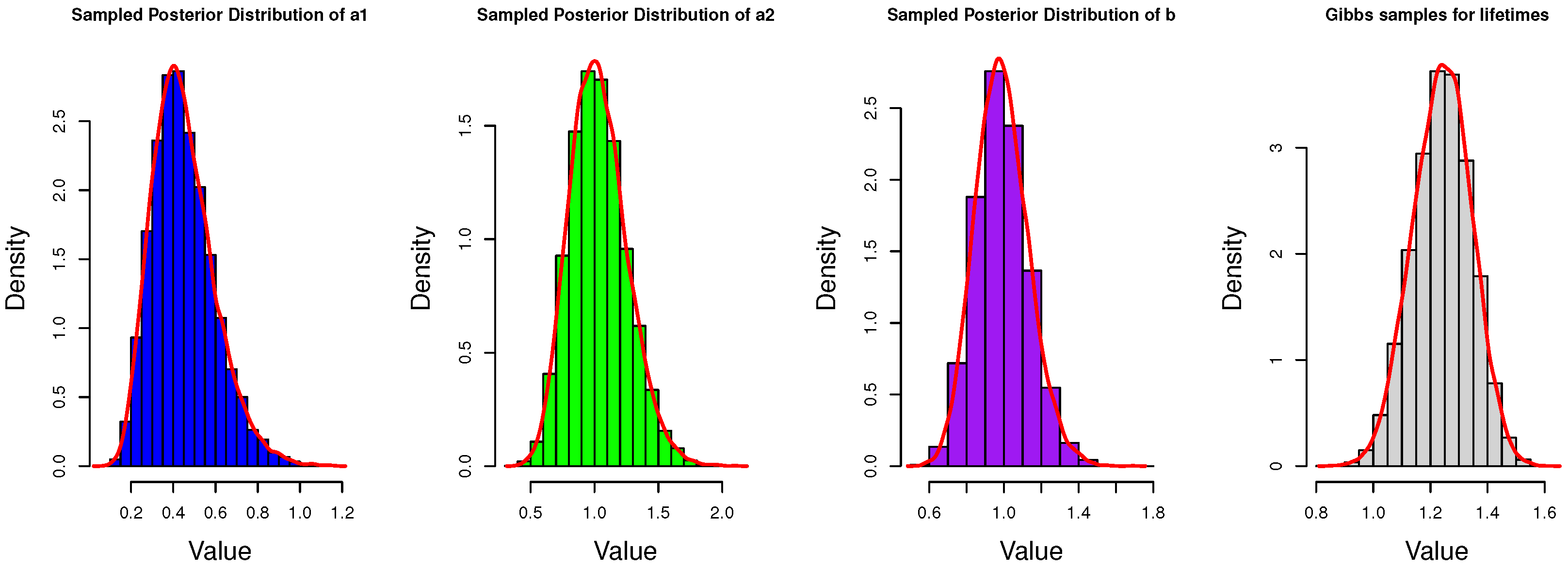
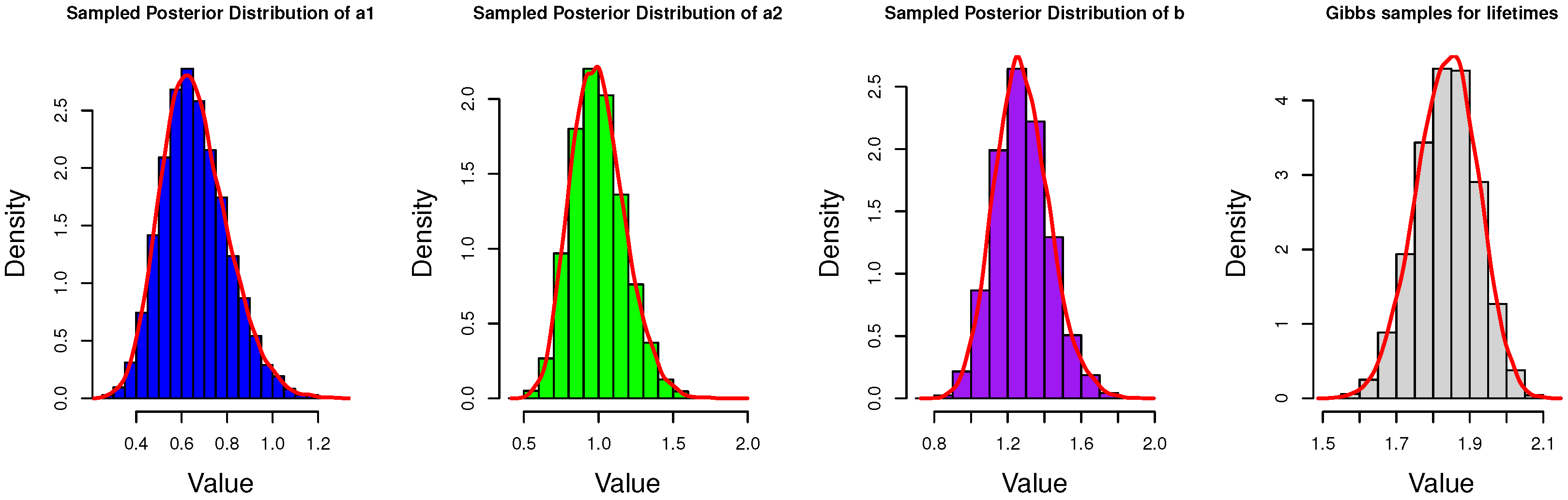
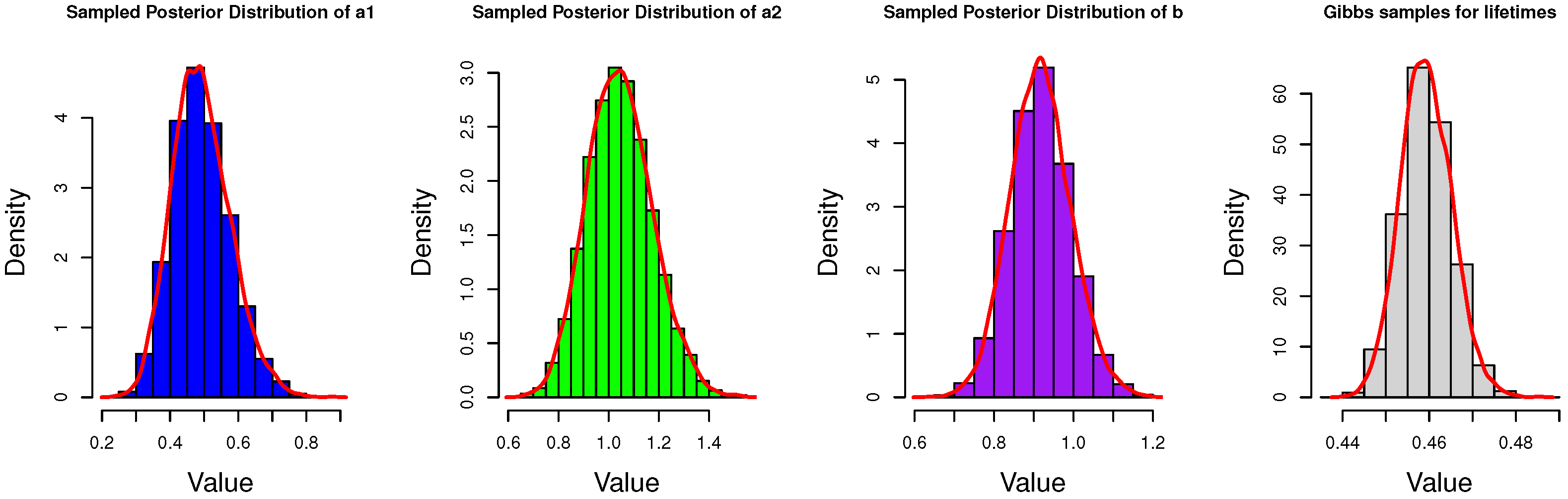
4.1. Gibbs Sampling
| Algorithm 2 Gibbs sampling method to Bayesian estimation |
| 1: Initialize the values of and . • Generate from , • Generate from , 2: for to N do 3: Sample from , then obtain 4: Sample through using the adaptive rejection sampling method proposed in [24]. 5: Sample from , where 6: end for |
- =, ,
4.2. HPD Credible Intervals
5. Simulation and Data Analysis
5.1. Simulation Study
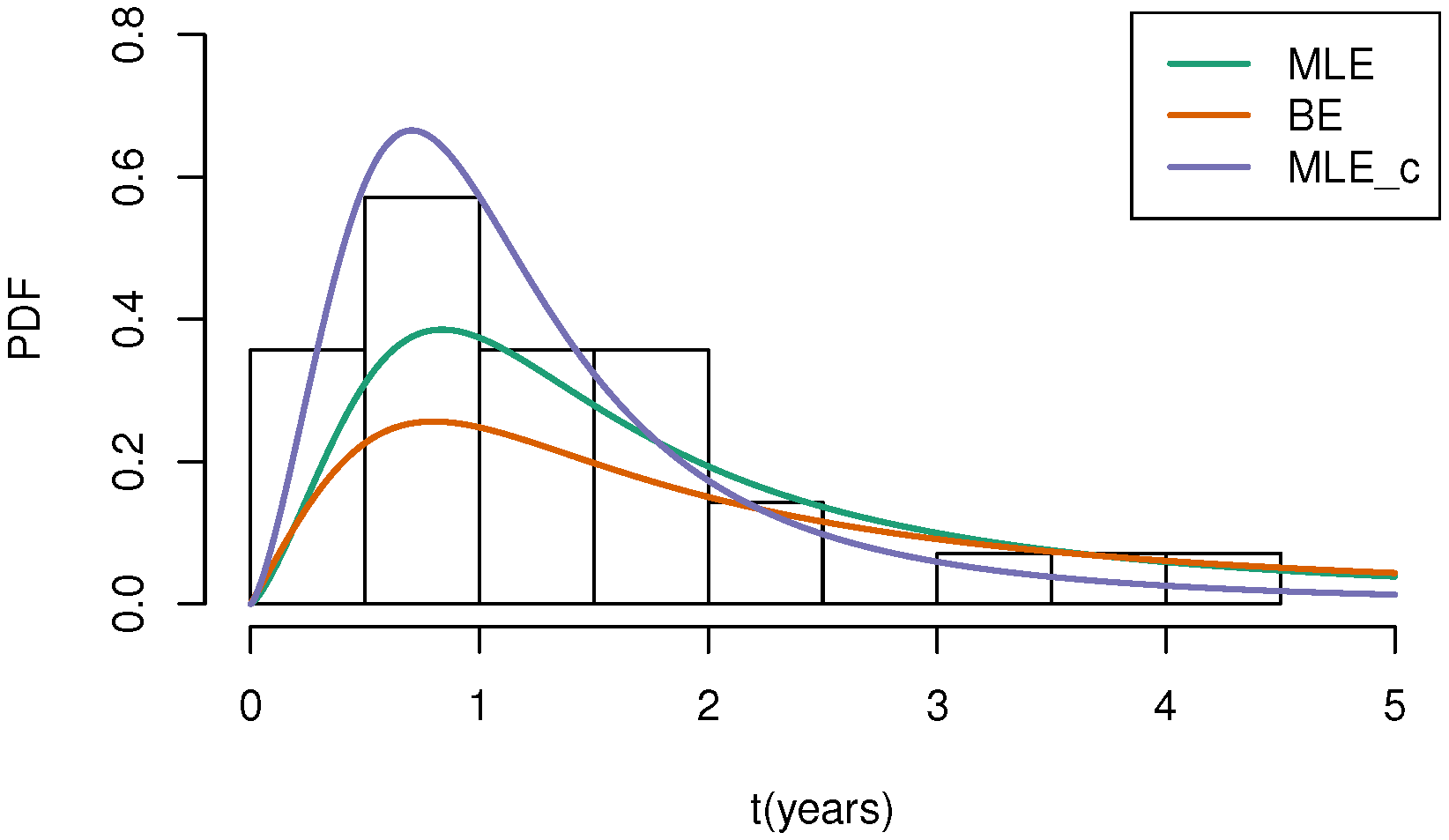
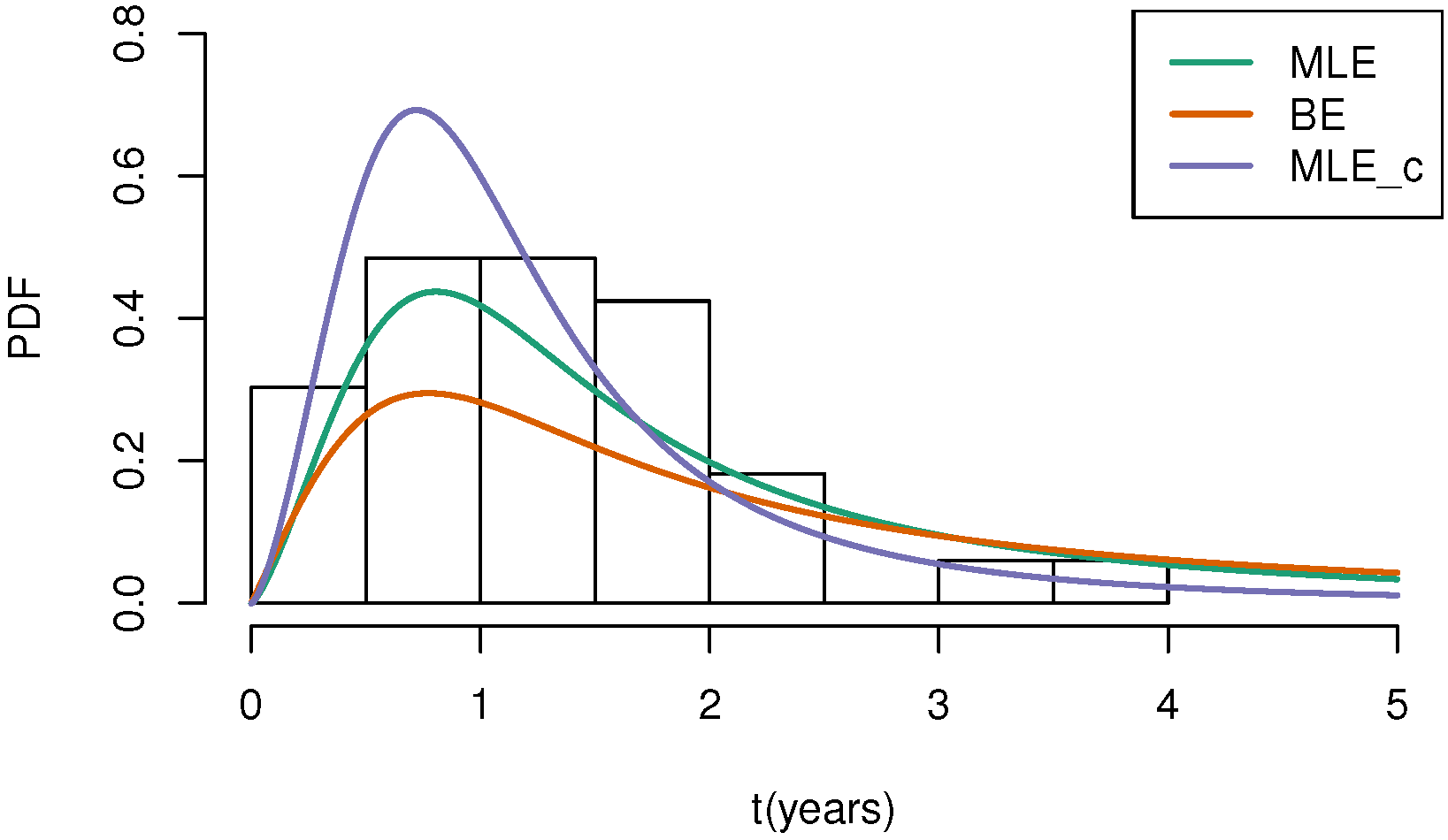
5.2. Real Data Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jammalamadaka, S.R.; Mangalam, V. Nonparametric estimation for middle-censored data. J. Nonparametr. Stat. 2003, 15, 253–265. [Google Scholar] [CrossRef]
- Jammalamadaka, S.R.; Iyer, S.K. Approximate self consistency for middle-censored data. J. Stat. Plan. Inference 2004, 124, 75–86. [Google Scholar] [CrossRef]
- Iyer, S.K.; Jammalamadaka, S.R.; Kundu, D. Analysis of middle-censored data with exponential lifetime distributions. J. Stat. Plan. Inference 2008, 138, 3550–3560. [Google Scholar] [CrossRef][Green Version]
- Davarzani, N.; Parsian, A. Statistical inference for discrete middle-censored data. J. Stat. Plan. Inference 2011, 141, 1455–1462. [Google Scholar] [CrossRef]
- Jammalamadaka, S.R.; Bapat, S.R. Middle censoring in the multinomial distribution with applications. Stat. Probab. Lett. 2020, 167, 108916. [Google Scholar] [CrossRef]
- Abuzaid, A.H.; El-Qumsan, M.K.A.; El-Habil, A.M. On the robustness of right and middle censoring schemes in parametric survival models. Commun. Stat. Simul. Comput. 2015, 46, 1771–1780. [Google Scholar] [CrossRef]
- Wang, L. Estimation for exponential distribution based on competing risk middle censored data. Commun. Stat. Theory Methods 2016, 45, 2378–2391. [Google Scholar] [CrossRef]
- Ahmadi, K.; Rezaei, M.; Yousefzadeh, F. Statistical analysis of middle censored competing risks data with exponential distribution. J. Stat. Comput. Simul. 2017, 87, 3082–3110. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Wu, M. Statistical inference for dependence competing risks model under middle censoring. J. Syst. Eng. Electron. 2019, 30, 209–222. [Google Scholar]
- Davarzani, N.; Parsian, A.; Peeters, R. Statistical Inference on Middle-Censored Data in a Dependent Setup. J. Stat. Res. 2014, 9, 646–657. [Google Scholar] [CrossRef]
- Sankaran, P.G.; Prasad, S. Weibull Regression Model for Analysis of Middle-Censored Lifetime Data. J. Stat. Manag. Syst. 2014, 17, 433–443. [Google Scholar] [CrossRef]
- Rehman, H.; Chandra, N. Inferences on cumulative incidence function for middle censored survival data with Weibull regression. J. Appl. Stat. 2022, 5, 65–86. [Google Scholar] [CrossRef]
- Sankaran, P.G.; Prasad, S. Additive risks regression model for middle censored exponentiated-exponential lifetime data. Commun. Stat. Simul. Comput. 2018, 47, 1963–1974. [Google Scholar] [CrossRef]
- Zimmer, W.J.; Keats, J.B.; Wang, F.K. The Burr XII Distribution in Reliability Analysis. J. Qual. Technol. 1998, 30, 386–394. [Google Scholar] [CrossRef]
- Soliman, A.A. Estimation of Parameters of Life from Progressively Censored Data Using Burr-XII Model. IEEE Trans. Reliab. 2005, 54, 34–42. [Google Scholar] [CrossRef]
- Yan, W.; Li, P.; Yu, Y. Statistical inference for the reliability of Burr-XII distribution under improved adaptive Type-II progressive censoring. Appl. Math. Model. 2021, 95, 38–52. [Google Scholar] [CrossRef]
- Du, Y.; Gui, W. Statistical inference of Burr-XII distribution under adaptive type II progressive censored schemes with competing risks. Results Math. 2022, 77, 81. [Google Scholar] [CrossRef]
- Abuzaid, A.H. The estimation of the Burr-XII parameters with middle-censored data. J. Appl. Probab. Stat. 2015, 4, 101. [Google Scholar] [CrossRef][Green Version]
- Cox, D.R. The analysis of exponentially distributed life - times with two types of failure. J. R. Stat. Soc. Ser. B Stat. Methodol. 1959, 21, 411–421. [Google Scholar] [CrossRef]
- Qin, X.; Gui, W. Statistical inference of Burr-XII distribution under progressive Type-II censored competing risks data with binomial removals. J. Comput. Appl. Math. 2020, 378, 112922. [Google Scholar] [CrossRef]
- Chacko, M.; Mohan, R. Bayesian analysis of Weibull distribution based on progressive type-II censored competing risks data with binomial removals. Comput. Stat. 2018, 34, 233–252. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1922, 222, 309–368. [Google Scholar]
- Gilks, W.R.; Wild, P. Adaptive Rejection Sampling for Gibbs Sampling. Appl. Stat. 1992, 41, 337–348. [Google Scholar] [CrossRef]
- Chen, M.-H.; Shao, Q.-M. Monte Carlo Estimation of Bayesian Credible and HPD Intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
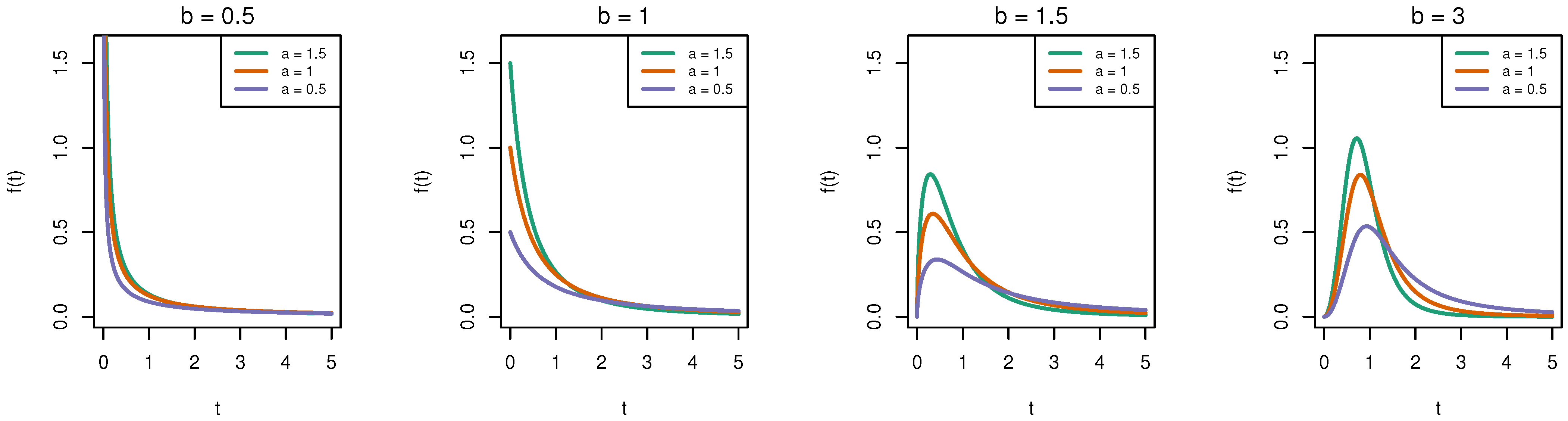
| b | |||
|---|---|---|---|
| 0.001 | 0.016977448 | 0.034834531 | 0.016680585 |
| 0.0001 | 0.016734582 | 0.035520978 | 0.016437775 |
| 0.00001 | 0.016355864 | 0.035480364 | 0.016265085 |
| pc | n | MLE | BE | ||||
|---|---|---|---|---|---|---|---|
| OPT | EM | Prior 1 | Prior 2 | ||||
| (0.5, 0.5) | 0.19 | 30 | bias | 0.0241 | 0.0241 | −0.0503 | 0.0099 |
| mse | 0.0328 | 0.0330 | 0.0348 | 0.0282 | |||
| 50 | bias | 0.0101 | 0.0100 | −0.0510 | 0.0010 | ||
| mse | 0.0166 | 0.0166 | 0.0310 | 0.0174 | |||
| 100 | bias | 0.0078 | 0.0077 | −0.0524 | −0.0049 | ||
| mse | 0.0077 | 0.0077 | 0.0265 | 0.0071 | |||
| (0.5, 1) | 0.14 | 30 | bias | 0.0188 | 0.0186 | −0.0421 | 0.0019 |
| mse | 0.0309 | 0.0311 | 0.0362 | 0.0246 | |||
| 50 | bias | 0.0102 | 0.0101 | −0.0501 | 0.0016 | ||
| mse | 0.0165 | 0.0165 | 0.0332 | 0.0154 | |||
| 100 | bias | 0.0074 | 0.0073 | −0.0640 | −0.0011 | ||
| mse | 0.0077 | 0.0077 | 0.0361 | 0.0076 | |||
| (1, 0.5) | 0.28 | 30 | bias | 0.0195 | 0.0195 | −0.0553 | −0.0036 |
| mse | 0.0318 | 0.0318 | 0.0399 | 0.0253 | |||
| 50 | bias | 0.0104 | 0.0103 | −0.0509 | −0.0098 | ||
| mse | 0.0169 | 0.0169 | 0.0317 | 0.0148 | |||
| 100 | bias | 0.0081 | 0.0080 | −0.0784 | −0.0111 | ||
| mse | 0.0078 | 0.0078 | 0.0382 | 0.0076 | |||
| () | pc | n | MLE | BE | |||
|---|---|---|---|---|---|---|---|
| OPT | EM | Prior 1 | Prior 2 | ||||
| (0.5, 0.5) | 0.19 | 30 | bias | 0.0249 | 0.0249 | −0.0860 | 0.0123 |
| mse | 0.0617 | 0.0622 | 0.0993 | 0.0542 | |||
| 50 | bias | 0.0182 | 0.0182 | −0.0969 | −0.0024 | ||
| mse | 0.0361 | 0.0361 | 0.1002 | 0.0352 | |||
| 100 | bias | 0.0139 | 0.0138 | −0.0994 | −0.0061 | ||
| mse | 0.0156 | 0.0156 | 0.0936 | 0.0164 | |||
| (0.5, 1) | 0.14 | 30 | bias | 0.0270 | 0.0267 | −0.0829 | 0.0066 |
| mse | 0.0636 | 0.0641 | 0.1024 | 0.0537 | |||
| 50 | bias | 0.0183 | 0.0182 | −0.0963 | 0.0011 | ||
| mse | 0.0354 | 0.0355 | 0.1008 | 0.0322 | |||
| 100 | bias | 0.0132 | 0.0129 | −0.1296 | −0.0044 | ||
| mse | 0.0153 | 0.0153 | 0.1324 | 0.0169 | |||
| (1, 0.5) | 0.28 | 30 | bias | 0.0275 | 0.0275 | −0.1150 | 0.0015 |
| mse | 0.0636 | 0.0636 | 0.1078 | 0.0593 | |||
| 50 | bias | 0.0188 | 0.0185 | −0.1198 | −0.0171 | ||
| mse | 0.0369 | 0.0368 | 0.1016 | 0.0313 | |||
| 100 | bias | 0.0145 | 0.0143 | −0.1562 | −0.0203 | ||
| mse | 0.0156 | 0.0155 | 0.1372 | 0.0182 | |||
| () | pc | n | MLE | BE | |||
|---|---|---|---|---|---|---|---|
| OPT | EM | Prior 1 | Prior 2 | ||||
| (0.5, 0.5) | 0.19 | 30 | bias | 0.0437 | 0.0440 | 0.0145 | 0.0756 |
| mse | 0.0294 | 0.0296 | 0.0819 | 0.0362 | |||
| 50 | bias | 0.0265 | 0.0267 | -0.0195 | 0.0460 | ||
| mse | 0.0163 | 0.0164 | 0.0892 | 0.0236 | |||
| 100 | bias | 0.0111 | 0.0117 | -0.0476 | 0.0324 | ||
| mse | 0.0072 | 0.0073 | 0.0879 | 0.0090 | |||
| (0.5, 1) | 0.14 | 30 | bias | 0.0407 | 0.0420 | -0.0032 | 0.0622 |
| mse | 0.0288 | 0.0290 | 0.0866 | 0.0364 | |||
| 50 | bias | 0.0267 | 0.0268 | -0.0342 | 0.0433 | ||
| mse | 0.0161 | 0.0159 | 0.0925 | 0.0212 | |||
| 100 | bias | 0.0105 | 0.0115 | -0.0916 | 0.0243 | ||
| mse | 0.0071 | 0.0073 | 0.1259 | 0.0101 | |||
| (1, 0.5) | 0.28 | 30 | bias | 0.0436 | 0.0436 | 0.0365 | 0.0942 |
| mse | 0.0305 | 0.0305 | 0.1037 | 0.0477 | |||
| 50 | bias | 0.0282 | 0.0280 | -0.0017 | 0.0818 | ||
| mse | 0.0168 | 0.0168 | 0.0937 | 0.0281 | |||
| 100 | bias | 0.0111 | 0.0111 | -0.0735 | 0.0618 | ||
| mse | 0.0072 | 0.0072 | 0.1349 | 0.0157 | |||
| () | pc | n | ACI | HPD-P1 | HPD-P2 | |||
|---|---|---|---|---|---|---|---|---|
| AW | CP | AW | CP | AW | CP | |||
| (0.5, 0.5) | 0.19 | 30 | 0.6490 | 0.9280 | 0.5367 | 0.8540 | 0.5914 | 0.9170 |
| 50 | 0.4938 | 0.9500 | 0.4204 | 0.8600 | 0.4610 | 0.9090 | ||
| 100 | 0.3480 | 0.9460 | 0.2993 | 0.8540 | 0.3288 | 0.9430 | ||
| (0.5, 1) | 0.14 | 30 | 0.6420 | 0.9220 | 0.5425 | 0.8610 | 0.5845 | 0.9290 |
| 50 | 0.4920 | 0.9530 | 0.4208 | 0.8500 | 0.4611 | 0.9320 | ||
| 100 | 0.3466 | 0.9430 | 0.2905 | 0.8280 | 0.3299 | 0.9410 | ||
| (1, 0.5) | 0.28 | 30 | 0.6495 | 0.9310 | 0.5273 | 0.8410 | 0.5781 | 0.9010 |
| 50 | 0.4966 | 0.9500 | 0.4174 | 0.8420 | 0.4521 | 0.9300 | ||
| 100 | 0.3498 | 0.9470 | 0.2823 | 0.7850 | 0.3242 | 0.9310 | ||
| () | pc | n | ACI | HPD-P1 | HPD-P2 | |||
|---|---|---|---|---|---|---|---|---|
| AW | CP | AW | CP | AW | CP | |||
| (0.5, 0.5) | 0.19 | 30 | 0.9264 | 0.9380 | 0.7919 | 0.8640 | 0.8571 | 0.9390 |
| 50 | 0.7095 | 0.9410 | 0.6088 | 0.8520 | 0.6638 | 0.9350 | ||
| 100 | 0.4987 | 0.9500 | 0.4309 | 0.8550 | 0.4719 | 0.9200 | ||
| (0.5, 1) | 0.14 | 30 | 0.9191 | 0.9370 | 0.7939 | 0.8800 | 0.8519 | 0.9320 |
| 50 | 0.7044 | 0.9420 | 0.6082 | 0.8730 | 0.6656 | 0.9300 | ||
| 100 | 0.4951 | 0.9530 | 0.4166 | 0.8210 | 0.4729 | 0.9400 | ||
| (1, 0.5) | 0.28 | 30 | 0.9374 | 0.9460 | 0.7697 | 0.8500 | 0.8484 | 0.9100 |
| 50 | 0.7170 | 0.9400 | 0.5983 | 0.8360 | 0.6563 | 0.9320 | ||
| 100 | 0.5035 | 0.9580 | 0.4046 | 0.8020 | 0.4671 | 0.9210 | ||
| () | pc | n | ACI | HPD-P1 | HPD-P2 | |||
|---|---|---|---|---|---|---|---|---|
| AW | CP | AW | CP | AW | CP | |||
| (0.5, 0.5) | 0.19 | 30 | 0.6830 | 0.9550 | 0.5951 | 0.9050 | 0.6172 | 0.9410 |
| 50 | 0.5181 | 0.9610 | 0.4467 | 0.8630 | 0.4705 | 0.9240 | ||
| 100 | 0.3592 | 0.9510 | 0.3064 | 0.8600 | 0.3296 | 0.9410 | ||
| (0.5, 1) | 0.14 | 30 | 0.6621 | 0.9430 | 0.5839 | 0.8920 | 0.6111 | 0.9430 |
| 50 | 0.5043 | 0.9550 | 0.4386 | 0.8740 | 0.4685 | 0.9260 | ||
| 100 | 0.3497 | 0.9660 | 0.2916 | 0.8240 | 0.3269 | 0.9460 | ||
| (1, 0.5) | 0.28 | 30 | 0.7239 | 0.9760 | 0.6167 | 0.8630 | 0.6341 | 0.9140 |
| 50 | 0.5486 | 0.9820 | 0.4585 | 0.8450 | 0.4906 | 0.9040 | ||
| 100 | 0.3783 | 0.9790 | 0.3003 | 0.7860 | 0.3416 | 0.8880 | ||
| Unit: Days | |||||||
|---|---|---|---|---|---|---|---|
| (266, 1) | (583, 1) | (79, 1) | (93, 1) | (805, 1) | (344, 1) | (306, 1) | (415, 1) |
| (178, 1) | (1484, 1) | (315, 1) | (1252, 1) | (642, 1) | (407, 1) | (356, 1) | (699, 1) |
| (667, 1) | (126, 1) | (350, 1) | (84, 1) | (392, 1) | (901, 1) | (276, 1) | (520, 1) |
| (503, 1) | (584, 1) | (355, 1) | (1302, 1) | (91, 2) | (154, 2) | (547, 2) | (707, 2) |
| (469, 2) | (1313, 2) | (790, 2) | (125, 2) | (777, 2) | (307, 2) | (637, 2) | (577, 2) |
| (517, 2) | (287, 2) | (717, 2) | (141, 2) | (427, 2) | (36, 2) | (588, 2) | (350, 2) |
| (567, 2) | (1140, 2) | (448, 2) | (904, 2) | (485, 2) | (248, 2) | (423, 2) | (285, 2) |
| (315, 2) | (727, 2) | (210, 2) | (409, 2) | (227, 2) | |||
| Cause | Data (Years) | |||
|---|---|---|---|---|
| Cause 1 | 0.7288 | 0.2164 | 0.2548 | 2.2055 |
| 0.9425 | 1.1370 | 4.0658 | 1.0740 | |
| 0.8630 | 3.4301 | 1.7589 | 1.1151 | |
| 1.9151 | 1.8274 | 0.9589 | 0.2301 | |
| 0.9726 | 3.5671 | 0.7562 | 1.4247 | |
| 1.6000 | [0.0911, 5.0378] | [0.6011, 1.7187] | [0.3192, 0.6168] | |
| [0.8229, 1.0968] | [0.0267, 0.5380] | [2.0658, 4.4214] | [0.1413, 2.1862] | |
| Cause 2 | 0.2493 | 1.4986 | 1.9370 | 1.2849 |
| 3.5973 | 2.1644 | 0.3425 | 2.1288 | |
| 1.7452 | 1.5808 | 1.9644 | 0.3863 | |
| 1.1699 | 0.0986 | 1.5534 | 1.2274 | |
| 2.4767 | 1.1589 | 0.7808 | 0.8630 | |
| 1.9918 | 0.5753 | 1.1205 | 0.6219 | |
| [0.1226, 0.9680] | [0.6727, 2.0312] | [0.4918, 2.2852] | [0.4439, 0.9947] | |
| [0.7571, 2.0435] | [0.0610, 1.6743] | [0.9411, 3.4598] | [0.3921, 1.3314] | |
| [0.1619, 1.0728] | ||||
| BE | ACI | HPD | |||
|---|---|---|---|---|---|
| 0.4339 | 0.4339 | 0.3025 | [0.2584, 0.6095] | [0.1832, 0.4357] | |
| 0.5114 | 0.5114 | 0.3571 | [0.3182, 0.7047] | [0.1664, 0.4951] | |
| b | 2.3292 | 2.3292 | 2.0231 | [1.6961, 2.9624] | [1.5444, 2.5151] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Gui, W. Parametric Estimation and Analysis of Lifetime Models with Competing Risks Under Middle-Censored Data. Appl. Sci. 2025, 15, 4288. https://doi.org/10.3390/app15084288
Liang S, Gui W. Parametric Estimation and Analysis of Lifetime Models with Competing Risks Under Middle-Censored Data. Applied Sciences. 2025; 15(8):4288. https://doi.org/10.3390/app15084288
Chicago/Turabian StyleLiang, Shan, and Wenhao Gui. 2025. "Parametric Estimation and Analysis of Lifetime Models with Competing Risks Under Middle-Censored Data" Applied Sciences 15, no. 8: 4288. https://doi.org/10.3390/app15084288
APA StyleLiang, S., & Gui, W. (2025). Parametric Estimation and Analysis of Lifetime Models with Competing Risks Under Middle-Censored Data. Applied Sciences, 15(8), 4288. https://doi.org/10.3390/app15084288







