Application of Improved Whale Algorithm to Optimize Dephosphorization Process Parameters in Converter Steelmaking

Abstract

Regulating the process parameters in converter steelmaking is crucial for reducing the phosphorus content in molten steel and enhancing its quality. However, immoderate alteration may result in raised production costs and the occurrence of phosphorus return. This study addresses process parameter optimization challenges in converter steelmaking by proposing an improved multi-objective whale optimization algorithm (IMOWOA) that synergistically integrates metallurgical thermodynamics with data-driven modeling. The methodology constructs a physics-informed objective function linking process parameters to optimization targets, thereby resolving the disconnect between mechanistic and data-driven modeling approaches. The algorithm innovatively combines Sobol quasi-random sequences with grey wolf social hierarchy strategies to prevent premature convergence in high-dimensional search spaces while maintaining Pareto front diversity, supplemented by a reward mechanism to ensure strict adherence to multi-objective constraints. Experimental validation using steel plant production data demonstrates IMOWOA’s efficacy, achieving a 10.8% reduction in endpoint phosphorus content and a 5.79% decrease in production costs per ton of steel. Comparative analyses further confirm its superior feasibility and stability in quality-cost co-optimization, evidenced by a 12.6% improvement in hypervolume (HV) over conventional swarm intelligence benchmarks, establishing a robust framework for industrial metallurgical process optimization.

1. Introduction

Converter steelmaking offers a series of advantages, including high efficiency and low cost, making it one of the mainstream steelmaking methods in the steel industry [1]. This method effectively reduces phosphorus content—a detrimental element in molten iron—through both physical heating and exothermic chemical reactions between components. The endpoint phosphorus content of molten steel serves as a critical indicator for assessing the quality of molten steel, which directly influences the steel’s plasticity and toughness [2]. Consequently, the reasonable regulation of converter steelmaking process parameters, effectively reducing the endpoint phosphorus content of molten steel is one of the significant challenges that the steel industry needs to overcome to meet the growing market demand and achieve the goal of high-quality and low-cost steel production.

Scholars globally have conducted extensive research on process optimization to improve steel quality. Early studies by Deng Yong [3] and Deng Nanyang [4] focused on adjusting slag-forming and scrap material ratios to reduce endpoint phosphorus content under fixed furnace temperature conditions. However, the inherent complexity of in-furnace chemical reactions limits the effectiveness of purely dosage-based control strategies. Subsequently, the literature [5] proposes a synergistic modeling strategy integrating principal component analysis (PCA) and neural networks (NNs) based on the characteristics of converter metallurgical processes and production data. This method employs PCA to perform linear orthogonal transformations on process parameters, thereby eliminating multicollinearity among variables. However, PCA—a linear projection technique rooted in variance maximization—fails to adequately address nonlinear coupling relationships inherent in metallurgical processes, resulting in the forced decoupling of critical nonlinear features. While the subsequently developed neural network prediction model enhances fitting capabilities through nonlinear activation functions, its fully connected architecture lacks embedded metallurgical thermodynamic constraints. Consequently, the weights of the hidden layer remain disconnected from actual physical processes, creating a fundamental disconnect between mechanistic principles and data-driven modeling. To enhance model performance, Han Kaifeng [6], Yang Rongzheng [7], and Azzaz [8], R. introduced optimization algorithms to refine neural networks and extreme learning machines (ELMs), aiming to improve prediction accuracy for endpoint phosphorus content in molten steel. Nevertheless, these approaches retain inherent limitations: neural networks remain prone to overfitting, while ELM suffers from random weight initialization defects. Furthermore, such methods rely on engineers to preset static combinations of process parameters for pre-production simulations, effectively reducing the dynamic smelting process to a discrete parameter search. This simplification inherently limits real-time responsiveness to raw material composition fluctuations and fails to capture time-varying couplings among process parameters. To address steel quality optimization challenges, researchers have adopted intelligent optimization algorithms such as particle swarm optimization [9,10], genetic algorithm [11,12], and grey wolf algorithm [13], among others. These algorithms iteratively adjust process parameters by holistically considering multiple influencing factors during smelting. However, conventional methods frequently converge to local optima, overlook critical process constraints, and struggle to balance model accuracy with industrial feasibility—particularly when simultaneously optimizing endpoint phosphorus content and production costs.

In addressing the optimization problem in the dephosphorization process paramters of the converter steelmaking production, this study employs the actual production data from an industrial steel plant as a case exemple. This paper describes the converter steelmaking process, numerically analyzing the objectives to be optimized along with their constraints, establishing the relationship model between process parameters and objective function through machine learning methods, and proposing the improved multi-objective whale optimization algorithm (IMOWOA). The scientific novelty manifested in three key innovations:

• A hybrid metallurgical-mechanism modeling framework is constructed to enhance the interpretability of data-driven models by embedding thermodynamic constraints directly into the optimization architecture;
• A Sobol sequence initialization and grey wolf collaborative search mechanism is designed to dynamically balance global exploration and local exploitation capabilities, addressing premature convergence in high-dimensional spaces;
• A reward function is introduced to enable multi-objective synergy, ensuring economically optimal solutions while rigorously satisfying process constraints.

Experimental validation demonstrates that the IMOWOA achieves a 12.6% improvement in hypervolume (HV) compared to the second-best performing MOBWO, confirming the enhanced quality and stability of the solution set. In full-scale production trials, parameters optimized by IMOWOA reduce endpoint phosphorus content by 10.8% and lower production costs by 5.79% per ton of steel relative to current industrial benchmarks. These results validate its capability to deliver a framework for metallurgical process optimization that harmonizes physical rationality with engineering applicability.

The subsequent sections of this paper are structured as follows: Section 1 research background and problem definition. Section 2 delves into the analysis of the objective to be optimized. Section 3 design principles of the improved multi-objective whale optimization algorithm. Section 4 encompasses experiments and analysis. Section 5 concludes and future directions.

2. Materials and Methods

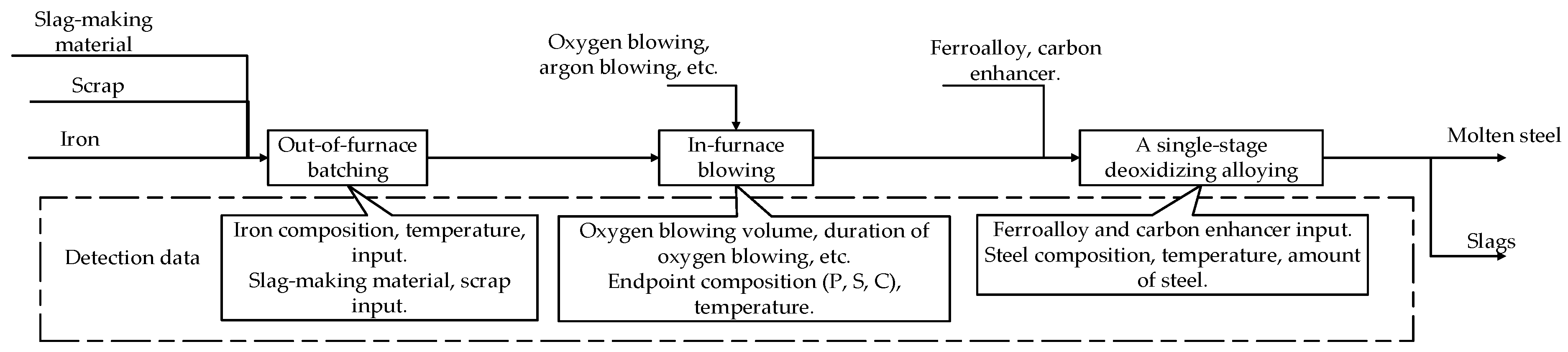
This study utilizes the converter steelmaking production process of a steel mill (Shanxi Province, China) manufacturing Q235B-Z grade steel as a case study, with the process flow presented in Figure 1. The production process encompasses out-of-furnace batching, in-furnace blowing, and a single-stage deoxidizing alloying process, which is aimed at initially refining the molten steel.

In the context of the industrial production process, dephosphorization predominantly occurs during the furnace-blowing stage. During this stage, the analytical assessment and monitoring of detection data from the batching and blowing stages of the furnace are critical for achieving precise control over the dephosphorization process. The test data encompass various parameters, including the composition of raw materials, temperature, and oxygen supply. Following the completion of the blowing process, a detailed evaluation of the process is conducted by measuring the steel composition data (i.e., endpoint composition). By meticulously adjusting the detection data to optimize the dephosphorization reaction, it is possible to effectively mitigate the occurrence of phosphorus reversion, thereby enhancing dephosphorization efficiency and reducing production costs [2]. Consequently, to tackle the optimization problem associated with the dephosphorization process parameters during the furnace blowing stage, the optimization objectives are established based on numerical analysis of the smelting process, with the focus being on minimizing the endpoint phosphorus content (f₁) and the steel production cost per ton (f₂). The selected process parameters include the detection data of both the incoming batch and the furnace blowing stage.

Through a comprehensive analysis of the physicochemical mechanism underlying the dephosphorization reaction within the furnace, as documented in the literature [2], several critical factors that influence the endpoint phosphorus content in steel were identified. These factors encompass the carbon, silicon, and phosphorus content in the molten iron, the quantity and temperature of the molten iron, the quantity of scrap utilized, the amounts of lime and ore input, the initial pouring temperature, and the volume of oxygen blowing, among other experimental parameters. Consequently, the relationship function for the phosphorus content at the endpoint was derived as follows:

$$f_1=f\left(w_{c0},w_{si0},w_{p0},W_{iron},T_{iron},W_{resteel},W_{\lim e},W_{ore},O,T\right).$$

(1)

In the formula, f₁ denotes the endpoint phosphorus content, while w_c0, w_si0, and w_p0, respectively, represent the iron-carbon, silicon, and phosphorus content. W_iron, W_resteel, W_lime, and W_ore, respectively, refer to the weight of iron, scrap, lime, and ore. T_iron represents the temperature of iron. O and T signify the amount of oxygen blowing and the temperature of a pour, and f signifies the function for calculating endpoint phosphorus content.

The primary constituent of lime is calcium oxide. To decrease the production cost per tonne of steel, limestone and raw dolomite are partially substituted for lime in practical production processes. The production cost per ton of steel can be articulated as follows:

$$\left\{\begin{array}{l}C={\displaystyle \frac{C_m+C_s+C_t}{W_t}}\\ W_t=\left(W_{\mathrm{iron}}+W_{\mathrm{resteel}}\right)\ast \mathrm{Qcover}\end{array}\right.,$$

(2)

$$\left\{\begin{array}{l}{C}_m=k_0{W}_{iron}+k_1{W}_{resteel}+k_2{w}_{si0}\\ {\mathrm{C}}_{\mathrm{s}}={\displaystyle \frac{k_3{W}_{\lim e}+k_4{W}_{ls}+k_5{W}_{rd}+k_6{W}_{ore}}{1000}}\\ C_t=k_{7}O+k_{8}T\end{array}\right..$$

(3)

In the formula, C represents the total cost of producing all tonnes of steel, C_m denotes the cost of raw materials, C_s signifies the cost of auxiliary materials, and C_t stands for the cost of process control. W_ls, W_rd, and W_t represent the weights of limestone, raw dolomite, and molten steel respectively. Q_cover refers to the smelting of molten steel with iron and scrap steel to achieve the conversion rate, typically around 90%. The parameters k₀ to k₈ denote the corresponding parameter unit price.

Based on the above, the relationship function for the production cost of tonnes of steel can be articulated as follows:

$$f_2=a_0+a_1{W}_{iron}+a^2{W}_{resteel}+a_3{w}_{si0}+ a_4{W}_{\lim e}+ a_5{W}_{ls}+a_6{W}_{rd}+a_7{W}_{ore}+a_{8}O+a_{9}T$$

(4)

In this equation, f₂ represents the total production cost of steel in tonnes, and a₀ to a₉ signify correlation coefficients.

The multi-objective function is constructed with the optimization goals of minimizing the endpoint phosphorus content (f₁) and minimizing the production cost per tonne of steel (f₂). The formulation of this multi-objective function is presented as depicted in the following equation:

$$\min f=[f_1,f_2].$$

(5)

According to the overall dephosphorization reaction equation [13], it is evident that the phosphorus content in molten iron undergoes chemical reactions with the composition of auxiliary materials, resulting in the formation of stable precipitates. To ensure that the phosphorus content in the molten iron is adequately reduced to meet practical production requirements while simultaneously controlling the production cost per tonne of steel, constraints have been introduced in the optimization study of process parameters, specifically aimed at the input materials during the charging phase.

$$s.t. \left\{\begin{array}{l}\begin{array}{c}{W}_{\lim e}+W_{ls}+W_{rd}+W_{ore}\ge 4500kg\\ W_{{iron}_{\min }}\le W_{iron}\le (1+30\%)W_{{iron}_{\max }}\end{array}\\ W_{{resteel}_{\min }}\le W_{resteel}\le (1+30\%)W_{{resteel}_{\max }}\\ 0<W_{{\lim e}_{\min }}\le W_{sh}\le (1+30\%)W_{{\lim e}_{\max }}\\ 0<W_{{ls}_{\min }}\le W_{shs}\le (1+30\%)W_{{ls}_{\max }}\\ 0<W_{{rd}_{\min }}\le W_{sbys}\le (1+30\%)W_{{rd}_{\max }}\\ 0<W_{{ore}_{\min }}\le W_{ks}\le (1+30\%)W_{{ore}_{\max }}\end{array}\right..$$

(6)

3. Proposed Methods

In the aforementioned multi-objective optimization problems, the multi-objective whale optimization algorithm (MOWOA) [14] simulates the foraging behavior of whales, employing global search and spiral encirclement techniques to strategy significantly enhance the acquisition of globally optimal solutions within the solution space. However, in addressing the optimization of dephosphorization process parameters, due to the conflicting relationships among multiple objectives, which may necessitate compromising the endpoint phosphorus content to achieve a globally optimal solution. To tackle this issue, an improved multi-objective whale optimization algorithm (IMOWOA) will be designed by refining the MOWOA algorithm through enhancements in the population initialization strategy, incorporation of a reward function, and enhancement of search capabilities.

3.1. Optimisation of the Initialization Population

The distribution of the initialized population significantly influences both the convergence speed and accuracy of the optimization algorithm [15]. In addressing the optimization problem of the dephosphorization process parameter, the initial set of process parameters is distributed as uniformly as possible within the search space. This uniform distribution enhances the search range of the algorithm in the solution space, thereby improving its exploration capabilities and diversity, ultimately obtaining a more optimal set of process parameters [16]. The Sobol sequence, recognized for its low-variance, high-efficiency characteristics, serves as a deterministic sequence suitable for generating uniformly distributed points within multidimensional spaces. By employing Sobol sequences to define the set of process parameters, one can ensure that the initial distribution of the population is more uniform in the solution space. This uniformity is instrumental in accelerating the algorithm’s convergence and enhancing the accuracy of the final solution. The locations of the initial process parameters, generated using Sobol sequences, can be expressed as follows:

$$x_n=x_{\min }+K_n\left(x_{\max }-x_{\min }\right).$$

(7)

In the aforementioned formula, x_min and x_max, respectively, represent the lower and upper limits of the process parameter values; K_n denotes the random number generated by the Sobol sequence constrained within the interval [0, 1].

3.2. Addition of Reward Function

In the multi-objective optimization algorithm, there often exists a certain degree of mutual exclusivity among the objective functions, necessitating the optimization of the overall objective at the expense of some individual objectives. In the dephosphorization process parameter optimization problem, the primary optimization objective is to enhance dephosphorization efficiency. Consequently, it is imperative to minimize the necessity of compromising endpoint phosphorus content in the pursuit of obtaining the optimal solution set. To address this challenge, the introduction of the reward function serves to realign the search direction of the algorithm, thus prompting the optimization algorithm to greater emphasis search and optimization of the endpoint phosphorus content for improved dephosphorization results.

The configuration of the reward function directly influences the optimization process and the resultant optimal solution set of the algorithm. When the reward value is set excessively high, the algorithm may disproportionately prioritize the optimization of the rewarded objectives, thereby compromising the potentially diminishing overall performance. Conversely, if the reward value is set too low, the reward function may fail to significantly affect the search direction of the algorithm, resulting in negligible optimization effect and difficulties in achieving the intended improvements in dephosphorization efficiency. Consequently, establishing a reasonable reward function is essential. By balancing the magnitude of the reward value, it can ensure that the algorithm adequately addresses the relationship between the endpoint phosphorus content and the production cost per tonne of steel throughout the optimization process, ultimately achieving enhanced optimization results. The increased reward items are delineated in the following formula:

$$reward=e^{\left(-beta\cdot f1\right)}.$$

(8)

In the formula, the term reward refers to the reward factor, while beta denotes the number of normals employed to modulate the rate of increase of the reward factor.

Consequently, the objective function f₁ has been updated to reflect these adjustments.

$$f_1=f_1-alpha\cdot reward.$$

(9)

In the context of this formulation, alpha represents the learning rate utilized for iterative updating of the objective function f₁.

3.3. Improvement of Search Capabilities

When addressing the multi-objective dephosphorization process parameter optimization problem, the MOWOA exhibits several inherent limitations, such as a propensity to converge prematurely to local optima and a relatively slow convergence speed. In contrast, the multi-objective grey wolf optimization (MOGWO) algorithm [17] emulates the collaborative foraging structure observed in natural grey wolf packs by employing a leader–follower structure along with a flexible individual update mechanism. This architecture facilitates effective information sharing and extensive exploration of the solution space. The synergistic integration of these algorithmic components markedly improves global exploration capabilities and diversity maintenance ability of the MOWOA algorithm, thereby effectively mitigating the solutions of converging to local optimal and improving the algorithm’s running efficiency.

Following the incorporation of the MOGWO algorithm, the MOWOA utilizes three distinct populations to identify the individual exhibiting the best fitness across the current populations, designating this individual as the target prey. The remaining individuals undergo updates based on the position of this target prey. The selection probability during the encircling prey phase and the bubble net predation phase of the algorithm is set at 50%. Furthermore, when the condition |A_i| < 1 is satisfied, the mathematical model is updated as follows:

$$\left\{\begin{array}{l}{D}_i=\left|C_i{X}_i^{*}\left(t\right)-X_i\left(t\right)\right|\\ D_i^{\prime }=\left|X_i^{*}\left(t\right)-X_i\left(t\right)\right|\end{array}\right. i=1,2,3 ,$$

(10)

$$X_i(t+1)=\left\{\begin{array}{l}{X}_i^{*}\left(t\right)-A_i{D}_i p<0.5\\ X_i^{*}\left(t\right)+D_i^{\prime }{e}^{bl}\cos \left(2\pi l\right) p\ge 0.5\end{array}\right. i=1,2,3 .$$

(11)

In the current, X(t) denotes the position vector of the current individual whale, while X_i^*(t) represents the position of the current optimal solution among various groups. The D_i signifies the distance between the individual whale and the optimal position, and D_i′ refers to the distance between each prey and the optimal position. The variable t indicates the current iteration number, while A_i and C_i are coefficient vectors that influence the algorithm’s search dynamics, Additionally, p is a randomly generated number within the interval [0, 1].

During the stochastic search phase, the algorithm randomly searches for prey throughout the search space, thereby increasing the likelihood of escaping from the local optimal. When the condition |A_i| ≥ 1 is satisfied, the mathematical model is subsequently updated as follows:

$$\left\{\begin{array}{l}{D}_i^{″}=\left|Ci{X}_{randi}(t)-X\left(t\right)\right|\\ X_i\left(t+1\right)=X_{randi}\left(t\right)-A_i{D}_i^{″}\end{array}\right. i=1,2,3,$$

(12)

where X_rand(t) denotes the position of the randomly selected individual whales within each population. The term D_i″ represents the distance between the randomly updated individual and the optimal solution in the search space.

The optimal individual of the population is updated by taking the arithmetic mean of the optimal individuals from the three distinct populations. This procedure can be mathematically represented as follows:

$$X\left(t+1\right)={\displaystyle \frac{{\displaystyle \sum _{i=1}^3{X}_i\left(t+1\right)}}{3}}$$

(13)

3.4. Optimization Algorithm Steps

The incremental multi-objective whale optimization algorithm (IMOWOA) first employs the Sobol sequence to initialize the population, thereby enhancing diversity. A reward factor is then integrated to refine the search direction, followed by the incorporation of the grey wolf optimization (GWO) algorithm to perturb the current optimal solution, thereby augmenting global search capabilities.

Step 1: Initialize algorithm parameters, including population size, data dimensions, number of iterations, alpha, beta, etc.

Step 2: The regression function was employed to formulate a relational model delineating the association between the objective variable and the process parameters. Subsequently, set objective function by Equation (5).

Step 3: Set the constraints according to Equation (6).

Step 4: Initialize three populations using Sobol in Equation (7).

Step 5: Select individuals exhibiting high adaptive capabilities among the whale population as reference points. Assess the value of the acceleration coefficient A_i. If the |A_i| < 1, incorporate a random perturbation (p) and update the optimal positions of the different groups following the Equation (11). Conversely, the optimal positions of the various groups will be updated following Equation (12) provided.

Step 6: The optimal position of the overall population is updated under Equation (13), and the validity of this optimal position is assessed against the established constraints utilizing Equation (6).

Step 7: Following a single iteration, the reward factor is incorporated, and the objective function f₁ is modified following Equation (9) to determine the current optimal position.

Step 8: the optimal position and its corresponding fitness value are updated based on the prevailing state of the whale population.

Step 9: The convergence criteria are evaluated using three termination conditions: (1) the relative change rate of the best fitness value F remains below 0.1% over five consecutive iterations, (2) the total iteration count reaches 800, (3) the relative fluctuations of both HV and Spacing metrics are maintained below 0.1% across five consecutive iterations. To ensure computational efficiency without compromising solution quality, the algorithm employs low-frequency evaluation and dynamic thresholds derived from sensitivity analysis. The optimization process terminates immediately upon satisfying any criterion; otherwise, it returns to Step 4 for continued iteration.

The flowchart of the IMOWOA is illustrated in Figure 2.

4. Experiment and Results

The objective of this study is to identify the optimal process parameters for converter steelmaking with reduced phosphorus content at the endpoint while minimizing the production cost per tonne of steel, utilizing an optimization algorithm. The original dataset comprises 14 process parameters recorded throughout the steelmaking process, including molten iron composition (C, Si, P content), operational parameters (oxygen blowing volume, temperature), and flux proportions (lime, dolomite, etc.). During preprocessing, heats failing to meet molten steel quality standards, lacking critical parameters (e.g., endpoint phosphorus content), or exhibiting statistical outliers were removed, resulting in 4000 validated data groups retained for subsequent analysis. A subset of the processed sample data is presented in

Table 1. Partial sample data.

	1	2	3	4	5	6	7	8
Ferric C (%)	4.68	4.62	4.59	4.66	4.91	4.95	4.72	4.80
Ferric Si (%)	0.32	0.25	0.30	0.31	0.39	0.32	0.41	0.39
Ferric P (%)	0.112	0.120	0.122	0.125	0.114	0.113	0.123	0.122
Temperature of iron (T)	1344	1330	1330	1280	1301	1320	1320	1300
Amount of iron (t)	116.00	116.90	113.70	110.05	109.10	109.00	112.30	108.80
Scrap quantity (t)	15.90	19.95	20.40	21.00	23.00	19.00	21.25	19.29
Lime (kg)	3200	1200	1700	1500	1800	1100	2000	1700
Limestone (kg)	600	3000	4100	1800	2200	3900	2700	3700
Raw dolomite (kg)	1000	1000	1500	2000	1600	1000	2600	1000
Ore (kg)	800	1500	1100	3400	3600	1300	700	1900
Oxygen blowing quantity (m3)	5566	5965	6242	5132	5326	6197	5755	5808
First pour temperature (°C)	1682	1646	1674	1640	1667	1680	1680	1644
Endpoint P (%)	0.019	0.015	0.024	0.018	0.021	0.020	0.022	0.010
Production cost (CNY/t)	3740.70	3429.21	3420.80	3420.58	3401.90	3426.18	3407.73	3428.74

Note: The table presents eight representative samples selected from the complete dataset comprising 4000 heats, with endpoint phosphorus content (Endpoint P) and production cost per ton of steel established as the dual optimization objectives.

. The preprocessed sample data that meet the specified requirements is utilized to construct a regression model that establishes the mapping relationship between process parameters (e.g., lime addition amount, oxygen blowing volume) and the endpoint phosphorus content of molten steel as well as the production cost per ton of steel. A dual-objective optimization problem is formulated by defining the objective function, and an improved multi-objective whale optimization algorithm is employed to optimize the process parameters. The parameter adjustment is specifically implemented through the following mechanisms.

To ensure physical feasibility, the optimization process integrates domain-specific constraints derived from metallurgical thermodynamics. For instance, lime dissolution exhibits nonlinear saturation when the addition exceeds 80 kg/ton (Section 2), and temperature thresholds govern reaction kinetics. These constraints are explicitly enforced via Equation (6), ensuring that optimized parameters align with industrial practice rather than arbitrary combinations. Parameter encoding and search space definition involve encoding the process parameters as 12-dimensional decision variables, with upper and lower bounds determined based on historical data ranges. Dynamic weight allocation adaptively adjusts the optimization weights of phosphorus content and cost according to the distribution state of the current solution set. A hybrid search strategy is designed based on social hierarchy cooperation, deeply integrating the hierarchical population structure of the MOGWO with the spiral contraction mechanism of the MOWOA to achieve collaborative optimization of process parameters in high-dimensional space. Constraint handling imposes an exponential penalty on solutions that violate process boundaries, ensuring that parameter adjustments comply with industrial feasibility. Finally, the optimal parameter combination satisfying production conditions is selected from the Pareto solution set.

4.1. Modeling Effects Analysis

The complex nonlinear relationship between process parameters and endpoint phosphorus content originates from fundamental metallurgical mechanisms: the temperature-dependent competitive reaction mechanism where lower temperatures promote dephosphorization through CaO-P₂O₅ formation while simultaneously reducing slag fluidity and reaction kinetics; the threshold effect of lime dissolution demonstrating nonlinear saturation characteristics when addition exceeds 80 kg/ton; and the time-dependent reaction kinetics exhibiting distinct inflection points during different blowing stages. These physicochemical complexities manifest mathematically as strong interaction effects and non-Gaussian residual distributions in linear models. 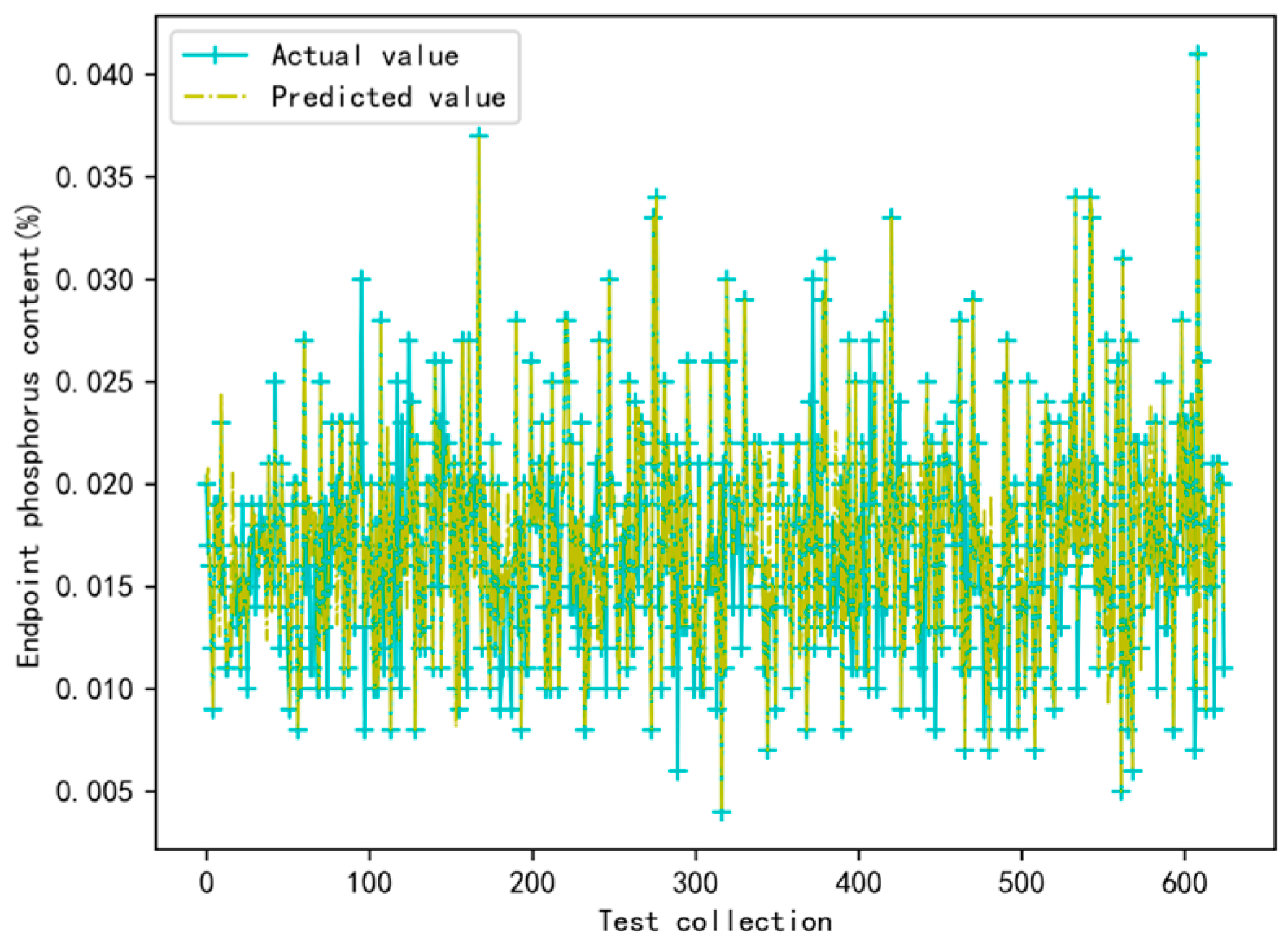The extremely random forest (ERT) [18] algorithm demonstrates superior capability in capturing these nonlinear relationships through three principal mechanisms: the ensemble of randomized decision trees intrinsically models multiplicative parameter interactions; the automatic feature selection weights reveal dominant nonlinear parameters; and the algorithm’s inherent robustness to collinear inputs effectively handles the strong correlation between slag-forming materials and furnace temperature. Consequently, the ERT algorithm was employed to construct a regression model for predicting the endpoint phosphorus content. To evaluate the predictive performance of this model, a random selection of 600 sets of sample data was utilized as test samples for experimentation, yielding the prediction results depicted in Figure 3. The results indicate that the fluctuations between the model-predicted values and the actual values exhibit a similar trend.

The root mean square error (RMSE) of the prediction model for endpoint phosphorus content was measured at 0.09, with an R² value of 0.79. Notably, the proportion of furnaces exhibiting a prediction error of endpoint phosphorus content in the range of −0.001% to 0.001% constituted 72.30% of the total furnaces, while those with a prediction error ranging from −0.003% to 0.003% accounted for 85.05% of the total furnaces. The results confirm that the model demonstrates a relatively low average prediction error and high precision, indicating its efficacy and reliability in predicting the endpoint phosphorus content.

4.2. Indicator Evaluation

Three evaluation metrics, inverted generational distance (IGD), hypervolume metric (HV), and spacing evaluation method (Spacing), are used to evaluate the convergence, diversity, and uniformity of the algorithm.

The IGD metric [19] serves as an evaluation criterion for assessing the convergence and distribution performance of optimization algorithms. It does so by computing the minimum sum of distances between each point on the true Pareto front and the set of solutions produced by the algorithm. A smaller IGD value indicates that the algorithm achieves faster convergence to the true Pareto front with fewer iterations while preserving comprehensive coverage of the solution set. The formula for calculation IGD is as follows:

$$\mathrm{IGD}(P,Q)={\displaystyle \frac{{\displaystyle \sum _{x\in P}d(x,Q)}}{\left|P\right|}}.$$

(14)

In the expression, P denotes the set of points uniformly distributed across the real Pareto front, with |P| representing the number of individuals in the set. Q refers to the Pareto optimal solution set generated by the algorithm, while d(x, Q) signifies the minimum Euclidean distance from an individual point x in P to the biological minimum of the population Q.

The HV metric [20] quantifies the volume enclosed by the Pareto optimal solution set and serves as an indicator of both the diversity and extent of coverage provided by the algorithm’s output. The growth rate of the HV metric across iterations serves as a critical indicator of convergence efficiency. A significant early-stage increase in HV values demonstrates the algorithm’s ability to rapidly identify high-quality solutions during initial iterations, while higher final HV values quantitatively reflect the enhanced accuracy of the Pareto optimal set. The method for computing HV is illustrated as follows:

$$HV(X,P)=\underset{x\in X}{\overset{X}{\cup }}v(x,P).$$

(15)

In this context, v(x, P) represents the hypervolume of the region delineated by the solution x in the optimal solution set X and the reference point P.

The Spacing metric [21] is defined as an assessment of the standard deviation of the minimum distance between each solution and its respective neighbors within the solutions set generated by her algorithm. This metric is employed to evaluate both the distribution and uniformity of solutions in the set. A smaller Spacing metric value indicates that the algorithm effectively avoids premature convergence to local optima during the search process while achieving uniform exploration of the objective space, thereby minimizing the generation of redundant or overlapping solutions. The calculation is expressed as follows:

$$Spacing(P)=\sqrt{{\displaystyle \frac{1}{\left|P\right|-1}}{\displaystyle \sum _{i=1}^{\left|P\right|}{(\overline{d}-d_i)}^2}},$$

(16)

where P denotes the total number of solutions in the solution set, d_i represents the distance between the ith solution and its nearest neighbor, and $\overline{d}$ signifies the mean of all di values.

4.3. Pareto Solution Set Analysis

In the context of the dephosphorization optimization problem, it is imperative to concurrently optimize two objectives to attain outcomes. Typically, the optimal solution is represented by a set, known as the Pareto optimal solution set, which characterizes the trade-offs between the competing objectives.

Table 2. IMOWOA algorithm parameter settings.

Type	Parameter
Population size	50
Data dimension	12
Number of iterations	800
Solenoidal morphology constant	1
Alpha	0.2
Beta	0.8

delineates the specific parameter configurations within the IMOWOA.All Pareto optimal solutions (

Table 3. Pareto optimal solution set.

Parameter	Practicality	1	2	3
Ferric C (%)	4.67	4.47	4.48	4.48
Ferric Si (%)	0.54	0.57	0.57	0.57
Ferric P (%)	0.101	0.103	0.103	0.103
Temperature of iron (T)	1340	1302	1300	1301
Amount of iron (t)	118.7	111.7	111.3	111.4
Scrap quantity (t)	21.90	38.91	38.90	38.93
Lime (kg)	2000	2246	2248	2243
Limestone (kg)	4000	4551	4609	4594
Raw dolomite (kg)	1500	1812	1807	1809
Ore (kg)	1000	806	792	791
Oxygen blowing quantity (m3)	6397	6394	6405	6399
First pour temperature (°C)	1641	1636	1634	1634
Endpoint P (%)	0.0120	0.0107	0.0108	0.0109
Production cost (CNY/t)	3414.68	3217.03	3216.65	3216.52

) were validated against historical production data, confirming that the proposed parameter adjustments (e.g., increased limestone substitution) adhere to known physicochemical limits (e.g., slag basicity requirements) while achieving measurable quality-cost improvements.

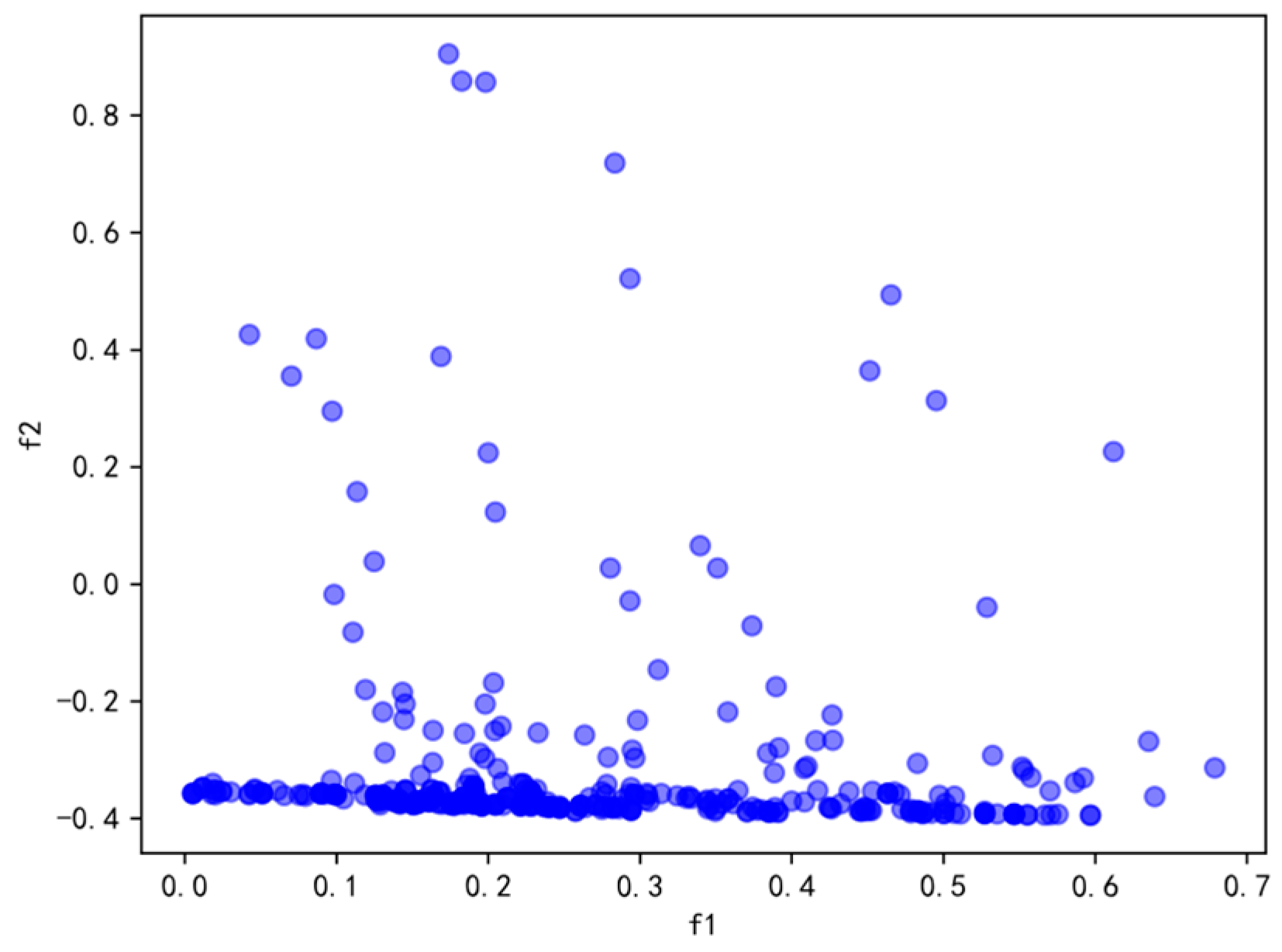
The IMOWOA was employed to address the multi-objective optimization model concerning the production process parameters of Q235B-Z steel grades, obtaining Pareto feasible solutions, as depicted in Figure 4. In this multi-objective optimization framework, the dual objectives are articulated as minimizing the endpoint phosphorus content and minimizing the production cost per tonne of steel. For a comprehensive analysis, the three most optimal solutions from further examination.

The Pareto feasible solution graph presented in Figure 4 illustrates that the IMOWOA effectively achieves a favorable trade-off between the dual objectives of minimizing endpoint phosphorous content and production cost per tonne of steel. The presence of multiple solutions in the feasible solution set makes the objectives of f₁ and f₂ research a better solution, reflecting the algorithm’s efficacy in navigating the iterative optimization process. In the optimal solution set displayed in Table 3, the endpoint phosphorus content of the first optimized solutions is recorded as 0.0107%, alongside the consumed production cost of 3217.03 CNY per tonne of steel. Compared with the actual production data with analogous processing parameters, the endpoint phosphorus content and the production cost of a tonne of steel have been reduced by 10.8% and 5.79%, respectively. The third optimized solution yields an endpoint phosphorous content of 0.0109%, and a steel production cost of 3216.52 CNY per tonne of steel. Compared with the actual production data, two objectives are reduced by 9.17% and 5.80%, respectively.

To evaluate the stability of the IMOWOA algorithm, the Pareto optimal solution set delineated in Table 3 underwent further verification. The first optimal objective function was selected as the initial solution, and the same parameter configurations were applied to conduct multiple experimental runs. The optimal endpoint phosphorus content and production cost per tonne of steel attained in each trial were systematically recorded to assess the robustness and stability of the algorithm.

Table 4. Algorithm validation results.

	1	2	3	4
Endpoint P (%)	0.0108	0.0109	0.0110	0.0109
Production cost (CNY/t)	3213.10	3215.97	3213.88	3210.48

presents the findings from these multiple experimental evaluations, revealing the optimal endpoint phosphorus content consistently falls within the range of 0.0108% to 0.0110%, while the optimal production cost per tonne of steel varies approximately between 3210.48 CNY/t and 3215.97 CNY/t. In comparison to the initial solution, the maximum error of the endpoint phosphorus content is 0.0004%, whereas the corresponding maximum error of the production cost of a tonne of steel reaches 6.55 CNY/t. These experimental outcomes substantiate the relative stability and reliability of the IMOWOA.

4.4. Ablation Experiment Analysis

To evaluate the efficacy of the three proposed enhancement strategies for the IMOWAO, ablation experiments were conducted for each improvement strategy. Following the execution of the algorithm 30 times for each strategy, the mean and standard deviation of the results were calculated and analyzed. The findings of the analysis are presented in

Table 5. Ablation experiments results.

	Endpoint P (%)		Production Cost (CNY/t)
Strategic	Mean Value	Standard Deviation	Mean Value	Standard Deviation
MOWOA	0.0135	0.0009	3207.15	2.30
+ Sobol + Reward	0.0129	0.0002	3201.27	1.54
+ Sobol + MOGWO	0.0130	0.0011	3215.81	8.42
+ Reward + MOGWO	0.0123	0.0008	3212.16	5.52
IMOWOA	0.0110	0.0006	3214.51	3.97

.

The impact of each strategic approach on the endpoint phosphorus content and the production cost per tonne of steel has been systematically analyzed, as detailed in Table 5. This analysis comprehensively evaluates how the different strategies influence both key performance metrics, thereby providing insights into their respective effectiveness in optimizing the steelmaking parameter process. The enhanced strategy that incorporates the Sobol sequence and reward function demonstrates notable superiority regarding endpoint phosphorus content, achieving the mean value reduction to 0.0129% with a standard deviation of merely 0.0002%. Additionally, this strategy results in a slight decrease in the production cost per tonne of steel, characterized by a standard deviation of 1.54 CNY/t, indicating its high stability and efficiency. In contrast, the improved strategy that integrates the Sobol sequence with the MOGWO algorithm results in a 0.0005% decrease in the mean endpoint phosphorus content. However, this approach led to an increase in production cost, rising to 3215.81 CNY/t with a corresponding standard deviation of 8.52 CNY/t. This observation suggests a relatively weak stability in cost control when adopting this particular strategy. When combining the reward function with the enhanced MOGWO algorithm, a significant reduction in the endpoint phosphorus content is achieved, reducing to 0.0123%. This improvement is realized without significant sacrifice in the production cost, showcasing a more favorable overall optimization effect. The IMOWOA proves particularly effective in reducing the endpoint phosphorus content, with an average value of only 0.0110%. Simultaneously, it maintains effective cost control over steel production, with an average cost noted at 3214.51 CNY/t, demonstrating a relatively small standard deviation, and indicating good stability. In summary, the IMOWOA successfully establishes an optimal balance between the endpoint phosphorus content and the production cost per tonne of steel, thereby validating its effectiveness and reasonableness in optimizing phosphorus removal during the converter steelmaking process.

4.5. Algorithm Comparison

To further substantiate the effectiveness of the IMOWOA in addressing the dephosphorization optimization problem in converter steelmaking, a comparison was conducted with several algorithms, including the mature multi-objective particle swarm algorithm [22] (MOPSO), the multi-objective grey wolf optimization (MOGWO) algorithm, known for its strong optimization capabilities with fewer parameters, the novel multi-objective beluga whale optimization (MOBWO) algorithm, distinguished by its distinctive search paradigm [23], the multi-objective crayfish optimization algorithm [24] (MOCOA), and the original MOWOA. The Pareto feasible solution graph for each algorithm is illustrated in Figure 5, while the first optimal solution in the respective solution sets is presented in

Table 6. Each algorithm’s Pareto optimal solutions.

Parameter	MOPSO	MOGWO	MOBWO	MOCOA	MOWOA
Ferric C (%)	4.53	4.86	4.52	4.67	4.73
Ferric Si (%)	0.44	0.18	0.24	0.25	0.30
Ferric P (%)	0.112	0.115	0.072	0.101	0.131
Temperature of iron (T)	1371	1276	1265	1370	1316
Amount of iron (t)	116.2	107.2	114.0	111.0	107.0
Scrap quantity (t)	12.86	39.51	13.85	19.61	39.52
Lime (kg)	2944	1271	916	2328	1323
Limestone (kg)	4546	1864	5549	1625	4710
Raw dolomite (kg)	2216	943	3292	2787	3737
Ore (kg)	892	2664	3228	2005	759
Oxygen blowing quantity (m3)	6694	6679	6271	6465	6799
First pour temperature (°C)	1624	1618	1615	1637	1634
Endpoint P (%)	0.0137	0.0128	0.0136	0.0132	0.0134
Production cost (CNY/t)	3510.56	3213.36	3505.53	3435.19	3205.89

.

As illustrated in Figure 5, the MOPSO, MOBWO, and MOCOA algorithms exhibit relatively poor Pareto optimal solution sets. During the iterative process, these algorithms are trapped in more local optimal solution cases, leading to an insufficient exploration of the search space. On the contrary, the MOGWO and MOWOA achieve a more favorable trade-off between the two objective functions; however, these algorithms compromise the performance of the objective function f₁ during the optimization search process. According to the data presented in Table 6, the MOGWO algorithm successfully obtains a lower endpoint phosphorus content of 0.0128%, while the MOWOA achieves a reduced cost of production cost at 3205.89 CNY per tonne of steel during the iterative process.

4.6. Evaluation Indicators Analysis

To evaluate the convergence, diversity, and uniformity of the algorithm, IGD, HV, and Spacing metrics are employed. Recognizing the stochastic nature inherent in optimization algorithms, each algorithm was executed independently 30 times for the dephosphorization process parameter optimization problem. Subsequently, the mean and standard deviation of each algorithm’s solution set indices were calculated, and the results of these evaluation metrics are presented in

Table 7. Each algorithm’s evaluation metrics.

Algorithm	IGD		HV		Spacing
	Mean Value	Standard Deviation	Mean Value	Standard Deviation	Mean Value	Standard Deviation
MOPSO	0.024	0.0018	1.05	1.60	0.012	0.002
MOGWO	0.007	0.0016	3.39	1.10	0.088	0.018
MOBWO	0.022	0.0035	8.92	0.50	0.211	0.005
MOWOA	0.012	0.0011	3.23	0.77	0.039	0.032
MOCOA	0.015	0.0053	5.13	2.44	0.071	0.033
IMOWOA	0.009	0.0025	7.80	1.18	0.033	0.019

.

Following extensive empirical evaluations, the mean IGD of the IMOWOA is approximately 0.009, which is close to zero, The mean HV attained is around 7.80, while the mean Spacing value stands at about 0.033. In terms of the IDG metric, although the IMOWOA slightly lags behind the 0.007 of the MOGWO algorithm, it is noteworthy that the IGD produced by the IMOWOA is relatively low, with a standard deviation of 0.0015. The statistically consistent convergence patterns across multiple independent runs demonstrate that the algorithm maintains stable convergence rates without succumbing to local optima entrapment caused by stochastic factors. Comparative analysis of the HV metric reveals that IMOWOA achieves broader coverage of the Pareto optimal front compared to benchmark algorithms, indicating superior solution diversity. Although IMOWOA exhibits a slightly less uniform distribution (Spacing metric) relative to MOPSO, its near-zero Spacing values (approximating 0.033) still confirm advantageous solution spread characteristics. Experimental results collectively demonstrate that IMOWOA’s lower IGD values, higher HV values, and near-zero Spacing metrics reflect dual strengths in computational efficiency and optimization accuracy. These findings validate the algorithm’s robust performance across convergence stability, solution quality, and distribution uniformity, thereby confirming the efficacy of its architectural design. Consequently, the IMOWOA shows significant potential and effectiveness when applied to the optimization of dephosphorization process parameters.

The experimental results indicate that the solutions derived from the IMOWOA are more effective in addressing the optimization problem associated with dephosphorization process parameters in converter steelmaking. This algorithm facilitates a more favorable tradeoff between the endpoint phosphorus content and production cost per tonne of steel, leading to improved steel quality with only a marginal increase in the production cost. Therefore, the IMOWOA evidences a remarkable optimization efficacy for this specific category of dephosphorization process parameter optimization problem.

5. Conclusions

This study addresses the multi-objective optimization challenges in dephosphorization processes during converter steelmaking by proposing an integrated solution that combines metallurgical mechanisms with intelligent algorithms. A thermodynamically constrained extreme random forest model is developed, where domain knowledge is embedded through feature selection prioritization, constructing an interpretable hybrid modeling framework. To enhance search capability and balance endpoint phosphorus content with production cost objectives, three key enhancements are implemented: an optimized population initialization strategy using quasi-random sampling, a dynamic reward-penalty function for objective equilibrium, and hybridized GWO social hierarchy mechanisms to reinforce global-local search coordination. Full-scale production trials validate the approach, demonstrating a 10.8% reduction in endpoint phosphorus content and a 5.79% decrease in production costs per ton of steel while maintaining minimum cost thresholds. The algorithm’s efficacy is further corroborated by superior hypervolume and spacing metrics compared to conventional methods, establishing a robust framework for industrial-scale metallurgical optimization.

The present research investigates the application of intelligent optimization algorithms in refining the process parameters of converter steelmaking, thereby providing an effective tool for technicians. However, the proposed approach still has some limitations, for example, the study focuses solely on the aggregate input quantities of auxiliary materials without delving into the optimization of input patterns as process parameters. For future work, we plan to extend the dataset to encompass a broader range of steel grades and variations in auxiliary material input patterns. Furthermore, we intend to explore advanced intelligent optimization algorithms to further enhance optimization outcomes. Additionally, we are keen on investigating the application of neural network models to improve the predictive accuracy of endpoint phosphorus content.