Shear Mechanical Properties of Rock Joints Under Non-Uniform Load Based on DEM
Abstract
1. Introduction
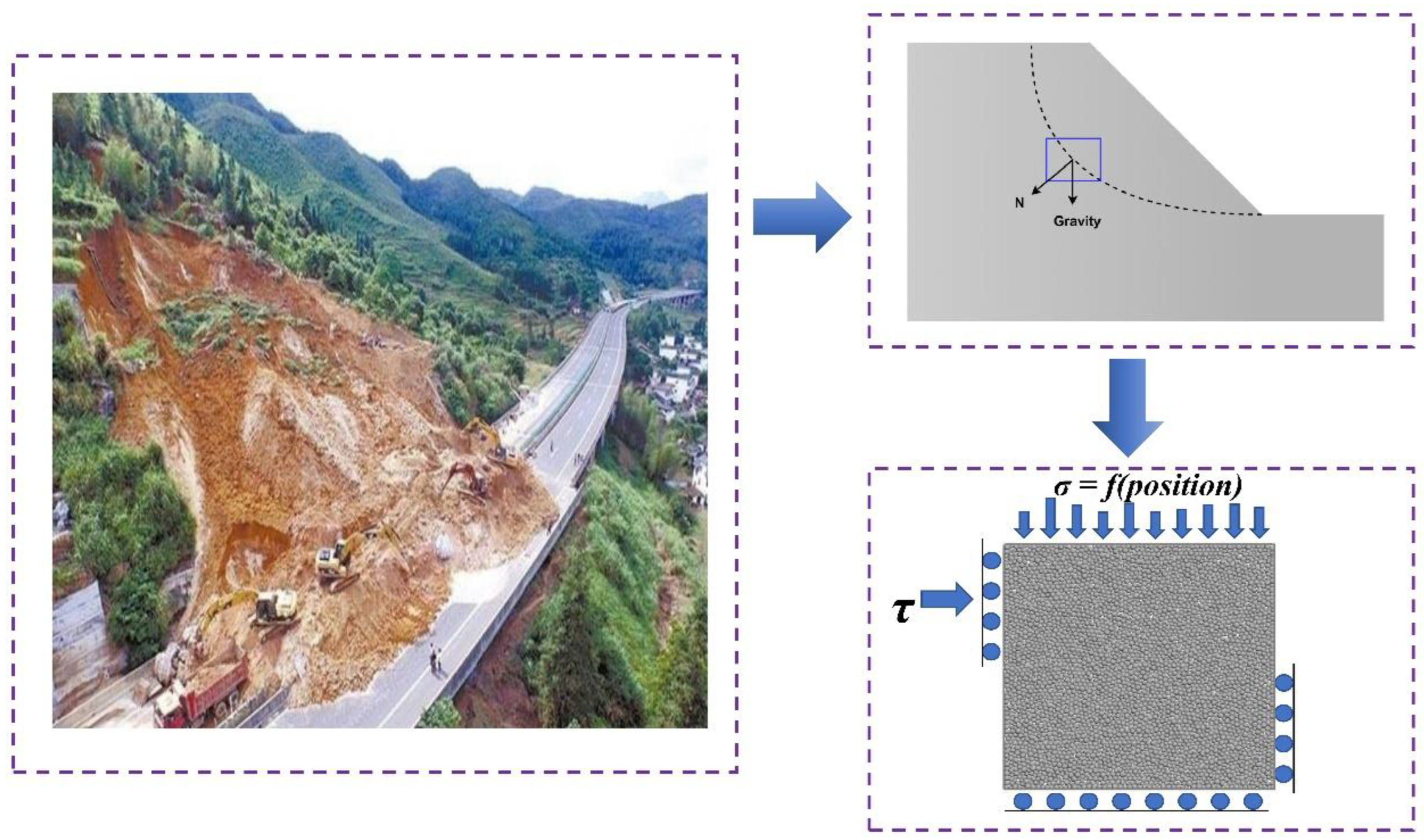
2. Modeling of Non-Uniform Load Mechanics
3. Numerical Modeling
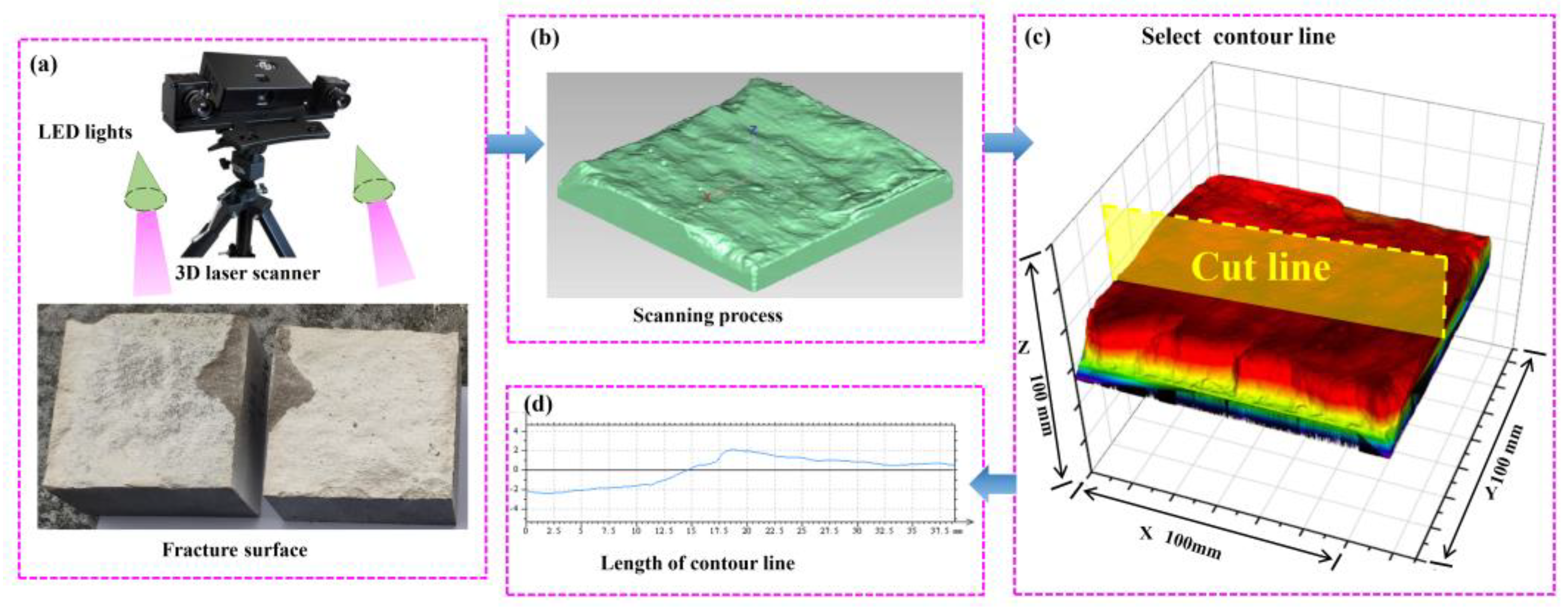
3.1. Geometric Model
3.2. Calibration of Microscopic Parameters
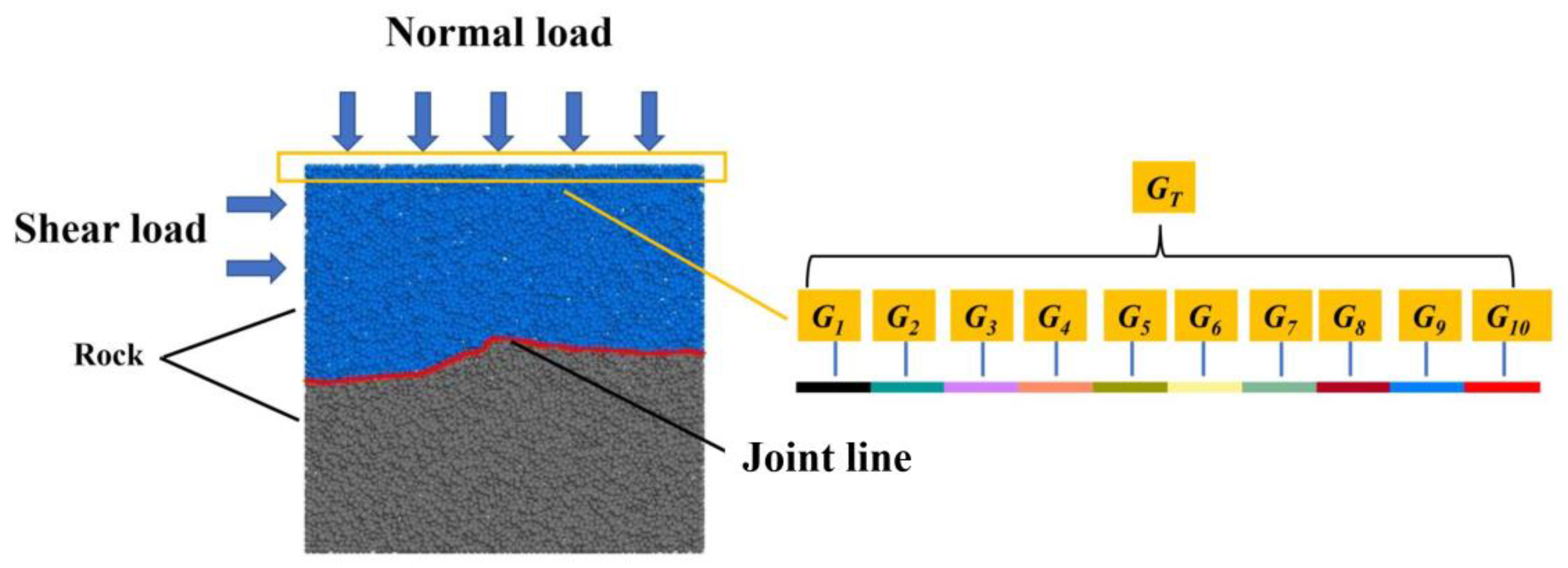
3.3. Boundary Conditions and Loading Scheme
4. Simulation Results and Analysis
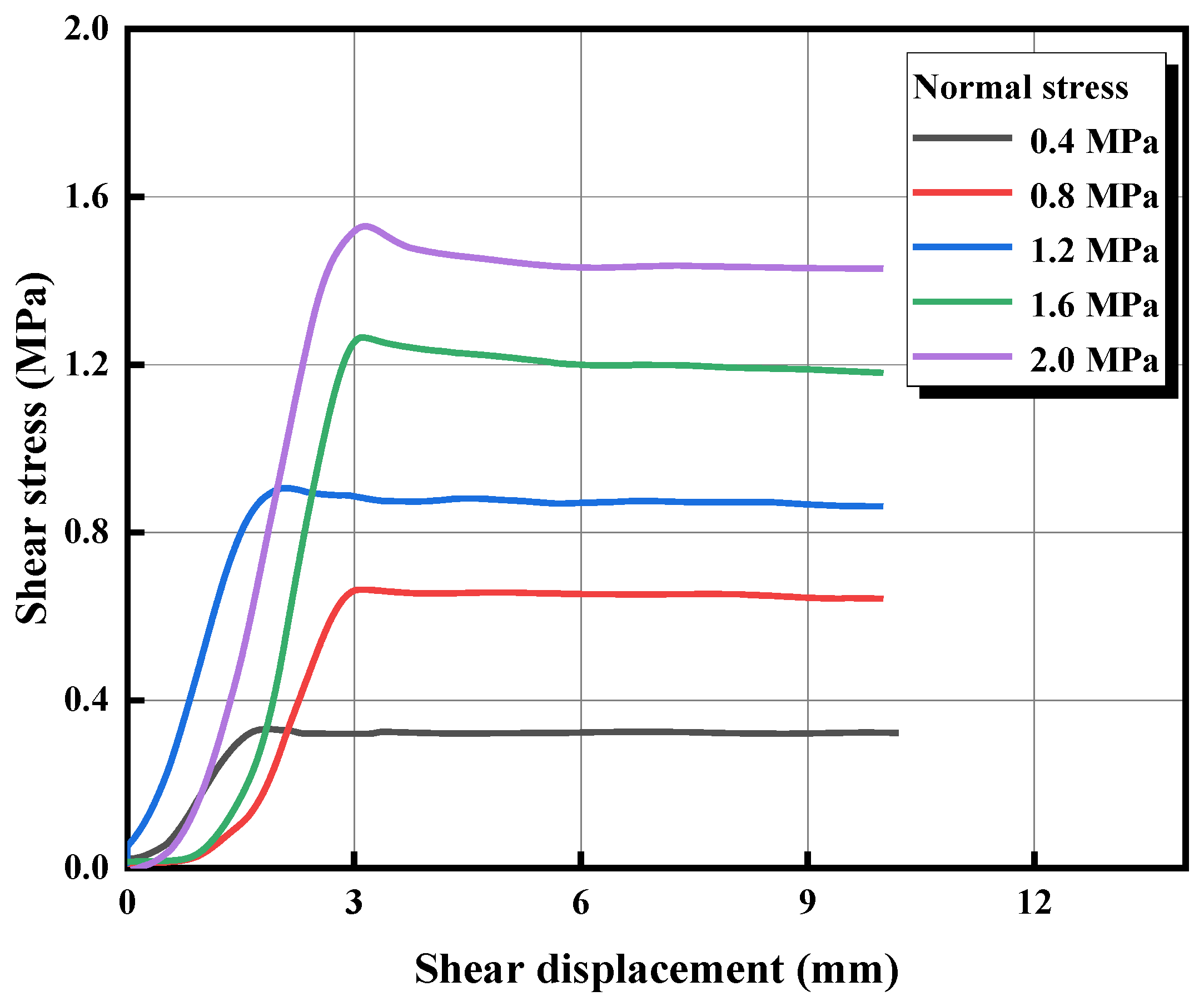
4.1. Shear Stress–Shear Displacement Curve
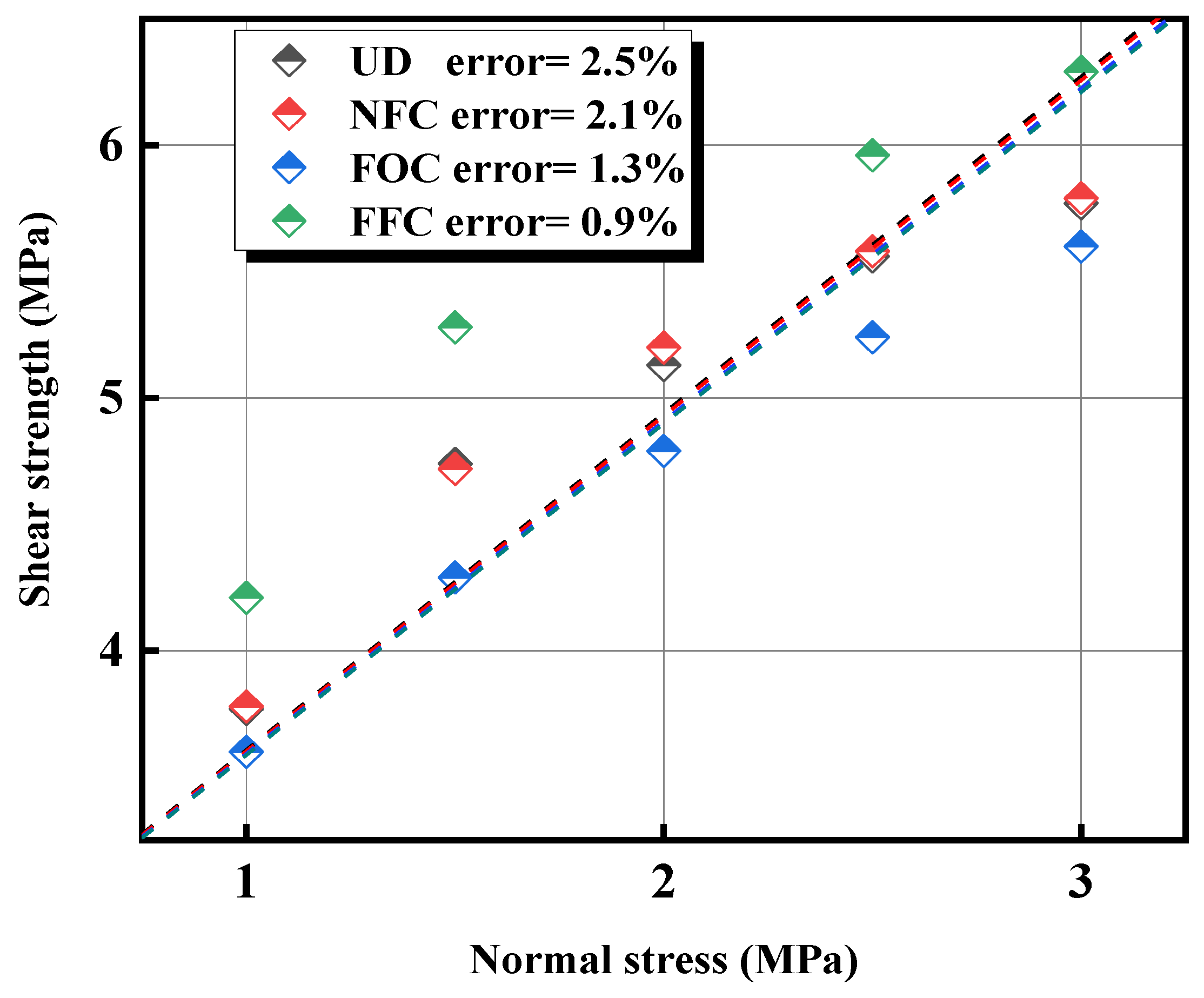
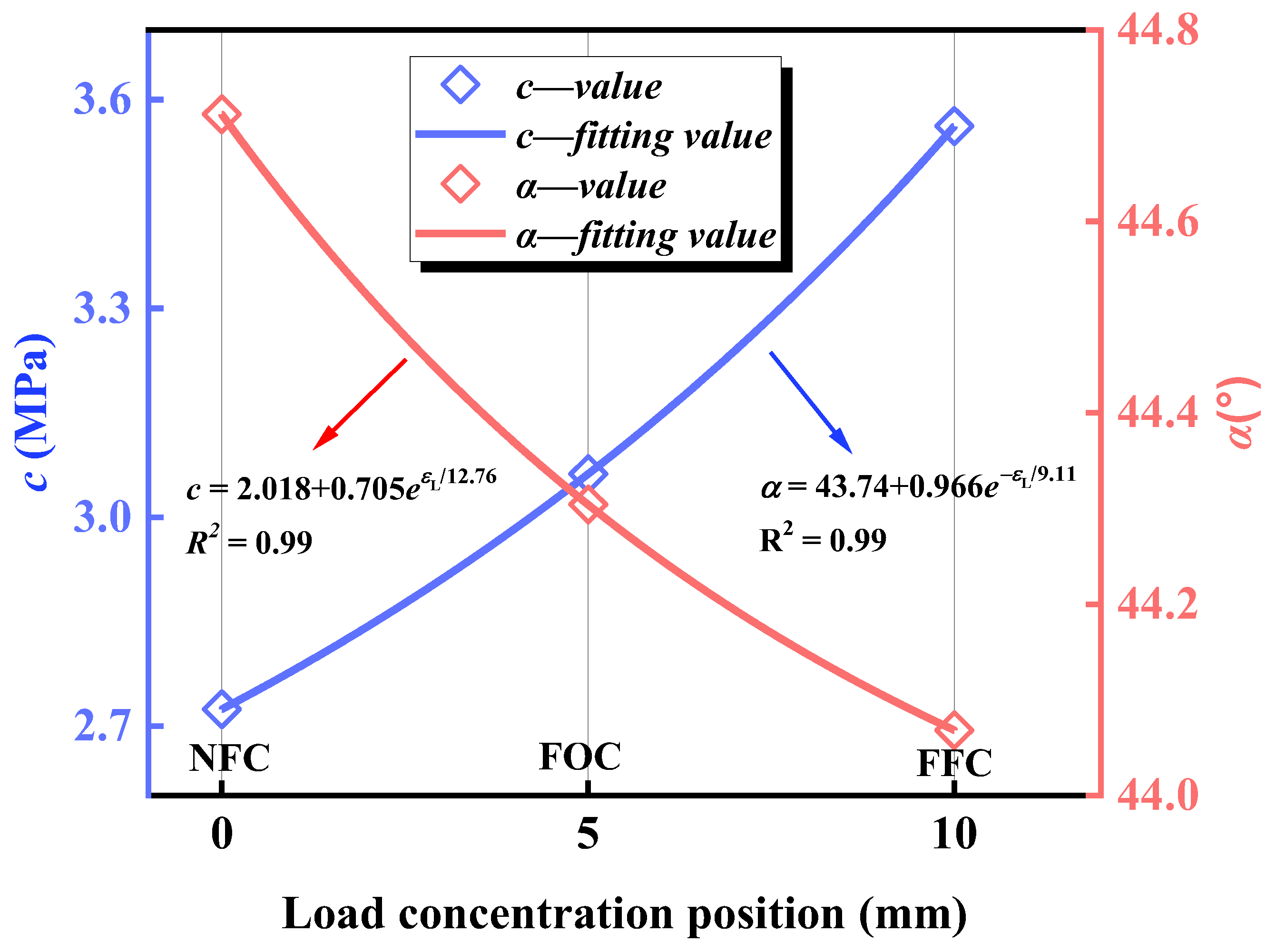
4.2. Main Shear Mechanical Parameters
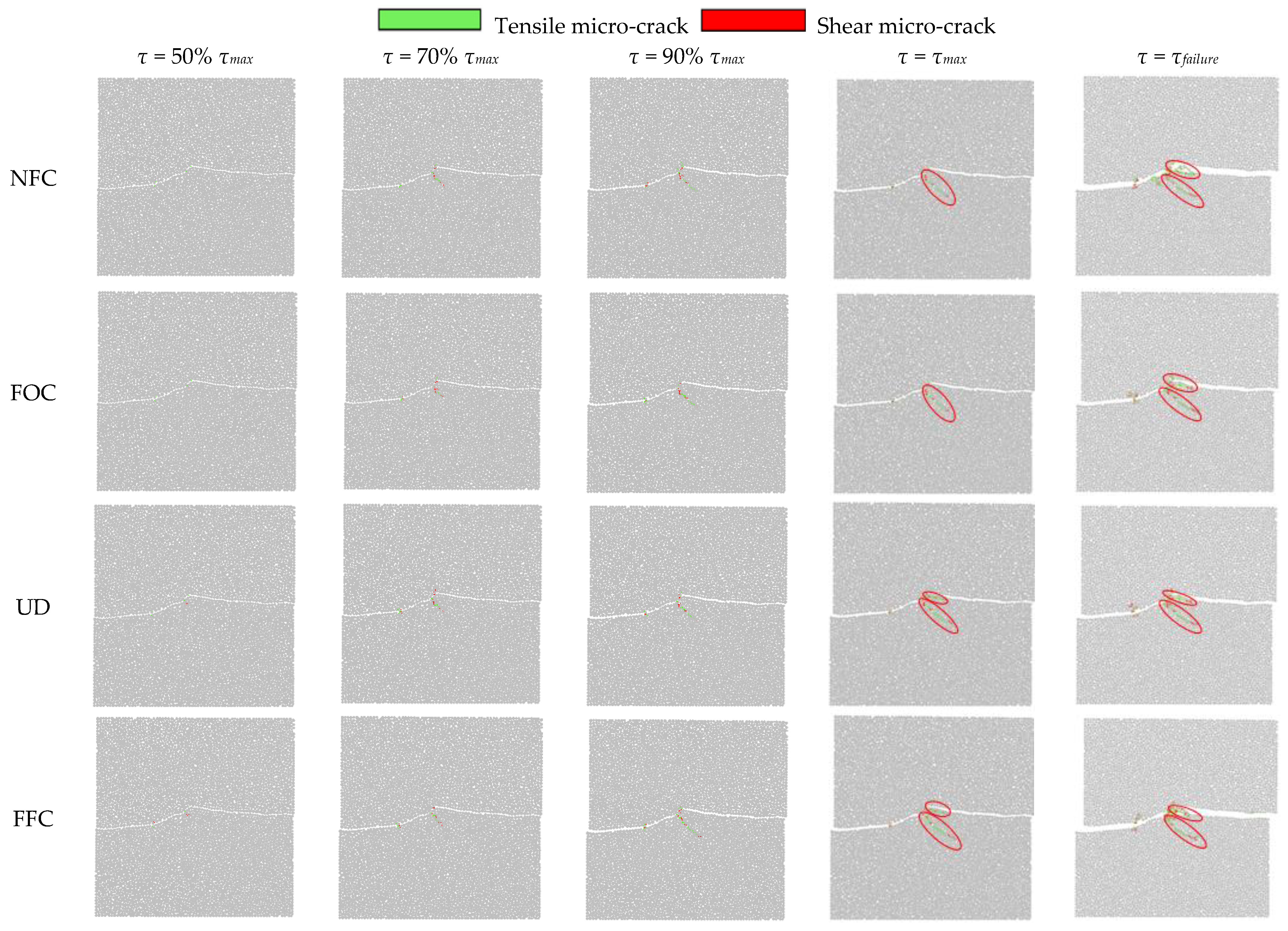
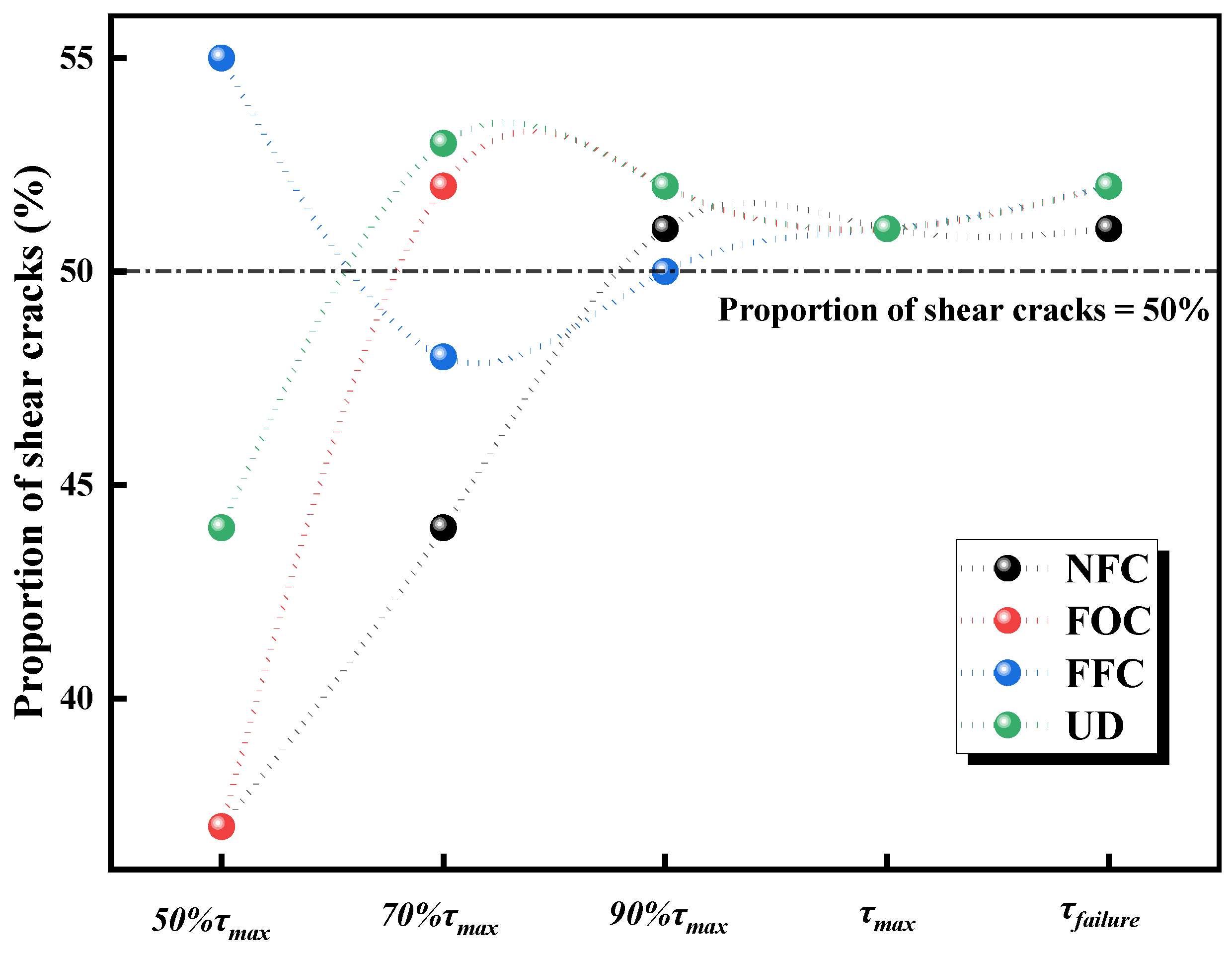
4.3. Crack Evolution
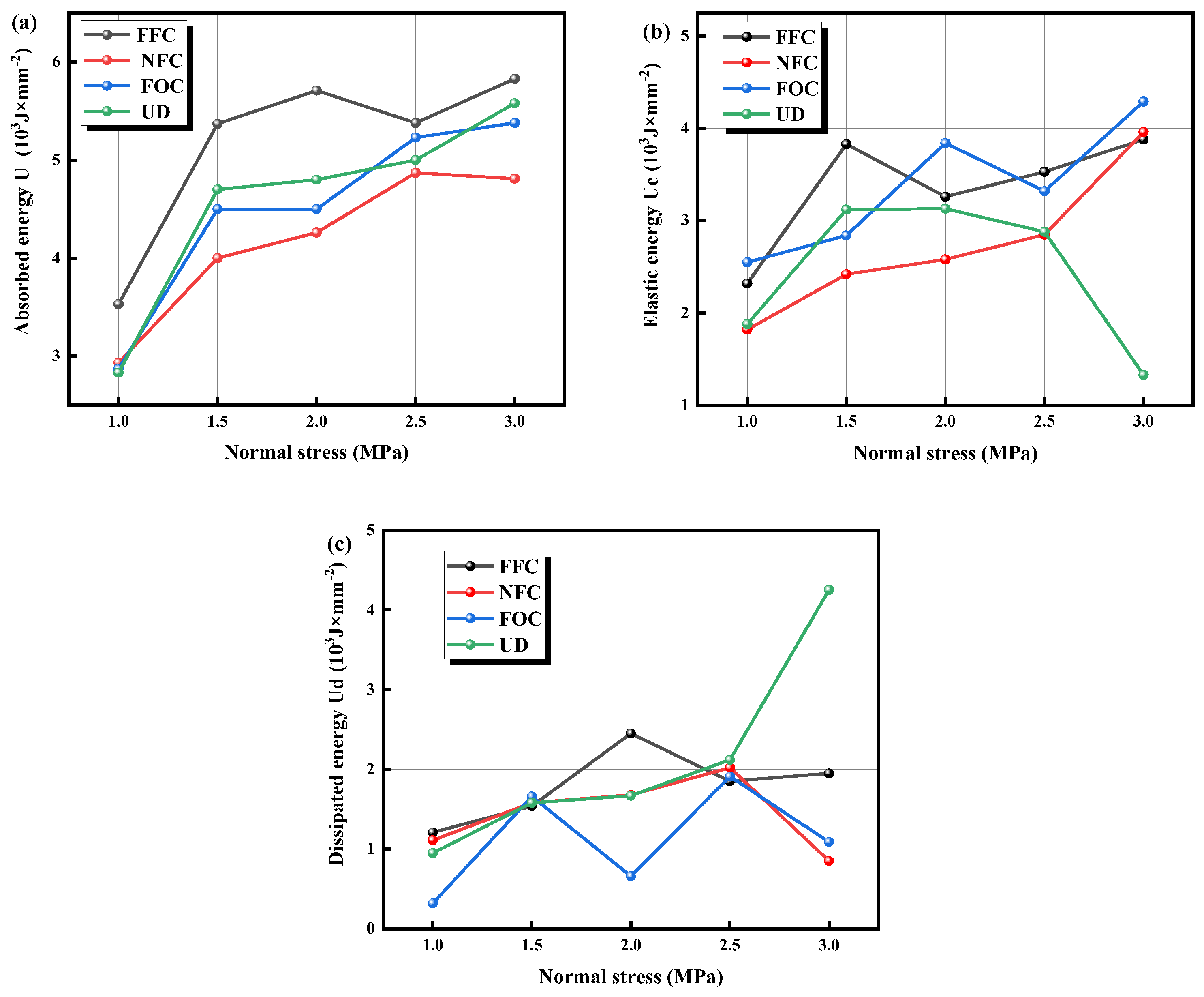
4.4. Energy Evolution Law
5. Non-Uniform-Load Shear Strength Criterion Based on Machine Learning Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Jiang, Y.; Asahina, D.; Wang, Z. Shear behavior and acoustic emission characteristics of en-echelon joints under constant normal stiffness conditions. Theor. Appl. Fract. Mech. 2020, 109, 102772. [Google Scholar] [CrossRef]
- Asadizadeh, M.; Hossaini, M.F.; Moosavi, M.; Masoumi, H.; Ranjith, P.G. Mechanical characterisation of jointed rock-like material with non-persistent rough joints subjected to uniaxial compression. Eng. Geol. 2019, 260, 105224. [Google Scholar] [CrossRef]
- Aziznejad, S.; Esmaieli, K.; Hadjigeorgiou, J.; Labrie, D. Responses of jointed rock masses subjected to impact loading. J. Rock Mech. Geotech. Eng. 2018, 10, 624–634. [Google Scholar] [CrossRef]
- Kou, M.; Liu, X.; Tang, S.; Wang, Y. Experimental study of the prepeak cyclic shear mechanical behaviors of artificial rock joints with multiscale asperities. Soil. Dyn. Earthq. Eng. 2019, 120, 58–74. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.Z.; Jiang, Y.J.; Liu, P.X.; Guo, Y.S.; Liu, J.K.; Ma, M.; Wang, K.; Wang, S.G. Shear Behaviour and Acoustic Emission Characteristics of Bolted Rock Joints with Different Roughnesses. Rock Mech. Rock Eng. 2018, 51, 1885–1906. [Google Scholar] [CrossRef]
- Xie, S.; Lin, H.; Wang, Y.; Chen, Y.; Xiong, W.; Zhao, Y.; Du, S. A statistical damage constitutive model considering whole joint shear deformation. Int. J. Damage Mech. 2020, 29, 988–1008. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, H.; Wang, Y.; Yong, R.; Zhao, Y.; Du, S. Damage evolution characteristics of saw-tooth joint under shear creep condition. Int. J. Damage Mech. 2021, 30, 453–480. [Google Scholar] [CrossRef]
- Oh, J.; Li, Y.; Mitra, R.; Canbulat, I. A Numerical Study on Dilation of a Saw-Toothed Rock Joint Under Direct Shear. Rock Mech. Rock Eng. 2017, 50, 913–925. [Google Scholar] [CrossRef]
- Saadat, M.; Taheri, A. A numerical study to investigate the influence of surface roughness and boundary condition on the shear behaviour of rock joints. Bull. Eng. Geol. Environ. 2020, 79, 2483–2498. [Google Scholar] [CrossRef]
- Singh, P.; Spearing, A.J.S. An Improved Analytical Model for the Elastic and Plastic Strain-hardening Shear Behaviour of Fully Grouted Rockbolts. Rock Mech. Rock Eng. 2021, 54, 3909–3925. [Google Scholar] [CrossRef]
- Tang, Z.C.; Wong, L.N.Y. New Criterion for Evaluating the Peak Shear Strength of Rock Joints Under Different Contact States. Rock Mech. Rock Eng. 2016, 49, 1191–1199. [Google Scholar] [CrossRef]
- Esaki, T.; Du, S.; Mitani, Y.; Ikusada, K.; Jing, L. Development of a shear-flow test apparatus and determination of coupled properties for a single rock joint. Int. J. Rock Mech. Min. Sci. 1999, 36, 641–650. [Google Scholar] [CrossRef]
- Xia, C.-C.; Yu, Q.-F.; Qian, X.; Gui, Y.; Zhuang, X.-Q. Experimental study of shear-seepage behaviour of rock joints under constant normal stiffness. Rock Soil Mech. 2020, 41, 57. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Wu, C.; Fei, X.; Hong, Y. Impacts of stress and roughness on steady-state creep of synthetic rock joints under shear. Geotech. Lett. 2019, 9, 46–52. [Google Scholar] [CrossRef]
- Liu, X.W.; Liu, Q.S.; Kang, Y.S.; Pan, Y.C. Improved Nonlinear Strength Criterion for Jointed Rock Masses Subject to Complex Stress States. Int. J. Geomech. 2018, 18, 04017164. [Google Scholar] [CrossRef]
- Li, X.; Gong, F.; Tao, M.; Dong, L.; Du, K.; Ma, C.; Zhou, Z.; Yin, T. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Okubo, S.; Fukui, K.; Hashiba, K. Long-term creep of water-saturated tuff under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2010, 47, 839–844. [Google Scholar] [CrossRef]
- Lajtai, E.Z.; Schmidtke, R.H.; Bielus, L.P. The effect of water on the time-dependent deformation and fracture of a granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 247–255. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, Y.; Gong, B.; Guan, Z.; Deng, T. Shear Performance of Rock Joint Reinforced by Fully Encapsulated Rock Bolt Under Cyclic Loading Condition. Rock Mech. Rock Eng. 2019, 52, 2681–2690. [Google Scholar] [CrossRef]
- Li, H.-Y.; Wang, Z.; Sun, Y.-F.; Li, W.-H. Terrain classification based on adaptive weights with airborne LiDAR data for mining area. Trans. Nonferrous Met. Soc. China 2011, 21, S648–S653. [Google Scholar] [CrossRef]
- Kim, Y.; Sim, T.E.; Chua, Y.S.; Bakytuly, N.; Satyanaga, A.; Pu, J.H. Harnessing Green Cover Systems for Effective Slope Stabilization in Singapore. Land 2025, 14, 436. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Sharrock, G.; Hebblewhite, B.K. Numerical direct shear tests to model the shear behaviour of rock joints. Comput. Geotech. 2013, 51, 101–115. [Google Scholar] [CrossRef]
- Mehranpour, M.H.; Kulatilake, P.H.S.W. Improvements for the smooth joint contact model of the particle flow code and its applications. Comput. Geotech. 2017, 87, 163–177. [Google Scholar] [CrossRef]
- Fereshtenejad, S.; Kim, J.; Song, J.-J. Experimental Study on Shear Mechanism of Rock-Like Material Containing a Single Non-Persistent Rough Joint. Energies 2021, 14, 987. [Google Scholar] [CrossRef]
- Xie, S.J.; Lin, H.; Duan, H.Y. A novel criterion for yield shear displacement of rock discontinuities based on renormalization group theory. Eng. Geol. 2023, 314, 107008. [Google Scholar] [CrossRef]
- Gell, E.M.; Walley, S.M.; Braithwaite, C.H. Review of the Validity of the Use of Artificial Specimens for Characterizing the Mechanical Properties of Rocks. Rock Mech. Rock Eng. 2019, 52, 2949–2961. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, X.; Qin, J.; Lin, H. Influence of Morphology Characteristics on Shear Mechanical Properties of Sawtooth Joints. Buildings 2022, 12, 886. [Google Scholar] [CrossRef]
- Cheng, Y.; Wong, L.N.Y. A study on mechanical properties and fracturing behavior of Carrara marble with the flat-jointed model. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 803–822. [Google Scholar] [CrossRef]
- Zhai, W.; Zhang, H.; Yang, Z.; Chen, Z.; Wu, B.; Zhou, J.; Cheng, S.; Tan, P. A semi-analytical model for predicting the mechanical responses around a non-circular wellbore by using complex variable method. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 26. [Google Scholar] [CrossRef]
- Tan, H.; Li, J.T.; Shi, Z.M.; Wang, M.X.; Wang, J.; Li, J. Damage evolution and failure characteristics of red sandstone with prefabricated crack under coupled dry-wet cycle-fatigue loading. Int. J. Fatigue 2023, 175, 107751. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Olbert, A.I. A comprehensive method for improvement of water quality index (WQI) models for coastal water quality assessment. Water Res. 2022, 219, 118532. [Google Scholar] [CrossRef] [PubMed]


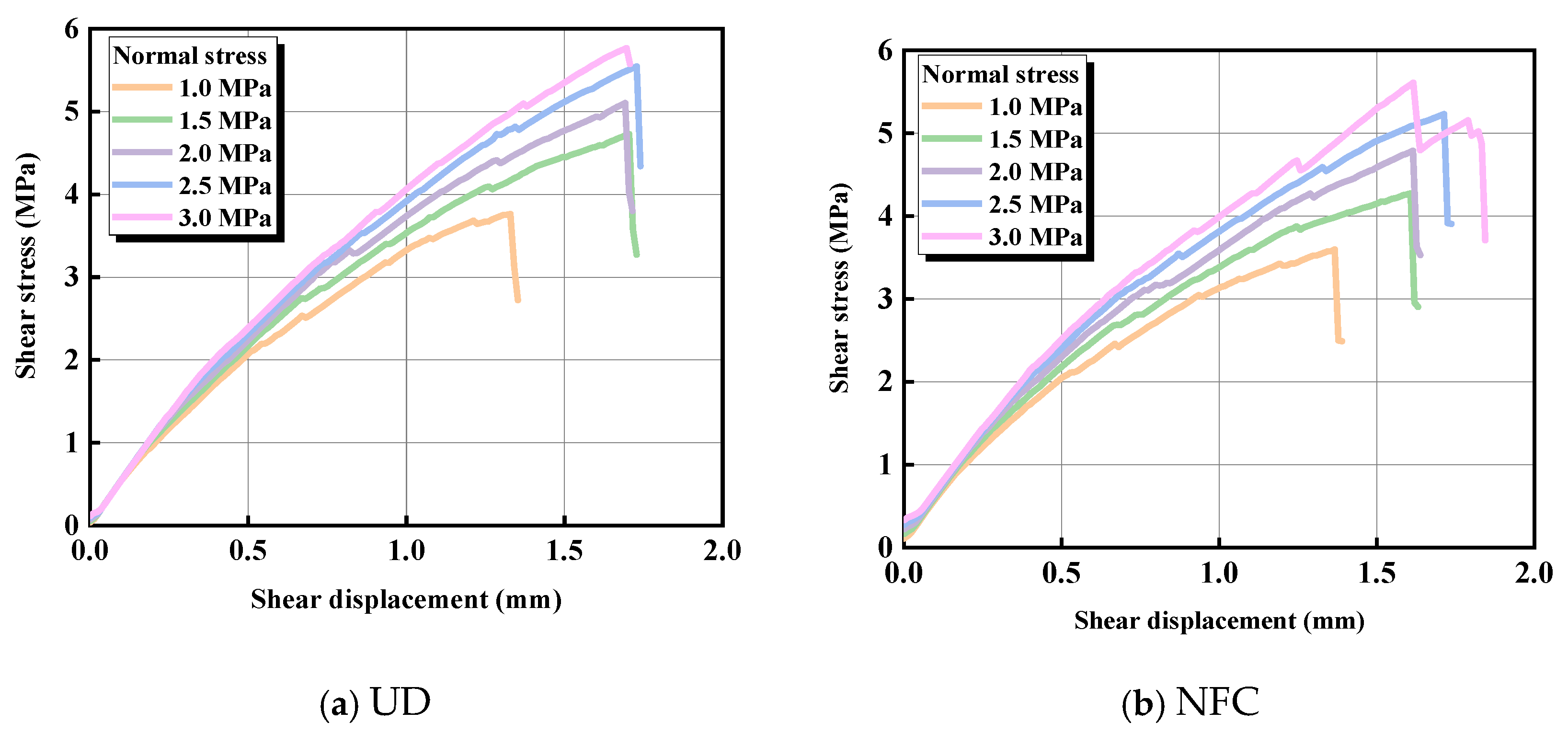
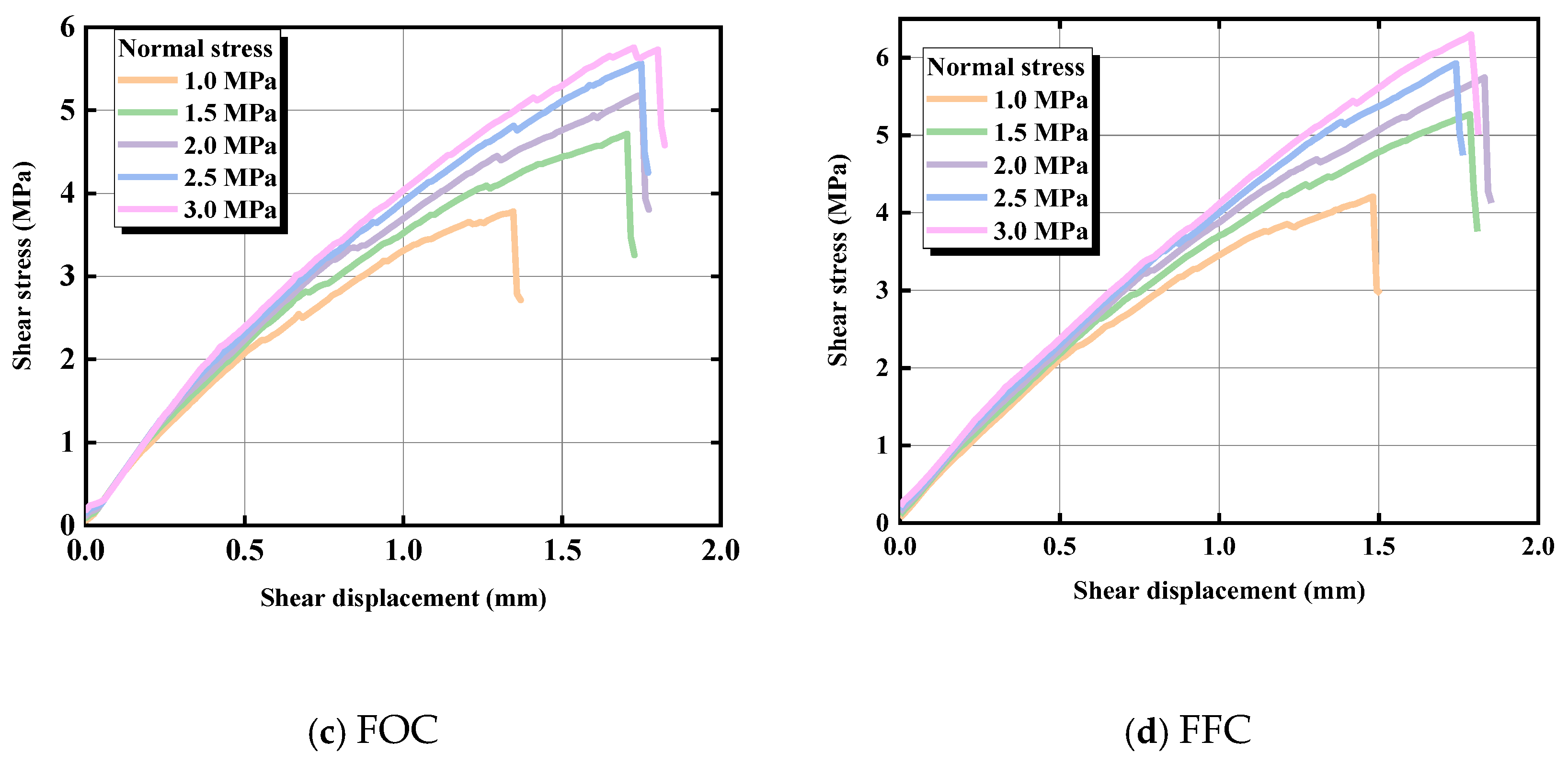
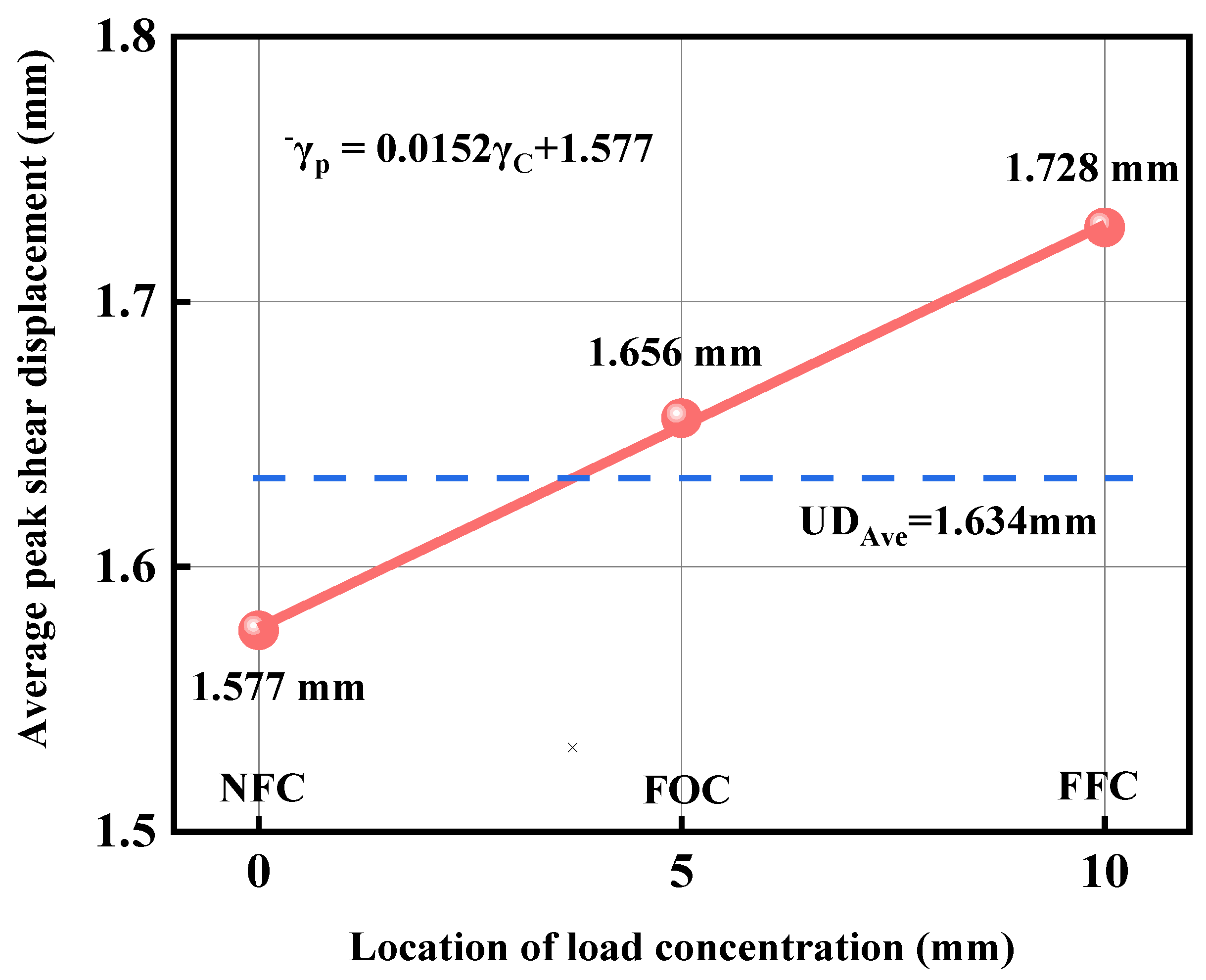
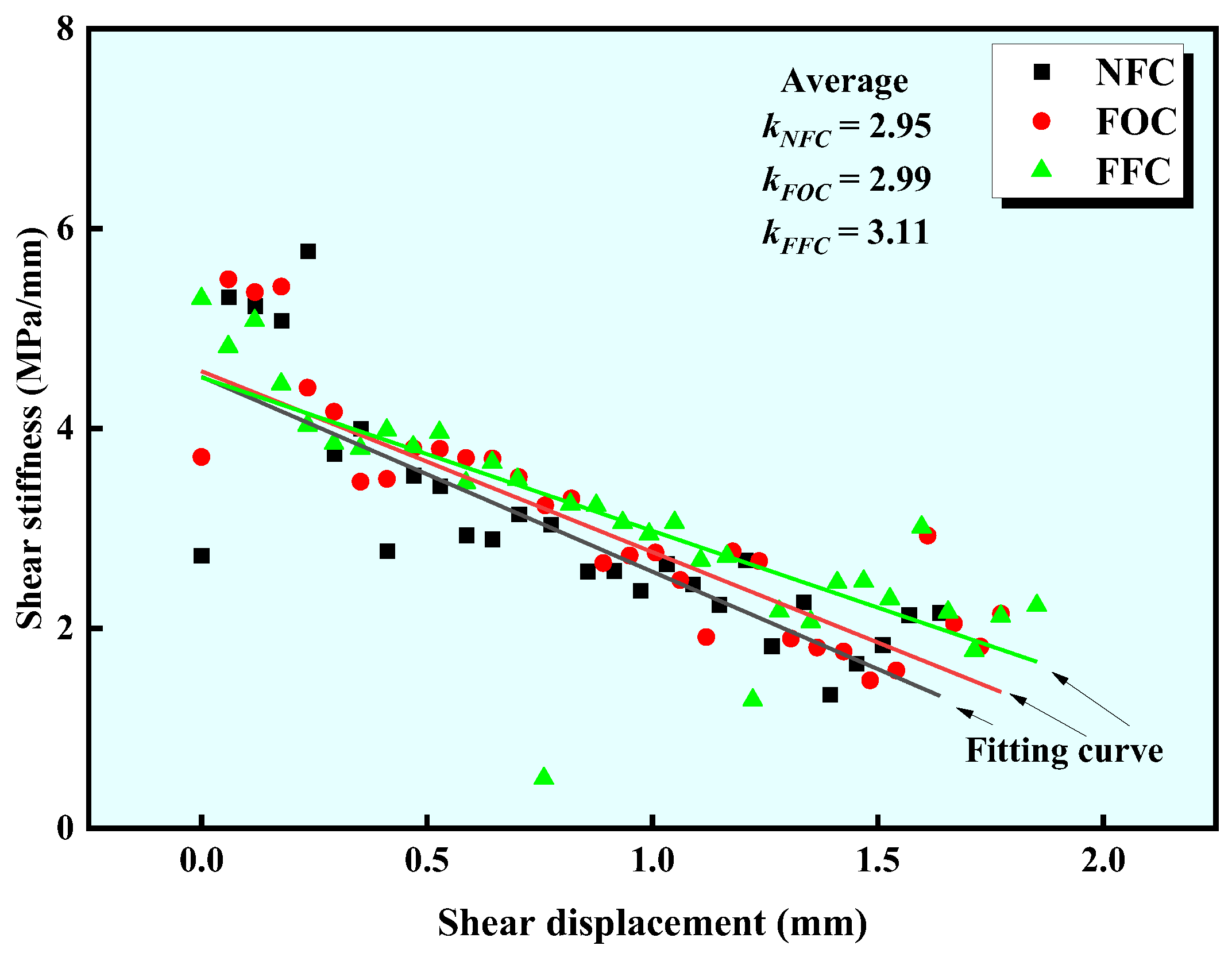

| Parameter Type | Microscopic Parameters | Value |
|---|---|---|
| Particle | Density (kg/m3) | 2500 |
| Radius (mm) | 0.6–0.9 | |
| Porosity | 0.1 | |
| Flat-joint contact model | Contact modulus, | 1.8 |
| Contact stiffness ratio, | 1.0 | |
| Tensile strength (MPa) | 13.8 | |
| Cohesion (MPa) | 28.8 | |
| Internal friction angle (°) | 32.5 | |
| Friction coefficient, f | 1.5 | |
| Smoot-joint contact model | Normal stiffness, | 100 |
| Shear stiffness, | 0.62 | |
| Friction coefficient, f | 0.92 |
| Distribution Form | Normal Stress σ | |
|---|---|---|
| Uniform distribution (UD) | 10 kN, 15 kN, 20 kN, 25 kN, 30 kN | 1 MPa, 1.5 MPa, 2 MPa, 2.5 MPa, 3 MPa |
| Far-field concentration (FFC) | ||
| Near-field concentration (NFC) | ||
| Focus on center (FOC) |
| Normal Stress (MPa) | Shear Strength Simulation (MPa) | |||
|---|---|---|---|---|
| NFC | FOC | FFC | UD | |
| 1 | 3.6 | 3.78 | 4.21 | 3.77 |
| 1.1 | 3.71 | 3.93 | 4.22 | 3.9 |
| 1.2 | 3.84 | 4.29 | 4.38 | 4.31 |
| 1.3 | 4.11 | 4.54 | 4.82 | 4.55 |
| 1.4 | 4.25 | 4.53 | 5.08 | 4.71 |
| 1.5 | 4.29 | 4.71 | 5.28 | 4.74 |
| 1.6 | 4.41 | 4.67 | 5.31 | 4.76 |
| 1.7 | 4.52 | 4.84 | 5.31 | 4.92 |
| 1.8 | 4.52 | 4.74 | 5.44 | 5.06 |
| 1.9 | 4.66 | 5.06 | 5.58 | 4.84 |
| 2 | 4.79 | 5.2 | 5.75 | 5.13 |
| 2.1 | 5.05 | 2.16 | 5.77 | 5.1 |
| 2.2 | 5.01 | 5.28 | 5.88 | 5.22 |
| 2.3 | 5.12 | 5.4 | 5.91 | 5.34 |
| 2.4 | 5.19 | 5.53 | 5.97 | 5.46 |
| 2.5 | 5.24 | 5.58 | 5.94 | 5.56 |
| 2.6 | 5.3 | 5.63 | 6.21 | 5.67 |
| 2.7 | 5.35 | 5.69 | 5.29 | 5.71 |
| 2.8 | 5.38 | 5.7 | 6.21 | 5.75 |
| 2.9 | 5.41 | 5.81 | 6.26 | 5.83 |
| 3 | 5.6 | 5.91 | 6.31 | 5.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhang, X.; Lin, H.; Chen, Y.; Yang, C.; Ou, K. Shear Mechanical Properties of Rock Joints Under Non-Uniform Load Based on DEM. Appl. Sci. 2025, 15, 4257. https://doi.org/10.3390/app15084257
Liu H, Zhang X, Lin H, Chen Y, Yang C, Ou K. Shear Mechanical Properties of Rock Joints Under Non-Uniform Load Based on DEM. Applied Sciences. 2025; 15(8):4257. https://doi.org/10.3390/app15084257
Chicago/Turabian StyleLiu, Hongwei, Xing Zhang, Hang Lin, Yifan Chen, Chaoyi Yang, and Ke Ou. 2025. "Shear Mechanical Properties of Rock Joints Under Non-Uniform Load Based on DEM" Applied Sciences 15, no. 8: 4257. https://doi.org/10.3390/app15084257
APA StyleLiu, H., Zhang, X., Lin, H., Chen, Y., Yang, C., & Ou, K. (2025). Shear Mechanical Properties of Rock Joints Under Non-Uniform Load Based on DEM. Applied Sciences, 15(8), 4257. https://doi.org/10.3390/app15084257







