A Distance-Encoded Bloom Filter for Fast NDN Name Lookup

Abstract

Named data networking (NDN) is a content-centric network architecture that requires efficient name lookup to forward packets based on hierarchical content names. Whereas IP lookup operates on fixed-length addresses, NDN name lookup must identify the longest matching prefix (LMP) from a variable-length name space, making it computationally challenging. Hash table-based approaches provide O (1) search complexity but often require multiple accesses due to the unknown LMP length. To mitigate excessive off-chip memory accesses, Bloom filter-assisted pre-checking is commonly employed. However, conventional Bloom filter-based approaches can only perform membership tests and do not provide information about the next search range, which limits their ability to effectively reduce Bloom filter accesses. This paper proposes a distance-encoded Bloom filter to improve name lookup efficiency. It encodes two distance values into the Bloom filter, enabling a more refined search range compared to binary search-based methods. By utilizing these encoded distances, the proposed scheme not only reduces the number of Bloom filter queries but also ensures that only prefix nodes need to be stored in the hash table. This helps reduce hash collisions and minimize off-chip memory accesses. Experimental evaluation using large-scale FIB datasets shows that the proposed approach reduces both Bloom filter accesses and hash table lookups, which contributes to improving overall lookup performance.

1. Introduction

Named data networking (NDN) is a promising future Internet architecture that delivers packets based on content names rather than destination addresses [1,2,3,4]. Traditional IP networks rely on host-to-host communication, which faces challenges with mobility, security vulnerabilities, and redundant data transmissions. The NDN, which delivers packets based on content name, has emerged to address the demands of recent network-enabled technologies such as the Internet of Things (IoT) and mobility [4]. Recent studies have focused on forwarding strategies in IoT and MANET [5,6].

In NDN, forwarding a packet to the next hop requires a name lookup. For a given content name, the name lookup process aims to find the longest matching prefix (LMP) in the forwarding information base (FIB) [7]. For example, if /net/ndn/codebase/main is given as a content name and there are two matching prefixes, /net/ndn and /net/ndn/codebase, in the FIB, then /net/ndn/codebase is the best matching prefix because it is longest among them.

Like IP address lookup, name lookup involves finding the longest matching prefix (LMP) but is more complex and challenging. Unlike IP addresses, which are fixed at 32 bits, content names have variable lengths, and the name space is unbounded. A lot of research has been conducted to achieve fast name lookup. One approach to achieving efficient lookups is to use a hash table. However, a key challenge in hash table lookup arises from the fact that the length of the key used for searching cannot be known in advance. The length of the search key should be the length of the LMP, but the LMP is determined as a result of the lookup. In the previous example, the length of the LMP is 3, meaning that taking three components from the given content name as the key would result in a successful hash table lookup. However, since the LMP is not known beforehand, the lookup process must start with the length of the longest possible prefix among all prefixes in the FIB and decrement the length iteratively until a match is found. Alternatively, a binary search by the length can be employed [8].

The hash table contains all the prefixes of the FIB and resides in off-chip memory due to its large size. Since off-chip memory has high latency, minimizing hash table accesses is crucial. A Bloom filter can help reduce these accesses by pre-checking whether the prefix of a specific length is present in the hash table. A Bloom filter is a space-efficient data structure that represents membership using bits [9]. In a Bloom filter, the membership of an element in a set may result in a false positive, but a negative result is always true. Implementing the Bloom filter in on-chip memory can improve name lookup performance by reducing the number of hash table accesses and instead relying on the faster Bloom filter.

There has been extensive research on Bloom filter-assisted name lookup schemes [10,11,12,13,14]. Just as multiple lookups are required in hash tables, multiple queries to the Bloom filter may also be necessary to determine the length corresponding to the LMP. The number of these membership queries can be reduced using a binary search based on length. A positive result from a Bloom filter query indicates that a matching node may exist at the current length or at a longer length, meaning the search should continue in a longer length region. Conversely, a negative result suggests that no match exists at the current length, so the search should proceed in a shorter length region. When the length of a given content name is n, the number of Bloom filter accesses in a binary search typically follows O (log₂ n). To further reduce both Bloom filter and hash table accesses, we propose encoding additional information in the Bloom filter, along with membership, such as the distance to the nearest (or farthest) matching prefix from the current length.

The set of name prefixes in the FIB can be represented as a trie. In this prefix trie, there are two types of nodes: prefix nodes and intermediate nodes, which are non-prefix nodes. To find the longest matching prefix for a given content name, a Bloom filter must include all nodes as members, not just prefix nodes but also intermediate nodes. As a result, the matching node identified by the Bloom filter test may be an intermediate node. Therefore, the hash table must store all nodes, including intermediate nodes. If the hash table contains only prefix nodes, additional backtracking may be required due to hash table lookup failures.

The proposed Bloom filter determines the next search range based on two distance values, which define the possible length range where descendant prefixes may exist. Consequently, the Bloom filter test indicates the existence of a matching prefix at a specific length, allowing the hash table to store only prefix nodes. This proposed method not only reduces the number of Bloom filter accesses by narrowing the search range based on distance values but also helps mitigate hash collisions by reducing the number of entries stored in the hash table.

The rest of this paper is organized as follows. Section 2 reviews related work on name lookup and introduces trie-based, hash-based, and Bloom filter-based approaches. Section 3 introduces the proposed scheme, which incorporates a distance-encoded Bloom filter. In Section 4, the proposed scheme is evaluated through experiments and compared to previous approaches. The experimental results are also discussed. Finally, Section 5 concludes this paper.

2. Related Works and Background

2.1. Related Works

Most NDN name lookup schemes can be classified into trie-based [15,16,17], hash table-based [8,18,19,20], and Bloom filter-based [10,11,12,13,14] approaches, among others [14,21,22,23,24,25].

In the trie-based approach, name prefixes are stored in a hierarchical tree structure, called a trie, where each node represents a name component. In the name prefix tree (NPT), the algorithm traverses from the root to the leaves to find the longest matching name prefix. However, it suffers from low performance due to the large number of sequential memory accesses, which depend on the length of each input name. To improve throughput, Wang et al. proposed parallel name lookup (PNL) [15]. The PNL processes multiple input names concurrently by dividing the NPT structure into several groups, which are mapped onto parallel modules. Additionally, they introduced name component encoding (NCE) to reduce memory usage, utilizing two types of tries: the component character trie (CCT) and the encoded name prefix trie (ENPT) [16].

The NPT contains many non-prefix internal nodes, which are referred to as empty nodes. Seo et al. observed that these empty nodes not only waste memory space but also increase the number of memory accesses required to find the longest matching prefix [17]. To address this issue, they proposed Priority-NPT, which stores longer prefixes in empty nodes. This approach not only reduces memory usage but also enables finding the longest matching prefix with fewer memory accesses.

In hash table-based lookup, all name prefixes are stored in the hash table. A hash table search for a given key can be completed in a single access if there are no collisions. However, since the key length is unknown in advance, multiple attempts are required to find the longest matching prefix. Wang et al. proposed a greedy strategy that determines the next prefix length to search in the hash table based on the popularity distribution of leaf prefixes [20]. This approach is compared to CCNx, which performs a linear search from the longest prefix downward. In the case of hash collisions, searching requires traversing the chain within the corresponding bucket and performing key comparisons, which increases lookup time. To mitigate this, So et al. proposed storing a Bloom filter in each bucket to maintain membership information, indicating whether the key exists in the chain. This allows for fast lookups without requiring a chain walk [18]. Additionally, they replace a name string with a 64-bit hash value in each bucket, significantly reducing comparison time for long name strings. Similarly, Yuan et al. proposed using fingerprints to reduce comparison time in both hash tables and Patricia trie lookups [19]. In another study, they introduced a binary search by length to optimize hash table-based lookup [8].

Most Bloom filter-based approaches are used in combination with or as an auxiliary component of other lookup techniques. Several studies have explored the use of on-chip Bloom filters to pre-check the presence of a prefix before performing a hash table lookup in off-chip memory [10,11,12]. Lee et al. proposed a method that progressively increases the prefix length and iteratively accesses the on-chip Bloom filter to determine the length of the longest matching prefix [10]. This approach reduces the number of off-chip hash table accesses. He et al. introduced an optimization that applies a binary search by prefix length to minimize the number of Bloom filter accesses [11]. In another study, Lee et al. proposed a dual-load Bloom filter, which contains two types of information within a single cell to assist hash table lookups [12]. One piece of information is membership, similar to a conventional Bloom filter, while the other represents a skip value in a path-compressed trie, indicating the length of a compressed path. Jing et al. proposed a name lookup architecture utilizing three types of Bloom filters: level-VBF, face-VBF, and en-BF [13]. The vectored-Bloom filter (VBF), originally introduced for IP lookup by Byun et al. [26], enables rapid output port retrieval using multiple Bloom filter vectors.

Some approaches addressed name lookup by incorporating hash tables and tries [14,21,22]. Quan et al. proposed a hybrid model that utilizes fixed-sized counting Bloom filters for higher-level components and variable-sized tries for lower-level components to optimize NDN lookup efficiency [14]. Kim et al. proposed constructing hash tables at each component level and using a Patricia trie instead of chaining to resolve hash table bucket collisions [21]. Byun et al. introduced a hybrid lookup scheme combining a level-priority trie with a hash table-based approach [22]. The level-priority trie is implemented through programming Bloom filters, called l-BF and p-BF.

Kraska et al. proposed machine learning-based index structures that predict the position or existence of data by learning their distribution [23]. Building on this idea, Wang et al. enhance name lookup by applying the learned indexes to Bloom filters [24]. Since neural network-based classifiers may produce false negatives unlike standard Bloom filters, a backup Bloom filter is employed to handle such cases. Similar to conventional methods, multiple accesses are still required to find the longest matching prefix, and this approach does not address this issue. Li et al. also proposed a neural network-based name lookup scheme [25]. In their approach, the input name string is split into fixed-length segments to be fed into neural network models and processed through a layered architecture of multiple sub-range models. All these neural network-based approaches face challenges with incremental FIB updates.

2.2. Trie-Based Name Lookup

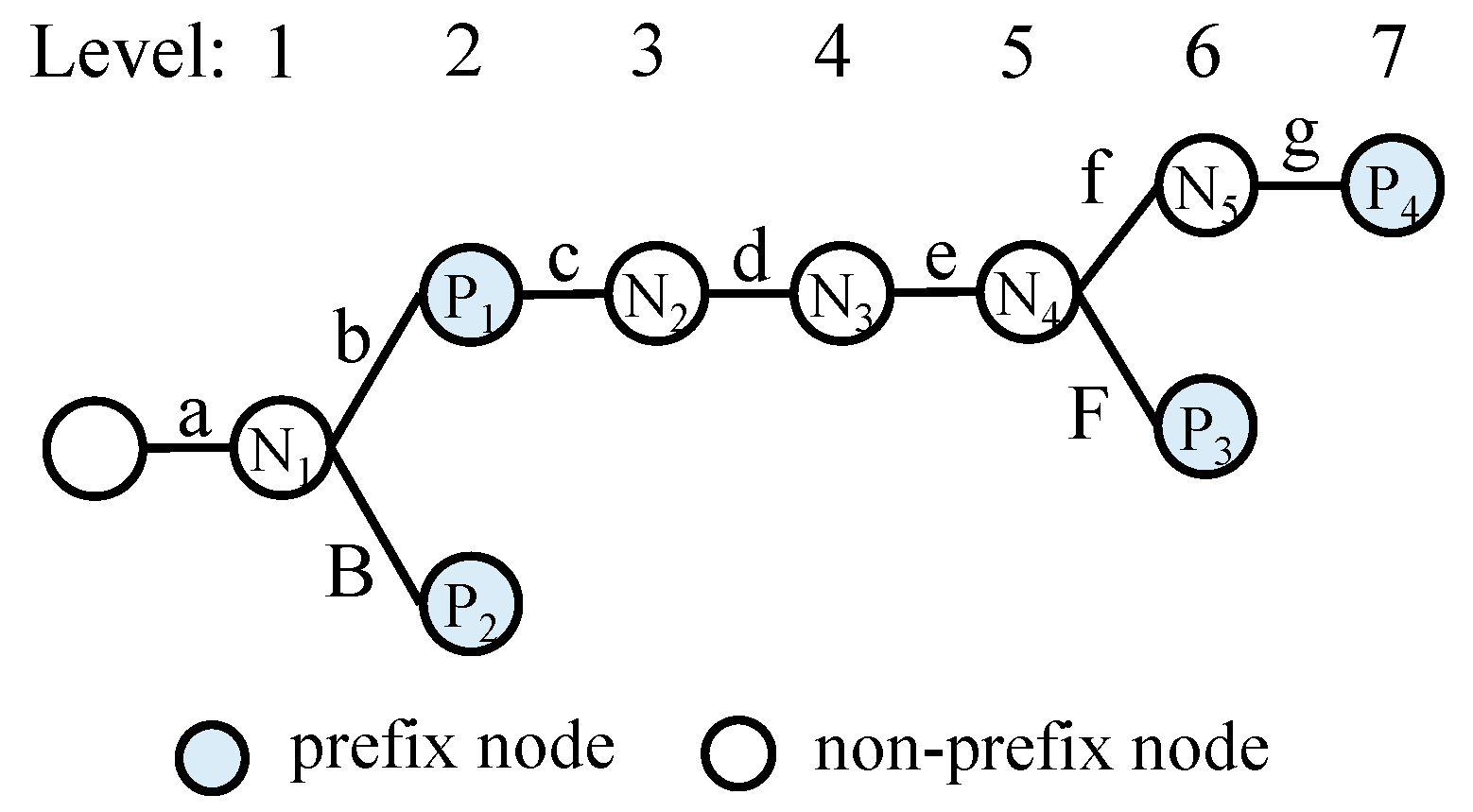
A trie consists of prefix nodes and non-prefix intermediate nodes. Figure 1 illustrates an example of a trie, which includes four prefix nodes (P₁ to P₄) and five intermediate nodes (N₁ to N₅). These prefixes are associated with output face information that is used for packet forwarding. To illustrate the name lookup process, suppose that the content name /a/b/c/d/e/F/s is queried. Starting from the root node of the trie and following the matching path, two name prefixes match in the trie: /a/b (P₁) and /a/b/c/d/e/F (P₃). Since /a/b/c/d/e/F is the longer of the two, it is chosen as the final lookup result.

2.3. Hash Table-Based Name Lookup

The hash table-based scheme for name lookup is one of the most effective approaches because each search can be performed in O (1) time in a hash table when there is no collision. However, for each hash search, the length of the key must be determined in advance since the hash table contains prefixes of varying lengths. As a result, multiple hash searches may be required to find the longest matching prefix during the lookup process.

2.3.1. Descending Order from the Longest Name

In CCNx, the search begins with the key corresponding to the length of the longest prefix in the FIB or the length of the full content name [27]. If the search fails, the search key length decrements and the search continues iteratively. Although the search stops upon finding the first match, in the worst-case scenario, up to O (min(k, n)) searches may be needed, where k is the longest prefix length in the FIB and n is the length of the given name. In this context, the prefix length is defined as the deepest component level rather than the length of the character string.

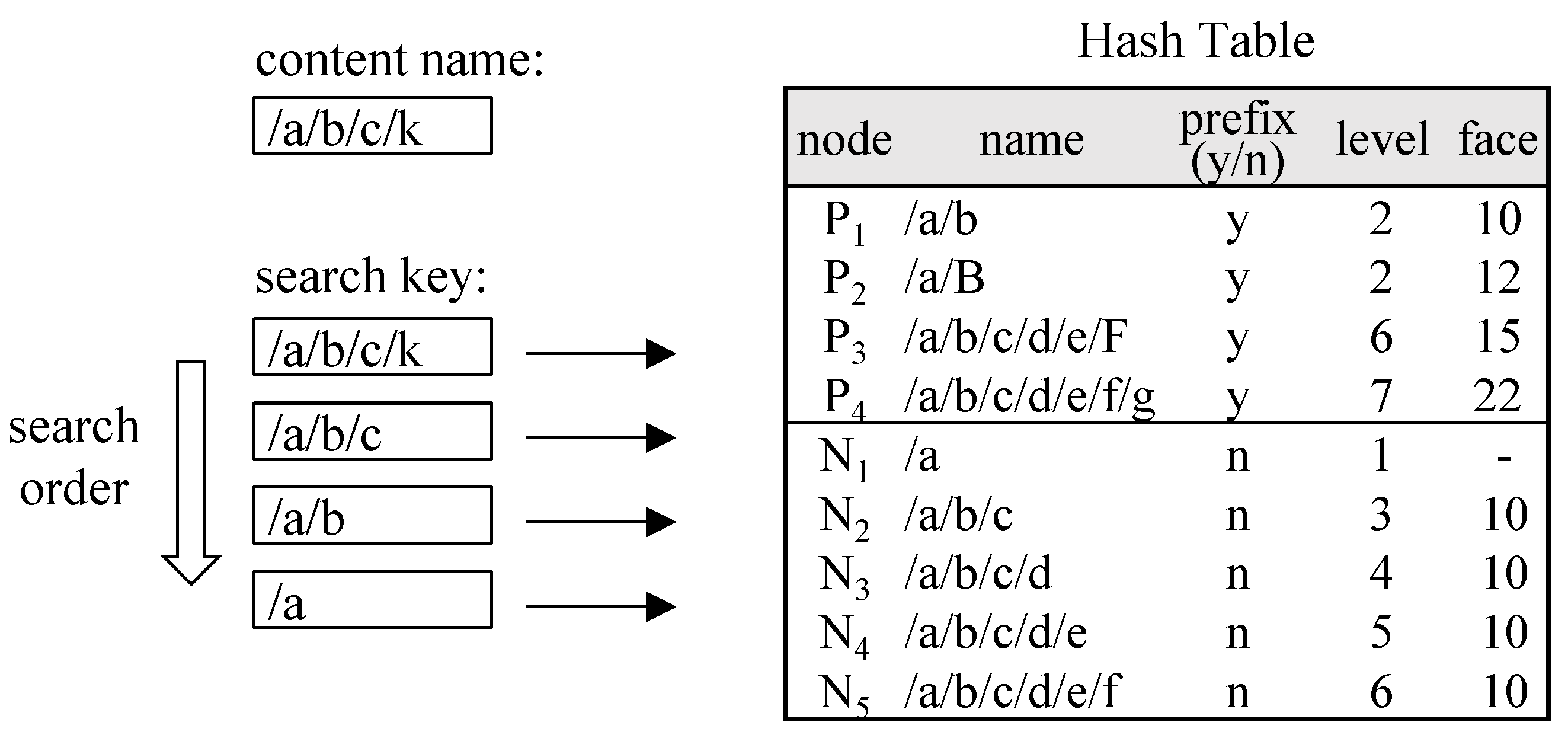
Figure 2 illustrates how the trie in Figure 1 is represented as a hash table. Given a content name /a/b/c/k for lookup, searches for each of its sub-prefixes—/a/b/c/k, /a/b/c, /a/b, and /a—may be conducted sequentially in the hash table until a matching prefix is found. In this case, the search stops at /a/b, which is the longest matching prefix, and the lookup returns 10 as the face value. The hash table can be constructed using only prefix nodes (P₁ to P₄), while non-prefix nodes (N₁ to N₅) can be omitted. However, as shown in Figure 2, the number of hash table accesses can be reduced if each non-prefix node inherits and retains the face value of the nearest ancestor prefix. Under this configuration, a lookup for /a/b/c successfully finds a match in the hash table and returns the correct face value. There is a trade-off between the number of hash table accesses and the increase in collisions as hash table entries grow.

2.3.2. Binary Search Order by Length

To reduce the hash table accesses, a binary search by prefix length is proposed [8]. This idea was originally proposed by Waldvogel in the field of IP lookup [28]. This binary search starts at the middle component level. If a match is found, the search range shifts to the longer half of the levels; otherwise, it shifts to the shorter half.

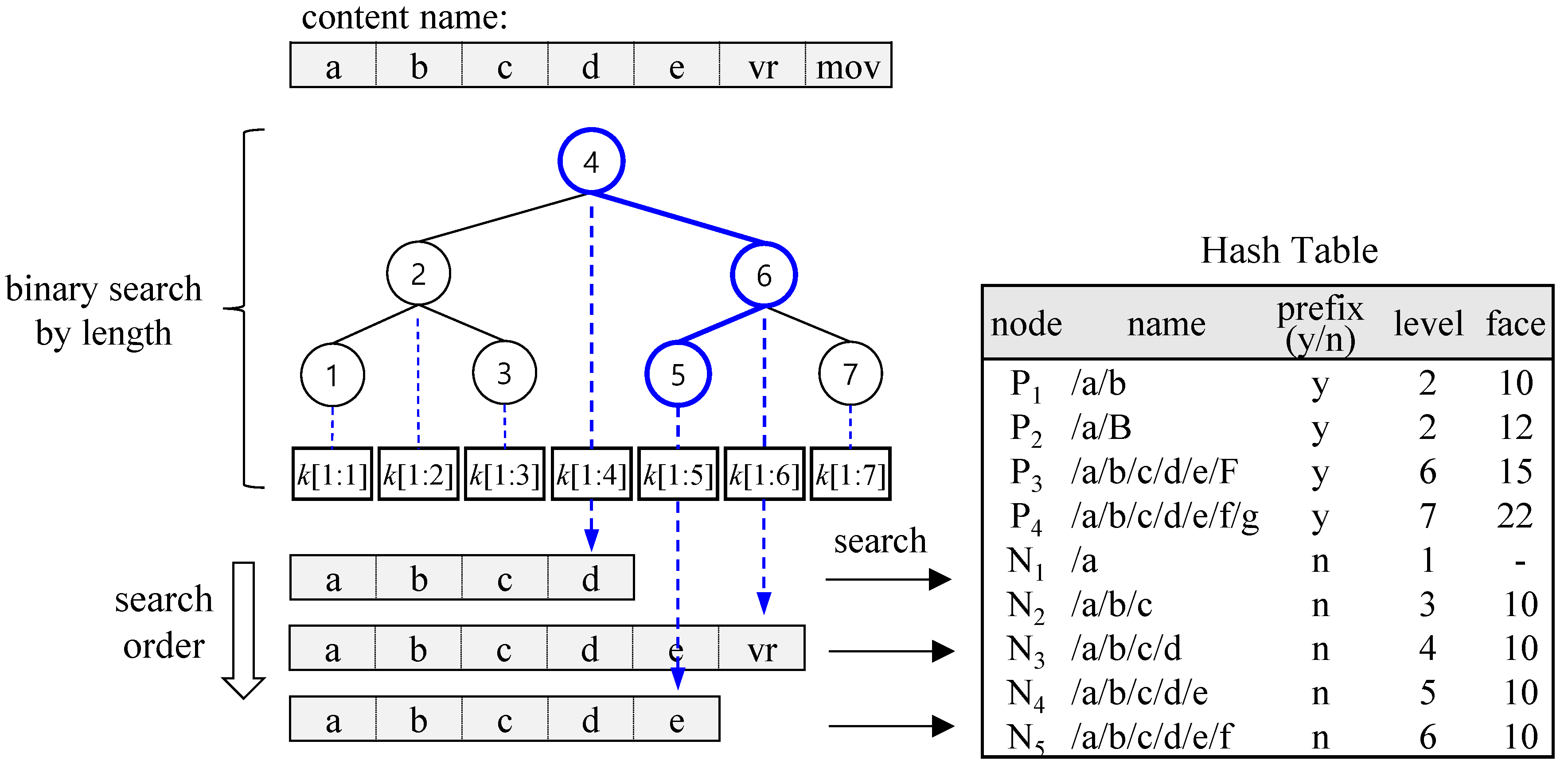
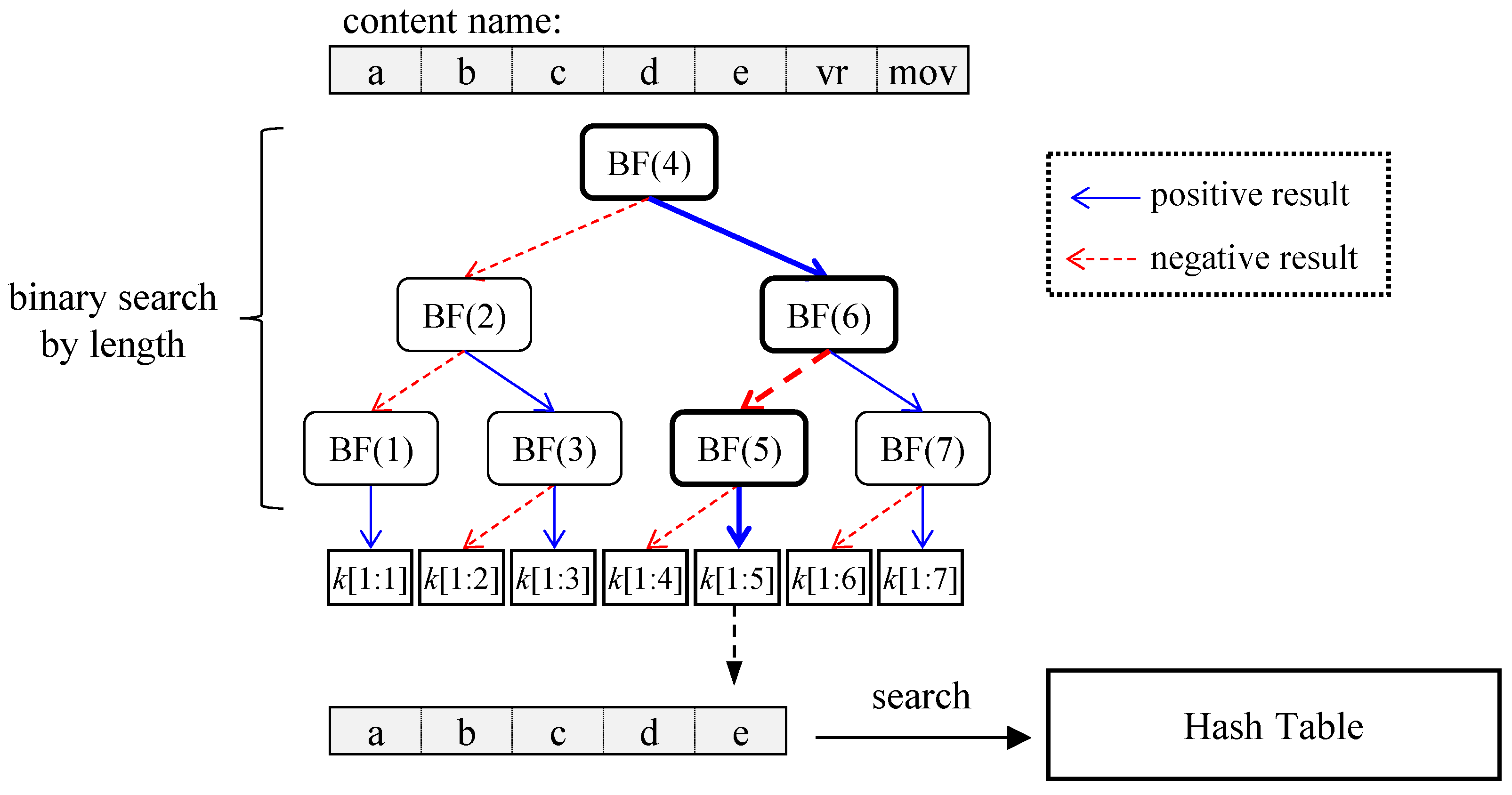
Figure 3 illustrates the lookup process using binary search by length. Given a content name /a/b/c/d/e/vr/mov, the hash search begins at level 4, where the search key corresponds to /a/b/c/d. k [1:4] represents a key composed of the first through the fourth components. Since the search result (N₃) is found in the hash table, the next search proceeds at level 6 with the key /a/b/c/d/e/vr. However, this search fails, so the next search is conducted at level 5. The final search result, N₄, is a non-prefix node, meaning that its result face is inherited from its ancestor prefix. Thus, the face of N₄ is the same as the face of P₁.

Note that for the binary search to work, the hash table must contain both prefix nodes (P₁ to P₄) and non-prefix nodes (N₁ to N₅). Unlike CCNx, which searches sequentially from the longest prefix downward, the binary search starts at the middle level. As a result, all non-prefix nodes must be stored in the hash table to enable further searches for a longer matching prefix. This method achieves O (log (r)) hash table accesses where r represents the longest prefix length in the FIB.

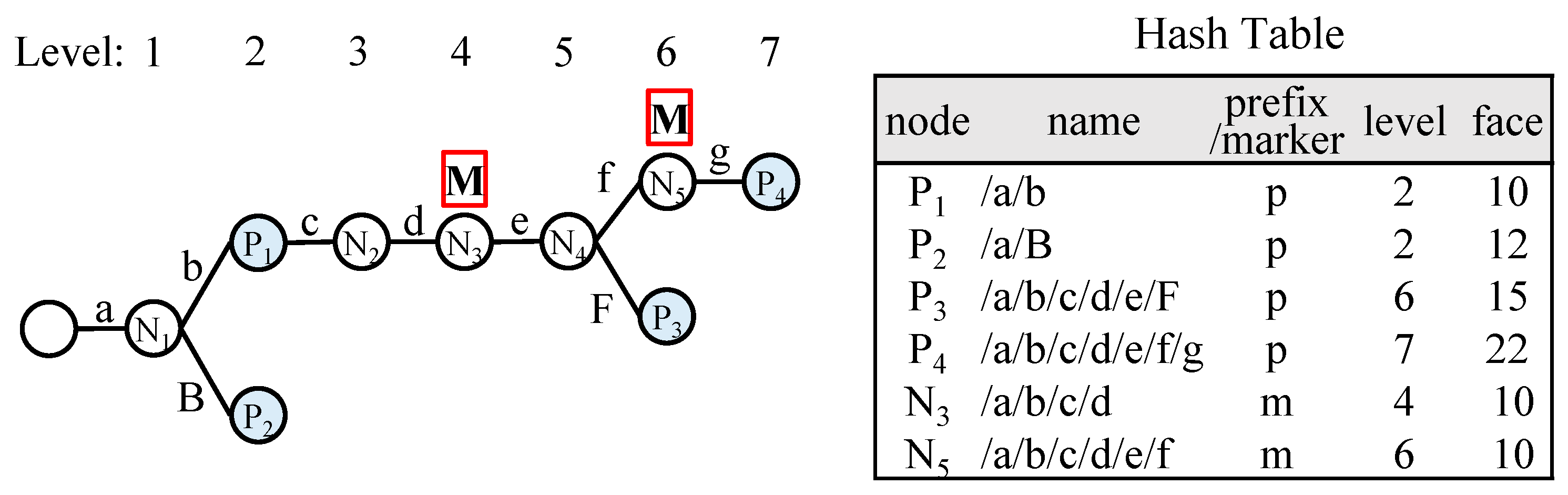
Waldvogel et al. discovered that not all non-prefix nodes are required for the next search. Instead, binary search can proceed as long as only specific non-prefix nodes, known as marker nodes, are stored in the hash table [28]. Figure 4 illustrates a name prefix trie with marker nodes indicated, along with the corresponding hash table reflecting this approach. In the figure, the N₄ node at level 5 is reached after confirming the match of N₃ at level 4 and passing through level 6. Since the result has already been obtained through the match of N₃, the match result for N₄ is unnecessary. Similarly, N₁ and N₂ nodes are not required in the hash table.

2.4. Bloom Filter-Assisteed Name Lookup

Since the hash table contains a large number of name prefixes and even includes non-prefix intermediate nodes for binary search, it resides in off-chip memory (DRAM), resulting in high access latency. To reduce the number of hash table accesses, Bloom filter-based pre-search approaches have been proposed [10,11,12]. A Bloom filter checks whether a specific element is in a set [9]. Such Bloom filters have been widely used to improve longest prefix matching in network applications [29,30,31,32].

Using a Bloom filter, we can efficiently check whether a matching node exists for a specific length. Since a Bloom filter is much smaller than a hash table, the length of the LMP can be identified at the speed of on-chip memory access.

A Bloom filter is a bit vector that indicates the existence of members by setting bits indexed by multiple hash functions. Figure 5 illustrates an example where the presence of a member is tested using three hash functions (h₁–h₃). For /net/ndn/lookup, at least one bit specified by the hash function (h₂) is not set, indicating the absence of the member. In contrast, for /net/ndn, all bits are set, suggesting the possible presence of the member.

By performing such pre-checking techniques before searching the hash table, the number of hash table accesses can be reduced. However, since bits may be set by other members, Bloom filters can produce false positives, meaning that a non-existent member may incorrectly appear as present.

As described in Section 2.3.2 in the context of hash tables, the binary search by length approach can also be applied to Bloom filters for membership testing. The hash table search is conducted only after the final Bloom filter access rather than after every Bloom filter access.

In Figure 6, BF (m) means a membership test for a key of length m, meaning a query to check whether a matching node exists at that length. During the binary search process, if the Bloom filter returns a positive result, the search continues for a longer length; otherwise, it proceeds with a shorter length. With each membership test, the search range halves, and the search position shifts to the midpoint of the remaining range. Once the search reaches a leaf of the search tree, a hash table search is initiated using the final length value.

The number of Bloom filter accesses follows an O (log (r)), where r is the length of the longest prefix in the FIB. Since a Bloom filter may produce false positives, the hash table search could fail, requiring backtracking.

A Bloom filter can be constructed by including either all nodes—both prefix nodes and non-prefix nodes—or only marker nodes among the non-prefix nodes. If only marker nodes are included, the number of elements in the Bloom filter is reduced, thereby lowering the false positive rate. However, since the positions of marker nodes are fixed within the given binary search tree, using marker nodes makes it difficult to dynamically adjust the initial search range.

The hash table can store (1) all nodes, (2) prefix nodes and marker nodes, or (3) only prefix nodes. Storing only prefix nodes reduces the number of entries, which helps decrease hash collisions. However, it also increases search failures, potentially leading to a significantly higher number of hash table accesses.

3. Proposed Scheme

The binary search with a conventional Bloom filter reduces the search range by half with each Bloom filter access. In contrast, the proposed method further reduces the search range to the span of descendant prefixes, making it less than half. Additionally, since the proposed Bloom filter identifies a prefix node at the final access, the hash table only needs to store prefix nodes. This reduces the number of table entries, helping to minimize hash collisions.

3.1. A Distance-Encoded Bloom Filter

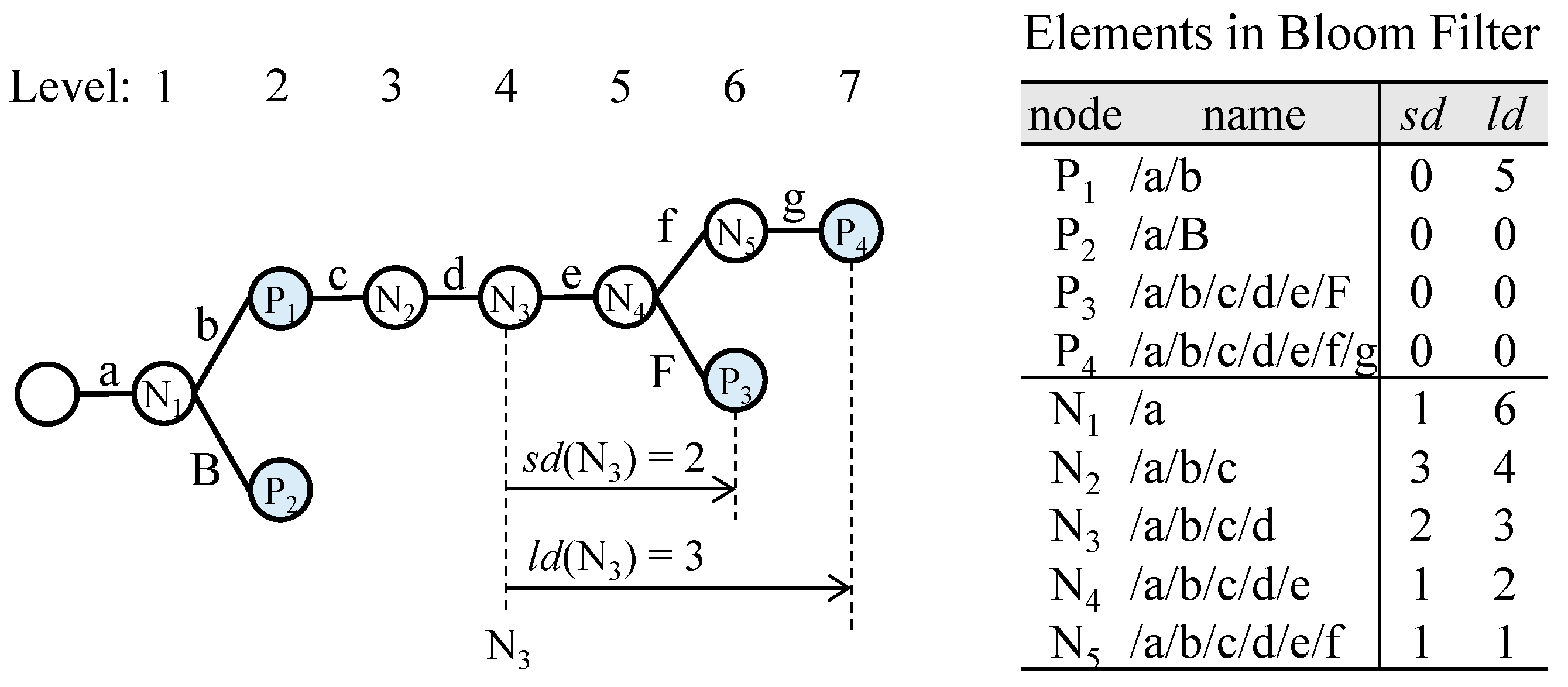
A distance-encoded Bloom filter provides the range of descendant prefixes when the membership test result is positive. This range, represented by two distance values, determines the next search range.

Definition 1.

(Shortest Distance): For a given node t in a trie, sd (t) is defined as the distance to its nearest descendant prefix.

Definition 2.

(Longest Distance): For a given node t in a trie, ld (t) is defined as the distance to its farthest descendant prefix.

For a given membership query on node t, if the distance-encoded Bloom filter returns a positive result, the next search range is derived from sd (t) and ld (t). In Figure 7, the nearest descendant of N₃ is P₃, with a distance of 2. Similarly, the farthest descendant of N₃ is P₄, with a distance of 3. Figure 7 presents a table showing sd and ld values for all nodes. If the membership test for N₃ returns positive, the next search range is given by the interval [4 + sd, 4 + ld], where 4 represents the level of N₃, resulting in the interval [6,7]. In contrast, the binary search approach would produce the interval [5,7], which is wider. Additionally, for any prefix node, sd is always 0, and for any leaf prefix node, ld is also 0.

In a basic Bloom filter of m bits, the membership checking is performed by examining the bits indexed by the k hash functions: h₁ (t), h₂ (t), …, h_k (t). If all k bits are set to 1, the membership check returns a positive result. Yang et al. proposed a shifting Bloom filter that utilizes an offset to represent element counters [33]. The distance-encoded Bloom filter also uses an offset but extends this approach by incorporating both negative and positive offsets to encode two distance values: sd and ld, respectively. Figure 8 illustrates how membership and distance values are represented in the distance-encoded Bloom filter, providing a comparison with the conventional Bloom filter.

3.2. Construction

In the distance-encoded Bloom filter, 2 k bits must be set to 1 to insert the membership of a node, where k is the number of hash functions. Each set bit is positioned at a distance sd or (ld − sd) from the location indexed by each hash function. A total of 2 k bits are set to 1 at the following locations: h₁ (t) − sd, h₂ (t) − sd, …, h_k (t) − sd, h₁ (t) + (ld − sd), h₂ (t) + (ld − sd), …, h_k (t) + (ld − sd). However, if sd and ld are equal, all the bits at h_i(t) + (ld − sd) are not set, meaning that only k bits are set to 1.

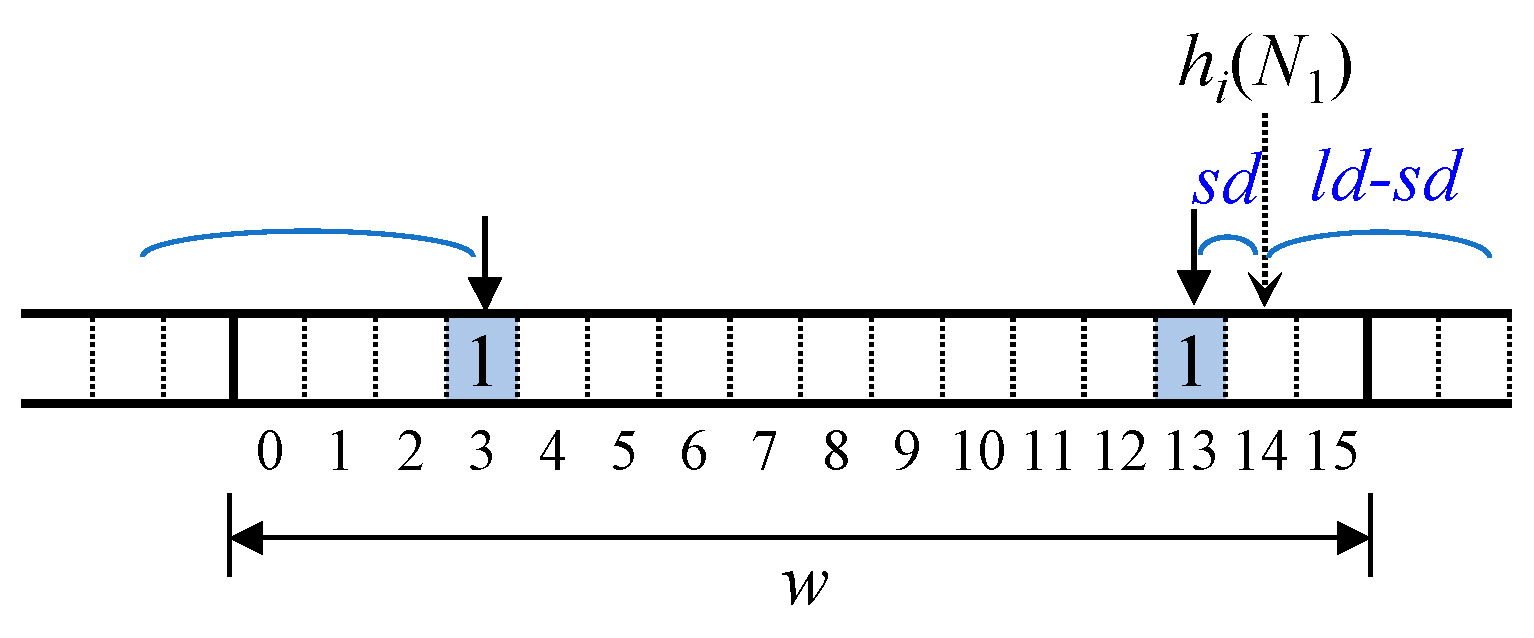
To minimize the number of Bloom filter accesses, it is desirable for both bits at sd and (ld − sd) positions to reside within the same word. To achieve this, if they fall outside the word boundary, they are wrapped around. Figure 9 illustrates how the bit position of (ld − sd) wraps around when inserting N₁, assuming a word size of 16 for convenience. The ⟨sd, ld⟩ values for N₁ are ⟨1, 6⟩, meaning (ld − sd) = 5. In the figure, h_i (N₁) + 5 exceeds the word boundary, so the actual bit position becomes 3 due to wrapping. The bit position of sd can be computed in a similar manner. The sd value is limited to w/2 − 1, and (ld − sd) is limited to w/2 where w represents the word size. These values indicate the maximum limits in the FIB rather than their actual values.

3.3. Query

The Bloom filter access for a node provides both distance information and the membership test result simultaneously. If valid sd and ld values are obtained, the membership test result for that node is positive. For a query on node t, a total of k words are retrieved from the Bloom filter. Each of these words contains a bit pointed to by the hash functions, h₁ (t), h₂ (t), …, h_k (t). If multiple hash functions point to the same word, the total number of retrieved words may be less than k.

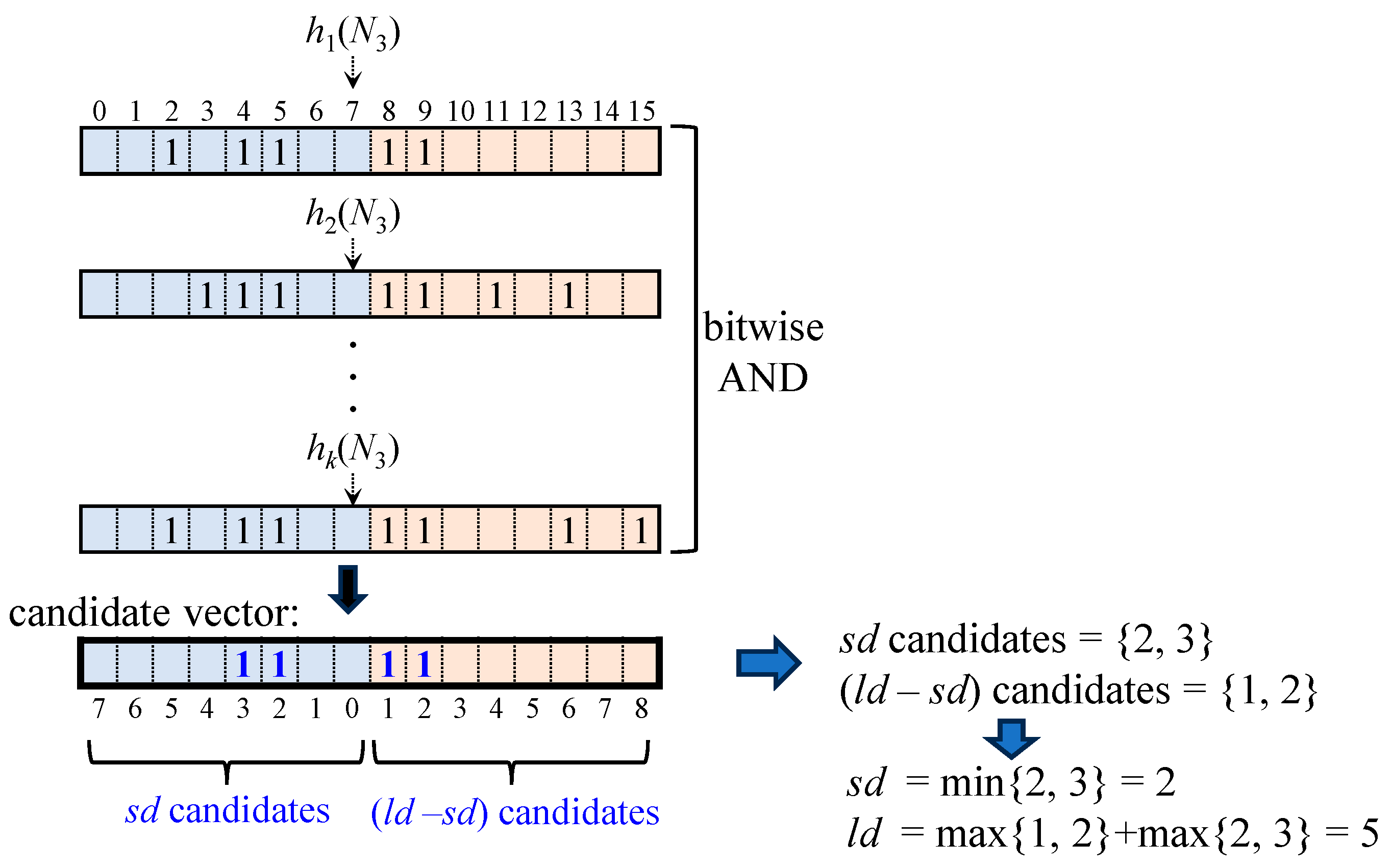
In each word, the bit position pointed to by h_i (t) varies. However, for ease of processing, these bit positions are aligned so that the designated bit is positioned at the center. Specifically, a circular shift is applied to ensure that, in all words, the bit specified by h_i (t) is located at the bit position (w/2 − 1). Figure 10 illustrates the process of obtaining sd and ld values from these aligned words.

The candidate vector is obtained by simply performing a bitwise-AND operation on k words. In this vector, the left half represents candidate values for sd, while the right half represents candidate values for (ld − sd). Since the candidate vector may contain bits that were set when other nodes were inserted into the Bloom filter, it can include spurious values. To obtain a valid next search range, sd must be interpreted as the smallest value, while ld must be the largest value.

For a given node t, the Bloom filter output, BF(t), produces ⟨sd, ld⟩. These values are computed from candidate values for sd and (ld − sd) as follows:

max_sd = max{x₀, x₁, …, x_c}

sd = min{x₀, x₁, …, x_c}

ld = max{y₀, y₁, …, y_d} + max_sd

where x_i and y_i are candidate values for sd and (ld − sd), respectively.

In Figure 10, the candidate values extracted from the set bit positions in the candidate vector are {2, 3} for sd and {1, 2} for (ld − sd). The sd value is chosen as 2, the smallest value in {2, 3}, while ld is computed as the sum of the largest value in {2, 3} and the largest value in {1, 2}, resulting in 5. Thus, the Bloom filter output for N₃, denoted as BF (N₃), is ⟨2, 5⟩. Since a valid ⟨sd, ld⟩ pair has been obtained, the presence of N₃ is regarded as positive.

Due to other nodes inserted into the Bloom filter, spurious values may appear. The result of BF (N₃) may cover a larger range than the actual ⟨sd, ld⟩ of N₃, but this range always encompasses the required search range.

Let a node t have the actual distance range [a, b], meaning that all of t’s descendant prefixes in the trie lie at distance d satisfying a ≤ d ≤ b. Suppose the Bloom filter returns BF(t) = ⟨sd, ld⟩. The returned range [sd, ld] always covers [a, b], i.e., sd ≤ a and ld ≥ b.

A search range that fully covers the length range of all the prefixes to be searched is called a valid search range. If the Bloom filter output for a node t, BF(t), is ⟨sd, ld⟩, then the interval [sd, ld] is always a valid search range and a positive membership result is indicated for t. On the other hand, if BF(t) produces no output, meaning that there is no candidate value for sd, then a negative membership result is indicated for t.

The decoding process to obtain the Bloom filter output, BF(t), can be efficiently performed with specialized hardware support. First, k words are fetched from on-chip memory based on k hash functions, as in a conventional Bloom filter. Then, a candidate vector is efficiently computed using hardware support for a k-way bitwise-AND operation. The bitwise-AND style operation is also required to perform the membership check in the conventional Bloom filter. In the next step, we need to identify the position of the rightmost set bit in each half word of the candidate vector in order to compute the ⟨sd, ld⟩ value. Given that many off-the-shelf processors support counting trailing zeros (CTZs), the ⟨sd, ld⟩ value can be easily extracted using the hardware feature. Although this incurs additional cycles for the CTZs, our Bloom filter provides more informative results than the conventional one, which enables a reduction in both off-chip hash table lookups and even on-chip Bloom filter accesses.

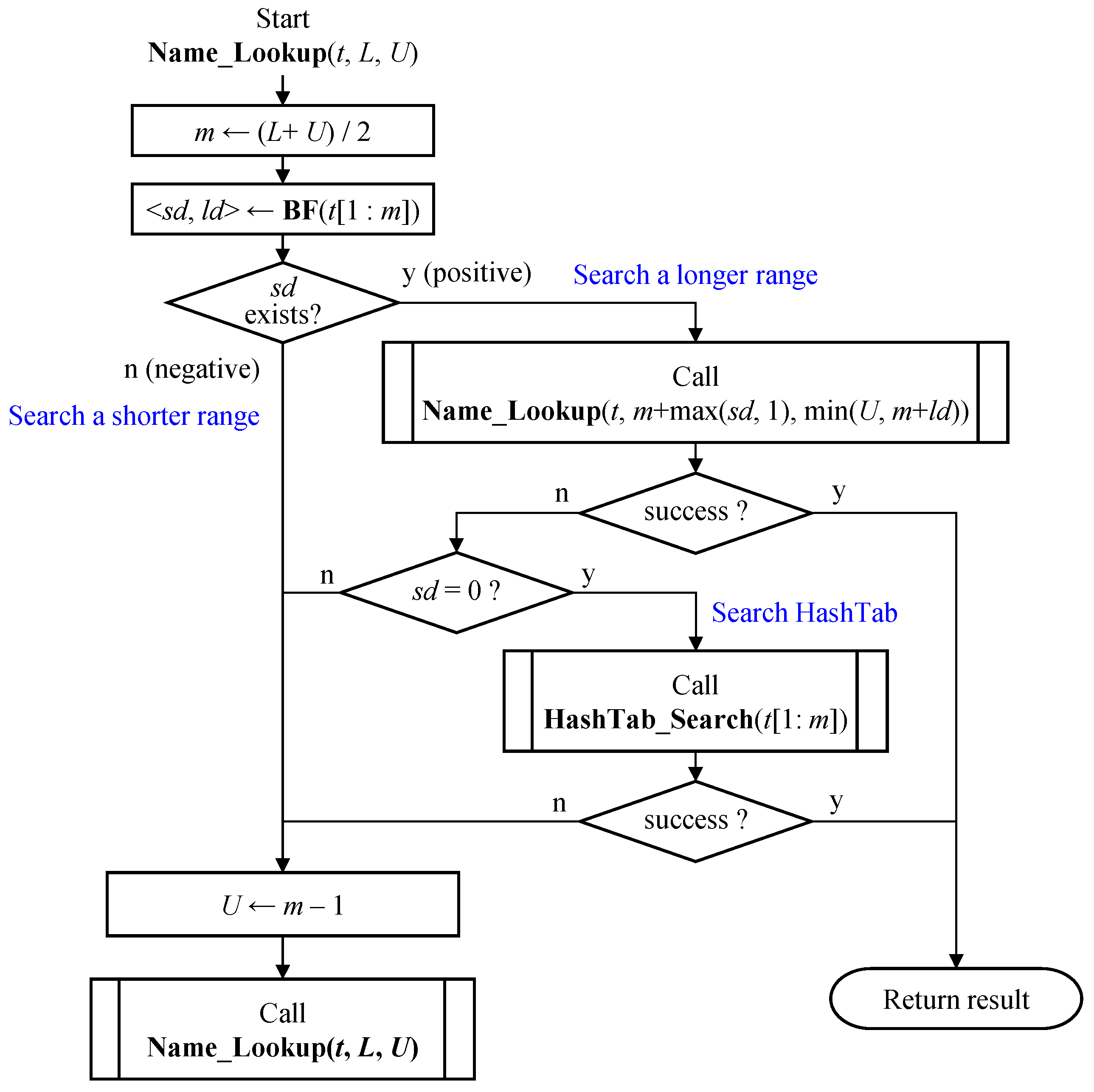
3.4. Name Lookup Using a Distance-Encoded Bloom Filter

Similar to binary search, name lookup using the distance-encoded Bloom filter advances to a longer range if the current level passes the membership test, and otherwise, shifts to a shorter range.

Figure 11 illustrates the name lookup process using a distance-encoded Bloom filter. Given a name t and an initial search range [L, U], the process first pre-checks whether the name at level m, denoted as t [1:m], is a matching node where m = (L + U)/2, or any initial starting level. Two distance values, ⟨sd, ld⟩, are obtained as the output of the Bloom filter, BF (t [1:m]). If the sd value exists in the output, it means the Bloom filter indicates a positive match. In this case, the search should continue to find a longer matching node. The new search range is the intersection of the interval derived from ⟨sd, ld⟩, and the right half of the current range, i.e., [m + sd, m + ld] ∩ [m + 1, U].

If the search in the longer range fails, meaning that there is no longer a matching node, then the name at the current level m can be the LMP. In the earlier step, the Bloom filter indicated there is a matching node at level m. If sd = 0, the node is considered a prefix since the closest prefix is at distance 0. At this point, a hash table search is performed using t [1:m] to find the LMP. Note that the hash table search is only performed when the distance-encoded Bloom filter indicates the presence of a matching prefix at the current level and that prefix is the longest one. If the search fails both at the current level m and in the longer range, the search proceeds in the shorter range [L, m − 1].

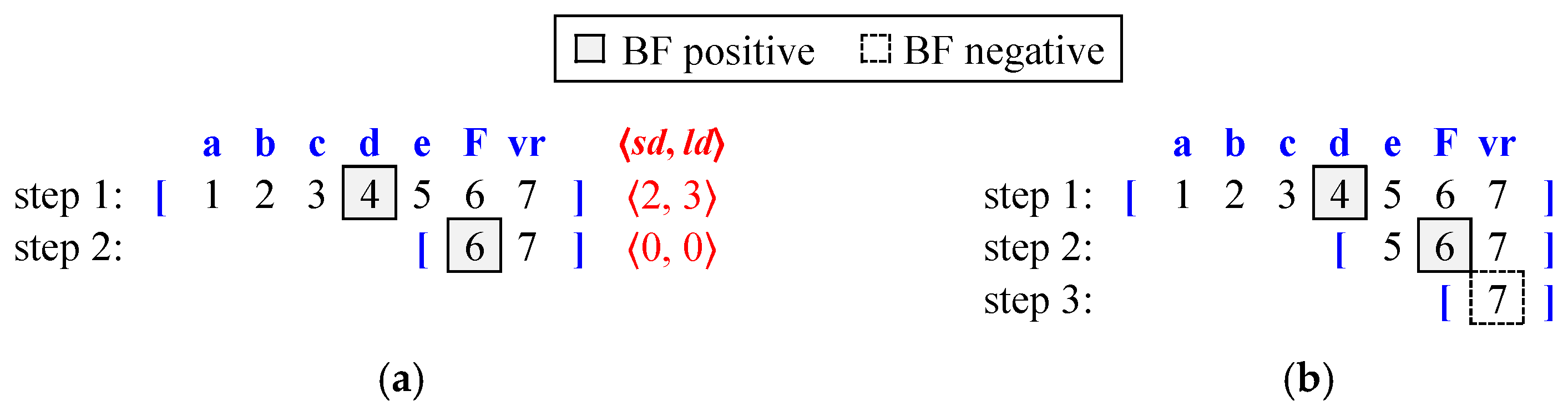
Figure 12 compares the distance-encoded Bloom filter and the conventional Bloom filter. We suppose that the FIB and distance-encoded Bloom filter contents are structured as shown in Figure 7 and that the lookup target content name is /a/b/c/d/e/F/vr. In Step 1, both Bloom filters begin with the search range [1,7], querying the Bloom filter at level 4 with /a/b/c/d. In the case of the conventional Bloom filter, which follows binary search, the lookup always starts at the middle level (level 4). However, for the distance-encoded Bloom filter, the starting level is flexible; it could begin at the most popular level (where most prefixes exist), but for this example, we assume it also starts at level 4.

In the distance-encoded Bloom filter, the BF (/a/b/c/d) output is ⟨2, 3⟩, indicating a positive result. Using the sd and ld values (⟨2, 3⟩), the next search range is obtained as [6,7], marking Step 2. At this step, the midpoint of the search range is level 6, and BF (/a/b/c/d/e/F) returns ⟨0, 0⟩, which is also positive. Since sd = ld = 0, this implies that the LMP may exist at the current level. As a result, Bloom filter access stops here, and a hash table lookup is performed for /a/b/c/d/e/F.

For binary search using the conventional Bloom filter, the search range halves with each Bloom filter access, and the next lookup level is always the midpoint of the current range. In Step 2, the Bloom filter access at level 6 returns a positive result, so the next step proceeds to level 7. For /a/b/c/d/e/F/vr, which corresponds to level 7, the Bloom filter lookup result is negative. Additionally, since no further search range remains, Bloom filter access terminates. Consequently, the last successful lookup at level 6 (/a/b/c/d/e/F) triggers the hash table search.

3.5. Update

A binary Bloom filter does not support incremental deletion of members. Moreover, for high-speed lookups, it is important to decouple the lookup structure from the structure supporting the updates. To enable incremental updates, an auxiliary structure known as a counting Bloom filter (CBF) is commonly used. A distance-encoded Bloom filter can also be updated in a similar way using a CBF.

When inserting a member, each hash function sets two bits in the distance-encoded Bloom filter—one for the sd value and the other for the (ld − sd) value. At the same time, the counting Bloom filter (CBF) increments the counters for those bit positions. For deletion, the CBF decrements the corresponding counters. If a counter reaches zero, the associated bit in the distance-encoded Bloom filter is cleared.

To update the Bloom filters described above, the distance values, sd and ld, of the nodes affected by the update must be recalculated. If a prefix is inserted as a leaf, its distance values are both zero, i.e., sd = ld = 0, and the only affected nodes are some of its ancestors, whose sd or ld values may change. For example, suppose that /a/b/c/D/E is newly inserted as a leaf prefix in Figure 7. The sd and ld of that node are ⟨0, 0⟩. The intermediate node/a/b/c/D must also be inserted, and its ⟨sd, ld⟩ is ⟨1, 1⟩. The distance of the ancestor /a/b/c was originally ⟨3, 4⟩, but it now becomes ⟨2, 4⟩. For an inserted prefix at level k, most k distance values are adjusted.

In the case of non-leaf prefix insertion, which means an intermediate (non-prefix) node becomes a prefix node, its sd value becomes 0 while its ld value remains unchanged. No descendant nodes are affected. The only affected nodes are some ancestors where only the sd values are adjusted to reflect the new distance to the inserted node; the ld values remain unchanged. For instance, suppose/a/b/c/d is newly inserted as a prefix in Figure 7. The node N₃ (/a/b/c/d) becomes a prefix node, and its sd value is adjusted to 0. The sd value of N₂ (/a/b/c) is adjusted to 1 while its ld value remains unchanged.

In the case of prefix deletion, the nodes affected by the update are also limited to some ancestors, similar to the insertion case. Therefore, the maximum number of nodes whose ⟨sd, ld⟩ values need to be updated is k when a prefix is inserted or deleted at level k. Instead of reconstruction of the entire distance table, only a limited number of entries need to be updated, which enables on-the-fly incremental updates.

3.6. Analysis

In a conventional standard Bloom filter, if the number of hash functions is k, each inserted element sets k bits. Given a Bloom filter of size m bits with n elements, the probability p₁ that a particular bit remains unset can be approximately calculated as follows:

$$p_1={\left(1-{\displaystyle \frac{1}{m}}\right)}^{kn}\approx e^{-kn/m}$$

(1)

The probability that all the bits pointed to by k hash functions are set to 1 is ${\left(1-p_1\right)}^k$. Therefore, the false positive probability FPP_S of the standard Bloom filter is given as follows [34].

$${FPP}_S={\left(1-p_1\right)}^k={\left(1-{\left(1-{\displaystyle \frac{1}{m}}\right)}^{kn}\right)}^k$$

(2)

In the distance-encoded Bloom filter, two bits for sd and (ld–sd) are set based on the hash value of a given element. If ld and sd are equal, meaning (ld–sd) = 0, then the (ld–sd) bit is not set, and only the sd bit is set. For each given ld and sd, the expected number of set bits, s, is given by s = r·1 + (1 − r)·2, where r is the probability that sd is equal to ld. The probability p₂ that a particular bit remains unset is approximated as follows:

$$p_2={\left(1-{\displaystyle \frac{s}{m}}\right)}^{kn}\approx e^{-kns/m}$$

(3)

The probability that all bits pointed to by k hash functions are set to 1 is given by ${\left(1-p_2\right)}^k$. Let p₀ be the probability that at least one of the k bits is not set. Then, p₀ = $1-{\left(1-p_2\right)}^k$. The distance-encoded Bloom filter returns a negative result if there is no sd candidate at all. The maximum number of sd candidates is h = w/2, where w is the word size. The probability of failing to reach a consensus from k bits for all the h bits is ${{p_0}^h=\left[1-{\left(1-p_2\right)}^k\right]}^h$. Thus, the false positive probability FPP_D of the distance-encoded Bloom filter that at least one sd candidate exists is given as follows:

$${FPP}_D=1-{p_0}^h={1-\left[1-{\left(1-p_2\right)}^k\right]}^h$$

(4)

For a given [L, U] range, the next search should be conducted within the range [c + sd, c + ld], where c represents the current component level. If c + sd > U, then the search cannot proceed further. In such a case, the distance-encoded Bloom filter returns a negative result instead of a positive one. Assuming c = 0 for simplicity, if U = 0, the only possible value for sd is 0. In this scenario, the probability of failing to yield a valid sd value, denoted as p_f, is p₀. For an arbitrary i representing U, there are i + 1 possible valid sd values. Thus, the probability that all of them fail, p_f, is given by ${p_0}^{i+1}$. Assuming U follows a uniform distribution, the overall failure probability p_f is as follows:

$$p_f={\displaystyle \frac{1}{h}}·\sum _{U=0}^{h-1}{p_0}^{U+1}={\displaystyle \frac{1}{h}}·\left[{\displaystyle \frac{p_0(1-{p_0}^h)}{1-p_0}}\right]$$

(5)

In Equation (4), FPP_D denotes the probability that at least one sd candidate exists. The effective false positive probability eFPP_D corresponds to the probability that such sd exists within the specified [L, U] range.

$${eFPP}_D=1-p_f=1-{\displaystyle \frac{1}{h}}·\sum _{U=0}^{h-1}{p_0}^{U+1}=1-{\displaystyle \frac{1}{h}}·\left[{\displaystyle \frac{p_0(1-{p_0}^h)}{1-p_0}}\right]$$

(6)

eFPP_D in Equation (6) is still higher than the FPP_S of Equation (4). However, the distance-encoded Bloom filter can predict the existence of a matching prefix at the current level based on whether the sd value is 0. The false positive probability of prefix prediction, FPP_pfx, is calculated as follows:

$${FPP}_{pfx}=1-p_0=1-\left[1-{\left(1-p_2\right)}^k\right]={\left(1-p_2\right)}^k={\left(1-{\left(1-{\displaystyle \frac{s}{m}}\right)}^{kn}\right)}^k$$

(7)

If s approaches 1, FPP_pfx gets closer to FPP_S. This means that predicting whether a matching prefix exists at the current level in the distance-encoded Bloom filter has an error probability comparable to that of predicting whether a matching node exists in a conventional Bloom filter.

4. Evaluation

The proposed name lookup scheme was evaluated using FIBs and name trace data constructed as follows. The FIBs were built using URL data provided by dmoz [35]. Each URL in the dataset was converted into a name prefix according to a predefined naming rule. For example, http://cs.some.edu/courseA/syllabus was transformed into /edu/some/cs/courseA/syllabus. The characteristics of the generated FIB data are shown in

Table 1. Characteristics of FIBs.

Type of Nodes	R0	R1	R2
Prefixes	2,900,962	3,135,491	3,370,019
Leaf prefixes	2,836,521	2,836,521	2,836,521
Non-leaf prefixes	64,441	298,970	533,498
Intermediate nodes	2,345,281	2,110,752	1,876,224
Markers	1,830,872	1,672,280	1,507,044
Non-marker nodes	514,409	438,472	369,180
Total no. of nodes	5,246,243	5,246,243	5,246,243

. The total number of prefixes is 2.9 million, and when including non-prefix intermediate nodes, the total number of nodes reaches 5.2 million. This dataset was named R0. Additionally, two more datasets, R1 and R2, were generated. In R1 and R2, 10% and 20% of the non-prefix nodes were, respectively, selected and converted into prefix nodes. As a result, the number of prefix nodes increased, but the total number of nodes remained the same across all datasets.

The name trace data used as input for name lookup consists of a collection of randomly generated content names, amounting to 10 million entries. To ensure that each generated content name has a matching prefix in the FIB, a prefix was first randomly selected from the FIB, and a suffix was then appended by randomly generating a component. The character strings of the suffix components were not generated uniformly at random; instead, they were produced using a 3 g model trained on the distribution of component strings in the FIBs [36]

Table 2. Comparison of name lookup schemes.

Scheme	Elems in BF	Nodes in Hash Table	Fixed Search Tree	Prefix Prediction
DEB	All	Prefixes	–	Yes
BS	All	All	No	No
BS-a-p	All	Prefixes	No	No
BS-m-m	Prefixes, markers	Prefixes, markers	Yes	No
BS-m-p	Prefixes, markers	Prefixes	Yes	No

compares the characteristics of the six name lookup schemes used in the experiment. DEB is the proposed scheme that utilizes a distance-encoded Bloom filter. BS employs a conventional Bloom filter based on binary search, where all nodes in the trie are stored in both the Bloom filter and the hash table. Other schemes with the ‘BS-‘ prefix are differentiated based on whether they include prefixes and markers in the Bloom filter and the hash table.

A key feature, prefix prediction, allows the Bloom filter to indicate whether a prefix exists at the current level. Among all schemes, only DEB supports this feature. Marker-based schemes (BS-m-m and BS-m-p) must use a fixed search tree rather than dynamically adjusting the search range, regardless of the content name length to take advantage of markers.

Four hash functions were used for the Bloom filters (k = 4). Additionally, the sizes of the Bloom filter and hash table are 64 Mbits and 32 million entries, respectively.

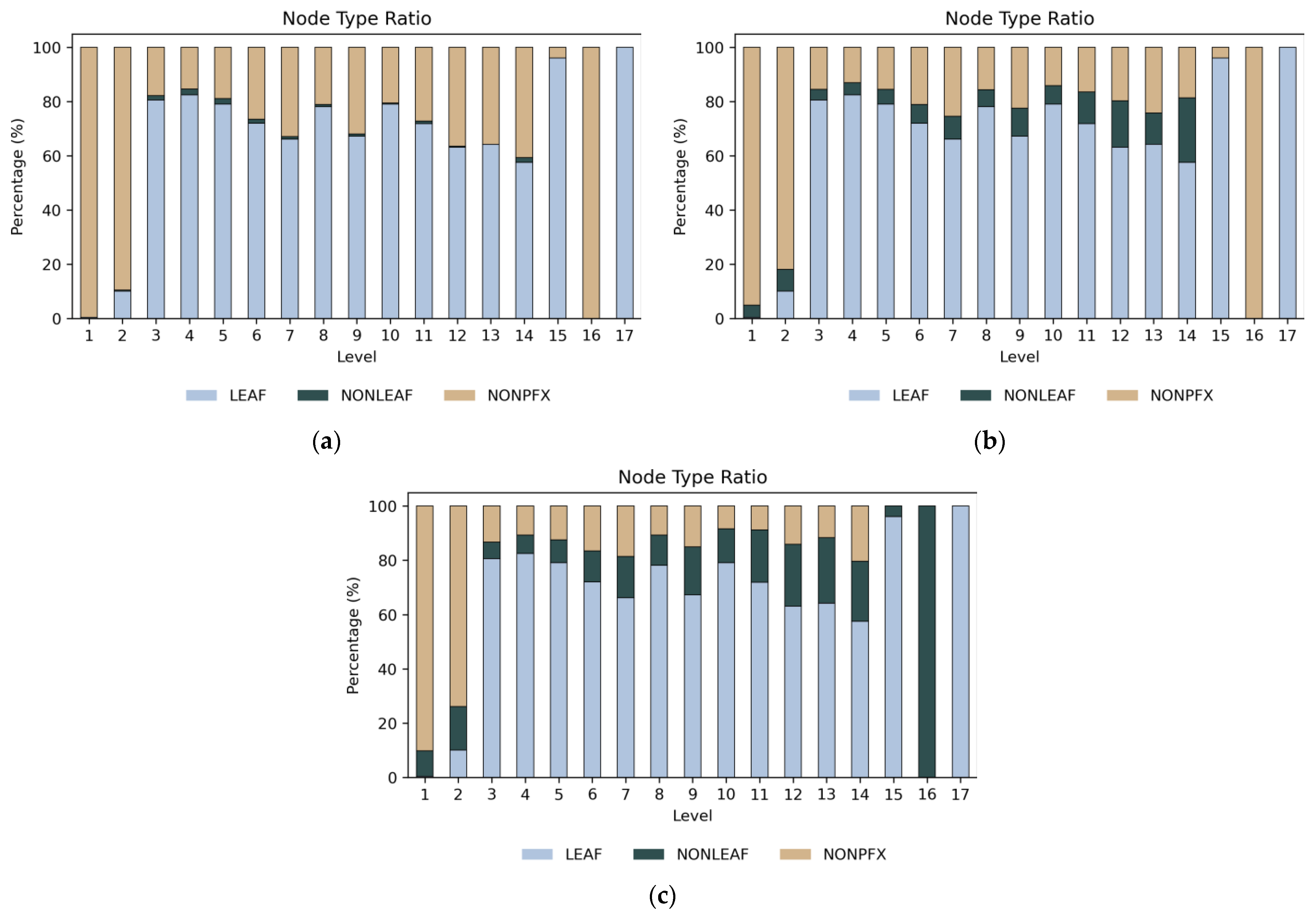
Figure 13 shows the ratio of different node types used in the experiment. At levels 1 and 2, non-prefix intermediate nodes are the most common, whereas leaf prefixes dominate at other levels. In R1 and R2, the proportion of non-leaf prefix nodes increases as 10% and 20% more of these nodes are added, respectively.

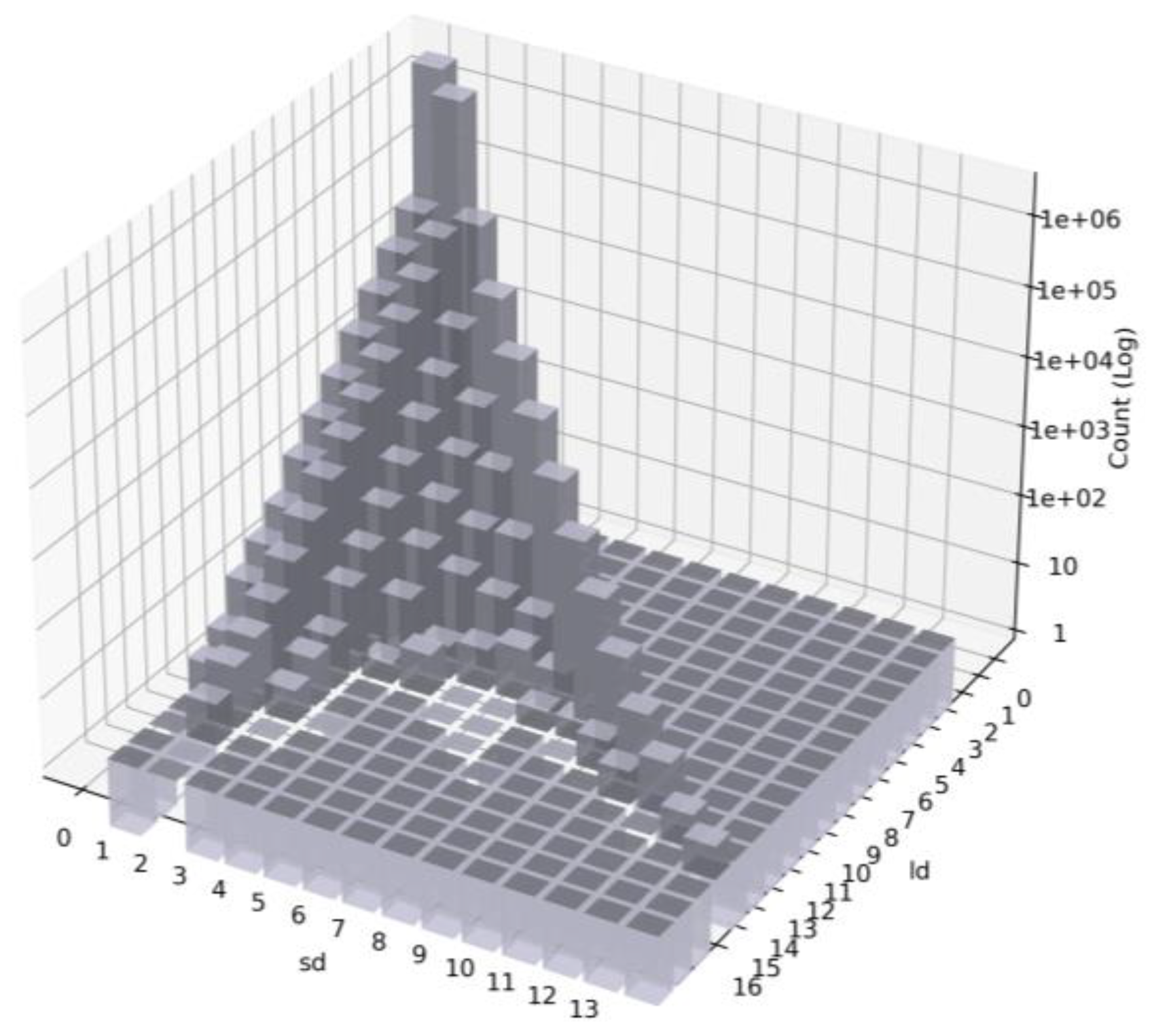
Figure 14 shows the distribution of ⟨sd, ld⟩ values for all nodes in R0. Nodes with sd = 0 are all prefix nodes. In particular, when both sd and ld are 0, the node is a leaf prefix, accounting for the largest proportion (54%) of the total.

A positive result in DEB indicates there exists a matching node at the current level, which is identified by the existence of a valid sd. The valid sd refers to the one that not only exists but also falls within a given range [L, U]. Thus, the false positive rate (FPR) of DEB corresponds to the effective false positive probability (eFPPD) defined in Equation (6). DEB sets one or two bits per node for each hash function, resulting in a higher FPR compared to other schemes. In this context, a positive result in Bloom filters indicates that there is a matching node at the current level, regardless of whether the node is a prefix node or an intermediate node. The primary performance goal is to reduce both on-chip and off-chip memory accesses required to find the longest matching prefix. Finding the longest matching node may require more Bloom filter and hash table accesses. DEB can predict whether a node at the current level is a prefix, whereas other schemes lack this prefix prediction capability. If the sd value in the Bloom filter output <sd, ld> is zero, DEB identifies the node at the current level as a prefix. This capability allows the hash table to store only prefix nodes, thereby reducing the number of off-chip memory accesses. 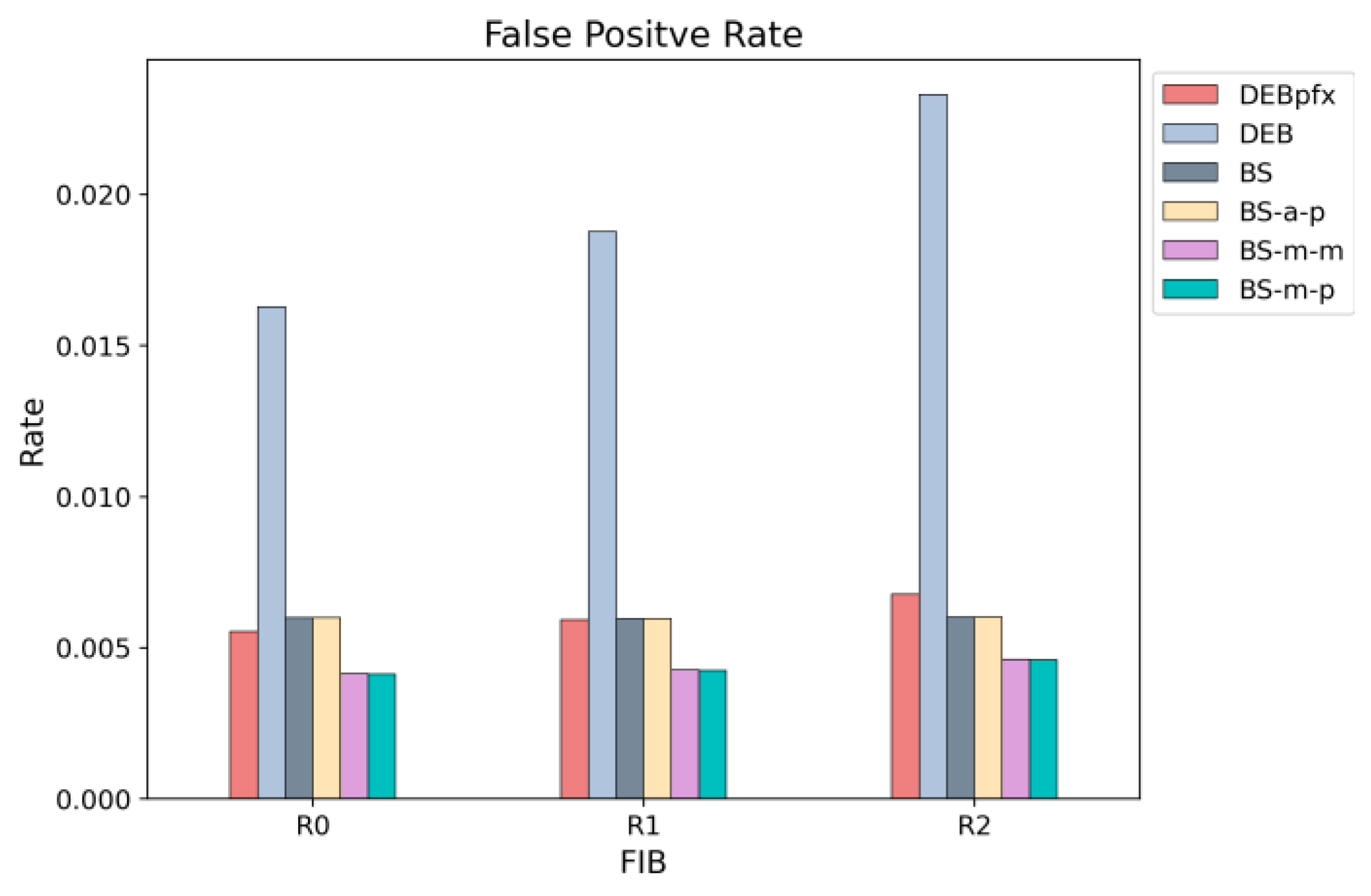In Figure 15, the FPR for prefix prediction in DEB is specifically marked as DEBpfx. The figure shows that DEBpfx achieves an FPR comparable to that of other schemes, even though the others focus on only node prediction.

As shown in Figure 15, the FPR of DEB increases across R0, R1, and R2 with rising prefix density. It implies that FIBs with more prefixes yield higher FPRs despite having the same total number of nodes. Whereas other schemes set one bit per node for each hash function, DEB sets either one or two bits depending on the sd and ld values. If sd equals ld, only one bit is set for that node, which is referred to as single-bit-set nodes. As prefix density increases, the portion of single-bit-set nodes decreases. It leads to more set bits and, consequently, more false positives. Nevertheless, even under very high prefix density, the FPR is bounded because leaf prefixes, which constitute a large portion of the FIB, always have distances where sd equals ld. Despite a high FPR, DEB achieves fewer on-chip and off-chip memory accesses due to the next search range information based on distance values, as illustrated in Figures 16, 17 and 19.

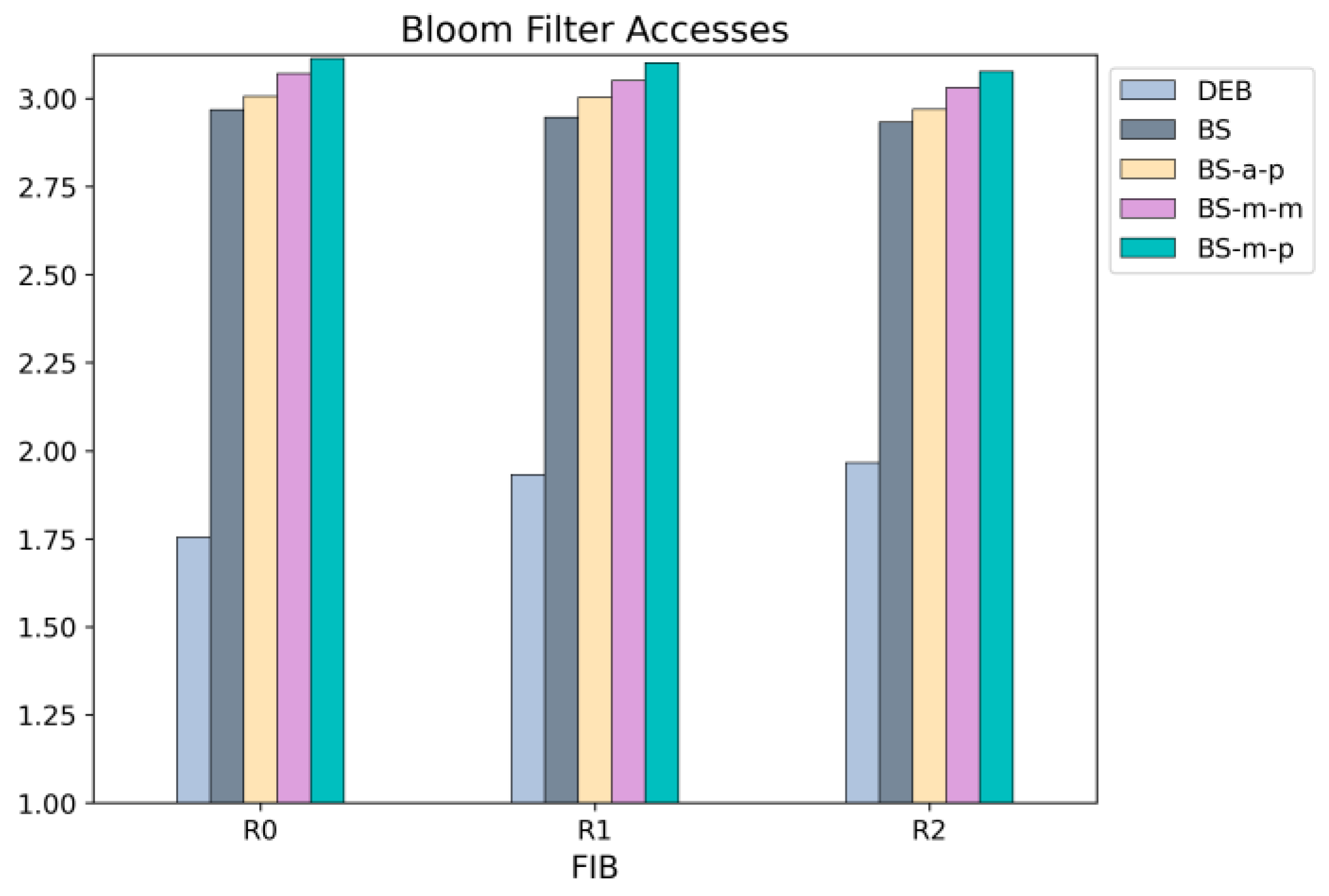
The name lookup process involves two types of memory accesses: one to the Bloom filter in on-chip memory and the other to the hash table in off-chip memory. The average number of Bloom filter accesses and hash table accesses is compared in Figure 16 and Figure 17, respectively. DEB outperforms all other schemes in both types of memory accesses.

Since DEB determines the next search range using ⟨sd, ld⟩, it requires fewer Bloom filter accesses than other schemes that rely on binary search. Figure 16 shows that in DEB, the Bloom filter is accessed 1.75 to 1.96 times, whereas in other schemes, the Bloom filter is accessed approximately three times on average.

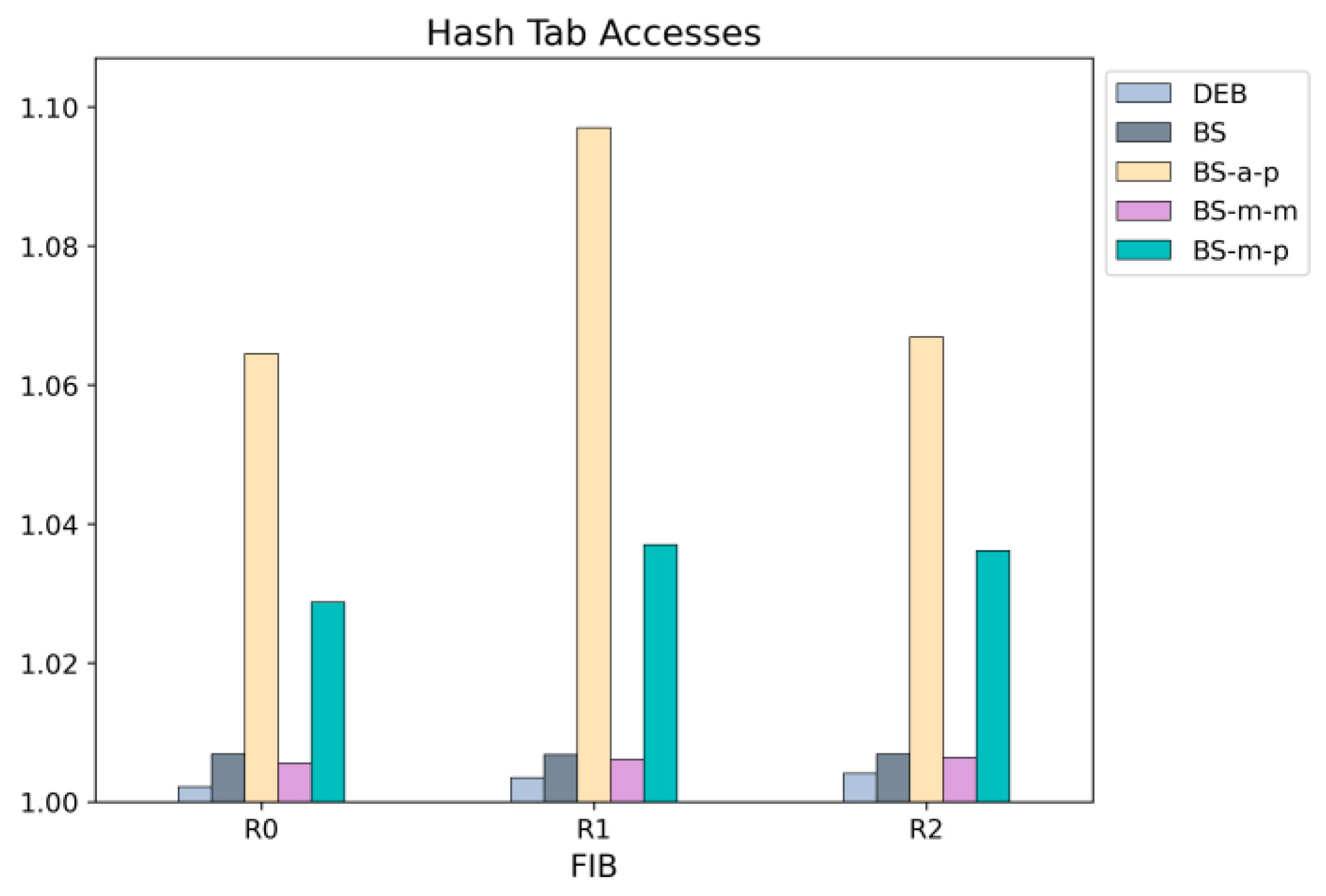
Additionally, DEB demonstrates a lower average number of hash table accesses compared to other schemes. The number of hash table accesses increases when a lookup in the hash table fails. As shown in Figure 17, schemes that store only prefix nodes in the hash table (BS-a-p and BS-m-p) require more accesses. In those schemes, a node identified as present by the Bloom filter may not necessarily be a prefix node but rather a non-prefix intermediate node. Since the hash table contains only prefix nodes, lookups for such non-prefix nodes result in failures, leading to an increased number of hash table accesses. While DEB also stores only prefix nodes in the hash table, it can predict whether a node is a prefix node using the Bloom filter, resulting in a lower hash table lookup failure rate.

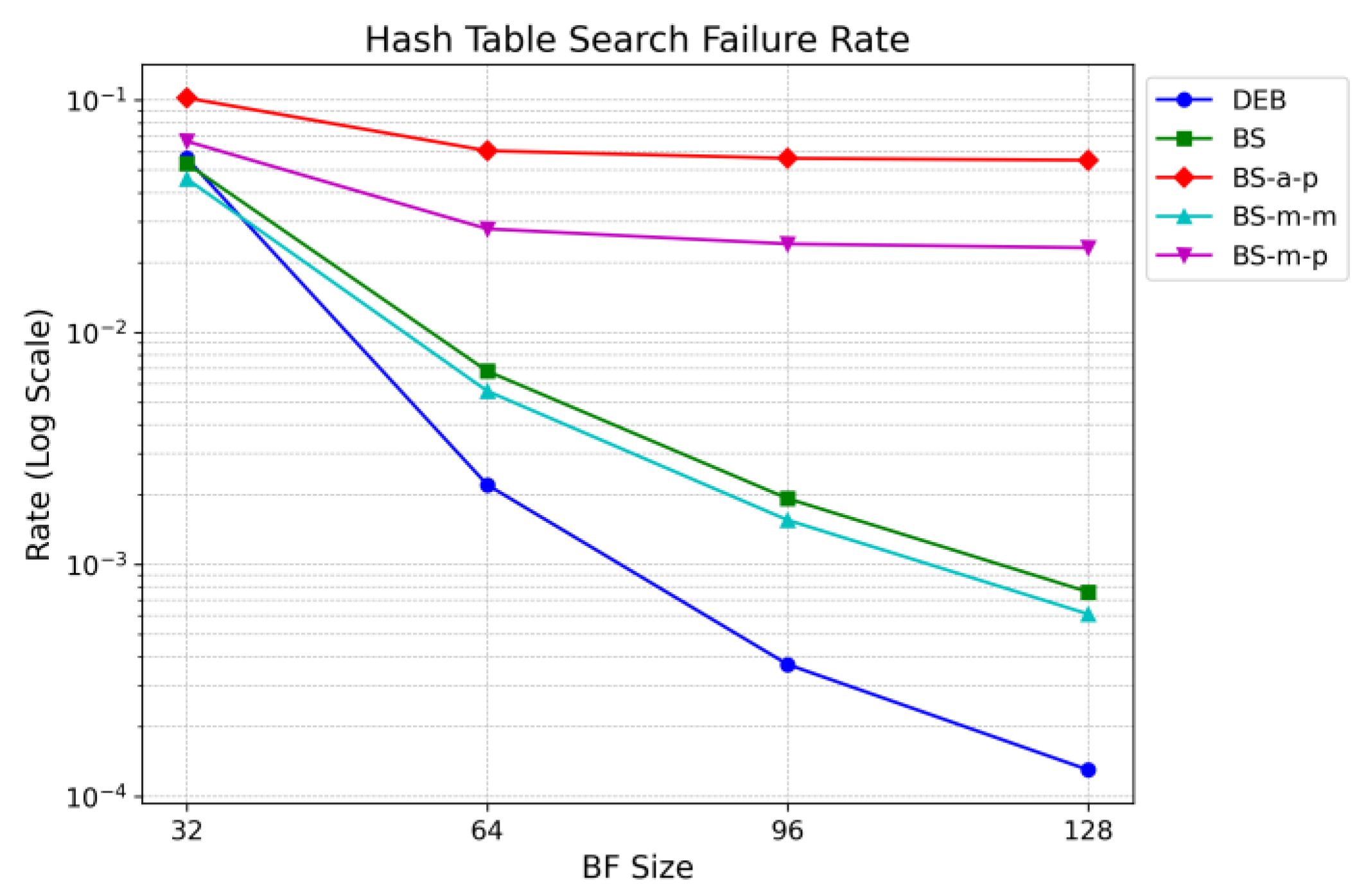
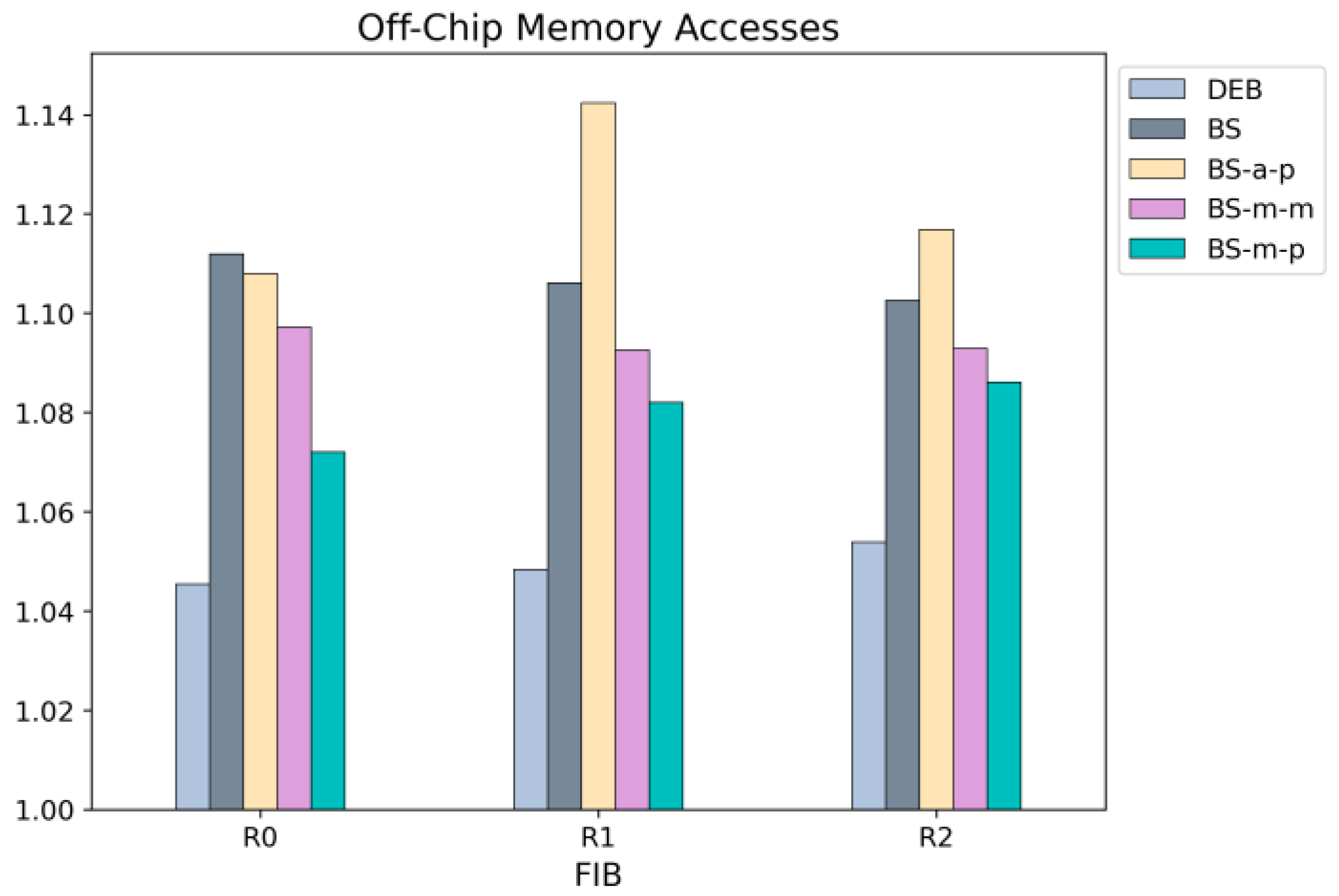
Figure 18 compares the hash table lookup failure rates of different lookup schemes. The results are obtained using various Bloom filter sizes. Since a larger Bloom filter reduces the false positive rate (FPR), the hash table lookup failure rate also decreases. As discussed earlier, schemes BS-a-p and BS-m-p, which store only prefix nodes in the hash table, exhibit significantly higher failure rates compared to other schemes.

Unlike the Bloom filter, which resides in on-chip memory, the hash table is stored in off-chip memory. Accessing off-chip memory is the most time-consuming operation and is a critical factor in affecting overall performance. Moreover, a single hash table lookup is not always complete with just one off-chip memory access. In cases of hash collisions, additional memory accesses may be required to check the overflow area. Figure 19 presents the average number of off-chip memory accesses per name lookup. As the number of nodes stored in the hash table increases, hash collisions also increase, leading to more off-chip memory accesses. However, since DEB stores only prefix nodes in the hash table, it experiences fewer hash collisions. As a result, DEB achieves the best average memory access count among all the schemes. While BS-a-p also stores only prefix nodes in the hash table, its high hash table lookup failure rate and excessive access count result in poor overall memory access performance.

5. Conclusions

In this paper, we propose a novel name lookup scheme for NDN that employs a distance-encoded Bloom filter to enhance lookup efficiency. The primary challenge in NDN name lookup is identifying the longest matching prefix in the FIB. For any given content name, multiple matching prefixes may exist, and the longest one should be identified among them.

Hash table-based approaches can efficiently determine whether a given prefix matches an entry in the FIB. However, multiple hash table lookups may be required to find the longest matching prefix since these approaches cannot determine the longest prefix length in advance. Given the large size of the FIB, the hash table must be stored in off-chip memory. Therefore, it is crucial to minimize table accesses to optimize performance.

Several pre-checking techniques using Bloom filters, which indicate the possible presence of a prefix before accessing the hash table, help reduce hash table accesses. A binary search approach in a Bloom filter can reduce the number of Bloom filter accesses, as the search range is halved each time the Bloom filter is queried.

Our proposed approach further narrows the search range by utilizing the distance to descendant prefixes. Two types of distance values—shortest distance (sd) and longest distance (ld)—are encoded into the Bloom filter. The Bloom filter based on these distance values provides not only membership testing but also a narrower search range compared to binary search. This narrower search range reduces Bloom filter accesses required to identify the longest matching prefix. Moreover, our proposed Bloom filter can identify the matching prefix nodes, whereas conventional Bloom filters identify only the matching nodes regardless of whether they are prefix nodes or non-prefix nodes. As a result, only prefix nodes are stored in the hash table in the proposed scheme, which reduces hash collisions and minimizes overall off-chip memory accesses.

Through experiments with large FIBs and name trace datasets, we demonstrated that the proposed distance-encoded Bloom filter significantly reduces both on-chip Bloom filter accesses and off-chip hash table accesses compared to other lookup schemes. Our results show that the proposed scheme achieves up to 44% fewer Bloom filter accesses and a lower hash table lookup failure rate. Furthermore, it stores only prefix nodes in the hash table, which reduces off-chip memory accesses and improves overall lookup performance.