From Phase Space to Non-Equilibrium Dynamics: Exploring Liouville’s Theorem and Its Implications
Abstract
1. Introduction
2. The Equation of Motion for Physical Quantities
2.1. Foundations of Hamiltonian and Liouville Dynamics
Liouville’s Theorem
2.2. Symplectic Structure and Phase-Space Dynamics
2.3. Beyond Liouville: Motivation for Modifications
2.4. Transition to Generalized Mechanics
3. Out-of-Equilibrium Dynamics
3.1. Basic Introduction to Extended Hamiltonian Dynamics in Non-Equilibrium Systems
3.2. Connection to GENERIC and Rayleigh Dissipation
- GENERIC Formalism: The General Equation for Non-Equilibrium Reversible–Irreversible Coupling (GENERIC) [33] separates dynamics into reversible (Hamiltonian) and irreversible (dissipative) components:where denotes Poisson brackets and dissipative brackets. Our entropy gradient term mirrors the dissipative bracket , coupling reversible mechanics to irreversible entropy production.
- Rayleigh Dissipation: The Rayleigh dissipation function models friction as a quadratic form of velocities. In contrast, our framework generalizes dissipation through entropy gradients , which act as configurational friction forces. For small deviations from equilibrium, , recovering Rayleigh’s formalism [28].
3.3. Extended Formulation of Canonical Momentum and Equation of Motion
3.4. Definition of
- denotes the entropy contribution from the -th particle or subsystem, reflecting the individual disorder or randomness contribution;
- signifies the total energy of the -th particle or subsystem;
- and represent the momentum and mass, respectively;
- and refer to the angular momentum and moment of inertia;
- represents the charge;
- and are the scalar and vector potentials;
- denotes the velocity;
- symbolizes external mechanical energy contributions;
- and are vectors of Lagrange multipliers related to translational and rotational velocities.
- It emphasizes the microscopic foundation of our thermodynamic analysis, allowing for the detailed tracking of individual contributions to the system’s overall entropy.
- It reminds us of the potential for statistical or collective constructions, facilitating a transition from a microscopic to a macroscopic perspective when necessary.
- It assures the flexibility of our approach, indicating that while the index is crucial for a nuanced understanding, it can be abstracted away or summarized for problems where a granular level of detail is not required.
3.5. Physical Interpretation of Lagrange Multipliers
3.5.1. Kinematic Meaning
- represents the collective drift velocity of the system: When is maximized, where is the center-of-mass velocity.
- corresponds to the thermodynamic angular velocity: At equilibrium, with being the rigid-body rotation vector.
3.5.2. Dissipative Dynamics
3.5.3. Field-Theoretic Connection
3.5.4. Measurement Protocol
3.6. Non-Negativity and Constraints of the Extended Entropy
3.6.1. Variational Principle and Lagrange Multipliers
3.6.2. Energy Constraints and Positivity of
3.6.3. Bounds on Linear Terms
3.6.4. Thermodynamic Consistency
- Energy constraints are satisfied: ;
- Lagrange multipliers are derived from variational principles to enforce conservation laws;
- Bounds on linear terms are respected via inequalities tied to kinetic/angular energies.
3.7. Physical Interpretation of Entropy Gradients
- Environmental Coupling: When the system interacts with a thermal reservoir (e.g., stochastic cooling), represents heat exchange. For example, in beam stacking [34], entropy gradients model energy loss to electromagnetic fields.
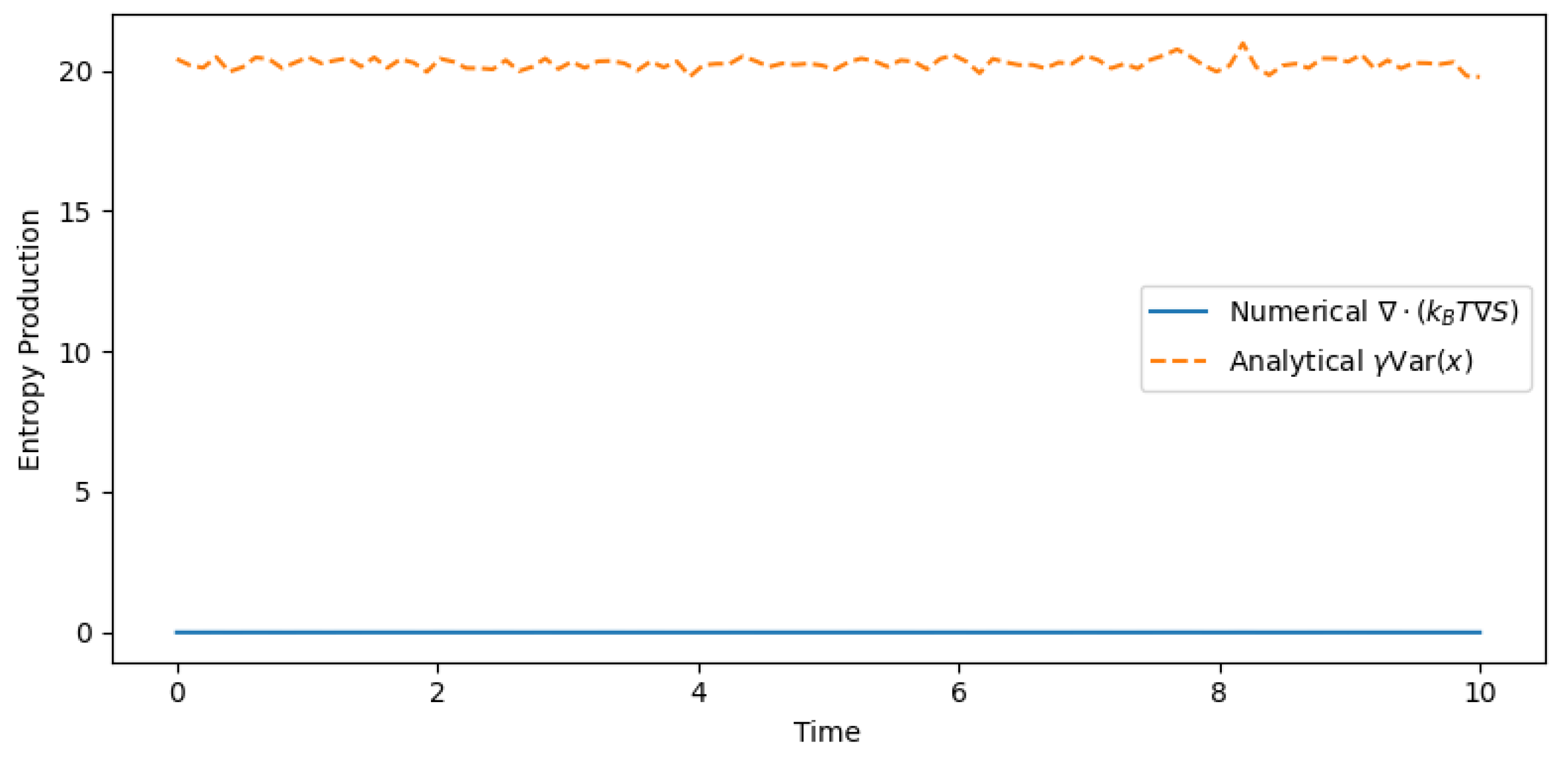
- Internal Irreversibility: For systems with self-interacting particles (e.g., turbulent plasmas), the entropy production has two equivalent representations:where is the damping coefficient, measures velocity fluctuations, and the right-hand side matches the entropy production term in Equation (7) and shwon in Figure 1. This dual form connects particle-scale dynamics to continuum-scale irreversibility.
3.8. Modified Dynamics with Entropy Coupling
3.8.1. Canonical Example: Harmonic Oscillator
- Hamiltonian:
- Entropy function:where (kg/s) and (dimensionless) are coupling parameters.
3.8.2. Dynamical Behavior
Equations of Motion
Resulting Second-Order Dynamics
3.9. Physical Regimes
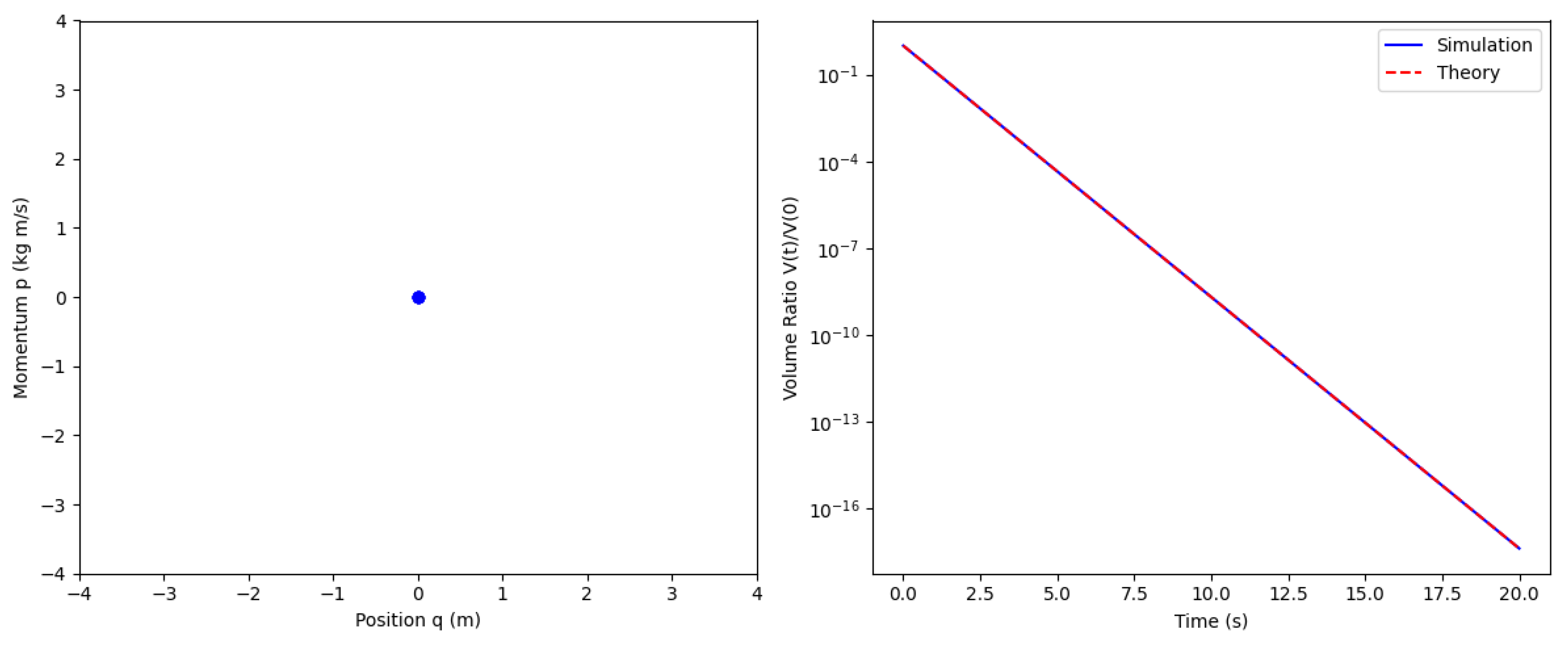
3.9.1. Case 1: Purely Dissipative ()
- Standard damped oscillator:
- Phase-space contraction (Figure 2(Left))
3.9.2. Case 2: Energy-Injecting ()
- Modified dynamics:
- Requires for stability;
- Models active matter systems.
3.10. Thermodynamic Consistency
3.10.1. Entropy Production
3.10.2. Stability Criterion
3.11. Derivation of Governing Equation
3.12. Implementation Guidelines
- For passive systems: ,
- For active systems:
- Numerical stability requires:
Relation to Liouville’s Theorem in Hamiltonian Systems
4. Adaptability of the Formulation
- For problems that emphasize the behavior of individual particles or specific interactions, the index can be maintained to take advantage of the full descriptive power of the model.
- For broader analyses where such specificity is not necessary, the index can be dropped or integrated over, simplifying the equations without compromising the theoretical integrity.
- This adaptability ensures that our extended entropy formulation remains applicable across a wide range of scenarios, from deeply microscopic investigations to more generalized thermodynamic studies.
4.1. Role of in Canonical Momentum and Dynamics
4.2. Implications and Applications
4.3. Foundational Justification of Equations (22) and (23)
4.3.1. Derivation of Extended Entropy
4.3.2. Entropy Gradients in Dynamics (Equations (33) and (34))
4.3.3. Quantum Field Equation
Wigner Function and Quantum Dynamics
4.4. Relaxation of an Initially Out-of-Equilibrium System Towards Thermal Equilibrium
4.4.1. Transition to Quantum Field Equations
4.4.2. Bridging Theory and Application: The Free-Energy Operator in QM
4.5. Detailed Analysis of Derived Equations
4.5.1. Modified Hamilton’s Equations (Equations (10) and (11))
4.5.2. Generalized Liouville Equation
4.6. Conservation of Total Probability
Example: Harmonic Oscillator with Entropy Gradient
4.7. Modified Poisson Brackets and Commutators
Quantum Field Equation (Equation (28))
4.8. Relaxation of an Initially Out-of-Equilibrium System Towards Thermal Equilibrium
4.9. Transition to Quantum Field Equations
- ★-product reduces to an ordinary product when ;
- Expectation values become phase-space integrals: ;
- This ensures that correspondence.
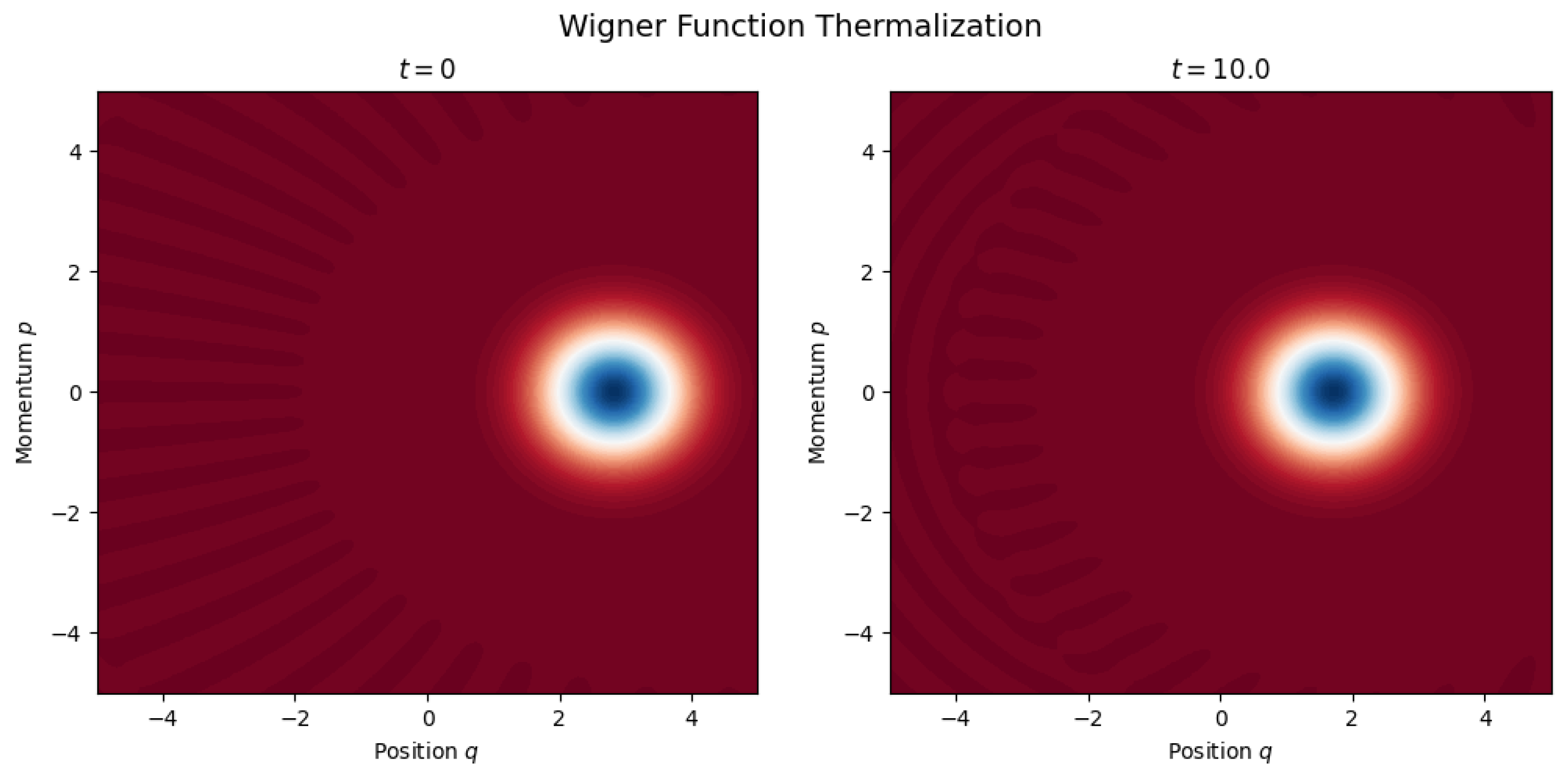
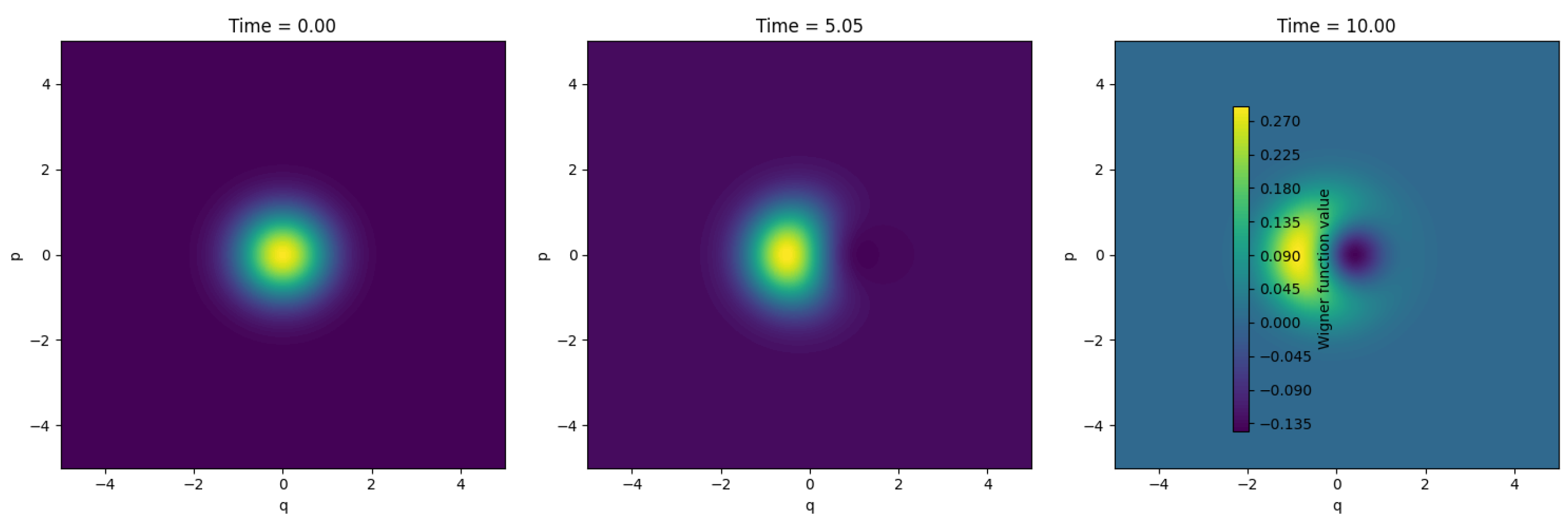
4.9.1. Wigner Function and Quantum Dynamics
4.9.2. Bridging Theory and Application: The Free-Energy Operator in QM
4.9.3. Note on Quantum Thermalization and Perturbation
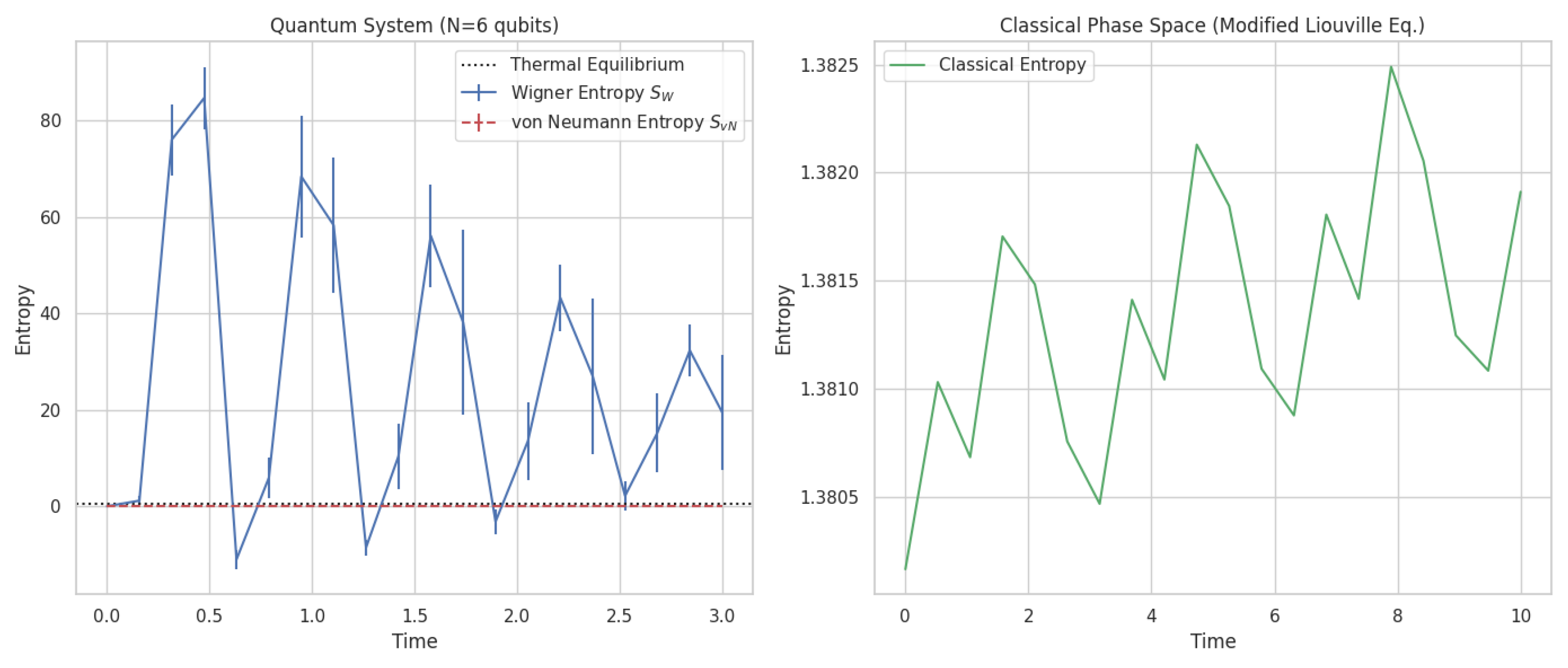
4.10. Quantum Thermalization via Entropy Gradients
4.11. Application and Simulation of Quantum Thermalization Using an Effective Hamiltonian
Relation to Lindblad and Quantum Master Equations
4.12. Nonelastic Collisions Between Particles
4.13. Brightness of an Atomic Beam Source
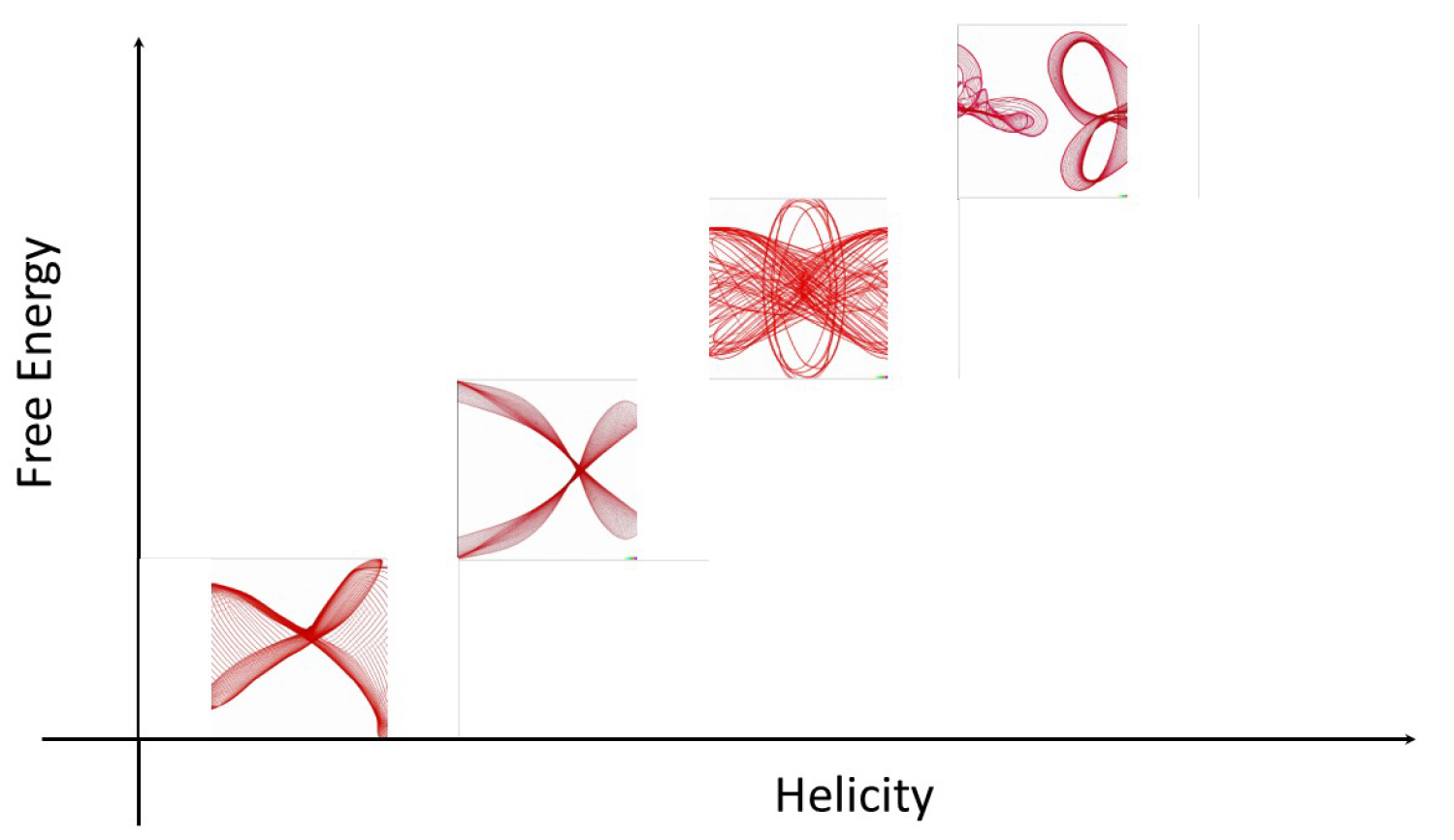
4.14. The Mechanics of Magnetic Helicity in Plasma
5. Fundamental Consistency Checks
5.1. Energy Conservation
5.2. Momentum and Angular Momentum
5.3. Time-Reversal Symmetry
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Preservation of Antisymmetry and Jacobi Identity
Appendix A.1. Classical Case: Poisson Brackets
Appendix A.2. Quantum Case: Commutators
Appendix A.3. Summary
Appendix A.4. Formal Proof of Probability Conservation
Appendix A.5. Example: Free Particle with Linear Entropy Gradient

Appendix B. Variational Derivation of Entropy-Gradient Terms
References
- Liouville, J. Note sur la Théorie de la Variation des constantes arbitraires. J. Math. Pures Appl. 1838, 3, 342–349. [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste; Gauthier-Villars: Paris, France, 1892; Volume III. [Google Scholar]
- Alberucci, A.; Jisha, C.P.; Peschel, U.; Nolte, S. Breaking the action-reaction principle in self-confined optical beams. Phys. Rev. A 2019, 100, 011802(R). [Google Scholar] [CrossRef]
- Arnold, V.I. Small denominators and problems of stability of motion in classical and celestial mechanics. Russ. Math. Surv. 1963, 18, 85. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Ehrenfest, P.; Ehrenfest, T. The Conceptual Foundations of the Statistical Approach in Mechanics; Moravcsik, M.J., Translator; Cornell University Press: Ithaca, NY, USA, 1959. [Google Scholar]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91. [Google Scholar] [CrossRef]
- Barton, G. Quantum mechanics of open systems. J. Phys. B 1987, 20, 879. [Google Scholar] [CrossRef]
- Becattini, F.; Piccinini, F.; Rizzo, J. Angular momentum conservation in heavy ion collisions at very high energy. Phys. Rev. C 2008, 77, 024906. [Google Scholar] [CrossRef]
- Berger, M.A. Rigorous new limits on magnetic helicity dissipation in the solar corona. Geophys. Astrophys. Fluid Dyn. 1984, 30, 79–104. [Google Scholar] [CrossRef]
- Blackman, E.G.; Field, G.B. Coronal activity from dynamo waves. Astrophys. J. 2000, 534, 984–988. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Bryce, T.; MacMillan, K. Momentum and kinetic energy: Confusable concepts in secondary school physics. J. Res. Sci. Teach. 2009, 46, 739–761. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Son, D.; Stephanov, M. Collisions in chiral kinetic theory. Phys. Rev. Lett. 2015, 115, 021601. [Google Scholar] [CrossRef] [PubMed]
- Walborn, S.P.; Cunha, M.O.T.; Pádua, S.; Monken, C.H. Double-slit quantum eraser. Phys. Rev. A 2002, 65, 033818. [Google Scholar] [CrossRef]
- Datsko, V.S. The fallacy of Liouville’s theorem and predictable atmosphere and climate. In Proceedings of the International Conference InterCarto.InterGIS, Wellington, New Zeland, 31 August–2 September 2016; Volume 22, pp. 311–321. [Google Scholar]
- Pinheiro, M.J. A reformulation of mechanics and electrodynamics. Heliyon 2017, 3, e00365. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Gallavotti, G. Foundations of Fluid Dynamics: With Applications to Physics and Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Toda, M. Theory of Nonlinear Lattices; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Denisov, V.Y. Improvements to the theory of time-dependent quantum correlations. Phys. Lett. B 2002, 526, 315–321. [Google Scholar] [CrossRef]
- Léontovitch, M. Introduction à la Thermodynamique-Physique Statistique; Editions MIR: Moscow, Russia, 1986. [Google Scholar]
- Ruggiero, A.G. Are we beating Liouville’s theorem? In Proceedings of the Workshop on Producing High-Luminosity High-Energetic Proton-Antiproton Collisions, Berkeley, CA, USA, 27–31 March 1978. [Google Scholar]
- Winston, R. Beating the optical Liouville theorem. In Optics and Photonics for Advanced Energy Technology; Paper WD8; Optical Society of America: Washington, DC, USA, 2009. [Google Scholar]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience Publishers: Hoboken, NJ, USA, 1967. [Google Scholar]
- Zubarev, D.N.; Morozov, V.; Röpke, G. Statistical Mechanics of Nonequilibrium Processes; Akademie Verlag: Berlin, Germany, 1996. [Google Scholar]
- Pinheiro, M.J. Ergontropic dynamics: Contribution to an extended particle dynamics. In Studies in Rhythm Engineering; Bandyopadhyay, A., Ray, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ruggiero, A.G. Are We Beating Liouville’s Theorem? In Proceedings of the Workshop High-Luminosity Proton-Antiproton Collisions, Berkeley, CA, USA, 27–31 March 1978; p. 123. [Google Scholar]
- Pinheiro, M.J. On Newton’s third law and its symmetry-breaking effects. Phys. Scr. 2011, 84, 055004. [Google Scholar] [CrossRef][Green Version]
- Wimmer, M.; Regensburger, A.; Bersch, C.; Miri, M.; Batz, S.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Optical diametric drive acceleration through action–reaction symmetry breaking. Nat. Phys. 2013, 9, 780–784. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1. In Course of Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 1980; Volume 5. [Google Scholar]
- Villani, C. A review of mathematical topics in collisional kinetic theory. In Handbook of Mathematical Fluid Dynamics; North-Holland: Amsterdam, The Netherlands, 2002; Volume 1, pp. 71–74. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Pinheiro, M.J.G. Entropy-Driven Classical and Quantum Dynamics, GitHub Repository. 2023. Available online: https://github.com/mjgpinheiro/Physics_models (accessed on 5 April 2025).
- Lent, C.S. Quantum operator entropies under unitary evolution. Phys. Rev. A 2020, 101, 012342. [Google Scholar] [CrossRef]
- Pinheiro, M.J. Quantum Thermalization and Entropy Influence: A Wigner Function Perspective. 2023. Available online: https://github.com/mjgpinheiro/Physics_models (accessed on 5 April 2025).
- Morozov, V.G.; Röpke, G. Non-Markovian quantum kinetics and conservation laws. J. Stat. Phys. 2001, 102, 285–316. [Google Scholar] [CrossRef]
- Peralta-Ramos, J.; Calzetta, E. Effective dynamics of a non-Abelian plasma out of equilibrium. Phys. Rev. D 2012, 86, 125024. [Google Scholar] [CrossRef]
- Prodan, I.; Scherson, D.; Metiu, H. Phase-space compression and the production of intense, collimated atomic beams. Phys. Rev. Lett. 1994, 73, 2992. [Google Scholar]
- Pierce, D.T. Bright source of slow atomic beams. Phys. Rev. Lett. 1983, 51, 2205. [Google Scholar]
- Sheehy, B.; Schlosser, M.; Raizen, M.G. Atomic beam brightness beyond the Liouville limit. Phys. Rev. Lett. 1999, 82, 3198. [Google Scholar]
- Kuyatt, C.E. The Liouville Theorem and Its Applications; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Kimble, H.J.; Dagenais, M.; Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Chasapis, A.; Matthaeus, W.H.; Parashar, T.N.; Haggerty, C.C.; Shay, M.A.; Gershman, D.J.; Giles, B.L.; Burch, J.L. Energy dissipation in turbulent reconnection. Phys. Plasmas 2021, 28, 112305. [Google Scholar] [CrossRef]
- Shafranov, V.D. Reviews of Plasma Physics; Consultants Bureau: New York, NY, USA, 1987; Volume 13. [Google Scholar]
- Helander, P.; Bird, T.; Jenko, F.; Kleiber, R.; Plunk, G.G.; Proll, J.H.E.; Riemann, J.; Xanthopoulos, P. Advances in stellarator gyrokinetics. Plasma Phys. Control. Fusion 2014, 56, 124009. [Google Scholar] [CrossRef]
| Equation | Mathematical Form | Physical Meaning |
|---|---|---|
| Modified Dynamics | Hamiltonian mechanics with entropy forces | |
| Extended Entropy | Non-equilibrium entropy with constraints | |
| Generalized Liouville | Compressible phase-space evolution | |
| Quantum Version | Wigner function with entropy coupling | |
| Plasma Free-Energy | Magnetic helicity contributions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinheiro, M.J. From Phase Space to Non-Equilibrium Dynamics: Exploring Liouville’s Theorem and Its Implications. Appl. Sci. 2025, 15, 4117. https://doi.org/10.3390/app15084117
Pinheiro MJ. From Phase Space to Non-Equilibrium Dynamics: Exploring Liouville’s Theorem and Its Implications. Applied Sciences. 2025; 15(8):4117. https://doi.org/10.3390/app15084117
Chicago/Turabian StylePinheiro, Mario J. 2025. "From Phase Space to Non-Equilibrium Dynamics: Exploring Liouville’s Theorem and Its Implications" Applied Sciences 15, no. 8: 4117. https://doi.org/10.3390/app15084117
APA StylePinheiro, M. J. (2025). From Phase Space to Non-Equilibrium Dynamics: Exploring Liouville’s Theorem and Its Implications. Applied Sciences, 15(8), 4117. https://doi.org/10.3390/app15084117






