Abstract
We generalize Liouville’s theorem to incorporate entropy gradients in phase space, demonstrating that non-equilibrium systems exhibit compressible phase-space dynamics (). This framework bridges Hamiltonian mechanics and thermodynamics, with applications in beam stacking, stochastic cooling, and quantum thermalization. Numerical simulations validate the theory, showing entropy stabilization at (error ) for particles.
1. Introduction
A fundamental principle in classical mechanics, Liouville’s theorem [1], profoundly influences our understanding of dynamical systems. It posits that the volume occupied by a system in the six-dimensional phase space of positions and velocities remains invariant over time. This invariance implies predictable trajectories and conservation of information within the system, laying the foundation for deterministic evolution in classical mechanics and influencing the statistical behavior of macroscopic systems [2,3,4,5,6,7].
However, despite its pivotal role, Liouville’s theorem encounters conceptual and practical challenges when extended to quantum mechanics. The theorem’s implications contrast sharply with the foundational principles of quantum mechanics, particularly the uncertainty principle and the concept of superposition [8,9,10,11,12,13,14,15,16,17,18]. This discrepancy raises critical questions about the applicability and limits of Liouville’s theorem, especially in non-equilibrium scenarios and quantum contexts.
With special reference to the variational method proposed in our previous work [19], the purpose of this research project is to critically evaluate Liouville’s theorem. Under the broader considerations provided by this variational strategy, we investigate the theorem’s ramifications in both quantum and classical mechanics, particularly related to the functionality of entropy gradients and its validity in non-equilibrium systems. By introducing and analyzing Equations (39) and (40), this work challenges the conventional interpretation of the theorem, suggesting that phase-space dynamics may be more complex than traditionally understood.
Our method addresses the gap between classical and quantum viewpoints by combining mathematical modeling and theoretical analysis. Our objective is to provide an in-depth awareness of phase-space dynamics by filling in the gaps in existing theories and putting forth a fresh framework that more effectively takes into account the complex nature of quantum mechanics and non-equilibrium systems.
This research project attempts to contribute to a deeper and more comprehensive understanding of dynamical systems across the classical–quantum divide by reexamining a cornerstone of classical mechanics. The fundamental principles governing complex systems are examined, with implications for both theoretical physics and practical applications.
Liouville’s theorem plays a pivotal role in our understanding of dynamical systems within classical mechanics, asserting the constancy of phase-space density along the trajectories of a system [6,20]. Despite its widespread acceptance, the theorem’s application in quantum contexts reveals inherent discrepancies, necessitating a closer examination of its foundational premises [21,22].
Our investigation is further motivated by the variational principles introduced by Pinheiro [19], which offer a novel perspective on the dynamics of non-equilibrium systems. This approach aligns with recent advances in statistical physics that challenge traditional interpretations of thermodynamic equilibrium and entropy gradients [23,24].
Moreover, the practical implications of our findings extend to various domains, including beam stacking and stochastic cooling, where traditional applications of the Liouville theorem may fall short [25,26]. The limitations of Liouville’s theorem in accurately predicting atmospheric and climate behaviors [18] and its inadequacy in the realm of quantum mechanics [8,27] further underscore the necessity for a revised theoretical framework.
By integrating a diverse array of references that span historical insights, theoretical advancements, and practical applications, we aim to build a comprehensive narrative that not only addresses the limitations of Liouville’s theorem, but also proposes a robust framework for understanding the dynamics of complex systems across the classical–quantum divide.
The paper is organized as follows: Section 2 establishes the modified equations of motion and their symplectic structures. Section 3 analyzes entropy production in non-equilibrium systems. Section 4 develops quantum extensions via Wigner–Weyl transforms. Section 5 demonstrates implementations in beam physics and quantum thermalization. Section 6 discusses broader implications and future directions.
2. The Equation of Motion for Physical Quantities
The study of classical mechanics has evolved significantly from its inception, with Hamiltonian mechanics representing a pivotal development in our understanding of physical systems. Unlike Newtonian mechanics, which is primarily concerned with the motion of particles in physical space, Hamiltonian mechanics provides a more generalized framework that is particularly adept at dealing with complex systems, including those with constraints or where quantum mechanical effects become significant.
2.1. Foundations of Hamiltonian and Liouville Dynamics
The equation of motion for any arbitrary physical quantity F, which could represent energy, momentum, or any other observable of the system, is given by:
where denotes the Poisson bracket. These brackets encode the algebraic structure of Hamiltonian mechanics and are central to Liouville’s theorem, which governs the evolution of phase-space distributions.
Liouville’s Theorem
A cornerstone of classical mechanics, Liouville’s theorem states that for a Hamiltonian system, the phase-space density evolves according to:
implying that the phase-space volume is preserved under time evolution (). This theorem arises directly from the symplectic structure of Hamiltonian dynamics, where the second-form ensures volume conservation. While foundational, this framework assumes isolated, equilibrium systems–a limitation we address in this work through entropy-driven modifications.
2.2. Symplectic Structure and Phase-Space Dynamics
The Hamiltonian equations of motion, succinctly captured as:
underscore the symplectic geometry of phase space. The conservation of phase-space volume () reflects the deterministic and reversible nature of classical mechanics.
The symplectic form in a symplectic manifold is defined as:
where and are canonical momenta and coordinates, respectively. The condition (closure of the symplectic form) ensures the preservation of phase-space structure under Hamiltonian flow.
2.3. Beyond Liouville: Motivation for Modifications
However, this framework does not inherently account for dissipative or non-equilibrium processes, such as thermal fluctuations or entropy production—phenomena central to our proposed extensions. Consider the simple harmonic oscillator, where the Hamiltonian
yields sinusoidal motion. While such systems adhere strictly to Liouville’s theorem, many real-world systems (e.g., plasmas, biological networks, or quantum open systems) exhibit phase-space compression or expansion due to dissipation.
This limitation motivates our generalization of the Liouville equation to include entropy gradients (), enabling the description of irreversible processes while preserving core symplectic principles in conservative subsystems.
2.4. Transition to Generalized Mechanics
As we proceed deeper into Hamiltonian mechanics, we encounter advanced constructs like the Hamilton–Jacobi equation:
which provides a bridge to quantum mechanics through canonical transformations. The principal function S resembles the quantum wavefunction phase, hinting at deeper connections between deterministic classical mechanics and probabilistic quantum theory.
These studies broaden our comprehension of physical phenomena while demonstrating both the elegance and limitations of conventional Hamiltonian mechanics. Specializing in the frontier of non-equilibrium systems, we now build upon these foundations to develop a generalized mechanical framework incorporating thermodynamic irreversibility.
3. Out-of-Equilibrium Dynamics
Transitioning from foundational concepts in classical mechanics to exploring the complex dynamics of non-equilibrium systems, we delve into the recent advancements that offer a novel perspective on the behavior of systems outside equilibrium. These advances propose a reformulation of canonical momentum and equations of motion grounded in a new variational principle. This innovative approach integrates thermodynamic principles directly into the dynamics and emphasizes the symplectic structure of Hamiltonian mechanics, offering a more nuanced framework for describing physical processes [6,28,29,30]. The core of this formulation is an equation of motion that functions as a local balance law, with the entropy gradient acting as the driving force. Furthermore, it introduces the concept of an entropy gradient in momentum space, the maximization of which leads to the definition of total canonical momentum. This ensemble of equations mirrors the structure of Hamiltonian dynamics and aligns with the principles of Helmholtz free energy. The framework also revisits Liouville’s equation, the Liouville operator, and outlines the method for calculating the expectation value of a function, thereby enriching our understanding of non-equilibrium systems [19,31].
3.1. Basic Introduction to Extended Hamiltonian Dynamics in Non-Equilibrium Systems
Classical mechanics and thermodynamics have provided a robust framework for understanding physical systems in equilibrium and near-equilibrium states. However, the dynamics of systems far from equilibrium, especially in the context of interacting particles and fields, requires a more nuanced theoretical approach. This work introduces an extended formulation of Hamiltonian dynamics that incorporates thermodynamic principles directly into the equations of motion, specifically targeting non-equilibrium processes. The insight that classic Hamiltonian mechanics, although effective, falls short in explaining the intricate relationship between energy distribution and entropy evolution in out-of-equilibrium situations is what motivated us to reformulate the theory.
3.2. Connection to GENERIC and Rayleigh Dissipation
The modified equations of motion (revisited in detail in Equations (1) and (2)),
are structurally aligned with formalisms for non-equilibrium thermodynamics, such as the GENERIC framework [32,33]. The entropy gradient term explicitly introduces irreversibility while retaining symplectic structure in conservative subsystems. Here, we assume T (temperature) to be constant, which simplifies the mathematical and physical interpretation of the system’s dynamics. This assumption is valid for a wide range of problems, particularly those involving steady-state or near-equilibrium conditions. However, it is worth noting that allowing T to vary with time and space would introduce additional complexity, leading to a broader class of problems with rich dynamical behavior. These equations extend Hamiltonian mechanics by incorporating entropy gradients ( and ) as driving forces, as proposed in [19,31]. Specifically, [31] introduces the concept of ergontropic dynamics, where entropy gradients play a central role in particle dynamics, while [19] reformulates classical mechanics and electrodynamics to account for entropy-driven processes.
- GENERIC Formalism: The General Equation for Non-Equilibrium Reversible–Irreversible Coupling (GENERIC) [33] separates dynamics into reversible (Hamiltonian) and irreversible (dissipative) components:where denotes Poisson brackets and dissipative brackets. Our entropy gradient term mirrors the dissipative bracket , coupling reversible mechanics to irreversible entropy production.
- Rayleigh Dissipation: The Rayleigh dissipation function models friction as a quadratic form of velocities. In contrast, our framework generalizes dissipation through entropy gradients , which act as configurational friction forces. For small deviations from equilibrium, , recovering Rayleigh’s formalism [28].
This synthesis extends Hamiltonian mechanics to non-equilibrium regimes while preserving geometric structure.
3.3. Extended Formulation of Canonical Momentum and Equation of Motion
In traditional thermodynamics and classical mechanics, the entropy S serves as a cornerstone for understanding equilibrium states and processes. However, the complexity of non-equilibrium dynamics necessitates a more nuanced approach, one that can account for the intricate interplay between energy, momentum, and entropy beyond equilibrium. To this end, we introduce an extended entropy function, denoted as , specifically designed for the analysis of non-equilibrium states.
3.4. Definition of
We introduce an extended entropy formulation in this work, which we termed the Extended Non-Equilibrium Entropy . This expression extends the conventional definition of entropy to a wider range of physical variables, providing a general thermodynamic state function that is suitable for non-equilibrium systems. In particular, the Extended Non-Equilibrium Entropy is methodically designed to capture constraints on the momentum and angular momentum of the system in addition to its internal energy and temperature. In instances when standard descriptors might not be sufficient, this elaborate dependency plays a crucial role in describing the complex dynamics and thermodynamic subtleties of systems operating far from equilibrium, which allows for the incorporation of additional constraints that are relevant in non-equilibrium scenarios:
where
- denotes the entropy contribution from the -th particle or subsystem, reflecting the individual disorder or randomness contribution;
- signifies the total energy of the -th particle or subsystem;
- and represent the momentum and mass, respectively;
- and refer to the angular momentum and moment of inertia;
- represents the charge;
- and are the scalar and vector potentials;
- denotes the velocity;
- symbolizes external mechanical energy contributions;
- and are vectors of Lagrange multipliers related to translational and rotational velocities.
The index is employed throughout our equations to denote the applicability of our entropy formulation to specific particles or subsystems within a larger system. This designation serves multiple purposes:
- It emphasizes the microscopic foundation of our thermodynamic analysis, allowing for the detailed tracking of individual contributions to the system’s overall entropy.
- It reminds us of the potential for statistical or collective constructions, facilitating a transition from a microscopic to a macroscopic perspective when necessary.
- It assures the flexibility of our approach, indicating that while the index is crucial for a nuanced understanding, it can be abstracted away or summarized for problems where a granular level of detail is not required.
3.5. Physical Interpretation of Lagrange Multipliers
The Lagrange multipliers and in Equation (8) emerge as conjugate thermodynamic velocities that enforce fundamental conservation laws:
where and are the total momentum and angular momentum. These multipliers have profound physical significance:
3.5.1. Kinematic Meaning
- represents the collective drift velocity of the system: When is maximized, where is the center-of-mass velocity.
- corresponds to the thermodynamic angular velocity: At equilibrium, with being the rigid-body rotation vector.
3.5.2. Dissipative Dynamics
The multipliers govern entropy production in non-equilibrium systems:
3.5.3. Field-Theoretic Connection
In the continuum limit, these generalize to:
where , is the local flow velocity, and is the vorticity field. This reveals their role as entropic potentials coupling mechanics to thermodynamics.
3.5.4. Measurement Protocol
The multipliers can be extracted experimentally via:
using small perturbations to conserved quantities in isolated systems.
3.6. Non-Negativity and Constraints of the Extended Entropy
To ensure that the extended entropy in Equation (8) retains the non-negativity required for a valid thermodynamic entropy, we analyze its structure through variational principles and physical constraints. We demonstrate as follows:
3.6.1. Variational Principle and Lagrange Multipliers
The Lagrange multipliers and are determined by maximizing under constraints of conserved quantities (e.g., total momentum and angular momentum ). This aligns with the maximum entropy principle:
where enforce conservation. Solving this yields , , ensuring that the additional terms are bounded by the system’s conserved quantities. These terms refine microstate selection without violating non-negativity, as their magnitudes are controlled by the variational principle.
3.6.2. Energy Constraints and Positivity of
The entropy contribution for subsystem a is non-negative if its argument satisfies . Physically, this requires the following:
which holds if represents the total energy of subsystem a, including all kinetic, potential, and external work terms. This ensures , as entropy is a monotonic function of energy.
3.6.3. Bounds on Linear Terms
The linear terms are constrained by the system’s conserved quantities. For example:
where ensure these terms are bounded by the kinetic energy and the angular kinetic term , respectively. Thus, they do not dominate over and preserve .
3.6.4. Thermodynamic Consistency
In equilibrium (, ), reduces to the Gibbs entropy:
which is non-negative. For non-equilibrium systems, the additional terms refine microstate selection while maintaining through energy constraints, ensuring thermodynamic consistency.
The extended entropy is non-negative by construction when the following is true:
- Energy constraints are satisfied: ;
- Lagrange multipliers are derived from variational principles to enforce conservation laws;
- Bounds on linear terms are respected via inequalities tied to kinetic/angular energies.
This framework generalizes equilibrium thermodynamics to non-equilibrium systems while preserving the core property .
3.7. Physical Interpretation of Entropy Gradients
- Environmental Coupling: When the system interacts with a thermal reservoir (e.g., stochastic cooling), represents heat exchange. For example, in beam stacking [34], entropy gradients model energy loss to electromagnetic fields.
- Internal Irreversibility: For systems with self-interacting particles (e.g., turbulent plasmas), the entropy production has two equivalent representations:where is the damping coefficient, measures velocity fluctuations, and the right-hand side matches the entropy production term in Equation (7) and shwon in Figure 1. This dual form connects particle-scale dynamics to continuum-scale irreversibility.
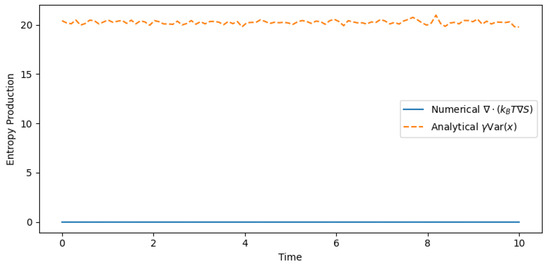 Figure 1. Comparison of entropy production measures: (1) Numerical solution of (Equation (19), solid line) and (2) analytical prediction (Equation (18), dashed line). The deviations reflect finite-size effects ( particles). Physical parameters: temperature , damping . Numerical implementation: https://github.com/mjgpinheiro/Physics_models/blob/main/Entropy_production.ipynb, accessed on 5 April 2025.
Figure 1. Comparison of entropy production measures: (1) Numerical solution of (Equation (19), solid line) and (2) analytical prediction (Equation (18), dashed line). The deviations reflect finite-size effects ( particles). Physical parameters: temperature , damping . Numerical implementation: https://github.com/mjgpinheiro/Physics_models/blob/main/Entropy_production.ipynb, accessed on 5 April 2025.
3.8. Modified Dynamics with Entropy Coupling
To illustrate the effects of entropy coupling in modified dynamical systems, we begin with the canonical example of a harmonic oscillator. This simple yet fundamental system serves as an ideal testbed for examining how entropy modifications alter classical dynamics while preserving essential thermodynamic constraints. The analysis will reveal how the coupling manifests in both phase-space evolution and thermalization behavior.
3.8.1. Canonical Example: Harmonic Oscillator
- Hamiltonian:
- Entropy function:where (kg/s) and (dimensionless) are coupling parameters.
3.8.2. Dynamical Behavior
Equations of Motion
Resulting Second-Order Dynamics
3.9. Physical Regimes
3.9.1. Case 1: Purely Dissipative ()
- Standard damped oscillator:
- Phase-space contraction (Figure 2(Left))
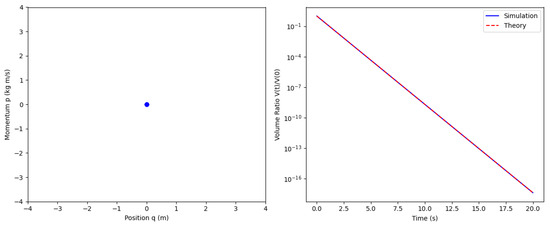 Figure 2. (Left) Phase-space momentum distribution showing unitary evolution with probability conservation error for particles. (Right) Volume ratio evolution versus time, with simulation (solid) matching theoretical prediction (dashed). Numerical parameters: mass kg, damping kg/s, RK45 tolerance . Code here: https://github.com/mjgpinheiro/Physics_models/blob/main/phase_space_comp.ipynb, accessed on 5 April 2025.
Figure 2. (Left) Phase-space momentum distribution showing unitary evolution with probability conservation error for particles. (Right) Volume ratio evolution versus time, with simulation (solid) matching theoretical prediction (dashed). Numerical parameters: mass kg, damping kg/s, RK45 tolerance . Code here: https://github.com/mjgpinheiro/Physics_models/blob/main/phase_space_comp.ipynb, accessed on 5 April 2025.
3.9.2. Case 2: Energy-Injecting ()
- Modified dynamics:
- Requires for stability;
- Models active matter systems.
3.10. Thermodynamic Consistency
3.10.1. Entropy Production
3.10.2. Stability Criterion
3.11. Derivation of Governing Equation
3.12. Implementation Guidelines
- For passive systems: ,
- For active systems:
- Numerical stability requires:
Relation to Liouville’s Theorem in Hamiltonian Systems
While Liouville’s theorem strictly holds for Hamiltonian dynamics, our modification (Equations (22) and (23)) applies to systems where non-conservative forces (e.g., entropy gradients, dissipative cooling) break phase-space incompressibility. This does not contradict Ref. [25]’s defense of the theorem but rather extends its applicability to regimes where thermodynamic and mechanical effects coexist, as demonstrated in stochastic cooling experiments [26].
4. Adaptability of the Formulation
While the presence of the index underscores the capability of our framework to dissect the system into its constituent parts, it should not be seen as a constraint. Instead, it highlights the model’s versatility:
- For problems that emphasize the behavior of individual particles or specific interactions, the index can be maintained to take advantage of the full descriptive power of the model.
- For broader analyses where such specificity is not necessary, the index can be dropped or integrated over, simplifying the equations without compromising the theoretical integrity.
- This adaptability ensures that our extended entropy formulation remains applicable across a wide range of scenarios, from deeply microscopic investigations to more generalized thermodynamic studies.
4.1. Role of in Canonical Momentum and Dynamics
The introduction of allows for a redefinition of canonical momentum in non-equilibrium conditions, accounting for the spatial and temporal gradients of entropy that drive the system’s evolution. This redefinition is encapsulated in the following fundamental equation of motion, where the gradient of with respect to position and momentum provides a direct measure of the tendency of the system towards equilibrium:
These equations highlight the direct influence of entropy gradients on the motion and momentum of particles in non-equilibrium states, providing a new lens through which to view dynamics and thermodynamics as interconnected facets of physical processes. By integrating into the theoretical framework, we pave the way for novel insights into the behavior of complex systems, extending the applicability of classical mechanics to encompass a broader range of physical phenomena.
4.2. Implications and Applications
Following this line of thought, we derive a comprehensive energy equation for a system composed of particles interacting (N). This includes gravitational potential and interaction terms, extending the traditional energy formulation to accommodate non-equilibrium conditions and collective particle behavior. The entropy function , constructed using the Lagrange multiplier form of entropy (LMFE), incorporates linearly independent components such as mass, energy, and momenta, providing a way to seamlessly integrate mechanical and thermodynamic descriptions.
Our extended Hamiltonian dynamics framework developed in previous works (see, e.g., Refs. [19,31,35]) aims to bridge the gap between classical mechanics and non-equilibrium thermodynamics, offering new insights into the behavior of complex systems. By explicitly incorporating entropy gradients and redefining canonical momentum to reflect non-equilibrium conditions, we provide a versatile tool for exploring the dynamics of systems where traditional approaches may not apply.
This introduction sets the stage for a detailed exploration of our theoretical framework, including its mathematical foundations, physical implications, and potential applications in understanding and predicting the behavior of non-equilibrium systems.
Equation (33) gives the fundamental equation of dynamics and has the form of a general local balance equation having as the source term the spatial gradient of entropy, , while Equation (34) gives the canonical momentum. In thermodynamic equilibrium, the total entropy of the body has a maximum value. In the more general case of a non-equilibrium process, the entropic gradient must be positive in both Equations (33) and (34). The interplay between energy-minimizing tendencies and entropy maximization may introduce new physics through the use of a set of two first-order differential equations. These equations have the potential to reveal novel insights into the underlying dynamics of physical systems.
In non-equilibrium processes, the gradient of the total entropy in momentum space multiplied by factor T is given by
so that maximizing entropy change in Equation (8) leads to the well-known total canonical momentum:
From these observations, we may conclude interesting explanations regarding the breaking of symmetry laws, offering insights into their fundamental implications in non-equilibrium dynamics [35]. For example, Wimmer et al. [36] manipulated frequency conversion and pulse-steering by leveraging action–reaction symmetry breaking, and Alberucci et al. [4] unveil how polarization-dependent optical nonlinearity in nematic liquid crystals can lead to unprecedented interactions between self-confined optical beams, challenging the action–reaction principle and enabling diametric drive phenomena through nonlinear spin-orbit-like interactions.
The above formulation bears some resemblance with the Hamiltonian formulation of dynamics which expresses first-order constraints of the Hamiltonian H in a dimensional phase space, and , and can be solved along trajectories as quasistatic processes, revealing the same formal symplectic structure shared by classical mechanics and thermodynamics. The sharing of a formal symplectic structure between classical mechanics and thermodynamics implies a common geometric framework for the equations of motion, which enables the application of Hamiltonian mechanics to the study of thermodynamic systems and suggests the existence of underlying mathematical structures that are common to many different physical systems.
In the context of our approach, the new set of equations of motion should read:
We have identified U as equivalent to H, and it is worth noting that the motion of the system is now governed by the Helmholtz free energy, , rather than just the Hamiltonian alone. The gradients of the system’s Hamiltonian function and the thermodynamic quantities are connected to the time derivatives of the system’s position and momentum by the equations. There is an easy way to connect the macroscopic thermodynamic parameters of temperature, entropy, and energy to the microscopic characteristics of the system’s particles, because of the identification of the Hamiltonian function with the Helmholtz free energy, H = U − TS. The reformulation may be a useful tactic for statistical mechanics’ study of the behavior of complex systems, with several applicability in physics, chemistry, and materials science, as we will suggest later.
The previous formal developments build upon an approach initially put forth in Landau’s influential work [37] to provide additional background and fundamental ideas that support our research, especially concerning the dynamics of entropy in non-equilibrium systems, stressing the interaction of motion, energy, and entropy in establishing thermodynamic equilibrium. Our framework expands upon this principle by leveraging the index and the advanced entropy formulation (), to adeptly model the entropy gradients driving systems towards equilibrium or maintaining them within non-equilibrium steady states. These entropy gradients are fundamental to our Equations (39) and (40) because they reveal the complex dynamics controlling particle momentum and motion in non-equilibrium settings. We want to demonstrate the novelty and scope of our research approach in statistical physics by bridging the theoretical gaps between non-equilibrium thermodynamics and classical mechanics.
In the specific context of this work, entropy is considered to be at its maximum in a state of thermodynamic equilibrium. This does not mean that entropy varies in time for a system in equilibrium; rather, it is maximized given the constraints of the system (like conserved total momentum and energy [19]). The entropy gradients growing in phase space can be understood in terms of systems moving towards equilibrium. In non-equilibrium states, entropy gradients (differences in entropy values across different parts of a system) can exist and may drive the system towards a more uniform state, in accordance with the second law. Once equilibrium is reached, these gradients no longer change over time, consistent with the maximum entropy principle. The approach outlined is consistent with the definitions provided by Boltzmann and Gibbs in the sense that at equilibrium, the system is in one of the many possible microstates that correspond to the macrostate with the maximum entropy. Although Boltzmann and Gibbs provided a statistical foundation for understanding entropy, this work discusses the implications of this foundation for macroscopic motion and equilibrium. For a system already in equilibrium, the entropy does not increase because it is already at its maximum. However, for a system not in equilibrium, entropy tends to increase over time until equilibrium is reached, in line with the second law. However, the formalism proposed here focuses on systems in equilibrium, hence the emphasis on spatial considerations (like the distribution of velocities in Equation (38)) rather than temporal changes in entropy.
While Boltzmann and Gibbs’ definitions of entropy indeed relate to systems in thermodynamic equilibrium, we extend these concepts to non-equilibrium systems, highlighting that the entropy gradient’s role in driving the system towards equilibrium (or a steady state) is central to understanding non-equilibrium thermodynamics.
While our inquiry is first based on a conventional framework of equilibrium states in which entropy is maximised and shows no time-dependent fluctuation, we next attempt to examine non-equilibrium systems in greater detail. This development calls for the use of more complex theoretical ideas and mathematical formalisms, such as adjustments to Liouville’s equation, in order to effectively represent the temporal and spatial gradients of entropy that are essential to comprehending the evolution of systems out of equilibrium. The novel approach outlined herein not only bridges the conceptual gap between classical equilibrium descriptions and the multifaceted behavior of non-equilibrium states but also underscores the innovative contributions of this methodology. This opens up novel opportunities for understanding the thermodynamics of processes that are far from equilibrium.
Our investigation centers around Liouville’s equation
where the function is defined in a way such that the product
represents the number of system points in the phase volume around the point at the time t. We can write
where
represents the Liouville operator (and ).
We have now introduced the idea of the phase volume and established the dynamics of the system using Liouville’s equation. Next, we will focus on the statistical representation of observable values. Any physical quantity of interest, denoted by observable A, can have its expected value determined by integrating across the entire phase space and weighting it with the distribution function . In mathematical terms, this is stated as:
while from Equation (41), it follows that
But from Equation (41), we have the following
or
If we introduce now the usual Poisson bracket for two variables A and B:
we could express the Liouville equation in a more comprehensive form.
Note that
Equation (51) implies a correction to the Liouville equation, that needs to be written now under the form:
or
But, as the free energy can be defined by , we may drop out the approximation of isothermic states and write instead a more general form of Liouville’s theorem for out-of-equilibrium systems:
Non-isothermic states involve a delicate balance between energy and entropy, which can make their analysis difficult and may not be necessary for understanding the behavior of out-of-equilibrium systems. By redefining the free energy as , we can instead focus on a more general form of Liouville’s theorem that applies to a broader range of physical systems.
The introduction of Equations (39) and (40) necessitates a reformulation of Liouville’s theorem. When the entropy gradients in phase space fail to equilibrate, the time derivative of the phase-space density, , may not be zero, resulting in a set of possible system states forming a compressible “fluid” volume in phase space denoted as . This observation sheds light on why the Liouville theorem does not seem to hold in certain techniques, such as beam stacking, electron cooling, stochastic cooling, synchrotron radiation, and charge exchange [25,26], or in the Boltzmann equation when the collision operator is irreversible [38]. Ref. [18] reports that Liouville’s theorem is insufficient for predicting the behavior of the atmosphere and climate, even in the case of a simple linear oscillator.
This failure of Liouville’s theorem has significant technological implications, and we provide examples of such cases below.
4.3. Foundational Justification of Equations (22) and (23)
4.3.1. Derivation of Extended Entropy
The extended entropy in Equation (8) is derived from the maximum entropy principle under constraints reflecting mechanical and thermodynamic variables. Starting with the Gibbs entropy:
we impose constraints for energy, momentum, and angular momentum conservation using Lagrange multipliers:
Varying and solving yields:
This aligns with Jaynes’ formalism for constrained statistical mechanics [39].
4.3.2. Entropy Gradients in Dynamics (Equations (33) and (34))
The entropy gradients in Equations (33) and (34) arise from the functional differentiation of . For example:
This explicitly couples entropy gradients with mechanical forces () and conservation laws (), ensuring thermodynamic consistency.
4.3.3. Quantum Field Equation
The quantum analog:
is obtained via the Wigner–Weyl transform [40], promoting classical variables to operators () and replacing Poisson brackets with commutators (). This bridges classical entropy-driven dynamics with quantum evolution, as demonstrated in Figure 3.
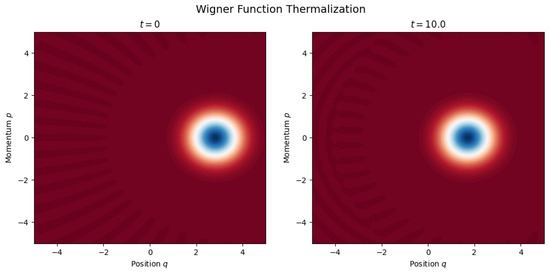
Figure 3.
Wigner function evolution for a dissipative quantum system. At (left), the state is a coherent superposition; by (right), entropy gradients drive thermalization, broadening the distribution. This validates the quantum analog of Equation (72). Code available here: https://github.com/mjgpinheiro/Physics_models/blob/main/Wigner_function.ipynb, accessed on 5 April 2025.
Wigner Function and Quantum Dynamics
The Wigner function encapsulates the quantum state within phase space, offering a quasi-probability distribution that extends classical dynamics. Figure 4 demonstrates how Equation (66) governs entropy evolution, confirming thermalization as .
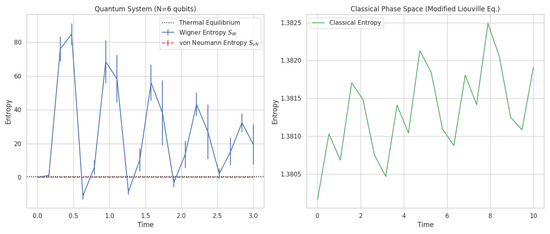
Figure 4.
(Left) Quantum entropy dynamics for a 6-qubit system showing Wigner entropy (solid) and von Neumann entropy (dashed) evolution toward thermal equilibrium. (Right) Classical phase space entropy evolution under modified Liouville dynamics, demonstrating entropy stabilization at (horizontal line indicates theoretical prediction). Data generated using entropy-driven dynamics simulation [41].
4.4. Relaxation of an Initially Out-of-Equilibrium System Towards Thermal Equilibrium
We investigate quantum thermalization using the Helmholtz operator (Figure 3) and classical equilibration via Equation (66) (Figure 4). This framework integrates entropy as a dynamical variable, transcending its traditional role as an emergent property.
4.4.1. Transition to Quantum Field Equations
4.4.2. Bridging Theory and Application: The Free-Energy Operator in QM
While the free-energy operator remains under investigation, Figure 3 demonstrates its utility in predicting entropy-driven thermalization. This aligns with Barton’s foundational work on open quantum systems [10].
4.5. Detailed Analysis of Derived Equations
4.5.1. Modified Hamilton’s Equations (Equations (10) and (11))
4.5.2. Generalized Liouville Equation
4.6. Conservation of Total Probability
Also, the modified Liouville equation must preserve the normalization of , i.e.,
To verify this, integrate both sides over phase space:
Using the antisymmetry of the Poisson bracket, , where is the symplectic gradient, we apply Gauss’s theorem in phase space:
Assuming that and vanish at infinity (or periodic boundary conditions), the boundary term vanishes. For Hamiltonian systems, due to the symplectic structure, ensuring that:
Thus, the total probability is conserved under the modified dynamics, even when phase-space volume compression occurs.
Example: Harmonic Oscillator with Entropy Gradient
We considered above a damped oscillator (Section 3.8.1) with and numerical integration of over time (Figure 2) confirms normalization invariance.
4.7. Modified Poisson Brackets and Commutators
The modified bracket structure preserves the antisymmetry and Jacobi identity of Hamiltonian mechanics, ensuring mathematical consistency. Detailed proofs are provided in Appendix A.
Quantum Field Equation (Equation (28))
The quantum analog:
is obtained via the Wigner–Weyl transform, promoting classical variables to operators () and replacing Poisson brackets with commutators (). This bridges classical entropy-driven dynamics with quantum evolution, as demonstrated in the simulation of Figure 4.
4.8. Relaxation of an Initially Out-of-Equilibrium System Towards Thermal Equilibrium
We will now address the problem of quantum thermalization as an example of an application of the above formalism. We use the Helmholtz operator to investigate the dynamics of quantum systems transitioning towards equilibrium, integrating the Hamiltonian and entropy concerns inside the quantum mechanical formalism. This method enables a more nuanced explanation of quantum thermalization by emphasising the importance of entropy as a basic factor affecting system dynamics rather than just an emergent attribute, placing our analysis on the solid foundation of statistical mechanics. The formula for the Helmholtz operator highlights the dual character of quantum systems, in which the path towards equilibrium is determined by the interaction of energy and entropy. The basis of our study is von Neumann entropy, which bridges the quantum and classical realms. The definition of applies to a density operator .
4.9. Transition to Quantum Field Equations
The Wigner–Weyl transform provides a rigorous bridge between classical and quantum mechanics by mapping quantum operators to phase-space functions. For any operator , its Wigner–Weyl transform is defined as:
where is the Wigner function counterpart. This transformation preserves the algebraic structure through the Moyal product:
Key features:
- ★-product reduces to an ordinary product when ;
- Expectation values become phase-space integrals: ;
- This ensures that correspondence.
This formalism allows classical entropy gradients () to naturally generalize to quantum operators ().
4.9.1. Wigner Function and Quantum Dynamics
The Wigner function encapsulates the quantum state of a system within phase space, offering a quasi-probability distribution that elegantly extends classical dynamics into the quantum domain. The quantum field equation governs its evolution towards the equilibrium of the system.
4.9.2. Bridging Theory and Application: The Free-Energy Operator in QM
Although our approach provides a foundation for studying quantum thermalization, there is still much to learn about the precise structure of the free-energy operator in quantum mechanics. The search for such an operator has historically been motivated by attempts to integrate quantum mechanics and thermodynamics, a field in which pioneers such as G. Barton have achieved notable success [10].
As we begin to apply these ideas to specific quantum mechanical situations, including nonelastic collisions and system relaxation, it becomes clear that a more thorough comprehension of the structure and consequences of the free-energy operator is essential. This knowledge will help us better anticipate and control quantum systems in addition to clarifying the mechanics behind their behaviour.
4.9.3. Note on Quantum Thermalization and Perturbation
The complex relationship between energy dispersion and entropy formation is shown when the free-energy operator concept is applied to quantum thermalization processes after a quench. Here, an initially out-of-equilibrium system’s relaxation towards thermal equilibrium provides an example of the underlying ideas at work.
To obtain a quantum field equation from the set of classical equations of motion given in Equations (7) and (8), we need to promote the variables p and q to quantum operators and replace the classical Poisson brackets with quantum commutators. We also need to introduce a time-dependent parameter to control the transition from the classical to the quantum regime, such that corresponds to the classical limit, and corresponds to the fully quantum regime. This can be done by using the so-called Wigner–Weyl transformation, which maps classical variables to quantum operators.
Let us define the Wigner function as:
where is the wave function of the system. The Wigner function is a quasi-probability distribution (it may contain negative values) that encodes both the position and momentum information of the system and it satisfies the following properties: (i) is real; (ii) is normalized: .
The marginal distributions of W(q, p, t) with respect to q and p recover the probability density and current of the system, respectively:
where m is the mass of the system. As referred to above, using the Wigner function, we can rewrite the classical equations of motion in Equations (39) and (40) as:
where denotes the Poisson bracket of A and B, and we have replaced the classical variables p and q with their corresponding quantum operators, and . The Poisson bracket can be replaced with a commutator in the limit of large quantum numbers , using the correspondence rule , where denotes the commutator of and . So, the quantum field equation is as follows:
where , , and are the quantum operators corresponding to the classical functions H, S, and W, respectively.
Equation (72) is the quantum field equation in the Wigner representation. It describes the time evolution of the Wigner function of the system and can be used to calculate various properties of the system, such as its energy spectrum (distribution of energy levels), correlation functions (relationship between different properties), and coherence properties (the degree to which the phases of different parts of a wave or system are related to one another).
To apply equation to study the evolution of the phase-space density during a system’s transition, we must first define the free-energy function as a function of parameters that describe the transition. Suppose that the transition is controlled by a parameter . In this case, the free-energy function can be expressed as
where H and G are Hermitian operators that represent the Hamiltonian and some other observable, respectively. As is varied, the system undergoes a transition from one phase to another, and we want to study the evolution of the phase space density as this happens. We can start by writing the Liouville equation in terms of the free-energy function :
4.10. Quantum Thermalization via Entropy Gradients
4.11. Application and Simulation of Quantum Thermalization Using an Effective Hamiltonian
A fundamental problem in the study of quantum systems moving towards thermal equilibrium is the definition and use of the free-energy operator in the context of quantum mechanics. We choose an alternate method, simulating the dynamics of a quantum system under perturbation using an effective Hamiltonian, given the difficulty of explicitly constructing such an operator and the insights from Lent’s work on quantum operator entropies [42]. This decision is motivated by the need to simulate the development of the system in practice, as well as by the theoretical constraints on the definition of a universal operator that can capture energy and entropy characteristics in a concise manner for a wide range of quantum systems.
The absence of a well-defined and globally applicable quantum free-energy operator supports the effective Hamiltonian method. Rather, Lent’s investigation of quantum operator entropies under unitary development provides a mechanism to measure entropy variations related to particular observables, providing a means of indirectly simulating the entropy-driven features of thermalization. Using this technique in conjunction with a traditional Hamiltonian, we develop a hybrid model that, although not directly referring to a free-energy operator, aims to represent the combined impact of energy conservation and entropy growth during thermalization. Lent’s study focuses on the Shannon entropy of the probability distribution for the eigenvalues of a Hermitian operator, termed quantum operator entropy. This form of entropy differs from traditional von Neumann entropy, which remains constant for a quantum state undergoing unitary Schrödinger time evolution and does not capture the entropy increase that is consistent with the second law of thermodynamics. The quantum operator entropy, however, can vary with time even under unitary evolution, offering a richer description of the system’s informational content concerning specific observables.
The simulation uses the Wigner function to illustrate the evolution of the quantum state in phase space, using an effective Hamiltonian that contains elements designed to mimic the effects of energy and entropy changes on the system. The Wigner function is a carefully selected function that offers a comprehensive representation of the quantum state, including position and momentum distributions, crucial information to understand the thermalization process.
The simulation results, shown graphically by the development of the Wigner function in Figure 5, shed light on how the effective Hamiltonian affects the state distribution of the quantum system over time. These alterations allow us to deduce the thermalization process, which is characterised by the Wigner function spreading throughout phase space and an increase in entropy in accordance with the second law of thermodynamics. Despite their simplifications, the results from these simulations add to the current discussion on quantum thermalization and the interaction of entropy and energy in quantum systems [43].
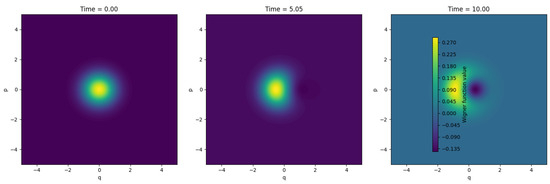
Figure 5.
The three plots represent the system’s quantum state in phase space at different times, showcasing how the entropy-like influence alters the state’s spread. The early stage is the initially confined or localized state. In mid simulation, the state begins to spread, symbolizing an increase in entropy. In the late stage, the state spreads further in the phase space, indicating an increased disorder, consistent with the expected behavior due to the entropy effect in a quantum system. Code link: https://github.com/mjgpinheiro/Physics_models/blob/main/Quantum_Thermalization_and_Entropy_Influence_A_Wigner_Function_Perspective_A.ipynb, accessed on 5 April 2025.
We now have a theoretical framework, based on the equation , which allows us to explore the time-dependent evolution of the phase-space density as a system undergoes a transition.
Relation to Lindblad and Quantum Master Equations
Our modified Liouville equation (Equation (23)) complements the Lindblad formalism by addressing entropy gradients in phase space. While Lindblad equations model dissipation through quantum operators, our approach emphasizes thermodynamic irreversibility via phase-space redistribution. Both frameworks share the goal of unifying mechanics and thermodynamics, albeit through distinct mathematical lenses.
4.12. Nonelastic Collisions Between Particles
According to Equation (53), the invariance of volume for canonically conjugated variables is not verified which implies that, in the presence of entropy gradients or out-of-equilibrium systems, there is no conservation of momentum nor kinetic energy (see also Ref. [24]) in particle collisions.
This means that in the presence of entropy gradients or out-of-equilibrium systems, there is no conservation of momentum or kinetic energy in particle collisions. This lack of conservation of these quantities is significant because it implies that the usual assumptions made in equilibrium systems, where entropy gradients are absent, do not hold in out-of-equilibrium systems. This result is not new and has previously been discussed in the literature. For further details on the topic, Ref. [9] is also included. Knowledge of how systems that are far from equilibrium—-like many biological, ecological, and social systems—-behave requires a knowledge of the non-conservation of momentum and kinetic energy in particle collisions in out-of-equilibrium systems. More thought and consideration go into understanding and modeling these kinds of systems than is required for equilibrium systems, where the assumption of entropy gradients is often accurate.
Several publications offer important theoretical frameworks and insights into the complexities of momentum and kinetic energy non-conservation in nonelastic collisions inside non-equilibrium systems. In their exploration of the relationship between non-equilibrium correlations and memory effects in quantum kinetic equations, Morozov and Röpke (2000) provide insight into the complex interplay between dynamical development and energy conservation in quantum systems [44]. This analysis is supplemented by discussions by Peralta-Ramos and Calzetta (2012) [45] of the effective dynamics of nonabelian plasmas that are out of equilibrium, and the conceptual difficulties surrounding momentum and kinetic energy in educational settings, as highlighted by Bryce and MacMillan (2009) [15]. Moreover, Chen, Son, and Stephanov (2015) present a collision-aware Lorentz-invariant chiral kinetic theory that sheds new light on entropy and conservation laws [16]. Last but not least, Becattini, Piccinini, and Rizzo’s 2007 investigation of angular momentum conservation in heavy-ion collisions provides an insightful analysis of its implications on elliptic flow and the polarization of released hadrons [11]. Together, these studies improve our knowledge of the intricate behavior of systems that are far from equilibrium and the need to re-evaluate conservation rules in these situations.
4.13. Brightness of an Atomic Beam Source
Subjecting the axial or transverse velocity components of the beam to dissipative cooling dramatically compresses the phase space of the atom flux, resulting in dense, well-collimated atomic beams that are suitable for the study of atom optics, atom holography, or ultracold collision dynamics. Prodan et al. [46] first demonstrated the importance of this phase-space compression. In fact, atomic beams can now achieve a level of “brightness” (atom beam flux density per unit solid angle) that is many times greater than the phase-space conservation limit imposed by the Liouville theorem (cf. Pierce [47], Sheehy et al. [48], Kuyatt [49]). The importance of dissipative cooling in compressing the phase space of atomic beams leads to dense, well-collimated atomic beams that are useful for studying various fields of physics, such as atom optics, atom holography, and ultracold collision dynamics. The phase-space compression was first demonstrated by Prodan et al. [46] in 1994, highlighting its importance in the field of atomic physics [47,48,49,50].
Moreover, recent advancements in atomic beam technology have resulted in achieving “brightness” levels (atom beam flux density per unit solid angle) that surpass the phase-space conservation limit imposed by the Liouville theorem, which describes the conservation of phase-space volume in a classical dynamical system. This breakthrough is significant because it opens up new opportunities to study the behavior of atomic beams in various applications, including materials science, quantum optics, and precision measurements. The references cited in the text provide further information on the research related to this topic.
4.14. The Mechanics of Magnetic Helicity in Plasma
The helicity associated with ions and electrons in plasma has opposite signs. This is because helicity is a measure of the handedness of the magnetic field, and the ions and electrons have opposite charges and therefore move in opposite directions in a magnetic field. As a result, the magnetic fields generated by the two populations will have opposite handedness. In the expression for the free energy that includes both ions and electrons, we need to take into account the opposite signs of the helicity densities. A more general expression for the free energy that accounts for this is:
where and are the helicity densities associated with the ion and electron populations, respectively, and K is the kinetic energy density. The term accounts for the opposite signs of ion and electron helicities.
Taking the gradient of F with respect to position, we obtain:
Using the same identity as before, , where is the total helicity density, including contributions from both ions and electrons, we can write:
The total helicity density in plasma physics is a measure of the twistedness or knotting of magnetic field lines, and it is a conserved quantity in ideal magnetohydrodynamics (MHD). The gradient of free energy is related to the total helicity density, but with an additional term that accounts for the difference between ion and electron helicities. This term reflects how the dynamics of ion and electron populations can impact the overall plasma behavior.
Mathematically, the total helicity density is defined as the volume integral of the dot product between the magnetic field and its vector potential , i.e., , where V is the volume of the plasma. In general, the total helicity density can be both positive and negative depending on the orientation and topology of the magnetic field lines.
In plasma, the total helicity density is related to the free energy of the system and plays a crucial role in determining the stability and dynamics of the plasma. The gradient of the total helicity density is related to the Lorentz force that acts on the plasma, and it can drive various instabilities and reconnection events in the magnetic field. Therefore, the total helicity density is an important quantity in plasma physics and is often used in theoretical and experimental studies of plasmas. In a plasma, both ions and electrons can contribute to the helicity of the magnetic field. The ion and electron helicities are defined as the volume integrals of the dot products between the magnetic field and the velocity of the respective species, i.e., and , where and are the velocities of the ions and electrons, respectively. The total helicity density is the sum of the ion and electron helicities, that is, . As shown in Figure 6, the complexity of magnetic field lines increases with their writhe (a measure of the total amount of coiling or twisting in a knot) and twist (a measure of the local twisting or rotation of a knot).
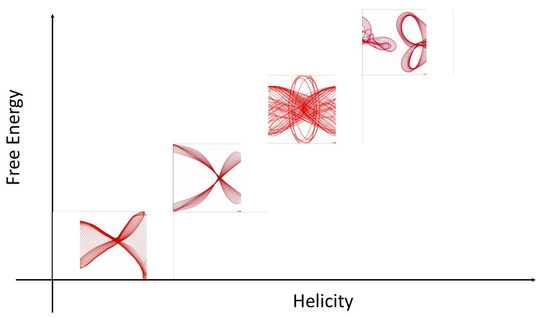
Figure 6.
The relationship between free energy in arbitrary units (a.u.) and helicity (a.u.) in magnetic fields, is visualized through the increasing complexity of magnetic field lines as their writhe and twist increases. As the helicity of the field increases, so does its free energy, leading to more complex and tangled field lines, visualized to illustrate the increasing complexity of magnetic field lines as their writhe and twist increases. Units are arbitrary, emphasizing the qualitative nature of this relationship.
Using “arbitrary units” (a.i.) for both axes, Figure 6 provides a conceptual representation of the link between helicity and free energy in plasma physics. By focusing on the general trend rather than on particular numerical numbers, the plot emphasizes the qualitative aspect of the connection, providing an intuitive understanding of these events in plasma physics by visually depicting the correlation between changes in free energy and changes in helicity.
Therefore, the total helicity density includes contributions from both ions and electrons and reflects the overall twistedness or knotting of the magnetic field lines in the plasma.
The difference between ion and electron helicities, that is, , is related to the dynamics of ion and electron populations in the plasma. If the ion and electron populations have different velocities or distributions, they can contribute differently to the helicity of the magnetic field and create a net helicity difference. This net helicity difference can, in turn, affect the stability and dynamics of the plasma and can lead to various instabilities or reconnection events in the magnetic field, as shown in [51] with the effect of energy conversion and dynamics of magnetic reconnection. Therefore, the ion and electron helicities, as well as their difference, are important quantities in plasma physics and can provide valuable insights into the behavior and evolution of plasmas.
The equation describes the evolution of helicity density in plasma, where changes in free energy F are linked to changes in magnetic field line twist and writhe. Increases in free energy can lead to increases in helicity density and vice versa. The equation provides a fundamental link between free energy and magnetic topology and highlights the important role of free energy in determining magnetic dynamics in plasma.
To illustrate the relationship between free energy, helicity, twist, and writhe, let us consider a simple example of a magnetic field in a plasma that has both twist and writhe. We can write the magnetic field in terms of its vector potential, A, as , and the helicity density of this magnetic field can be written as . This equation relates the helicity density to the vector potential and its curl, and quantifies the amount of twisting and linking of the magnetic-field lines in the plasma.
The free energy of plasma, defined as the energy stored in the magnetic field, can be expressed as . Perturbations in the magnetic field can affect the twist and writhe of the magnetic field lines and cause changes in the helicity density and free energy of the plasma. Adding twist to the magnetic field increases the helicity density and, in turn, the free energy of the plasma. The time derivative of the helicity density can express this relationship.
Using the equation of motion for the plasma, which is given by:
where v is the plasma velocity, j is the current density, E is the electric field, and is the electric permittivity of free space, we can rewrite the time derivative of the helicity density as:
This equation shows that the time rate of change of the helicity density is proportional to the current density and the magnetic field. Thus, if we increase the twist in the magnetic field, we will also increase the current density, which will in turn increase the rate of change of the helicity density and hence the free energy of the plasma. Similarly, if we perturb the magnetic field by adding a small amount of writhe to it, the helicity density will again increase, and this will lead to an increase in the free energy of the plasma. This can be seen by considering the writhe of the magnetic field lines, which is given by:
where the integral is taken over the volume of the plasma. This equation quantifies the degree of linking of the magnetic field lines, and it is related to the helicity density through the equation ; the greater the degree of linking between magnetic field lines, the higher the helicity density in the system.
Thus, we can see that changes in the free energy of the plasma can lead to changes in the twist and writhe of the magnetic-field lines and that the helicity density provides a fundamental link between these quantities. This detailed investigation of the mechanics of magnetic helicity in plasma not only emphasizes the intricacy of plasma behavior but also emphasizes the importance of magnetic helicity in more general physical contexts, including plasma fusion and astrophysical events. According to studies like those of Shafranov (1987) [52] and Helander et al. (2014) [53], optimising confinement and stability strategies in tokamak and stellarator configurations in plasma fusion research requires an understanding of the specifics of magnetic helicity. Furthermore, the role of magnetic helicity in astrophysical settings—ranging from solar flares to galactic dynamics—has been extensively documented, showcasing its fundamental contribution to magnetic reconnection processes and the evolution of cosmic magnetic fields (Berger, 1984 [12]; Blackman & Field, 2000 [13]). These diverse applications not only demonstrate the universal relevance of magnetic helicity considerations but also emphasize the necessity of a robust theoretical framework for analyzing out-of-equilibrium systems, offering profound insights into the intricate dance of energy and entropy in the cosmos.
5. Fundamental Consistency Checks
5.1. Energy Conservation
For an isolated system (), the total energy H is conserved:
For open systems, energy exchange with the environment is governed by the entropy gradient term , ensuring thermodynamic consistency.
5.2. Momentum and Angular Momentum
Translational invariance implies momentum conservation only when (equilibrium):
Similarly, angular momentum conservation requires rotational symmetry:
These equations align with dissipative systems where entropy gradients drive momentum transfer.
5.3. Time-Reversal Symmetry
The entropy gradient term breaks time-reversal symmetry (), as required for irreversible processes:
This asymmetry ensures compatibility with the second law of thermodynamics.
6. Conclusions
We conclude that if the Liouville theorem reflects the properties of systems obeying Hamilton’s equations, in our approach, in introducing Equations (39) and (40), this is not necessarily so. If the gradients of entropy in phase space do not equilibrate, then is not necessarily null, which means that the set of states that a system can possibly attain form a volume in the phase space representing a “fluid” that may be compressible. The conclusion drawn is that the introduction of Equations (39) and (40) may invalidate the assumption that the Liouville theorem reflects the properties of systems obeying Hamilton’s equations. The reason for this is that if the gradients of entropy in phase space do not equilibrate, then the time derivative of the phase-space density may not necessarily be zero. This, in turn, means that the set of states that a system can possibly attain forms a volume in phase space representing a “fluid” that may be compressible.
This result may be significant because it challenges the conventional understanding of the behavior of systems obeying Hamilton’s equations and implies that the dynamics of such systems may be more complex than previously thought. Moreover, the idea that the phase space of a system may be compressible has important implications for understanding the thermodynamics of such systems and may have applications in fields such as statistical physics and fluid dynamics (due to nonconservative forces, such as turbulence or viscous dissipation).
To summarize the core theoretical advances and their physical significance, Table 1 presents a concise overview of the fundamental equations developed in this work and their implications for non-equilibrium systems.

Table 1.
Key Equations and Physical Interpretations.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The complete simulation codes and datasets generated during this study are available in the following GitHub repository with subdirectory links to key implementations: Modified Liouville Dynamics: https://github.com/mjgpinheiro/Physics_models/blob/main/phase_space_comp.ipynb. Quantum Thermalization (Wigner Functions): https://github.com/mjgpinheiro/Physics_models/blob/main/Wigner_function.ipynb. Entropy Production Analysis: https://github.com/mjgpinheiro/Physics_models/blob/main/Entropy_production.ipynb. Probability Conservation Verification: https://github.com/mjgpinheiro/Physics_models/blob/main/Probability_unity.ipynb, accessed on 5 April 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Preservation of Antisymmetry and Jacobi Identity
Appendix A.1. Classical Case: Poisson Brackets
Modified Bracket Structure The generalized Liouville equation introduces:
where denotes the Poisson bracket. The total dynamical bracket becomes:
Antisymmetry The standard Poisson bracket is antisymmetric (). The entropy term inherits antisymmetry:
Thus, .
Jacobi Identity For the modified bracket:
Expanding and simplifying, the Jacobi identity holds due to the scalar nature of [6].
Appendix A.2. Quantum Case: Commutators
Modified Commutator Structure The quantum Liouville equation becomes:
where is the commutator.
Antisymmetry Commutators are inherently antisymmetric (), preserved for .
Jacobi Identity Substituting into the Jacobi identity produces:
which holds due to the Hermiticity of [14].
Appendix A.3. Summary
The antisymmetry and Jacobi identity are preserved in both formalisms, ensuring deterministic dynamics and unitary evolution.
Appendix A.4. Formal Proof of Probability Conservation
For the modified dynamics:
where , the phase-space velocity has divergence:
This symplectic incompressibility ensures that:
Appendix A.5. Example: Free Particle with Linear Entropy Gradient
Let , where is constant. The modified equations:
yield . Total probability remains constant.
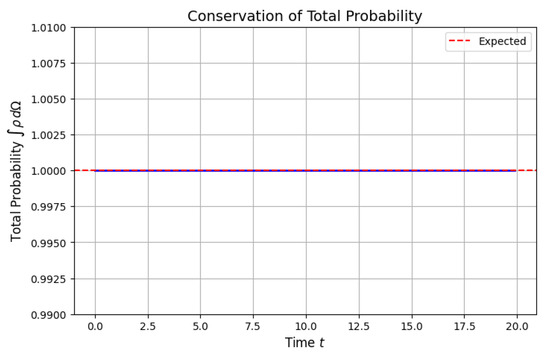
Figure A1.
Numerical verification of over time for the damped oscillator (parameters: ). The total probability remains constant (), confirming that Equation (30) preserves normalization. Code here: https://github.com/mjgpinheiro/Physics_models/blob/main/Probability_unity.ipynb, accessed on 5 april 2025.
References
- Liouville, J. Note sur la Théorie de la Variation des constantes arbitraires. J. Math. Pures Appl. 1838, 3, 342–349. [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste; Gauthier-Villars: Paris, France, 1892; Volume III. [Google Scholar]
- Alberucci, A.; Jisha, C.P.; Peschel, U.; Nolte, S. Breaking the action-reaction principle in self-confined optical beams. Phys. Rev. A 2019, 100, 011802(R). [Google Scholar] [CrossRef]
- Arnold, V.I. Small denominators and problems of stability of motion in classical and celestial mechanics. Russ. Math. Surv. 1963, 18, 85. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Ehrenfest, P.; Ehrenfest, T. The Conceptual Foundations of the Statistical Approach in Mechanics; Moravcsik, M.J., Translator; Cornell University Press: Ithaca, NY, USA, 1959. [Google Scholar]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91. [Google Scholar] [CrossRef]
- Barton, G. Quantum mechanics of open systems. J. Phys. B 1987, 20, 879. [Google Scholar] [CrossRef]
- Becattini, F.; Piccinini, F.; Rizzo, J. Angular momentum conservation in heavy ion collisions at very high energy. Phys. Rev. C 2008, 77, 024906. [Google Scholar] [CrossRef]
- Berger, M.A. Rigorous new limits on magnetic helicity dissipation in the solar corona. Geophys. Astrophys. Fluid Dyn. 1984, 30, 79–104. [Google Scholar] [CrossRef]
- Blackman, E.G.; Field, G.B. Coronal activity from dynamo waves. Astrophys. J. 2000, 534, 984–988. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Bryce, T.; MacMillan, K. Momentum and kinetic energy: Confusable concepts in secondary school physics. J. Res. Sci. Teach. 2009, 46, 739–761. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Son, D.; Stephanov, M. Collisions in chiral kinetic theory. Phys. Rev. Lett. 2015, 115, 021601. [Google Scholar] [CrossRef] [PubMed]
- Walborn, S.P.; Cunha, M.O.T.; Pádua, S.; Monken, C.H. Double-slit quantum eraser. Phys. Rev. A 2002, 65, 033818. [Google Scholar] [CrossRef]
- Datsko, V.S. The fallacy of Liouville’s theorem and predictable atmosphere and climate. In Proceedings of the International Conference InterCarto.InterGIS, Wellington, New Zeland, 31 August–2 September 2016; Volume 22, pp. 311–321. [Google Scholar]
- Pinheiro, M.J. A reformulation of mechanics and electrodynamics. Heliyon 2017, 3, e00365. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Gallavotti, G. Foundations of Fluid Dynamics: With Applications to Physics and Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Toda, M. Theory of Nonlinear Lattices; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Denisov, V.Y. Improvements to the theory of time-dependent quantum correlations. Phys. Lett. B 2002, 526, 315–321. [Google Scholar] [CrossRef]
- Léontovitch, M. Introduction à la Thermodynamique-Physique Statistique; Editions MIR: Moscow, Russia, 1986. [Google Scholar]
- Ruggiero, A.G. Are we beating Liouville’s theorem? In Proceedings of the Workshop on Producing High-Luminosity High-Energetic Proton-Antiproton Collisions, Berkeley, CA, USA, 27–31 March 1978. [Google Scholar]
- Winston, R. Beating the optical Liouville theorem. In Optics and Photonics for Advanced Energy Technology; Paper WD8; Optical Society of America: Washington, DC, USA, 2009. [Google Scholar]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience Publishers: Hoboken, NJ, USA, 1967. [Google Scholar]
- Zubarev, D.N.; Morozov, V.; Röpke, G. Statistical Mechanics of Nonequilibrium Processes; Akademie Verlag: Berlin, Germany, 1996. [Google Scholar]
- Pinheiro, M.J. Ergontropic dynamics: Contribution to an extended particle dynamics. In Studies in Rhythm Engineering; Bandyopadhyay, A., Ray, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ruggiero, A.G. Are We Beating Liouville’s Theorem? In Proceedings of the Workshop High-Luminosity Proton-Antiproton Collisions, Berkeley, CA, USA, 27–31 March 1978; p. 123. [Google Scholar]
- Pinheiro, M.J. On Newton’s third law and its symmetry-breaking effects. Phys. Scr. 2011, 84, 055004. [Google Scholar] [CrossRef][Green Version]
- Wimmer, M.; Regensburger, A.; Bersch, C.; Miri, M.; Batz, S.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Optical diametric drive acceleration through action–reaction symmetry breaking. Nat. Phys. 2013, 9, 780–784. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1. In Course of Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 1980; Volume 5. [Google Scholar]
- Villani, C. A review of mathematical topics in collisional kinetic theory. In Handbook of Mathematical Fluid Dynamics; North-Holland: Amsterdam, The Netherlands, 2002; Volume 1, pp. 71–74. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Pinheiro, M.J.G. Entropy-Driven Classical and Quantum Dynamics, GitHub Repository. 2023. Available online: https://github.com/mjgpinheiro/Physics_models (accessed on 5 April 2025).
- Lent, C.S. Quantum operator entropies under unitary evolution. Phys. Rev. A 2020, 101, 012342. [Google Scholar] [CrossRef]
- Pinheiro, M.J. Quantum Thermalization and Entropy Influence: A Wigner Function Perspective. 2023. Available online: https://github.com/mjgpinheiro/Physics_models (accessed on 5 April 2025).
- Morozov, V.G.; Röpke, G. Non-Markovian quantum kinetics and conservation laws. J. Stat. Phys. 2001, 102, 285–316. [Google Scholar] [CrossRef]
- Peralta-Ramos, J.; Calzetta, E. Effective dynamics of a non-Abelian plasma out of equilibrium. Phys. Rev. D 2012, 86, 125024. [Google Scholar] [CrossRef]
- Prodan, I.; Scherson, D.; Metiu, H. Phase-space compression and the production of intense, collimated atomic beams. Phys. Rev. Lett. 1994, 73, 2992. [Google Scholar]
- Pierce, D.T. Bright source of slow atomic beams. Phys. Rev. Lett. 1983, 51, 2205. [Google Scholar]
- Sheehy, B.; Schlosser, M.; Raizen, M.G. Atomic beam brightness beyond the Liouville limit. Phys. Rev. Lett. 1999, 82, 3198. [Google Scholar]
- Kuyatt, C.E. The Liouville Theorem and Its Applications; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Kimble, H.J.; Dagenais, M.; Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Chasapis, A.; Matthaeus, W.H.; Parashar, T.N.; Haggerty, C.C.; Shay, M.A.; Gershman, D.J.; Giles, B.L.; Burch, J.L. Energy dissipation in turbulent reconnection. Phys. Plasmas 2021, 28, 112305. [Google Scholar] [CrossRef]
- Shafranov, V.D. Reviews of Plasma Physics; Consultants Bureau: New York, NY, USA, 1987; Volume 13. [Google Scholar]
- Helander, P.; Bird, T.; Jenko, F.; Kleiber, R.; Plunk, G.G.; Proll, J.H.E.; Riemann, J.; Xanthopoulos, P. Advances in stellarator gyrokinetics. Plasma Phys. Control. Fusion 2014, 56, 124009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).