Complementary Filter Optimal Tuning Methodology for Low-Cost Attitude and Heading Reference Systems with Statistical Analysis of Output Signal
Abstract
1. Introduction
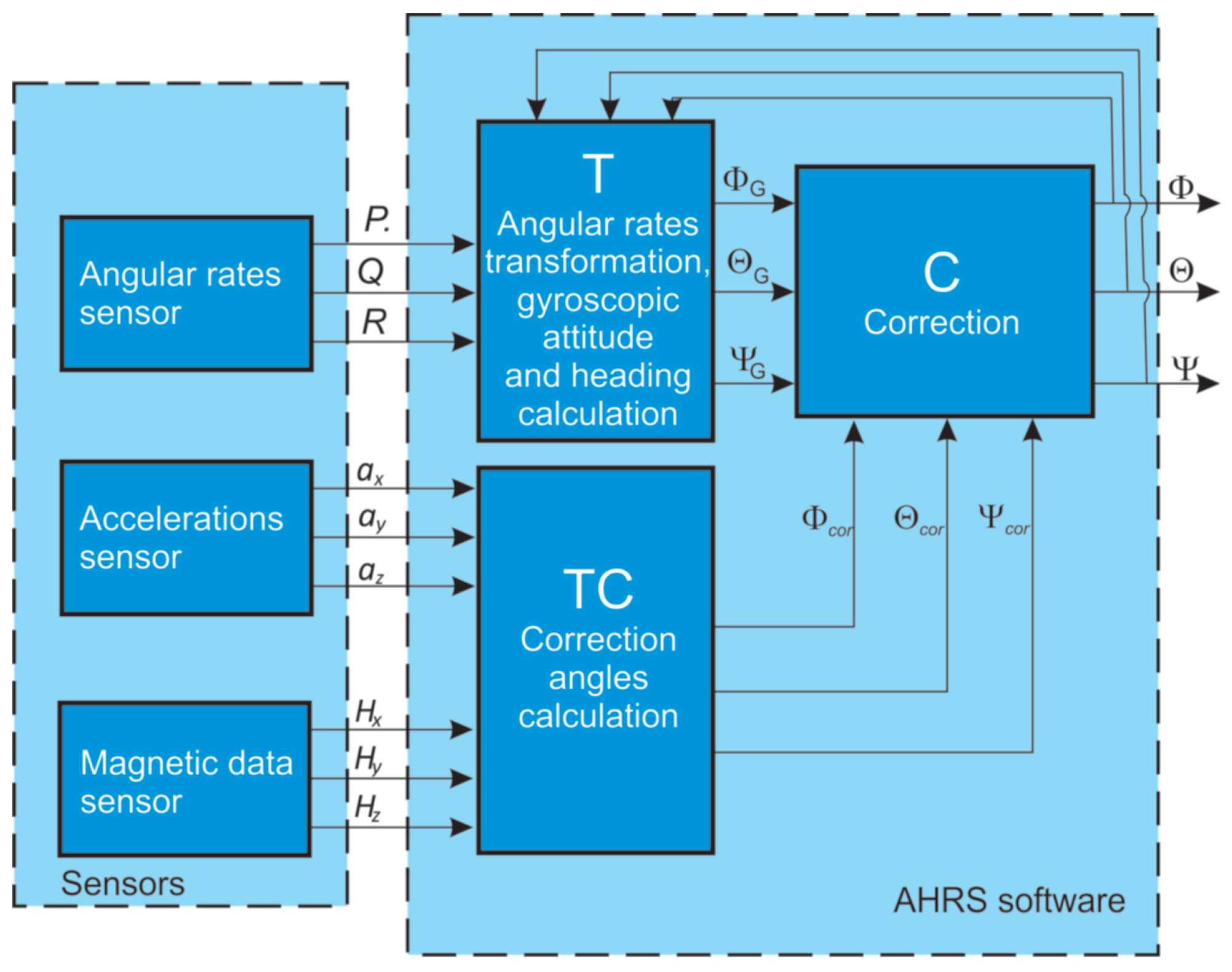
2. AHRS Principles of Operation
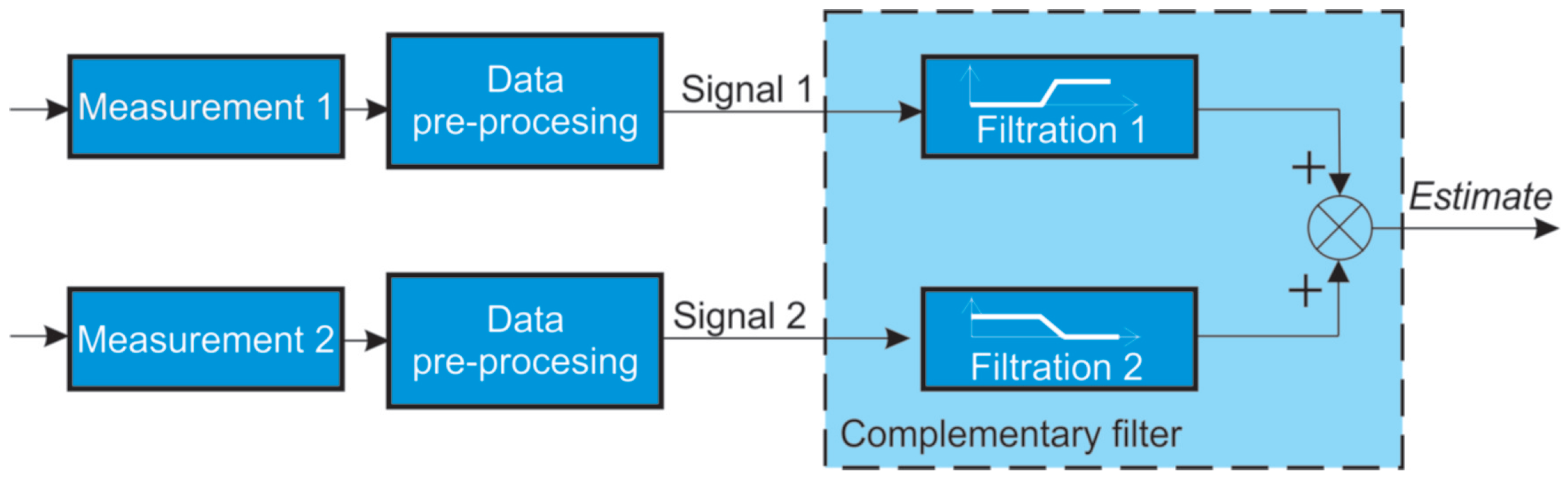
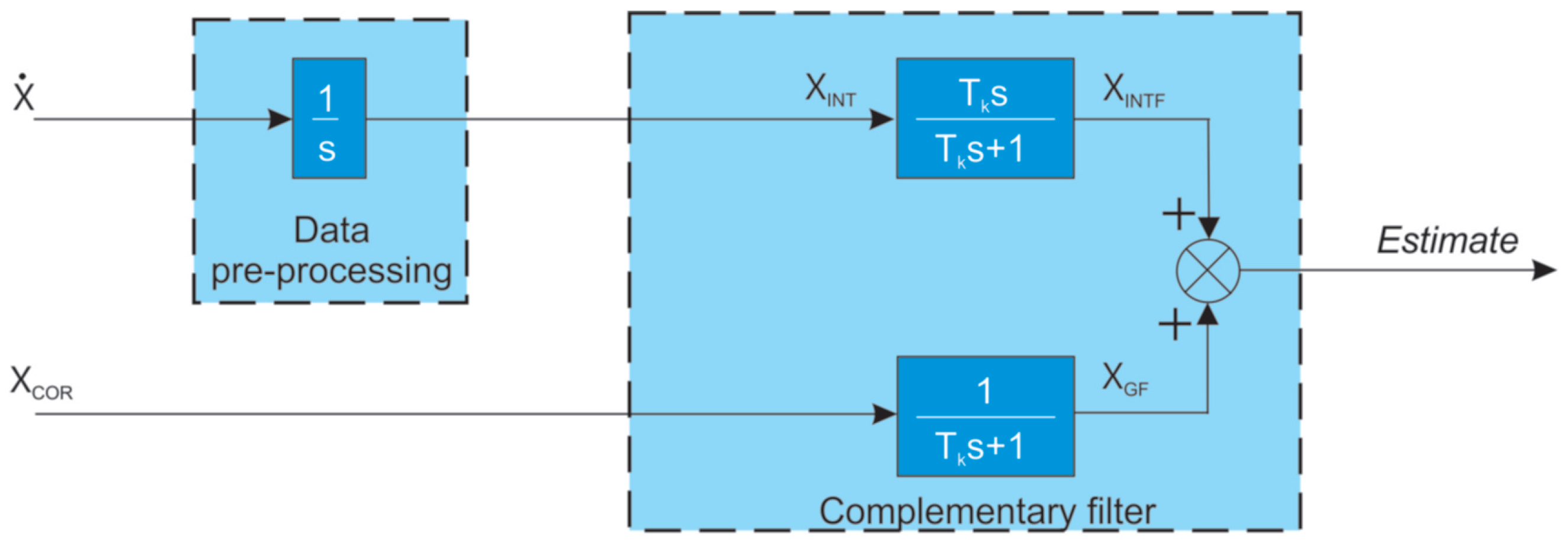
3. Methodology of Complementary Filter Calibration
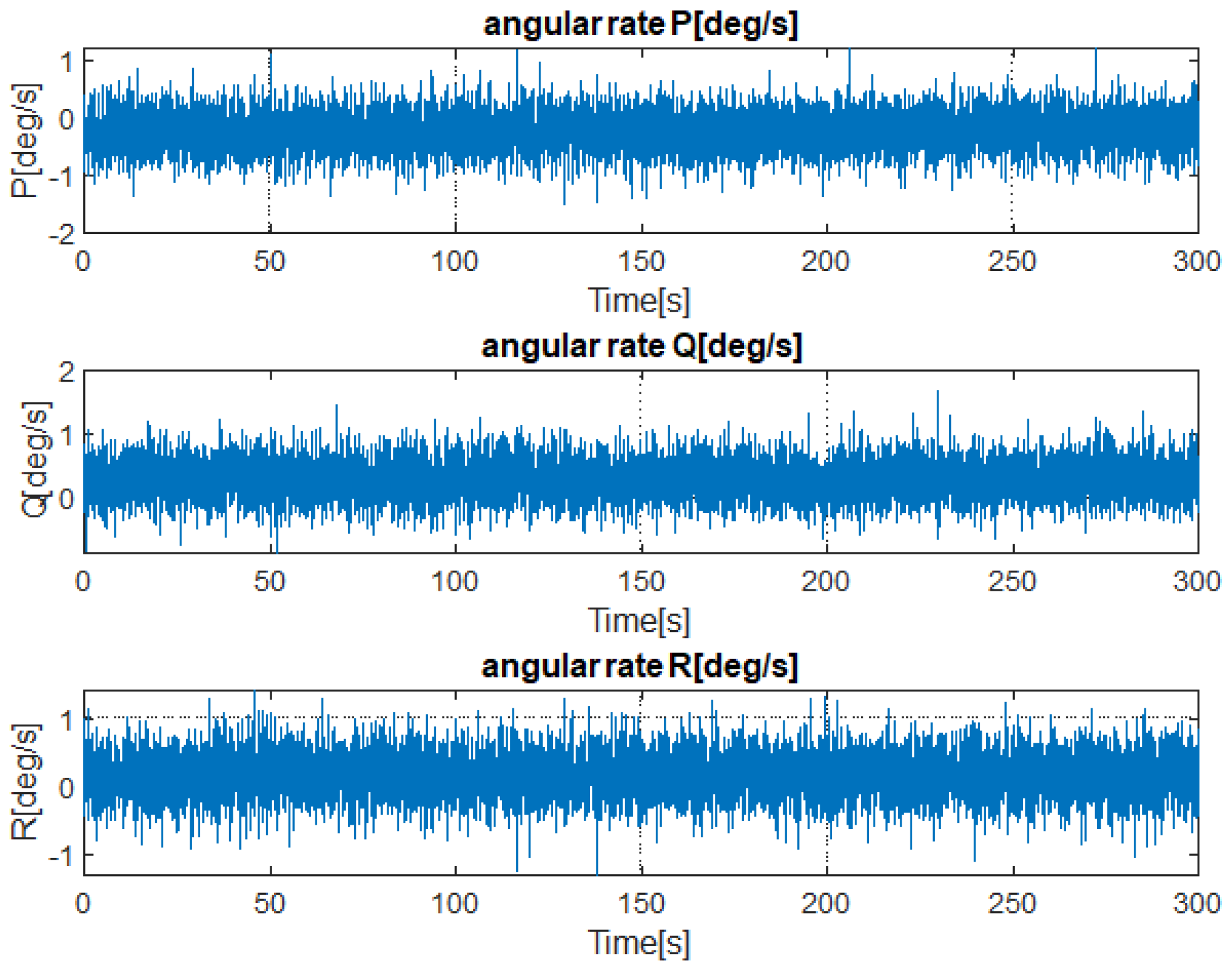
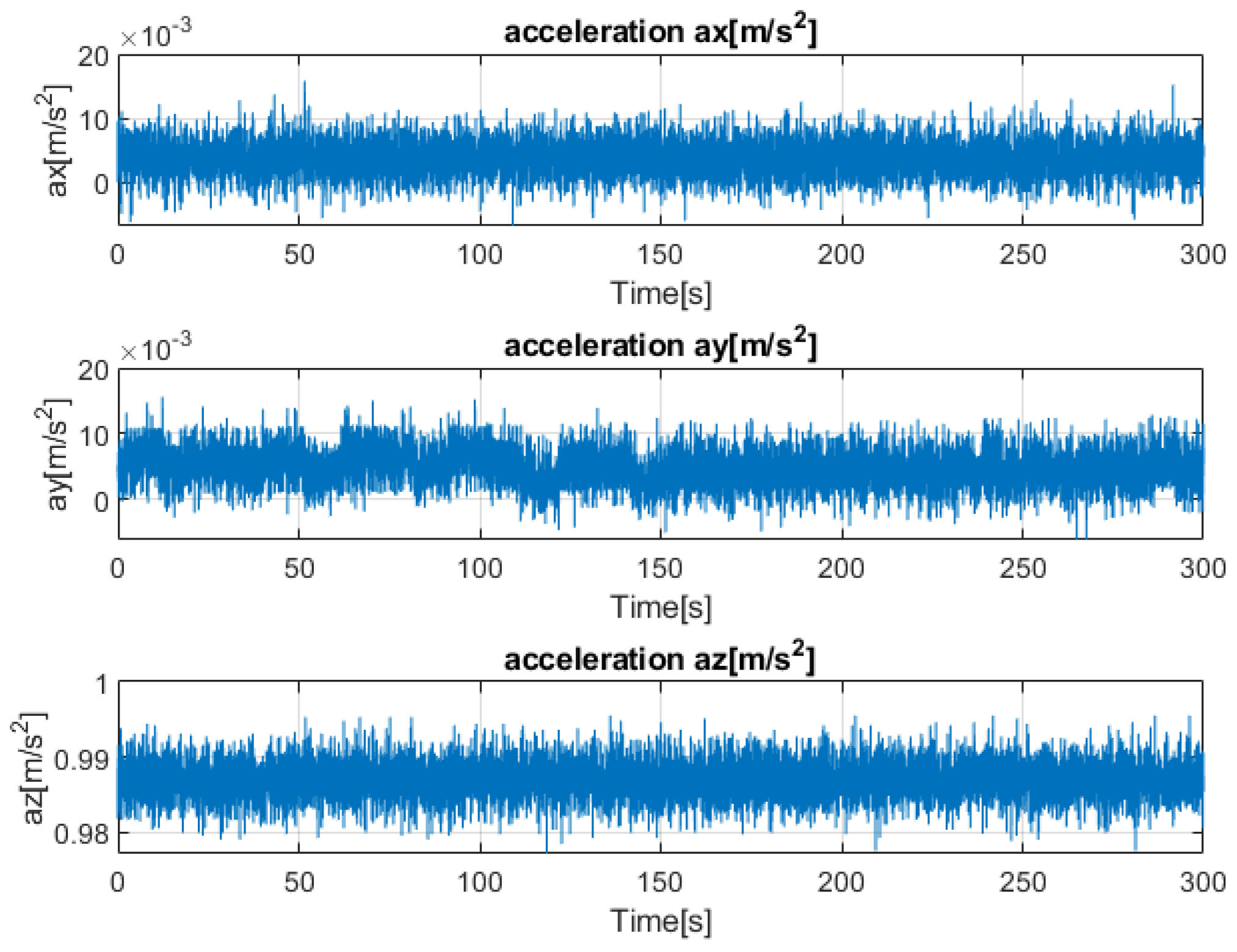
3.1. Data Collection
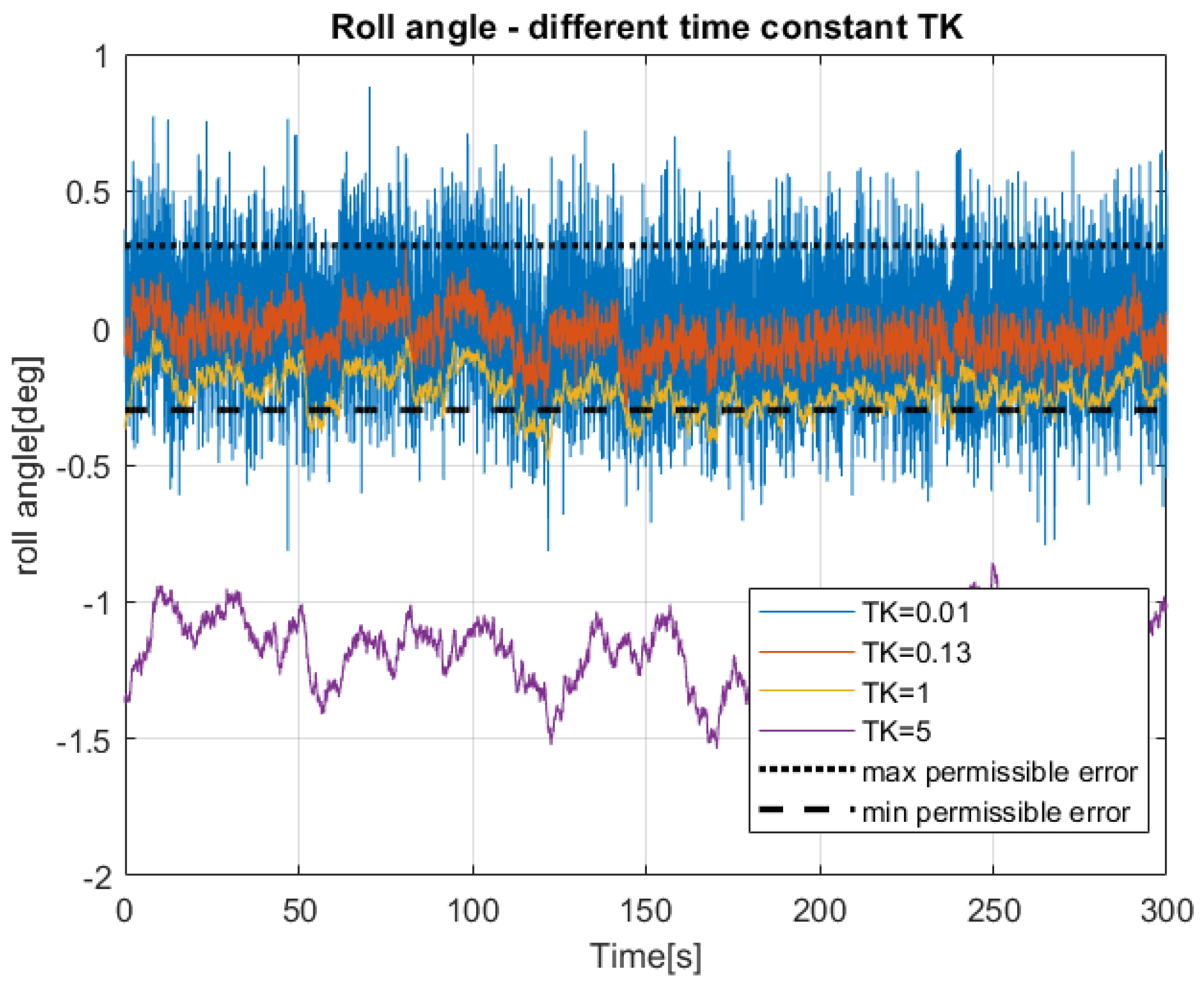
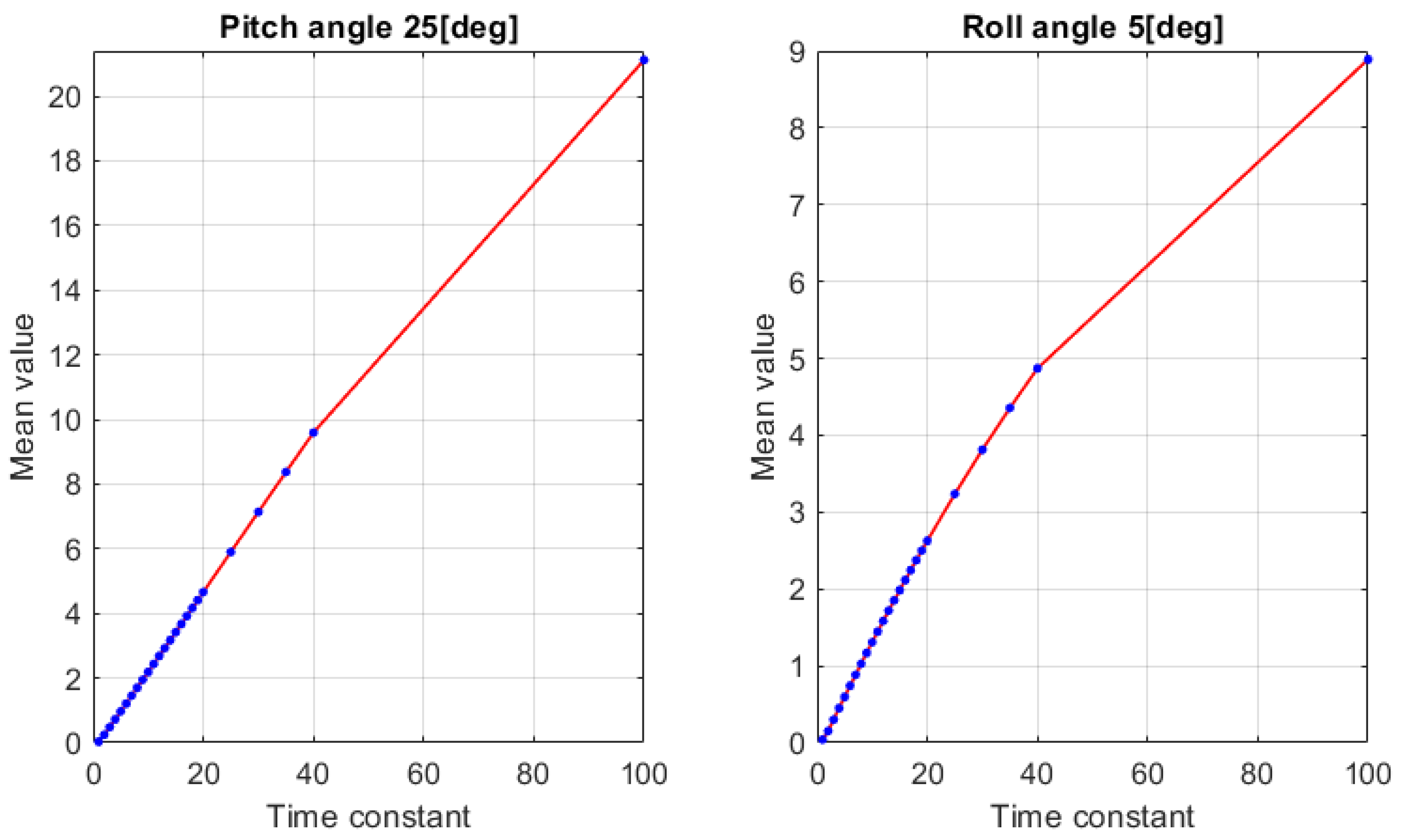
3.2. Optimization Methodology
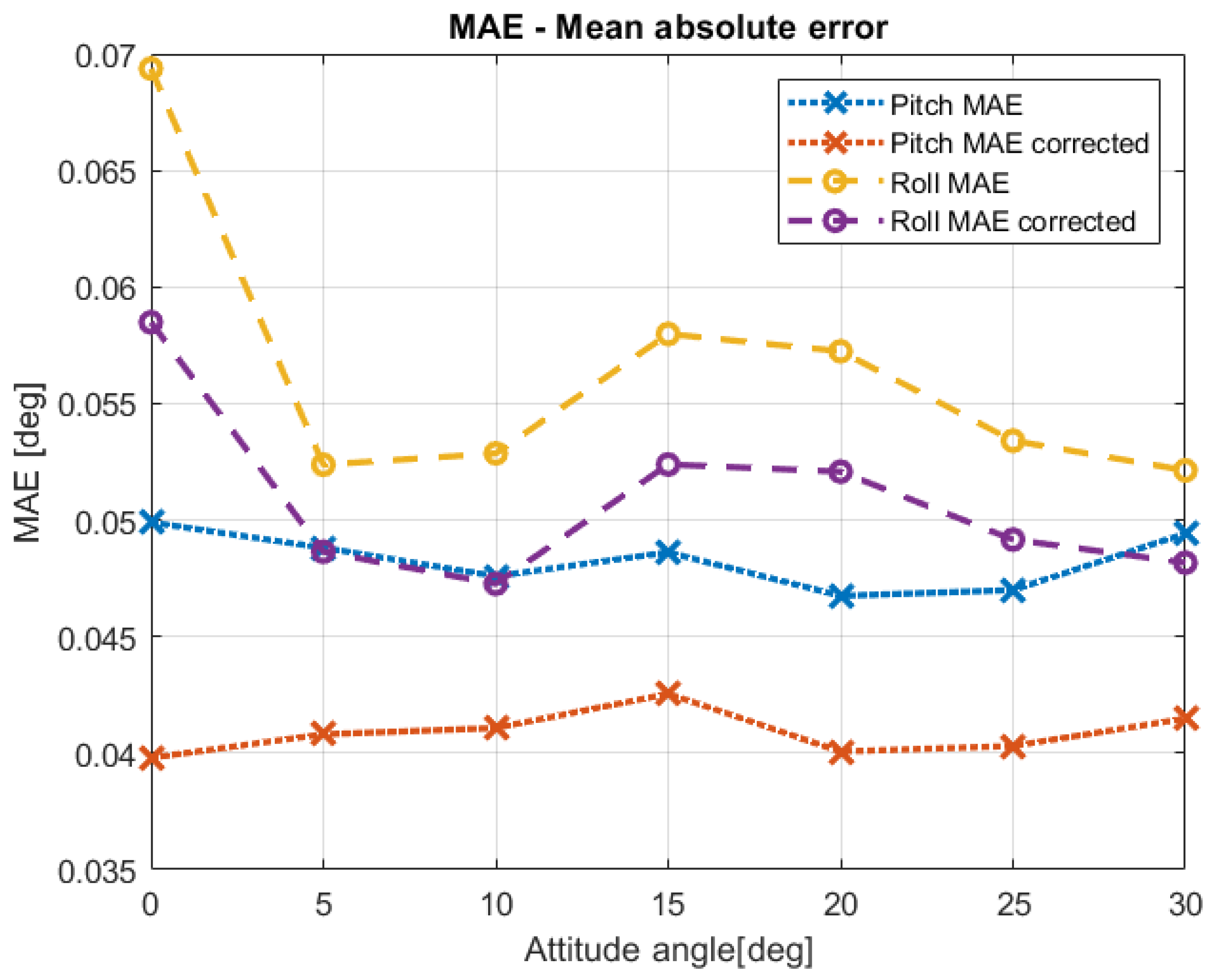
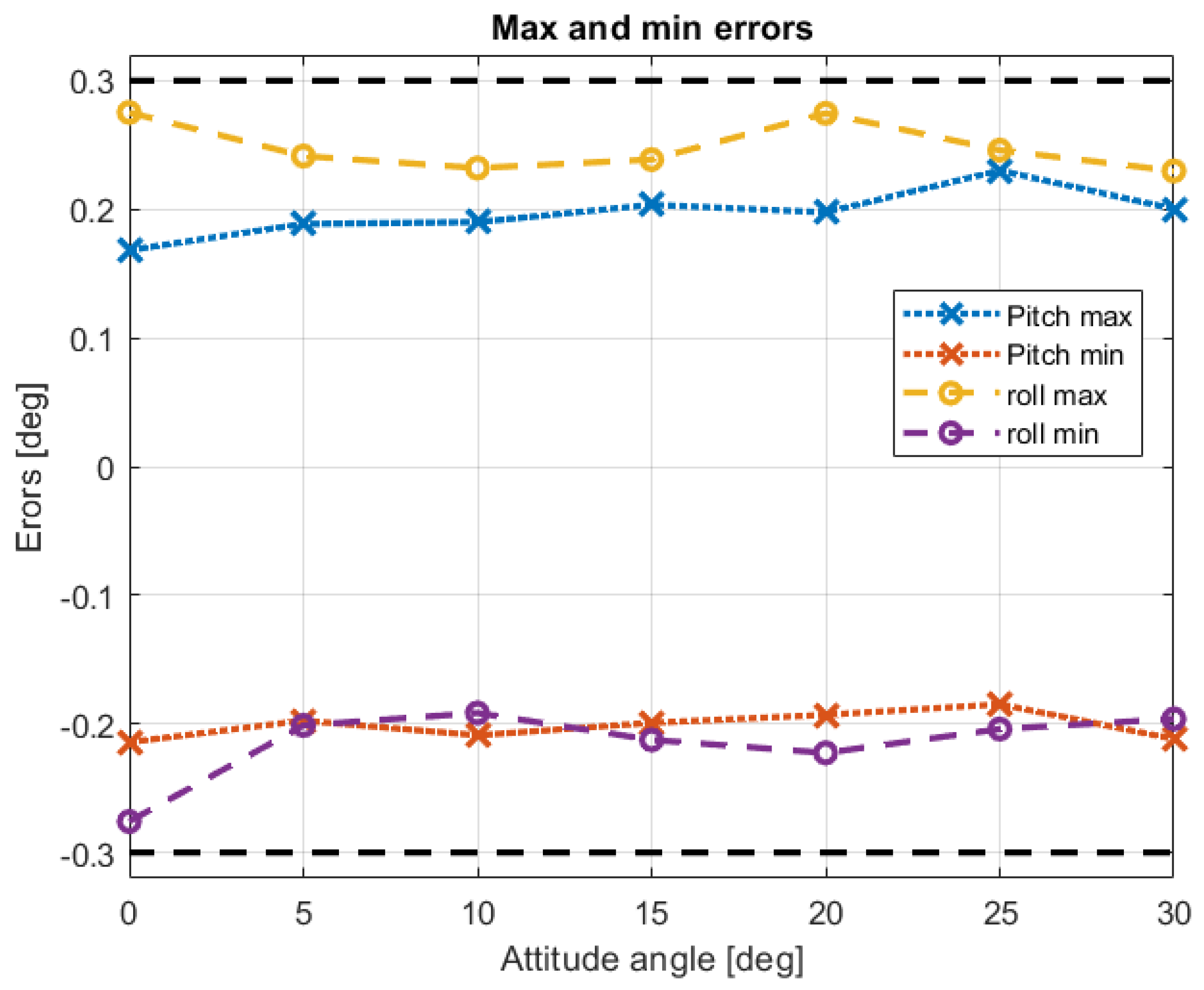
3.3. Performance Evaluation of the Optimized Signal
4. Conclusions, Discussion, and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kowalik, R.; Łuksiak, T.; Novak, A. A Mathematical Model for Controlling a Quadrotor UAV. Trans. Aerosp. Res. 2021, 3, 58–70. [Google Scholar] [CrossRef]
- Steffensen, R.; Ginnell, K.; Holzapfel, F. Practical System Identification and Incremental Control Design for a Subscale Fixed-Wing Aircraft. Actuators 2024, 13, 130. [Google Scholar] [CrossRef]
- Pecho, P.; Velky, P.; Kapustik, S.; Novak, A. Use of Computer Simulation to Optimize UAV Swarm Flying. In Proceedings of the 2022 New Trends in Aviation Development (NTAD), Novy Smokovec, Slovakia, 24–25 November 2022. [Google Scholar] [CrossRef]
- Kusmirek, S.; Socha, V.; Urban, D.; Hanakova, L.; Kripsky, F.; Walton, R.; Pecho, P. Design of Pitot-Static Tube Shapes and Their Influence on Airspeed Measurement Accuracy. J. Aerosp. Eng. 2024, 37, 04024045. [Google Scholar] [CrossRef]
- Qu, G.; Zhou, Z.; Li, J.; Shao, Z.; Dong, Y.; Guo, A. UAV Attitude Angle Measurement Method Based on Magnetometer-Satellite Positioning System. Appl. Sci. 2022, 12, 5947. [Google Scholar] [CrossRef]
- Sedlackova, A.N.; Kurdel, P.; Mrekaj, B. Synthesis criterion of ergatic base complex with focus on its reliability. In Proceedings of the 2017 IEEE 14th International Scientific Conference on Informatics, INFORMATICS 2017, Poprad, Slovakia, 14–16 November 2017; pp. 318–321. [Google Scholar] [CrossRef]
- Kopecki, G.; Dołęga, B.; Rzucidło, P. Fault Detection and Identification in the Doubled Attitude and Heading Reference System (AHRS). Sensors 2025, 25, 1603. [Google Scholar] [CrossRef]
- Islam, M.S.; Shajid-Ul-Mahmud, M.; Islam, T.; Amin, M.S.; Hossam-E-Haider, M. A low cost MEMS and complementary filter based attitude heading reference system (AHRS) for low speed aircraft. In Proceedings of the 2016 3rd International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 22–24 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Zarchan, P.; Musoff, H. Fundamentalsof Kalman Filtering: A Practical Approach, 3rd ed.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2009. [Google Scholar]
- Collinson, R.P.G. Introduction to Avionics; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Grygiel, R.T.; Bieda, R. Angles from gyroscope to complementary filter in IMU. Przegląd Elektrotechniczny 2014, 90, 217–224. [Google Scholar] [CrossRef]
- Narkhede, P.; Poddar, S.; Walambe, R.; Ghinea, G.; Kotecha, K. Cascaded Complementary Filter Architecture for Sensor Fusion in Attitude Estimation. Sensors 2021, 21, 1937. [Google Scholar] [CrossRef] [PubMed]
- Kopecki, G.; Rogalski, T. Aircraft Attitude Calculation with the Use of Aerodynamic Flight Data as Correction Signals. Aerosp. Sci. Technol. 2013, 32, 267–273. [Google Scholar] [CrossRef]
- Li, X.; Xu, Q.; Shi, Q.; Tang, Y. Complementary Filter for Attitude Estimation Based on MARG and Optical Flow Sensors. J. Phys. Conf. Ser. 2021, 2010, 012160. [Google Scholar]
- Pitieeraphab, Y.; Jusing, T.; Chotikunnan, P.; Thongpance, N.; Lekdee, W.; Teersoradech, A. The Effect of Average Filter for Complemetary Filter And Kalman Filter Based on Measurement Angle. In Proceedings of the 2016 Biomedical Engineering International Conference, Laung Prabang, Laos, 7–9 December 2016; BMEiCON-2-16. [Google Scholar]
- Poulose, A.; Senouci, B.; Han, D.S. Performance Analysis of Sensor Fusion Techniques for Heading Estimation Using Smpartphone Sensors. IEEE Sens. J. 2019, 19, 12369–12380. [Google Scholar]
- Wag, Y.; Li, N.; Chen, X.; Liu, M. Design and Implementation of an AHRS Based on MEMS Sensors and Complementary Filtering. Adv. Mech. Eng. 2014, 6, 214726. [Google Scholar] [CrossRef]
- Ryzhkov, L. Complementary Filter Design for Attitude Determination. In Proceedings of the IEEE 5th International Conference on Methodz and Systems on Navigation and Motion Control (MSNMC), Kyiv, Ukraine, 16–18 October 2018. [Google Scholar]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. Keeping a Good Attitude: A Quaternion-Based Orientation Filter for IMUs and MARGs. Sensors 2015, 15, 19302–19330. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.; Padayachee, K.; Broughton, B.A. A robust complementary filter approach for attitude estimation of unmanned aerial vehicles using AHRS. In Proceedings of the 2019 CEAS EuroGNC Conference, Milan, Italy, 3–5 April 2019; CEAS-GNC-2019-036. [Google Scholar]
- Rzucidło, P.; Kopecki, G.; Szczerba, P.; Szwed, P. Analysis of Stochastic Properties of MEMS Accelerometers and Gyroscopes Used in the Miniature Flight Data Recorder. Appl. Sci. 2024, 14, 1121. [Google Scholar] [CrossRef]
- Yoo, T.S.; Hong, S.K.; Yoon, H.M.; Park, S. Gain-scheduled complementary filter design for a MEMS based attitude and heading reference system. Sensors 2011, 11, 3816–3830. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Thomas, D.; Mohit, V.; Christophe, C. Complementary Filters Shaping Using Hinf Synthesis. In Proceedings of the 2019 7th International Conference on Control, Mechatronics and Automation (ICCMA), Delft, The Netherlands, 6–8 November 2019; pp. 459–464. [Google Scholar] [CrossRef]
- Duong, D.Q.; Sun, J.; Nguyen, T.P.; Luo, L. Attitude estimation by using MEMS IMU with Fuzzy Tuned Complementary Filter. In Proceedings of the 2016 IEEE International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 August 2016; pp. 372–378. [Google Scholar] [CrossRef]
- Kopecki, G.; Tomczyk, A.; Rzucidło, P. Algorithms of Measurement System for a Micro UAV. Solid State Phenom. 2013, 198, 165–170. [Google Scholar] [CrossRef]
- Kopecki, G.; Banicki, M. A proposal of AHRS yaw angle correction with the use of roll angle. Aircr. Eng. Aerosp. Technol. 2023, 95, 1435–1443. [Google Scholar] [CrossRef]
- Dolega, B.; Kopecki, G.; Tomczyk, A. Possibilities of using software redundancy in low cost aeronautical control systems. In Proceedings of the 3rd IEEE International Workshop on Metrology for Aerospace (MetroAeroSpace) 2016, 2016 IEEE Metrology for Aerospace (Metroaerospace), Florence, Italy, 22–23 June 2016; pp. 33–37. [Google Scholar]
- Rzucidlo, P.; Kopecki, G.H.; deGroot, K.; Kucaba-Pietal, A.; Smusz, R.; Szewczyk, M.; Szumski, M. Data acquisition system for PW-6U in flight boundary layer mapping. Aircr. Eng. Aerosp. Technol. 2016, 88, 572–579. [Google Scholar]
- Kopecki, G.; Rzucidlo, P. Integration of optical measurement methods with flight parameter measurement systems. Meas. Sci. Technol. 2016, 27, 054003. [Google Scholar] [CrossRef]
- Durham, W. Aircraft Flight Dynamics and Control; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Gosiewski, Z.; Ortyl, A. Algorithms of an Inertial Gimbal-Free Orientation and Positioning System for an Object in Spatial Motion; Scientific Publishing House of the Institute of Aviation: Warsaw, Poland, 1999; ISBN/ISSN 83-910906-1-2. (In Polish) [Google Scholar]
- Tomczyk, A. Testing of the attitude and heading reference system. Aircr. Eng. Aerosp. Technol. 2002, 74, 154–160. [Google Scholar] [CrossRef]
- Gruszecki, J. (Ed.) Unmanned Aerial Vehicles: Control and Navigation Systems; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2002. (In Polish) [Google Scholar]

| Pitch Angle | TC | Minimum MAE | Roll Angle | TC | Minimum MAE |
|---|---|---|---|---|---|
| 0 | 0.11 | 0.049626 | 0 | 0.13 | 0.069190 |
| 5 | 0.12 | 0.048810 | 5 | 0.19 | 0.051458 |
| 10 | 0.13 | 0.047545 | 10 | 0.17 | 0.052601 |
| 15 | 0.13 | 0.048458 | 15 | 0.16 | 0.057899 |
| 20 | 0.12 | 0.046747 | 20 | 0.17 | 0.056838 |
| 25 | 0.12 | 0.046995 | 25 | 0.19 | 0.052498 |
| 30 | 0.12 | 0.049422 | 30 | 0.19 | 0.050939 |
| Pitch Angle | 0_LM | 5_LM | 10_LM | 15_LM | 20_LM | 25_LM | 30_LM |
| (Intercept) | 0.043588 | 0.026875 | 0.025521 | 0.035361 | 0.037425 | 0.034270 | 0.026435 |
| t | −0.000055 | 0.000033 | 0.000000 | −0.000044 | −0.000052 | 0.000000 | 0.000038 |
| Roll Angle | 0_LM | 5_LM | 10_LM | 15_LM | 20_LM | 25_LM | 30_LM |
| (Intercept) | 0.010557 | −0.014750 | −0.026526 | −0.030684 | −0.020162 | −0.018307 | −0.023530 |
| t | −0.000305 | −0.000055 | −0.000004 | 0.000020 | −0.000042 | −0.000039 | −0.000010 |
| Roll Angle | MSE | RMSE | Pitch Angle | MSE | RMSE |
|---|---|---|---|---|---|
| 0 | 0.005352 | 0.073161 | 0 | 0.002493 | 0.049934 |
| 5 | 0.003722 | 0.061010 | 5 | 0.002609 | 0.051075 |
| 10 | 0.003526 | 0.059377 | 10 | 0.002682 | 0.051790 |
| 15 | 0.004319 | 0.065719 | 15 | 0.002828 | 0.053177 |
| 20 | 0.004270 | 0.065346 | 20 | 0.002550 | 0.050495 |
| 25 | 0.003805 | 0.061685 | 25 | 0.002570 | 0.050691 |
| 30 | 0.003597 | 0.059972 | 30 | 0.002725 | 0.052202 |
| P_Ang | Pr_Up | Pr_Down | Pr | R_Ang | Pr_Up | Pr_Down | Pr |
|---|---|---|---|---|---|---|---|
| 0 | 0.000467 | 0.001133 | 0.001600 | 0 | 0.000467 | 0.001200 | 0.001667 |
| 5 | 0.000867 | 0.001200 | 0.002067 | 5 | 0.002000 | 0.000133 | 0.002133 |
| 10 | 0.000933 | 0.001733 | 0.002666 | 10 | 0.002067 | 0.000067 | 0.002133 |
| 15 | 0.000400 | 0.000533 | 0.000933 | 15 | 0.000667 | 0.000067 | 0.000733 |
| 20 | 0.001200 | 0.000933 | 0.002133 | 20 | 0.002133 | 0.000133 | 0.002267 |
| 25 | 0.001533 | 0.000933 | 0.002467 | 25 | 0.001200 | 0.000200 | 0.001400 |
| 30 | 0.000867 | 0.001000 | 0.001867 | 30 | 0.000867 | 0.000067 | 0.000933 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopecki, G.; Łagodowski, Z.A. Complementary Filter Optimal Tuning Methodology for Low-Cost Attitude and Heading Reference Systems with Statistical Analysis of Output Signal. Appl. Sci. 2025, 15, 4114. https://doi.org/10.3390/app15084114
Kopecki G, Łagodowski ZA. Complementary Filter Optimal Tuning Methodology for Low-Cost Attitude and Heading Reference Systems with Statistical Analysis of Output Signal. Applied Sciences. 2025; 15(8):4114. https://doi.org/10.3390/app15084114
Chicago/Turabian StyleKopecki, Grzegorz, and Zbigniew A. Łagodowski. 2025. "Complementary Filter Optimal Tuning Methodology for Low-Cost Attitude and Heading Reference Systems with Statistical Analysis of Output Signal" Applied Sciences 15, no. 8: 4114. https://doi.org/10.3390/app15084114
APA StyleKopecki, G., & Łagodowski, Z. A. (2025). Complementary Filter Optimal Tuning Methodology for Low-Cost Attitude and Heading Reference Systems with Statistical Analysis of Output Signal. Applied Sciences, 15(8), 4114. https://doi.org/10.3390/app15084114






