Determination of Kinematic and Dynamic Characteristics of Oscillating Conveyor Mechanism
Abstract
1. Introduction
2. Materials and Methods
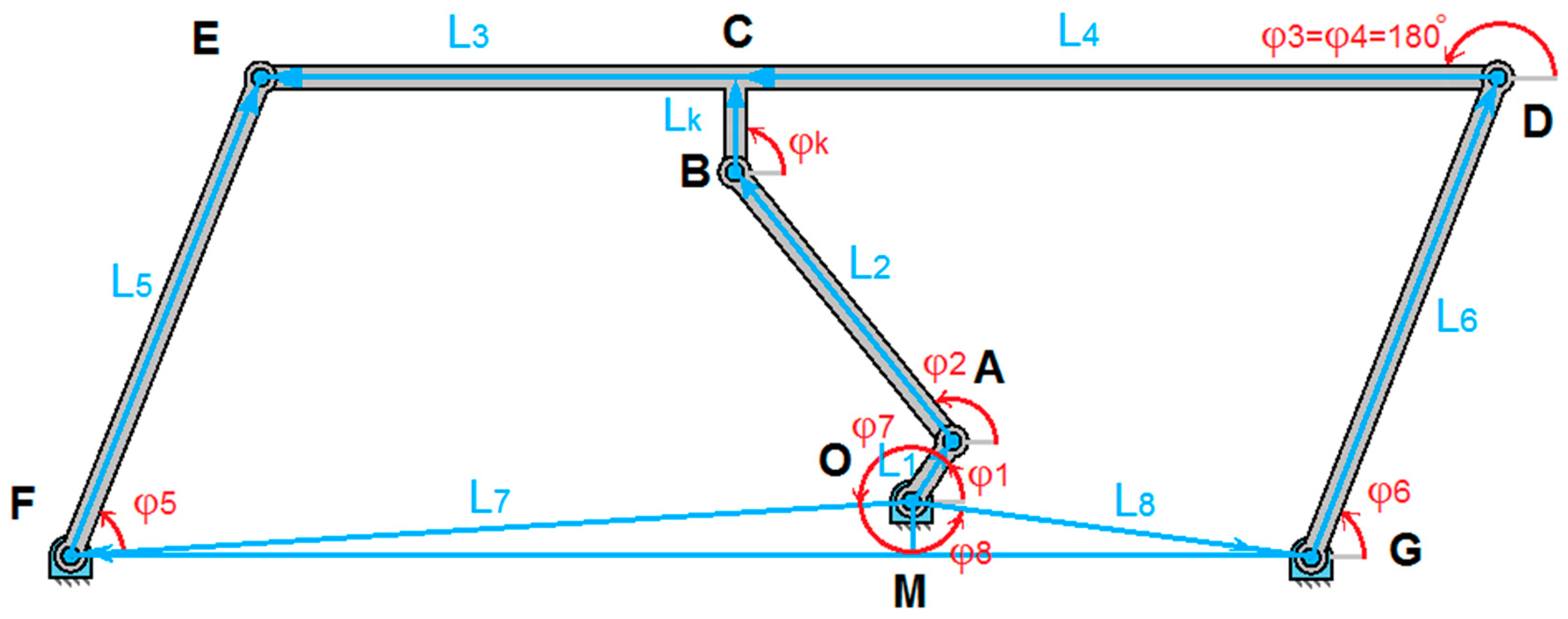
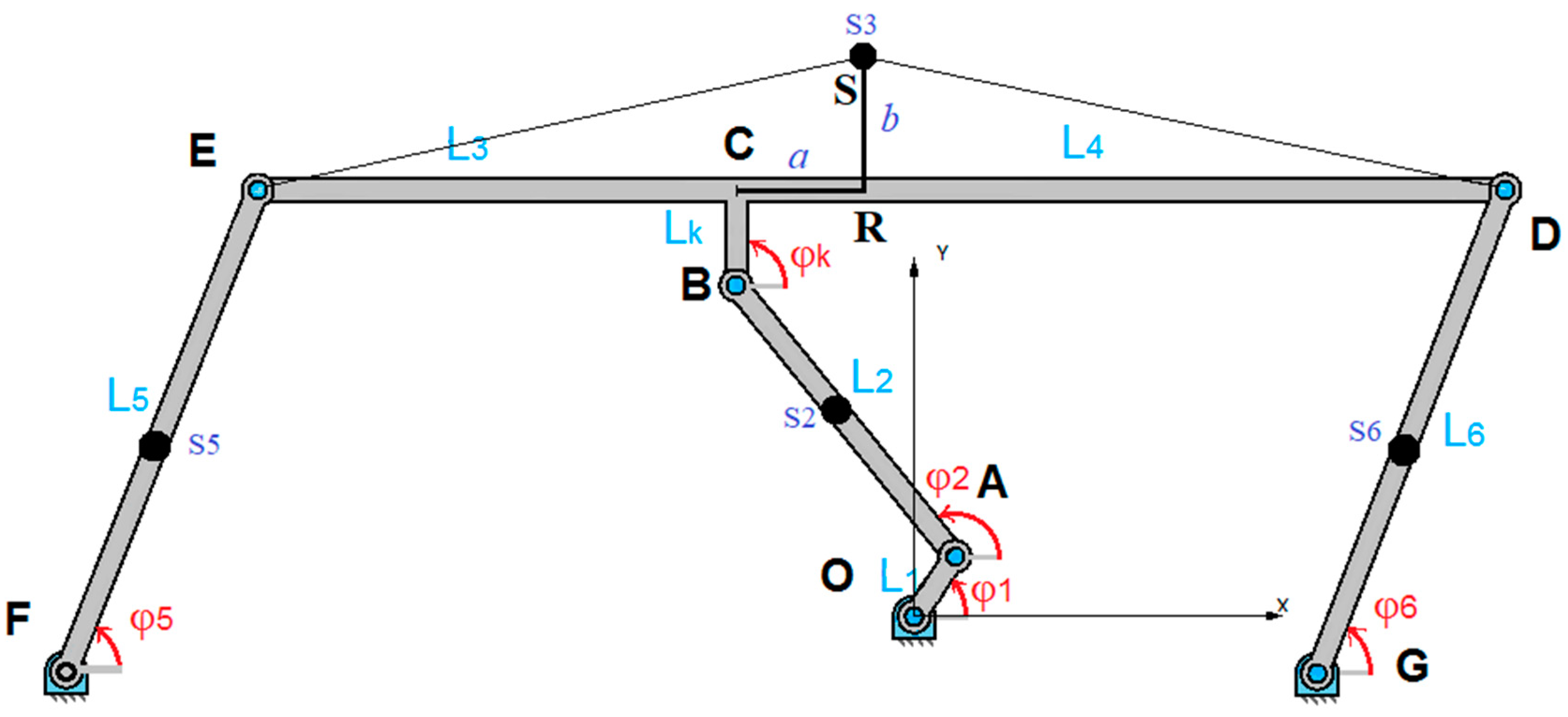
2.1. Geometric and Trigonometric Constraints
- -
- Semi-major axis (horizontal extent);
- -
- Semi-minor axis b (vertical extent);
- -
- Offset determined by and , which places the ellipse at a specific location in the coordinate system.
2.2. Differential Equations of Motion of the Joints of an Oscillating Conveyor Mechanism
2.3. Solving the Differential Equation of an Oscillating Conveyor Mechanism Using the Approximate Calculation Method
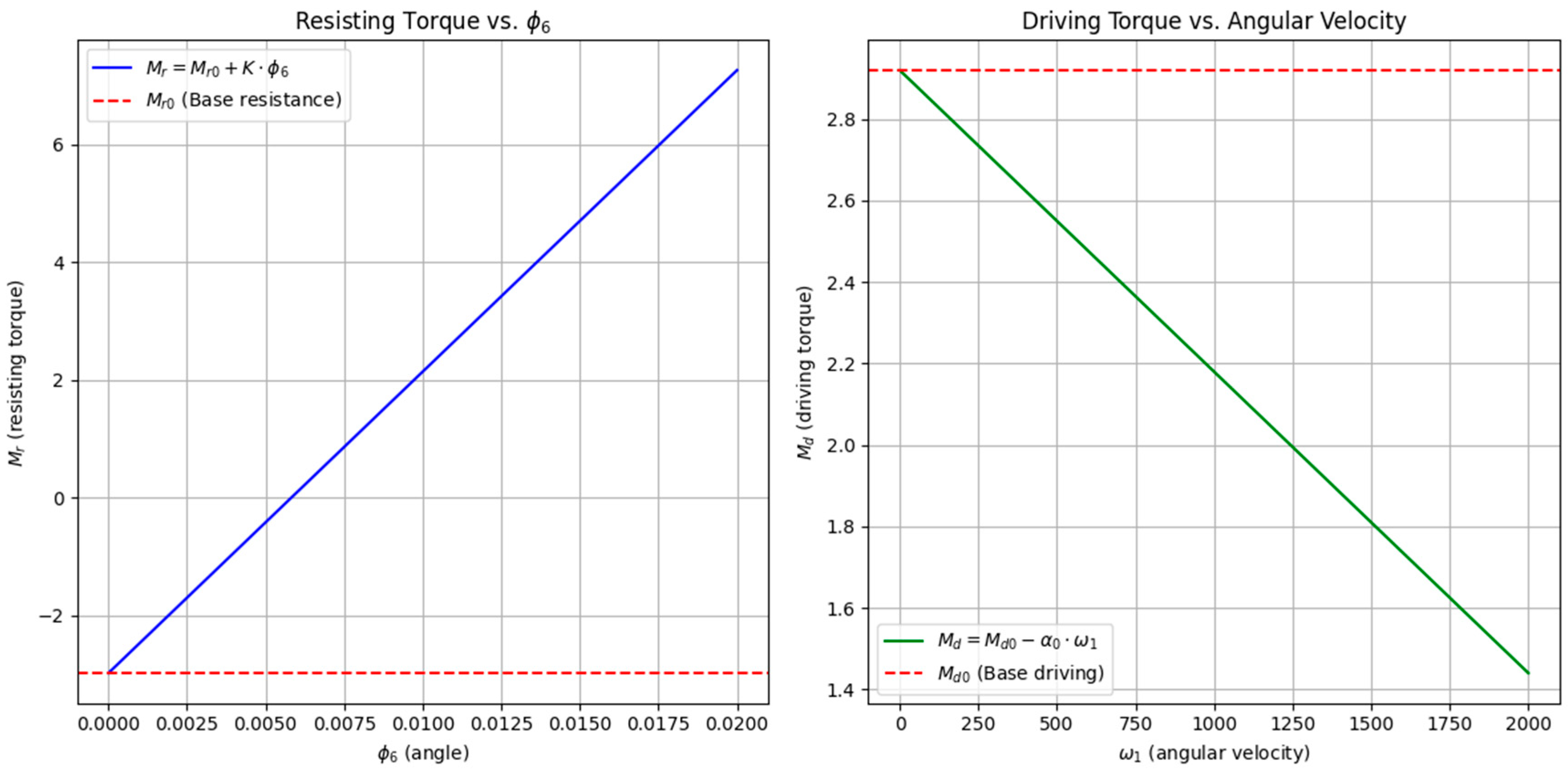
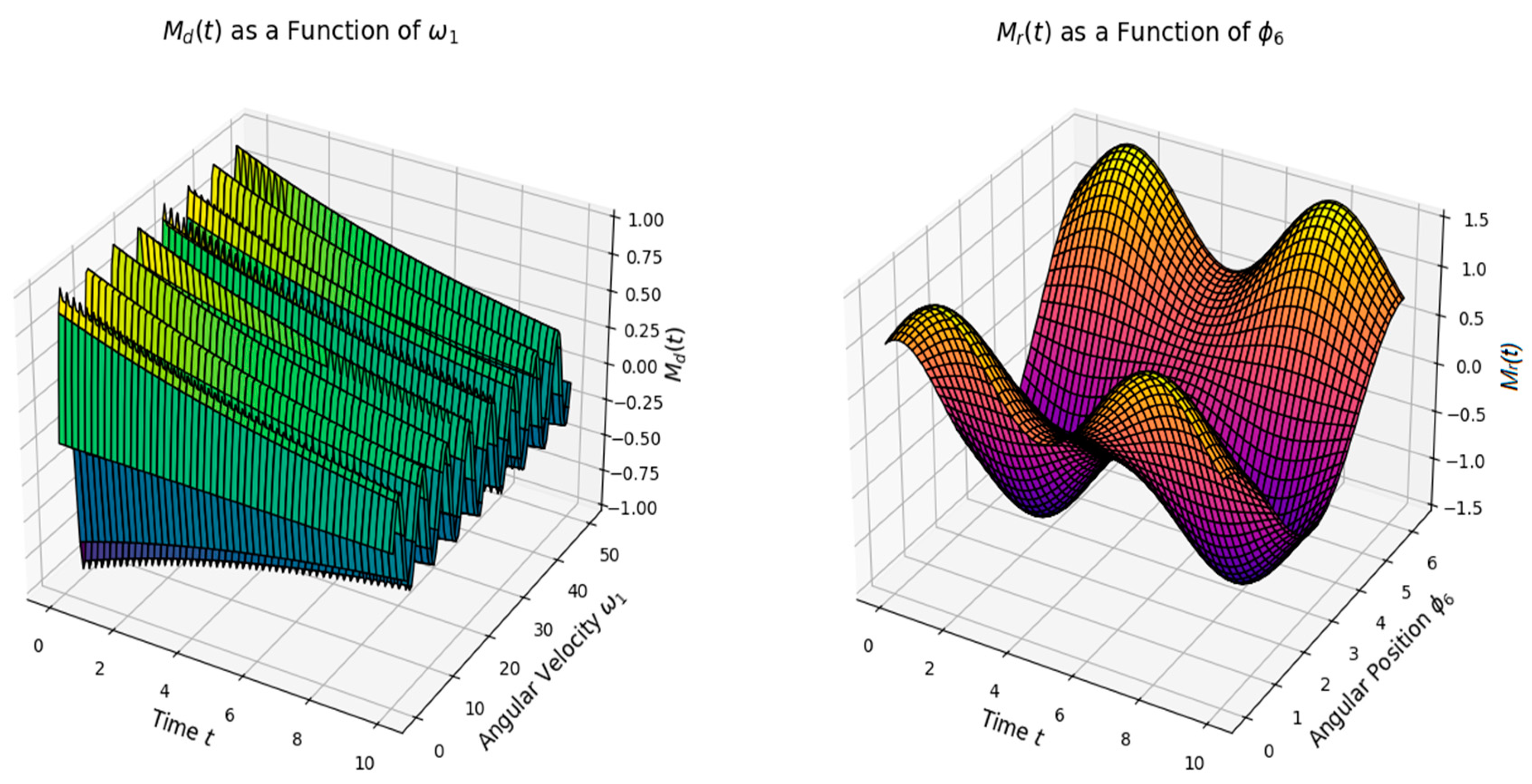
- Influence of driving torque (Md) on system behavior
- -
- higher Md values lead to increased energy input, causing larger oscillation amplitudes and potential instability;
- -
- higher torque may shift the system’s natural frequency, leading to resonance risks.
- -
- if Md is too low, the conveyor may experience damped oscillations, limiting material transport efficiency.
- 2.
- Effect of resistance coefficient (K) on damping and stability
- -
- a higher K results in faster energy dissipation, reducing oscillation persistence;
- -
- if K is too low, oscillations may persist longer than desired, potentially affecting material transport consistency;
- -
- excessively high K values could lead to overdamping, preventing efficient oscillatory motion.
- 3.
- Influence of moment of inertia on system response
- -
- higher reduces acceleration, slowing oscillation growth;
- -
- lower increases system reactivity, which may lead to excessive motion variations;
- -
- higher inertia requires more energy to maintain oscillations.
3. Methodology
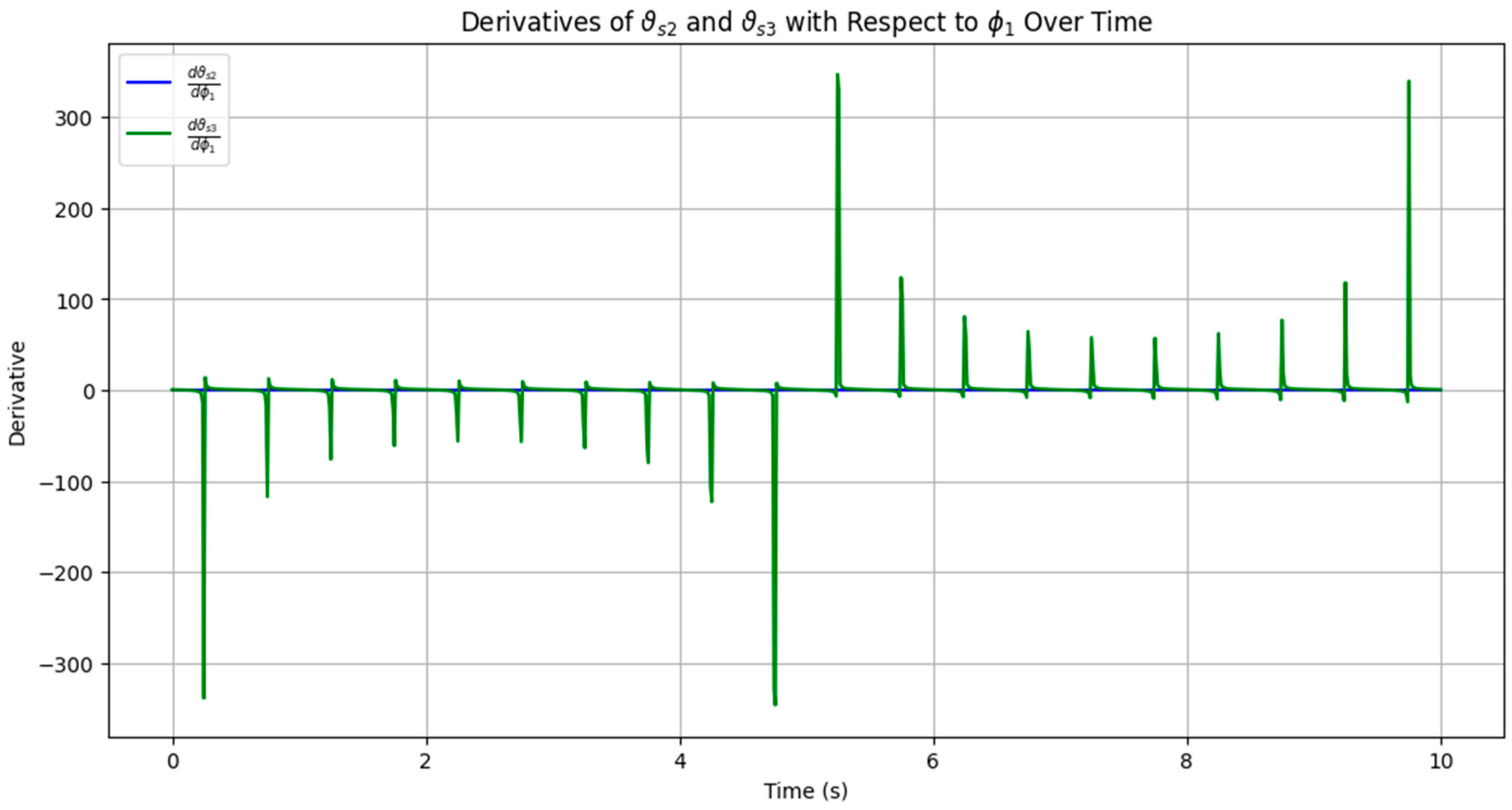
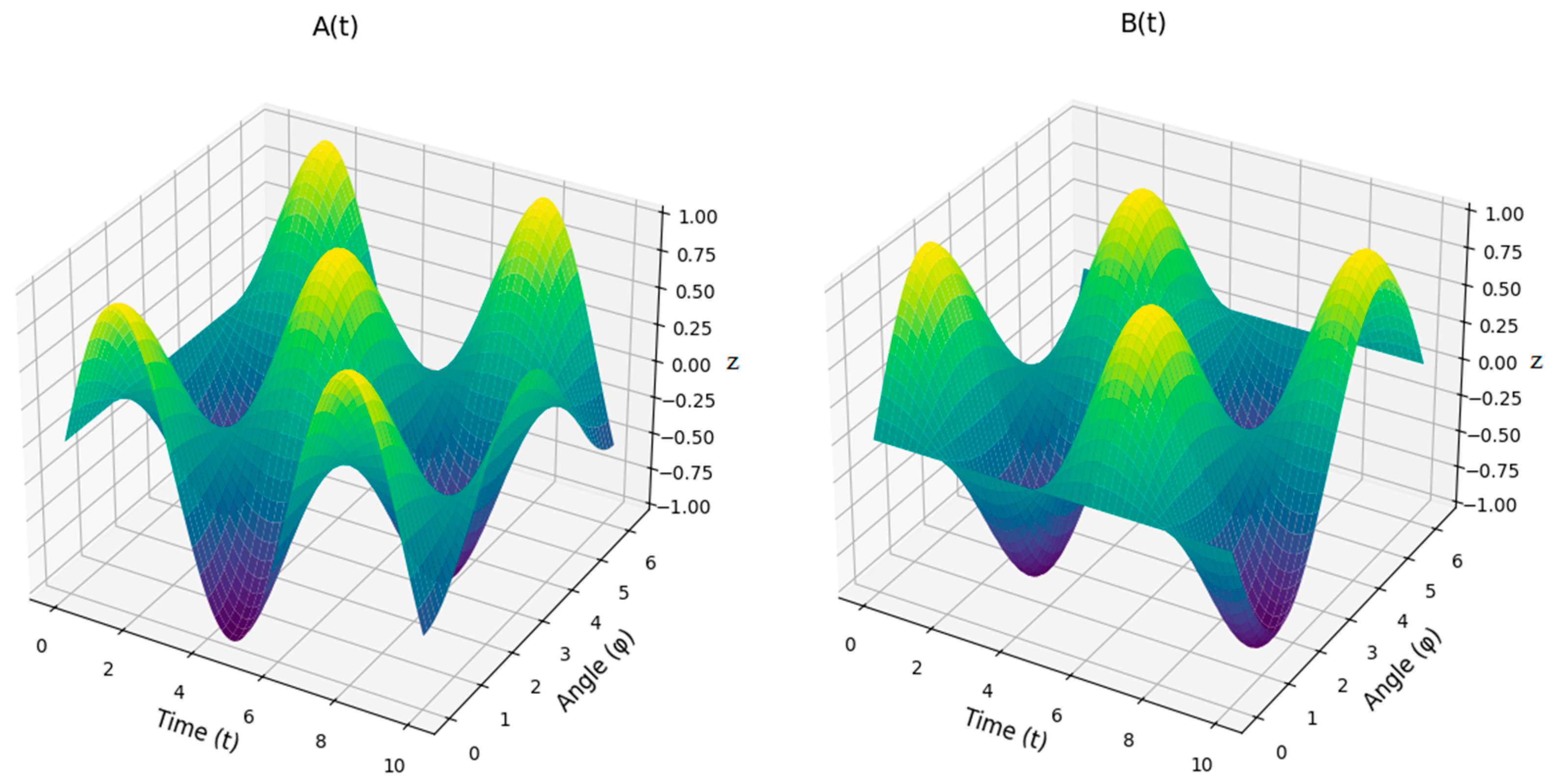
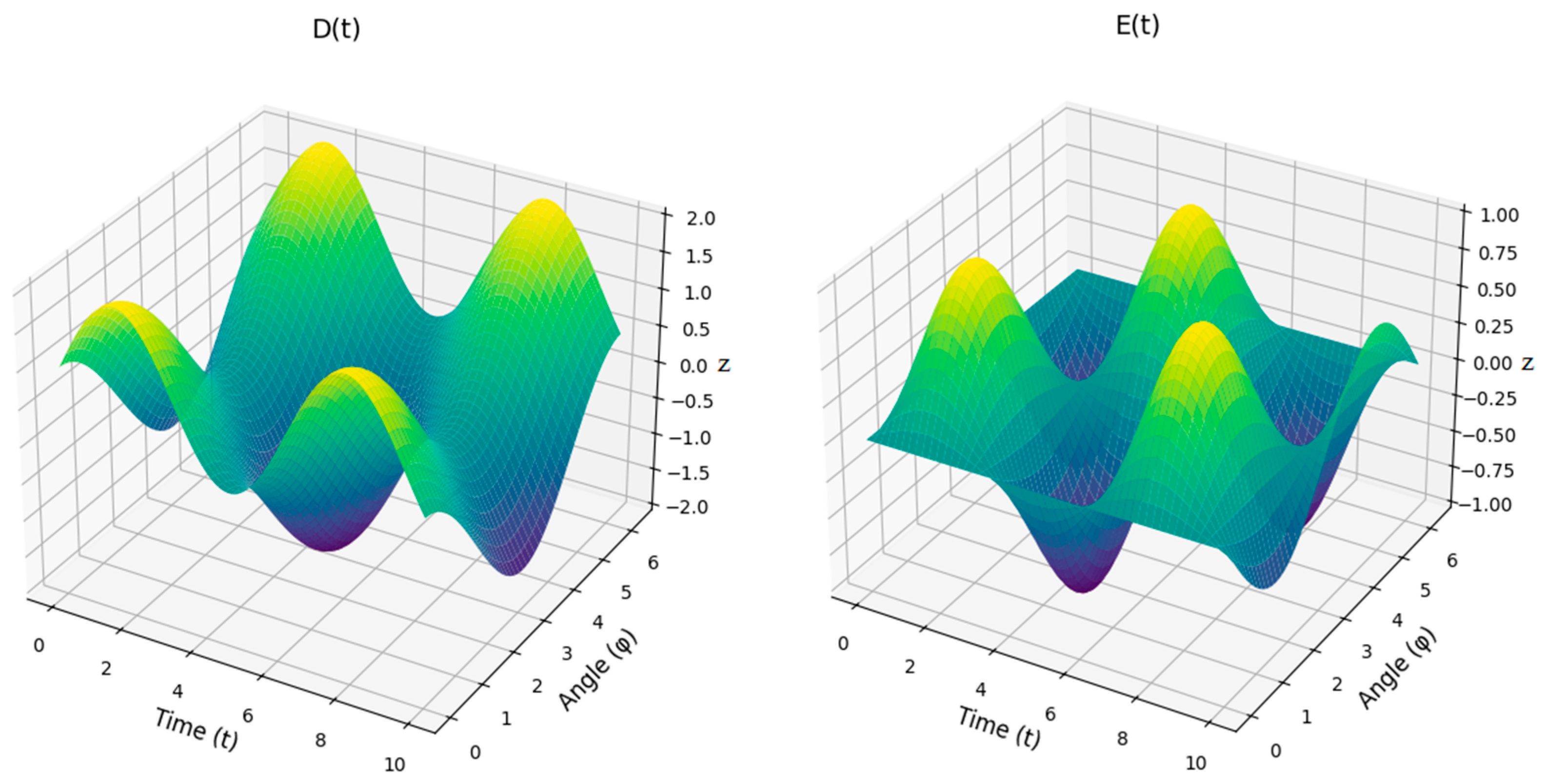
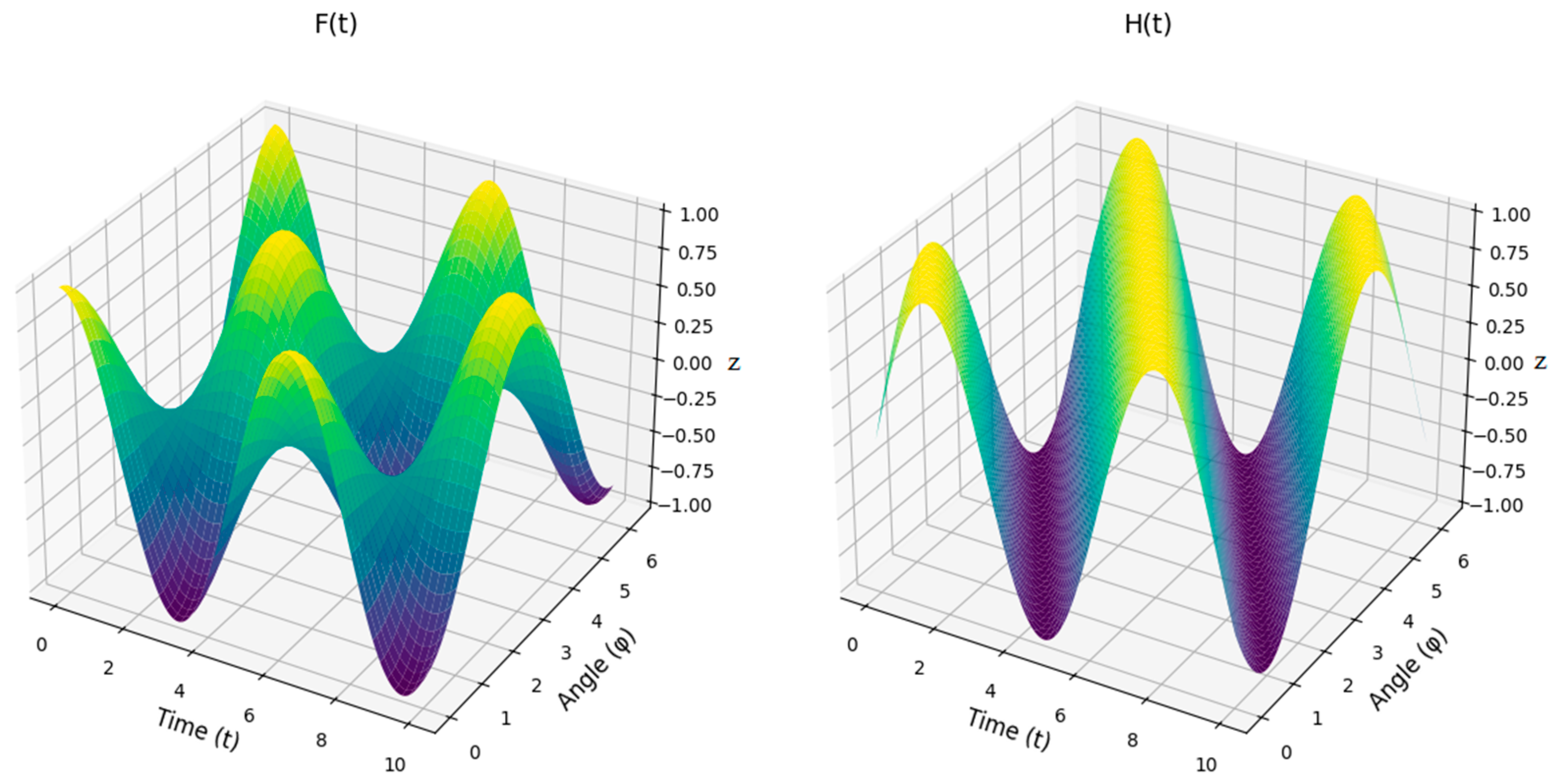
- Kinematic analysis. The kinematic analysis focused on describing the motion of the system’s components without considering the forces or torques causing the motion: (a) System modeling—the conveyor mechanism was modeled as a system of interconnected rigid links with specified lengths (, , …) and joints. Angular displacements () were used to describe the positions of the links relative to reference points. (b) Geometric and trigonometric relationships—constraints between the links were expressed as equations involving sines and cosines of the angular variables. Relationships such as were used to ensure consistency in the system’s geometry. (c) Velocities and accelerations—the angular velocities and angular accelerations were derived using time differentiation of the position equations. The motion constraints were used to compute velocities and accelerations for all components. (d) Visualization—3D plots of angular displacement, velocity, and acceleration were generated to illustrate the motion behavior over time.
- Dynamic analysis. The dynamic analysis incorporated the forces and torques acting on the system to evaluate its response under load. (a) Derivation of equations of motion—Newton’s Second Law and the principle of virtual work were applied to derive equations governing the system’s dynamics. Inertia terms were computed using the mass distribution and geometry of the system. (b) Force and torque calculations—driving torques and resisting torques were modeled as functions of angular velocity and angular displacement . External factors, such as damping and load resistance, were incorporated into the dynamic equations. (c) Nonlinear effects—nonlinear terms, such as those involving products of angular velocities and displacements, were explicitly included to account for real-world interactions. (d) System stability—stability conditions were analyzed by evaluating the balance of forces and torques during operation. Parameters like stiffness K and base moments were studied to ensure system stability.
- Numerical approximation. The numerical approximation was used to solve the nonlinear differential equations derived in the dynamic analysis. (a) Differential equation formulation—the equations were expressed in the standard form:where , and are time-dependent coefficients. (b) Discretization—Euler’s method was employed to approximate the derivatives using finite time steps h:angular displacement was updated iteratively:
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Gurskyi, V.; Korendiy, V.; Krot, P.; Dyshev, O. Determination of kinematic and dynamic characteristics of a reversible vibratory conveyor with an electromagnetic drive. Vibroeng. Procedia 2024, 55, 138–144. [Google Scholar] [CrossRef]
- Korendiy, V.; Kachur, O.; Dmyterko, P. Kinematic analysis of an oscillatory system of a shaking conveyor-separator. In Advanced Manufacturing Processes III; Springer International Publishing: Cham, Switzerland, 2022; pp. 592–601. [Google Scholar] [CrossRef]
- Gurskyi, V.; Korendiy, V.; Krot, P.; Zimroz, R.; Kachur, O.; Maherus, N. On the dynamics of an enhanced coaxial inertial exciter for vibratory machines. Machines 2023, 11, 97. [Google Scholar] [CrossRef]
- Shah, K.P. Construction, Working and Maintenance of Electric Vibrators and Vibrating Screens. Available online: https://practicalmaintenance.net/wp-content/uploads/Construction-Working-and-Maintenance-of-Vibrators-and-Vibrating-Screens.pdf (accessed on 8 December 2022).
- Cieplok, G.; Wójcik, K. Conditions for self-synchronization of inertial vibrators of vibratory conveyors in general motion. J. Theor. Appl. Mech. 2020, 58, 513–524. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.X.; Nguyen, K.L.; Dinh, G.N. Study of the dynamics and analysis of the effect of the position of the vibration motor to the oscillation of vibrating screen. J. Phys. Conf. Ser. 2019, 1384, 012035. [Google Scholar] [CrossRef]
- Nazarenko, I.; Gaidaichuk, V.; Dedov, O.; Diachenko, O. Investigation of vibration machine movement with a multimode oscillation spectrum. East.-Eur. J. Enterp. Technol. 2017, 6, 28–36. [Google Scholar] [CrossRef][Green Version]
- Chen, Z.; Tong, X.; Li, Z. Numerical investigation on the sieving performance of elliptical vibrating screen. Processes 2020, 8, 1151. [Google Scholar] [CrossRef]
- Gursky, V.; Krot, P.; Korendiy, V.; Zimroz, R. Dynamic analysis of an enhanced multi-frequency inertial exciter for industrial vibrating machines. Machines 2022, 10, 130. [Google Scholar] [CrossRef]
- Gursky, V.; Kuzio, I.; Krot, P.; Zimroz, R. Energy-saving inertial drive for dual-frequency excitation of vibrating machines. Energies 2021, 14, 71. [Google Scholar] [CrossRef]
- Yaroshevich, N.; Puts, V.; Yaroshevich, T.; Herasymchuk, O. Slow oscillations in systems with inertial vibration exciters. Vibroeng. Procedia 2020, 32, 20–25. [Google Scholar] [CrossRef]
- Yaroshevich, N.; Yaroshevych, O.; Lyshuk, V. Drive dynamics of vibratory machines with inertia excitation. In Vibration Engineering and Technology of Machinery; Balthazar, J.M., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 37–47. [Google Scholar]
- Chen, B.; Yan, J.; Yin, Z.; Tamma, K. A new study on dynamic adjustment of vibration direction angle for dual-motor-driven vibrating screen. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 186–196. [Google Scholar] [CrossRef]
- Cieplok, G. Verification of the nomogram for amplitude determination of resonance vibrations in the run-down phase of a vibratory machine. J. Theor. Appl. Mech. 2009, 47, 295–306. [Google Scholar]
- Michalczyk, J.; Cieplok, G. Disturbances in self-synchronisation of vibrators in vibratory machines. Arch. Min. Sci. 2014, 59, 225–237. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, Q.; Gong, Z.; Wen, B. Synchronization of two self-synchronous vibrating machines on an isolation frame. Shock. Vib. 2011, 55, 73–90. [Google Scholar] [CrossRef]
- Zhauyt, A. The substantiating of the dynamic parameters of the shaking conveyor mechanism. Vibroeng. Procedia 2015, 5, 15–20. [Google Scholar]
- Wyk, J.; Snyman, A.; Heyns, S. Optimization of a vibratory conveyor for reduced support reaction force. N&O J. 1994, 1, 12–17. [Google Scholar]
- Andrea, V.; Nicolae, U.; Loana, M. Contribution to the optimization of relative motion on a vibrating conveyor. ACTA Tech. Napoc. 2012, 2, 519–522. [Google Scholar]
- Chu, Y.; Li, C. Helical vibratory conveyors for bulk materials. Bulk Solid Handl. 1987, 1, 103–112. [Google Scholar]
- Sloot, E.M.; Kruyt, N.P. Theoretical and experimental study of the conveyance of granular materials by inclined vibratory conveyors. Powder Technol. 1996, 87, 203–210. [Google Scholar] [CrossRef]
- Despotovic, Z.; Stojiljkovic, Z. A realization AC/DC transistor power converter for driving electromagnetic vibratory conveyors. In Proceedings of the V Symposium of Industrial Electronics-INDEL, Banja, Luka, 11–13 September 2004; Volume T2A, pp. 34–40. [Google Scholar]
- Despotovic, Z.; Stojiljkovic, Z. Power converter control circuits for two-mass vibratory conveying system with electromagnetic drive: Simulations and experimental results. IEEE Trans. Ind. Electron. 2007, 54, 453–466. [Google Scholar] [CrossRef]
- Winkler, G. Analysing the vibrating conveyor. Int. J. Mech. 1978, 20, 561–570. [Google Scholar] [CrossRef]
- Stoicovici, D.I. Movement regimes and determining the main parameters of oscillating and vibrating conveyors. In Environmental and Human Impact of Buildings; Springer: Berlin/Heidelberg, Germany, 2021; pp. 149–182. [Google Scholar] [CrossRef]

| Step | Description |
|---|---|
| Inputs | , N, h |
| Increment n | Set n: = n + 1 |
| Compute A(tn) | Compute A(tn) |
| Compute B(tn) | Compute B(tn) |
| Compute D(tn) | Compute D(tn) |
| Compute E(tn) | Compute E(tn) |
| Compute F(tn) | Compute F(tn) |
| Compute H(tn) | Compute H(tn) |
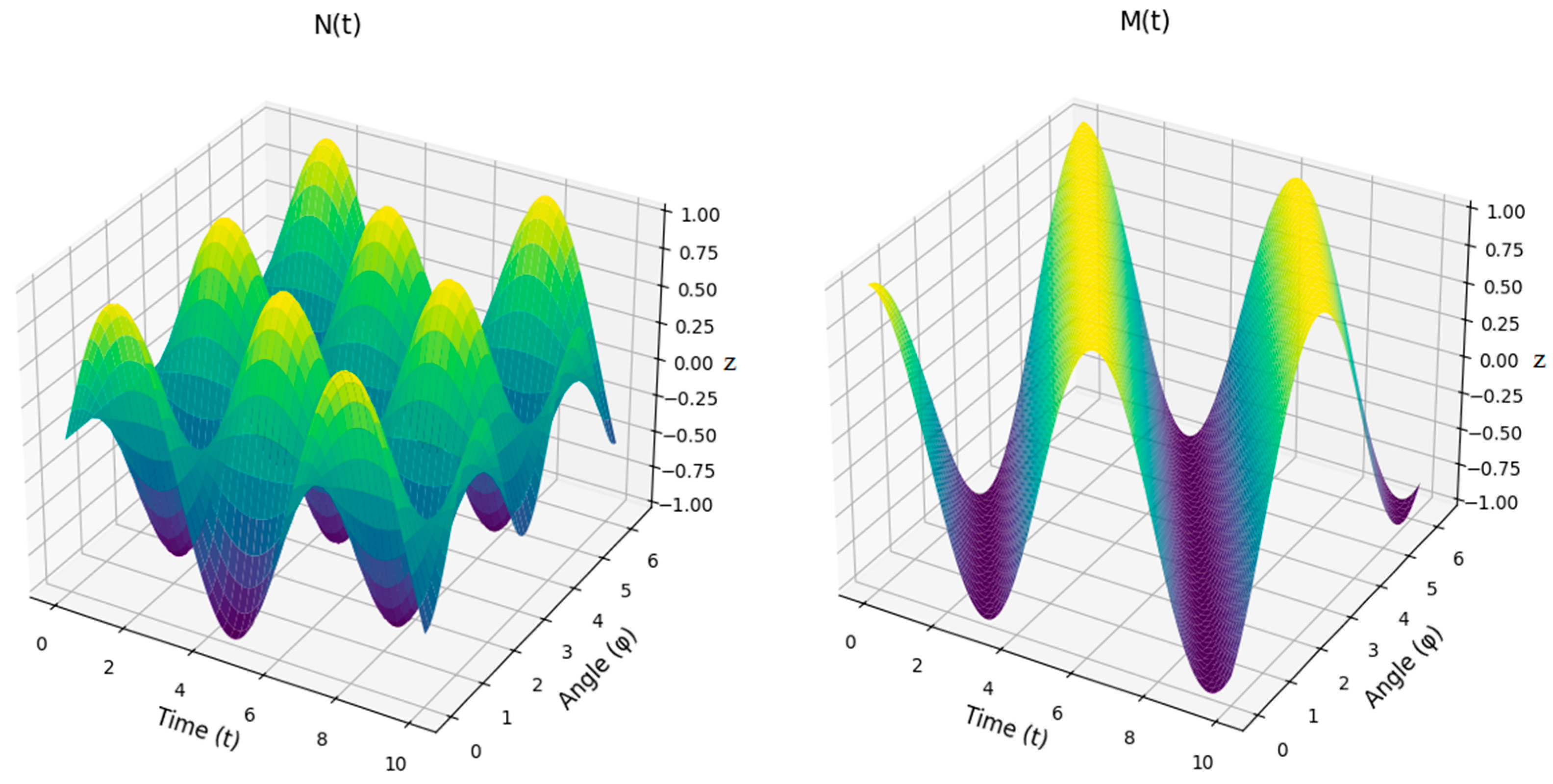
| Compute N(tn) | Compute N(tn) |
| Compute M(tn) | Compute M(tn) |
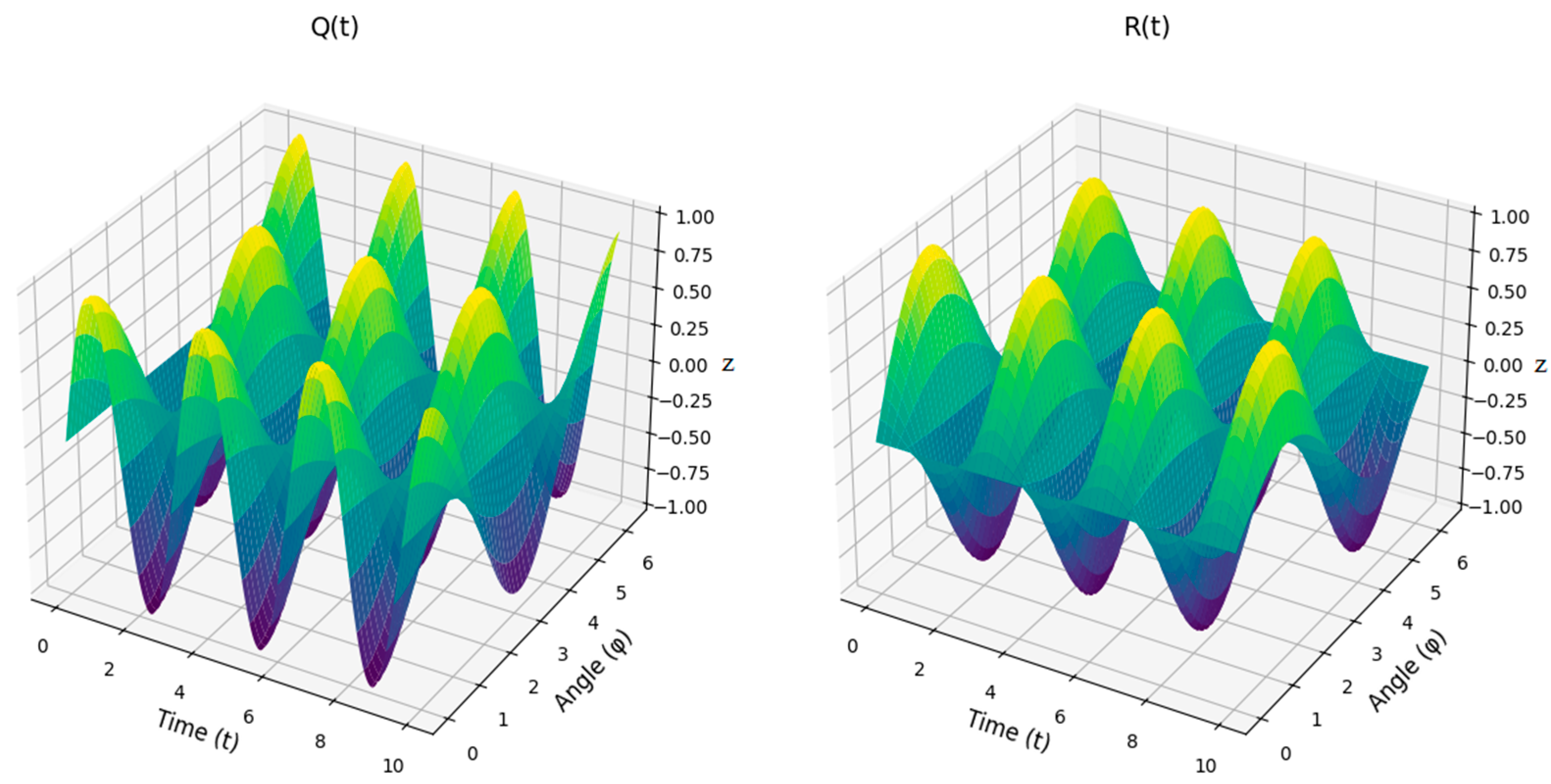
| Compute Q(tn) | Compute Q(tn) |
| Compute R(tn) | Compute R(tn) |
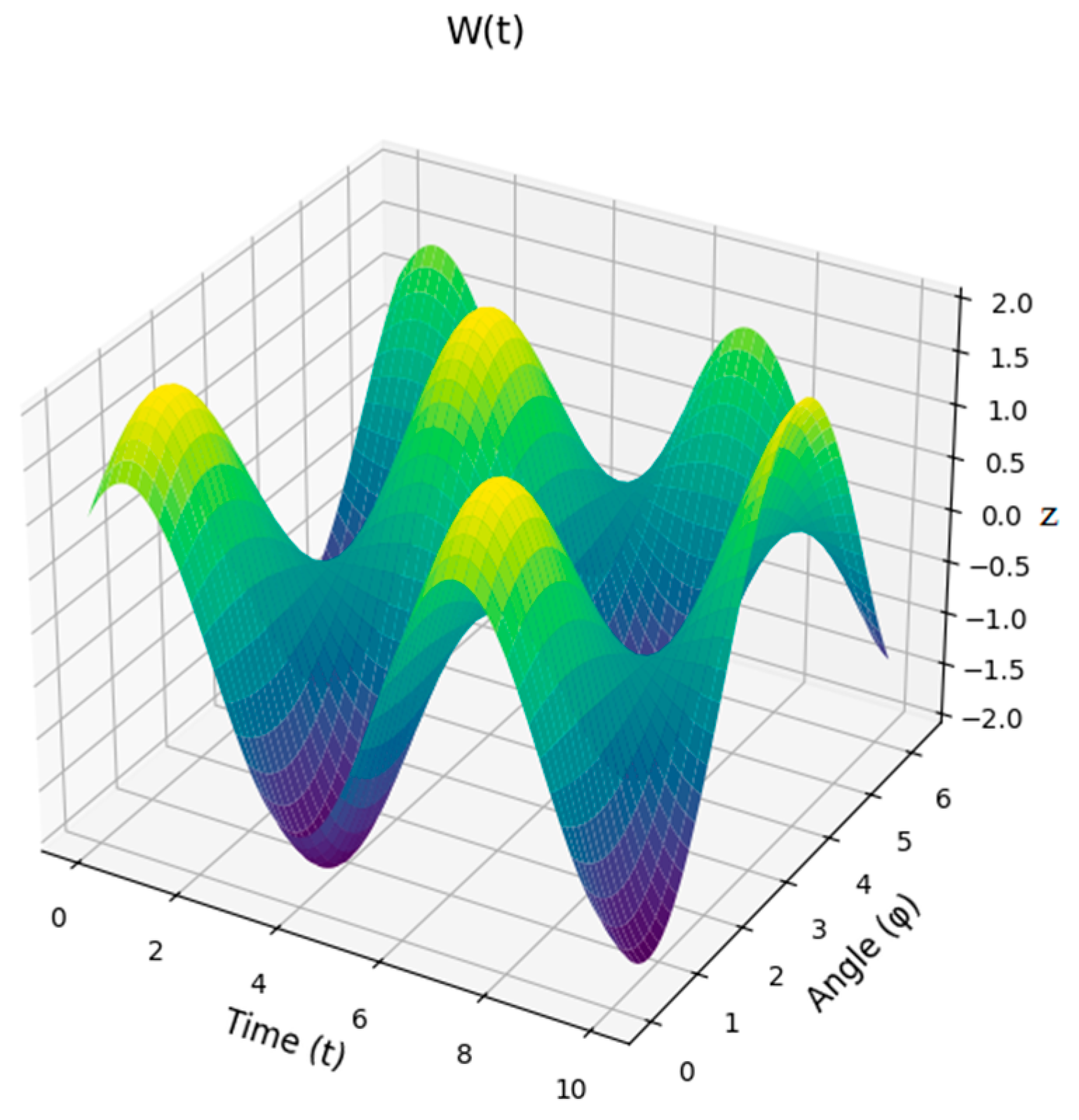
| Compute W(tn) | Compute W(tn) |
| ) | |
| Check if n < N | Check if n < N |
| and Repeat | and Repeat |
| End | End of process |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhauyt, A.; Alipbayev, K.; Aden, A.; Orazaliyeva, A.; Bikhozhayeva, G. Determination of Kinematic and Dynamic Characteristics of Oscillating Conveyor Mechanism. Appl. Sci. 2025, 15, 1676. https://doi.org/10.3390/app15031676
Zhauyt A, Alipbayev K, Aden A, Orazaliyeva A, Bikhozhayeva G. Determination of Kinematic and Dynamic Characteristics of Oscillating Conveyor Mechanism. Applied Sciences. 2025; 15(3):1676. https://doi.org/10.3390/app15031676
Chicago/Turabian StyleZhauyt, Algazy, Kuanysh Alipbayev, Alisher Aden, Aray Orazaliyeva, and Gulmira Bikhozhayeva. 2025. "Determination of Kinematic and Dynamic Characteristics of Oscillating Conveyor Mechanism" Applied Sciences 15, no. 3: 1676. https://doi.org/10.3390/app15031676
APA StyleZhauyt, A., Alipbayev, K., Aden, A., Orazaliyeva, A., & Bikhozhayeva, G. (2025). Determination of Kinematic and Dynamic Characteristics of Oscillating Conveyor Mechanism. Applied Sciences, 15(3), 1676. https://doi.org/10.3390/app15031676







