ROLQ-TEE: Revocable and Privacy-Preserving Optimal Location Query Based on Trusted Execution Environment
Abstract
1. Introduction
- First, we design a query architecture for sensitive location data based on the TEE, ensuring that no information of either customer, apart from the intersection, is disclosed, and that the intersection results are not exposed to the cloud service provider. Meanwhile, the TEE leverages its features to guarantee the confidentiality and integrity of both data and code within its enclave.
- Second, we propose a revocable and privacy-preserving optimal location query scheme based on the above architecture (ROLQ-TEE), which not only enables the data users to obtain an optimal location of the new facility securely but also realizes the revocability of the query permission of the data users.
- Third, we introduce a practical scenario where the data users (i.e., banks) are required to perform any of the three optimal location query operations (namely RNN Query (RNNQ), Average Distance Query (AVGQ), and Maximum Distance Query (MAXQ)) we designed on the cloud server (i.e., cloud service provider) according to their own needs within a specified time; otherwise, the data user’s query permission will be revoked once the specified time has passed.
- Finally, we conduct a security analysis and performance evaluation of the optimal location query protocols. Subsequently, we demonstrate the security of the ROLQ-TEE scheme, illustrating that ROLQ-TEE scheme effectively preserves the privacy of both the location data owner and the requesting user. Finally, we theoretically analyze the performance and provide the experimental results.
2. Related Work
2.1. Optimal Location Query
2.2. Privacy-Preserving Location-Based Query
3. Preliminaries
3.1. Bilinear Pairings
- Bilinearity: ∈ and ∈, .
- Non-degeneracy: , where 1 is an unit of .
- Computability: , there exists an efficient algorithm to compute .
3.2. Discrete Logarithm Problem
3.3. Collision-Resistant Hash Function
- The input X can be of arbitrary length, while the output has a fixed length of n bits (with ).
- The hash function must be one-way, meaning that, given a Y in the range of H, it is hard to find a message X such that . Furthermore, given X and , it should be challenging to find another message such that .
- The hash function must be collision-resistant, meaning that it is difficult to find two distinct messages that produce the same hash result.
3.4. NN and RNN Query
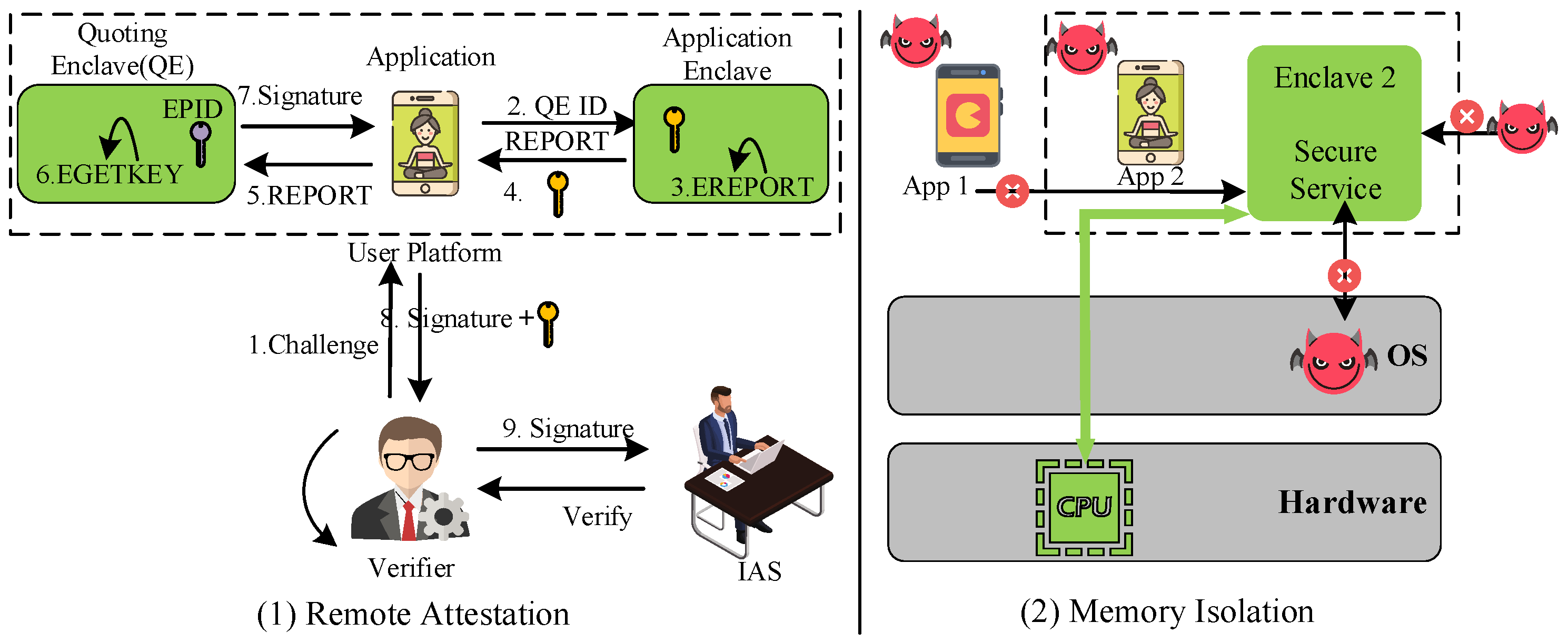
3.5. Trusted Execution Environment
- Remote attestation: Remote attestation offers cryptographic verification to ensure that the enclave operates securely on the cloud server. When the enclave is created, a remote attestation signature is generated with the assistance of the SGX component, which is known as quote enclave (QE), to ensure the security of the enclave. Additionally, a secure channel is established for secret sharing between the enclave and the client using Elliptic-curve Diffie–Hellman (ECDH) [33].
- Memory isolation: When a project runs on an SGX platform, the project is divided into an untrusted (or semi-trusted) storage area and a trusted isolation area, called an enclave. The enclave is an independent physical RAM block where the code and data contained within it are protected and inaccessible to privileged software, operating systems, hypervisors, and system firmware. When the SGX program is suspended or closed, the encrypted sensitive data separated from the enclave are stored in an untrusted area. When the SGX program is running, these data can only be accessed within the enclave through a dedicated interface designed for decryption and integrity checking.
4. ROLQ-TEE Scheme
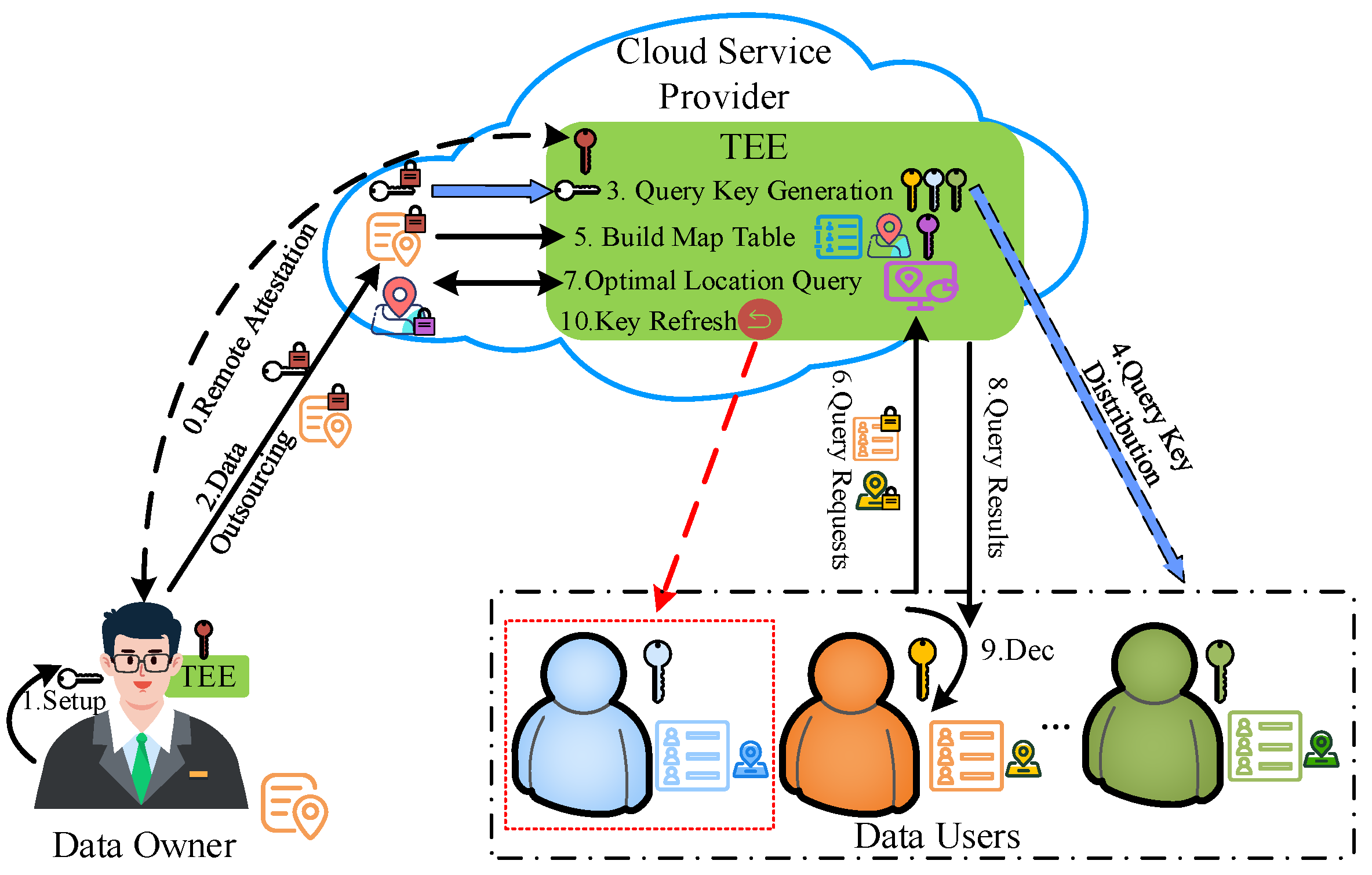
4.1. System Architecture
- Data owner (): The data owner is mainly responsible for system setup, data encryption and ciphertext uploading. In addition, the establishes the secure channel through remote attestation with the TEE of the and generates the session key to transfer the secret key and data.
- Cloud service provider (): This is mainly divided into two areas: one is the TEE area, and the other is the storage area. The TEE is mainly responsible for query key generation, map table construction, optimal location query, and query key refresh. The storage area is mainly responsible for storing encrypted data.
- Data users (): The is mainly responsible for providing a candidate set = and generating query requests for the candidate set. Additionally, the is also responsible for decrypting the optimal location query results.
4.2. Threat Model
- Data privacy: Data privacy means that the outsourced location data, query tokens, customer lists, and query results cannot be broken by the adversary.
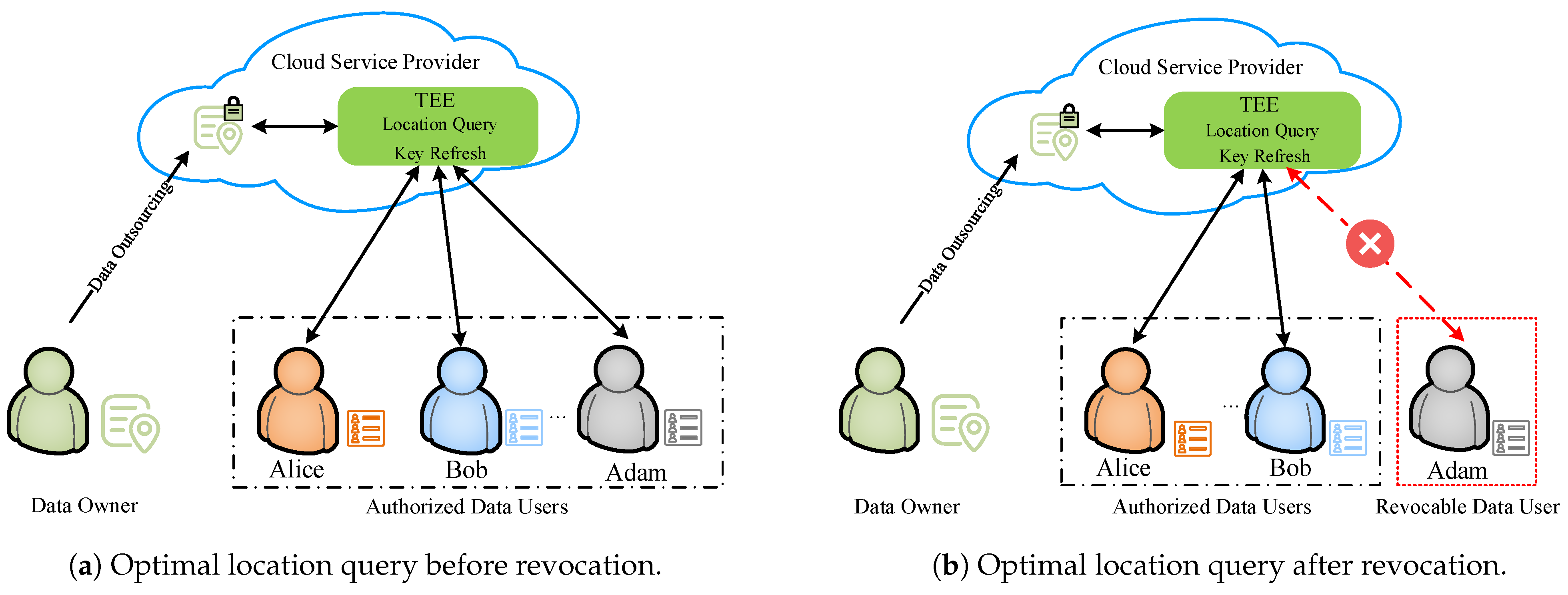
- Revocation security: The data users whose access has been revoked are unable to initiate new optimal location queries and are also prevented from decrypting any ciphertext data associated with subsequent queries.
- Data anonymity: The data users cannot utilize the obtained information to infer the locations stored in the database of the data owner, other than the intersection location data.
4.3. Detailed Construction
- →. The algorithm is run by the . It takes as input a security parameter . It outputs the master secret key and system master public key .
- The chooses a bilinear map →, where and are two cyclic groups with order q. Then, the randomly chooses a generator g of and a generator of , respectively. After that, the chooses two different collision-resistant hash functions, :→ and :→, randomly. Additionally, the chooses an pseudo-random function F.
- The chooses some random values , and computes h = and = , 1 ≤ ≤ n.
- The executes remote attestation with the TEE of the to generate the session key . Meanwhile, both parties establish a secure channel.
- Finally, the publishes as the system parameters, and sends the encrypted = to the TEE through the secure channel.
- →. The algorithm is run by the . It takes as input the data , the master system key , the initial vector , the additional authentication data , and the session key . It outputs the ciphertexts and , and the encrypted tags and , where .
- →. The KeyGen algorithm is run by the TEE. It takes as input the encrypted master secret key and the master public key . It outputs the query key , a storage key , a data user list , an empty revocation list , and an timestamp list .
- First, the TEE decrypts to and randomly generates a unique identifier for each registered data user . Meanwhile, the TEE also generates a unique identifier for the .
- Second, the TEE creates a timestamp and sets a counter , where . After that, the TEE computes the corresponding query key , where ·, , and .
- Next, the TEE computes the storage key for the and uses it for data encryption.
- Finally, the TEE distributes to the through a secure channel, and distributes to the corresponding through the secure sockets layer (SSL) protocol.
- →. The algorithm is run by the TEE. It takes as input the session key , the ciphertext , and the secret key . It outputs the map table and encrypted location data. The detailed process is as follows:
- First, the TEE decrypts the ciphertext to plaintext and splits the to obtain the customer identity and corresponding location information , .
- Second, the TEE computes , and calls the algorithm to generate the encrypted location data ciphertext ; that is, .
- Finally, the TEE constructs a map table and stores the ciphertext to the store area of the .
- →. The algorithm is run by the . It takes as input a list of candidate facility locations , the query key , and the private customer set of the data user . It outputs an encrypted candidate set and an encrypted customer list set . The detailed steps are as in Algorithm 1:
- The chooses a random value and computes the encrypted candidate set , where , , , and .
- Next, the computes the encrypted customer list , where , , , , and .
- Finally, the sends the encrypted query token to the .
- →. The algorithm is run by the TEE. It takes as input the encrypted location data set , the encrypted query token , the query key , the secret key , the map table , and public system parameters . It outputs an encrypted optimal location query result . The detailed steps are as in Algorithm 2:
- The TEE decrypts the to the using Equation (3), as shown below, and obtains a list of the candidate facility locations .
- According to the decryption method in Step 1, TEE decrypts the encrypted customer list to .
- Meanwhile, the TEE compares whether and are equal using Equation (4), as shown below. If equal, the TEE loads , corresponding to , and decrypts it to obtain the location data . Otherwise, TEE continues to match the next token.
- Subsequently, the TEE loads the encrypted location data of and decrypts the to the . Next, the TEE obtains , corresponding to the intersection of the customers of the and the .
- The TEE uses the and the to compute the ranking result of the optimal location query (RNNQ/AVGQ/MAXQ) according to the Euclidean distance (Section 3.1) and Definition 1 (or Definition 2 or Definition 3).
- The TEE encrypts the optimal location query results to using , and sends the to the .
- Dec()→. The algorithm is run by the . It takes as input the query results and the query key . It outputs the ranking results , as follows:
- →. The algorithm is run by the TEE. It takes as input a set of revoked identities , the master secret key , and the system master public key . It outputs the updated query keys , an updated revocation list , an updated data user list , and an updated timestamp list .
- Upon the expiration of the subscription period, the TEE first identifies the user identities to be revoked in the data user list, and obtains an updated revocation list and an updated request user list , where .
- Then, the TEE recreates the timestamp onto the original list , and obtains a new timestamp list .
- TEE randomly chooses a for the corresponding unrevoked user set -, and recomputes · and , .
- Finally, the TEE sends the to the corresponding unrevoked data user .
| Algorithm 1: GenToken Algorithm |
| Input: The candidate facility list , the query key , and the customer set |
| Output: The encrypted candidate set and the encrypted customer list set |
| 1: Select a random value ; |
| 2: Construct the facility candidate set ; |
| 3: Compute the encrypted candidate set , where , |
| , and ; |
| 4: Select a random value ; |
| 5: Construct the customer list ; |
| 6: Compute the encrypted customer list set , where , |
| , and ; |
| 7: Generate the query token and send to the . |
| Algorithm 2: OptLocQue Algorithm |
| Input: The encrypted location data set , the encrypted query token , the query key , the secret key |
| , the map table , and the public system parameters |
| Output: The encrypted optimal query result |
| 1: Load the encrypted query token ; |
| 2: Decrypt to ; |
| 3: Decrypt to ; |
| 4: for do |
| 5: for do |
| 6: if |
| 7: Load the of and decrypt to ; |
| 8: Obtain the location intersection set ; |
| 9: for do |
| 10: foreach in do |
| 11: Compute the euclidean distance between and ; |
| 12: Compute accumulated value ; |
| 13: Select the query type, namely RNNQ, AVGQ, or MAXQ; |
| 14: Obtain the optimal query result ; |
| 15: Select a random value ; |
| 16: Compute encrypted optimal query result |
| ; |
| 17: Send the to the . |
5. Security Analysis
6. Performance Evaluation
6.1. Complexity Analysis
6.2. Memory Usage
6.3. Communication
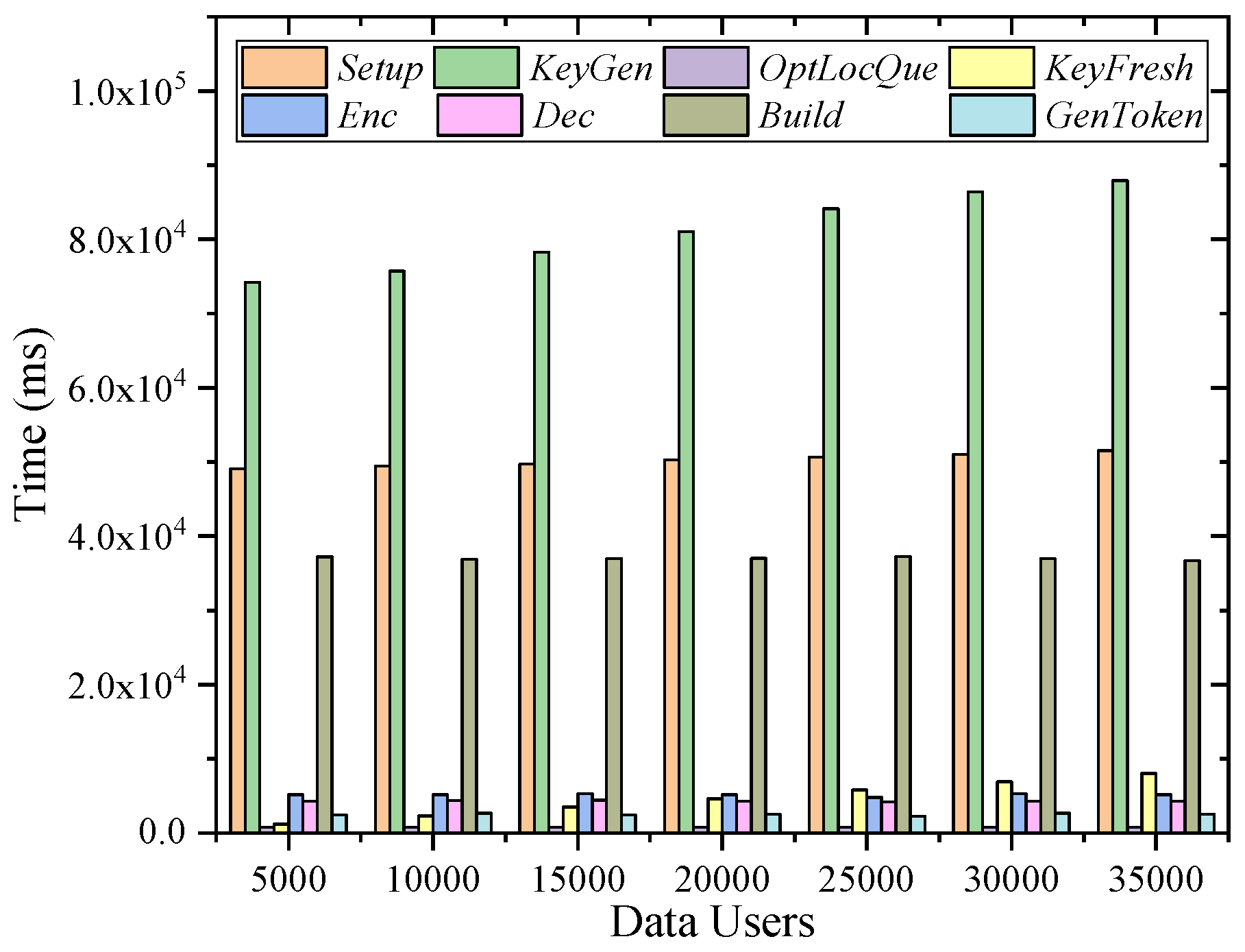
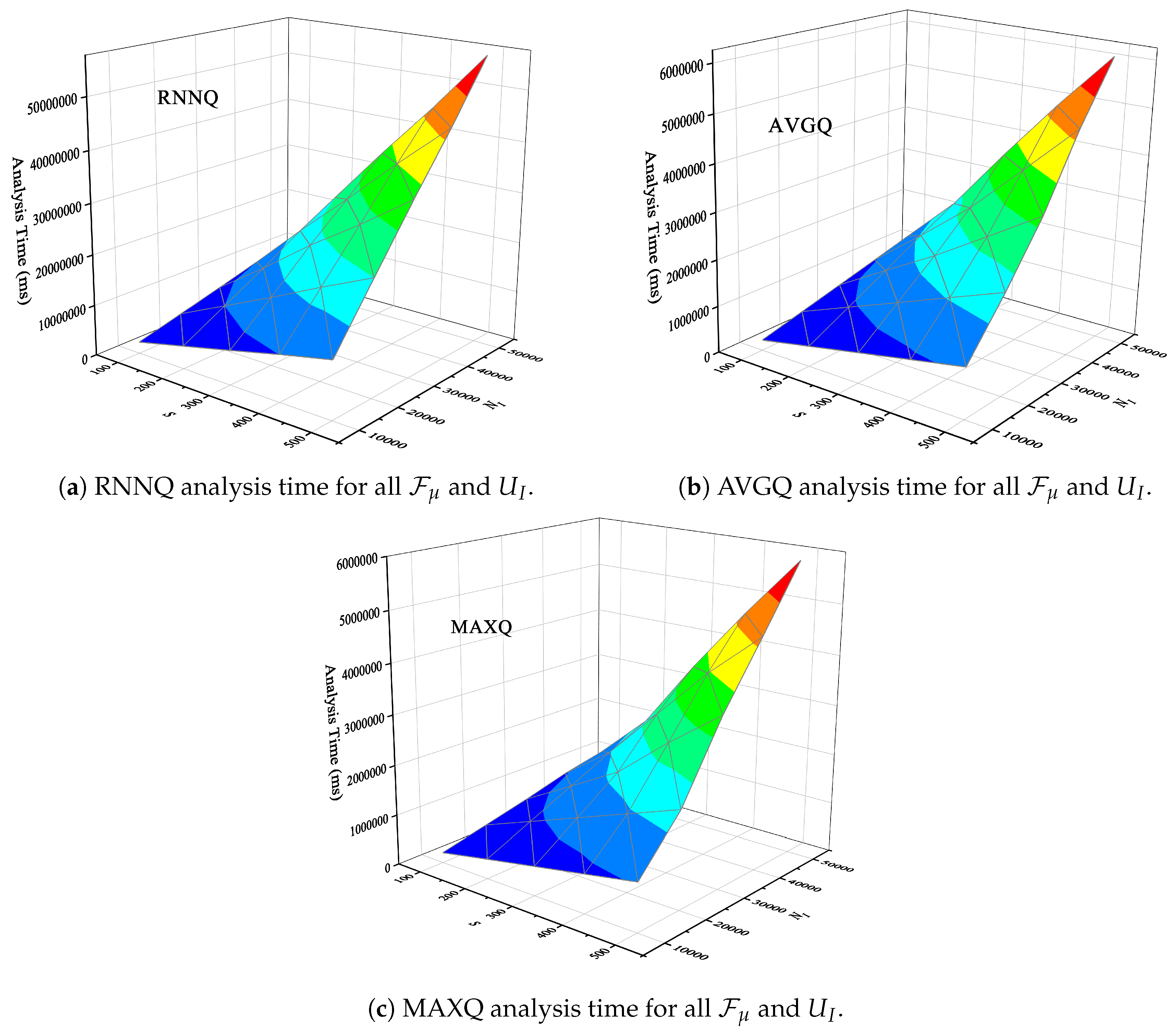
6.4. Efficiency
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, X.; Yao, B.; Li, F. Optimal location queries in road network databases. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 804–815. [Google Scholar]
- Lin, X.; Zhou, L.; Chen, P.; Gu, J. Privacy preserving reverse nearest-neighbor queries processing on road network. In Proceedings of the Web-Age Information Management: WAIM 2012 International Workshops: GDMM, IWSN, MDSP, USDM, and XMLDM, Harbin, China, 18–20 August 2012; pp. 19–28. [Google Scholar]
- Zhang, H.; Xu, Z.; Yu, X.; Du, X. LPPS: Location privacy protection for smartphones. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 1–6 May 2016; pp. 1–6. [Google Scholar]
- Hu, L.; Qian, Y.; Chen, M.; Hossain, M.S.; Muhammad, G. Proactive Cache-Based Location Privacy Preserving for Vehicle Networks. IEEE Wirel. Commun. 2018, 25, 77–83. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Li, H.; Ma, J.; Ma, X. Spatiotemporal correlation-aware dummy-based privacy protection scheme for location-based services. In Proceedings of the IEEE INFOCOM 2017—IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Islam, M.S.; Shen, B.; Wang, C.; Taninar, D.; Wang, J. Efficient processing of reverse nearest neighborhood queries in spatial databases. Inf. Syst. 2020, 92, 101530. [Google Scholar] [CrossRef]
- Du, Y. Privacy-Aware RNN Query Processing on Location-Based Services. In Proceedings of the 2007 International Conference on Mobile Data Management, Mannheim, Germany, 7–11 May 2007; pp. 253–257. [Google Scholar]
- Li, X.; Xiang, T.; Guo, S.; Li, H.; Mu, Y. Privacy-Preserving Reverse Nearest Neighbor Query Over Encrypted Spatial Data. IEEE Trans. Serv. Comput. 2022, 15, 2954–2968. [Google Scholar] [CrossRef]
- Yilmaz, E.; Ferhatosmanoglu, H.; Ayday, E. Aksoy, R.C. Privacy-Preserving Aggregate Queries for Optimal Location Selection. IEEE Trans. Dependable Secur. Comput. 2019, 16, 329–343. [Google Scholar] [CrossRef]
- Han, L.; Luo, W.; Yang, Y.; Yang, A.; Lu, R.; Lai, J.; Zheng, Y. PPOLQ: Privacy-Preserving Optimal Location Query with Multiple-Condition Filter in Outsourced Environments. IEEE Trans. Serv. Comput. 2023, 16, 3564–3577. [Google Scholar] [CrossRef]
- Huang, Q.; Du, J.; Yan, G.; Yang, Y.; Wei, Q. Privacy-Preserving Spatio-Temporal Keyword Search for Outsourced Location-Based Services. IEEE Trans. Serv. Comput. 2022, 15, 3443–3456. [Google Scholar] [CrossRef]
- Guan, Y.; Lu, R.; Zheng, Y.; Shao, J.; Wei, G. Toward Oblivious Location-Based k-Nearest Neighbor Query in Smart Cities. IEEE Internet Things J. 2021, 8, 14219–14231. [Google Scholar] [CrossRef]
- Zhu, X.; Ayday, E.; Vitenberg, R. A Privacy-Preserving Framework for Outsourcing Location-Based Services to the Cloud. IEEE Trans. Dependable Secur. Comput. 2021, 18, 384–399. [Google Scholar] [CrossRef]
- Nieminen, R.; Järvinen, K. Practical Privacy-Preserving Indoor Localization Based on Secure Two-Party Computation. IEEE Trans. Mob. Comput. 2021, 20, 2877–2890. [Google Scholar] [CrossRef]
- Shao, J.; Lu, R.; Lin, X. FINE: A fine-grained privacy-preserving location-based service framework for mobile devices. In Proceedings of the IEEE INFOCOM 2014—IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 244–252. [Google Scholar]
- Korn, F.; Muthukrishnan, S. Influence sets based on reverse nearest neighbor queries. ACM Sigmod Rec. 2000, 29, 201–212. [Google Scholar] [CrossRef]
- Stanoi, I.; Agrawal, D.; EI Abbadi, A. Reverse nearest neighbor queries for dynamic databases. In Proceedings of the ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, Dallas, TX, USA, 14 May 2000. [Google Scholar]
- Tao, Y.; Lung, Y.M.; Mamoulis, N. Reverse Nearest Neighbor Search in Metric Spaces. IEEE Trans. Knowl. Data Eng. 2006, 18, 1239–1252. [Google Scholar]
- Zhang, D.; Du, Y.; Xia, T.; Tao, Y. Progressive computation of the min-dist optimal-location query. In Proceedings of the 32nd International Conference on Very Large Data Bases, Seoul, Republic of Korea, 12–15 September 2006; pp. 643–654. [Google Scholar]
- Chen, Z.; Liu, Y.; Wong, R.C.W.; Xiong, J.; Mai, G.; Long, C. Efficient algorithms for optimal location queries in road networks. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, Snowbird, UT, USA, 22–27 June 2014; pp. 123–134. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. In Proceedings of the Annual International Cryptology Conference, Berlin, Germany, 19–23 August 2001; pp. 213–229. [Google Scholar]
- Nyberg, K.; Rueppel, R.A. Message recovery for signature schemes based on the discrete logarithm problem. In Workshop on the Theory and Application of of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1994; pp. 182–193. [Google Scholar]
- Preneel, B. Cryptographic hash functions. Eur. Trans. Telecommun. 1994, 5, 431–448. [Google Scholar] [CrossRef]
- Putra, M.A.P.; Kim, D.S.; Lee, J.M. DB-BiLSTM: Euclidean Distance-Based Sensor Data Prediction for IoT Applications. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 20–22 October 2021; pp. 814–817. [Google Scholar]
- Shih, F.Y.; Wu, Y.-T. The efficient algorithms for achieving Euclidean distance transformation. IEEE Trans. Image Process. 2004, 13, 1078–1091. [Google Scholar] [CrossRef] [PubMed]
- Roussopoulos, N.; Kelley, S.; Vincent, F. Nearest neighbor queries. In Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data, San Jose, CA, USA, 22–25 May 1995; pp. 71–79. [Google Scholar]
- Zheng, W.; Wu, Y.; Wu, X.; Feng, C.; Sui, Y.; Luo, Y. Zhou, Y. A survey of Intel SGX and its applications. Front. Comput. Sci. 2021, 15, 1–15. [Google Scholar] [CrossRef]
- Costan, V. Intel SGX explained. IACR Cryptol. ePrint Arch. 2016, 86. [Google Scholar]
- Arnautov, S.; Trach, B.; Gregor, F.; Knauth, T.; Martin, A.; Priebe, C.; Priebe, C.; Lind, J.; Muthukumaran, D.; Fetzer, C. SCONE: Secure linux containers with intel SGX. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 689–703. [Google Scholar]
- Li, B.; Zhou, F.; Wang, Q.; Xu, J.; Feng, D. SEDCPT: A secure and efficient Dynamic Searchable Encryption scheme with cluster padding assisted by TEE. J. Syst. Archit. 2024, 154, 103221. [Google Scholar] [CrossRef]
- Jiang, Q.; Qi, S.; Yang, X.; Qi, Y.; Wang, J.; Lu, Y.; An, B.C.; Chang, E.C. Reducing Paging and Exit Overheads in Intel SGX for Oblivious Conjunctive Keyword Search. IEEE Trans. Comput. 2023, 1–14. [Google Scholar] [CrossRef]
- Murdock, K.; Oswald, D.; Garcia, F.D.; Van Bulck, J.; Gruss, D.; Piessens, F. Plundervolt: Software-based Fault Injection Attacks against Intel SGX. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–21 May 2020; pp. 1466–1482. [Google Scholar]
- Haakegaard, R.; Lang, J. The Elliptic Curve Diffie-Hellman (ecdh). 2015. Available online: https://koclab.cs.ucsb.edu/teaching/ecc/project/2015Projects/Haakegaard+Lang.pdf (accessed on 2 December 2024).
- Boneh, D.; Waters, B. Constrained pseudorandom functions and their applications. In Proceedings of the Advances in Cryptology-ASIACRYPT 2013: 19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 1–5 December 2013; pp. 280–300. [Google Scholar]
- Bao, L.; Fu, Z.; Qiang, W.; Feng, D. A Secure and Efficient Dynamic Analysis Scheme for Genome Data within SGX-Assisted Servers. Electronics 2023, 12, 5004. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, D.; Zheng, V.W.; Yu, Z. Modeling User Activity Preference by Leveraging User Spatial Temporal Characteristics in LBSNs. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 129–142. [Google Scholar] [CrossRef]
- Corrigan-Gibbs, H.; Kogan, D. The discrete-logarithm problem with preprocessing. In Proceedings of the Advances in Cryptology–EUROCRYPT 2018: 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Proceedings, Part II 37, Tel Aviv, Israel, 29 April–3 May 2018; pp. 415–447. [Google Scholar]
- Rogaway, P.; Shrimpton, T. Cryptographic hash-function basics: Definitions, implications, and separations for preimage resistance, second-preimage resistance, and collision resistance. In Proceedings of the Fast Software Encryption: 11th International Workshop, FSE 2004, Delhi, India, 5–7 February 2004; pp. 371–388. [Google Scholar]

| Symbol | Descriptions |
|---|---|
| System master secret key | |
| System master public key | |
| The query key of | |
| The storage key of | |
| The timestamp list | |
| The revocation list | |
| The data user list | |
| The customer sets of | |
| The customer sets of -th | |
| The location information set of | |
| n, s | The total number of users and existing facilities |
| The total number of customers of | |
| The total number of customers of the -th | |
| The total number of data in intersection I | |
| The query result of the optimal location query | |
| The i-th customer data of | |
| The j-th customer data of the | |
| The intersection set of the customer of and | |
| A distance function that computes the euclidean | |
| distance between any two objects a and b |
| Schemes | Query Computation Complexity | Storgae | RNN | Revocation | TEE | |||
|---|---|---|---|---|---|---|---|---|
| S(TEE) | C() | C() | C() | S | ||||
| RNNQ/S [9] | () | ()Mu | ||||||
| (2E+Mu) | s(2E+Mu) | ✔ | ✘ | ✘ | ||||
| s(Div+E+Mu) | ||||||||
| AVGQ/S [9] | () | 2Mu | ||||||
| 2(2E+Mu) | 2(2E+Mu) | ✔ | ✘ | ✘ | ||||
| 2(Div+E+Mu) | 1 Div | |||||||
| MAXQ/S [9] | () | ()Mu | ||||||
| (2E+Mu) | E | ✔ | ✘ | ✘ | ||||
| w(Div+E+Mu) | ||||||||
| RNNQ/C [9] | () | |||||||
| s(2E+Mu) | s(Div+E+Mu) | ✔ | ✘ | ✘ | ||||
| ()Mu | ||||||||
| AVGQ/C [9] | () | 2(Div+E+Mu) | ||||||
| 2(2E+Mu)+2Mu | 1 Div | ✔ | ✘ | ✘ | ||||
| E | ||||||||
| MAXQ/C [9] | () | (w-q)(Div+E+Mu) | ||||||
| ·Mu | Div+E+Mu | ✔ | ✘ | ✘ | ||||
| E ≤w(2E+Mu) | ||||||||
| RNNQ | () | 2(3E+P+2H+Mu) | ||||||
| ·Dec | 2P+Mu+Div | ✔ | ✔ | ✔ | ||||
| 5P+3Mu+2Div+3E+2H | ||||||||
| AVGQ | ()+sDiv | 2(3E+P+2H+Mu) | ||||||
| ·Dec | 2P+Mu+Div | ✔ | ✔ | ✔ | ||||
| 5P+3Mu+2Div+3E+2H | ||||||||
| MAXQ | ()+(s-1)Com | 2(3E+P+2H+Mu) | ||||||
| ·Dec | 2P+Mu+Div | ✔ | ✔ | ✔ | ||||
| 5P+3Mu+2Div+3E+2H | ||||||||
| Schemes | Memory Usage | |
|---|---|---|
| [9] | 250 MB | 25 KB |
| ROLQ-TEE | 28.61 MB | 29.3 KB |
| Schemes | Communication | ||
|---|---|---|---|
| C() | S | ||
| RNNQ/S [9] | / | ||
| AVGQ/S [9] | / | ||
| MAXQ/S [9] | / | ||
| RNNQ/C [9] | / | ||
| AVGQ/C [9] | / | ||
| MAXQ/C [9] | / | ||
| RNNQ | |||
| AVGQ | |||
| MAXQ | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhou, F.; Xu, J.; Wang, Q.; Li, J.; Feng, D. ROLQ-TEE: Revocable and Privacy-Preserving Optimal Location Query Based on Trusted Execution Environment. Appl. Sci. 2025, 15, 1641. https://doi.org/10.3390/app15031641
Li B, Zhou F, Xu J, Wang Q, Li J, Feng D. ROLQ-TEE: Revocable and Privacy-Preserving Optimal Location Query Based on Trusted Execution Environment. Applied Sciences. 2025; 15(3):1641. https://doi.org/10.3390/app15031641
Chicago/Turabian StyleLi, Bao, Fucai Zhou, Jian Xu, Qiang Wang, Jiacheng Li, and Da Feng. 2025. "ROLQ-TEE: Revocable and Privacy-Preserving Optimal Location Query Based on Trusted Execution Environment" Applied Sciences 15, no. 3: 1641. https://doi.org/10.3390/app15031641
APA StyleLi, B., Zhou, F., Xu, J., Wang, Q., Li, J., & Feng, D. (2025). ROLQ-TEE: Revocable and Privacy-Preserving Optimal Location Query Based on Trusted Execution Environment. Applied Sciences, 15(3), 1641. https://doi.org/10.3390/app15031641







