Intelligent Optimization Pathway and Impact Mechanism of Age-Friendly Neighborhood Spatial Environment Driven by NSGA-II and XGBoost
Abstract
1. Introduction
2. Literature Review
2.1. Impacts of Outdoor Environmental Performance on the Physical and Mental Health of the Elderly
2.2. Urban Spatial Morphology and Outdoor Environmental Performance
2.3. Research Progress on the Relationship Between Urban Morphology and Environmental Performance
- (1)
- Accuracy: On nonlinear datasets, XGBoost provides more precise predictions and interpretable analyses [55].
- (2)
- Handling high-dimensional data: XGBoost includes built-in regularization, effectively managing high-dimensional data and preventing overfitting [56]. In contrast, traditional methods require manual adjustment of regularization parameters and often face overfitting or computational complexity in high-dimensional cases.
- (3)
2.4. Research Objectives and Significance
3. Methodology
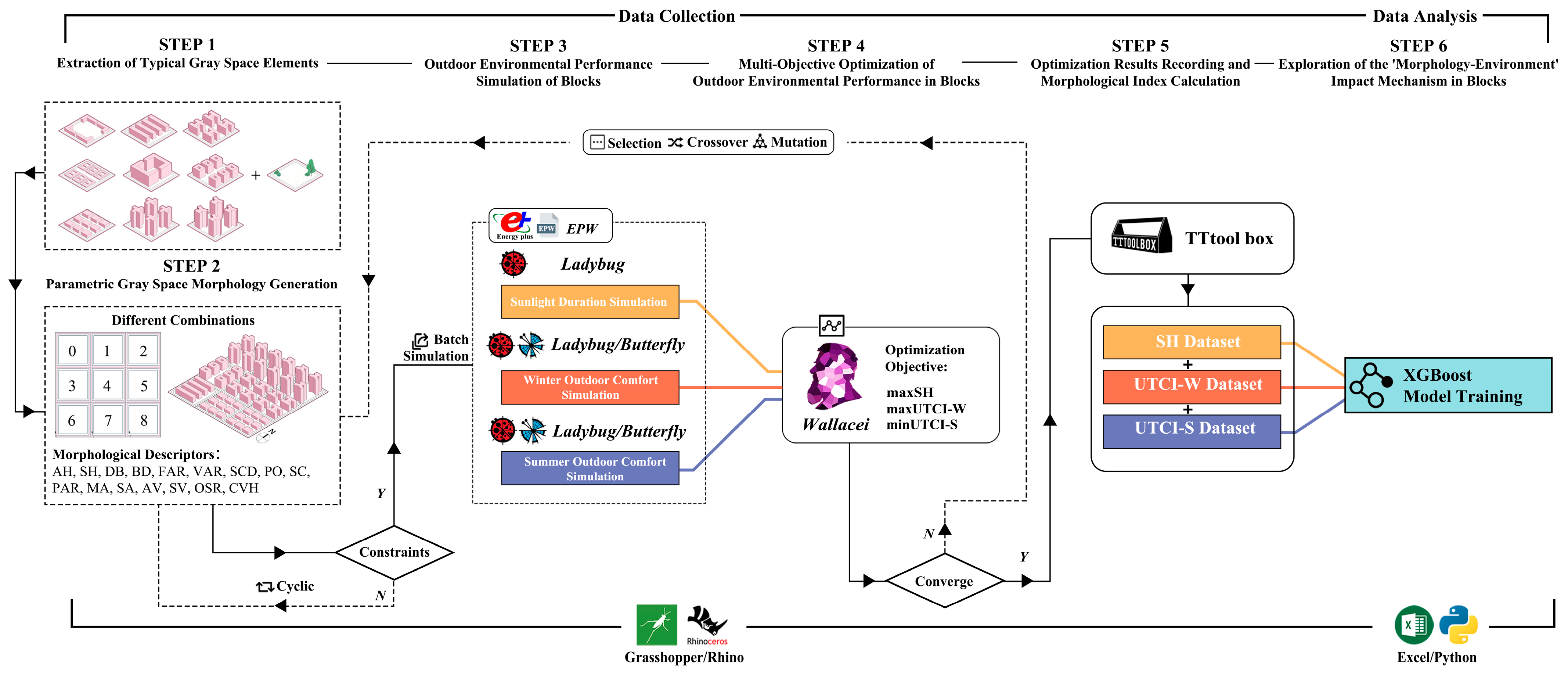
3.1. Overview of the Framework
3.2. Study Area
3.3. Parametric Urban Block Morphology Intelligent Generation
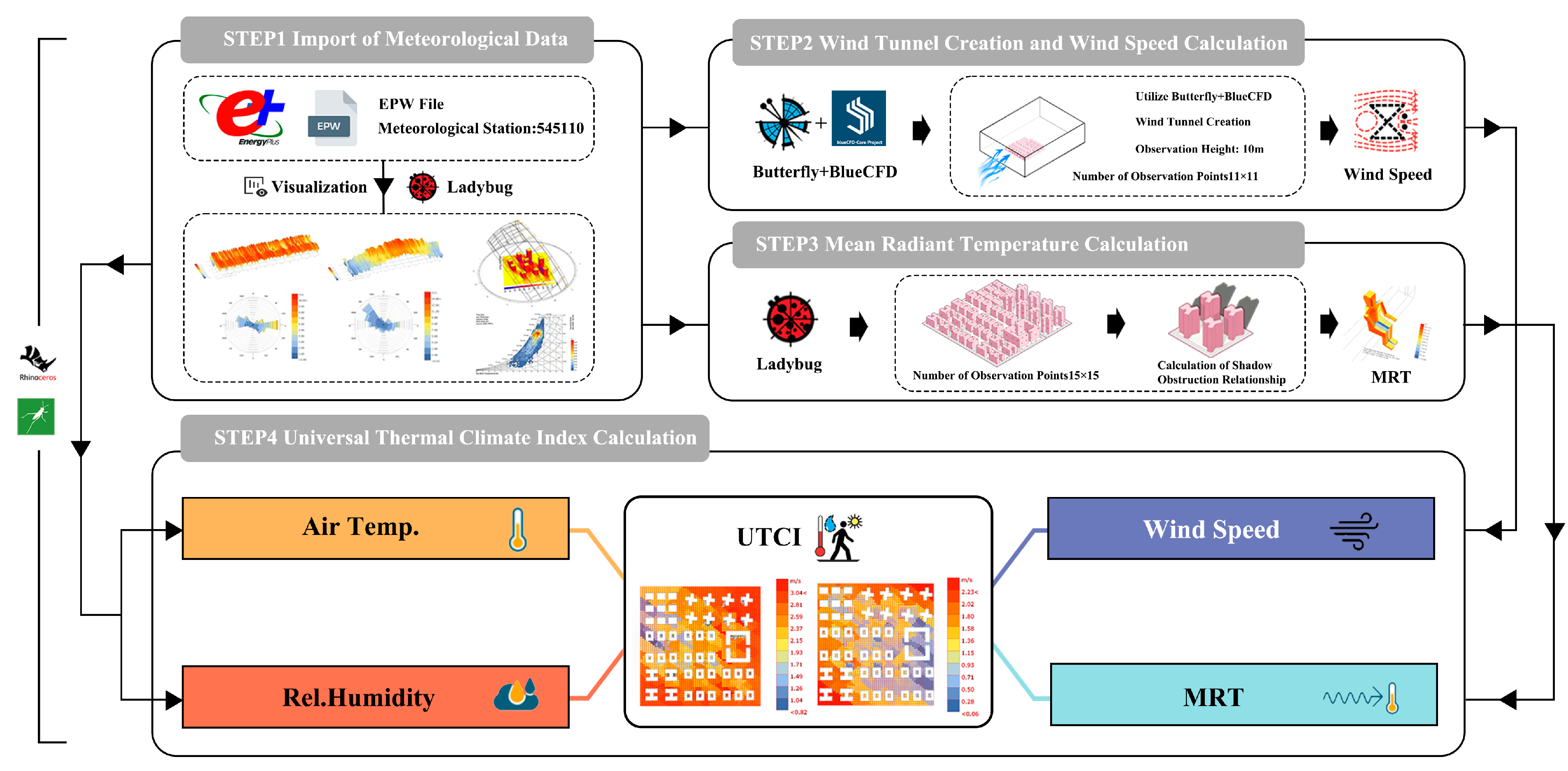
3.4. Simulation of Outdoor Environmental Performance in Urban Blocks
3.4.1. Simulation of Universal Thermal Climate Index (UTCI) at Pedestrian Height
3.4.2. Sunlight Hours (SHs)
3.5. Multi-Objective Optimization of Outdoor Environmental Performance
- (1)
- Maximizing winter pedestrian UTCI (UTCI-W): to reduce the impact of cold temperatures and winds on elderly people’s outdoor activities in winter.
- (2)
- Minimizing summer pedestrian UTCI (UTCI-S): to mitigate the adverse effects of high temperatures on physical and mental health in summer.
- (3)
- Maximizing sunlight hours (SHs): to extend the duration of outdoor activities for the elderly.
3.6. Exploring the “Morphology–Environment” Interaction Mechanism
4. Results and Discussion
4.1. Multi-Objective Optimization Results of Outdoor Environmental Performance
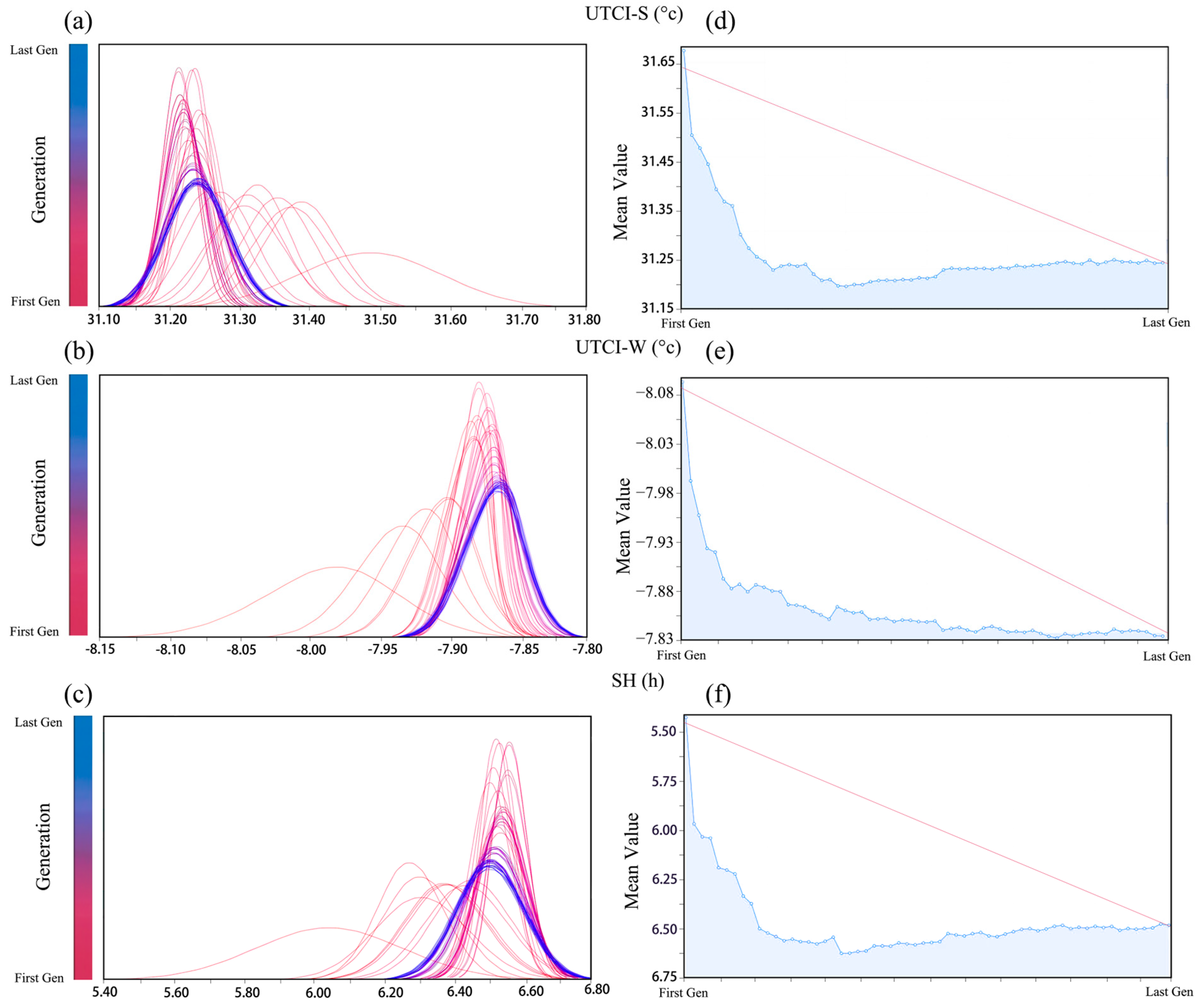
4.1.1. Optimization Process
4.1.2. Analysis of Optimization Results
- (1)
- Outdoor Environmental Performance Optimization Results
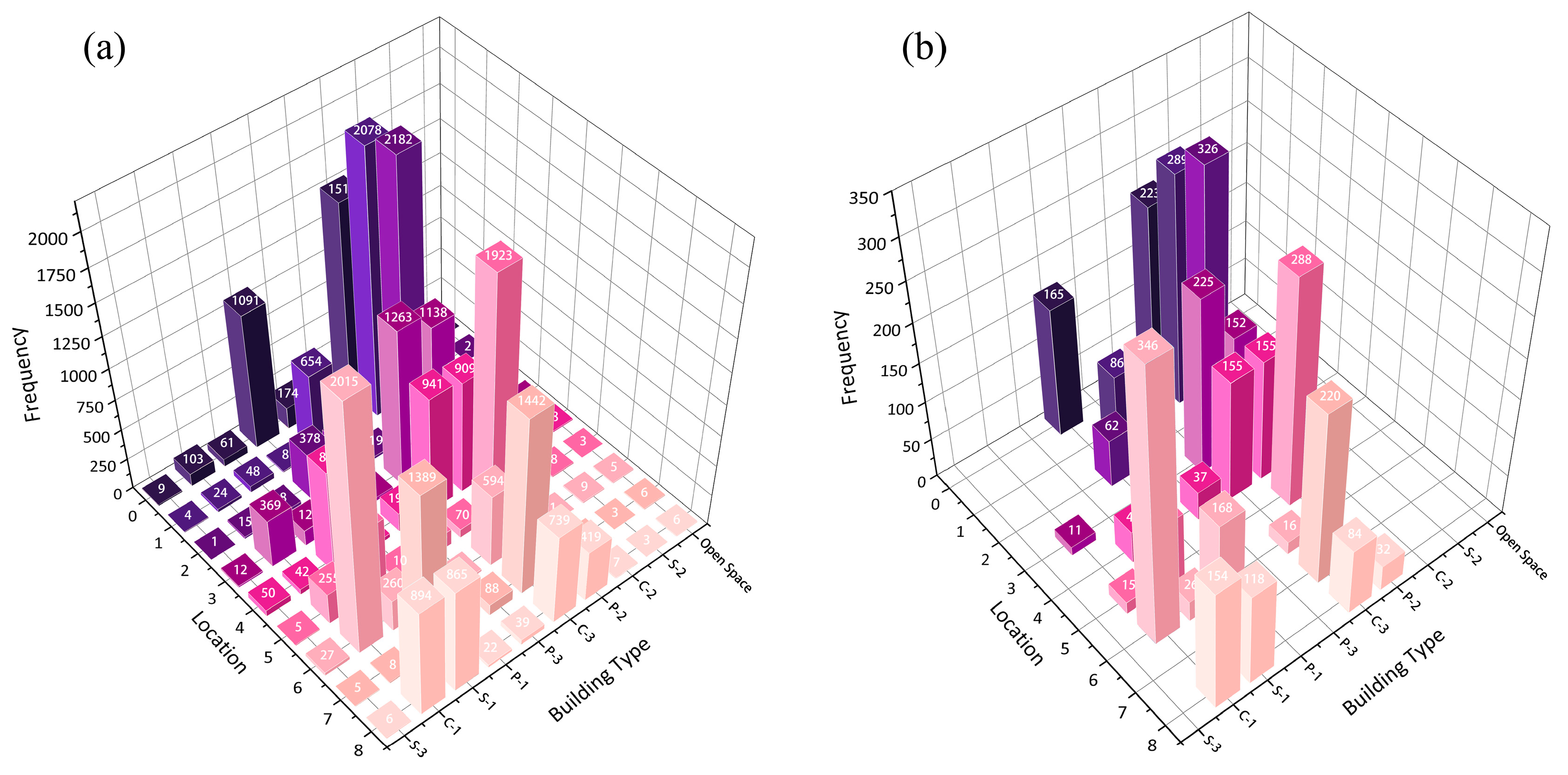
- (2)
- Optimization Results of Urban Spatial Form
4.2. Impact Mechanism of Urban Spatial Form on Outdoor Environmental Performance
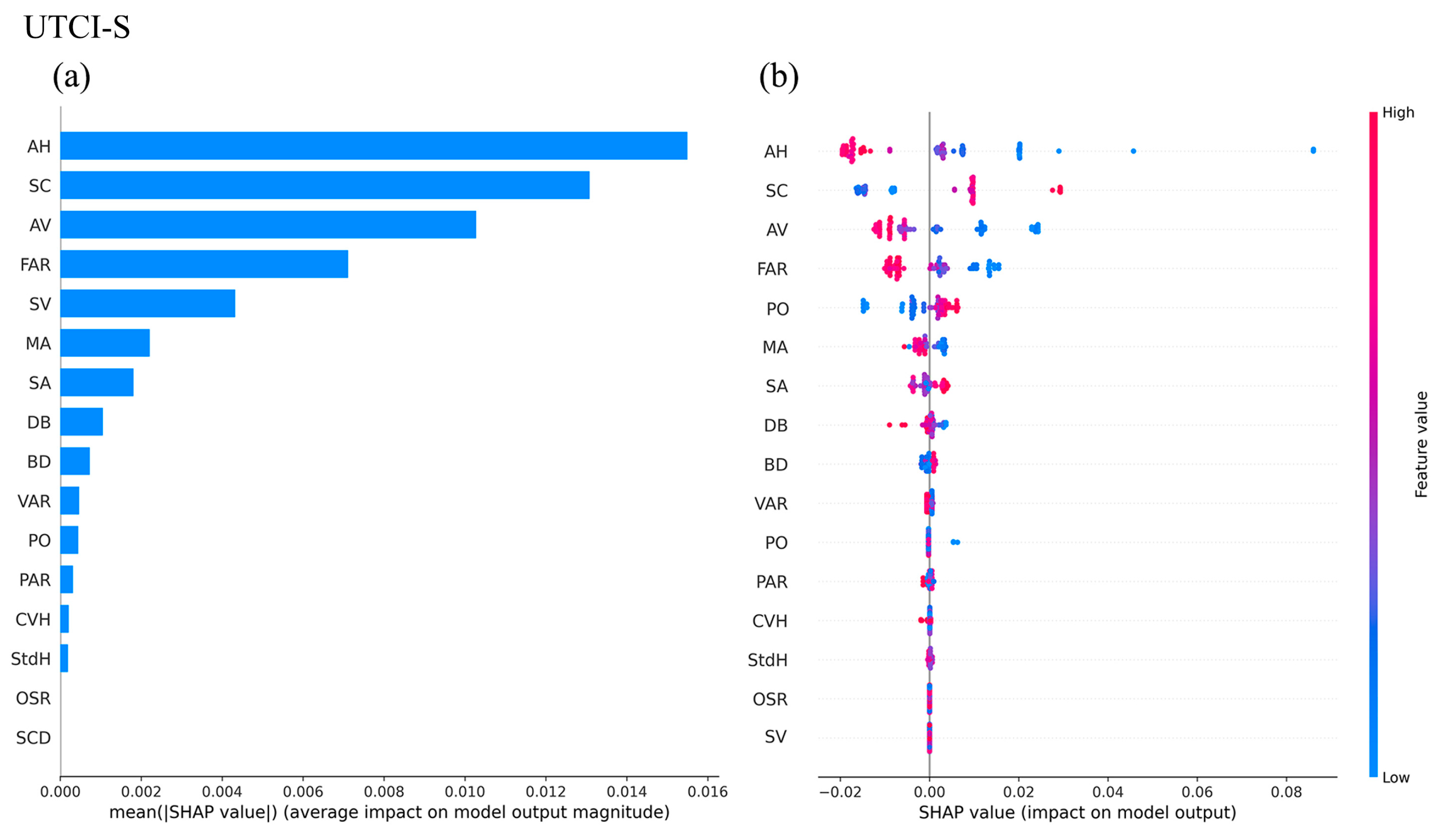
4.2.1. Impact Mechanism of Urban Spatial Form on UTCI-S
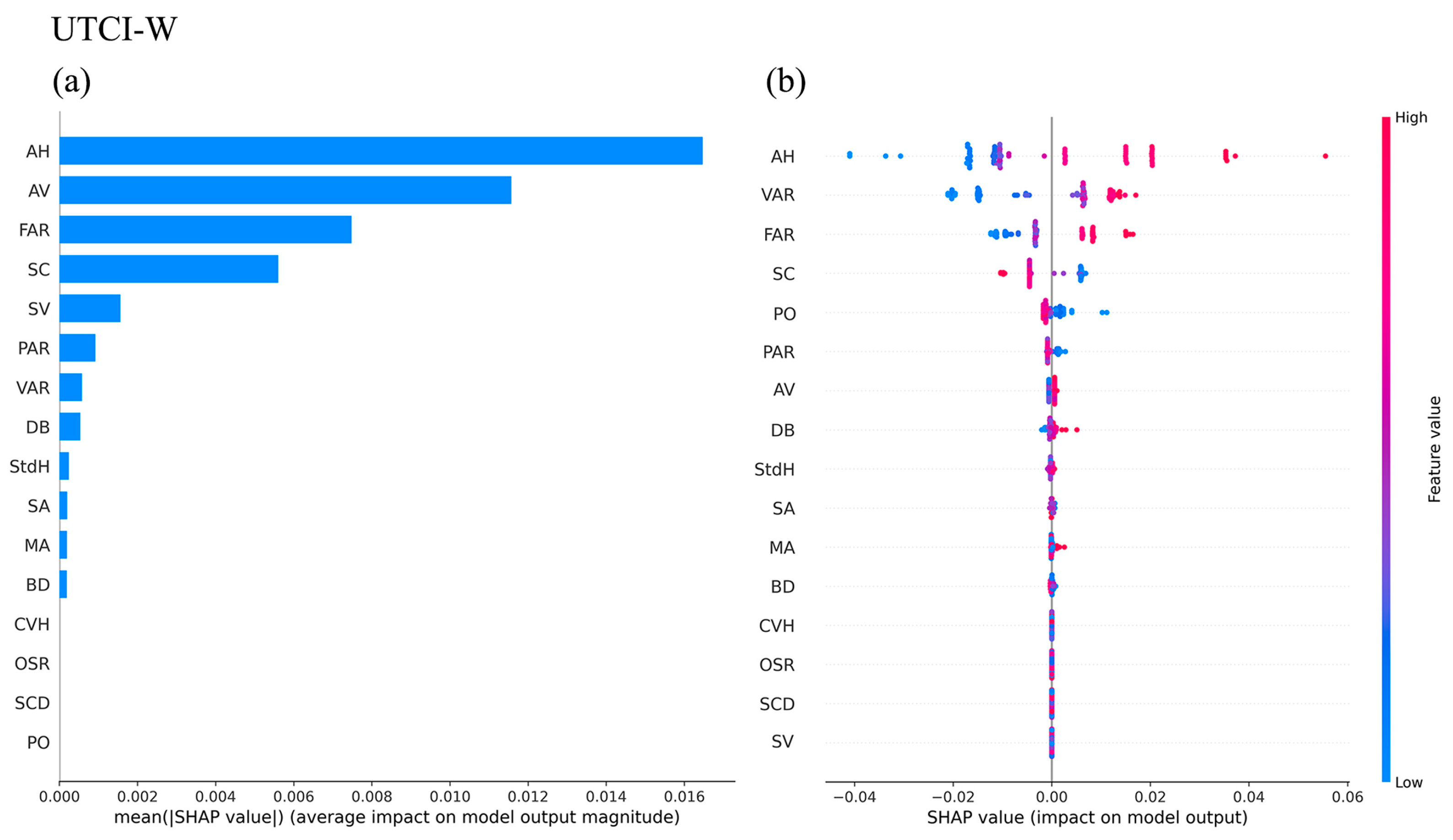
4.2.2. Impact Mechanism of Urban Spatial Form on UTCI-W
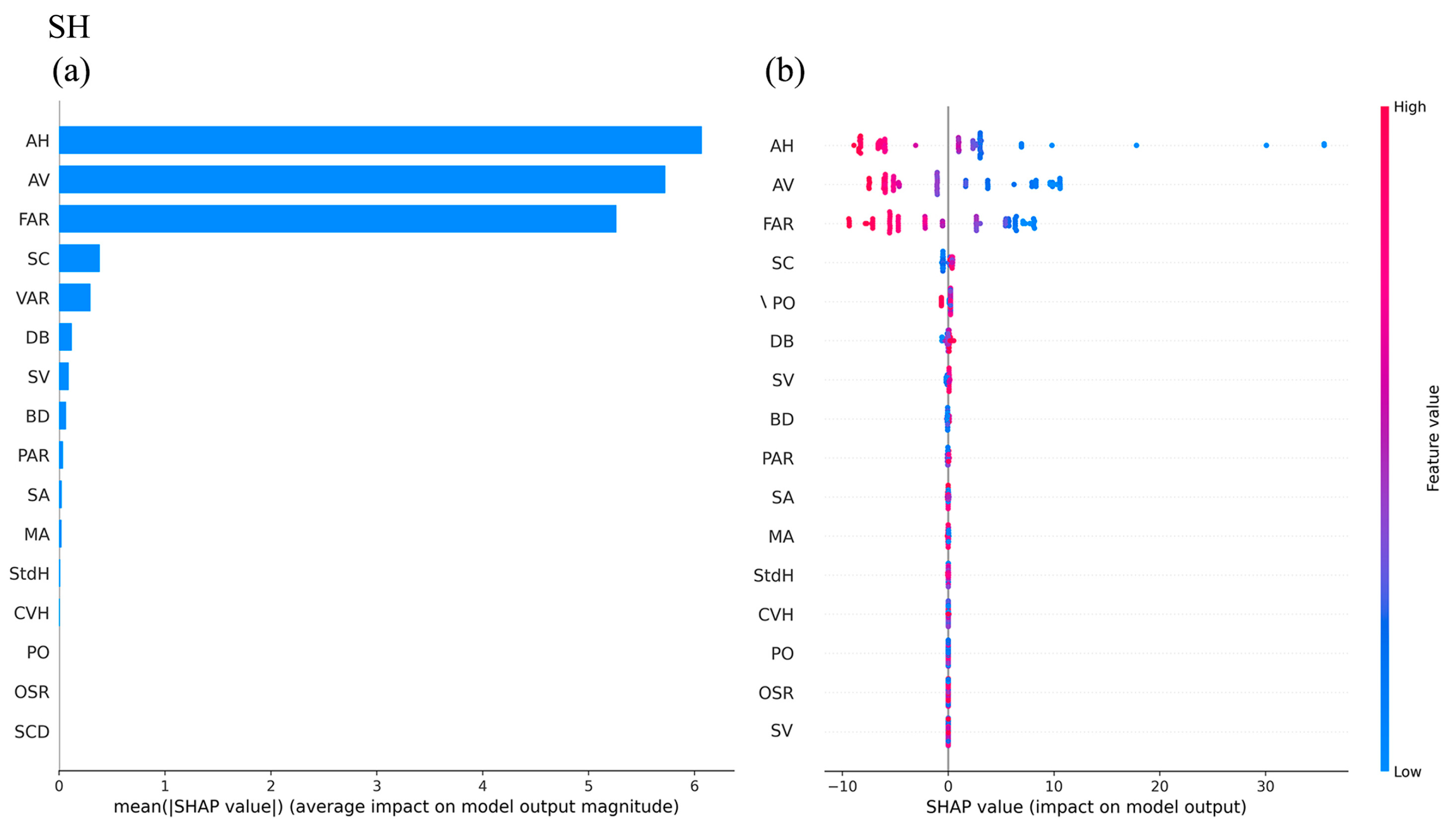
4.2.3. Impact Mechanism of Urban Spatial Form on SHs
5. Conclusions
- (1)
- High-rise buildings should be set on the north side of the block to ensure a high floor–area ratio while blocking winter cold winds.
- (2)
- Mid-to-high-rise buildings should be placed on the west side of the block to maintain natural ventilation in summer while reducing the impact of westward heat.
- (3)
- Low-rise buildings should be placed on the east and south sides to ensure direct sunlight penetration and increase sunlight hours.
- (4)
- The overall block layout should be considered, forming an enclosed shape with higher buildings on the outside and lower buildings on the inside, following the northwest-high, southeast-low principle, to ensure comfortable outdoor environments within the block.
- (5)
- The building forms should be simple, reducing the form factor, and clustered building types should be prioritized.
- (1)
- A “pre-evaluation” optimization framework considering outdoor comfort and lighting duration was applied to the shape design of the elderly block in cold areas, filling the gap in the quantitative study of the elderly block shape.
- (2)
- Through field research, performance simulation, and data analytics, the nonlinear relationship between the block shape of elderly residential buildings and environmental performance indicators was explained, and the key factors affecting elderly people’s outdoor environmental experience were accurately identified.
- (3)
- We translated the research results into design strategies, provided early design decisions for senior-friendly block form design, reduced the cost of later environmental performance optimization and transformation, provided a reference for block planning and layout, improved the outdoor environment of elderly people, improved the overall quality of life of elderly people, and promoted the physical and mental health of elderly people.
- (1)
- It only considers the climate conditions of cold regions, and the applicability to extreme cold, hot summers, and cold winters; climates with hot summers and mild winters need further verification.
- (2)
- The parametric generation of the block form based on the Grasshopper platform’s shape syntax is limited by preset rules, lacking diversity and flexibility.
- (3)
- The optimization process, based on a static genetic algorithm, takes a long time and has a high convergence difficulty.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UTCI-S | Universal Thermal Climate Index in summer (°C) |
| UTCI-W | Universal Thermal Climate Index in winter (°C) |
| SH | sunlight hour (h) |
| AH | average building height (m) |
| StdH | standard deviation of building height (m) |
| BD | building density (%) |
| DB | Distance Between Buildings |
| FAR | floor–area ratio |
| VAR | Volume–Area Ratio (%) |
| SCD | Space Crowding Density |
| PO | porosity (%) |
| SC | Shape Coefficient |
| PAR | perimeter–area ratio |
| MA | Mean Building Area (m2) |
| SA | Standard Deviation of Building Area (m2) |
| AV | Average Building Volume (m3) |
| SV | Volume Standard Deviation (m3) |
| OSR | Open Space Ratio (%) |
| CVH | Coefficient of Variation for Building Height |
| MOO | multi-objective optimization |
| SVF | sky view factor |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| XGBoost | eXtreme Gradient Boosting |
| MRT | mean radiant temperature (°C) |
| SD | standard deviation |
| SHAP | Shapley Additive Explanations |
References
- Ageing and Health, n.d. Available online: https://www.who.int/news-room/fact-sheets/detail/ageing-and-health (accessed on 14 January 2025).
- Population Division World Population Prospects 2024-United Nations, n.d. Available online: https://population.un.org/wpp/ (accessed on 14 January 2025).
- National Bureau of Statistics of China. Total Population Growth is Maintained and the Level of Urbanisation Is steadily Increasing. Available online: http://www.stats.gov.cn/xxgk/jd/sjjd2020/202201/t20220118_1826609.html (accessed on 14 January 2025). (In Chinese)
- Liu, T.Y.; Wang, J.X.; Zhou, D.; Meng, X.Z.; Luo, X.L.; Wang, Y.P. Research on Optimization Design Strategies for Natural Ventilation in Living Units of Institutional Elderly Care Facilities Based on Computational Fluid Dynamics Simulation. Buildings 2024, 14, 1648. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Fung, I.W.H.; Tsang, Y.T.; Chan, L. Development of a Universal Design-Based Guide for Handrails: An Empirical Study for Hong Kong Elderly. Sustainability 2018, 10, 4233. [Google Scholar] [CrossRef]
- Zhou, S.; Li, B.Z.; Du, C.Q.; Liu, H.; Wu, Y.X.; Hodder, S.; Chen, M.Z.; Kosonen, R.; Ming, R.; Ouyang, L.Y.; et al. Opportunities and challenges of using thermal comfort models for building design and operation for the elderly: A literature review. Renew. Sust. Energ. Rev. 2023, 183, 18. [Google Scholar] [CrossRef]
- Kang, K.; Kim, T.; Kim, H. Effect of indoor and outdoor sources on indoor particle concentrations in South Korean residential buildings. J. Hazard. Mater. 2021, 416, 9. [Google Scholar] [CrossRef]
- Sander, B.; Markvart, J.; Kessel, L.; Argyraki, A.; Johnsen, K. Can sleep quality and wellbeing be improved by changing the indoor lighting in the homes of healthy, elderly citizens? Chronobiol. Int. 2015, 32, 1049–1060. [Google Scholar] [CrossRef] [PubMed]
- Petersen, J.; Austin, D.; Kaye, J.A.; Pavel, M.; Hayes, T.L. Unobtrusive in-home detection of time spent out-of-home with applications to loneliness and physical activity. IEEE J. Biomed. Health Inf. 2014, 18, 1590–1596. [Google Scholar] [CrossRef] [PubMed]
- Cedervall, Y.; Torres, S.; Åberg, A.C. Maintaining well-being and selfhood through physical activity: Experiences of people with mild Alzheimer’s disease. Aging Ment. Health 2015, 19, 679–688. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Liu, G.Y.; Lv, Z.; Wen, S.R.; Bi, S.; Wang, W.Z. Inverse associations of outdoor activity and vitamin D intake with the risk of Parkinson’s disease. J. Zhejiang Univ.-Sci. B 2014, 15, 923–927. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Murase, S. Influence of Outdoor Activity and Indoor Activity on Cognition Decline: Use of an Infrared Sensor to Measure Activity. Telemed. J. E-Health 2010, 16, 686–690. [Google Scholar] [CrossRef]
- Blais, M.; Martin, E.; Albaret, J.M.; Tallet, J. Preservation of perceptual integration improves temporal stability of bimanual coordination in the elderly: An evidence of age-related brain plasticity. Behav. Brain Res. 2014, 275, 34–42. [Google Scholar] [CrossRef]
- Smith, R.M. Immunity, trauma and the elderly. Inj.-Int. J. Care Inj. 2007, 38, 1401–1404. [Google Scholar] [CrossRef]
- Hua, Y.; Qiu, Z.; Luo, W.J.; Wang, Y.; Wang, Z. Correlation between Elderly Migrants’ Needs and Environmental Adaptability: A Discussion Based on Human Urbanization Features. Int. J. Environ. Res. Public Health 2021, 18, 5068. [Google Scholar] [CrossRef] [PubMed]
- Aydelott, J.; Leech, R.; Crinion, J. Normal Adult Aging and the Contextual Influences Affecting Speech and Meaningful Sound Perception. Trends Amplif. 2010, 14, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Chun, S.A.; Nam, K. A public healthscape framework for assessing geriatric long-term care public hospitals in South Korea by a Delphi expert consultation. Build. Environ. 2019, 165, 13. [Google Scholar] [CrossRef]
- Zhou, H.X.; Yu, W.; Zhao, K.Y.; Shan, H.Y.; Zhou, S.; Wei, S.; Ouyang, L.Y. Thermal demand characteristics of elderly people with varying levels of frailty in residential buildings during the summer. J. Build. Eng. 2024, 84, 16. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.; Oz, F. Effect of psychosocial care model applied in an “elderly day care center” on loneliness, depression, quality of life, and elderly attitude. Niger. J. Clin. Pract. 2020, 23, 189–197. [Google Scholar] [CrossRef]
- Aylaz, R.; Aktürk, Ü.; Erci, B.; Öztürk, H.; Aslan, H. Relationship between depression and loneliness in elderly and exami-nation of influential factors. Arch. Gerontol. Geriatr. 2012, 55, 548–554. [Google Scholar] [CrossRef]
- Antoine, P.; Antoine, C.; Poinsot, R. Elderly distress: Cognitive schemas identification. Psychol. NeuroPsychiatr. Vieil. 2007, 5, 305–314. [Google Scholar] [PubMed]
- Pokorski, M.; Cajdler, A.; Menzyk, K. SENSE OF SOCIAL INTERACTION IN THE ELDERLY. J. Physiol. Pharmacol. 2008, 59, 579–584. [Google Scholar]
- Yajima, M.; Asakawa, Y.; Yamaguchi, H. Contents and Construct of Subjective Enjoyment of Community-dwelling Elderly People Performing Physical Activities. J. Phys. Ther. Sci. 2013, 25, 207–209. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.Y.; Wu, Z.Q.; Wu, Z.Y.; Liu, Y.D.; Yang, Z.Z. Using Space Syntax in Close Interaction Analysis between the Elderly: Towards a Healthier Urban Environment. Buildings 2023, 13, 1456. [Google Scholar] [CrossRef]
- Yin, Y.D.; Zhang, D.; Zhen, M.; Jing, W.Q.; Luo, W.; Feng, W. Combined effects of the thermal-acoustic environment on subjective evaluations in outdoor public spaces. Sust. Cities Soc. 2022, 77, 9. [Google Scholar] [CrossRef]
- Huang, J.X.; Zhou, C.B.; Zhuo, Y.B.; Xu, L.Y.; Jiang, Y. Outdoor thermal environments and activities in open space: An experiment study in humid subtropical climates. Build. Environ. 2016, 103, 238–249. [Google Scholar] [CrossRef]
- Cleary, M.; Raeburn, T.; West, S.; Childs, C. The environmental temperature of the residential care home: Role in thermal comfort and mental health? Contemp. Nurse 2019, 55, 38–46. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, H.; Kim, D.S. Association between daily environmental temperature and suicide mortality in Korea (2001–2005). Psychiatry Res. 2011, 186, 390–396. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Meng, S.Q.; Lee, J.; Kwak, H.B.; Liu, Y.Q. Effects of walking and sun exposure on bone density and balance in elderly with osteopenia. J. Bone Miner. Metab. 2022, 40, 528–534. [Google Scholar] [CrossRef]
- Cui, Y.F.; Gong, Q.; Huang, C.; Guo, F.; Li, W.; Wang, Y.X.; Cheng, X. The relationship between sunlight exposure duration and depressive symptoms: A cross-sectional study on elderly Chinese women. PLoS ONE 2021, 16, 9. [Google Scholar] [CrossRef]
- Ishii, N.; Terao, T.; Araki, Y.; Kohno, K.; Mizokami, Y.; Arasaki, M.; Iwata, N. Risk factors for suicide in Japan: A model of predicting suicide in 2008 by risk factors of 2007. J. Affect. Disord. 2013, 147, 352–354. [Google Scholar] [CrossRef] [PubMed]
- Kööts, L.; Realo, A.; Allik, J. The Influence of the Weather on Affective Experience An Experience Sampling Study. J. Individ. Differ. 2011, 32, 74–84. [Google Scholar] [CrossRef]
- Martín, L.; March, L. Urban Space and Structures; Cambridge University Press: Cambridge, UK, 1972. [Google Scholar]
- Qaoud, R.; Adel, B.; Sayad, B.; Alkama, D.; Attia, S. Assessing the influence of neighborhood urban form on outdoor thermal conditions in the hot dry city of Biskra, Algeria. Ain Shams Eng. J. 2023, 14, 10. [Google Scholar] [CrossRef]
- Blocken, B.; Janssen, W.D.; van Hooff, T. CFD simulation for pedestrian wind comfort and wind safety in urban areas: General decision framework and case study for the Eindhoven University campus. Environ. Modell. Softw. 2012, 30, 15–34. [Google Scholar] [CrossRef]
- Ramponi, R.; Blocken, B.; de Coo, L.B.; Janssen, W.D. CFD simulation of outdoor ventilation of generic urban configurations with different urban densities and equal and unequal street widths. Build. Environ. 2015, 92, 152–166. [Google Scholar] [CrossRef]
- Ng, E. Policies and technical guidelines for urban planning of high-density cities—Air ventilation assessment (AVA) of Hong Kong. Build. Environ. 2009, 44, 1478–1488. [Google Scholar] [CrossRef]
- Li, J.N.; Niu, J.L.; Huang, T.Y.; Mak, C.M. Dynamic effects of frequent step changes in outdoor microclimate environments on thermal sensation and dissatisfaction of pedestrian during summer. Sustain. Cities Soc. 2022, 79, 17. [Google Scholar] [CrossRef]
- Yu, Y.C.; de Dear, R.; Chauhan, K.; Niu, J.L. Impact of wind turbulence on thermal perception in the urban microclimate. J. Wind Eng. Ind. Aerodyn. 2021, 216, 14. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.G.; Sandberg, M.; Buccolieri, R.; Di Sabatino, S. The influence of building height variability on pollutant dispersion and pedestrian ventilation in idealized high-rise urban areas. Build. Environ. 2012, 56, 346–360. [Google Scholar] [CrossRef]
- Chao, Y. Mitigating Urban Heat Island Effects of High Density Cities: A Study at Hong Kong. Archit. J. 2010, 54, 120–123, (In Chinese with English Abstract). [Google Scholar]
- Yan, L.; Moyan, Z.; Qimeng, C.; Xin, R.; Xiangfei, G.; Liu, Y. Research on total daily solar radiation in the middle and low density block. Ind. Constr. 2020, 50, 151–158, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Hong, P. Correlation between From Elements and Temperature of Commercial Block in Harbin Central Street. Build. Sci. 2019, 35, 11–17, (In Chinese with English abstract). [Google Scholar]
- Tian, J.; Xu, S. A morphology-based evaluation on block-scale solar potential for residential area in central China. Sol. Energy 2021, 221, 332–347. [Google Scholar] [CrossRef]
- Darbani, E.S.; Parapari, D.M.; Boland, J.; Sharifi, E. Impacts of urban form and urban heat island on the outdoor thermal comfort: A pilot study on Mashhad. Int. J. Biometeorol. 2021, 65, 1101–1117. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Xu, X.D.; Huang, W.X.; Zhang, R.; Kong, L.Y.; Wang, X. A multi-objective optimization framework for designing urban block forms considering daylight, energy consumption, and photovoltaic energy potential. Build. Environ. 2023, 242, 19. [Google Scholar] [CrossRef]
- Wang, S.S.; Yi, Y.K.; Liu, N.X. Multi-objective optimization (MOO) for high-rise residential buildings’ layout centered on daylight, visual, and outdoor thermal metrics in China. Build. Environ. 2021, 205, 19. [Google Scholar] [CrossRef]
- Deng, X.D.; Nie, W.X.; Li, X.H.; Wu, J.; Yin, Z.; Han, J.J.; Pan, H.N.; Lam, C.K.C. Influence of built environment on outdoor thermal comfort: A comparative study of new and old urban blocks in Guangzhou. Build. Environ. 2023, 234, 18. [Google Scholar] [CrossRef]
- Wang, B.; Cot, L.D.; Adolphe, L.; Geoffroy, S.; Sun, S. Cross indicator analysis between wind energy potential and urban morphology. Renew. Energy 2017, 113, 989–1006. [Google Scholar] [CrossRef]
- Zheng, Y.S.; Ren, C.; Shi, Y.; Yim, S.H.L.; Lai, D.Y.F.; Xu, Y.; Fang, C.; Li, W.J. Mapping the spatial distribution of nocturnal urban heat island based on Local Climate Zone framework. Build. Environ. 2023, 234, 17. [Google Scholar] [CrossRef]
- Ding, C.; Cao, X.; Liu, C. How does the station-area built environment influence Metrorail ridership? Using gradient boosting decision trees to identify non-linear thresholds. J. Transp. Geogr. 2019, 77, 70–78. [Google Scholar] [CrossRef]
- Dong, W.; Cao, X.Y.; Wu, X.Y.; Dong, Y. Examining pedestrian satisfaction in gated and open communities: An integration of gradient boosting decision trees and impact-asymmetry analysis. Landsc. Urban Plan. 2019, 185, 246–257. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C.; Assoc Comp, M. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N.; Assoc Comp, M. Explanation of Machine Learning Models Using Improved Shapley Additive Explanation. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics (ACM-BCB), Niagara Falls, NY, USA, 7–10 September 2019; p. 546. [Google Scholar]
- Wu, X.Y.; Tao, T.; Cao, J.S.; Fan, Y.L.; Ramaswami, A. Examining threshold effects of built environment elements on travel-related carbon-dioxide emissions. Transport. Res. Part D-Transport. Environ. 2019, 75, 1–12. [Google Scholar] [CrossRef]
- Liu, J.X.; Wang, B.; Xiao, L.Z. Non-linear associations between built environment and active travel for working and shopping: An extreme gradient boosting approach. J. Transp. Geogr. 2021, 92, 12. [Google Scholar] [CrossRef]
- Yang, L.; Ao, Y.; Ke, J.; Lu, Y.; Liang, Y. To walk or not to walk? Examining non-linear effects of streetscape greenery on walking propensity of older adults. J. Transp. Geogr. 2021, 94, 103099. [Google Scholar] [CrossRef]
- Tao, T.; Wu, X.Y.; Cao, J.; Fan, Y.L.; Das, K.; Ramaswami, A. Exploring the Nonlinear Relationship between the Built Environment and Active Travel in the Twin Cities. J. Plan. Educ. Res. 2023, 43, 637–652. [Google Scholar] [CrossRef]
- Liang, J.H.; Huang, S.; Bao, W.W.; Pu, Y.Q.; Liu, M.L.; Yang, X.Z.; Wu, Z.W.; Chen, J.Q.; Dong, G.H.; Chen, Y.J. Longitudinal relationship between built environment and physical fitness in Chinese children and adolescents: Findings from the COHERENCE study. Build. Environ. 2025, 267, 9. [Google Scholar] [CrossRef]
- Nejati, F.; Tahoori, N.; Sharifian, M.A.; Ghafari, A.; Nehdi, M.L. Estimating Heating Load in Residential Buildings Using Multi-Verse Optimizer, Self-Organizing Self-Adaptive, and Vortex Search Neural-Evolutionary Techniques. Buildings 2022, 12, 1328. [Google Scholar] [CrossRef]
- Ladybug Tools|Ladybug, (n.d.). Available online: https://www.ladybug.tools/ladybug.html (accessed on 14 January 2025).
- Ladybug Tools|Butterfly, (n.d.). Available online: https://www.ladybug.tools/butterfly.html (accessed on 14 January 2025).
- Evolutionary Engine for Grasshopper3D, Wallacei (n.d.). Available online: https://www.wallacei.com (accessed on 14 January 2025).
- TT Toolbox, Food4Rhino. 2013. Available online: https://www.food4rhino.com/en/app/tt-toolbox (accessed on 14 January 2025).
- National Bureau of Statistics of China. Report on the Development of the Elderly Career in Beijing. 2023. Available online: https://www.gov.cn/lianbo/difang/202410/content_6979496.htm (accessed on 4 December 2024). (In Chinese)
- Alothaimeen, I.; Arditi, D.; Türkakin, O.H. Multi-objective optimization for LEED-new construction using BIM and genetic algorithms. Autom. Constr. 2023, 149, 22. [Google Scholar] [CrossRef]
- Joshi, M.Y.; Rodler, A.; Musy, M.; Guernouti, S.; Cools, M.; Teller, J. Identifying urban morphological archetypes for microclimate studies using a clustering approach. Build. Environ. 2022, 224, 15. [Google Scholar] [CrossRef]
- Li, H.D.; Liu, Y.G.; Zhang, H.W.; Xue, B.; Li, W.L. Urban morphology in China: Dataset development and spatial pattern characterization. Sust. Cities Soc. 2021, 71, 12. [Google Scholar] [CrossRef]
- Geng, X.T.; Xie, D.; Gou, Z.H. Optimizing urban block morphologies for net-zero energy cities: Exploring photovoltaic potential and urban design prototype. Build. Simul. 2024, 17, 607–624. [Google Scholar] [CrossRef]
- Naskar, P.R.; Mohapatra, M.; Singh, G.P.; Das, U. Spatiotemporal variations of UTCI based discomfort over India. J. Earth Syst. Sci. 2024, 133, 21. [Google Scholar] [CrossRef]
- China Meteorological Administration. China Climate Bulletin. 2022. Available online: https://www.cma.gov.cn/zfxxgk/gknr/qxbg/202303/t20230324_5396394.html (accessed on 14 January 2025).
- Ohashi, Y.; Katsuta, T.; Tani, H.; Okabayashi, T.; Miyahara, S.; Miyashita, R. Human cold stress of strong local-wind “Hijikawa-arashi” in Japan, based on the UTCI index and thermo-physiological responses. Int. J. Biometeorol. 2018, 62, 1241–1250. [Google Scholar] [CrossRef]
- Blazejczyk, K.; Twardosz, R. Secular changes (1826–2021) of human thermal stress according to UTCI in Krakow (southern Poland). Int. J. Climatol. 2023, 43, 4220–4230. [Google Scholar] [CrossRef]
- Kuchcik, M. Mortality and thermal environment (UTCI) in Poland-long-term, multi-city study. Int. J. Biometeorol. 2021, 65, 1529–1541. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.Y.; Zhang, G.J.; Yao, J.W.; Wang, X.X.; Calautit, J.K.; Zhao, C.R.; An, N.; Peng, X. Accelerated environmental performance-driven urban design with generative adversarial network. Build. Environ. 2022, 224, 22. [Google Scholar] [CrossRef]
- Ma, H.P.; Zhang, Y.J.; Sun, S.Y.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Alam, S.M.K.; Li, P.Y.; Rahman, M.; Fida, M.; Elumalai, V. Key factors affecting groundwater nitrate levels in the Yinchuan Region, Northwest China: Research using the eXtreme Gradient Boosting (XGBoost) model with the SHapley Additive exPlanations (SHAP) method. Environ. Pollut. 2025, 364, 11. [Google Scholar] [CrossRef]
- Panda, C.; Mishra, A.K.; Dash, A.K.; Nawab, H. Predicting and explaining severity of road accident using artificial intelligence techniques, SHAP and feature analysis. Int. J. Crashworthiness 2023, 28, 186–201. [Google Scholar] [CrossRef]


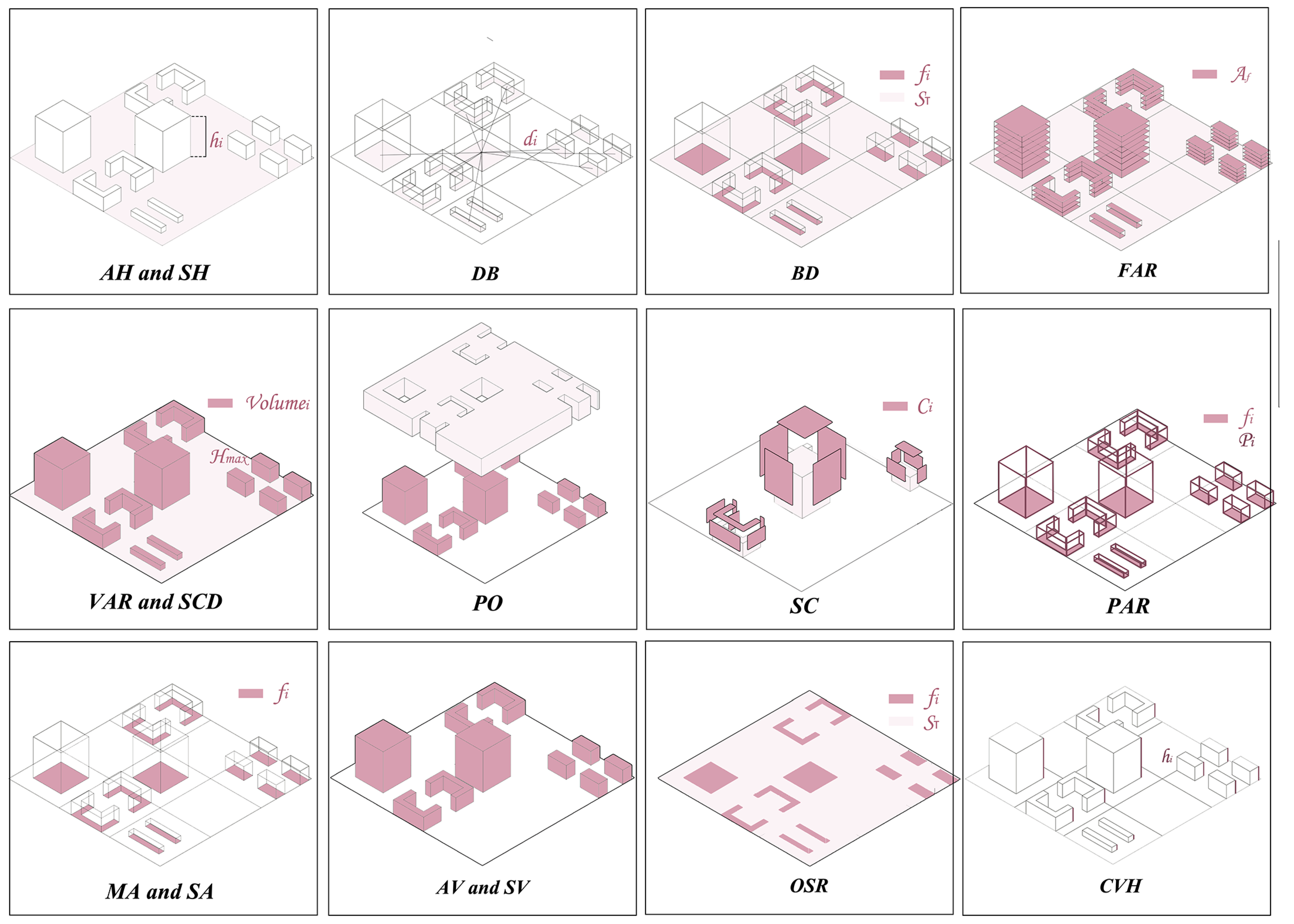

| Indicator Name | Indicator Symbol | Formula | Indicator Unit |
|---|---|---|---|
| Average Building Height | AH | m | |
| Standard Deviation of Building Height | StdH | m | |
| Distance Between Buildings | DB | m | |
| Building Density | BD | % | |
| Floor–Area Ratio | FAR | - | |
| Volume–Area Ratio | VAR | m | |
| Space Crowding Density | SCD | - | |
| Porosity | PO | % | |
| Shape Coefficient | SC | - | |
| Perimeter–Area Ratio | PAR | - | |
| Mean Building Area | MA | m2 | |
| Standard Deviation of Building Area | SA | m2 | |
| Average Building Volume | AV | m3 | |
| Standard Deviation of Building Volume | SV | m3 | |
| Open Space Ratio | OSR | % | |
| Coefficient of Variation for Building Height | CVH | m |
| Elitism | Mutation Probability | Mutation Rate | Crossover Rate | Mutation Distribution Index | Generation Size | Generation Count |
|---|---|---|---|---|---|---|
| 0.5 | 0.3 | 0.5 | 0.9 | 20 | 50 | 60 |
| Dataset | Training Set (R2) | Testing Set (R2) |
|---|---|---|
| UTCI-S | 0.944 | 0.712 |
| UTCI-W | 0.993 | 0.843 |
| SH | 1.000 | 0.966 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Qi, Z.; Yang, X.; Jiang, L. Intelligent Optimization Pathway and Impact Mechanism of Age-Friendly Neighborhood Spatial Environment Driven by NSGA-II and XGBoost. Appl. Sci. 2025, 15, 1449. https://doi.org/10.3390/app15031449
Zhang L, Qi Z, Yang X, Jiang L. Intelligent Optimization Pathway and Impact Mechanism of Age-Friendly Neighborhood Spatial Environment Driven by NSGA-II and XGBoost. Applied Sciences. 2025; 15(3):1449. https://doi.org/10.3390/app15031449
Chicago/Turabian StyleZhang, Lu, Zizhuo Qi, Xin Yang, and Ling Jiang. 2025. "Intelligent Optimization Pathway and Impact Mechanism of Age-Friendly Neighborhood Spatial Environment Driven by NSGA-II and XGBoost" Applied Sciences 15, no. 3: 1449. https://doi.org/10.3390/app15031449
APA StyleZhang, L., Qi, Z., Yang, X., & Jiang, L. (2025). Intelligent Optimization Pathway and Impact Mechanism of Age-Friendly Neighborhood Spatial Environment Driven by NSGA-II and XGBoost. Applied Sciences, 15(3), 1449. https://doi.org/10.3390/app15031449






