High-Pressure Hydrogen Charge Check-Valve Energy Loss-Based Correlation Analysis Affecting Internal Flow Characterizations
Abstract
1. Introduction
2. Numerical Analysis Method
2.1. Check-Valve Shape and Analysis Conditions
2.2. Turbulence Models
3. Result and Discussions
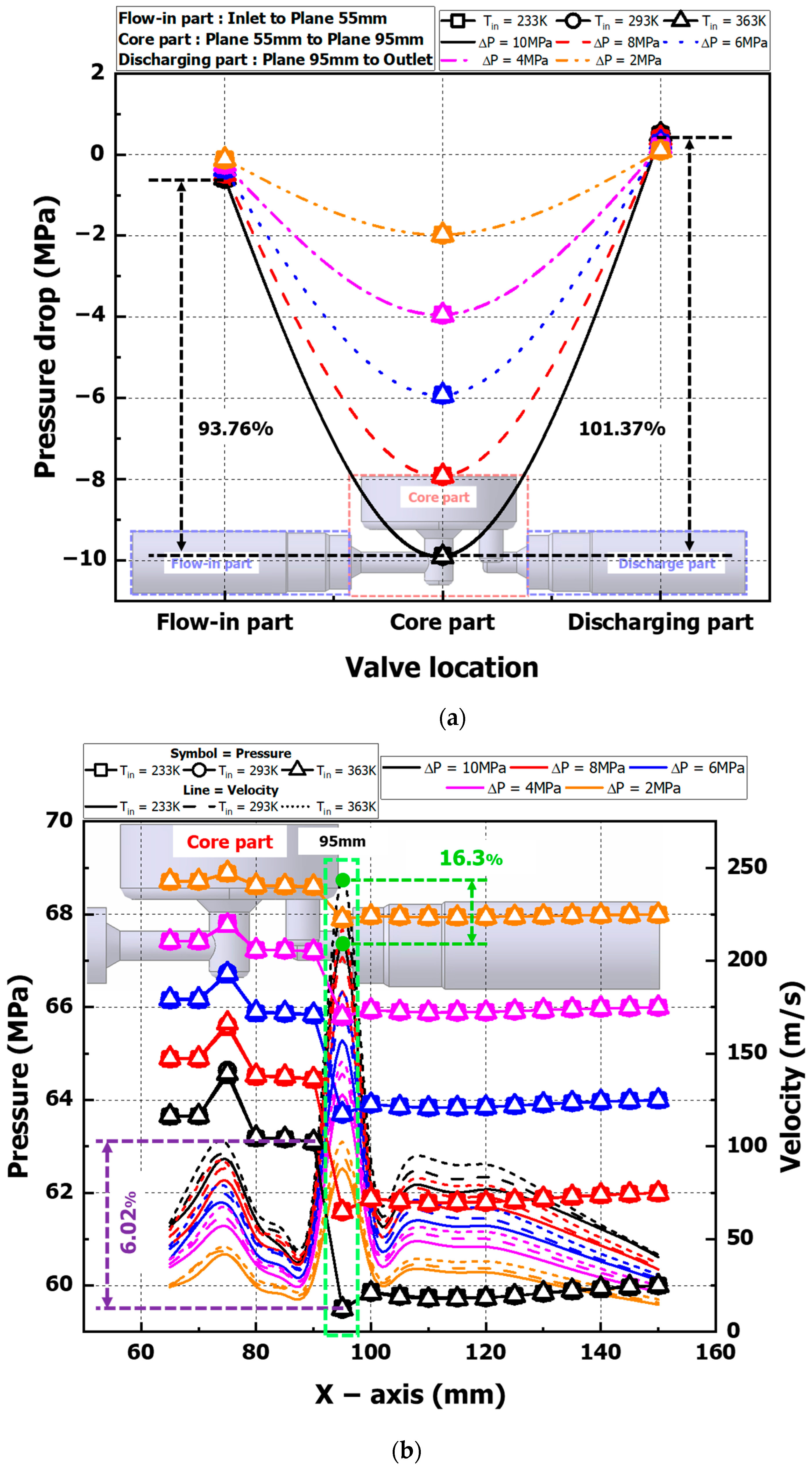
3.1. Analysis of Pressure and Velocity Results According to Inlet Temperature and Differential Pressure Change
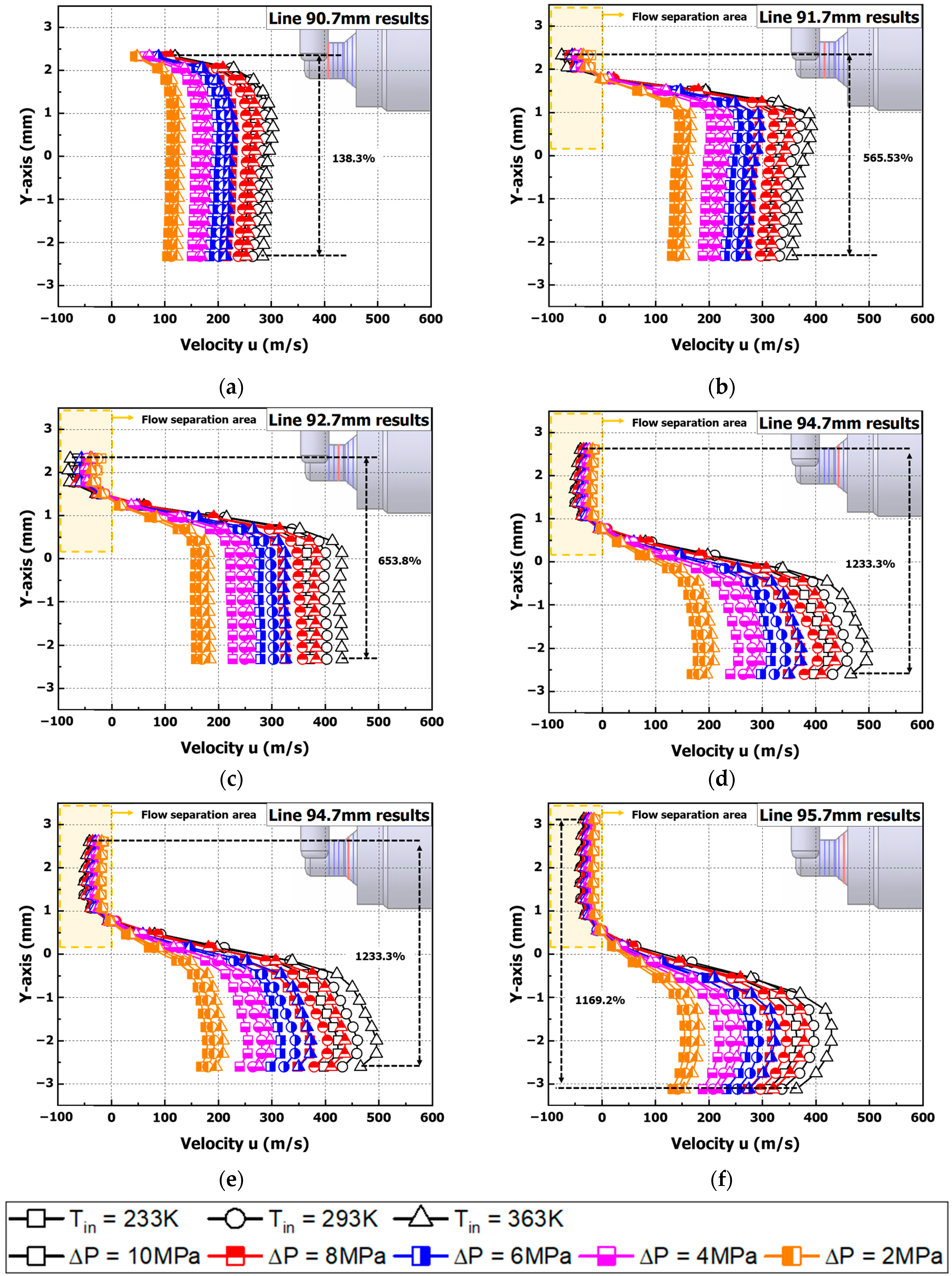
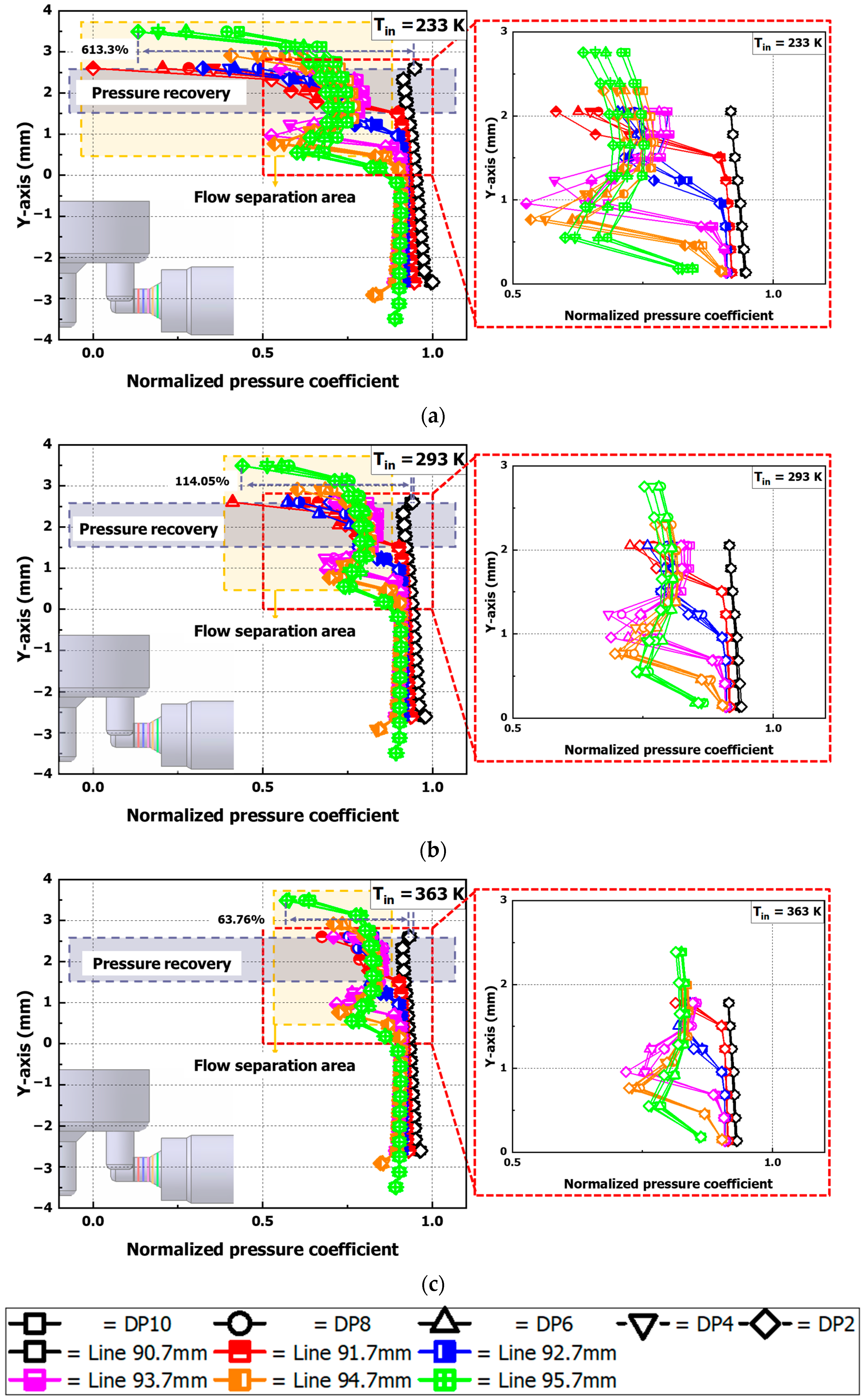
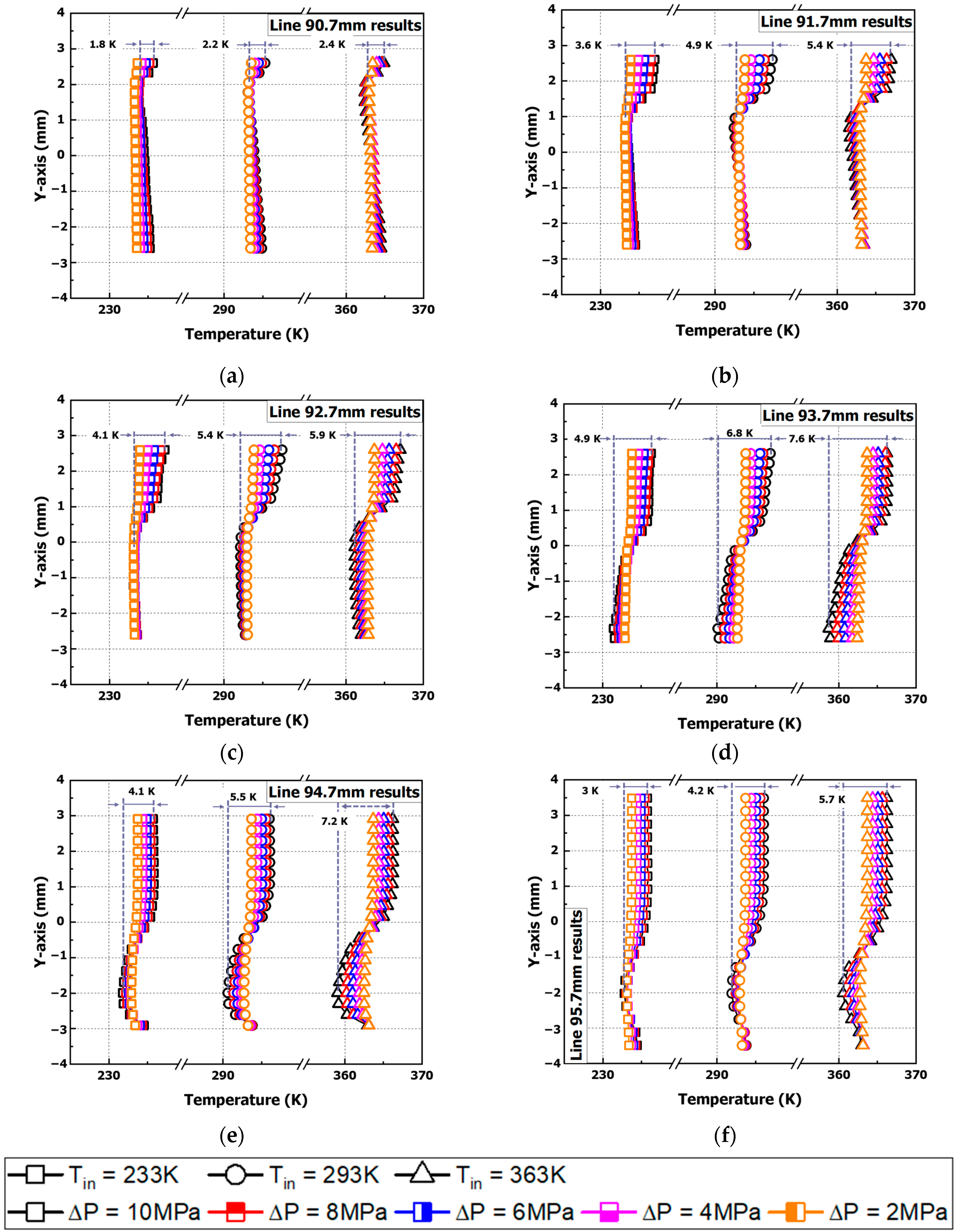
3.2. Analysis of Pressure Coefficient (CP) and Velocity Results in L-Shaped Bend of Check Valve
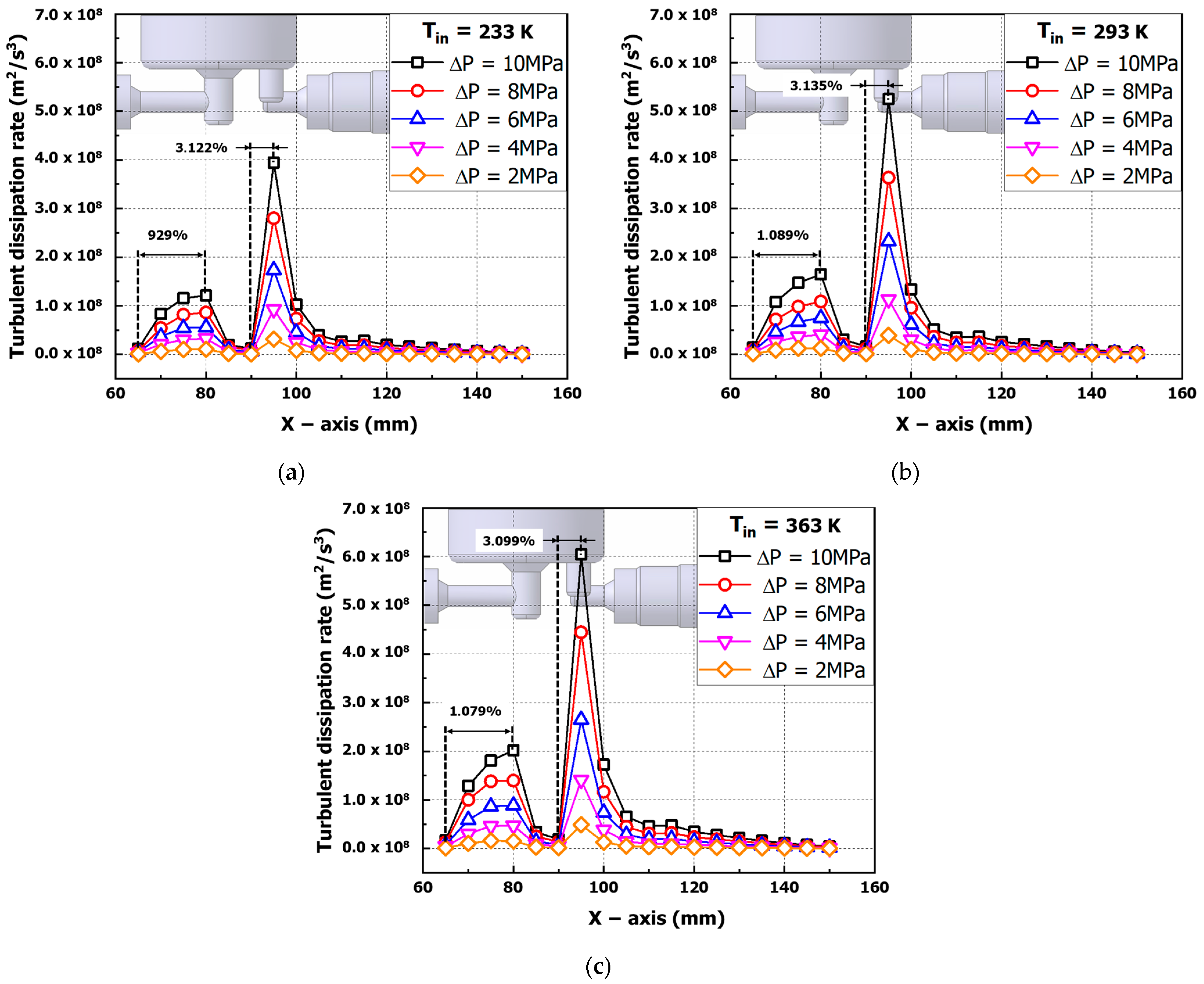
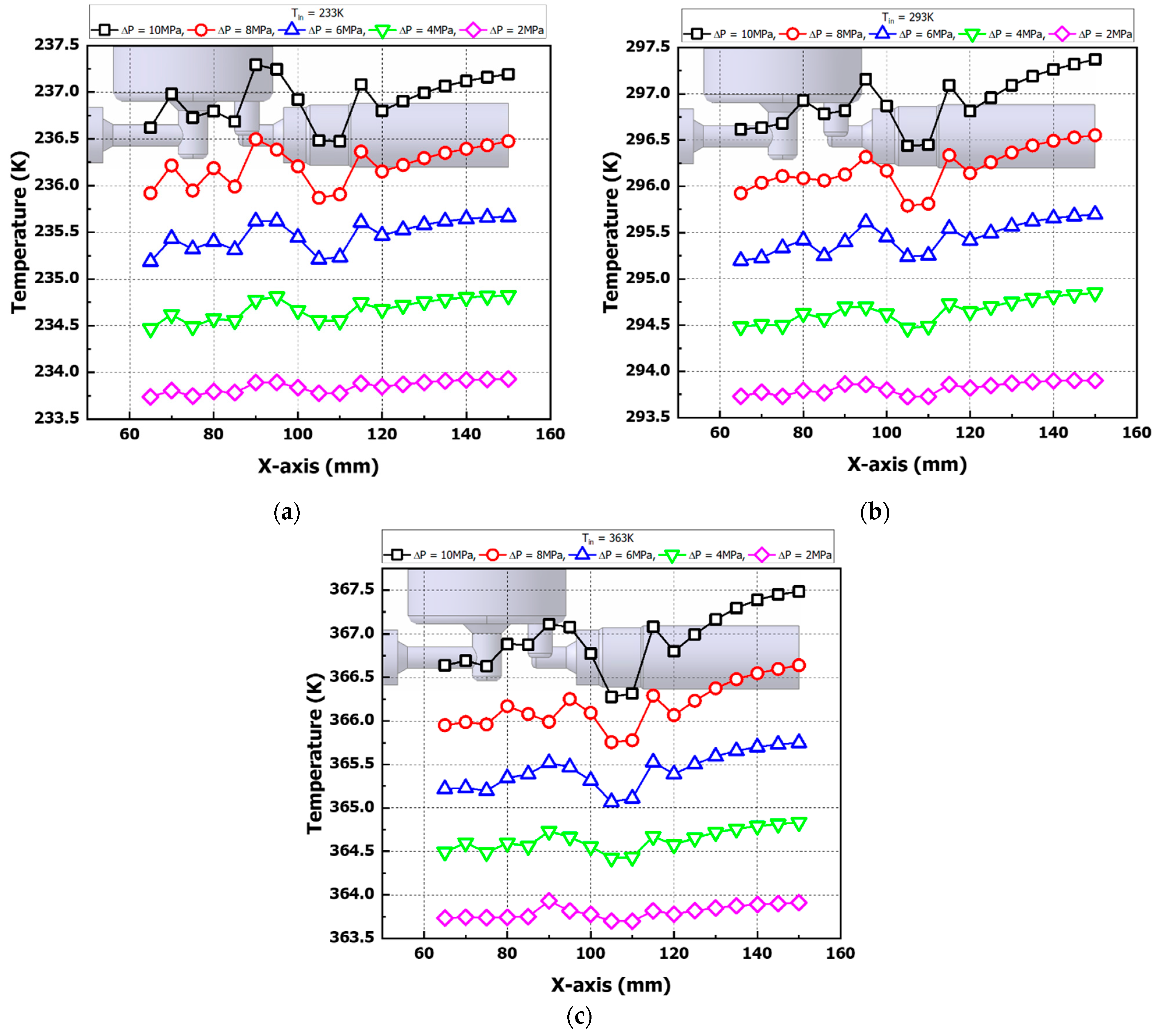
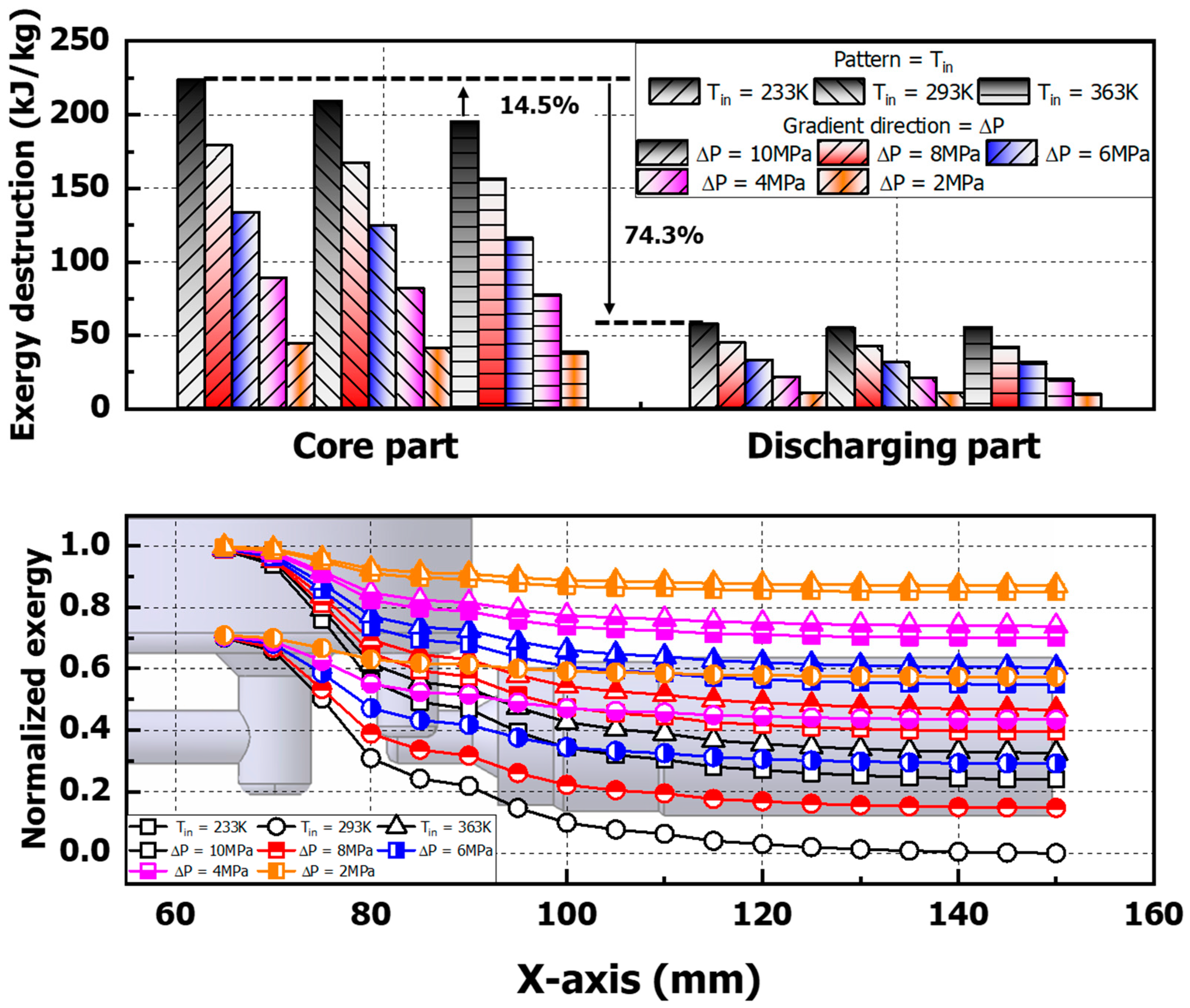
3.3. Analysis of Turbulent Dissipation Rate (TDR) and Exergy Destruction Results at Check-Valve Part Location
4. Conclusions
- (1)
- In the case of a differential pressure (ΔP) of 10 MPa and a hydrogen-inlet temperature (Tin) of 363 K at the point X = 90.7 mm in the L-shaped curved tube area of the check valve, the flow rate at the point Y = 2.3 mm at the top of the valve decreases by up to approximately 60%, and it is found that the flow rate decreases and the pressure increases due to the viscosity of the wall surface, forming a separation point.
- (2)
- The flow separation that occurs in an L-shaped curved tube causes a wake and reverse flow to form in the downstream region, which affects the delay in pressure recovery at the boundary layer and the occurrence of a recirculation area, and it reduces the flow area of the main flow, resulting in a bias towards the bottom of the check valve.
- (3)
- The pressure coefficient (CP) analysis shows that the pressure coefficient increases by up to 98% at the X = 91.7 mm measurement position in the (Tin) 233 K condition compared to the (Tin) 363 K condition. This is believed to be due to the fact that the increase in hydrogen-inlet temperature promotes flow reattachment within the boundary layer of the flow-separation region, which reduces the pressure change.
- (4)
- In the L-shaped curved tube region of the core part, the turbulent dissipation rate (TDR) at the X = 95 mm point increased by up to about 3000% compared to the X = 90 mm point, and the temperature results also increased by up to about 4.5 K compared to the inlet temperature. This is due to the conversion of the dissipated turbulent kinetic energy into heat energy, which is the major contributor to the temperature rise and energy loss of hydrogen.
- (5)
- The exergy destruction results show a 74% decrease in the discharging part compared to the core part for the (Tin) 233 K condition, and the differential pressure (∆P) increases by up to 14.6% for the 233 K condition compared to the (Tin) 363 K hydrogen-inlet temperature condition under the same conditions. This is believed to be due to the higher density at Tin of 233 K, which increases the viscosity dissipation within the boundary layer of the flow-separation zone and increases the temperature-rise rate and energy-dissipation rate, resulting in increased exergy destruction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Raorane, C.J.; Xia, C.; Wu, Y.; Tran, T.K.N.; Khademi, T. Latest Approaches on Green Hydrogen as a Potential Source of Renewable Energy Towards Sustainable Energy: Spotlighting of Recent Innovations, Challenges, and Future Insights. Fuel 2023, 334, 126684. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Q.; Yu, D. The Future of Hydrogen Energy: Bio-Hydrogen Production Technology. Int. J. Hydrog. Energy 2022, 47, 33677–33698. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Nasreen, S.; Hammoudeh, S.; Selmi, R. Dynamic Dependence of Oil, Clean Energy and the Role of Technology Companies: New Evidence from Copulas with Regime Switching. Energy 2021, 220, 119590. [Google Scholar] [CrossRef]
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen Production, Storage, Transportation and Key Challenges with Applications: A Review. Energy Convers. Manag. 2018, 165, 602–627. [Google Scholar] [CrossRef]
- Moradi, R.; Groth, K.M. Hydrogen Storage and Delivery: Review of the State of the Art Technologies and Risk and Reliability Analysis. Int. J. Hydrog. Energy 2019, 44, 12254–12269. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, X.; Xu, P.; Liu, P.; Zhao, Y.; Yang, J. Development of High Pressure Gaseous Hydrogen Storage Technologies. Int. J. Hydrog. Energy 2012, 37, 1048–1057. [Google Scholar] [CrossRef]
- Apostolou, D.; Xydis, G. A Literature Review on Hydrogen Refuelling Stations and Infrastructure. Current Status and Future Prospects. Renew. Sustain. Energy Rev. 2019, 113, 109292. [Google Scholar] [CrossRef]
- J2601_201612; Fueling Protocols for Light Duty Gaseous Hydrogen Surface Vehicles (J2601_201612). SAE International: Warrendale, PA, USA; p. 2016.
- Li, M.; Bai, Y.; Zhang, C.; Song, Y.; Jiang, S.; Grouset, D.; Zhang, M. Review on the Research of Hydrogen Storage System Fast Refueling in Fuel Cell Vehicle. Int. J. Hydrog. Energy 2019, 44, 10677–10693. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, X.; Bujlo, P.; Chen, B.; Zhang, X.; Sheng, X.; Liang, C. Review on the Safety Analysis and Protection Strategies of Fast Filling Hydrogen Storage System for Fuel Cell Vehicle Application. J. Energy Storage 2022, 45, 103451. [Google Scholar] [CrossRef]
- Soboleva, J.A.; Kerimov, A.M.; Anudinov, S.S.; Kocharov, M.A. Operation Simulation for a Check Valve used in High-Performance Systems. Civ. Eng. J. 2023, 9, 3202–3217. [Google Scholar] [CrossRef]
- Ye, J.; Zhao, Z.; Cui, J.; Hua, Z.; Peng, W.; Jiang, P. Transient Flow Behaviors of the Check Valve with Different Spool-Head Angle in High-Pressure Hydrogen Storage Systems. J. Energy Storage 2022, 46, 103761. [Google Scholar] [CrossRef]
- Yu, L.; Yang, X.; Zhang, Z.; Lin, Z.; Jin, Z.; Qian, J. Parametric Analysis on Throttling Elements of Conical Throttling Valve for Hydrogen Decompression in Hydrogen Fuel Cell Vehicles. J. Energy Storage 2023, 65, 107342. [Google Scholar] [CrossRef]
- Qian, J.; Chen, M.; Gao, Z.; Jin, Z. Mach Number and Energy Loss Analysis Inside Multi-Stage Tesla Valves for Hydrogen Decompression. Energy 2019, 179, 647–654. [Google Scholar] [CrossRef]
- Ariyadi, H.M.; Jeong, J.; Saito, K. Computational Analysis of Hydrogen Flow and Aerodynamic Noise Emission in a Solenoid Valve during Fast-Charging to Fuel Cell Automobiles. J. Energy Storage 2022, 45, 103661. [Google Scholar] [CrossRef]
- Jin, X.; Shen, C.; Wu, X. Numerical Study on Regenerative Cooling Characteristics of Kerosene Scramjets. Int. J. Aerosp. Eng. 2020, 2020, 8813929. [Google Scholar] [CrossRef]
- Mi, J.; Yu, J.; Huang, G. Direct-Drive Electro-Hydraulic Servo Valve Performance Characteristics Prediction Based on Big Data and Neural Networks. Sensors 2023, 23, 7211. [Google Scholar] [CrossRef]
- Dindorf, R. Study of the Energy Efficiency of Compressed Air Storage Tanks. Sustainability 2024, 16, 1664. [Google Scholar] [CrossRef]
- Oosthuizen, P.H.; Carscallen, W.E. Introduction to Compressible Fluid Flow; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty due to Discretization in CFD Applications. J. Fluids Eng. Trans. ASME 2008, 130, 078001. [Google Scholar] [CrossRef]
- Shih, T. A Realizable Reynolds Stress Algebraic Equation Model; National Aeronautics and Space Administration: Washington, DC, USA, 1993; Volume 105993. [Google Scholar]
- Shih, T.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New K-Ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Shih, T.; Zhu, J.; Lumley, J.L. A New Reynolds Stress Algebraic Equation Model. Comput. Methods Appl. Mech. Eng. 1995, 125, 287–302. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, B.; She, X.; Luo, Y.; Sun, Q.; Teng, L. Numerical Study on the Behavior and Design of a Novel Multistage Hydrogen Pressure-Reducing Valve. Int. J. Hydrog. Energy 2022, 47, 14646–14657. [Google Scholar] [CrossRef]
- Ansys Fluent Theory Guide; Ansys lnc.: Canonsburg, PA, USA, 2023.
- Liu, X.; Farhat, M.; Li, Y.; Liu, Z.; Yang, W. Onset of Flow Separation Phenomenon in a Low-Specific Speed Centrifugal Pump Impeller. J. Fluids Eng. 2023, 145, 021206. [Google Scholar] [CrossRef]
- Hwang, H.; Woo, S.; Han, S. Boil-Off Gas Generation in Vacuum-Jacketed Valve used in Liquid Hydrogen Storage Tank. Energies 2024, 17, 2341. [Google Scholar] [CrossRef]
- Wang, Y.; Semlitsch, B.; Mihaescu, M.; Fuchs, L. Flow Induced Energy Losses in the Exhaust Port of an Internal Combustion Engine. J. Fluids Eng. 2015, 137, 011105. [Google Scholar] [CrossRef]
- Hendricks, R.C.; Peller, I.C.; Baron, A.K. Joule-Thomson Inversion Curves and Related Coefficients for several Simple Fluids. In Joule-Thomson Inversion Curves and Related Coefficients for Several Simple Fluids; National Aeronautics and Space Administration: Washington, DC, USA, 1972. [Google Scholar]

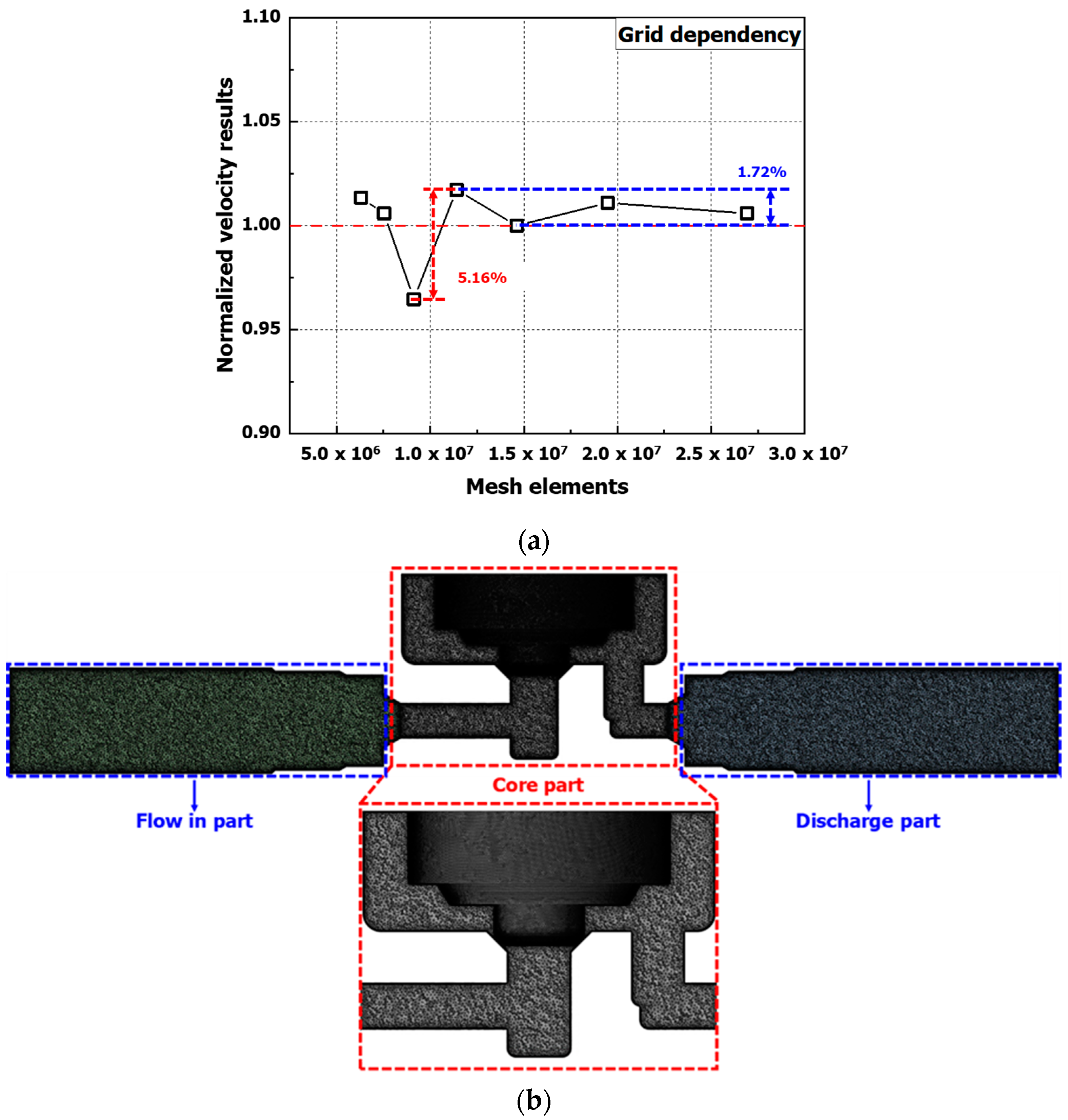

| Specification of Check Valve | |
|---|---|
| Valve length (mm) | 150 |
| Valve height (mm) | 29 |
| Inlet and outlet diameter (mm) | 15.2 |
| Parameters | Conditions |
|---|---|
| Turbulence model | Realizable |
| Real gas equation | SRK EOS |
| Inlet pressure (MPa) | 70 |
| Differential pressure (MPa) | 2, 4, 6, 8, 10 |
| H2 temperature (K) | 233, 293, 363 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, S.-H.; Jang, S.-M.; Suh, H.-K. High-Pressure Hydrogen Charge Check-Valve Energy Loss-Based Correlation Analysis Affecting Internal Flow Characterizations. Appl. Sci. 2025, 15, 1428. https://doi.org/10.3390/app15031428
Oh S-H, Jang S-M, Suh H-K. High-Pressure Hydrogen Charge Check-Valve Energy Loss-Based Correlation Analysis Affecting Internal Flow Characterizations. Applied Sciences. 2025; 15(3):1428. https://doi.org/10.3390/app15031428
Chicago/Turabian StyleOh, Seung-Hun, Sun-Min Jang, and Hyun-Kyu Suh. 2025. "High-Pressure Hydrogen Charge Check-Valve Energy Loss-Based Correlation Analysis Affecting Internal Flow Characterizations" Applied Sciences 15, no. 3: 1428. https://doi.org/10.3390/app15031428
APA StyleOh, S.-H., Jang, S.-M., & Suh, H.-K. (2025). High-Pressure Hydrogen Charge Check-Valve Energy Loss-Based Correlation Analysis Affecting Internal Flow Characterizations. Applied Sciences, 15(3), 1428. https://doi.org/10.3390/app15031428






