New Hybrid Approaches Based on Swarm-Based Metaheuristic Algorithms and Applications to Optimization Problems
Abstract
1. Introduction
- Based on HHO, the WOA, and PSO, this work has presented four novel hybrid approaches dubbed HHHOWOA1, HHHOWOA2, HHHOWOA1PSO, and HHHOWOA2PSO.
- The HHHOWOA1 and HHHOWOA2 methodologies are developed by modifying the equations utilized in the exploitation phase of the WOA and subsequently applying these modifications in the exploitation phase of Harris Hawks Optimization (HHO). The HHHOWOA1PSO and HHHOWOA2PSO methodologies are developed by using modified PSO equations during the final stages of the HHHOWOA1 and HHHOWOA2 algorithms. Both the WOA and HHO algorithms have been improved because of these new hybrid techniques.
- The general problems of metaheuristic algorithms that often involve getting stuck in local optima, low diversity, and imbalanced exploitation capabilities have been further improved. So, the optimization search capability has been further improved, and the probability of the optimal value falling to a local minimum has been further reduced.
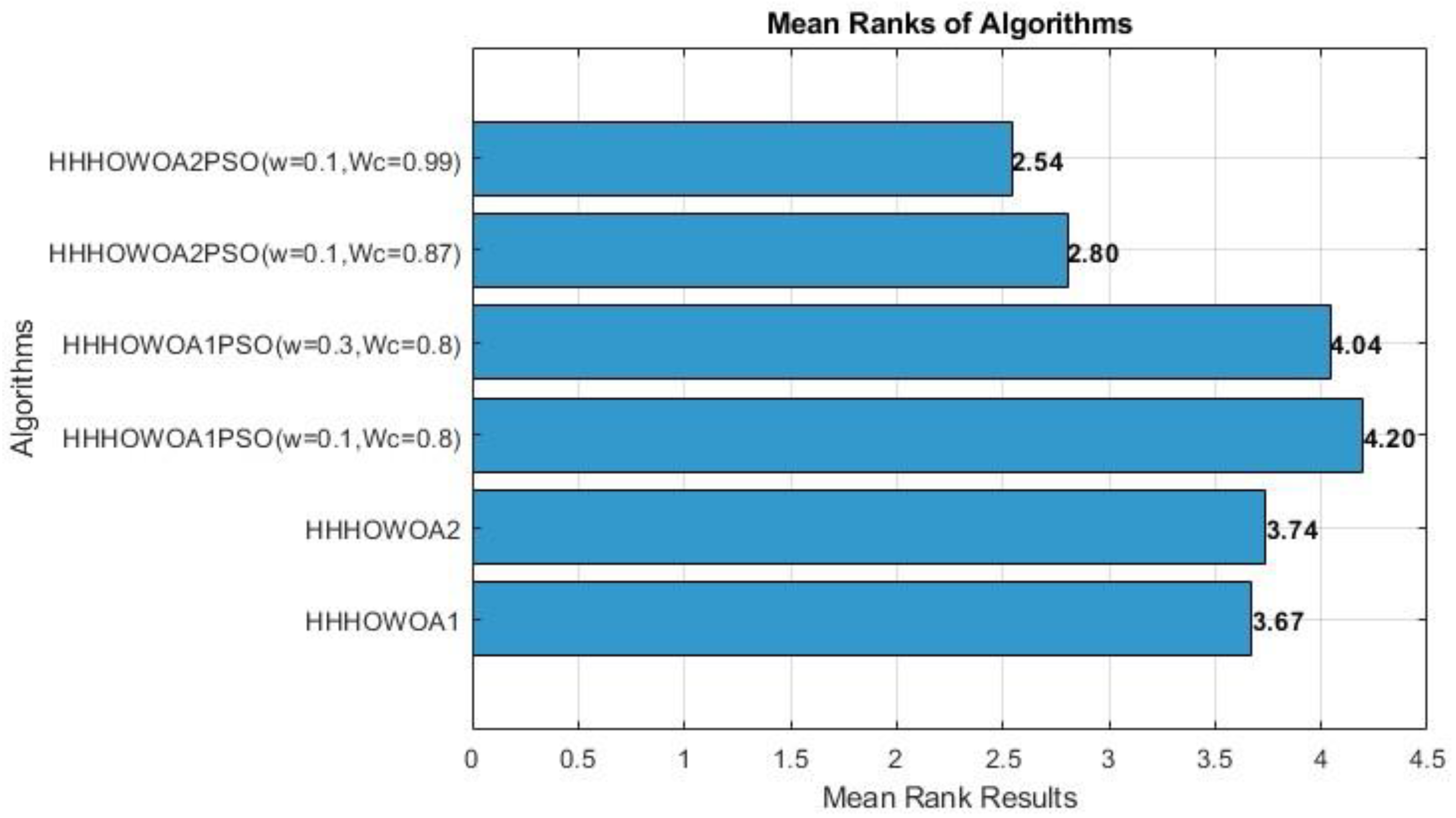
- The proposed four novel hybrid approaches were evaluated on 23 benchmark functions and compared to the results of the publications using the same parameters. For these 23 functions, Friedman rank tests were performed based on the average optimization results of all algorithms. It was observed that the HHHOWOA2PSO approach is ranked first, followed by the HHHOWOA1 approach, in the success ranking for the F1–F23 functions.
- The HHHOWOA1, HHHOWOA2, and HHHOWOA2PSO approaches are applied to three benchmark problems in engineering, and the optimum values obtained are compared with the literature.
2. Preliminaries
2.1. Harris Hawks Optimization (HHO)
2.2. Exploration Phase of HHO
2.3. Exploration to Exploitation Transition of HHO
2.4. Exploitation Phase of HHO
2.5. Whale Optimization Algorithm (WOA)
2.6. Exploitation Phase of WOA
2.7. Exploration Phase of WOA
2.8. Particle Swarm Optimization (PSO)
3. The Proposed Approaches
3.1. HHHOWOA1 and HHHOWOA2 Approaches
3.2. HHHOWOA1PSO and HHHOWOA2PSO Approaches
4. Results and Discussion
4.1. Experimental Setup and Benchmark Sets
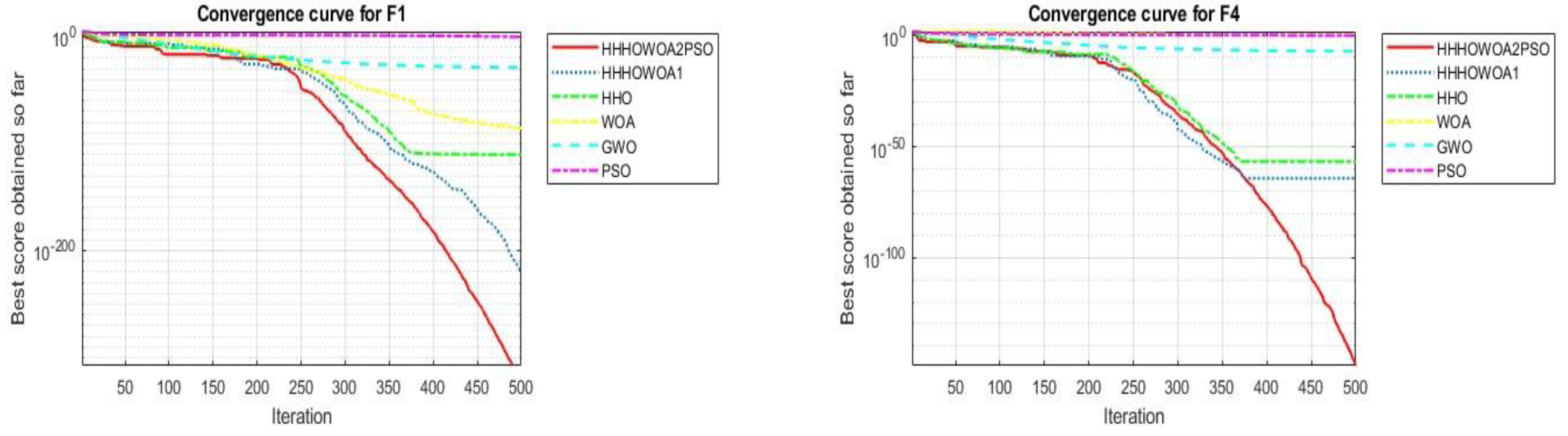
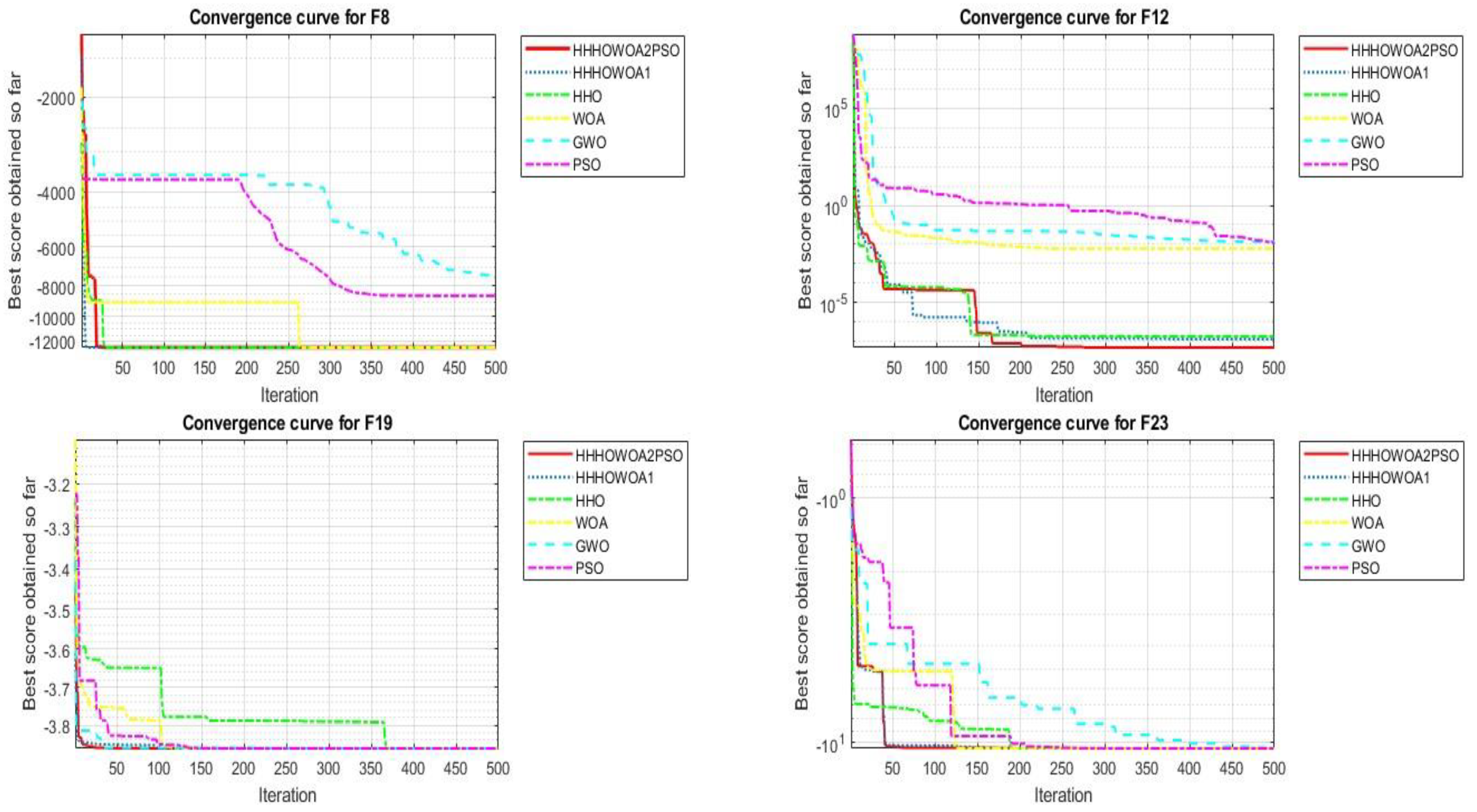
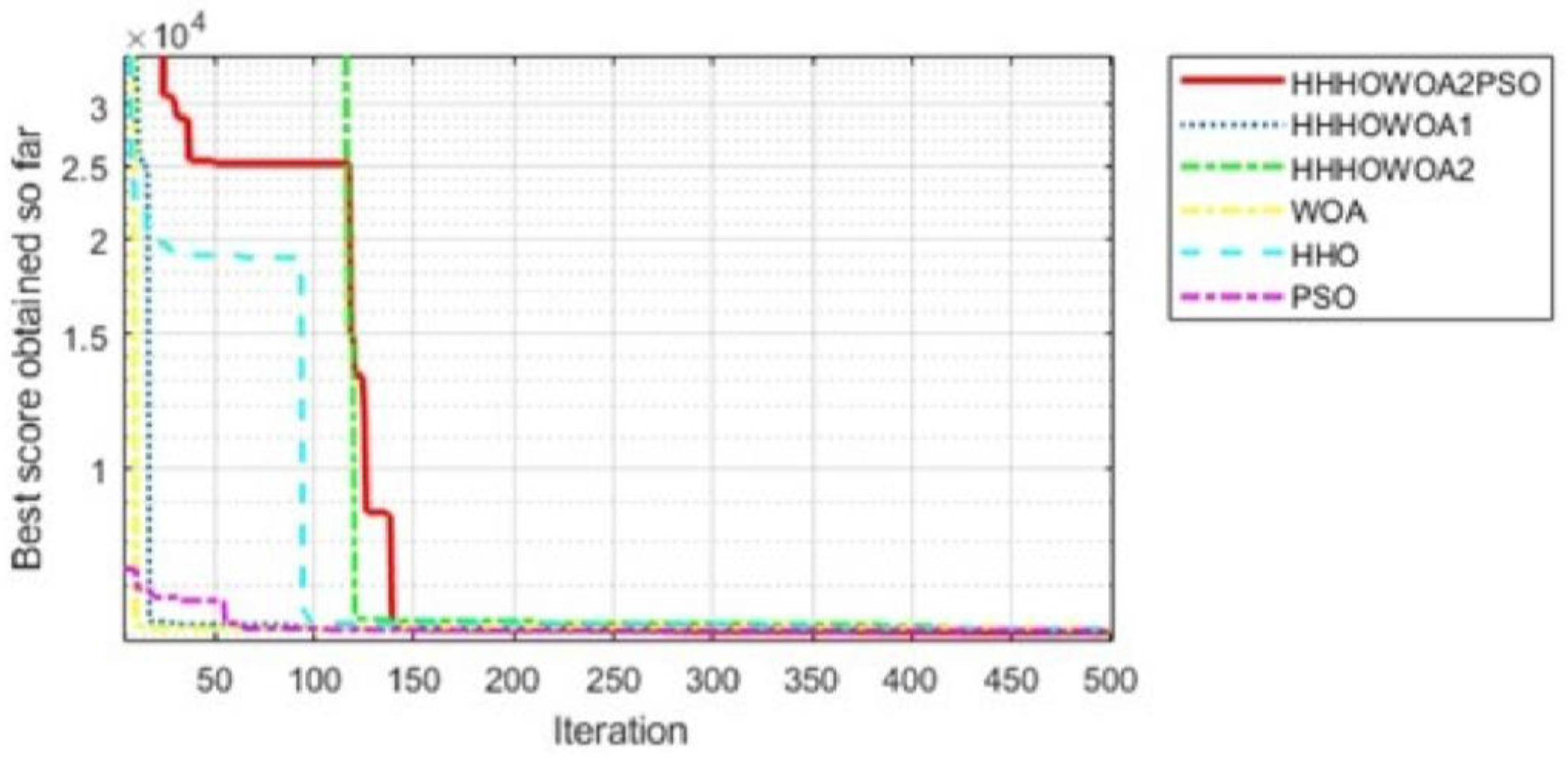
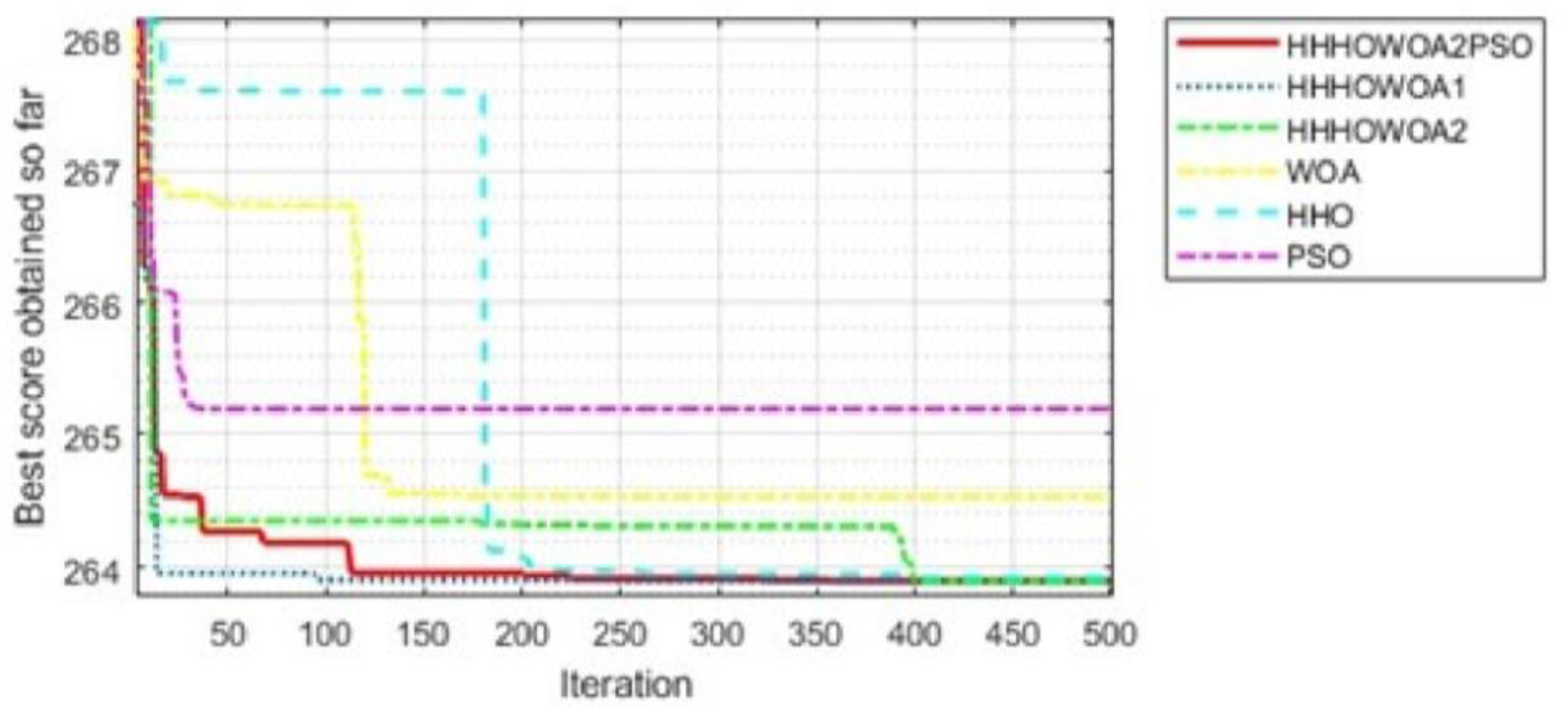
4.2. Comparison of Proposed Algorithms Among Themselves
4.3. Comparison of the Proposed Approaches with the Literature
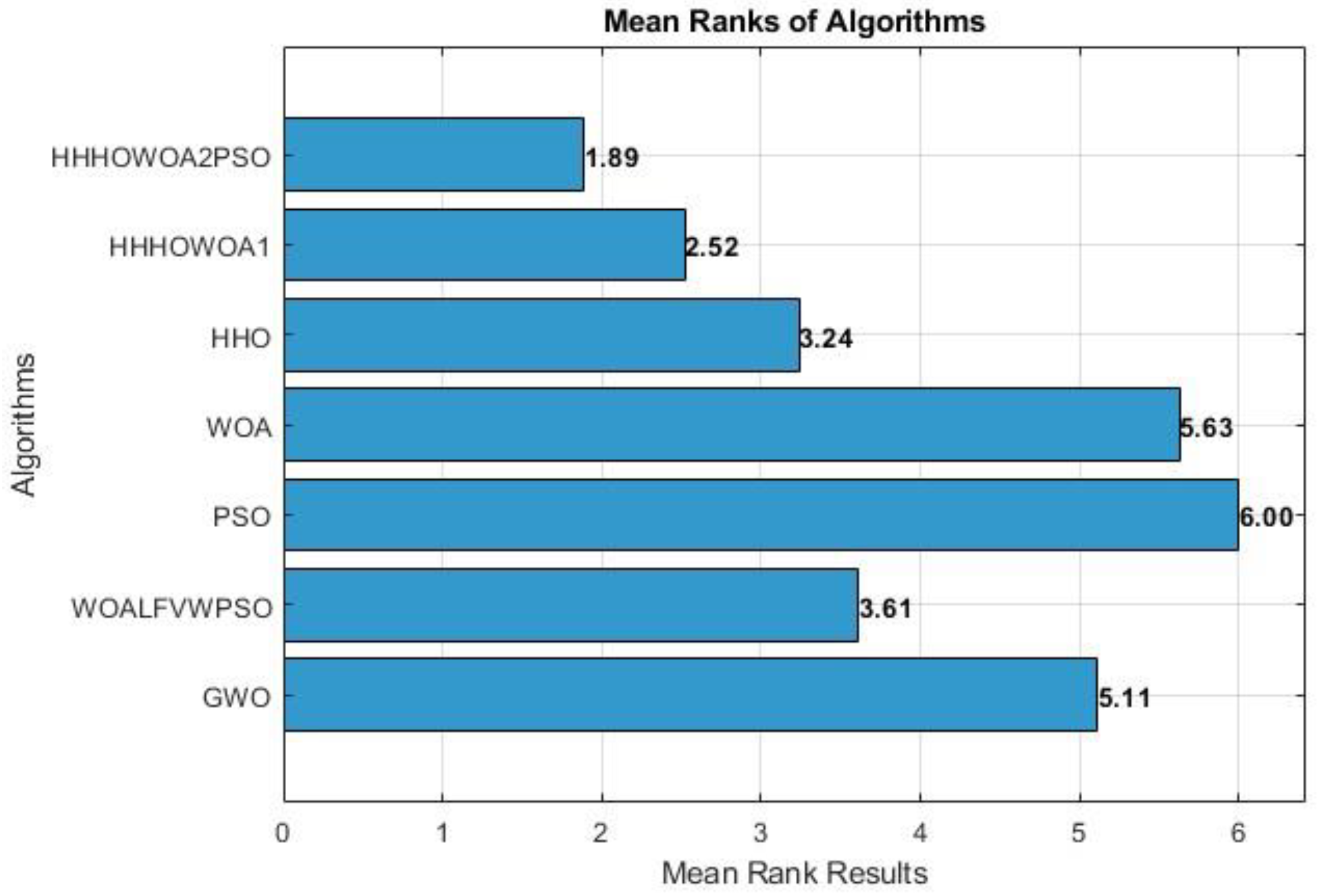
4.4. Statistical Analysis
4.5. Application of the Proposed Approaches to Engineering Problems
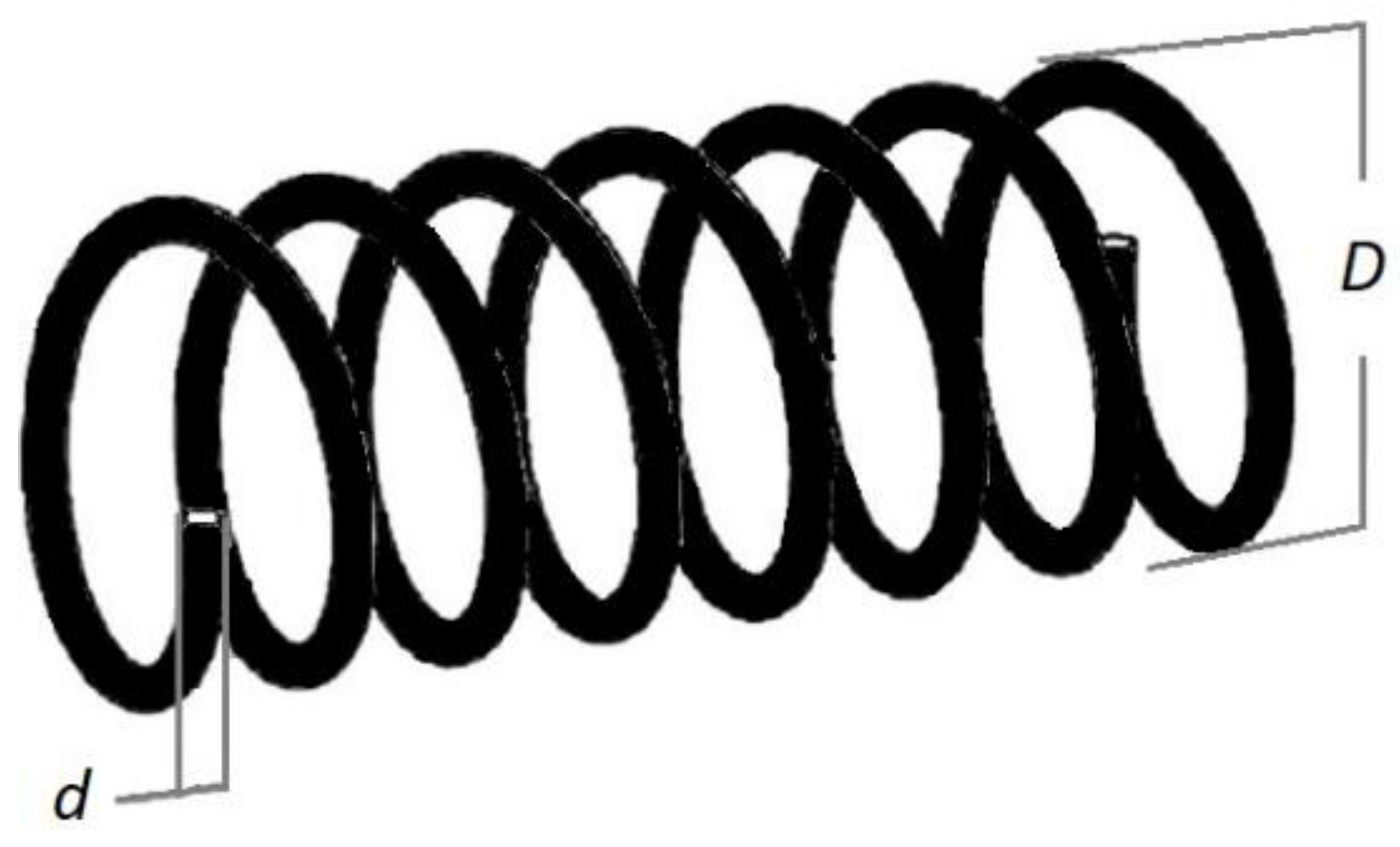
4.6. Tension–Compression Spring Design Problem
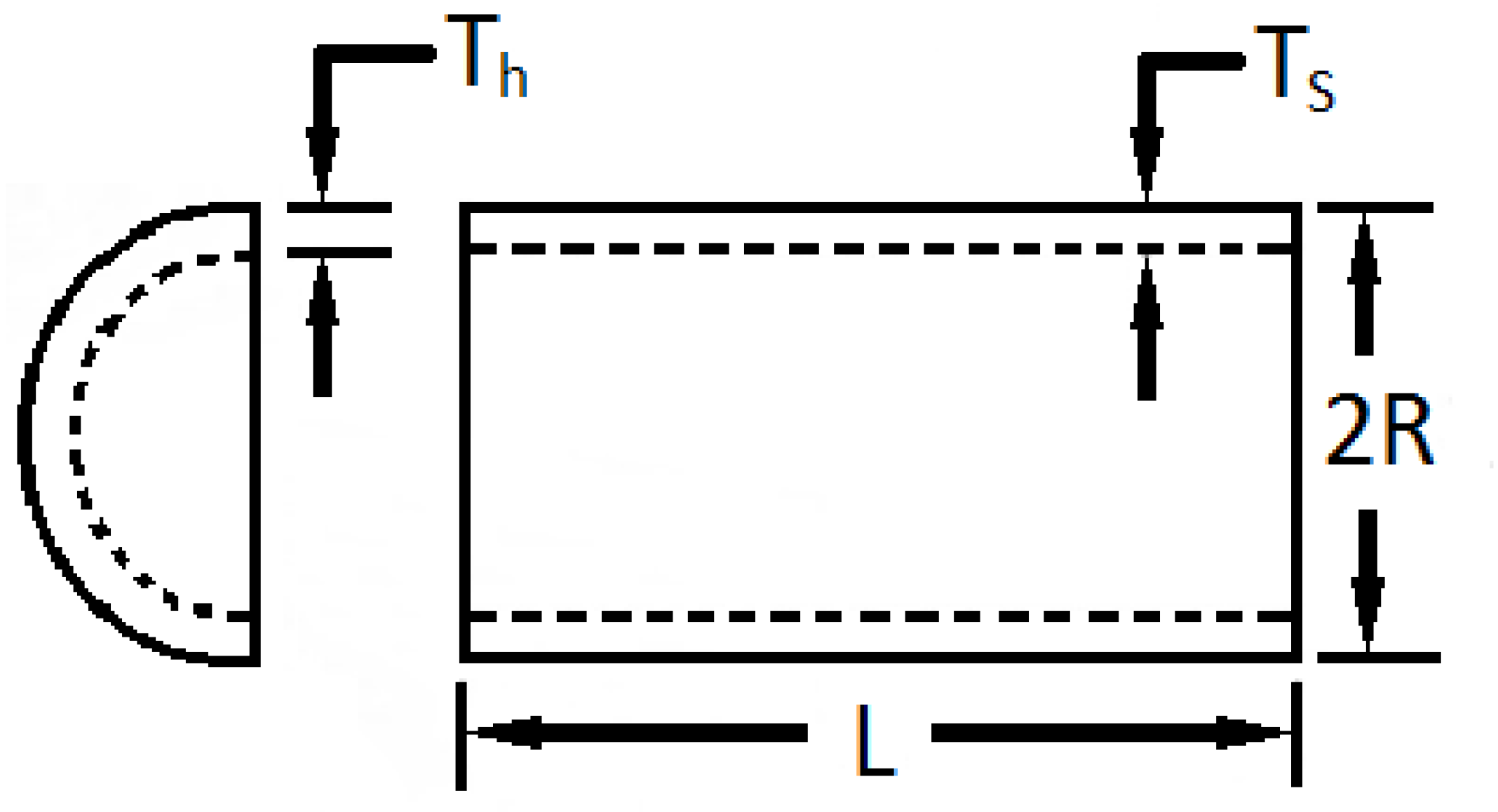
4.7. Pressure Vessel Design Problem
4.8. Three-Bar Truss Design Problem
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asghari, K.; Masdari, M.; Gharehchopogh, F.S.; Saneifard, R. Multi-swarm and chaotic whale-particle swarm optimization algorithm with a selection method based on roulette wheel. Expert Syst. 2021, 38, 44. [Google Scholar] [CrossRef]
- Wang, L.P.; Han, J.H.; Ma, F.J.; Li, X.K.; Wang, D. Accuracy design optimization of a CNC grinding machine towards low-carbon manufacturing. J. Clean. Prod. 2023, 406, 14. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Fogel, D.B. How to Solve It: Modern Heuristics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Hromkovič, J. Algorithmics for Hard Problems: Introduction to Combinatorial Optimization, Randomization, Approximation, and Heuristics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Uzer, M.S.; Inan, O. Application of improved hybrid whale optimization algorithm to optimization problems. Neural Comput. Appl. 2023, 35, 12433–12451. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L. A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization. J. Appl. Math. 2013, 2013, 696491. [Google Scholar] [CrossRef]
- Irmak, B.; Karakoyun, M.; Gülcü, S. An improved butterfly optimization algorithm for training the feed-forward artificial neural networks. Soft Comput. 2023, 27, 3887–3905. [Google Scholar] [CrossRef]
- Nguyen, P.T. Construction site layout planning and safety management using fuzzy-based bee colony optimization model. Neural Comput. Appl. 2021, 33, 5821–5842. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D. Fuzzy adaptive teaching–learning-based optimization for global numerical optimization. Neural Comput. Appl. 2018, 29, 309–327. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hosney, M.E.; Mohamed, W.M.; Ali, A.A.; Younis, E.M.G. Fuzzy-based hunger games search algorithm for global optimization and feature selection using medical data. Neural Comput. Appl. 2023, 35, 5251–5275. [Google Scholar] [CrossRef] [PubMed]
- Uzer, M.S.; Inan, O. A novel feature selection using binary hybrid improved whale optimization algorithm. J. Supercomput. 2023, 79, 10020–10045. [Google Scholar] [CrossRef]
- Hussain, K.; Mohd Salleh, M.N.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Meraihi, Y.; Gabis, A.B.; Mirjalili, S.; Ramdane-Cherif, A. Grasshopper Optimization Algorithm: Theory, Variants, and Applications. IEEE Access 2021, 9, 50001–50024. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated Local Search. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; Springer: Boston, MA, USA, 2003; pp. 320–353. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Voudouris, C.; Tsang, E. Guided local search and its application to the traveling salesman problem. Eur. J. Oper. Res. 1999, 113, 469–499. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H.L. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Kaya, E.; Gorkemli, B.; Akay, B.; Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Eng. Appl. Artif. Intell. 2022, 115, 105311. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Arora, S.; Anand, P. Binary butterfly optimization approaches for feature selection. Expert Syst. Appl. 2019, 116, 147–160. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowl.-Based Syst. 2018, 159, 20–50. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Zhu, G.Y.; Zhang, W.B. Optimal foraging algorithm for global optimization. Appl. Soft Comput. 2017, 51, 294–313. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Furio, C.; Lamberti, L.; Pruncu, C.I. An Efficient and Fast Hybrid GWO-JAYA Algorithm for Design Optimization. Appl. Sci. 2024, 14, 9610. [Google Scholar] [CrossRef]
- Knypinski, L.; Devarapalli, R.; Gillon, F. The hybrid algorithms in constrained optimization of the permanent magnet motors. IET Sci. Meas. Technol. 2024, 18, 613–619. [Google Scholar] [CrossRef]
- Ramachandran, M.; Mirjalili, S.; Nazari-Heris, M.; Parvathysankar, D.S.; Sundaram, A.; Charles Gnanakkan, C.A.R. A hybrid Grasshopper Optimization Algorithm and Harris Hawks Optimizer for Combined Heat and Power Economic Dispatch problem. Eng. Appl. Artif. Intell. 2022, 111, 104753. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Wunnava, A.; Jena, B.; Abraham, A. A leader Harris hawks optimization for 2-D Masi entropy-based multilevel image thresholding. Multimed. Tools Appl. 2021, 80, 35543–35583. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Heidari, A.A.; Fujita, H.; Moayedi, H. A competitive chain-based Harris Hawks Optimizer for global optimization and multi-level image thresholding problems. Appl. Soft Comput. 2020, 95, 106347. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Loganathan, A.; Ahmad, N.S. A Hybrid HHO-AVOA for Path Planning of a Differential Wheeled Mobile Robot in Static and Dynamic Environments. IEEE Access 2024, 12, 25967–25979. [Google Scholar] [CrossRef]
- Prakasa, M.A.; Robandi, I.; Nishimura, R.; Djalal, M.R. A New Scheme of Harris Hawk Optimizer with Memory Saving Strategy (HHO-MSS) for Controlling Parameters of Power System Stabilizer and Virtual Inertia in Renewable Microgrid Power System. IEEE Access 2024, 12, 73849–73878. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Chelloug, S.; Alduailij, M.; Al-qaness, M.A.A. Boosted Reptile Search Algorithm for Engineering and Optimization Problems. Appl. Sci. 2023, 13, 3206. [Google Scholar] [CrossRef]
- Li, Q.H.; Shi, H.; Zhao, W.T.; Ma, C.L. Enhanced Dung Beetle Optimization Algorithm for Practical Engineering Optimization. Mathematics 2024, 12, 1084. [Google Scholar] [CrossRef]
- Ouyang, C.T.; Liao, C.; Zhu, D.L.; Zheng, Y.Y.; Zhou, C.J.; Zou, C.Y. Compound improved Harris hawks optimization for global and engineering optimization. Clust. Comput. 2024, 27, 9509–9568. [Google Scholar] [CrossRef]
- Shehadeh, H.A. A hybrid sperm swarm optimization and gravitational search algorithm (HSSOGSA) for global optimization. Neural Comput. Appl. 2021, 33, 11739–11752. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Xu, Y.B.; Zhang, J.Z. A Hybrid Nonlinear Whale Optimization Algorithm with Sine Cosine for Global Optimization. Biomimetics 2024, 9, 602. [Google Scholar] [CrossRef]
- Hubálovsky, S.; Hubálovská, M.; Matousová, I. A New Hybrid Particle Swarm Optimization-Teaching-Learning-Based Optimization for Solving Optimization Problems. Biomimetics 2024, 9, 8. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Kadir, S.J.A.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Binary Optimization Using Hybrid Grey Wolf Optimization for Feature Selection. IEEE Access 2019, 7, 39496–39508. [Google Scholar] [CrossRef]
- Heidari, A.A.; Ali Abbaspour, R.; Rezaee Jordehi, A. An efficient chaotic water cycle algorithm for optimization tasks. Neural Comput. Appl. 2017, 28, 57–85. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng. Appl. Artif. Intell. 2007, 20, 89–99. [Google Scholar] [CrossRef]
- Liu, H.; Cai, Z.; Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]






| Num. of Func. | Function | Var. Num | Boundary (Lower–Upper) | fmin |
|---|---|---|---|---|
| 30 | LB = −100, UB = 100 | 0 | ||
| 30 | LB = −10, UB = 10 | 0 | ||
| 30 | LB = −100, UB = 100 | 0 | ||
| 30 | LB = −100, UB = 100 | 0 | ||
| 30 | LB = −30, UB = 30 | 0 | ||
| 30 | LB = −100, UB = 100 | 0 | ||
| 30 | LB = −1.28, UB = 1.28 | 0 |
| Num. of Func. | Function | Var. Num | Boundary (Lower–Upper) | fmin |
|---|---|---|---|---|
| 30 | LB = −500, UB = 500 | −418.9829×D | ||
| 30 | LB = −5.12, UB = 5.12 | 0 | ||
| 30 | LB = −32, UB = 32 | 0 | ||
| 30 | LB = −600, UB = 600 | 0 | ||
| 30 | LB = −50, UB = 50 | 0 | ||
| 30 | LB = −50, UB = 50 | 0 |
| Num. of Func. | Function | Var. Num | Boundary (Lower–Upper) | fmin |
|---|---|---|---|---|
| 2 | LB = −65, UB = 65 | 1 | ||
| 4 | LB = −5, UB = 5 | 0.00030 | ||
| 2 | LB = −5, UB = 5 | −1.0316 | ||
| 2 | LB = −5, UB = 5 | 0.398 | ||
| 2 | LB = −2, UB = 2 | 3 | ||
| 3 | LB = 1, UB = 3 | −3.86 | ||
| 6 | LB = 0, UB = 1 | −3.32 | ||
| 4 | LB = 0, UB = 10 | −10.1532 | ||
| 4 | LB = 0, UB = 10 | −10.4028 | ||
| 4 | LB = 0, UB = 10 | −10.5363 |
| Func Num | fmin (Target Value) | HHHOWOA1 | HHHOWOA2 | HHHOWOA1PSO (w = 0.1, Wc = 0.8) | HHHOWOA1PSO (w = 0.3, Wc = 0.8) | HHHOWOA2PSO (w = 0.1, Wc = 0.87) | HHHOWOA2PSO (w = 0.1, Wc = 0.99) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | ||
| F1 | 0 | 7.5688 × 10−163 | 3.1435 × 10−162 | 4.4183 × 10−279 | 0 | 4.9168 × 10−223 | 0 | 1.7489 × 10−185 | 0 | 0 | 0 | 0 | 0 |
| F2 | 0 | 6.3749 × 10−112 | 1.4659 × 10−111 | 5.3520 × 10−141 | 1.6592 × 10−140 | 2.6277 × 10−144 | 7.7444 × 10−144 | 9.3859 × 10−116 | 1.4463 × 10−115 | 5.0998 × 10−165 | 0 | 1.3642 × 10−143 | 2.4035 × 10−143 |
| F3 | 0 | 9.7687 × 10−86 | 2.6715 × 10−85 | 1.0246 × 10−247 | 0 | 5.2309 × 10−139 | 1.8573 × 10−138 | 3.3371 × 10−122 | 7.6236 × 10−122 | 5.5734 × 10−297 | 0 | 5.8706 × 10−257 | 0 |
| F4 | 0 | 7.2856 × 10−58 | 1.4966 × 10−57 | 3.3849 × 10−140 | 7.6830 × 10−140 | 5.9403 × 10−88 | 1.3481 × 10−87 | 5.7732 × 10−76 | 8.4847 × 10−76 | 5.1158 × 10−163 | 0 | 5.1401 × 10−143 | 8.5271 × 10−143 |
| F5 | 0 | 1.58 × 10−2 | 1.28 × 10−2 | 1.80 × 10−2 | 1.5347 × 10−2 | 3.00 × 10−3 | 3.100 × 10−3 | 1.700 × 10−3 | 1.500 × 10−3 | 1.700 × 10−3 | 1.300 × 10−3 | 8.1582 × 10−3 | 5.99452 × 10−3 |
| F6 | 0 | 5.5635 × 10−5 | 5.2482 × 10−5 | 6.9172 × 10−5 | 5.2127 × 10−5 | 6.4207 × 10−6 | 5.9199 × 10−6 | 6.4379 × 10−6 | 5.1401 × 10−6 | 5.6822 × 10−6 | 5.0890 × 10−6 | 4.7299 × 10−5 | 3.30251 × 10−5 |
| F7 | 0 | 4.1742 × 10−5 | 1.2773 × 10−4 | 6.1309 × 10−5 | 1.3507 × 10−4 | 5.4657 × 10−5 | 6.6645 × 10−5 | 5.0220 × 10−5 | 9.1324 × 10−5 | 5.1236 × 10−5 | 1.3246 × 10−4 | 4.1047 × 10−5 | 1.2278 × 10−4 |
| F8 | −418.9829 × D(30) | −1.2569 × 104 | 1.628 × 10−1 | −1.2569 × 104 | 5.435 × 10−2 | −1.2569 × 104 | 4.451 × 10−1 | −1.2569 × 104 | 6.4170 × 10−1 | −1.2569 × 104 | 8.7722 × 10−4 | −1.2569 × 104 | 1.0250 × 10−1 |
| F9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F10 | 0 | 4.4409 × 10−16 | 0 | 4.4409 × 10−16 | 0 | 4.4409 × 10−16 | 0 | 4.4409 × 10−16 | 0 | 4.4409 × 10−16 | 0 | 4.4409 × 10−16 | 0 |
| F11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F12 | 0 | 2.9442 × 10−6 | 3.3438 × 10−5 | 4.2180 × 10−6 | 3.0745 × 10−6 | 9.6399 × 10−7 | 6.0726 × 10−7 | 1.0427 × 10−6 | 6.6825 × 10−7 | 1.2621 × 10−6 | 8.3728 × 10−7 | 1.4922 × 10−6 | 1.3570 × 10−5 |
| F13 | 0 | 4.1390 × 10−5 | 4.4308 × 10−5 | 4.5853 × 10−5 | 3.2563 × 10−5 | 1.1479 × 10−5 | 8.4429 × 10−6 | 8.2899 × 10−6 | 5.8436 × 10−6 | 1.4609 × 10−5 | 1.2821 × 10−5 | 2.84662 × 10−5 | 2.10999 × 10−5 |
| F14 | 1 | 9.980 × 10−1 | 3.7366 × 10−10 | 9.980 × 10−1 | 3.1807 × 10−13 | 9.980 × 10−1 | 5.6249 × 10−9 | 9.980 × 10−1 | 6.5476 × 10−8 | 9.980 × 10−1 | 1.6636 × 10−7 | 9.980 × 10−1 | 3.16591 × 10−10 |
| F15 | 0.00030 | 3.0959 × 10−4 | 2.8224 × 10−5 | 3.1268 × 10−4 | 4.0431 × 10−6 | 3.2521 × 10−4 | 8.9993 × 10−6 | 3.2340 × 10−4 | 1.0263 × 10−5 | 3.1874 × 10−4 | 3.2332 × 10−5 | 3.0873 × 10−4 | 2.5451 × 10−4 |
| F16 | −1.0316 | −1.0316 | 4.3281 × 10−11 | −1.0316 | 4.8945 × 10−10 | −1.0314 | 1.3373 × 10−4 | −1.0314 | 1.5692 × 10−4 | −1.0316 | 1.8940 × 10−5 | −1.0316 | 8.81347 × 10−8 |
| F17 | 0.398 | 3.979 × 10−1 | 3.8425 × 10−6 | 0.3979 | 1.4877 × 10−8 | 0.3997 | 6.7899 × 10−2 | 3.979 × 10−1 | 9.3412 × 10−5 | 3.979 × 10−1 | 4.6079 × 10−5 | 3.979 × 10−1 | 1.8607 × 10−5 |
| F18 | 3 | 3.0000 | 2.9879 × 10−14 | 3.0000 | 1.1148 × 10−14 | 3.0003 | 2.9895 × 10−4 | 3.0003 | 2.4535 × 10−4 | 3.0000 | 3.2568 × 10−5 | 3.0000 | 8.0118 × 10−8 |
| F19 | −3.86 | −3.8623 | 7.1386 × 10−4 | −3.8618 | 8.5670 × 10−4 | −3.8564 | 4.6 × 10−3 | −3.8559 | 7.3651 × 10−3 | −3.8617 | 9.5276 × 10−4 | −3.8615 | 9.7288 × 10−4 |
| F20 | −3.32 | −3.3188 | 2.7279 × 10−3 | −3.3182 | 6.9643 × 10−2 | −3.2752 | 2.80 × 10−2 | −3.2851 | 2.20 × 10−2 | −3.3060 | 7.8 × 10−3 | −3.3191 | 2.1882 × 10−3 |
| F21 | −10.1532 | −1.01531 × 101 | 1.0309 × 10−4 | −1.01529 × 101 | 2.3945 × 10−4 | −9.8868 | 1.767 × 10−1 | −1.00392 × 101 | 6.43 × 10−2 | −1.00735 × 101 | 3.66 × 10−2 | −1.01530 × 101 | 1.5709 × 10−4 |
| F22 | −10.4028 | −1.04027 × 101 | 2.4422 × 10−4 | −1.04027 × 101 | 1.6608 × 10−4 | −1.00626 × 101 | 1.696 × 10−1 | −1.02935 × 101 | 7.40 × 10−2 | −1.03223 × 101 | 5.26 × 10−2 | −1.04028 × 101 | 1.6801 × 10−4 |
| F23 | −10.5363 | −1.05363 × 101 | 1.4095 × 10−4 | −1.05362 × 101 | 1.7339 × 10−4 | −1.02332 × 101 | 1.818 × 10−1 | −1.03978 × 101 | 8.14 × 10−2 | −1.04300 × 101 | 5.85 × 10−2 | −1.05363 × 101 | 1.0364 × 10−4 |
| Friedman mean rank results | 3.6739 | 3.7391 | 4.1957 | 4.0435 | 2.8043 | 2.5435 | |||||||
| Friedman rank | 3 | 4 | 6 | 5 | 2 | 1 | |||||||
| Func Num | fmin (Target Value) | GWO [25] | WOALFVWPSO [5] | PSO [28] | WOA [28] | HHO [17] | HHHOWOA1 | HHHOWOA2PSO (w = 0.1, Wc = 0.99) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | ||
| F1 | 0 | 6.5900 × 10−28 | 6.3400 × 10−5 | 0 | 0 | 1.3600 × 10−4 | 2.0200 × 10−4 | 1.4100 × 10−30 | 4.9100 × 10−30 | 3.95 × 10−97 | 1.72 × 10−96 | 7.5688 × 10−163 | 3.1435 × 10−162 | 0 | 0 |
| F2 | 0 | 7.1800 × 10−17 | 2.9014 × 10−2 | 6.1126 × 10−186 | 0 | 4.2144 × 10−2 | 4.5421 × 10−2 | 1.0600 × 10−21 | 2.3900 × 10−21 | 1.56 × 10−51 | 6.98 × 10−51 | 6.3749 × 10−112 | 1.4659 × 10−111 | 1.3642 × 10−143 | 2.4035 × 10−143 |
| F3 | 0 | 3.2900 × 10−6 | 7.9150 × 101 | 4.9407 × 10−323 | 0 | 7.0126 × 101 | 2.2119 × 101 | 5.3900 × 10−7 | 2.9300 × 10−6 | 1.92 × 10−63 | 1.05 × 10−62 | 9.7687 × 10−86 | 2.6715 × 10−85 | 5.8706 × 10−257 | 0 |
| F4 | 0 | 5.6100 × 10−7 | 1.3151 × 100 | 7.0830 × 10−175 | 0 | 1.0865 × 100 | 3.1704 × 10−1 | 7.2581 × 10−2 | 3.9747 × 10−1 | 1.02 × 10−47 | 5.01 × 10−47 | 7.2856 × 10−58 | 1.4966 × 10−57 | 5.1401 × 10−143 | 8.5271 × 10−143 |
| F5 | 0 | 2.6813 × 101 | 6.9905 × 101 | 2.7672 × 101 | 4.3000 × 10−1 | 9.6718 × 101 | 6.0116 × 101 | 2.7866 × 101 | 7.6363 × 10−1 | 1.32 × 10−2 | 1.87 × 10−2 | 1.58 × 10−2 | 1.28 × 10−2 | 8.1582 × 10−3 | 5.99452 × 10−3 |
| F6 | 0 | 8.1658 × 10−1 | 1.2600 × 10−4 | 2.6074 × 10−1 | 2.2076 × 10−1 | 1.0200 × 10−4 | 8.2800 × 10−5 | 3.1163 × 100 | 5.3243 × 10−1 | 1.15 × 10−4 | 1.56 × 10−4 | 5.5635 × 10−5 | 5.2482 × 10−5 | 4.7299 × 10−5 | 3.30251 × 10−5 |
| F7 | 0 | 2.2130 × 10−3 | 1.0029 × 10−1 | 6.0582 × 10−5 | 5.8660 × 10−5 | 1.2285 × 10−1 | 4.4957 × 10−2 | 1.4250 × 10−3 | 1.1490 × 10−3 | 1.40 × 10−4 | 1.07 × 10−4 | 4.1742 × 10−5 | 1.2773 × 10−4 | 4.1047 × 10−5 | 1.2278 × 10−4 |
| F8 | −418.9829 × D(30) | −6.1231 × 103 | −4.0874 × 103 | −5.2568 × 103 | 1.3258 × 103 | −4.8413 × 103 | 1.1528 × 103 | −5.0808 × 103 | 6.9580 × 102 | −1.25 × 104 | 1.47 × 102 | −1.2569 × 104 | 1.628 × 10−1 | −1.2569 × 104 | 1.0250 × 10−1 |
| F9 | 0 | 3.1052 × 10−1 | 4.7356 × 101 | 0 | 0 | 4.6704 × 101 | 1.1629 × 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F10 | 0 | 1.0600 × 10−13 | 7.7835 × 10−2 | 8.8818 × 10−16 | 0 | 2.7602 × 10−1 | 5.0901 × 10−1 | 7.4043 × 100 | 9.8976 × 100 | 8.88 × 10−16 | 4.01 × 10−31 | 4.4409 × 10−16 | 0 | 4.4409 × 10−16 | 0 |
| F11 | 0 | 4.4850 × 10−3 | 6.6590 × 10−3 | 0 | 0 | 9.2150 10−3 | 7.7240 × 10−3 | 2.8900 × 10−4 | 1.5860 × 10−3 | 0 | 0 | 0 | 0 | 0 | 0 |
| F12 | 0 | 5.3438 × 10−2 | 2.0734 × 10−2 | 2.3036 × 10−2 | 1.4120 × 10−2 | 6.9170 × 10−3 | 2.6301 × 10−2 | 3.3968 × 10−1 | 2.1486 × 10−1 | 2.08 × 10−6 | 1.19 × 10−5 | 2.9442 × 10−6 | 3.3438 × 10−5 | 1.4922 × 10−6 | 1.3570 × 10−5 |
| F13 | 0 | 6.5446 × 10−1 | 4.4740 × 10−3 | 4.5032 × 10−1 | 2.4475 × 10−1 | 6.6750 × 10−3 | 8.9070 × 10−3 | 1.8890 × 100 | 2.6609 × 10−1 | 1.57 × 10−4 | 2.15 × 10−4 | 4.1390 × 10−5 | 4.4308 × 10−5 | 2.84662 × 10−5 | 2.10999 × 10−5 |
| F14 | 1 | 4.0425 × 100 | 4.2528 × 100 | 1.1968 × 100 | 4.0440 × 10−1 | 3.6272 × 100 | 2.5608 × 100 | 2.1120 × 100 | 2.4986 × 100 | 9.98 × 10−1 | 9.23 × 10−1 | 9.980 × 10−1 | 3.7366 × 10−10 | 9.980 × 10−1 | 3.16591 × 10−10 |
| F15 | 0.00030 | 3.3700 × 10−4 | 6.2500 × 10−4 | 3.2711 × 10−4 | 1.3308 × 10−5 | 5.7700 × 10−4 | 2.2200 × 10−4 | 5.7200 × 10−4 | 3.2400 × 10−4 | 3.10 × 10−4 | 1.97 × 10−4 | 3.0959 × 10−4 | 2.8224 × 10−5 | 3.0873 × 10−4 | 2.5451 × 10−4 |
| F16 | −1.0316 | −1.0316 × 100 | −1.0316 × 100 | −1.0316 × 100 | 3.7458 × 10−5 | −1.0316 × 100 | 6.2500 × 10−16 | −1.0316 × 100 | 4.2000 × 10−7 | −1.03 × 100 | 6.78 × 10−16 | −1.0316 | 4.3281 × 10−11 | −1.0316 | 8.81347 × 10−8 |
| F17 | 0.398 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9804 × 10−1 | 1.9193 × 10−4 | 3.9789 × 10−1 | 0 | 3.9791 × 10−1 | 2.7000 × 10−5 | 3.98 × 10−1 | 2.54 × 10−6 | 3.979 × 10−1 | 3.8425 × 10−6 | 3.979 × 10−1 | 1.8607 × 10−5 |
| F18 | 3 | 3.0000 × 100 | 3.0000 × 100 | 3.0000 × 100 | 3.0908 × 10−7 | 3.0000 × 100 | 1.3300 × 10−15 | 3.0000 × 100 | 4.2200 × 10−15 | 3.00 × 100 | 0 | 3.0000 | 2.9879 × 10−14 | 3.0000 | 8.0118 × 10−8 |
| F19 | −3.86 | −3.8626 × 100 | −3.8628 × 100 | −3.8626 × 100 | 8.9319 × 10−5 | −3.8628 × 100 | 2.5800 × 10−15 | −3.8562 × 100 | 2.7060 × 10−3 | −3.86 × 100 | 2.44 × 10−3 | −3.8623 | 7.1386 × 10−4 | −3.8615 | 9.7288 × 10−4 |
| F20 | −3.32 | −3.2865 × 100 | −3.2506 × 100 | −3.3022 × 100 | 3.5700 × 10−2 | −3.2663 × 100 | 6.0516 × 10−2 | −2.9811 × 100 | 3.7665 × 10−1 | −3.322 × 100 | 1.37406 10−1 | −3.3188 | 2.7279 × 10−3 | −3.3191 | 2.1882 × 10−3 |
| F21 | −10.1532 | −1.0151 × 101 | −9.1402 × 100 | −9.8275 × 100 | 9.2493 × 10−1 | −6.8651 × 100 | 3.0196 × 100 | −7.0492 × 100 | 3.6296 × 100 | −1.01451 × 101 | 8.85673 × 10−1 | −1.01531 × 101 | 1.0309 × 10−4 | −1.01530 × 101 | 1.5709 × 10−4 |
| F22 | −10.4028 | −1.0402 × 101 | −8.5844 × 100 | −1.0119 × 101 | 9.5309 × 10−1 | −8.4565 × 100 | 3.0871 × 100 | −8.1818 × 100 | 3.8292 × 100 | −1.04015 × 101 | 1.352375 × 100 | −1.04027 × 101 | 2.4422 × 10−4 | −1.04028 × 101 | 1.6801 × 10−4 |
| F23 | −10.5363 | −1.0534 × 101 | −8.5590 × 100 | −1.0397 × 101 | 1.0899 × 10−1 | −9.9529 × 100 | 1.7828 × 100 | −9.3424 × 100 | 2.4147 × 100 | −1.05364 × 101 | 9.27655 × 10−1 | −1.05363 × 101 | 1.4095 × 10−4 | −1.05363 × 101 | 1.0364 × 10−4 |
| Friedman mean rank results | 5.1087 | 3.6087 | 6.0000 | 5.6304 | 3.2391 | 2.5217 | 1.8913 | ||||||||
| Friedman rank | 5 | 4 | 7 | 6 | 3 | 2 | 1 | ||||||||
| Total number of the most optimum results obtained by comparing the proposed methods one by one according to the literature | 15 | 18 | |||||||||||||
| Algorithms | Optimum Variables | Optimum Cost | ||
|---|---|---|---|---|
| d | D | N | ||
| GWO [25] | 0.05169 | 0.356737 | 11.28885 | 0.012666 |
| MFO [43] | 0.051994457 | 0.36410932 | 10.868421862 | 0.0126669 |
| SSA [27] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 |
| WOA [28] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 |
| HHO [17] | 0.051796393 | 0.359305355 | 11.138859 | 0.012665443 |
| RSRFT [39] | 0.05147146 | 0.3515050 | 11.6013141 | 0.01266617 |
| RFO [39] | 0.052667011 | 0.3806680 | 10.0213925 | 0.0126934 |
| EDBO [40] | 0.0500156 | 0.31777 | 13.7778 | 0.012718751 |
| HHHOWOA1 | 0.0517709162 | 0.3586901539 | 11.174259208 | 0.0126653548 |
| HHHOWOA2 | 0.0516725910 | 0.3563216437 | 11.312225467 | 0.0126652377 |
| HHHOWOA2PSO | 0.0516901857 | 0.3567431404 | 11.2876518173 | 0.0126654334 |
| Algorithms | Optimum Variables | Optimum Cost | |||
|---|---|---|---|---|---|
| Ts | Th | R | L | ||
| WOALFVWPSO [5] | 0.7831596 | 0.3944979 | 40.35439 | 200 | 5955.7996 |
| CPSO [50] | 0.8125 | 0.4375 | 42.091266 | 176.7465 | 6061.0777 |
| MFO [43] | 0.8125 | 0.4375 | 42.098445 | 176.636596 | 6059.7143 |
| WOA [28] | 0.8125 | 0.4375 | 42.0982699 | 176.638998 | 6059.741 |
| HHO [17] | 0.81758383 | 0.4072927 | 42.09174576 | 176.7196352 | 6000.46259 |
| RSRFT [39] | 0.81612257 | 0.403409949 | 42.2861349 | 174.325078 | 5953.4364 |
| RFO [39] | 0.81425 | 0.44521 | 42.20231 | 176.62145 | 6113.3195 |
| EDBO [40] | 0.7827496 | 0.3943 | 40.38594 | 200 | 5957.489796 |
| CIHHO [41] | 1.07055 | 0.52863 | 55.38854 | 60.615468 | 5962.00814 |
| HHHOWOA1 | 0.8049634 | 0.3890709 | 40.88383 | 192.6467 | 6023.1709 |
| 0.8125 | 0.4375 | 42.0974671 | 176.64872135 | 6059.8335 | |
| HHHOWOA2 | 0.7818555 | 0.3920745 | 40.31962 | 200 | 5933.5439 |
| 0.8125 | 0.4375 | 42.095787915 | 176.66953154 | 6060.0380 | |
| HHHOWOA2PSO | 0.7869923 | 0.3888867 | 40.77421 | 193.7898 | 5901.0625 |
| 0.8125 | 0.4375 | 42.0984444394 | 176.63768237 | 6059.7395 | |
| Algorithms | Optimum Variables | Optimum Cost | |
|---|---|---|---|
| A1 | A2 | ||
| PSO-DE [51] | 0.7886751 | 0.4082482 | 263.8958433 |
| MFO [43] | 0.788244770931922 | 0.409466905784741 | 263.895979682 |
| MBA [52] | 0.788244771 | 0.409466905784741 | 263.8959797 |
| CS [53] | 0.78867 | 0.40902 | 263.9716 |
| HHO [17] | 0.788662816 | 0.4082831338329 | 263.8958434 |
| RSRFT [39] | 0.78875052 | 0.4080351 | 263.89584 |
| RFO [39] | 0.75356 | 0.55373 | 268.51195 |
| EDBO [40] | 0.78821 | 0.40958 | 263.8979156 |
| CIHHO [41] | 0.78829 | 0.40934 | 263.89584 |
| HHHOWOA1 | 0.78867397436 | 0.4082515721132 | 263.8958433 |
| HHHOWOA2 | 0.7886718168799 | 0.4082576744595 | 263.89584338 |
| HHHOWOA2PSO | 0.788547951539648 | 0.4086082820095 | 263.89586973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzer, M.S. New Hybrid Approaches Based on Swarm-Based Metaheuristic Algorithms and Applications to Optimization Problems. Appl. Sci. 2025, 15, 1355. https://doi.org/10.3390/app15031355
Uzer MS. New Hybrid Approaches Based on Swarm-Based Metaheuristic Algorithms and Applications to Optimization Problems. Applied Sciences. 2025; 15(3):1355. https://doi.org/10.3390/app15031355
Chicago/Turabian StyleUzer, Mustafa Serter. 2025. "New Hybrid Approaches Based on Swarm-Based Metaheuristic Algorithms and Applications to Optimization Problems" Applied Sciences 15, no. 3: 1355. https://doi.org/10.3390/app15031355
APA StyleUzer, M. S. (2025). New Hybrid Approaches Based on Swarm-Based Metaheuristic Algorithms and Applications to Optimization Problems. Applied Sciences, 15(3), 1355. https://doi.org/10.3390/app15031355





