Study on Vibration Characteristics of Multi-Beam Structures with Stick and Slip at Joints
Abstract
1. Introduction
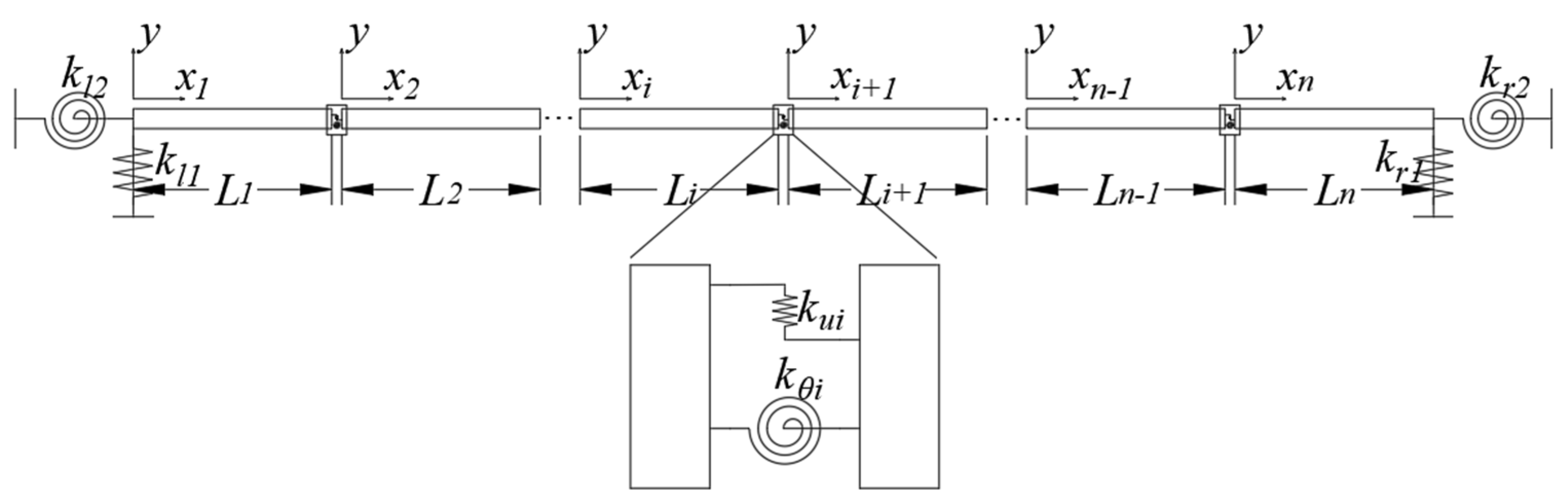
2. Theoretical Modeling
2.1. Energy Equation of Beam Structure
2.2. Improved Fourier Series Expansion Vibration Displacement
2.3. Nonlinear Connecting
2.4. Theoretical Solution of Displacement Series Coefficients
3. Result Analysis and Discussion
3.1. Validation
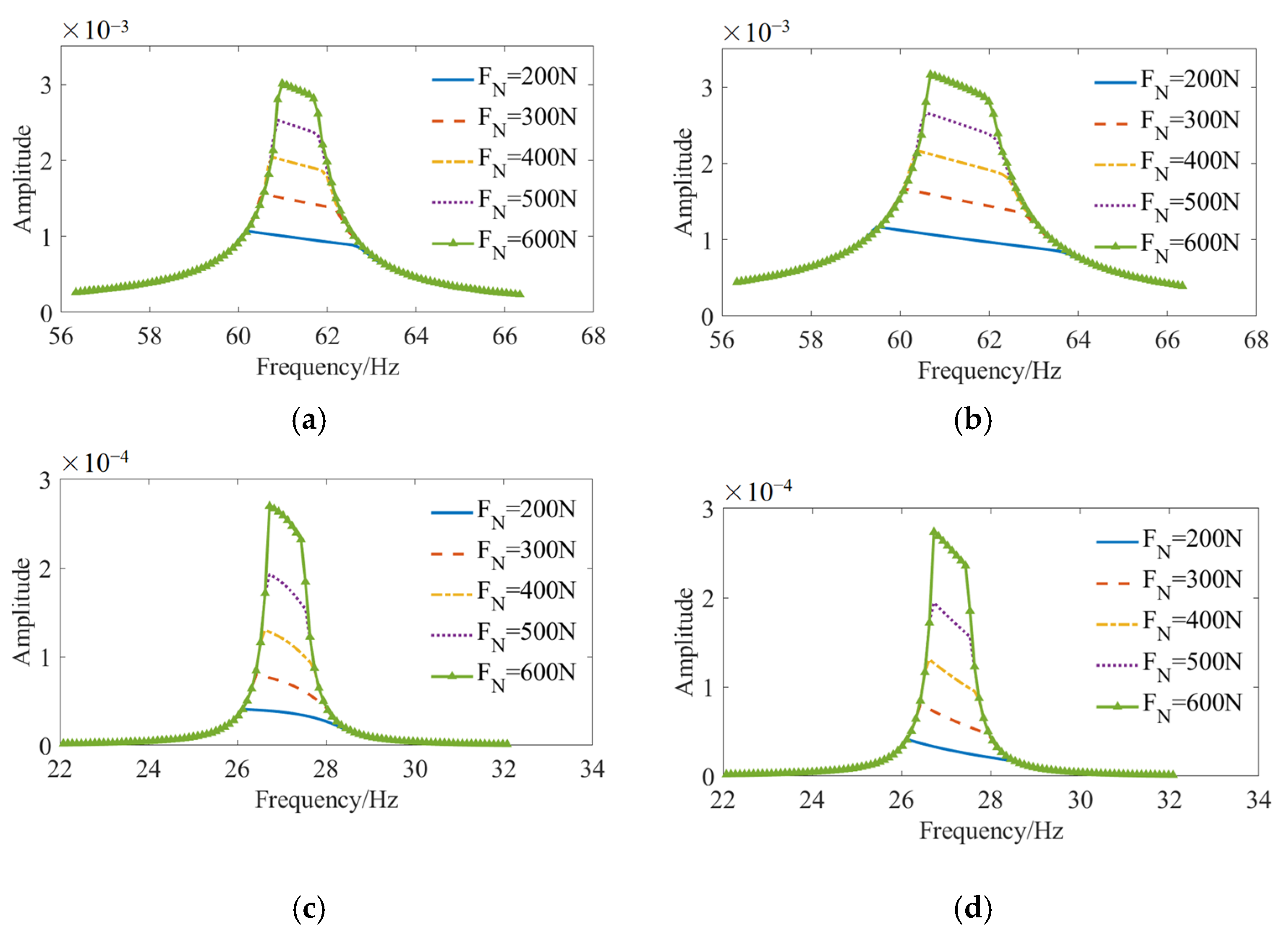
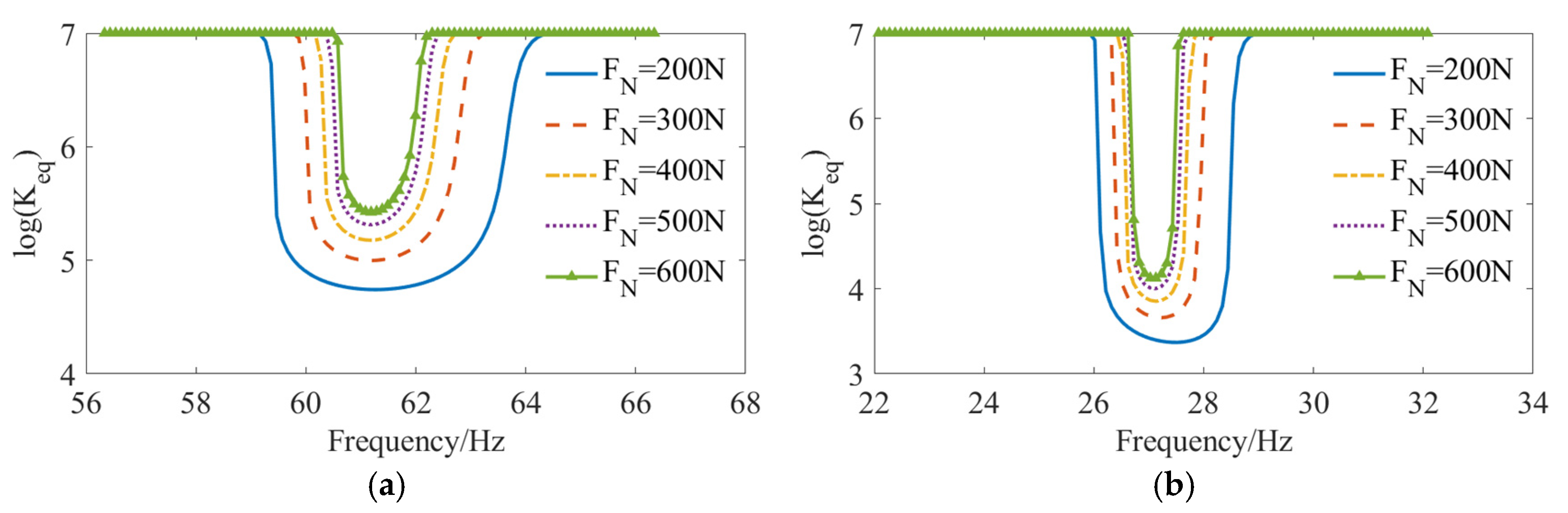
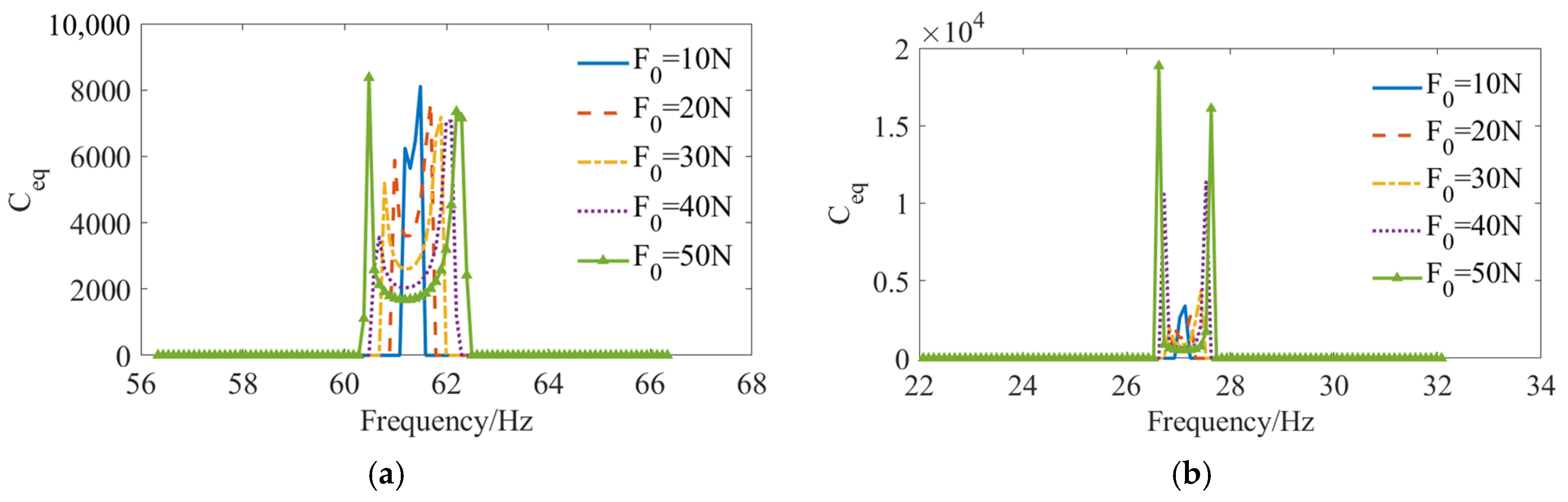
3.2. Response Under Different Contact Pressure Conditions
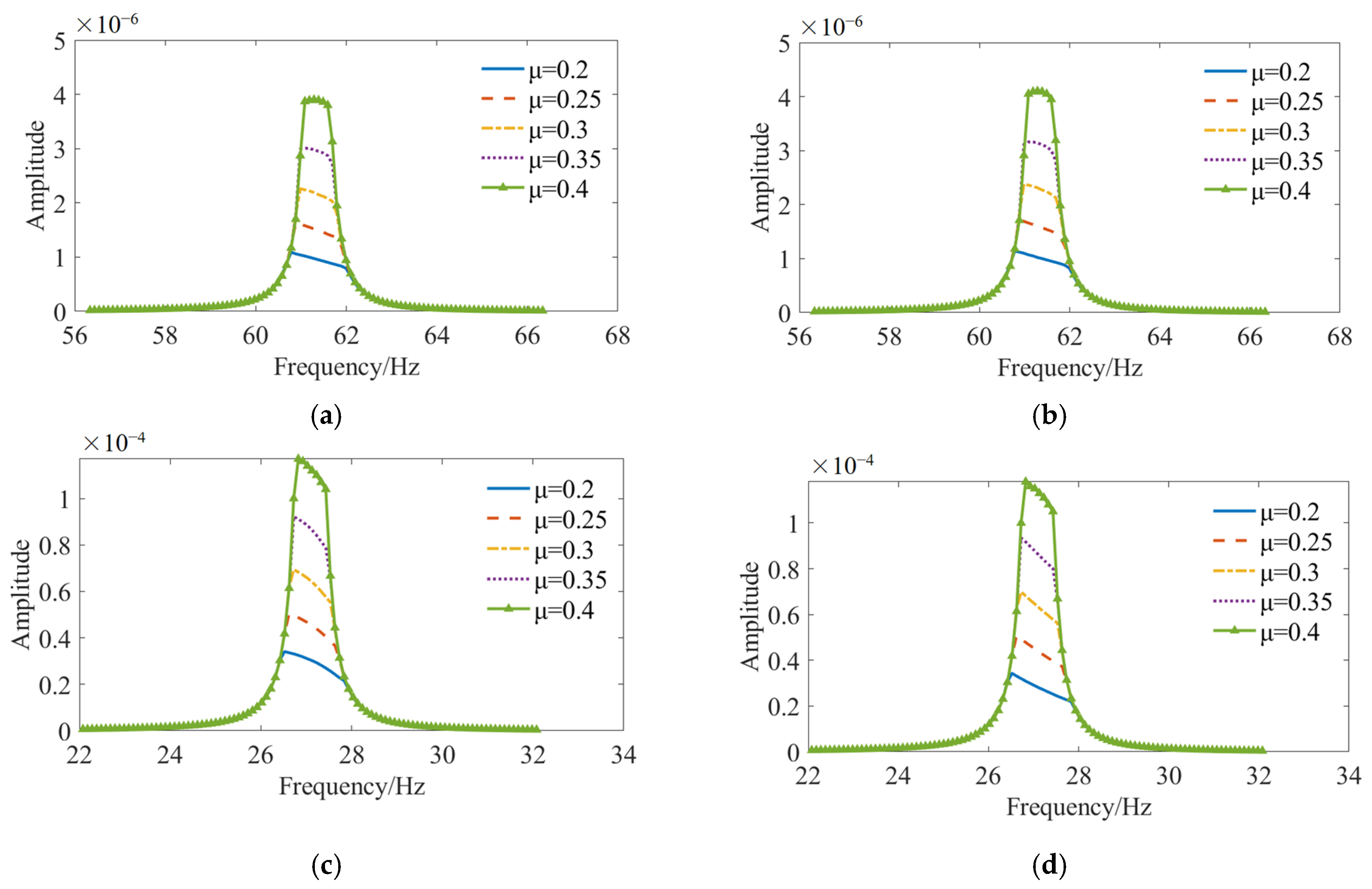
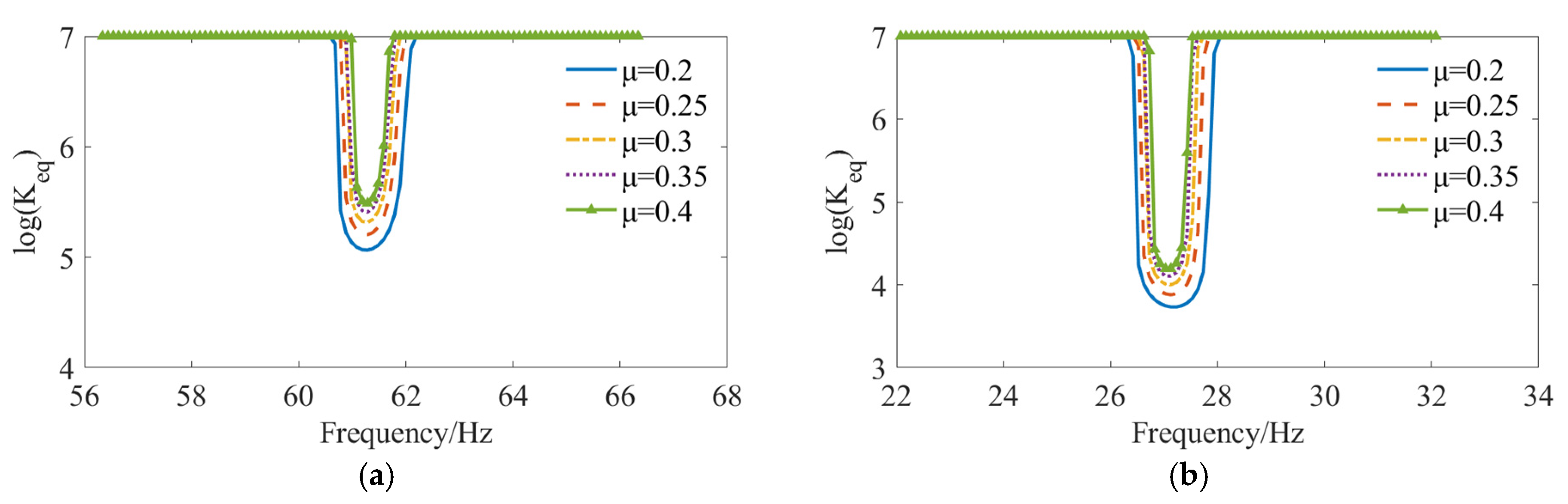
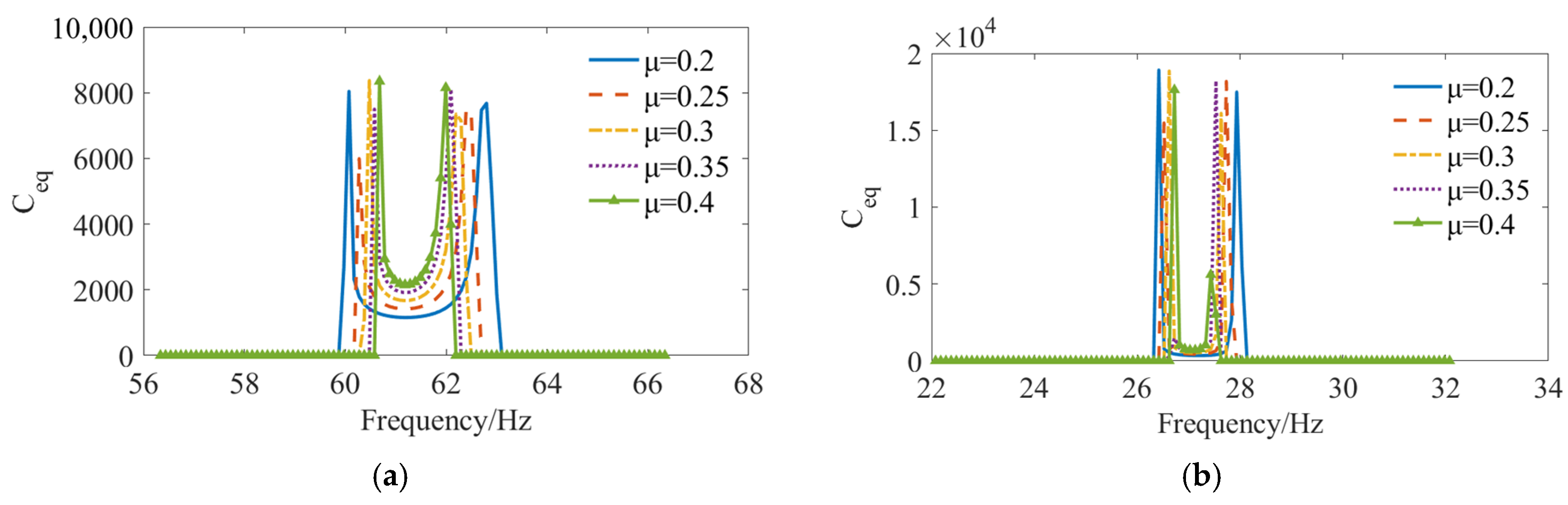
3.3. Structural Amplitude–Frequency Curves with Different Friction Coefficients
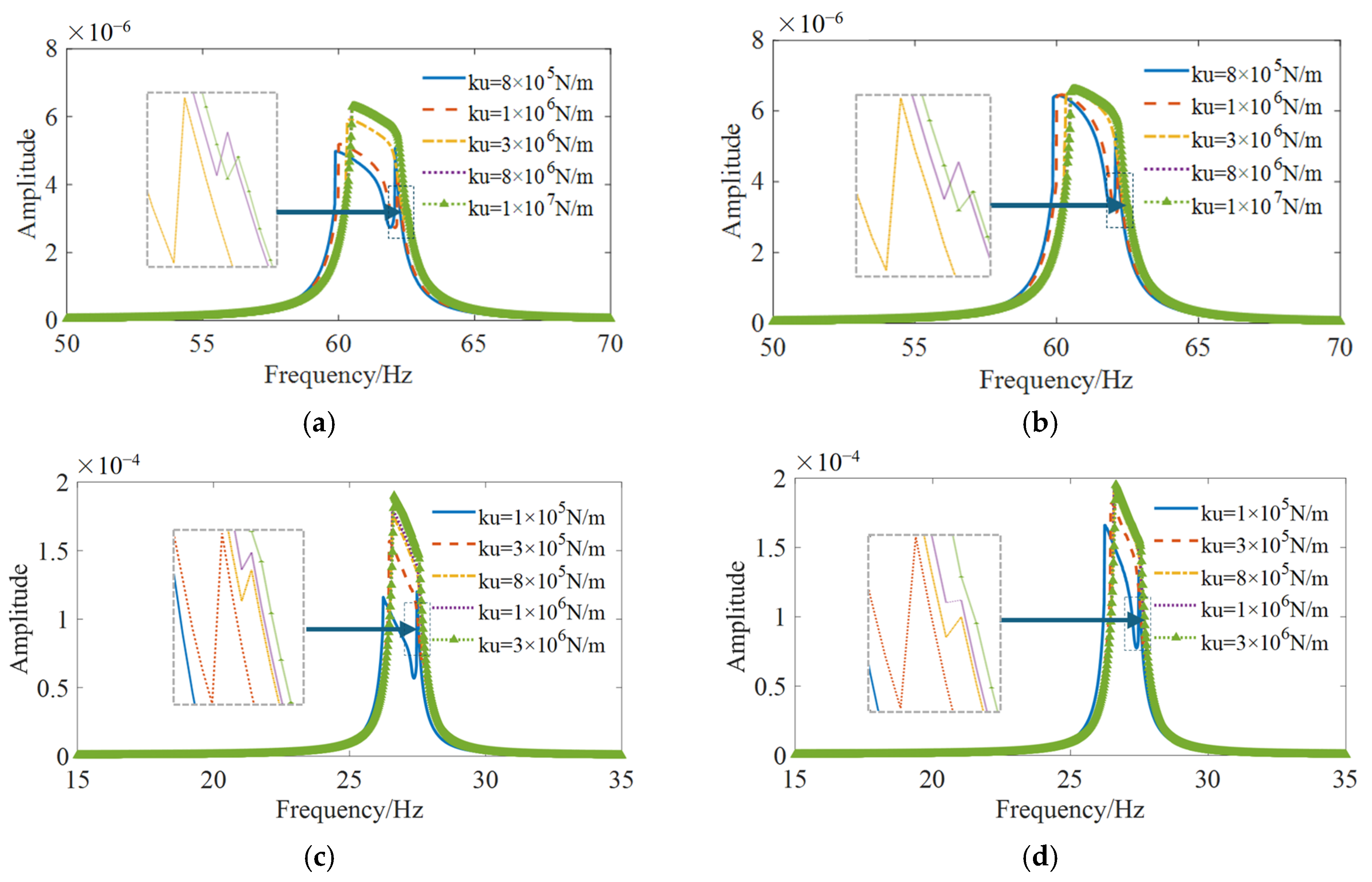
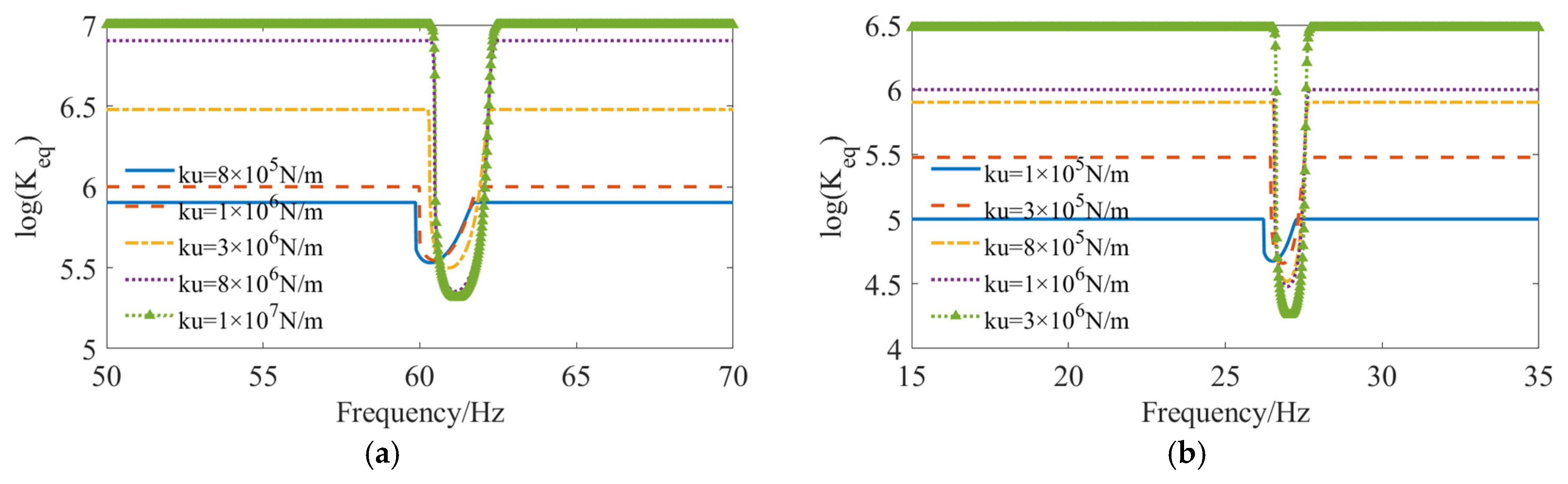
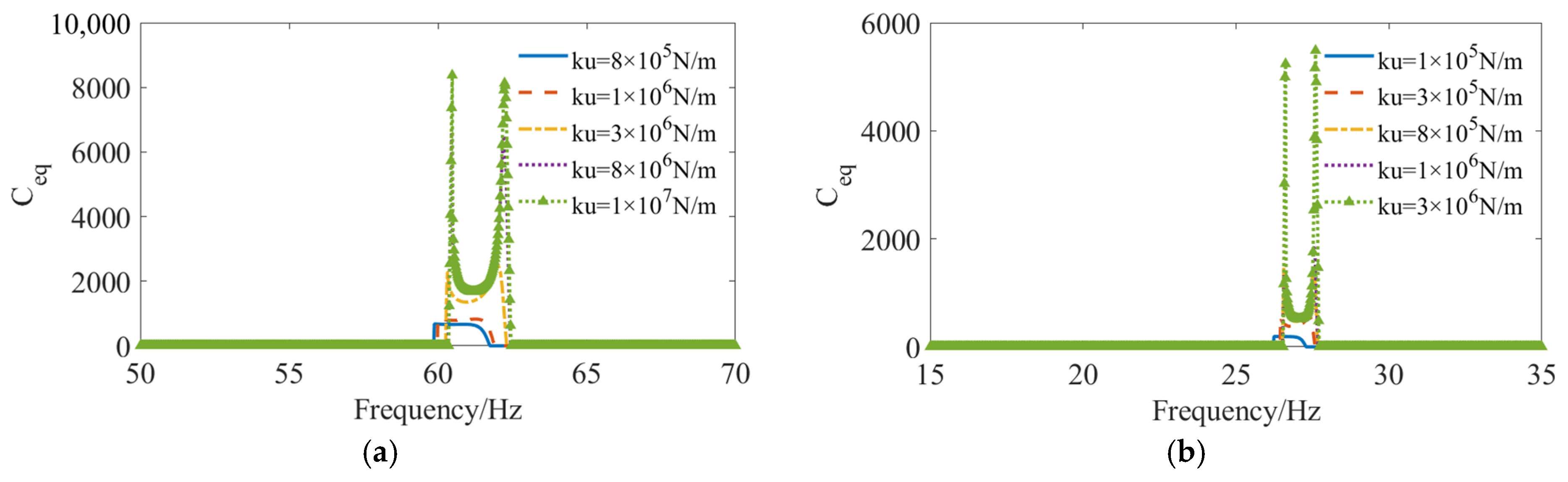
3.4. Different Connection Translation Stiffness
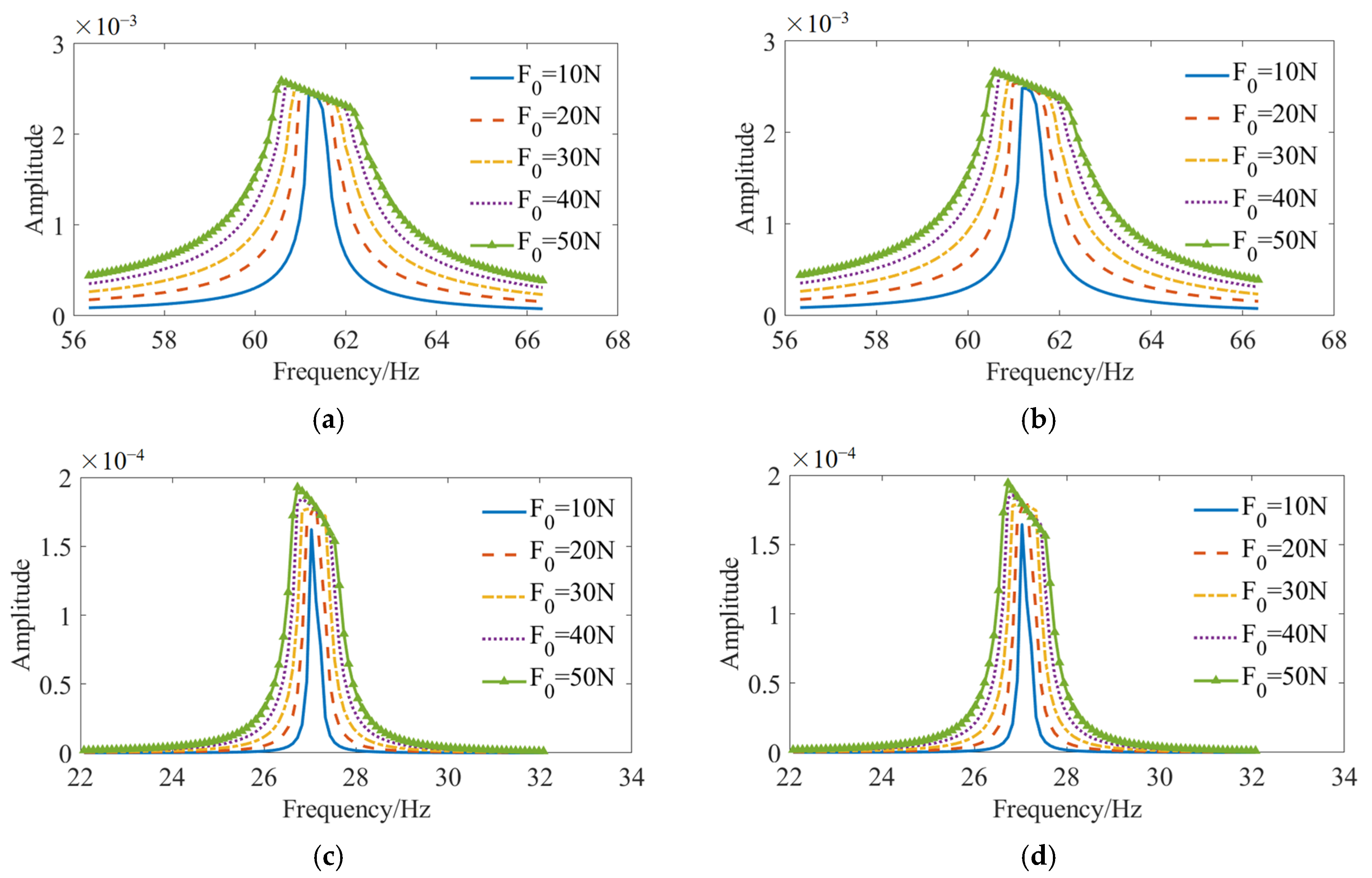
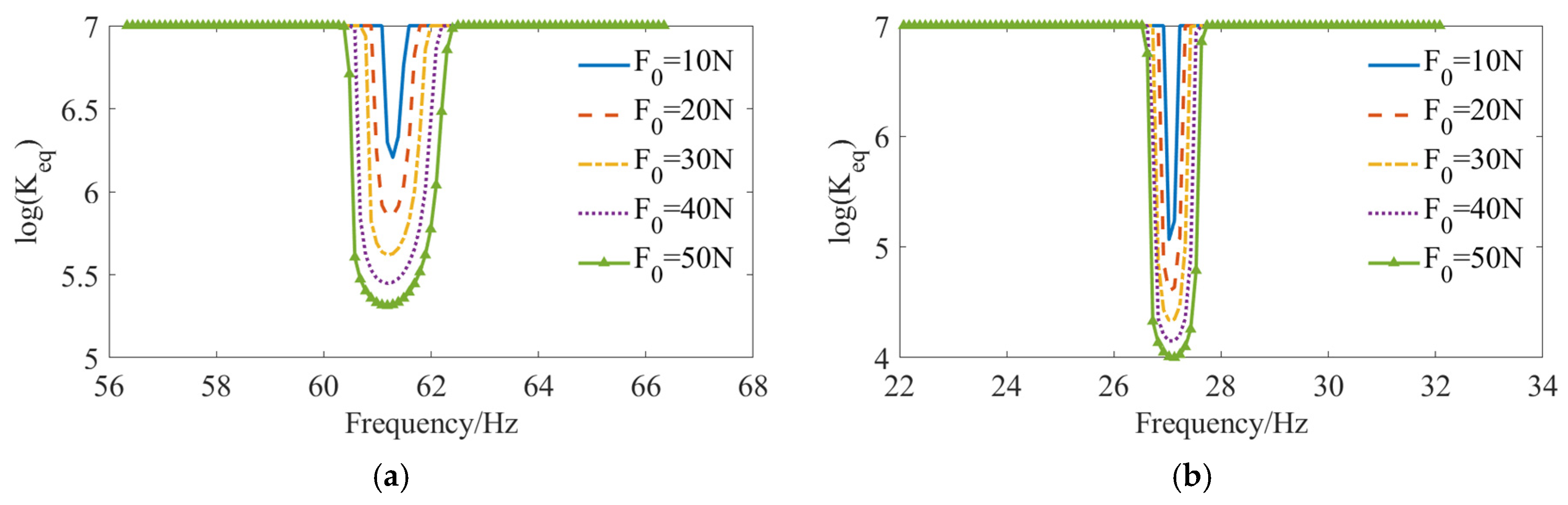
3.5. Effect of Excitation
3.6. Multi-Beam Situation
3.6.1. Beams of Different Lengths
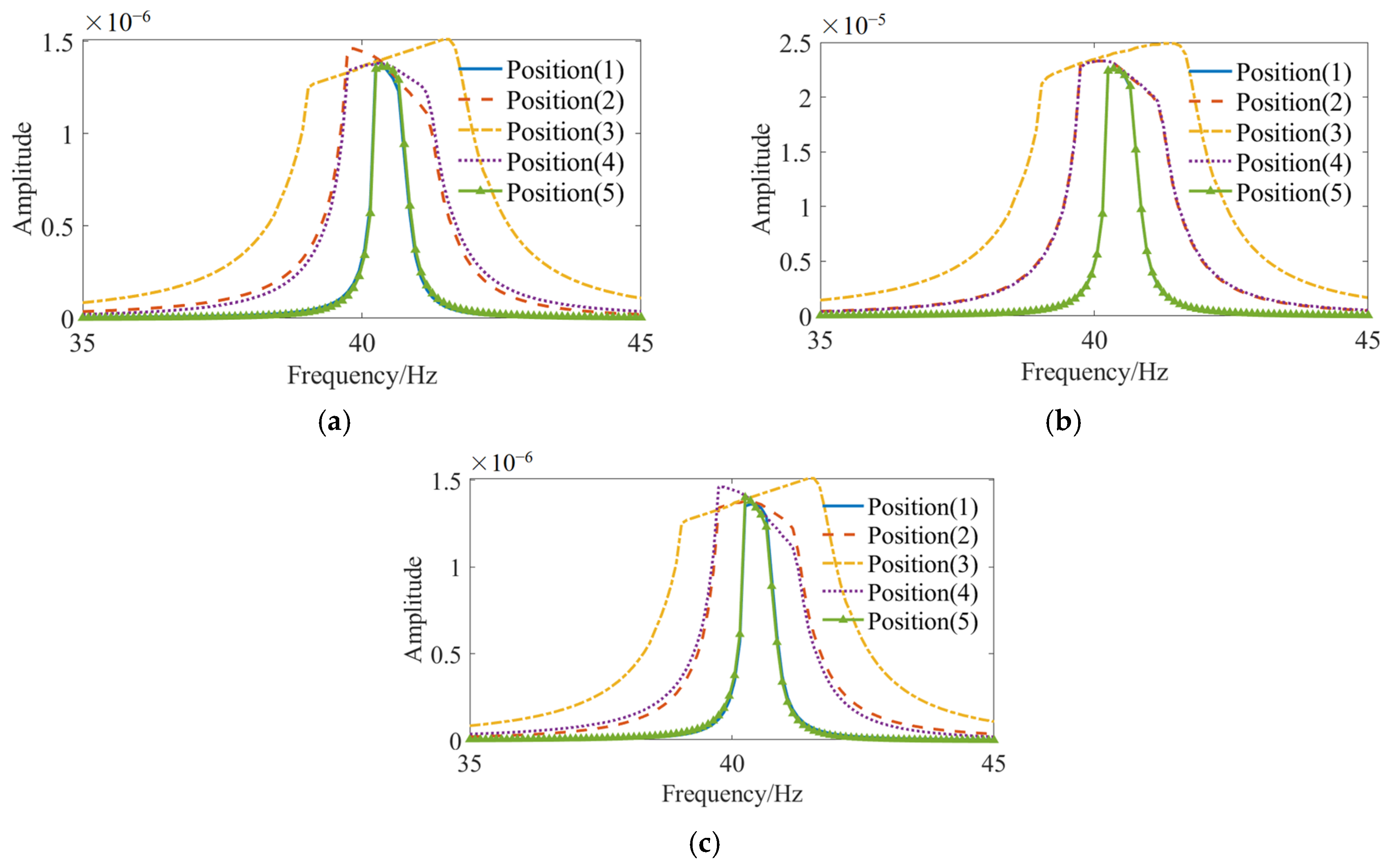
3.6.2. Influence of Excitation Position
4. Conclusions
- (1)
- The alterations in the state of structural connections primarily manifest as a decrease in connection stiffness near the resonance frequency, with the reduction being more pronounced in the simply supported condition than the fixed condition. The “tracking” phenomenon caused by the abrupt change of damping and the variation in resonance frequency results in a relatively stable vibration response amplitude over a larger frequency range.
- (2)
- As the contact pressure and friction diminish, the frequency response curve progressively flattens, indicating a resonance frequency range. The peak response frequency is observed at the lower end of this resonance range, which is situated below the linear natural frequency.
- (3)
- When the connection stiffness is reduced, the resonance peaks broaden and diverge, exhibiting the characteristics of internal resonance in nonlinear systems. This feature becomes increasingly pronounced as the stiffness decreases.
- (4)
- The magnitude of external excitation serves as a direct factor in inducing nonlinear softening of the connection. When the excitation amplitude is minimal, its impact on the connection state remains limited. As the external excitation escalates, the structure’s frequency response curve exhibits a resonance region.
- (5)
- Various sub-beam combinations display distinct nonlinear characteristics when used in multi-beam structures. In asymmetric configurations, alterations in connection states are primarily induced by excitation and predominantly manifest at the junctions of shorter beams. As the excitation point approaches the structural center, it is more likely to cause significant changes in connection states, thereby broadening the range of resonant intervals.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Timoshenko, S. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Courier Corporation: Chelmsford, MA, USA, 1983. [Google Scholar]
- Timoshenko, S.P.X. On the transverse vibrations of bars of uniform cross-section. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Strutt, J.W.; Rayleigh, J.W.S. The Theory of Sound; Macmillan: London, UK, 1877; Volume 1. [Google Scholar]
- Abbas, B.A.H.; Thomas, J. The second frequency spectrum of Timoshenko beams. J. Sound Vib. 1977, 51, 123–137. [Google Scholar] [CrossRef]
- Mao, Q.; Pietrzko, S. Free vibration analysis of stepped beams by using Adomian decomposition method. Appl. Math. Comput. 2010, 217, 3429–3441. [Google Scholar] [CrossRef]
- Kiani, K.; Soltani, S. Nonlocal longitudinal, flapwise, and chordwise vibrations of rotary doubly coaxial/non-coaxial nanobeams as nanomotors. Int. J. Mech. Sci. 2020, 168, 105291. [Google Scholar] [CrossRef]
- Guler, S. Free vibration analysis of a rotating single edge cracked axially functionally graded beam for flap-wise and chord-wise modes. Eng. Struct. 2021, 242, 112564. [Google Scholar] [CrossRef]
- Banerjee, J.R. Dynamic stiffness formulation and free vibration analysis of centrifugally stiffened Timoshenko beams. J. Sound Vib. 2001, 247, 97–115. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bazoune, A. Effect of tapering on natural frequencies of rotating beams. Shock Vib. 2007, 14, 169–179. [Google Scholar] [CrossRef]
- Bograd, S.; Reuss, P.; Schmidt, A.; Gaul, L.; Mayer, M. Modeling the dynamics of mechanical joints. Mech. Syst. Signal Process. 2011, 25, 2801–2826. [Google Scholar] [CrossRef]
- Sun, D.; Li, W.Y.; Lyu, B.L. Overview of mechanical modeling methods for bolted connections. J. Vib. Acoust. 2012, 32, 8–12. [Google Scholar]
- Iwan, W.D. A distributed-element model for hysteresis and its steady-state dynamic response. J. Appl. Mech. 1966, 33, 893–900. [Google Scholar] [CrossRef]
- Iwan, W.D. On a class of models for the yielding behavior of continuous and composite systems. J. Appl. Mech. 1966, 34, 612–617. [Google Scholar] [CrossRef]
- An, W.W.; Gong, Z.R.; Zhao, T. Dynamic Properties of Machine Bolted Joints Summary. Appl. Mech. Mater. 2013, 423, 1594–1602. [Google Scholar] [CrossRef]
- Valanis, K.C. Fundamental consequences of a new intrinsic time measure: Plasticity as a limit of the endochronic theory. Arch. Mech. Stossowanej 1980, 32, 171–191. [Google Scholar]
- Bouc, R. Forced vibrations of mechanical systems with hysteresis. In Proceedings of the Fourth Conference on Nonlinear Oscillations, Prague, Czech Republic, 5–9 September 1967. [Google Scholar]
- Wen, Y.K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, J.C.; Kang, B.S. Finite element analysis and modelling of structure with bolted joints. Appl. Math. Model. 2007, 31, 895–911. [Google Scholar] [CrossRef]
- Qin, Z.; Han, Q.; Chu, F. Bolt loosening at rotating joint interface and its influence on rotor dynamics. Eng. Fail. Anal. 2016, 59, 456–466. [Google Scholar] [CrossRef]
- Rao, C.K.; Mirza, S. A note on vibrations of generally restrained beams. J. Sound Vib. 1989, 130, 453–465. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, M.S. Vibration of beams with generally restrained boundary conditions using Fourier series. J. Sound Vib. 2001, 245, 771–784. [Google Scholar] [CrossRef]
- Abbas, B.A.H. Vibrations of Timoshenko beams with elastically restrained ends. J. Sound Vib. 1984, 97, 541–548. [Google Scholar] [CrossRef]
- Elishakoff, I.; Lin, Y.K.; Zhu, L.P. Random vibration of uniform beams with varying boundary conditions by the dynamic-edge-effect method. Comput. Methods Appl. Mech. Eng. 1995, 121, 59–76. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhao, X.; Li, Y.H. Green’s functions of the forced vibration of Timoshenko beams with damping effect. J. Sound Vib. 2014, 333, 1781–1795. [Google Scholar] [CrossRef]
- Li, W.L. Free vibrations of beams with general boundary conditions. J. Sound Vib. 2000, 237, 709–725. [Google Scholar] [CrossRef]
- Copetti, R.D.; Claeyssen, J.R.; de Rosso Tolfo, D.; Pavlack, B.S. The fundamental modal response of elastically connected parallel Timoshenko beams. J. Sound Vib. 2022, 530, 116920. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Li, B.; Wen, B.; Ma, Q. Analysis of natural vibration characteristics of continuous multi-span beams with concentrated mass under arbitrary boundary conditions. J. Vib. Acoust. 2024, 44, 52–58+85. [Google Scholar]
- Hao, Q.; Zhai, W.; Chen, Z. Free vibration of connected double-beam system with general boundary conditions by a modified Fourier–Ritz method. Arch. Appl. Mech. 2018, 88, 741–754. [Google Scholar] [CrossRef]
- Li, W.L.; Xu, H. An exact fourier series method for the vibration analysis of multispan beam systems. J. Comput. Nonlinear Dyn. 2009, 4, 710–733. [Google Scholar] [CrossRef]
- Couch, L.; Tehrani, F.M.; Naghshineh, A.; Frazao, R. Shake Table response of a dual system with inline friction damper. Eng. Struct. 2023, 281, 115776. [Google Scholar] [CrossRef]
- Li, Y.; Long, T.; Luo, Z.; Wen, C.; Zhu, Z.; Jin, L.; Li, B. Numerical and experimental investigations on dynamic behaviors of a bolted joint rotor system with pedestal looseness. J. Sound Vib. 2024, 571, 118036. [Google Scholar] [CrossRef]
- Kang, B.; Tan, C.A. Nonlinear response of a beam under distributed moving contact load. Commun. Nonlinear Sci. Numer. Simul. 2006, 11, 203–232. [Google Scholar] [CrossRef]
- Sinou, J.J.; Dereure, O.; Mazet, G.B.; Thouverez, F.; Jezequel, L. Friction-induced vibration for an aircraft brake system-Part 1: Experimental approach and stability analysis. Int. J. Mech. Sci. 2006, 48, 536–554. [Google Scholar] [CrossRef]
- Joglekar, D.M. Analysis of nonlinear frequency mixing in Timoshenko beams with a breathing crack using wavelet spectral finite element method. J. Sound Vib. 2020, 488, 115532. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J. Nonlinear vibration analysis of a generally restrained double-beam structure coupled via an elastic connector of cubic nonlinearity. Nonlinear Dyn. 2022, 109, 563–588. [Google Scholar] [CrossRef]
- Krack, M.; Bergman, L.A.; Vakakis, A.F. On the efficacy of friction damping in the presence of nonlinear modal interactions. J. Sound Vib. 2016, 370, 209–220. [Google Scholar] [CrossRef]
- Tüfekci, M.; Sun, Y.; Yuan, J.; Maharaj, C.; Liu, H.; Dear, J.P.; Salles, L. Analytical vibration modelling and solution of bars with frictional clamps. J. Sound Vib. 2024, 577, 118307. [Google Scholar] [CrossRef]
- Tang, Q.; Li, C.; She, H.; Wen, B. Nonlinear response analysis of bolted joined cylindrical-cylindrical shell with general boundary condition. J. Sound Vib. 2019, 443, 788–803. [Google Scholar] [CrossRef]
- Lu, K.; Jin, Y.; Chen, Y.; Cao, Q.; Zhang, Z. Stability analysis of reduced rotor pedestal looseness fault model. Nonlinear Dyn. 2015, 82, 1611–1622. [Google Scholar] [CrossRef]
- Lu, K.; Cheng, H.; Zhang, W.; Zhang, H.; Zhang, K.; Fu, C. Nonlinear dynamic behavior of a dual-rotor bearing system with coupling misalignment and rubbing faults. Meas. Sci. Technol. 2022, 34, 014005. [Google Scholar]
- Casini, P.; Vestroni, F. Mitigation of Structural Vibrations of MDOF Oscillators by Modal Coupling Due to Hysteretic Dampers. Appl. Sci. 2022, 12, 10079. [Google Scholar] [CrossRef]
- Jewell, E.; Allen, M.S.; Zare, I.; Wall, M. Application of quasi-static modal analysis to a finite element model and experimental correlation. J. Sound Vib. 2020, 479, 115376. [Google Scholar] [CrossRef]
- Zang, J.; Yuan, T.C.; Lu, Z.Q.; Zhang, Y.W.; Ding, H.; Chen, L.Q. A lever-type nonlinear energy sink. J. Sound Vib. 2018, 437, 119–134. [Google Scholar] [CrossRef]
- Dai, W.; Yang, J.; Wiercigroch, M. Vibration energy flow transmission in systems with Coulomb friction. Int. J. Mech. Sci. 2022, 214, 106932. [Google Scholar] [CrossRef]
- Alberto, J.; Fuentes, A. On the Influence of Piecewise Defined Contact Geometries on Friction Dampers; KIT Scientific Publishing: Karlsruhe, Germany, 2023; p. 182. [Google Scholar]
- Riddoch, D.J.; Cicirello, A.; Hills, D.A. Response of a mass-spring system subject to Coulomb damping and harmonic base excitation. Int. J. Solids Struct. 2020, 193, 527–534. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A.; Hills, D.A. Displacement transmissibility of a Coulomb friction oscillator subject to joined base-wall motion. Nonlinear Dyn. 2019, 98, 2595–2612. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A. Experimental investigation of a single-degree-of-freedom system with Coulomb friction. Nonlinear Dyn. 2020, 99, 1781–1799. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A. Multi-degree-of-freedom systems with a Coulomb friction contact: Analytical boundaries of motion regimes. Nonlinear Dyn. 2021, 104, 35–63. [Google Scholar] [CrossRef]
- Asadi, K.; Ahmadian, H.; Jalali, H. Micro/macro-slip damping in beams with frictional contact interface. J. Sound Vib. 2012, 331, 4704–4712. [Google Scholar] [CrossRef]
- Won, H.I.; Chung, J. Numerical analysis for the stick-slip vibration of a transversely moving beam in contact with a frictional wall. J. Sound Vib. 2018, 419, 42–62. [Google Scholar] [CrossRef]
- Won, H.I.; Lee, B.; Chung, J. Stick-slip vibration of a cantilever beam subjected to harmonic base excitation. Nonlinear Dyn. 2018, 92, 1815–1828. [Google Scholar] [CrossRef]
- Baek, S.; Epureanu, B. Reduced-order modeling of bladed disks with friction ring dampers. J. Vib. Acoust. 2017, 139, 061011. [Google Scholar] [CrossRef]
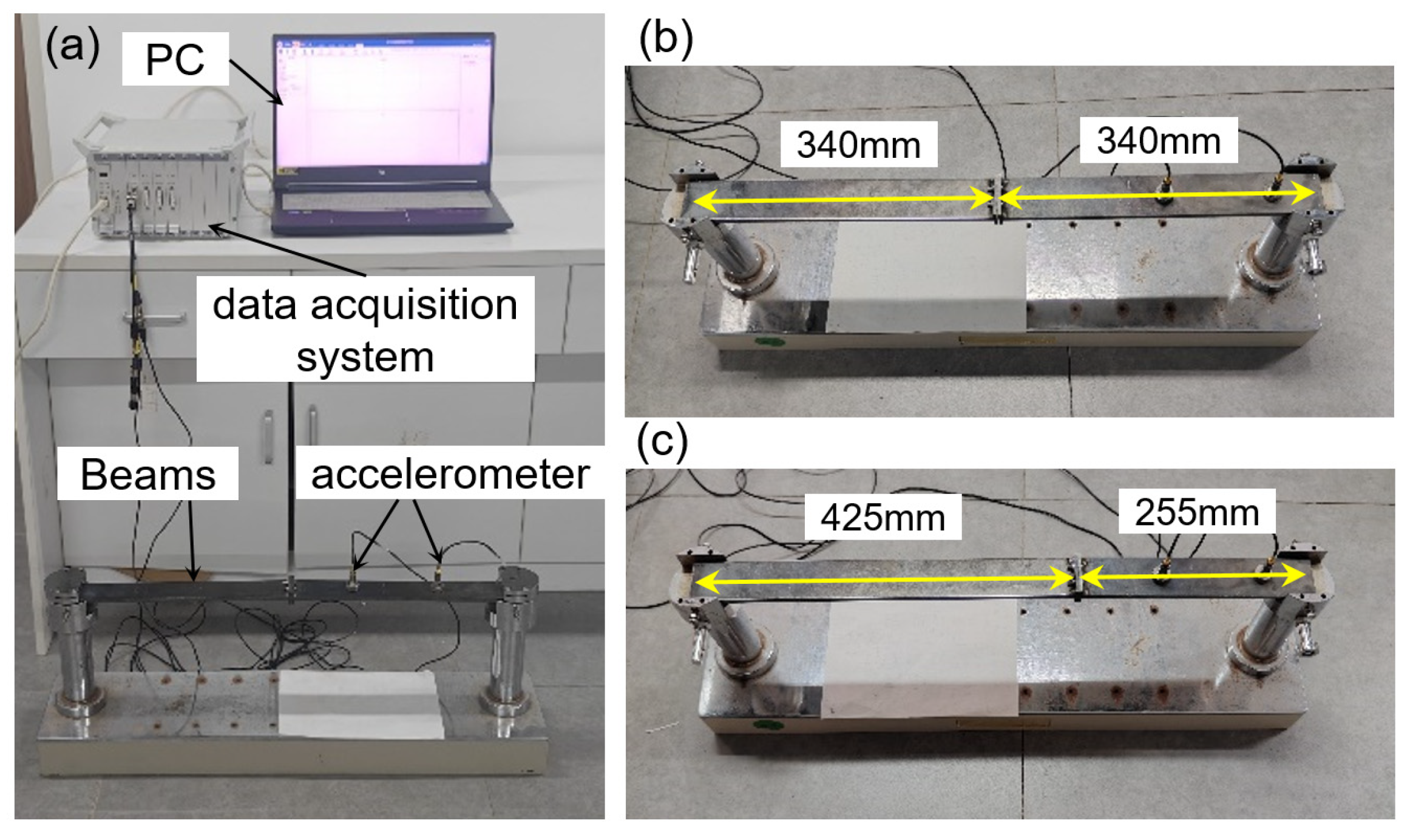





| Case I | Case II | ||||||
|---|---|---|---|---|---|---|---|
| Experiment | Present | Error | Experiment | Present | Error | ||
| Simply supported | 1st | 38.156 | 36.736 | 3.8% | 37.109 | 35.969 | 3.1% |
| 2nd | 154.297 | 155.771 | 1.0% | 146.484 | 149.145 | 1.8% | |
| 3rd | 322.326 | 326.375 | 1.3% | 332.031 | 333.604 | 0.5% | |
| Clamped | 1st | 81.055 | 83.322 | 2.8% | 83.008 | 85.279 | 2.7% |
| 2nd | 245.117 | 241.488 | −1.5% | 231.445 | 231.747 | 0.1% | |
| 3rd | 439.453 | 443.556 | 0.9% | 460.938 | 458.237 | −0.6% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xie, Y.; Lyu, P.; Ning, D.; Li, Z. Study on Vibration Characteristics of Multi-Beam Structures with Stick and Slip at Joints. Appl. Sci. 2025, 15, 1141. https://doi.org/10.3390/app15031141
Zhang X, Xie Y, Lyu P, Ning D, Li Z. Study on Vibration Characteristics of Multi-Beam Structures with Stick and Slip at Joints. Applied Sciences. 2025; 15(3):1141. https://doi.org/10.3390/app15031141
Chicago/Turabian StyleZhang, Xian, Yingchun Xie, Peng Lyu, Donghong Ning, and Zhixiong Li. 2025. "Study on Vibration Characteristics of Multi-Beam Structures with Stick and Slip at Joints" Applied Sciences 15, no. 3: 1141. https://doi.org/10.3390/app15031141
APA StyleZhang, X., Xie, Y., Lyu, P., Ning, D., & Li, Z. (2025). Study on Vibration Characteristics of Multi-Beam Structures with Stick and Slip at Joints. Applied Sciences, 15(3), 1141. https://doi.org/10.3390/app15031141









