Abstract
The limits of direct current (DC) injection and output current distortion of grid-connected photovoltaic (PV) inverters are specified in the IEEE 1547-2018 standard. The standard prescribes limits of output current harmonics, but the input voltage and power at which output current distortion is measured are not specified. This manuscript presents the results of DC injection and output current distortion measurements for three commercial single-phase PV inverters, with 3 kVA, 3.3 kVA, and 6 kVA rated power. During the measurements, the inverters are powered by a programmable DC source that emulates the power voltage characteristic of a PV array, providing different input conditions. In addition to steady-state measurements at constant input voltage and power, the change in the output current spectrum over time during the maximum power point tracking (MPPT) is also measured. The results show that the output current distortion depends on the input voltage and power. Moreover, the current distortion of some of the tested inverters exceeds the limits specified by the standard in some cases. The presented results suggest that further research on the dependence of the output current distortion from PV inverters on their input power and voltage is needed.
1. Introduction
Climate change is primarily caused by anthropogenic greenhouse gas emissions from fossil fuels. As awareness of global climate change continues to grow, efforts to mitigate it have intensified. As a result, significant efforts are being made to expand the use of renewable energy sources. In response to these challenges, widespread adoption of photovoltaic (PV) technologies began in the early 2000s. In 2023 alone, the total capacity of solar power plants installed worldwide has increased by 410 GW, almost half of the previously installed capacity [1].
Most of the total PV capacity consists of systems installed on residential and commercial buildings connected to the low-voltage grid [2]. A typical PV system includes a PV array, a DC/AC converter, called also PV inverter, and a battery energy storage system. The PV inverter is equipped with a controller with a function that determines the maximum power of the PV array. This controller employs a maximum power point tracking (MPPT) algorithm to accomplish this task. There are several implementations of the MPPT algorithm, and a detailed description of their features can be found in [3,4,5].
One of the leading research challenges in electricity production and delivery is the widespread integration of PV accompanied by power electronic-based inverters [6]. These inverters represent low-inertia sources in the utility grid, which, depending on the inverter design, control strategy, and output filters, generate certain harmonic distortions. Harmonic emissions can cause certain problems, which have prompted extensive research into the effects of harmonics generated by inverters [7,8,9]. The authors of [10] examined the impact of PV system integration in utility grids, particularly harmonic generation. Specifically, this research focused on the voltage and current distortions with and without the integration of PV inverters in a distribution grid. The research included total harmonic distortion analysis and individual voltage and current harmonics analysis. The authors of [11] investigated different conditions influencing the harmonics at the point of common coupling for PV systems. It provided a detailed review of grid-connected PV inverters with different topologies, control techniques, sources of generated harmonic, and their mitigation strategies. Subsequently, various cases involving different sources of harmonics in a distribution grid with connected PV inverters were modeled and simulated using MATLAB/Simulink.
Reference [12] evaluated the behavior of higher harmonics due to the parallel operation of multiple PV inverters connected to a low-voltage grid. The results were collected through field measurements to characterize the harmonic generation in a PV system consisting of six identical three-phase PV inverters with 20 kW rated power. The analysis indicated three harmonic current emission ranges: low-frequency 0–2 kHz range, broad 2–5 kHz range due to resonance, and narrow high-frequency range near 16 kHz due to the inverters’ switching frequency. The authors of [13] examined the power quality at different locations within an academic institution’s grid. One of the key findings was that PV inverters generate a total harmonic distortion in the output current ranging from 2.94% to 327.67%. The authors of [14] explored how household PV systems affect voltage quality in a three-phase low-voltage grid. This case study analyzed data collected remotely from two specially designed three-phase Y-connected power meters to evaluate the PV system’s impact on the grid. The main finding of this study is that a three-phase PV system in the presence of household loads can create or increase grid unbalance and cause a current in the neutral wire.
A simulation model for a microgrid was proposed in [15]. The model was developed in MATLAB/Simulink to investigate power quality when the microgrid operates connected to the conventional grid. In the study of [16], the power factor variation in a grid-connected PV system based on solar irradiance was modeled and analyzed using MATLAB/Simulink. In addition, Reference [17] proposed a detailed mathematical model for the inter-harmonic current in an on-grid PV system, utilizing a transfer function approach. The authors of [18] analyzed the effect of environmental factors on inverter operation, specifically power quality, through simulation. An experimental analysis of the power quality of PV microinverters operating under different operating conditions was conducted in [19]. Moreover, energy efficiency and current distortion measurements of PV inverters together with the associated validation procedures were considered in [20]. The analysis was conducted through a series of experimental laboratory tests on 26 contemporary PV inverters available on the market. In addition to research addressing the causes of output current distortion and quantitative analysis of harmonics generated by PV inverters, extensive research was also conducted on methods for their detection and mitigation [21,22,23,24,25].
In most studies, PV inverters were tested at a single maximum power point (MPP), typically chosen at the inverter’s nominal power. All tests on PV inverters regarding output current distortion found in the literature were carried out under steady-state operation, maintaining constant input power and voltage. The authors of [20] conducted steady-state measurements of the 3rd, 5th, 7th, 9th, 11th, and 15th harmonics across three different input voltages at 25%, 50%, 75%, and 100% of the nominal power. Based on the present review of literature, a need for further research that can include a quantitative analysis of the output current distortion from PV inverters through a broader spectrum (up to the 50th harmonic) for various input voltages and power levels has been identified. Additionally, there is a lack of research focusing on inverters in unsteady-state operation, specifically analyses of current distortion time evolution during MPPT.
Alongside the growing interest in this research area, the increasing number of PV systems connected to the power grid has led to practical issues related to interconnection and interoperability. The IEEE 1547-2018 and IEC 61727:2004 standards address these challenges by specifying requirements that must be met, particularly concerning power quality [26,27]. These standards prescribe power quality aspects, including DC injection (the presence of a DC component in the output current) and current distortion (the existence of higher harmonics in the output current spectrum).
Another critical issue is the performance of PV inverters. One relevant standard that addresses this is the European standard EN 50530:2010 [28], which focuses on the efficiency of PV inverters. This standard outlines procedures for measuring and evaluating the efficiency of PV inverters under various environmental conditions, particularly those connected to the utility grid. To assess efficiency, the starting parameters include the input power (DC) and the inverter’s output power (AC). These measurements allow for the estimation of losses under specific test conditions. This process involves calculating the AC/DC conversion efficiency and analyzing how the converters perform under different loads, temperatures, and other climatic factors. Unlike the previous standards, EN 50530:2010 does not address issues related to power quality.
The IEEE 1547-2018 standard does not specify precise test conditions regarding the voltage, current, or power supplied to the input of the PV inverter, which directly depends on solar irradiance and other environmental conditions. The research presented here aims to evaluate PV inverters by analyzing the DC injection and output current distortion at different MPPs of the PV array. The measurements are performed at the MPPs chosen according to the test specifications for the conversion and static MPPT efficiency of the EN 50530:2010 standard [28] and compared with the limits prescribed by IEEE 1547-2018 standard [26]. Additionally, the DC injection and output current distortion during MPPT are measured from the instance when the DC voltage was switched on to the inverter input until the MPP was reached. These analyses are crucial because, under actual operating conditions, the position of MPP is not constant and depends on environmental factors. Additionally, the illumination of PV modules can change due to variable irradiance, leading to fluctuations in the MPP. It is essential to assess how these variations affect harmonic generation.
This manuscript is organized as follows: The second section summarizes the IEEE 1547-2018 [26], IEC 61727:2004 [27], and EN 50530:2010 [28] standards. The IEEE 1547-2018 standard is summarized concerning only aspects of power quality, especially DC injection and current distortion. The third section describes the laboratory for microgrids and renewable energy sources, including test setup and instrumentation used for testing and evaluating the PV inverters. The fourth section presents the experimental results, including DC injection measurements and current distortion for three single-phase dual-stage PV inverters with 3 kVA, 3.3 kVA, and 6 kVA rated power. Measurements are conducted at different input voltages and power levels and represented numerically. The time evolution of the current distortion during MPPT is given graphically. The fifth section discusses the results, while the sixth one provides conclusions.
2. Overview of the Relevant Standards
2.1. IEEE 1547-2018 Standard
The “IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Related Power System Interfaces”, labeled as IEEE 1547-2018, specifies criteria for connecting and integrating distributed energy resources (DERs) such as PV installations containing inverters, modules, and optional battery storage to the power grid [26]. It focuses on the requirements necessary to ensure that DERs, when connected to the utility grid, operate safely, reliably, and efficiently. This section describes parts relevant to the research, specifically focusing on the limitations of DC injection and the limitations of current distortion [26].
The standard IEEE 1547-2018 defines current distortion limits based on the standard IEEE 519-2022 [29]. However, there are notable differences between these two standards. Firstly, there has been a change from using total harmonic distortion (THD) limits, as seen in the previous IEEE 1547-2003 standard, to total rated current distortion (TRD) [26]. This change aims to include inter-harmonics in the total distortion calculation.
Secondly, there is a change concerning the limits on even harmonics. Tighter limits—precisely 25% of the odd harmonic limits—should apply to even harmonics due to concerns about the DC offset effect. This effect can lead to the misoperation of electronic switches by affecting zero crossing and other control logic. The main contributor to this DC offset effect is the 2nd harmonic, while the influence of higher-order harmonics decreases rapidly with increasing harmonic order [26].
Moreover, despite the findings regarding tighter limits for higher-order harmonics, the standard IEEE 1547-2018 has relaxed these limits. Specifically, the limits for the 8th harmonic and higher are now the same as those for their corresponding odd harmonics. The limits for the 2nd harmonic remain unchanged. A stepped approach has been taken for the 4th and 6th harmonics, which have been adjusted to 50% and 75% of the corresponding odd harmonic limits, respectively. Voltage distortion limits for DERs are not defined, and current distortion limits are intended to exclude from consideration current distortions caused by the harmonic voltage distortion of the power system that exists when the DER is not connected [26].
The limitations related to current distortion, i.e., the maximum values of individual current harmonics and the DC component, are summarized in Table 1. The total current of all inter-harmonics with frequencies within ±5 Hz of the frequency of a given harmonic is limited to the maximum magnitude of that harmonic. The total current of inter-harmonics, with frequencies ranging from fh + 5 Hz to fh+1 − 5 Hz, is limited by a lower limit for order h and h + 1 harmonics [26].

Table 1.
Maximum harmonic current distortion, given in percent of the rated current capacity, Ir.
The TRD is calculated using the following formula:
Irms represents the RMS value of generated current in A, I1 is the RMS value of the fundamental harmonic in A, and Ir stands for the rated current capacity of DER in A. The standard limits the TRD to 5%.
2.2. IEC 61727:2004 Standard
IEC 61727:2004 is an international standard specifying requirements for connecting PV inverters to the distribution grid [27]. It applies to PV systems using non-island inverters. The standard addresses several key aspects of the inverter–utility interface, including power quality. Like IEEE 1547-2018, the standard IEC 61727:2004 also aims to ensure high power quality by limiting power distortion and DC injection from DERs. This section describes parts of the standard relevant to the research, specifically focusing on the limitations of DC injection and the harmonics and waveform distortion [27].
In addition to the fact that IEEE 1547-2018 offers more detailed and, for some limitations, stricter requirements, one of the main differences is that the THD factor is used as a quantitative parameter for power distortion, which does not consider inter-harmonics. The limitations related to the maximum values of individual current harmonics and the DC injection are given in Table 2. The THD factor is limited to 5%.

Table 2.
Maximum DC injection and harmonic current distortion, given in percent of the rated current capacity, Ir.
2.3. EN 50530:2010 Standard
EN 50530:2010 is a European standard that specifies a methodology for testing and evaluating the performance of PV inverters [28]. It defines procedures for evaluating inverters’ efficiency under different operating conditions and establishes a uniform methodology for measuring the efficiency of grid-connected PV inverters. The standard applies to single-phase and three-phase inverters, ensuring that they are tested under controlled conditions to determine their overall efficiency and performance under different conditions. The description provided in this section is limited to MPPT efficiency test conditions [28].
The standard specifies testing over a defined range of DC input voltages and loads connected to the inverter output. The tests consider different environmental conditions, such as temperature and radiation, but usually assume nominal parameters. During testing, the inverter’s performance is compared to its nominal efficiency to predict its performance under field operating conditions [28].
In EN 50530:2010, efficiency serves as the primary performance indicator. This concept includes maximum efficiency, usually evaluated under full load or optimal operating conditions. In addition, weighted efficiency is also defined, which considers different load scenarios to reflect use in real-world conditions. In addition to assessing the inverter’s performance during unchanging conditions (static MPPT efficiency), the testing also assesses its ability to cope with fluctuations in input power caused by different environmental conditions (dynamic MPPT efficiency). For this research, test specifications and conditions for static MPPT efficiency are used to evaluate PV inverters regarding the generation of current harmonics in steady-state operations. Measurements were performed for MPP normalized to 100%, 75%, 50%, 30%, 25%, 20%, 10%, and 5% of the nominal DC power, with measurements being conducted for minimum MPP voltage, rated input voltage, and maximum input voltage [28].
3. The Measurement Setup
Laboratory measurements for this research were conducted on a prototype microgrid that emulates DER, utilizing several single-phase commercial grid inverters. The PV inverters are powered by a programmable DC source (specifically, the ITECH model IT6000C [30]), which can simulate the characteristics of PV modules and energy storage batteries. This testing system was initially designed to validate the steady-state performance of new grid inverter control algorithms.
The laboratory microgrid setup for testing PV inverters includes several main components: PV inverters under test, a programmable bidirectional DC supply to emulate PV arrays, local inductive and resistive loads, and instrumentation for measuring current harmonics. This setup includes a programmable logic controller (PLC) for managing grid topology, complemented by a suitable supervisory control and data acquisition (SCADA) to synchronize testing procedures and collect measurement results.
Figure 1 shows a photo and schematic representation of the microgrid setup’s main components. The microgrid can operate in two modes: a grid-connected mode with contactor Q1 closed or a grid-isolated mode with this contactor open. Local loads can be switched on and off using individual contactors in six different combinations.
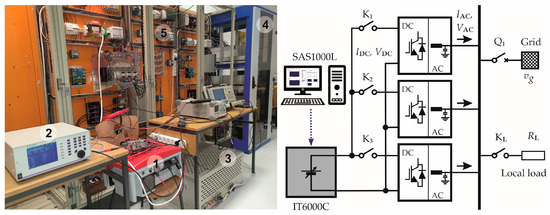
Figure 1.
Photo of laboratory microgrid site (left): 1—device under test, 2—LMG450, 3—local load, 4—DC source, 5—grid connection. A schematic of a test setup with three PV inverters, powered by a programmable DC power source (right). On-grid mode is achieved by closing contactor Q1.
A programmable DC source emulates the characteristics of a PV array comprising several connected modules to test the PV inverters. The output current of the DC source (IDC) is injected into the PV inverter.
The DC source is programmed using the Solar Array Simulation software SAS1000L version 2.2.0, which provides numerous features, including the option to generate current–voltage (I–V) characteristics of the modules based on various technological and environmental parameters [31]. For the purpose of this research, a built-in EN 50530 test program was used to provide static and dynamic MPP efficiency tests in compliance with the given standard [28]. Specifically, static tests with predefined power and voltages are performed.
The inverter output current (IAC), DC component, and harmonic distortion are measured using a precise LMG450 power analyzer and LabVIEW virtual instrumentation designed to validate DERs in compliance with the IEEE 1547-2018 standard [32]. LMG450 power analyzer is a reference device for LabVIEW virtual instrument verification. This LabVIEW testing environment uses the virtual instrumentation approach, utilizing NI USB-9264 acquisition module and USM-3IV isolated voltage and current sensor module to measure electrical quantities. The current harmonics and TRD factor calculations are processed on a computer. A crucial part of the testing environment is the software operating on a computer, performing real-time calculations and analyses based on the data collected from the acquisition modules. The DER testing environment can simultaneously perform all measurements required by the IEEE 1547-2018 standard using a single measurement setup. Additionally, it generates a comprehensive validation assessment report detailing the measured parameters.
4. Test Results
Experimental tests were conducted with three PV inverters having nominal powers of 3.6 kVA [33], 3.3 kVA [34], and 6 kVA [35]. The parameters of the tested inverters are summarized in Table 3. For safety reasons and to ensure compatibility with the laboratory’s electrical protection system, the grid inverters were connected to a three-phase power grid through a three-phase isolation transformer (400 V/230 V) with a rated power of 6 kVA and a vector group of Yd5.

Table 3.
The characteristics of the tested inverters.
4.1. Output Current Distortion During Steady-State Operation at MPP
For these tests, static MPPT efficiency test specifications and conditions according to EN 50530 are utilized to assess PV inverters’ current distortion during steady-state operations at MPP [15]. Measurements were carried out for MPP normalized at 100%, 75%, 50%, 30%, 25%, 20%, 10%, and 5% of the specified nominal DC power, with assessments conducted at maximum MPP voltage (VMPP,max), rated input voltage (VDC,r), and minimum MPP voltage (VMPP,min).
4.1.1. SOLIS S5-EH1P3.6K-l Steady-State Operation
The test results of the SOLIS S5-EH1P3.6K-l inverter, with rated current that is 15.6A, are shown in Table 4. The values of the TRD factor, DC component of the output current, fundamental, and higher harmonics are shown. The results are shown for 5%, 25%, 50%, 75%, and 100% of the nominal power of the PV array (10%, 20%, and 30% are omitted due to lack of space). The DC component and harmonics values are given in the percentage of the rated current.

Table 4.
The TRD factor, DC component, fundamental, and higher output current harmonics obtained for the SOLIS S5-EH1P3.6K-l inverter.
4.1.2. SMA Sunny Boy SB 3300-11 Steady-State Operation
Table 5 shows the SMA Sunny Boy SB 3300-11 test results, with a rated current of 14.3 A.

Table 5.
The TRD factor, DC component, fundamental, and higher output current harmonics obtained for the SMA Sunny Boy SB 3300-11 inverter.
4.1.3. DIEHL Platinum 6300TLD-ENS1-DCT-UNI Steady-State Operation
Table 6 shows the test results of the DIEHL Platinum 6300TLD-ENS1-DCT-UNI inverter, which has a rated current of 26.1 A.

Table 6.
The TRD factor, DC component, fundamental, and higher output current harmonics obtained for the DIEHL Platinum 6300TLD-ENS1-DCT-UNI inverter.
4.2. Output Current Distortion During MPPT
The distortion of the PV inverter output current during MPPT was measured from the moment when the inverter was powered up—when DC voltage was applied to the inverter input—until MPP was tracked. The harmonics of the output current were calculated in real time over ten periods, lasting 200 ms. Specifically, the DC voltage, DC current, and power at the inverter input were measured simultaneously.
4.2.1. SOLIS S5-EH1P3.6K-l-Based MPPT
Figure 2 shows the operation of the SOLIS S5-EH1P3.6K-l inverter during MPPT. The DC voltage and power at the inverter input are shown in Figure 2a. For clarity, only the 3rd, 5th, 7th, 9th, and 11th harmonics of the output current are shown in Figure 2b. MPP was achieved after 115.77 s from the inverter switching on.
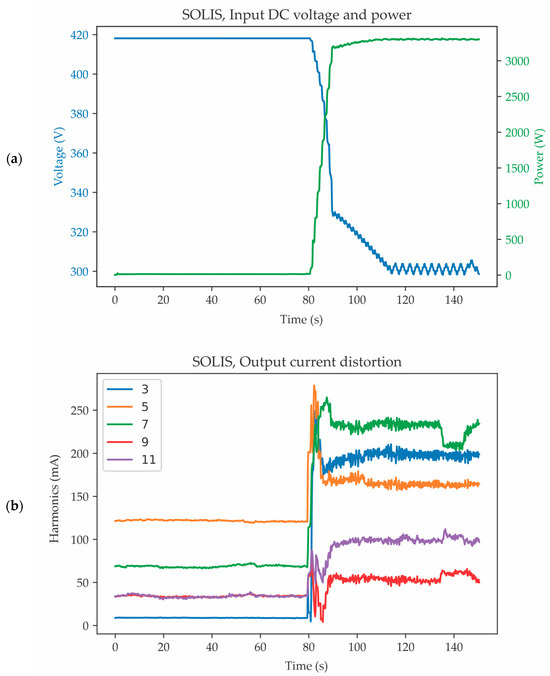
Figure 2.
The results obtained for SOLIS S5-EH1P3.6K-l inverter testing in dynamic operation. (a) Input voltage and power. (b) Output current distortion—higher harmonics in the output current spectrum.
4.2.2. SMA Sunny Boy SB 3300-11-Based MPPT
Figure 3 depicts the operation of the SMA Sunny Boy SB 3300-11 inverter during MPPT, namely Figure 3a illustrates the DC voltage and power at the inverter’s input, and Figure 3b presents the 3rd, 5th, 7th, 9th, and 11th harmonics of the output current. MPP reached 344.35 s after the inverter was powered on.
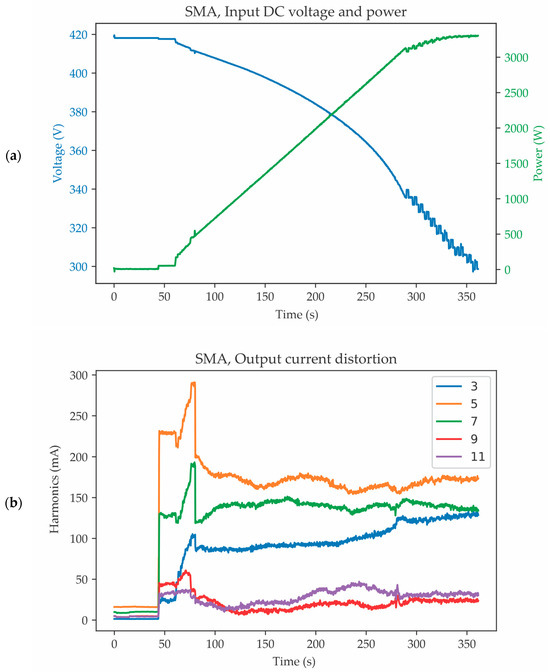
Figure 3.
(a) Input voltage and power. (b) Higher harmonics in the output current spectrum of SMA Sunny Boy SB 3300-11 inverter.
4.2.3. DIEHL Platinum 6300TLD-ENS1-DCT-UNI-Based MPPT
Figure 4 illustrates the operation of the DIEHL Platinum 6300TLD-ENS1-DCT-UNI inverter during the MPPT process. The input DC voltage and power levels for this inverter are depicted in Figure 4a. Only the 3rd, 5th, 7th, 9th, and 11th harmonics of the output current are presented in Figure 4b. MPPT was successfully achieved 67.94 s after the inverter was powered on.
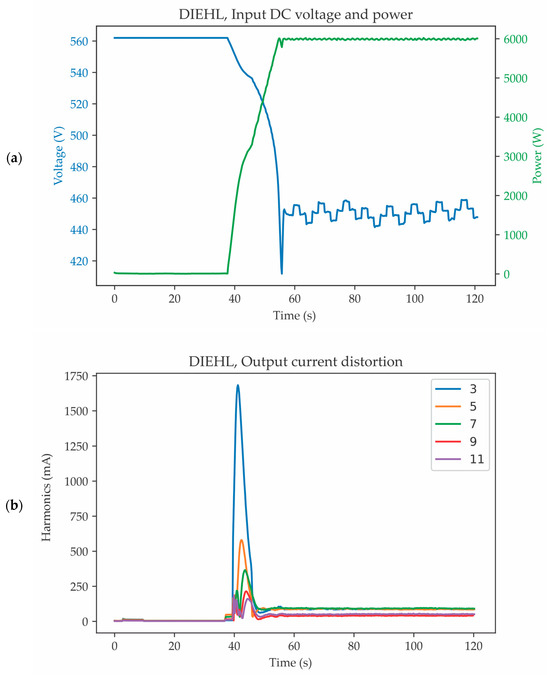
Figure 4.
(a) Voltage and power at the input of DIEHL Platinum 6300TLD-ENS1-DCT-UNI inverter. (b) Higher harmonics in the inverter’s output current spectrum.
5. Discussion
The experimental results obtained during PV inverters’ testing by measuring and analyzing the output current spectrum clearly show that the output current distortion, i.e., magnitudes of individual harmonics in the output current spectrum, depends on the input DC voltage and power. Although most tests defined by DC input voltage and power confirm that the tested inverters comply with the IEEE 1547-2018 standard, in some instances, deviations exist.
Measurements of the DC component of the output currents show that all tested inverters comply with the DC injection limits prescribed by the IEEE 1547-2018 standard (Table 1). The maximum DC injection was measured for the SMA Sunny Boy SB 3300-11 inverter for the input voltage VDC,r, at 25% of the nominal power. That value is 0.34% of the rated current.
In all associated tests, the measurements show that the SOLIS S5-EH1P3.6K-l inverter complies with the current distortion limits specified in the standard, except for the lowest power (5% to 25% of nominal power) and at the maximum DC input voltage (VMPP,max). In tests with a negative outcome, deviations from the standard were observed only for the 47th harmonic. These deviations are relatively small (less than 0.01%), within the error tolerance for this type of measurement. The trends of the influence of the input power on the harmonics measured for the steady-state operation of the SOLIS S5-EH1P3.6K-l inverter, outlined in Table 4, are practically observed during the process of the MPPT illustrated in Figure 2. For example, the 3rd and 5th harmonics have higher magnitudes at the beginning of the MPPT when the input power is smallest. When approaching the MPP, these harmonics decrease. The 7th harmonic is almost constant, which is also the trend seen in Table 4. The 3rd, 5th, 7th, 11th, and 13th harmonics are most pronounced in the output current spectrum.
All magnitudes of higher harmonics in the output current spectrum of the SMA Sunny Boy SB 3300-11 inverter are within the limits prescribed by the IEEE 1547-2018 standard [26] (Table 4). However, this inverter executes the slowest MPPT algorithm (344.35 s). Regarding the output current spectrum, the time evolution of harmonics observed during the MPPT corresponds to the results from Table 5. For example, the 5th and 7th harmonics have increased amplitudes at the beginning at lower input power, while the 3rd harmonic has an amplitude that increases in time, corresponding to the results from the mentioned table with increasing input power. The 3rd, 5th, 7th, and 11th harmonics have the highest magnitudes in the output current spectrum.
The DIEHL Platinum 6300TLD-ENS1-DCT-UNI PV inverter does not pass the validation tests according to the standard for low input powers, i.e., for 10–30% of nominal power, at all considered input voltages. Measurements show that the 3rd harmonic (greater than 5%, limit is 4%) and the TRD factor (greater than 5%, limit is 5%) are above the upper limit prescribed by the standard (Table 6). For 25% of nominal power, these values that exceeded the limits prescribed by the standard are 5.88% for VMPP,max, 5.44% for VDC,r, and 5.9% for VMPP,min. This is reflected in the results presented in Figure 4, where one can observe that at the beginning of the MPPT, the 3rd harmonic is significantly pronounced at low input power. In the later MPPT stages, the higher harmonic magnitudes become significantly smaller as input power increases. This inverter exhibits the fastest MPPT. The 3rd harmonic dominates the output current spectrum at low input power, while the proportion of higher harmonics at higher input power is more pronounced. The magnitude of higher harmonics decreases with the harmonics order.
Measurements of current distortion during MPPT show that the harmonic magnitudes are not constant and change over time. The harmonic evolution profiles of tested PV inverters differ significantly. The current distortion in steady-state operation depends on many factors, such as the inverter circuit topology, control algorithms, and output filter topologies. In addition to these factors, in an unsteady-state during MPPT, the harmonic changes depend on the MPPT algorithm. The current distortions during MPPT are most pronounced for the DIEHL Platinum 6300TLD-ENS1-DCT-UNI inverter (Figure 4b). During rapid changes in the illumination of PV modules caused by fluctuating irradiance, the input power of the inverter varies, leading to perpetual MPPT. These changes can further cause variable current distortion, which can affect sensitive electronic devices.
In the DC-coupled configuration, if a battery does not back up the PV inverter, the input power is only supplied from the PV array, as in the measurements conducted. It is a trivial fact that solar irradiance depends on the time of day, the day of the year, and variable climatic factors. For these reasons, for a significant part of the operating time of the PV inverter, the input power is less than the nominal one. Since the distortion of the output current from the PV inverter depends on its input power, which is the main conclusion of this research, it is expected that the current distortion differs in various periods. Moreover, lower solar irradiance is expected to produce less current distortion from the PV inverter if it is backed up by a battery in a DC-coupled configuration because the battery compensates for the input power deficit. In addition to the DC-coupled configuration, there is also an AC-coupled configuration. For both coupling configurations, during the one-day operation, the battery charging and discharging periods can be distinguished [36]. In the case of battery discharge, the input power of the PV inverter is equal to the total power of the PV array and the battery for the DC-coupled configuration, or only to the PV array power for an AC-coupled configuration [36]. In the case of battery charging, the input power of the PV inverter is the PV array power [36]. Since the distortion in the output current from each coupling configuration depends on the input power of the PV inverter, it is obvious that the current distortion must differ in various operating intervals. The observations presented here indicate the need for further research in this direction.
6. Conclusions
The IEEE 1547-2018 standard prescribes limits on inverter output current distortion, but the standard does not prescribe input DC voltage and power measurement conditions. The standard implicitly suggests that the recommended limits apply for all input voltages and power in all operating modes. This vagueness may lead to deviations in inverter output current distortion not being registered and documented, negatively affecting the power system during operation.
Three commercial single-phase, two-stage PV inverters were tested. The DC injection and output current distortion were measured for the input powers and voltages specified for static MPPT efficiency tests according to the EN 50530:2010 standard. The SOLIS S5-EH1P3.6K-l inverter did not comply with the IEEE 1547-2018 standard regarding the 47th harmonic for maximum MPP voltage and 5–25% of rated power. The current distortion of the SMA Sunny Boy SB 3300-11 inverter was within the limits permitted by the standard in all tests. The current distortion of the DIEHL Platinum 6300TLD-ENS1-DCT-UNI inverter exceeded the limits of the TRD factor and the 3rd harmonic at 25% of the nominal power and for all input voltages. Furthermore, this inverter exhibited high-magnitude peaks for odd harmonics during MPP tracking.
The results presented in this paper suggest that further work is needed to encourage additional research on the dependence existing between the output current distortions from different PV inverters and the associated input powers and voltages.
Author Contributions
Conceptualization, M.D. and M.P.; methodology, M.D. and M.P.; software, M.D.; validation, D.K.; formal analysis D.K.; investigation, M.D. and M.P.; resources, M.P.; data curation, M.D.; writing—original draft preparation, M.D.; writing—review and editing, M.D., M.P. and D.K.; visualization, M.D. and M.P.; supervision, M.P.; project administration, M.P.; funding acquisition, M.P. and D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This manuscript is a part of the research supported by the Agreement No. 451-03-65/2024-03/200102 on the realization and financing of scientific research work of the Faculty of Electronic Engineering, University of Niš in 2024 by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- International Energy Agency. Renewables 2023: Analysis and Forecast to 2028; International Energy Agency: Paris, France, 2023; Available online: https://www.iea.org/reports/renewables-2023 (accessed on 18 December 2024).
- Eltawil, M.A.; Zhao, Z. MPPT Techniques for Photovoltaic Applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Hache, E.; Palle, A. Renewable Energy Source Integration into Power Networks, Research Trends and Policy Implications: A Bibliometric and Research Actors Survey Analysis. Energy Policy 2019, 124, 23–35. [Google Scholar] [CrossRef]
- Kamarzaman, N.A.; Tan, C.W. A Comprehensive Review of Maximum Power Point Tracking Algorithms for Photovoltaic Systems. Renew. Sustain. Energy Rev. 2014, 37, 585–598. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Shandilya, A.M.; Dash, S.K. Maximum Power Point Tracking (MPPT) Techniques: Recapitulation in Solar Photovoltaic Systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Hossain, J.; Blaabjerg, F. Evolution of Microgrids with Converter-Interfaced Generations: Challenges and Opportunities. Int. J. Electr. Power Energy Syst. 2019, 109, 160–186. [Google Scholar] [CrossRef]
- Yaghoobi, J.; Alduraibi, A.; Martin, D.; Zare, F.; Eghbal, D.; Memisevic, R. Impact of High-Frequency Harmonics (0–9 kHz) Generated by Grid-Connected Inverters on Distribution Transformers. Int. J. Electr. Power Energy Syst. 2020, 122, 106177. [Google Scholar] [CrossRef]
- Anurangi, R.O.; Rodrigo, A.S.; Jayatunga, U. Effects of High Levels of Harmonic Penetration in Distribution Networks with Photovoltaic Inverters. In Proceedings of the 2017 IEEE International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 15–16 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Nicolae, P.-M.; Marinescu, R.-F.; Marinescu, D.-C.; Nicolae, M.-Ş.; Nicolae, I.-D. Harmonics Induced by Inverters from a Photovoltaic Plant in the Power Grid. In Proceedings of the 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility (EMC/APEMC), Suntec City, Singapore, 14–18 May 2018; pp. 821–826. [Google Scholar] [CrossRef]
- Pereira, J.L.M.; Leal, A.F.R.; Almeida, G.O.d.; Tostes, M.E.d.L. Harmonic Effects Due to the High Penetration of Photovoltaic Generation into a Distribution System. Energies 2021, 14, 4021. [Google Scholar] [CrossRef]
- Naidu, T.A.; Ali Ahmed Albeshr, H.M.; Al-Sabounchi, A.; Sadanandan, S.K.; Ghaoud, T. A Study on Various Conditions Impacting the Harmonics at Point of Common Coupling in On-Grid Solar Photovoltaic Systems. Energies 2023, 16, 6398. [Google Scholar] [CrossRef]
- Peiris, K.; Elphick, S.; David, J.; Robinson, D. Impact of Multiple Grid-Connected Solar PV Inverters on Harmonics in the High-Frequency Range. Energies 2024, 17, 2639. [Google Scholar] [CrossRef]
- Alawasa, K.M.; Al-Badi, A.H. Investigation and Analysis of the Power Quality in an Academic Institution’s Electrical Distribution System. Energies 2024, 17, 3998. [Google Scholar] [CrossRef]
- Apse-Apsitis, P.; Krievs, O.; Avotins, A. Impact of Household PV Generation on the Voltage Quality in 0.4 kV Electric Grid—Case Study. Energies 2023, 16, 2554. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Jiménez-Román, C.R.; Enriquez-Santiago, J.A.; López-López, A.; González-Domínguez, R.A.; Ramírez-Torres, J.A.; Rodríguez-Romero, J.D.; Jaramillo, O.A. Power Quality Analysis of a Microgrid-Based on Renewable Energy Sources: A Simulation-Based Approach. Computation 2024, 12, 226. [Google Scholar] [CrossRef]
- Adak, S. Power Factor Analysis of Grid-Connected Solar Inverter under Different Irradiance Levels throughout the Day. Energies 2024, 17, 3632. [Google Scholar] [CrossRef]
- Mao, M.; Ni, X.; Xu, Z.; Sun, H.; Yin, C. A Comprehensive Analysis of the Influencing Factors of Interharmonics on a Distributed PV Grid-Connected Power Generation System. Energies 2024, 17, 5958. [Google Scholar] [CrossRef]
- Asma, R.; Zahzouh, Z.; Boulahchiche, S. Impact of Grid-Connected Photovoltaic System under Different Weather Conditions and Load Types. J. Appl. Eng. Sci. 2023, 21, 721–728. [Google Scholar] [CrossRef]
- Tamrakar, E.; Patel, R.N.; Kumar, A.; Sahu, A.; Singla, R. Experimental Investigation and Power Quality Analysis of Solar Micro-Inverter for Different Operating Conditions. E3S Web Conf. 2023, 405, 02024. [Google Scholar] [CrossRef]
- Chmielowiec, K.; Topolski, Ł.; Piszczek, A.; Rodziewicz, T.; Hanzelka, Z. Study on Energy Efficiency and Harmonic Emission of Photovoltaic Inverters. Energies 2022, 15, 2857. [Google Scholar] [CrossRef]
- Jaiswal, A.; Sachan, S.; Deb, S. A Novel Technique to Detect and Mitigate Harmonics during Islanding in Grid-Connected PV Systems. Energy Rep. 2024, 12, 3940–3956. [Google Scholar] [CrossRef]
- Gada, S.; Fekik, A.; Mahdal, M.; Vaidyanathan, S.; Maidi, A.; Bouhedda, A. Improving Power Quality in Grid-Connected Photovoltaic Systems: A Comparative Analysis of Model Predictive Control in Three-Level and Two-Level Inverters. Sensors 2023, 23, 7901. [Google Scholar] [CrossRef] [PubMed]
- Bandahalli Mallappa, P.K.; Garcia, H.M.; Quesada, G.V. Power Quality Enhancement in a Grid-Integrated Photovoltaic System Using Hybrid Techniques. Appl. Sci. 2021, 11, 10120. [Google Scholar] [CrossRef]
- Benabdelkader, A.; Draou, A.; AlKassem, A.; Toumi, T.; Denai, M.; Abdelkhalek, O.; Ben Slimene, M. Enhanced Power Quality in Single-Phase Grid-Connected Photovoltaic Systems: An Experimental Study. Energies 2023, 16, 4240. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P.; Alkahtani, A.A.; PG Abas, A.E. Power quality assessment of grid-connected PV system in compliance with the recent integration requirements. Electronics 2020, 9, 366. [Google Scholar] [CrossRef]
- IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003); IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018; pp. 1–138. [CrossRef]
- IEC 61727:2004; Photovoltaic (PV) Systems—Characteristics of the Utility Interface. International Electrotechnical Commission: Geneva, Switzerland, 2004.
- EN 50530:2010+A1:2013 (Amendment to EN 50530:2010); Overall Efficiency of Grid Connected Photovoltaic Inverters. European Committee for Electrotechnical Standardization; CENELEC: Brussels, Belgium, 2013; pp. 1–40.
- IEEE Std 519-2022 (Revision of IEEE Std 519-2014); IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; pp. 1–31. [CrossRef]
- IT6000C Bidirectional Programmable DC Power Supply. Available online: https://www.itechate.com/en/product/dc-power-supply/IT6000C.html (accessed on 19 December 2024).
- SAS1000 Solar Array Simulation Software. Available online: https://www.itechate.com/uploadfiles/catalogue/SAS1000-en.pdf (accessed on 19 December 2024).
- Dimitrijević, M.; Petronijević, M. The System for Distributed Energy Resources Testing According to the IEEE 1547-2018 Standard. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2023, 42, 1019–1036. [Google Scholar] [CrossRef]
- SOLIS S5-EH1P3.6K-l. Available online: https://www.solisinverters.com/uk/energy_storage_inverter5/3_6k_s5_l_en.html (accessed on 19 December 2024).
- SMA Sunny Boy Operating Parameters. Available online: https://files.sma.de/downloads/SB_SMC_WB_Par-TB-TEN113160.pdf (accessed on 19 December 2024).
- PLATINUM® Inverter, Monitoring & Energy Management. Available online: http://www.avdira-solar.eu/pdf/diehl/en/diehl_catalogue_en.pdf (accessed on 19 December 2024).
- Sandelic, M.; Sangwongwanich, A.; Blaabjerg, F. Reliability evaluation of PV systems with integrated battery energy storage systems: DC-coupled and AC-coupled configurations. Electronics 2019, 8, 1059. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).