Preliminary Test of Source Parameters of M_wp6 Italian Earthquakes: Revisiting Kinematic Function Method

Abstract

Macroseismic intensity data are the only source of information for historical earthquakes; it is therefore necessary to devise methods that allow us to retrieve as many source parameters as possible on the basis of these data. We present the inversion of macroseismic data as a first validation of an improved version of the kinematic function, KF. Following the previous results of some earthquakes on Italian territory and several validations by Californian events provided with instrumental solutions, we have now simplified the KF by reducing some degrees of freedom of the parameters and rearranging the code for parallel calculation. This approach will allow for a more extensive application of the KF technique. We present the inversion of the macroseismic intensity pattern of the M_wp6 earthquake of 27 March 1928 (8:32 GMT), which occurred in Northeastern Italy (Carnia), and we retrieved source parameters that are compatible with the solutions of other authors who independently treat instrumental data. The 1928 event is located a few tens of kilometers west of the more destructive M_w6.5 of 6 May 1976 and northeast of the subsequent earthquake M_wp6.1 of 18 October 1936. The inversion was performed as a blind test, without prior knowledge for fault plane solutions and tectonic information; it resulted in a minimum variance model with a strike of 62°, a dip of 10°, and a rake of 101°. This solution is not consistent with the entire tectonic framework of the eastern Southalpine chain, but it is in agreement with the But-Chiarsò line. This result encourages us to test further improvements to the KF method and to treat other cases from the Italian macroseismic catalog.

1. Introduction

Italy has allegedly the best historical seismic catalog in the world. It is the CPTI15 [1] and its associated macroseismic database [2], which spans from 1000 to 2018. This catalog is the last iteration of a series of parametric catalogs that summarize all of, hopefully, the relevant studies on each known event that affected the Italian territory in the above-mentioned time window. Starting from 1903, instrumental information was also added.

In this catalog, macroseismic fields, expressed in terms of MCS, are associated with several thousands of events. Following the CPTI15 format, we express macroseismic intensities as regular digits or as non-numerical values throughout this paper. Since Italian seismicity is moderate (only eight events with M > six occurred since 1976, the year when digital seismology started worldwide), it is essential to include historical information to correctly assess hazards. Intensity, however, is often quite tricky.

First, it must be stated that since damage can be caused both by positive and negative pulses, it is impossible to recover a complete focal mechanism; it means that we can theoretically distinguish between a strike-slip solution and a normal/reverse one, but we cannot hope to refine it to say that it is a right or left strike-slip rupture or, alternatively, a normal versus a reverse one.

To add to the complexity, we must consider that there can be regional variations in Q and local seismic effects, but we will not tackle these issues here, since they would require investigating a large number of events. Usually, local effects are not a serious problem, since we generally observe them only in few spots. Q effects are a more serious problem, even more so if the macroseismic field lies partially on a mountain range and partially on a plane. In this case, the general shape can be altered.

However, another important issue is the seismic vulnerability of buildings. The EMS98 scale, for example, organizes vulnerability correctly, based on building types and considering vulnerability explicitly. Theoretically, this aspect should be consistent with the previous macroseismic scales MSK, MCS, and MM. In fact, the historical scales considered vulnerability based on a visual (or esthetic) survey of building types, considering the substantial equivalence between building types and vulnerability. On the contrary, the variations in resistance within each building type are often as great as those between different vulnerability classes. Following this approach, the seismic vulnerability of buildings has historically often been neglected, considered as a secondary parameter, and thus poorly conditioned. In fact, the seismic vulnerability of buildings and its distribution has not generally been considered in attenuation laws (e.g., but not limited to [3,4,5]).

In addition, the incorrect assessment of seismic vulnerability could significantly affect the assessment of cumulative damage after the main shock of each seismic sequence. Consequently, there may be significant problems in assigning seismic intensity for earthquake events in the catalog. The correct definition of the seismic vulnerability of buildings for events in the historical catalog is an extremely complex problem; this topic is beyond the scope of the present study but is an important topic of study for our research group.

Up to now, source parameters, i.e., fault surface projection and macroseismic magnitude expressed as M_w proxy (M_wp), in Italy are generally recovered using a method shown in [6,7], which is known as “boxer”. It has been widely used by other investigators aside from the main authors [8,9].

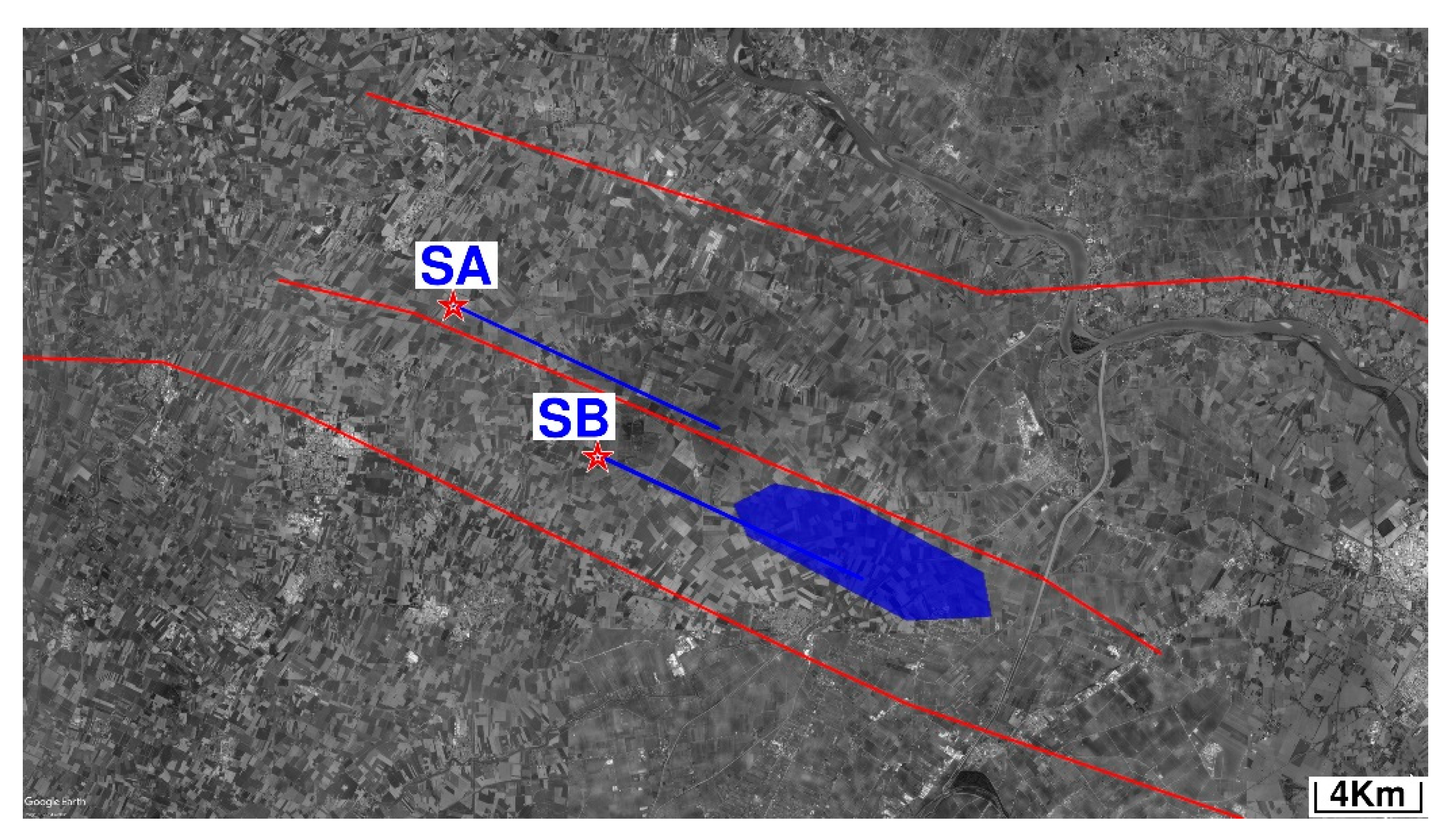
It assumes that the fault surface projection corresponds to that of the area of maximum intensities. As it can be understood, it is extremely rough, since often the fault is shifted to the side of the main area of damage but allows for a wide application even in cases where relatively few intensity points are available. To better understand the problem, in Figure 1, we show two cases in Italy where the source is markedly shifted with respect to the area of main damage. In Figure 1a, the case of the M_w6.45 on 6 May 1976 is depicted. A summary of the hypotheses of sources for 1976 is reported in [10], where the more accredited sources are distributed in the Gemona area. One of the older ones is [11], revalued by [12,13,14]. In blue is shown the area involving the largest asperities of the 6 May 1976 M_w6.45 Friuli earthquake [15]—slightly NE to the area in [14] and similarly, we show the area of main deformation of the 20 May 2012 M_w6.09 Mirandola earthquake [16]. Incidentally, the Friuli earthquake occurred in the same area as the 1928 event, which is the one investigated in this paper.

The 2012 event occurred in the Po plain (Figure 1b) and, contrary to the usual expectation of strong amplification in such an environment, the macroseismic field yields a macroseismic magnitude of M_wp5.15. The nearby Po River had probably saturated the terrain sediments that compose the upper layers of the plain over a thickness of several kilometers, effectively attenuating the S-waves. In contrast to the case of the 1976 alluvial fan, it was observed that at the transition from the lower to the upper part of the fan—and thus at greater thickness—the intensity increases by up to three degrees, which represents a very large difference in international case history [10].

In this paper, we further develop the KF method in order to make it more widely applicable to as many historical macroseismic fields as possible. The obvious conclusion is that we cannot obtain a totally unconstrained source solution because often the degrees of freedom yielded by the macroseismic field are less than those required by the KF source description method that in turn is already a simplified version of the true one. This is because a macroseismic field described in terms of MCS provides at most 11 possible values and quite often even less, much less, than that. We want to clarify here that the CPTI15 strictly abides to the quantization of intensity values. Even whenever two intensities are given (e.g., I_MCS = 7–8), it means that there is an uncertainty between the two values, but the quantization still holds.

As a showcase for our theoretical development, we choose an M_wp6 event that occurred in Northeastern Italy in 1928. This choice is almost obliged, since it is the only event in the CPTI16 catalog that fulfills all the necessary requirements; it is an event that occurred before the widespread use of concrete, which means that the building quality should not be too different from that of the previous centuries, there are instrumental data, and the magnitude is in the correct range, since it is large enough to be modeled as a linear horizontal rupture but is also small enough to be relatively simple.

2. Improved KF Version

This work is a new step toward the development of the quantitative treatment of the so-called macroseismic intensity in order to obtain geophysical information on the source of mostly pre-instrumental earthquakes on Italian territory [17,18]. To retrieve this information, we use the method of inversion of kinematic function, KF. This method of inversion has already been used in the Italian territory. The first inversion was carried out for the Noto earthquake M_wp7.4 of 11 January 1693, which struck southeastern Sicily [17]. Despite many qualitative works localizing the source offshore on the Ibleo Maltese structure, the source of January 11 and its ninth foreshock is inland and linked to the Scicli Monte Lauro structure, which was recently confirmed by the work in [19]. In recent years we have performed the inversion of the earthquake of 7 September 1920 [20] and the earthquake of 14 April 1895 at M_wp6.1 in Ljubljana, which struck part of northeastern Italy. The former confirms the hypothesis of a normal fault linked with the Garfagnana graben, the latter, despite the complexity of the macroseismic dataset, leads to the source being associated with the Dinaric style of the area. The aim of this article is to retrieve some information on the source of the earthquake M_wp6 of 27 March 1928 in the Friuli Venezia Giulia (FVG) region in Northeast Italy. In the same region, the KF method was used for the M_wp6.2 earthquake of 18 October 1936 [21] (see in Section 2) and the previously cited M_w6.45 of 6 May 1976 [10]. Information on the sources of historical earthquakes is important for hazard assessment and the development of damage scenarios for engineering planning [22].

The KF inversion method is based on a kinematic function (KF) [23], developed in [24]. The kinematic function, KF, has already been presented in other publications, and the details can be found in Appendix A.

The first version of the KF has already been validated using the regional intensity patterns of Californian earthquakes, which have been provided with instrumental solutions. Following these validations, we applied the method in other regions of the world [25]. Our hypothesis of the M8.2 Bihar–Nepal 1934 earthquake is confirmed in the recent study of [26] and the epicenter of M8.5 Shillong 1895 is confirmed in [27]. The algorithm is also useful for earthquakes that occurred offshore [28], overcoming the concept of other macroseismic methods where a surface projection corresponds to that of the area of maximum intensities. Indeed, the KF inversion method is based on the radiation pattern of S-waves, as in the example of Sirovich et al. (2009) [22].

Regarding the KF formula (see Appendix A, Formula (A1)), we only want to emphasize here that it agrees with the asymptotic approximation [29,30,31]. This means that the KF uses as a propagation medium an elastic half-space in the distance range of about 5 to 100 km from the source and wavelengths shorter than the shortest distance between the observer and source. If a site is within 5 km from the epicenter, the method assigns the maximum intensity value of the computed dataset. We also recall that in our convention, the fault plane is dipping to the right of the positive direction of the strike; the rake angle is seen on the fault plane from the hanging wall of the fault and measured anticlockwise from 0° to 360° between the positive direction of the strike and the direction of the slip vector.

It should also be kept in mind that since the intensity has no polarity, our KF method is unable to distinguish between the results of mechanisms that differ in the rake angle by 180°, since it produces the same radiation but with reversed polarities in both cases. This ambiguity can only be resolved by instrumental records or additional tectonic/geodynamic information. Secondly, our KF inversion problem is close to bimodality in the case of almost pure dip-slip mechanisms [21].

In this paper, we propose a simplified version of the standard method that allows us to systematically explore the whole parameter space. This need arises from a simple fact, that intensity data are discrete and can assume only 11 possible values; this strongly limits the amount of possible free parameters. It is true that intensity spatial distribution plays a role as well, as we will see. This means that there are many possible equivalent solutions unless we somehow limit the free parameters making use of as much a priori information as possible. This is even more dramatic if we consider that often, only a subset of intensities is available, that is, there are only seven or eight intensity values out of the possible eleven.

With 12 parameters, even in principle, this would lead to an underdetermined problem. Most of the Italian events, however, are small enough (M < 6.5) such that a uniform rupture velocity is sufficient.

Moreover, excellent S-wave velocity models are now available. This means that we can use one of these [32] instead of inverting for the S-wave velocity. In this case, we choose a simplified approach, in line with the general simplicity of the original method, that is, to select the average velocity in the area comprised between the fault and the intensity point. Finally, a magnitude estimate usually exists a priori. The “boxer” method in fact has a good feature that we will make use of, that is, the magnitude estimation. It is in fact the main tool to compute macroseismic magnitudes in the CPTI15 catalog that are scaled to correspond to M_w proxies (M_wp). It is also possible to constrain the fault to have a fixed length that depends on the assumed magnitude, e.g., in [33]. In our case, however, we do not straightforwardly use the RLD, the subsurface rupture length (Formula (A3) of Appendix A) general relation, but a function of it, namely 80% of its value. We tentatively selected this value on the base of admittedly very few available observations. In Italy, in fact, only four events occurred after 1976 that (1) yielded M_w > 6, (2) occurred on land, (3) were not intermixed with other events that occurred nearby, and 4) were investigated in terms of slip distribution. We show these in

Table 1. Four modern Italian events where total length of asperities is known compared to 0.8*RLD as obtained in [35]. They are organized in descending order of magnitude. (Magnitude from CPTI15.)

Date	Mw	80% RLD	Observed
6 May 1976	6.45	18.6	18
6 April 2009	6.29	14.9	15
24 August 2016	6.18	12.9	13
20 May 2012	6.09	11.4	11

. We roughly estimated the along strike length of the principal asperities using the literature data, namely [15] for the 6 May 1976 Friuli event; [34] for the 6 April 2009 L’Aquila event; [35] for the 24 August 2016 Accumoli event; and [16] for the 20 May 2012 Mirandola event.

The above reasoning reduces the number of free parameters to eight and consequently helps stabilize the solution. We also rewrote the inversion program to optimize it as much as possible. This program is now fully parallel with respect to the epicentral location, that is, the computation is performed in parallel with respect to the grid of possible epicentral locations. Its main limit, however, is not related to the computation workload but to the speed of memory access in the CPU cache. The final improvement is in the way intensity data are treated. As is known, real valued intensities do not exist; whenever we obtain an uncertainty between two intensity values or, even worse, a non-numeric value such as a generic damage assessment, we need to evaluate the probability that this value assumes a given intensity. Since we use the current version of the [1,2] historical catalog, we pre-computed the probability of uncertain intensities on the assumption that they are distributed in such a way that the relative proportion between the intensity values does not change. In the case of non-numeric values, we normalized the values proposed in [2]. This means that for a calculated intensity $I_c=M$ and an observed intensity $I_o=N÷N+1$, the residual value will be:

$$R{\left(M\right)}^2=\left[P_N{\left(M-N\right)}^2\right]+\left[P_{N+1}{\left(M-N-1\right)}^2\right]$$

(1)

where $P_N$ P() and $P_{N+1}$ are the normalized partition coefficients. The partition coefficients are reported in Appendix B.

3. Validation of the Improved KF Version

To give a sense of what is the resolution of our approach, we tested it on the macroseismic field of the 20 May 2012 event. The macroseismic field of this event is extremely poor (53 intensity points), since only localities within the immediate surrounding area are reported, even though it was felt over a wide area. This earthquake source is, however, extremely well investigated and reasonably simple, so that we can be sure that an along strike representation of the main asperity will be satisfactory. Following [16], we selected a source with a length of 11 km, unilateral rupture, a 12 km depth, 114° strike, 30° dip, 90° rake, and an M_w = 6.09, according to [1,2]. So, we basically left the program as free to choose the epicenter and the Mach value (rupture propagation velocity with respect to S-wave velocity). This is because the intensity (MCS) points only give three possible values (I_MCS = 7, 6, 5) and eight points out of fifty-three are uncertain, while another 12 are expressed as non-numerical values (I_MCS = D), an overall situation that is even worse than most historical events available in [1,2]. In Figure 2, we show the two best solutions, SA and SB, of two different families. As the results show quite evidently, it is SB, the second best, which is most similar to the real one. This means that there is a distinct probability that in many cases, we will need to choose one family over another not only on the basis of the absolute best residual but also on the basis of tectonic considerations. As far as the choice between SA and SB is concerned, in case we did not know the source’s true geometry and location, we could only prefer SB on the basis that it is nearer to the area of maximum damage. However, we note that the epicentral error is still about 6 km, and we should never forget that due to variations in vulnerability, local effects, and improper and simplified modeling, we cannot hope to obtain a better accuracy. There is another crucial point, which is that it is necessary to fix a priori the correct fault length and magnitude, otherwise weird solutions start to appear, particularly in an area of about 20 km to the southwest of the true epicenter. These latter solutions allow for much better matching of the macroseismic data obviously, with completely wrong fault lengths.

We also need to understand what the meaning of the macroseismic epicenter is. In general, according to the Boxer method [6,7], this is in fact conceptually very similar to a centroid in a moment expansion representation. Conversely, we consider it as the surface projection of the point where the rupture of the main asperities starts. Another issue we need to address is how to perform inversion. Since our data are quantized, there is no derivative continuity. This means that none of the classic derivative-based inversion methods can be applied. Even random approaches such as the Monte Carlo method will fail, since the quantified data will induce strong nonlinearity effects, as small variations in a parameter can induce large variations in the residual. The only way we found is to resolve the issue by brute force, that is, to explore the whole space parameter and find possible epicentral areas and a family of solutions, progressively refining them. This approach needs to be necessarily coarse at the beginning, since an initial in-depth exploration would require exploring a number of solutions that could easily be in excess of 1015. To give an example, we explored the case of the 2012 earthquake, an area that was almost 0.5° × 0.5°, precisely 47 lines in latitude by 51 rows in longitude. Since we were using only another parameter, this computation is extremely fast, but in cases where we are exploring seven or eight parameters, using hundreds of intensity points, this computation rapidly approaches levels of CPU time that are simply not affordable. This means that it is necessary to follow a refinement approach. Moreover, there is a maximum distance for the application of this method that is about 100 km, the distance in Italy for which we have direct S-wave propagation using an elastic half-space; this implies that we need to keep the number of intensity points that falls within the 100 km range at each step constant. This distance within 100 km obviously depends on epicentral locations, fault lengths, and strikes. Since at each refinement step, the parameter range is reduced, this introduces another source of strong nonlinearity. This is tantamount to saying that there is a small but non-negligible degree of subjectivity in defining an optimal solution. This is another reason why we will, in general, identify a few families of possible solutions, represented by the best one for each family, and then we will try to select the preferred one on the basis of tectonic considerations and not on the basis of residuals only.

It would be natural to test this approach on some modern event where the source is well known. However, none of those with M > 6 shows a full range of intensity values. The event we selected, however, yields intensities from I_MCS = 2 to I_MCS = 9 and has an instrumental magnitude estimate (M_wp = 6.09) that is not dissimilar to the macroseismic-based one (M_wp = 5.99) [1].

The epicentral area of the M_wp6 earthquake of 27 March 1928 (

Table 2. Events that struck the 1928 area in the previous 20 years (data from CPTI15, n.a. is not available).

Earthquake Date	Mwp	I0	Epicenter Macroseismic	Epicenter Instrumental	I at Tolmezzo
27 March 1928 08:32	6.0	9	46.372 N 12.975 E	46.270 N 13.020 E	7–8
26 March 1928 14:40	5.7	n.a.	46.490 N 13.180 E	46.490 N 13.180 E	n.a.
12 December 1924 03:29	5.4	7	46.462 N 12.982 E	46.400 N 13.020 E	7
12 May 1924 08:46	5.0	7	46.409 N 12.912 E	46.460 N 12.850 E	6
5 May 1920 14:41	5.3	6–8	46.384 N 13.144 E	n.a.	5
10 July 1908 02:13	5.3	7–8	46.465 N 13.191 E	n.a.	6

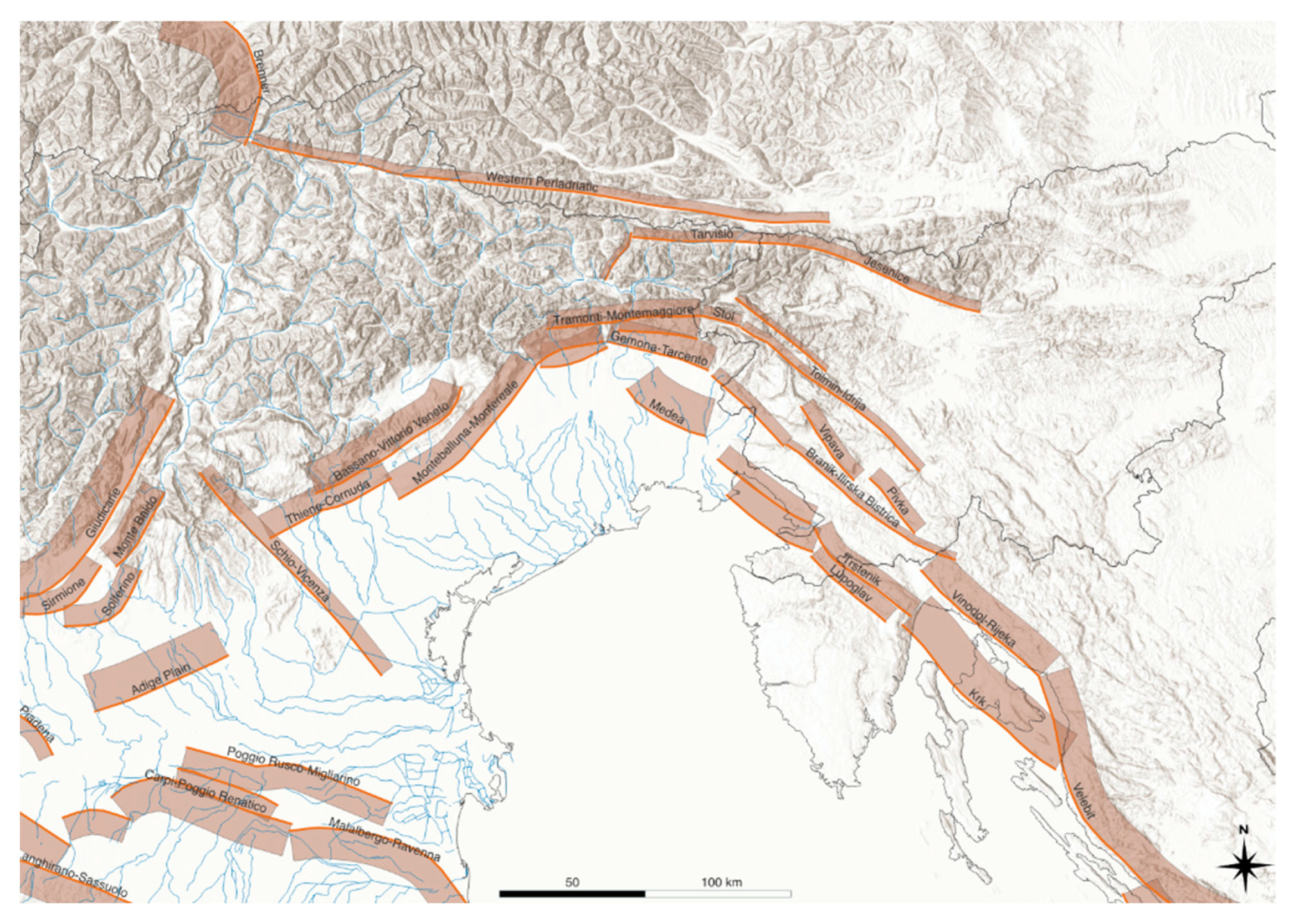
) is located in the central part of the Italian Region of Friuli Venezia Giulia (Figure 3), in the eastern portion of the Southern Alps. The area (Figure 4) of the 1928 M_wp6 earthquake is located at the boundary between the fold and thrust belt of the Southern Alps and the Venetian Friulian plain and follows the Pliocene–Quaternary front of the eastern Southalpine Chain [37].

The eastern part of the Southern Alps is affected by high seismicity, the highest in the entire Alpine chain. The shortening and thickening of the crust are still active and the most seismic activity has been recorded along the southern edge of the eastern Southalpine Chain. The seismicity is almost exclusively due to the activation of compressional sources, with the main compression oriented between NNW-SSE and N-S [38]; associated with the evolution of the S-SE verging trending overthrust fronts, focal mechanisms of strike-slip characterize the western Slovenian territory [39,40] and the Alto Tagliamento area north of Tolmezzo [38,39,40,41,42]. The central part of eastern Southern Alps Chain—the area affected by the 1928 earthquake—is located in the transition zone between the Southern Alps and the Dinarides. The transition is marked by the southern front or Periadriatic Lineament [43]. The geological units of the area consist mainly of limestones and carbonate rocks from Triassic to Cretaceous, which belong to the thick shelf complex of the Friuli Platform [44]. Flysch and molasse compose the Cenozoic and Quaternary deposits. To the north, the area borders the Paleozoic Carnic Chain, which consists mainly of limestones (Permian and Devonian), evaporitic, terrigenous, and volcanic deposits. As already mentioned, the main directions of the tectonic lineaments are E-W, generated by N-S trending Alpine compression (Pliocene) and turning ENE-WSW toward west (late Pliocene). In the central part (1928 area), shown in [38], a series of E-W lineaments is indicated. South of Tolmezzo are the Dof-Auda and Pinedo-Uccea lines. They also show a series of faults running from northeast to southwest, except the But-Chiarsò, which continues toward southwest at the Tramonti–Verzegnis line, shown by [43]. In recent years, there have been numerous studies on active faults of the zone. The most recent is in, which points to Quaternary activity. These authors show a quaternary active line with a direction of east–west at the Alto Tagliamento and Resiutta-Pont Avons line= and NNW-SSE for the San Florian fault in the area of the 1928 event.

In this area, the KF was used to invert the M_w6.5 6 May 1976 Friuli earthquake [10], the M_w6.1 18 October 1936 Cansiglio event [21], and the M_w6.1 14 April 1895 Ljubljana (Slovenia) event [45]. The main shock occurred on 27 March 1928 at 8:32 GMT and caused 11 fatalities and 40 injuries. The heaviest damage was reported in some towns and small settlements in the upper Tagliamento valley and in the surrounding mountains. Aside from the [1,2] catalog, there is another available catalog, the CFTI5med [46], that spans from 461 B.C. to 1997 and reports an in-depth description of effects for a large number of events. In our case, it shows that the three most damaged villages were Chiaicis, Pusea, and Verzegnis (I = 9); many houses completely collapsed and most buildings were severely damaged. In this work, we have used the [1,2] catalog for the inversion, which, in addition to the three villages mentioned above, also assigns I = 9 to other settlements in the epicentral area, namely Faeit, Pozzis, Santo Stefano, and Villa. The settlements of Marins, about 10 km south of the epicenter, were severely damaged (“semi-destroyed township”) according to the CFTI5med. The most important town near the epicenter was Tolmezzo (I_MCS = VII-VIII), where the damage was exacerbated by injuries from previous earthquakes. The cathedral and the courthouse were damaged, as well as some schools. The day before the main shock, an M_wp5.7 earthquake occurred at 14:40 GMT about 18 km northeast of the March 27 epicenter and 14 km from Tolmezzo. In Table 2, we list the most important earthquakes in the area and in the twenty years prior to the 1928 earthquake, with an indication of the epicentral intensity I₀. The studies [1,2] report two aftershocks of at least M_wp ≥ 4 in 1928 close the epicenter of the March 27 event. There are a total of 359 intensities in terms of MCS scale (Mercalli Calcani Sieberg) through mainly Italy, Austria, and Slovenia (Figure 4). The dataset shows a gap in the southwestern area of the epicenter due to a mountainous zone, but the intensities within the first 20 km are fairly homogeneous in terms of attenuation. The local effects of many sites in the region have already been analyzed for other earthquakes. In [10], for distances above 40 km, one degree of intensity can be seen only for sites with soft soil, confirmed in [45] for sites with soft soil with a thickness > 30 m (C1) but not for soft soil with a thickness less than 30 m (C2).

A detailed study of the Gemona alluvial fan, which was characterized by the highest intensities for the 1976 M_w6.5 earthquake, ref. [10] denies the amplifications for the 1928 earthquake, being I = V-VI in Gemona, about 15 km from the epicenter. The small (in 1928) settlement of Majano experienced an I_MCS = IV, and this does not justify the strong motion amplification of the same magnitude (M6) and distance from the epicenter of the 15 September 1976 9:21 GMT aftershock [32] (I = VIII-IX from [1,2]). In 1928, the assigned intensity was significantly lower than the main shock of 1976 (IX). Moreover, the resident population in 1928 was practically double that of 1976. That is, the town was depopulated and probably regressed. This may have resulted in an increased vulnerability of buildings due to a lack of maintenance and the sequence of shocks in 1976.

As such, many of the possible local effects assessed in the historical catalog should be revised based on a broad and thorough vulnerability assessment [47]. In the case under consideration, for the 1928 earthquake, available information and archive images would allow for a new assessment of the vulnerability of buildings. In this regard, recent events have highlighted similar cases. For example, in the 2016 Central Italy earthquake [48], Accumoli village has been classified as the VIII-IX grade of EMS98. Several partial collapses have been surveyed, and based on the survey, the high vulnerability of the buildings has been highlighted. Nevertheless, the effects of tie beams must be highlighted. The difference with the city of Amatrice is evident. However, in a pre-earthquake typological survey, the building types could have been considered similar. Finally, because of what has just been said, for the September 15 aftershock, Majano appears to be a clear case of cumulative damage.

KF Inversion

As we stated previously, the KF inversion is a nonlinear problem. Moreover, since we know that sometimes the epicentral area does not coincide with the macroseismic epicenter, it is necessary to probe a rather large area to pinpoint the true epicenter. Therefore, we initially scanned with a rough parameterization (0.02° in latitude and longitude, 2.5 km in depth, 10° steps for strike dip and rake, fixed magnitude according to [1,2], 0.1 Mach steps) the two segments that can compose the fault subdivided according to Table 1 in an area that at least exceeds that which includes all the values I ≥ I_max−1, with a 12 × 19 grid. In our case, the magnitude is the macroseismic one from [1,2], that is, M_wp = 5.99. The total fault length accordingly becomes 10 km. These two values were not modified throughout the whole process of inversion.

After this first test, we observed that the eastern portion of the grid was systematically yielding very high residual values, that is, the epicenter must be located to the west of our tentative research area. We therefore restricted our search to the central and western portion of the area using, in this case, a 24 × 26 grid, 0.01° step, and reducing strike and rake steps to 5° and depth step to 1 km. What is more relevant is the fact that we subdivided our search in four blocks, using the same geographical grid. We separated strike in 0° ÷ 180° and 180° ÷ 360°, with rake comprised, respectively, between −60° ÷ 60° and 60° ÷ 120°. We progressively refined our search to end with 1° steps for strike, rake, and dip, 1 km for fault length, and 0.01 for Mach. We contemporaneously reduced our search area and the range of variations for most of the parameters (all but total lengths of the two fault segments). In doing so, we strictly maintained the commonality of the intensity points dataset within each of the progressive refinements. Obviously at each refinement, the number of intensity points increased progressively to the final value of 256 (Figure 5).

It is also noteworthy that at each refinement, the local minima can shift from one location to a nearby location; this means that it is better not to discard possible epicenters up to what we decide to be the very last iteration. In

Table 3. Best solution parameters.

Solution	Intensity	Mwp	Lat	Long	Strike	Dip	Rake	Depth	Along Strike Length	Antistrike Length	Mach
S1	0.8477	5.99	46.34	12.95	108	1	−30	14.0	3.0	7.0	0.52
S2	0.8516	5.99	46.36	12.93	63	9	99	14.0	1.0	9.0	0.53
S3	0.8543	5.99	43.36	12.93	236	81	89	13.0	9.0	1.0	0.53

, we report the best solutions, with one for each family that we selected as a possible representative of the real one.

4. Discussion

Two focal mechanisms of the M_wp6 27 March 1928 earthquake are available in [49]. This allows for a first validation of the improved version of the KF and the obtained solution (Figure 6). The first positive aspect is that all the three possible macroseismic epicenters are spaced at most 6 km west apart from that in [49]. However, all three of our solutions yield impossibly low dip values. There is, however, an explanation; we need first to compute the isoseismals with the method proposed in [50].

In our case, isoseismals are roughly circular. This shape is typical of dip-slip events: we know [21] in this case that dip is often not well constrained and it can yield unrealistically low values. We prefer, therefore, solution S2, even though we trust only strike (the auxiliary plan of S2 = 234°, 81°, 86°, similar to S3) and a rake ± 180°. By tectonic considerations, we prefer a rake of 99°.

This solution places the 1928 rupture directly in southern continuation with the But-Chiarsò line. At first it may seem odd, but we must remember that where arcs merge, tectonic styles can coexist [51]. We suppose therefore that the solutions proposed by the authors of [52], although not very different from ours, were maybe influenced by an inappropriate depth that led to a strike-slip rupture. A final remark is linked to the relation between the 1928 event and the 1976 event (Figure 7).

It is extremely interesting that the 1928 earthquake is placed between the two main asperities ascribed to the 1976 event. Our finding therefore seems to give a powerful indication that when investigating seismic hazards, we should take into account mainly the asperities and not the whole fault. This is deeply intertwined with the open question of what the return times of events are. According to our finding, it would probably be more appropriate to think in terms of return times on asperities, since the rest of the fault might slip almost passively whenever a previous event occurred in the same volume. Obviously, this is only a first case, and this behavior should be proved or disproved by studying many other possible similar situations. In fact, if we examine all the over 200 macroseismic fields available in the CPTI15 catalog for events with M_wp > 5.5, we note that only in two cases we might assume that there is a qualitative similarity between them. Conversely, as a rough estimate, we can affirm that about 80% of the events in the catalog occur within at most 20 km from a previous event. In particular, cases where differently shaped macroseismic fields are overlapped, such as the 1928–1976 pairing, are extremely common. This consideration is only qualitative, but it should clearly be investigated in depth.

As far as the methodological approach is concerned, it is obvious that the main issue is an evaluation of solution stability. There is no straightforward answer to this problem; however, when it is possible to recover a trend in the isoseismals, almost circular versus lobate, it helps in distinguishing between a dip-slip solution versus a strike-slip one. As far as the magnitude is concerned, we understand that the “boxer” approach is definitely a good starting point. That is, in most cases, it is within 0.15 degrees of the true M_w. A magnitude assessment gives us automatically a binding into the RLD and from this, we can retrieve the effective length of the involved asperities. In this paper, we confirmed that the instrumental epicenter normally is within a few kilometers from where the relevant portion of the rupture starts. Combining all these relevant pieces of information, it means that we can recover a strike direction with an error of less than 5°, we can assess where the main asperity lies with an error of about 5 to 8 km, and we can distinguish between a dip-slip versus a strike-slip solution. This in turn allows us to tentatively associate the event to a known fault system. This is the most significant piece of information that a macroseismic field can yield. It must finally be added that there is a lower limit to the event magnitude, and it is about M~6; for smaller events, there is a high chance that the rupture will not be mostly horizontal, and this will not allow for an application of the method.

We must clarify, moreover, that starting from an independent measure of magnitude, e.g., the Boxer one, is necessary because from the test we conducted, fixing the combination of magnitude–asperity length is by far the most important parameter in obtaining a correct solution. In the case of the 2012 event, allowing for free research of these parameters could lead to a solution that is numerically more satisfying but is located 20 km away and with a totally different strike, even if we were to fix all the other parameters to the correct values.

As a final remark, we need to stress that when we discuss stability, we also refer to the fact that in previous papers, KF solutions were often expressed in terms of three decimal digits for locations, a fraction of kilometers for asperity length, etc. We can still carry this out, but it is meaningless because there is a trade-off between the various parameters due to the discrete values of intensities.

5. Conclusions

The improved KF approach we present here seems to be rather effective. In particular, we note the following:

• Given the nonlinearity, systematic parameter research without specific inversion algorithms seems to be particularly suited at retrieving the most significant families of possible solutions;
• Limiting the number of free parameters seems to help with stabilizing such solutions;
• However, a limitation of free parameters means that when the macroseismic field is not particularly developed, there is no hope to find a solution without a priori constraints;
• Isoseismal shape is at least as important as the macroseismic field, since it can help distinguish between families of solutions;
• Our approach yields a solution that is compatible with fault kinematics in the area, even though it is rather different from that retrieved on the base of focal mechanisms; this is a point that should be better understood;
• The epicentral location is within 5 to 6 km from the instrumental location, but it is clear that an excessive refinement of the solution serves only a numerical purpose;
• An error of one MCS degree in intensity estimates appears to be physiological; this is important because we must remember that intensities are, in a sense, a logarithmic measure and this means that the intrinsic error is relatively high, even though the inversion can yield a correct event solution.

In particular, we think that with this analysis, we have gained experience of how to correctly apply the KF to as many historical events as possible. It has also provided us with an understanding of its intrinsic limitations.

In the next steps of the research, the proposed study will be developed to investigate and better understand the relationship between fault kinematics in the area and the differences from those recovered on the base of focal mechanisms. In addition, in the future, the study will explore how vulnerability affects individual intensity measurements within a macroseismic field.