Grasp Pattern Recognition Using Surface Electromyography Signals and Bayesian-Optimized Support Vector Machines for Low-Cost Hand Prostheses

Featured Application

This work presents a low-cost, sEMG-based prosthetic control interface optimized for grasp pattern recognition, which can be applied in the development of affordable, functional prosthetic hands. It holds significant potential in healthcare settings where cost-effective solutions are crucial, providing an accessible alternative for individuals with upper limb amputations in low-resource environments.

Abstract

Every year, thousands of people undergo amputations due to trauma or medical conditions. The loss of an upper limb, in particular, has profound physical and psychological consequences for patients. One potential solution is the use of externally powered prostheses equipped with motorized artificial hands. However, these commercially available prosthetic hands are prohibitively expensive for most users. In recent years, advancements in 3D printing and sensor technologies have enabled the design and production of low-cost, externally powered prostheses. This paper presents a pattern-recognition-based human–prosthesis interface that utilizes surface electromyography (sEMG) signals, captured by an affordable device, the Myo armband. A Support Vector Machine (SVM) algorithm, optimized using Bayesian techniques, is trained to classify the user’s intended grasp from among nine common grasping postures essential for daily life activities and functional prosthetic performance. The proposal is viable for real-time implementations on low-cost platforms with 85% accuracy in grasping posture recognition.

1. Introduction

The loss of a limb, particularly an upper limb, has severe implications at a physical level, as well as significant psychological consequences. After an amputation, the recovery phase can be particularly challenging, with patients potentially experiencing phantom limb pain. Furthermore, the hand plays a crucial role in social interactions, and its loss can lead to a devastating reduction in autonomy, hindering the patient’s ability to engage in social, work-related, and daily activities. Limb loss affects approximately 2 million people in the United States and can result from various factors, including trauma, neoplasia, and vascular or infectious diseases [1].

Recent technological advancements in hardware (such as sensors, mechanical designs, and materials) and artificial intelligence for signal processing have shifted researchers’ focus towards active prostheses, particularly body-powered options. Externally powered prostheses typically feature an artificial hand as an end effector, actuated by motors driven by batteries. Significant progress has been made in their development, leading to the availability of many complex artificial hands on the market [2]. Some examples include the i-Limb [3], Bebionic [4], and Michelangelo [5], which enable a wide range of grasping capabilities.

Externally powered prostheses require a robust interface to translate the user’s intent into control signals for the hand’s actuators. This interface must allow for intuitive and natural control, minimizing cognitive load and reducing training time. Surface electromyography (sEMG) is a highly promising bio-signal for decoding a user’s intended movement. As sEMG reflects the natural signals that command human muscle movement, it enables smooth and biologically intuitive control. Additionally, sEMG can be acquired non-invasively, making it ideal for use in prosthetic applications. Consequently, EMG-controlled prostheses have gained significant attention in research and have become a standard for externally powered prostheses.

With recent advancements in 3D printing, control systems, and sensors, there has been a growing focus on designing low-cost, externally powered prostheses. While high-end commercial prostheses can cost upwards of USD 10,000, recent innovations in 3D printing have brought these costs down significantly, with some models priced as low as USD 500.

This paper presents a pattern-recognition-based human–prosthesis interface utilizing the Myo armband, an affordable sensor for acquiring sEMG signals. A Support Vector Machine (SVM) algorithm is employed to classify nine different grasping postures based on the sEMG data. These postures were selected from a study by Vergara et al. [6], which identified the nine most commonly used grasps in daily life activities.

2. Related Work

The analysis of surface electromyography (sEMG) signals is inherently complex due to their stochastic nature [7]. Numerous factors significantly impact the characteristics of sEMG signals in the context of myoelectric control for upper-limb prostheses [8]. Key challenges include temporal variations in signal properties, electrode displacement, muscle fatigue, inter-subject differences, fluctuations in muscle contraction intensity, and changes in limb position or forearm orientation [9,10,11].

In pattern-recognition-based myoelectric control, the interface between the user and the prosthesis is a classifier. This classifier is an algorithm trained to recognize the movements the patient intends to perform by analyzing patterns in the sEMG signals. Through this control strategy, the classifier maps sEMG signal patterns to their corresponding movements and controls the prosthesis motors to replicate them. This approach can be used for the simultaneous control of multiple degrees of freedom (DOF), which would significantly reduce the cognitive load required to operate the prosthesis.

To effectively address the intricate and variable nature of sEMG signals in advanced applications, a substantial volume of data is often required. Existing techniques face limitations in enabling simultaneous and proportional control of multiple degrees of freedom (DOF) [10]. Many of them have not yet been adequately tested in practical or clinical settings. As a result, achieving control simplicity and maintaining low costs are critical objectives in the development of prosthetic hands.

Among the existing machine-learning (ML) techniques, Support Vector Machine (SVM) is a supervised ML method commonly used for sEMG signal classification. Although originally a binary classifier, distinguishing between two classes, SVM can be extended to multi-class classification by combining multiple SVMs. SVM has attracted significant attention due to its superior performance in EMG data classification compared to other methods.

Dhindsa et al. [12] conducted a comparison of different ML algorithms for sEMG signal classification to predict knee joint angles. They compared k-Nearest Neighbor (kNN), Linear Discriminant Analysis (LDA), Naive Bayes (NB), and Support Vector Machine (SVM) with various kernels. The results showed that SVM with a quadratic kernel performed best, achieving an accuracy of 93.07 ± 3.84%. They used EMG signals from four different muscles and extracted 15 features from both the time and frequency domains for classification.

Purushothaman and Vikas [13] acquired multi-channel EMG signals to recognize fifteen different finger movements (constituting five individual finger movements and ten combined finger movements) with 16 features, comparing NN, LDA, and SVM. Additionally, they employed two feature selection algorithms: Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO). The results demonstrated that a naive Bayes classifier with ACO showed an average classification accuracy of 88.89% using features such as MAV, ZC, SSC, and WL (definitions of these features can be found in Appendix A for completeness).

SVM has also been applied in the diagnosis of muscular dystrophy disorders. Kehri and Awale [14] achieved 95% accuracy using an SVM with a polynomial kernel to detect this disorder. They pre-processed the signal using wavelet-based decomposition techniques.

Purushothaman [15] designed a low-cost mechatronics platform for the development of robotic hands controlled via sEMG. Using this platform, they compared several classification algorithms, including ANN, LDA, and SVM. By employing temporal features such as MAV, SSV, WL, ZC, and fourth-order AR coefficients with normalized data, they achieved 92.8% accuracy.

Amirabdollahian and Walters [16] used the Myo armband from Thalmic Labs, the same device used in this project, to acquire sEMG signals from the forearm and classify hand gestures using an SVM with a linear kernel. With eight electrodes, they achieved 94.9% accuracy in classifying four different grasp gestures. A good review of the initiatives in this sense can be found in [10], which examined the suitability of upper limb prostheses in the healthcare sector from their technical control perspective. This paper reviewed the overall structure of pattern recognition schemes for myo-controlled prosthetic systems and summarized the existing challenges and future research recommendations.

In recent years, this topic has attracted public interest. Gopal et al. [17] investigated various ML and Deep Learning (DL) models for sEMG-based gesture classification and found that ensemble learning and deep learning algorithms outperform classical approaches for assistive robotic applications. Kadavath et al. [18] used four traditional ML models for classifying finger movements across seven distinct gestures. They concluded that the Random Forest emerges as the top performer, consistently delivering superior precision.

Real-time performance and low memory consumption are requirements that greatly influence the selection of the technique to be used. In fact, methods such as LDA and kNN cannot meet real-time requirements. Similarly, complex DL networks (CNN, RNN, etc.) cannot meet the memory requirements of low-cost platforms [19].

Among the topics in which greater activity is observed in the research field, the elucidation of how to best adapt the acquired signal to the identification process to which it will be subjected stands out strongly. The problem of determining which characteristics have the greatest influence on signal detection and identification, and how to fuse them for their use through ML techniques, constitutes a notable focus of activity in the literature. In [20], Hellara et al. studied a total of 37 time and frequency-domain features extracted from each sEMG channel. Their results highlight the significance of employing an appropriate feature selection method to significantly reduce the number of necessary features while maintaining classification accuracy. In parallel, Sahoo et al. [21] proposed other sets of features, this being an open question for the time being.

On the other hand, Chaplot et al. [22] have addressed the important question of optimizing sensor placement for accurate hand gesture classification. They also proposed the use of an SVM for solving the problem.

In a previous work [19], the authors explored the possibility of using ML algorithms for grasping posture recognition. In that study, a straightforward multi-layer perceptron was designed in MATLAB and deployed on a GPU. The model was optimized to identify nine hand gestures, accounting for 90% of Activities of Daily Living (ADL), in real-time. Achieving an overall success rate of 73% with just two features, the GPU implementation enabled the evaluation of optimal architectures that balanced generalization ability, robustness to electrode displacement, low memory usage, and real-time operation.

In this work, the selected algorithm for the classification task is a Support Vector Machine [23] with the aim of increasing the grasping posture recognition accuracy of the previous work [19]. The literature review shows higher recognition accuracies using an SVM than other ML algorithms and also shows that, although there is a remarkable research activity in sEMG classification, many of the previous studies neither focus on real-time implementation on low-cost platforms nor deal with grasping postures. In fact, those that do often use a reduced set of postures are not properly justified and probably insufficient for fully functional prostheses [24].

This work addresses this limitation by considering the most used grasping postures in 90% of ADL, with experimental data obtained offline from the NinaPro public database [25]. This approach aims to provide the prosthesis with a higher level of dexterity, granting the user greater functionality.

3. Materials and Methods

3.1. Dataset, Acquisition Device, and Implementation Details

The dataset selected for this project was the publicly available NinaPro Database 5 (DB5) [25]. The NinaPro series consists of EMG datasets acquired using various devices, and the NinaPro DB5 utilizes the Myo armband as its acquisition device [26]. It includes data collected from 10 healthy subjects using two Thalmic Myo armbands. The subjects wore the upper armband closer to the elbow, with the first electrode positioned on the radio-humeral joint. The lower Myo armband was placed just below the upper one, closer to the hand, and tilted by 22.5 degrees to cover the gaps left by the electrodes of the upper armband. Additionally, the subjects wore a glove (CyberGlove II dataglove) equipped with 22 sensors to record hand kinematics.

The Myo armband acquisition system (Figure 1 left) from Thalmic Labs is a wearable band placed right below the elbow that contains 8 electrodes for sEMG acquisition, at 200 Hz and 8-bit resolution, and a nine-axis IMU composed of a three-axis accelerometer, gyroscope, and magnetometer [26]. It is also equipped with a tactile sensor to transmit feedback to the user with short, medium, and long vibrations. The device includes a Freescale Kinetis ARM Cortex M4 120 MHz, MK22FN1M MCU, and BLE (Bluetooth low energy) NRF51822 chip to communicate with other devices. The device is powered by 2 × lithium batteries 3.7 V—260 mAh.

The Myo armband transmits data via Low-Energy Bluetooth, which is a great advantage for a robotic prosthesis as it consumes less power and allows the system to last longer before needing to be charged. The typical placement and configuration for acquisition can be seen in Figure 1 (right).

The complete dataset contains sEMG signals from both Myo armbands, accelerometer data from the upper Myo, and finger joint angles from the glove. However, for the purposes of this project, only the sEMG data from the upper Myo was used.

The data acquisition process was divided into two phases: a training phase and the actual recording of three different exercises. During both phases, the subjects were seated comfortably in a chair, resting their dominant arm on a desk. A laptop was placed in front of each subject to provide visual instructions and to record the data. In the training phase, each subject was instructed to replicate the movements displayed on the screen. These movements were chosen randomly to allow the subjects to familiarize themselves with the task.

In the recording phase, each subject was instructed to repeat three different exercises. Each exercise was made of different movements, and every movement was repeated 6 times lasting 5 s each, with a 3 s rest between every movement to avoid muscular fatigue. The dataset contains 52 different movements from the hand taxonomy and robotics literature. The 10 subjects that participated in these experiments were all healthy but had substantial differences in gender, height, and weight (

Table 1. Information about the subjects of the experiments and the exercises from NinaPro DB5.

	Ninapro DB5 Thalmic Myo (Double and Single)
Available subjects	10
Considered subjects	10
Males	8
Females	2
Right-handed	10
Left-handed	0
Avg. age (years)	28 ± 3.97
Avg. height (cm)	172.2 ± 9.88
Avg. Weight (kg)	68.6 ± 9.1
Avg. BMI (kg/m2)	23.17 ± 2.66
Exercise	NinaPro DB5 Exercises B (Posture 7) and C (Postures 1, 4, 8, 9, 14, 15, 18)

).

After the sEMG signal was acquired, the raw data underwent pre-processing. The Myo armbands are equipped with a Notch Filter that removes powerline interference (set at 50 Hz). However, there was a slight desynchronization between the visual input from the computer and the actual recorded sEMG signals due to the delay caused by human reaction time. These discrepancies were corrected using movement detection algorithms, such as the generalized likelihood ratio algorithm or the Lidierth threshold-based algorithm.

From the NinaPro DB5 dataset, only a subset of movements was selected for classification. The goal was to classify movements as described by Vergara et al. [6], so a comparison was made between the hand postures in NinaPro DB5 and those described by Vergara. Based on this comparison, nine hand postures were chosen as classes for the SVM to predict: cylindrical grasp (Cyl), pinch grasp (Pinch), lateral pinch (LatP), oblique palmar grasp (Obl), lumbrical grasp (Lum), hook grasp (Hook), intermediate power-precision grasp (intPP), special pinch/tripod (SpP), and pointing index (nonP). The non-prehensile grasp in [6] was not present in the NinaPro DB5 dataset, and thus it was replaced with the “pointing index” posture. These postures are described and represented in

Table 2. Description of grasping postures.

Grasp Type (NinaPro Posture)	Contact with Object	Image	Grasp Type (NinaPro Posture)	Contact with Object	Image
Cyl (C1)	Palm and fingers		Hook (C3)	Fingers
Pinch (C15)	Thumb and some fingertips		intPP (C4)	Thumb, fingers, and part of the palm
LatP (C14)	Thumb and lateral part of some fingers		SpP/Tripod (C9)	Thumb and some tips/lateral part of the fingers
Obl (C8)	Palm and fingers		Pointing Index (B7)	No contact
Lum (C18)	Thumb and proximal part of the fingers

.

The frequencies of use of each grasp type during the day are shown in

Table 3. Distribution of daily frequencies of use of each grasping posture [6].

Grasp	%use	Color
Cyl	9.4%
Pinch	36.9%
LatP	6.6%
Obl	11.9%
Lum	10.9%
Hook	2.3%
intPP	5.8%
SpP	5.7%
nonP	7.6%
Not analyzed	3%

, where it can be seen that the most used grasp is the Pinch grasp (grasping with the fingertips, at least the thumb and the index fingers) with a 36.9% frequency. The next most used grasps have frequencies around 10% and are the Cylindrical grasp (grasping with the whole hand in contact, including the palm, and with the thumb in opposition to the fingers), the Oblique grasp (similar to the Cylindrical grasp, but with adduction of the thumb), and the Lumbrical grasp (grasping with all the fingers contacting the object but not the palm).

All the implementations were carried out offline in MATLAB, for the following reasons:

• The NinaPro dataset is provided in MATLAB format, ready to be imported.
• It has many toolboxes for implementing machine-learning techniques and for fast training classifiers. In this work, the Statistics and Machine Learning Toolbox was employed.
• It allows fast prototyping and easy code debugging.

3.2. Feature Extraction

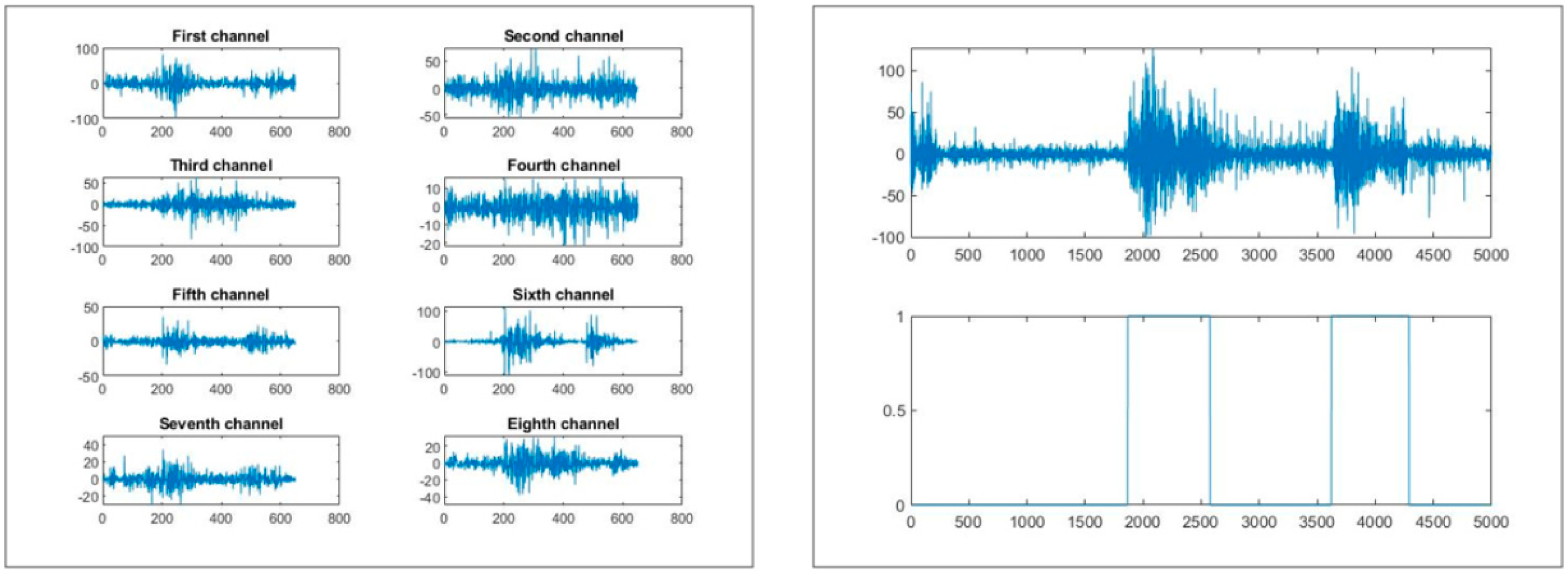
The following paragraphs outline the procedure for processing one subject’s data. The same procedure was applied uniformly to all the subjects. Once the data were imported into MATLAB, only the sEMG signals from the electrodes of the first Myo (the one placed on the forearm) and the gesture labels were used, the latter indicating when and which grasp was performed in the sEMG signal (Figure 2).

Once the sEMG signals for the 9 selected grasping postures were obtained, feature extraction was performed to create the dataset used for SVM training. The system is designed to operate in real-time with minimal delay: for an actual prosthesis, the time required for acquiring and classifying each signal should be under 300 ms [23]. With this in mind, a 250 ms window was chosen for signal acquisition, leaving the remaining 50 ms for classification. As previously mentioned, the Myo armband records sEMG signals at 200 Hz, meaning that in 250 ms it collects 50 data points, on which various features are evaluated. With fewer data points, classifier performance would degrade significantly.

In total, 8 features were extracted: 6 from the time domain and 2 from the frequency domain. The selected time domain features include:

• MAV: Mean absolute value;
• SD: Standard deviation;
• VAR: Variance;
• WL: Waveform Length;
• RMS: Root Mean Square;
• IEMG: Integrated EMG.

The selected frequency domain features were:

• MF: Median Frequency;
• MPF: Mean Power Frequency.

For a mathematical description of these features, we refer the reader to Appendix A. These features were selected based on their proven effectiveness in sEMG classification using an SVM [23], as well as their widespread use in the field of pattern recognition for myoelectric control. The full dataset was then divided into two parts: 70% of the data was used to train the SVM, while the remaining 30% was reserved for testing the classifier.

3.3. SVM Training and Test

Once the dataset was prepared, the training and optimization of the SVMs began. The chosen approach was “one-vs-one”, where an SVM is trained for each possible pair of grasping postures (with each grasping posture corresponding to a class). For k classes, the number of binary classifiers (NBC) required is:

$$NBC(k)={\displaystyle \frac{k(k-1)}{2}}.$$

(1)

NBC covers all possible grasping posture combinations. In this case, there are 9 grasp types, so the multi-class model consists of 36 binary SVMs.

Before training, the data were standardized, and the selected kernel was a Radial Basis Function (RBF).

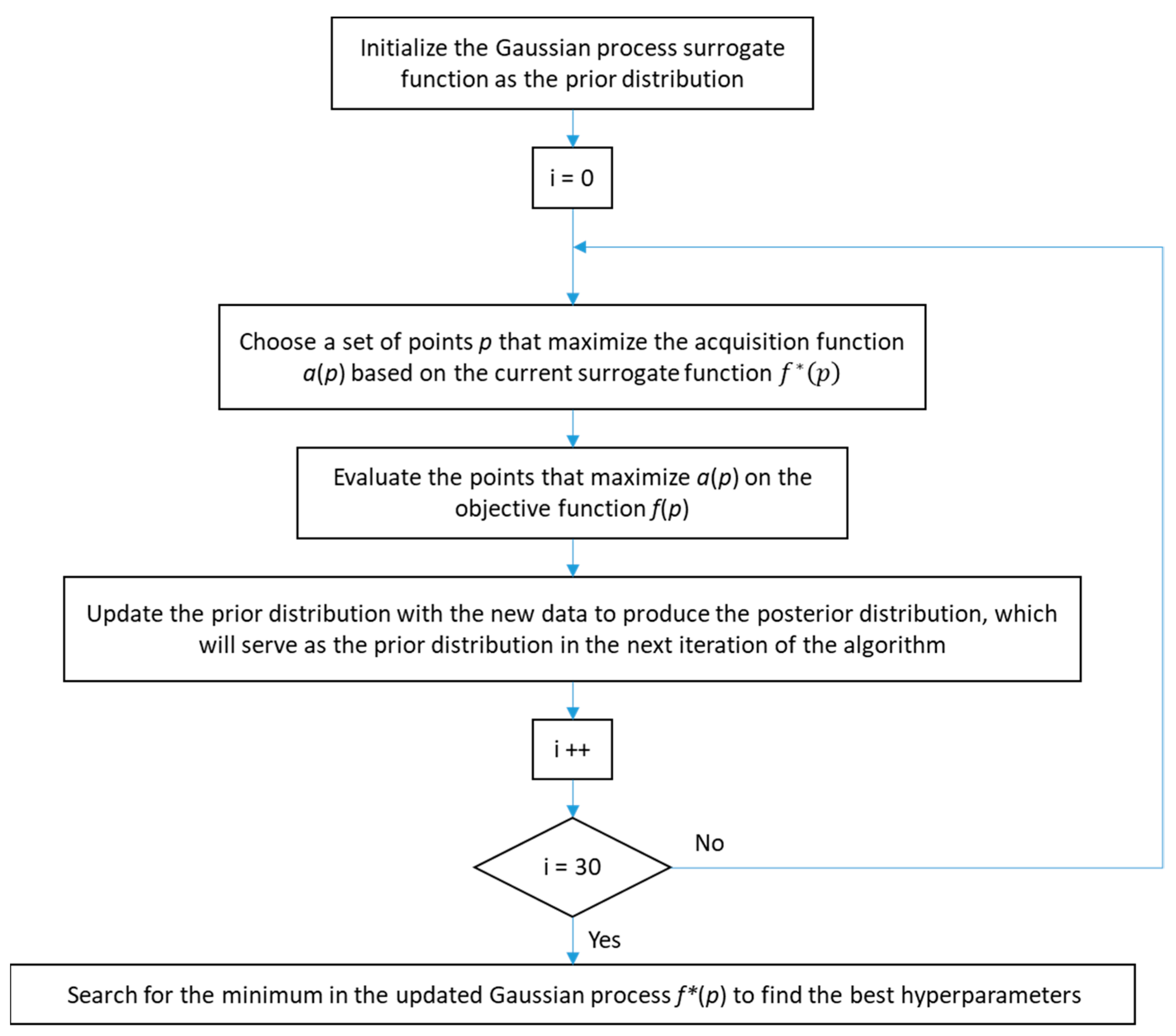
The SVMs were optimized using 10-fold cross-validation and a Bayesian optimization process. Bayesian optimization is a technique used to fine-tune the model’s hyperparameters, which is a critical step since the model’s accuracy heavily depends on selecting the correct hyperparameters. This iterative algorithm minimizes an objective function by creating a probability model, also known as a surrogate function, which is easier to optimize than the original target function. At each iteration, the next point to evaluate is selected based on previous evaluations of the surrogate function, limiting the exploration of unpromising hyperparameters and reducing the search space. In this case, the target function to be optimized is the cross-validation error (CVE) of the SVM, with the goal of finding the best set of hyperparameters that minimize error and maximize accuracy. Given $y_i$ as the true label and ${\widehat{y}}_i$ as the label estimated by the classifier, the CVE is formulated as follows:

$$CVE={\displaystyle \frac{1}{N}}\sum _{i=0}^{N}L\left(y_i,{\widehat{y}}_i\right) where L\left(y_i,{\widehat{y}}_i\right)=\left\{\begin{array}{c}0, if y_i={\widehat{y}}_i\\ 1, otherwise\end{array}\right.$$

(2)

Let p represent the set of hyperparameters to tune in the SVM, and denote the CVE as a function of these hyperparameters, CVE(p). In Bayesian optimization, a Gaussian process is initialized as the surrogate function for the CVE. The final component required for this process is the acquisition function, (p), which is used to select the hyperparameter values to evaluate at each iteration of the optimization. The chosen acquisition function is the Expected Improvement (EI), meaning that the next hyperparameter values to be evaluated are those that are expected to improve the target function the most. Letting $f^{*}\left(p\right)$ denote the surrogate function, (p) the objective function, p the hyperparameters at the current iteration, and $p_{-}$ the hyperparameters from the previous step, the EI is formulated as follows:

$$a\left(p\right)=EI\left(p\right)=E[\mathrm{m}\mathrm{a}\mathrm{x}(0,f^{*}\left(p\right)-f\left(p_{-}\right)\left)\right],$$

(3)

where E[x] is the expectation operation.

The workflow of the Bayesian optimization algorithm is depicted in Figure 3.

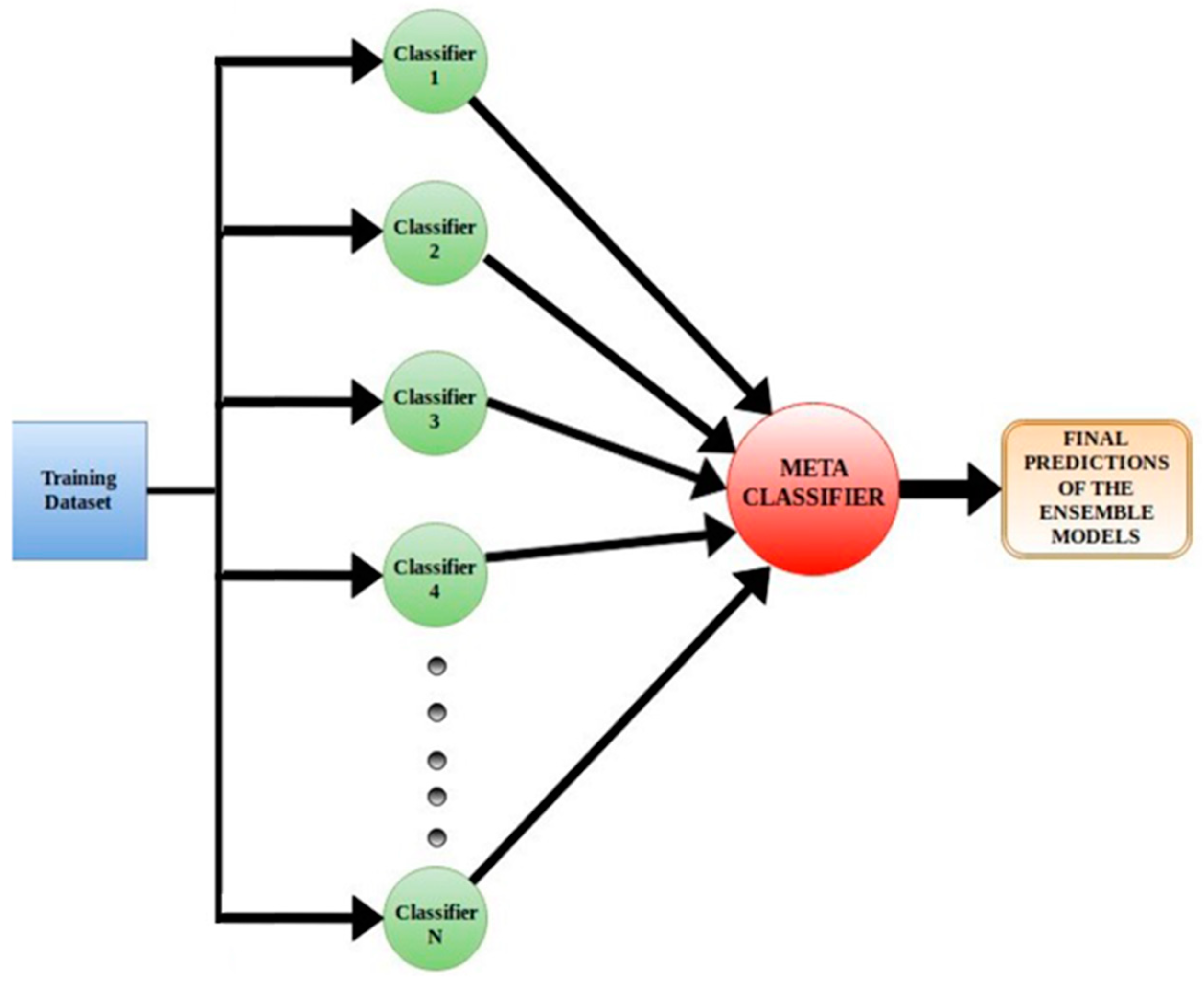
Once all the binary SVMs were trained and optimized, they were combined into a single model for multi-class classification. In this phase, the model was tested using the test set. For this type of model, classification works as follows: when a new, unknown observation is presented to the model, it is classified by all 36 binary classifiers, and the final class is determined using a majority vote technique. Each classifier votes for a class, and the class that receives the most votes is selected as the output by the multi-class model (Figure 4).

4. Results

The first set of experiments aimed to evaluate the classifier. Initially, individual features were tested for accuracy across the 10 subjects (

Table 4. Accuracy for every subject of the single feature classifier for 9 grasping postures.

Subject	MAV	SD	IEMG	WL	VAR	RMS	MPF	MF
1	78%	78%	79%	76%	75%	80%	40%	31%
2	81%	80%	81%	80%	79%	83%	42%	36%
3	86%	85%	85%	84%	82%	84%	32%	27%
4	70%	71%	70%	69%	70%	72%	31%	26%
5	76%	76%	77%	75%	73%	78%	44%	35%
6	80%	79%	81%	75%	74%	77%	38%	34%
7	78%	75%	75%	72%	73%	76%	39%	33%
8	80%	78%	79%	79%	76%	78%	47%	40%
9	85%	83%	85%	80%	84%	86%	52%	43%
10	80%	77%	79%	79%	75%	79%	42%	36%
Mean	79%	78%	79%	76%	76%	79%	40%	34%

).

A simple glance at the table reveals a noticeable difference in accuracy when comparing the time-domain features to the frequency-domain features (MPF and MF). This performance gap is largely due to the sampling frequency of the acquisition device. The Myo armband’s electrodes capture sEMG signals at 200 Hz, which effectively covers the dominant energy range of surface sEMG signals, typically between 50 Hz and 150 Hz. However, certain frequency components can extend up to 500 Hz, a bandwidth beyond the Myo armband’s capabilities [27]. The exclusion of these higher frequencies results in poorer classification accuracy. Consequently, frequency-domain features were discarded for sEMG signal classification.

Table 5. Accuracy for every subject of the multi-features classifier for 9 grasping postures and 3 different groups of features.

Subject	Group 1 (WL, MAV, SD)	Group 2 (IEMG, MAV, RMS)	Group 3 (IEMG, WL, MAV, VAR)
1	83%	84%	86%
2	87%	87%	88%
3	88%	89%	88%
4	80%	83%	78%
5	83%	81%	80%
6	84%	84%	85%
7	80%	82%	80%
8	85%	81%	83%
9	89%	90%	90%
10	84%	85%	84%
Mean	84%	85%	84%

presents the classification accuracy using three different feature sets: Group 1 (WL, MAV, and SD), Group 2 (IEMG, MAV, and RMS), and Group 3 (IEMG, WL, MAV, and VAR).

As can be observed, a multi-feature classifier performs better than those trained with a single feature, achieving an average accuracy of 85% with the Group 2 features while requiring slightly less training and computational time.

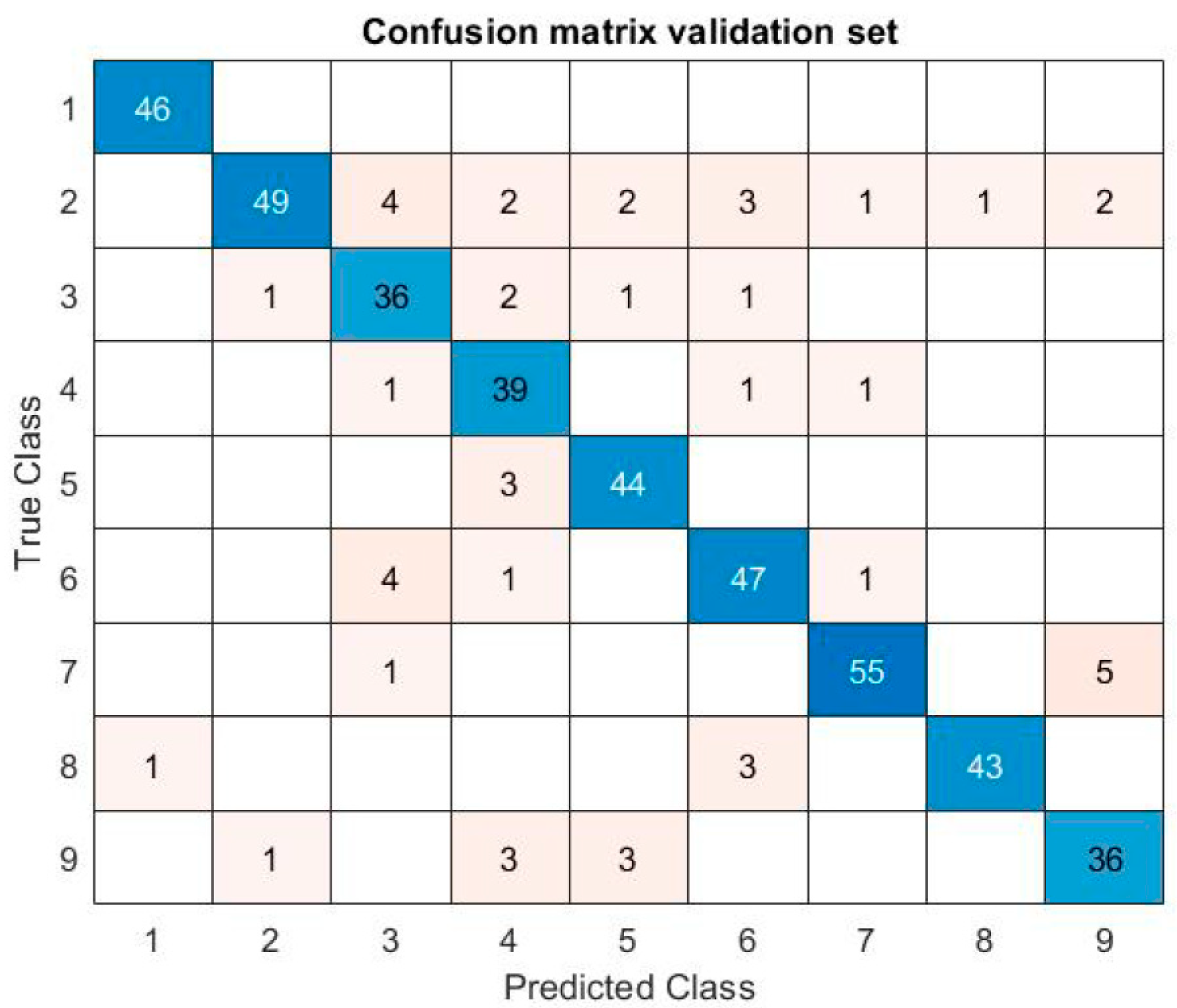
The confusion matrix (Figure 5) shows the predicted versus actual labels for each grasping posture classification. In this figure, each number represents a grasping posture: (1) pointing index, (2) cylindrical grasp, (3) hook grasp, (4) parallel grasp, (5) oblique palmar, (6) intermediate power precision, (7) pinch grasp, (8) lateral pinch, and (9) special pinch.

Regarding the implementation of the algorithm, it takes an average of 15 ms to extract the features and classify the signal in MATLAB, running on a laptop with an Intel Core i5-8300H 2.3 GHz CPU and 8 GB of RAM.

In order to check the feasibility of the real-time implementation of this classifier on a low-cost platform, time calculations have been performed. The algorithm devotes 15 ms to feature computation and classification. Adding the 250 ms required for signal acquisition, the overall process takes an average of 265 ms, which complies with the 300 ms limit reported in the literature.

There are some differences in pattern recognition depending on the grasping type. Hook grasp (number 3 in Figure 5) is sometimes confused with cylindrical grasp (number 2 in Figure 5). This is due to the similar muscles and tendons activated along the grasping process, and in fact both grasps look very similar. It also happens when special pinch (number 9 in Figure 5) is recognized and confused with pinch grasp (number 7 in Figure 5).

Cost Analysis

To analyze the cost of an SVM, it is necessary to evaluate various factors related to performance, time, and computational resources necessary to train and use the model. This section describes the process in detail. This analysis evaluates the computational cost, real-time feasibility, and resources required for the posture classification algorithm based on sEMG and SVM signals. The described system is meant to operate in real-time with strict time constraints, using a multiple SVM approach (one vs. one) and optimizing the hyperparameters using Bayesian optimization.

First, let us consider the features of the system:

• Inputs: eight channels of sEMG signals, 200 Hz, 50 ms window (50 points per channel).
• Classes: nine postures.
• Multi-class model: 36 binary classifiers (one vs. one).
• Features: eight features per channel.
• Tasks:
• Feature extraction: 50 data per channel.
• Classification: SVM algorithm, RBF kernel optimized through 10-fold cross-validation and Bayesian optimization.

The feature extraction task involves calculations in the time and frequency domain for each channel. There are 64 features per window (8 sEMG channels × 8 features). For the six time-domain features, the calculation is linear with the number of samples, O(n). For the two frequency-domain features, the calculation requires a fast Fourier transform (FFT), with complexity O(n·log n). So, for a window of 50 samples,

• Time-domain features: 8 channels × 6 features × O(50) = 2400 operations.
• Frequency-domain features: 8 channels × 2 features × O(50·log 50) ≈ 2700 operations.
• Combined cost: Approximately O(5000) operations per window of 50 samples.

In the classification step, each of the 36 classifiers processes an input vector of 64 features (8 × 8 vector).

• At training, the complexity is O(n³), where n is the number of training vectors. This does not apply in real-time but is relevant during development.
• In the inference step, complexity is O(m⋅d), where m is the number of support vectors (estimated at 50), and d is the dimensionality of the vector (d = 64). This way, the cost per SVM is estimated as O(50·64) = O(3200).
• Finally, there is the majority voting of the 36 binary classificators to determine the final class, which gives a total cost for a classification of 36·3200 = 115,200. These tasks must be completed in less than 50 ms.

The Bayesian Optimization is an offline process. Each iteration evaluates a set of hyperparameters using 10-fold cross-validation. The SVM training complexity with RBF is O(n³), where n is the size of the data set. With 30 iterations, the total cost includes 300 model evaluations, which is computationally intensive during development, but it does not have an influence on the real-time operation.

Regarding the use of memory, each sample of the sEMG signal occupies four bytes (32-bit floating point). Then, for the 8 sEMG signals, the amount of memory required is 8 channels × 50 samples × 4 bytes = 1.6 kB per window. For the extracted features, the requirements are 64 features × 4 bytes = 256 bytes per window. Therefore, the total amount of memory necessary per window is approximately 1856 kB, which is a manageable quantity even on resource-constrained hardware.

Additionally, each SVM stores the support vectors (m = 50): 50 vectors × 64 features × 4 bytes = 12.8 kB per SVM. For 36 SVMs, this means a memory use of 460.8 kB.

These numbers sustain the feasibility of a real-time implementation. The estimated time for signal acquisition is 250 ms and for the feature extraction is about 20 ms (estimated with hardware optimization). The estimated time for the inference is about 30 ms for 36 SVMs. All this leads to a 50 ms limit for real-time, which involves 300 ms including signal acquisition.

This calculation has been made using a conservative approach in a worst-case scenario and indicates that the algorithm can be successfully implemented on low-cost platforms such as Arduino Portenta H7, Arduino Due, or ESP32-S3.

5. Discussion

The results indicate that classifiers that use multiple features outperform those with a single feature, with an average accuracy of 85%. This is consistent with the current state-of-the-art SVM classifiers using acquisition devices at 200 Hz, such as those by Phinyomark et al. [28,29]. However, there are two key differences in the feature selection of this project.

First, no frequency-domain features, such as mean frequency or cepstral coefficients, were used in the training process. This significantly reduces the computational time since the Fourier Transform is not required. The second difference is that two well-known time-domain features, Zero Crossing (ZC) and slope sign change (SSC), were also excluded. While these features are common in sEMG analysis, they require the definition of a threshold, which introduces an additional parameter to tune during SVM training. Discarding these features is a step toward generalizing and simplifying the classifier.

To better understand the accuracy obtained, it is necessary to delve into the anatomy of the classifier. As previously described, the multiclass SVM consists of 36 individual binary SVMs, one for each pair of possible postures. This means that the overall accuracy of the model is influenced by the performance of each individual SVM. Examining their individual accuracy reveals that some postures are highly separable from others. For instance, the SVMs responsible for recognizing the “pointing index” posture achieve accuracy between 98% and 100%. This posture is highly distinguishable from the other postures using this feature set.

Conversely, the SVM responsible for classifying the “cylindrical grasp” and “hook grasp” shows significantly lower accuracy, around 79% to 82%. This indicates that, with this feature set, these two movements are not highly separable, which lowers the overall accuracy of the classifier. This behavior is evident in the confusion matrix (Figure 5), where misclassification between these postures is more common.

As mentioned earlier, the ’pointing index’ posture is highly separable from the other postures, as every predicted class matches the true class. However, the remaining postures are not perfectly separable, and the predicted class does not always correspond to the actual class.

The present work also contributes to the existing literature. Other SVM approaches for upper limb movement classification do not address grasping postures in activities of daily living or focus on only a subset of them. In this project, the nine most common grasping postures used in daily life activities are considered, with the goal of restoring as much dexterity as possible to prostheses users.

Finally, regarding the real-time low-cost implementation, improvements have been made with respect to the authors’ previous work presented in [19]. In that work, an NN-based algorithm was developed that took 600.66 ms to recognize a grasping posture from the sEMG signal provided by the Myo armband, with a global percentage success of 73%. In the present work, a total time of 265 ms is needed for the whole classification process with an accuracy of 85%. These results imply a reduction of the computational time of 56% and an increase in accuracy of more than 16%. In addition, the time required in MATLAB is 265ms and it should be shorter on a low-cost specific microprocessor. As the classification time required is small, the grasping posture recognition of nine hand postures using SVMs seems feasible for low-cost platforms.

6. Conclusions and Future Work

This work presents a machine-learning technique for myoelectric hand prostheses based on the recognition of grasp patterns using sEMG signals and SVM algorithms optimized with Bayesian techniques. The results obtained demonstrate an average accuracy of 85% in the classification of nine grasp types that represent 90% of the activities of daily living, highlighting the use of features in the time domain to improve computational efficiency and reduce processing times. These findings suggest that the use of accessible acquisition devices, such as the Myo armband, can provide effective and affordable solutions for monitoring low-cost prostheses.

Despite the promising results, this study has certain limitations. For example, the low separation capacity between some grasp types, such as “cylindrical grasp” and “hook grasp”, reduces the overall accuracy of the model. In future works, additional features and more advanced algorithms could be explored to improve classification. Furthermore, the integration of haptic feedback could be another important step towards a more intuitive user experience for prosthetic users.

This study is based on the analysis of previously collected offline data (the NinaPro Database), enabling a detailed evaluation of the proposed system’s capabilities. Real-time implementation on low-cost platforms will be tackled in the near future. Such investigations will involve the evaluation of new features, such as sparse domains and model-based approaches, as well as the development of a real-time classification system using low-cost hardware platforms. In this way, the practical feasibility of the system in everyday applications will be validated.