A Prognostic Theory of Treatment Response for Major Depressive Disorder: A Dynamic Systems Framework for Forecasting Clinical Trajectories
Abstract
1. Introduction
- Therapeutic Impulse Function (TIF): A formal characterisation of a treatment’s properties, including its pharmacodynamic and pharmacokinetic profile, which acts as a specific input or “impulse” to the patient’s system [37].
- Predicted Recovery Trajectory (PRT): The forecasted, continuous path of a patient’s symptom severity over time, which emerges from the dynamic interaction between their unique PSV and a given TIF.
2. The Limits of the Current Static Prediction Paradigm
3. A New Paradigm from Engineering: Damage Prognosis
- Current State Assessment: A precise characterisation of the system’s current condition, including any existing damage. This was achieved using data collected from the SHM sensor network.
- Future Loading Conditions: An estimation of the operational and environmental loads that the system will be subjected to in the future (e.g., flight cycles for an aircraft and traffic patterns for a bridge).
- Damage Evolution Model: A predictive model, often physics-based or data-driven, that simulates the propagation of existing damage under estimated future loads.
4. A Prognostic Theory of Treatment Response
4.1. The “What”: Core Theoretical Constructs
- Clinical Data: Standardised assessments of symptom severity (e.g., PHQ-9 scores), diagnostic history, comorbidities, and demographic information [17,18]. This domain includes information typically collected in clinical trials and practice, captured longitudinally. Data sources include Electronic Health Records (EHRs) and Patient-Reported Outcome Measures (PROMs). Metrics include symptom severity (e.g., PHQ-9, HAM-D, tracked weekly), diagnostic history (e.g., ICD-10 codes for MDD and comorbidities), and demographics.
- Biological Data: Genotypic information (e.g., pharmacogenetic markers), neuroimaging data (e.g., fMRI, EEG), and other biomarkers (e.g., inflammatory markers, metabolic indices) that may moderate treatment response [46,47,54,55,57]. This domain captures neurobiological and physiological substrates. These data are often static or low-frequency. Data sources include genetic assays, neuroimaging, and blood samples. Metrics include pharmacogenetics (e.g., genotypes for CYP2D6, CYP2C19), neuroimaging (e.g., functional connectivity), and peripheral biomarkers (e.g., inflammatory markers, cortisol).
- Digital Phenotype Data: High-frequency, real-world behavioural data passively collected from personal devices, such as smartphones and wearables. This includes objective measures and feature-engineered metrics reflect behavioural domains such as mobility patterns (e.g., GPS/location entropy, time spent at home), social activity (e.g., call/text frequency, log metadata), and circadian rhythms (e.g., inferred sleep duration from phone usage patterns), sleep cycles, and physical activity, which provide a continuous and ecologically valid window into the behavioural manifestations of depression [35,36]. The integration of these dynamic real-world data streams is a key innovation of the PSV construct. Collecting these data streams, especially from personal devices, presents significant HCI challenges related to ensuring user engagement while minimising the burden [58].
- Pharmacotherapy TIF: A vector representation for a medication would include:
- –
- Mechanism of Action: A multi-hot encoded vector representing primary targets (e.g., for an SSRI, for an SNRI targeting Serotonin and Norepinephrine).
- –
- Half-life Elimination: A numerical feature (in hours) governing time to steady state.
- –
- Metabolism: A categorical feature for the primary CYP450 enzyme (e.g., CYP2D6), enabling direct modelling of gene-drug interactions with the PSV.
- –
- Dose: A normalised numerical feature for the prescribed daily dosage.
- Psychotherapy TIF: A vector representation for a psychotherapy would include:
- –
- Modality: A one-hot encoded vector (e.g., Cognitive Behavioural Therapy, Psychodynamic).
- –
- Dose and Schedule: Numerical features for session duration (minutes) and frequency (sessions per week). This structured TIF serves as a static or dynamic input to the prognostic model, allowing it to learn not only that treatments differ in outcome, but how and why they do so, based on their intrinsic properties.
4.2. The “How”: Propositions of the Prognostic Framework
4.2.1. Proposition 1: The Patient State Vector (PSV) Predicts an Unperturbed Trajectory
4.2.2. Proposition 2: The Effect of a Therapeutic Impulse Function (TIF) on the Predicted Recovery Trajectory (PRT) Is Conditional upon the Patient State Vector (PSV)
4.2.3. Proposition 3: Early Changes in PRT Are Predictive of Long-Term Treatment Outcomes
4.2.4. Proposition 4: Clinical Recovery Represents a Critical State Transition (Bifurcation) in a Patient’s Dynamic System
5. Causal Mechanisms and Multi-Level Integration
5.1. Neurobiological and Pharmacological Mechanisms
5.2. Behavioural and Psychological Mechanisms
5.3. Integration via Dynamic Systems Theory
6. Implications, Future Directions, and a Research Agenda
6.1. Clinical and Human-Computer Interaction (HCI) Implications
Illustrative Use Case
6.2. Methodological Implications
6.2.1. A Computational Architecture for Prognosis
6.2.2. A Protocol for Empirical Validation
- Data Preprocessing: All continuous input features (e.g., step count, symptom scores) will be standardised (e.g., z-score normalisation). High-frequency digital phenotype data will be aggregated to a consistent temporal resolution (e.g., daily summaries).
- Validation: To prevent information leakage and ensure the model generalises to unseen patients, a patient-level, nested cross-validation (CV) scheme must be employed. The outer loop splits patients into training and test sets; the inner loop performs hyperparameter tuning on a validation set carved from the training set.
- Evaluation Metrics: The evaluation must reflect the prognostic goal of forecasting the entire trajectory. This provides the direct mechanism for falsifiability; the theory’s propositions (e.g., Proposition 3) are supported only if a dynamic model (like the LSTM) significantly outperforms static benchmarks. Key metrics include:
- –
- Trajectory-wise Root Mean Squared Error (RMSE) or Mean Absolute Error (MAE): The average error across all forecasted time points. This is the primary measure of path accuracy.
- –
- Endpoint MAE: The error at the final time point only (e.g., week 12). This allows for direct comparison with traditional static models.
- –
- Dynamic Time Warping (DTW): A metric that measures the similarity between two temporal sequences, even if they are out of phase. This assesses if the model correctly predicted the shape of recovery (e.g., “fast-responder”) even if its timing was slightly off.
- Benchmarks: To prove its value, the proposed model must be benchmarked against simpler alternatives, as outlined in Table 3.
6.3. Ethical Considerations
- Data Privacy and Informed Consent: The continuous, passive nature of digital phenotyping is incompatible with traditional, one-time consent models.
- Methodological Solution: We propose implementing a dynamic consent interface within any data collection application. This would allow patients granular control to view, pause, or withdraw specific data streams at any time. This must be paired with privacy-preserving machine learning techniques, such as federated learning, where the model is trained on the user’s device, and only anonymised model weights—not raw personal data—are sent to a central server.
- Algorithmic Bias and Fairness: AI models trained on historical data risk learning and amplifying existing societal biases and health disparities, which can lead to poor performance in underrepresented populations.
- Methodological Solution: A mandatory algorithmic bias audit must be part of the validation protocol (Section 6.2.2). This involves disaggregating all key performance metrics (e.g., Trajectory RMSE) across demographic subgroups (e.g., race, gender, socioeconomic status). If significant performance disparities are identified, mitigation strategies (e.g., data reweighting, fairness constraints) must be employed and reported transparently.
- Accountability and Responsibility: If a model’s forecast contributes to an adverse outcome, who is responsible?
- Methodological Solution: The framework must establish clear lines of accountability. The model must be legally and ethically framed as a Clinical Decision Support (CDS) tool, not an autonomous medical device. The final clinical judgement and responsibility must always reside with the human clinician. The system’s interface and documentation must clearly state its probabilistic nature, its limitations, and its role as an assistive tool to augment, rather than replace, professional expertise.
6.4. Limitations of the Prognostic Framework
6.5. Boundary Conditions and Scope of the Theory
6.6. A Research Agenda for a Prognostic Psychiatry
- Establishment of Longitudinal, Multi-Modal Cohorts: The primary focus should be on creating large-scale, openly shared datasets. These studies must collect longitudinal data from patients with MDD, capturing the full PSV (clinical, biological, and high-frequency digital phenotype data) before, during, and after various treatment interventions (TIFs).
- Development and Validation of Prognostic Models: Using these new datasets, the next step is to develop and rigorously validate computational models that can forecast individual PRTs. This work (which will be the subject of our subsequent paper) should focus on time-series models (e.g., LSTMs) and benchmark their prognostic accuracy against the current static prediction methods.
- Testing of Causal Propositions: The propositions of the theory should be empirically tested. For example, studies should investigate whether early changes in the PRT (Proposition 3) are indeed more predictive than baseline data alone and whether specific PSV-TIF interactions (Proposition 2) can be identified that lead to differential treatment outcomes.
- Human-Centred Design and Implementation Studies: Parallel to model development, HCI research is required to co-design and evaluate clinical decision support tools based on this framework. Usability studies, qualitative interviews with clinicians and patients, and pilot implementation trials are necessary to understand how to ethically and effectively integrate prognostic information into clinical care.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| CBT | Cognitive Behavioural Therapy |
| CRP | C-reactive Protein |
| CYP2D6 | Cytochrome P450 2D6 |
| DP | Damage Prognosis |
| DST | Dynamic Systems Theory |
| EEG | Electroencephalography |
| EHR | Electronic Health Record |
| fMRI | Functional Magnetic Resonance Imaging |
| GPS | Global Positioning System |
| HAM-D | Hamilton Depression Rating Scale |
| HCI | Human-Computer Interaction |
| HPA | Hypothalamic-Pituitary-Adrenal (axis) |
| LSTM | Long Short-Term Memory (networks) |
| MDD | Major Depressive Disorder |
| ML | Machine Learning |
| PHQ-9 | Patient Health Questionnaire-9 |
| PRT | Predicted Recovery Trajectory |
| PSV | Patient State Vector |
| RNNs | Recurrent Neural Networks |
| RULs | Remaining Useful Life |
| SHM | Structural Health Monitoring |
| SSRI | Selective Serotonin Reuptake Inhibitor |
| TIF | Therapeutic Impulse Function |
| WHO | World Health Organization |
| XAI | Explainable AI |
References
- Abrahams, A.B.; Beckenstrom, A.; Browning, M.; Dias, R.; Goodwin, G.M.; Gorwood, P.; Kingslake, J.; Morriss, R.; Reif, A.; Ruhe, H.G.; et al. Exploring the incidence of inadequate response to antidepressants in the primary care of depression. Eur. Neuropsychopharmacol. 2024, 83, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Penn, E.M.; Tracy, D.K. The drugs don’t work? Antidepressants and the current and future pharmacological management of depression. Ther. Adv. Psychopharmacol. 2012, 2, 179–188. [Google Scholar] [CrossRef]
- Alharbi, A. Treatment-resistant depression: Therapeutic trends, challenges, and future directions. Patient Prefer. Adherence 2012, 6, 369. [Google Scholar] [CrossRef] [PubMed]
- Zelek-Molik, A.; Litwa, E. Trends in research on novel antidepressant treatments. Front. Pharmacol. 2025, 16, 1544795. [Google Scholar] [CrossRef]
- Voineskos, D.; Daskalakis, Z.J.; Blumberger, D.M. Management of treatment-resistant depression: Challenges and opportunities. Neuropsychiatr. Dis. Treat. 2020, 16, 221–234. [Google Scholar] [CrossRef]
- Rush, A.J.; Trivedi, M.H.; Wisniewski, S.R.; Nierenberg, A.A.; Stewart, J.W.; Warden, D.; Niederehe, G.; Thase, M.E.; Lavori, P.W.; Lebowitz, B.D.; et al. Acute and longer-term outcomes in depressed outpatients requiring one or several treatment steps: A STAR* D report. Am. J. Psychiatry 2006, 163, 1905–1917. [Google Scholar] [CrossRef]
- Trivedi, M.H.; Rush, A.J.; Wisniewski, S.R.; Nierenberg, A.A.; Warden, D.; Ritz, L.; Norquist, G.; Howland, R.H.; Lebowitz, B.; McGrath, P.J.; et al. Evaluation of outcomes with citalopram for depression using measurement-based care in STAR* D: Implications for clinical practice. Am. J. Psychiatry 2006, 163, 28–40. [Google Scholar] [CrossRef]
- Crown, W.H.; Finkelstein, S.; Berndt, E.R.; Ling, D.; Poret, A.W.; Rush, A.J.; Russell, J.M. The impact of treatment-resistant depression on health care utilization and costs. J. Clin. Psychiatry 2002, 63, 963–971. [Google Scholar] [CrossRef]
- Lépine, J.P.; Briley, M. The increasing burden of depression. Neuropsychiatr. Dis. Treat. 2011, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Ozomaro, U.; Wahlestedt, C.; Nemeroff, C.B. Personalized medicine in psychiatry: Problems and promises. BMC Med. 2013, 11, 132. [Google Scholar] [CrossRef]
- Baminiwatta, A. Global trends of machine learning applications in psychiatric research over 30 years: A bibliometric analysis. Asian J. Psychiatry 2022, 69, 102986. [Google Scholar] [CrossRef]
- Iyortsuun, N.K.; Kim, S.; Jhon, M.; Yang, H.; Pant, S. A review of machine learning and deep learning approaches on mental health diagnosis. Healthcare 2023, 11, 285. [Google Scholar] [CrossRef]
- Sun, J.; Lu, T.; Shao, X.; Han, Y.; Xia, Y.; Zheng, Y.; Wang, Y.; Li, X.; Ravindran, A.; Fan, L.; et al. Practical AI application in psychiatry: Historical review and future directions. Mol. Psychiatry 2025, 30, 4399–4408. [Google Scholar] [CrossRef]
- Shatte, A.; Hutchinson, D.; Teague, S. Machine learning in mental health: A scoping review of methods and applications. Psychol. Med. 2019, 49, 1426–1448. [Google Scholar] [CrossRef] [PubMed]
- Karvelis, P.; Charlton, C.E.; Allohverdi, S.G.; Bedford, P.; Hauke, D.J.; Diaconescu, A.O. Computational approaches to treatment response prediction in major depression using brain activity and behavioral data: A systematic review. Netw. Neurosci. 2022, 6, 1066–1103. [Google Scholar] [CrossRef]
- Li, H.; Song, S.; Wang, D.; Zhang, D.; Tan, Z.; Lian, Z.; Wang, Y.; Zhou, X.; Pan, C.; Wu, Y. Treatment response prediction for major depressive disorder patients via multivariate pattern analysis of thalamic features. Front. Comput. Neurosci. 2022, 16, 837093. [Google Scholar] [CrossRef]
- Ntam, V.A.; Huebner, T.; Steffens, M.; Scholl, C. Machine learning approaches in the therapeutic outcome prediction in major depressive disorder: A systematic review. Front. Psychiatry 2025, 16, 1588963. [Google Scholar] [CrossRef]
- Curtiss, J.; DiPietro, C.P. Machine learning in the prediction of treatment response for emotional disorders: A systematic review and meta-analysis. Clin. Psychol. Rev. 2025, 120, 102593. [Google Scholar] [CrossRef] [PubMed]
- Sheu, Y.; Magdamo, C.; Miller, M.; Das, S.; Blacker, D.; Smoller, J.W. Ai-assisted prediction of differential response to antidepressant classes using electronic health records. npj Digit. Med. 2023, 6, 73. [Google Scholar] [CrossRef]
- Sajjadian, M.; Lam, R.W.; Milev, R.; Rotzinger, S.; Frey, B.N.; Soares, C.N.; Parikh, S.V.; Foster, J.A.; Turecki, G.; Müller, D.J.; et al. Machine learning in the prediction of depression treatment outcomes: A systematic review and meta-analysis. Psychol. Med. 2021, 51, 2742–2751. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Vekaria, V.; Wang, F.; Cukor, J.; Su, C.; Adekkanattu, P.; Brandt, P.; Jiang, G.; Kiefer, R.C.; Luo, Y.; et al. Using machine learning to predict antidepressant treatment outcome from electronic health records. Psychiatr. Res. Clin. Pract. 2023, 5, 118–125. [Google Scholar] [CrossRef]
- Stephan, K.E.; Bach, D.R.; Fletcher, P.C.; Flint, J.; Frank, M.J.; Friston, K.J.; Heinz, A.; Huys, J.M.; Owen, M.J.; Binder, E.B.; et al. Charting the landscape of computational psychiatry. Lancet Psychiatry 2017, 4, 324–334. [Google Scholar] [CrossRef]
- Scheffer, M.; Bockting, C.; Borsboom, D.; Cools, R.; Delecroix, C.; Hartmann, J.; Kendler, K.S.; Leemput, I.v.d.; Maas, H.L.J.v.d.; Nes, E.H.v.; et al. A dynamical systems view of psychiatric disorders—Theory. JAMA Psychiatry 2024, 81, 618. [Google Scholar] [CrossRef]
- Gauld, C.; Depannemaecker, D. Dynamical systems in computational psychiatry: A toy-model to apprehend the dynamics of psychiatric symptoms. Front. Psychol. 2023, 14, 1099257. [Google Scholar] [CrossRef]
- Bosl, W.J.; Enlow, M.B.; Nelson, C.A. A dynamical systems framework for precision psychiatry. npj Digit. Med. 2025, 8, 586. [Google Scholar] [CrossRef]
- Öngür, D.; Paulus, M.P. Embracing complexity in psychiatry—From reductionistic to systems approaches. Lancet Psychiatry 2025, 12, 220–227. [Google Scholar] [CrossRef]
- Voerman, S.A.; Strijbos, D.; Staring, A.B.P.; Boer, F.d.; Dijk, M.v.; Driessen, J.; Glas, G.; Goekoop, R.; Mulder, A.; Tromp, N.; et al. Problem-sustaining patterns: Redesigning the concept of mental disorder. Front. Psychiatry 2025, 16, 1382915. [Google Scholar] [CrossRef]
- Friston, K.; Redish, A.D.; Gordon, J.A. Computational nosology and precision psychiatry. Comput. Psychiatry 2017, 1, 2. [Google Scholar] [CrossRef] [PubMed]
- Nelson, B.; McGorry, P.D.; Wichers, M.; Wigman, J.T.W.; Hartmann, J. Moving from static to dynamic models of the onset of mental disorder. JAMA Psychiatry 2017, 74, 528. [Google Scholar] [CrossRef] [PubMed]
- Does, F.H.S.v.d.; Nagamine, M.; Kitano, M.; Saito, T.; Wee, N.J.v.d.; Vermetten, E.; Giltay, E.J. The potential of personalized post-traumatic stress disorder networks. Psychiatry Clin. Psychopharmacol. 2025, 35, S141–S151. [Google Scholar] [CrossRef] [PubMed]
- Farrar, C.R.; Lieven, N.A.J. Damage prognosis: The future of structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 623–632. [Google Scholar] [CrossRef]
- Worden, K.; Dulieu-Barton, J.M. An overview of intelligent fault detection in systems and structures. Struct. Health Monit. 2004, 3, 85–98. [Google Scholar] [CrossRef]
- Durstewitz, D.; Huys, Q.J.M.; Koppe, G. Psychiatric illnesses as disorders of network dynamics. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2021, 6, 865–876. [Google Scholar] [CrossRef] [PubMed]
- Hayes, A.M.; Andrews, L.A. A complex systems approach to the study of change in psychotherapy. BMC Med. 2020, 18, 197. [Google Scholar] [CrossRef]
- Insel, T.R. Digital phenotyping: An overarching framework to capture our extended mental states. Lancet Psychiatry 2018, 5, 194–195. [Google Scholar] [CrossRef]
- Torous, J.; Onnela, J.; Keshavan, M.S. New dimensions and new tools to realize the potential of rdoc: Digital phenotyping via smartphones and connected devices. Transl. Psychiatry 2017, 7, e1053. [Google Scholar] [CrossRef]
- Hiemke, C.; Baumann, P.; Bergemann, N.; Conca, A.; Dietmaier, O.; Egberts, K.; Fric, M.; Gerlach, M.; Greiner, C.; Gründer, G.; et al. AGNP consensus guidelines for therapeutic drug monitoring in psychiatry: Update 2011. Pharmacopsychiatry 2011, 44, 195–235. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Ragguett, R.M.; Mansur, R.B.; Boutilier, J.J.; Rosenblat, J.D.; Trevizol, A.P.; McIntyre, R.S. Applications of machine learning algorithms to predict antidepressant treatment response in patients with major depressive disorder: A systematic review and meta-analysis. J. Affect. Disord. 2018, 241, 573–584. [Google Scholar] [CrossRef]
- Rost, N.; Binder, E.B.; Brückl, T. Predicting treatment outcome in depression: An introduction into current concepts and challenges. Eur. Arch. Psychiatry Clin. Neurosci. 2022, 273, 113–127. [Google Scholar] [CrossRef]
- Uyar, A.; Gönül, A.S. New and emerging pharmacologic treatments for mdd. Front. Psychiatry 2025, 16, 1621887. [Google Scholar] [CrossRef] [PubMed]
- Elsaesser, M.; Feige, B.; Kriston, L.; Schumacher, L.; Peifer, J.; Hautzinger, M.; Härter, M.; Schramm, E. Longitudinal clusters of long-term trajectories in patients with early-onset chronic depression: 2 years of naturalistic follow-up after extensive psychological treatment. Psychother. Psychosom. 2023, 93, 65–74. [Google Scholar] [CrossRef]
- Frässle, S.; Marquand, A.F.; Schmaal, L.; Dinga, R.; Veltman, D.J.; Wee, N.J.v.d.; Tol, M.v.; Schöbi, D.; Penninx, B.W.; Stephan, K.E. Predicting individual clinical trajectories of depression with generative embedding. NeuroImage Clin. 2020, 26, 102213. [Google Scholar] [CrossRef]
- Lai, W.; Liao, Y.; Zhang, H.; Zhao, H.; Li, Y.; Chen, R.; Shi, G.; Liu, Y.; Hao, J.; Li, Z.; et al. The trajectory of depressive symptoms and the association with quality of life and suicidal ideation in patients with major depressive disorder. BMC Psychiatry 2025, 25, 310. [Google Scholar] [CrossRef] [PubMed]
- Schmaal, L.; Marquand, A.F.; Rhebergen, D.; Tol, M.v.; Ruhé, H.G.; Wee, N.J.v.d.; Veltman, D.J.; Penninx, B.W. Predicting the naturalistic course of major depressive disorder using clinical and multimodal neuroimaging information: A multivariate pattern recognition study. Biol. Psychiatry 2015, 78, 278–286. [Google Scholar] [CrossRef]
- Fried, E.I. The 52-symptom challenge: The measurement of depression. Lancet Psychiatry 2017, 4, 181–183. [Google Scholar] [CrossRef]
- Kang, S.; Cho, S. Neuroimaging biomarkers for predicting treatment response and recurrence of major depressive disorder. Int. J. Mol. Sci. 2020, 21, 2148. [Google Scholar] [CrossRef]
- Liu, R.; Hou, X.; Liu, S.; Zhou, Y.; Zhou, J.; Qiao, K.; Qi, H.; Li, R.; Yang, Z.; Zhang, L.; et al. Predicting antidepressant response via local-global graph neural network and neuroimaging biomarkers. npj Digit. Med. 2025, 8, 515. [Google Scholar] [CrossRef] [PubMed]
- Athira, K.V.; Bandopadhyay, S.; Samudrala, P.K.; Naidu, V.; Lahkar, M.; Chakravarty, S. An overview of the heterogeneity of major depressive disorder: Current knowledge and future prospective. Curr. Neuropharmacol. 2020, 18, 168–187. [Google Scholar] [CrossRef]
- Lynall, M.; McIntosh, A.M. The heterogeneity of depression. Am. J. Psychiatry 2023, 180, 703–704. [Google Scholar] [CrossRef]
- Li, X.; Pei, C.; Wang, X.; Wang, H.; Tian, S.; Yao, Z.; Lü, Q. Predicting neuroimaging biomarkers for antidepressant selection in early treatment of depression. J. Magn. Reson. Imaging 2021, 54, 551–559. [Google Scholar] [CrossRef]
- Joyce, D.W.; Kormilitzin, A.; Smith, K.; Cipriani, A. Explainable artificial intelligence for mental health through transparency and interpretability for understandability. npj Digit. Med. 2023, 6, 6. [Google Scholar] [CrossRef]
- Probierz, B.; Straś, A.; Rodek, P.; Kozak, J. Explainable ai in psychiatry. In Explainable Artificial Intelligence for Sustainable Development; Routledge: London, UK, 2025; pp. 245–262. [Google Scholar] [CrossRef]
- Yadav, P.; Kumar, Y.; Kumar, S. Evaluating the impact of machine learning models on adult major depressive disorder using conventional treatment strategies: A systematic review approach. Discov. Public Health 2025, 22, 410. [Google Scholar] [CrossRef]
- Cai, H.; Song, H.; Yang, Y.; Xiao, Z.; Zhang, X.; Jiang, F.; Liu, H.; Tang, Y. Big-five personality traits and depression: Chain mediation of self-efficacy and walking. Front. Psychiatry 2024, 15. [Google Scholar] [CrossRef]
- Chen, J.; Huang, H. The influence of big five personality traits on depression and suicidal behavior. In The Association Between Depression and Suicidal Behavior; InTechOpen: Rijeka, Croatia, 2024. [Google Scholar] [CrossRef]
- Whetten, D.A. What constitutes a theoretical contribution? Acad. Manag. Rev. 1989, 14, 490–495. [Google Scholar] [CrossRef]
- Watson, M.; Protzner, A.B.; McGirr, A. Five-factor personality and antidepressant response to intermittent theta burst stimulation for major depressive disorder. Transcranial Magn. Stimul. 2025, 5, 100196. [Google Scholar] [CrossRef]
- Thieme, A.; Hanratty, M.; Lyons, M.; Palacios, J.; Marques, R.F.; Morrison, C.; Doherty, G. Designing human-centered AI for mental health: Developing clinically relevant applications for online CBT treatment. ACM Trans. Comput.-Hum. Interact. 2022, 29, 1–44. [Google Scholar] [CrossRef]
- Salvi, J.D.; Rauch, S.L.; Baker, J.T. Behavior as physiology: How dynamical-systems theory could advance psychiatry. Am. J. Psychiatry 2021, 178, 791–792. [Google Scholar] [CrossRef]
- Delgadillo, J.; de Jong, K.; Lucock, M.; Lutz, W.; Rubel, J.; Gilbody, S.; Ali, S.; Aguirre, E.; Appleton, M.; Nevin, J.; et al. Feedback-informed treatment versus usual psychological treatment for depression and anxiety: A multisite, pragmatic, cluster-randomised controlled trial. Lancet Psychiatry 2018, 5, 564–572. [Google Scholar] [CrossRef]
- Alowais, S.A.; Alghamdi, S.S.; Alsuhebany, N.; Alqahtani, T.; Alshaya, A.I.; Almoaiqel, M. Revolutionizing healthcare: The role of artificial intelligence in clinical practice. BMC Med Educ. 2023, 23, 689. [Google Scholar] [CrossRef] [PubMed]
- Bauer, M.; Glenn, T.; Monteith, S.; Bauer, R.; Whybrow, P.C.; Geddes, J. Ethical perspectives on recommending digital technology for patients with mental illness. Int. J. Bipolar Disord. 2017, 5, 6. [Google Scholar] [CrossRef]
- Tilala, M.H.; Chenchala, P.K.; Choppadandi, A.; Kaur, J.; Naguri, S.; Saoji, R.; Devaguptapu, B. Ethical considerations in the use of artificial intelligence and machine learning in health care: A comprehensive review. Cureus 2024, 16, e62443. [Google Scholar] [CrossRef] [PubMed]
- Ratti, E.; Morrison, M.; Jakab, I. Ethical and social considerations of applying artificial intelligence in healthcare—A two-pronged scoping review. BMC Med Ethics 2025, 26, 68. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO Calls for Safe and Ethical AI for Health. 2023. Available online: https://www.who.int/news/item/16-05-2023-who-calls-for-safe-and-ethical-ai-for-health (accessed on 13 August 2024).
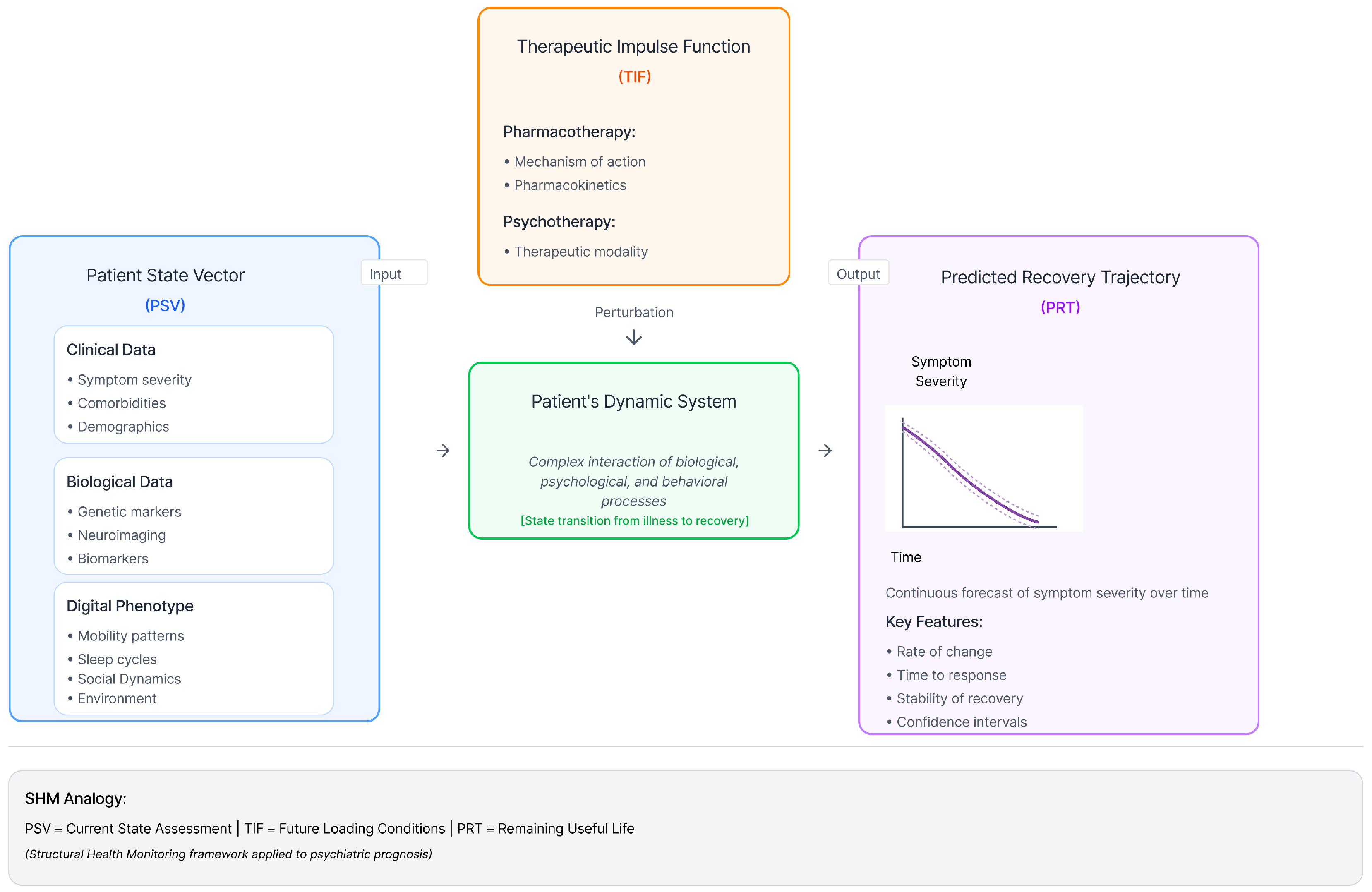
| Damage Prognosis in Engineering | Prognostic Framework in Psychiatry |
|---|---|
| System: A physical structure (e.g., bridge or aircraft wing). | System: An individual patient’s mental health state. |
| Current State Assessment: Data from embedded sensors (e.g., strain, vibration) quantifying existing damage. | Patient State Vector (PSV): Multimodal data (clinical, biological, digital) quantifying the patient’s baseline state. |
| Future Loading Conditions: Anticipated operational and environmental loads (e.g., traffic, weather). | Therapeutic Impulse Function (TIF): The properties of a specific intervention (e.g., pharmacokinetics, therapeutic modality). |
| Remaining Useful Life (RUL): Forecast of the time until the structure can no longer perform its function safely. | Predicted Recovery Trajectory (PRT): Forecast of the patient’s symptom severity over time (e.g., time to remission). |
| Domain | Example Variable | Data Source | Hypothesised Role |
|---|---|---|---|
| Core PSV | |||
| Clinical | Baseline PHQ-9/HAM-D score | Electronic Health Record (EHR) | Measures initial severity |
| Clinical | Comorbidity history | EHR | Moderates overall prognosis |
| Digital Phenotype | Step count/Mobility | Smartphone/Wearable | Objective measure of psychomotor activity |
| Digital Phenotype | Sleep duration/timing | Smartphone/Wearable | Objective measure of sleep disturbance |
| Extended PSV | |||
| Biological | Inflammatory markers (e.g., CRP) | Blood Assay | Moderates response to specific TIFs |
| Biological | Pharmacogenetic markers (e.g., CYP2D6) | Genetic Test | Moderates drug metabolism (TIF) |
| Biological | fMRI (e.g., amygdala reactivity) | Neuroimaging | Identifies neural circuit dysfunction |
| Digital Phenotype | Social communication (call/text logs) | Smartphone | Objective measure of social withdrawal |
| Model | Input Data | Evaluation Metrics |
|---|---|---|
| Multiple Linear Regression (Baseline) | Baseline PSV only (static features) | Endpoint MAE, AUC at 12 weeks |
| Standard LSTM (no time-awareness) | Full time-series of PSV + TIF | Trajectory RMSE, Endpoint MAE, DTW |
| Time-Aware LSTM (Proposed) | Full time-series of PSV + TIF (with time-awareness) | Trajectory RMSE, Endpoint MAE, DTW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngabo-Woods, H.; Dunai, L.; Verdú, I.S. A Prognostic Theory of Treatment Response for Major Depressive Disorder: A Dynamic Systems Framework for Forecasting Clinical Trajectories. Appl. Sci. 2025, 15, 12524. https://doi.org/10.3390/app152312524
Ngabo-Woods H, Dunai L, Verdú IS. A Prognostic Theory of Treatment Response for Major Depressive Disorder: A Dynamic Systems Framework for Forecasting Clinical Trajectories. Applied Sciences. 2025; 15(23):12524. https://doi.org/10.3390/app152312524
Chicago/Turabian StyleNgabo-Woods, Harold, Larisa Dunai, and Isabel Seguí Verdú. 2025. "A Prognostic Theory of Treatment Response for Major Depressive Disorder: A Dynamic Systems Framework for Forecasting Clinical Trajectories" Applied Sciences 15, no. 23: 12524. https://doi.org/10.3390/app152312524
APA StyleNgabo-Woods, H., Dunai, L., & Verdú, I. S. (2025). A Prognostic Theory of Treatment Response for Major Depressive Disorder: A Dynamic Systems Framework for Forecasting Clinical Trajectories. Applied Sciences, 15(23), 12524. https://doi.org/10.3390/app152312524








