Soil Parameter Inversion Considering the Influence of Temperature Effects
Abstract
1. Introduction
2. Influence of Temperature on Underground Structural Deformation
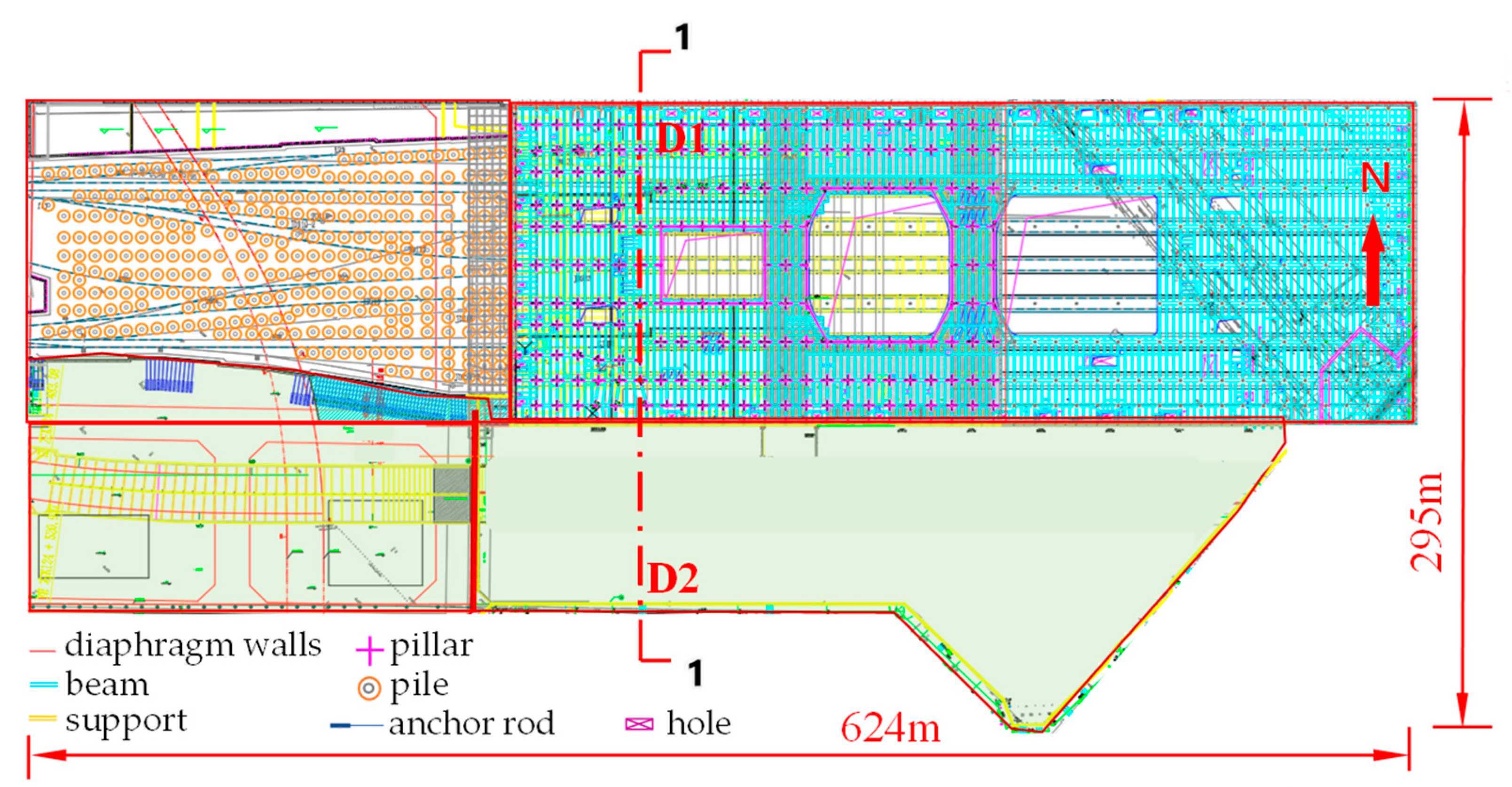
2.1. Experimental Monitoring of Displacement and Temperature in Underground Structures
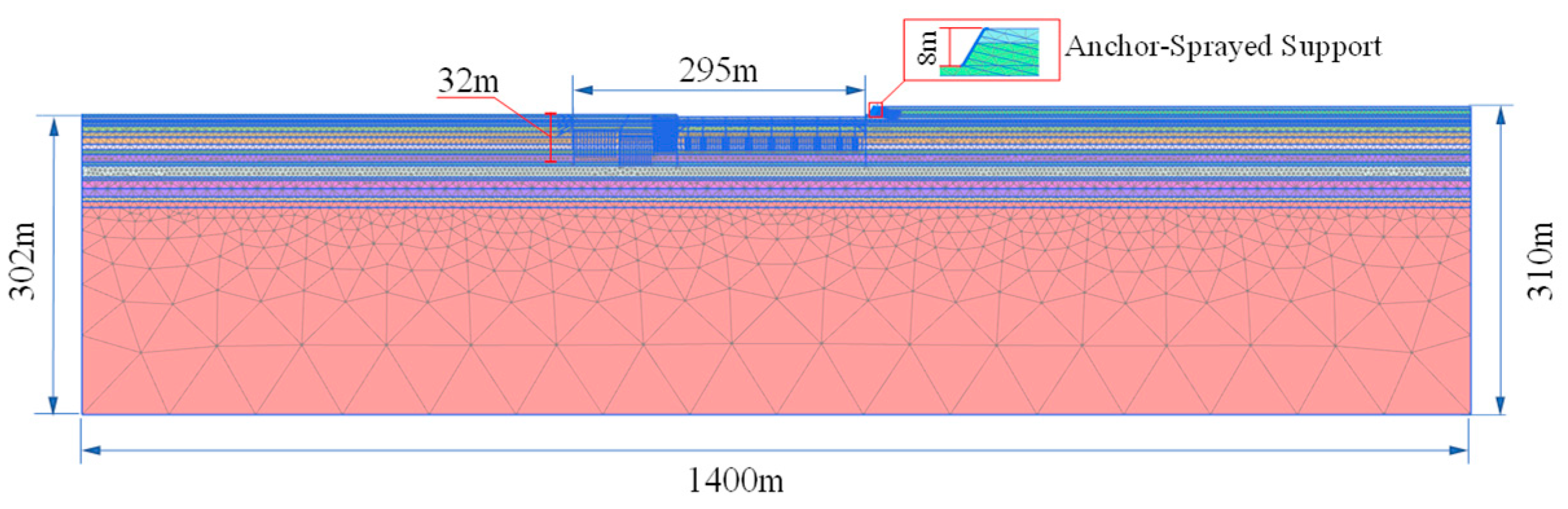
2.2. Finite Element Model
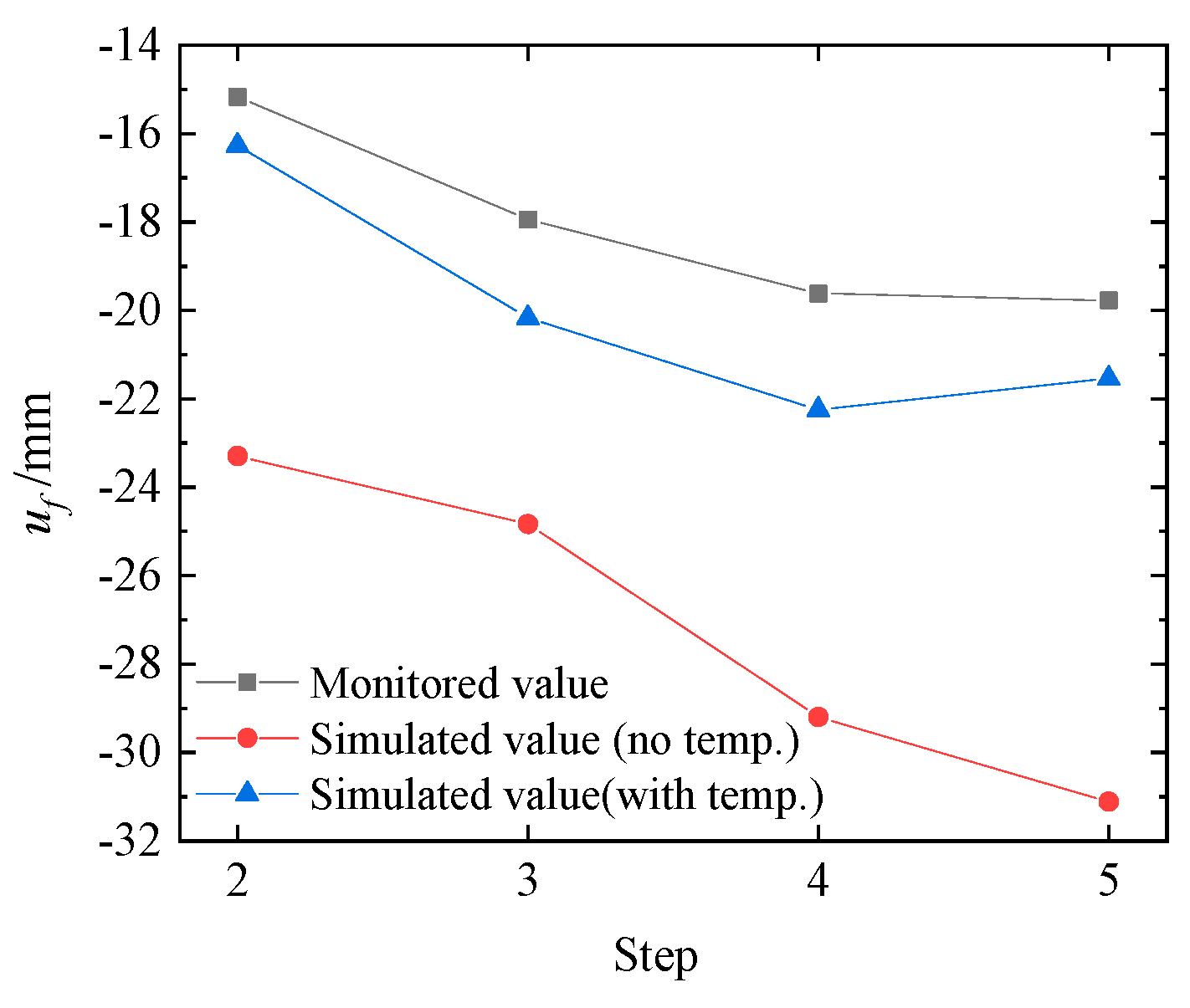
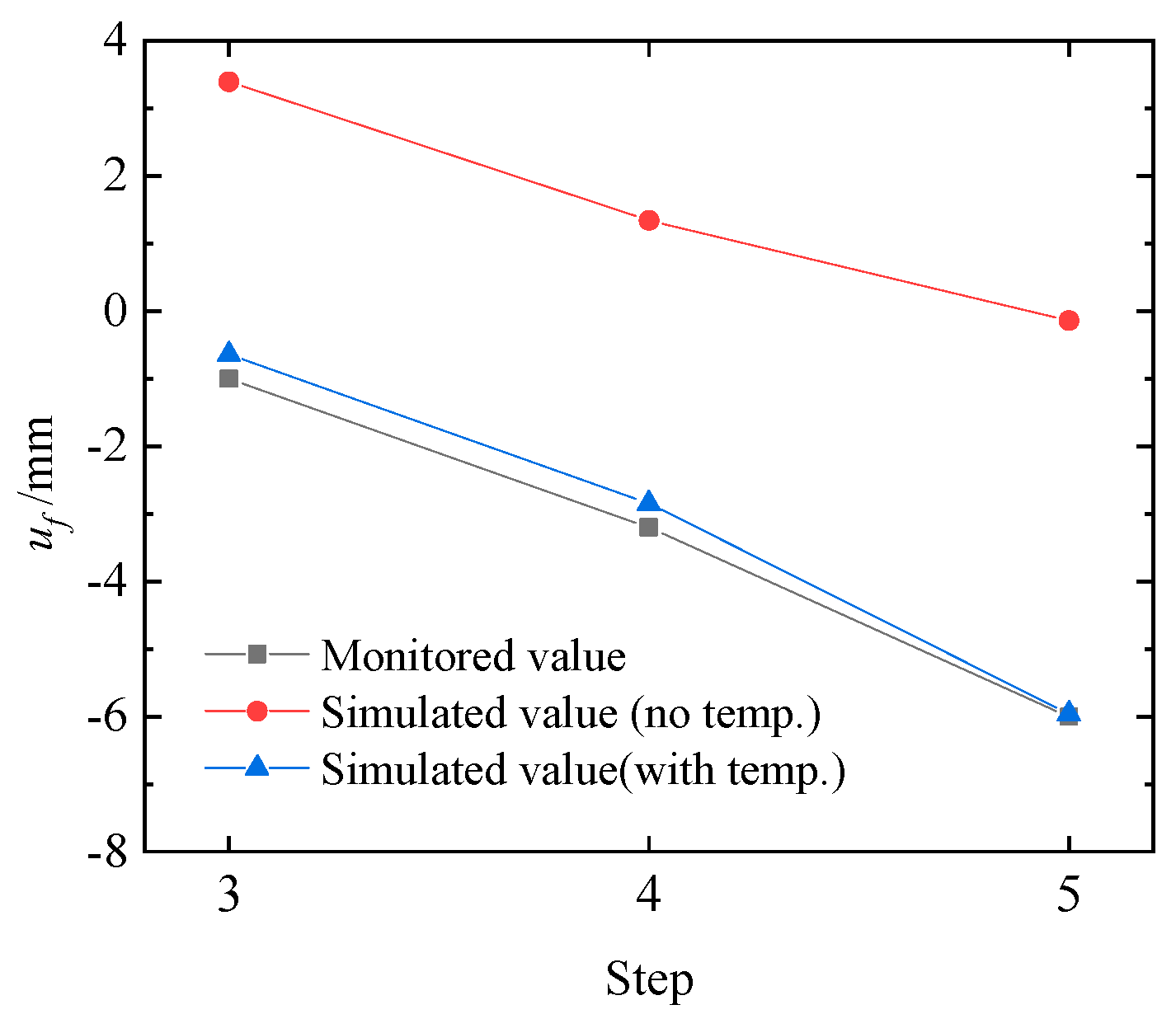
2.3. Finite Element Analysis Results
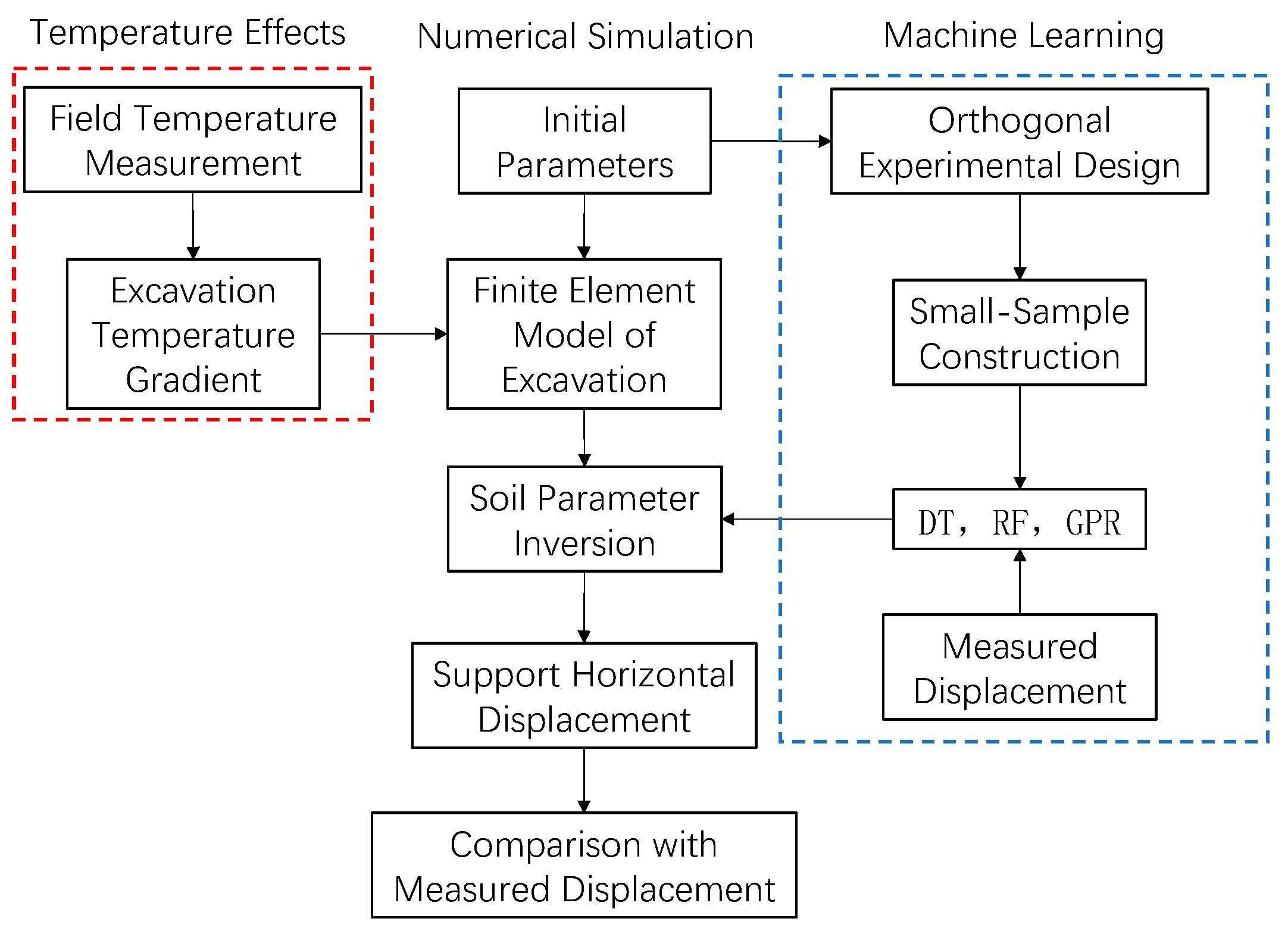
3. Soil Parameter Inversion Considering Temperature Effects
3.1. Machine Learning Methods for Small-Sample Datasets
3.1.1. DT Algorithm
3.1.2. RF Algorithm
3.1.3. GPR Algorithm
3.2. Soil Parameter Inversion
3.2.1. Dataset Preparation
3.2.2. Model Construction for Training
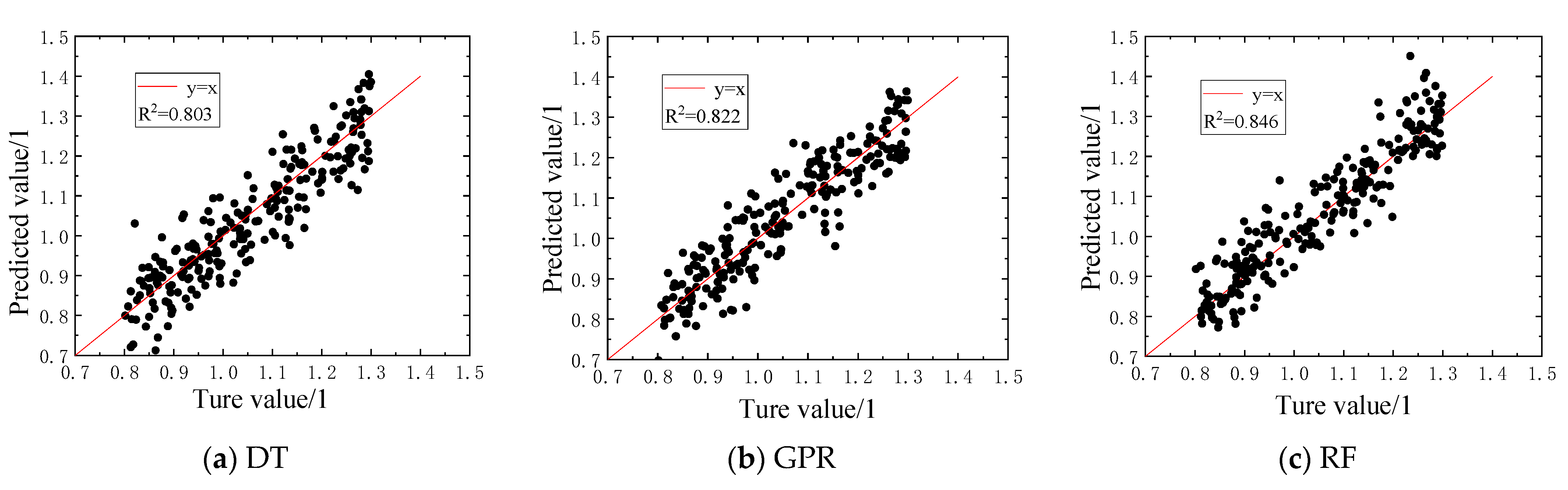
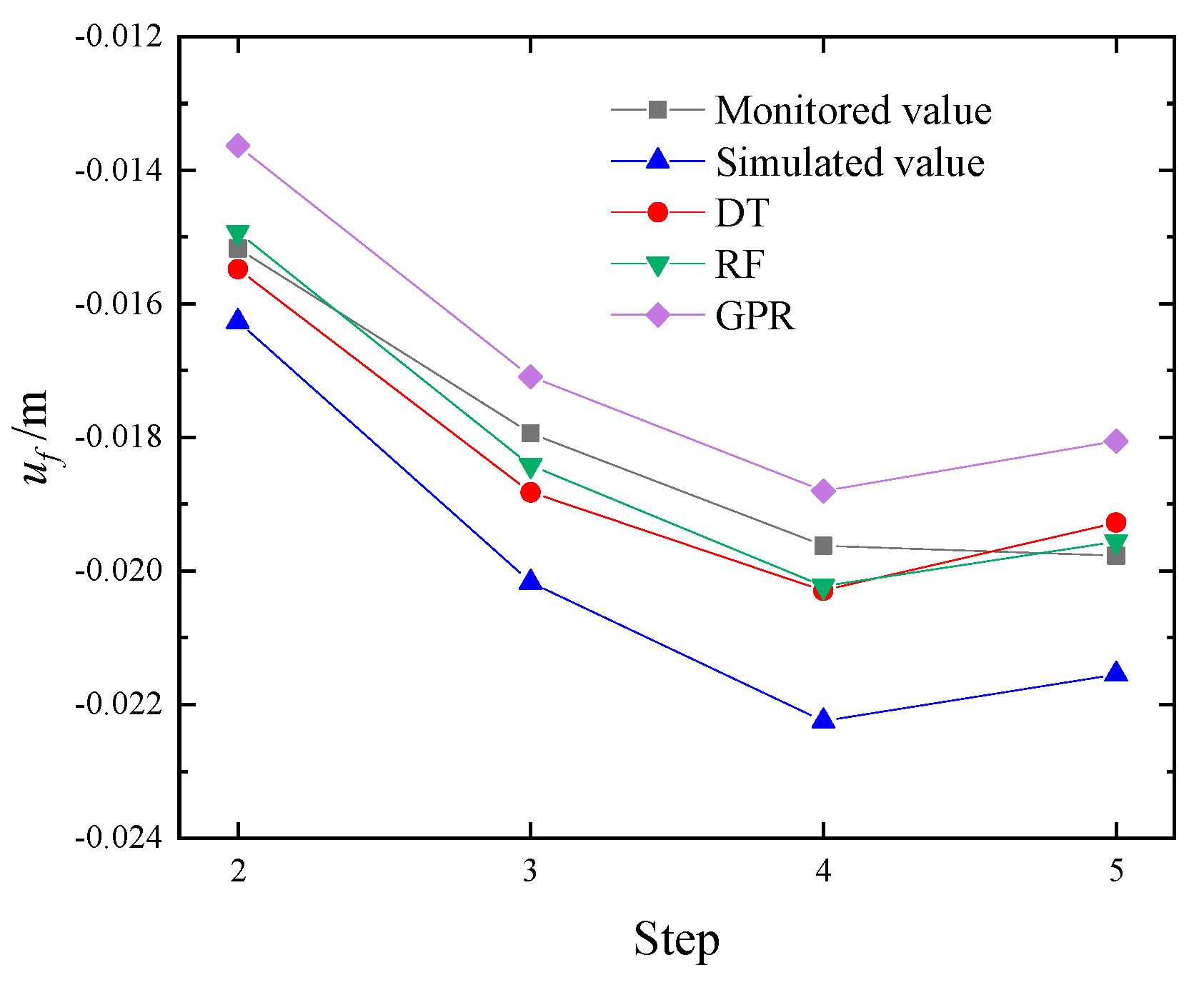
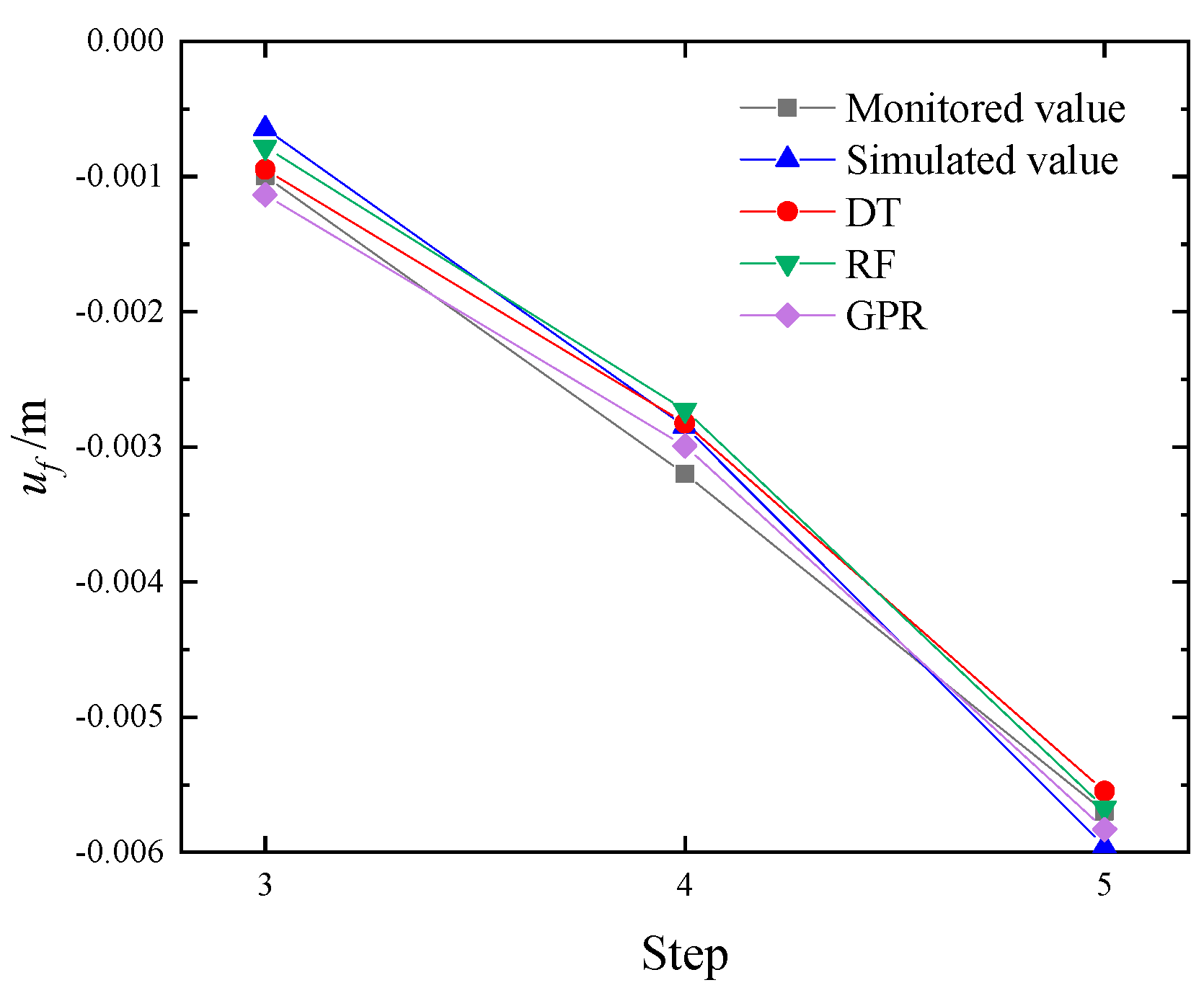
3.2.3. Analysis of Inversion Results
4. Conclusions
- A method was proposed that accounts for the combined effects of excavation and temperature during the construction of super-large pits, and the results show that temperature is a non-negligible factor in deformation analysis. Compared with previous studies that ignored thermal influences, this work provides a more accurate representation of structural deformation behavior and demonstrates the necessity of considering temperature effects in the design and analysis of deep and large-scale excavations.
- Soil layer parameter inversion was conducted based on the finite element model incorporating temperature effects. Training samples were constructed using soil layer grouping and orthogonal experimental design, and the accuracy of DT, RF, and GPR machine learning algorithms was compared. Inverting the soil parameters effectively reduced computational errors, with the RF algorithm achieving the lowest error.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PSO | Particle Swarm Optimization |
| HSS | Hardening Soil Small Strain |
| DT | Decision Tree |
| RF | Random Forest |
| GPR | Gaussian Process Regression |
References
- Tang, L.; Liao, S.; Yang, Y.; Fan, Y.; Liu, Z. A Spatiotemporal Data Mining Method for Advanced Prediction and Assessment of Large Combined Excavation-Induced Wall Deformations and Risks. J. Rock Mech. Geotech. Eng. 2025, 17, 2758–2777. [Google Scholar] [CrossRef]
- Johari, A.; Pourbeirak, S. Impact of Soil Heterogeneity on Stochastic SANISAND Constitutive Model and Static Liquefaction Potential. Iran. J. Sci. Technol. 2025, 49, 5003–5020. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Levenberg, K.A. Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN′95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Goh, A.T.C. Empirical Design in Geotechnics Using Neural Networks. Géotechnique 1995, 45, 709–714. [Google Scholar] [CrossRef]
- Cheng, Q.; Yang, Z.; Qin, S. Application of Soil Parameters Inversion Based on PSO-MLSSVR in Deep Foundation Pit Engineering. J. Eng. Geol. 2022, 30, 520–532. [Google Scholar] [CrossRef]
- Ji, H.; Jin, Y.; Yin, Z. Enhancement of Genetic Algorithm and Its Application to the Identification of Soil Parameters by Inverse Analysis. Chin. J. Comput. Mech. 2018, 35, 224–229. [Google Scholar] [CrossRef]
- Cao, J.; Tang, B.; Li, H. Optimization of LS-SVM Based on SA-PSO Algorithm for Inversion of Equivalent Parameters of Foundation Soil Layers. Ind. Saf. Environ. Prot. 2023, 49, 15–20. [Google Scholar]
- Zhao, C. A Modified Back Analysis Method for Deep Excavation with Multi-Objective Optimization Procedure. J. Rock Mech. Geotech. Eng. 2024, 16, 1373–1387. [Google Scholar] [CrossRef]
- Liu, M.; Zhuang, P.; Lai, F. A Bayesian Optimization-Genetic Algorithm-Based Approach for Automatic Parameter Calibration of Soil Models: Application to Clay and Sand Model. Comput. Geotech. 2024, 176, 106717. [Google Scholar] [CrossRef]
- Li, B.Y.; Sima, J. Horizontal Displacement Back-Analysis for Deep Excavation Using MEC-BP Neural Network. J. Railw. Sci. Eng. 2021, 18, 1764–1772. [Google Scholar]
- Liu, W.; Tong, L.; Li, H.; Wang, Z.; Sun, Y.; Gu, W. Multi-Parameter Intelligent Inverse Analysis of a Deep Excavation Considering Path-Dependent Behavior of Soils. Comput. Geotech. 2024, 174, 106597. [Google Scholar] [CrossRef]
- Sun, L.; Liu, S.; Zhang, L.; He, K.; Yan, X. Prediction of the Displacement in a Foundation Pit Based on Neural Network Model Fusion Error and Variational Modal Decomposition Methods. Measurement 2025, 240, 115534. [Google Scholar] [CrossRef]
- Hu, H.; Tian, Y.; Zheng, N.; Du, X.; Guo, H.; Xu, Z. Numerical Simulation on an Ultra-Large Seven-Ring Internal Support System Considering the Effects of Soil–Structure Interaction and Temperature. Buildings 2025, 15, 463. [Google Scholar] [CrossRef]
- Yang, J.; Cui, F.; Zhang, Y.; Li, B.; Li, B.; Mei, W. Influence of Seasonal Ambient Temperature on the Temperature and Deformation Behaviors of Underground Utility Tunnels. Soil Mech. Found. Eng. 2025, 62, 253–260. [Google Scholar] [CrossRef]
- Ji, F.; Shi, S. Temperature Effect Analysis of Mechanical Behavior of Deep Foundation Pit Supporting Structure. Chin. J. Undergr. Space Eng. 2024, 20, 298–309. [Google Scholar]
- Park, S.; Son, Y.; Kim, J.; Won, D.; Choi, H. Thermal and Mechanical Impact of Artificial Ground-Freezing on Deep Excavation Stability in Nakdong River Deltaic Deposits. Eng. Geol. 2024, 343, 107796. [Google Scholar] [CrossRef]
- Lu, P.; Han, L.; Yu, Y. Finite Element Analysis of Temperature Stress in Strut of Foundation Pit. Rock Soil Mech. 2008, 29, 1290–1294. [Google Scholar]
- Liu, C.; Zhang, Y.; Zheng, G. Effects of Seasonal Temperature Change on a Large-Excavation Project. Chin. J. Geotech. Eng. 2016, 38, 627–635. [Google Scholar] [CrossRef]
- Wang, X.; Li, M.; Chen, J.; Zhu, Y. Performance of a Deep Excavation with the Composite Retaining Wall Using Artificial Ground Freezing Method. Cold Reg. Sci. Technol. 2022, 204, 103676. [Google Scholar] [CrossRef]
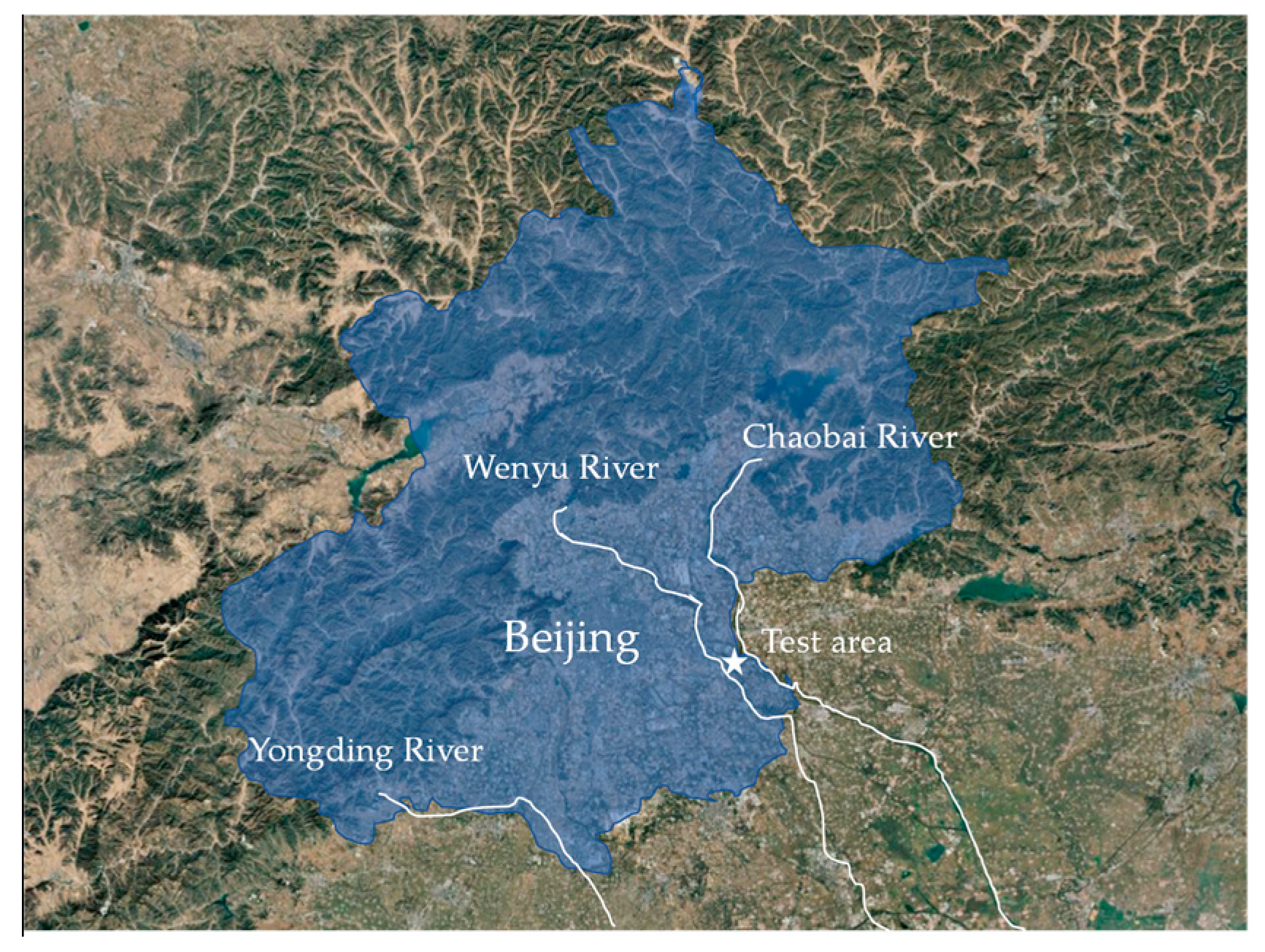
- Luo, Y.; Zhao, L.; Zhu, L.; Tian, F.; Lei, K.; Sun, A. Land Subsidence Characteristics and Disaster Prevention in the Tongzhou Area, Beijing. PIAHS 2020, 382, 715–722. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Yan, Q.; Zhang, M.; Liang, W. The Research on 3D Modelling and Visualization of the Quaternary in Tongzhou Area, Beijing. Geo-Spat. Knowl. Intell. 2018, 848, 3–12. [Google Scholar] [CrossRef]
- Bentley PLAXIS 2D Materials Models Manual. Available online: https://files.seequent.com/PLAXIS/Manuals/PLAXIS_2D/English/PLAXIS_2D_3_Material%20Models%20Manual.pdf (accessed on 16 November 2025).
- Hu, J.; Du, Q. Parameter Study and Engineering Verification of the Hardening Soil Model with Small-Strain Stiffness for Loess in the Xi’an Area. Appl. Sci. 2025, 15, 1278. [Google Scholar] [CrossRef]
- Li, M.; Chen, H.; Zhang, Z.; Chen, J. Numerical Analysis of a Deep and Oversized Group Excavation: A Case Study. Undergr. Space 2025, 21, 178–197. [Google Scholar] [CrossRef]
- Kawa, M.; Puła, W.; Truty, A. Probabilistic Analysis of the Diaphragm Wall Using the Hardening Soil-Small (HSs) Model. Eng. Struct. 2021, 232, 111869. [Google Scholar] [CrossRef]
- Hu, H.; Luo, X.; Wang, W.; Xu, C.; Zheng, G. Soil Parameter Inversion Modeling Using Deep Learning Algorithms and Its Application to Settlement Prediction: A Comparative Study. Acta Geotech. 2023, 18, 4703–4720. [Google Scholar] [CrossRef]


| Construction Step | Description | D1 (m) | D2 (m) | T1 (°C) | T2 (°C) | T3 (°C) |
|---|---|---|---|---|---|---|
| step 1 | B0.5 slab construction | |||||
| step 2 | Local excavation to 8 m; B0.5 excavation; B1 slab construction | −0.01517 | Not arranged | 30 | Not arranged | Not arranged |
| step 3 | Overall excavation to 12 m; completion of B1 excavation; B2 slab construction | −0.01794 | −0.001 | 26 | 22 | Not arranged |
| step 4 | B2 excavation to 50%; installation of B2 raking struts | −0.01962 | −0.0032 | 27 | 23 | Not arranged |
| step 5 | Excavation to 22 m; completion of B2 excavation; B2 base slab construction | −0.01977 | −0.0057 | 29 | 24.5 | 22.5 |
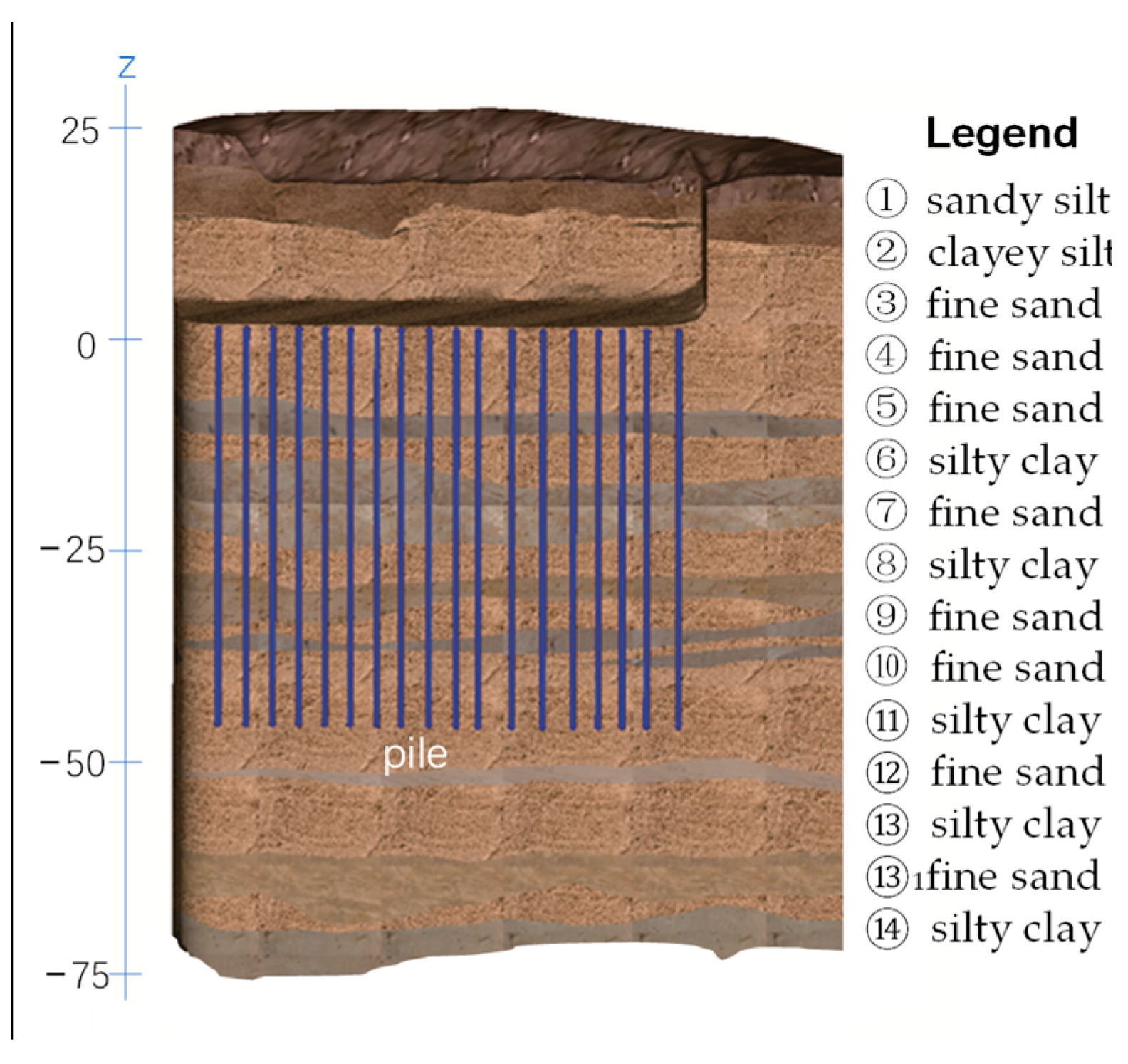
| Soil Texture | Layer Thickness (m) | (MPa) | (MPa) | (MPa) | (kPa) | (×10−4) | (MPa) | kg/m3 | |
|---|---|---|---|---|---|---|---|---|---|
| sandy silt | 3.1 | 10.4 | 9.4 | 92.3 | 2 | 10 | 2.00 | 120 | 15.50 |
| clayey silt | 7.1 | 10.4 | 9.4 | 92.3 | 15 | 23.6 | 2.00 | 120 | 19.03 |
| fine sand | 4.1 | 18.9 | 11.1 | 82.1 | 2 | 28 | 2.00 | 107 | 15.43 |
| fine sand | 5 | 21.2 | 12.5 | 92.4 | 2 | 32 | 3.00 | 120 | 16.98 |
| fine sand | 5.9 | 25.4 | 14.9 | 111 | 2 | 32 | 3.00 | 144 | 16.98 |
| silty clay | 5.55 | 11.0 | 9.97 | 97.7 | 35 | 10 | 3.00 | 127 | 20.35 |
| fine sand | 7.05 | 33.8 | 19.9 | 147 | 2 | 34 | 3.00 | 191 | 20.21 |
| silty clay | 5.49 | 16.4 | 14.9 | 146 | 59 | 16 | 3.00 | 190 | 19.49 |
| fine sand | 4.61 | 42.1 | 24.8 | 183 | 2 | 35 | 3.00 | 238 | 20.4 |
| fine sand | 8.02 | 51.3 | 30.2 | 223 | 2 | 36 | 3.00 | 290 | 20.4 |
| silty clay | 3.48 | 20.7 | 18.8 | 184 | 55 | 14 | 3.00 | 239 | 19.72 |
| fine sand | 11.7 | 61.2 | 36.0 | 266 | 2 | 36 | 3.00 | 346 | 20.6 |
| silty clay | 2.6 | 24.4 | 22.2 | 218 | 55 | 14.4 | 3.00 | 283 | 19.52 |
| fine sand | 8.8 | 69.7 | 41.0 | 303 | 2 | 36 | 3.00 | 394 | 20.60 |
| silty clay | 8.36 | 25.1 | 22.8 | 223 | 77 | 19.7 | 3.00 | 290 | 19.94 |
| silty clay | 4.36 | 28.6 | 26.0 | 255 | 79 | 15.2 | 3.00 | 331 | 19.82 |
| fine sand | 214.98 | 89.8 | 52.8 | 391 | 2 | 38 | 3.00 | 508 | 20.60 |
| Algorithms | Training Parameter | Value |
|---|---|---|
| DT | Maximum Depth | 5 |
| Minimum Samples to Split a Node | 3 | |
| Minimum Samples per Leaf Node | 2 | |
| RF | Number of Base Learners | 120 |
| Number of Features per Split | 14 | |
| Bootstrap Sampling | True | |
| GPR | Kernel Function | RBF |
| Noise Term | ||
| Number of Optimizer Restarts | 4 |
| Monitoring Point | Simulated Value | DT | RF | GPR |
|---|---|---|---|---|
| D1 | 11.10% | 3.41% | 2.30% | 7.11% |
| D2 | 11.00% | 7.80% | 6.16% | 4.20% |
| Mean value | 11.05% | 5.61% | 4.23% | 5.65% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Shen, X.; Pan, D. Soil Parameter Inversion Considering the Influence of Temperature Effects. Appl. Sci. 2025, 15, 12511. https://doi.org/10.3390/app152312511
Liu D, Shen X, Pan D. Soil Parameter Inversion Considering the Influence of Temperature Effects. Applied Sciences. 2025; 15(23):12511. https://doi.org/10.3390/app152312511
Chicago/Turabian StyleLiu, Dong, Xingrui Shen, and Danguang Pan. 2025. "Soil Parameter Inversion Considering the Influence of Temperature Effects" Applied Sciences 15, no. 23: 12511. https://doi.org/10.3390/app152312511
APA StyleLiu, D., Shen, X., & Pan, D. (2025). Soil Parameter Inversion Considering the Influence of Temperature Effects. Applied Sciences, 15(23), 12511. https://doi.org/10.3390/app152312511






