Dynamic Modeling and Adaptive Dimension Improvement Method for Smart Distribution Network Stations Based on Koopman Theory

Abstract

Aiming at the dynamic characteristics and stability of smart distribution network stations under the combined effect of the uncertainty of new energy output and the control logic of power electronics, an adaptive dimensionally increasing linear dynamic modeling method based on Koopman theory is proposed. Firstly, a regional nonlinear model of an intelligent transformer integrating photovoltaic, wind power, battery, hydrogen fuel cell, and synchronous generator is constructed. The control logic of the virtual synchronous generator is then integrated to characterize the dynamic response of the power electronic interface. Secondly, by constructing a set of nonlinear observation functions, including high-order polynomials, exponents, and periodic functions, the dimensional upgrade mapping of the system state is carried out. The dynamic mode decomposition algorithm is adopted to adaptively extract the dominant dynamic modes in the dimensional upgrade space, achieving global linear approximation of complex nonlinear dynamical systems. Finally, the simulation example results show that the average RMAE error of the Koopman method proposed in this paper in voltage spatiotemporal reconstruction is 0.1419, and the maximum RMSE error is 0.1915, significantly improving the accuracy and stability of dynamic modeling.

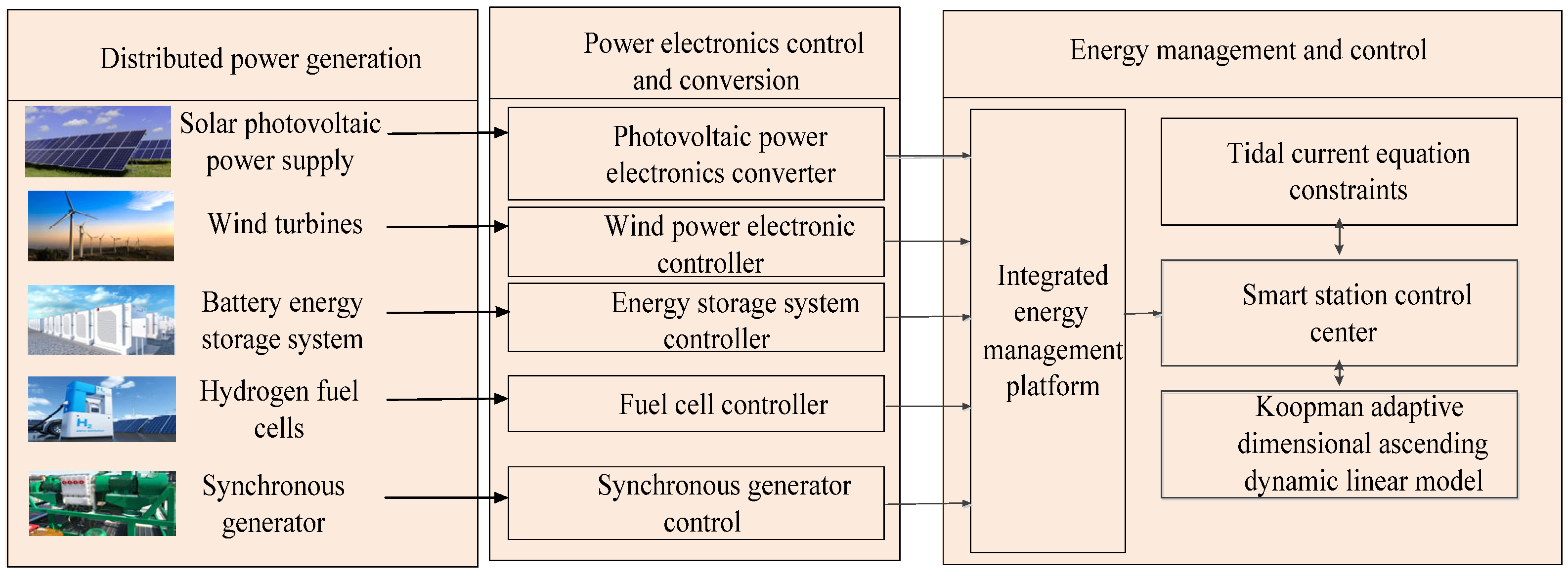
1. Introduction

With the continuous advancement of the integration of source, grid, load, and storage in the power system [1], the distribution station area, which is an important part of the modern power system, is accelerating its evolution into a smart station area. The smart station area deeply integrates advanced sensing, communication, computing, and control technologies with a variety of distributed energy and power electronic equipment, aiming to achieve more efficient energy management, optimized control, and intelligent operation. However, the high proportion of renewable energy penetration, complex power electronic control logic, and the time-varying uncertainty of operating conditions have led to significant nonlinearity, strong coupling, and time-varying dynamic behavior in the smart station area, presenting new challenges for precise and real-time system modeling and control [2].

The existing research can be roughly divided into four technical paths. The first is the flexible interconnection and local control. The flexible interconnection system for low-voltage distribution transformer areas proposed in Reference [3] has enhanced the reliability of power supply and the capacity to accept distributed power sources. Based on this, Reference [4] constructed a planning model considering the total investment cost and comprehensive carrying capacity. Reference [5] effectively alleviated the voltage over-limit and fluctuation problems caused by high-permeability distributed generation through a local interconnection and control strategy based on soft open points. These works focus on achieving flexible power regulation through power electronic devices, laying the foundation for the application of advanced control strategies. However, their underlying device-level dynamic models are often simplified and fail to fully reveal the nonlinear evolution process of the system. The second is big data and edge computing. Reference [6] combined the autocorrelation feature detection and information fusion recognition to construct a risk assessment model for a smart station area. References [7,8] utilized edge computing technology to address the latency issue between intelligent terminal devices and cloud platforms, meeting the demands of business scenarios with high real-time requirements and enhancing the local perception and decision-making capabilities of the distribution area. Reference [9] further proposed an intelligent transformer area design method based on cloud-edge collaboration, achieving real-time resource monitoring and power quality governance. These studies have addressed the platform issues for real-time data analysis and execution. However, their performance is highly dependent on the quality of the models themselves running on the edge side. A dynamic model that is both precise and computationally efficient is the key to realizing its potential. The third is the optimization and risk management methods. Reference [10] constructed a risk-power interaction control model using mixed integer linear optimization, providing a tool for the quantitative management of risks in the distribution area. The fourth is the method based on operators or extended linearization. Reference [11] introduced the Koopman method into the power flow calculation of the distribution system and constructed a high-precision linear mapping model. References [12,13] constructed a global linear dynamic model of wind turbine units by applying the Koopman operator theory and an extended dynamic mode decomposition algorithm.

The above-mentioned work has made significant progress in its respective dimensions. But there are still systematic deficiencies. Most precise mechanism models struggle to strike a balance between accuracy and computational complexity, thus failing to meet the demands of real-time control and online applications. The existing data-driven linear or local models are usually only effective under limited working conditions, and it is difficult to uniformly characterize the global nonlinear behavior of the system and cross-device interaction. In terms of constructing a universal observation/feature space to ensure the generalization ability of the model, there is still a lack of systematic adaptive methods, especially in the scenario of high-dimensional and multi-source perturbations in smart station areas.

To address the aforementioned deficiencies, the Koopman operator theory offers an effective approach. By mapping the original nonlinear dynamics to a high-dimensional observation function space, the system evolution is approximately described by linear operators in this space. Thus, not only can the linear system theory be utilized for analysis and control, but also the representational observation functions can be automatically learned through data-driven methods. Based on this idea, this paper proposes an adaptive high-dimensional dynamic modeling method based on the Koopman operator. The core of this method lies in achieving high-precision modeling of the global dynamic characteristics of smart station areas under high penetration of renewable energy and complex power electronics control by adaptively constructing and selecting a set of high-dimensional observation functions. The main contributions of this article are as follows:

• A mathematical model of the smart distribution network stations, including wind, solar, hydrogen storage, and synchronous generators, was constructed. Through dynamic power allocation strategies and SOC constraint management, the energy interaction characteristics at multiple time scales were accurately depicted, providing a physical basis for subsequent stability analysis.
• A construction method of hybrid nonlinear basis functions is proposed. Compared with the traditional single-type basis functions, this paper innovatively combines seven types of nonlinear observation functions, including cubic nonlinearity, square nonlinearity, exponential decay, trigonometric function oscillation, and logarithmic function. Through the function selection strategy based on the typical nonlinear characteristics of power electronic systems, the Koopman operator’s ability to capture the strong nonlinear dynamics of power electronic systems is significantly enhanced.
• A two-stage state reconstruction framework based on least squares regression was designed. A post-regression mapping was introduced based on the standard Koopman method to achieve an accurate transformation from the high-dimensional observation space to the original state space, solving the problem of insufficient state reconstruction accuracy in traditional methods and providing a more reliable numerical tool for nonlinear system analysis.
• A modal analysis method based on SVD truncation was adopted. The singular value decomposition was used to automatically screen the dominant modes. The eigenvalue analysis was combined to identify the dynamic patterns of the system, providing a data-driven analysis tool for the stability assessment of smart transformer areas.

2. Basic Architecture of the Smart Station Area

The smart distribution network stations constructed in this study integrate solar photovoltaic (PV) power sources, wind turbines, battery energy storage systems (BESSs), hydrogen fuel cells (HFCs), and traditional synchronous generators (SGs). It also incorporates the control logic of power electronic devices and embeds the power flow equations of the station area network. This architecture not only combines multiple types of power sources to leverage their respective advantages but also employs an adaptive dimension-lifting linear dynamic model based on Koopman operator theory to comprehensively capture potential nonlinear characteristics within the system.

By designing high-dimensional observation function sets and applying principal component analysis (PCA), the model emphasizes the dominant dynamic modes of the system, enabling efficient analysis and dimensionality reduction for real-time data reconstruction. This ensures precise online modeling even under islanded operation conditions. Ultimately, smart distribution network stations optimize the coordinated scheduling of internal resources while balancing renewable energy utilization, flexible power electronic control, and power flow constraints. This approach significantly enhances the stability, response speed, and economic efficiency of the smart station area. The structural model of the smart distribution network stations is illustrated in Figure 1.

3. Mathematical Model of the Smart Station Area

In the smart transformer area, to achieve the collaborative optimization and dynamic regulation of multiple types of energy and power electronic equipment, this paper constructs a multi-level and multi-module coupled mathematical model. This model is based on renewable energy sources such as solar photovoltaic and wind power generation, combines the regulation capabilities of BESS, HFC, and SG, and incorporates the standard adaptive control characteristics of power electronic equipment, achieving real-time feedback control of the system’s operating status. The model comprehensively considers the balance of energy supply and demand, the constraints of battery State Of Charge (SOC), the coupling of physical topological power flow, and cost-driven scheduling strategies, providing fundamental support for the safe and stable operation and efficient scheduling of smart transformer areas.

3.1. Solar Photovoltaic Power Model

The solar photovoltaic power generation system builds a model based on the meteorological characteristics of solar radiation and the actual installed capacity, breaking through the simplified assumption of traditional linear interpolation and introducing the intraday radiation pattern and the fluctuation characteristics within an hour, which is more in line with the actual output characteristics.

Assuming the installed capacity of photovoltaic power is $P_{pv,rated}$, the solar radiation within a day varies periodically (the effective radiation period is from 6:00 to 18:00), and the radiation intensity function is:

$$G(t)=\sin ({\displaystyle \frac{\pi (t-6)}{12}})\ge 0$$

(1)

where

$t$ denotes continuous time.

Considering the random fluctuations of photovoltaic output within an hour (such as disturbances caused by cloud cover), the photovoltaic output at any time $t$ is obtained through a three-layer calculation of “radiation intensity-installed capacity-fluctuation correction”, and at the same time, a 24 h modulus operation is utilized to achieve a periodic cycle:

$$P_{pv}(t)=P_{pv,rated}G(t)[1+{\delta }_{pv}randn(1)]Interp(t_h,P_{pv,h}, \mathrm{mod}(\mathrm{t},24))$$

(2)

where

$P_{pv}(t)$ represents the PV power output of the smart station area at time $t$;

${\delta }_{pv}$ represents the hourly fluctuation coefficient of photovoltaic power;

$randn(1)$ represents the random fluctuation simulation operator;

$Interp(\cdot )$ ensures linear interpolation between hourly data points;

$t_h$ represents a 24 h discrete moment;

$P_{pv,h}$ represents the basic output of photovoltaic power at discrete moments within 24 h;

$\mathrm{mod}(t,24)$ indicates the realization of a 24 h cycle loop.

3.2. Wind Turbine Model

The wind turbine model [14] is established based on the physical characteristics of wind speed and power. It combines the entry, rated, and exit wind speed thresholds to reflect the correlation between wind power output and meteorological conditions, avoiding the defect of “no physical meaning” of traditional interpolation methods.

• Wind speed periodic characteristics: The wind speed within a day shows a pattern of being higher at night and stable during the day. The wind speed function is:

$$v(t)=v_0+A\sin ({\displaystyle \frac{\pi (t-t_0)}{T_0}})$$

(3)

where

$v(t)$ represents the wind speed at time $t$;

$v_0$ represents the average wind speed;

$A$ represents the fluctuation range of wind speed;

$t_0$ represents the time offset of the peak wind speed;

$T_0$ represents the period adjustment coefficient.

2.

Wind speed–power segmentation characteristics: Based on the physical principles of wind turbine units, the output varies in three segments with wind speed: cut-in, rated, and cut-out wind speed.

$$P_{wt,base}(t)=\left\{\begin{array}{l}0 , v(t) <v_{ci} or v(t)>v_{co}\\ P_{wt,rated}{\displaystyle \frac{v(t)-v_{ci}}{v_r-v_{ci}}}, v_{ci}\le v(t)<v_r\\ P_{wt,rated} , v_r\le v(t)<v_{co}\end{array}\right.$$

(4)

where

$P_{wt,base}(t)$ represents the base power of wind power generation in the smart substation at time $t$;

$P_{wt,rated}$ represents the installed capacity of the wind turbine;

$v_{ci}$ represents the cut-in wind speed;

$v_r$ indicates the rated wind speed;

$v_{co}$ represents the cutting air velocity.

3.

Hourly fluctuation correction: Considering short-term disturbances such as gusts, the final wind power output is:

$$P_{wt}(t)=P_{wt,base}(t)[1+{\delta }_{wt}randn(1)]Interp(t_h,P_{wt,h},\mathrm{mod}24)$$

(5)

where

$P_{wt}(t)$ represents the output power of wind power generation in the smart substation at time $t$;

${\delta }_{wt}$ represents the hourly fluctuation coefficient of wind power;

$P_{wt,h}$ represents the base output of wind power at discrete moments within 24 h.

3.3. Battery Energy Storage System (BESS) Model

The core function of BESS [15] is to compensate for power gaps. Its scheduling logic combines time period characteristics with SOC safety constraints to ensure that the energy storage system takes into account both lifespan and regulation capacity during “peak shaving and valley filling”.

3.3.1. Objective Function

BESS selects charging and discharging strategies based on the load–renewable energy supply, and demand difference, and time period characteristics:

• The power gap is defined as:

$$\Delta P(t)=P_{load}(t)-(P_{pv}(t)+P_{wt}(t))$$

(6)

where

$\Delta P(t)$ represents the system power imbalance at time $t$, defined as the difference between load demand and total renewable energy output;

$P_{load}(t)$ denotes the load demand power of the smart station area at time $t$.

2.

The time-based charging and discharging strategy is:

During the period when photovoltaic power is sufficient and there is remaining electricity in the smart transformer area, BESS prioritizes charging operations, and its expression is:

$$\left\{\begin{array}{l}\Delta P(t)<0\\ P_{bess}^{ch}(t)=\max (\Delta P(t),-P_{bess}^{\max })\end{array}\right.$$

(7)

where

$P_{bess}^{ch}(t)$ represents the charging power of BESS at time $t$;

$P_{bess}^{\max }$ indicates the maximum allowable charging/discharging power limit.

During peak load periods, when a power gap occurs in the smart transformer area, BESS prioritizes discharging operations, and its expression is:

$$\left\{\begin{array}{l}\Delta P(t)>0\\ P_{bess}^{dis}(t)=\min (\Delta P(t),P_{bess}^{\max })\end{array}\right.$$

(8)

where

$P_{bess}^{dis}(t)$ denotes the discharging power of BESS at time $t$.

3.3.2. Operational Constraints

To ensure safe operation within specified boundaries, the charging/discharging power of BESS must satisfy the following constraints:

$$\left\{\begin{array}{l}\left|P_{bess}^{ch}(t)\right|\le P_{bess}^{\max }\\ \left|P_{bess}^{dis}(t)\right|\le P_{bess}^{\max }\end{array}\right.$$

(9)

The State of Charge (SOC) reflects the current energy storage level of the battery, expressed as:

$$SOC(t+\Delta t)=SOC(t)-{\displaystyle \frac{P_{bess}(t)\Delta t}{E_{bess}}}$$

(10)

where

$SOC(t)$ represents the state of charge at time $t$, bounded within $[0,1]$;

$P_{bess}(t)$ indicates the charging/discharging power (negative for charging, positive for discharging);

$\Delta t$ is the discrete time step for calculating BESS state transitions;

$E_{bess}$ denotes the rated energy capacity of BESS.

BESS maintains adequate regulation capability during prolonged operation while protecting the battery from extreme conditions to extend the battery lifespan and guarantee the operational safety of the smart station area. The SOC must comply with upper and lower limit constraints:

$$SO{C}_{\min }\le SOC(t+\Delta t)\le SO{C}_{\max }$$

(11)

where

$SO{C}_{\min }$ represents the minimum energy threshold to prevent the over-discharge;

$SO{C}_{\max }$ indicates the maximum energy threshold to prevent overcharging.

3.4. Hydrogen Fuel Cell (HFC) Model

In the smart transformer area, HFC [16] serves as a supplementary power supply, making up for the insufficient power of the system after BESS regulation. A cost-driven sharing strategy is adopted, taking into account both the economy and reliability of the system power supply.

The remaining power gap $P_{deficit}(t)$ after BESS regulation is:

$$P_{deficit}(t)=\Delta P(t)-P_{bess}(t)$$

(12)

where

$P_{bess}(t)$ represents the charge and discharge power of the BESS at time $t$.

The output allocation of HFC and SG is based on the optimization of unit generation cost: if the unit cost of HFC is defined as $C_{fc}$ and that of SG as $C_{gen}$. The cost-weighted sharing ratio is:

$$\left\{\begin{array}{l}{\lambda }_{fc}={\displaystyle \frac{C_{gen}}{C_{fc}+C_{gen}}}\\ {\lambda }_{gen}={\displaystyle \frac{C_{fc}}{C_{fc}+C_{gen}}}\end{array}\right.$$

(13)

where

${\lambda }_{fc}$ and ${\lambda }_{gen}$ represent the proportion coefficients of the remaining power gap borne by HFC and SG, respectively.

$C_{fc}$ and $C_{gen}$ represent the unit costs of HFC and SG, respectively.

The actual output of the HFC needs to meet the maximum capacity constraint:

$$P_{fc}(t)=\min (\max (P_{deficit}(t){\lambda }_{fc},0),k{P}_{fc}^{\max })$$

(14)

where

$P_{fc}(t)$ represents the output power of the HFC in the intelligent transformer area’s adaptive dimensional escalation dynamic linear model at time $t$;

$k$ represents the short-term overload coefficient;

$P_{fc}^{\max }$ represents the upper limit of the maximum output of the HFC in the adaptive dimensional escalation dynamic linear model of the smart transformer area at time $t$.

3.5. Synchronous Generator (SG) Model

As a traditional backup power supply, SG fills the gap when the output of HFC is still insufficient. It works in tandem with HFC to achieve the dual goals of “economy and reliability” while also playing a core role in maintaining the stability of the system frequency.

Based on the cost-weighted sharing ratio of Equation (13), the output of SG is:

$$P_{gen}(t)=\min (\max (P_{deficit}(t){\lambda }_{gen},0),P_{gen}^{\max })$$

(15)

where

$P_{gen}(t)$ represents the output power of SG at time $t$;

$P_{gen}^{\max }$ represents the maximum output limit of SG at time $t$.

The final system power balance needs to meet:

$$P_{load}(t)=P_{pv}(t)+P_{wt}(t)+P_{bess}(t)+P_{fc}(t)+P_{gen}(t)$$

(16)

3.6. Power Electronic Device Control Logic

3.6.1. Foundation Sag Control

In the smart transformer area system, power electronic devices are responsible for controlling and regulating the output of distributed energy and balancing power fluctuations. The standard adaptive Virtual Synchronous Generator (VSG) control is adopted to imitate the inertia and damping characteristics of traditional synchronous machines. The parameters are set in accordance with IEEE and GB/T standards to enhance the frequency, voltage stability, and dynamic adaptability of the system.

VSG adopts a droop control mechanism, converting the power deviation of the system into adjustments for frequency and voltage. The expression for frequency drop is:

$$\left\{\begin{array}{l}\Delta f(t)=-D_p(P_{inj}(t)-P_{ref}(t))\\ P_{ref}(t)=P_{pv}(t)+P_{wt}(t)+P_{bess}(t)\\ +P_{fc}(t)+P_{gen}(t)\end{array}\right.$$

(17)

where

$\Delta f(t)$ represents the frequency adjustment amount caused by the active power deviation at time $t$;

$D_p$ represents the frequency drop coefficient;

$P_{inj}(t)$ represents the active power injected at time $t$;

$P_{ref}(t)$ represents the system reference power at time $t$.

The expression of voltage sag is:

$$\Delta V(t)=-D_q{Q}_{inj}(t)$$

(18)

where

$\Delta V$ represents the voltage adjustment caused by the reactive power deviation at time $t$;

$D_q$ represents the voltage sag coefficient;

$Q_{inj}$ represents the reactive power injected at time $t$.

3.6.2. Adaptive Inertia and Damping Control

To enhance transient stability, the adaptive parameter adjustment based on standard thresholds is introduced. The core logic is “increasing inertia in transient states and decreasing inertia in steady states”.

• Frequency change rate calculation: By calculating the difference in frequency deviation between the current moment and the previous moment, combined with the time step, the frequency change rate is calculated to reflect the intensity of the system’s transient process:

$${\displaystyle \frac{df}{dt}}={\displaystyle \frac{\left|\Delta f(t)-\Delta f_{prev}\right|}{\Delta t}}$$

(19)

where

$\Delta f_{prev}$ represents the frequency deviation at the previous moment.

2.

Adaptive virtual inertia adjustment: This is adjusted according to the system operation status. The core logic is that “transient inertia increases and steady-state inertia decreases.”

$$J(t)=\left\{\begin{array}{l}{k}_{J1}{J}_{base}, \left|\Delta f(t)\right|>{\left|\Delta f\right|}_{th}\\ k_{J2}{J}_{base},{ (\mathrm{df}/\mathrm{dt})>(\mathrm{df}/\mathrm{dt})}_{th}\\ J_{base}, \mathrm{Other} \mathrm{working} \mathrm{conditions}\end{array}\right.$$

(20)

where

$k_{J1}$ and $k_{J2}$ represent the inertia amplification coefficients, respectively;

$J_{base}$ represents the basic virtual inertia;

${\left|\Delta f\right|}_{th}$ represents the frequency deviation threshold;

${(\mathrm{df}/\mathrm{dt})}_{th}$ represents the threshold of the rate of frequency change.

3.

Adaptive damping coefficient adjustment: $D_{ad}$ is adjusted according to the system operation conditions in different scenarios. The core logic is “transient strong damping and steady-state weak damping”.

$$D(t)=\left\{\begin{array}{l}{k}_{D1}{D}_{base}, \left|\Delta f(t)\right|>{\left|\Delta f\right|}_{th}\\ k_{D2}{D}_{base},{ (\mathrm{df}/\mathrm{dt})>(\mathrm{df}/\mathrm{dt})}_{th}\\ D_{base}, \mathrm{Other} \mathrm{working} \mathrm{conditions}\end{array}\right.$$

(21)

where

$k_{D1}$ and $k_{D2}$ represent the damping amplification coefficients, respectively;

$D_{base}$ represents the basic damping coefficient.

3.6.3. Final VSG Control Equation

Adaptive parameters are integrated into the VSG frequency control while keeping the voltage control logic unchanged:

$$\left\{\begin{array}{l}{\omega }_{\mathrm{vsg}}(t)={\omega }_{norm}+{\displaystyle \frac{\Delta f(t)}{J(t)}}-D(t)\times (P_{inj}(t)-P_{ref}(t))\\ V_{vsg}(t)=V_{nom}+\Delta V(t)\end{array}\right.$$

(22)

where

${\omega }_{vsg}(t)$ represents the actual frequency of VSG under control at time $t$;

${\omega }_{nom}$ represents the rated frequency of the system;

$V_{vsg}(t)$ represents the voltage setting value of VSG under control at time $t$;

$V_{nom}$ represents the rated voltage of the system.

Finally, under the VSG control strategy, the expression of the state equation for the dynamic change in node voltage $V=V_r+j{V}_i$ is:

$$\left\{\begin{array}{l}{\displaystyle \frac{d{V}_{re}(t)}{dt}}={\omega }_{vsg}(t)V_{re}(t)-V_{im,vsg}(t)V_{im}(t)\\ {\displaystyle \frac{d{V}_{im}(t)}{dt}}={\omega }_{vsg}(t)V_{im}(t)+V_{re,vsg}(t)V_{re}(t)\end{array}\right.$$

(23)

where

$V_{re}(t)$ and $V_{im}(t)$ represent the real and imaginary parts of the voltage at time $t$, respectively.

$V_{im,vsg}(t)$ and $V_{re,vsg}(t)$ represent the real and imaginary parts of the target voltage $V_{vsg}$ at time $t$, respectively.

3.7. Power Flow Equations

The power flow calculation is based on the physical significance and numerical stability of the admittance matrix of the 33-node distribution network topology, which is in line with the actual grid structure of the transformer area. The complex admittance matrix $Y_{bus}$ of a single line is:

$$Y_{bus}={\displaystyle \frac{1}{R+jX}}$$

(24)

where

$R$ represents the line resistance;

$X$ represents the line reactance.

The self-admittance of node $i$ is the sum of the admittances of all the lines connected to this node:

$$Y_{ii}={\displaystyle \sum Y_{bus}}$$

(25)

If node $i$ is directly connected to node $j$, the mutual admittance is the negative value of the line admittance:

$$Y_{ij}=-Y_{bus}$$

(26)

The injection current of the $i$ node is:

$$I_i(t)={\displaystyle \sum _{j=1}^n{Y}_{ij}{V}_j(t)}$$

(27)

where

$V_j(t)$ represents the complex voltage of node $j$.

The injection complex power $S_i$ of the $i$ node is:

$$S_i(t)=V_i(t)\cdot I_i^{*}(t)$$

(28)

where

$V_i(t)$ represents the complex voltage of node $i$;

$I_i^{*}(t)$ represents the conjugate complex number of $I_i(t)$.

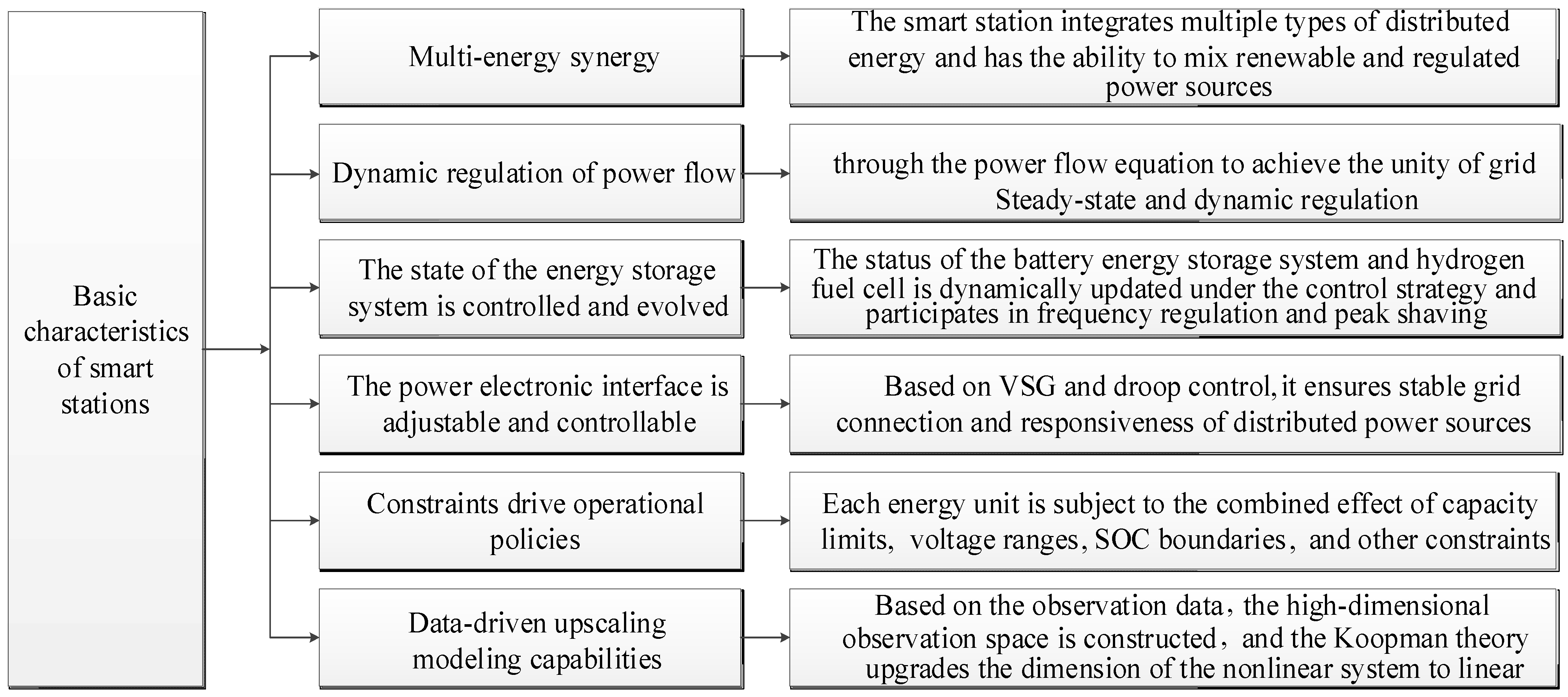
In summary, based on the core principles of nonlinear dynamic characteristic modeling, the mathematical model of the smart station area should possess the features illustrated in Figure 2. These include multi-energy coordination, dynamic power flow regulation, controlled evolution of energy storage system states, adjustable and controllable power electronic interfaces, constraint-driven operation strategies, and data-driven dimensionality augmentation modeling capabilities. By integrating the output characteristics of various distributed energy resources, observation functions, and dynamic modes, the model establishes an efficient and reliable operational and analytical platform for the station area.

4. Adaptive Ascending Linear Dynamic Modeling Based on Koopman Theory

4.1. Fundamental Concepts of Koopman Theory

The Koopman operator is a theory that describes the evolution of Hamiltonian dynamical systems in terms of quantity measurement. Its function is to transform finite-dimensional nonlinear systems into infinite-dimensional linear systems. This theory has the ability to characterize the dynamic evolution process of nonlinear systems, and it can transform the originally finite-dimensional nonlinear system into an infinite-dimensional linear system for research. Therefore, modeling methods based on the Koopman operator have received widespread attention [17,18].

Consider a continuous nonlinear dynamical system evolving in the state space $\mathit{ℳ}\subseteq {ℝ}^n$. Its state-space representation can be expressed as:

$$\dot{x}=f(x)$$

(29)

where

$x\in \mathit{ℳ}$ denotes the $n$ dimensional state variable on a smooth manifold, encompassing quantities such as voltage magnitude and phase angle.

The mapping $f$: $\mathit{ℳ}\to \mathit{ℳ}$ describes the temporal evolution of the state variables in the dynamical system.

Define a complex-valued scalar function $g$: ${ℝ}^n\to C$ on the state space as an observable function, representing the mapping from state variables to observables. The Koopman operator $\kappa$ is a linear operator acting on the observable function $g$ such that:

$${\displaystyle \frac{d}{dt}}g(x(t))=\kappa g(x(t))$$

(30)

where

$g(x)$ denotes one or a set of observable functions, representing the result of a nonlinear transformation applied to $x$.

$\kappa$ is the Koopman operator, an infinite-dimensional linear operator acting on observable functions, capable of capturing global dynamic information in nonlinear systems.

To convert the nonlinear system into a linear representation, a nonlinear mapping—termed the ascending operator—is defined as:

$$y=\theta (x)$$

(31)

where the new variable $y$ approximately satisfies a linear dynamic:

$$\dot{y}=Ay$$

(32)

Here, $A$ represents the finite-dimensional approximation of the Koopman operator within the selected observable subspace.

4.2. Construction of Koopman Dimensionality Ascension

The nonlinear mapping is achieved by constructing diverse observable functions, expressed as:

$$\left\{\begin{array}{l}{g}_1(x)=x\\ g_2(x)=x{\left|x\right|}^2\\ g_3(x)=x^2\\ g_4(x)=x\exp (-\left|x\right|)\\ g_5(x)=x\sin (\left|x\right|)\\ g_6(x)=x\cos (\left|x\right|)\end{array}\right.$$

(33)

where

$x$ denotes the original state vector;

$g_1(x)=x$ preserves the original state variables directly, retaining primary system information;

$g_2(x)=x{\left|x\right|}^2$ introduces third-order nonlinearity by multiplying the state variables by their squared norm;

$g_3(x)=x^2$ captures quadratic nonlinear effects through component-wise squaring;

$g_4(x)=x\exp (-\left|x\right|)$ enhances local smoothness via exponential decay;

$g_5(x)=x\sin (\left|x\right|)$ and $g_6(x)=x\cos (\left|x\right|)$ employ trigonometric functions to characterize the system’s periodicity and oscillations.

Thus, the constructed high-dimensional observable vector is formulated as:

$$y(x)=\left\{\begin{array}{l}{g}_1(x)\\ g_2(x)\\ g_3(x)\\ g_4(x)\\ g_5(x)\\ g_6(x)\end{array}\right.$$

(34)

Here, $y(x)$ defines a nonlinear mapping:

$$\theta :{ℝ}^n\to {ℝ}^m,m>n$$

(35)

where

$m$ represents the number of observable functions in $\theta$;

$m>n$ indicates that the new observable space has a significantly higher dimensionality than the original state space, effectively “linearizing” nonlinear relationships in this extended space.

To implement this, the original data matrix $X$ is expanded into:

$$Y=\left[\begin{array}{l}X\\ X{\left|X\right|}^2\\ X^2\\ X\exp (-\left|X\right|)\\ X\sin (\left|X\right|)\\ X\cos (\left|X\right|)\end{array}\right]$$

(36)

To avoid numerical overflow and information loss, the observation functions in Equation (26) are standardized:

• Polynomial function: By using state variable normalization, let the normalized state vector $x_{norm}=(x-x_{\min })/(x_{\max }-x_{\min })$, where $x_{\min }$ and $x_{\max }$ represent the minimum and maximum values of the original state vector, respectively, and compress the input range to $[0,1]$.
• Exponential function: Introduce the scaling factor $\alpha =0.15$ (determined through cross-validation) to balance the attenuation rate and information retention.
• Trigonometric functions: Add amplitude constraints to avoid high-frequency oscillations.

Based on the modal energy contribution screening function, the steps are as follows:

• Calculate the Koopman mode energy corresponding to each observation function.
• Sort functions in descending order by energy proportion, with a cumulative energy proportion reaching 99.5%, to form a sparse function set.
• Define the sparsity index S as the filtered function/the original function. When S < 0.5, the energy threshold needs to be recalculated to avoid information loss due to excessive sparsity.

In the construction of the data matrix in Equation (29), a regularization term is introduced and corrected to:

$$\tilde{X}=X+\lambda I$$

(37)

where

$\lambda$ represents the regularization parameter;

$I$ represents the identity matrix.

Noise robustness is achieved through data preprocessing, with a third-order moving average filter applied to the original state variable x:

$$\overline{x}(t)={\displaystyle \frac{x_{t-2}+2x_{t-1}+x_t}{4}}$$

(38)

where

$\overline{x}(t)$ represents the filtered state variable at time $t$;

$x_t$ represents the original state vector at time $t$;

$x_{t-1}$ and $x_{t-2}$ represent the original state vectors of the previous moment and the previous two moments, respectively.

4.3. Linear Approximation Based on Dynamic Mode Decomposition (DMD)

There are many methods for finite-dimensional approximation of the Koopman operator. This paper chooses the method of Dynamic Mode Decomposition (DMD) [19,20].

Following the dimensionality ascension process, the new variable $y$ satisfies an approximate linear dynamic model expressed as:

$$y(t+\Delta t)\approx Ay(t)$$

(39)

where

$y(t)$ represents the ascended state at time step $t$;

$A$ denotes a linear transformation matrix characterizing the temporal evolution of $y$.

To approximate the matrix A from data, the Dynamic Mode Decomposition (DMD) method is employed. The specific implementation steps are as follows:

• Data Matrix Construction:

To capture low-frequency dominant modes, a delay embedding matrix $X_{aug}$ is constructed using the Hankel matrix formulation. Assuming a delay step number of r, we have:

$$X_{aug}=\left[\begin{array}{c}X(:,1:T-\tau +1)\\ X(:,2:T-\tau +2)\\ ⋮\\ X(:,\tau :T)\end{array}\right]$$

(40)

where

$X(:,1:T-\tau +1)$ means taking the first $T-\tau +1$ columns of $X$ as the first delay layer;

$T$ represents the total number of time sampling points.

The reshaped delay embedding matrix $X_{aug}$ is then partitioned into $X_1$ and $X_2$, corresponding to temporally adjacent delay embedding vectors:

$$\left\{\begin{array}{l}{X}_1=X_{aug}(:,1:end-1)\\ X_2=X_{aug}(:,2:end)\end{array}\right.$$

(41)

where

$1:end-1$ represents, in the delay-embedded data matrix, from the first column to the second-last column;

$2:end$ represents from the second column to the last column.

2.

Singular Value Decomposition (SVD):

The matrix $X_1$ undergoes SVD:

$$X_1=U{\mathrm{SV}}^T$$

(42)

where

$U$ contains orthogonal basis vectors representing principal data directions $U\in {ℝ}^{m\times r}$;

$S$ is a diagonal matrix of singular values indicating modal energy levels $S\in {ℝ}^{r\times r}$;

$V$ contains the right singular vectors $V\in {ℝ}^{(T-1)\times r}$;

$r$ denotes the truncation order.

3.

Low-dimensional Linear Operator Construction:

Using SVD results, the reduced-order linear operator is constructed as:

$$\tilde{A}=U^T{X}_{2}V{S}^{-1}$$

(43)

where

$\tilde{A}$ represents the approximate Koopman operator in the reduced-order space;

$U^T$ is the conjugate transpose of $U$;

$S^{-1}$ denotes the inverse of the singular value matrix.

4.

Eigen decomposition and Mode Recovery:

Performing eigenvalue decomposition on $\tilde{A}$ yields:

$$\tilde{A}W=W\Lambda$$

(44)

where

$W$ contains eigenvectors representing modal characteristics in the reduced space;

$\Lambda$ is a diagonal matrix whose elements ${\lambda }_i$ are eigenvalues, reflecting each mode’s growth/decay and oscillatory properties.

The high-dimensional Koopman modes are recovered as:

$$\varphi =X_{2}V{S}^{-1}W$$

(45)

where $\varphi$ is the high-dimensional modal matrix, with each column representing a dynamic mode in the ascended space.

5.

Continuous-time Frequency Calculation:

The continuous-time characteristic frequencies are derived from discrete eigenvalues ${\lambda }_i$:

$${\omega }_i={\displaystyle \frac{\ln ({\lambda }_i)}{\Delta t}}$$

(46)

where

${\omega }_i$ represents the characteristic frequency of the $i$ dynamic mode;

$\Delta t$ denotes the sampling interval.

6.

Initial Condition Expansion and Signal Reconstruction:

For the initial time $y(0)$, the least squares projection on Koopman modes gives:

$$b={\varphi }^{†}y(0)$$

(47)

where

$b$ represents the modal expansion coefficients, indicating the contribution of each Koopman mode to the initial state;

${\varphi }^{†}$ denotes the Moore–Penrose pseudoinverse of matrix $\varphi$.

Finally, the reconstructed expression at time $t$ is given by:

$$y(t)\approx \varphi diag(e^{\omega t})b$$

(48)

where

$diag(e^{\omega t})$ is a diagonal matrix with elements $e^{{\omega }_{i}t}$, describing the temporal evolution of each mode;

$y(t)$ represents the reconstructed high-dimensional observation vector.

4.4. Online Adaptive Dimensionality Upgrade Model

A sliding window of length $N$ (taking 12 time steps, corresponding to 1 h) is adopted, and the data matrix within the window is defined as:

$$X_{win}=[x_t,x_{t-1},\dots ,x_{t-N+1}]$$

(49)

where

$x_{t-N+1}$ represents the original state vector at the earliest moment.

When the new data $x_{t+1}$ arrives, the update window is:

$$X_{win}^{new}=[x_{t+1},X_{win}(:,1:N-1)]$$

(50)

Based on the historical SVD result $X_{win}=U{\displaystyle \sum V^T}$, the calculation steps for the incremental SVD of the new window data matrix $X_{win}^{new}=[a,X_{win}(:,1:N-1)]$ are:

• Calculate the projection residual $r=a-U{U}^{T}a$ of the new vector $a$ in the historical left singular space.
• If ${‖r‖}_2>\epsilon$, update the left singular matrix: $U_{new}=[U,r/{‖r‖}_2]$.
• Update the singular value matrix. The right singular matrix $V_{new}$ is reconstructed through QR decomposition.
• Calculate the modal contribution of each observation function.
• Calculate the Koopman operator to complete the model update.

In summary, this paper proposes an adaptive dimension-lifting linear dynamic model based on Koopman theory. By constructing diverse nonlinear observable functions (including higher-order polynomials, exponentials, and periodic functions) combined with time-delay embedding, we achieve high-dimensional linearization of the original nonlinear system states. Through truncated SVD and DMD algorithms, the model adaptively identifies dominant modes and computes the Koopman operator, thereby establishing a linear evolution mapping for the system in the lifted dimensional space. The workflow of this Koopman theory-based adaptive dimension-lifting linear dynamic model is illustrated in Figure 3.

5. Case Studies

This paper takes the IEEE 33-node standard test system as the research object. This system is the benchmark network for power system research. The network topology and basic parameters are derived from the Matpower public database, covering five types of multi-functional equipment: solar photovoltaic, wind power generation, BESS, HFC, and SG. The simulation time domain selects 0:00 to 23:00 of the next day, with a total of 24 time intervals. The load data is based on the typical daily variation pattern of residential electricity consumption, and the profiles of photovoltaic and wind power generation refer to the standard typical daily data provided by NREL. The specific parameter settings are shown in

Table 1. System main parameter settings.

Parameter	Value
Number of nodes	33
The number of branch roads	32
Reference power (MVA)	100
Reference voltage (kV)	12.66
BESS charge/discharge efficiency	0.9
SOC Min	0.15
SOC Max	0.95

.

The system load balance is shown in Figure 4. During the period from 0:00 to 04:00, the photovoltaic system has no output. At this stage, the load demand is mainly borne by the output of the wind turbine, the power supply from the fuel cell, and a small amount of generator power. The battery charging and discharging show slight fluctuations, and the battery state of charge remains in the range of 0.75 to 0.85, indicating that the battery has not undergone large-scale charging and discharging operations. During the period from 05:00 to 12:00, the photovoltaic output gradually increases to approximately 300 kW, and the wind turbine output remains at a relatively high level. The system’s power generation exceeds the load demand, and the battery begins to charge, with the SOC gradually rising from around 0.85. During the period from 12:00 to 15:00, the photovoltaic and wind turbines maintain a high-output state continuously, significantly exceeding the load demand, and the SOC rises to 0.95. During the period from 15:00 to 20:00, the output of photovoltaic power gradually decreases, and the output of wind turbines also drops. When the system’s power generation capacity is insufficient to fully cover the load demand, the battery begins to discharge, and the SOC drops accordingly. At the same time, the power of fuel cells and generators participates in load compensation. After 20:00, the photovoltaic output approaches zero, while the load demand remains at a certain level. The battery continues to discharge, and the SOC further drops. At this stage, the load demand is mainly met by the output of the wind turbine, the power supply of the fuel cell, and the power of the generator, ensuring the stable operation of the system.

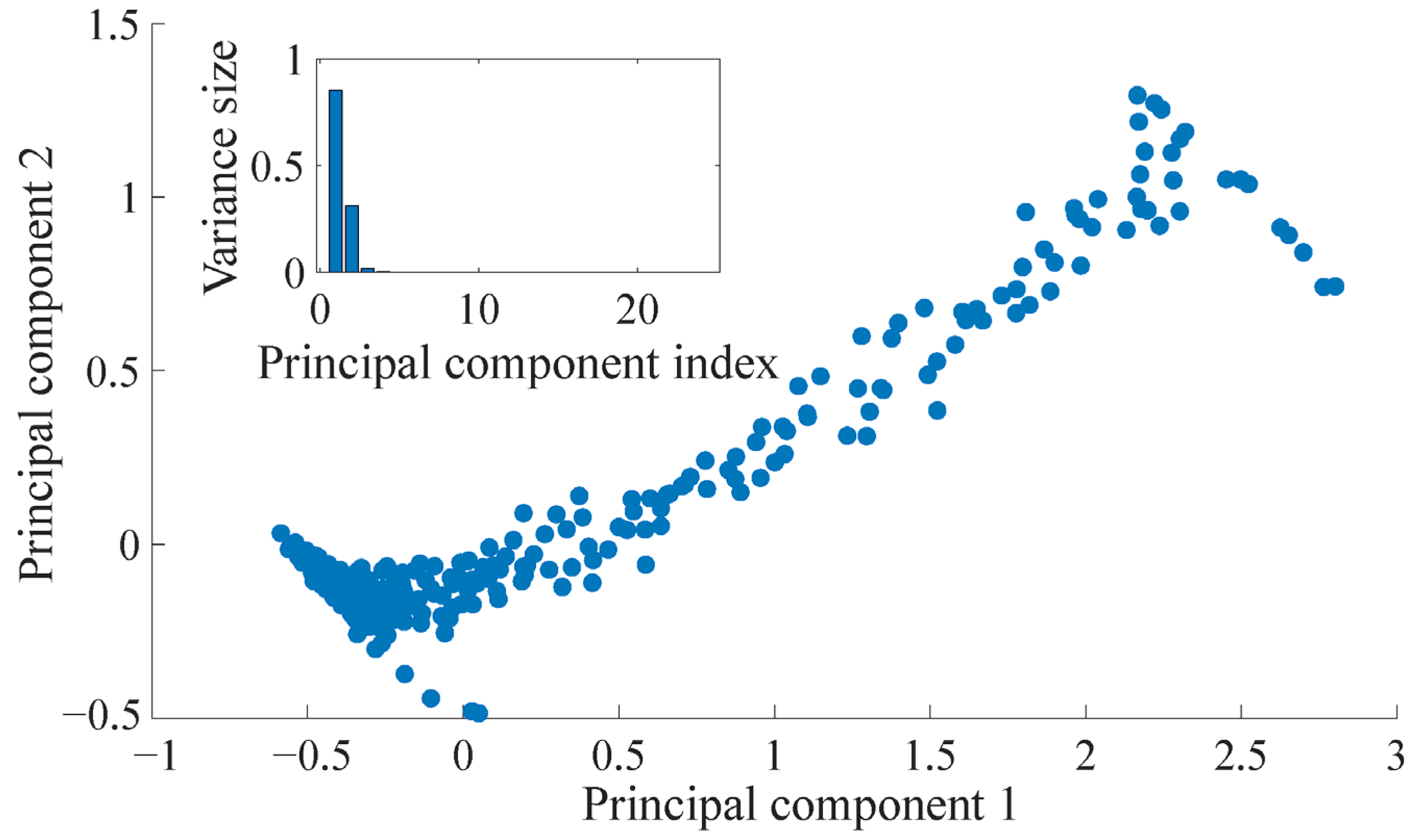
Principal component analysis is shown in Figure 5. Among them, the principal component 1 on the x-coordinate and the principal component 2 on the y-coordinate are dimensionless.

Figure 5 illustrates the primary trends and disturbance features of node voltages in the smart station area. The scatter plot shows that Principal Component 1 (PC1) corresponds to voltage gradient variations, with left-to-right increments reflecting spatial transitions from low- to high-voltage zones. PC2 captures non-uniformities caused by load fluctuations. The variance bar chart quantifies each component’s contribution: PC1 explains 70–90% of spatial variations, while PC2, though smaller, remains significant. This confirms that a two-dimensional reduction effectively preserves data features, reduces computational complexity, and suppresses random noise interference in DMD and Koopman analyses. Compared to the raw high-dimensional data, PCA achieves an optimal balance between information retention and computational efficiency, enhancing the stability and accuracy of the dynamic mode extraction.

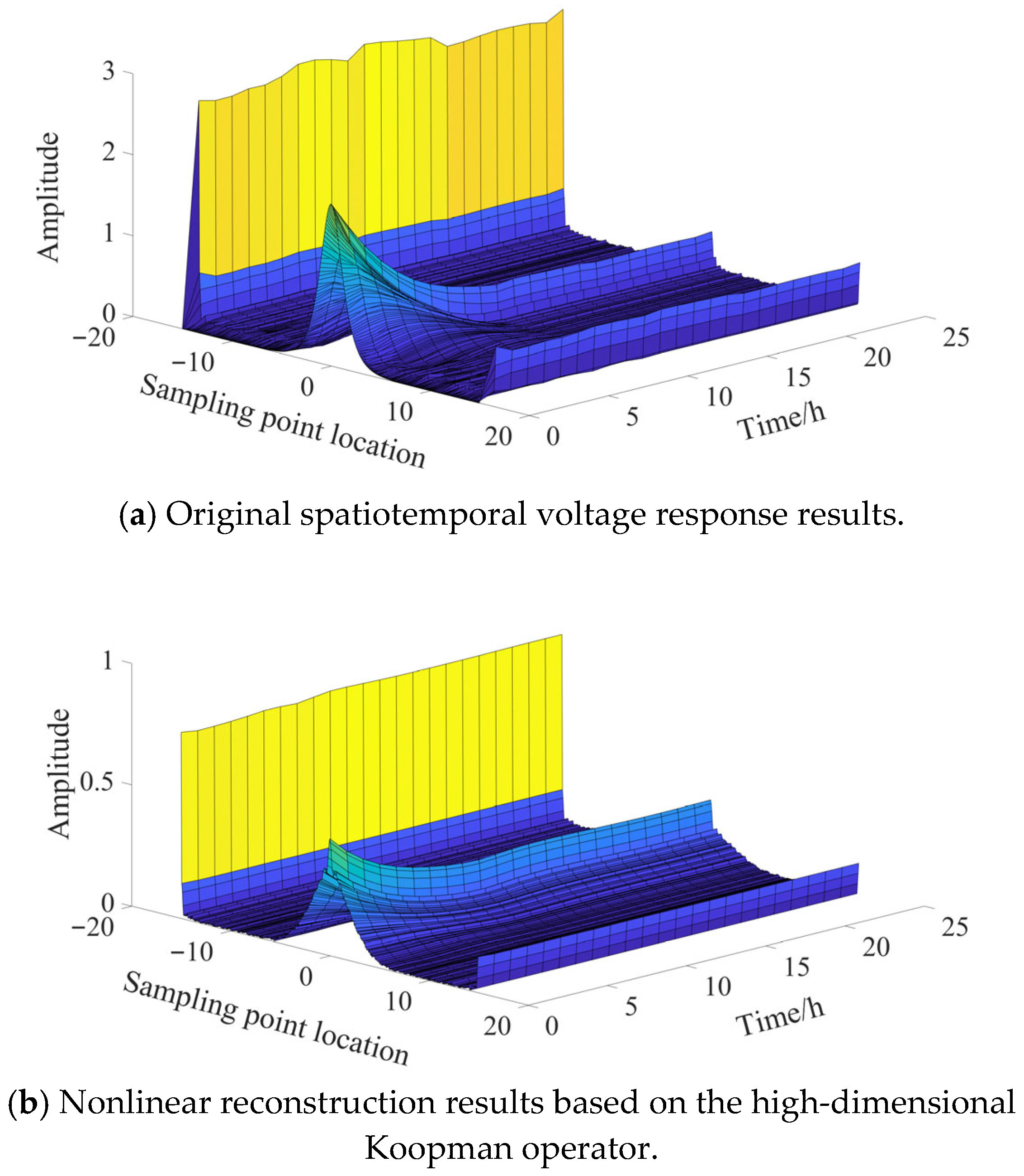
Figure 6 shows the reconstruction results of the original data and Koopman. Among them, the position and amplitude of the sampling points on the coordinate axes are dimensionless.

As shown in Figure 6a, the original spatiotemporal voltage response exhibits multimodal coupling characteristics. The high-frequency components decay slowly in the early stage, there is obvious oscillation in the middle stage, and only weak noise remains in the later stage. Figure 6b shows that the nonlinear reconstruction results based on the high-dimensional Koopman operator significantly improve the fitting accuracy. It is more in line with the original data in terms of the capture process, pulse peak, and phase control, with a peak time error of less than 0.1 h. Moreover, the overall response is smoother, and the noise suppression is more effective, demonstrating a better modeling ability for the nonlinear dynamics of the system.

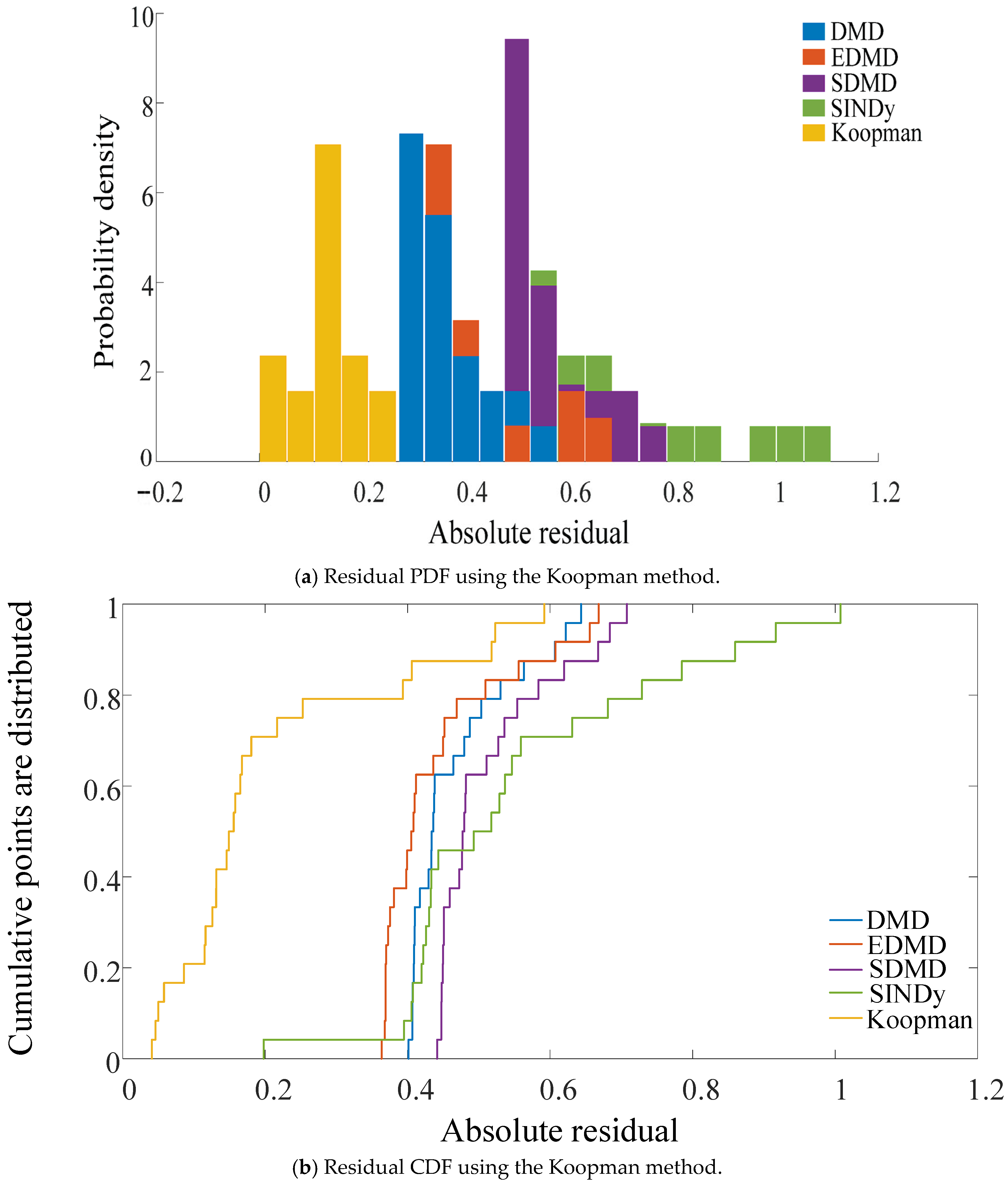
The absolute distribution of the residual is shown in Figure 7. Among them, the probability density and cumulative distribution of the vertical coordinate are dimensionless. The expression of the absolute residual is:

$$r(t)=\left|r(m,t)-o(m,t)\right|$$

(51)

where

$r(m,t)$ represents the reconstructed value;

$o(m,t)$ represents the original value.

The residual PDF is shown in Figure 7a. The peak probability density of the proposed Koopman method is concentrated in the 0–0.2 range with a relatively small absolute residual, demonstrating an advantage in fitting samples with low residuals. The probability density distribution of other methods is relatively more inclined towards the high residual interval. The residual CDF is shown in Figure 7b. The cumulative distribution curve of the Koopman method rises the earliest and fastest. Within the interval with a smaller absolute residual, its cumulative probability increases rapidly, indicating that the proportion of samples with a smaller residual is significantly higher under this method. However, the cumulative curves of other methods, such as DMD, rise more slowly, and the proportion of low-residual samples is lower. In conclusion, the Koopman model performs better in error control and fitting accuracy and can cover more low-residual samples.

The RMSE error of the model is shown in Figure 8. The calculation formula for RMSE is:

$$\mathrm{RMSE}(t)\hspace{0.17em}=\sqrt{(1/n)\times {\displaystyle \sum {(r(x,t)-o(x,t))}^2}}$$

(52)

where

$r(x,t)$ represents the reconstructed value;

$o(x,t)$ represents the original value.

The RMSE error of the model is shown in Figure 8. The simulation mainly compared the performance of the Koopman model with other models under the RMSE index. Four typical moments of the day, namely 00:00, 08:00, 14:00, and 18:00, were selected. The selected time covers the low load period at night, the peak photovoltaic output period during the day, the afternoon period when photovoltaic output decreases and load is relatively high, and the evening peak electricity consumption period, which can represent different operating conditions. At the same time, these periods often correspond to voltage fluctuations or inflection points, which are conducive to revealing the evaluation characteristics of the model under high-fluctuation working conditions. The performance comparison of the Koopman model with other models is shown in

Table 2. Comparison of model RMSE indicators.

Indicator/Method	DMD	EDMD	SINDY	SDMD	Koopman
Average RMSE	0.1579	0.1858	0.3407	0.1579	0.1419
Maximum RMSE	0.1941	0.5385	0.3539	0.1941	0.1915

.

Based on the analysis of the RMSE error of the model, the performance differences of several methods were evaluated from the perspective of modal characteristics. By comparing the distribution of eigenvalues extracted from the dynamic data of the intelligent transformer region by Koopman and other methods, the overall dynamic trend reflected by the error curve was verified, highlighting Koopman’s unique capabilities in modal capture and system stability.

The eigenvalue distribution is shown in Figure 9. The proposed Koopman method linearizes the nonlinear dynamics through an adaptive high-dimensional observation mapping, resulting in more concentrated eigenvalues with smaller modulus values, demonstrating better stability, reconstruction accuracy, and robustness. In contrast, although the SINDY method can obtain a concise nonlinear model through sparse recognition, its performance is highly dependent on the completeness of the pre-selected basis functions, and it has poor stability in high-dimensional or noisy scenarios. The linear approximation ability of DMD is limited. EDMD relies on the selection of artificial basis functions. Although SDMD is sparse, it is prone to unstable modes when there is noise or insufficient samples.

6. Conclusions

This study addresses the dynamic characteristics and stability challenges of smart station areas under the combined effects of uncertain renewable energy output and power electronic control logic. A Koopman theory-based adaptive dimensionality-lifting linear dynamic modeling method is proposed and validated through a 24 h case study. The key conclusions are as follows:

• Dynamic Modeling Framework for Smart Station Areas: Under conditions of uncertain PV/wind output and load fluctuations, the proposed framework achieves adaptive load regulation and maximizes energy utilization in BESS through dynamic power allocation and SOC constraint optimization.
• The reconstruction effect of the adaptive dimensionality enhancement modeling method based on Koopman theory on the system is verified through numerical examples. Compared with methods such as DMD, EDMD, SDMD, and SINDY, the Koopman model has the lowest average and maximum RMSE errors, demonstrating its advantages in terms of accuracy and robustness in nonlinear feature extraction and system dynamic response modeling.
• The results of the eigenvalue distribution show that the proposed method has a significant effect in extracting the dynamic characteristics of the system and improving its stability. Compared with methods such as DMD, EDMD, SDMD, and SINDY, the Koopman model more effectively retains key modes and avoids excessive attenuation, fully demonstrating the advantages of the proposed method in dynamic modeling and system stability.

Future research will deepen multi-scale dynamic modeling, break through resilience strategies in extreme scenarios, develop lightweight real-time early warning algorithms, expand multi-energy collaborative control, and promote the engineering application of smart transformer area modeling.