Feature Extraction from Flow Fields: Physics-Based Clustering and Morphing with Applications ^†

Abstract

The high dimensionality of flow fields obtained from Computational Fluid Dynamics (CFD) poses major challenges for Machine Learning (ML), especially when the scarcity of training data combines with strong geometric variability. Most existing ML approaches for inference from CFD data rely on expert-defined features, primarily quantities computed over manually selected regions. However, this strategy does not scale well, since regions must be redefined for each new geometry, requiring expert knowledge and significant effort. To overcome this limitation, we introduce two complementary methods to extract features from CFD flow fields: the first identifies meaningful flow regions by clustering features derived from the governing equations; the second employs mesh morphing to align each flow field onto a common reference geometry, enabling consistent use of expert-defined regions across cases. Both require minimal human intervention on new samples and ensure scalability across diverse CFD scenarios. We validate our methods on two distinct applications: first, by accurately identifying airfoil shapes and geometric defects; second, by classifying nasal pathologies from 3D CFD simulations of human upper airways reconstructed from CT scans. Both methods show robustness and high accuracy, highlighting their potential for automated, generalizable, and scalable CFD analysis within ML frameworks.

1. Introduction

Computational Fluid Dynamics (CFD) plays a central role in modeling, analyzing, and optimizing fluid flows in a wide spectrum of scientific and engineering applications [1], including aerospace or automotive design [2,3,4,5], energy systems optimization, and biomedical diagnostics [6]. By numerically solving the Navier–Stokes equations on discretized and often highly complex geometries, CFD provides detailed spatio-temporal fields of velocity, pressure, and turbulent quantities. Typically, in real-world applications, these simulations involve dense discretizations of the spatial (2D or 3D) domain, producing highly detailed and high-dimensional flow data, often resulting in tens of Gigabytes per simulation. The combination of high dimensionality and variability in the CFD data hinders the application of ML models, which require compact, structured, and comparable input representations.

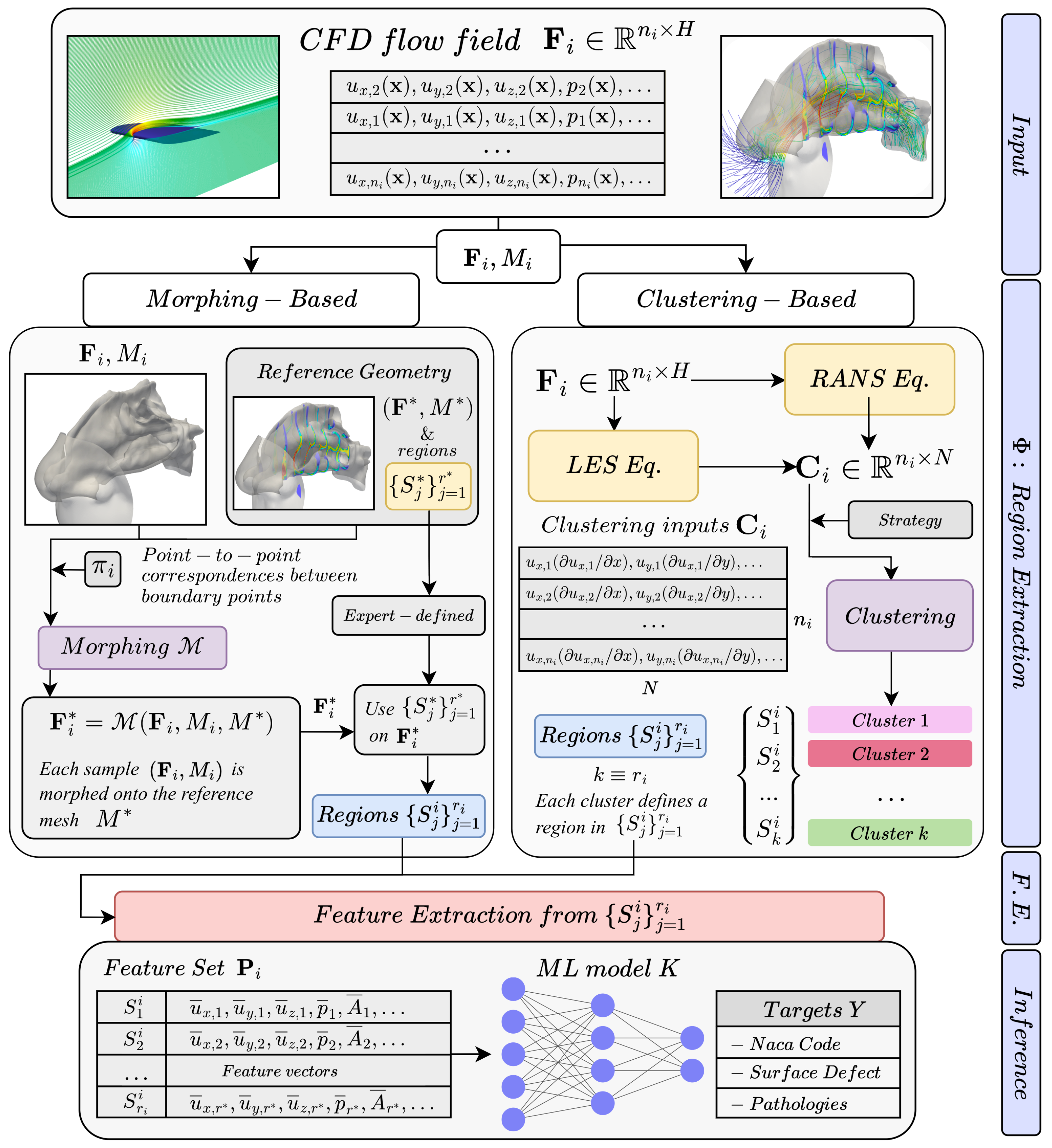
Most existing ML approaches for inference from CFD data are tailored to scenarios with large datasets and limited geometric variability [7,8,9]. We target the opposite situation, where limited training data and high geometric variability across samples make feature extraction particularly challenging. In this context, the classical way to feed CFD data into an ML model relies on handcrafted features designed by domain experts, who manually define regions of interest within the flow field and extract selected physical quantities as regional averages (see Figure 1). These aggregated features are then classified using standard ML models. Averaging flow quantities over the selected regions serves as a dimensionality reduction step that extracts the most relevant information based on prior knowledge. Although intuitive and effective, this process introduces critical limitations: the selected regions must be consistently identified across all simulated flow fields, which becomes non-trivial when geometries vary.

A representative example is the work of Schillaci et al. [10], where flow features are extracted from cross-sectional planes placed a priori in simplified nasal geometries to classify respiratory pathologies. A similar approach was applied in our previous work [11], where the above ML approach was extended to real anatomies of human upper airways by performing CFD simulations on CT-derived surfaces. Features were then extracted from regions located in fixed anatomical sections, as shown on the left-hand side of Figure 1. In this case, cross-sectional planes had to be manually positioned and adapted for each patient to account for anatomical variability. Such handcrafted features have important strengths: they leverage expert knowledge (medical or fluid mechanical) to define interpretable regions tied to anatomical landmarks or aerodynamic structures, and they remain a valid strategy that we also adopt as a baseline. However, the main drawback of this approach is scalability: because regions must be redefined case-by-case, especially in geometrically diverse datasets, the process is time-intensive, costly, and prone to inconsistency.

To overcome these constraints, in this work, we extend our previous study [12] by introducing two alternative methods to define regions for feature extraction: (i) a Clustering-based method, where features are computed in flow regions that are automatically identified; and (ii) a Morphing-based method, where regions are manually defined once on a reference mesh by an expert and then consistently used across simulations by mapping each flow field onto this reference. This approach eliminates the need for case-by-case region definition and enables automated, consistent feature extraction.

Within the Clustering-based method, the CFD domain is segmented into physically meaningful regions by clustering the terms of the governing equations, so that cells with similar local balance of physical contributions (e.g., advection, diffusion, pressure gradient) are grouped together. This removes the need for predefined regions and allows adaptive, simulation-specific and physics-based flow region definition. This approach opens new challenges and benefits: on one hand, it takes a step toward fully data-driven feature extraction, as regions are identified directly from data. On the other hand, since clusters are generated independently for each simulation, the regions may differ from case to case. As a consequence, areas capturing similar physical phenomena in two simulations may not correspond spatially, leading to unordered and potentially inconsistent feature sets across cases. To address this drawback, we implement two complementary clustering strategies: (i) we adopt alignment techniques to explicitly establish correspondences between clusters across samples, such that features can be classified by a standard ML model, and (ii) we train a permutation-invariant ML model that can process unordered sets of data. While effective, features extracted from automatically identified regions may lack interpretability, which is a critical aspect for domain experts, such as clinicians, who rely on descriptors directly linked to anatomical landmarks in their work.

Overcoming the lack of interpretability and providing features that remain directly accessible to medical experts is the rationale behind the Morphing-based method, inspired by [13], which ensures spatial alignment across samples by mapping each simulation onto a unique reference geometry. After a reference geometry is selected, each CFD field in the training set is morphed onto this by fitting a smooth deformation model based on radial basis functions [14]. By doing so, mesh topologies and flow fields of each sample are aligned to the reference, allowing features to be extracted from consistent regions defined only once on the common reference. This method embeds domain knowledge into the reference and propagates it automatically, eliminating repetitive manual interventions. As a result, it enables scalable learning across CFD datasets with varying geometries and boundary conditions, and is particularly effective in scenarios involving parametric variations, surface defects, or anatomical variability, where consistent region definition is challenging.

The two proposed methods thus address complementary challenges: adaptability (clustering), where regions conform to the specific flow field, and transferability (morphing), where expert-defined regions are consistently applied across geometries. Together, they define two key strategies for extracting meaningful and reusable features from CFD data. In particular, the Morphing-based method is preferable when reliable geometric or anatomical landmarks are available and expert knowledge plays a central role, as it preserves spatial interpretability and consistency across complex or patient-specific geometries. Conversely, the Clustering-based method is more suitable when such expert information is not available and inference relies primarily on the physical structure of the flow, since it automatically adapts to each case and identifies meaningful flow regions directly from the CFD data. This distinction provides a practical guideline for selecting the most suitable method depending on the availability of prior knowledge and the nature of the problem.

In this work, we compute features with the proposed methods and use them to train ML models, validating and comparing their performance across scenarios of increasing complexity and variability. Our first evaluation focuses on two large datasets of 2D CFD simulations around NACA (National Advisory Committee for Aeronautics) airfoils, including a publicly available dataset [15] and an extended version that we have generated to include defects. In this setting, where thousands simulations are available, we address two regression tasks: (i) predicting the NACA 4-digit airfoil code, and (ii) estimating geometric defects, such as bumps, cavities, or cut trailing edges. The second test considers a dataset of 3D CFD simulations of airflow in the human upper airways. In this case, we tackle (iii) the classification of frequent nasal pathologies, namely septal deviation and turbinate hypertrophy. Despite the limited number of available flow fields and the complexity of anatomical geometries, our method demonstrates consistent performance in both 2D and 3D domains, confirming its ability to generalize in both data-rich and data-scarce conditions.

Our main contributions are:

-

We introduce two complementary methods for feature extraction: a Clustering-based method that adaptively identifies flow-consistent regions, and a Morphing-based method that transfers expert-defined regions across geometries.

-

We generate a dataset of CFD simulations including controlled geometric defects on NACA airfoils, which will be publicly released upon acceptance to foster reproducibility and further research.

-

We validate our methods on real-world applications of increasing complexity, including biomedical and aerodynamic CFD scenarios, and demonstrate improved performance and practical value compared to established methods [10,11].

-

We provide a solution to a fundamental problem in applying ML to CFD data: the lack of standardized and scalable feature extraction procedures that remain valid across simulations with heterogeneous geometries.

The paper is organized as follows: in Section 2, we review works related to the use of ML in CFD. In Section 3, we formulate the problem we address and introduce the notation. In Section 4, we describe our methodology, detailing the Clustering-based and Morphing-based methods for feature extraction, together with the adopted inference models. Finally, in Section 5, we present the experimental evaluation, including datasets, conducted experiments, feature extraction procedures, training settings, and results.

2. Related Works

Over the past decade, the use of Machine Learning (ML) in fluid mechanics has expanded rapidly, as demonstrated by the increasing number and quality of publications in the field [1,16,17]. Several existing studies focus on making CFD faster or more accurate, either by reducing the cost of solving the governing equations or by improving the quality of simulated flow fields. Within these works, a prominent line of research develops surrogate models that bypass the direct numerical solution of the governing equations, with Physics-Informed Neural Networks (PINNs) as a leading example [18,19,20,21]. Another active direction is turbulence modeling, where deep neural networks have been used to refine the additional equations used to account for the turbulence effects [22,23,24,25]. Among these approaches, researchers have also leveraged decision-tree methods [26], ensemble learning [27], Tensor-Basis Neural Networks [28], and genetic programming [29] to improve closure modeling and enhance predictive accuracy. In addition, ML has been applied to address regression tasks [30] and super-resolution problems on flow fields using convolutional neural networks (CNNs) [31], enabling the reconstruction of fine-scale flow structures from limited-resolution data.

While these contributions showcase the potential of ML to accelerate simulations and augment CFD outputs, they typically use fluid-dynamic variables both as the input and the target, aiming to reproduce or enhance what CFD can, in principle, compute. In contrast, our work focuses on a less explored problem: inferring from CFD information that is not directly computable by numeric solvers, such as whether an airfoil presents a structural defect or a patient is affected by a specific pathology. Inference on flow fields is particularly challenging, since CFD data are inherently high-dimensional and vary significantly across geometries, while annotated datasets are costly to gather and scarce. In this context, the classical strategy to extract features from CFD data relies on handcrafted regions defined a priori by domain experts. For example, Schillaci et al. [10] averaged flow quantities on predefined cross-sections to predict airfoil codes and classify nasal pathologies in simplified and parametric upper airways geometries, an approach later extended to real CT-derived anatomies in [11]. While interpretable and grounded in domain knowledge, this strategy does not scale well: regions must be redefined for each geometry or patient, making the process costly and poorly portable across heterogeneous datasets. This motivates the introduction of more general strategies for feature definition.

Recent advances in ML, particularly in unsupervised learning and deep learning models, offer new opportunities to overcome the limitations of expert-driven approaches and highlight a growing trend toward end-to-end methods. Callaham et al. [32] combined Gaussian Mixture Models (GMMs) with Sparse PCA to partition CFD fields in terms of their local balance relationships in the Navier–Stokes equations. Their goal was to reveal zones where different subsets of terms dominate, providing a visualization of the underlying physical regimes, rather than for extracting features for downstream inference. Similarly, Saetta et al. [2] used GMMs to automatically extract homogeneous regions such as boundary layers, shocks, and inviscid zones, avoiding heuristic thresholds and manual intervention. Kaiser et al. [7] introduced a clustering framework to segment time-resolved flow snapshots (e.g., 20,000 PIV frames in a mixing layer) into a small number of representative states (called centroids), and then described the temporal evolution between these states using a Markov model. This enables the identification of flow transitions in an unsupervised manner. Foroozan et al. [4] applied clustering on DNS data of a transitional boundary layer, embedding high-dimensional observations and analyzing the transitions between flow states through a probabilistic model. More recently, Tran et al. [33] integrated optimal transport distances into autoencoder latent embeddings for separated flows, producing latent variables interpretable in terms of physical quantities such as recirculation region size and control performance, but assuming abundant flow fields computed from a fixed geometry. These works illustrate how unsupervised learning can reveal structure and dynamics in fluid flows, typically relying on large numbers of snapshots or simulations over the same geometry, and aim at data exploration or reduced-order modeling rather than prediction. By contrast, our framework extends this paradigm to supervised inference: physics-based clustering is used to define adaptive regions, and morphing to transfer expert-defined ones, thereby extracting compact, geometry-consistent features from a few simulations, which are then processed by ML models to predict non-computable quantities such as airfoil defects or pathologies.

A major limitation of data-driven approaches, such as clustering, lies in their reduced interpretability and portability. Our morphing-based method takes the opposite perspective: by aligning all flow fields to a common reference domain, we reintroduce expert knowledge in the definition of regions and ensure that features remain directly interpretable across cases. In CFD, mesh morphing has traditionally been employed for shape optimization and aerodynamic design, where geometry and mesh deformation techniques are used to explore parametric variations (as changes in shape strongly affect aerodynamic performance) while preserving mesh quality [34,35,36]. Beyond aerodynamic optimization, morphing is also widely used in moving boundary problems, where solid–fluid interfaces undergo displacements or rotations (e.g., valves, pistons, turbomachinery blades) [37]. Another key application is fluid–structure interaction (FSI), where mesh boundaries deform in response to structural displacements, ranging from weakly coupled rigid-body motions to strongly coupled phenomena such as vortex-induced vibrations [38]. The MMGP framework presented in [13] was among the first to extend morphing beyond these applications, applying it to non-parametric variability: each mesh is morphed to a reference geometry, fields are interpolated onto a common mesh, and dimensionality reduction in a latent space precedes Gaussian Process regression. This strategy makes it possible to handle complex geometric variability with classical ML regressors, while providing predictive uncertainty estimates at low computational cost. Inspired by this idea, we do not adopt morphing as a tool for model reduction, but rather as a means to transfer expert-defined regions across all samples, ensuring feature consistency without the need for case-by-case redefinition.

3. Problem Formulation

Let ${\mathsf{\Omega }}_i\subset {\mathbb{R}}^D,D\in \{2,3\}$ denote the spatial domain of the i-th CFD simulation, discretized into $n_i$ cells defining the mesh $M_i$, which provides a numerical approximation of ${\mathsf{\Omega }}_i$. Each cell of $M_i$ is associated with H physical quantities (e.g., velocity $\mathit{u}$, pressure p, turbulence-related terms, etc.), resulting in a data matrix ${\mathbf{F}}_i\in {\mathbb{R}}^{n_i\times H}$ (visible in the top part of Figure 2). In typical high-fidelity CFD simulations, $n_i$ can easily reach the order of ${10}^7$, making it infeasible to directly use ${\mathbf{F}}_i$ as input to standard ML models.

Our objective is to train a model K that predicts a target quantity $Y\in \mathcal{Y}$ from CFD data, where $\mathcal{Y}$ may denote either a continuous (regression) or discrete (classification) output space. In both cases, it is necessary to derive from ${\mathbf{F}}_i$ a compact and structured representation that can be effectively processed by K. To this end, we introduce a region extraction operator $\mathsf{\Phi }:({\mathbf{F}}_i,M_i)\to {\left\{S_j^i\right\}}_{j=1}^{r_i}$ (bottom part of Figure 2) which segment the computational domain ${\mathsf{\Omega }}_i$ of the i-th sample into a collection of regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$, with each region satisfying $S_j^i\subset M_i$ for $j=1,\dots ,r_i$. Here, $r_i$ denotes the number of regions and j is the region index within sample i. In each region, we compute regional averages of flow quantities, producing a compact and informative representation ${\mathbf{P}}_i$ of features suitable for inference, namely:

$$({\mathbf{F}}_i,M_i)\stackrel{\mathsf{\Phi }}{\to }{\left\{S_j^i\right\}}_{j=1}^{r_i}\underset{Averages}{\overset{Regional}{\to }}{\mathbf{P}}_i.$$

The focus of our work is to design $\mathsf{\Phi }$ so that the resulting regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ and the extracted features in ${\mathbf{P}}_i$ are consistent and comparable across simulations, even when the geometries ${\mathsf{\Omega }}_i$ differ significantly. At the same time, ${\mathbf{P}}_i$ must be sufficiently expressive to capture the relevant physical structures of the flow field. Training the ML model $K:\mathbf{P}\to Y$ requires a labeled dataset $\mathcal{D}={\left\{({\mathbf{P}}_i,Y_i)\right\}}_{i=1}^m$, obtained by processing flow fields using a shared feature extraction procedure based on the region extraction function $\mathsf{\Phi }$.

4. Method

We tackle the challenge of learning from high-dimensional CFD data through a feature extraction pipeline that segments each flow field into regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ (top part of Figure 2). Within each region, we compute representative flow quantities and aggregate them in the feature set ${\mathbf{P}}_i$, which we then feed as input to the Machine Learning model K. Our Morphing-based and Clustering-based methods are illustrated in Figure 2, in the left and right boxes respectively. The key difference between the two lies in how the operator $\mathsf{\Phi }$ defines regions: in the Clustering-based method, the regions are data-driven, guided by the physics of the governing equations; in the Morphing-based method, the regions are instead expert-driven, being manually defined on a single reference geometry and then propagated to all simulations via morphing based on Radial Basis Functions (RBFs) [14].

In the Clustering-based method [12], $\mathsf{\Phi }$ is obtained as follows. We insert the raw flow variables computed in ${\mathbf{F}}_i$ into the governing equations of the CFD solver [39], obtaining N derived quantities corresponding to the terms of the equations (top part of the right box in Figure 2). Collecting these values for all cells yields the matrix ${\mathbf{C}}_i\in {\mathbb{R}}^{n\times N}$, where each row corresponds to a CFD cell and stores the N derived quantities. A clustering algorithm is then applied to the rows of ${\mathbf{C}}_i$ (central part of the right box in Figure 2) thus grouping the flow field into regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ characterized by coherent physical behavior. Within these regions, we compute regional averages of fluid-dynamic quantities, resulting in a set of features ${\mathbf{P}}_i$ (bottom part of the right box in Figure 2) given as input to a ML model K.

In the Morphing-based method, each CFD simulation in ${\mathbf{F}}_i$, together with its associated mesh in $M_i$, is geometrically aligned onto a common reference domain ${\mathsf{\Omega }}^{*}$ through $\mathcal{M}:{\mathbb{R}}^{n_i\times H}\to {\mathbb{R}}^{n^{*}\times H}$ (top part of the left box in Figure 2). The region extraction operator $\mathsf{\Phi }$ partially implements the procedure presented in [13], which requires a point-to-point correspondence ${\pi }_i$ between the boundaries of the two domains, $\partial {\mathsf{\Omega }}_i$ and $\partial {\mathsf{\Omega }}^{*}$. From these correspondences, the displacements of the boundary nodes are computed as the coordinate differences between each boundary point of $\partial {\mathsf{\Omega }}_i$ and its matched counterpart on $\partial {\mathsf{\Omega }}^{*}$. These boundary displacements are then smoothly propagated throughout the domain using Radial Basis Functions (RBFs) [14]. Finally, all CFD fields in ${\mathbf{F}}_i$ are interpolated from ${\mathsf{\Omega }}_i$ onto ${\mathsf{\Omega }}^{*}$ using a finite element (FEM) basis. Thus, applying the morphing operator $\mathcal{M}$ yields a new CFD matrix ${\mathbf{F}}_i^{*}=\mathcal{M}({\mathbf{F}}_i,M_i,M^{*})$, where ${\mathbf{F}}_i^{*}\in {\mathbb{R}}^{n^{*}\times D}$ corresponds to the i-th flow field mapped onto the reference mesh $M^{*}$ (center part of the left box in Figure 2). Each morphed flow field ${\mathbf{F}}_i^{*}$ shares the same domain discretization $M^{*}$, on which the regions ${\left\{S_j\right\}}_{j=1}^{r^{*}}$ are defined a priori by an expert. Therefore, regions need to be defined only once on ${\mathsf{\Omega }}^{*}$, and can be used to extract features from all morphed flow fields ${\mathbf{F}}_i^{*}$. As a result, the extracted features are perfectly comparable across simulations and can be consistently organized in the feature set ${\mathbf{P}}_i$, which is then processed by a standard ML model K (bottom part of the left box in Figure 2). In what follows, we describe in detail the two proposed methods and their role within the overall feature extraction framework.

4.1. Clustering-Based Method

To automate the extraction of regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ through the operator $\mathsf{\Phi }$ without relying on geometry-specific landmarks (such as cross-sections visible in Figure 1), we derive physics-based quantities from each ${\mathbf{F}}_i$ and apply a clustering procedure to extract coherent flow structures. This approach ensures adaptability and scalability across different geometric configurations, while reducing data complexity. Here, we leverage the governing equations of the CFD model, namely the Reynolds-averaged Navier–Stokes (RANS) and the Large Eddy Simulation (LES) formulations [39], described in the following. In RANS, flow variables are decomposed into mean and fluctuating components through time-averaging, whereas in LES, the large turbulent scales are resolved and the smaller ones are modeled via spatial filtering. The terms derived from these formulations serve as inputs to our clustering algorithm.

4.1.1. Clustering Inputs

Inspired by [32], we apply clustering not directly to the CFD data matrix ${\mathbf{F}}_i\in {\mathbb{R}}^{n_i\times H}$, but to a transformed representation ${\mathbf{C}}_i\in {\mathbb{R}}^{n_i\times N}$ obtained by mapping ${\mathbf{F}}_i$ through the governing equations (see top part of the right box in Figure 2). In the CFD data matrix ${\mathbf{F}}_i$, each cell of the computational mesh $M_i$ is described by a row vector of raw flow variables $f_j^i\in {\mathbb{R}}^H$ (with $j=1,\dots ,n_i$), which includes fluid quantities such as velocity $\mathbf{u}$, pressure p, and turbulence-related terms. In the transformed space, each cell is associated with a vector $c_j^i\in {\mathbb{R}}^N,j=1,\dots ,n_i$ (the rows of ${\mathbf{C}}_i$) whose components correspond to the terms of the equations employed by the CFD solver. This mapping converts ${\mathbf{F}}_i\in {\mathbb{R}}^{n_i\times H}$ into ${\mathbf{C}}_i\in {\mathbb{R}}^{n_i\times N}$, typically with $N<H$, providing a compact and physics-based feature space. Clustering is then applied to the rows of ${\mathbf{C}}_i$, so that the cells of the computational domain are partitioned into groups. As shown in the center of the right box in Figure 2, each cluster corresponds to a region $S_j^i$, and the collection ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ defines a physically guided segmentation of the domain. In this way, the identification of regions derives from the underlying governing equations, ensuring that feature extraction relies on meaningful and physics-consistent structures. Hereafter, we describe how the matrices ${\mathbf{C}}_i$ are constructed in the cases of RANS and LES formulations of the Navier–Stokes equations.

4.1.2. RANS and LES Formulations of the Navier–Stokes Equations

To perform CFD simulations, we adopted two common turbulence modeling approaches for the solver: Reynolds-averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES) [39]. In (1) we report the LES equations, an analytical model for turbulent flows obtained by applying a spatial filtering operation, denoted by the tilde $\widetilde{(·)}$, to the Navier–Stokes equations. This filtering separates the resolved large-scale motions from the subgrid-scale (SGS) fluctuations, which are modeled through turbulence closures. Although LES are inherently unsteady, in this work we consider flow quantities that are time-averaged after the initial transient, so that the extracted features represent statistically stationary conditions. Therefore, for LES, ${\mathbf{C}}_i$ includes the Cartesian components of the advection term, pressure gradient, laminar diffusion, and subgrid-scale (SGS) stress terms, namely:

$$\begin{array}{cc}\hfill \underset{\mathrm{Unsteadiness}}{\underbrace{{\displaystyle \frac{\partial \tilde{\mathbf{u}}}{\partial t}}}}+\underset{\mathrm{Advection}}{\underbrace{\nabla ·\left(\tilde{\mathbf{u}}\otimes \tilde{\mathbf{u}}\right)}}& =\underset{\mathrm{Laminar}\mathrm{diffusion}}{\underbrace{\nu {\nabla }^2\tilde{\mathbf{u}}}}-\underset{\mathrm{Pressure}\mathrm{gradient}}{\underbrace{{\displaystyle \frac{1}{\rho }}\nabla \tilde{p}}}-\underset{\mathrm{SGS}\mathrm{stress}}{\underbrace{\nabla ·\left({\mathit{\tau }}^{SGS}\right)}},\hfill \end{array}$$

(1)

where $\tilde{\mathbf{u}}$ and $\tilde{p}$ denote the filtered velocity and pressure, $\rho$ is the fluid density (assumed constant for incompressible flows), and $\nu$ is the kinematic viscosity. The subgrid-scale stress tensor is defined as ${\mathit{\tau }}^{sgs}=\widetilde{\mathbf{u}\mathbf{u}}-\tilde{\mathbf{u}}\tilde{\mathbf{u}}$, and represents the effect of unresolved scales. In our case, it is modeled using the WALE (Wall-Adapting Local Eddy-viscosity) model [40], which introduces an eddy viscosity ${\nu }_{SGS}$ that properly accounts for near-wall behavior without requiring damping functions. The operator ∇ denotes the gradient, while $\nabla ·$ and ${\nabla }^2$ represent the divergence and Laplacian, respectively.

For the RANS setting, we define ${\mathbf{C}}_i$ in a similar way to the LES case, but here a time-averaging operation, denoted by the overbar $\overline{(·)}$, replaces spatial filtering. Each flow variable is decomposed into a mean component and a fluctuating one, e.g., $\mathbf{u}\left(t\right)=\overline{\mathbf{u}}\left(t\right)+{\mathbf{u}}^{\prime }\left(t\right)$, where $\overline{\mathbf{u}}$ denotes the time-averaged velocity and ${\mathbf{u}}^{\prime }$ the corresponding fluctuation. The unresolved turbulent stresses are modeled using the Spalart–Allmaras (SA) one-equation closure [41], which introduces a transport equation for a modified turbulent viscosity ${\nu }_t$. The RANS equations are outlined in (2), and based on their structure, we construct ${\mathbf{C}}_i$ by collecting the Cartesian components of the following terms: advection, pressure gradient, laminar diffusion, turbulent diffusion (modeled via SA viscosity), and the contribution of turbulent kinetic energy (TKE):

$$\begin{array}{cc}\hfill \underset{\mathrm{Advection}}{\underbrace{\nabla ·\left(\overline{\mathbf{u}}\otimes \overline{\mathbf{u}}\right)}}& =-\underset{\mathrm{Pressure}\mathrm{gradient}}{\underbrace{{\displaystyle \frac{1}{\rho }}\nabla \overline{p}}}+\underset{\mathrm{Laminar}\mathrm{diffusion}}{\underbrace{\nu {\nabla }^2\overline{\mathbf{u}}}}+\underset{\mathrm{Turbulent}\mathrm{diffusion}}{\underbrace{\nabla ·({\nu }_{\mathrm{t}}\nabla \overline{\mathbf{u}})}}-\underset{\mathrm{TKE}}{\underbrace{\nabla \left(\frac{2}{3}\overline{k}\right)}},\hfill \end{array}$$

(2)

where $\overline{\mathbf{u}}$ is the mean velocity, $\overline{p}$ the mean pressure, $\rho$ the constant density (for incompressible flows), $\nu$ the kinematic viscosity, ${\nu }_{\mathrm{t}}$ the turbulent viscosity computed by the SA model, and $\overline{k}$ the turbulent kinetic energy defined as $\overline{k}=\frac{1}{2}\overline{{\mathbf{u}}^{\prime }·{\mathbf{u}}^{\prime }}$. Once ${\mathbf{C}}_i$ has been assembled in this way, the next step is to apply a clustering algorithm to its rows, grouping CFD cells into regions characterized by coherent physical behavior.

4.1.3. Clustering Algorithm

We leverage a Bayesian Gaussian Mixture Model (BGMM) [42] to cluster the rows of ${\mathbf{C}}_i$. By doing that, we identify flow regions based on the underlying physical properties of the flow (at the bottom-right of Figure 2), which we then use to extract features that form the set ${\mathbf{P}}_i$. In more detail, the distinctive advantage of the BGMM lies in employing full covariance matrices to describe the distribution of each cluster extracted from ${\mathbf{C}}_i$, thereby capturing correlations between the equation terms in (1) or (2). Such correlations reflect the dominant physical mechanisms in each region: for instance, strong correlations between advection and pressure-gradient terms typically indicate free-stream areas, whereas higher covariance among diffusion or turbulence-related terms is more often associated with boundary layers or recirculation zones. By modeling these correlations, the BGMM automatically captures variations in the local balance between physical contributions, allowing it to distinguish regions governed by distinct flow behaviors such as boundary layer growth, shear-layer formation, separation, or wake development [32]. Unlike heuristic or geometry-based segmentation, clusters emerge directly from the statistical relationships among the governing equation terms, providing a physically meaningful and adaptive description of the flow field.

Another important property of the BGMM is that the variational Bayesian inference framework automatically estimates the best number of clusters k, allowing each flow field to yield a cluster structure adapted to its specific flow physics. This makes the method flexible and generally applicable across different geometries and flow regimes. To improve numerical stability and convergence, we set an upper bound $k_{max}$ for the number of clusters and initialize the Gaussian components of the BGMM using the centroids obtained from a k-means run with $k_{max}$ clusters. During inference, the variational Bayesian framework automatically removes redundant components, thus estimating the effective number of clusters $k\le k_{max}$. In the following, we describe two alternative clustering strategies that differ in how clusters are defined and propagated across simulations.

4.1.4. Clustering Strategies

The clustering process, followed by feature extraction, condenses the CFD data in ${\mathbf{C}}_i\in {\mathbb{R}}^{n_i\times N}$ into a more compact representation ${\mathbf{P}}_i$. However, the BGMM does not enforce a consistent ordering of the clusters and lets their number potentially vary across ${\left\{{\mathbf{F}}_i\right\}}_{i=1}^m$. Consequently, the feature vectors extracted from the clusters form an unordered set ${\mathbf{P}}_i$ whose cardinality may differ from case to case. As a result, ${\mathbf{P}}_i$ cannot be directly provided as input to the ML model K, which requires a fixed input size. To address the variability in both the number and the ordering of clusters across simulations, we adopt two different approaches:

• Free clustering (C-FREE): In this setting, both the order and the number of clusters are allowed to vary across simulations, as a BGMM is applied independently to each CFD flow field ${\mathbf{F}}_i$. Consequently, the k feature vectors in ${\mathbf{P}}_i$ form a set having no predefined order or cardinality, which must be explicitly considered when choosing the learning model K. In this case, we adopt a set-learning model [43] for K, which naturally handles unordered inputs. The main advantage of this strategy is its flexibility, since no fixed clustering structure is imposed, and the representation can adapt to different flow regimes and geometrical configurations. In principle, increasing the number of clusters in each CFD simulation can be beneficial, as it allows capturing additional flow features that would otherwise be lost with a less detailed segmentation. However, when set-learning models are employed to process these variable-size representations, they aggregate features in a permutation-invariant manner. While this allows processing unordered inputs, it may also smooth out subtle but potentially useful information, which could affect inference performance.
• Clustering propagation (C-PROP): To mitigate the potential loss of information introduced by set-learning models, and to enable the use of standard architectures such as MLPs (Multi-Layer Perceptrons), we enforce a consistent definition of clusters across all ${\left\{{\mathbf{F}}_i\right\}}_{i=1}^m$. Specifically, we select a reference CFD simulation ${\mathbf{F}}^{*}$ in which clusters are computed using the C-FREE strategy. These reference clusters are then propagated to all other simulations by matching each row of ${\mathbf{C}}_i$ to its nearest counterpart in the reference ${\mathbf{C}}^{*}$ according to the Euclidean distance. This matching procedure is efficiently implemented through a k-d tree [44], ensuring that similarity is preserved in the feature space spanned by the columns of ${\mathbf{C}}_i$. Because the rows of ${\mathbf{C}}_i$ are derived from the governing equations, the propagation inherently respects the underlying flow physics. This strategy guarantees that both the number and the ordering of clusters in ${\mathbf{P}}_i$ remain consistent across simulations, enabling direct comparison of features vectors and compatibility with conventional supervised learning models. However, this comes at the cost of restricting simulations to the set of flow regions present in the reference case, which may reduce flexibility and generalization.

The clustering process yields regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ corresponding to the k clusters, each representing a coherent physical zone within the flow field, so that the number of regions satisfies $r_i=k$. These regions are identified either independently for each simulation (C-FREE) or propagated from a reference case to ensure consistency across samples (C-PROP). In both cases, clustering provides a data-driven and physics-guided segmentation of the domain, allowing features to be extracted from regions that reflect the underlying flow behavior. We now describe our Morphing-based method, which reintroduces expert knowledge and ensures spatial alignment across geometries.

4.2. Morphing-Based Method

In the Morphing-based method, the operator $\mathsf{\Phi }$ relies on regions of the flow field defined by domain experts. However, instead of specifying ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ separately for each geometry, the regions are defined once on a single reference mesh $M^{*}$, yielding a fixed set ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$ (see top part of the left box in Figure 2). We then leverage a morphing operator $\mathcal{M}$ to map each CFD flow field ${\mathbf{F}}_i$ computed on the mesh $M_i$, to the reference mesh $M^{*}$, obtaining the morphed field ${\mathbf{F}}_i^{*}$ on which the reference partition ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$ can be consistently applied.

In more detail, we transfer ${\mathbf{F}}_i\in {\mathbb{R}}^{n_i\times H}$ defined on $M_i$, onto a common reference domain ${\mathsf{\Omega }}^{*}$ discretized into $n^{*}$ cells forming the mesh $M^{*}$. Without alignment, the CFD fields ${\left\{{\mathbf{F}}_i\right\}}_{i=1}^m$ are not directly comparable, preventing the consistent application of the same expert-defined regions across simulations. By mapping both the geometry $M_i$ and the associated CFD data ${\mathbf{F}}_i$ onto the common reference mesh $M^{*}$, we obtain a consistent CFD data matrix ${\mathbf{F}}_i^{*}\in {\mathbb{R}}^{n^{*}\times H}$, built on the same spatial support, namely, the same boundary $\partial {\mathsf{\Omega }}^{*}$ and computational mesh $M^{*}$ on which regions ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$ are defined.

We denote the morphing operator that performs this transformation as $\mathcal{M}:({\mathbf{F}}_i,M_i,M^{*})\to {\mathbf{F}}_i^{*}$ and decompose it into two distinct operators $\mathcal{M}=\mathcal{I}\circ \mathcal{T}$, where the symbol “∘” denotes the composition of operators. Here, $\mathcal{T}:(M_i,M^{*})\to M_i^{\prime }$ is the geometric transformation that aligns the boundary nodes of $M_i$ onto those of the reference $M^{*}$, yielding a deformed mesh $M_i^{\prime }$ whose boundary coincides with $\partial {\mathsf{\Omega }}^{*}$, but differs in its internal discretization. The operator $\mathcal{T}$ requires as input a point-to-point correspondence ${\pi }_i$ between the boundaries of the two domains, $\partial {\mathsf{\Omega }}_i$ and $\partial {\mathsf{\Omega }}^{*}$. From these correspondences, the displacements of the boundary nodes are computed and then smoothly propagated to the interior nodes using Radial Basis Functions (RBFs) [14], i.e., smooth functions whose value depends only on the distance from a center point, which are commonly used to interpolate boundary displacements into the interior of the mesh.

Subsequently, a projection operator $\mathcal{I}:({\mathbf{F}}_i,M_i^{\prime })\to {\mathbf{F}}_i^{*}$ transfers both the internal nodes of and the CFD field ${\mathbf{F}}_i$ from the morphed mesh $M_i^{\prime }$ to the common reference mesh $M^{*}$, ensuring that CFD data refer to the same spatial support, and enabling consistent feature extraction across samples using ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$. In the following, we detail how the two operators, $\mathcal{T}$ and $\mathcal{I}$, are defined and implemented.

4.2.1. $\mathcal{T}$: Mesh Deformation to a Common Shape

Let ${\mathbf{x}}_j$ be the coordinates of the j-th node of $M_i$. The transformation $\mathcal{T}:(M_i,M^{*})\to M_i^{\prime }$ applies a displacement field ${\mathbf{d}}_i\left(\mathbf{x}\right)$ such that

$${\mathbf{x}}_j^{\prime }={\mathbf{x}}_j+{\mathbf{d}}_i\left({\mathbf{x}}_j\right).$$

Following the mesh deformation method of De Boer et al. [14], the displacement ${\mathbf{d}}_i\left(\mathbf{x}\right)$ is interpolated from the boundary to the interior nodes by means of RBFs. Specifically, we denote by ${\left\{{\mathbf{b}}_{i,k}\right\}}_{k=1}^{n_b}$ the set of boundary nodes of $M_i$ that discretize $\partial {\mathsf{\Omega }}_i$, each associated with a corresponding boundary node on the reference mesh $M^{*}$, denoted by ${\left\{{\mathbf{b}}_{k^{\prime }}^{*}\right\}}_{k^{\prime }=1}^{n_b^{*}}$. The correspondence between the two sets is defined through a mapping ${\pi }_i:\partial {\mathsf{\Omega }}_i\to \partial {\mathsf{\Omega }}^{*},$ such that $k^{\prime }={\pi }_i\left(k\right),\forall k=1,\dots ,n_b$. Thus, the prescribed displacement of the $k$-th boundary node of $\partial {\mathsf{\Omega }}_i$ is then defined as ${\mathbf{d}}_{i,k}^b={\mathbf{b}}_{{\pi }_i\left(k\right)}^{*}-{\mathbf{b}}_{i,k},$ indicating how this node must be shifted to match the corresponding node on the reference boundary $\partial {\mathsf{\Omega }}^{*}$. In practice, the correspondence mapping ${\pi }_i$ is obtained through domain-specific knowledge (detailed in Section 5.4): in our aerodynamic application, boundary correspondences are based on a few unambiguous geometric landmarks, namely, the leading edge, trailing edge, uniformly spaced points along the pressure and suction sides, and the farfield boundary. For the human upper airways, instead, ${\pi }_i$ is computed following the method proposed in [11], which derives dense point-to-point correspondences from a small number of easily identifiable anatomical landmarks via functional maps [45,46,47]. This strategy considerably simplifies the process compared to manually redefining the regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ for each geometry, while ensuring accurate and reproducible boundary alignment across all cases.

Given the displacement ${\mathbf{d}}_i^b$ of all the boundary nodes, the displacement field ${\mathbf{d}}_i$ inside the domain is then obtained by RBF interpolation (for the sake of readability, the subscript i identifying the i-th mesh is omitted hereafter):

$$\mathbf{d}\left(\mathbf{x}\right)=\sum _{k=1}^{n_b}{\alpha }_k\psi (\parallel \mathbf{x}-{\mathbf{b}}_k\parallel )+\mathbf{R}\left(\mathbf{x}\right).$$

(3)

Here, ${\alpha }_k$ are interpolation coefficients, $\mathbf{R}\left(\mathbf{x}\right)=[1,x,y,z]\mathit{\beta }$ is a low-order polynomial that guarantees the reproduction of rigid transformations (translations and rotations), with the z term included only in the 3D formulation, and $\psi (·)$ is a compactly supported $C^2$ radial basis function defined on normalized coordinates,

$$\psi \left(r\right)=\left\{\begin{array}{cc}{(1-r)}^4(4r+1)\hfill & r\le 1,\hfill \\ 0\hfill & r>1,\hfill \end{array}\right.r={\displaystyle \frac{\parallel \mathbf{x}-\mathbf{b}\parallel }{r_s}},$$

(4)

where $r_s>0$ is the support radius, i.e., the distance beyond which the influence of a boundary control point vanishes. Rather than being fixed, $r_s$ is adapted to a characteristic scale of the problem (e.g., domain size or boundary spacing), allowing the interpolation to remain robust across applications characterized by different spatial scales, such as aerodynamic airfoils and anatomical airways.

The coefficients $\mathit{\alpha }$ and $\mathit{\beta }$ in (3) are determined by enforcing the interpolation conditions at the boundary nodes and the orthogonality between the radial and polynomial terms. This leads to the following linear system:

$$\left[\begin{array}{cc}\mathsf{\Psi }& {\mathit{R}}_b\\ {{\mathit{R}}_b}^T& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{d}}^b\\ \mathbf{0}\end{array}\right],$$

(5)

where ${\mathsf{\Psi }}_{ij}=\psi (\parallel {\mathbf{x}}_i^b-{\mathbf{x}}_j^b\parallel )$ and ${\mathit{R}}_b$ is the matrix containing the polynomial basis evaluated at the boundary nodes. The orthogonality condition ${\mathit{R}}_b^T\mathit{\alpha }=\mathbf{0}$ in (5) ensures the uniqueness of the interpolant and guarantees that rigid transformations are exactly recovered. The system only involves the boundary nodes, and can be solved efficiently by LU decomposition or, for large-scale cases, by fast iterative methods [48].

4.2.2. $\mathcal{I}$: Projection on Common Mesh

After the geometry has been deformed by $\mathcal{T}$ to match the boundary $\partial {\mathsf{\Omega }}^{*}$ of $M^{*}$, each flow field ${\mathbf{F}}_i$, defined on $M_i^{\prime }$, must be interpolated onto the reference mesh $M^{*}$, as $M_i^{\prime }$ and $M^{*}$ do not share nodes and connectivity. Following [13], we adopt a finite element (FEM) projection, which formulates the interpolation in a variational setting and guarantees both stability and consistency of the transferred CFD fields. Since finite element fields are by construction represented on the mesh, the FEM projection is particularly suited for transferring solutions between non-conforming meshes $M_i$ and $M^{*}$.

As in [13], we adopt a Lagrange ${\mathbb{P}}_1$ finite element basis, so that any scalar field $q_i$ defined on the morphed mesh $M_i^{\prime }$ can be expressed as

$$q_i\left(\mathbf{x}\right)=\sum _{I=1}^{n_i}{Q}_I^i{\lambda }_I^i\left(\mathbf{x}\right),$$

where $Q_I^i$ are the nodal values and $\left\{{\lambda }_I^i\right\}$ is the finite element basis associated with $M_i^{\prime }$. The projection $q_i^{*}=P\left(q_i\right)$ on the common mesh $M^{*}$ is then defined as

$$q_i^{*}\left(\mathbf{x}\right)=\sum _{J=1}^{n^{*}}{q}_i\left({\mathbf{x}}_J^{*}\right){\lambda }_J^{*}\left(\mathbf{x}\right)=\sum _{I=1}^{n_i}\sum _{J=1}^{n^{*}}{Q}_I^i{\lambda }_I^i\left({\mathbf{x}}_J^{*}\right){\lambda }_J^{*}\left(\mathbf{x}\right),$$

where $\left\{{\lambda }_J^{*}\right\}$ denotes the finite element basis associated with $M^{*}$ and ${\mathbf{x}}^{*}$ the coordinates of its nodes. Applying this procedure to all the CFD fields of ${\mathbf{F}}_i$ defines the projection operator $\mathcal{I}$, and yields

$${\mathbf{F}}_i^{*}=\mathcal{M}({\mathbf{F}}_i,M_i,M^{*})=\mathcal{I}\left({\mathbf{F}}_i,\mathcal{T}(M_i,M^{*})\right).$$

The combined action of $\mathcal{T}$ and $\mathcal{I}$ ensures that both geometry and CFD fields are consistently represented on the same reference mesh $M^{*}$, leading to a unified dataset ${\left\{{\mathbf{F}}_i^{*}\right\}}_{i=1}^m$ where we can adopt regions ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$.

4.3. Extraction of Features from Regions ${\left\{{\mathit{S}}_{\mathit{j}}^{\mathit{i}}\right\}}_{\mathit{j}=\mathbf{1}}^{{\mathit{r}}_{\mathit{i}}}$

Once the flow regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ have been identified, either through clustering or defined by experts on morphed data, the next step is to extract the feature set ${\mathbf{P}}_i$ (bottom part of Figure 2) that will serve as input to the learning model K. This stage aims to transform high-dimensional CFD data into compact and informative descriptors that are consistent across simulations, despite variations in geometry and flow conditions.

Both for the Clustering-based and Morphing-based methods, from each region we extract a feature vector composed of aggregated flow and geometrical quantities. Specifically, we compute the weighted average of the fluid dynamics quantities reported in

Table 1. Summary of the complete set of features composing ${\mathbf{P}}_i$, including both the regional averages of flow quantities (denoted as “Avg.”) defined in (6) and the geometrical features. On the left, RANS (2D, time-averaged); on the right, LES (3D, filtered). The notation ${|}_x$, ${|}_{x,y}$, ${|}_{x,y,z}$ indicates that we use the corresponding vector components. In LES we explicitly report the subgrid stress term ${\mathit{\tau }}_{\mathrm{SGS}}$, although it is modeled in practice through an eddy viscosity ${\nu }_{\mathrm{SGS}}$ [40].

Features in ${\mathbf{P}}_{\mathit{i}}$
Category	RANS (2D)	LES (3D)
Avg. Flow variables	${\overline{u}}_x,{\overline{u}}_y,\overline{p},{\nu }_t$	${\tilde{u}}_x,{\tilde{u}}_y,{\tilde{u}}_z,\tilde{p},{\nu }_{SGS}$
Avg. Advection	$\nabla ·(\overline{\mathbf{u}}\otimes \overline{\mathbf{u}}){|}_{x,y}$	$\nabla ·(\tilde{\mathbf{u}}\otimes \tilde{\mathbf{u}}){|}_{x,y,z}$
Avg. Laminar diffusion	$\nu {\nabla }^2\overline{\mathbf{u}}{|}_{x,y}$	$\nu {\nabla }^2\tilde{\mathbf{u}}{|}_{x,y,z}$
Avg. Turbulent diffusion	$\nabla ·({\nu }_t\nabla \overline{\mathbf{u}}){|}_{x,y},\nabla \left(\frac{2}{3}\overline{k}\right){|}_{x,y}$	$\nabla ·{\mathit{\tau }}_{\mathrm{SGS}}{|}_{x,y,z}$
Avg. Pressure	$\frac{1}{\rho }\nabla \overline{p}{|}_{x,y}$	$\frac{1}{\rho }\nabla \tilde{p}{|}_{x,y,z}$
Geometrical	Centroids $(x,y)$, Area	Centroids $(x,y,z)$, Volume

and marked with “Avg.”, using cell area (in 2D) or volume (in 3D) as weights. In particular, let $S_r\subset M_i$ denote a region and let q be a generic flow quantity (e.g., pressure, velocity components), the corresponding regional average is defined as:

$$q_{S_r}={\displaystyle \frac{{\sum }_{j\in S_r}{q}_j{w}_j}{{\sum }_{j\in S_r}{w}_j}},$$

(6)

where $q_j$ is the value of q at cell j and $w_j$ is its area or volume.

The feature vector also includes geometrical information like the total area (or volume in 3D) of each cluster, and, to preserve spatial information which is crucial in CFD data, centroid coordinates. The complete set of features in ${\mathbf{P}}_i$ is reported in Table 1.

Feature extraction reduces the high-dimensional CFD data ${\mathbf{F}}_i$ to a compact set of feature vectors ${\mathbf{p}}_j^i$:

$${\mathbf{P}}_i=\{{\mathbf{p}}_j^i\in {\mathbb{R}}^l,j=1,\dots ,r_i\},$$

(7)

where $r_i\ll n_i$ is the number of regions (clusters when using the Clustering-based method, or expert-defined regions when using the Morphing-based method), and $l=\mathcal{O}\left(N\right)$ is the number of features per cluster.

For the Clustering-based method, regions correspond to the k clusters estimated by the BGMM as described in Section 4.1. This generalizes the regional averaging strategy of [10], replacing manually defined spatial regions with data-driven clusters that adapt to the local flow structures of each simulation. In the Morphing-based method, expert knowledge is explicitly reintroduced into the feature extraction process. Here, the expert-defined regions on the reference mesh $M^{*}$ replace the clusters, and the same feature computation described above is applied. Depending on the application, expert-defined regions may correspond to probe-like measurements in aerodynamic cases (e.g., vertical lines placed upstream and downstream of an airfoil, subdivided into segments as in [10]) or to anatomically meaningful sections in biomedical flows (e.g., cross-sectional cuts along the nasal cavity, as in [11]). Compared to clustering, which offers flexibility and adaptivity by tailoring regions to the specific flow structures of each simulation, expert-defined regions yield standardized and interpretable features, since they are defined once on the reference mesh and consistently applied to all flow fields through morphing. However, this standardization comes at the cost of reduced sensitivity to localized or case-specific flow variations, making morphing potentially less effective in capturing small-scale phenomena.

4.4. Inference Models

The choice of inference model K depends on how the regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ are defined, as clustering and morphing can generate feature sets with different structural properties, which guide the selection of the inference model.

4.4.1. Clustering-Based Method

When regions are obtained through clustering, the inference model depends on the adopted clustering strategy described in Section 4.1. In the C-PROP setting, clusters are propagated from a reference case, which ensures that the resulting feature vectors ${\mathbf{p}}_j^i$ in (7) have fixed size and ordering across simulations, allowing us to employ a simple MLP to classify ${\mathbf{P}}_i$, by stacking all the feature vectors. In contrast, the C-FREE strategy produces sets of clusters with variable cardinality and no predefined order, so ${\mathbf{P}}_i$ cannot be directly aligned across flow fields and must be processed as a set by using permutation-invariant models. For this case, we adopt a Point Transformer (PT) [43], i.e., a permutation-invariant architecture specifically designed for point sets. Since we included the centroid coordinates in each feature vector ${\mathbf{p}}_j^i$ (see Section 4.3), the remaining components can be interpreted as point features. This allows the PT to leverage the self-attention to build spatially aware representations of the clusters, an essential property in CFD, where spatial relations underpin the flow physics.

4.4.2. Morphing-Based Method

When features are extracted from morphed fields ${\left\{{\mathbf{F}}_i^{*}\right\}}_{i=1}^m$, all simulations are aligned to the same reference geometry $M^{*}$ as explained in Section 4.2. As a result, the feature sets ${\mathbf{P}}_i$ are directly comparable across cases, with fixed size and consistent ordering imposed by the expert that defines regions ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$. This regularity makes an MLP the natural choice, as the network can exploit the standardized input structure without the need for permutation invariance or set-based processing.

5. Experiments

We evaluate our methods on three distinct tasks of increasing complexity, each corresponding to a different application of CFD analysis: (i) airfoil shape identification, (ii) surface defect detection on airfoils, and (iii) pathology classification in real human upper airways. In each scenario, we compare experiments where features in the set ${\mathbf{P}}_i$ are extracted using different alternatives, as detailed in the following section. As baseline, we consider the handcrafted feature approaches proposed by Schillaci et al. [10] and also adopted in [11], which represent well-established references for ML inference on CFD data.

We first validate our methods on a publicly available dataset [15], complemented with an extended version we generated. The two datasets consist of 2D flow fields with a large number of samples, allowing for extensive evaluation. We then move to a more realistic and challenging scenario, that is, pathology identification in human upper airways directly extracted from CT scans. In this case, the dataset contains far fewer samples, as these are expensive to acquire. Moreover, the CFD simulations are fully three-dimensional, increasing complexity due to the additional spatial dimension and greater geometric variability of human anatomies. This transition from controlled, data-rich 2D settings to a real-world, data-scarce 3D scenario enables a comprehensive assessment of the method’s adaptability and robustness.

5.1. Datasets and Tasks

5.1.1. Airfoil Shape Identification (AirNACA)

We focus on the family of NACA (National Advisory Committee for Aeronautics) four-digit airfoils, with the goal of training a regressor K that predicts the corresponding NACA code, and thus the airfoil shape, directly from the CFD solution. The geometry of a NACA airfoil is fully determined by its four-digit code: the first digit specifies the maximum camber as a percentage of the chord length c (ranging from 0 to 9, where c is the straight-line distance from the airfoil leading to the trailing edge), the second digit its position along the chord in tenths of c (0–9), and the last two digits together define the maximum thickness as a percentage of c (from 05 to 50). Identifying the airfoil, therefore, reduces to a regression problem over three integer parameters.

The 2D computational domain $\mathsf{\Omega }$ is centered on the airfoil and extends radially up to $500c$, with unitary chord length c, and is discretized into $\mathcal{O}\left({10}^5\right)$ cells. Simulations are performed at a fixed angle of attack $\alpha ={10}^{\circ }$ and a freestream velocity of 30 m/s, using RANS for turbulence modeling. The dataset comprises 3025 flow fields obtained by varying the NACA digits and solving the corresponding CFD problems. The complete dataset of RANS simulations and the source code for the Clustering-based method applied to the AirNACA task are publicly available on Zenodo [15,49].

5.1.2. Surface Defect Detection (AirDEF)

The second dataset extends the NACA airfoil benchmark by introducing controlled geometric deformations to mimic manufacturing defects, structural damage, or ice accretion. The simulation setup is identical to the previous case, with the same computational domain, boundary conditions, and freestream parameters.

We consider three classes of defects, namely bumps, cavities, and cut trailing edges, parameterized through a compact 3-digit code $(i,j,k)$. Each airfoil undergoes controlled deformations by introducing a set of 18 different surface defects applied individually or in combination, for a total of 3600 CFD flow fields. Bumps and cavities, summarized and illustrated in

Table 2. NACA deformation codes and corresponding shapes for the 0012 airfoil. All rows except the last represent surface modifications in the form of bumps or cavities, with the right-hand column displaying more pronounced deformations (higher intensity) of the same type. The last row corresponds instead to the cut at the trailing edge.

Code	Shape	Code	Shape
$\left(1,\hspace{1em}0,\hspace{1em}0\right)$		$\left(2,\hspace{1em}0,\hspace{1em}0\right)$
$\left(0,\hspace{1em}1,\hspace{1em}0\right)$		$\left(0,\hspace{1em}2,\hspace{1em}0\right)$
$\left(-1,\hspace{1em}0,\hspace{1em}0\right)$		$\left(-2,\hspace{1em}0,\hspace{1em}0\right)$
$\left(0,\hspace{1em}-1,\hspace{1em}0\right)$		$\left(0,\hspace{1em}-2,\hspace{1em}0\right)$
$\left(1,\hspace{1em}1,\hspace{1em}0\right)$		$\left(2,\hspace{1em}2,\hspace{1em}0\right)$
$\left(-1,\hspace{1em}-1,\hspace{1em}0\right)$		$\left(-2,\hspace{1em}-2,\hspace{1em}0\right)$
$\left(1,\hspace{1em}-1,\hspace{1em}0\right)$		$\left(2,\hspace{1em}-2,\hspace{1em}0\right)$
$\left(-1,\hspace{1em}1,\hspace{1em}0\right)$		$\left(-2,\hspace{1em}2,\hspace{1em}0\right)$
$\left(0,\hspace{1em}0,\hspace{1em}1\right)$		$\left(0,\hspace{1em}0,\hspace{1em}2\right)$

on a NACA0012 airfoil, are modeled using Gaussian functions centered at the chord midpoint: a bump produces a local elevation of the profile, while a cavity generates a small indentation. The first digit $i\in [-2,2]$ encodes the deformation on the suction side: a positive value corresponds to a bump, a negative value to a cavity, and the absolute value specifies the intensity, which can reach up to $4\%$ of the chord c. The second digit $j\in [-2,2]$ is defined analogously for the pressure side. The third digit $k\in [0,2]$ controls the trailing-edge cut, whose depth can reach up to $5\%$ of c. The complete dataset of the AirDEF experiments will be publicly released upon acceptance.

Pathology Identification in Real Upper Airways (NosePAT and NoseREAL)

The third dataset consists of LES simulations of airflows in human upper airways, focusing on the identification of septal deviations and turbinate hypertrophies on 3D patient geometries obtained from CT scan segmentation. A septal deviation is a condition where the nasal septum is deviated to one side, potentially obstructing airflow and causing breathing difficulties. Turbinate hypertrophy refers to the excessive enlargement of the nasal turbinates, leading to nasal congestion.

The dataset is derived from 7 CT scans of healthy patients provided by ASST Santi Paolo e Carlo in Milan (Italy), a medical institution we are collaborating with. To generate pathological variants, we follow the approach described in [11], where functional maps [45,47,50] are employed to transfer controlled geometric deformations across anatomically consistent meshes. This methodology allows ENT (Ear, Nose, and Throat) specialists to introduce synthetic deformations that mimic septal deviations and turbinate hypertrophies on real CT scans, while ensuring anatomical plausibility and preserving geometric variability. By adopting the approach proposed in [11], we generated 309 pathological geometries, on which we performed LES simulations of a steady-state inspiration. The CFD simulations were performed using OpenFOAM v9, employing the LES model under incompressible flow assumptions (see Section 4.1).

In addition to the 309 synthetic geometries, we extracted 10 real pathological cases (5 septal deviations, 5 hypertrophies) from CT scans, all diagnosed by medical experts, to evaluate whether a model trained on synthetic data can accurately detect real conditions (we refer to this experiment as NoseREAL). (Due to sensitivity reasons, the NosePAT and NoseREAL datasets are available from the corresponding author upon reasonable request.)

The computational domain contains the full internal volume of the upper airways, bounded externally by a spherical surface around the nostrils to mimic an open environment. Each mesh contains on the order of $\mathcal{O}\left({10}^7\right)$ cells, storing several tens of fluid-dynamic variables per element. Running one LES simulation requires about 96 HPC cores, 160 GB of RAM, and tens of thousands of core-hours, producing roughly 40 GB of data per case. The generation of real human upper-airway CFD data is therefore highly resource-demanding and requires specialized expertise.

Figure 3 reports the cumulative distribution of cell counts and total volume as a function of cell size. While most cells have volumes between $2\times {10}^{-13}$ m³ and $5\times {10}^{-13}$ m³, they account for only a negligible fraction of the total volume, which is instead concentrated (about 80%) in cells around $3\times {10}^{-10}$ m³. To reduce computational costs, after LES simulations we discard all cells smaller than $3\times {10}^{-12}$ m³ (violet line in Figure 3). This filtering removes 91% of the cells while still preserving 95% of the domain volume. The discarded cells, located in the near-wall region at millimetric scales, are crucial for CFD fidelity but provide little information for pathology-related effects, which arise at larger anatomical scales. Hence, this filtering step is adopted solely for efficiency: including these cells would increase the data size without altering the information content relevant to our task.

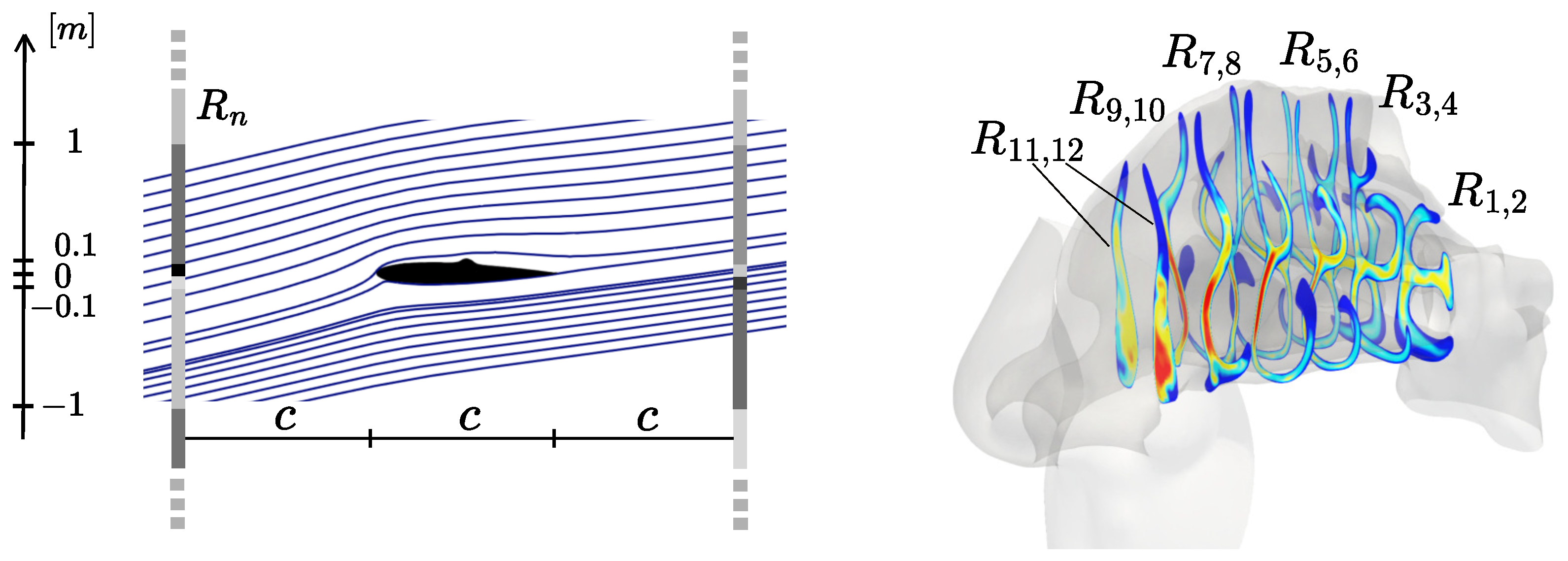
5.2. Baseline: Hand-Crafted Regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$

As baseline to our experiments, we manually extract the same regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ as in [10,11]. In AirNACA and AirDEF, these regions are defined along three vertical lines perpendicular to the airfoil chord (left-hand side of Figure 4), located at $x=-c$, $x=c$, and $x=10c$. Each line is divided into 8 regions, symmetrically distributed around $y=0$, with boundaries defined by the y-coordinates at $[-500,-10,-1,-0.1,0,0.1,1,10,500]c$. On these regions, we compute the regional averages of velocity magnitude $\left|\mathit{u}\right|$ and pressure p weighted by the cell area to account for non-uniform mesh resolution as described in Section 4.3.

In NosePAT and NoseREAL, we define 6 cross-sections as in [11]: the first and last correspond to the beginning and end of the olfactory region (right-hand side of Figure 4), while the remaining four are evenly spaced between them. Each cross-section is split into left and right semi-sections, yielding a total of 12 handcrafted regions ($R_1,\dots ,R_{12}$) on which we compute the average of the velocity magnitude $\left|\mathit{u}\right|$. It is worth noting that, in the dataset generation procedure adopted here, sections are defined once for each of the 7 healthy patients and then transferred to the corresponding pathological variants using functional mapping [11]. In a real application scenario, however, the sections would need to be manually defined on all 309 patient-specific geometries, highlighting the limited scalability of this expert-driven approach. This procedure compresses each LES simulation into 12 features, corresponding to the 12 sections shown in Figure 4, which are then used as inputs to the inference model K.

5.3. Conducted Experiments

In this section, we describe the experiments carried out to evaluate the proposed methods. We consider 6 approaches for constructing the feature set ${\mathbf{P}}_i$, which differ in the definition of regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ and their associated features.

(I) The first approach, named HC (Hand-Crafted features), serves as a baseline. It reproduces the expert-driven strategies proposed by Schillaci et al. [10] for airfoils and by our previous work [11] for nasal flows. In this setting, the regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ on which we compute features are defined a priori by experts on each geometry $M_i$ as described in Section 5.2 and shown in Figure 4. For inference, since the resulting feature sets ${\left\{{\mathbf{P}}_i\right\}}_{i=1}^m$ have fixed size and ordering across cases, we adopt a MLP consistently with [10,11] (details on the ML models in Section 5.6).

(II) In CR+HC (Clustering Regions with Hand-Crafted features), we introduce clustering to identify regions with the operator $\mathsf{\Phi }$, but retain the same regional averages of fluid-dynamic quantities as in the HC setting. This allows us to assess how clustering influences performance without altering the definition of features. For AirNACA and AirDEF, we apply the C-PROP clustering strategy described in Section 4.1, using as reference a NACA0012, while for NosePAT and NoseREAL, the first of the seven healthy patients in the training set is adopted as reference. Since we rely on C-PROP, the resulting feature sets ${\left\{{\mathbf{P}}_i\right\}}_{i=1}^m$ are directly comparable across flow fields, enabling the use of a MLP as model K.

(III) In FREE-CR+FC (C-FREE strategy, Clustering Regions, Features inside Clusters), the operator $\mathsf{\Phi }$ implements the Clustering-based method as described in Section 4.1 using as features the regional averages of quantities in Table 1. Here, clusters are computed independently on each simulation using the BGMM, so both the number and order of clusters may vary. The resulting feature vectors ${\left\{{\mathbf{p}}_j^i\right\}}_{j=1}^k\in {\mathbf{P}}_i$ are processed using a Point Transformer (PT), which naturally handles unordered sets of varying size, as discussed in Section 4.4.

(IV) In PROP-CR+FC (C-PROP strategy, Clustering Regions, Features inside Clusters), $\mathsf{\Phi }$ enforces consistency across simulations by propagating clusters from a reference case using the C-PROP approach described in Section 4.1, adopting the same references as in CR+HC. This guarantees that the number and ordering of the feature vectors ${\left\{{\mathbf{p}}_j^i\right\}}_{j=1}^k\in {\mathbf{P}}_i$ remain fixed across the training set, enabling direct comparison of the sets of features across the training set. As in CR+HC and HC, we employ an MLP for training and testing.

(V) In MORPH+HC (MORPHing with Hand-Crafted features), $\mathsf{\Phi }$ extracts the same features as in HC (introduced in [10,11], and described in Section 5.2), but computed on the common regions ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$ defined once on the reference geometry $M^{*}$. To this end, all simulations are first morphed onto $M^{*}$ (see Section 5.4 for details on the morphing procedure), so that each CFD flow field ${\mathbf{F}}_i$ is mapped to ${\mathbf{F}}_i^{*}$. Regional averages are then consistently computed within the fixed regions defined on $M^{*}$, ensuring that the resulting feature vectors have fixed size and consistent ordering across simulations. Therefore, as in HC, CR+HC, and PROP-CR+FC, we employ an MLP for inference.

(VI) Finally, in MORPH+FC (MORPHing with Features inside Clusters), the operator $\mathsf{\Phi }$ performs morphing as in MORPH+HC, mapping all flow fields ${\mathbf{F}}_i$ onto the reference mesh $M^{*}$ and employing the same expert-defined regions ${\left\{S_j^{*}\right\}}_{j=1}^{r^{*}}$. Unlike MORPH+HC, however, we adopt the set of features used in PROP-CR+FC and FREE-CR+FC, namely, regional averages of quantities in Table 1. This experiment combines the richness of clustering-derived features with the consistency and interpretability of expert-defined regions. Since the regions are fixed and ordered, being defined once by an expert on $M^{*}$, we adopt an MLP for inference.

Table 3. Summary of the conducted experiments. Each setting differs in how regions are defined, which features are extracted, and the inference model employed.

Experiment	Regions ${\left\{{\mathit{S}}_{\mathit{j}}^{\mathit{i}}\right\}}_{\mathit{j}=1}^{{\mathit{r}}_{\mathit{i}}}$	Model K
HC (Baseline)	Expert-defined (expert-defined regions and features described in Section 5.2)	MLP
CR+HC	Clustering-based (regions from clustering, same features as HC)	MLP
FREE-CR+FC	Clustering-based (regions from clustering, features in Table 1)	PT
PROP-CR+FC	Clustering-based (clusters propagated from a reference, features in Table 1)	MLP
MORPH+HC	Expert-defined (regions and features of HC transferred via morphing)	MLP
MORPH+FC	Expert-defined (regions transferred via morphing, features in Table 1)	MLP

summarizes the different experimental settings, highlighting how regions, features, and models are combined.

5.4. Morphing onto the Reference $M^{*}$

In this section, we provide additional details on the morphing procedure described in Section 4.2. In general, the morphing procedure requires as input the correspondence mapping ${\pi }_i$ between the boundaries of the current and reference geometries. Therefore, for the i-th mesh $M_i$, the boundary displacements ${\mathbf{d}}_i^b$ are prescribed on the boundary nodes ${\left\{{\mathbf{b}}_{i,k}\right\}}_{k=1}^{n_b}$ as the coordinate differences between corresponding points on $\partial {\mathsf{\Omega }}_i$ and $\partial {\mathsf{\Omega }}^{*}$, and are smoothly propagated to the interior nodes through RBF interpolation [14].

Based on the work by Casenave et al. [13], in the case of airfoils (AirNACA and AirDEF experiments), we directly assign boundary displacements based on aerodynamic prior knowledge of the boundary conditions illustrated on the left-hand side of Figure 5. Here, the domain boundary $\partial {\mathsf{\Omega }}_i$ consists of the airfoil surface and the external farfield. Points on the farfield are kept fixed to enforce a zero displacement mapping, while the leading (LE) and trailing (TE) edges are associated with the corresponding points of the reference geometry. The nodes lying on the suction side (upper surface in blue in Figure 5) and on the pressure side (lower surface in red in Figure 5) are matched with nodes on the respective curves of the reference, preserving the local node density relative to the boundary length. The support radius $r_s$ is set proportionally to the chord length, ensuring that deformations remain localized around the airfoil while maintaining mesh quality in the outer regions of the domain.

For the upper airways (NosePAT and NoseREAL), boundary displacements are obtained from anatomically consistent point-to-point maps computed with functional maps [45,47,50] following [11]. The functional maps framework establishes point-to-point correspondences between shapes by projecting them onto a spectral domain, namely the space spanned by the eigenfunctions of the Laplace–Beltrami operator [51]. In this basis, smooth maps between shapes can be compactly represented as linear operators acting on spectral coefficients, providing a stable and efficient way to encode correspondences. In practice, ${\pi }_i$ is obtained by projecting descriptors (e.g., landmarks, geodesic segments, spectral descriptors) into the Laplace–Beltrami basis, solving for the optimal linear operator in the functional domain, and then converting this map into vertex-wise correspondences. The resulting dense point-to-point mapping ${\pi }_i$ (illustrated on the right-hand side of Figure 5) associates each vertex of $\partial {\mathsf{\Omega }}_i$ with the corresponding vertex on the reference surface $\partial {\mathsf{\Omega }}^{*}$ that best preserves spectral and geometric consistency. By leveraging functional mapping, we ensure robust alignment of complex anatomical surfaces, even in the presence of local variability or partial data, guaranteeing consistent correspondences across the septum, turbinates, and lateral walls of the nasal cavity. The computation of ${\pi }_i$ requires as input a small set of corresponding points between $\partial {\mathsf{\Omega }}_i$ and $\partial {\mathsf{\Omega }}^{*}$, which serve as landmarks to guide the functional alignment. These landmarks are defined manually but are few in number and easily identifiable, making the process simple and considerably less costly than manually redefining the regions ${\left\{S_j^i\right\}}_{j=1}^{r_i}$ for each geometry. More details can be found in [11]. From the point-to-point map ${\pi }_i$, we derive the prescribed boundary displacements ${\mathbf{d}}_i^b$ introduced in Section 4.2 and used in (5) to interpolate the displacement field ${\mathbf{d}}_i\left(\mathbf{x}\right)$ within the interior mesh. Here, the support radius $r_s$ is set to an average value of the inter-nostril distance, which provides a natural global scale for the upper-airways scenario and allows the deformation to propagate smoothly inside the volume while adapting to anatomical variability.

5.5. Challenges in the 3D Extension and Computational Costs

Moving from two- to three-dimensional CFD simulations introduces several practical challenges that affect both computation and geometry handling. First, the computational cost increases considerably, since 3D meshes may contain tens of millions of cells, leading to high memory usage and long simulation times. In our implementation, the clustering step was performed on the Leonardo Data Centric General Purpose (DCGP) partition of the CINECA HPC system, running one process per core across three compute nodes equipped with dual Intel Xeon Platinum 8480+ CPUs (56 cores per CPU). For 2D airfoil simulations (around 300,000 cells), clustering through the BGMM required approximately 10–12 min per sample. For 3D nasal geometries, where the filtered meshes contained about 1.5–1.7 million cells per case, clustering took around 1.5 h per sample, consistent with the expected linear scaling of the BGMM with the number of cells. The morphing procedure was executed on the same HPC infrastructure used for clustering. For the airfoil datasets, each morphing process required approximately 30 min per case, including both the RBF deformation and finite element interpolation stages. In the 3D nasal geometries, where the number of mesh nodes and control points increases by roughly one order of magnitude, the morphing requires about 4–5 h per sample.

Second, defining accurate point-to-point correspondences on complex anatomical 3D surfaces may be difficult, especially when boundaries have irregular shapes or partial occlusions. To address this, we leverage the shared topological structure across patients’ anatomies and employ advanced computer-graphics tools based on functional maps to recover dense and anatomically consistent correspondences from a few manually identified landmarks, as described in Section 5.4. The point-to-point correspondence between boundaries is computed offline on a personal workstation following [11], and takes approximately 15 min per geometry while requiring no HPC resources.

Finally, maintaining mesh quality during the morphing process is critical. As in [13], we address this issue by using compactly supported $C^2$ radial basis functions (see Section 4.2) with an adaptive support radius, which ensures smooth deformations and avoids mesh distortion. Despite the increase in computational cost, these methods remain efficient and practical for realistic 3D applications, enabling the proposed framework to be applied to complex geometries such as human upper airways while preserving numerical stability, accuracy, and scalability.

5.6. Models Training and Evaluation

As in [10,11], we train simple MLPs for HC, CR+HC, PROP-CR+FC, MORPH+HC, and MORPH+FC, while we adopt a Point Transformer model for FREE-CR+FC. All models are defined with a comparable number of parameters in order to evaluate the performance of different feature extraction strategies under similar learning capacity. We report the details on the model architectures and training setup in

Table 4. Summary of the inference model architectures used for K. As in [10,11], we train simple MLPs for HC, CR+HC, PROP-CR+FC, MORPH+HC, and MORPH+FC, and adopt a Point Transformer (PT) for FREE-CR+FC. All models are defined with a comparable number of parameters to ensure similar learning capacity. The output dimension is left unspecified, as it depends on the target variable in each experimental scenario (AirNACA, AirDEF, or NosePAT).

Model	Experiments	Architecture	Training Setup
MLP	HC, CR+HC, PROP-CR+FC, MORPH+HC, MORPH+FC	Flatten, Dense (256, 128, 64, 32, 16, 8, output dimension)	Batch size: 16 Optimizer: Adam + exponential decay (LR 0.001, decay 0.985, steps 150) Epochs: up to 1000 with early stopping (patience = 10)
PT	FREE-CR+FC	2× Attention (32, 64), Dense (128, 64, 32, 16, output dimension)	Batch size: 16 Optimizer: Adam (LR 0.0001) Epochs: up to 1000 epochs with early stopping (patience = 10)

.

For both AirNACA and AirDEF, we preprocess the data by standardizing and randomly shuffling the samples, then partition them into 5 folds for cross-validation. At each iteration, one fold is reserved for testing, while the remaining folds are further divided into training (80%) and validation (20%). As these are regression tasks, the models are optimized using the mean squared error (MSE) loss. Since the predicted values are not necessarily integers, they are rounded to obtain the final output code. We report the performance corresponding to the average over the 5 folds, evaluated through the mean absolute error (MAE) on each digit of the code and the overall accuracy, defined as the proportion of codes correctly reconstructed after rounding the prediction to the nearest integer.

In NosePAT, performance is assessed through a Leave-One-Patient-Out Cross-Validation (LOPOCV). Here, in each fold, all synthetic samples associated with one of the 7 healthy patients are excluded from training and used for testing, ensuring that models are always evaluated on anatomies never seen during training. For every iteration, the remaining patients’ data are divided into 85% for training and 15% for validation, and the outcomes are averaged across folds. Pathology identification is formulated as a binary classification problem, with models trained using categorical cross-entropy as the loss. Classification accuracy is adopted as the main evaluation metric.

Finally, in the NoseREAL experiment, models are trained on all 309 samples from NosePAT using the same hyperparameters and loss function, and evaluated on 10 real pathological patients, simulating a realistic diagnostic scenario. As a performance metric, we report the modal score, defined as the number of correctly classified patients most frequently obtained over multiple trainings of the same model. This measure provides a compact summary of the typical performance in this small-scale evaluation.

5.7. Results

The outcomes of our experiments are summarized in

Table 5. Test accuracy across all tasks. On the right-hand side, we also report the modal score on the set of real pathological patients. Best results are highlighted in bold, while second-best results are underlined.

	Test Accuracy			Score
	AirNACA	AirDEF	NosePAT	NoseREAL
HC (Baseline)	84.6%	65.6%	88.8%	8/10
CR+HC	85.0%	83.2%	71.5%	6/10
PROP-CR+FC	86.5%	88.7%	86.8%	8/10
FREE-CR+FC	85.1%	84.2%	77.5%	7/10
MORPH+HC	82.4%	64.1%	84.3%	7/10
MORPH+FC	82.5%	64.3%	88.5%	8/10

and

Table 6. Mean Absolute Error (MAE) and standard deviation ($\sigma$) for each digit of the regression code in AirNACA and AirDEF tasks. Best results (lowest MAE) are highlighted in bold, while second-best results are underlined.

	Mean Absolute Error (MAE) and Standard Deviation ($\mathit{\sigma }$)
	AirNACA						AirDEF
	I Digit		II Digit		III Digit		I Digit		II Digit		III Digit
	MAE	±$\mathbf{\sigma }$	MAE	±$\mathbf{\sigma }$	MAE	±$\mathbf{\sigma }$	MAE	±$\mathbf{\sigma }$	MAE	±$\mathbf{\sigma }$	MAE	±$\mathbf{\sigma }$
Range	[0:9]		[0:9]		[05:50]		[−2:2]		[−2:2]		[0:2]
HC (Baseline)	0.17	0.23	0.30	0.24	0.17	0.26	0.35	0.25	0.33	0.18	0.11	0.15
CR+HC	0.16	0.20	0.28	0.21	0.16	0.23	0.22	0.21	0.21	0.17	0.03	0.12
PROP-CR+FC	0.14	0.19	0.24	0.21	0.15	0.24	0.18	0.19	0.19	0.18	0.01	0.11
FREE-CR+FC	0.14	0.21	0.26	0.20	0.16	0.19	0.21	0.22	0.21	0.18	0.02	0.09
MORPH+HC	0.18	0.23	0.30	0.25	0.19	0.30	0.38	0.27	0.37	0.22	0.12	0.15
MORPH+FC	0.17	0.23	0.29	0.24	0.16	0.27	0.36	0.25	0.35	0.18	0.11	0.14

. Table 5 reports the test accuracy of all inference models across the considered tasks, while Table 6 details the mean absolute error (MAE) and the standard deviation for each digit of the regression codes.

5.7.1. AirNACA and AirDEF

The results on the airfoils datasets in Table 5 show that the Clustering-based method is overall beneficial when compared to the expert-driven handcrafted baseline (HC) proposed in [10]. This is demonstrated by the consistent increase in accuracy from HC, to CR+HC (where the same features are extracted from regions defined by clustering), and further to the full clustering settings FREE-CR+FC and PROP-CR+FC (where additional features derived from clusters are used). As expected, MORPH+HC and MORPH+FC yield performances very similar to HC. In the aerospace scenario, in fact, the handcrafted regions of [10] (visible on the left-hand side of Figure 4) are defined far from the airfoil surface and are therefore almost unaffected by the morphing procedure. For this reason, the morphing experiments in AirNACA and AirDEF should be regarded primarily as a validation of the morphing pipeline itself: they confirm that the deformation procedure preserves consistency across geometries without degrading the CFD data, while the slight performance decrease with respect to HC simply reflects the limited sensitivity of the employed regions to small geometric variations.

In AirNACA, PROP-CR+FC achieves the highest accuracy (86.5%), while FREE-CR+FC outperforms HC but remains slightly behind PROP-CR+FC. This indicates that enforcing both ordering and cardinality of clusters to be consistent across simulations, as described in Section 4.1, yields a more stable and directly comparable representation, which in turn benefits regression tasks. Although FREE-CR+FC adapts flexibly to each simulation and captures relevant local information, the lack of ordering among clusters makes the learning problem more challenging, which justifies its slightly lower performance compared to PROP-CR+FC. A similar trend is observed in AirDEF, where improvements over the handcrafted baseline are even more apparent: while HC yields the lowest accuracy (65.6%), PROP-CR+FC reaches 88.7% and FREE-CR+FC achieves 84.3%. We attribute the large gap between HC and clustering-based approaches to the nature of the handcrafted regions proposed in [10]: being positioned far from the airfoil surface, they fail to capture the localized flow perturbations induced by surface defects such as bumps, cavities, and trailing-edge cuts. By contrast, physics-based clustering defines regions directly from the governing equations, which makes them more localized around the relevant aerodynamic structures. As a result, the extracted features better reflect the underlying physics of the flow and provide more informative and discriminative descriptors for the learning task.

Table 6 provides further insights into the regression tasks. In AirNACA, the second digit (position of maximum camber) consistently exhibits the highest MAE across all experiments, confirming that it is the most difficult parameter to predict. By contrast, the thickness (third digit) is predicted with the lowest error relative to its range, indicating that flow features strongly encode thickness information. In AirDEF, a similar pattern is observed: the trailing-edge cut (third digit of the defect code) is the easiest to infer, as its presence produces a distinct and structured wake that is reliably captured by physics-based clustering. The first two digits, encoding bump or cavity intensity and location, remain more challenging due to their subtler aerodynamic signatures, leading to higher errors.

5.7.2. NosePAT

In the medical application, the trends partially differ. Table 5 shows that including features of Table 1 enhances the classification performance also in this case: PROP-CR+FC attains 86.8% accuracy, while FREE-CR+FC remains at 77.5%. However, the handcrafted baseline (HC) achieves the highest test performance (88.8%), outperforming both clustering strategies. This result is not unexpected: in HC, the six cross-sectional sections used to extract features (see Figure 4) were defined ad hoc for this task to capture the pathological deformations associated with septal deviations and turbinate hypertrophies. As a result, HC benefits from a strong inductive bias provided by medical expertise, which is not available to clustering. Nevertheless, PROP-CR+FC remains close to HC and achieves competitive results without requiring any expert-driven feature definition, demonstrating the portability of clustering-based methods to anatomically complex domains.

Regarding the morphing-based experiments, MORPH+HC (84.3%) achieves performance comparable to HC, confirming that morphing can reliably transfer handcrafted regions onto a common reference while ensuring consistency across anatomies. MORPH+FC attains 88.5%, almost matching the baseline and surpassing both clustering strategies. This demonstrates the benefit of combining the richer feature set derived from clustering with the spatial consistency of morphing: expert-defined sections provide interpretability, while the additional physical descriptors enhance discriminative capability. Overall, morphing makes it possible to exploit expert knowledge across all samples without case-by-case redefinition, thus combining the strengths of HC with the scalability required in medical applications, where anatomical variability would otherwise make manual definition impractical.

5.7.3. NoseREAL

The results on real pathological anatomies further confirm the robustness of our methods. Here, models are trained on synthetic deformations described in [11] and then tested on unseen real pathological patients. Despite the small dataset size (ten pathological cases), both PROP-CR+FC and MORPH+FC achieve an 8/10 modal score, while FREE-CR+FC and HC obtain slightly lower results. These outcomes suggest that our methods can generalize beyond synthetic training data and reliably identify real pathologies using only CFD information, even in the presence of limited samples. The ability to correctly classify the majority of real patients highlights the potential of Clustering-based and Morphing-based feature extraction for clinical applications.

6. Conclusions and Future Works

In this work, we have addressed the problem of training a classifier directly from CFD data, where the high dimensionality and complexity of flow fields typically require a preprocessing step to obtain more compact and structured representations. To address this challenge, we proposed two complementary methods.

First, we introduce a Clustering-based method which automatically identifies regions within the flow field based on the local balance of physical terms in the governing equations. This approach is particularly effective when the flow field exhibits clearly distinguishable physical phenomena, such as boundary layers, separation bubbles, or wake regions. In these cases, clustering isolates zones governed by distinct flow behaviors, yielding physically meaningful descriptors without any manual intervention. This method proved especially effective in aerodynamic applications, reaching 86.5% accuracy in airfoil identification and 88.7% in defect detection, outperforming the handcrafted baseline.

Second, we presented a Morphing-based method that aligns heterogeneous geometries and their CFD fields onto a common reference mesh using Radial Basis Function deformation. In these settings, morphing ensures spatial consistency and preserves interpretability, achieving 88.5% accuracy in pathology classification, comparable to expert-driven baselines. However, unlike fully handcrafted approaches [10,11], it requires significantly less expert intervention, since the regions are defined once on a reference geometry and automatically reused across all patients. This approach is preferable in applications where expert knowledge remains fundamental, such as medical CFD, where regions correspond to anatomical areas (e.g., nasal cavities or sinuses) that must retain a clear physical and clinical interpretation. Morphing is inherently designed for geometries that share a consistent topological structure, making it naturally well-suited for anatomical datasets or families of shapes with stable connectivity. The results demonstrate that the morphing strategy successfully transfers anatomical knowledge across patients and geometries, enabling consistent learning despite limited data availability.

Overall, the findings of our experiments confirm that the proposed methods preserve physical consistency across geometries and remain effective in both aerospace and clinical applications. Together, they substantially reduce the need for expert intervention and establish a scalable framework for automated inference from CFD data, grounded on both physics- or expert-based principles.

In future work, we plan to integrate the clustering and morphing components within end-to-end Physics-Informed Neural Networks (PINNs) architectures, enabling inference models to be directly constrained by governing equations for fully differentiable flow representations. We also aim to extend our methods to unsteady and fully three-dimensional CFD scenarios to capture time-dependent dynamics and more realistic operating conditions. A further step will involve developing inference models capable of exploiting sparse or incomplete CFD data, thus enabling applications where only partial flow measurements or limited simulations are available. Another interesting research direction consists of exploring techniques for uncertainty quantification and domain adaptation across different geometries and boundary conditions, improving generalization and robustness on unseen configurations. These developments will be supported by stronger collaborations with aerospace and medical experts, combining experimental, numerical, and clinical data to validate the methodology in practical contexts such as aerodynamic optimization, sensor placement, and non-invasive diagnosis based on airflow patterns. Pursuing these research directions will further enhance the flexibility, interpretability, and practical impact of the proposed framework. Ultimately, our goal is to develop classifiers and inference models capable of operating directly on CFD data with minimal preprocessing, enabling faster, more scalable, and more interpretable applications across both engineering and healthcare domains.