Bow-Tie-Based Risk Assessment of Fishing Vessel Marine Accidents in the Open Sea Using IMO GISIS Data
Abstract
1. Introduction
- A systematic analysis of open-sea fishing vessel accidents that addresses the existing research gap concerning accident patterns in areas characterized by fragmented jurisdiction and limited regulatory oversight;
- Development of an integrated bow-tie-based analytical framework connecting FTA, Firth logistic regression, ETA, and QRA, enabling holistic risk modeling that simultaneously accounts for accident causation, outcome severity, and rare-event characteristics;
- Identification of accident-type-specific risk profiles, demonstrating that human factors primarily drive collisions, structural instability underlies capsizing events, and technical deterioration is the dominant factor in sinkings;
- Quantification of accident probabilities and resultant severities, providing evidence-based priorities for targeted safety interventions in remote maritime regions where enforcement and emergency response capabilities are inherently constrained.
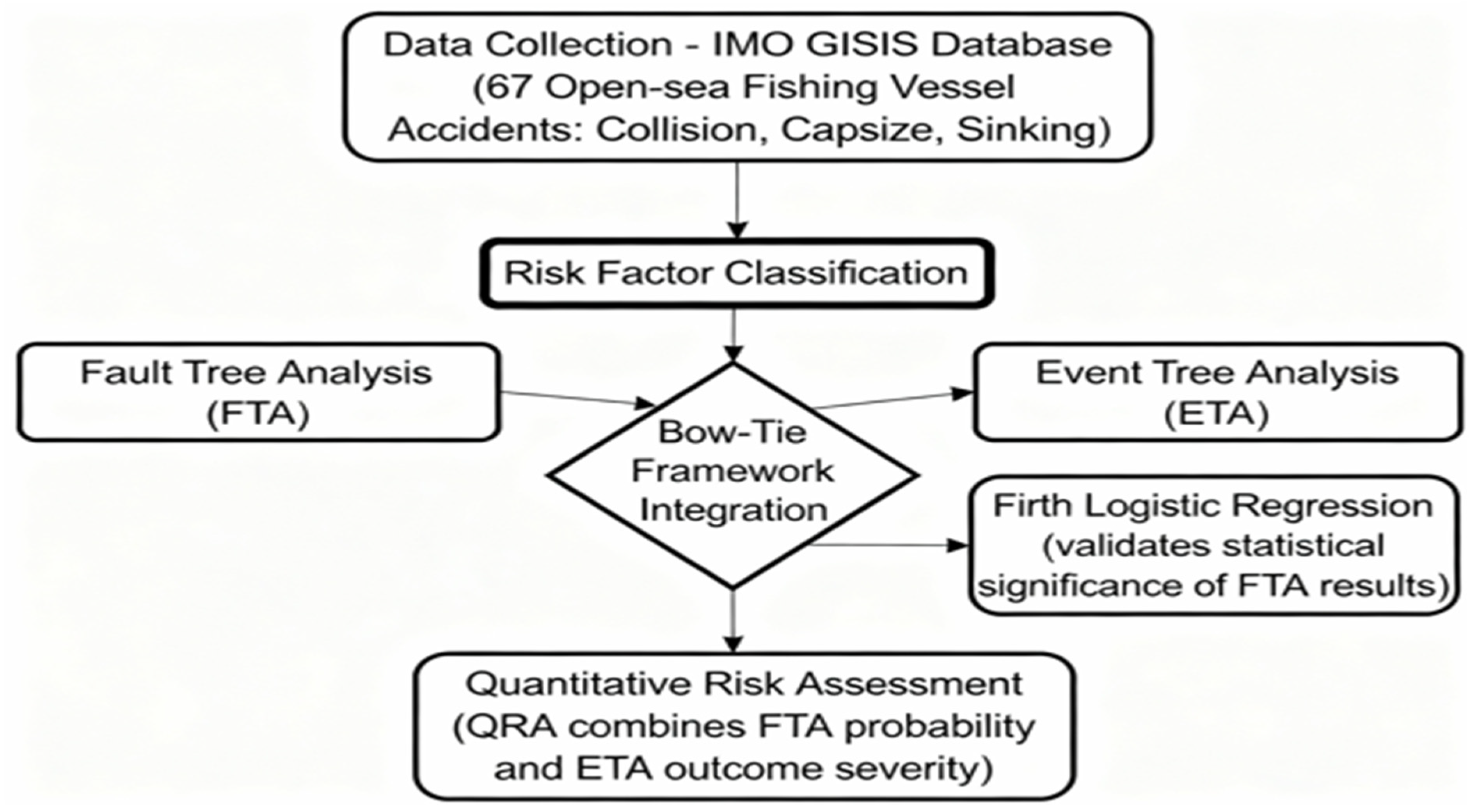
2. Materials and Methods
2.1. Data
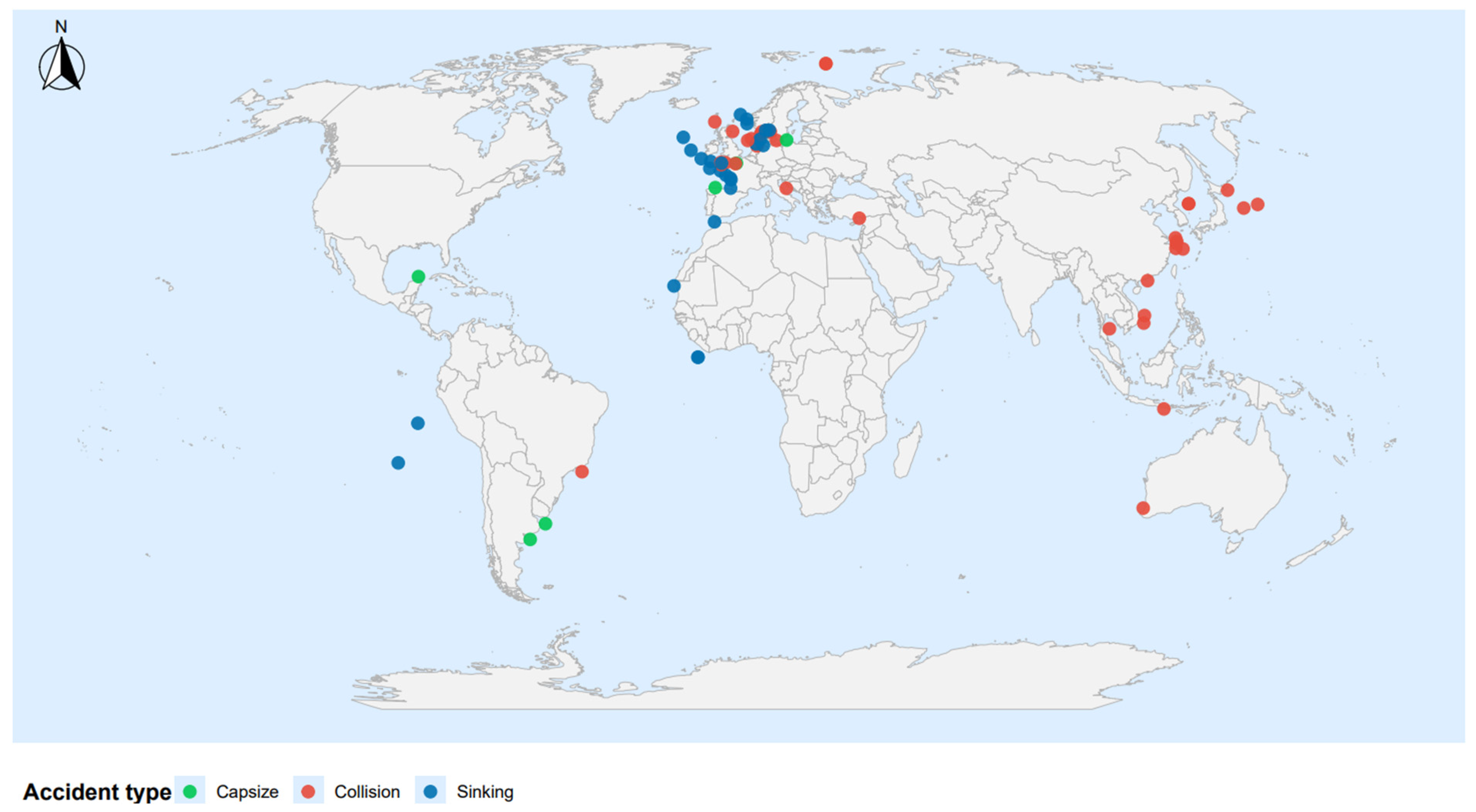
2.1.1. Ship Accident Database
2.1.2. Risk Influential Factors
2.2. Methods
2.2.1. Bow-Tie
2.2.2. Fault Tree Analysis (FTA)
2.2.3. Firth Logistic Regression
2.2.4. Event Tree Analysis (ETA)
2.2.5. Bow-Tie-Based QRA
2.2.6. Sensitivity Analysis
3. Results
3.1. Descriptive Statistics
- (1)
- COLREG violation/navigation error. Failures in collision-avoidance maneuvers and non-compliance with COLREG Rules.
- (2)
- Watch and communication failure. Inadequate look-out or breakdown in communication among bridge or engine personnel.
- (3)
- Hull failure/leakage. Structural deterioration or localized hull damage leading to flooding.
- (4)
- Improper hatch closure. Unsealed hatches or open fish-hold covers permitting seawater ingress.
- (5)
- Pump failure/insufficient capacity. Malfunction or insufficient discharge rate of bilge pumps.
- (6)
- Overload/stability issues. Loss of stability due to excessive loading or improper weight distribution.
3.2. Bow-Tie
3.2.1. FTA
3.2.2. Firth Logistic Regression Analysis
3.2.3. ETA
3.3. Bow-Tie-Based QRA
3.4. Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CI | Confidence interval |
| EMSA | European Maritime Safety Agency |
| EPV | Events per variable |
| ETA | Event tree analysis |
| FSA | Formal Safety Assessment |
| FTA | Fault tree analysis |
| FWSI | Fatalities and Weighted Serious Injuries |
| GISIS | Global Integrated Shipping Information System |
| IMO | International Maritime Organization |
| MCI | Marine Casualties and Incidents |
| MLE | Maximum likelihood estimation |
| OR | Odds ratio |
| QRA | Quantitative risk assessment |
| RIF | Risk influential factors |
| RR | Relative risk |
| SOLAS | Safety of Life at Sea |
Appendix A
| Event | RIFs | OR | p-Value |
|---|---|---|---|
| Capsize | Season—Winter | 1.82 | 0.623 |
| Wave(m) ≥2 | 1.884 | 0.659 | |
| Length (m) ≥24 | 0.653 | 0.684 | |
| Age of vessel (years) ≥30 | 0.85 | 1 | |
| Beam (B/L) ≥0.30 | 0.694 | 1 | |
| Wind (m/s) ≥10 | 0.975 | 1 | |
| Visibility (nm) <2 | 1.717 | 1 |
References
- Jin, D.; Thunberg, E. An analysis of fishing vessel accidents in fishing areas off the Northeastern United States. Saf. Sci. 2005, 43, 523–540. [Google Scholar] [CrossRef]
- Jensen, O.C.; Petursdottir, G.; Holmen, I.M.; Abrahamsen, A.; Lincoln, J. A review of fatal accident incidence rate trends in fishing. Int. Marit. Health 2014, 65, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Pillay, A.; Kwon, Y.S.; Wall, A.D.; Loughran, C.G. An analysis of fishing vessel accidents. Accid. Anal. Prev. 2005, 37, 1019–1024. [Google Scholar] [CrossRef] [PubMed]
- Collins, C.; Nuno, A.; Broderick, A.; Curnick, D.J.; de Vos, A.; Franklin, T.; Jacoby, D.M.P.; Mees, C.; Moir-Clark, J.; Pearce, J.; et al. Understanding persistent non-compliance in a remote, large-scale marine protected area. Front. Mar. Sci. 2021, 8, 650276. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, L.; Zhang, F.; Yan, Z.; Ruan, X.; Min, K.; Li, M. Integrating island spatial information and integer optimization for locating maritime search and rescue bases: A case study in the South China Sea. ISPRS Int. J. Geo-Inf. 2019, 8, 88. [Google Scholar] [CrossRef]
- Bielić, T.; Hasanspahić, N.; Čulin, J. Preventing marine accidents caused by technology-induced human error. Pomorstvo 2017, 31, 33–37. [Google Scholar]
- Hasanspahić, N.; Bošnjak, R.; Brčić, D. The role of the human factor in marine accidents. J. Mar. Sci. Eng. 2021, 9, 261. [Google Scholar] [CrossRef]
- Maternová, A.; Materna, M. Research of maritime accidents based on HFACS framework. Transp. Res. Procedia 2023, 74, 1224–1231. [Google Scholar] [CrossRef]
- Maternová, A.; Materna, M.; Dávid, A. Revealing causal factors influencing sustainable and safe navigation in Central Europe. Sustainability 2022, 14, 2231. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, S. Framework for Process Analysis of Maritime Accidents Caused by the Unsafe Acts of Seafarers: A Case Study of Ship Collision. J. Mar. Sci. Eng. 2022, 10, 1793. [Google Scholar] [CrossRef]
- Zhang, W.; Meng, X.; Yang, X.; Lyu, H.; Zhou, X.-Y.; Wang, Q. A practical risk-based model for early warning of seafarer errors using integrated Bayesian network and SPAR-H. Int. J. Environ. Res. Public Health 2022, 19, 10271. [Google Scholar] [CrossRef] [PubMed]
- Kose, E.K.; Dincer, A.C.; Durukanoglu, H.F. Risk assessment of fishing vessels. Tr. J. Eng. Environ. Sci. 1998, 22, 417–428. [Google Scholar]
- Jin, D.; Kite-Powell, H.L.; Thunberg, E.; Solow, A.R.; Talley, W.K. A model of fishing vessel accident probability. J. Saf. Res. 2002, 33, 497–510. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Du, W.; Feng, H.; Ye, Y.; Grifoll, M.; Liu, G.; Zheng, P. Identification of Risk Influential Factors for Fishing Vessel Accidents Using Claims Data from Fishery Mutual Insurance Association. Sustainability 2023, 15, 13427. [Google Scholar] [CrossRef]
- Obeng, F.; Domeh, V.; Khan, F.; Bose, N.; Sanli, E. Capsizing accident scenario model for small fishing trawler. Saf. Sci. 2022, 145, 105500. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). Revised Guidelines for the Implementation of the Casualty Investigation Code (Resolution MSC.255(84)). In MSC-MEPC. 3/circ.4/Rev.1; IMO: London, UK, 2013. [Google Scholar]
- Su, G. Research on cause analysis and management of coal mine safety risk based on social network and bow-tie model. Sci. Rep. 2025, 15, 29850. [Google Scholar] [CrossRef] [PubMed]
- Antão, P.; Guedes Soares, C. Analysis of the influence of human errors on the occurrence of coastal ship accidents in different wave conditions using Bayesian Belief Networks. Accident Anal. Prev. 2019, 133, 105262. [Google Scholar] [CrossRef] [PubMed]
- Firth, D. Bias reduction of maximum likelihood estimates. Biometrika 1993, 80, 27–38. [Google Scholar] [CrossRef]
- Heinze, G.; Schemper, M. A solution to the problem of separation in logistic regression. Stat. Med. 2002, 21, 2409–2419. [Google Scholar] [CrossRef] [PubMed]
- Puhr, R.; Heinze, G.; Nold, M.; Lusa, L.; Geroldinger, A. Firth’s logistic regression with rare events: Accurate effect estimates and predictions? Stat. Med. 2017, 36, 2302–2317. [Google Scholar] [CrossRef] [PubMed]
- European Maritime Safety Agency (EMSA). Risk Acceptance Criteria (Study 1); DNV GL: Lisbon, Portugal, 2015. [Google Scholar]
- International Maritime Organization (IMO). Revised guidelines for formal safety assessment (FSA) for use in the IMO rule-making process. In MSC-MEPC.2/Circ.12/Rev.2; Appendix 4; IMO: London, UK, 2018. [Google Scholar]
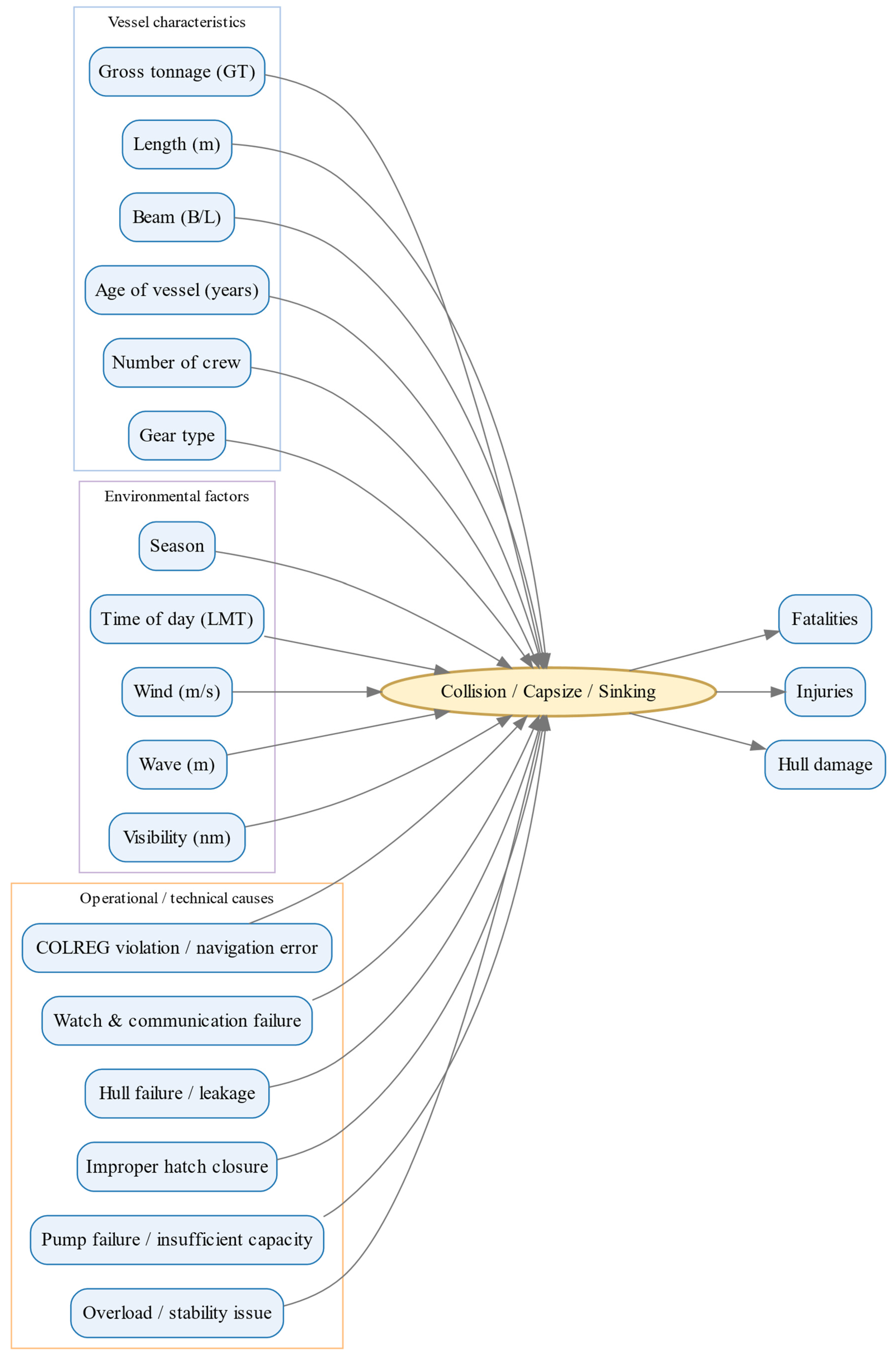
| Group | RIFs | Classification | Group | RIFs | Classification |
|---|---|---|---|---|---|
| Vessel characteristics | Gross tonnage (GT) | <100 GT | Environmental factors | Season | Spring (3–5) |
| 100–500 GT | Summer (6–8) | ||||
| >500 GT | Fall (9–11) | ||||
| Length (m) | <24 m | Winter (12–2) | |||
| ≥24 m | Time of day (LMT) | Day | |||
| Beam (B/L) | <0.20 | Night | |||
| 0.20–0.30 | Wind (m/s) | 0–5 | |||
| >0.30 | 5–10 | ||||
| Age of vessel (years) | <15 years | 10–15 | |||
| 15–30 years | >15 | ||||
| >30 years | Wave (m) | <1.0 | |||
| Number of crew | <5 | 1.0–2.5 | |||
| 5–10 | >2.5–4.0 | ||||
| >10 | ≥4.0 | ||||
| Gear type | Trawl | Visibility (nm) | <2 | ||
| 2–6 | |||||
| Non-Trawl | ≥6 |
| RIFs | Classification | Collision | Capsize | Sinking | Total |
|---|---|---|---|---|---|
| Gross tonnage * (GT) | <100 GT | 15 | 4 | 11 | 30 |
| 100–500 GT | 16 | 2 | 12 | 30 | |
| >500 GT | 3 | 0 | 3 | 6 | |
| Length (m) | <24 m | 18 | 4 | 15 | 37 |
| ≥24 m | 17 | 2 | 11 | 30 | |
| Beam/Length ratio * (B/L) | <0.20 | 10 | 0 | 4 | 14 |
| 0.20–0.30 | 19 | 5 | 10 | 34 | |
| >0.30 | 5 | 1 | 12 | 18 | |
| Age of vessel * (years) | <15 years | 14 | 0 | 4 | 18 |
| 15–30 years | 13 | 4 | 8 | 25 | |
| >30 years | 7 | 2 | 14 | 23 | |
| Number of crew | <5 | 11 | 2 | 12 | 25 |
| 5–10 | 16 | 3 | 5 | 24 | |
| >10 | 8 | 1 | 9 | 18 | |
| Gear type | Trawl | 16 | 5 | 20 | 41 |
| Non-trawl | 19 | 1 | 6 | 26 |
| RIFs | Classification | Collision | Capsize | Sinking | Total |
|---|---|---|---|---|---|
| Season | Spring | 11 | 1 | 7 | 19 |
| Summer | 8 | 1 | 4 | 13 | |
| Fall | 9 | 2 | 8 | 19 | |
| Winter | 7 | 2 | 7 | 16 | |
| Time of day (LMT) | Day | 7 | 3 | 12 | 22 |
| Night | 28 | 3 | 14 | 45 | |
| Wind * (m/s) | 0–5 | 12 | 2 | 6 | 20 |
| 5–10 | 14 | 2 | 11 | 27 | |
| 10–15 | 8 | 2 | 4 | 14 | |
| >15 | 1 | 0 | 4 | 5 | |
| Wave * (m) | <1.0 | 11 | 3 | 6 | 20 |
| 1.0–2.5 | 17 | 2 | 11 | 30 | |
| >2.5–4.0 | 6 | 1 | 4 | 11 | |
| ≥4.0 | 1 | 0 | 4 | 5 | |
| Visibility (nm) | <2 | 5 | 1 | 3 | 9 |
| 2–6 | 10 | 0 | 1 | 11 | |
| ≥6 | 20 | 5 | 22 | 47 |
| Causal Factors | Collision | Capsize | Sinking | Total |
|---|---|---|---|---|
| COLREG violation/navigation error | 33 | 0 | 4 | 37 |
| Watch & communication failure | 35 | 1 | 14 | 50 |
| Hull failure/leakage | 0 | 1 | 19 | 20 |
| Improper hatch closure | 0 | 2 | 12 | 14 |
| Pump failure/insufficient capacity | 0 | 0 | 20 | 20 |
| Overload/stability issue | 0 | 5 | 2 | 7 |
| Initiating Accident | Casualties | Vessel Damage Level | |||
|---|---|---|---|---|---|
| Fatalities | Injuries | L | S | V | |
| Collision | 85 | 4 | 6 | 10 | 19 |
| Capsize | 14 | 0 | 0 | 0 | 6 |
| Sinking | 4 | 1 | 0 | 0 | 26 |
| Top Event | RIFs | P(TE|x = 1) | P(TE|x = 0) | RR |
|---|---|---|---|---|
| Collision | Watch and communication failure | 0.714 | 0 | - |
| COLREG violation/navigation error | 0.892 | 0.067 | 13.31 | |
| Time of day (LMT)—night | 0.622 | 0.318 | 1.96 | |
| Length (m) ≥ 24 m | 0.567 | 0.486 | 1.17 | |
| Gross tonnage (GT) 100–500 | 0.533 | 0.500 | 1.07 | |
| Visibility (nm) < 2 | 0.556 | 0.517 | 1.08 | |
| Gross tonnage (GT) ≥ 500 | 0.500 | 0.517 | 0.97 | |
| Wind (m/s) ≥ 10 | 0.500 | 0.548 | 0.91 | |
| Number of crew > 10 | 0.444 | 0.551 | 0.81 | |
| Wave (m) ≥ 2 | 0.458 | 0.571 | 0.80 | |
| Season–Winter | 0.438 | 0.549 | 0.80 | |
| Number of crew < 5 | 0.440 | 0.571 | 0.77 | |
| Beam (B/L) ≥ 0.30 | 0.333 | 0.583 | 0.57 | |
| Gear type–Trawl | 0.390 | 0.731 | 0.53 | |
| Age of vessel (years) ≥ 30 | 0.308 | 0.650 | 0.47 | |
| Hull failure/leakage | 0 | 0.745 | 0.00 | |
| Improper hatch closure | 0 | 0.660 | 0.00 | |
| Pump failure/insufficient capacity | 0 | 0.745 | 0.00 | |
| Overload/stability issue | 0 | 0.583 | 0.00 |
| Top Event | RIFs | P(TE|x = 1) | P(TE|x = 0) | RR |
|---|---|---|---|---|
| Capsize | Overload/stability issue | 0.714 | 0.017 | 42.00 |
| Gear type–Trawl | 0.122 | 0.038 | 3.21 | |
| Improper hatch closure | 0.143 | 0.075 | 1.91 | |
| Wave (m) ≥ 2 | 0.125 | 0.071 | 1.76 | |
| Season—Winter | 0.125 | 0.078 | 1.60 | |
| Visibility (nm) < 2 | 0.111 | 0.086 | 1.29 | |
| Wind (m/s) ≥ 10 | 0.083 | 0.095 | 0.87 | |
| Number of crew < 5 | 0.080 | 0.095 | 0.84 | |
| Age of vessel (years) ≥ 30 | 0.077 | 0.100 | 0.77 | |
| Length (m) ≥ 24 | 0.067 | 0.108 | 0.62 | |
| Gross tonnage (GT) 100–500 | 0.067 | 0.111 | 0.60 | |
| Number of crew > 10 | 0.056 | 0.102 | 0.55 | |
| Beam (B/L) ≥ 0.30 | 0.056 | 0.104 | 0.54 | |
| Time of day (LMT)—night | 0.067 | 0.136 | 0.49 | |
| Hull failure/leakage | 0.050 | 0.106 | 0.47 | |
| Watch and communication failure | 0.020 | 0.278 | 0.07 | |
| COLREG violation/navigation error | 0 | 0.200 | 0.00 | |
| Pump failure/insufficient capacity | 0 | 0.128 | 0.00 | |
| Gross tonnage (GT) ≥ 500 | 0 | 0.100 | 0.00 |
| Top Event | RIFs | P(TE|x = 1) | P(TE|x = 0) | RR |
|---|---|---|---|---|
| Sinking | Gear type–Trawl | 0.488 | 0.231 | 2.11 |
| Pump failure/insufficient capacity | 0.488 | 0.231 | 2.11 | |
| Hull failure/leakage | 1.000 | 0.660 | 1.52 | |
| Wind (m/s) ≥ 10 | 1.000 | 0.660 | 1.52 | |
| Number of crew > 10 | 0.958 | 0.643 | 1.49 | |
| Number of crew < 5 | 0.500 | 0.347 | 1.44 | |
| Improper hatch closure | 0.480 | 0.333 | 1.44 | |
| Wave (m) ≥ 2 | 1.000 | 0.698 | 1.43 | |
| Overload/stability issue | 1.000 | 0.733 | 1.36 | |
| Age of vessel (years) ≥ 30 | 0.846 | 0.700 | 1.21 | |
| Beam (B/L) ≥ 0.30 | 0.778 | 0.771 | 1.01 | |
| Season—Winter | 0.750 | 0.765 | 0.98 | |
| Gross tonnage (GT) 100–500 | 0.733 | 0.778 | 0.94 | |
| Length (m) ≥ 24 | 0.733 | 0.784 | 0.93 | |
| Gross tonnage (GT) ≥ 500 | 0.667 | 0.767 | 0.87 | |
| Watch & communication failure | 0.673 | 1.000 | 0.67 | |
| COLREG violation/navigation error | 0.568 | 1.000 | 0.57 | |
| Time of day (LMT)—night | 0.311 | 0.545 | 0.57 | |
| Visibility (nm) < 2 | 0.444 | 0.810 | 0.55 |
| Accident | Variable | β (Coef) | Odds Ratio (OR) | 95% CI (Lower) | 95% CI (Upper) | p-Value | Significance |
|---|---|---|---|---|---|---|---|
| Collision | Age of vessel (years) ≥ 30 | −1.492 | 0.225 | 0.068 | 0.671 | 0.007 | ** |
| Wave (m) ≥ 2 | −0.887 | 0.412 | 0.125 | 1.237 | 0.115 | ||
| Beam (B/L) ≥ 0.30 | −0.878 | 0.416 | 0.1 | 1.637 | 0.21 | ||
| Season—Winter | −0.186 | 0.83 | 0.244 | 2.822 | 0.762 | ||
| Length (m) ≥ 24 | −0.168 | 0.845 | 0.238 | 2.913 | 0.79 |
| Accident | RIFs | β (Coef) | Odds Ratio (OR) | 95% CI (Lower) | 95% CI (Upper) | p-Value | Significance |
|---|---|---|---|---|---|---|---|
| Capsize | Age of vessel (years) ≥ 30 | −0.162 | 0.85 | 0.139 | 4.167 | 0.844 |
| Accident | RIFs | β (Coef) | Odds Ratio (OR) | 95% CI (Lower) | 95% CI (Upper) | p-Value | Significance |
|---|---|---|---|---|---|---|---|
| Sinking | Age of vessel (years) ≥ 30 | 1.589 | 4.9 | 1.596 | 16.885 | 0.005 | ** |
| Beam (B/L) ≥ 0.30 | 1.433 | 4.193 | 1.008 | 19.912 | 0.049 | * | |
| Wave (m) ≥ 2 | 0.814 | 2.256 | 0.707 | 7.964 | 0.172 | ||
| Length (m) ≥ 24 | 0.713 | 2.04 | 0.54 | 8.809 | 0.298 | ||
| Season—Winter | −0.075 | 0.928 | 0.254 | 3.2 | 0.906 |
| Casualties | Fatality | Injury Only | No Injury | N |
|---|---|---|---|---|
| Collision | 0.457 | 0.000 | 0.543 | 35 |
| Capsize | 0.667 | 0.000 | 0.333 | 6 |
| Sinking | 0.115 | 0.038 | 0.846 | 26 |
| Hull Damage Severity | V | S | L | N |
|---|---|---|---|---|
| Collision | 0.543 | 0.286 | 0.171 | 35 |
| Capsize | 1.000 | 0.000 | 0.000 | 6 |
| Sinking | 1.000 | 0.000 | 0.000 | 26 |
| Joint Probabilities of Human-Damage Scenarios | |
|---|---|
| Collision–Fatality–V | 0.371 |
| Collision–Fatality–S | 0.029 |
| Collision–Fatality–L | 0.057 |
| Collision–No injury–V | 0.171 |
| Collision–No injury–S | 0.257 |
| Collision–No injury–L | 0.114 |
| Capsize–Fatality–V | 0.667 |
| Capsize–No injury–V | 0.333 |
| Sinking–Fatality–V | 0.115 |
| Sinking–Injury only–V | 0.038 |
| Sinking–No injury–V | 0.846 |
| Accident | Human-Damage Scenarios | P (Top Event) | P (Consequence∣Event) | Severity | |
|---|---|---|---|---|---|
| Collision | Fatality–V | 0.522 | 0.371 | 1.0 × 0.8 | 0.155 |
| Capsize | Fatality–V | 0.090 | 0.667 | 1.0 × 0.8 | 0.048 |
| Sinking | Fatality–V | 0.388 | 0.115 | 1.0 × 0.8 | 0.036 |
| Accident | Scenarios | P (Gate) | Ratio | ||
|---|---|---|---|---|---|
| Collision | human_OR | 0.73 | 0.33 | 0.24 | 1.40 |
| Collision | human_AND | 0.55 | 0.25 | 0.24 | 1.06 |
| Capsize | overload_only | 0.10 | 0.07 | 0.06 | 1.17 |
| Capsize | overload_OR_env | 0.41 | 0.27 | 0.06 | 4.57 |
| Capsize | overload_AND_env | 0.06 | 0.04 | 0.06 | 0.67 |
| Sinking | pump_OR_hull | 0.33 | 0.13 | 0.30 | 0.43 |
| Sinking | pump_AND_hull | 0.27 | 0.11 | 0.30 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-H.; Kim, S.-H.; Ryu, K.-J.; Kwon, S.-Y.; Lee, Y.-W. Bow-Tie-Based Risk Assessment of Fishing Vessel Marine Accidents in the Open Sea Using IMO GISIS Data. Appl. Sci. 2025, 15, 12330. https://doi.org/10.3390/app152212330
Lee S-H, Kim S-H, Ryu K-J, Kwon S-Y, Lee Y-W. Bow-Tie-Based Risk Assessment of Fishing Vessel Marine Accidents in the Open Sea Using IMO GISIS Data. Applied Sciences. 2025; 15(22):12330. https://doi.org/10.3390/app152212330
Chicago/Turabian StyleLee, Seung-Hyun, Su-Hyung Kim, Kyung-Jin Ryu, Soo-Yeon Kwon, and Yoo-Won Lee. 2025. "Bow-Tie-Based Risk Assessment of Fishing Vessel Marine Accidents in the Open Sea Using IMO GISIS Data" Applied Sciences 15, no. 22: 12330. https://doi.org/10.3390/app152212330
APA StyleLee, S.-H., Kim, S.-H., Ryu, K.-J., Kwon, S.-Y., & Lee, Y.-W. (2025). Bow-Tie-Based Risk Assessment of Fishing Vessel Marine Accidents in the Open Sea Using IMO GISIS Data. Applied Sciences, 15(22), 12330. https://doi.org/10.3390/app152212330








