Stability Assessment of Unilateral External Fixator Configurations for Open Tibial Fractures: An Experimental Study
Abstract
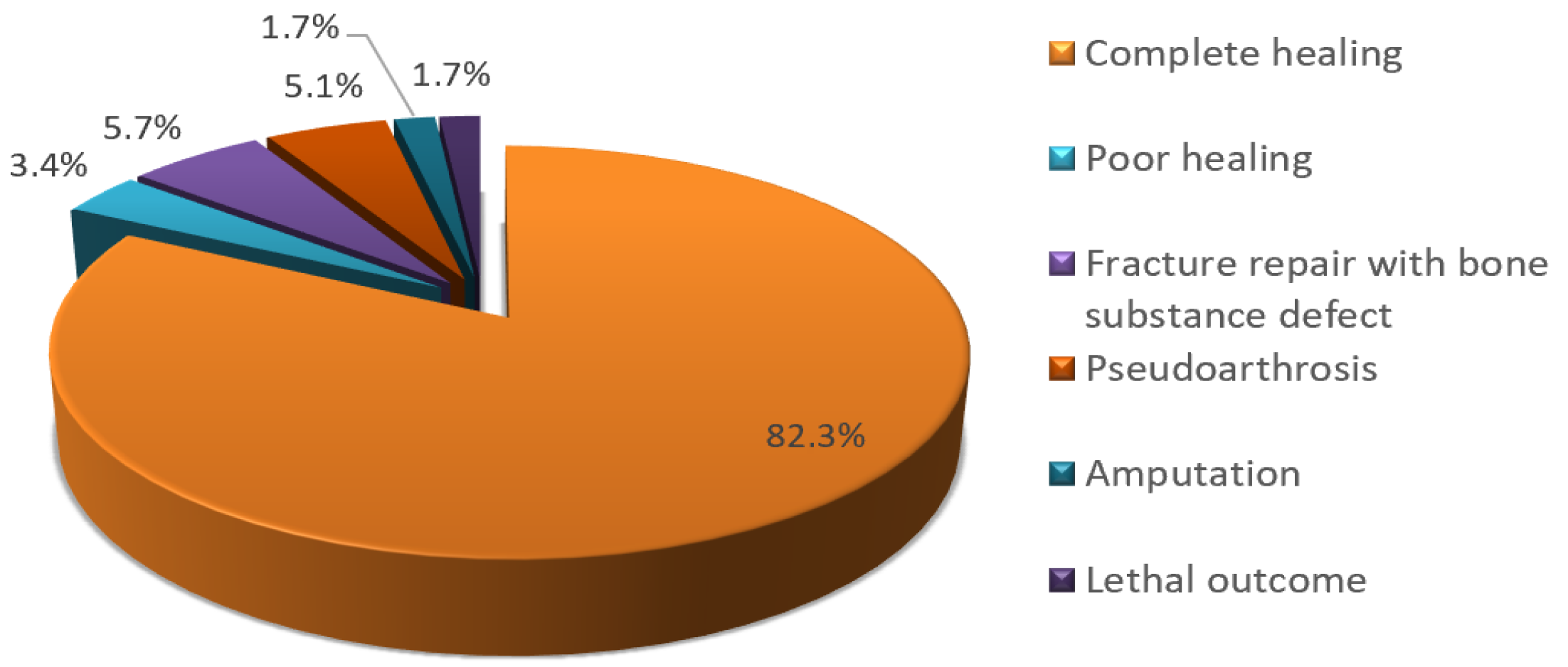
1. Introduction
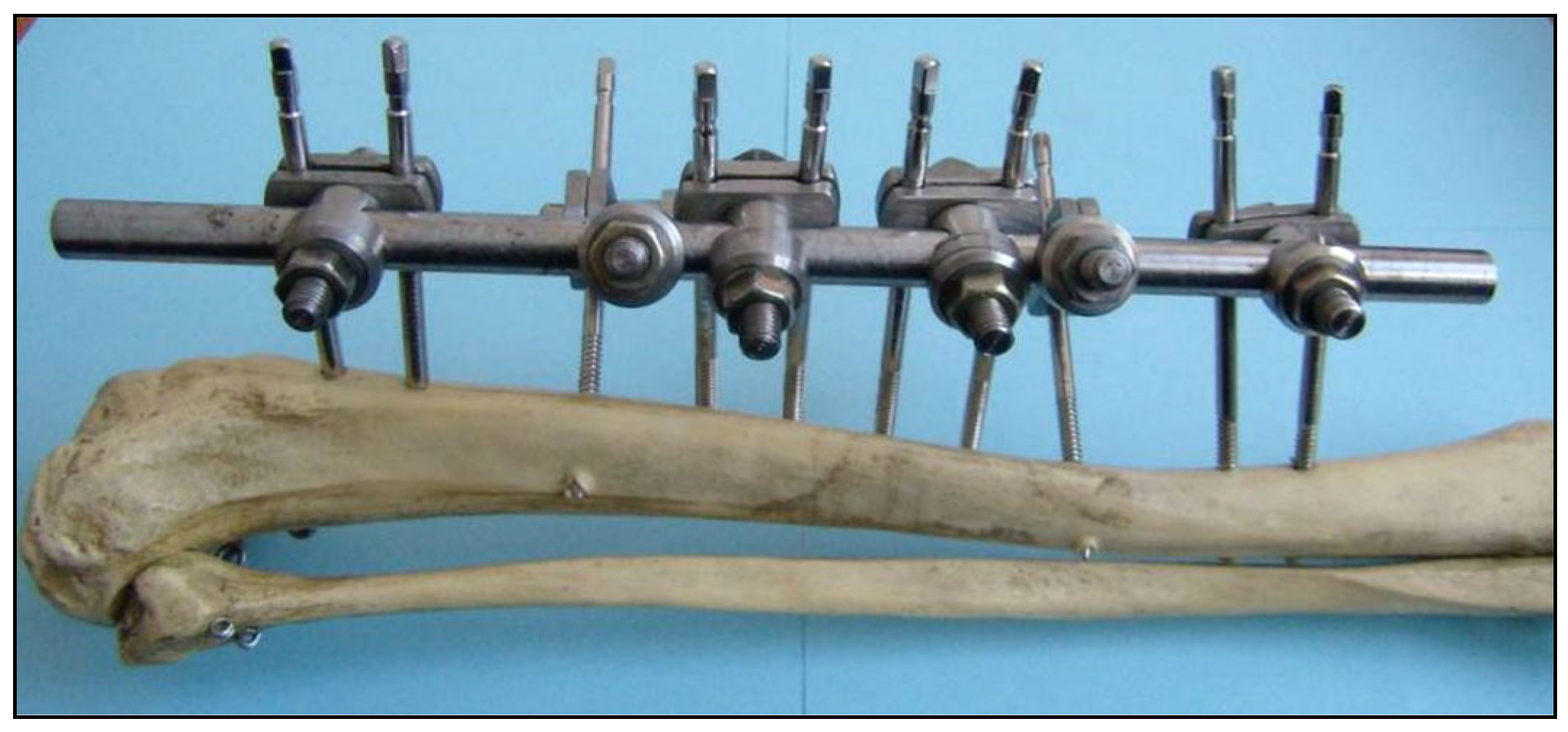
Sarafix External Fixation System
2. Materials and Methods
2.1. Test Configurations of the Sarafix External Fixation System
2.2. Methodology for Evaluating the Stiffness of Fixator Configurations
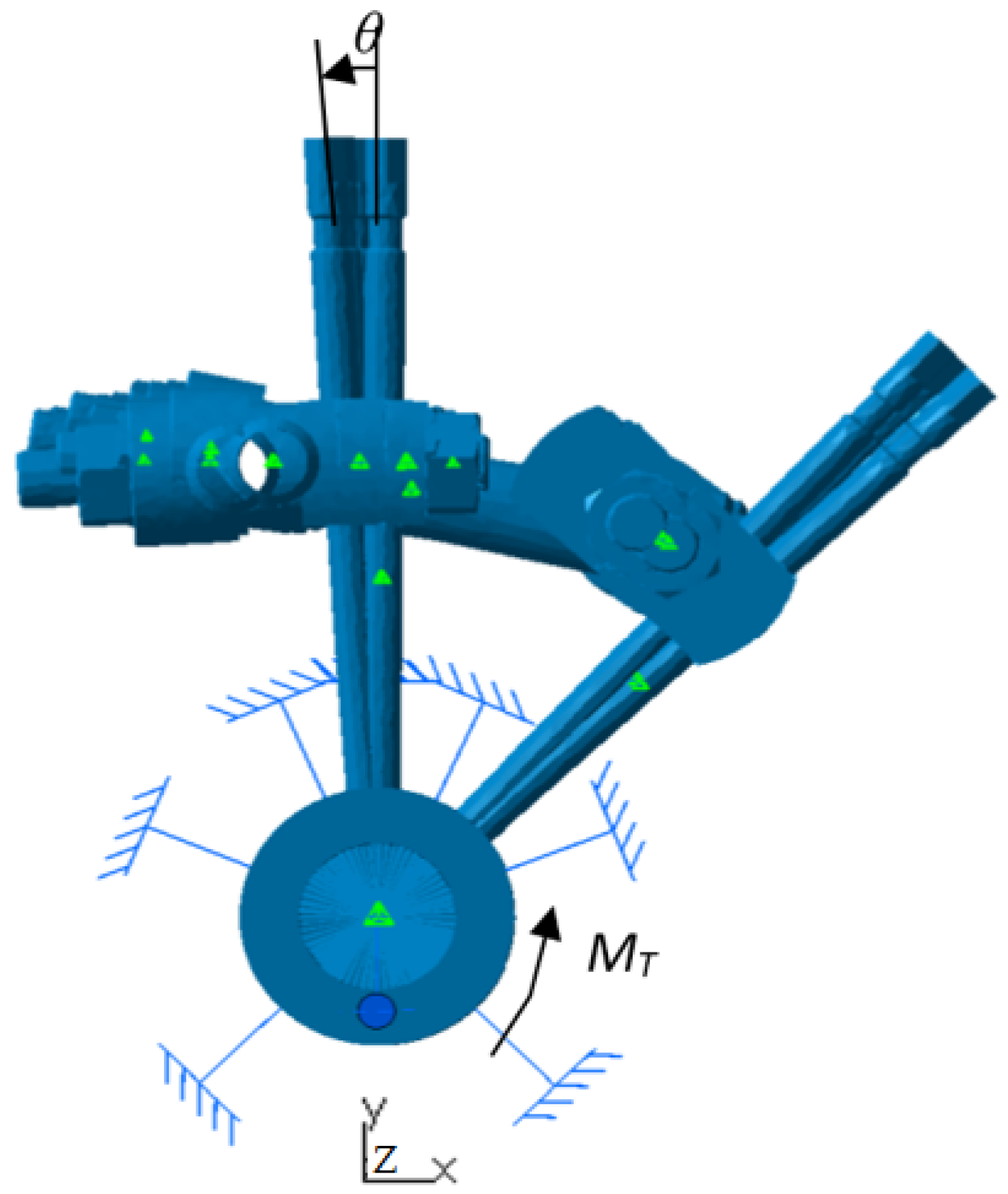
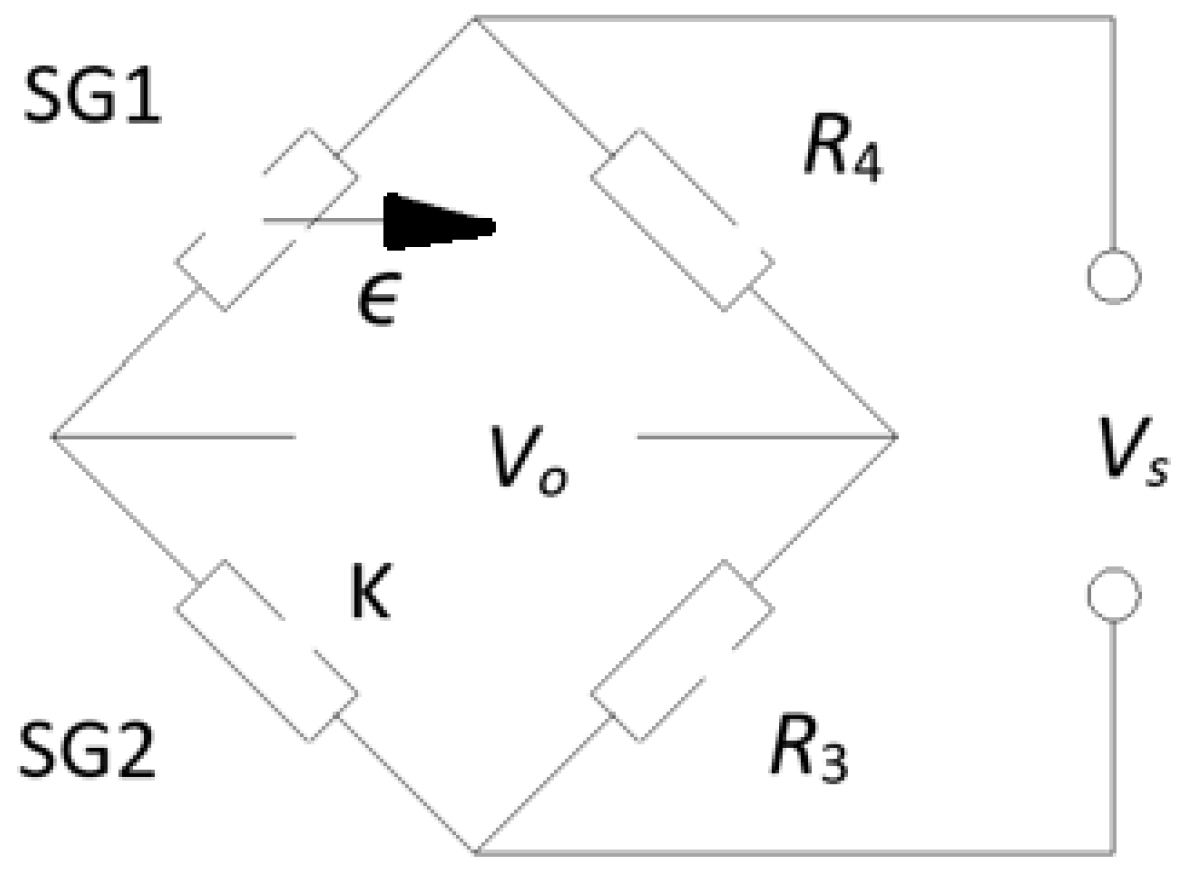
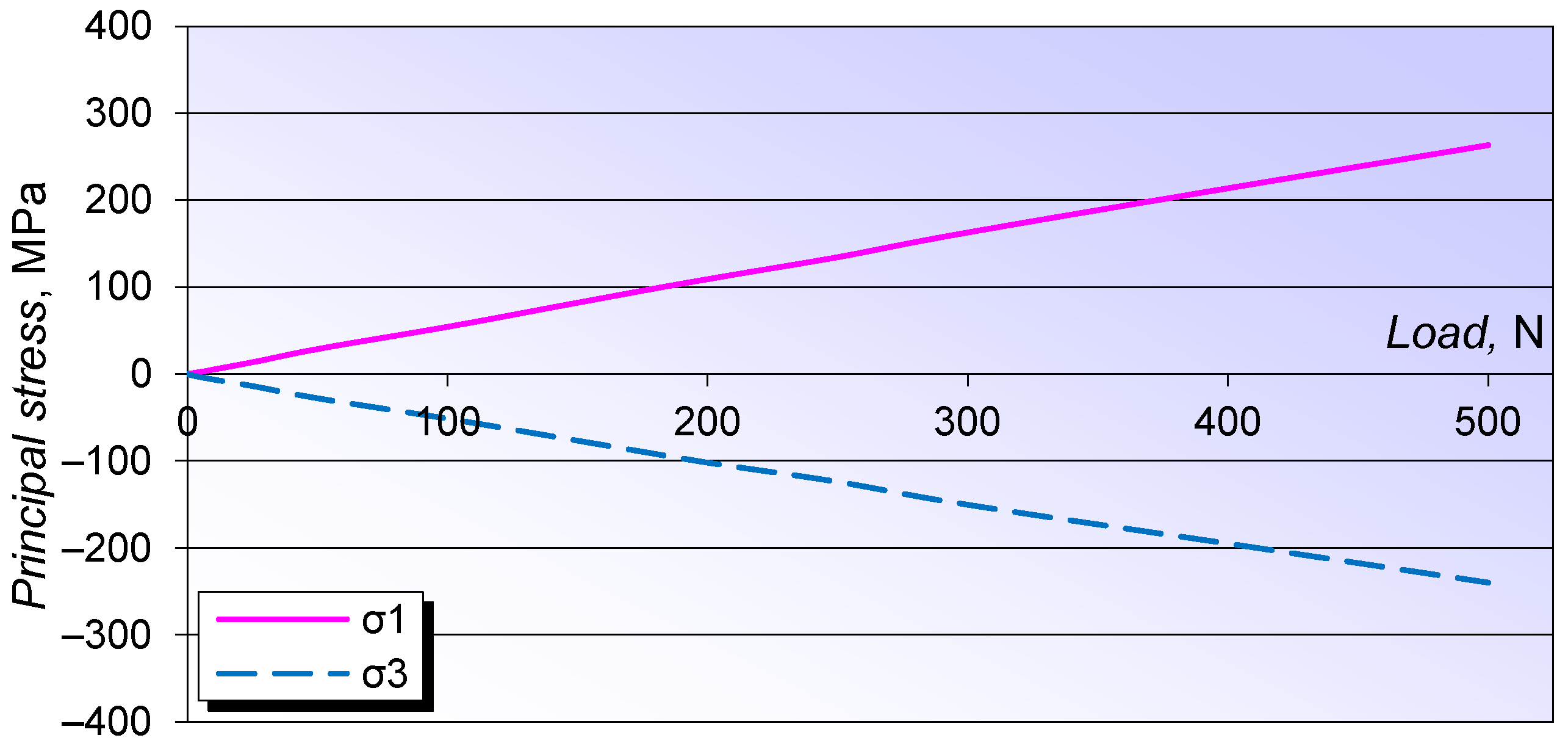
2.3. Experimental Stress Analysis
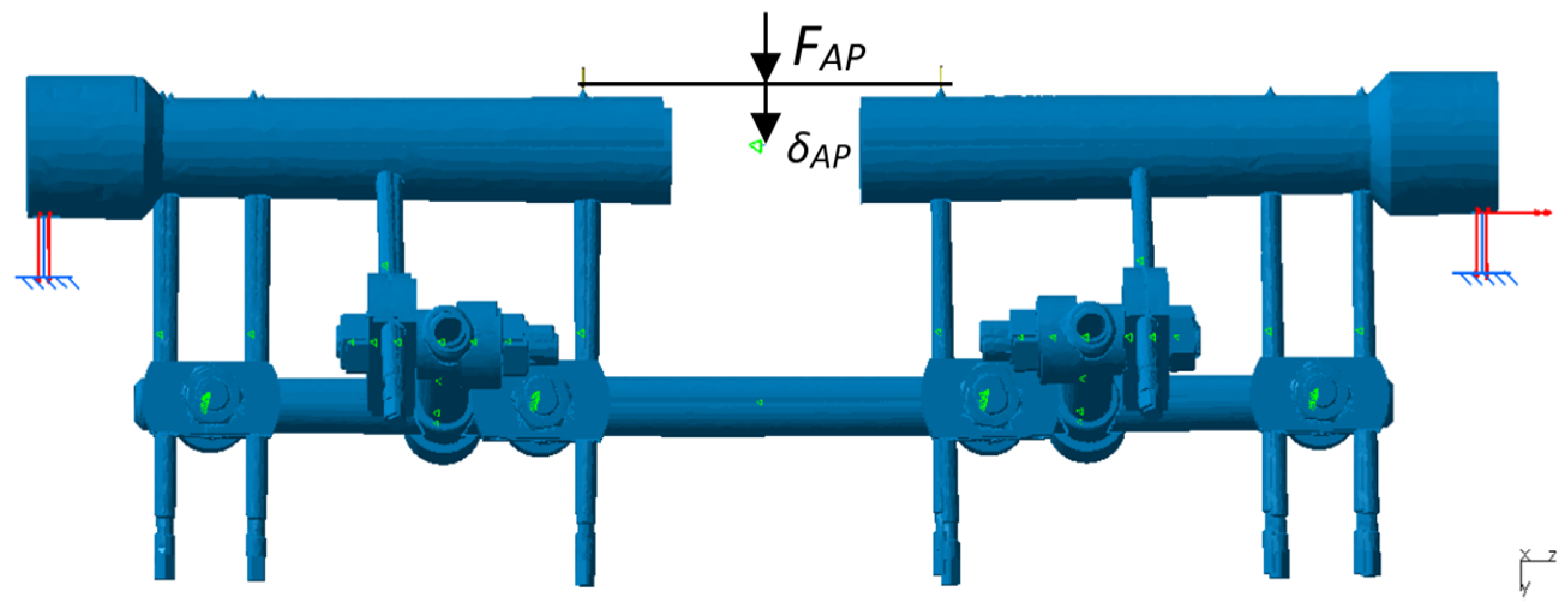
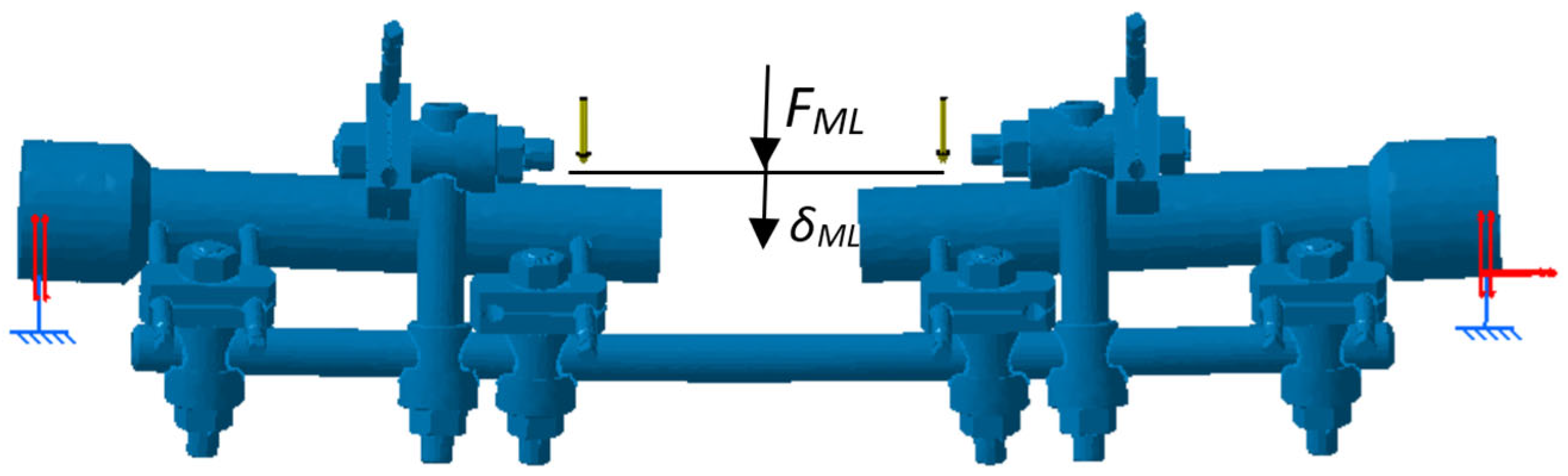
2.4. Experimental Testing of Fixator Configurations
3. Results
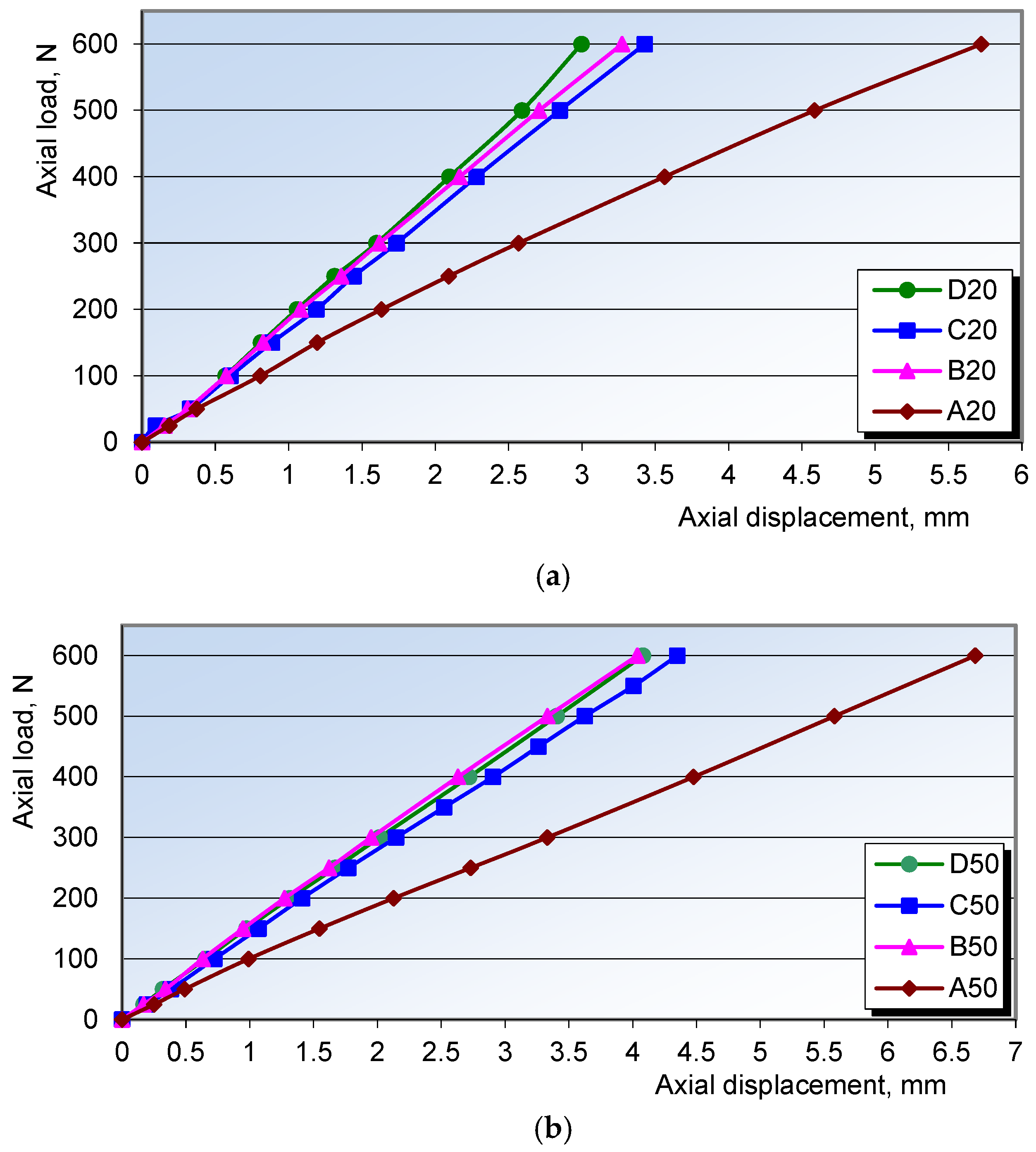
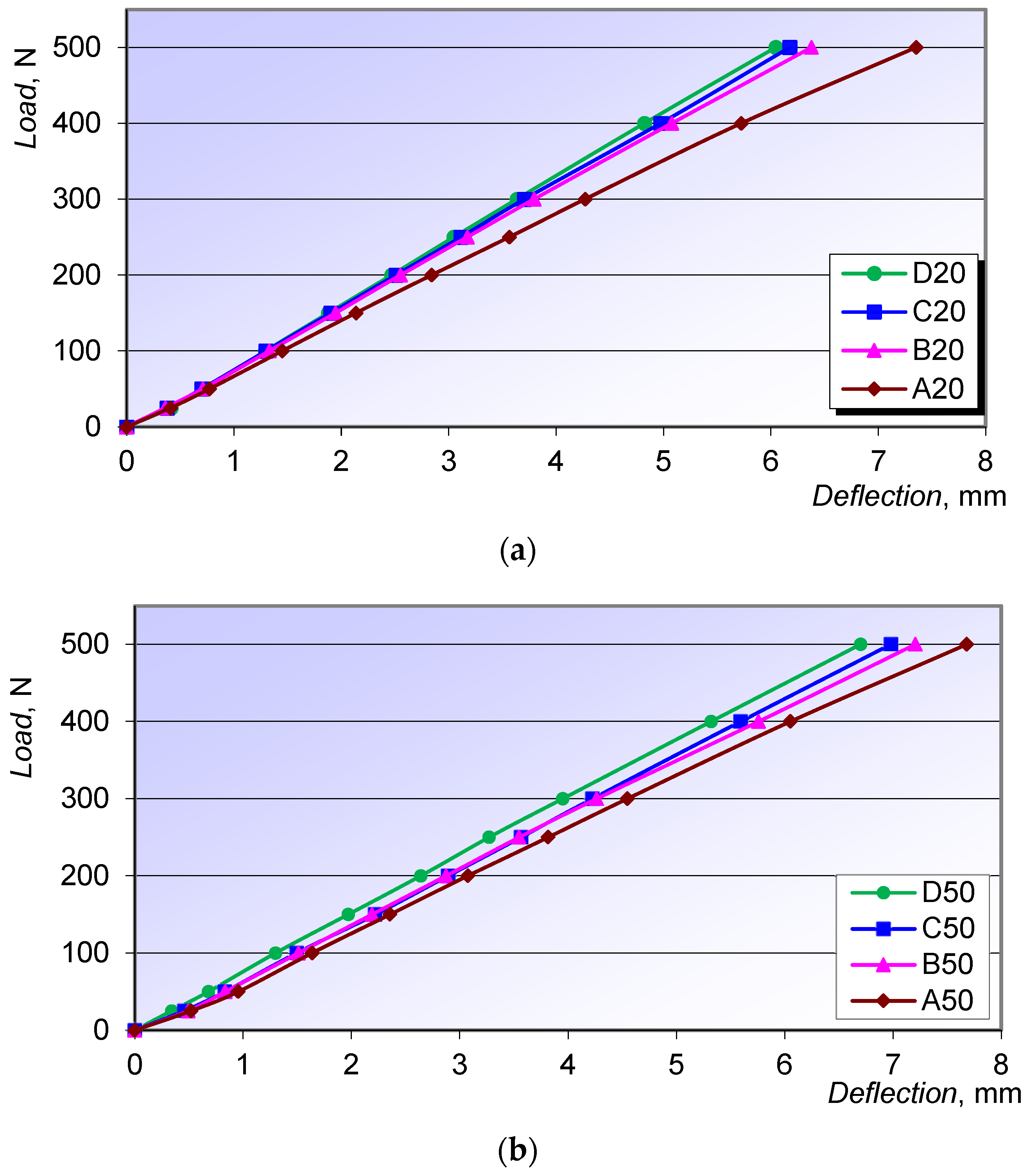
3.1. Results of Axial Compression Testing
3.2. Test Results for Four-Point AP and ML Bending
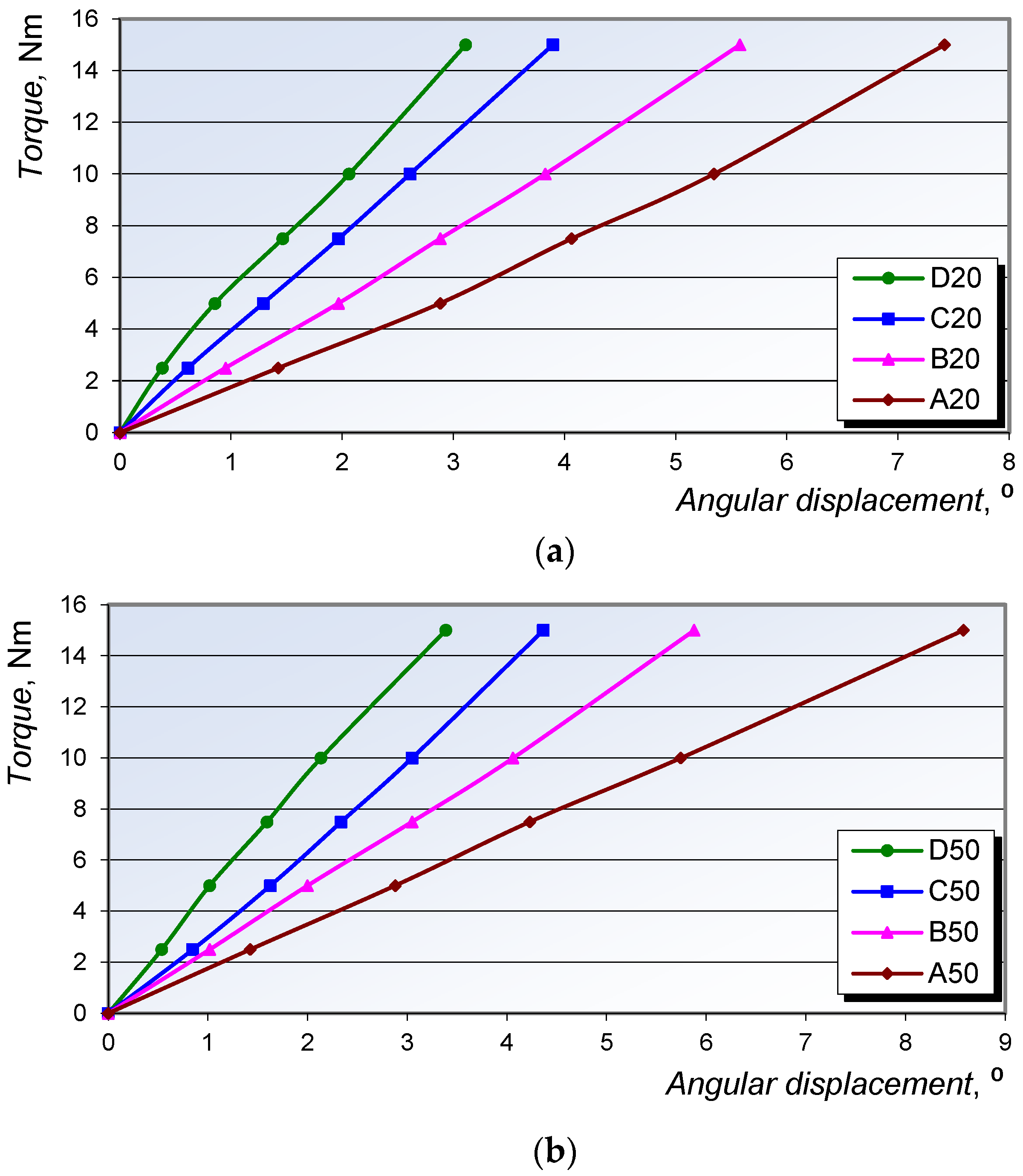
3.3. Torsional Testing Results
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Behrens, F. A Primer of Fixator Devices and Configurations. Clin. Orthop. 1989, 241, 5–14. [Google Scholar] [CrossRef]
- Behrens, F.; Searls, K. External fixation of the tibia. Basic concepts and prospective evaluation. J. Bone Jt. Surg. 1986, 68, 246–254. [Google Scholar] [CrossRef] [PubMed]
- Behrens, F. General Theory and Principles of External Fixation. Clin. Orthop. 1989, 241, 15–23. [Google Scholar] [CrossRef]
- Karunakar, M.A.; Bosse, M.J. Principles of External Fixation. In Rockwood & Green’s: Fractures, 5th ed.; LWW: New York, NY, USA, 2001; Chapter 7. [Google Scholar]
- Agrawal, H.K.; Garg, M.; Singh, B.; Jaiman, A.; Khatkar, V.; Khare, S.; Batra, S.; Sharma, V.K. Management of complex femoral nonunion with monorail external fixator: A prospective study. J. Clin. Orthop. Trauma 2016, 7, 191–200. [Google Scholar] [CrossRef]
- Simpson, A.H.R.W.; Robiati, L.; Jalal, M.M.K.; Tsang, S.T.J. Non-union: Indications for external fixation. Injury 2019, 50, S73–S78. [Google Scholar] [CrossRef]
- Bliven, E.K.; Greinwald, M.; Hackl, S.; Augat, P. External fixation of the lower extremities: Biomechanical perspective and recent innovations. Injury 2019, 50, S10–S17. [Google Scholar] [CrossRef]
- Abd Aziz, A.U.; Abdul Wahab, A.H.; Abdul Rahim, R.A.; Abdul Kadir, M.R.; Ramlee, M.H. A finite element study: Finding the best configuration between unilateral, hybrid, and ilizarov in terms of biomechanical point of view. Injury 2020, 51, 2474–2478. [Google Scholar] [CrossRef]
- Emami, A.; Mjoberg, B.; Karlstrom, G.; Larsson, S. Treatment of closed tibial shaft fractures with unilateral external fixation. Injury 1995, 26, 299–303. [Google Scholar] [CrossRef]
- Perren, S.M. Evolution of the internal fixation of long bone fractures. The scientific basis of biological internal fixation: Choosing a new balance between stability and biology. J. Bone Jt. Surg. Br. 2002, 84, 1093–1100. [Google Scholar]
- Chao, E.Y.; Inoue, N. Biophysical stimulation of bone fracture repair, regeneration and remodelling. Eur. Cell Mater. 2003, 6, 72–84; discussion 84–85. [Google Scholar] [CrossRef] [PubMed]
- Fleming, B.; Paley, D.; Kristiansen, T.; Pope, M. A biomechanical analysis of the Ilizarov external fixator. Clin. Orthop. Relat Res. 1989, 241, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Pollack, A.; Ziran, B.H. Principles of External Fixators, Skeletal Injury, 3rd ed.; Browner and Jupiter, Ed.; W.B. Saunders: Philadelphia, PA, USA, 2003; Volume 1, Chapter 9; pp. 179–194. [Google Scholar]
- Heim, D.; Regazzoni, P.; Perren, S.M. Current use of external fixation in open fractures. Injury 1992, 23 (Suppl. 2), S1–S35. [Google Scholar]
- Terzini, M.; Sicuranza, S.; Alberghina, F.; Ravera, L.; Aloj, D.C.; Bignardi, C. Evaluation of the Structural Behaviour of a Unilateral External Fixator for Osteosynthesis. Open Biomed. Eng. J. 2021, 15, 29–36. [Google Scholar] [CrossRef]
- Giotakis, N.; Narayan, B. Stability with unilateral external fixation in the tibia. Strateg. Trauma Limb Reconstr. 2007, 2, 13–20. [Google Scholar]
- Burgers, P.T.P.W.; Van Riel, M.P.J.M.; Vogels, L.M.M.; Stam, R.; Patka, P.; Van Lieshout, E.M.M. Rigidity of unilateral external fixators—A biomechanical study. Injury 2011, 42, 1449–1454. [Google Scholar] [CrossRef]
- Loi, F.; Córdova, L.A.; Pajarinen, J.; Lin, T.; Yao, Z.; Goodman, S.B. Inflammation, fracture and bone repair. Bone 2016, 86, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Fernando, P.L.N.; Abeygunawardane, A.; Wijesinghe, P.C.I.; Dharmaratne, P.; Silva, P. An engineering review of external fixators. Med. Eng. Phys. 2021, 98, 91–103. [Google Scholar] [PubMed]
- Yang, L.; Saleh, M.; Nayagam, S. The Effects od Different Wire and Screw Combinations on the Stiffness of a Hybrid External Fixator. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2000, 214, 669–676. [Google Scholar]
- Vossoughi, J.; Youm, Y.; Bosse, M.; Burgess, A.R.; Poka, A. Structural Stiffness of the Hoffmann Simple Anterior Tibial External Fixation Frame. In Proceedings of the 5th Southern Biomedical Engineering Conference, Baton Rouge, LA, USA, 20–21 October 1986. [Google Scholar]
- Alkalay, R.N.; Sharpe, D.; Bader, D.L. The effects of design and configuration on the biomechanical response of an internal spinal fixator. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1999, 213, 137–146. [Google Scholar] [CrossRef]
- Moroz, T.K.; Finlay, J.B.; Rorabeck, C.H.; Bourne, R.B. Stability of the Original Hoffmann and AO Tubular External Fixation Devices. Med. Biol. Eng. Comput. 1988, 26, 271–276. [Google Scholar]
- Remiger, A.R. Mechanical Properties of the Pinless External Fixator on Human Tibiae. Br. J. Accid. Surg. Inj. 1992, 23 (Suppl. 3), S28–S42. [Google Scholar] [CrossRef]
- Kumara, R.; Guptab, R.C.; Mishra, S. Experimental Testing of Joshi’s External Stabilizing System (JESS) under Axial Compression. Int. J. Eng. Res. Technol. 2014, 3, 599–603. [Google Scholar]
- Martins Amaro, A.; Fátima Paulino, M.; Manuel Roseiro, L.; Augusta Neto, M. The Effect of External Fixator Configurations on the Dynamic Compression Load: An Experimental and Numerical Study. Appl. Sci. 2020, 10, 3. [Google Scholar] [CrossRef]
- Simpson, A.H.R.W.; Cunningham, J.L.; Kenwright, J. The Forces which Develop in the Tissues During Leg Lenghtening: A Clinical Study. J. Bone Jt. Surg. Br. Vol. 1996, 78, 979–983. [Google Scholar] [CrossRef]
- Windolf, M.; Varjas, V.; Gehweiler, D.; Schwyn, R.; Arens, D.; Constant, C.; Zeiter, S.; Richards, R.G.; Ernst, M. Continuous implant load monitoring to assess bone healing status—Evidence from animal testin. Medicina 2022, 58, 858. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.; Hetreau, C.; Ernst, M.; Varga, P.; Schwarzenberg, P. Sensor-validated simulations predict fracture healing outcomes in an ovine model. Results Eng. 2025, 25, 104518. [Google Scholar] [CrossRef]
- Carrera-Pinzón, A.F.; Leyton, A.; Machado Caicedo, A.; García, J.J.; Casanova, F. Development of an easy-to-assemble external fixation system for bone transport. DYNA 2019, 86, 53–59. [Google Scholar]
- Sellei, R.M.; Kobbe, P.; Dienstknecht, T.; Lichte, P.; Pfeifer, R.; Behrens, M.; Brianza, S.; Pape, H.-C. Biomechanical properties of different external fixator frame configurations. Eur. J. Trauma Emerg. Surg. 2014, 41, 313–318. [Google Scholar] [CrossRef]
- Pavić, A.; Kodvanj, J.; Surjak, M. Determining the stability of novel external fixator by using measuring system Aramis. Tech. Gaz. 2013, 20, 995–999. [Google Scholar]
- Padovec, Z.; Růžička, P.; Sedláček, R.; Růžička, M. Design, analysis and testing of an external fixation device manufactured from composite materials. Appl. Comput. Mech. 2017, 11, 145–154. [Google Scholar] [CrossRef]
- Sellahewa, T.; Weerasinghe, C.; Silva, P. Biomechanical Evaluation Method to Optimize External Fixator Configuration in Long Bone Fractures—Conceptual Model and Experimental Validation Using Pilot Study. Appl. Sci. 2021, 11, 8481. [Google Scholar] [CrossRef]
- Zhao, X.; Li, J.; Chen, Y.; Tao, C.; Ji, R. Investigation of load transfer process between external fixator and bone model by experimental and finite element methods. J. Appl. Biomater. Funct. Mater. 2019, 17, 2280800019826512. [Google Scholar] [CrossRef]
- Paulino, M.F.; Roseiro, L.M.; Balacó, I.; Neto, M.A.; Amaro, A.M. Evaluation of Bone Consolidation in External Fixation with an Electromechanical System. Appl. Sci. 2022, 12, 2328. [Google Scholar] [CrossRef]
- Grasa, J.; Gomez-Benito, M.J.; Gonzalez-Torres, L.A.; Asiain, D.; Quero, F.; Garcia-Aznar, J.M. Monitoring In Vivo Load Transmission Through an External Fixator. Ann. Biomed. Eng. 2010, 38, 605–612. [Google Scholar] [CrossRef]
- Đozić, Š.; Salihefendić, R.; Baralić, E.; Fazlagić, S.; Đikić, S.; Bašić, S.; Kulenović, F. External Fixator Sarafix in the Treatment of War Injuries of the Extremities at the State Hospital Sarajevo from May 1992 to May 1995. In Proceedings of the 1st Congress of War Surgery with International Participation, Sarajevo, Bosnia and Herzegovina, 12–15 May 1996. [Google Scholar]
- EN 10088-1:2014; Stainless Steels – Part 1: List of Stainless Steels. European Committee for Standardization (CEN): Brussels, Belgium, 2014.
- Salihefendic, R.; Djozic, S.; Fazlagic, S.; Basic, S.; Baralic, E.; Djikic, S.; Beavis, J.P. The use of the Sarafix external fixator for the treatment of war injuries. Inj. Int. J. Care Inj. 1997, 28, 242–243. [Google Scholar]
- ASTM Standard F1541-02; Specification and Test Methods for External Skeletal Fixation Devices. ASTM International: West Conshohocken, PA, USA, 2015.
- Koo, T.K.K.; Chao, E.Y.S.; Mak, A.F.T. Fixation Stiffness of Dynafix Unilateral External Fixator in Neutral and Non-neutral Configurations. Bio-Med. Mater. Eng. 2005, 15, 433–444. [Google Scholar]
- Oh, J.K.; Lee, J.J.; Jung, D.K.; Kim, B.J.; Oh, C.W. Hybrid External Fixation of Distal Tibial Fractures: New Strategy to Place Pins and Wires without Penetrating The Anterior Compartment. Arch. Orthop. Trauma Surg. 2004, 124, 542–546. [Google Scholar] [CrossRef]
- Grubor, P.; Grubor, M.; Asotic, M. Comparison of stability of different types of external fixation. Med. Arch. 2011, 65, 157–159. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.S.; Wang, X. Strain Measurements and Stress Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 2001. [Google Scholar]
- Mešić, E.; Pervan, N.; Muminović, A.J.; Muminović, A.; Čolić, M. Development of knowledge-based engineering system for structural size optimization of external fixation device. Appl. Sci. 2021, 11, 10775. [Google Scholar] [CrossRef]
- Mešić, E.; Muminović, A.; Čolić, M.; Petrović, M.; Pervan, N. Development and Experimental Verification of a Generative CAD/FEM Model of an External Fixation Device. Tech. J. 2020, 14, 1–6. [Google Scholar] [CrossRef]
- Mešić, E.; Muminović, A.; Čolić, M.; Petrović, M.; Pervan, N. Structural Size Optimization of an External Fixation Device. Adv. Sci. Technol. Res. J. 2020, 14, 233–240. [Google Scholar] [CrossRef]
- Seide, K.; Weinrich, N.; Wenzl, M.E.; Wolter, D.; Jürgens, C. Three-dimensional load measurements in an external fixator. J. Biomech. 2004, 37, 1361–1369. [Google Scholar] [CrossRef]
- Fu, X.; Liu, S.; Wang, N.; Ji, Y.; Lu, L.; Chen, T.; Gu, M.; Chai, Z.; Yu, D.; Liu, Y.; et al. Measurement of the dynamic axial load-share ratio in vivo could indicate sufficient callus healing in external fixators. BMC Musculoskelet. Disord. 2025, 26, 139. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Claes, L.; Laule, J.; Wenger, K.; Suger, G.; Liener, U.; Kinzl, L. The Influence of the Stiffness of the Fixator on Maturation of Callus after Segmental Transport. J. Bone Jt. Surg. 2000, 82, 142–148. [Google Scholar] [CrossRef]
- Murdoch, A.H.; Mathias, K.J.; Shepherd, D.E. Investigation into the material properties of beech wood and cortical bone. Biomed. Mater. Eng. 2004, 14, 1–4. [Google Scholar]
- Nefjodovs, V.; Andze, L.; Andzs, M.; Filipova, I.; Tupciauskas, R.; Vecbiskena, L.; Kapickis, M. Wood as Possible Renewable Material for Bone Implants—Literature Review. J. Funct. Biomater. 2023, 14, 266. [Google Scholar] [CrossRef] [PubMed]
- Kretschmann, D.E. Mechanical properties of wood. Environments 2010, 5, 34. [Google Scholar]
- Yilmaz, F.; Bllhan, O.; Karakurt, L.; Arslan, N.; Serin, E. Mechanical performance of hybrid Ilizarov External Fixator in comparison with Ilizarov Circular External Fixator. Clin. Biomech. 2003, 18, 518–522. [Google Scholar] [CrossRef]
- Taylor, K.F.; Sharma, J.; Davisson, N.A.; Roush, E.P.; Jones, C.M.; Lewis, G.S. Effect of Metacarpal Fixation Configuration on Strength and Fracture Gap Displacements in a Cadaveric Model of Externally Fixed Distal Radius Fractures. Hand 2021, 16, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Sternick, M.B.; Dallacosta, D.; Bento, D.Á.; Reis, M.L.D. Relationship Between Rigidity of External Fixator and Number of Pins: Computer Analysis Using Finite Elements. Rev. Bras. Ortop. 2012, 47, 646–650. [Google Scholar] [CrossRef]
- Salas, C.; Hoopes, D.; Reda Taha, M.M.; DeCoster, T.A. External Fixation for Treating Tibial Shaft Fractures Using a Triangular Two-Planar Frame: A Computational and Biomechanical Study. Univ. New Mex. Orthop. Res. J. 2017, 6, 25. [Google Scholar]
- Lovisetti, G.; Rohilla, R.; Siwach, K. Circular external fixation as definitive treatment for open or comminuted femoral fractures: Radiologic and functional outcomes. J. Clin. Orthop. Trauma 2019, 10 (Suppl. 1), S115–S122. [Google Scholar] [CrossRef] [PubMed]
- Kouassi, K.J.; Cartiaux, O.; Fonkoué, L.; Detrembleur, C.; Cornu, O. Biomechanical study of a low-cost external fixator for diaphyseal fractures of long bones. J. Orthop. Surg. Res. 2020, 15, 247. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Pervan, N.; Mešić, E.; Muminović, A.J.; Delić, M.; Muratović, E.; Trobradović, M.; Hadžiabdić, V. Biomechanical Performance Analysis of the Monolateral External Fixation Devices with Steel and Composite Material Frames under the Impact of Axial Load. Appl. Sci. 2022, 12, 722. [Google Scholar] [CrossRef]
- Mešić, E.; Avdić, V.; Pervan, N.; Muminović, A. A new Proposal on Analysis of the Interfragmentary Displacements in the Fracture Gap. TEM J. 2015, 4, 270–275. [Google Scholar] [CrossRef]













| Configuration | Type | Number of Half-Pins | Number of Clamps | Number of Clamp Holders |
|---|---|---|---|---|
| A50 | Unilateral uniplanar | 4 | 4 | – |
| A20 | ||||
| B50 | Unilateral uniplanar | 8 | 4 | – |
| B20 | ||||
| C50 | Unilateral biplanar | 6 + 2/45° | 6 | 2 |
| C20 | ||||
| D50 | Unilateral biplanar | 8 + 2/45° | 6 | 2 |
| D20 |
| Sum of Squares | df | Mean Square | F | p | η2 | η2p | ω2 | |
|---|---|---|---|---|---|---|---|---|
| Configuration | 86.3 | 7 | 12.33 | 5.84 | <0.001 | 0.088 | 0.088 | 0.073 |
| Residuals | 897.1 | 425 | 2.11 |
| Comparison | |||||||
|---|---|---|---|---|---|---|---|
| Configuration | Configuration | Mean Difference | SE | df | t | ptukey | |
| A20 | - | B20 | 0.7869 | 0.294 | 425 | 2.678 | 0.132 |
| - | C20 | 0.7171 | 0.294 | 425 | 2.440 | 0.225 | |
| - | D20 | 0.8913 | 0.277 | 425 | 3.217 | 0.030 | |
| - | A50 | −0.4985 | 0.277 | 425 | −1.800 | 0.621 | |
| - | B50 | 0.5265 | 0.277 | 425 | 1.901 | 0.551 | |
| - | C50 | 0.0394 | 0.262 | 425 | 0.150 | 1.000 | |
| - | D50 | 0.4909 | 0.277 | 425 | 1.772 | 0.639 | |
| B20 | - | C20 | −0.0698 | 0.310 | 425 | −0.225 | 1.000 |
| - | D20 | 0.1044 | 0.294 | 425 | 0.355 | 1.000 | |
| - | A50 | −1.2855 | 0.294 | 425 | −4.375 | <0.001 | |
| - | B50 | −0.2604 | 0.294 | 425 | −0.886 | 0.987 | |
| - | C50 | −0.7475 | 0.280 | 425 | −2.674 | 0.133 | |
| - | D50 | −0.2960 | 0.294 | 425 | −1.007 | 0.973 | |
| C20 | - | D20 | 0.1741 | 0.294 | 425 | 0.593 | 0.999 |
| - | A50 | −1.2157 | 0.294 | 425 | −4.137 | 0.001 | |
| - | B50 | −0.1906 | 0.294 | 425 | −0.649 | 0.998 | |
| - | C50 | −0.6778 | 0.280 | 425 | −2.425 | 0.232 | |
| - | D50 | −0.2262 | 0.294 | 425 | −0.770 | 0.995 | |
| D20 | - | A50 | −1.3898 | 0.277 | 425 | −5.017 | <0.001 |
| - | B50 | −0.3647 | 0.277 | 425 | −1.316 | 0.892 | |
| - | C50 | −0.8519 | 0.262 | 425 | −3.254 | 0.027 | |
| - | D50 | −0.4004 | 0.277 | 425 | −1.445 | 0.836 | |
| A50 | - | B50 | 1.0251 | 0.277 | 425 | 3.700 | 0.006 |
| - | C50 | 0.5379 | 0.262 | 425 | 2.055 | 0.446 | |
| - | D50 | 0.9895 | 0.277 | 425 | 3.571 | 0.009 | |
| B50 | - | C50 | −0.4872 | 0.262 | 425 | −1.861 | 0.579 |
| - | D50 | −0.0356 | 0.277 | 425 | −0.129 | 1.000 | |
| C50 | - | D50 | 0.4515 | 0.262 | 425 | 1.725 | 0.671 |
| Configuration | Maximum Axial Displacement δp, mm | Axial Stiffness Cp, N/mm | Principal Stresses, MPa | |
|---|---|---|---|---|
| σ1, SG+ | σ3, SG− | |||
| D50 | 4.08 (0.03) | 147.05 | 325 (2.24) | −380 (3.54) |
| D20 | 3.00 (0.09) | 200 | 325 (2.83) | −378 (3.96) |
| C50 | 4.35 (0.04) | 137.93 | 330 (2.38) | −375 (3.59) |
| C20 | 3.43 (0.02) | 174.93 | 320 (2.15) | −366 (3.18) |
| B50 | 4.04 (0.12) | 148.51 | 334 (1.28) | −374 (3.42) |
| B20 | 3.27 (0.04) | 183.49 | 319 (1.26) | −370 (2.50) |
| A50 | 6.69 (0.06) | 89.69 | 326 (4.65) | −379 (4.69) |
| A20 | 5.72 (0.12) | 104.9 | 326 (2.89) | −381 (3.87) |
| Sum of Squares | df | Mean Square | F | p | η2 | η2p | ω2 | |
|---|---|---|---|---|---|---|---|---|
| Configuration AP bending | 1.75 | 7 | 0.251 | 0.388 | 0.909 | 0.007 | 0.007 | −0.011 |
| Residuals | 240.06 | 372 | 0.645 |
| Configuration | Max. Deflection in the AP Plane δAP, mm | AP Bending Stiffness CAP, N/mm | Principal Stresses, MPa | |
|---|---|---|---|---|
| σ1, SG+ | σ3, SG− | |||
| D50 | 2.36 | 211.86 | 269 | −274 |
| D20 | 2.38 | 210.08 | 268 | −272 |
| C50 | 2.54 | 196.85 | 268 | −271 |
| C20 | 2.59 | 193.05 | 267 | −272 |
| B50 | 2.48 | 201.61 | 263 | −269 |
| B20 | 2.35 | 212.77 | 264 | −270 |
| A50 | 2.81 | 177.94 | 262 | −265 |
| A20 | 2.77 | 180.51 | 260 | −264 |
| Sum of Squares | df | Mean Square | F | p | η2 | η2p | ω2 | |
|---|---|---|---|---|---|---|---|---|
| Configuration ML bending | 14.2 | 6 | 2.37 | 0.507 | 0.803 | 0.010 | 0.010 | −0.010 |
| Residuals | 1370.3 | 293 | 4.68 |
| Configuration | Max. Deflection in the ML Plane δML, mm | AP Bending Stiffness CML, N/mm | Principal Stresses, MPa | |
|---|---|---|---|---|
| σ1, SG+ | σ3, SG− | |||
| D50 | 6.70 | 74.63 | 278 | −282 |
| D20 | 6.05 | 82.65 | 276 | −280 |
| C50 | 6.98 | 71.63 | 283 | −286 |
| C20 | 6.18 | 80.91 | 280 | −284 |
| B50 | 7.21 | 69.35 | 292 | −297 |
| B20 | 6.38 | 78.37 | 290 | −295 |
| A50 | 7.68 | 65.10 | 292 | −297 |
| A20 | 7.35 | 68.03 | 291 | −296 |
| Sum of Squares | df | Mean Square | F | p | η2 | η2p | ω2 | |
|---|---|---|---|---|---|---|---|---|
| Configuration Torsion | 47.9 | 7 | 6.841 | 18.5 | <0.001 | 0.323 | 0.323 | 0.305 |
| Residuals | 100.4 | 272 | 0.369 |
| Comparison | |||||||
|---|---|---|---|---|---|---|---|
| Configuration | Configuration | Mean Difference | SE | df | t | ptukey | |
| A20 | - | B20 | 0.45086 | 0.145 | 272 | 3.10377 | 0.043 |
| - | C20 | 0.93696 | 0.145 | 272 | 6.45012 | <0.001 | |
| - | D20 | 0.93823 | 0.145 | 272 | 6.45892 | <0.001 | |
| - | A50 | −0.14935 | 0.145 | 272 | −1.02814 | 0.970 | |
| - | B50 | 0.46187 | 0.145 | 272 | 3.17955 | 0.035 | |
| - | C50 | 0.92264 | 0.145 | 272 | 6.35155 | <0.001 | |
| - | D50 | 0.89655 | 0.145 | 272 | 6.17195 | <0.001 | |
| B20 | - | C20 | 0.48610 | 0.145 | 272 | 3.34636 | 0.021 |
| - | D20 | 0.48738 | 0.145 | 272 | 3.35515 | 0.020 | |
| - | A50 | −0.60021 | 0.145 | 272 | −4.13191 | 0.001 | |
| - | B50 | 0.01101 | 0.145 | 272 | 0.07578 | 1.000 | |
| - | C50 | 0.47178 | 0.145 | 272 | 3.24778 | 0.028 | |
| - | D50 | 0.44569 | 0.145 | 272 | 3.06818 | 0.048 | |
| C20 | - | D20 | 0.00128 | 0.145 | 272 | 0.00879 | 1.000 |
| - | A50 | −1.08631 | 0.145 | 272 | −7.47827 | <0.001 | |
| - | B50 | −0.47509 | 0.145 | 272 | −3.27058 | 0.026 | |
| - | C50 | −0.01432 | 0.145 | 272 | −0.09857 | 1.000 | |
| - | D50 | −0.04041 | 0.145 | 272 | −0.27817 | 1.000 | |
| D20 | - | A50 | −1.08758 | 0.145 | 272 | −7.48706 | <0.001 |
| - | B50 | −0.47637 | 0.145 | 272 | −3.27937 | 0.026 | |
| - | C50 | −0.01560 | 0.145 | 272 | −0.10737 | 1.000 | |
| - | D50 | −0.04169 | 0.145 | 272 | −0.28696 | 1.000 | |
| A50 | - | B50 | 0.61122 | 0.145 | 272 | 4.20769 | <0.001 |
| - | C50 | 1.07199 | 0.145 | 272 | 7.37969 | <0.001 | |
| - | D50 | 1.04590 | 0.145 | 272 | 7.20009 | <0.001 | |
| B50 | - | C50 | 0.46077 | 0.145 | 272 | 3.17200 | 0.036 |
| - | D50 | 0.43468 | 0.145 | 272 | 2.99241 | 0.060 | |
| C50 | - | D50 | −0.02609 | 0.145 | 272 | −0.17960 | 1.000 |
| Configuration | Max. Angular Displacement θ, ° | Torsional Stiffness CT, Nm/° |
|---|---|---|
| D50 | 3.8 | 3.95 |
| D20 | 2.78 | 5.40 |
| C50 | 4.36 | 3.44 |
| C20 | 3.89 | 3.86 |
| B50 | 5.88 | 2.55 |
| B20 | 5.58 | 2.69 |
| A50 | 8.58 | 1.75 |
| A20 | 7.42 | 2.02 |
| Stiffness/Fixator | Meyrueis’s (One Rod) | Noor’s (One Rod) | Hoffmann 3 (One Rod) | Orthofix Modul System | Dynafix (EBI) | Sarafix C20 |
|---|---|---|---|---|---|---|
| Axial (N/mm) | 48.9 | 71.8 | 35 | 261 | 340 | 174.93 |
| AP bending (N/mm) | - | - | 31 | 220 | 230 | 193 |
| ML bending (N/mm) | 4.4 | 4.7 | 6.5 | - | 62 | 80.91 |
| Torsional (Nm/deg) | 1.8 | 1.6 | 1.03 | - | 3.2 | 3.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mešić, E.; Pervan, N.; Muminović, A.; Rahman, E.; Muminović, B. Stability Assessment of Unilateral External Fixator Configurations for Open Tibial Fractures: An Experimental Study. Appl. Sci. 2025, 15, 12327. https://doi.org/10.3390/app152212327
Mešić E, Pervan N, Muminović A, Rahman E, Muminović B. Stability Assessment of Unilateral External Fixator Configurations for Open Tibial Fractures: An Experimental Study. Applied Sciences. 2025; 15(22):12327. https://doi.org/10.3390/app152212327
Chicago/Turabian StyleMešić, Elmedin, Nedim Pervan, Adil Muminović, Edvin Rahman, and Bakir Muminović. 2025. "Stability Assessment of Unilateral External Fixator Configurations for Open Tibial Fractures: An Experimental Study" Applied Sciences 15, no. 22: 12327. https://doi.org/10.3390/app152212327
APA StyleMešić, E., Pervan, N., Muminović, A., Rahman, E., & Muminović, B. (2025). Stability Assessment of Unilateral External Fixator Configurations for Open Tibial Fractures: An Experimental Study. Applied Sciences, 15(22), 12327. https://doi.org/10.3390/app152212327






