Abstract
Among the various active cooling methods, transpiration cooling currently attracts significant attention because of its efficient cooling effect and less coolant consumption, in applications such as the combustion chamber of the rockets, turbine blades, leading edges of a hypersonic vehicle, etc. With the development of advanced manufacturing technology and extremely high thermal protection demand, transpiration cooling has become more promising in the future thermal management of aerospace high-temperature components. Compared with other CFD simulations, the calculation of transpiration cooling is more complex, which couples heat transfer and fluid flow in porous media, phase change, etc. This work reviews the mathematical modeling of transpiration cooling in aerospace applications, which mainly includes four aspects: structural modeling of porous media, heat transfer modeling, turbulence modeling, and phase change modeling. For each aspect, the modeling details are provided and the advantage and limitations of each modeling method is summarized. Finally, this paper analyzes the current challenges and future research directions for transpiration cooling.
1. Introduction
1.1. Background and Industrial Applications
Hypersonic vehicles (Ma > 5) that are designed for long cruise times face extraordinarily high thermal loads due to aerodynamic and combustion heating. Leading edges and nose cones may see surface temperatures in excess of 2000 K at local pressures of several megapascals, which jeopardize the structural integrity of the vehicle. A similar challenge is faced in modern rocket engine combustion chambers, where temperatures often reach 3500 K, and on the turbine blades of advanced gas turbines, whose operating environment exceeds 1800 K.
Active thermal protection systems are therefore needed to handle these conditions. Of these, the transpiration cooling method is very effective owing to its high heat removal efficiency with minimal consumption of coolant. This technique involves forcing a coolant either in liquid or gas form through a porous structure. As the coolant percolates through a network of interconnected pores, it picks up heat from the solid matrix through internal convection and emerges to eventually form an insulating surface film. This dual mechanism, consisting of internal convection and external film cooling, as illustrated in Figure 1, provides robust thermal protection capable of managing heat fluxes up to 1000 MW/m2.
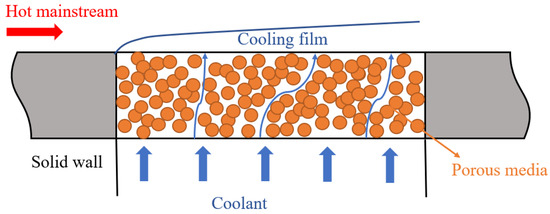
Figure 1.
Schematic of the transpiration cooling principle.
1.2. Research Gaps, Novelty, and Paper Structure
Transpiration cooling inherently represents a very complex process to model due to the presence of strongly coupled fluid flow and heat transfer within a porous medium, with a possibility for phase change. For these reasons, numerical modeling is usually required for design and analysis. A wide range of modeling techniques has been developed to capture these physics, from early Darcy-based representations of the flow in porous media to modern approaches that make use of advanced turbulence models, such as LES and multi-phase frameworks.
Notwithstanding these advances, there is still a lack of a structured and critical review of these methods in the context of aerospace. This review addresses key research gaps: a fragmented landscape of models with little guidance on how to choose the best trade-off between accuracy and computational cost in different application scenarios, such as Darcy versus Forchheimer and LTE versus LTNE; the lack of direct comparisons that outline the advantages, limitations, and operational ranges of different groups of models in a single, easy-to-access format; persistent challenges in modeling multi-physics coupling, especially in turbulence and phase change interaction, for which no clear summary of the state of the art is available; and inadequacy of classical porous media models to represent novel material geometries created by additive manufacturing.
In this respect, the present paper covers a systematic review of numerical modeling approaches for transpiration cooling. It is organized along four main technical sections: Section 2 revisits porous media modeling; Section 3 discusses heat transfer models; Section 4 covers turbulence approaches; and Section 5 presents multi-phase field modeling. Each section closes with a comparison table to summarize the key characteristics of the models reviewed. Section 6 concludes the review with both a summary of findings and a discussion of promising directions of research.
It is important to note the scope of this review. Our focus is primarily on continuum-scale numerical methods (CFD-based) for transpiration cooling. We do not provide an exhaustive review of pore-scale modeling techniques, purely analytical solutions, or experimental diagnostic methods, although we acknowledge their critical importance for model development and validation.
2. Modeling of Porous Media
It is challenging to characterize the internal structure of a porous medium using a standard mathematical model due to its extreme complexity and the typically disorganized and unpredictable spatial distribution of its skeleton and pores [1,2]. The Darcy model [3] remains the foundation for current theoretical models of fluid seepage in porous media. These models have been continuously updated and expanded, culminating in the development of the widely used Darcy–Brinkman–Forchheimer model, as depicted in Figure 2.
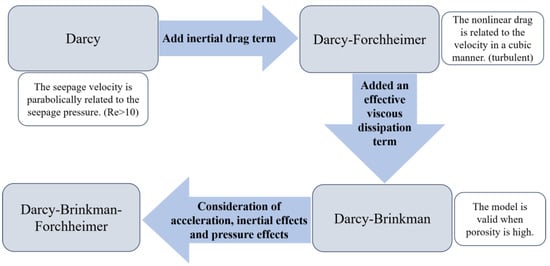
Figure 2.
Development of the Darcy model.
2.1. Darcy’s Law
Henry Darcy published an extensive study on the public water supply of Dijon [3]. In this work, he detailed experiments that led to his renowned filtration law, as expressed by Equation (1):
Darcy’s empirical law establishes a linear relationship between the filtration velocity, vFV, and the hydraulic head gradient, h. In this context, grad(·) is the gradient operator ∂(·)/∂x, and x represents the position vector. The law is shown in both its fundamental one-dimensional (1D) form and its contemporary three-dimensional (3D) notation. The filtration velocity vFV has units of m/s, while the hydraulic conductivity, kF, has units of m/s (equivalent to m3/(m2·s)). The hydraulic head gradient h is dimensionless, as it is defined as the ratio of the hydraulic pressure head (in meters) to the characteristic length (also in meters), typically expressed as shown in Equation (2):
2.2. Forchheimer’s Law
According to Darcy’s seepage model, the seepage velocity bears a linear relationship to the seepage pressure, implying the Reynolds number has no effect. However, this linear relationship between the hydraulic head gradient and the filtration velocity becomes inaccurate at higher flow rates. Forchheimer [4] found that the Darcy model is only applicable for Reynolds numbers below 10. Through experiments on coarse sand, he observed that the hydraulic conductivity decreased with an increasing hydraulic gradient, thereby invalidating the constant ratio between vFV and gradh. Beyond this range, the relationship between seepage velocity and pressure becomes parabolic. On this basis, Forchheimer proposed a modification to Darcy’s law (Equation (1)) by introducing a quadratic velocity term, as shown in Equation (3):
Here, a = 1/kF and b is a non-Darcian flow coefficient. In earlier literature, for instance, in the work of Markert [5], b was defined as b = 1/bs, where bs is a solid curvature parameter with units of (m/s)2 that accounts for the inherent irregularities of the pore spaces. By extending Forchheimer’s work, Equation (3) can be rearranged to solve for the filtration velocity, vFV. In this formulation, the hydraulic gradient is represented by the pressure gradient. Consequently, the gradient h in Equation (3) must be substituted with the expression given in Equation (4):
Substituting into Equation (4), the summable is
Here, is equal to Equation (6):
The parameter kF has been replaced by KS, and bS has been substituted with the curvature parameter BS (which has a dimension of meters), using the relation bS = BS|g|. This substitution integrates the curvature effect with the gravitational force paradigm, represented by the gravitational acceleration vector g. In cases where the body force is negligible, the equation simplifies to Equation (7):
It should be noted that in Equations (5) and (7), the term represents the hydraulic conductivity. This contrasts with kF, which also incorporates the effects of zigzag-induced inertial forces [5]. Furthermore, the intrinsic parameters KS and BS are generally preferred for characterization, as they are independent of the specific permeable fluid.
2.3. Brinkman’s Law
Like Forchheimer, Brinkman [6] proposed a modification of Darcy’s law to calculate the viscous force exerted by a flowing fluid on a dense particle population. Starting with Darcy’s law and neglecting gravitational forces, he arrived at the following relationship between the filtration velocity and the modified pressure gradient:
However, Brinkman concluded that this equation was unsuitable for solving the problem because it lacked a proper definition of the viscous force. Subsequently, he turned to the Navier–Stokes equations for viscous, incompressible fluids:
In Equation (9), vF represents the fluid velocity relative to the undeformed solid skeleton, also termed the seepage velocity. This seepage velocity is related to the filtration velocity vFV by vFV = nFvF, where nF is the fluid volume fraction. However, the Navier–Stokes equations combine first- and second-order partial differential operators, making it challenging to formulate rational boundary conditions. To resolve this issue, Brinkman proposed a combined approach, integrating the Darcy and Navier–Stokes equations as follows:
Here, μF = nFμFR defines the partial shear viscosity of the pore fluid, with Brinkman postulating a distinction between the two viscosity parameters μF and μFR. A key advantage of the combined equation is its asymptotic behavior: it approximates the Stokes-type Equation (9) for low values of the intrinsic permeability KS, and converges to the Darcy-type Equation (10) for high values of KS.
2.4. Applications in Transpiration Cooling
Numerous researchers have employed these three models to numerically simulate transpiration cooling effects [7,8,9,10,11,12]. Ding et al. [7] integrated transpiration and film cooling in separate porous matrices, utilizing the Brinkman–Forchheimer extension of the Darcy equation to model nitrogen flow through pores with an average diameter of 39 μm. In a subsequent study, Ding et al. [8] proposed a novel two-layer combined cooling configuration, consisting of an inner layer with discrete slots for localized coolant injection and an outer layer with a uniform porous matrix for enhanced coolant diffusion. Within the porous region, the coolant flow through randomly distributed pores was modeled using the Brinkman–Forchheimer-extended Darcy equation for momentum conservation and the local thermal equilibrium (LTE) model for energy balance. Xiao et al. [10] applied the Darcy–Forchheimer model along with a local thermal non-equilibrium model to numerically investigate transpiration cooling in a porous nose cone, analyzing liquid coolant behavior under transonic flow across varying enthalpy conditions. Their results demonstrate that coolant injection markedly influences the boundary layer structure. Similarly, Wu et al. [11] adopted the Darcy–Brinkman–Forchheimer equation to characterize fluid flow in the porous region, showing that coolant distribution in the leading and trailing edge regions significantly affects the development of the blade flow boundary layer and overall cooling performance.
While the Darcy–Brinkman–Forchheimer model is the most comprehensive, its practical application is often limited by the challenge of empirically determining its multiple coefficients for specific porous materials. This underscores a pivotal disparity between theoretical completeness and industrial applicability. To illustrate this point, consider the applications of the leading edges of hypersonic vehicles, where high flow velocities and the dominance of inertial effects are characteristic. In such cases, the Forchheimer model frequently offers an optimal balance between accuracy and computational efficiency. Conversely, in the context of transpiration cooling in lower-velocity regions or in materials with high porosity where viscous shear near the solid matrix is significant, neglecting the Brinkman term could lead to inaccurate predictions of the boundary layer behavior. Consequently, simpler models such as the Forchheimer equation are frequently employed during the preliminary design stages or when boundary layer effects are of secondary importance. The full Darcy–Brinkman–Forchheimer model is reserved for detailed analyses where high fidelity is imperative. The following Table 1 presents a comparison of the porous media models.

Table 1.
Comparison of porous media flow models.
3. Heat Transfer Modeling
To simulate heat transfer within porous media, two main approaches are typically utilized: the local thermal equilibrium (LTE) and the local thermal non-equilibrium (LTNE) models [13]. The LTE model assumes a negligible temperature difference between the fluid and the solid matrix, thereby utilizing a single energy equation. In contrast, the LTNE model accounts for interphase heat transfer by solving two separate energy equations for the fluid and solid phases [14]. The LTE model is widely used in porous media research because it is simpler to implement numerically and treat analytically. The LTNE model, while more physically detailed, introduces greater complexity and has consequently received significant research attention only in recent years.
3.1. Local Thermal Equilibrium (LTE)
To achieve a continuous temperature distribution in porous medium flows, the solid and fluid phases are often assumed to be thermally coupled and approximated under the local thermal equilibrium (LTE) condition. Numerous studies have employed the LTE model to investigate heat transfer characteristics in porous media [15,16,17,18]. For example, Alazmi and Vafai [15] examined the influence of various velocity and thermal boundary conditions at the porous medium–fluid interface. Their results indicate that variations in these conditions exert a more significant effect on the velocity field, a comparatively smaller effect on the temperature field, and an even lesser influence on the Nusselt number distribution. Vafai and Tien [17] analyzed the effects of solid boundary and inertial forces on flow and heat transfer, concluding that these factors are more pronounced in highly permeable media, fluids with high Prandtl numbers, under large pressure gradients, and in regions near the boundary layer leading edge. In a related study, Hooman and Gürgenci [18] investigated the role of viscous dissipation in forced convection within a porous channel, where the viscous dissipation function is given by Equation (11):
Three viscous dissipation models have been developed based on Equation (11) [19,20,21]. Vadasz [19] addressed a paradox arising in heat conduction problems involving a combination of Dirichlet and insulating boundary conditions, which surprisingly leads to a local thermal equilibrium solution. Meanwhile, to characterize heat transfer under high-Reynolds-number flows, Masuoka and Takatsu [20] developed a zero-equation model that incorporates eddy diffusion coefficients dependent on particle and void sizes. Separately, Wang and Li [21] focused on the combined effects of viscous dissipation and bidispersity (the presence of two distinct pore sizes) on the thermal characteristics of porous channels.
Partial filling with porous media has emerged as a novel strategy to enhance heat transfer while maintaining a relatively small pressure drop [22,23,24,25]. Mohamad [23] compared the performance of heat exchangers with fully and partially filled porous media, concluding that the partial-filling configuration is more effective for heat transfer enhancement. This approach offers two key advantages: it significantly increases the heat transfer rate while generating a much lower pressure drop than a fully porous-filled conduit. In a similar study, Shokouhmand et al. [24] investigated heat transfer characteristics in partially filled porous channels, finding that near-wall porous structures perform better with high thermal conductivity and high Darcy number, whereas low values of these parameters are less favorable. Ghazian et al. [25] further examined Couette flow in a partially porous channel between parallel plates. This confirmed that for the best heat transfer results, near-wall porous structures should preferably have a high Darcy number and high thermal conductivity.
Furthermore, the application of nanofluids as working fluids significantly enhances the heat transfer performance of porous media systems [26,27,28,29,30,31,32,33]. Matin and Pop [26] investigated the heat transfer characteristics of nanofluids flowing through porous media, accounting for the effects of viscous dissipation and catalytic reactions on the porous walls. Their study provided closed-form analytical solutions for the dimensionless governing equations of momentum, energy, and concentration. Zhang et al. [28] also examined the impacts of thermal radiation and chemical reactions on nanofluid flow and heat transfer in porous media, reporting that both the wall shear stress and the heat transfer rate increase with higher nanoparticle volume fractions. In a numerical study, Bhowmick et al. [29] analyzed the thermo-hydraulic performance of forced convection in channels with different corrugation shapes (triangular, sinusoidal, and trapezoidal), concluding that corrugated walls promote mixing between hot and cold fluids. Additionally, Hassan et al. [30] derived an analytical solution for the convective heat transfer of nanofluids over porous wavy surfaces under liquid–solid phase transition conditions.
3.2. Local Thermal Non-Equilibrium (LTNE)
The local thermal equilibrium (LTE) model is only applicable when the interfacial temperature can be considered constant, and the thermal disparity between the solid and fluid components is insignificant [34]. However, the temperature difference between the fluid and the solid matrix becomes important and plays a crucial role in complicated systems like those with high-speed flows; this condition cannot be explained under the LTE assumption [35]. In such cases, to effectively represent the characteristics of conjugate heat transfer, utilizing the local thermal non-equilibrium (LTNE) model is crucial. The LTNE model specifically considers the internal heat exchange between the flowing fluid and the solid phase within the porous medium.
A comparative analysis of the predictions from the local thermal equilibrium (LTE) and local thermal non-equilibrium (LTNE) models has been conducted by several researchers [34,36]. Vafai and Sozen [34] highlighted a critical limitation: LTE models may yield inaccurate results when applied to porous media flows. Furthermore, the assumptions underlying the LTE model were found to be invalid under conditions of high Reynolds and high Darcy numbers [36]. Subsequent studies have examined non-Darcy flow phenomena, incorporating the effects of thermal dispersion and exponential porosity variations under LTNE conditions. To guide model selection, error plots illustrating the applicability ranges of various simplified assumptions for specific working conditions were developed. The suitability of the LTE assumption is quantitatively determined by the local temperature difference at each grid point, defined as . The LTE assumptions are classified as “good” if %LTE < 1%, “very good” for 1–5%, “fair” for 5–10%, “poor” for 10–15%, and “very poor” if exceeding 15%. These results are presented graphically in Figure 3.
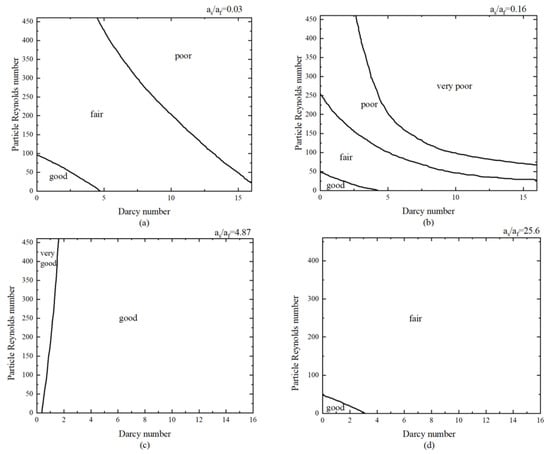
Figure 3.
Qualitative assessment of LTE using several thermal Amiri and Vafai’s diffusivities, (a) αs/αf = 0.03; (b) αs/αf = 0.16; (c) αs/αf = 4.87; (d) αs/αf = 25.6 [36].
Building upon this foundation, Kuznetsov [37] conducted further research on LTNE modeling. He utilized the Brinkman–Forchheimer-extended Darcy equation to analyze a porous parallel-plate channel under thermal non-equilibrium conditions. The results indicate that the temperature difference between the solid and fluid phases increases with the Darcy number in the central region of the channel, while the opposite trend is observed within the fluid boundary layer. In a separate analysis [38], the problem is described using two energy equations, with the fluid-phase energy equation given by Equation (12):
And the solid phase energy equation is
where kf,eff and ks,eff denote the effective thermal conductivities of the fluid and solid phases, respectively. The variables Tf and Ts represent the temperatures of the fluid and solid, hsf is the interstitial heat transfer coefficient, and asf is the interfacial area per unit volume of the porous medium.
These governing equations were applied to analyze flow in a porous parallel-plate channel. The results demonstrate that the heat transfer characteristics are predominantly governed by fluid conduction, solid conduction, and internal heat exchange between the phases [39,40]. For instance, Parhizi et al. [39] employed the LTNE model to study thermally developing flow in porous media with a spatially varying Biot number. Based on the dominance of the different heat transfer mechanisms, they categorized the flow’s thermal behavior into three distinct zones. In a related study, Filho et al. [40] investigated thermal radiation transport under LTNE conditions, showing that for a periodically varying Biot number, the peaks and troughs in the temperature field align with the corresponding maxima and minima of the Bi function.
The geometry of the porous medium, including factors such as wall thickness, is a key parameter governing its heat transfer characteristics [35,41,42,43,44,45,46,47]. Nield and Kuznetsov [41] investigated forced convection in a porous parallel-plate channel using the LTNE model, revealing that the degree of thermal non-equilibrium is directly influenced by the solid-to-fluid thermal conductivity ratio (KR). They found that the LTNE effect is more pronounced when KR > 1 and is diminished when KR < 1. In a related study, Alazmi et al. [35] identified heat flow bifurcation under LTNE conditions, noting that while certain parameters significantly alter the flow velocity, their impact on temperature and the Nusselt number is minimal. They also observed that constant-temperature boundary conditions can induce such a bifurcation. Furthermore, Al-Sumaily et al. [47] emphasized the role of particle size, concluding that larger spherical particles are more effective at enhancing heat transfer while maintaining lower pressure losses.
3.3. LTE and LTNE Comparison
Researchers have offered logical justifications and correlations for the application of LTE and LTNE models at various points in time to address this problem. The comparison of LTE and LTNE model applications by numerous researchers is given in Table 2.

Table 2.
Comparison of heat transfer models.
4. Modeling of Turbulent Flows
Modeling of turbulent flows represents another critical aspect in transpiration cooling studies. Three primary approaches are commonly used: Reynolds-averaged Navier–Stokes (RANS), large eddy simulation (LES), and direct numerical simulation (DNS).
4.1. RANS
The two-equation model of RANS is often used in numerical studies of transpiration cooling [11,12,48,49,50,51,52] because this kind of model can predict relatively accurate temperature distributions. Lv et al. [48] proposed a new optimized composite cooling structure for aero-engine combustion chamber thermal protection using Menter’s two-square-equation SST model. The results show that the overall cooling effect of the combined structure is improved by 30%. Wang et al. [49] proposed an optimization scheme for composite cooling, and a full-field coupled numerical method was developed. The RANS equations were employed to characterize the turbulent supersonic velocity in the main flow area and the coolant movement within the cooling cavity. The RANS equations were employed to characterize the turbulent supersonic velocity in the main flow area and the coolant movement within the cooling cavity.
The validation of these RANS models is a critical step, which is often performed against well-established experimental benchmarks. For instance, experimental data from transpiration cooling experiments on flat plates or in turbine blade cascades provide essential test cases for assessing the accuracy of turbulence closures in predicting wall temperatures and film effectiveness. The selection of the turbulence model has been demonstrated to exert a substantial influence on the predictions, particularly in regions characterised by pronounced pressure gradients or flow curvature.
Numerical investigations were carried out by Wu et al. [11] to investigate the transpiration cooling performance of two wedge-shaped cone heads by the RNG k-ε turbulence model. It is indicated that non-uniform permeability combined with optimized transpiration cooling results in optimal coolant distribution and a decrease in the driving force needed to deliver coolant to the stagnation zone. The critical importance of validating these models is highlighted in recent studies. For example, Ma et al. conducted a combined numerical and experimental investigation on a transpiration-cooled turbine blade, demonstrating that while RANS models can predict overall cooling effectiveness reasonably well, accurately capturing the complex near-wall flow physics remains a challenge that requires careful model selection and validation against high-quality experimental data [51]. A powerful example of this is the community-wide validation effort from the 5th AIAA Propulsion Aerodynamics Workshop, summarized by Georgiadis et al. [53]. Their findings highlighted that RANS simulations tightly coupled with a three-dimensional conjugate heat transfer (CHT) analysis were required to accurately predict plate surface temperatures, yielding results that matched experimental data much more closely than simpler adiabatic wall treatments. This underscores that for practical engineering applications, the fidelity of the heat transfer model is as critical as the turbulence model itself for achieving predictive accuracy. Table 3 summarizes the RANS approach.

Table 3.
Summary of studies using the RANS approach.
4.2. Large Eddy Simulation (LES)
Advances in computational capabilities have enabled researchers, beginning in 1963, to employ large eddy simulation (LES) for simulating the physics of wall injection [54,55]. LES is used to simulate flow structures in transpiration cooling studies [56,57,58,59,60]. Brillante et al. [57] used LES to study the change of the turbulent boundary layer induced by flowing through a porous plate. The results show that the longitudinal velocities obtained by the simulation are in good agreement with the experimental results. Xiao et al. [59] used LES to study the behavior of eddy flow in a thermal mainstream. A recurring vortex pattern with a 1.25 ms cycle was identified in both the experimental and numerical results. It is observed that there are three processes, including vortex generation, development, and fragmentation in one complete cycle. Zhang et al. [60] numerically simulated the near-wall flow structure and heat transfer characteristics of transpiration cooling using a validated internal lattice Boltzmann method and a LES method. The results show that the development of the coolant layer is affected by the local velocity gradient. Additionally, a blowing ratio of more than 2% to 3% leads to flow separation and instability of the coolant coverage.
Hybrid RANS-LES Models
In order to balance the high computational cost of LES with the robustness of RANS, Hybrid RANS-LES models have emerged as a powerful alternative. Approaches such as Detached Eddy Simulation (DES) and its variants utilise a RANS model in the near-wall region of the boundary layer (where turbulence is anisotropic and computationally expensive to resolve) and transition to an LES formulation in regions away from the wall where large, unsteady eddies are dominant. This renders them especially well-suited for applications involving transpiration cooling, which encompasses intricate interactions between the wall-bounded coolant flow and external separated or vortical structures. It is evident that these models offer a significant improvement in accuracy over RANS for predicting flow separation and heat transfer in unsteady flow fields, without the prohibitive cost of a full wall-resolved LES. The practical application and benefit of hybrid models in a formal benchmark setting were demonstrated in the 5th AIAA Propulsion Aerodynamics Workshop, as summarized by Georgiadis et al. [53]. It is evident that a number of participating organisations have applied hybrid RANS-LES approaches, including delayed detached eddy simulation (DDES) and improved delayed detached eddy simulation (IDDES), to the complex film-cooling problem. A salient finding was that these scale-resolving simulations (SRS), a category that includes the hybrid methods, yielded substantially more accurate predictions of the thermal boundary layer in comparison to traditional RANS approaches. This underscores the significance of hybrid models in capturing the intricate turbulent mixing physics that are paramount for precise heat transfer analysis, even when the overall surface temperature can be reasonably predicted by less sophisticated methods.
4.3. Direct Numerical Simulation (DNS)
Direct numerical simulation (DNS) has the advantage of capturing the behaviors of individual eddies at all scales with large computational efforts [61]. Researchers have used DNS for transpiration cooling because of the great improvements in computational efficiency and resources [62,63]. Avsarkisov et al. [62] studied a fully developed turbulent Poiseuille flow with wall transpiration using an incompressible transpiration DNS analysis.
Kraheberger et al. [63] also employed incompressible DNS to model transpiration cooling within turbulent Couette flow, allowing for an examination of the flow’s turbulent structure and internal scaling. They noticed that the turbulence intensity dropped when the rate of transpiration increased. Changes in the frictional Reynolds number have a negligible effect on the mean velocity and intensity; they only fall if the transpiration rate is constant.
Besides the uniform blowing boundary condition mentioned above, some researchers have investigated transpiration cooling using DNS to capture the flow details. Coolant for transpiration cooling is injected through many individual holes, and there are many researchers working on this approach [60,64,65,66]. Cerminara et al. [64] used compressible DNS for transpiration cooling through pores in a hypersonic laminar flow flat plate boundary layer. In actual use, the coolant is injected from individual holes. They made use of these data to investigate the areas where the boundary layer and pores interact, as well as to evaluate the multiscale DNS methods for these flows. Keller and Kloker [65] carried out effusion cooling into a laminar supersonic boundary layer through several rows of distinct perforations using DNS methods. In the case of mainstream turbulence, it was determined that the pressurization conditions of the simulated coolant channels are optimal for thin film cooling. Christopher et al. [66] investigated the problem of evaporative cooling in a flat plate turbulent boundary layer using DNS to obtain all the relevant properties of the full three-dimensional flow and thermal fields. When the stripes get smaller, the results converge to the case of uniform injection for a fixed total mass flow rate and wall porosity. Two-domain analytical method proposed by Nakayama et al. [60], which applies RANS and DNS to achieve agreement in the results, was proposed to solve the coupled problem of forced convective flow in a transpiration-cooled channel with uniformly porous walls. A summary of these turbulence modeling approaches is presented in Table 4.

Table 4.
Comparison of turbulence modeling approaches.
5. Modeling of Multi-Phase Field
Theoretical analyses of complex phase change phenomena in porous structures are mainly divided into three categories: separated-phase model (SPM), two-phase mixture model (TPMM), and semi-mixed model (SMM). The turbulence particle mixture model (TPMM) is the most widely used due to its consistent form of conservation equations and ease of implementation in commercial simulation software.
The modeling of multi-phase phenomena in porous media is inherently complex due to the presence of moving interfaces between liquid and vapour phases within an intricate solid matrix. The primary challenge confronting researchers in this field is the mathematical representation of the system without the necessity of resolving every individual pore. The models examined in this section, SPM, TPMM, and SMM, embody divergent philosophical approaches to this issue. The choice between these two models is often dependent on the expected nature of the phase transition: is it a sharp, distinct interface, or a diffuse, mixed region? The response to this question is pivotal in determining the most suitable and computationally efficient framework.
Furthermore, understanding the transient response of the system is critical for ensuring operational stability. Recent work by Liu et al. investigated the dynamic behavior of transpiration cooling with phase change under unsteady heat flux conditions [67]. Their findings highlight the complex interplay between phase-change front movement and pressure fluctuations, demonstrating that transient effects can significantly influence cooling performance and stability, a factor that must be captured by robust numerical models.
5.1. Classical Physical Modeling of Phase Change
Figure 4 shows a schematic of the typical two-phase flow problem, illustrating a porous medium of thickness L with a heat flux q applied to its heated surface.
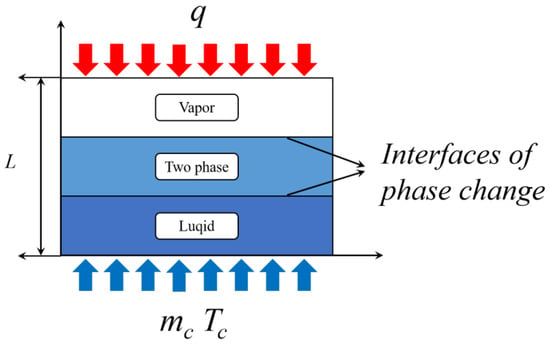
Figure 4.
Physical model of two-phase flow in porous media.
A fluid at temperature Tc and with a mass flow rate mc enters the pore from the outside. It absorbs heat from the porous matrix until it undergoes a phase transition, generating vapor before exiting. Based on the fluid state, the porous matrix is divided into three distinct zones: the liquid zone, the liquid-vapor mixing zone, and the vapor zone. For such two-phase flow problems, three models are commonly employed to characterize the flow, heat transfer, and phase change: the standard-pore model (SPM), the two-phase mixture model (TPMM), and the more recently developed semi-mixed model (SMM). All three models are formulated under the assumption of local thermal non-equilibrium (LTNE) to account for heat exchange between the fluid and solid matrix within the pores. Consequently, each model comprises two energy conservation equations—one for the fluid phase and another for the solid phase.
5.2. Separated-Phase Model (SPM)
The phase separation modeling approach formulates separate governing equations for the gas and liquid phases, coupling them at interfaces through specific boundary conditions and interfacial parameters. As described by Bear [68], the separated flow model (SFM) applies this methodology to two-phase flow in porous media. Although SFM achieves high computational accuracy, it treats the two phases as distinct fluids, which complicates the solution process due to the need to solve numerous coupled nonlinear differential equations. Ramesh and Torrance [69] successfully implemented SFM using a front-tracking method; however, unlike front-capturing methods, this technique requires continuous mesh reconstruction to explicitly determine the phase interface. Additionally, numerical analysis with SFM often necessitates the introduction of correction equations [70,71].
Recent studies have seen proposals for improved SFM variants [72,73]. Specifically, Xin et al. [72] developed a modified separated flow model (MSFM) to numerically investigate heat and mass transfer in porous media under LTNE conditions. Their results demonstrated that the direction of heat flow significantly influences thermal and fluid flow behaviors. Notably, a distinct non-isothermal phenomenon was observed in the two-phase region under one heating mode, while a pronounced LTNE phenomenon was identified under the other. In another study, Wang et al. [73] enhanced the standard-pore model (SPM) by incorporating coupled pressure and phase equations. This modification allows the solution process to be implemented within the OpenFOAM framework, thereby significantly simplifying the computations. Collectively, these new models and algorithms provide efficient tools for transpiration cooling research.
The governing equations of the standard-pore model (SPM) are presented in Table 5. These equations are solved for the primary variables: saturation, fluid temperature, and solid temperature. In the two-phase region, separate sets of conservation equations are defined for the liquid and vapor phases, respectively. In a single-phase region, these two sets of equations reduce to a single set for the prevailing phase. Consequently, since no phase change occurs in single-phase regions, the mass transfer term is absent from the corresponding mass conservation equations.

Table 5.
LTNE-SPM conservation equation.
5.3. Two-Phase Mixture Model (TPMM)
The primary limitation of the standard-pore model (SPM) lies in its requirement to track phase transition interfaces and solve numerous coupled nonlinear equations. To address this, Wang and Beckerman [74,75] introduced mixing variables and a series of algebraic relations, consolidating the differential equations from the three regions of the SPM into a unified mathematical expression. This approach significantly reduced the number of differential equations needed for the main variables, leading to the development of the two-phase mixture model (TPMM). This new formulation facilitates the solution of complex problems, such as boundary layer two-phase flow, multi-regional conjugate two-phase and single-phase flow, and transient flow.
However, the fluid enthalpy equations in the TPMM are notably complex due to numerous ontological relations and have undergone various modifications to enhance their practicality [76,77,78,79]. A known issue is the discontinuity in the effective diffusion coefficient of the TPMM [76], which causes unphysical “jumps” in predicted temperatures. To mitigate this, several smoothing functions have been proposed. For instance, Dong et al. [77] developed a novel mathematical model for a two-dimensional evaporative cooling problem with liquid-cooled phase transition. This enthalpy-based model circumvented the use of mixture density and velocity, thereby avoiding errors associated with the TPMM. Similarly, after analyzing shortcomings in existing enthalpy formulations based on TPMM, Ray and Alomar [78] proposed an improved version that readily adapts to density variations in single-phase regions, resulting in significantly reduced computational time. In another study, Li et al. [79] employed a modified Kirchhoff method to numerically investigate transient flow boiling in a vertical porous channel. The findings showed that for auxiliary flow, the lowest liquid saturation was at the end of the heated portion, while for opposing flow, it was found inside the heated area.
Subsequently, researchers have integrated the modified enthalpy formulation of the TPMM with the local thermal non-equilibrium (LTNE) model, creating new frameworks for investigation [67,76,80,81,82,83,84,85,86,87,88]. Alomar et al. [76,80] performed numerical simulations of phase change within a porous plate using both LTE and LTNE models, revealing that the LTNE approach yields more accurate results for low inlet Reynolds numbers and high thermal inputs. Chen et al. [82] proposed an integrated numerical method incorporating TPMM for transient transpiration cooling, which additionally accounted for gas compressibility, actual physical properties, and LTNE effects between gas and solid phases. Shi and Wang [83] introduced an enhanced local thermal non-equilibrium two-phase mixture model (LTNE-TPMM) along with a multi-region numerical strategy to solve coupled heat and mass transfer in a porous cone. Validation against experimental data under supersonic conditions confirmed the model’s effectiveness, demonstrating reduced numerical simulation difficulties and improved computational accuracy. Further studies [67,84,85,86,87,88] have applied LTNE-TPMM to explore transpiration cooling under diverse conditions.
The conservation equations of the TPMM are unified into a single set applicable across all regions by introducing mixture density (ρ), velocity (u), and enthalpy (h). These mixing variables characterize the combined behavior of liquid and vapor phases within a control volume. Consequently, the primary variables for computation become the mixture pressure, mixture enthalpy, and solid temperature, rather than individual phase parameters. The specific TPMM formulation discussed herein was developed by Shi and Wang [83].
The mixing variables and supplementary equations involved in the TPMM are listed in Table 6.

Table 6.
Related equations for the LTNE-TPMM method.
5.4. Semi-Mixed Model (SMM)
Although the two-phase mixture model (TPMM) reduces the number of differential equations and eliminates the need for interface tracking, it introduces numerical complexities due to the proliferation of mixing variables. To address these limitations, Dong and Wang [89] recently proposed the semi-mixed model (SMM), formulated as shown below. This model accounts for localized fluid–solid heat transfer within the pores, offering a closer representation of actual transpiration cooling conditions. A key distinction from both the SPM and TPMM is that the SMM overcomes the challenge of tracking the phase-change interface while avoiding the numerical uncertainties associated with potential insulating layers inside the porous matrix. Building upon this foundation, Dong and Wang [90] developed a transient formulation of the SMM under local thermal non-equilibrium (LTNE) conditions to investigate the stability and reliability of phase-change transpiration cooling in complex, variable thermal environments. Their results demonstrate that pressure-controlled coolant injection remains stable only under low heat fluxes and when phase change occurs on the hot side. In contrast, mass-flow-controlled coolant injection exhibits stability irrespective of the external thermal conditions.
The mixing variables and supplementary equations involved in the SMM are listed in Table 7.

Table 7.
Related equations for SMM.
5.5. Comparison of the Phase-Change Models
The three presented models (SPM, TPMM, and SMM) constitute different methodologies for governing the mass, momentum, and energy conservation of two-phase flow with phase change in a porous medium. Despite their mathematical differences, they are all capable of characterizing the same physical phenomena and generating consistent overall results. A comparative summary is provided in Table 8. The key distinction lies in the variables: SPM and SMM are based on actual physical quantities, while TPMM uses pseudo-physical quantities. This results in SPM and SMM generating closely aligned numerical outcomes, whereas TPMM exhibits notable discrepancies, particularly in fluid temperature and phase distribution. Among them, TPMM predicts the largest two-phase zone thickness, and SMM the smallest.

Table 8.
Comparison of phase-change models.
In practice, the selection of a multi-phase model is a trade-off. The SPM, with its high physical fidelity, is best suited to problems where the liquid-vapor interface is relatively sharp and its location is critical. The TPMM has been demonstrated to be more robust when confronted with complex, transient problems where tracking an interface is impractical, such as boiling spread throughout a large porous volume. The SMM endeavours to identify a median position, but its development is less advanced. A fundamental constraint pervasive across all models is the precise determination of empirical parameters governing phase interaction, which frequently necessitates extensive experimental calibration.
5.6. Validation, Verification, and Uncertainty Quantification (VV&UQ)
A critical aspect underpinning the reliability of all the numerical models discussed is a rigorous VV&UQ process. Verification is the process of ascertaining the correctness of the solution to mathematical models. In contrast, validation involves the comparison of model predictions with high-quality experimental data to confirm that the model accurately represents physical reality. In the context of transpiration cooling, this process involves the comparison of model predictions against established test cases and high-quality experimental datasets. A powerful example of a community-wide validation effort is the 5th AIAA Propulsion Aerodynamics Workshop, summarized by Georgiadis et al. [53]. This study benchmarked a wide range of computational approaches, including both Reynolds-averaged Navier–Stokes (RANS) and scale-resolving simulations, against a detailed experimental dataset for a film-cooled plate, providing an invaluable resource for assessing the predictive capabilities of multiphysics models. The process of validating numerical frameworks is also a critical preliminary step in studies of novel cooling concepts. For instance, before investigating their proposed cavity-transpiration cooling system for a hypersonic leading edge, Wang et al. first validated their numerical method by comparing their simulations against prior experimental data, confirming that the Standard k-ε model provided the closest agreement [49]. These examples highlight the critical and ongoing role that well-documented experimental benchmarks play in advancing modeling fidelity.
Uncertainty quantification is of equal importance, as it addresses the impact of uncertainties in model inputs (e.g., material properties, boundary conditions, empirical coefficients) on the simulation output. It is imperative to understand the sensitivity of the predicted wall temperature to parameters such as permeability and the interstitial heat transfer coefficient, given the difficulty in precisely measuring these properties. This understanding is crucial for the development of robust engineering design. While a comprehensive evaluation of VV&UQ methodologies lies beyond the purview of this study, it is imperative to acknowledge that the reliability of any numerical simulation is contingent on this process.
A powerful example of a community-wide validation effort is the 5th AIAA Propulsion Aerodynamics Workshop, summarized by Georgiadis et al. [53]. This study benchmarked a wide range of computational approaches, from RANS to hybrid RANS-LES and scale-resolving simulations, against a detailed experimental dataset for a film-cooled plate. The findings highlighted that while RANS models coupled with conjugate heat transfer (CHT) could provide viable surface temperature predictions, scale-resolving approaches were superior in capturing the thermal boundary layer and the complex mixing between the coolant and the hot exhaust. Such comprehensive benchmark studies are invaluable for assessing the state-of-the-art and guiding the development of more predictive numerical models.
6. Conclusions and Future Research Direction
This paper has presented a state-of-the-art review of numerical modeling methodologies for transpiration cooling—a critical thermal management technology for aerospace applications. Four major areas were analyzed: porous media flow, heat transfer, turbulence, and multi-phase physics. Although noteworthy advances have been made in these areas, the ever-growing complexity of aerospace systems further necessitates enhanced modeling fidelity, efficiency, and predictive capability. Based on the developed review, the following can be outlined as important directions for further research:
Multi-Scale and Multi-Physics Modeling: The most important challenge is the strong coupling of the phenomena discussed in this review. Future efforts need to be directed toward developing high-fidelity frameworks that couple advanced turbulence models, say LES, with a model for LTNE heat transfer and multi-phase flow. In addition, multi-scale modeling can be used as a bridge between the pore-scale physics-dominated characteristics, such as permeability and heat transfer, and component-scale performance.
Modeling of Advanced Porous Materials: Additive manufacturing enables the design of porous media with precisely controlled, graded, and anisotropic structures. Current modeling approaches, which often assume homogeneous and isotropic properties, are insufficient. Future research must develop new models that can accurately capture the flow and thermal characteristics of these complex and engineered materials, potentially by directly incorporating pore-scale geometry or using homogenization techniques.
High-Fidelity Simulation for Design: As computational resources continue to increase, it will be possible to supplant RANS-based models with wall-resolved LES and hybrid RANS-LES methods within an industrial design framework. These higher-fidelity simulations can provide important insights into unsteady phenomena such as coolant jet interaction with the external boundary layer and flow separation, both key to predicting cooling effectiveness and the prevention of component failure.
Validation and Uncertainty Quantification (VV&UQ): There is an urgent need for more high-quality, well-documented experimental data for the validation of complex multi-physics models under the relevant conditions concerning aerospace test cases, namely at high temperatures, pressures, and Mach numbers. Rigorous VV&UQ should be an integral part of establishing the predictive credibility of numerical models and quantifying margins of uncertainty in their predictions.
Data-Driven and AI-Assisted Modeling: Detailed simulations are computationally expensive and, therefore, cannot be used in rapid design optimization. Machine learning and artificial intelligence are promising pathways toward the development of computationally inexpensive surrogate models. Such models, which would be trained on data from high-fidelity simulations or experiments, will be able to accelerate design cycles and explore immense design spaces to optimize transpiration cooling systems.
Addressing these areas of investigation will be essential to unlock the full potential of transpiration cooling and enable the next generation of reusable hypersonic vehicles and high-performance aerospace engines.
Author Contributions
Conceptualization, J.L.; software, W.Y.A. and J.Z.; data curation, J.Z. and G.Z.; writing—original draft preparation, W.Y.A. and J.Z.; writing—review and editing, W.X. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Hunan Province, China (Grant No. 2023JJ40733).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Abbreviation | Full Form | |
| BFED | Brinkman–Forchheimer-Extended Darcy Equation | |
| DNS | Direct Numerical Simulation | |
| LES | Large Eddy Simulation | |
| LTE | Local Thermal Equilibrium | |
| RANS | Reynolds-Averaged Navier–Stokes | |
| SMM | Semi-Mixed Model | |
| SPM | Separated-Phase Model | |
| TPMM | Two-Phase Mixture Model | |
| LTNE | Local thermal non-equilibrium | |
| Nomenclature | ||
| Symbol | Description | Units |
| asf | Interfacial area per unit volume | |
| a,b | A non-Darcian flow coefficient | |
| bs, BS | Solid curvature parameter | (m/s)2 |
| cp | Specific heat | J/(kg·K) |
| dp | Particle diameter | m |
| g | Gravity vector | |
| h1 | Hydraulic diameter | m |
| hsf | Heat transfer coefficient | W/(m2·K) |
| h | Specific enthalpy | J/kg |
| k | Thermal conductivity | |
| Ks | Intrinsic permeability | m2 |
| Hydraulic conductivity | ||
| L | Length of porous matrix | m |
| m | Mass flow rate per unit area | kg/(m2·s) |
| nF | Fluid volume fraction | |
| p | Pressure | Pa |
| q | Heat flux | W/m2 |
| s | Liquid saturation | |
| T | Temperature | K |
| u | Superficial or Darcy velocity vector | |
| Ug | Gravitation potential | |
| v | Velocity | |
| x,y | Position vector | |
| γFR | Intrinsic specific gravity of the fluid | |
| ε | Porosity | |
| μ | Dynamic viscosity | Ns/m2 |
| ρ | Density | kg/m3 |
| σ | Interfacial tension | N/m |
| φ | Viscous dissipation | |
| c | Coolant | |
| eff | Effective | |
| FV | Filter velocity | |
| FR | Intrinsic pore fluid | |
| F | Pore fluid | |
| i, f | Fluid in different regions | |
| l | Liquid | |
| v | Vapor | |
| s | Solid | |
| sat | Saturated state | |
References
- Wu, J.; Yu, B. A fractal resistance model for flow through porous media. Int. J. Heat Mass Transf. 2007, 50, 3925–3932. [Google Scholar] [CrossRef]
- Liu, J.; Guo, W.; Yin, M.; Xi, W.; Sunden, B. Flow and heat transfer characteristic of regenerative cooling channels using supercritical CO2 with circular tetrahedral lattice structures. Case Stud. Therm. Eng. 2025, 71, 106204. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes À Suivre et des Formules À Employer Dans Les Questions de Distribution D’eau: Ouvrage Terminé Par Un Appendice Relatif Aux Fournitures D’eau de Plusieurs Villes, Au Filtrage des Eaux et À La Fabrication des Tuyaux de Fonte, de Plomb, de Tôle et de Bitume; Dalmont, V., Ed.; Victor Dalmont: Paris, France, 1856; Volume 2. [Google Scholar]
- Ph, F. Wasserbewegung durch boden. Z. Des Vereines Dtsch. Ingenieure 1901, 45, 1781–1788. [Google Scholar]
- Markert, B. A Biphasic Continuum Approach for Viscoelastic High-Porosity Foams: Comprehensive Theory, Numerics, and Application. Arch. Comput. Methods Eng. 2008, 15, 371–446. [Google Scholar] [CrossRef]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Flow Turbul. Combust. 1949, 1, 27–34. [Google Scholar] [CrossRef]
- Ding, R.; Wang, J.; He, F.; Dong, G.; Tang, L. Numerical investigation on the performances of porous matrix with transpiration and film cooling. Appl. Therm. Eng. 2019, 146, 422–431. [Google Scholar] [CrossRef]
- Ding, R.; Wang, J.; He, F.; Wang, M.; Luan, Y.; Dong, G.; Tang, L. Numerical investigation on a double layer combined cooling structure for aerodynamic heat control of hypersonic vehicle leading edge. Appl. Therm. Eng. 2020, 169, 114949. [Google Scholar] [CrossRef]
- Wang, W.; Tao, G.; Ke, D.; Luo, J.; Cui, J. Transpiration cooling of high pressure turbine vane with optimized porosity distribution. Appl. Therm. Eng. 2023, 223, 119831. [Google Scholar] [CrossRef]
- Xiao, X.; Zhao, G.; Zhou, W. Numerical investigation of transpiration cooling for porous nose cone with liquid coolant. Int. J. Heat Mass Transf. 2018, 121, 1297–1306. [Google Scholar] [CrossRef]
- Wu, N.; Wang, J.; He, F.; Chen, L.; Ai, B. Optimization transpiration cooling of nose cone with non-uniform permeability. Int. J. Heat Mass Transf. 2018, 127, 882–891. [Google Scholar] [CrossRef]
- Dahmen, W.; Mueller, S.; Rom, M.; Schweikert, S.; Selzer, M.; von Wolfersdorf, J. Numerical boundary layer investigations of transpiration-cooled turbulent channel flow. Int. J. Heat Mass Transf. 2015, 86, 90–100. [Google Scholar] [CrossRef]
- Quintard, M.; Kaviany, M.; Whitaker, S. Two-medium treatment of heat transfer in porous media: Numerical results for effective properties. Adv. Water Resour. 1997, 20, 77–94. [Google Scholar] [CrossRef]
- Pati, S.; Borah, A.; Boruah, M.P.; Randive, P.R. Critical review on local thermal equilibrium and local thermal non-equilibrium approaches for the analysis of forced convective flow through porous media. Int. Commun. Heat Mass Transf. 2022, 132, 105889. [Google Scholar] [CrossRef]
- Alazmi, B.; Vafai, K. Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Int. J. Heat Mass Transf. 2001, 44, 1735–1749. [Google Scholar] [CrossRef]
- Vafai, K. Convective flow and heat transfer in variable-porosity media. J. Fluid Mech. 1984, 147, 233–259. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and inertia effects on flow and heat transfer in porous media. Int. J. Heat Mass Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Hooman, K.; Gurgenci, H. Effects of viscous dissipation and boundary conditions on forced convection in a channel occupied by a saturated porous medium. Transp. Porous Media 2007, 68, 301–319. [Google Scholar] [CrossRef]
- Vadasz, P. On the paradox of heat conduction in porous media subject to lack of local thermal equilibrium. Int. J. Heat Mass Transf. 2007, 50, 4131–4140. [Google Scholar] [CrossRef]
- Masuoka, T.; Takatsu, Y. Turbulence model for flow through porous media. Int. J. Heat Mass Transf. 1996, 39, 2803–2809. [Google Scholar] [CrossRef]
- Wang, K.; Li, P. Forced convection in bidisperse porous media incorporating viscous dissipation. Appl. Therm. Eng. 2018, 140, 86–94. [Google Scholar] [CrossRef]
- Teamah, M.A.; El-Maghlany, W.M.; Dawood, M.M.K. Numerical simulation of laminar forced convection in horizontal pipe partially or completely filled with porous material. Int. J. Therm. Sci. 2011, 50, 1512–1522. [Google Scholar] [CrossRef]
- Mohamad, A.A. Heat transfer enhancements in heat exchangers fitted with porous media Part I: Constant wall temperature. Int. J. Therm. Sci. 2003, 42, 385–395. [Google Scholar] [CrossRef]
- Shokouhmand, H.; Jam, F.; Salimpour, M.R. The effect of porous insert position on the enhanced heat transfer in partially filled channels. Int. Commun. Heat Mass Transf. 2011, 38, 1162–1167. [Google Scholar] [CrossRef]
- Ghazian, O.; Rezvantalab, H.; Ashjaee, M. Analytical Investigation of the Effect of Viscous Dissipation on Couette Flow in a Channel Partially Filled with a Porous Medium. Transp. Porous Media 2011, 89, 1–13. [Google Scholar] [CrossRef]
- Matin, M.H.; Pop, I. Forced convection heat and mass transfer flow of a nanofluid through a porous channel with a first order chemical reaction on the wall. Int. Commun. Heat Mass Transf. 2013, 46, 134–141. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Ganji, D.D. Nanofluid flow and heat transfer in an asymmetric porous channel with expanding or contracting wall. J. Mol. Liq. 2014, 195, 230–239. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, L.; Zhang, X.; Chen, G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. Appl. Math. Model. 2015, 39, 165–181. [Google Scholar] [CrossRef]
- Bhowmick, D.; Randive, P.R.; Pati, S. Implication of corrugation profile on thermo-hydraulic characteristics of Cu-water nanofluid flow through partially filled porous channel. Int. Commun. Heat Mass Transf. 2021, 125, 105329. [Google Scholar] [CrossRef]
- Hassan, M.; Marin, M.; Alsharif, A.; Ellahi, R. Convective heat transfer flow of nanofluid in a porous medium over wavy surface. Phys. Lett. A 2018, 382, 2749–2753. [Google Scholar] [CrossRef]
- Saryazdi, A.B.; Talebi, F.; Armaghani, T.; Pop, I. Numerical study of forced convection flow and heat transfer of a nanofluid flowing inside a straight circular pipe filled with a saturated porous medium. Eur. Phys. J. Plus 2016, 131, 78. [Google Scholar] [CrossRef]
- Moghadasi, H.; Aminian, E.; Saffari, H.; Mahjoorghani, M.; Emamifar, A. Numerical analysis on laminar forced convection improvement of hybrid nanofluid within a U-bend pipe in porous media. Int. J. Mech. Sci. 2020, 179, 105659. [Google Scholar] [CrossRef]
- Nazari, M.; Ashouri, M.; Kayhani, M.H.; Tamayol, A. Experimental study of convective heat transfer of a nanofluid through a pipe filled with metal foam. Int. J. Therm. Sci. 2015, 88, 33–39. [Google Scholar] [CrossRef]
- Vafai, K.; Sozen, M. Analysis of Energy and Momentum Transport for Fluid Flow Through a Porous Bed. J. Heat Transf. 1990, 112, 690–699. [Google Scholar] [CrossRef]
- Yang, K.; Vafai, K. Analysis of temperature gradient bifurcation in porous media—An exact solution. Int. J. Heat Mass Transf. 2010, 53, 4316–4325. [Google Scholar] [CrossRef]
- Amiri, A.; Vafai, K. Analysis of dispersion effects and non-thermal equilibrium, non-Darcian, variable porosity incompressible flow through porous media. Int. J. Heat Mass Transf. 1994, 37, 939–954. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Thermal nonequilibrium, non-darcian forced convection in a channel filled with a fluid saturated porous medium—A perturbation solution. Appl. Sci. Res. 1996, 57, 119–131. [Google Scholar] [CrossRef]
- Lee, D.Y.; Vafai, K. Analytical characterization and conceptual assessment of solid and fluid temperature differentials in porous media. Int. J. Heat Mass Transf. 1999, 42, 423–435. [Google Scholar] [CrossRef]
- Parhizi, M.; Torabi, M.; Jain, A. Local thermal non-equilibrium (LTNE) model for developed flow in porous media with spatially-varying Biot number. Int. J. Heat Mass Transf. 2021, 164, 120538. [Google Scholar] [CrossRef]
- Moro, R.C.; Malalasekera, W. An Analysis of Thermal Radiation in Porous Media Under Local Thermal Non-equilibrium. Transp. Porous Media 2020, 132, 683–705. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. Local thermal nonequilibrium effects in forced convection in a porous medium channel: A conjugate problem. Int. J. Heat Mass Transf. 1999, 42, 3245–3252. [Google Scholar] [CrossRef]
- Alazmi, B.; Vafai, K. Analysis of variants within the porous media transport models. J. Heat Transf. -Trans. Asme 2000, 122, 303–326. [Google Scholar] [CrossRef]
- Jiang, P.X.; Ren, Z.P. Numerical investigation of forced convection heat transfer in porous media using a thermal non-equilibrium model. Int. J. Heat Fluid Flow 2001, 22, 102–110. [Google Scholar] [CrossRef]
- Kuwahara, F.; Shirota, M.; Nakayama, A. A numerical study of interfacial convective heat transfer coefficient in two-energy equation model for convection in porous media. Int. J. Heat Mass Transf. 2001, 44, 1153–1159. [Google Scholar] [CrossRef]
- Elliott, A.; Torabi, M.; Karimi, N.; Cunningham, S. On the effects of internal heat sources upon forced convection in porous channels with asymmetric thick walls. Int. Commun. Heat Mass Transf. 2016, 73, 100–110. [Google Scholar] [CrossRef]
- Davarzani, H.; Marcoux, M.; Quintard, M. Effect of solid thermal conductivity and particle-particle contact on effective thermodiffusion coefficient in porous media. Int. J. Therm. Sci. 2011, 50, 2328–2339. [Google Scholar] [CrossRef]
- Al-Sumaily, G.F.; Nakayama, A.; Sheridan, J.; Thompson, M.C. The effect of porous media particle size on forced convection from a circular cylinder without assuming local thermal equilibrium between phases. Int. J. Heat Mass Transf. 2012, 55, 3366–3378. [Google Scholar] [CrossRef]
- Lv, Y.M.; Liu, T.L.; Huang, X.; He, F.; Tang, L.S.; Zhou, J.X.; Wang, J.H. Numerical investigation and optimization of flat plate transpiration-film combined cooling structure. Int. J. Therm. Sci. 2022, 179, 107673. [Google Scholar] [CrossRef]
- Wang, D.; Pan, K.; Li, J.G.; Wang, L.Y.; Liu, Z.C. Numerical investigation on the characteristics of cavity-transpiration combined cooling for hypersonic vehicle leading edge. Appl. Therm. Eng. 2023, 226, 120275. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, J.K.; Chen, P.T.; Zhang, H.; Tang, H.W. Numerical investigation on transpiration cooling performance with different porosities and mainstream pressure gradients. Int. J. Therm. Sci. 2023, 184, 107991. [Google Scholar] [CrossRef]
- Ma, H.F.; Sun, H.O.; Fu, H.; Luan, Y.G.; Sun, T.; Zunino, P. Numerical investigation on transpiration cooling performance of turbine blades with non-uniform porosity. Appl. Therm. Eng. 2023, 235, 121394. [Google Scholar] [CrossRef]
- Kim, M.; Shin, D.H.; Lee, B.J.; Lee, J. Flow characterization of microscale effusion and transpiration air cooling on single blade. Case Stud. Therm. Eng. 2022, 31, 101863. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Wernet, M.P.; Crowe, D.S.; Woeber, C.D.; Karaman-Shoemake, K.C.; Winkler, C.M. Assessment of Multiphysics Computations of Flow over a Film-Cooled Plate. J. Thermophys. Heat Transf. 2025, 39, 704–723. [Google Scholar] [CrossRef]
- Bouffanais, R. Advances and challenges of applied large-eddy simulation. Comput. Fluids 2010, 39, 735–738. [Google Scholar] [CrossRef]
- Yang, Z.Y. Large-eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef]
- Xi, W.; Liu, P.; Shao, Q.; Guo, W.; Liu, J. Parametric Study of Flow and Combustion Characteristic in a Cavitied Scramjet with Multi-Position Injection. Fire 2024, 7, 176. [Google Scholar] [CrossRef]
- Brillant, G.; Bataille, F.O.; Ducros, F. Large-eddy simulation of a turbulent boundary layer with blowing. Theor. Comput. Fluid Dyn. 2004, 17, 433–443. [Google Scholar] [CrossRef]
- Wang, C.H.; Zhang, J.Z.; Feng, H.K.; Huang, Y. Large eddy simulation of film cooling flow from a fanshaped hole. Appl. Therm. Eng. 2018, 129, 855–870. [Google Scholar] [CrossRef]
- Xiao, X.F.; Zhao, G.B.; Zhou, W.X.; Martynenko, S. Large-eddy simulation of transpiration cooling in turbulent channel with porous wall. Appl. Therm. Eng. 2018, 145, 618–629. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Sun, X.C.; Wang, X.; Xie, G.N. Flow structure and heat transfer of transpiration cooling by using a LBM: The effects of wall blowing and spatially nonuniform injection. Int. Commun. Heat Mass Transf. 2021, 127, 105491. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD, 3rd ed.; DCW Industries, Inc.: Philadelphia, PA, USA, 2006. [Google Scholar]
- Avsarkisov, V.; Oberlack, M.; Hoyas, S. New scaling laws for turbulent Poiseuille flow with wall transpiration. J. Fluid Mech. 2014, 746, 99–122. [Google Scholar] [CrossRef]
- Kraheberger, S.; Hoyas, S.; Oberlack, M. DNS of a turbulent Couette flow at constant wall transpiration up to Reτ = 1000. J. Fluid Mech. 2018, 835, 421–443. [Google Scholar] [CrossRef]
- Cerminara, A.; Deiterding, R.; Sandham, N. Direct Numerical Simulation of Hypersonic Flow Through Regular and Irregular Porous Surfaces. In Proceedings of the 7th European Conference on Computational Fluid Dynamics, Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Keller, M.A.; Kloker, M.J. Effusion Cooling and Flow Tripping in Laminar Supersonic Boundary-Layer Flow. Aiaa J. 2015, 53, 902–919. [Google Scholar] [CrossRef]
- Christopher, N.; Peter, J.M.F.; Kloker, M.J.; Hickey, J.P. DNS of turbulent flat-plate flow with transpiration cooling. Int. J. Heat Mass Transf. 2020, 157, 119972. [Google Scholar] [CrossRef]
- Liu, T.; Su, H.; Chen, Z.; He, F.; Wang, J. Numerical investigation on the transient transport and heat transfer characteristics of transpiration cooling with liquid phase change during coolant adjustment. Appl. Therm. Eng. 2022, 209, 118277. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Ramesh, P.S.; Torrance, K.E. Numerical Algorithm for Problems Involving Boiling and Natural Convection in Porous Materials. Numer. Heat Transf. Part B Fundam. 1990, 17, 1–24. [Google Scholar] [CrossRef]
- Chavent, G. A new formulation of diphasic incompressible flows in porous media. In Proceedings of the Applications of Methods of Functional Analysis to Problems in Mechanics; Springer: Berlin/Heidelberg, Germany, 1976; pp. 258–270. [Google Scholar]
- Tung, V.X.; Dhir, V.K. Finite element solution of multi-dimensional two-phase flow through porous media with arbitrary heating conditions. Int. J. Multiph. Flow 1990, 16, 985–1002. [Google Scholar] [CrossRef]
- Xin, C.Y.; Rao, Z.H.; You, X.Y.; Song, Z.C.; Han, D.T. Numerical investigation of vapor-liquid heat and mass transfer in porous media. Energy Convers. Manag. 2014, 78, 1–7. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.H.; Pu, J.; He, F. Transient heat dissipation performances of transpiration cooling with coolant phase change. Int. Commun. Heat Mass Transf. 2022, 135, 106082. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Beckermann, C. A two-phase mixture model of liquid-gas flow and heat transfer in capillary porous media—I. Formulation. Int. J. Heat Mass Transf. 1993, 36, 2747–2758. [Google Scholar]
- Wang, C.Y. A Fixed-Grid Numerical Algorithm for Two-Phase Flow and Heat Transfer in Porous Media. Numer. Heat Transf. Part B Fundam. 1997, 32, 85–105. [Google Scholar] [CrossRef]
- Alomar, O.R.; Mendes, M.A.A.; Trimis, D.; Ray, S. Simulation of complete liquid vapour phase change process inside porous evaporator using local thermal non-equilibrium model. Int. J. Therm. Sci. 2015, 94, 228–241. [Google Scholar] [CrossRef]
- Dong, W.J.; Wang, J.H.; Chen, S.Y.; Ai, B.C.; Luo, X.G. Modelling and investigation on heat transfer deterioration during transpiration cooling with liquid coolant phase-change. Appl. Therm. Eng. 2018, 128, 381–392. [Google Scholar] [CrossRef]
- Ray, S.; Alomar, O.R. Simulation of liquid-vapour phase change process inside porous media using modified enthalpy formulation. Int. J. Therm. Sci. 2016, 105, 123–136. [Google Scholar] [CrossRef]
- Li, H.Y.; Leong, K.C.; Jin, L.W.; Chai, J.C. Transient behavior of fluid flow and heat transfer with phase change in vertical porous channels. Int. J. Heat Mass Transf. 2010, 53, 5209–5222. [Google Scholar] [CrossRef]
- Alomar, O.R.; Mendes, M.A.A.; Trimis, D.; Ray, S. Numerical simulation of complete liquid-vapour phase change process inside porous media: A comparison between local thermal equilibrium and non-equilibrium models. Int. J. Therm. Sci. 2017, 112, 222–241. [Google Scholar] [CrossRef]
- Alomar, O.R.; Mendes, M.A.A.; Ray, S.; Trimis, D. Numerical investigation of complete evaporation process inside porous evaporator using staggered and non-staggered grid arrangements. Int. J. Therm. Sci. 2018, 129, 56–72. [Google Scholar] [CrossRef]
- Chen, Y.; Du, S.; Li, D.; Gao, Y.; He, Y.L. Numerical investigation of transient phase-change transpiration cooling based on variable properties of coolant. Appl. Therm. Eng. 2021, 184, 116204. [Google Scholar] [CrossRef]
- Su, H.; Wang, J.H.; He, F.; Chen, L.; Ai, B.C. Numerical investigation on transpiration cooling with coolant phase change under hypersonic conditions. Int. J. Heat Mass Transf. 2019, 129, 480–490. [Google Scholar] [CrossRef]
- Alomar, O.R.; Mohammed, R.R.; Mendes, M.A.A.; Ray, S.; Trimis, D. Numerical investigation of two-phase flow in anisotropic porous evaporator. Int. J. Therm. Sci. 2019, 135, 1–16. [Google Scholar] [CrossRef]
- Alomar, O.R. Numerical investigation of two-phase flow in a horizontal porous evaporator with localised heating using non-Darcian flow and two equations model. Heat Mass Transf. 2020, 56, 1203–1221. [Google Scholar] [CrossRef]
- Su, H.; He, F.; Wang, J.H.; Wu, N.; Yao, R.; Han, H.T.; Chu, M. Numerical investigation on the characteristics of coolant flow, heat absorption and phase change in transpiration cooling process. Int. J. Therm. Sci. 2019, 142, 68–76. [Google Scholar] [CrossRef]
- Alomar, O.R. Transient behaviour of heat transfer with complete evaporation process in Porous Channel with localised heating using non-Darcian flow and LTNE model. Heat Mass Transf. 2021, 57, 1921–1948. [Google Scholar] [CrossRef]
- Su, H.; He, F.; Wang, J.H.; Luo, X.G.; Ai, B.C. Numerical investigation on the effects of porous cone parameters on liquid transpiration cooling performance. Int. J. Therm. Sci. 2021, 161, 106743. [Google Scholar] [CrossRef]
- Dong, W.J.; Wang, J.H. A New Model and its Application to Investigate Transpiration Cooling with Liquid Coolant Phase Change. Transp. Porous Media 2018, 122, 575–593. [Google Scholar] [CrossRef]
- He, F.; Dong, W.J.; Wang, J.H.; Zhou, J.X.; Tang, L.S. Transient model and its application to investigate the injection mode and periodical operation of transpiration cooling with liquid coolant phase change. Appl. Therm. Eng. 2020, 181, 115956. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).