Tensile Creep Behavior of PP/CF Wet-Laid Nonwoven Composite: Short-Term and Long-Term Creep Behavior
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Composite Preparation
2.2. Testing and Characterization
2.2.1. Short-Term Tensile Creep Behavior
2.2.2. Long-Term Tensile Creep Behavior Test Method
2.2.3. Void Content Test Method
3. Results and Discussions
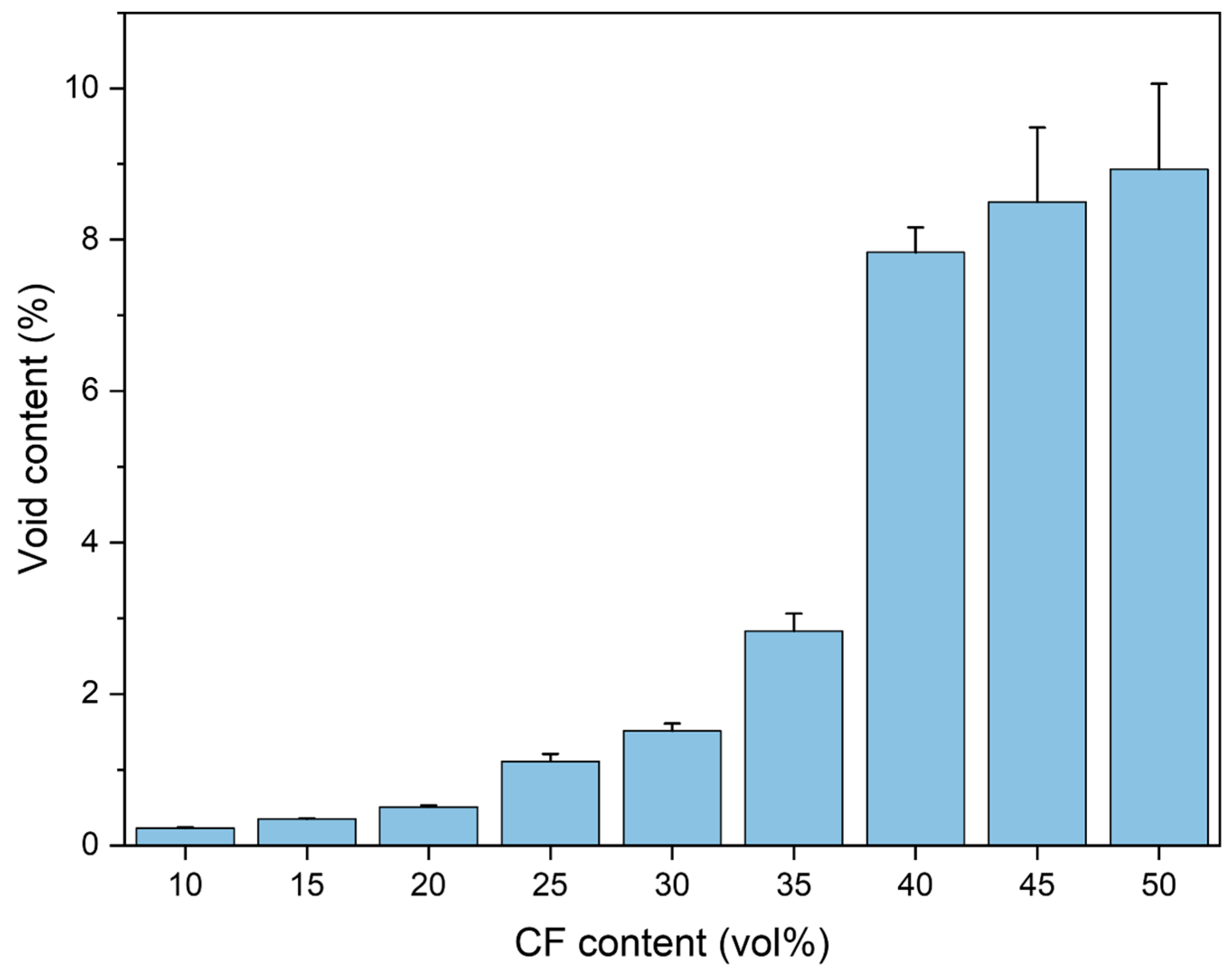
3.1. Void Content
3.2. Short-Term Creep Behavior
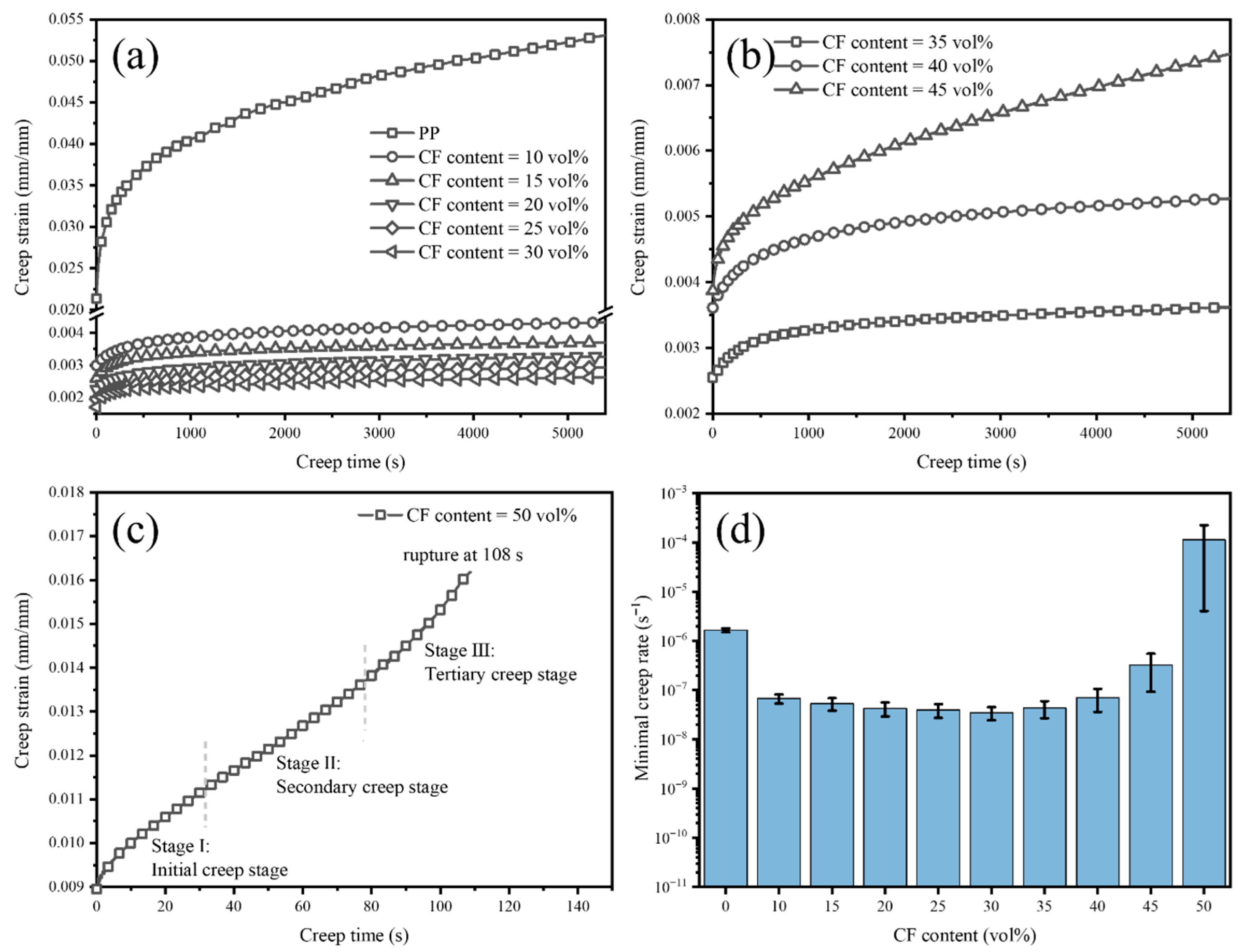
3.2.1. Effect of CF Content on Short-Term Tensile Creep Behavior
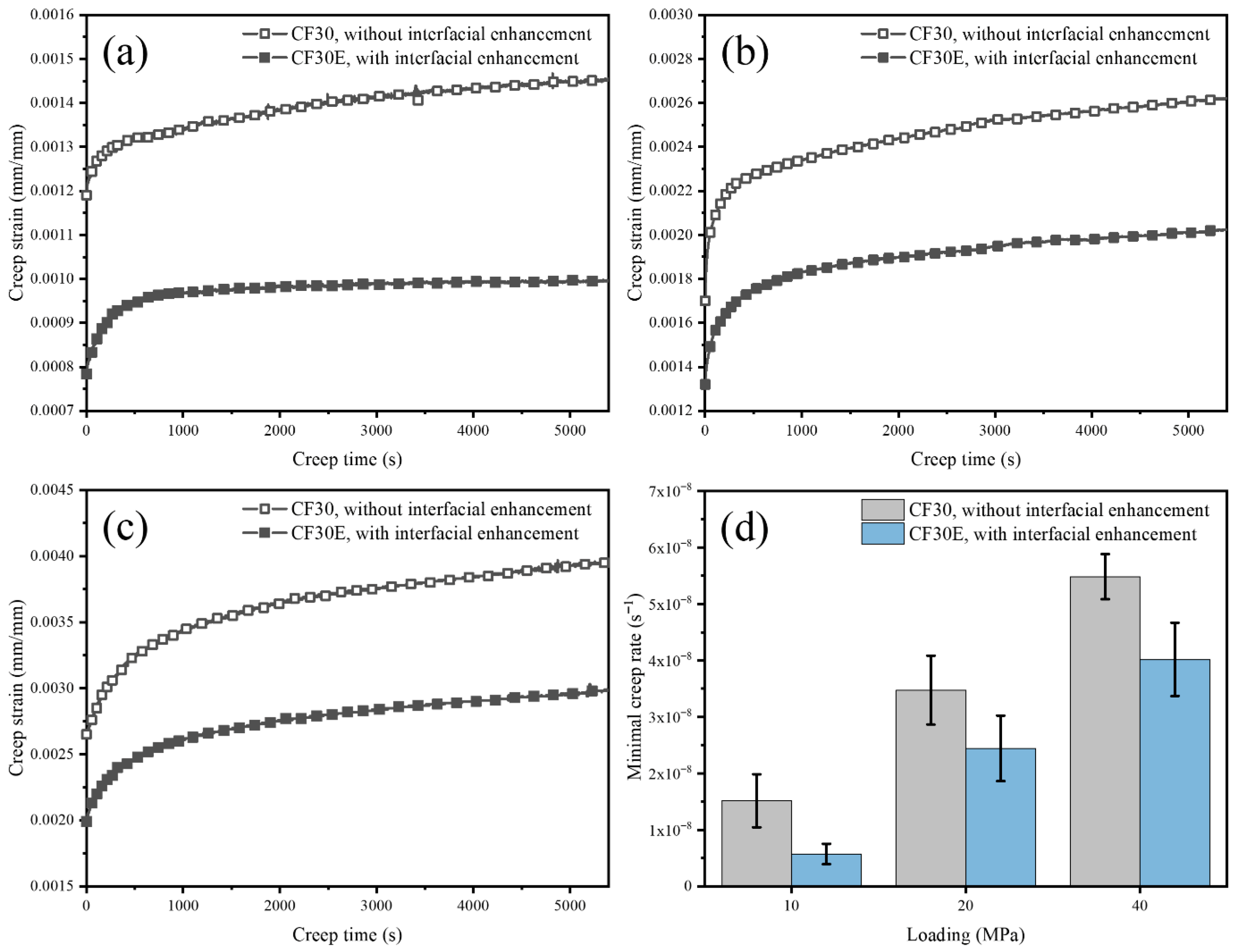
3.2.2. Effects of Load Level and Interfacial Enhancement on Short-Term Tensile Creep Behavior
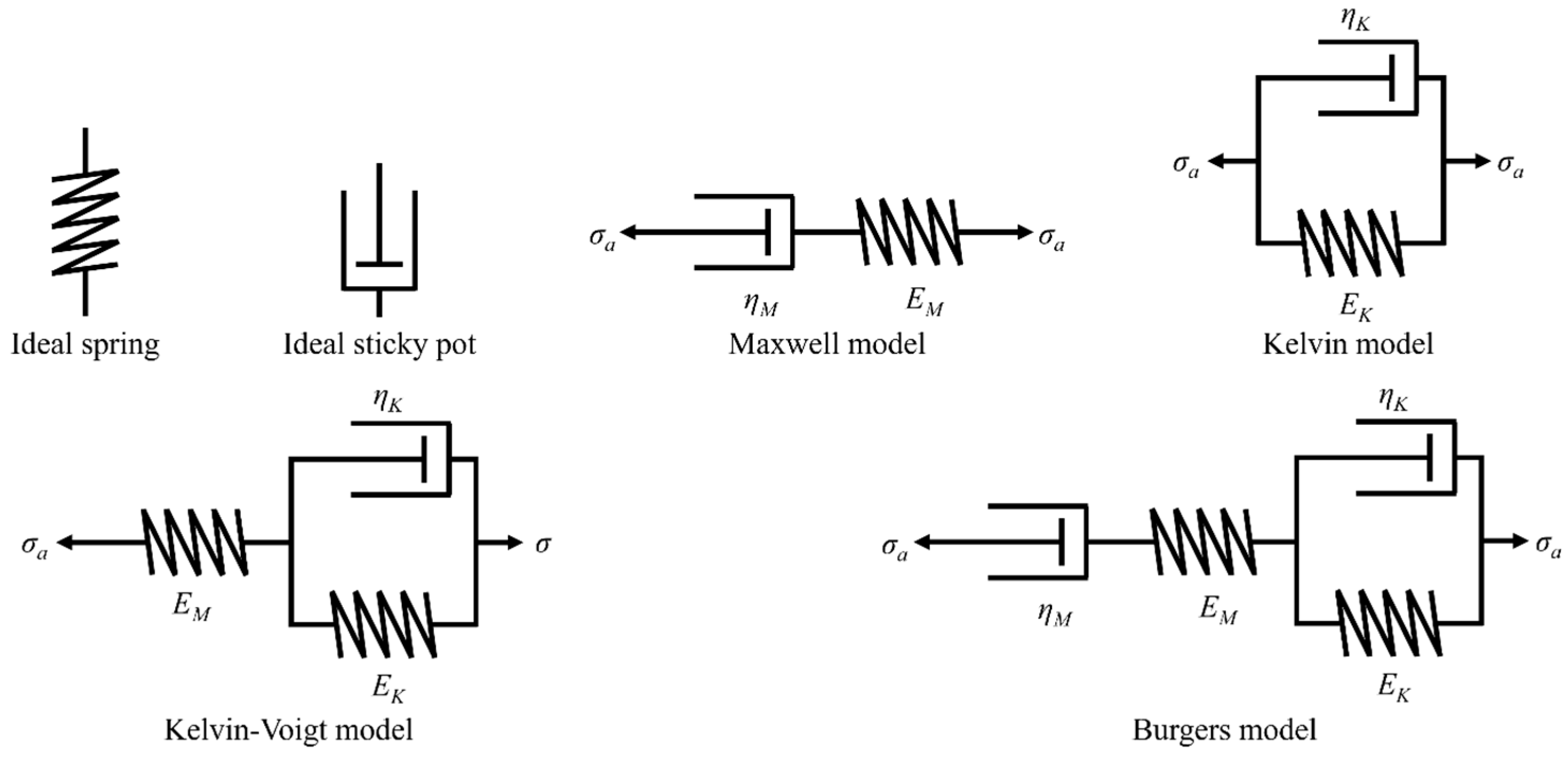
3.2.3. Fitting of Short-Term Tensile Creep Curves
- 1.
- Fitting with the Findley model
- 2.
- Fitting with the Burgers model
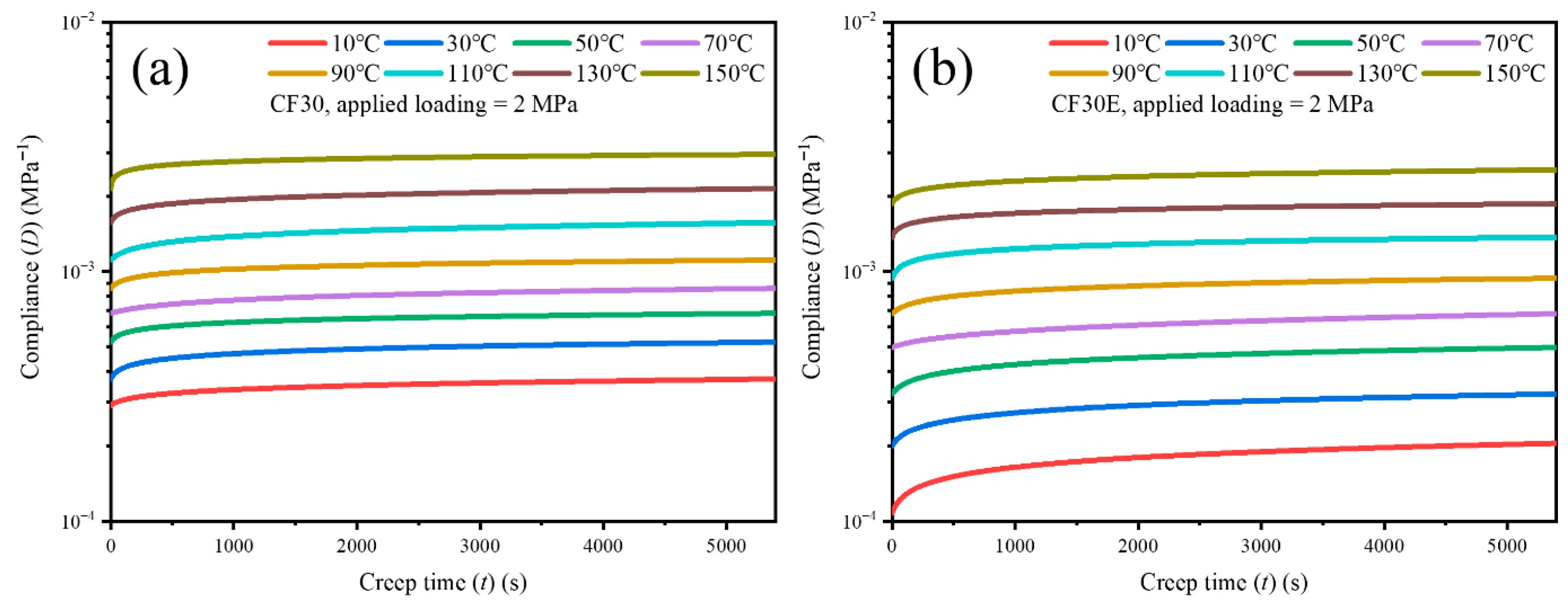
3.3. Long-Term Tensile Creep Behavior
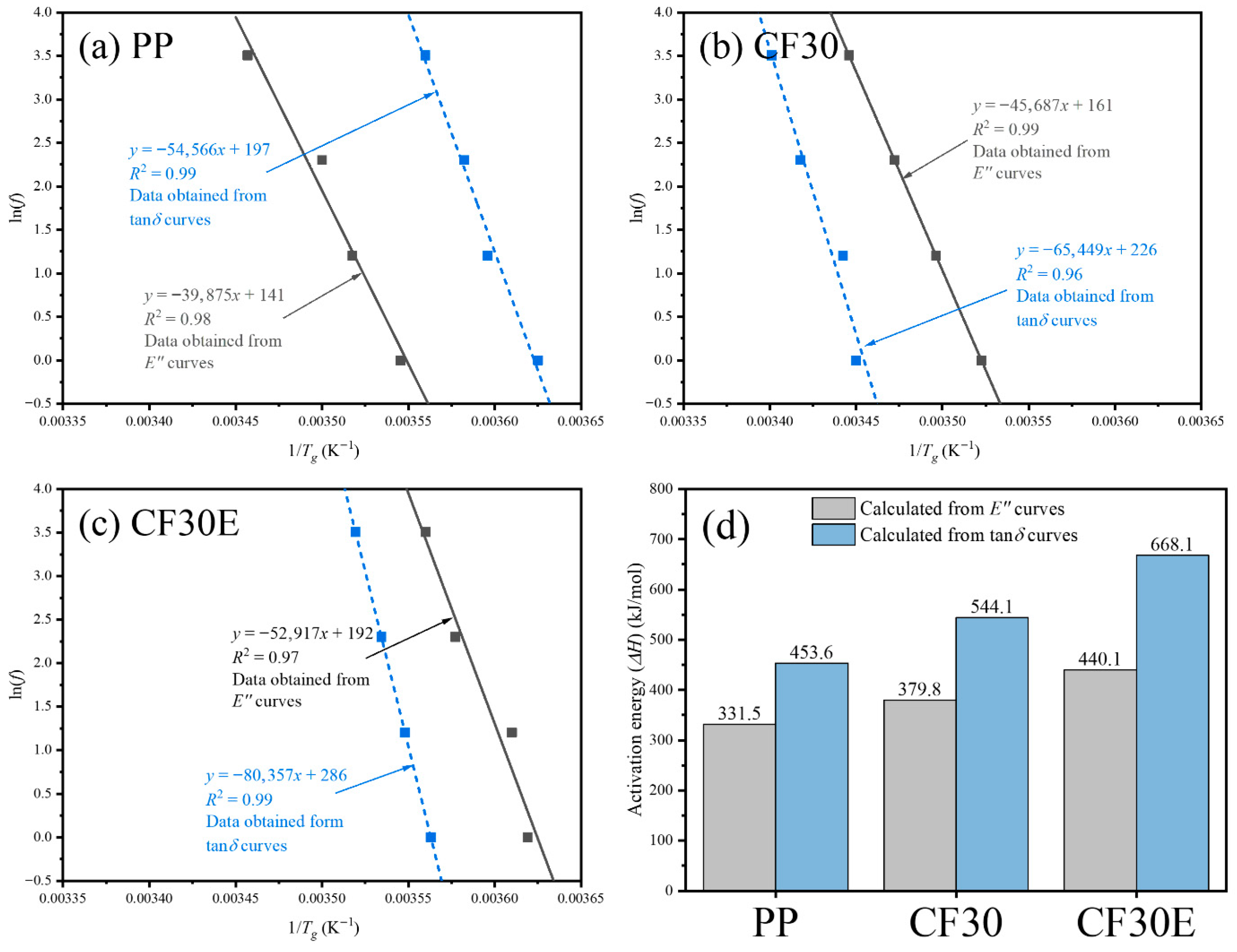
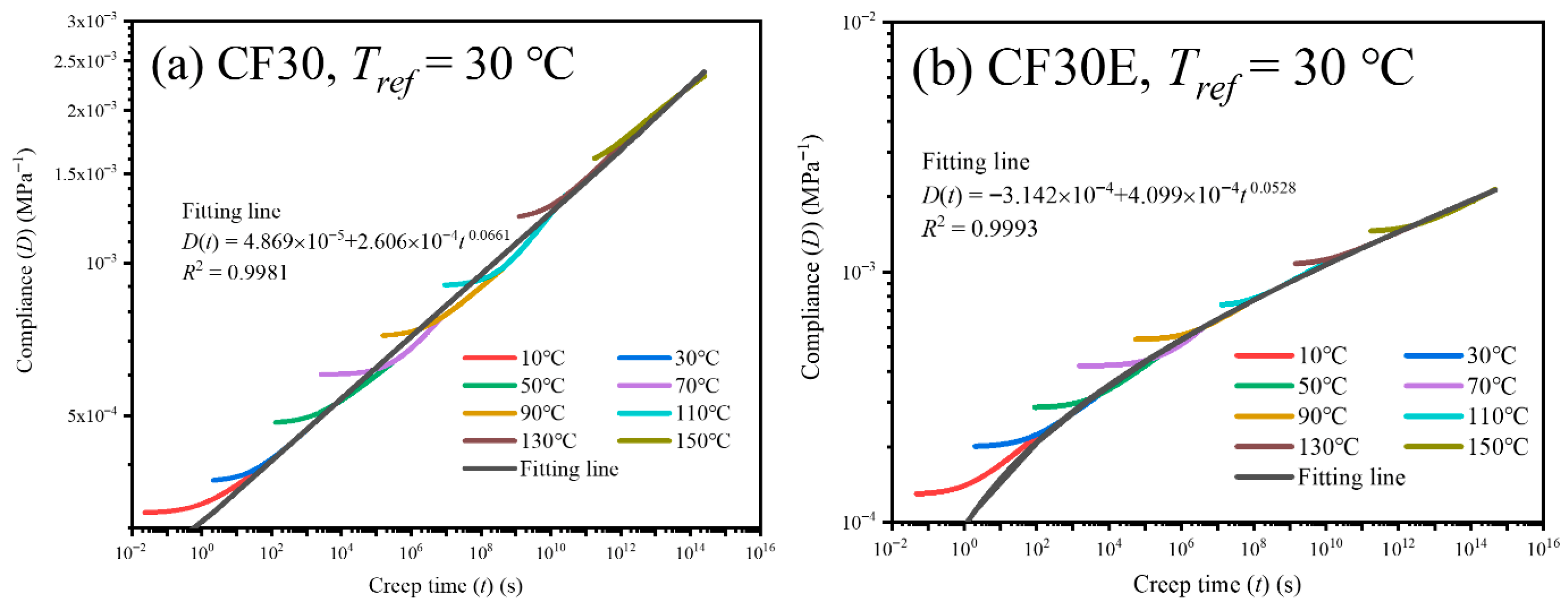
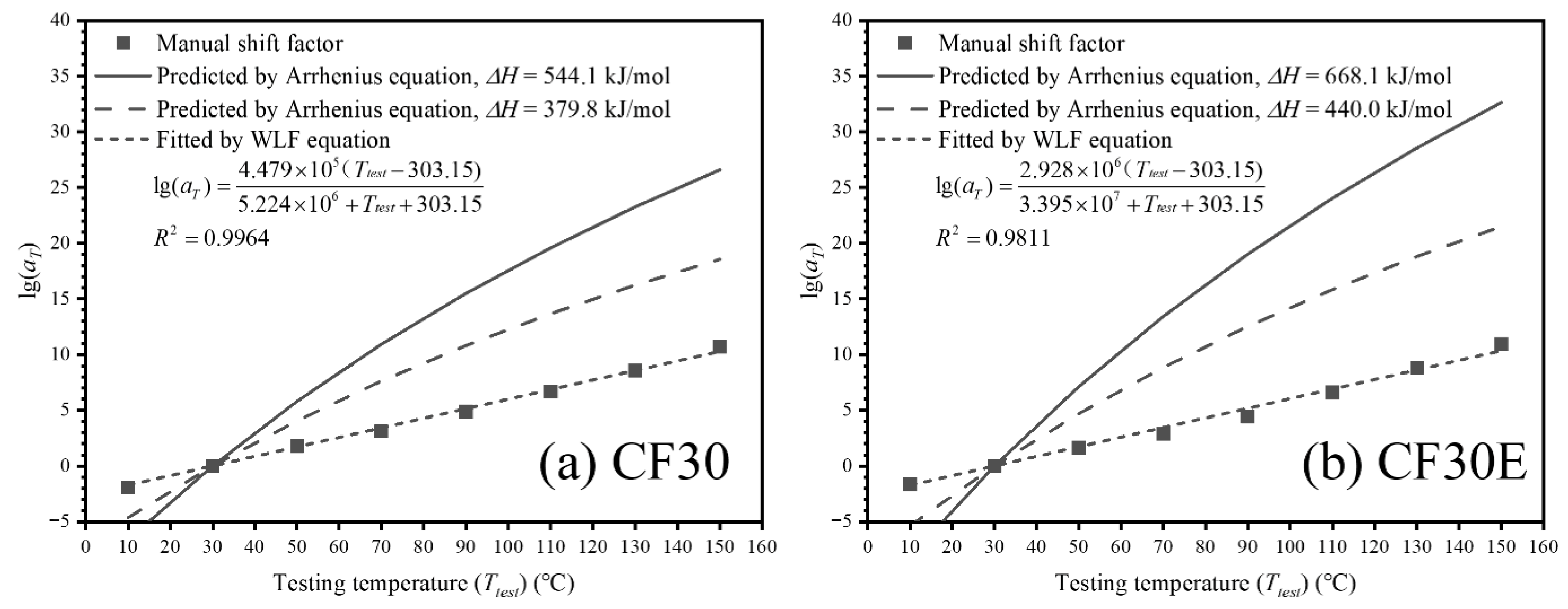
3.3.1. Time–Temperature Superposition Principle
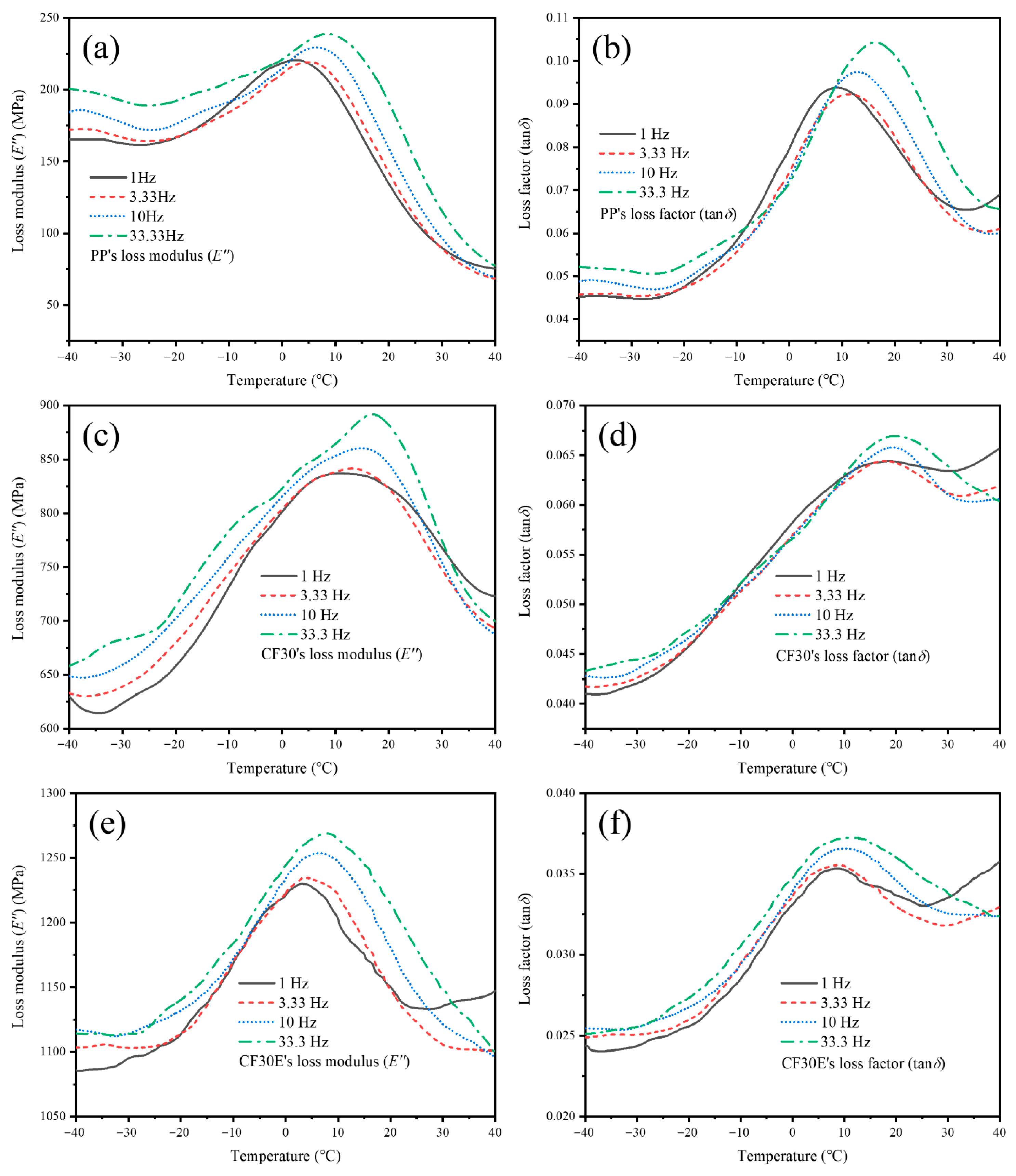
3.3.2. Results of Dynamic Mechanical Test
3.3.3. Isothermal Tensile Creep Curves and Creep Master Curves
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, Y.; Yan, N.; Kortschot, M.T. A simplified fabrication process for biofiber-reinforced polymer composites for automotive interior trim applications. J. Mater. Sci. 2013, 49, 2630–2639. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, G.; Yang, J.; Wang, X. Improving the interfacial shear strength of polypropylene/carbon fiber nonwoven composite by three different methods. J. Reinf. Plast. Compos. 2023, 42, 1207–1219. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, G.-l.; Yang, J.; Wang, X.-w. Void content of polypropylene/carbon fiber wet-laid nonwoven composites: Effect of fiber content and molding conditions, and void elimination mechanism. Polym. Compos. 2023, 44, 7181–7196. [Google Scholar] [CrossRef]
- Alves, F.C.; Monticeli, F.M.; Neves, R.M.; Voorwald, H.J.C.; Cioffi, M.O.H.; Ornaghi, H.L. Influence of void content and morphology on the creep behavior on glass/epoxy composites. Compos. Commun. 2021, 25, 100712. [Google Scholar] [CrossRef]
- GB/T 11546.1-2008; Plastic—Determination of Creep Behaviour—Part 1: Tensile Creep. General Administration of Quality Supervision, Inspection and Quarantine (AQSIQ): Beijing, China, 2008.
- ASTM D 2584; Standard Test Method for Ignition Loss of Cured Reinforced Resins. ASTM: West Conshohocken, PA, USA, 2018.
- ASTM D2734; Standard Test Methods for Void Content of Reinforced Plastics. ASTM: West Conshohocken, PA, USA, 2023.
- Dobeš, F.; Milička, K. The relation between minimum creep rate and time to fracture. Met. Sci. 1976, 10, 382–384. [Google Scholar] [CrossRef]
- Raghavan, J.; Meshii, M. Creep of polymer composites. Compos. Sci. Technol. 1998, 57, 1673–1688. [Google Scholar] [CrossRef]
- Alves, F.C.; Monticeli, F.M.; Voorwald, H.J.C.; Cioffi, M.O.H. The relation of porosity and creep behavior of glass fiber/epoxy composite: Design of experiments approach. Polym. Compos. 2021, 42, 5869–5879. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Sun, Z.; Li, Y.-Q.; Huang, P.; Chen, Q.; Fu, S.-Y. Tensile creep behavior of short-carbon-fiber reinforced polyetherimide composites. Compos. Part B Eng. 2021, 212, 108717. [Google Scholar] [CrossRef]
- Zhai, Z.Y.; Jiang, B.Y.; Drummer, D. Tensile Creep Behavior of Quasi-Unidirectional E-Glass Fabric Reinforced Polypropylene Composite. Polymers 2018, 10, 661. [Google Scholar] [CrossRef]
- Abdel-Magid, B.; Lopez-Anido, R.; Smith, G.; Trofka, S. Flexure creep properties of E-glass reinforced polymers. Compos. Struct. 2003, 62, 247–253. [Google Scholar] [CrossRef]
- Plaseied, A.; Fatemi, A. Tensile Creep and Deformation Modeling of Vinyl Ester Polymer and Its Nanocomposite. J. Reinf. Plast. Compos. 2009, 28, 1775–1788. [Google Scholar] [CrossRef]
- Zhao, L.L.; Wei, Y.; Zhang, G.W.; Xi, F. Short-term creep properties and creep model of wood-plastic composites. Polym. Compos. 2022, 43, 924–933. [Google Scholar] [CrossRef]
- Karabal, M.; Yıldız, A. Creep resistance enhancement and modeling of 3D printed Polyetherimide/carbon black composites. Compos. Struct. 2024, 345, 118398. [Google Scholar] [CrossRef]
- Georgiopoulos, P.; Kontou, E.; Christopoulos, A. Short-term creep behavior of a biodegradable polymer reinforced with wood-fibers. Compos. Part B-Eng. 2015, 80, 134–144. [Google Scholar] [CrossRef]
- Tang, X.-G.; Hou, M.; Zou, J.; Truss, R.; Zhu, Z. The creep behaviour of poly(vinylidene fluoride)/”bud-branched” nanotubes nanocomposites. Compos. Sci. Technol. 2012, 72, 1656–1664. [Google Scholar] [CrossRef]
- Dong, C.X.; Zhu, S.J.; Mizuno, M.; Hashimoto, M. Modeling and prediction of compressive creep of silane-treated TiO2/high-density polyethylene. J. Mater. Sci. 2010, 45, 3506–3513. [Google Scholar] [CrossRef]
- Nakazato, Y.; Zhu, S.; Usuki, A.; Kato, M. Analysis and Prediction of Creep Viscoelasticity in Nylon 6 Clay Hybrid Nanocomposites. J. Solid Mech. Mater. Eng. 2010, 4, 856–863. [Google Scholar] [CrossRef]
- ASTM D 4065-94; Standard Practice for Plastics: Dynamic Mechanical Properties: Determination and Report of Procedures. ASTM: West Conshohocken, PA, USA, 2001.
- Ghernaout, D.; Belaadi, A.; Boumaaza, M.; Chai, B.X.; Jawaid, M.; Abdullah, M.M.S.; Krishnasamy, P.; Al-Khawlani, A. Effects of incorporating cellulose fibers from Yucca treculeana L. on the thermal characteristics of green composites based on high-density poly-ethylene: An eco-friendly material for cleaner production. J. Mater. Res. Technol. 2024, 31, 787–798. [Google Scholar] [CrossRef]
- Gao, N.; Li, J.; Li, S.; Peng, Z. The dynamic mechanical properties of EPDM/Al(OH)3 composites. J. Appl. Polym. Sci. 2005, 98, 2454–2460. [Google Scholar] [CrossRef]
- Ayyagari, S.; Al-Haik, M. Enhancing the Viscoelastic Performance of Carbon Fiber Composites by Incorporating CNTs and ZnO Nanofillers. Appl. Sci. 2019, 9, 2281. [Google Scholar] [CrossRef]
- Spoljaric, S.; Genovese, A.; Shanks, R.A. Polypropylene–microcrystalline cellulose composites with enhanced compatibility and properties. Compos. Part A Appl. Sci. Manuf. 2009, 40, 791–799. [Google Scholar] [CrossRef]
- Ragoubi, M.; George, B.; Molina, S.; Bienaimé, D.; Merlin, A.; Hiver, J.M.; Dahoun, A. Effect of corona discharge treatment on mechanical and thermal properties of composites based on miscanthus fibres and polylactic acid or polypropylene matrix. Compos. Part A Appl. Sci. Manuf. 2012, 43, 675–685. [Google Scholar] [CrossRef]
- Paul, S.A.; Sinturel, C.; Joseph, K.; Mathew, G.D.G.; Pothan, L.A.; Thomas, S. Dynamic Mechanical Analysis of Novel Composites from Commingled Polypropylene Fiber and Banana Fiber. Polym. Eng. Sci. 2010, 50, 384–395. [Google Scholar] [CrossRef]
- Jabbar, A.; Militký, J.; Madhukar Kale, B.; Rwawiire, S.; Nawab, Y.; Baheti, V. Modeling and analysis of the creep behavior of jute/green epoxy composites incorporated with chemically treated pulverized nano/micro jute fibers. Ind. Crops Prod. 2016, 84, 230–240. [Google Scholar] [CrossRef]
- Pilz, G.; Wurzer, S.; Morak, M.; Pinter, G. Assessment of the stepped isothermal method for accelerated creep testing of high-density polyethylene. Mech. Time-Depend. Mater. 2022, 26, 775–790. [Google Scholar] [CrossRef]
- Chae, S.-H.; Zhao, J.-H.; Edwards, D.R.; Ho, P.S. Characterization of the Viscoelasticity of Molding Compounds in the Time Domain. J. Electron. Mater. 2010, 39, 419–425. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Z.; Sheng, B.; Wang, W.; Zhang, K. Experimental characterization of creep behavior of laminated bamboo composites based on stepped isothermal method. Polym. Compos. 2023, 44, 4551–4564. [Google Scholar] [CrossRef]
- Reis, A.K.d.; Monticelli, F.M.; Neves, R.M.; de Paula Santos, L.F.; Botelho, E.C.; Luiz Ornaghi, H., Jr. Creep behavior of polyetherimide semipreg and epoxy prepreg composites: Structure vs. property relationship. J. Compos. Mater. 2020, 54, 4121–4131. [Google Scholar] [CrossRef]

| CF Content/vol% | Molding Pressure/MPa |
|---|---|
| 10 | 2 |
| 15 | 2 |
| 20 | 2 |
| 25 | 5 |
| 30 | 5 |
| 35 | 7 |
| 40 | 7 |
| 45 | 10 |
| 50 | 12 |
| Specimen Dimensions | Temperature Gradient/°C | Load/MPa |
|---|---|---|
| 30 mm × 5 mm × 1 mm | 10, 30, 50, 70, 90, 110, 130, 150 | 2 |
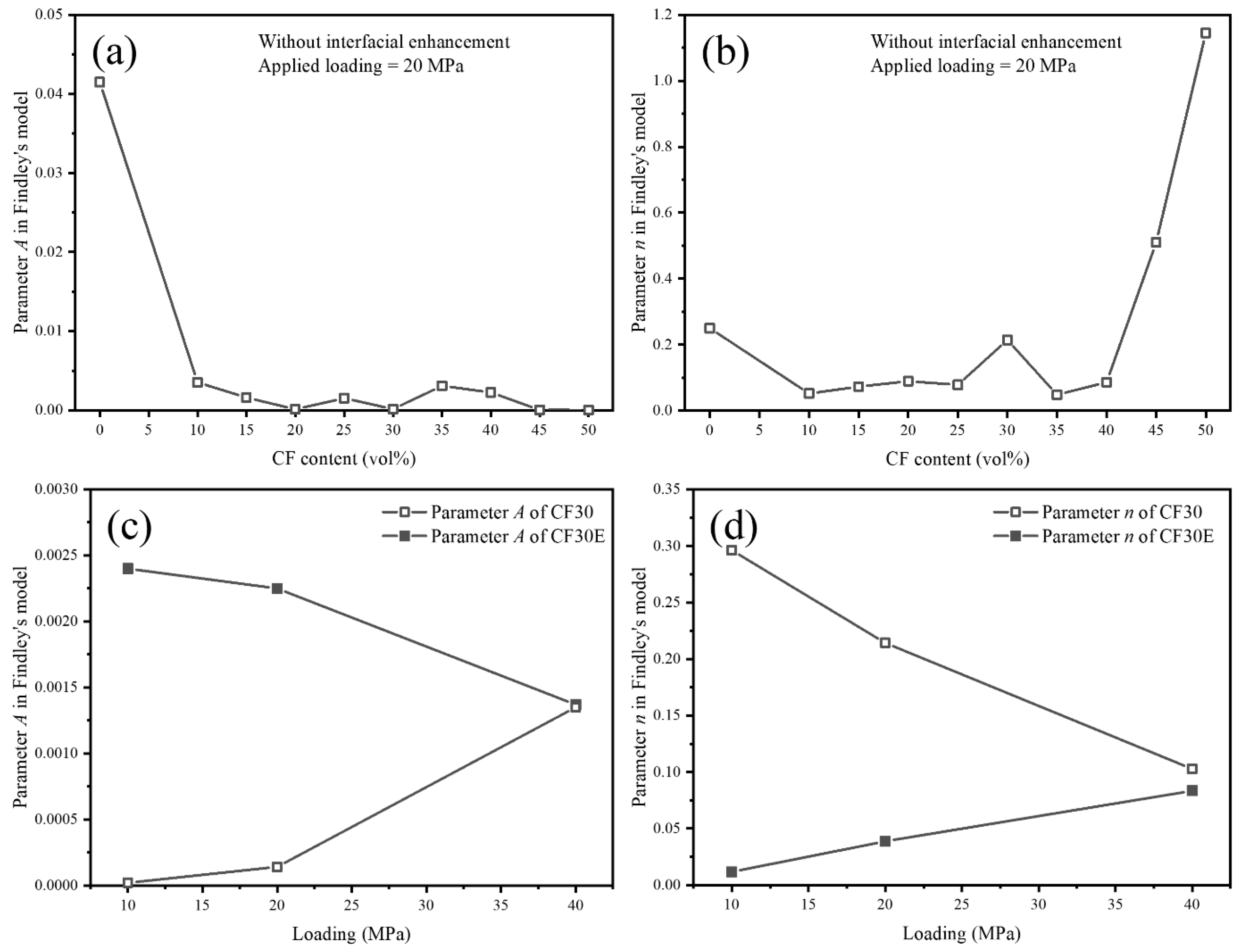
| CF Content/vol% | Load/MPa | Interfacial Condition | ε0 | A | n | R2 |
|---|---|---|---|---|---|---|
| 0 | 20 | Without interfacial enhancement | 1.79 × 10−2 | 4.15 × 10−2 | 0.25 | 0.9997 |
| 10 | −1.18 × 10−3 | 3.52 × 10−3 | 0.05211 | 0.9999 | ||
| 15 | 7.38 × 10−4 | 1.60 × 10−3 | 0.07271 | 0.9965 | ||
| 20 | 6.50 × 10−4 | 1.22 × 10−4 | 0.08942 | 0.9994 | ||
| 25 | −3.35 × 10−5 | 1.52 × 10−3 | 0.0783 | 0.9970 | ||
| 30 | 1.72 × 10−3 | 1.42 × 10−4 | 0.2143 | 0.9973 | ||
| 35 | −1.06 × 10−3 | 3.09 × 10−3 | 0.04823 | 0.9963 | ||
| 40 | 5.70 × 10−4 | 2.25 × 10−3 | 0.08617 | 0.9983 | ||
| 45 | 4.15 × 10−3 | 4.10 × 10−5 | 0.5101 | 0.9997 | ||
| 50 | 9.63 × 10−3 | 2.86 × 10−5 | 1.145 | 0.9957 | ||
| 30 | 10 | Without interfacial enhancement | 1.18 × 10−3 | 2.17 × 10−5 | 0.2962 | 0.9950 |
| 30 | 40 | 6.83 × 10−4 | 1.35 × 10−3 | 0.1028 | 0.9990 | |
| 30 | 10 | With interfacial enhancement | −1.65 × 10−3 | 2.40 × 10−3 | 0.01178 | 0.9942 |
| 30 | 20 | −1.12 × 10−3 | 2.25 × 10−3 | 0.03878 | 0.9986 | |
| 30 | 40 | 1.75 × 10−4 | 1.37 × 10−3 | 0.08348 | 0.9995 |
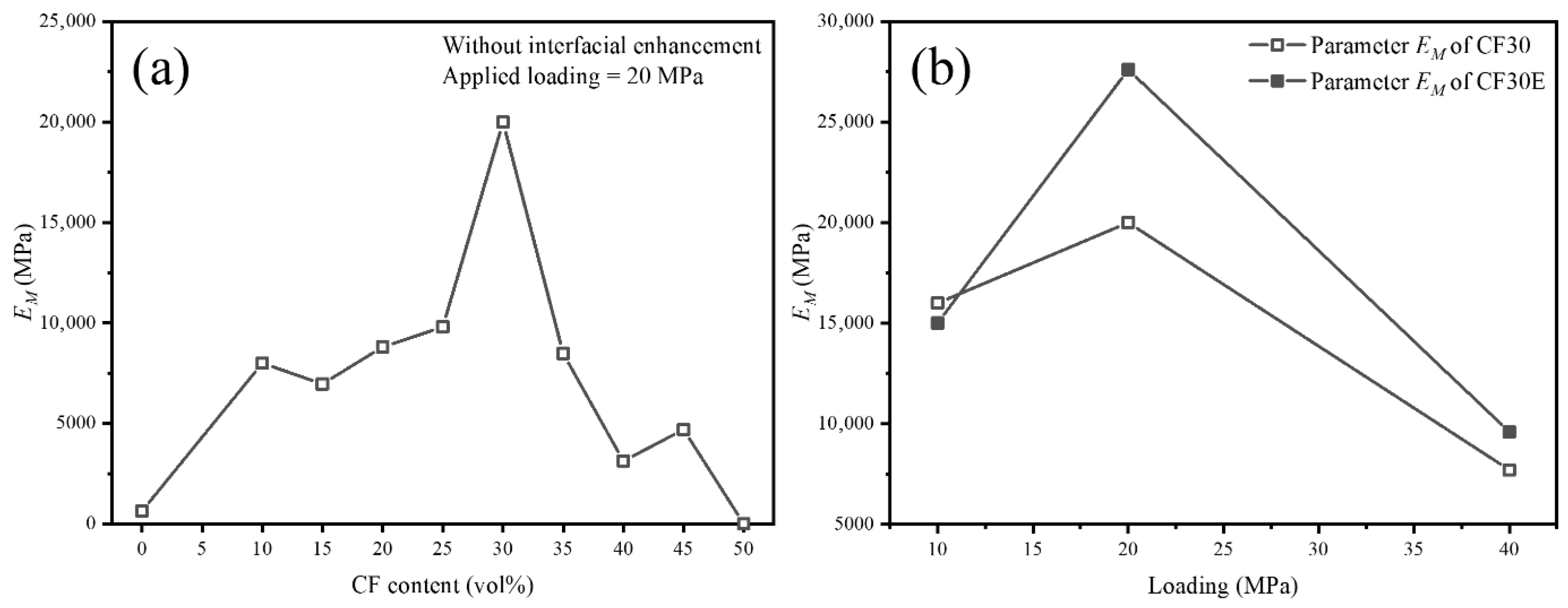
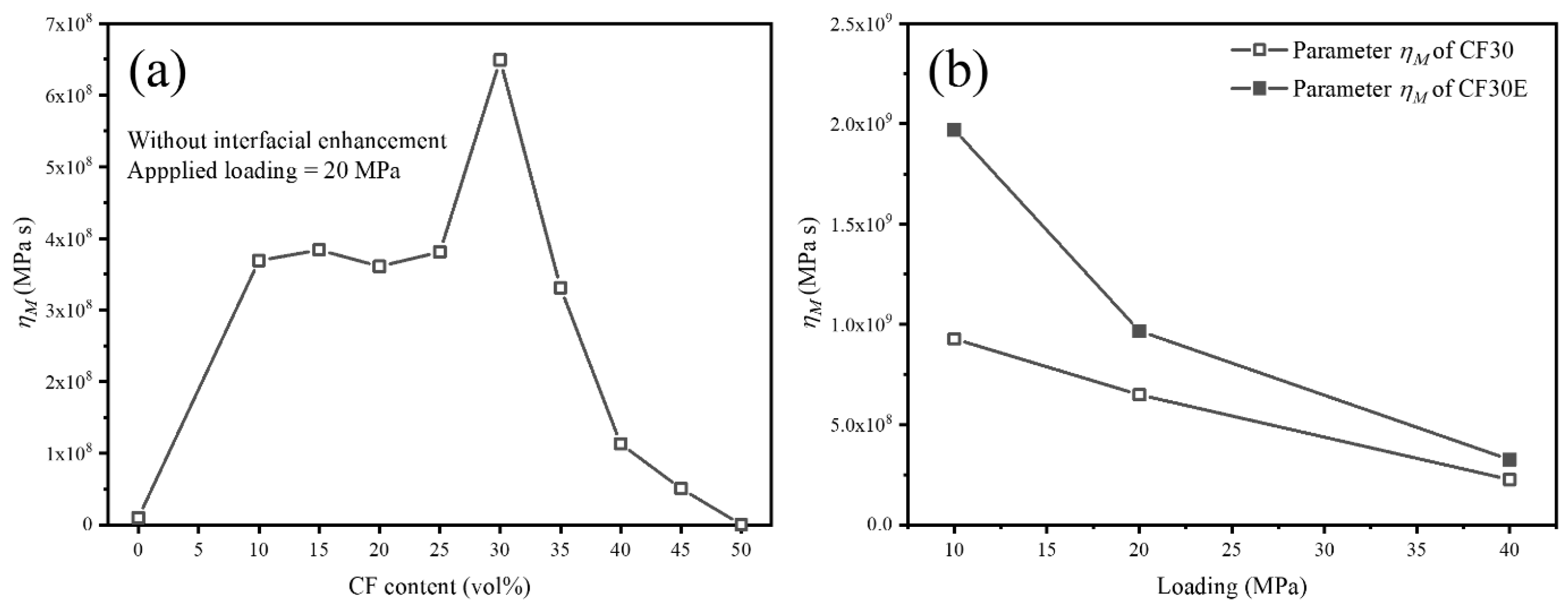
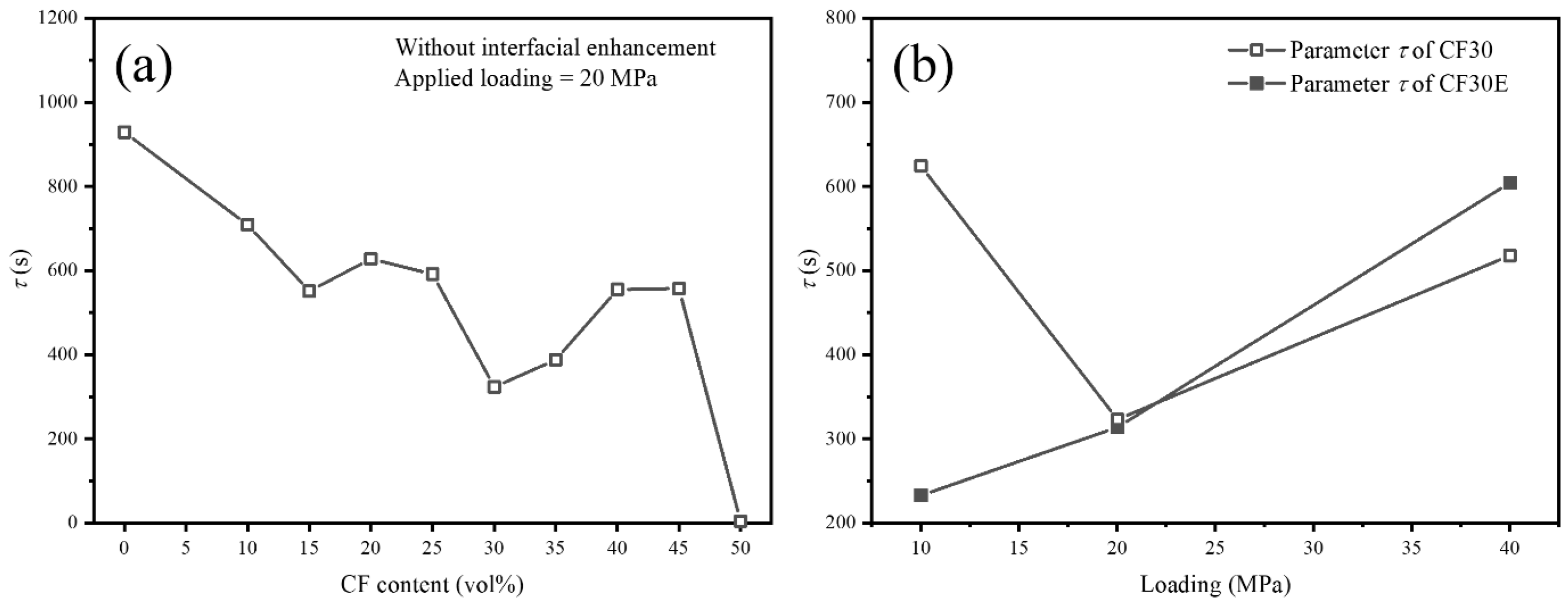
| CF Content/vol% | Load/MPa | Interfacial Condition | EM/MPa | EK/MPa | ηM/MPa s | ηK/MPa s | R2 |
|---|---|---|---|---|---|---|---|
| 0 | 20 | Without interfacial enhancement | 6.35 × 102 | 1.68 × 103 | 1.00 × 107 | 1.56 × 106 | 0.9997 |
| 10 | 7.99 × 103 | 4.12 × 104 | 3.69 × 108 | 2.92 × 107 | 0.9990 | ||
| 15 | 6.96 × 103 | 3.81 × 104 | 3.84 × 108 | 2.10 × 107 | 0.9981 | ||
| 20 | 8.80 × 103 | 4.19 × 104 | 3.61 × 108 | 2.63 × 107 | 0.9986 | ||
| 25 | 9.80 × 103 | 3.23 × 104 | 3.81 × 108 | 1.91 × 107 | 0.9966 | ||
| 30 | 2.00 × 104 | 1.30 × 105 | 6.49 × 108 | 4.20 × 107 | 0.9912 | ||
| 35 | 8.47 × 103 | 3.20 × 104 | 3.31 × 108 | 1.24 × 107 | 0.9963 | ||
| 40 | 3.12 × 103 | 1.18 × 104 | 1.13 × 108 | 6.55 × 106 | 0.9967 | ||
| 45 | 4.69 × 103 | 2.01 × 104 | 5.07 × 107 | 1.12 × 107 | 0.9997 | ||
| 50 | 2.19 × 10−3 | 4.65 × 104 | 3.75 × 105 | 1.68 × 105 | 0.9993 | ||
| 30 | 10 | Without interfacial enhancement | 1.60 × 104 | 2.13 × 105 | 9.28 × 108 | 1.33 × 108 | 0.9612 |
| 30 | 40 | 7.71 × 103 | 2.82 × 104 | 2.26 × 108 | 1.46 × 107 | 0.9980 | |
| 30 | 10 | With interfacial enhancement | 1.50 × 104 | 7.14 × 104 | 1.97 × 109 | 1.66 × 107 | 0.9780 |
| 30 | 20 | 2.76 × 104 | 1.10 × 105 | 9.67 × 108 | 3.45 × 107 | 0.9979 | |
| 30 | 40 | 9.59 × 103 | 4.12 × 104 | 3.26 × 108 | 2.49 × 107 | 0.9989 |
| Test Method | Frequency/Hz | Tg/°C | ||
|---|---|---|---|---|
| PP | CF30 | CF30E | ||
| Peak of Loss Modulus Curve | 1 | 8.90 | 10.73 | 3.17 |
| 3.33 | 11.14 | 12.87 | 3.86 | |
| 10 | 12.56 | 14.86 | 6.40 | |
| 33.3 | 16.13 | 17.05 | 7.75 | |
| Peak of Loss Modulus Curve | 1 | 2.71 | 16.71 | 7.51 |
| 3.33 | 4.95 | 17.35 | 8.70 | |
| 10 | 6.01 | 19.44 | 9.79 | |
| 33.3 | 7.77 | 20.87 | 10.99 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Deng, X.; Liao, J.; Zhong, J. Tensile Creep Behavior of PP/CF Wet-Laid Nonwoven Composite: Short-Term and Long-Term Creep Behavior. Appl. Sci. 2025, 15, 12167. https://doi.org/10.3390/app152212167
Yan X, Deng X, Liao J, Zhong J. Tensile Creep Behavior of PP/CF Wet-Laid Nonwoven Composite: Short-Term and Long-Term Creep Behavior. Applied Sciences. 2025; 15(22):12167. https://doi.org/10.3390/app152212167
Chicago/Turabian StyleYan, Xin, Xiaoxu Deng, Jingwen Liao, and Jinyi Zhong. 2025. "Tensile Creep Behavior of PP/CF Wet-Laid Nonwoven Composite: Short-Term and Long-Term Creep Behavior" Applied Sciences 15, no. 22: 12167. https://doi.org/10.3390/app152212167
APA StyleYan, X., Deng, X., Liao, J., & Zhong, J. (2025). Tensile Creep Behavior of PP/CF Wet-Laid Nonwoven Composite: Short-Term and Long-Term Creep Behavior. Applied Sciences, 15(22), 12167. https://doi.org/10.3390/app152212167