Numerical Study on the Aerodynamic and Structural Response Characteristics of a High-Altitude Wind-Capturing Umbrella
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.1.1. Fluid Dynamics
2.1.2. Structure Dynamics
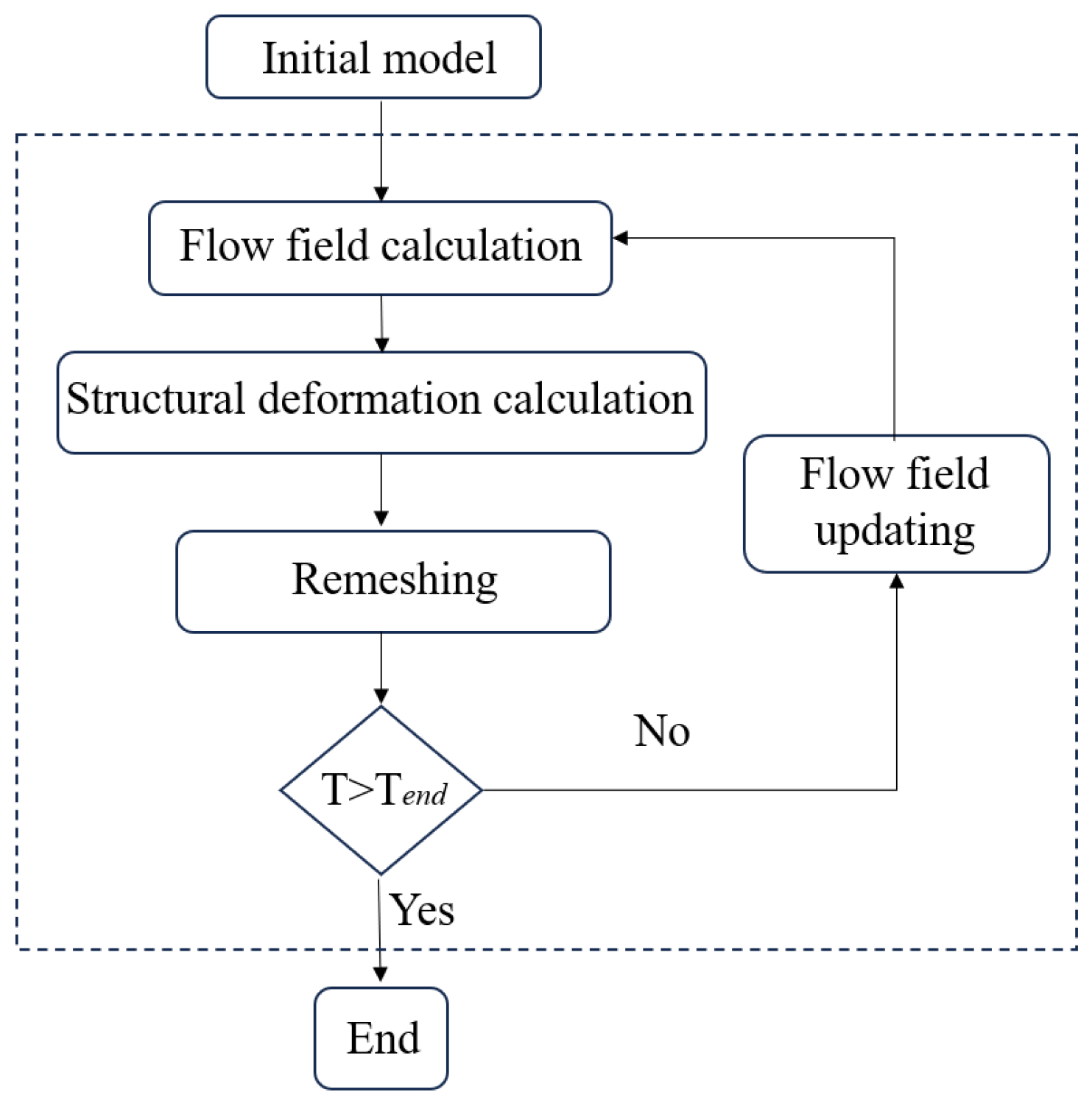
2.2. Fluid–Structure Interaction
2.3. Canopy Permeability
2.4. Model Assumptions
- The initial shape of the canopy is a flat circular shape, with no initial fabric prestress, ignoring the influence of fabric friction on the structural mechanical behavior.
- The suspension line is in an approximately straightened state, ignoring the aerodynamic force acting on the suspension line and the cable line.
- Only studying the aerodynamic effects of the canopy, ignoring the potential collision between the canopy and the cable, and using a bracket instead of the cable to restrict the movement of the canopy.
- In the flow field model, the velocity direction of the fluid is constant, and the velocity of 15 m/s remains unchanged. The fluid is incompressible.
- The inflation process of the canopy is an infinite mass situation, ignoring the influence of gravity.
3. High-Altitude Wind-Catching Umbrella Model
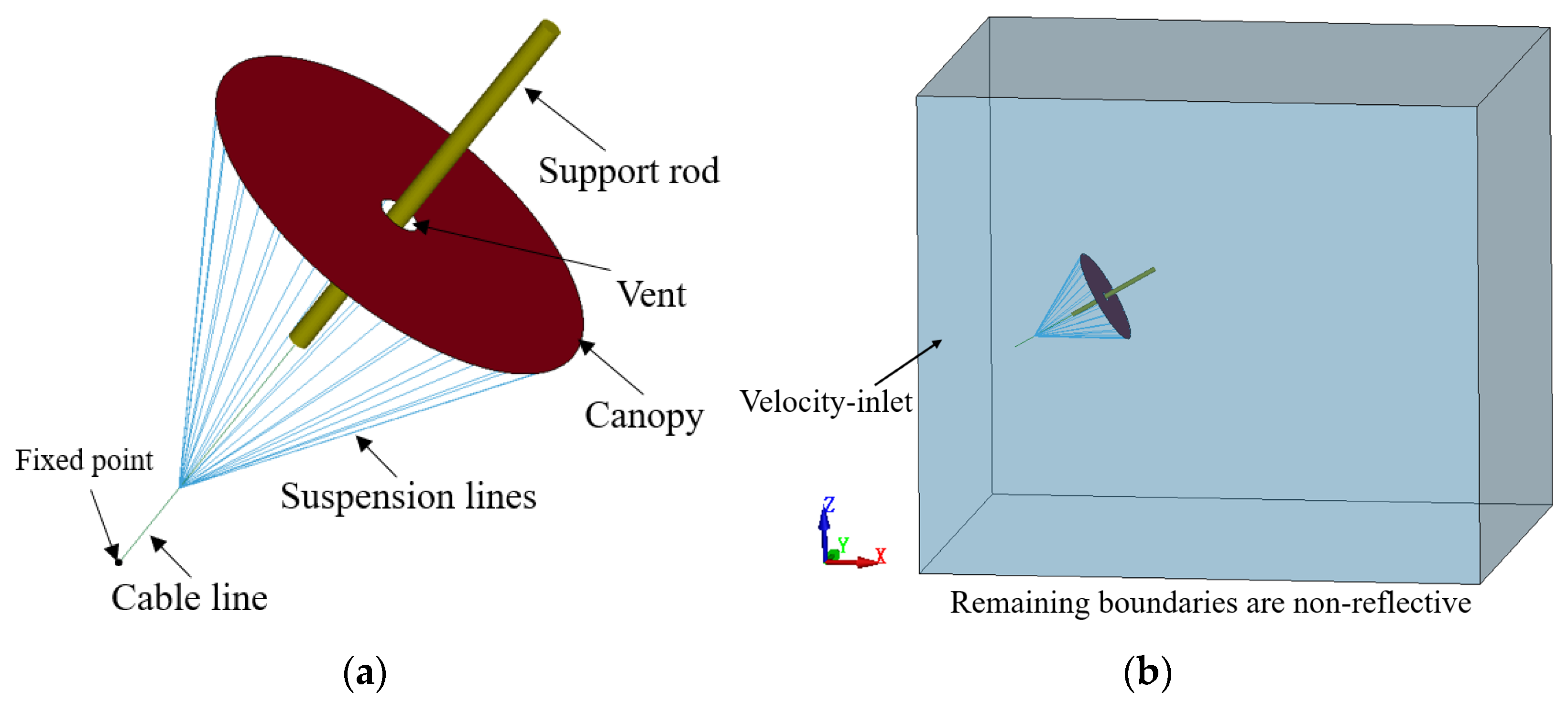
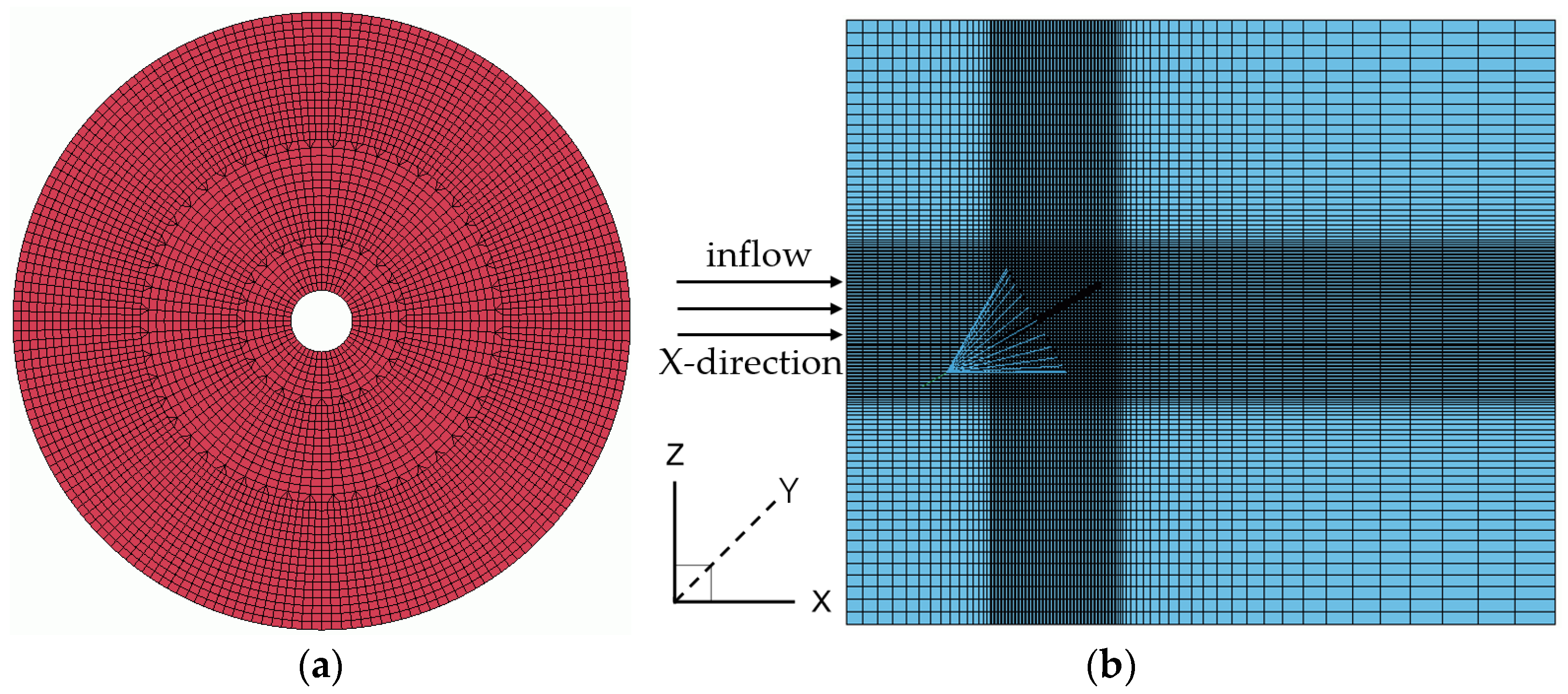
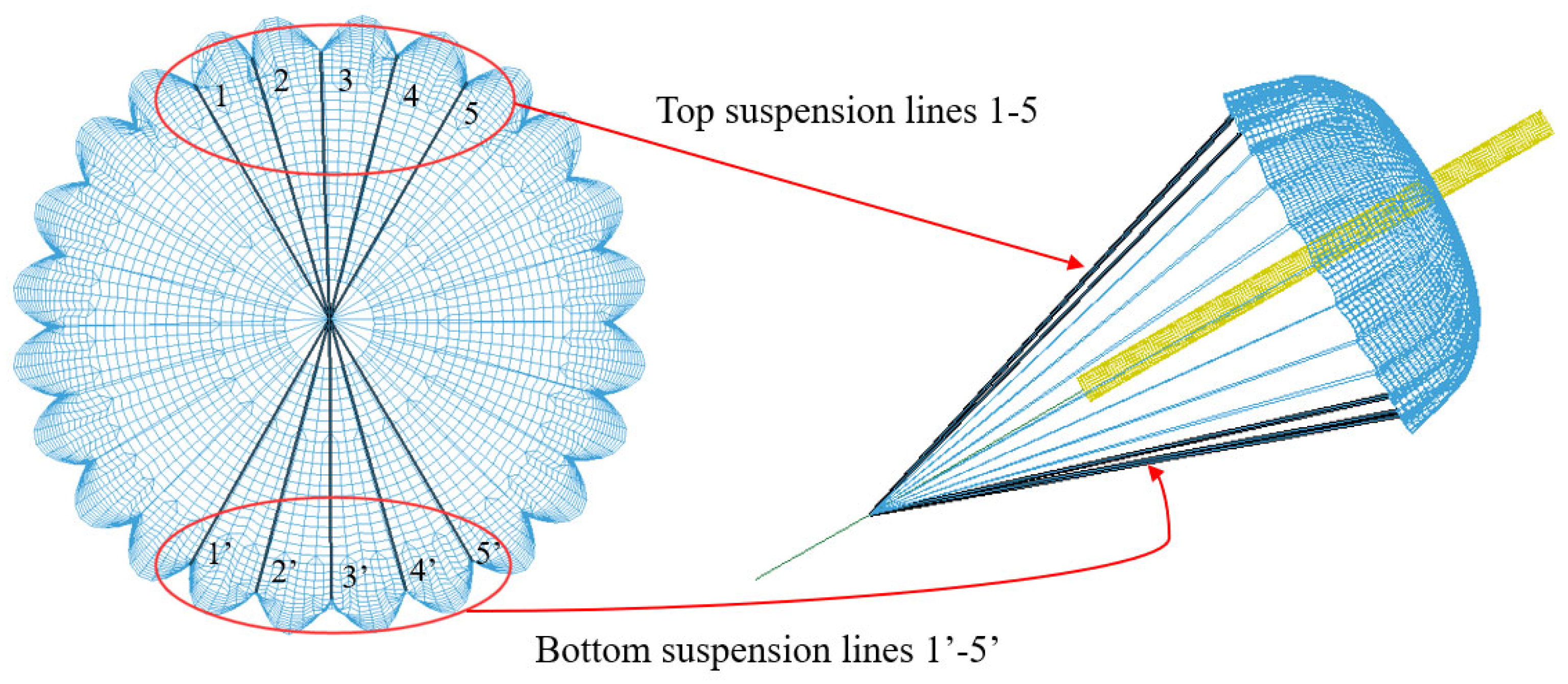
3.1. Geometric and Finite Element Model
3.2. Computational Case
3.3. Measurement Criteria
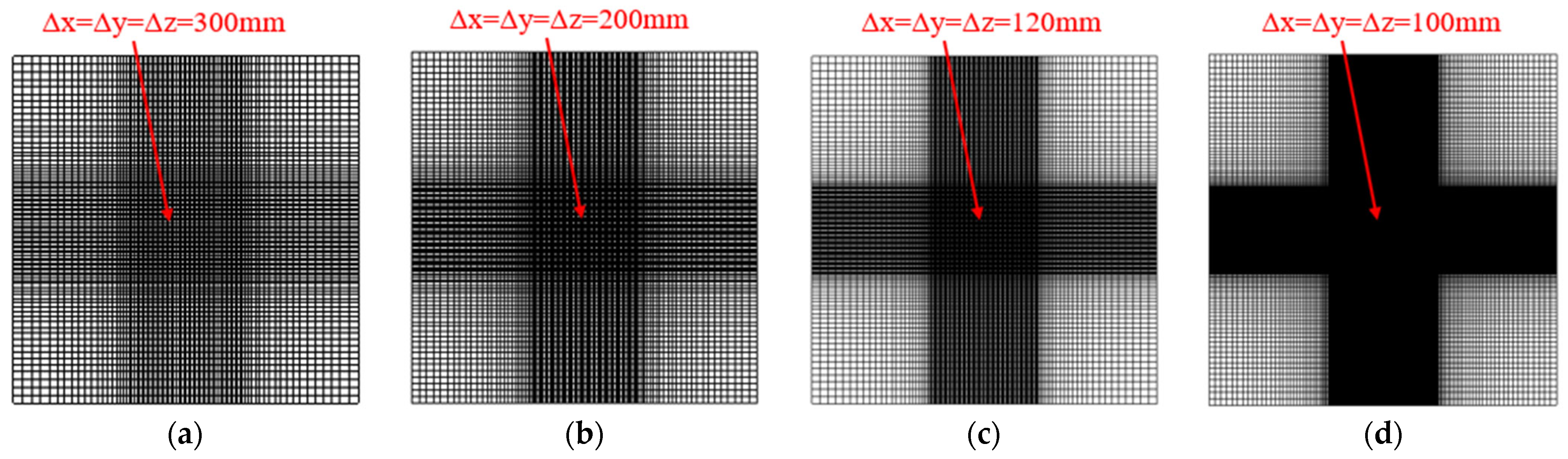
3.4. Mesh Convergence Test and Verification
4. Results and Discussion
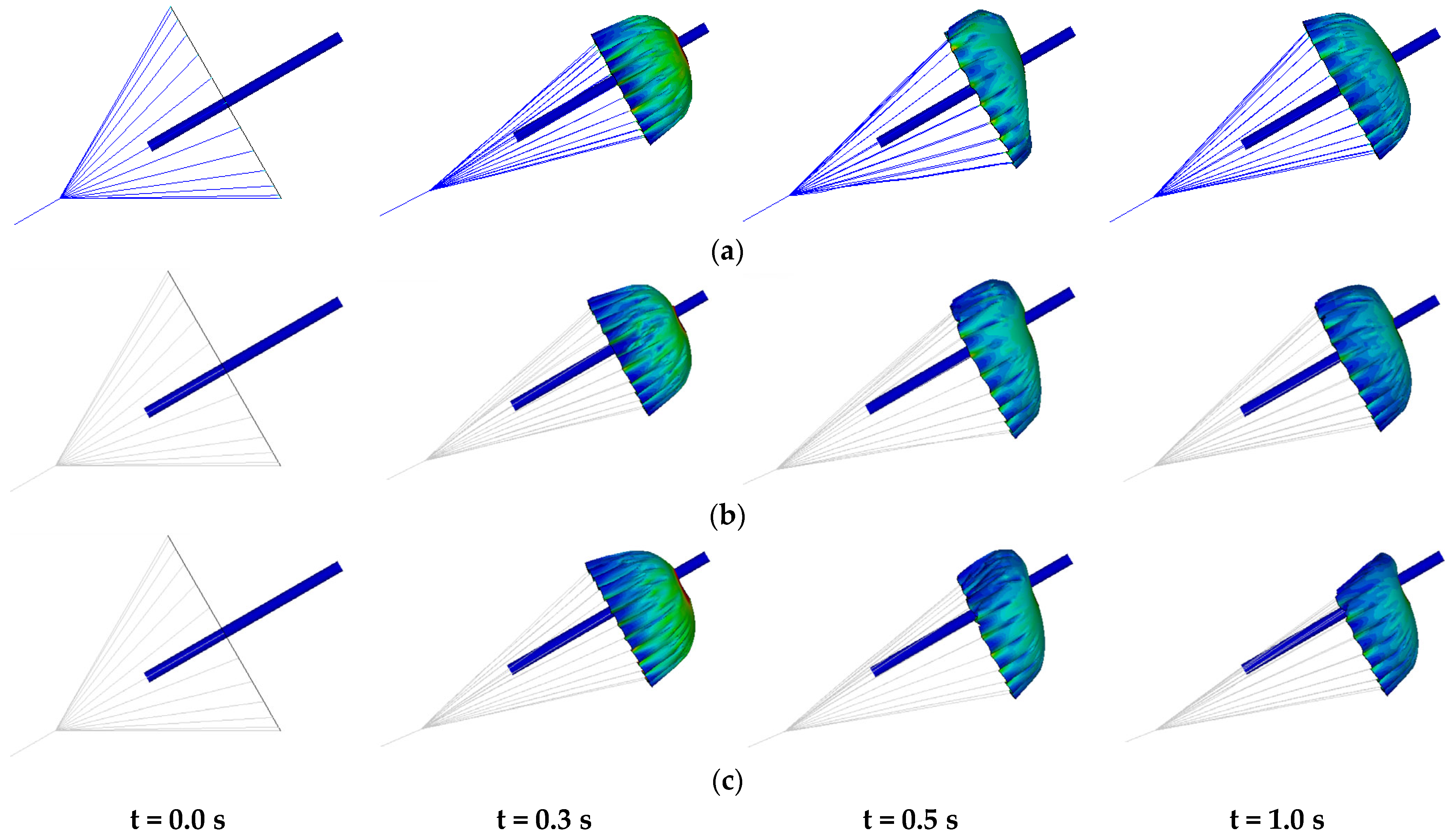
4.1. Inflation Shape
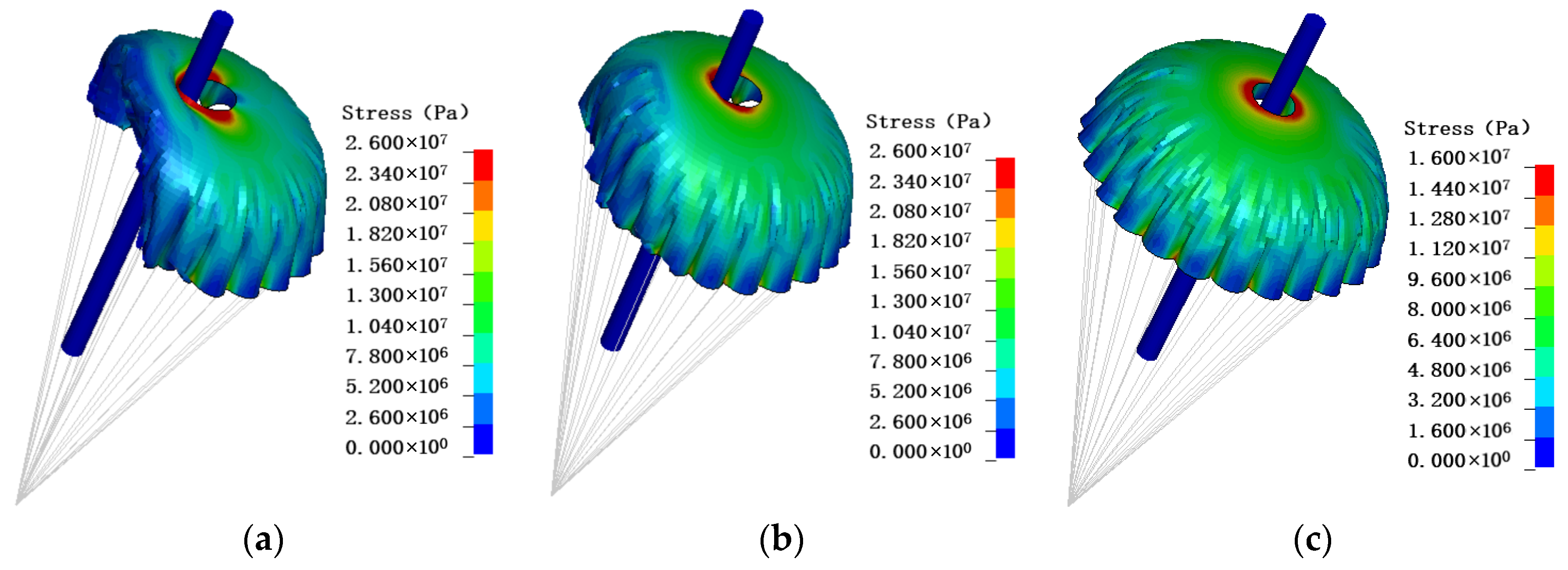
4.2. Stress Distribution
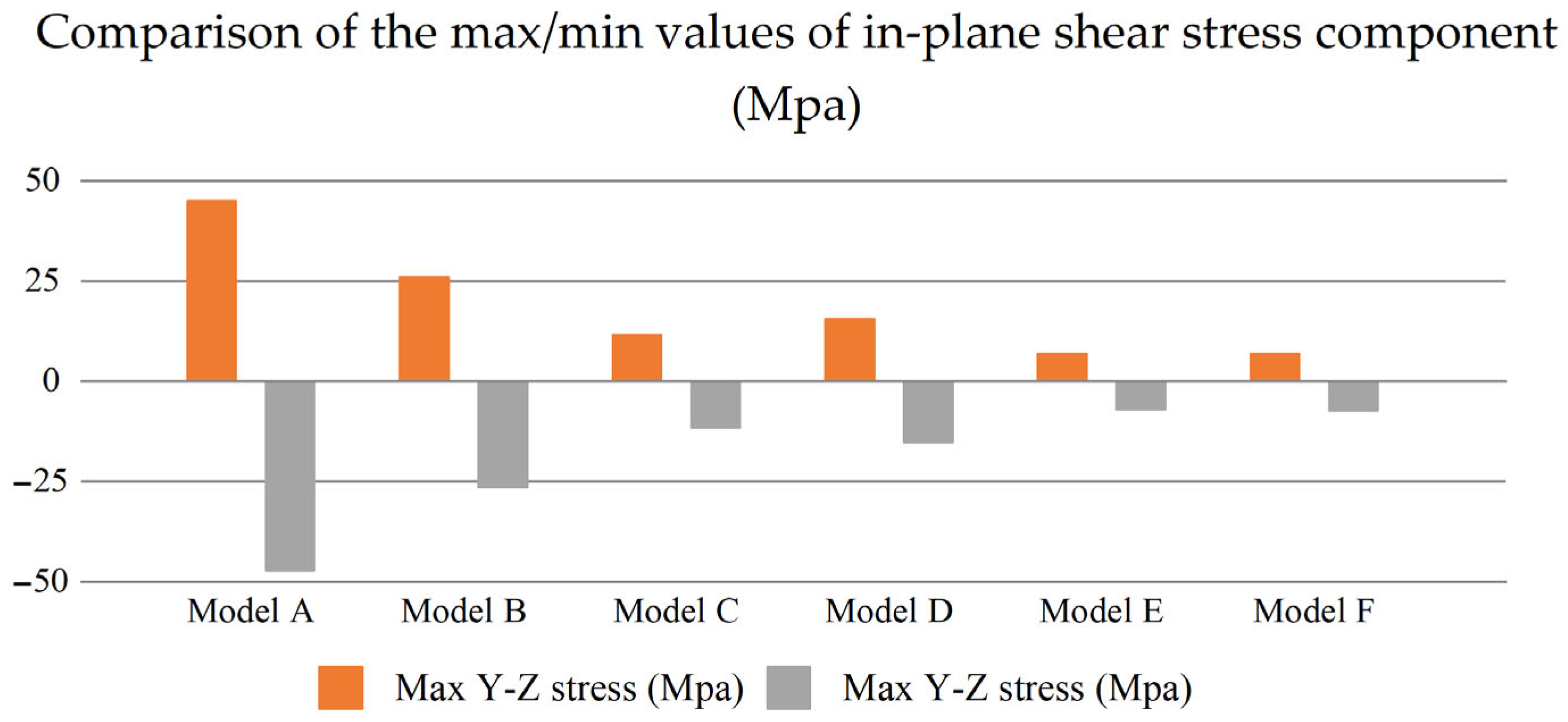
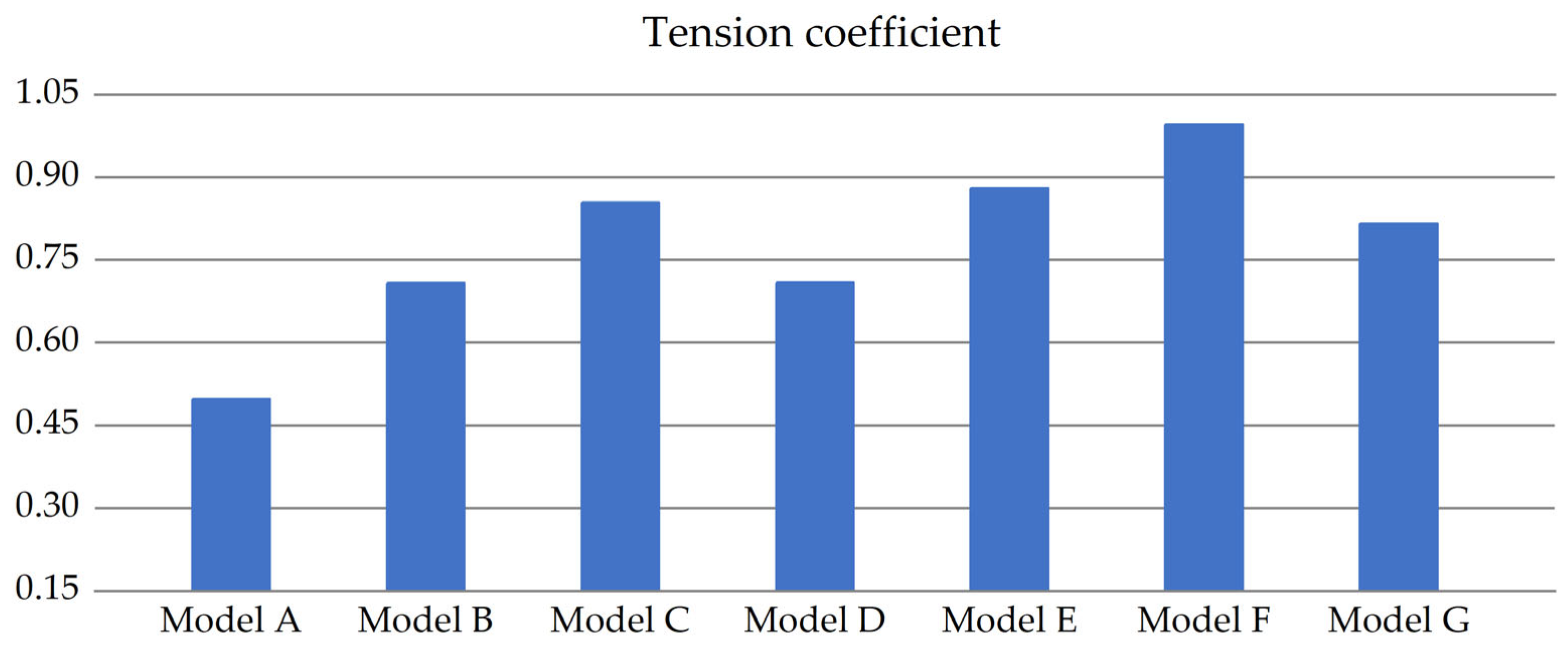
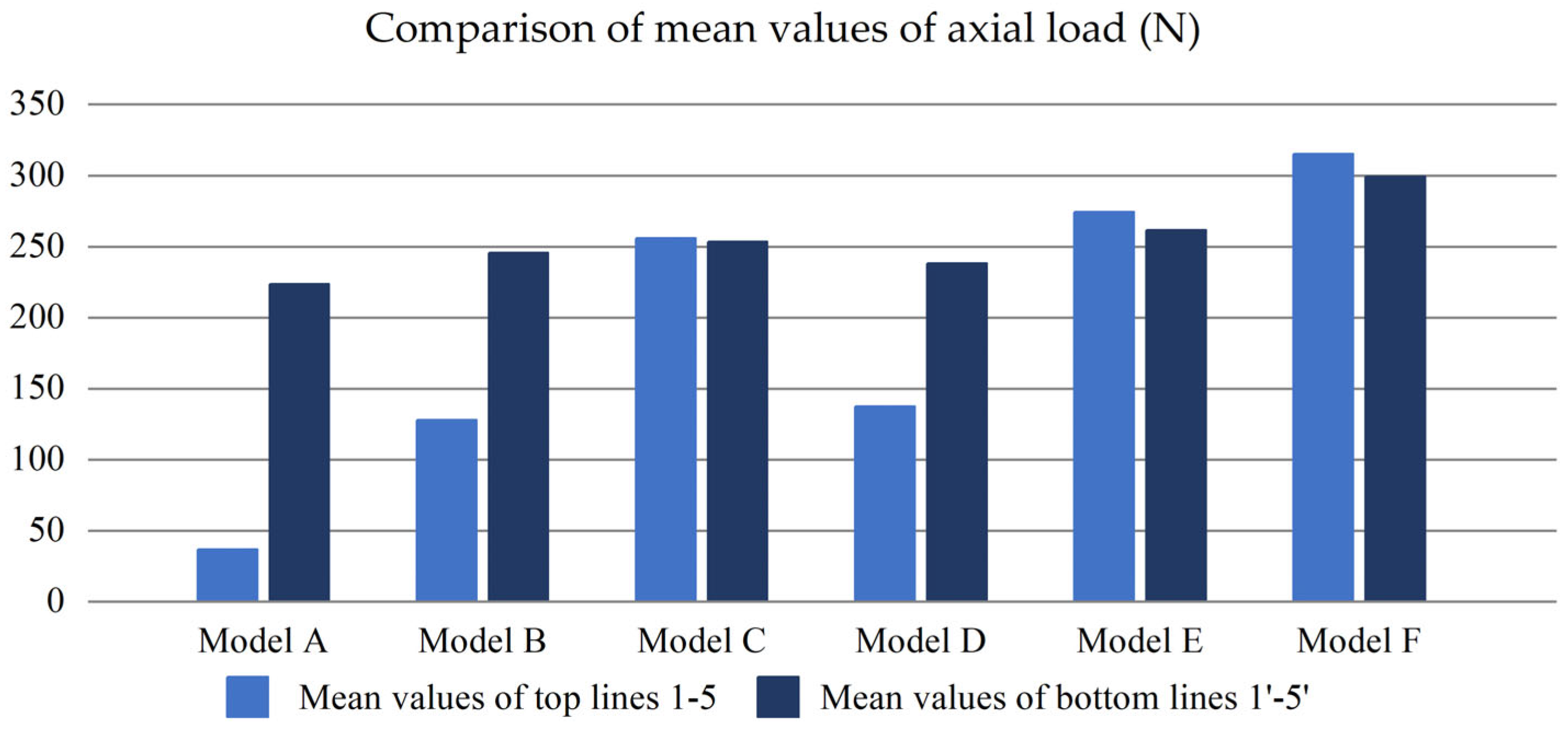
4.3. Tension Coefficient and Axial Load in Suspension Lines
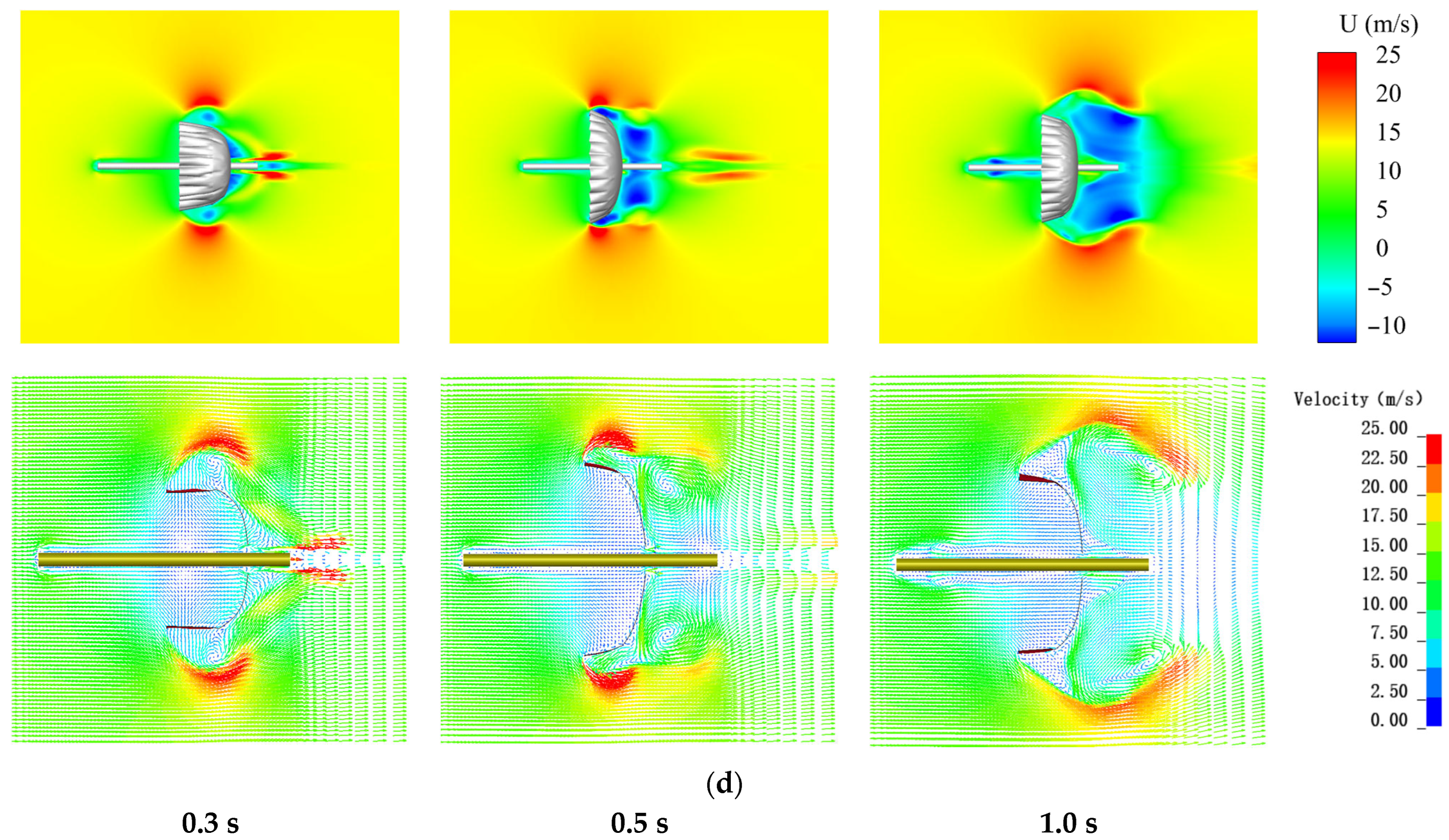
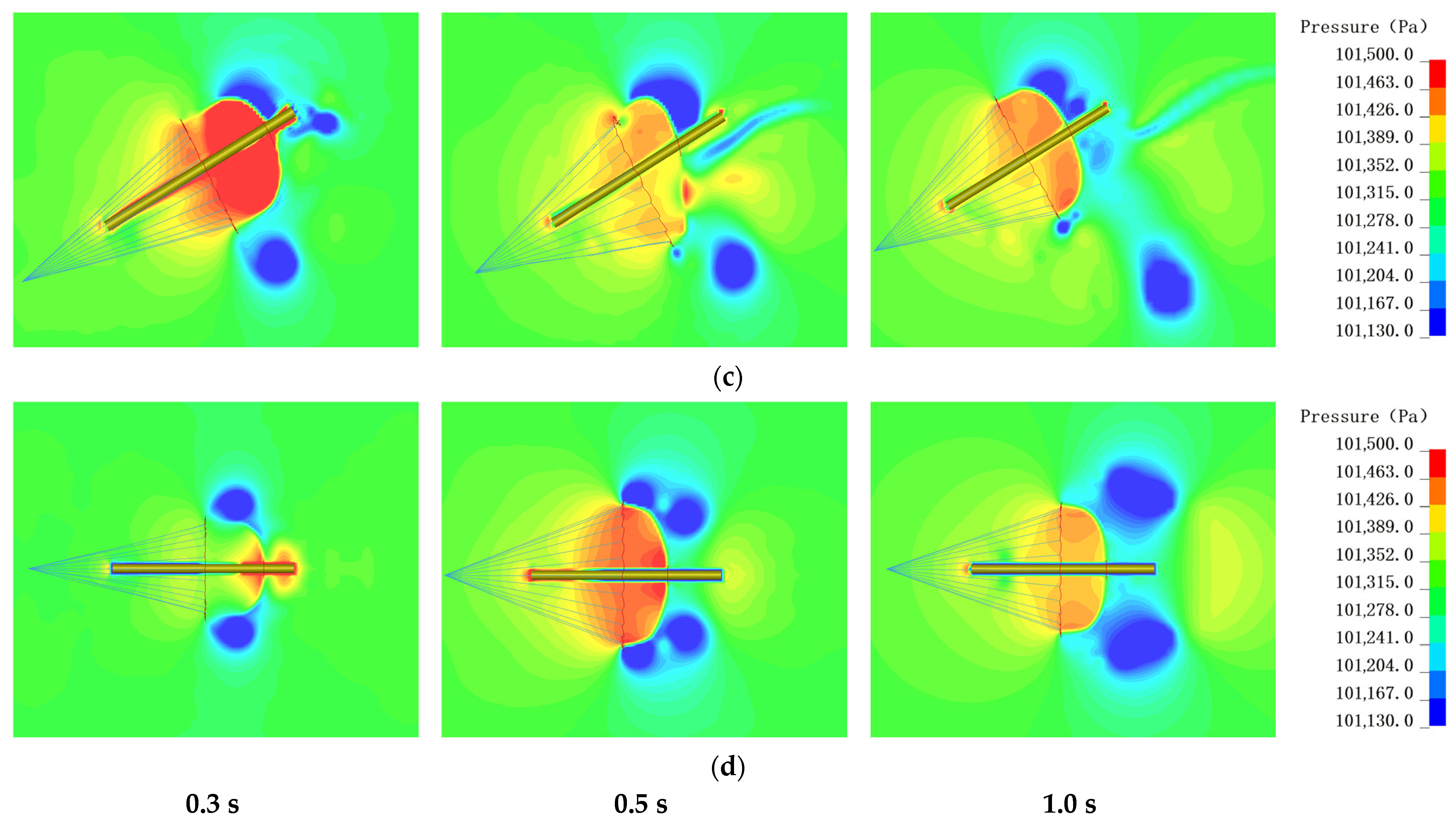
4.4. Flow Field Analysis
5. Conclusions
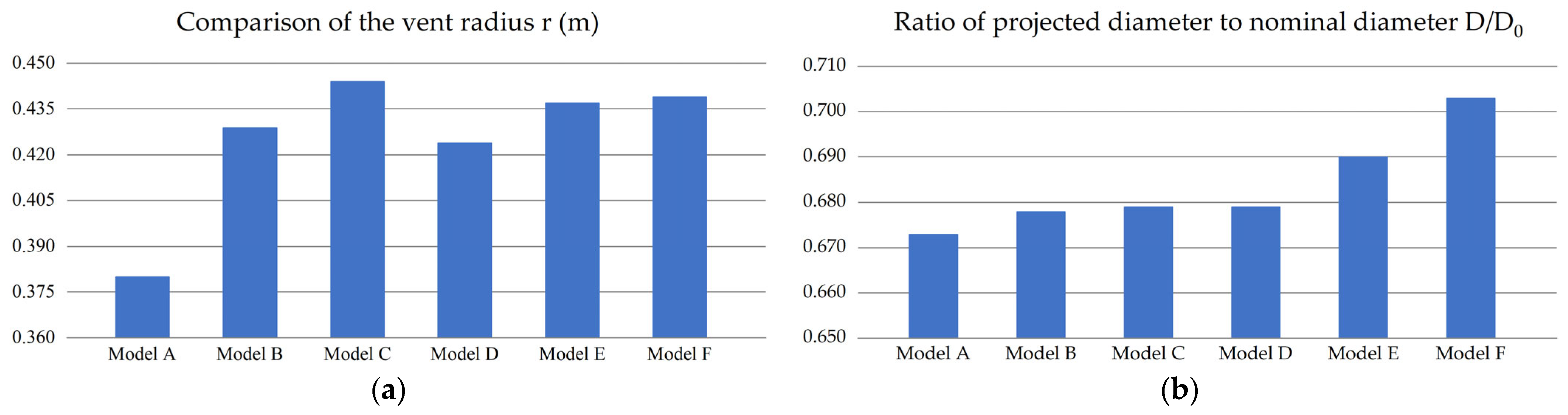
- Under the same canopy thickness, the smaller the viscosity coefficient a and the inertia coefficient b are, the more permeable the canopy becomes, making it harder to inflate the upper part. Permeability has little impact on the radius of the vent and the diameter of the canopy projection.
- The canopy is prone to stress concentration at the vent and at the connection between the canopy and the rope. The greater the permeability, the greater the stress generated by the contact with the support, and the smaller the permeability, the more uniform the stress distribution of the canopy. The max/min in-plane shear stress of the Model F with the smallest permeability is about 85% lower than the Model A with the most significant permeability.
- At the same canopy thickness, the tensile coefficient increases as canopy thickness increases, and halving the canopy’s thickness results in a tensile coefficient similar to doubling the coefficients of viscosity a and inertia b. The axial load on the top suspension line is slightly higher than that on the bottom line in the filled state, with a difference of up to 92.3% during slight collapse. Additionally, this difference becomes much more significant during severe collapse.
- The fluid field is always asymmetric when there is an angle of attack, and the acceleration zone at the outer edge of the lower part of the canopy affects the downstream flow field. The pressure difference between the inside and outside of the canopy causes it to generate a lift force, which increases the tension coefficient with angle of attack compared to the same conditions without an angle of attack.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Msigwa, G.; Ighalo, J.; Yap, P. Considerations on environmental, economic, and energy impacts of wind energy generation: Projections towards sustainability initiatives. Sci. Total Environ. 2022, 849, 157755. [Google Scholar] [CrossRef]
- Tleubergenova, A.; Tanasheva, N.; Shaimerdenova, K.; Kassymov, S.; Bakhtybekova, A.; Shuyushbayeva, N.; Uzbergenova, S.; Ranova, G. Mathematical modeling of the aerodynamic coefficients of a sail blade. Adv. Aerodyn. 2023, 5, 14. [Google Scholar] [CrossRef]
- Caduff, M.; Huijbregts, M.; Althaus, H.; Koehler, A.; Hellweg, S. Wind power electricity: The bigger the turbine, the greener the electricity? Environ. Sci. Technol. 2012, 46, 4725–4733. [Google Scholar] [CrossRef]
- Khan, Z.; Rehan, M. Harnessing airborne wind energy: Prospects and challenges. J. Control Autom. Electr. Syst. 2016, 27, 728–740. [Google Scholar] [CrossRef]
- Malz, E.; Hedenus, F.; Göransson, L.; Verendel, V.; Gros, S. Drag-mode airborne wind energy vs. wind turbines: An analysis of power production, variability and geography. Energy 2020, 193, 116765. [Google Scholar] [CrossRef]
- Weliwaththage, S.; Yildirim, M.; Aksac, G.; Ulku, M. Airborne Wind Energy Technology. J. Res. Technol. Eng. 2021, 2, 22–29. [Google Scholar]
- Malz, E.; Walter, V.; Göransson, L.; Gros, S. The value of airborne wind energy to the electricity system. Wind Energy 2022, 25, 281–299. [Google Scholar] [CrossRef]
- Loyd, M. Crosswind kite power. J. Energy 1980, 4, 106–111. [Google Scholar] [CrossRef]
- Fagiano, L.; Milanese, M. Airborne wind energy: An overview. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012. [Google Scholar]
- Fagiano, L.; Quack, M.; Bauer, F.; Carnel, L.; Oland, E. Autonomous airborne wind energy systems: Accomplishments and challenges. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 603–631. [Google Scholar] [CrossRef]
- Cherubini, A.; Papini, A.; Vertechy, R.; Fontana, M. Airborne Wind Energy Systems: A review of the technologies. Renew. Sustain. Energy Rev. 2015, 51, 1461–1476. [Google Scholar] [CrossRef]
- Canale, M.; Fagiano, L.; Milanese, M.; Ippolito, M. KiteGen project: Control as key technology for a quantum leap in wind energy generators. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007. [Google Scholar]
- Lansdorp, B.; Williams, P. The laddermill-innovative wind energy from high altitudes in holland and Australia. In Proceedings of the Global Windpower, Adelaide, Australia, 18–21 September 2006. [Google Scholar]
- Vermillion, C.; Cobb, M.; Fagiano, L.; Leuthold, R.; Diehl, M.; Smith, R.; Wood, T.; Rapp, S.; Schmehl, R.; Olinger, D.; et al. Electricity in the air: Insights from two decades of advanced control research and experimental flight testing of airborne wind energy systems. Annu. Rev. Control 2021, 52, 330–357. [Google Scholar] [CrossRef]
- Vermillion, C.; Grunnagle, T.; Kolmanovsky, I. Modeling and control design for a proto-type lighter-than-air wind energy system. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012. [Google Scholar]
- Sola, P.; McDonald, A.; Oterkus, E. A lightweight approach for airborne wind turbine drivetrains. In Proceedings of the European Wind Energy Association, Paris, France, 17–20 November 2015. [Google Scholar]
- Luo, B.; Ren, Z.; Liu, H. Analysis of Current Status and Prospects of Parachute-Based Airborne Wind Energy Technology. Electr. Power Constr. 2025, 46, 45–53. [Google Scholar]
- Li, J. Study on the Electromechanical Coupling Dynamics Modeling and Dynamic Characteristics of Ground Transmission Systems in High-Altitude Wind Power. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 1 June 2024. [Google Scholar]
- Luo, B.; Hu, J.; Yang, Y.; Ren, Z.; He, Y. Modeling and stable operation control method for airborne wind energy system considering longitudinal disturbance stability. South Energy Constr. 2025, 12, 1–11. [Google Scholar]
- Zhang, Y.; Pu, T.; Jia, H.; Wu, S.; Zhou, C. Extension of a sharp-interface immersed-boundary method for simulating parachute inflation. Adv. Aerodyn. 2024, 6, 3. [Google Scholar] [CrossRef]
- Taguchi, M.; Semba, N.; Mori, K. Effects of flexibility and gas permeability of fabric to supersonic performance of flexible parachute. In Proceedings of the 23rd AIAA Aerodynamic Decelerator Systems Technology Conference, Daytona Beach, FL, USA, 30 March–2 April 2015. [Google Scholar]
- Xu, X.; Jia, H.; Chen, Y. Influence mechanism of fabric permeability of canopy on aerodynamics of Mars parachute. Acta Areonaut. Astronaut. Sin. 2022, 43, 307–324. [Google Scholar]
- Yang, X.; Yu, L.; Nie, S.; Zhang, S. Aerodynamic performance of the supersonic parachute with material permeability. J. Ind. Text. 2021, 50, 812–829. [Google Scholar] [CrossRef]
- Yu, L.; Ming, X.; Chen, L. Experimental investigation on the flow-field of different vent canopy. Acta Aerodyn. Sin. 2008, 26, 19–25. [Google Scholar]
- Zeng, Y.; Wang, Y.; Yuan, H. A stable and efficient semi-implicit coupling method for fluid-structure interaction problems with immersed boundaries in a hybrid CPU-GPU framework. J. Comput. Phys. 2025, 534, 114026. [Google Scholar] [CrossRef]
- Guan, L.; Yu, G.; He, X. Inflation process of radially closed parachute. Phys. Fluids 2025, 37, 025109. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, S.; Zhang, Y. Effect of different steering approaches on gliding performance of cruciform parachute. Manned Spacefl. 2024, 30, 52–59. [Google Scholar]
- Huang, Y.; Wu, S.; Wang, Y. Numerical and experimental investigation of the steering performance of a ringsail parachute. J. Northwest. Polytech. Univ. 2024, 42, 1021–1029. [Google Scholar] [CrossRef]
- Cao, H.; Huang, L.; Li, X. Research on control force of parafoil based on fluid structure interaction method. Acta Aeronaut. Astronaut. Sin. 2025, 46, 148–158. [Google Scholar]
- Hou, X.; Hu, J.; Yu, Y. Numerical Study of Aerodynamic Characteristics of No-Swinging and Free-to-Swing Cross Parachute. AIAA J. 2023, 61, 5018–5031. [Google Scholar] [CrossRef]
- Li, K.; Wang, Z.; Ma, Y.; Wang, Y.; Li, H. Research on the inflation process of underwater parachute by numerical simulation and model test. Ocean Eng. 2024, 293, 116554. [Google Scholar] [CrossRef]
- Souli, M.; Ouahsine, A.; Lewin, L. ALE formulation for fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 2000, 190, 659–675. [Google Scholar] [CrossRef]
- Lee, H.; Xu, S. Fully discrete error estimation for a quasi-Newtonian fluid–structure interaction problem. Comput. Math. Appl. 2016, 71, 2373–2388. [Google Scholar] [CrossRef]
- Yu, L.; Cheng, H.; Zhan, Y.; Li, S. Study of parachute inflation process using fluid–structure interaction method. Chin. J. Aeronaut. 2014, 27, 272–279. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89. [Google Scholar]
- Nie, S.; Yu, L.; Li, Y.; Sun, Z.; Qiu, B. Influence of fabric permeability on breathing phenomenon of supersonic parachute. J. Ind. Text. 2023, 53, 15280837231171733. [Google Scholar] [CrossRef]
- Li, Z. Wind Tunnel Special Tests Technique; Aviation Industry Press: Beijing, China, 2010; p. 493. [Google Scholar]

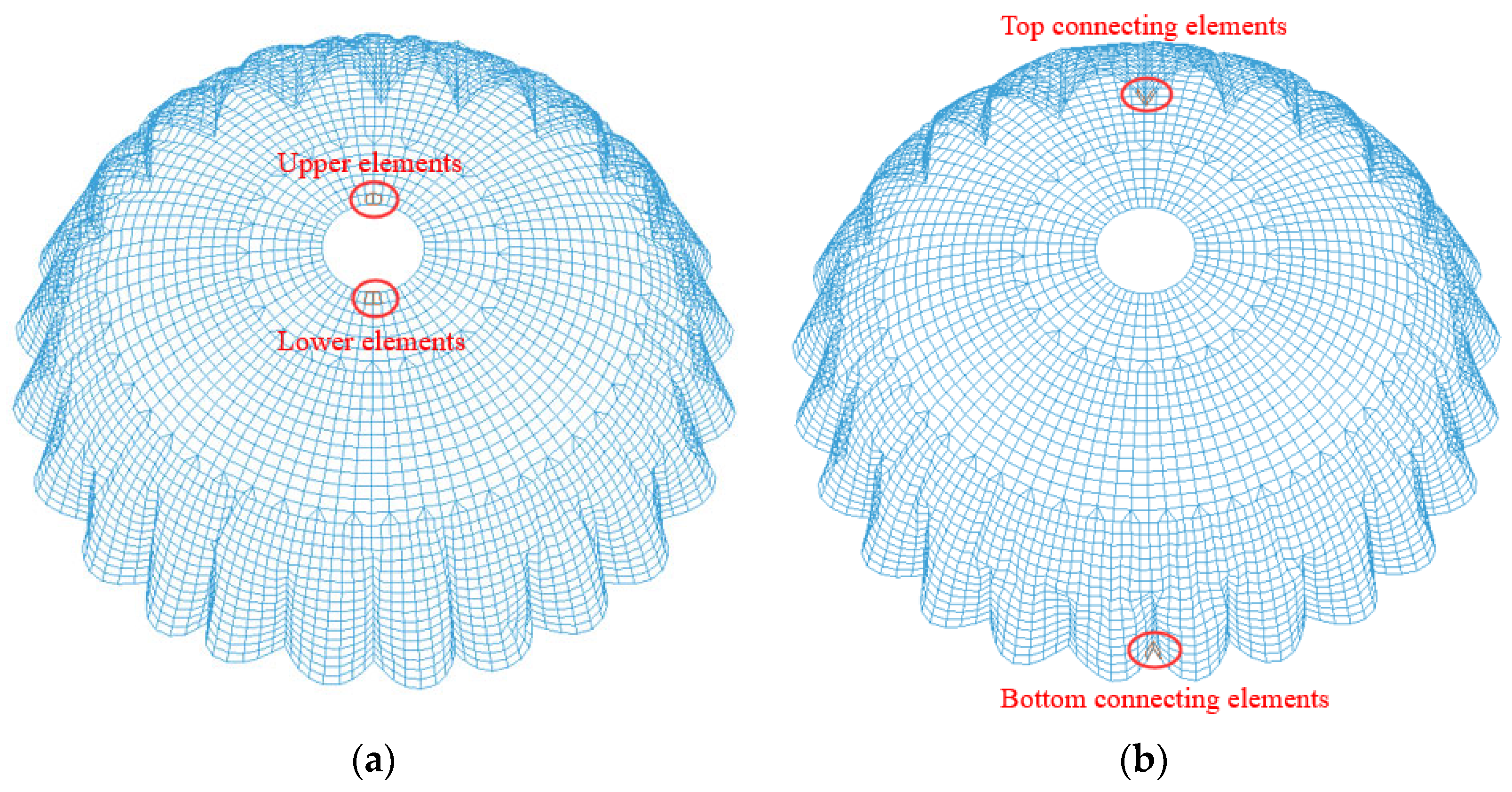



| Parameter | Value |
|---|---|
| Canopy nominal diameter D0 (m) | 8.4 |
| Suspension line length (m) | 8.4 |
| Vent diameter (m) | 0.84 |
| Support rod diameter (m) | 0.42 |
| Support rod length (m) | 8.35 |
| Parameter | Canopy | Suspension Line | Fluid |
|---|---|---|---|
| Type of elements | Shell | Beam | Solid |
| Density (kg·m−3) | 533.77 | 1154 | 1.225 |
| Young’s modulus (Pa) | 4.31 × 108 | 7.3 × 1010 | - |
| Poisson’s ratio | 0.14 | - | - |
| Materials | Fabric | Cable | Null |
| Number of elements | 4704 | 1008 | 2,729,712 |
| Models | Attack Angle | Thickness (m) | Viscosity Coefficient (a) (kg/(m3·s)) | Inertial Coefficient (b) (kg·m−4) |
|---|---|---|---|---|
| A | 30° | 5 × 10−5 | 8 × 105 | 2.4 × 105 |
| B | 1.6 × 106 | 4.8 × 105 | ||
| C | 3.2 × 106 | 9.6 × 105 | ||
| D | 30° | 1 × 10−4 | 8 × 105 | 2.4 × 105 |
| E | 1.6 × 106 | 4.8 × 105 | ||
| F | 3.2 × 106 | 9.6 × 105 | ||
| G | 0° | 1 × 10−4 | 1.6 × 106 | 4.8 × 105 |
| Mesh | Minimum Mesh Size (mm) | Simulation Time (hour) | Number of Mesh Elements | Drag Coefficient | Error |
|---|---|---|---|---|---|
| A | 300 × 300 × 300 | 2 | 499,800 | 0.535 | 31% |
| B | 200 × 200 × 200 | 4.1 | 1,205,936 | 0.754 | 2.7% |
| C | 120 × 120 × 120 | 9 | 2,729,712 | 0.816 | 5.3% |
| D | 100 × 100 × 100 | 67.5 | 4,818,975 | 0.792 | 2.2% |
| Model | Shape |
|---|---|
| A | Severely collapsed |
| B | Slightly collapsed |
| C | Fully inflated |
| D | Slightly collapsed |
| E | Fully inflated |
| F | Fully inflated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Wang, J.; Wang, Y.; Cai, C.; Wang, T. Numerical Study on the Aerodynamic and Structural Response Characteristics of a High-Altitude Wind-Capturing Umbrella. Appl. Sci. 2025, 15, 12161. https://doi.org/10.3390/app152212161
Jiang J, Wang J, Wang Y, Cai C, Wang T. Numerical Study on the Aerodynamic and Structural Response Characteristics of a High-Altitude Wind-Capturing Umbrella. Applied Sciences. 2025; 15(22):12161. https://doi.org/10.3390/app152212161
Chicago/Turabian StyleJiang, Jian, Jiaqi Wang, Yan Wang, Chang Cai, and Tengyuan Wang. 2025. "Numerical Study on the Aerodynamic and Structural Response Characteristics of a High-Altitude Wind-Capturing Umbrella" Applied Sciences 15, no. 22: 12161. https://doi.org/10.3390/app152212161
APA StyleJiang, J., Wang, J., Wang, Y., Cai, C., & Wang, T. (2025). Numerical Study on the Aerodynamic and Structural Response Characteristics of a High-Altitude Wind-Capturing Umbrella. Applied Sciences, 15(22), 12161. https://doi.org/10.3390/app152212161






