An Exact Approach for Multitasking Scheduling with Two Competitive Agents on Identical Parallel Machines
Featured Application
Abstract
1. Introduction
2. Related Work
| Literature | Single Machine | Parallel Machine | Multitasking Scheduling | Two-Agent | Due Date | Approach | Complexity |
|---|---|---|---|---|---|---|---|
| Hall et al. [4] | ✓ | - | ✓ | - | - | Polynomial algorithm | |
| Li et al. [9] | ✓ | - | ✓ | ✓ | ✓ | Polynomial algorithm | |
| Yang et al. [11] | ✓ | - | ✓ | ✓ | ✓ | Dynamic programming | |
| Wang et al. [12] | ✓ | - | ✓ | - | ✓ | Polynomial algorithm | |
| Wang et al. [3] | ✓ | - | ✓ | ✓ | - | Polynomial algorithm | |
| Wu et al. [10] | ✓ | - | ✓ | ✓ | - | Branch-and-bound, genetic algorithm, simulated annealing algorithm, cloud-simulated algorithm | - |
| Lee et al. [13] | - | ✓ | - | ✓ | ✓ | Branch-and-bound | - |
| Xiong et al. [14] | - | ✓ | ✓ | - | - | Branch-and-price | - |
| Gao et al. [15] | - | ✓ | ✓ | - | - | Branch-and-price | - |
3. Problem Statement and Optimal Solution Properties
3.1. The Problem
- Parameters
| : | The processing time and weight of job , where . |
| : | The number of jobs contained in and . |
| : | The due date coefficient and the due date of . |
| : | A job interruption factor, where . |
| : | The job switching time, the time consumption required once switching. |
- Variables
| : | The position-dependent processing time of job , where . |
| : | The makespan of jobs from the second agent. |
| : | The completion time of job from the first agent, where . |
| Algorithm 1 Polynomial Algorithm PolALG |
| Input: , |
| Output: , , , . |
| 1: Let , , , . |
| 2: Determine duration of and : |
| , . |
| 3: for starts from the last job to the first job in do |
| 4: |
| 5: if then |
| 6: Record the inserted position of block |
| 7: break |
| 8: end if |
| 9: end for |
| 10: for starts from the first job to the last job in do |
| 11: if then |
| /* Determine the completion time of block */ |
| 12: ,. |
| 13: end if |
| 14: , ,. |
| 15: end for |
3.2. Mathematical Model of the Problem
- Variables of MIP along with their brief descriptions
| Binary variable, if is arranged at th position of block on machine , ; otherwise, . | |
| Binary variable, if is arranged at th position of block on machine , ; otherwise, . | |
| Binary variable, if the block is inserted after th position of on machine , ; otherwise, . | |
| Non-negative variable, the duration of th position of block which is allocated to machine . | |
| Non-negative variable, the makespan of th position job from on machine . | |
| Non-negative variable, the duration of the block which is allocated to machine . | |
| Non-negative variable, the makespan of job . |
3.3. Structural Property of the Problem
4. Branch-and-Price Algorithm
4.1. Restricted Master Problem
4.2. Pricing Problem
4.3. Two-Phase Label-Setting Algorithm
- Symbols of the first phase label-setting algorithm
| The label associates with node , and it ends with job, where . | |
| The partitioning schedule of label , which only includes the set of jobs belonging to and ends with job . | |
| The set of jobs that are available and can be extended at job . | |
| The reduced cost of label . | |
| The recursive algorithm of the first phase label-setting algorithm, where the inputs are . |
- Symbols of the second phase label-setting algorithm
| The label associates with node , and ends with job , where . | |
| The partitioning schedule of label , which only includes the set of jobs belonging to and ends with job . | |
| The set of jobs that are available and can be extended at job . | |
| The reduced cost of label . | |
| The overall schedule includes the transferred and , and it is obtained by PolALG. | |
| The duration of the block. | |
| The completion time of the job , where . | |
| The total weighted completion time of jobs at label . | |
| The recursive algorithm of the second phase of the label-setting algorithm, where the inputs are , and is set to before starts. |
4.3.1. First Phase Label-Setting Algorithm
| Algorithm 2 First phase label-setting algorithm FPLS |
| Input |
| Output |
| 1: while do |
| 2: , |
| 3: Initialize consecutive label |
| 4: Initialize dummy label |
| 5: /* Initialize data structure of SPLS */ |
| 6: |
| 7: if then |
| 8: |
| 9: end if |
| 10: if then / *Lemma 1 */ |
| 11: / * Start next recursion */ |
| 12: end if |
| 13: end while |
4.3.2. Second Phase Label-Setting Algorithm
| Algorithm 3 Second phase label-setting algorithm SPLS |
| Input: |
| Output: |
| 1: while do |
| 2: , |
| 3: Initialize consecutive label |
| 4: |
| 5: Obtain reduced cost: |
| 6: if then |
| 7: , |
| 8: end if |
| 9: if then |
| 10: , |
| 11: end if |
| 12: if then / *Lemma 3 */ |
| 13: if then / *Lemma 4 */ |
| 14: |
| 15: if is in and then / *Lemma 2 */ |
| 16: / * Start next recursion */ |
| 17: end if |
| 18: end if |
| 19: end if |
| 20: end while |
| a Remove the last item from the sequence. b Insert at the head of . c Obtain the last item from the sequence. |
4.4. Primary Heuristic
4.5. Branching Rule
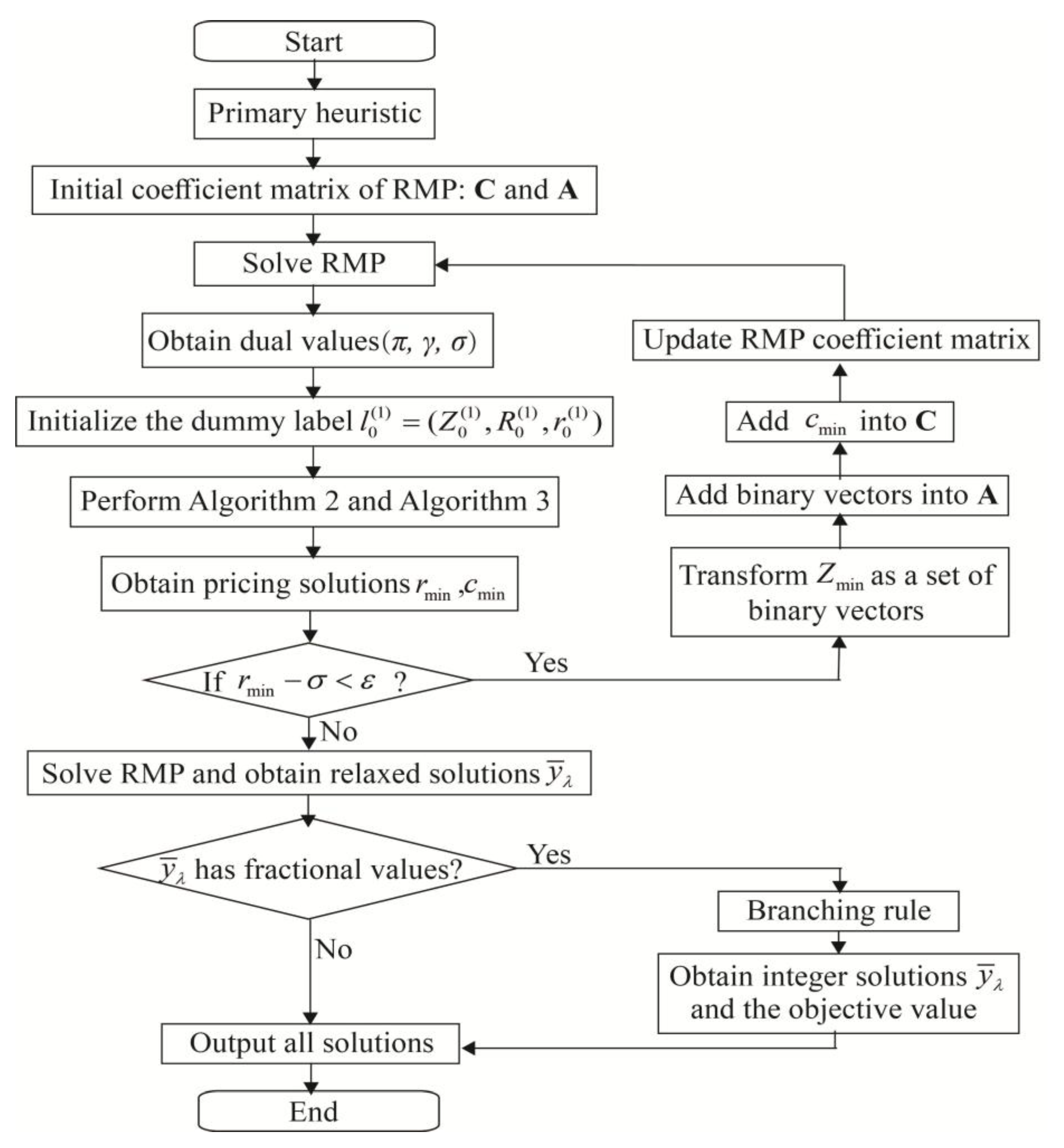
4.6. The Structure of the Branch-and-Price Algorithm
| Step 1 | Perform the primary heuristic (see Section 4.4) 5000 times, then store the 10 best solutions found. Initial coefficient matrix , and of the RMP; go to Step 2. |
| Step 2 | Solve the RMP and obtain the dual values (, and ). Initialize the dummy label of Algorithm 2, where , , and , and perform Algorithm 2. Simultaneously, input from Algorithm 1 to Algorithm 2, then perform Algorithm 2 (see Section 4.3). Obtain a set of pricing solutions ,, and ; go to Step 3. |
| Step 3 | If the reduced cost , transform as a set of binary vectors, then add and the binary vectors into the coefficient matrix ( and ) of the RMP and go to Step 2; otherwise, terminate B&P iteration. Go to Step 4. |
| Step 4 | If has fractional values, perform the branching rule (see Section 4.5), which obtains a series of integer solutions of and the corresponding objective value; otherwise, record solutions of and the corresponding objective value. Output all solutions. |
5. Computational Experiments
5.1. Description of Datasets
5.2. Comparison Results of Problems
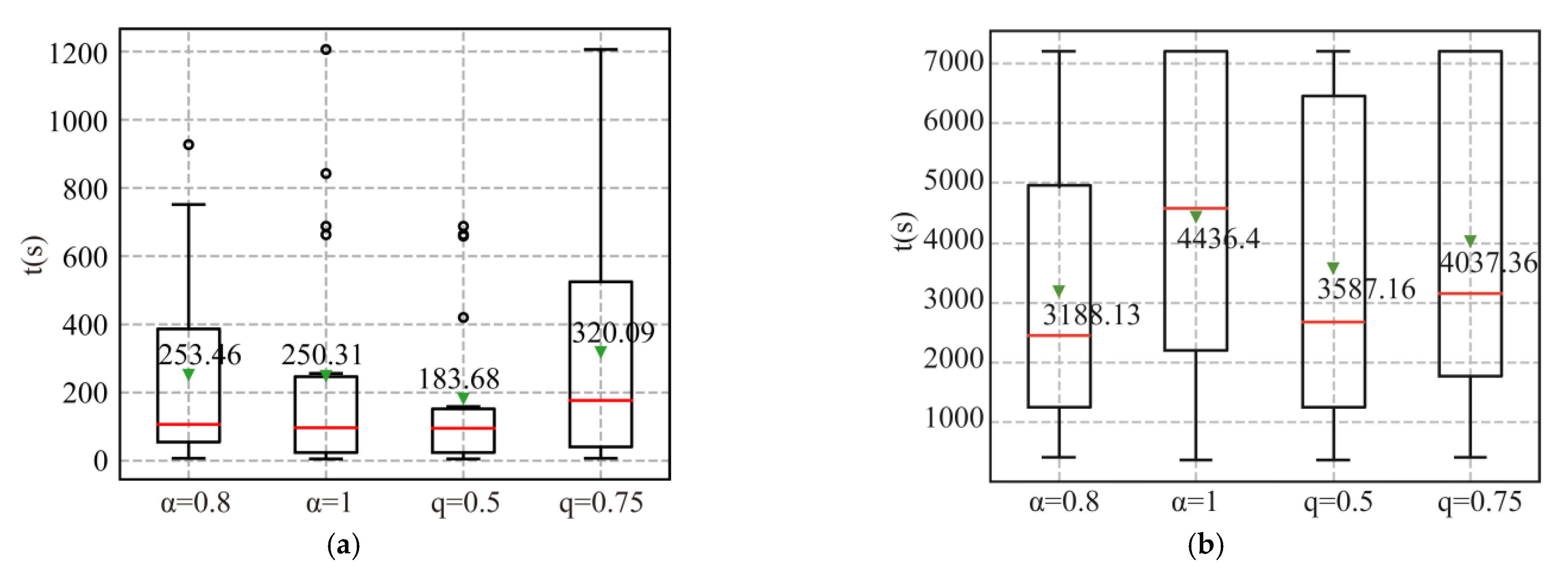
5.3. Computational Results of Large-Sized Problems
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, C.; Wang, Y. Design and strategy selection for quality incentive mechanisms in the public cloud manufacturing model. Comput. Ind. Eng. 2024, 198, 110681. [Google Scholar] [CrossRef]
- Jiang, Y.; Tang, D.; Zhu, H.; Liu, C.; Chen, K.; Zhang, Z.; Chen, J. A skill vector-based multi-task optimization algorithm for achieving objectives of multiple users in cloud manufacturing. Adv. Eng. Inform. 2025, 65, 103295. [Google Scholar] [CrossRef]
- Wang, D.; Yu, Y.; Yin, Y.; Cheng, T.C.E. Multi-agent scheduling problems under multitasking. Int. J. Prod. Res. 2021, 59, 3633–3663. [Google Scholar] [CrossRef]
- Hall, N.G.; Leung, J.Y.T.; Li, C.-L. The effects of multitasking on operations scheduling. Prod. Oper. Manag. 2015, 24, 1248–1265. [Google Scholar] [CrossRef]
- Xu, S.; Hall, N.G. Fatigue, personnel scheduling and operations: Review and research opportunities. Eur. J. Oper. Res. 2021, 295, 807–822. [Google Scholar] [CrossRef]
- Xue, H.; Bai, D.; Shu, X.; Wang, L.; Chu, F.; Cai, G. A multitasking scheduling problem of emergency medical response in mass casualty incident. IISE Trans. 2025, 1–19. [Google Scholar] [CrossRef]
- Graham, R.; Lawler, E.; Lenstra, J.; Kan, A. Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey. Ann. Discrete Math. 1979, 5, 287–326. [Google Scholar] [CrossRef]
- Hall, N.G.; Leung, J.Y.T.; Li, C.-L. Multitasking via alternate and shared processing: Algorithms and complexity. Discrete Appl. Math. 2016, 208, 41–58. [Google Scholar] [CrossRef]
- Li, S.-S.; Chen, R.-X.; Tian, J. Multitasking scheduling problems with two competitive agents. Eng. Optim. 2020, 52, 1940–1956. [Google Scholar] [CrossRef]
- Wu, C.-C.; Azzouz, A.; Chen, J.-Y.; Xu, J.; Shen, W.-L.; Lu, L.; Ben Said, L.; Lin, W.-C. A two-agent one-machine multitasking scheduling problem solving by exact and metaheuristics. Complex Intell. Syst. 2022, 8, 199–212. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, G.; Wang, C.; Yin, Y. Due date assignment and two-agent scheduling under multitasking environment. J. Comb. Optim. 2020, 44, 2207–2223. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.-Q.; Yin, Y. Due date assignment and multitasking scheduling with deterioration effect and efficiency promotion. Comput. Ind. Eng. 2020, 146, 106569. [Google Scholar] [CrossRef]
- Lee, W.-C.; Wang, J.-Y.; Lin, M.-C. A branch-and-bound algorithm for minimizing the total weighted completion time on parallel identical machines with two competing agents. Knowl. Based Syst. 2016, 105, 68–82. [Google Scholar] [CrossRef]
- Xiong, X.; Zhou, P.; Yin, Y.; Cheng, T.C.E.; Li, D. An exact branch-and-price algorithm for multitasking scheduling on unrelated parallel machines. Nav. Res. Logist. 2019, 66, 502–516. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, X.; Zhang, R. A branch-and-price approach to the multitasking scheduling with batch control on parallel machines. Int. Trans. Oper. Res. 2022, 29, 3464–3485. [Google Scholar] [CrossRef]
- Santos, F.; Fukasawa, R.; Ricardez-Sandoval, L. An integrated machine scheduling and personnel allocation problem for large-scale industrial facilities using a rolling horizon framework. Optim. Eng. 2021, 22, 2603–2626. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, J.; Chu, C. Multitasking scheduling problems with deterioration effect. Math. Probl. Eng. 2017, 2017, 4750791. [Google Scholar] [CrossRef]
- Zhu, Z.; Zheng, F.; Chu, C. Multitasking scheduling problems with a rate-modifying activity. Int. J. Prod. Res. 2017, 55, 296–312. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, M.; Chu, C.; Li, J. Multitasking scheduling with multiple rate-modifying activities. Int. Trans. Oper. Res. 2019, 26, 1956–1976. [Google Scholar] [CrossRef]
- Ji, M.; Zhang, Y.; Zhang, Y.; Cheng, T.C.E.; Jiang, Y. Single-machine multitasking scheduling with job efficiency promotion. J. Comb. Optim. 2022, 44, 446–479. [Google Scholar] [CrossRef]
- Liu, M.; Wang, S.; Zheng, F.; Chu, C. Algorithms for the joint multitasking scheduling and common due year assignment problem. Int. J. Prod. Res. 2017, 55, 6052–6066. [Google Scholar] [CrossRef]
- Ji, M.; Zhang, W.; Liao, L.; Cheng, T.C.E.; Tan, Y. Multitasking parallel-machine scheduling with machine-dependent slack due-window assignment. Int. J. Prod. Res. 2019, 57, 1667–1684. [Google Scholar] [CrossRef]
- Xu, C.; Xu, Y.; Zheng, F.; Liu, M. Multitasking scheduling problems with a common due-window. RAIRO–Oper. Res. 2021, 55, 1787–1798. [Google Scholar] [CrossRef]
- Xu, X.; Yin, G.; Wang, C. Multitasking scheduling with batch distribution and due data assignment. Comput. Int. Syst. 2021, 7, 191–202. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Gao, L.; Wang, C.; Chen, H. A multitasking workforce-constrained flexible job shop scheduling problem: An application from a real-world workshop. J. Manuf. Syst. 2025, 83, 196–215. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, W.; Ren, X.; Qin, S.; Chen, H.; Zhang, J. A novel resilient scheduling method based on multi-agent system for flexible job shops. Int. J. Prod. Res. 2025, 1–21. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, Y.; Hu, Y. Dynamic flexible scheduling with transportation constraints by multi-agent reinforcement learning. Eng. Appl. Artif. Intell. 2024, 134, 108699. [Google Scholar] [CrossRef]
- Agnetis, A.; Mirchandani, P.B.; Pacciarelli, D.; Pacifici, A. Scheduling problems with two competing agents. Oper. Res. 2004, 52, 229–242. [Google Scholar] [CrossRef]
- Leung, J.Y.-T.; Pinedo, M.; Wan, G. Competitive two-agent scheduling and its applications. Oper. Res. 2010, 58, 458–469. [Google Scholar] [CrossRef]
- Gerstl, E.; Mosheiov, G. Scheduling problems with two competing agents to minimized weighted earliness-tardiness. Comput. Oper. Res. 2013, 40, 109–116. [Google Scholar] [CrossRef]
- Shabtay, D.; Dover, O.; Kaspi, M. Single-machine two-agent scheduling involving a just-in-time criterion. Int. J. Comput. Prod. Res. 2015, 53, 2590–2604. [Google Scholar] [CrossRef]
- Li, H.; Gajpal, Y.; Bector, C. Single machine scheduling with two-agent for total weighted completion time objectives. Appl. Soft Comput. 2018, 70, 147–156. [Google Scholar] [CrossRef]
- Zhang, X. Two competitive agents to minimize the weighted total late work and the total completion time. Appl. Math. Comput. 2021, 406, 126286. [Google Scholar] [CrossRef]
- Lin, W.-C.; Yin, Y.; Cheng, S.-R.; Cheng, T.; Wu, C.-H.; Wu, C.-C. Particle swarm optimization and opposite-based particle swarm optimization for two-agent multi-facility customer order scheduling with ready times. Appl. Soft Comput. 2017, 52, 877–884. [Google Scholar] [CrossRef]
- Choi, B.C.; Park, M.J. Two-agent parallel machine scheduling with a restricted number of overlapped reserved tasks. Eur. J. Oper. Res. 2017, 260, 514–519. [Google Scholar] [CrossRef]
- Smith, W.E. Various optimizers for single-stage production. Nav. Res. Logist. Q. 1956, 3, 59–66. [Google Scholar] [CrossRef]
- Bruno, J.; Coffman, E.G.; Sethi, R. Scheduling independent tasks to reduce mean finishing time. Commun. ACM 1974, 17, 382–387. [Google Scholar] [CrossRef]
- Chen, Z.-L.; Powell, W.B. Solving Parallel Machine Scheduling Problems by Column Generation. INFORMS J. Comput. 1999, 11, 78–94. [Google Scholar] [CrossRef]
- Kowalczyk, D.; Leus, R. A branch-and-price algorithm for parallel machine scheduling using ZDDs and generic branching. INFORMS J. Comput. 2018, 30, 768–782. [Google Scholar] [CrossRef]
- Kramer, A.; Dell’Amico, M.; Iori, M. Enhanced arc-flow formulations to minimize weighted completion time on identical parallel machines. Eur. J. Oper. Res. 2019, 275, 67–79. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Zuo, X. Solving multi-depot electric vehicle scheduling problem by column generation and genetic algorithm. Appl. Soft Comput. 2021, 112, 107774. [Google Scholar] [CrossRef]
- Gunawan, A.; Widjaja, A.T.; Vansteenwegen, P.; Yu, V.F. A matheuristic algorithm for the vehicle routing problem with cross-docking. Appl. Soft Comput. 2021, 103, 107163. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, X.; Zhang, R. Scheduling for trial production with a parallel machine and multitasking scheduling model. Appl. Intell. 2023, 53, 26907–26926. [Google Scholar] [CrossRef]
- Azizoglu, M.; Kirca, O. On the minimization of total weighted Flow time with identical and uniform parallel machines. Eur. J. Oper. Res. 1999, 32, 91–100. [Google Scholar] [CrossRef]
- Elmaghraby, S.E.; Park, S.H. Scheduling jobs on a number of identical machines. AIIE Trans. 1974, 6, 1–13. [Google Scholar] [CrossRef]
- Muts, P.; Bruche, S.; Nowak, I.; Wu, O.; Hendrix, E.M.T.; Tsatsaronis, G. A column generation algorithm for solving energy system planning problems. Optim. Eng. 2023, 24, 317–351. [Google Scholar] [CrossRef]
- Jepsen, M.; Petersen, B.; Spoorendonk, S.; Pisinger, D. Subset-row inequalities applied to the vehicle-routing problem with time windows. Oper. Res. 2008, 56, 497–511. [Google Scholar] [CrossRef]
- Sedeño-Noda, A.; González-Martín, C. An efficient label setting/correcting shortest path algorithm. Comput. Optim. Appl. 2012, 51, 437–455. [Google Scholar] [CrossRef]
- Li, C.; Gong, L.; Luo, Z.; Lim, A. A branch-and-price-and-cut algorithm for a pickup and delivery problem in retailing. Omega 2019, 89, 71–91. [Google Scholar] [CrossRef]
- Muter, I. Exact algorithms to minimize makespan on single and parallel batch processing machines. Eur. J. Oper. Res. 2020, 285, 470–483. [Google Scholar] [CrossRef]
- Kramer, H.H.; Uchoa, E.; Fampa, M.; Köhler, V.; Vanderbeck, F. Column generation approaches for the software clustering problem. Comput. Optim. Appl. 2016, 64, 843–864. [Google Scholar] [CrossRef]
- van den Akker, J.M.; Hoogeveen, J.; van de Velde, A.S.L. Parallel Machine Scheduling by Column Generation. Oper. Res. 1999, 47, 862–872. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Iori, M.; Martello, S.; Monaci, M. Heuristic and exact algorithms for the identical parallel machine scheduling problem. INFORMS J. Comput. 2008, 20, 333–344. [Google Scholar] [CrossRef]
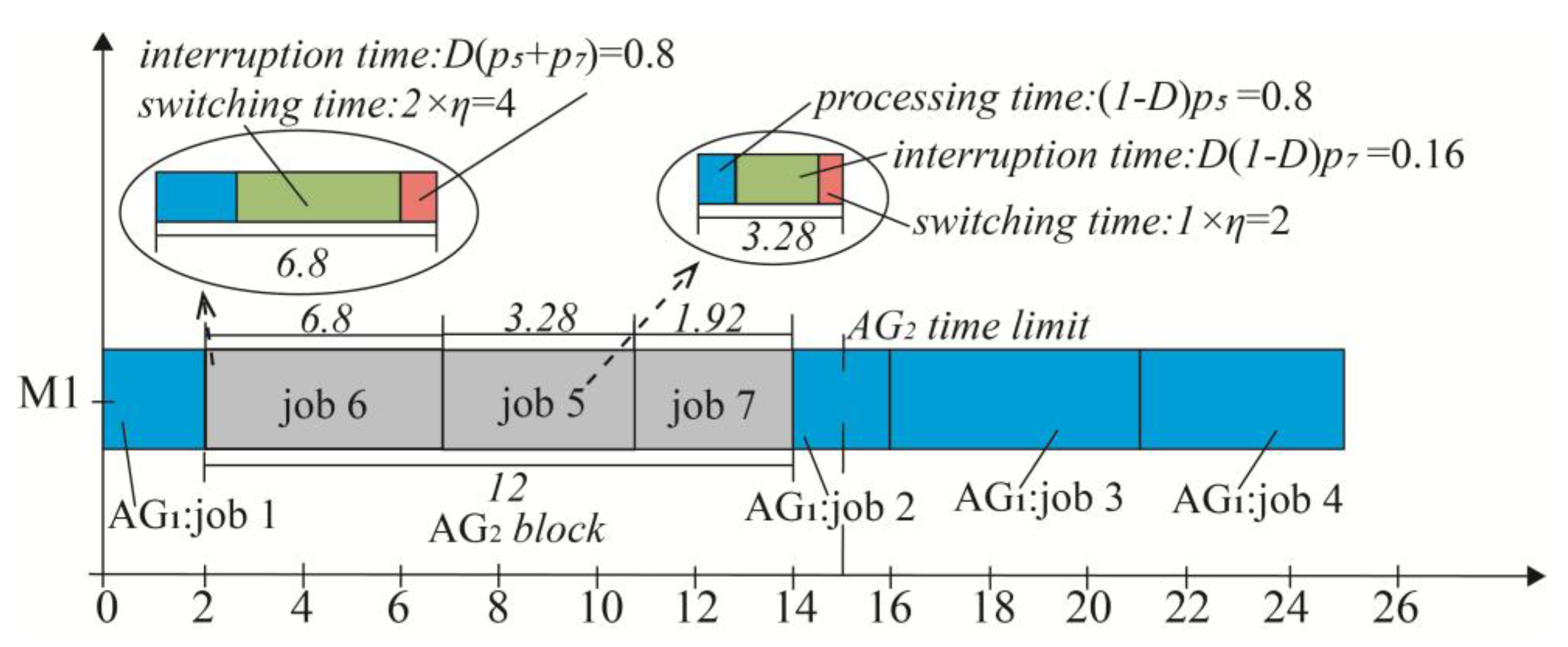
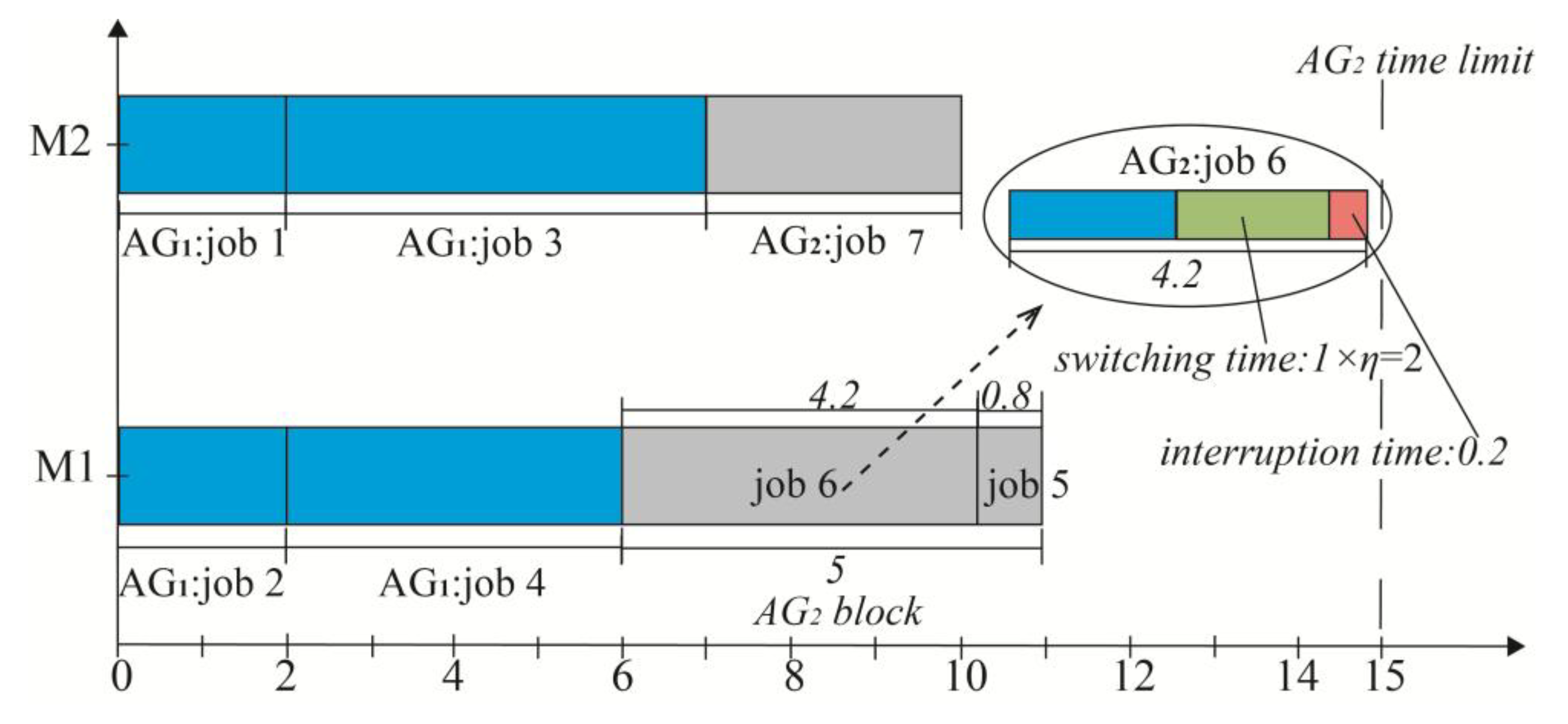
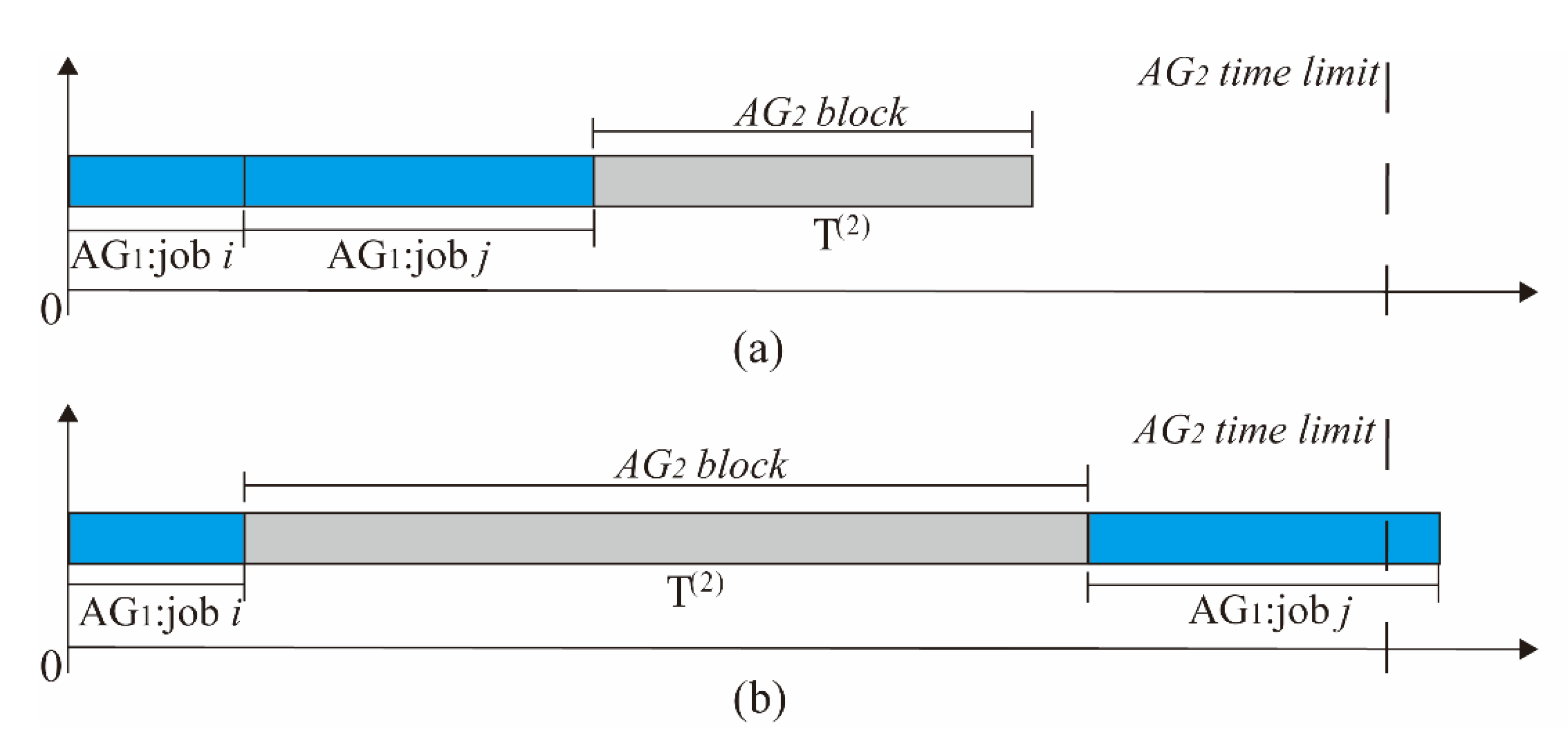
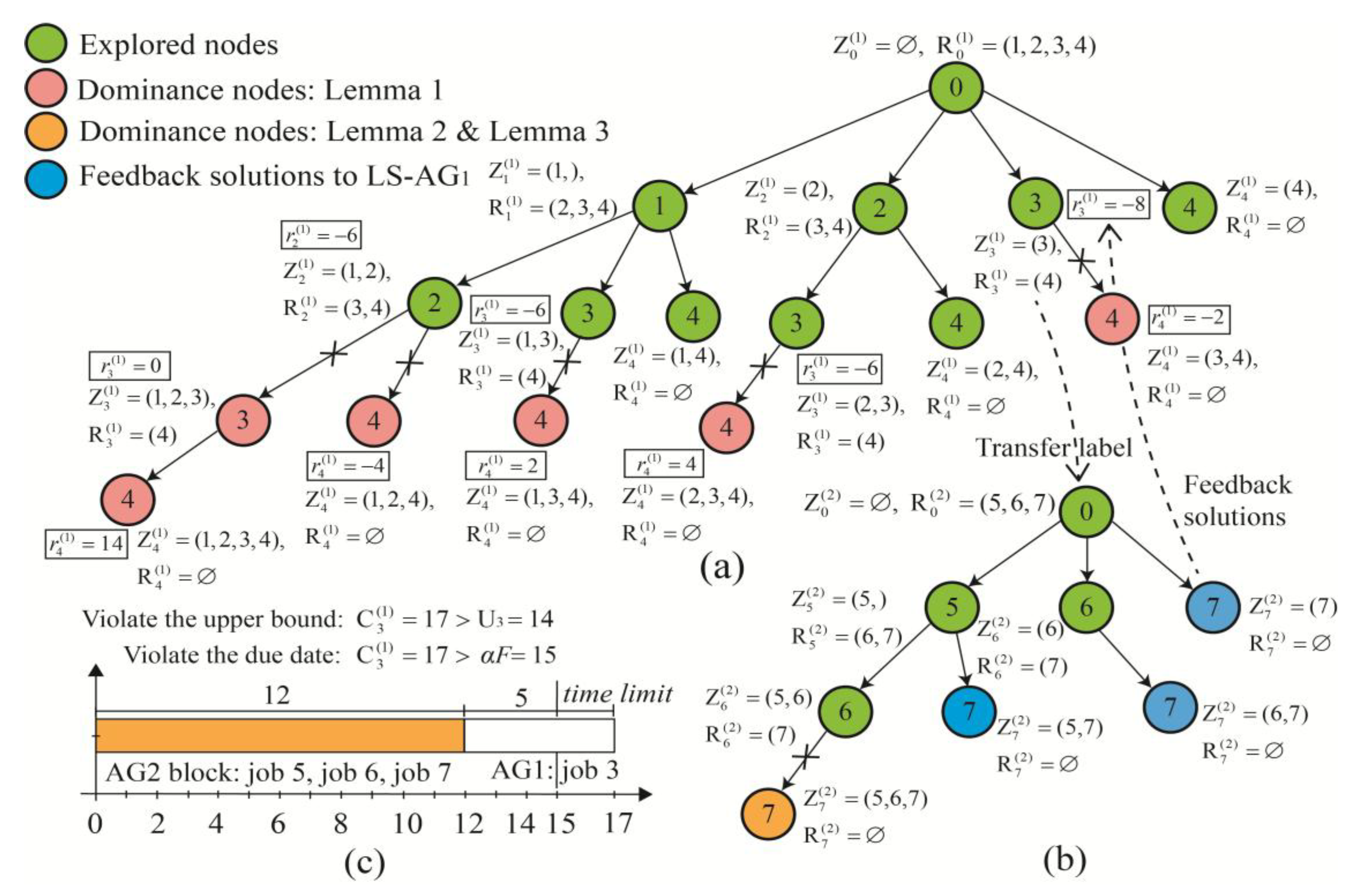
| Job | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 2 | 2 | 5 | 4 | 1 | 2 | 3 | |
| 6 | 2 | 3 | 2 | ||||
| 1 | 2 | 3 | 4 | ||||
| 5 | 6 | 7 |
| Job | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 18.0 | 10.0 | 21.0 | 14.0 | 0.0 | 0.0 | 2.0 | |
| −6.0 | |||||||
| {1,2,7} | {2,4,7} | ||||||
| −2.0 | −2.0 | ||||||
| 12.5 | 12.5 | 14.0 | 12.0 |
| −6.0 | 15.0 | 5.0 | 5.0 | 0.0 | |
| (5) | −6.0 | 15.0 | 6.0 | 6.0 | 1.0 |
| (5,6) | −6.0 | 15.0 | 10.0 | 10.0 | 5.0 |
| (5,6,7) | 28.0 | 51.0 | 17.0 | 12.0 | 12.0 |
| (5,7) | −8.0 | 15.0 | 11.0 | 11.0 | 6.0 |
| (6) | −6.0 | 15.0 | 7.0 | 7.0 | 2.0 |
| (6,7) | −8.0 | 15.0 | 12.0 | 12.0 | 7.0 |
| (7) | −8.0 | 15.0 | 8.0 | 8.0 | 3.0 |
| Parameters | MIP | B&P | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | m | α | q | ub | t(s) | lb | ub | gap | t(s) |
| 10 | 2 | 1.0 | 0.25 | 685.00 | 0.19 | 685.00 | 685.00 | 0.00 | 4.51 |
| 0.50 | 425.00 | 1.17 | 425.00 | 425.00 | 0.00 | 4.02 | |||
| 0.75 | 586.00 | 18.03 | 586.00 | 586.00 | 0.00 | 3.83 | |||
| 1.5 | 0.25 | 160.00 | 0.98 | 160.00 | 160.00 | 0.00 | 2.51 | ||
| 0.50 | 335.00 | 1.49 | 335.00 | 335.00 | 0.00 | 3.12 | |||
| 0.75 | 586.00 | 41.20 | 586.00 | 586.00 | 0.00 | 3.56 | |||
| 2.0 | 0.25 | 160.00 | 0.75 | 160.00 | 160.00 | 0.00 | 2.73 | ||
| 0.50 | 335.00 | 0.62 | 335.00 | 335.00 | 0.00 | 3.00 | |||
| 0.75 | 586.00 | 27.72 | 586.00 | 586.00 | 0.00 | 4.33 | |||
| 3 | 1.0 | 0.25 | 480.00 | 3.07 | 472.50 | 480.00 | 0.02 | 2.93 | |
| 0.50 | 345.00 | 5.61 | 345.00 | 345.00 | 0.00 | 3.10 | |||
| 0.75 | 466.00 | 63.84 | 466.00 | 466.00 | 0.00 | 3.68 | |||
| 1.5 | 0.25 | 140.00 | 0.61 | 140.00 | 140.00 | 0.00 | 3.00 | ||
| 0.50 | 280.00 | 4.18 | 280.00 | 280.00 | 0.00 | 2.93 | |||
| 0.75 | 463.00 | 46.97 | 463.00 | 463.00 | 0.00 | 3.43 | |||
| 2.0 | 0.25 | 140.00 | 0.19 | 140.00 | 140.00 | 0.00 | 2.89 | ||
| 0.50 | 280.00 | 4.91 | 280.00 | 280.00 | 0.00 | 3.27 | |||
| 0.75 | 463.00 | 80.62 | 463.00 | 463.00 | 0.00 | 3.53 | |||
| 4 | 1.0 | 0.25 | 287.50 | 2.66 | 287.50 | 287.50 | 0.00 | 2.61 | |
| 0.50 | 300.00 | 3.35 | 300.00 | 300.00 | 0.00 | 2.90 | |||
| 0.75 | 411.00 | 302.89 | 411.00 | 411.00 | 0.00 | 3.72 | |||
| 1.5 | 0.25 | 140.00 | 0.47 | 140.00 | 140.00 | 0.00 | 2.73 | ||
| 0.50 | 250.00 | 11.17 | 250.00 | 250.00 | 0.00 | 3.29 | |||
| 0.75 | 410.00 | 600.85 | 410.00 | 410.00 | 0.00 | 3.77 | |||
| 2.0 | 0.25 | 140.00 | 1.43 | 140.00 | 140.00 | 0.00 | 2.90 | ||
| 0.50 | 250.00 | 5.93 | 250.00 | 250.00 | 0.00 | 3.51 | |||
| 0.75 | 410.00 | 366.35 | 410.00 | 410.00 | 0.00 | 3.75 | |||
| Avg. | 352.35 | 59.16 | 352.07 | 352.35 | 0.00 | 3.32 | |||
| Parameters | MIP | B&P | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | m | α | q | ub | t(s) | lb | ub | gap | t(s) |
| 11 | 3 | 1.0 | 0.25 | 560.00 | 13.18 | 552.50 | 560.00 | 0.01 | 2.86 |
| 0.50 | 467.50 | 8.58 | 459.17 | 467.50 | 0.02 | 3.84 | |||
| 0.75 | 510.00 | 393.00 | 510.00 | 510.00 | 0.00 | 4.73 | |||
| 1.5 | 0.25 | 140.00 | 0.74 | 140.00 | 140.00 | 0.00 | 2.65 | ||
| 0.50 | 425.00 | 16.25 | 425.00 | 425.00 | 0.00 | 3.25 | |||
| 0.75 | 502.00 | 235.24 | 502.00 | 502.00 | 0.00 | 3.59 | |||
| 2.0 | 0.25 | 140.00 | 0.86 | 140.00 | 140.00 | 0.00 | 2.98 | ||
| 0.50 | 425.00 | 3.70 | 425.00 | 425.00 | 0.00 | 3.31 | |||
| 0.75 | 502.00 | 350.86 | 502.00 | 502.00 | 0.00 | 3.93 | |||
| 4 | 1.0 | 0.25 | 515.00 | 4.20 | 515.00 | 515.00 | 0.00 | 2.71 | |
| 0.50 | 400.00 | 49.31 | 400.00 | 400.00 | 0.00 | 3.50 | |||
| 0.75 | 448.00 | 600.99 | 448.00 | 448.00 | 0.00 | 4.00 | |||
| 1.5 | 0.25 | 140.00 | 0.22 | 140.00 | 140.00 | 0.00 | 2.72 | ||
| 0.50 | 385.00 | 1.85 | 385.00 | 385.00 | 0.00 | 3.52 | |||
| 0.75 | 439.00 | 601.40 | 439.00 | 439.00 | 0.00 | 3.73 | |||
| 2.0 | 0.25 | 140.00 | 0.31 | 140.00 | 140.00 | 0.00 | 2.91 | ||
| 0.50 | 385.00 | 43.14 | 385.00 | 385.00 | 0.00 | 3.50 | |||
| 0.75 | 439.00 | 601.24 | 439.00 | 439.00 | 0.00 | 3.72 | |||
| Avg. | 386.81 | 162.50 | 385.93 | 386.81 | 0.00 | 3.41 | |||
| Parameters | B&P | MIP | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | α | q | lb | ub | Gap | Cols | Nodes | PRI: t(s) | TP-LS: t(s) | B&P: t(s) | ub | t(s) |
| 15 | 2 | 0.8 | 0.50 | 78,330.19 | 78,330.19 | 0.00 | 1842 | 1,738,714 | 1.01 | 376.07 | 658.83 | 78,276.89 | 193.45 |
| 0.75 | 116,426.39 | 116,426.39 | 0.00 | 2202 | 2,154,347 | 1.43 | 340.43 | 604.58 | 116,955.56 | 1800.42 | |||
| 1.0 | 0.50 | 44,198.89 | 44,198.89 | 0.00 | 1531 | 1,835,517 | 1.24 | 449.52 | 687.62 | 44,198.89 | 178.99 | ||
| 0.75 | 106,393.50 | 106,495.82 | 0.00 | 2182 | 2,785,770 | 1.46 | 763.49 | 1206.14 | 106,495.82 | 1800.59 | |||
| 3 | 0.8 | 0.50 | 56,024.53 | 56,518.96 | 0.01 | 433 | 61,980 | 1.06 | 2.61 | 10.44 | 56,518.96 | 1800.38 | |
| 0.75 | 86,621.24 | 86,621.24 | 0.00 | 463 | 69,021 | 1.73 | 2.90 | 11.98 | 86,987.59 | 1800.45 | |||
| 1.0 | 0.50 | 33,028.01 | 34,638.56 | 0.05 | 393 | 68,886 | 1.21 | 2.26 | 8.36 | 34,638.56 | 1800.26 | ||
| 0.75 | 78,439.15 | 79,191.70 | 0.01 | 403 | 71,685 | 1.77 | 2.78 | 9.30 | 79,281.75 | 1800.53 | |||
| 4 | 0.8 | 0.50 | 48,128.18 | 48,128.18 | 0.00 | 482 | 18,082 | 1.10 | 0.74 | 7.46 | 48,128.17 | 1800.54 | |
| 0.75 | 73,730.05 | 74,221.20 | 0.01 | 484 | 16,397 | 1.85 | 0.56 | 7.35 | 74,438.17 | 1800.39 | |||
| 1.0 | 0.50 | 28,776.00 | 29,460.59 | 0.02 | 444 | 15,378 | 1.18 | 0.44 | 5.40 | 29,460.59 | 1800.45 | ||
| 0.75 | 65,440.23 | 65,440.23 | 0.00 | 504 | 19,511 | 2.05 | 0.79 | 8.20 | 65,440.23 | 1800.94 | |||
| 20 | 3 | 0.8 | 0.50 | 88,532.83 | 94,205.17 | 0.06 | 553 | 1,729,284 | 2.08 | 64.80 | 97.04 | 94,206.81 | 1800.48 |
| 0.75 | 126,989.07 | 126,989.07 | 0.00 | 703 | 3,967,908 | 3.58 | 170.73 | 224.84 | 127,798.66 | 1800.54 | |||
| 1.0 | 0.50 | 52,881.61 | 55,769.08 | 0.05 | 513 | 2,302,331 | 2.34 | 72.11 | 99.79 | 55,769.08 | 1800.49 | ||
| 0.75 | 119,253.78 | 120,826.33 | 0.01 | 523 | 3,080,361 | 3.47 | 106.05 | 135.62 | 120,826.33 | 1800.48 | |||
| 4 | 0.8 | 0.50 | 70,811.74 | 70,811.74 | 0.00 | 690 | 444,790 | 2.09 | 14.83 | 57.49 | 72,070.62 | 1800.53 | |
| 0.75 | 103,672.25 | 103,672.25 | 0.00 | 884 | 820,929 | 4.04 | 42.62 | 115.38 | 104,421.42 | 1800.94 | |||
| 1.0 | 0.50 | 44,510.11 | 45,794.58 | 0.03 | 544 | 417,733 | 4.85 | 9.37 | 33.07 | 45,856.64 | 1800.65 | ||
| 0.75 | 97,343.53 | 98,008.15 | 0.01 | 584 | 608,800 | 8.81 | 19.50 | 47.61 | 98,032.81 | 1800.64 | |||
| 5 | 0.8 | 0.50 | 61,302.55 | 61,302.55 | 0.00 | 785 | 153,399 | 4.54 | 6.24 | 54.12 | 61,302.56 | 1800.65 | |
| 0.75 | 90,439.54 | 90,439.54 | 0.00 | 865 | 230,383 | 9.10 | 11.39 | 70.94 | 91,162.53 | 1800.62 | |||
| 1.0 | 0.50 | 40,081.34 | 40,895.45 | 0.02 | 585 | 108,626 | 4.89 | 2.26 | 21.06 | 41,708.16 | 1800.76 | ||
| 0.75 | 84,663.37 | 84,663.37 | 0.00 | 685 | 177,894 | 9.81 | 6.18 | 38.56 | 85,542.54 | 1800.95 | |||
| 25 | 4 | 0.8 | 0.50 | 107,660.68 | 107,753.99 | 0.00 | 644 | 7,471,863 | 5.13 | 348.50 | 420.16 | 109,493.80 | 1800.73 |
| 0.75 | 139,394.71 | 139,830.08 | 0.00 | 744 | 13,463,151 | 9.39 | 826.42 | 927.03 | 144,093.18 | 1801.35 | |||
| 1.0 | 0.50 | 79,371.90 | 81,746.38 | 0.03 | 684 | 13,446,980 | 5.94 | 574.76 | 662.84 | 81,746.38 | 1800.64 | ||
| 0.75 | 129,004.21 | 129,328.13 | 0.00 | 694 | 14,909,496 | 15.38 | 755.33 | 842.20 | 130,433.97 | 1802.39 | |||
| 5 | 0.8 | 0.50 | 93,173.99 | 93,782.08 | 0.01 | 735 | 1,890,998 | 13.68 | 79.94 | 159.01 | 95,846.96 | 1800.65 | |
| 0.75 | 119,732.21 | 119,732.21 | 0.00 | 1155 | 5,416,879 | 24.40 | 515.62 | 751.31 | 121,681.37 | 1800.98 | |||
| 1.0 | 0.50 | 69,143.25 | 71,763.16 | 0.04 | 645 | 2,125,189 | 15.64 | 77.31 | 131.55 | 71,819.30 | 1800.67 | ||
| 0.75 | 110,957.15 | 110,992.30 | 0.00 | 795 | 3,488,210 | 51.64 | 163.53 | 256.29 | 111,878.72 | 1801.12 | |||
| 6 | 0.8 | 0.50 | 83,606.20 | 84,087.62 | 0.01 | 783 | 569,407 | 14.22 | 25.45 | 98.21 | 84,301.89 | 1800.76 | |
| 0.75 | 107,101.66 | 107,101.66 | 0.00 | 1086 | 1,397,517 | 23.77 | 106.55 | 286.06 | 107,717.38 | 1801.01 | |||
| 1.0 | 0.50 | 62,619.33 | 63,794.71 | 0.02 | 766 | 751,901 | 14.99 | 27.82 | 93.71 | 64,353.01 | 1800.86 | ||
| 0.75 | 99,084.44 | 99,084.44 | 0.00 | 976 | 1,302,097 | 28.08 | 80.75 | 218.22 | 100,095.40 | 1801.06 | |||
| Avg. | 83,246.33 | 83,945.72 | 0.01 | 805.11 | 2,475,872 | 8.48 | 168.07 | 251.88 | 84,527.24 | 1711.04 | |||
| n | m | α | q | lb | ub | Gap | Cols | Nodes | PRI: t(s) | TP-LS: t(s) | B&P: t(s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 5 | 0.8 | 0.50 | 113,122.32 | 117,753.70 | 0.04 | 835 | 32,325,486 | 14.75 | 1489.58 | 1685.38 |
| 0.75 | 140,269.97 | 140,269.97 | 0.00 | 925 | 53,811,784 | 24.84 | 2425.67 | 2679.59 | |||
| 1.0 | 0.50 | 86,097.85 | 97,561.69 | 0.13 | 845 | 52,159,442 | 15.10 | 2002.12 | 2192.45 | ||
| 0.75 | 128,957.39 | 129,302.14 | 0.00 | 784 | 54,781,101 | 25.73 | 2078.74 | 2255.38 | |||
| 6 | 0.8 | 0.50 | 100,796.61 | 101,964.21 | 0.01 | 916 | 8,711,009 | 28.58 | 408.87 | 596.20 | |
| 0.75 | 124,382.63 | 124,429.46 | 0.00 | 896 | 10,292,371 | 46.27 | 558.26 | 745.84 | |||
| 1.0 | 0.50 | 76,949.98 | 78,568.54 | 0.02 | 866 | 11,570,983 | 29.53 | 484.76 | 650.05 | ||
| 0.75 | 114,096.30 | 115,286.22 | 0.01 | 906 | 14,739,758 | 54.51 | 824.72 | 1021.76 | |||
| 7 | 0.8 | 0.50 | 92,070.50 | 93,195.19 | 0.01 | 1037 | 3,346,906 | 29.87 | 187.75 | 442.95 | |
| 0.75 | 113,438.54 | 113,557.99 | 0.00 | 1027 | 3,718,211 | 46.44 | 183.93 | 421.49 | |||
| 1.0 | 0.50 | 70,476.24 | 71,684.05 | 0.02 | 977 | 4,234,235 | 31.67 | 165.75 | 364.59 | ||
| 0.75 | 103,774.07 | 103,849.07 | 0.00 | 1007 | 3,973,022 | 53.12 | 210.61 | 431.37 | |||
| 35 | 6 | 0.8 | 0.50 | 126,532.95 | 127,063.87 | 0.00 | 986 | 86,135,136 | 31.52 | 4499.18 | 4893.70 |
| 0.75 | 157,242.97 | 157,253.16 | 0.00 | 966 | 126,152,708 | 60.43 | 6972.74 | 7158.08 | |||
| 1.0 | 0.50 | 98,828.25 | 120,761.19 | 0.22 | 796 | 159,800,770 | 33.60 | 7065.99 | >7200 | ||
| 0.75 | 149,226.55 | 149,332.14 | 0.00 | 926 | 129,151,861 | 68.98 | 6864.57 | >7200 | |||
| 7 | 0.8 | 0.50 | 114,736.16 | 115,274.64 | 0.00 | 1037 | 23,692,184 | 31.85 | 1187.67 | 1546.92 | |
| 0.75 | 141,919.85 | 142,012.00 | 0.00 | 1087 | 39,414,771 | 53.96 | 2465.73 | 2901.59 | |||
| 1.0 | 0.50 | 93,220.18 | 142,030.19 | 0.52 | 857 | 116,901,416 | 32.00 | 7064.76 | >7200 | ||
| 0.75 | 134,518.58 | 134,518.58 | 0.00 | 1187 | 52,679,587 | 64.61 | 2740.06 | 3295.96 | |||
| 8 | 0.8 | 0.50 | 105,791.98 | 106,335.85 | 0.01 | 1208 | 11,298,645 | 33.83 | 630.34 | 1151.21 | |
| 0.75 | 130,570.07 | 130,570.07 | 0.00 | 1268 | 14,863,205 | 57.83 | 984.72 | 1604.50 | |||
| 1.0 | 0.50 | 116,786.66 | 118,634.66 | 0.02 | 1278 | 67,811,664 | 33.56 | 4027.68 | 4963.75 | ||
| 0.75 | 139,292.02 | 139,420.54 | 0.00 | 1208 | 135,978,900 | 58.36 | 6521.38 | >7200 | |||
| 40 | 7 | 0.8 | 0.50 | 127,375.42 | 162,542.08 | 0.28 | 927 | 123,963,985 | 33.64 | 6903.67 | >7200 |
| 0.75 | 163,976.81 | 181,855.49 | 0.11 | 867 | 144,152,434 | 53.40 | 6910.64 | >7200 | |||
| 1.0 | 0.50 | 94,693.90 | 126,979.43 | 0.34 | 827 | 125,265,054 | 33.75 | 7156.75 | >7200 | ||
| 0.75 | 153,104.34 | 171,587.34 | 0.12 | 797 | 167,750,518 | 67.94 | 7388.95 | >7200 | |||
| 8 | 0.8 | 0.50 | 116,786.66 | 118,634.66 | 0.02 | 1278 | 67,811,664 | 33.56 | 4027.68 | 4963.75 | |
| 0.75 | 149,624.30 | 150,011.23 | 0.00 | 1238 | 105,409,675 | 52.03 | 6119.58 | 6930.18 | |||
| 1.0 | 0.50 | 86,087.85 | 88,017.02 | 0.02 | 1208 | 134,854,300 | 35.12 | 6189.11 | 6949.22 | ||
| 0.75 | 139,292.02 | 139,420.54 | 0.00 | 1208 | 135,978,900 | 58.36 | 6521.38 | >7200 | |||
| 9 | 0.8 | 0.50 | 108,858.27 | 109,523.23 | 0.01 | 909 | 28,050,329 | 34.88 | 1668.32 | 2232.17 | |
| 0.75 | 139,180.53 | 139,300.04 | 0.00 | 1319 | 42,391,554 | 46.96 | 2243.02 | 3032.78 | |||
| 1.0 | 0.50 | 80,705.75 | 82,478.08 | 0.02 | 1309 | 51,827,245 | 33.48 | 2397.94 | 3136.61 | ||
| 0.75 | 129,405.30 | 129,442.47 | 0.00 | 1409 | 66,722,646 | 54.23 | 3221.44 | 4194.05 | |||
| Avg. | 118,394.16 | 124,188.91 | 0.05 | 1031.14 | 66,992,318.31 | 41.62 | 3410.94 | 3812.26 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, X.; Zhou, S.; Gao, J. An Exact Approach for Multitasking Scheduling with Two Competitive Agents on Identical Parallel Machines. Appl. Sci. 2025, 15, 12111. https://doi.org/10.3390/app152212111
Xin X, Zhou S, Gao J. An Exact Approach for Multitasking Scheduling with Two Competitive Agents on Identical Parallel Machines. Applied Sciences. 2025; 15(22):12111. https://doi.org/10.3390/app152212111
Chicago/Turabian StyleXin, Xin, Suxia Zhou, and Jinsheng Gao. 2025. "An Exact Approach for Multitasking Scheduling with Two Competitive Agents on Identical Parallel Machines" Applied Sciences 15, no. 22: 12111. https://doi.org/10.3390/app152212111
APA StyleXin, X., Zhou, S., & Gao, J. (2025). An Exact Approach for Multitasking Scheduling with Two Competitive Agents on Identical Parallel Machines. Applied Sciences, 15(22), 12111. https://doi.org/10.3390/app152212111






