Exploring the Dynamic Properties of Tropical and Temperate Wood Species for Musical Instruments
Featured Application
Abstract
1. Introduction
2. Materials and Methods
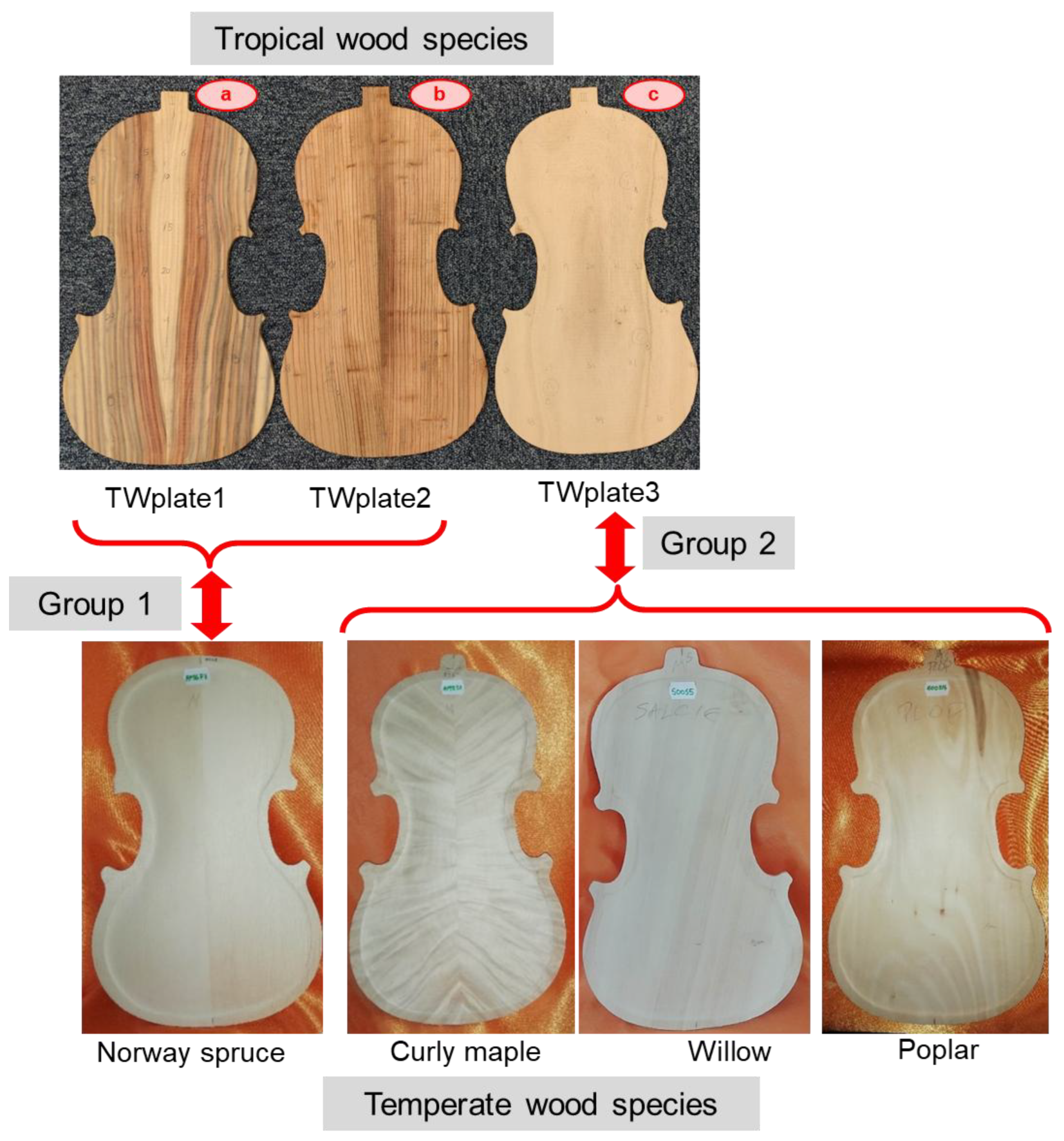
2.1. Materials
2.2. Methods
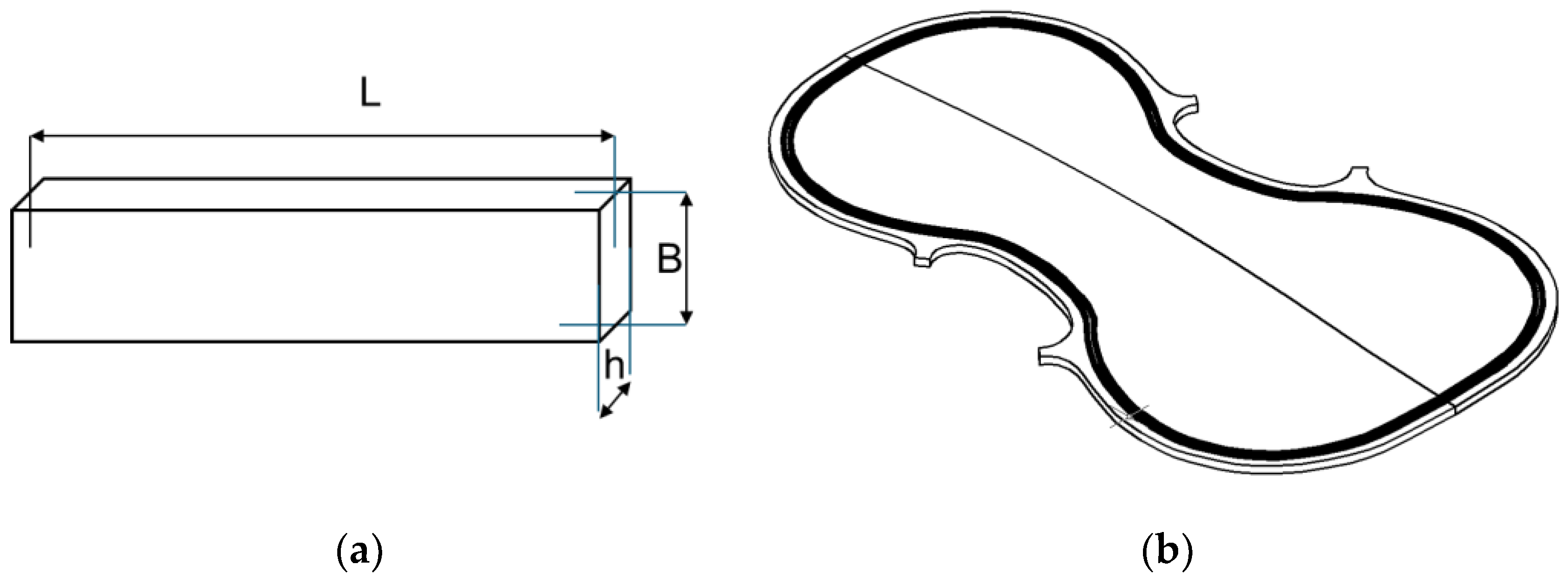
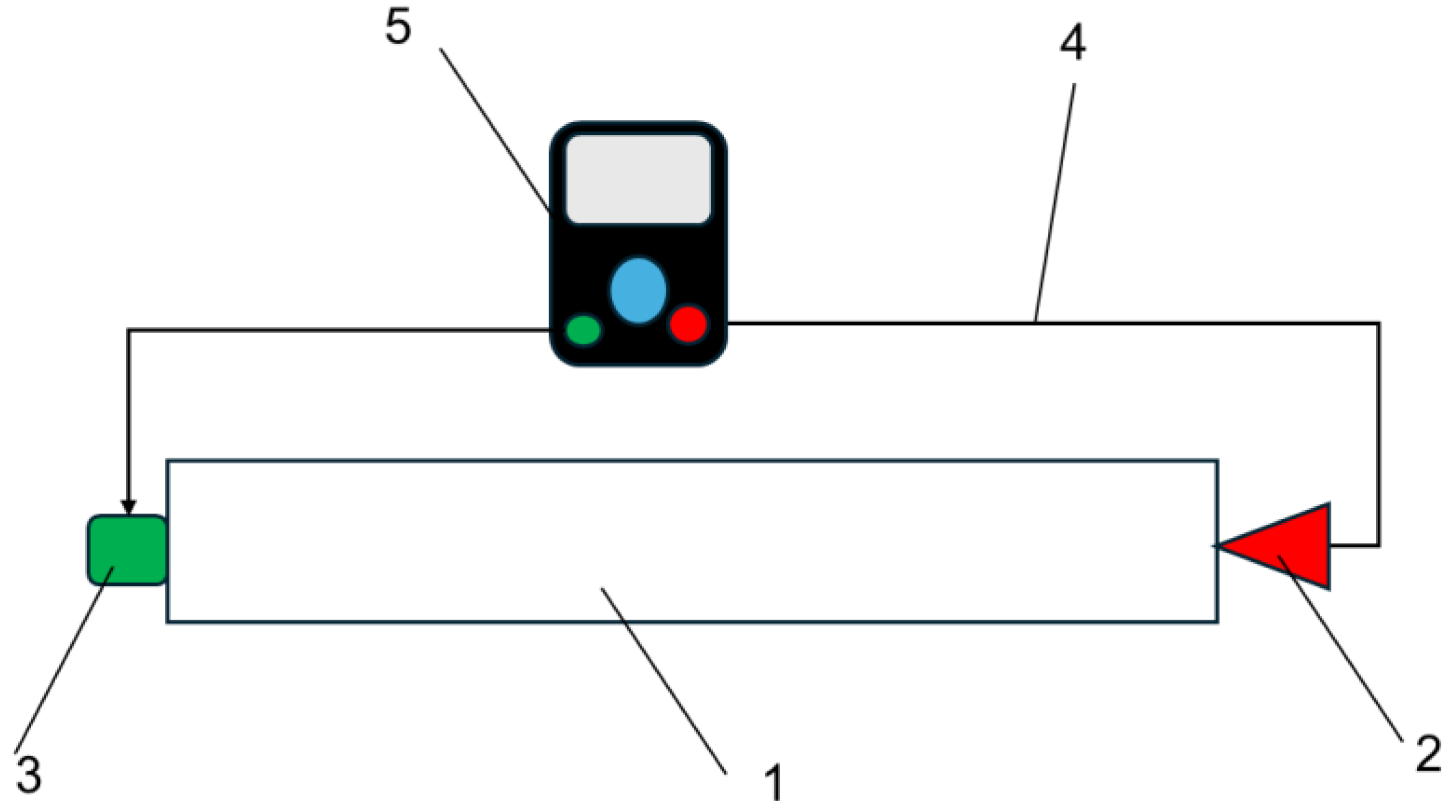
2.2.1. Determination of Acoustic Properties
- Sound velocity in wood (SV)
- Dynamic Modulus of Elasticity (DMOE)
- The acoustic impedance, , is calculated according to relation Equation (2):
- The sound radiation coefficient, , is determined by Equation (3):
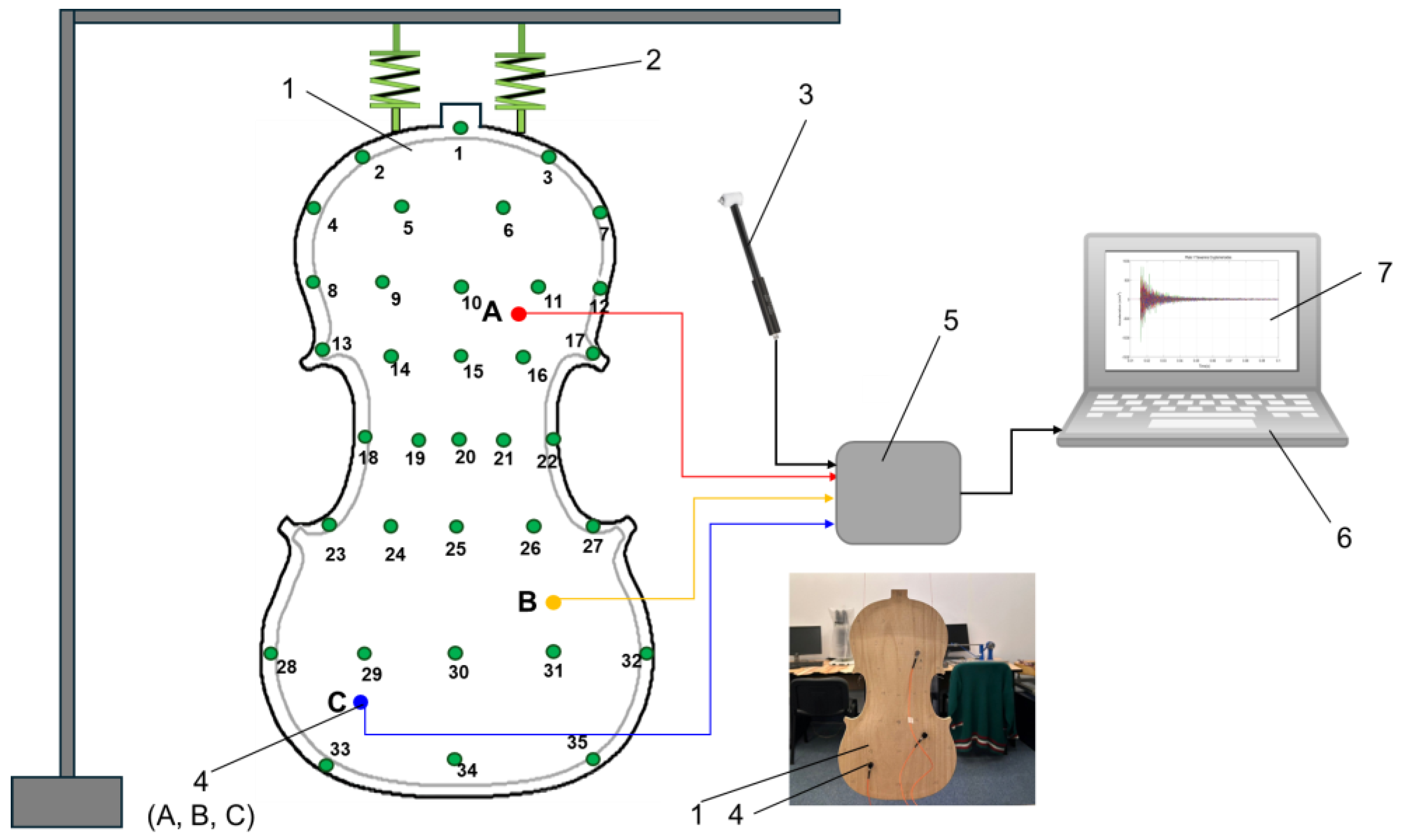
2.2.2. Experimental Modal Analysis (EMA)
2.2.3. Processing Signals
3. Results
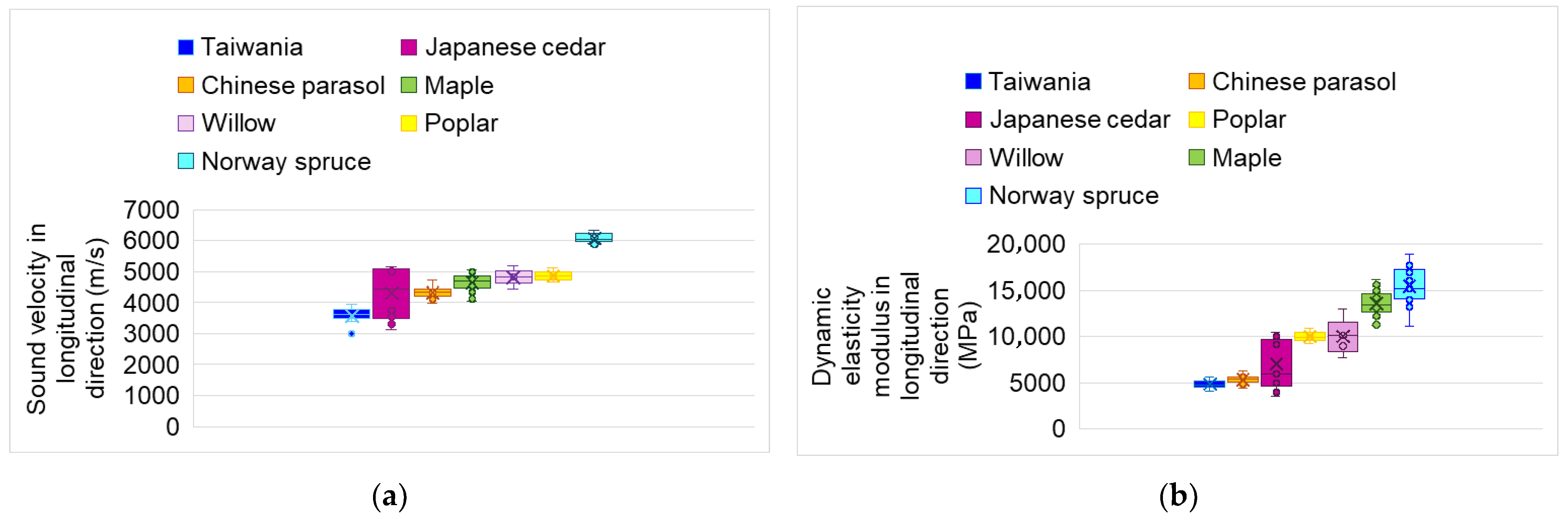
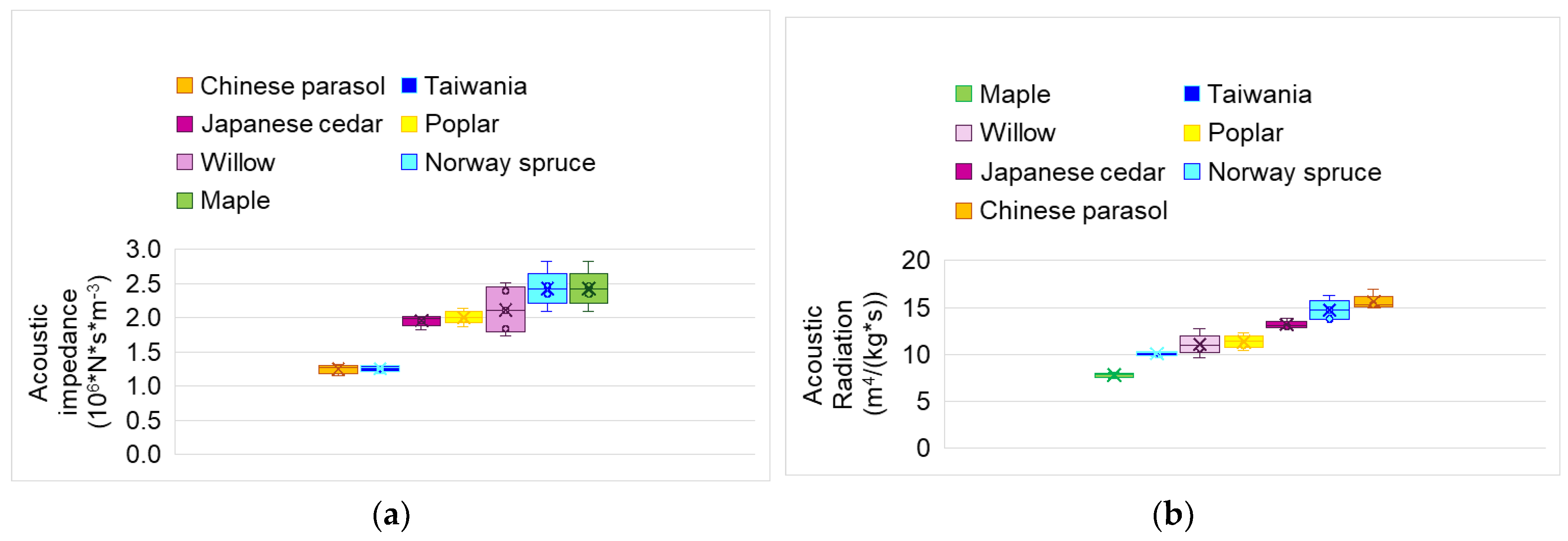
3.1. Acoustic and Elastic Parameters
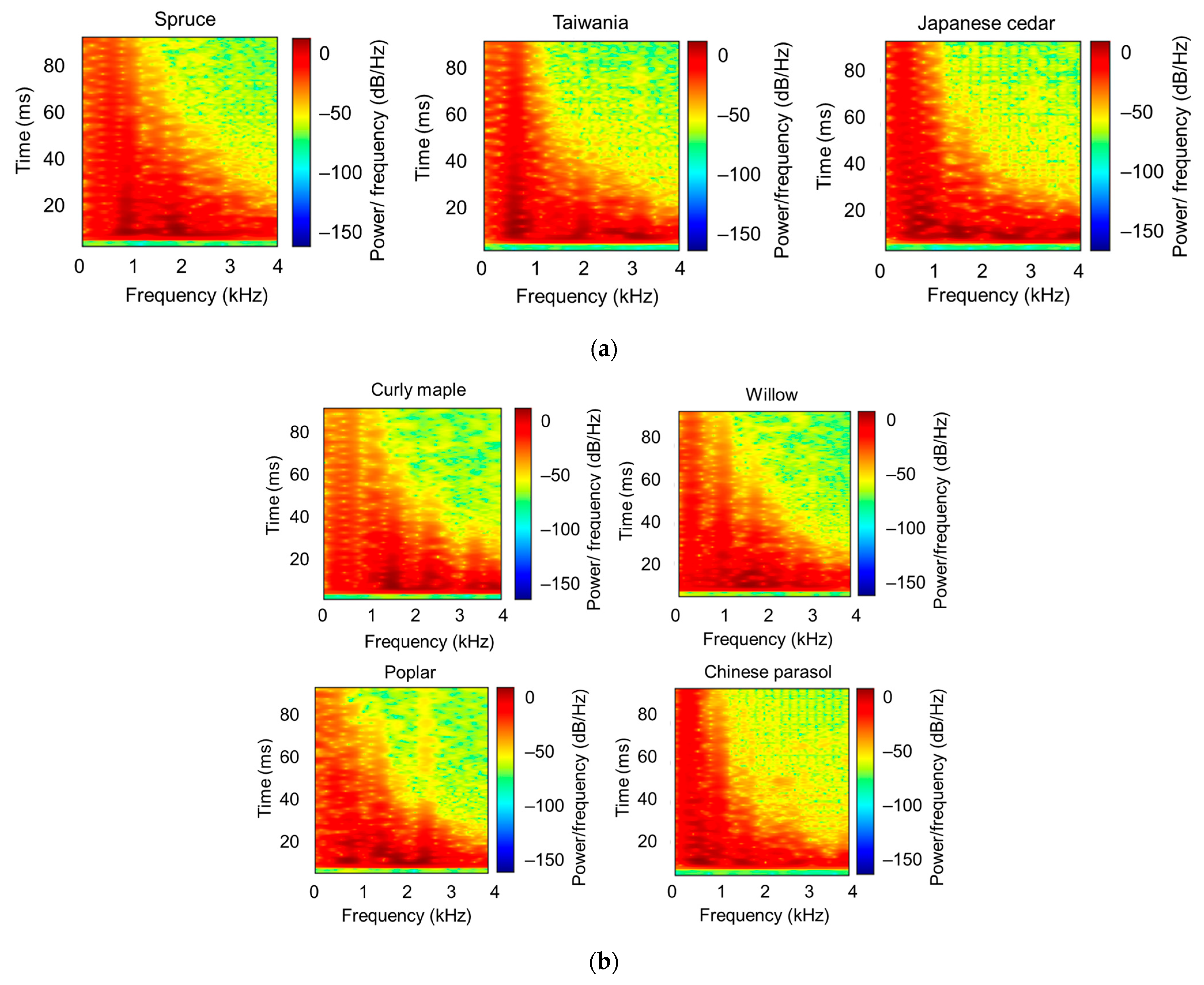
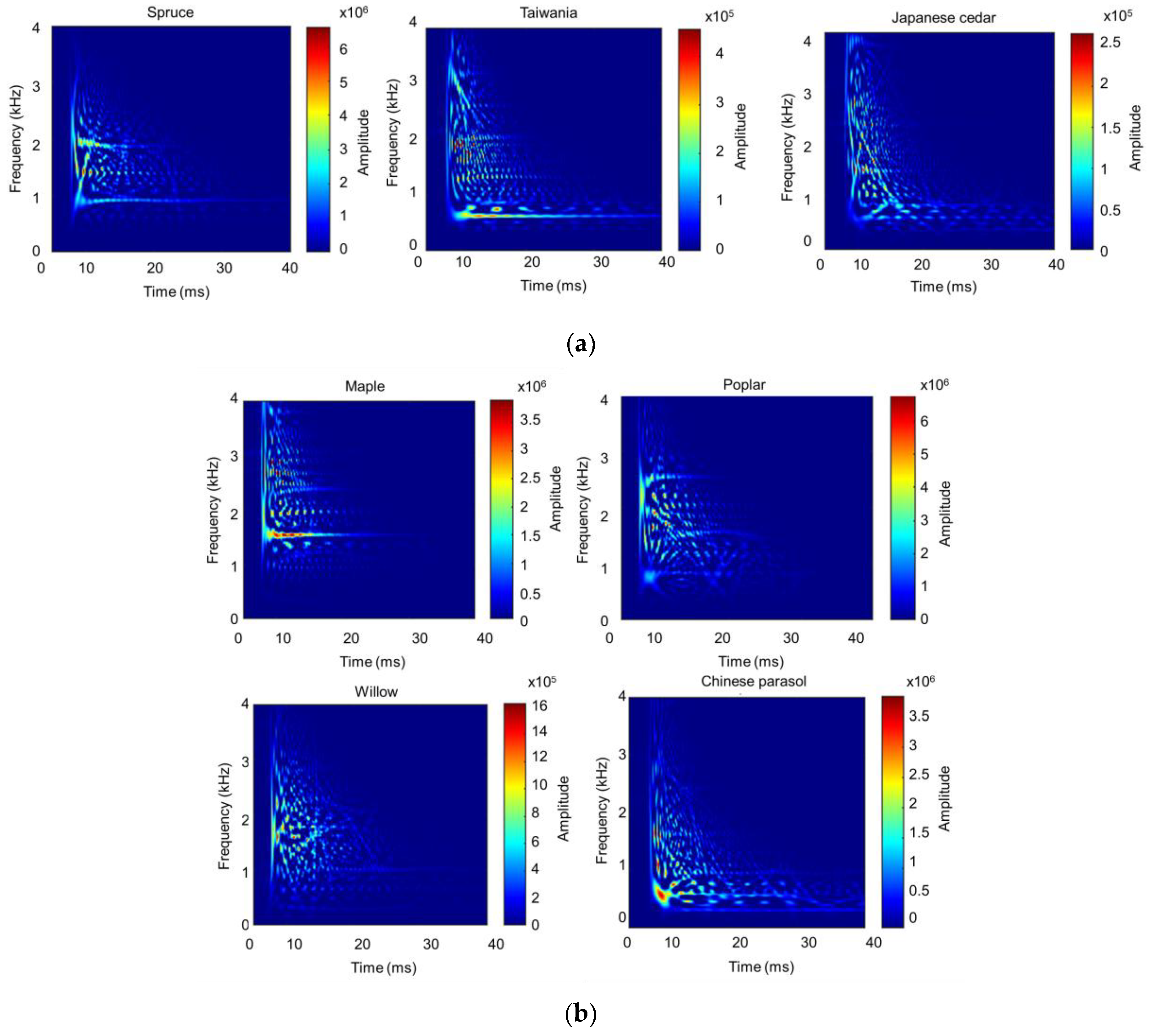
3.2. Experimental Modal Analysis
3.2.1. Spectrograms of Signals
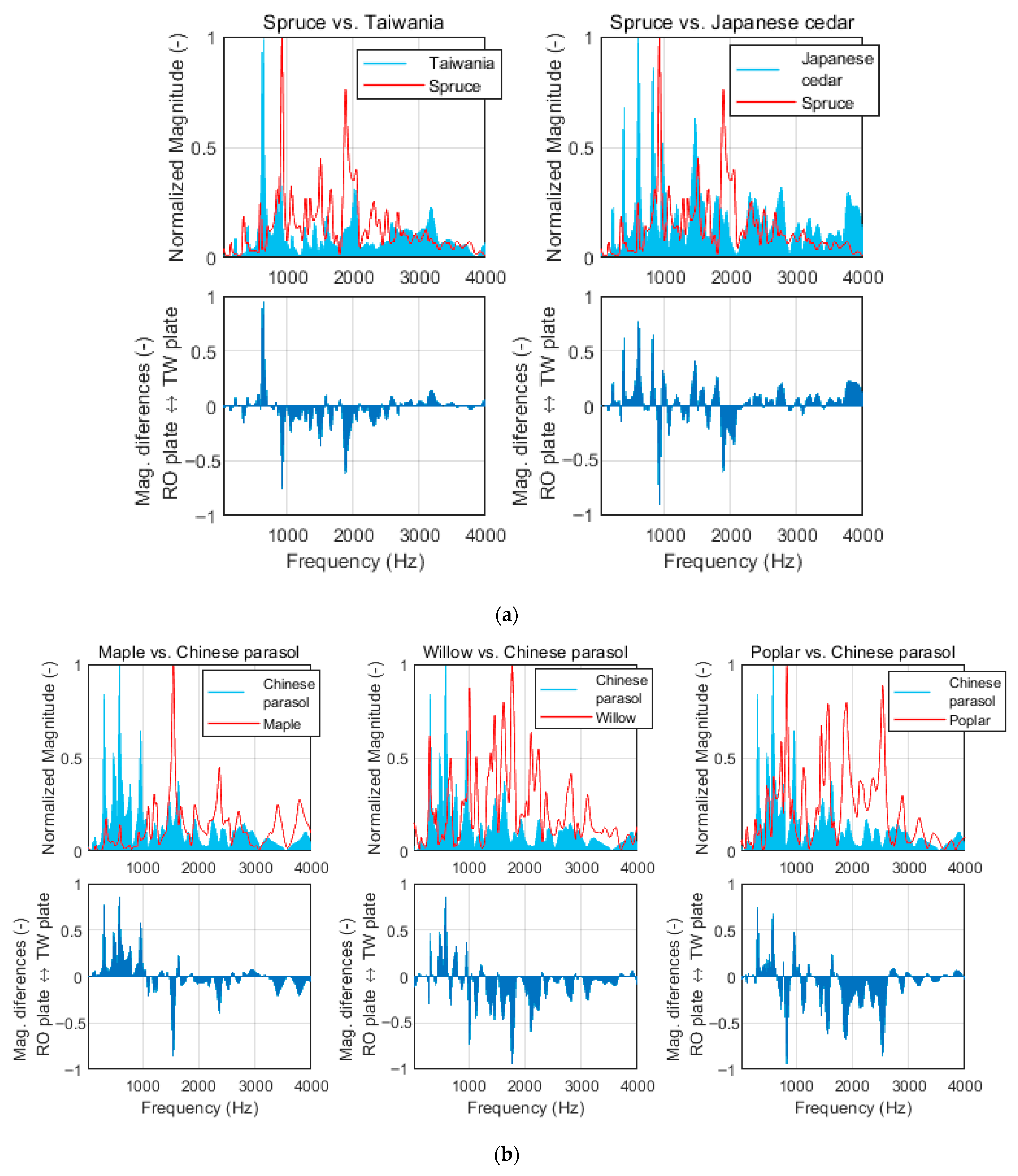
3.2.2. Comparison of Frequency Spectrum
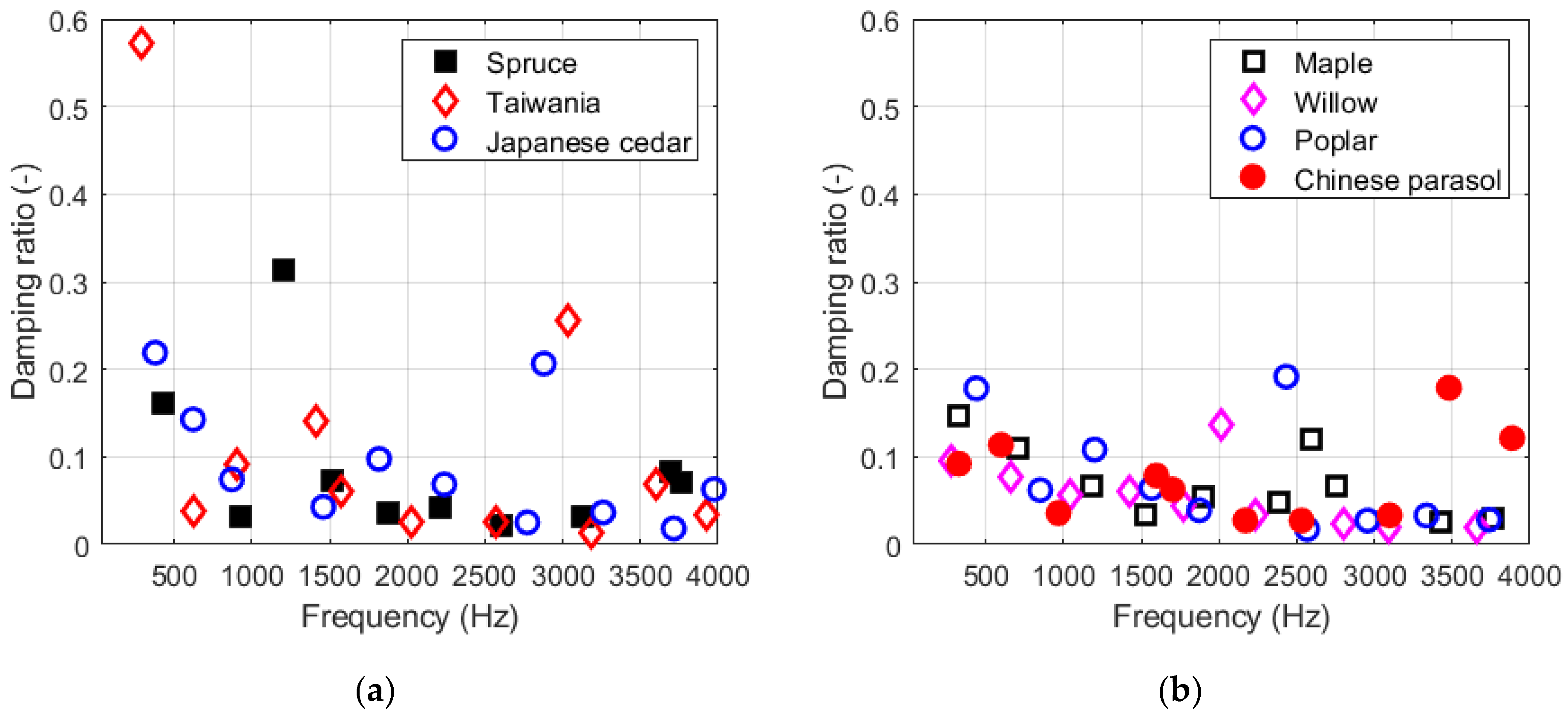
3.2.3. Damping Ratio
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schelleng, J.C. Wood for violins. Catgut Acoust. Soc. Newsl. 1982, 37, 8–19. [Google Scholar]
- Wegst, U.G.K. Wood for sound. Am. J. Bot. 2006, 93, 1439–1448. [Google Scholar] [CrossRef] [PubMed]
- Brémaud, I. Acoustical properties of wood in string instruments soundboards and tuned idiophones: Biological and cultural diversity. J. Acoust. Soc. Am. 2012, 131, 807–818. [Google Scholar] [CrossRef] [PubMed]
- Brémaud, I. What do we know on resonance wood properties? Selective review and ongoing research. In Proceedings of the Acoustics 2012 Nantes Conference, Nantes, France, 23–27 April 2012; pp. 2760–2764. [Google Scholar]
- Brezas, S.; Katsipis, M.; Orphanos, Y.; Kaselouris, E.; Kechrakos, K.; Kefaloyannis, N.; Papadaki, H.; Sarantis-Karamesinis, A.; Petrakis, S.; Theodorakis, I.; et al. An Integrated Method for the Vibroacoustic Evaluation of a Carbon Fiber Bouzouki. Appl. Sci. 2023, 13, 4585. [Google Scholar] [CrossRef]
- Brezas, S.; Katsipis, M.; Kaleris, K.; Papadaki, H.; Katerelos, D.T.G.; Papadogiannis, N.A.; Bakarezos, M.; Dimitriou, V.; Kaselouris, E. Review of Manufacturing Processes and Vibro-Acoustic Assessments of Composite and Alternative Materials for Musical Instruments. Appl. Sci. 2024, 14, 2293. [Google Scholar] [CrossRef]
- Gliga, V.G.; Stanciu, M.D.; Nastac, S.M.; Campean, M. Modal analysis of violin bodies with back plates made of different wood species. BioResources 2020, 15, 7687–7713. [Google Scholar] [CrossRef]
- Bucur, V. Acoustics of Wood, 2nd ed.; Springer: Berlin, Germany, 2006; pp. 173–196. [Google Scholar]
- Bucur, V. Chapter 3—Mechanical characterization of materials for string instruments. In Handbook of Materials for String Musical Instruments; Springer: Berlin, Germany, 2016; pp. 93–132. [Google Scholar]
- Bucur, V. Chapter 8—Ageing of musical instruments—About the old and new instruments. In Handbook of Materials for String Musical Instruments; Springer: Berlin, Germany, 2016. [Google Scholar]
- Bremaud, I.; Cabrolier, P.; Minato, K.; Gérard, J.; Thibaut, B. Vibrational properties of tropical woods with historical uses in musical instruments. In Proceedings of the International Conference of COST Action IE0601 Wood Science for the Preservation of Cultural Heritage, Braga, Portugal, 5–7 November 2008; pp. 17–23. [Google Scholar]
- Pérez-Pulido, M.; Bucur, V.; Morrow, A.; Ngo, D. Making Violins with Tasmanian Tonewood: Expect the unexpected. In Proceedings of the 20th International Congress on Acoustics, ICA 2010, Sydney, Australia, 23–27 August 2010. [Google Scholar]
- Zhang, T.; Bai, S.L.; Bardet, S.; Alméras, T.; Thibaut, B.; Beauchêne, J. Radial variations of vibrational properties of three tropical woods. J. Wood Sci. 2011, 57, 377–386. [Google Scholar] [CrossRef]
- Sproßmann, R.; Zauer, M.; Wagenführ, A. Characterization of acoustic and mechanical properties of common tropical woods used in classical guitars. Results Phys. 2017, 7, 1737–1742. [Google Scholar] [CrossRef]
- Wang, B.-T.; Su, B.-S.; Wu, Y.H. Vibroacoustic analysis for violin and discussions on sound generation mechanism. In Proceedings of the 28th International Congress on Sound and Vibration, ICSV28, Singapore, 24–28 July 2022. [Google Scholar]
- Wang, Y.; Wang, Y.; Shen, L.; Wu, Z.; Li, H.; Hu, M.; Liu, Q.; Chen, C.; Hu, X.; Zhong, Y. Evaluation of Wood Anatomical Properties from 18 Tree Species in the Subtropical Region of China. Forests 2023, 14, 2344. [Google Scholar] [CrossRef]
- Dinulică, F.; Stanciu, M.D.; Savin, A. Correlation between Anatomical Grading and Acoustic–Elastic Properties of Resonant Spruce Wood Used for Musical Instruments. Forests 2021, 12, 1122. [Google Scholar] [CrossRef]
- Dinulica, F.; Savin, A.; Stanciu, M.D. Physical and Acoustical Properties of Wavy Grain Sycamore Maple (Acer pseudoplatanus L.) Used for Musical Instruments. Forests 2023, 14, 197. [Google Scholar] [CrossRef]
- West, A.J.; Lin, C.W.; Lin, T.C.; Hilton, R.G.; Liu, S.H.; Chang, C.T.; Lin, K.C.; Galy, A.; Sparks, R.B.; Hovius, N. Mobilization and transport coarse woody debris to the oceans triggered by an extreme tropical storm. Limnol. Oceanogr. 2011, 56, 77–85. [Google Scholar] [CrossRef]
- Nguyen, K.-A.; Liou, Y.-A.; Vo, T.-H.; Cham, D.D.; Nguyen, H.S. Evaluation of urban greenspace vulnerability to typhoon in Taiwan. Urban For. Urban Green. 2021, 63, 127191. [Google Scholar] [CrossRef]
- Peereman, J.; Hogan, J.A.; Lin, T.-C. Intraseasonal interactive effects of successive typhoons characterize canopy damage of forests in Taiwan: A remote sensing-based assessment. For. Ecol. Manag. 2022, 521, 120430. [Google Scholar] [CrossRef]
- Li, C.-F.; Chytrý, M.; Zelený, D.; Chen, M.-Y.; Chen, T.-Y.; Chiou, C.-R.; Hsia, Y.-J.; Liu, H.-Y.; Yang, S.-Z.; Yeh, C.-L.; et al. Classification of Taiwan forest vegetation. Appl. Veg. Sci. 2013, 16, 698–719. [Google Scholar] [CrossRef]
- Jang, E.S.; Kang, C.W. Investigation of the pore structure and sound-absorbing capability of the Chinese parasol tree (Firmiana simplex (L.) W.Wight) and Chinese tulip poplar (Liriodendron chinense) transverse sections as eco-friendly, porous, sound-absorbing materials. J. Porous Mater. 2022, 29, 1791–1796. [Google Scholar] [CrossRef]
- Buksnowitz, C.; Teischinger, A.; Müller, U.; Pahler, A.; Evans, R. Resonance wood [Picea abies (L.) Karst.]—Evaluation and prediction of violin makers’ quality-grading. J. Acoust. Soc. Am. 2007, 121, 2384–2395. [Google Scholar] [CrossRef]
- Hwang, S.K. The Anatomy of Some Important Taiwan Woods. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 1962. Available online: https://open.library.ubc.ca/soa/cIRcle/collections/ubctheses/831/items/1.0105871 (accessed on 31 October 2025).
- Gurău, L.; Timar, M.C.; Coșereanu, C.; Cosnita, M.; Stanciu, M.D. Aging of Wood for Musical Instruments: Analysis of Changes in Color, Surface Morphology, Chemical, and Physical-Acoustical Properties during UV and Thermal Exposure. Polymers 2023, 15, 1794. [Google Scholar] [CrossRef]
- Sotomayor Castellanos, J.R.; Guridi Gomez, L.I.; Garcia Moreno, T. Características acústicas de la madera de 152 especies mexicanas. Velocidad del ultrasonido, módulo de elasticidad, índice material y factor de calidad. Base de datos. Investig. Ing. Madera 2010, 6, 3–32. [Google Scholar]
- Stanciu, M.D.; Chen, C.W.; Wang, Y.W.; Zheng, G.T.; Lin, Y.K.; Way, L.; Gall, R.; Salca, E.A. Analysis of the physical and acoustic properties of tropical wood species from Taiwan for stringed musical instruments. In Proceedings of the 18th Edition of the Interdisciplinarity in Engineering—INTER-ENG 2024, Târgu Mureș, Romania, 3–4 October 2024. [Google Scholar]
- Nastac, S.M.; Way, K.; Stanciu, M.D.; Guiman, M.V.; Chen, C.-W.; Wang, Y.-W.; Zheng, G.-T.; Lin, Y.-K. Comparative Analyses of Violin Back Plate Modal Responses between Tropical and Romanian Tone Woods. In Proceedings of the 16th International Conference on Vibration Problems (ICOVP-2025) & 11th International Conference on Wave Mechanics and Vibrations (WMVC-2025), Lisbon, Portugal, 2–5 September 2025. [Google Scholar]
- Casazza, M.; Barone, F.; Bonisoli, E.; Dimauro, E.; Venturini, S.; Masoero, C.M.; Shtrepi, L. A procedure for the characterization of a music instrument vibro-acoustic fingerprint: The case of a contemporary violin. Acta IMEKO 2023, 12, 1–6. [Google Scholar] [CrossRef]
- Sedik, Y.; Hamdan, S.; Jusoh, I.; Hasan, M. Acoustic Properties of Selected Tropical Wood Species. J. Nondestruct. Eval. 2010, 29, 38–42. [Google Scholar] [CrossRef]
- Lewandowski, M.; Foltynowicz, Z. Selected aspects of resonance properties of different woods and the construction of string instruments. Drewno 2022, 65, 21. [Google Scholar] [CrossRef]
- Wang, S.Y.; Lin, C.J.; Chiu, C.M.; Chen, J.H.; Yung, T.H. Dynamic modulus of elasticity and bending properties of young Taiwania trees grown with different thinning and pruning treatments. J. Wood Sci. 2005, 51, 1–6. [Google Scholar] [CrossRef]
- Okon, K.E.; Ndulue, N. Thermal modification of fast-growing Firmiana simplex wood using tin alloy: Evaluation of physical and mechanical properties. Maderas. Cienc. Tecnol. 2024, 27, e0325. [Google Scholar] [CrossRef]
- Brémaud, I.; El Kaïm, Y.; Giubal, D.; Minato, K.; Thibaut, B.; Gril, J. Characterisation and categorisation of the diversity in viscoelastic vibrational properties between 98 wood types. Annu. For. Sci. 2012, 69, 373–386. [Google Scholar] [CrossRef]
- Beldeanu, E.C. Produse Forestiere și Studiul Lemnului; Editura Universității Transilvania din Brașov: Brașov, Romania, 1999; pp. 324–340. [Google Scholar]
- Barlow, C.Y. Materials selection for musical instruments. Proc. Inst. Acoust. 1997, 19, 69–78. [Google Scholar]
- Liu, M.; Lyu, S.; Peng, L.; Fan, Z.; Cai, L.; Huang, Z.; Lyu, J. Study on properties of radiata pine wood treated with furfuryl alcohol as fretboard materials for string instruments. Eur. J. Wood Prod. 2022, 80, 1185–1200. [Google Scholar] [CrossRef]
- Holz von, D.; Schmidt, J. Untersuchungenan Resonanzholz. 3: Über die gleichzeitige Bestimmung des dynamischen Elastizitätsmodulus und der Dümpfungan Holzstäbenimhörbaren Frequenzbereich. Holztechnologie 1968, 9, 225–229. [Google Scholar]
- Macareva, T.A. The influence of various factors on the radiation ratio of resonance wood. Деревooбрабатывающая прoмышленнoсть 1968, 10, 14–15. (In Russian) [Google Scholar]
- Ghelmeziu, N.; Beldie, I.P. Despre caracteristicile lemnului de rezonanță de molid. Bull. Univ. Transilv. 1970, 12, 315–326. [Google Scholar]
- Beretos, J.; Santamaria, C.; Moral, J.A. Vibrational Patterns and Frequency Responses of the Free Plates and Box of a Violin Obtained by Finite Element Analysis. J. Acoust. Soc. Am. 1999, 105, 1942–1950. [Google Scholar] [CrossRef]
- Ono, T.; Morimoto, M. Anisotropy of Dynamic Young’s Modulus and Internal Friction in Wood. Jpn. J. Appl. Phys. 1985, 24, 960–964. [Google Scholar] [CrossRef]
- Haines, D.W. On musical instruments wood. Catgut Acoust. Soc. Newsl. 1979, 31, 23–32. [Google Scholar]
- Spycher, M.; Schwarze, F.W.M.R.; Steiger, R. Assessment of resonance wood quality by comparing its physical and histological properties. Wood Sci. Technol. 2008, 42, 325–342. [Google Scholar] [CrossRef]
| The Main Groups of Samples | Wood Species | Moisture Content MC (%) | Density (g/cm3) |
|---|---|---|---|
| Group 1 Coniferous species | Norway spruce | 7.0 | 0.430 |
| (Picea abies) | (0.90) | (0.045) | |
| Taiwania | 6.2 | 0.357 | |
| (Taiwania cryptomerioides Hayata) | (0.8) | (0.030) | |
| Japanese cedar | 6.5 | 0.392 | |
| (Cryptomeria japonica) | (0.7) | (0.020) | |
| Group 2 Deciduous species | Maple | 7.5 | 0.640 |
| (Acer pseudoplatanus) | (0.90) | (0.043) | |
| Poplar | 7.6 | 0.420 | |
| (Populus nigra) | (0.7) | (0.027) | |
| Willow | 7.3 | 0.450 | |
| (Salix alba) | (1.05) | (0.044) | |
| Chinese parasol | 6.8 | 0.279 | |
| (Firmiana simplex L.) | (0.7) | (0.020) |
| Wood Species | Weight (g) | Resonance Frequency (Hz) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Norway spruce | 92 | 848 | 922 * | 1062 | 1282 | 1349 | 1508 | 1660 | 1886 | 2045 | 2307 |
| Taiwania | 95 | 403 | 635 * | 836 | 903 | 1270 | 1416 | 1593 | 2026 | 2588 | 3180 |
| Japanese cedar | 97 | 385 | 604 * | 824 | 970 | 1459 | 1794 | 2289 | 2368 | 2765 | 3778 |
| Maple | 129 | 1105 | 1208 | 1245 | 1550 * | 1685 | 1929 | 2368 | 2710 | 3406 | 3790 |
| Poplar | 125 | 604 | 739 | 842 * | 1135 | 1453 | 1569 | 1898 | 2142 | 2368 | 2539 |
| Willow | 83 | 311 | 677 | 1019 | 1135 | 1392 | 1465 | 1624 | 1770 * | 2112 | 2246 |
| Chinese parasol | 76 | 323 | 360 | 488 | 525 | 592 * | 781 | 964 | 1477 | 1636 | 1929 |
| Wood Species | Damping Ratio, ζ, for Dominant Frequency | Quality Factor Q (1/2 ζ) | Resonance Response Time (sec.) |
|---|---|---|---|
| Norway spruce | 0.0176 | 28 | 0.0309 |
| Taiwania | 0.0239 | 21 | 0.0330 |
| Japanese cedar | 0.0252 | 20 | 0.0329 |
| Maple | 0.0145 | 34 | 0.0222 |
| Willow | 0.0164 | 30 | 0.0172 |
| Poplar | 0.0218 | 23 | 0.0272 |
| Chinese parasol | 0.0264 | 19 | 0.0320 |
| Acoustic and Dynamic Properties | Norway Spruce | Taiwania | Japanese Cedar | Maple | Willow | Poplar | Chinese Parasol |
|---|---|---|---|---|---|---|---|
| Density (kg/m3) | 430 (45) | 357 (30) | 392 (20) | 640 (43) | 450 (44) | 420 (27) | 280 (20) |
| Sound velocity (m/s) | 5875 (423) | 3573 (282) | 4310 (825) | 4653 (247) | 4820 (268) | 4872 (166) | 4325 (182) |
| DMOE (MPa) | 14,500 (2500) | 4834 (461) | 9724 (488) | 13,570 (1500) | 9997 (1965) | 9994 (617) | 5336 (463) |
| Acoustic radiation (m4 kg−1 s−1) | 15.22 (1.007) | 10.088 (0.254) | 13.167 (0.400) | 7.790 (0.259) | 11.082 (1.112) | 11.339 (0.695) | 15.585 (0.801) |
| Acoustic impedance (×106 N s m−3) | 2.43 (0.268) | 1.26 (0.048) | 1.96 (0.081) | 3.06 (0.133) | 2.12 (0.335) | 2.01 (0.094) | 1.25 (0.068) |
| Dominant frequency (Hz) | 922 | 635 | 604 | 1550 | 842 | 1770 | 592 |
| Quality factor Q | 28 | 21 | 20 | 34 | 30 | 23 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanciu, M.D.; Nastac, S.M.; Chen, C.-W.; Long, W. Exploring the Dynamic Properties of Tropical and Temperate Wood Species for Musical Instruments. Appl. Sci. 2025, 15, 11926. https://doi.org/10.3390/app152211926
Stanciu MD, Nastac SM, Chen C-W, Long W. Exploring the Dynamic Properties of Tropical and Temperate Wood Species for Musical Instruments. Applied Sciences. 2025; 15(22):11926. https://doi.org/10.3390/app152211926
Chicago/Turabian StyleStanciu, Mariana Domnica, Silviu Marian Nastac, Chi-Wen Chen, and Way Long. 2025. "Exploring the Dynamic Properties of Tropical and Temperate Wood Species for Musical Instruments" Applied Sciences 15, no. 22: 11926. https://doi.org/10.3390/app152211926
APA StyleStanciu, M. D., Nastac, S. M., Chen, C.-W., & Long, W. (2025). Exploring the Dynamic Properties of Tropical and Temperate Wood Species for Musical Instruments. Applied Sciences, 15(22), 11926. https://doi.org/10.3390/app152211926








