Enhanced Single-Objective Optimization Algorithm with Progressive Exploration Strategy for RF Accelerating Structure Optimization

Abstract

In many engineering applications, multi-objective optimization problems can be reformulated as single-objective problems with multiple constraints to improve computational efficiency. This paper discusses the characteristics and challenges of RF accelerating structure optimizations and proposes an enhanced single-objective optimization strategy based on progressive exploration method to find the global optimal solution within a large solution space characterized by a continuous and confined distribution of feasible solutions. It begins from an arbitrary feasible solution and progressively slides and expands the solution space fragment along the distribution path of feasible solutions to rapidly explore the entire space. By incorporating a re-initialization mechanism to enhance swarm diversity and introducing penalty factors in place of constraints to increase the number of feasible solutions, the algorithm significantly improves its ability to escape local optima traps. The proposed algorithm is applied to optimize a DAA structure, yielding satisfactory results and convergence speed. These results highlight the method’s effectiveness and its potential applicability to other complex constrained optimization problems.

1. Introduction

For complex, high-dimensional, and nonlinear optimization problems, it may be challenging to find the optimal solution using traditional optimization algorithms. In contrast, meta-heuristic algorithms do not rely on the specific structure or characteristics of the problem. Instead, they iteratively explore the solution space by simulating natural systems or other phenomena from real life to search for the optimal solution. These algorithms have proven highly effective in addressing such complex problems and have been widely utilized across diverse domains including engineering, science, business and so on. Within the paradigm of meta-heuristics, numerous Swarm Intelligence (SI) techniques and their variants have been proposed, including Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Differential Evolution (DE) and others. While they cannot guarantee always finding the global optimum, they provide efficient approximate optimal solutions in scenarios where exact solutions are difficult to obtain [1,2,3].

The RF (Radio Frequency) accelerating structures are crucial components in particle accelerators used to accelerate charged particles to high energies. When RF power is applied, they generate the RF electromagnetic field. The optimization challenge inherent to RF accelerating structures entails seeking the optimal solution within a high-dimensional parameter space, given the involvement of numerous geometric parameters, material properties, and other factors. Such optimization problems frequently demonstrate pronounced nonlinearity and multimodality, implying the presence of numerous local optimal solutions. Traditional optimization algorithms frequently encounter difficulties in effectively addressing this complexity. In practice, the optimization of RF accelerating structures typically involves a blend of theoretical analysis and practical experimentation. This involves the repetitive tuning of specific parameters while keeping others constant. However, structures derived through this approach often represent local optima rather than global optima, despite their satisfactory performance. Moreover, this methodology demands a considerable investment of time and effort from researchers. To enhance optimization efficiency, various swarm intelligence (SI) algorithms have been applied to both single-objective (SOO) and multi-objective optimization (MOO) designs of RF accelerating structures, achieving promising results [4,5,6,7,8,9,10]. Nevertheless, when dealing with complex real-world engineering problems such as RF accelerating structure optimization, mechanical fabrication and other technical limitations often impose highly restrictive constraints, which significantly narrow the feasible solution space and make it extremely challenging to identify optimal designs [11,12,13]. Consequently, a critical research question arises: under stringent multi-constraint conditions, how can swarm intelligence algorithms generate a sufficient number of feasible solutions, avoid premature convergence, and more effectively explore the solution space? Addressing this issue holds important practical significance.

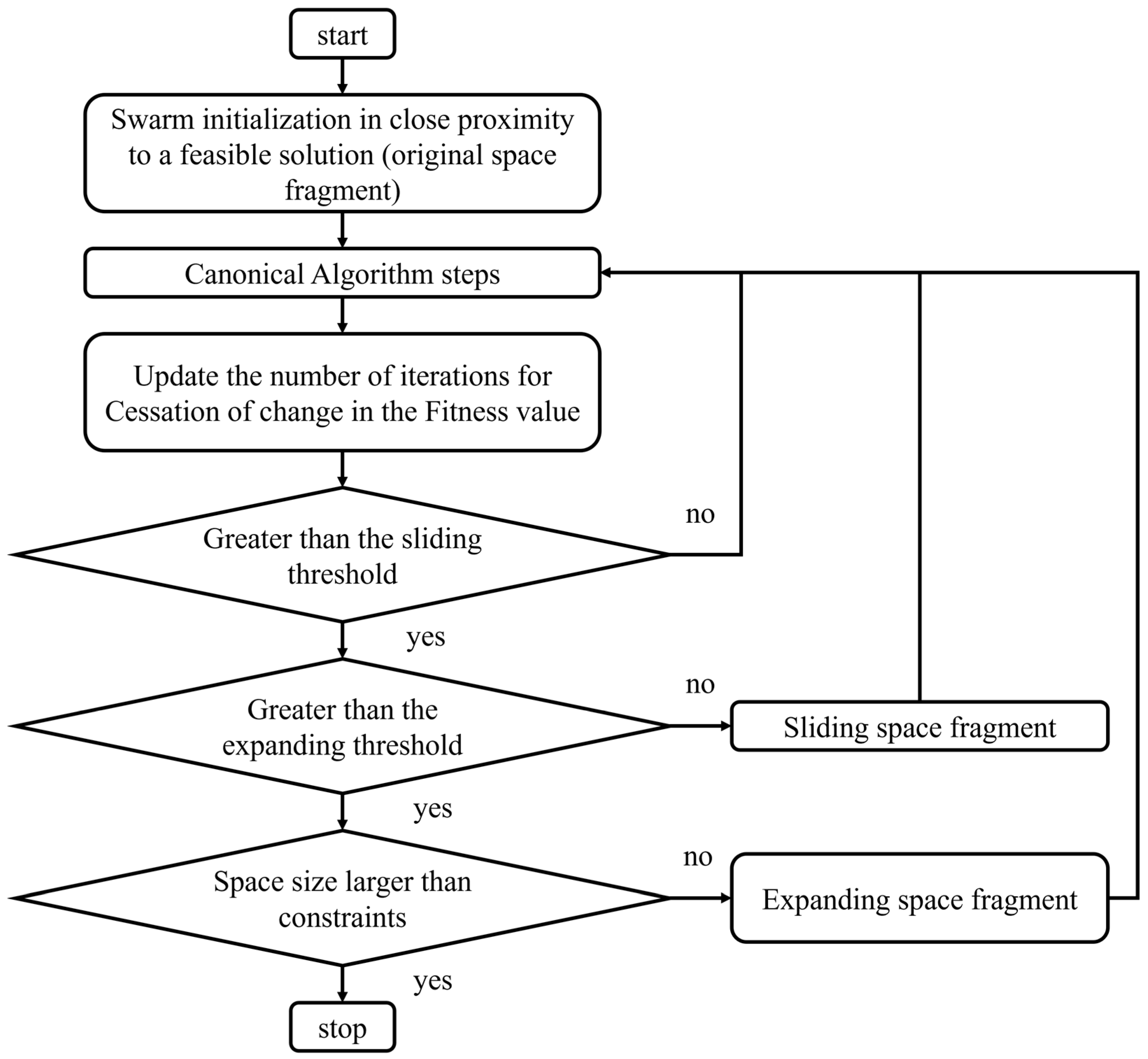
This paper uses the normal-conducting Dielectric Assist Accelerating (DAA) structure as a case study and proposes an improved single-objective optimization strategy based on a progressive exploration method to address the challenges of RF accelerating structures optimization. This strategy demonstrates strong compatibility and has been integrated with various single-objective optimization algorithms, including classical methods such as PSO, GA, and DE, as well as well-known enhanced algorithms such as CSO (Competitive Swarm Optimizer) and JADE (Adaptive Differential Evolution with Optional External Archive). The software was developed in Python 3.9.13, utilizing the NumPy 1.26.4 and Pandas 1.5.0 libraries for data processing and analysis, and Matplotlib 3.8.2 for generating visualizations. It has been applied to the optimization of the DAA structure, achieving consistently promising results. Among various optimization algorithms, this method effectively mitigates premature convergence caused by an excessive number of infeasible solutions due to multiple stringent constraints and enables rapid, progressive exploration of the solution space from a known feasible solution. The approach also demonstrates a degree of generality and can be extended to other single-objective or multi-objective optimization problems with similar multi-constraint characteristics.

This paper is organized as follows: Section 2 introduces the optimization objectives and constraints involved in the design of RF acceleration structures. It also discusses the reasons for adopting the single-objective optimization algorithm for DAA structure along with the challenges that lurk in this approach. Section 3 introduces the progressive exploration strategy with the penalty factor to increase the number of feasible solutions. In Section 4, we analyze the experimental results and the performance of the algorithm. Finally, Section 5 concludes this work.

2. Optimization of RF Accelerating Structure

Recent advances in RF accelerating structure optimization increasingly employ computational and intelligent algorithms to enhance performance metrics such as shunt impedance and quality factor while satisfying constraints on surface fields and operating frequency. Genetic algorithms have proven effective for single-objective optimization, enabling systematic exploration of geometrical parameters to improve shunt impedance. Multi-objective optimization algorithm, combined with Pareto front visualization, facilitate the simultaneous optimization of competing objectives, such as maximizing shunt impedance while minimizing peak surface fields, thereby providing designers with clear insights into trade-offs. More recent developments integrate neural networks as surrogate models with multi-objective algorithms, significantly reducing computational costs and enabling dynamic, high-dimensional exploration of complex design spaces. Overall, the trend in RF structure optimization is toward automated, multi-objective, and machine-learning-enhanced frameworks that deliver efficient, flexible, and performance-optimized designs. However, in practical engineering applications, under conditions where multiple constraints lead to a scarcity of feasible solutions, the ability to rapidly explore high-dimensional solution spaces and identify the global optimum is even more critical.

2.1. Objectives

In the optimization design of RF accelerating structures, several crucial objectives must be meticulously tuned.

One of the objectives is the shunt impedance, which is given by the following formula:

$${\mathrm{R}}_{sh}={\displaystyle \frac{{\left|V_{\mathrm{acc}}\right|}^2}{2P_{loss}}},$$

(1)

where ${\mathrm{R}}_{sh}$ (Ω) is the shunt impedance, $V_{acc}$ (V) is the accelerating voltage, and $P_{loss}$ (W) is the power loss. The shunt impedance reflects the efficiency that the power supply transfer energy to the charged particles. Maximizing the shunt impedance can achieve the maximum acceleration of particles for a given available power.

The accelerating voltage is defined as the follows:

$$V_{acc}={\int }_0^{\mathrm{L}}{E}_z{e}^{-j{\displaystyle \frac{\mathsf{\omega }\mathrm{Z}}{\mathsf{\beta }\mathrm{c}}}}\mathrm{d}\mathrm{z},$$

(2)

where $E_z$ (V/m) is the electric field component in the longitudinal direction, $\mathsf{\omega }$ (rad/s) is the angular frequency of the electromagnetic wave, $\mathsf{\beta }\mathrm{c}$ (m/s) is the speed of particle and L is the length of the accelerating gap. The power loss $P_{loss}$ (W) is the result of Ohmic heating, arising from the interaction between the tangential magnetic field and the surface resistance of the metallic walls. It is defined as follows:

$${\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\displaystyle \frac{1}{2}}{∯}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}{\mathrm{R}}_{\mathrm{s}}{\left|{\mathrm{H}}_{\mathrm{t}}\right|}^2\mathrm{dA},$$

(3)

where $R_S$ (Ω) represents the surface resistance, and $H_t$ (A/m) represents the tangential component of the magnetic field strength.

Another objective is the quality factor Q_0 (dimensionless), which is defined as the ratio of the energy stored in the structure to the energy dissipated per radian. It is given by the following:

$$Q_0={\displaystyle \frac{{\mathsf{\omega }}_{0}W}{P_{loss}}},$$

(4)

where ${\mathsf{\omega }}_0$ (rad/s) the resonant frequency, and $\mathrm{W}$ (J) is the stored energy. Maximizing cavity Q means minimizing the power required from the power supply to maintain the same stored energy.

The third crucial optimization objective is R/Q (Ω), which is given as follows:

$${\displaystyle \frac{R}{Q}}={\displaystyle \frac{{\left|V_{\mathrm{acc}}\right|}^2}{2{\mathsf{\omega }}_{0}W}},$$

(5)

Higher R/Q ratio reflects the higher efficiency of energy transfer to the charged particles from the stored energy in the RF accelerating structure.

Ideally, achieving the three primary optimization objectives of RF accelerating structures (shunt impedance $R_{sh}$, quality factor $Q_0$ and $\mathrm{R}/\mathrm{Q}$) simultaneously would be desirable. However, this is typically infeasible, as the optimization of one objective often compromises another. In practical engineering applications, it is more pragmatic to focus on optimizing a single objective, contingent upon the other two meeting the necessary requirements, tailored to the specific application scenario and cavity type. Due to the extremely low surface impedance in the superconducting state, the power loss of the metal wall is no longer the performance bottleneck of the accelerating structure. Typically, the aim is to maximize the quality factor $Q_0$ while ensuring the peak electric field on the surface remains below a predefined threshold to avert instances of field emission and breakdown. Conversely, in normal conducting accelerating structures, characterized by relatively high surface resistance leading to noticeable energy dissipation, the predominant optimization objective is to maximize the shunt impedance. This type of optimization seeks to enhance the efficiency of energy transfer per unit consumption and achieve the highest possible acceleration gradient. In normal conducting accelerating structures, the peak surface electric field is typically not a focal point, as it always meets the design specifications in almost any situation. Finally, for certain small-scale accelerators like medical radiation therapy devices, there is often a focus on maximizing R/Q. This optimization leads to more efficient energy transfer from the accelerating structure to charged particles, thereby enhancing the cost-effectiveness of the system.

2.2. Constraints

In the optimization of RF accelerating structures, some constraints must be meticulously considered. These constraints confine the solution space within specific boundaries and significantly impact the final design.

Ideally, the operating mode frequency of an RF cavity must exactly match the design frequency. This alignment is fundamental because the cavity’s interaction with charged particles relies on the intended frequency. However, achieving perfect coincidence between them is challenging in practical applications due to potential errors in design, manufacturing, and environmental variations such as temperature. Typically, frequency adjustments are made using mechanical methods, but the range of adjustment is often limited. Therefore, during the design phase, it is essential to constrain the frequency within a specific range around the ideal design frequency.

Several other important RF properties must be considered, such as the peak electric field on the surface and the frequency of higher-order modes (HOMs). Exceeding certain thresholds of the peak electric field on the surface can lead to undesirable effects such as field emission and breakdown. For RF accelerating structures operating in the fundamental mode, maintaining a sufficient frequency separation between HOM and the fundamental mode is crucial to ensure that HOM can be effectively suppressed using HOM dampers, minimizing the impact of non-operational modes on the beam. This constraint is also significant for structures operating in non-fundamental modes, where the influence of neighboring modes must be carefully managed.

In addition to considering radio frequency characteristics, we must address mechanical constraints. The dimensions of RF accelerating structures and internal components are influenced by factors like available space within accelerator facilities and beam aperture design specifications. Moreover, it is crucial to anticipate increased detuning from Lorentz forces, especially when optimizing RF structures for pulsed beams, because these optimization processes may inadvertently compromise mechanical integrity. This implies that the geometric parameters cannot be arbitrarily optimized for the best RF performance. Furthermore, due to manufacturing tolerances, pursuing excessively precise solutions is impractical. Therefore, it is essential to establish limits on achievable precision.

2.3. Optimizing DAA Structure

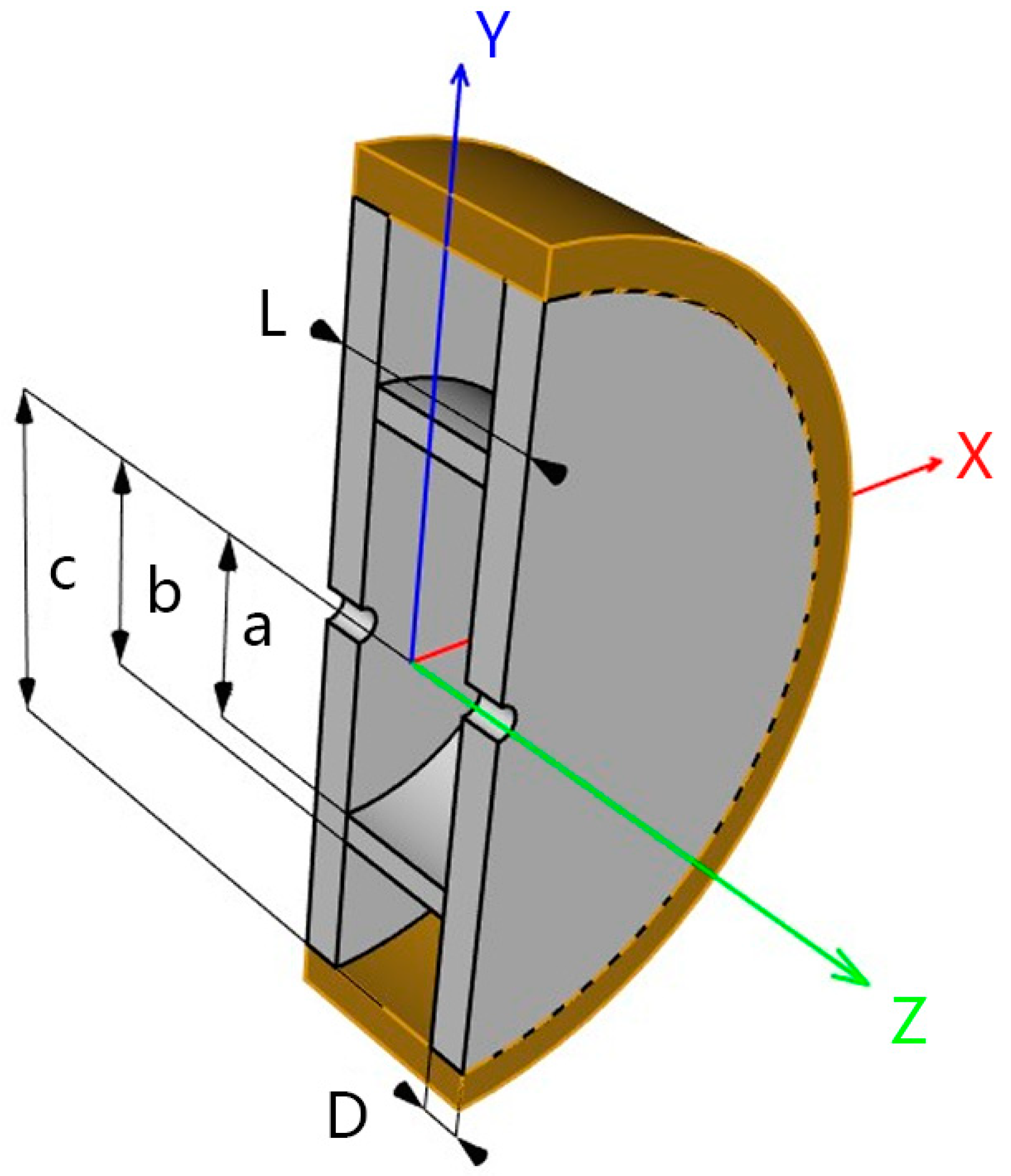
DAA structure is a novel normal conducting dielectric loaded RF accelerating structure. It is a TM₀₂₀ mode standing wave accelerating structure with ultralow-loss dielectric material for electromagnetic field distribution control. The longitudinal cross-section of the DAA acceleration cell, depicted in Figure 1, features a constant length, denoted as L, equivalent to half the wavelength. In the design of DAA structures, the primary objective is typically to maximize the shunt impedance while ensuring that R/Q remains above a specified threshold. Consequently, R/Q can also be treated as a constraint, defining the optimization of the DAA structure as a single-objective problem with multiple constraints [14,15]. Furthermore, another ancillary objective that is the frequency separation between the operating mode and adjacent modes has been overlooked. This objective is chiefly governed by the aperture radius, exhibiting minimal susceptibility to alterations in other geometric parameters. And the aperture radius determined by accelerator physics design maintains a constant value throughout the optimization process.

Therefore, when the material properties are identical, the geometric variables a, b, c, and D define the configuration of the DAA acceleration cell and have a significant impact on its performance.

The PSO, DE and the GA algorithm are the most popular swarm intelligence algorithms. For the RF accelerating structure optimization problem, the distribution of feasible solutions is continuous within the constraint range. Due to the inherent continuity of the PSO and DE algorithm, they are very suitable for solving this type of optimization problem, as particles move continuously according to certain laws. While many studies have reported successful applications of the GA algorithm in such optimization problems, the GA algorithm explores the solution space discretely rather than continuously [16,17,18,19].

The progressive exploration strategy was applied respectively to three improved single-objective swarm intelligence algorithms: PSO, DE, and GA, for the optimization of the DAA structure.

3. Progressive Exploration Strategy for Optimization Algorithm

Swarm intelligence algorithms guide stochastic exploration of the solution space by maintaining a population to find the global optimum with the maximum or minimum fitness value. Despite variations among specific algorithms (e.g., PSO, GA, DE), their general procedure can be summarized as follows:

• Generate an initial population of agents (Swarm) and assign random vectors in solution space, where each agent represents a candidate solution.
• Compute the fitness (objective value) of each agent, and record the best solution.
• Update the population according algorithm rules.
• Repeat step 2 until a converged optimal solution is obtained or a predefined number of iterations is reached.

3.1. Fitness Function for DAA Structure Optimization

The solution vector of the DAA structure is defined as $\mathbf{x}=\left(D,{\displaystyle \frac{\mathrm{a}}{\mathsf{\lambda }}},{\displaystyle \frac{\mathrm{c}}{\mathsf{\lambda }}},\mathrm{b}-\mathrm{a}\right)$, where a, b, c, D represent the geometric parameters as illustrated in Figure 1, and the $\mathsf{\lambda }$ denotes the wavelength. Taking into account some mechanical and physical design limitations, the entire solution space should be limited to a certain size. Based on these variable parameters and other constants, the model is established using commercial electromagnetic numerical simulation software. Its performance is evaluated, including mode frequency, shunt impedance, quality factor, and R/Q.

The DAA structure optimization problem is a maximization problem with constraints aimed at maximizing the shunt impedance. Its fitness function is depicted as the follows:

$${\mathcal{F}}_{fitness}=\left\{\begin{array}{c}{R}_{sh}={\mathcal{F}}_{sh}(x), R/Q\ge {R/\mathrm{Q}}_{min}, \left|f-f_{ideal}\right|\le {\displaystyle \frac{{\Delta f}_{tune}}{2}}\\ {\displaystyle \frac{R_{sh}·{\Delta f}_{tune}}{2·\left|f-f_{ideal}\right|}}=\delta ·R_{sh}, R/Q\ge {R/\mathrm{Q}}_{min}, \left|f-f_{ideal}\right|>{\displaystyle \frac{{\Delta f}_{tune}}{2}}\\ 0, R/Q<{R/\mathrm{Q}}_{min}\end{array}\right.,$$

(6)

Because the values of the shunt impedances are much greater than 0, it is reasonable to set the fitness value of infeasible solution to 0. All solutions with R/Q lower than the design value are treated as infeasible solutions. Additionally, imposing constraints on R/Q allows for the elimination of non-TM₀₂₀ modes. The $f_{ideal}$ is the ideal design operation frequency, and the ${\mathsf{\Delta }f}_{tune}$ is the frequency range that can be tuned. From a practical engineering perspective, if the calculated frequency exceeds the tunable range, the solution should be classified as an infeasible solution. However, this would result in a sharp decrease in the number of feasible solutions, thus causing the PSO algorithm to fail to function properly. Therefore, the penalty factor $\delta$ is introduced to penalize the fitness value by adding a term proportional to the degree of frequency constraint violation, where $0<\delta <1$. If the deviation between the optimized mode frequency and the ideal frequency falls within the tunable range, it is considered acceptable and feasible in engineering practice, and, therefore, no penalty is applied. However, if the deviation exceeds the tunable range, a penalty is imposed, and the farther the deviation is beyond this range, the larger the penalty applied. The penalty factor $\delta$ is depicted as follows:

$$\delta =\left\{\begin{array}{r}1, if \left|f-f_{ideal}\right|\le {\Delta f}_{tune}\\ 1-{\displaystyle \frac{\left|f-f_{ideal}\right|-{\Delta f}_{tune}}{{\Delta f}_{tune}}}, if \left|f-f_{ideal}\right|>{\Delta f}_{tune}\end{array}\right.,$$

(7)

${\mathcal{F}}_{sh}\left(\mathbf{x}\right)$ is a virtual function, and the $R_{sh}$, $R/\mathrm{Q}$ and frequency f are all calculated through numerical simulation software.

Figure 2 shows the distribution of solutions in a two-dimensional solution space near an initial feasible solution $\mathit{x}=(5.4683, 0.4331, 0.8055, 3.6837)$ while keeping D and ${\displaystyle \frac{\mathrm{c}}{\mathsf{\lambda }}}$ constant. The colored points represent feasible solutions, while the gray points represent infeasible ones. As shown in the figure, replacing the frequency constraint with a penalty factor significantly increases the number of feasible solutions.

3.2. Progressive Exploration Strategy

The depicted solution space in Figure 2 represents a minute fraction of the expansive realm requiring exploration, accounting for approximately 7.4074 × 10⁻⁹% of the total solution space. The continuous distribution of feasible solutions is observed, which is consistent with electromagnetic field theory. Consequently, as the explored space expands, the proportion of feasible solutions diminishes. Figure 3 depicts the distribution of random feasible solutions near the same initial feasible solution, spanning a much larger range, approximately 25 times the solution space illustrated in Figure 2. Therefore, applying the single-objective optimization algorithm directly to search for the optimal solution across the entire solution space may lead to operational challenges due to the scarcity of feasible solutions, even with the incorporation of a frequency penalty factor.

Based on the characteristics of the feasible solution distribution in the DAA structure optimization problem, and inspired by exploration strategies employed in some improved algorithms, this paper introduces a new progressive exploration strategy for single-objective swarm intelligence optimization algorithm [20,21,22,23,24,25]. This strategy commences its exploration from the vicinity of a feasible solution and gradually moves or expands its search scope, guided by the swarm global best solution and the convergence criteria, until the entirety of the solution space is thoroughly explored. The process of progressive exploration strategy is shown in Figure 4.

Firstly, the swarm is initialized in close proximity to a feasible solution within a narrow range called space fragment. The space fragment is defined as follows:

$${space\_fragment}_n={{\mathit{X}}_{group\_best}}_n+F_{fragment}\times F_{scale}\times ({\mathit{X}}_{\mathit{U}}-{\mathit{X}}_{\mathit{L}}),$$

(8)

where $F_{fragment}$ is the fragment factor, a constant that defines the proportion of the initial search space relative to the entire solution space; $F_{scale}$ is a variable that gradually increases to expand the search range if the algorithm gets trapped in a local optimum; ${{\mathit{X}}_{group\_best}}_n$ is the global best solution after the n-th iteration; and ${\mathit{X}}_{\mathit{U}}$ and ${\mathit{X}}_{\mathit{L}}$ are the upper and lower bounds of the solution space, respectively.

To augment the quantity of feasible solution particles, we employ a normal random distribution of particles. The convergence criterion is defined by the cessation of change in the fitness value. Upon sustaining convergence for a predetermined number of iterations, the algorithm is deemed to have discovered a local optimum within the original solution space fragment. Subsequently, the previous solution space fragment is shifted to center around this newfound local optimum, and the entire swarm is reinitialized within it, followed by the execution of the swarm intelligence algorithm once more. We refer to this process as the sliding of space fragments. If the local optimum remains unchanged following the sliding of the space fragment, its scope is expanded. Subsequently, the swarm undergoes reinitialization, followed by the repeated execution of the PSO algorithm. This process is referred to as the expansion of the space fragment. The algorithm will repeat the sliding and expanding process of the space fragment until the entire solution space is explored. At every sliding or expanding process, the global best solution particle from the previous swarm is incorporated into the reinitialized swarm as a guarantee mechanism. This ensures that subsequent iterations can find better solutions.

Figure 5 illustrates the sliding and expansion of the solution space fragment in PSO, DE and GAs. The $F_{fragment}$ is set to 0.05, that is, 6.25 parts per million of the entire solution space. The red rectangle denotes the original solution space fragment, while rectangles of varying colors depict solution space fragments re-initialized at different stages. The black lines and arrows delineate the trajectory of the sliding solution space fragments. From this visual representation, we also observed that the centers of certain sliding space fragments are not within the space fragments before sliding. This behavior arises from the inherent properties of the PSO and DE algorithms, where particle movements and vector updates are not constrained by the initial spatial limits. Such flexibility significantly accelerates convergence compared to GA and other algorithms based on binary encoding. Additionally, occasional overlaps between space fragments are observed, typically occurring when the swarm becomes trapped in a local suboptimal solution. In such scenarios, re-initialization plays a crucial role in restoring diversity within the swarm, enabling it to escape local suboptimalities and prevent premature convergence. This technique is well-established in many improved algorithms maintaining optimization performance.

4. Result and Analysis

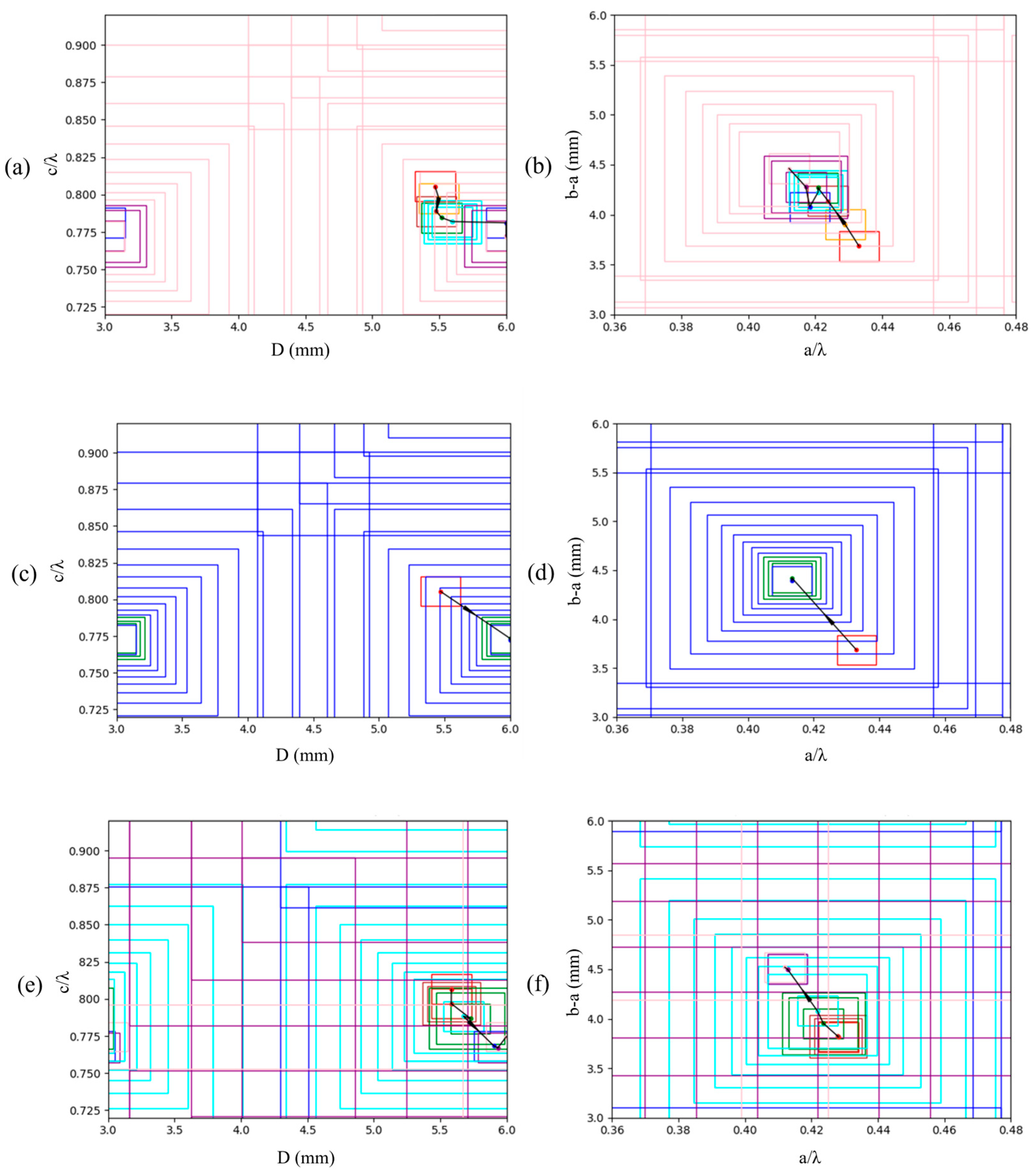
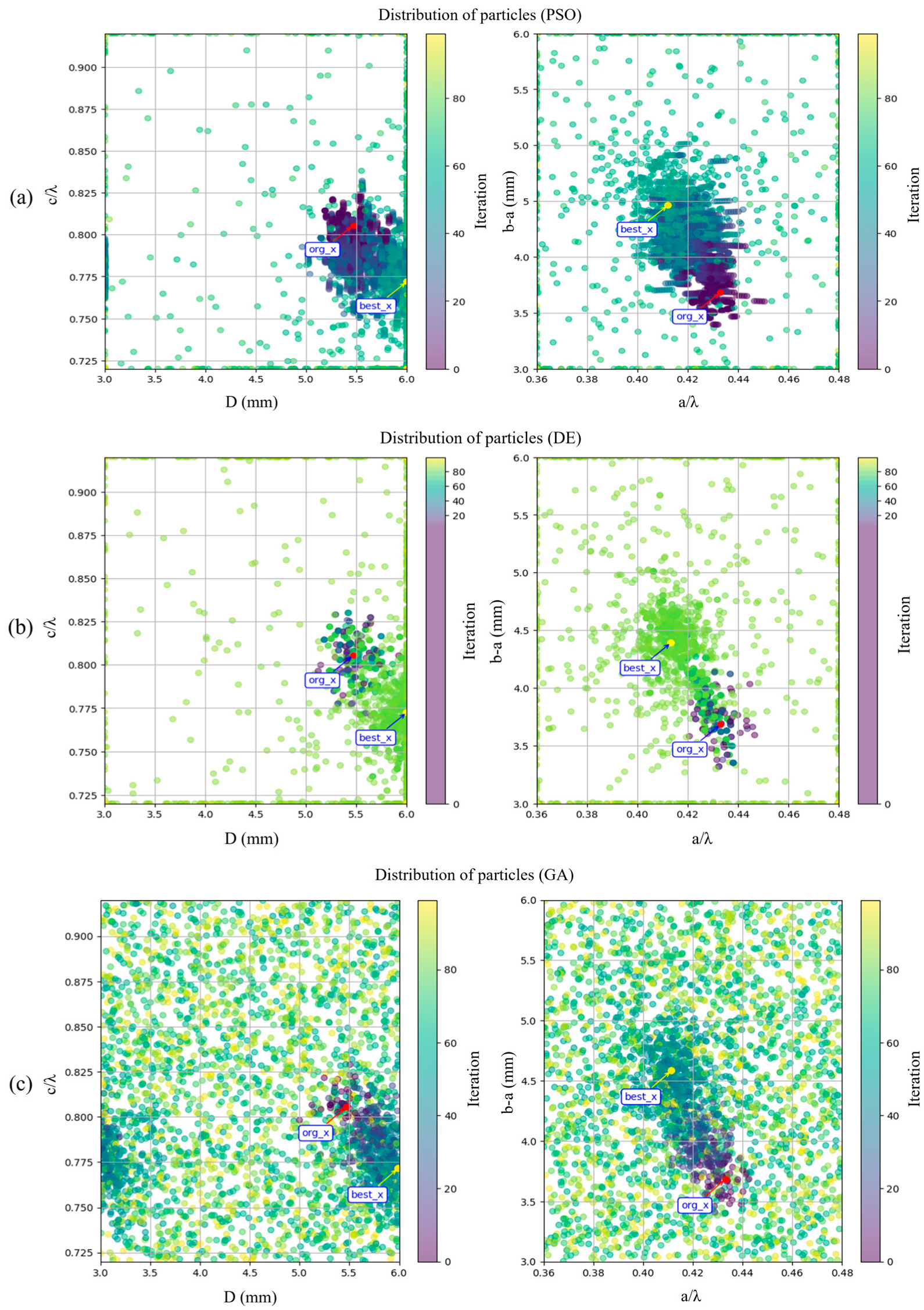
With the progressive exploration strategy the swarm intelligence algorithm can explore the entire solution space along the path of feasible solutions rapidly. In the actual algorithm implementation, the swarm is configured to consist of 50 particles, with a maximum of 100 iterations. In the PSO and CSO algorithms, the inertia weight is set to 1.0, and both the cognitive and social learning factors are 2.0. The competition ratio in CSO is 0.5. For the DE and JADE algorithms, the scaling factor is 0.8, and the crossover rate is 0.9. In the GA algorithm, the crossover probability is 0.5, and the mutation probability is 0.1. The distribution of particles during the iteration process is illustrated in Figure 6, while the distribution of feasible solutions is depicted in Figure 7. The particle named ‘org_x’ is the original feasible solution which our exploration start from, and the particle named ‘best_x’ is the global optimal solution found by the enhanced swarm intelligence algorithm. From these two figures, it can be seen that as the number of iterations increases, the particles gradually disperse throughout the solution space that needs to be explored. Most of the particles gather around the path formed by the feasible solutions and move along this path towards the global optimal solution.

The primary role of the progressive exploration strategy is to restrict the exploration space to a localized region, thereby increasing the number of feasible solutions in each iteration. This method is suitable for cases where feasible solutions are continuously distributed within the solution space but occupy only a small portion of it. If a swarm intelligence optimization algorithm is applied directly to the entire solution space, the algorithm may fail to work due to the lack of sufficient feasible solutions, or it may require a large increase in the number of initial particles, which would significantly increase the execution time. The progressive exploration strategy can be combined with classical swarm intelligence optimization algorithms, such as PSO, GA, and DE, as well as well-known, state-of-the-art enhanced algorithms, including the CSO and adaptive DE variants, etc.

Figure 8 delineates the convergence trajectory of the enhanced swarm intelligence algorithms. The DE and (Adaptive Differential Evolution with Optional External Archive) JADE algorithms demonstrate superior convergence speed, followed by the PSO and CSO algorithms, with the GA algorithm being the slowest. The final converged fitness values are 19,442,656.00 for PSO, 19,430,028.00 for DE, 19,441,840.00 for GA, 19,425,332.00 for CSO, and 19,431,379 for JADE. Furthermore, the visual representation reveals that the integration of the progressive exploration strategy with both the PSO, DE, GA, CSO and JADE algorithms effectively enables evasion from the traps of local optimal solutions.

The boxplot of the results from multiple independent runs of the five algorithms is shown in Figure 9. The medians of the algorithms do not differ significantly, indicating that the optimization results achieved by these algorithms are quite similar. The boxes for CSO and JADE are smaller and the results are more concentrated, suggesting better stability during runs. The PSO results distribution is wider, with one particularly low outlier (around 19,129,437), indicating that the algorithm may sometimes fall into a local trap. DE and GA can achieve relatively high fitness values but occasionally produce lower results, indicating that their stability is not as good as that of CSO and JADE. In summary, the progressive exploration strategy has been applied to various single-objective swarm intelligence algorithms, yielding good optimization results and demonstrating good stability.

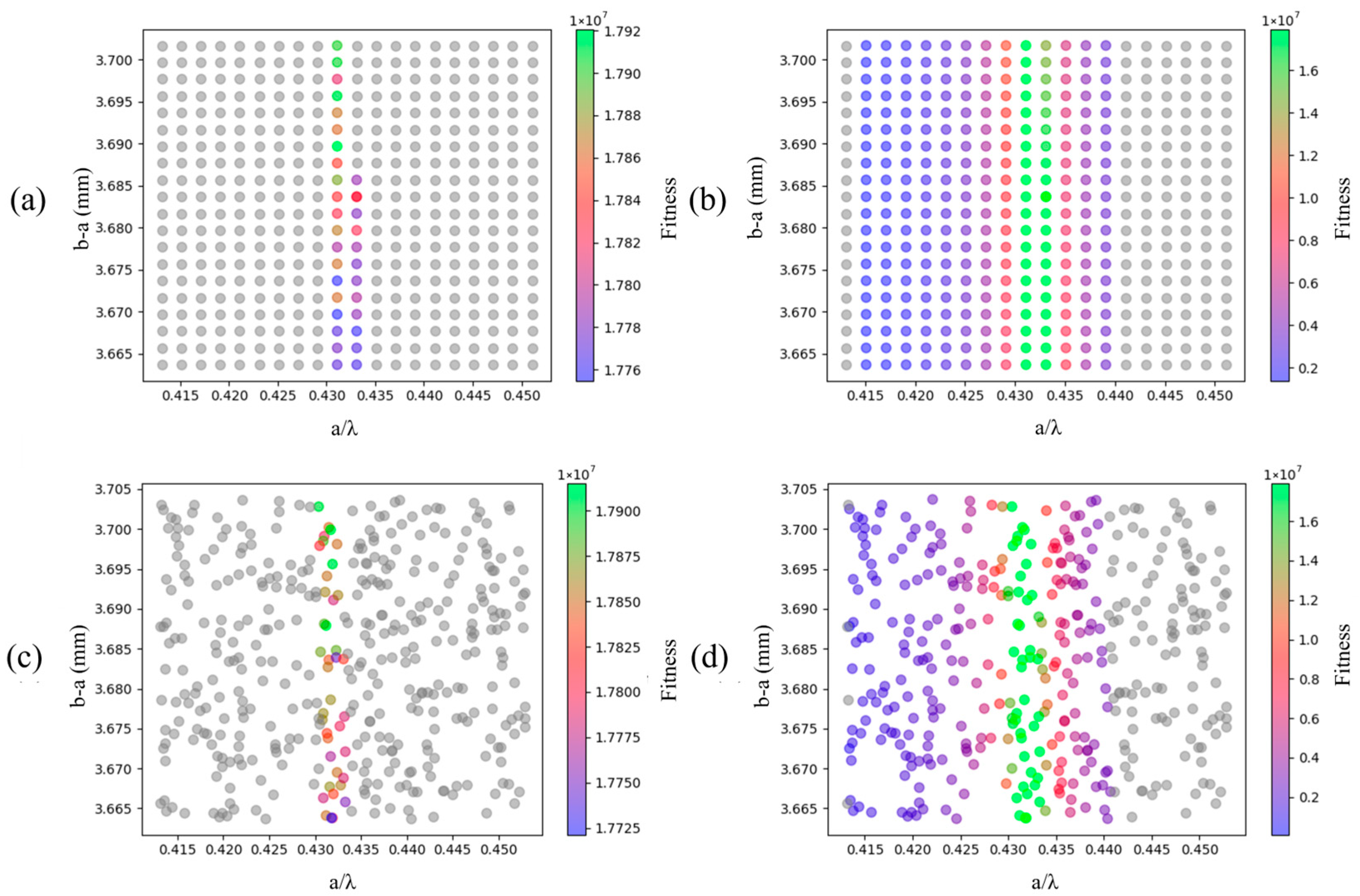
The Progressive Exploration Strategy involves three key hyperparameters: the sliding and the expanding threshold, the expanding factor, and the initial size of the space fragment. The smaller the sliding and expanding threshold is set, the faster the algorithm converges. However, if it is too small, the number of iterations within the same space fragment decreases, causing the fragment’s center point to short-step movement between two nearby local optima. This increases the number of fragment shifts and may, in fact, slow down the algorithm’s convergence. As observed in the convergence process shown in Figure 8, when a better solution exists nearby, the algorithm does not remain trapped in a suboptimal solution for more than three iterations. Therefore, setting the sliding and expanding thresholds to 3 yields the fastest convergence. However, the threshold value is also dependent on the initial size of the space fragment. If the initial fragment size is increased, the sliding and expanding threshold should also be increased to ensure sufficient exploration within the same fragment. The initial size of the space fragment determines the proportion of feasible solutions. A smaller initial fragment size generally yields a higher ratio of feasible solutions; however, if it is too small, the algorithm’s ability to explore the entire solution space is hindered, thereby slowing overall convergence. Conversely, a larger initial fragment size accelerates exploration of the solution space, but the lower proportion of feasible solutions may reduce stability and increase the risk of the algorithm becoming trapped in local optima, ultimately leading to slower convergence. Figure 10 presents the feasibility ratio and the global best fitness values for different initial space fragment sizes over 20 iterations.

The feasibility ratio increases with the number of iterations, as solutions tend to cluster within the feasible region. However, each sliding and expansion of the search space redistributes the solutions randomly, causing a sudden drop in the feasibility ratio. In Figure 10b, the initial space fragment size achieves faster convergence. In Figure 10a, the feasibility ratio reaches the highest level, but the convergence speed is slower due to the small initial search space. In Figure 10c, the feasibility ratio is too low, which makes the algorithm prone to becoming trapped in local optima, thereby hindering convergence.

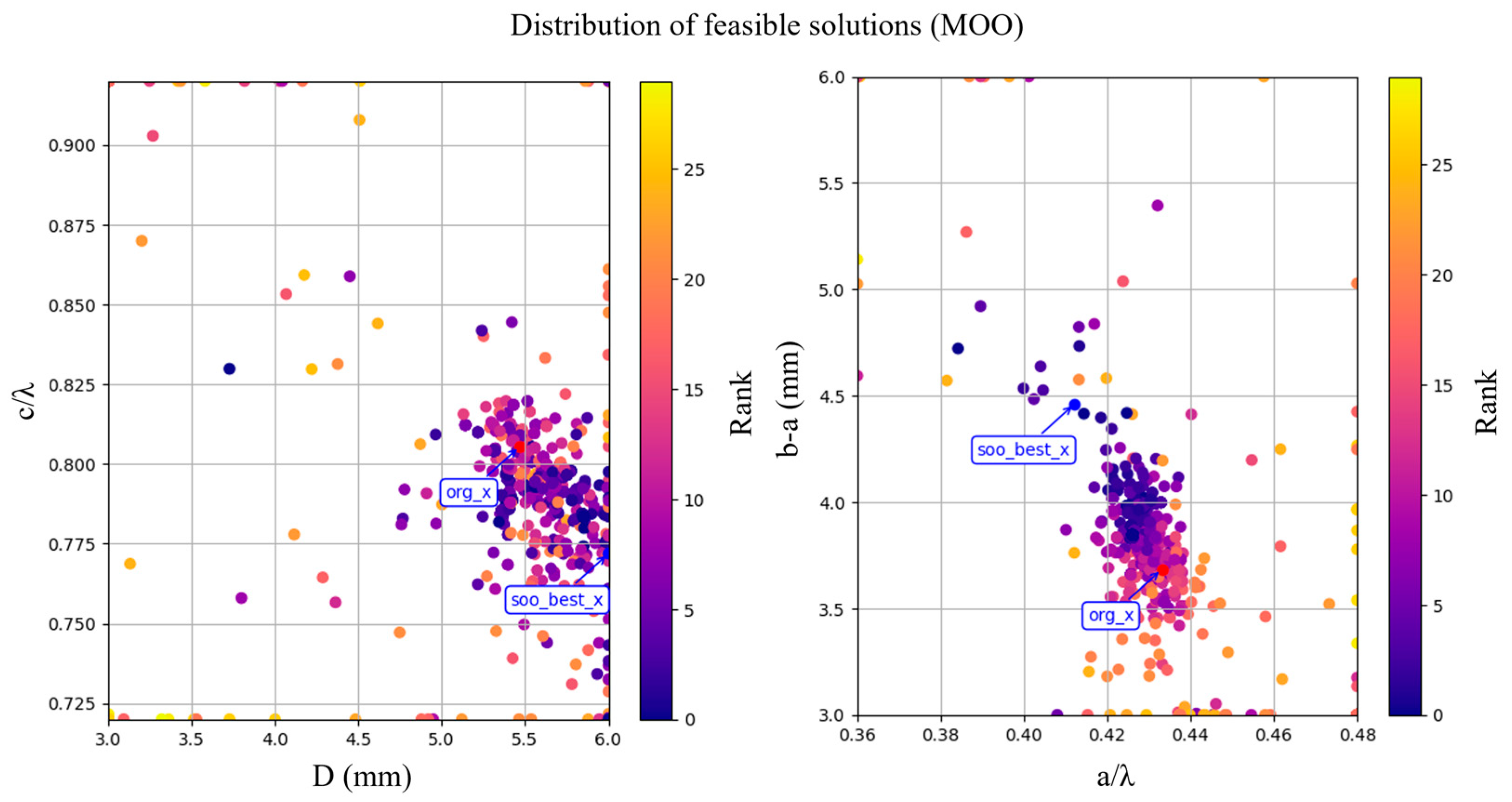
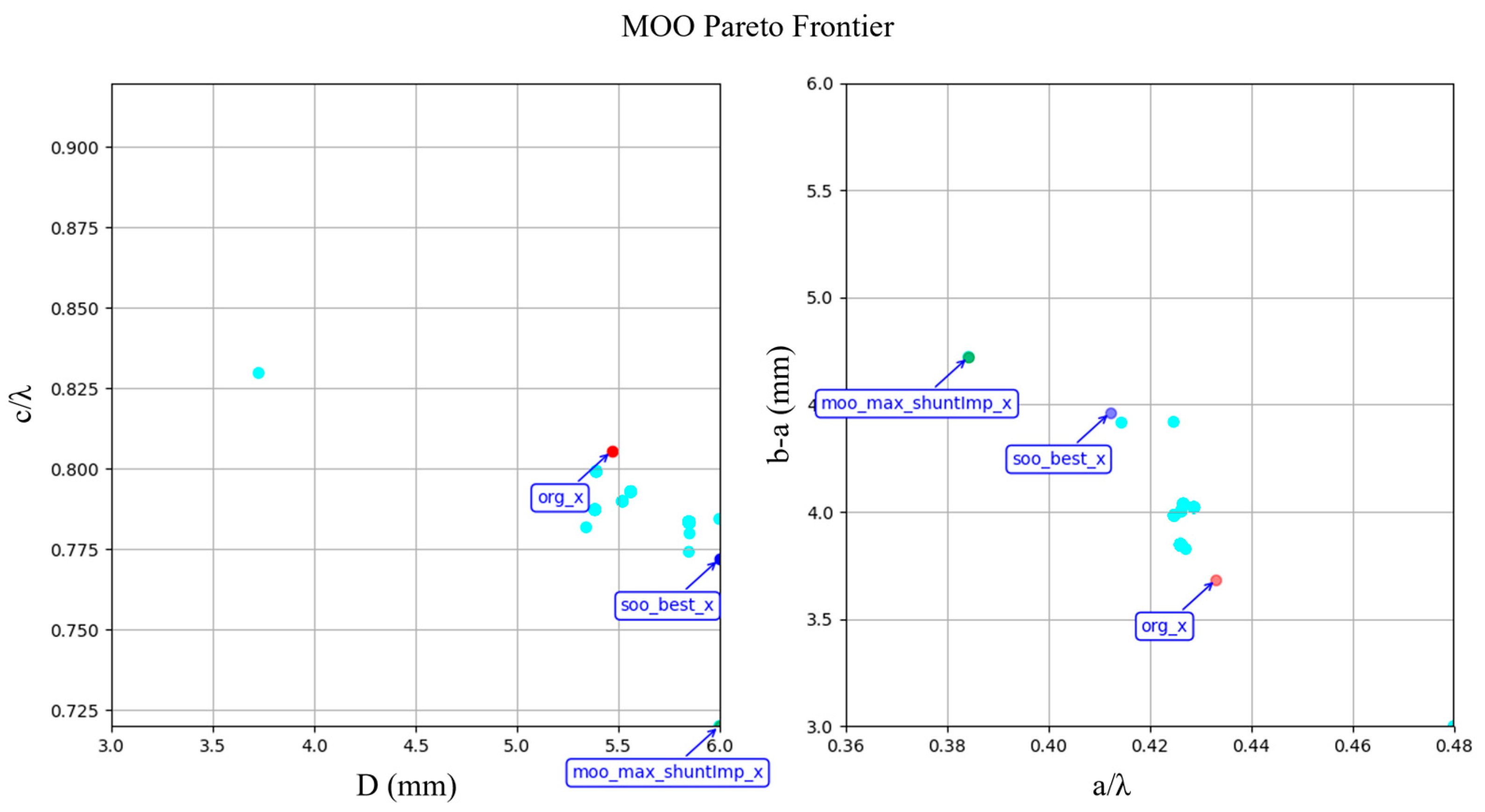
We also applied the Progressive Exploration Strategy to the multi-objective algorithm and optimized the DAA structure. The distribution of solutions and the resulting Pareto front, in comparison to the optimal solution obtained via the single-objective approach, are illustrated in the solution space in Figure 11 and Figure 12 respectively.

The SOO optimal solution is close to the MOO Pareto front, but it is not one of the solutions contained within the Pareto front. The feasible solution with the highest shunt impedance found by the MOO algorithm has a shunt impedance of 18377959.0 ohms, and it belongs to the Pareto front. The resonant frequency of the accelerating structure optimized by the MOO approach is closer to 5.71 GHz. However, its shunt impedance and quality factor (170,522.76) are both lower than those of the structure optimized by the SOO algorithm (19,442,656.00 ohms and 171,484.6877). Therefore, from the perspective of engineering applications, the SOO-optimized result is clearly the more appropriate choice.

The global optimal solution obtained after the convergence of the optimization algorithm is ${\mathit{x}}_{\mathit{o}\mathit{p}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{l}}=\left\{\mathrm{5.9995,\; 0.4122,\; 0.7719,\; 4.4621}\right\}$. The electric field distribution $E_z(r,\theta ,z)$ and the magnetic field distribution $H_{\theta }(r,\theta ,z)$ of the TM020 mode in the optimized DAA structure are shown in Figure 13. These contour plots are the results of eigenmode simulation with CST Microwave studio 2020. The RF parameters of the operating mode in the optimized DAA structure are shown in

Table 1. The RF parameters of the TM020 mode in the optimized DAA structure.

TM020 RF Parameter	Value
$\mathrm{Effective} \mathrm{Shunt} \mathrm{Impedance} {\mathrm{Z}}_{eff}$	19.442656 MΩ
R/Q	113.37838 Ω
Quality factor Q0	171,484.6877
Frequency	5.712 GHz
$\mathrm{Ideal} \mathrm{wavelength} \mathsf{\lambda }$	52.48 mm

. In Table 1, ${\mathrm{Z}}_{eff}$ represents the effective shunt impedance with the transit time factor taken into account. When the influence of the transit time factor is removed, the shunt impedance per accelerating distance ${\mathrm{R}}_{sh}$= 1297.71705 MΩ/m. Compared to the shunt impedance per unit length ${\mathrm{R}}_{sh}$ = 797 MΩ/m and Q₀ = 136,000 given for a single cell of the DAA structure in [8], the optimized structure has much higher shunt impedance ${\mathrm{R}}_{sh}$ and quality factor Q₀.

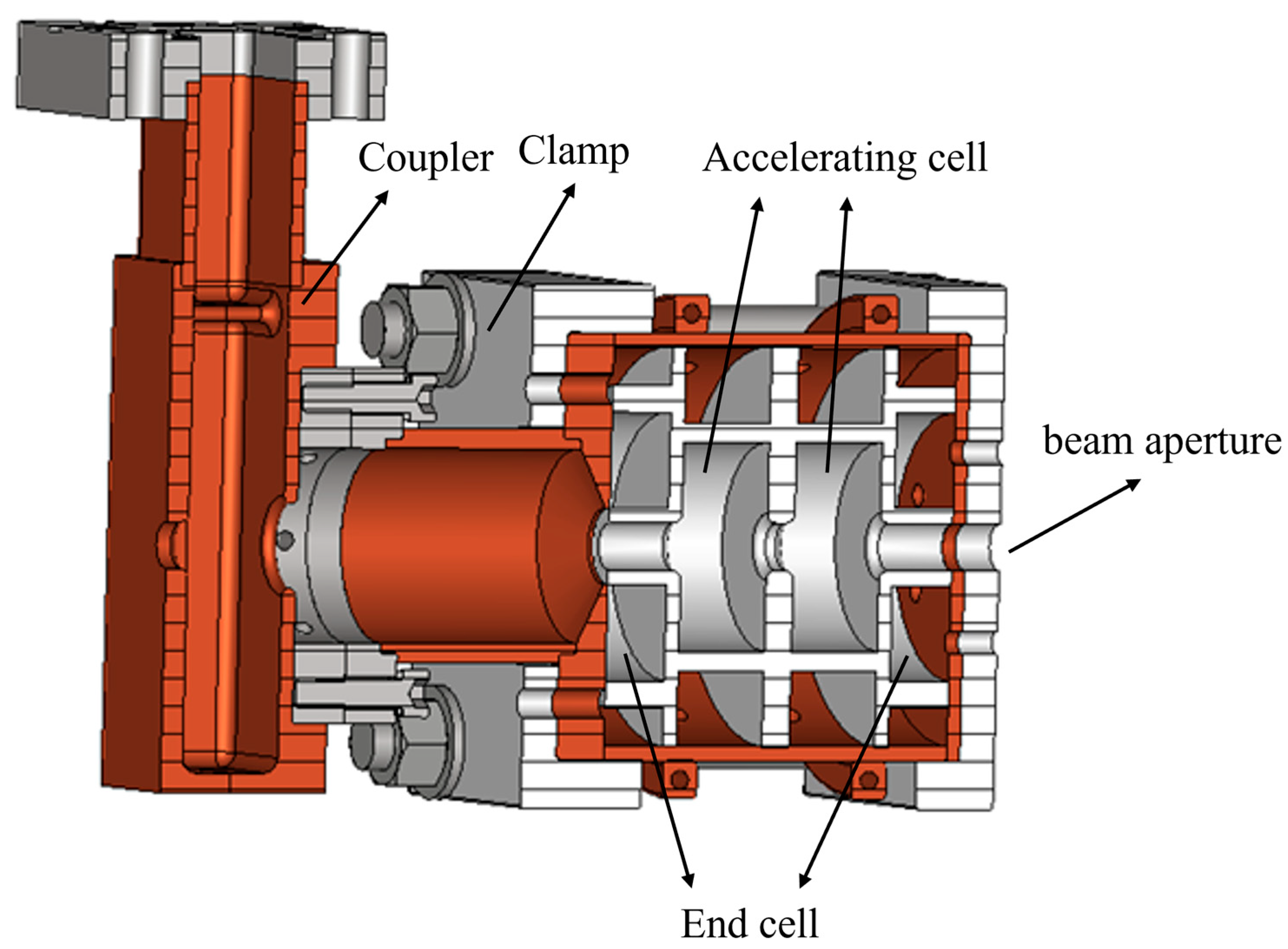
Based on the optimized results of the accelerating structure, we designed and fabricated a 2-cell cavity comprising two accelerating cells and two end cells for cold testing, see Figure 14. Since it is difficult and expensive to fabricate a cavity using a dielectric material as high-performance as the TiO₂-doped alumina mentioned in the references, alumina ceramic with a relative permittivity of 10 and a loss tangent of 2 × 10⁻⁵ was used for the cavity design and manufacture instead. The final simulation results of the complete cavity are: R_sh = 15.37 MΩ, f = 5.71203 GHz, Q₀ = 73185; R/Q = 210. Due to manufacturing errors, the actual performance of the cavity is inevitably lower than the simulation results. The measured results, which are 92% of the simulated values, are: R_sh = 14.14 MΩ, f = 5.71203 GHz, Q₀ = 67330, R/Q = 210.

5. Conclusions

In this paper, we analyze the characteristics of the optimization problem in RF accelerator structures and propose an enhanced single-objective optimization strategy based on a progressive exploration method, considering the confined continuous distribution of feasible solutions within its large solution space. For this type of optimization problem, algorithms based on continuous exploration mechanisms, such as PSO and DE, have an advantage in exploration efficiency compared to algorithms based on discrete exploration mechanisms, such as GA. The enhanced algorithms are applied to optimize the multi-constrained single-objective optimization problem of the DAA single-cell accelerating structure. By introducing a frequency penalty factor in place of frequency constraint conditions, the algorithm mitigates the issue of an insufficient quantity of feasible solutions.

The progressive exploration strategy enables the swarm to slide and expand along a reasonable path within the feasible solution region, thereby accelerating the exploration of the required solution space. During each phase of sliding and expansion, a re-initialization mechanism is introduced to restore swarm diversity, which significantly enhances the algorithm’s ability to escape local optima traps.

The progressive exploration strategy has been applied to various single-objective swarm intelligence algorithms and tested on the optimization of the DAA structure, all achieving satisfactory results. The strategy demonstrates fast convergence and strong capability in avoiding local optima. It effectively addresses the issue of insufficient feasible solutions caused by multiple stringent constraints and enables rapid exploration of the entire solution space. The performance and stability of the algorithm have also been verified. However, it is evident that this strategy is not suitable for cases where feasible solutions are uniformly distributed and occupy a relatively large proportion of the solution space.

The entire optimization algorithm was executed on a workstation equipped with an Intel Core i9 CPU and 32 GB of RAM. The algorithm required approximately 12 h to converge through iterations and identify the global optimum, which is about one-fifth to one-sixth of the time typically spent on manual parameter tuning, greatly improving the efficiency of the optimization process.

Future research could extend this strategy to both single-objective and multi-objective optimization problems in other types of RF accelerator structures, such as superconducting cavities, normal-conducting copper cavities, and ferrite-loaded cavities. In addition, integrating this method with parallel computing frameworks could further enhance convergence efficiency.