Ternary vs. Right-Angled Plots in Agricultural Research: An Assessment of Data Representation Efficiency and User Perception
Abstract
Featured Application
Abstract
1. Introduction
Visualizing Compositional Data
2. Materials and Methods
2.1. Theoretical Comparative Study
- Plotting area;
- Construction of axis;
- Zone indicators, including connections between the middle points of edges, and connections within the middle sections linking the barycenter to the midpoints of the triangle sides;
- Readability of data point values;
- Visual determination of dominance of one of the variables;
- Interpretation of linear and nonlinear relationships between variables.
2.2. Online Survey
- The rate of error-free answers for each kind of plot, separately for each coordinate (X, Y, Z), and all together (XYZ);
- The rate of respondents’ answers in which X + Y + Z = 100 (where X, Y, and Z were the values provided by the respondent) (A) for each plot, defined as “correct-coord” answers; (See Section 2.4 Data Analysis) and (B) for both plots at the same time;
- The bias of readings, where the bias was represented by the sum of the differences between the values given by the respondents and the correct value of the variable;
- The precision of readings of the values from the plots represented by the absolute value of the aforementioned differences;
- The time needed to read the values from the plots;
- The respondents’ perception of ease in reading the plots.
2.3. Technical Aspects of the Survey and the Experimental Design
2.4. Data Analysis
3. Results
3.1. Theoretical Comparison
- The plots have different coordinate systems: an atypical coordinate system exploiting the Cartesian coordinate system for the right-angled plot, and the barycentric coordinate system for the ternary plot;
- The ternary plot has a greater variation of construction elements (the value axes for the variables may appear along the sides or altitudes of the triangle, and the values can be interpreted either clockwise or counterclockwise along these axes). Therefore, it can be constructed in more ways than a right-angled plot. Because of this variability, ternary plots constructed by different authors can be difficult and confusing to read. The construction of a right-angled plot does not present such variability;
- The ternary plot has the isometric property for all three scales, so the relation between the physical distance on a plot and the distance in the data scale is the same for the three axes; a right-angled plot has the isometric property only for the two perpendicular axes;
- Given the triangle base, the right-angled plot has a larger plotting region than does the ternary plot; however, the former has one axis within the plotting region, while the whole plotting region of the latter is devoted to the data.
3.2. CAWI Survey
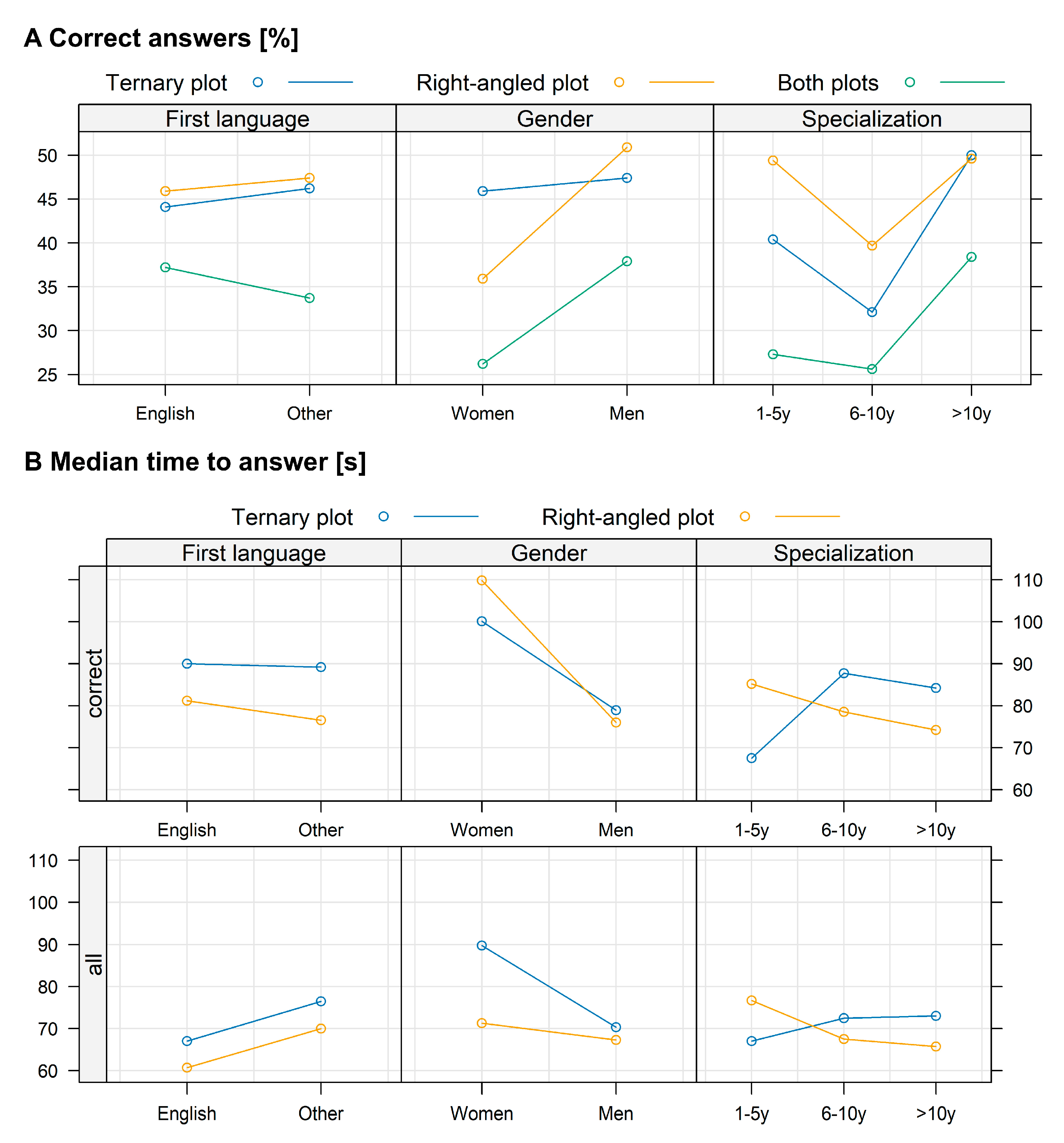
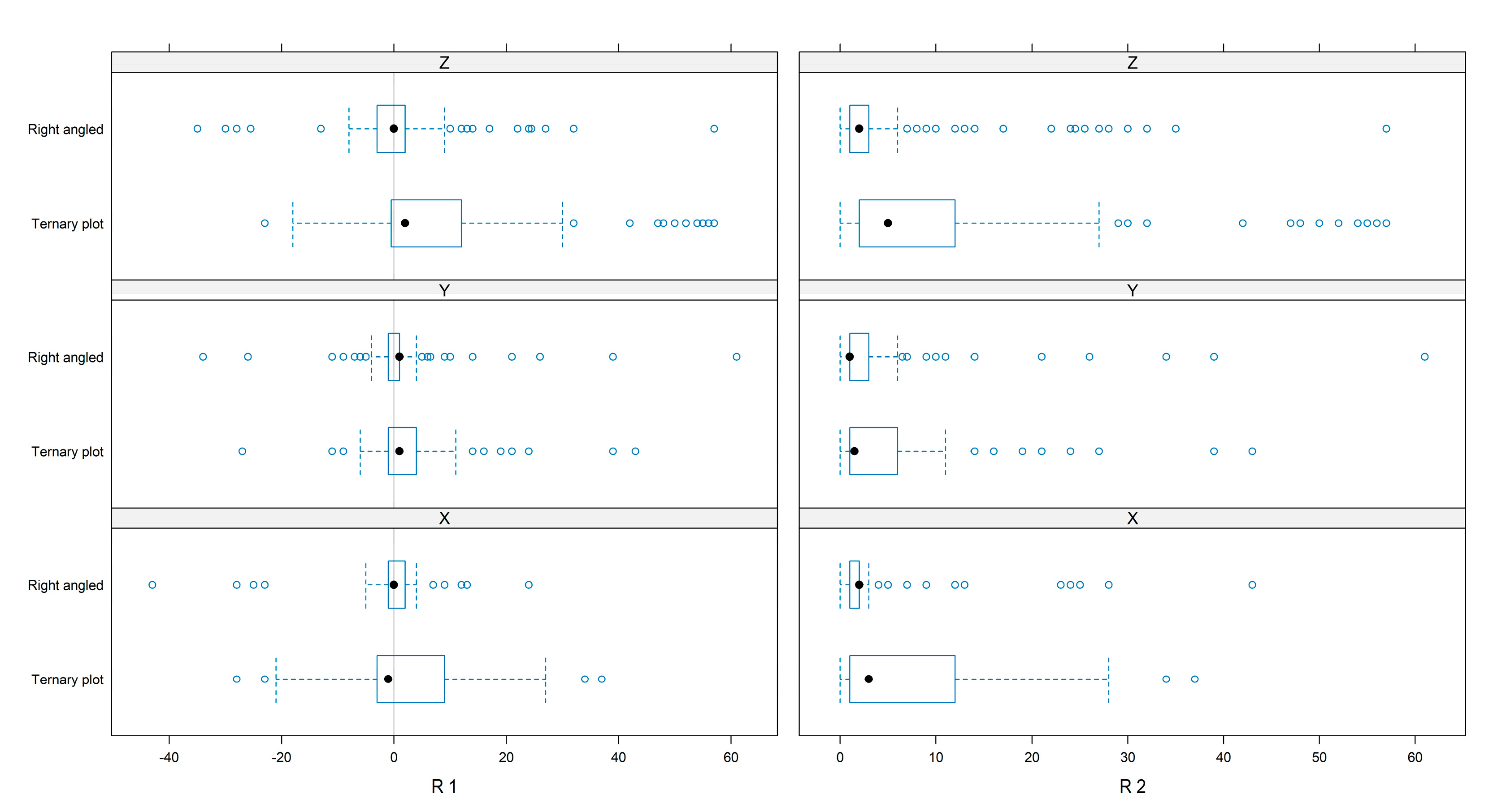
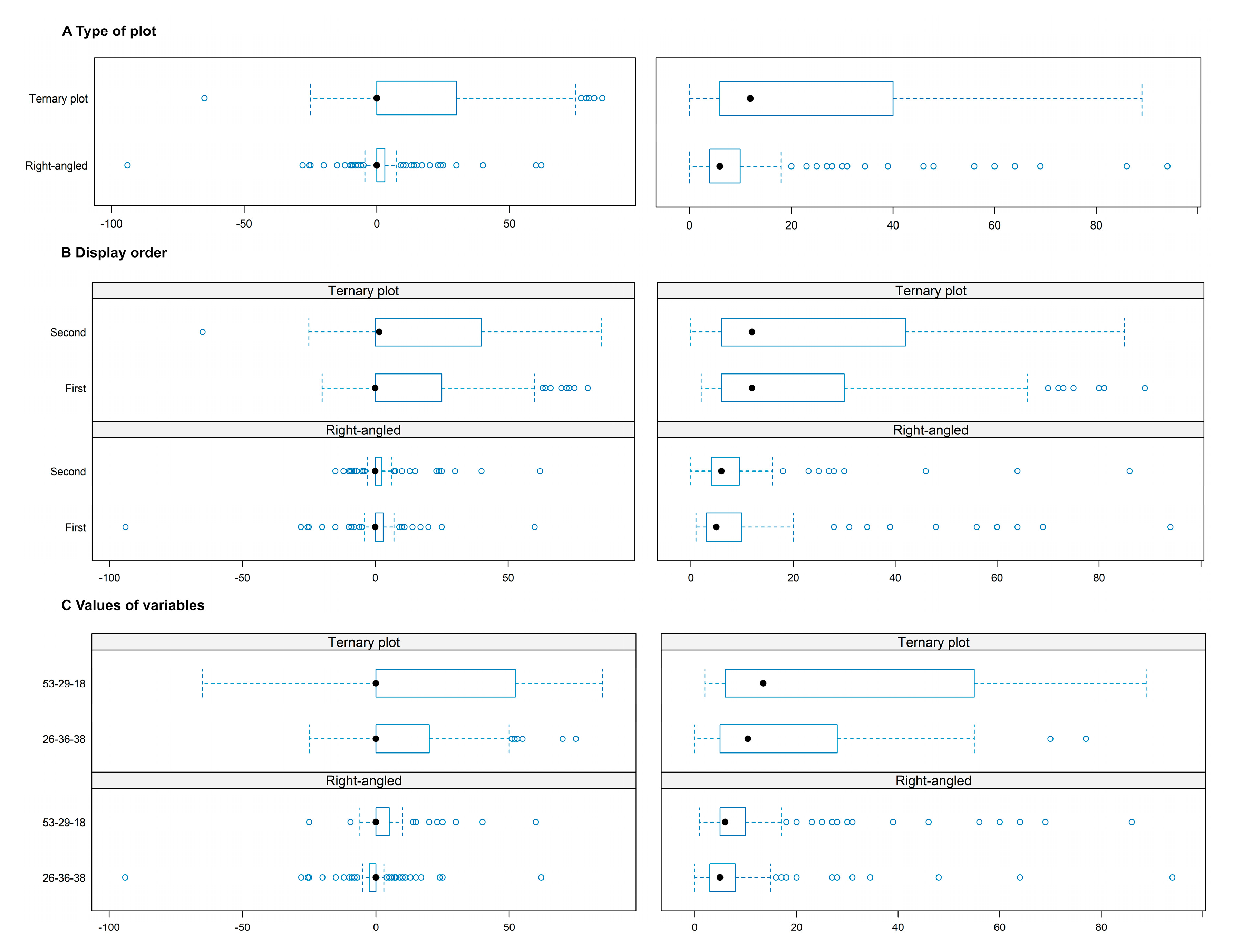
3.2.1. Rate of Correct Plot Reading
3.2.2. Analysis of the Bias and Precision in Plot Evaluation
3.2.3. Perceived Ease in Using the Two Kinds of Plots
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jolliffe, P.A.; Courtney, W.H. Plant Growth Analysis: Additive and Multiplicative Components of Growth. Ann. Bot. 1984, 54, 243–254. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Kozak, M. Note on two methods of additive yield component analysis. Biom. Lett. 2010, 47, 129–132. [Google Scholar]
- Kozak, M.; Gozdowski, D.; Wyszyński, Z. An approach to analyzing a response variable as affected by its additive components: Example for spring barley grain yield. Cereal Res. Commun. 2006, 34, 981–988. [Google Scholar] [CrossRef]
- Brzezinski, M.; Barszczak, T. Zawartość glinu wymiennego w glebie w świetle trwałych doświadczeń nawozowych w Skierniewicach. Zesz. Probl. Postęp. Nauk Rol. 2009, 541, 67–72. [Google Scholar]
- Skorupska, A.; Lacka, A. The response of the two-spotted spider mite (Tetranychus urticae koch) to different cereal crop species. Prog. Plant Prot. 2009, 49, 142–144. [Google Scholar]
- Karg, J.; Bałazy, S. Effect of landscape structure on the occurrence of agrophagous pests and their antagonists. Prog. Plant Prot./Postęp. Ochr. Rośl. 2009, 49, 1015–1034. [Google Scholar]
- Łabanowska-Bury, D.; Dąbrowski, Z.T.; Eyre, M.D.; Leifert, C.; White, R. The importance of field surrounding flora in protection of vegetable crops against pests. Prog. Plant Prot./Postęp. Ochr. Rośl. 2009, 49, 1066–1073. [Google Scholar]
- Złotkowski, J. Seasonal changes in aphid migration dynamics in the surrounding area of Winna Góra (Wielkopolska district) in 2007–2008. Prog. Plant Prot./Postęp. Ochr. Rośl. 2009, 49, 1242–1246. [Google Scholar]
- European Commission. Directive 2009/128/EC of the European Parliament and of the Council of 21 October 2009 establishing a framework for Community action to achieve the sustainable use of pesticides. Off. J. Eur. Union 2009, 309, 71–86. [Google Scholar]
- GUS. Statistical Yearbook of Poland; Zakład Wydawnictw Statystycznych: Warszawa, Poland, 2010; p. 700. [Google Scholar]
- Tufte, E.R.; Graves-Morris, P.R. The Visual Display of Quantitative Information; Graphics Press: Cheshire, CT, USA, 1983. [Google Scholar]
- Cleveland, W.S.; McGill, R. Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods. J. Am. Stat. Assoc. 1984, 79, 531–554. [Google Scholar] [CrossRef]
- Möbius, A.F. Der Barycentrische Calcul (Der barycentrische Calcul: Ein Neues Hülfsmittel zur Analytischen Behandlung der Geometrie); Barth: Leipzig, Germany, 1827; p. 426. [Google Scholar]
- Pawlowsky-Glahn, V.; Egozcue, J.J. Geometric approach to statistical analysis on the simplex. Stoch. Environ. Res. Risk Assess. 2001, 15, 384–398. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barcelo-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V. Groups of Parts and Their Balances in Compositional Data Analysis. Math. Geol. 2005, 37, 795–828. [Google Scholar] [CrossRef]
- Palmajumder, M.; Chaudhuri, S.; Das, V.K.; Nag, S.K. An appraisal of geohydrological status and assessment of groundwater quality of Indpur Block, Bankura District, West Bengal, India. Appl. Water Sci. 2021, 11, 59. [Google Scholar] [CrossRef]
- Chidambaram, S.; Prasanna, M.V.; Venkatramanan, S.; Nepolian, M.; Pradeep, K.; Panda, B.; Thivya, C.; Thilagavathi, R. Groundwater quality assessment for irrigation by adopting new suitability plot and spatial analysis based on fuzzy logic technique. Environ. Res. 2022, 204 Pt A, 111729. [Google Scholar] [CrossRef]
- Tamrakar, N.K. Riverbed-material texture and composition of Bishnumati River, Kathmandu, Nepal; implications in provenance analysis. Bull. Dep. Geol. 1970, 12, 55–62. [Google Scholar] [CrossRef][Green Version]
- Flemming, B.W. A revised textural classification of gravel-free muddy sediments on the basis of ternary diagrams. Cont. Shelf Res. 2000, 20, 1125–1137. [Google Scholar] [CrossRef]
- Rilo, E.; Ferreira, A.G.M.; Fonseca, I.M.A.; Cabeza, O. Densities and derived thermodynamic properties of ternary mixtures 1-butyl-3-methyl-imidazolium tetrafluoroborate + ethanol + water at seven pressures and two temperatures. Fluid Phase Equilibria 2010, 296, 53–59. [Google Scholar] [CrossRef]
- Selkirk, K.E. Triangular Graphs and League Tables. Teach. Stat. 1983, 5, 29–30. [Google Scholar] [CrossRef]
- Cox, N.J. Speaking Stata: Graphing Categorical and Compositional Data. Stata J. Promot. Commun. Stat. Stata 2004, 4, 190–215. [Google Scholar] [CrossRef]
- Potente, S.; Ramsthaler, F.; Federspiel, J.M. A useful data presentation tool: Ternary plots in forensic medicine. Leg. Med. 2025, 76, 102652. [Google Scholar] [CrossRef]
- Lang, P.; Modla, G.; Benadda, B.; Lelkes, Z. Homoazeotropic distillation of maximum azeotropes in a batch rectifier with continuous entrainer feeding I. Feasibility studies. Comput. Chem. Eng. 2000, 24, 1665–1671. [Google Scholar] [CrossRef]
- Cho, J.H.; Jeon, J.K. Comparison of three-and two-column configurations in ethanol dehydration using azeotropic distillation. J. Ind. Eng. Chem. 2006, 12, 206–215. [Google Scholar]
- Milano, G.; Di Giovambattista, R.; Ventura, G. Seismic activity in the transition zone between Southern and Central Apennines (Italy): Evidences of longitudinal extension inside the Ortona–Roccamonfina tectonic line. Tectonophysics 2008, 457, 102–110. [Google Scholar] [CrossRef]
- Yang, Z. Bayes Empirical Bayes Inference of Amino Acid Sites Under Positive Selection. Mol. Biol. Evol. 2005, 22, 1107–1118. [Google Scholar] [CrossRef] [PubMed]
- Siemes, H.; Schaeben, H.; Rosière, C.A.; Quade, H. Crystallographic and magnetic preferred orientation of hematite in banded iron ores. J. Struct. Geol. 2000, 22, 1747–1759. [Google Scholar] [CrossRef]
- Kruhl, J.H.; Peternell, M. The equilibration of high-angle grain boundaries in dynamically recrystallized quartz: The effect of crystallography and temperature. J. Struct. Geol. 2002, 24, 1125–1137. [Google Scholar] [CrossRef]
- Vdović, N.; Obhođaš, J.; Pikelj, K. Revisiting the particle-size distribution of soils: Comparison of different methods and sample pre-treatments. Eur. J. Soil Sci. 2010, 61, 854–864. [Google Scholar] [CrossRef]
- Gerakis, A.; Baer, B. A computer program for soil textural classification. Soil Sci. Soc. Am. J. 1999, 63, 807–808. [Google Scholar] [CrossRef]
- Thomas, W. Foliar diagnosis: Principles and practice. Plant Physiol. 1937, 12, 571. [Google Scholar] [CrossRef][Green Version]
- Golba, J.; Rozbicki, J.; Gozdowski, D.; Sas, D.; Mądry, W.; Piechociński, M.; Kurzyńska, L.; Studnicki, M.; Derejko, A. Adjusting yield components under different levels of N applications in winter wheat. Int. J. Plant Prod. 2013, 7, 139–150. [Google Scholar][Green Version]
- Dennis, R.L.H. Mate location behavior of the large skipper butterfly Ochlodes venata: Flexible strategies and spatial components. J. Lepid. Soc. 1987, 41, 45–64. [Google Scholar][Green Version]
- Hadian, S.; Smith, D.L.; Supronienė, S. Modulating the Plant Microbiome: Effects of Seed Inoculation with Endophytic Bacteria on Microbial Diversity and Growth Enhancement in Pea Plants. Microorganisms 2025, 13, 570. [Google Scholar] [CrossRef]
- Herman, I.; Melancon, G.; Marshall, M.S. Graph visualization and navigation in information visualization: A survey. IEEE Trans. Vis. Comput. Graph. 2000, 6, 24–43. [Google Scholar] [CrossRef]
- Tufte, E.R. Envisioning Information; Graphics Press: Cheshire, CT, USA, 1990. [Google Scholar]
- Cleveland, W.S. Visualizing Data; AT&T Bell Laboratories: Murray Hill, NJ, USA, 1993. [Google Scholar]
- Cleveland, W.S. The Elements of Graphing Data, rev. ed.; AT&T Bell Laboratories: Murray Hill, NJ, USA, 1994. [Google Scholar]
- Wilkinson, L. The grammar of graphics. In Handbook of Computational Statistics: Concepts and Methods; Springer: Berlin/Heidelberg, Germany, 2011; pp. 375–414. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Doubleday: Toronto, ON, Canada, 2011; p. 512. [Google Scholar]
- Wang, C.; Han, Q.; Li, J.; Li, C.; Zou, X. YOLO-BLBE: A Novel Model for Identifying Blueberry Fruits with Different Maturities Using the I-MSRCR Method. Agronomy 2024, 14, 658. [Google Scholar] [CrossRef]
- Tartanus, M.; Wnuk, A.; Kozak, M.; Hartley, J. Graphs and prestige in agricultural journals. J. Am. Soc. Inf. Sci. Technol. 2013, 64, 1946–1950. [Google Scholar] [CrossRef]
- Alter, A.L.; Oppenheimer, D.M. Uniting the tribes of fluency to form a metacognitive nation. Personal. Soc. Psychol. Rev. 2009, 13, 219–235. [Google Scholar] [CrossRef] [PubMed]
- Kozak, M.; Hartley, J. Presenting numerical values within sentences and text tables. J. Am. Soc. Inf. Sci. Technol. 2012, 63, 108–113. [Google Scholar] [CrossRef]
- Connelly, N.A.; Brown, T.L.; Decker, D.J. Factors Affecting Response Rates to Natural Resource—Focused Mail Surveys: Empirical Evidence of Declining Rates Over Time. Soc. Nat. Resour. 2003, 16, 541–549. [Google Scholar] [CrossRef]
- Soni, U.; Lu, Y.; Hansen, B.; Purchase, H.C.; Kobourov, S.; Maciejewski, R. The Perception of Graph Properties in Graph Layouts. Comput. Graph. Forum 2018, 37, 169–181. [Google Scholar] [CrossRef]
- Tartanus, M.; Kozak, M.; Sas, D. The use of ternary and right-angled plots in data visualization in agricultural applications. Zesz. Probl. Postęp. Nauk Rol. 2017, 589, 93–107. [Google Scholar] [CrossRef]
- Keith, T.Z.; Reynolds, M.R.; Patel, P.G.; Ridley, K.P. Sex differences in latent cognitive abilities ages 6 to 59: Evidence from the Woodcock–Johnson III tests of cognitive abilities. Intelligence 2008, 36, 502–525. [Google Scholar] [CrossRef]
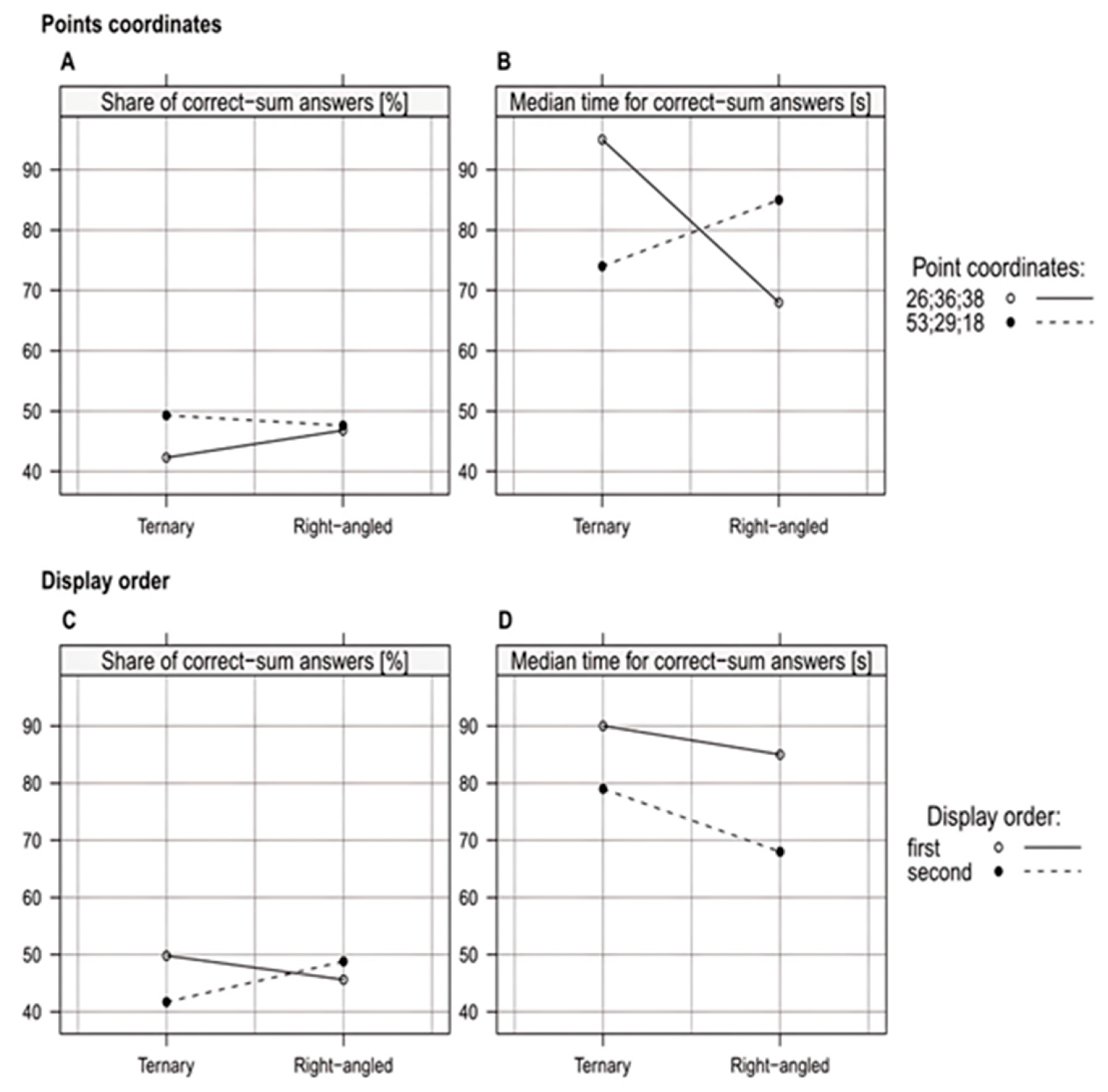


| Questionnaire Number | Plot | Position in the Questionnaire | Values of Variables | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| 1 | Ternary | First | 26 | 36 | 38 |
| Right-angled | Second | 53 | 29 | 18 | |
| 2 | Ternary | First | 53 | 29 | 18 |
| Right-angled | Second | 26 | 36 | 38 | |
| 3 | Right-angled | First | 53 | 29 | 18 |
| Ternary | Second | 26 | 36 | 38 | |
| 4 | Right-angled | First | 26 | 36 | 38 |
| Ternary | Second | 53 | 29 | 18 | |
| Ternary Plot | Right-Angled | |||||||
|---|---|---|---|---|---|---|---|---|
| Construction of the plots | ||||||||
| Kind of triangle | Equilateral triangle (which uses the barycentric coordinates) | Isosceles right triangle (which uses the Cartesian coordinate system for two axes) | ||||||
| Plotting area | Surface area ST-surface area of the ternary plot; SRA-surface area of the right-angled plot | Surface area SRA-surface area of the right-angled plot; a-length of the side of the triangle | ||||||
| The axes are located on the corresponding altitudes. The axes can be further projected onto the sides of the triangle, so that the plotting area is used only for drawing data points. | The axes are located on the corresponding altitudes, but one of the axes is within the plotting area. Two heights are the sides of the triangle. The three axes are directly shown and thus do not have to be projected. | |||||||
| Location of axes | All at the altitudes of the triangle. | Two at the heights and one at the angle bisecting line. | ||||||
| Typically, they require projection on the edges of the triangle. | They do not require projection on the edges of the triangle; one axis is within the plotting region. | |||||||
| Length of axes | The same for all the variables. | One is longer than the other two. | ||||||
| Distance between tick marks on axes | The same for all the scales. | Shorter on the inside axis than on the other two. | ||||||
| Use of zone indicators | ||||||||
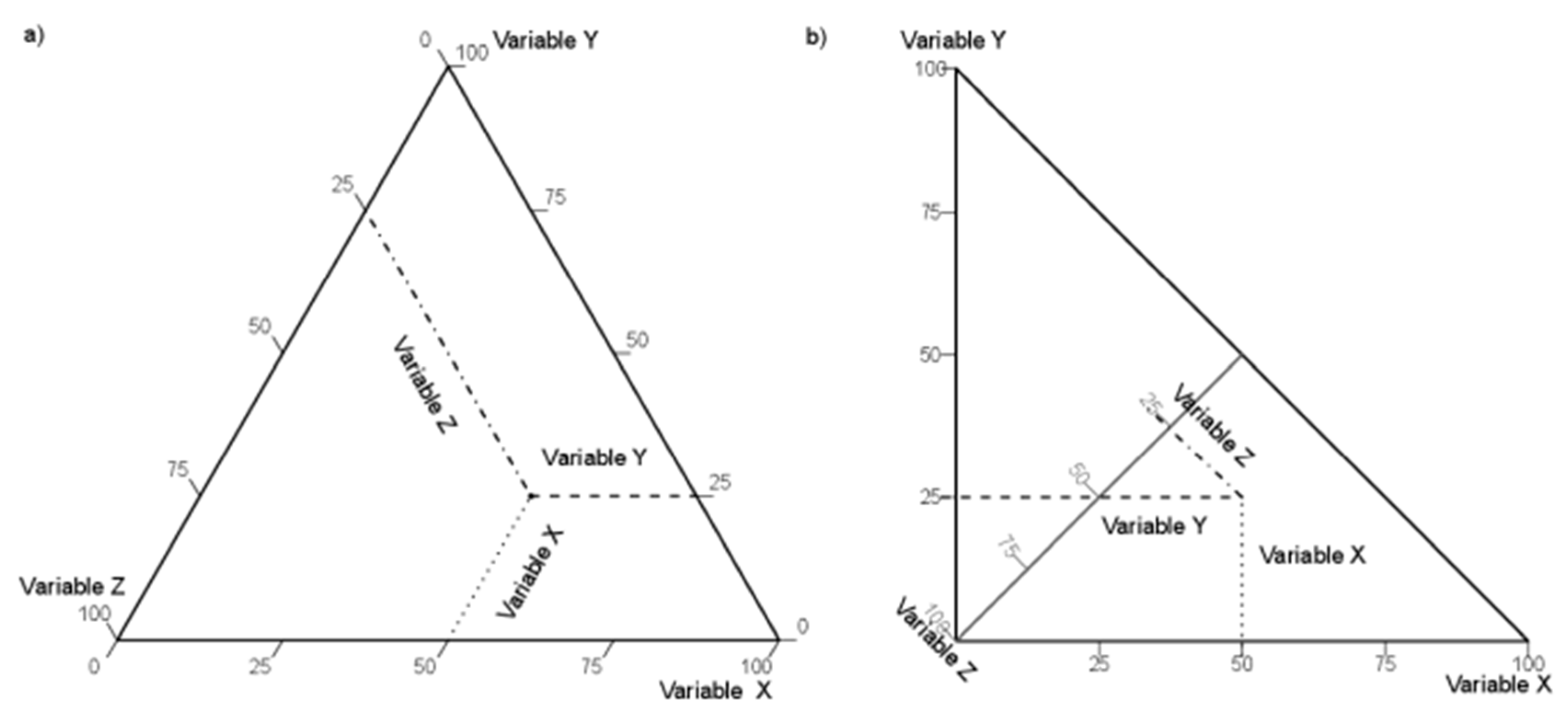
| Connections between the middle points of edges | 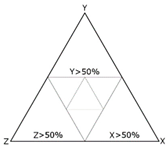 | 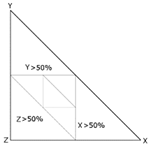 | ||||||
| Connections of the middle sections that join the barycenter to the midpoints of the sides of the triangle | 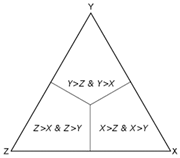 | 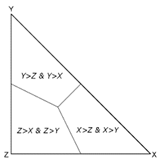 | ||||||
| Grid lines On both graphs, grid lines can be used. | Grid lines intersect at an angle of 60°. | Two grid lines form a right angle, and the third one intersects this point at an angle of 45°. | ||||||
| Reading values of variables in data points | ||||||||
| Interpretation | See Figure 1. To read values of data points, a user should know how these plots are constructed. On the right-angled plot, values of two variables are read on the sides perpendicular to each other, which resembles common graph layouts. On the ternary plot, every 2 axes create angles of 60 degrees with each other | |||||||
| Visual determination of the dominance of one of the variables | ||||||||
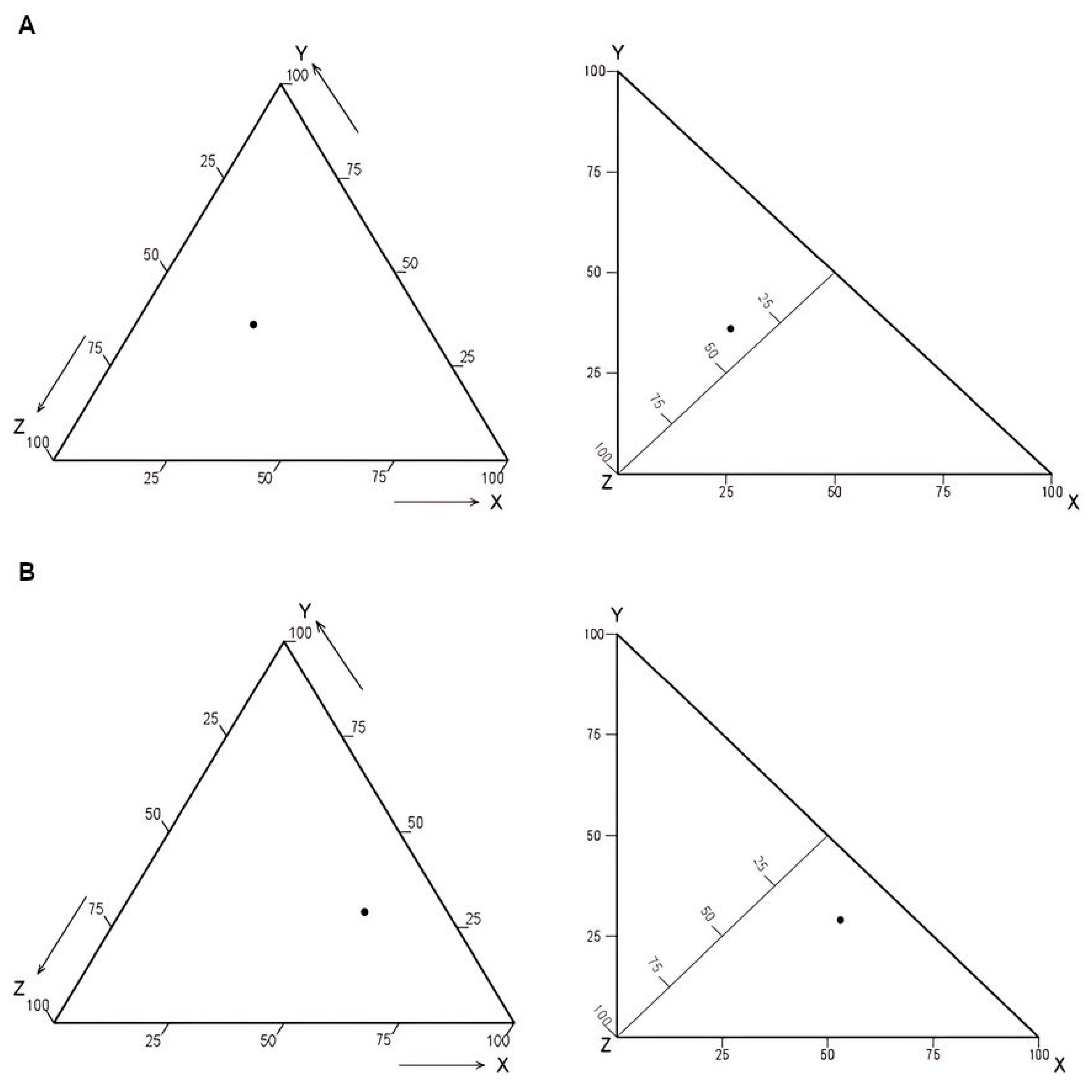
| Dominance of one of the variables | 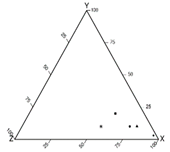 | 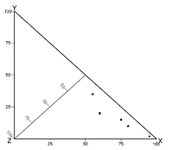 | ||||||
| If points are located closer to one of the vertices, the variable located in this vertex is dominant. | ||||||||
| Location of points on the graph when two variables have the same values at a point (this phenomenon can be observed for all pairs of variables; here for variables Y and Z) | 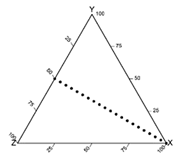 | 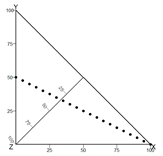 | ||||||
| Distribution of data points on a plot when one variable has the same value at several points of observation (this phenomenon can be observed for any variable; here for three example values of variable X) | 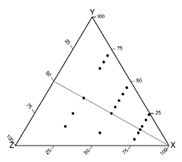 | 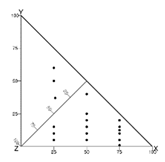 | ||||||
| Relationships between variables | ||||||||
| Linear correlation between variables (data generated artificially) | Correlation of 0.77: X vs. Y X vs. Z Y vs. Z | Correlation of 0.77: X vs. Y X vs. Z Y vs. Z | ||||||
| Nonlinear relationship between variables (data generated artificially) | Nonlinear relationship: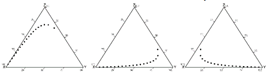 X vs. Y X vs. Z Y vs. Z | Nonlinear relationship: X vs. Y X vs. Z Y vs. Z | ||||||
| Questionnaire | No. of Respondents | Years of Experience [%] | First Language of Respondent [%] | Gender [%] | ||||
|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | >10 | English | Other | Woman | Man | ||
| 1 | 112 | 8.9 | 21.4 | 69.6 | 41.1 | 58.9 | 20.5 | 79.5 |
| 2 | 109 | 6.4 | 23.8 | 69.7 | 29.3 | 70.6 | 28.4 | 71.5 |
| 3 | 105 | 3.8 | 20.0 | 76.2 | 28.6 | 71.4 | 17.1 | 82.8 |
| 4 | 115 | 9.6 | 21.7 | 68.7 | 39.1 | 60.9 | 26.9 | 73.0 |
| Total | 441 | 7.2 | 21.7 | 71.0 | 34.5 | 65.4 | 23.2 | 76.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tartanus, M.; Sas, D.; Borowski, B.; Malusà, E.; Kozak, M. Ternary vs. Right-Angled Plots in Agricultural Research: An Assessment of Data Representation Efficiency and User Perception. Appl. Sci. 2025, 15, 9949. https://doi.org/10.3390/app15189949
Tartanus M, Sas D, Borowski B, Malusà E, Kozak M. Ternary vs. Right-Angled Plots in Agricultural Research: An Assessment of Data Representation Efficiency and User Perception. Applied Sciences. 2025; 15(18):9949. https://doi.org/10.3390/app15189949
Chicago/Turabian StyleTartanus, Małgorzata, Daniel Sas, Bartłomiej Borowski, Eligio Malusà, and Marcin Kozak. 2025. "Ternary vs. Right-Angled Plots in Agricultural Research: An Assessment of Data Representation Efficiency and User Perception" Applied Sciences 15, no. 18: 9949. https://doi.org/10.3390/app15189949
APA StyleTartanus, M., Sas, D., Borowski, B., Malusà, E., & Kozak, M. (2025). Ternary vs. Right-Angled Plots in Agricultural Research: An Assessment of Data Representation Efficiency and User Perception. Applied Sciences, 15(18), 9949. https://doi.org/10.3390/app15189949







