Vehicle Collision Frequency Prediction Using Traffic Accident and Traffic Volume Data with a Deep Neural Network
Abstract
Featured Application
Abstract
1. Introduction
2. Data and Variables
2.1. Accident Case Data
2.2. Traffic Volume Data
2.3. Data Preprocessing
2.3.1. Variable Organization and Handling of Missing Values
2.3.2. Categorical Variable Encoding
2.3.3. Continuous Variable Normalization
2.3.4. Dataset Splitting
- Elimination of bias in the model performance estimation and enhancement of the generalization capability;
- Reliable performance estimation, as all data samples were included once in validation;
- Robust evaluation even when outliers or imbalanced data are present.
3. Theoretical Basis for Crash Frequency Prediction
4. Deep Learning-Based Crash Risk Rate () Estimation
4.1. Theoretical Background
4.2. Input Variables
- Crash-related variables included travel speed (TRAV_SPNAME), collision direction (IMPACT1NAME), crash severity (HARM_EVNAME), and vehicle type (BODY_TYPNAME). These reflect the dynamics of the crash event.
- Environmental factors included the road surface condition (VSURCONDNAME), state location (STATENAME), and day of week (WEEKDAY_NAME). These contextual variables indirectly reflect risk levels and driver behavior.
4.3. DNN Model Structure and Hyperparameters
4.3.1. Definition of and the Dependent Variable in the DNN Model
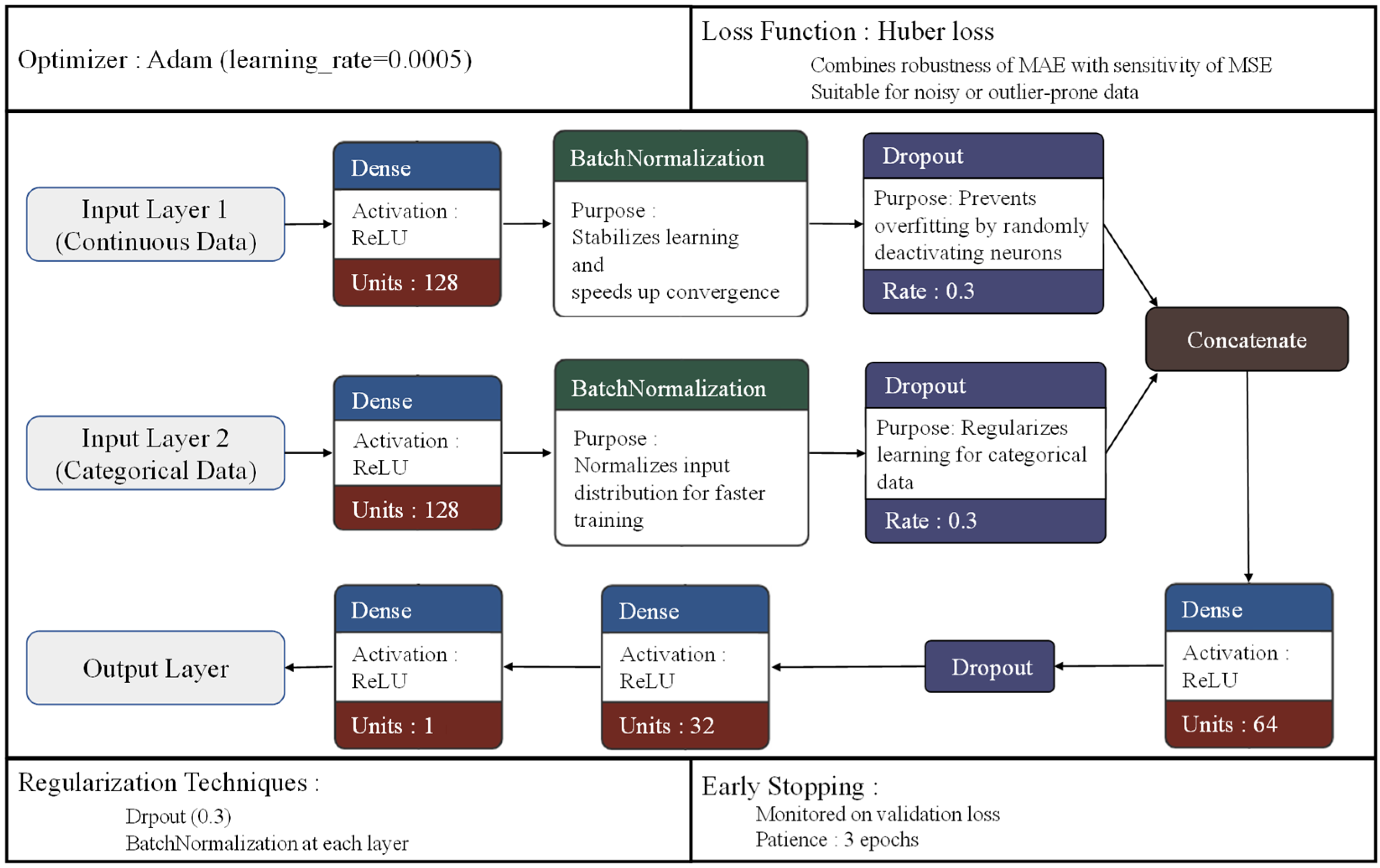
4.3.2. DNN Architecture
- Input layer—processes continuous inputs (2 variables) and categorical inputs (approximately 170 variables after one-hot encoding) using a dual-input structure.
- Hidden layers—
- ‑
- Continuous input pathway—Dense (128) → Batch Normalization → Dropout (0.3)
- ‑
- Categorical input pathway—Dense (128) → Batch Normalization → Dropout (0.3)
- ‑
- Merged pathway—Dense (64) → Dropout (0.3) → Dense (32)
- Activation function—ReLU was applied to all Dense layers.
- Normalization and dropout—Batch normalization and dropout (rate = 0.3) were applied to each input pathway.
- Output layer—ReLU activation (activation = ‘relu’) for positive continuous outputs.
4.3.3. Hyperparameter Configuration
4.4. Model Training and Performance Evaluation
4.4.1. Quantitative Performance
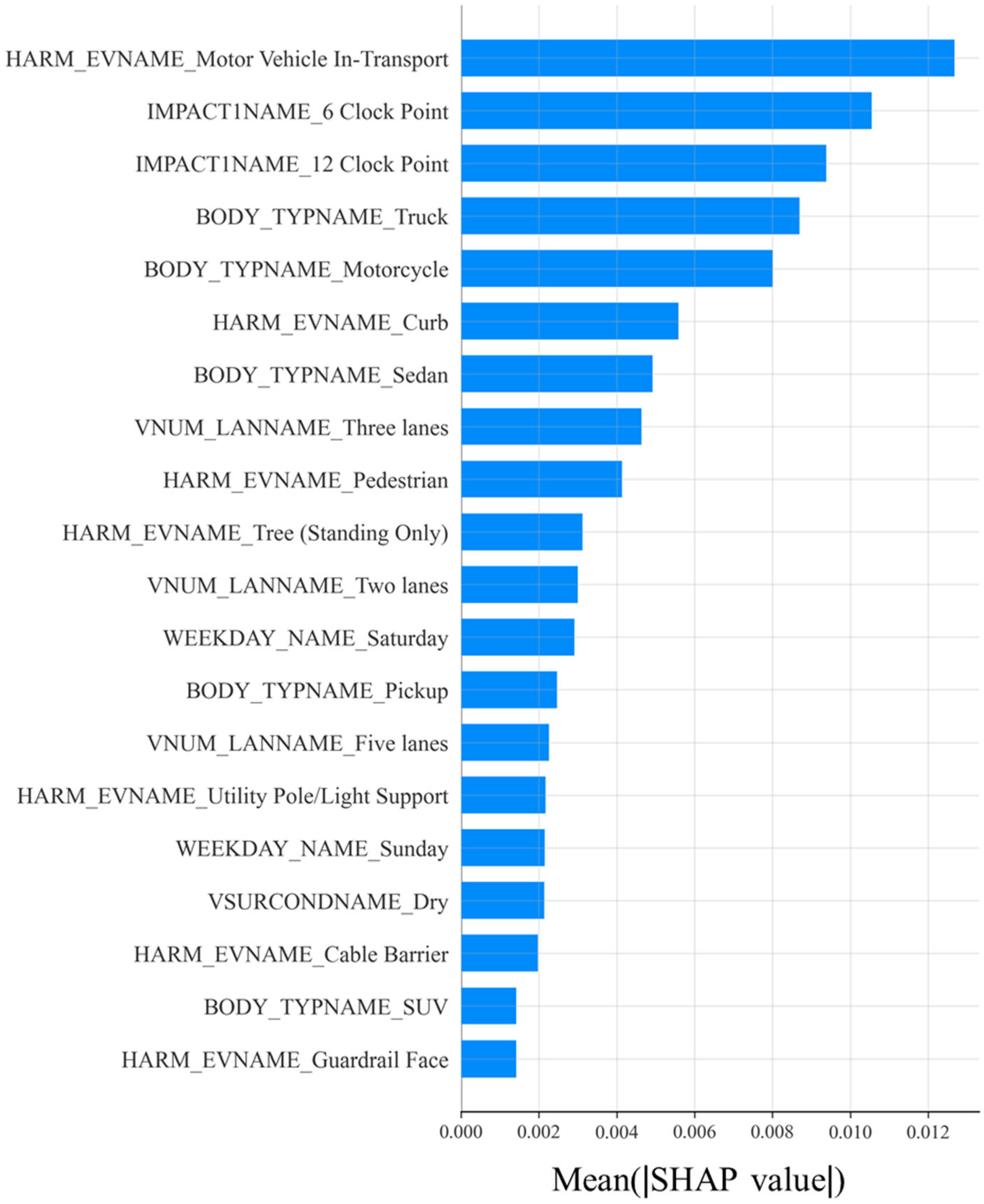
4.4.2. Post Hoc Interpretability Analysis
5. Exposure Frequency () Estimation Method
5.1. Data Composition and Key Variables
5.2. Safety Performance Function (SPF) Theory
- Truck Ratio = ;
- Traffic density, lane width, and road length are considered together to estimate actual exposure in a multidimensional manner;
- A scaling coefficient of dividing by 1000 is included for unit conversion.
5.3. Exposure Frequency Calculation Results
6. Crash Frequency () Prediction and Result Analysis
6.1. Overview of the Calculation Procedure
6.2. Predicted Value Distribution and Visualization
- Urban congested areas— was elevated where AADT and traffic density were both high;
- Logistics and industrial corridors—a high proportion of heavy vehicles increased both and , amplifying ;
- Major highway interchanges—multilane arterials with heavy flow showed peak values;
- Rural segments—typically associated with a low due to minimal exposure and risk.
6.3. Prediction Performance Evaluation and Implications
- Structural insights—the separate calculation of and enables the attribution of the crash risk;
- Accuracy—the DNN model captures complex nonlinearities overlooked in traditional models;
- Policy relevance—the model informs targeted countermeasures based on specific risk contributors.
7. Conclusions and Future Research Directions
- Combining interpretability and predictive power—by separating and λ, the framework ensures both the ability to analyze contributing factors and high predictive precision;
- The DNN model, designed to account for high-dimensional and complex variable structures, demonstrated robust performance (R2 = 0.7482);
- Identification of high-risk segments—the framework clearly identified high- segments (e.g., logistics hubs, urban congestion zones, and major highway interchanges).
- Mitigating data imbalance—applying data augmentation techniques such as SMOTE and GAN for high-risk segments;
- Advancing model architecture—enhancing learning performance through Residual, Attention, and Ensemble structures;
- Integrated risk estimation—combining crash severity indicators to develop a comprehensive risk measure in the form of Risk = Fi × C;
- Assessing real-time applicability—building a real-time crash risk prediction system integrated with intelligent transportation systems (ITSs) and autonomous driving support platforms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AADT | Annual Average Daily Traffic |
| DNN | Deep Neural Network |
| SPF | Safety Performance Function |
| AASHTO | American Association of State Highway and Transportation Officials |
| HSM | Highway Safety Manual |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| MLP | Multilayer Perceptron |
| FHWA | Federal Highway Administration |
| FARS | Fatality Analysis Reporting System |
| ITS | Intelligent Transportation System |
| NHTSA | National Highway Traffic Safety Administration |
| KDE | Kernel Density Estimation |
References
- National Highway Traffic Safety Administration (NHTSA). U.S. Traffic Deaths Statistics; NHTSA: Washington, DC, USA, 2022. [Google Scholar]
- Lord, D.; Mannering, F. The statistical analysis of crash-frequency data: A review and assessment of methodological alternatives. Transp. Res. Part A Policy Pract. 2010, 44, 291–305. [Google Scholar] [CrossRef]
- Washington, S.; Karlaftis, M.; Mannering, F. Statistical and Econometric Methods for Transportation Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Miaou, S.P. The relationship between truck accidents and geometric design of road sections: Poisson versus negative binomial regressions. Accid. Anal. Prev. 1994, 26, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aty, M.; Radwan, A.E. Modeling traffic accident occurrence and involvement. Accid. Anal. Prev. 2000, 32, 633–642. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, Y. Prediction of urban traffic accident risk based on XGBoost algorithm. Appl. Sci. 2022, 12, 298. [Google Scholar] [CrossRef]
- Xu, C.; Wang, W.; Zhang, M. A deep learning approach for urban traffic accident risk prediction and visualization. PLoS ONE 2020, 15, e0231907. [Google Scholar] [CrossRef]
- Chang, L.Y. Analysis of freeway accident frequencies: Negative binomial regression versus artificial neural network. Saf. Sci. 2005, 43, 541–557. [Google Scholar] [CrossRef]
- Kamrani, M.; Arvin, R.; Khattak, A.J. Extracting useful information from connected vehicle data: An empirical study of driving volatility measures and crash frequency at intersections. Accid. Anal. Prev. 2018, 121, 114–122. [Google Scholar] [CrossRef]
- Zuo, C.; Zhang, X.; Zhao, G.; Yan, L. PCR: A Parallel Convolution Residual Network for Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2025, 9, 3072–3083. [Google Scholar] [CrossRef]
- Chen, J.; Pan, S.; Peng, W.; Xu, W. Bilinear Spatiotemporal Fusion Network: An Efficient Approach for Traffic Flow Prediction. Neural Netw. 2025, 187, 107382. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Lü, J.; Liu, K.; Zhu, A.; Snoussi, H.; Zhang, B. Synchronous Spatiotemporal Graph Transformer: A New Framework for Traffic Data Prediction. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 10589–10603. [Google Scholar] [CrossRef]
- Al Mamun, M.M.; Hossain, S.; Ahmed, F. Traffic accident severity prediction using machine learning algorithms and feature selection techniques. Appl. Sci. 2023, 13, 2455. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). Highway Safety Manual; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Khattak, A.J.; Ahmed, M.M.; Lu, C. Truck traffic exposure and crash risk: Disaggregated AADT impacts by truck type. Sustainability 2024, 16, 1537. [Google Scholar] [CrossRef]
- Kloeden, C.N.; McLean, A.J.; Moore, V.M.; Ponte, G. Travelling Speed and the Risk of Crash Involvement on Rural Roads; Federal Office of Road Safety: Canberra, Australia, 2001.
- Wali, B.; Zou, Y.; Ozbay, K. Understanding traffic crash patterns using traffic density and modeling congestion effects. arXiv 2018, arXiv:1803.05074. [Google Scholar]
- Ma, Y.; Ma, W.; Wang, Y.; Zhang, W.; Huang, H. Modeling crash frequency on urban road segments using a hybrid deep learning framework: A comparative study with traditional statistical and machine learning models. Accid. Anal. Prev. 2023, 195, 107282. [Google Scholar] [CrossRef]
- Tang, J.; Liang, J.; Han, C.; Li, Z.; Huang, H. Crash injury severity analysis using a two-layer Stacking framework. Accid. Anal. Prev. 2019, 122, 226–238. [Google Scholar] [CrossRef]
- Zhuang, Z.; Liu, Y. A deep learning-based model for identifying blackspots on highways using historical traffic data. Appl. Sci. 2023, 13, 5296. [Google Scholar] [CrossRef]
- Bao, J.; Liu, P.; Ukkusuri, S.V. A Spatiotemporal Deep Learning Approach for Citywide Short-Term Crash Risk Prediction with Multi-Source Data. Accid. Anal. Prev. 2019, 122, 239–254. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, Q.; Lin, Y. Traffic accident forecasting based on time series and deep learning approaches. Appl. Sci. 2022, 12, 3592. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J. Comparison of machine learning models for crash prediction on rural highways. Appl. Sci. 2021, 11, 1120. [Google Scholar] [CrossRef]

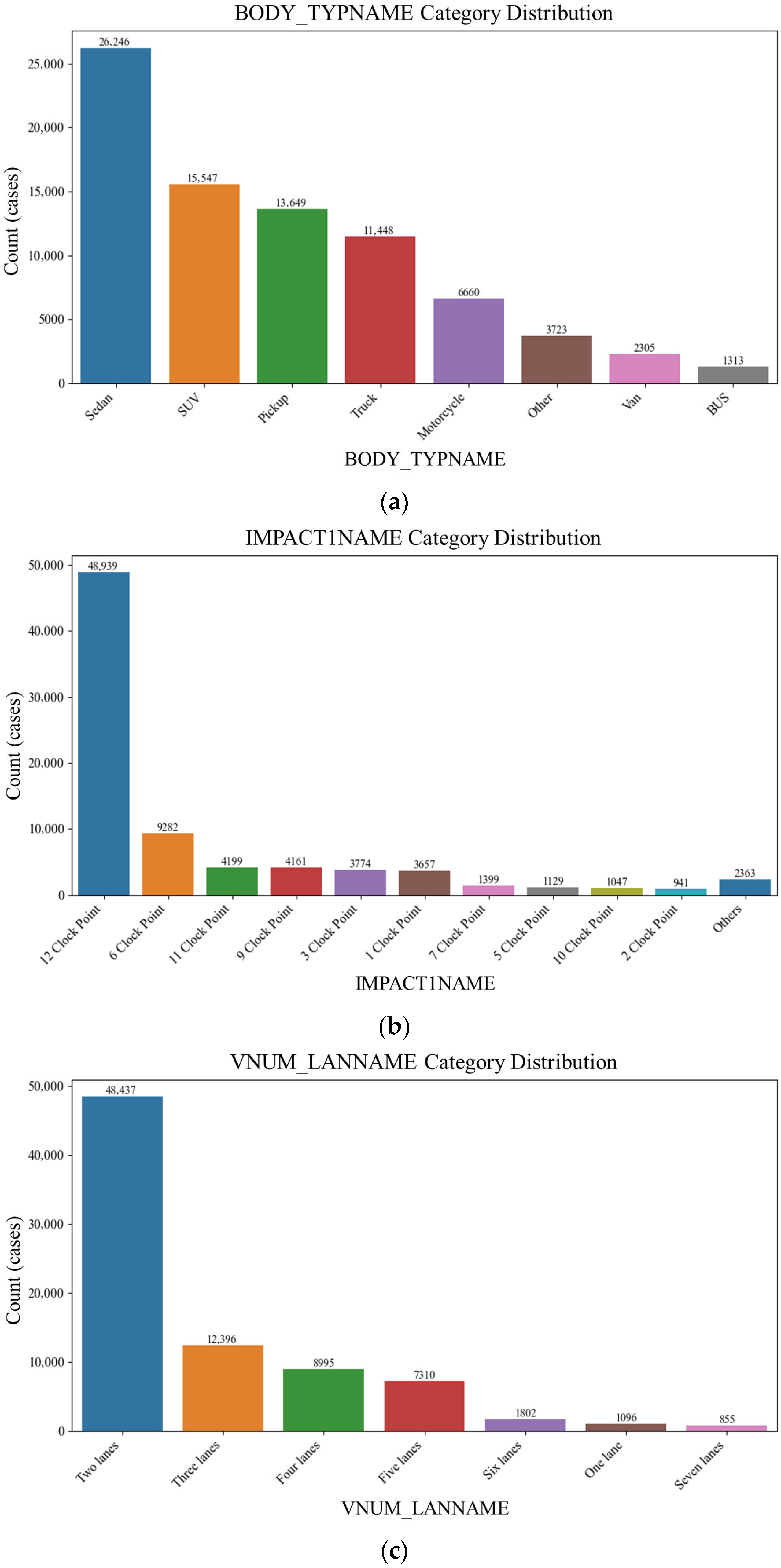
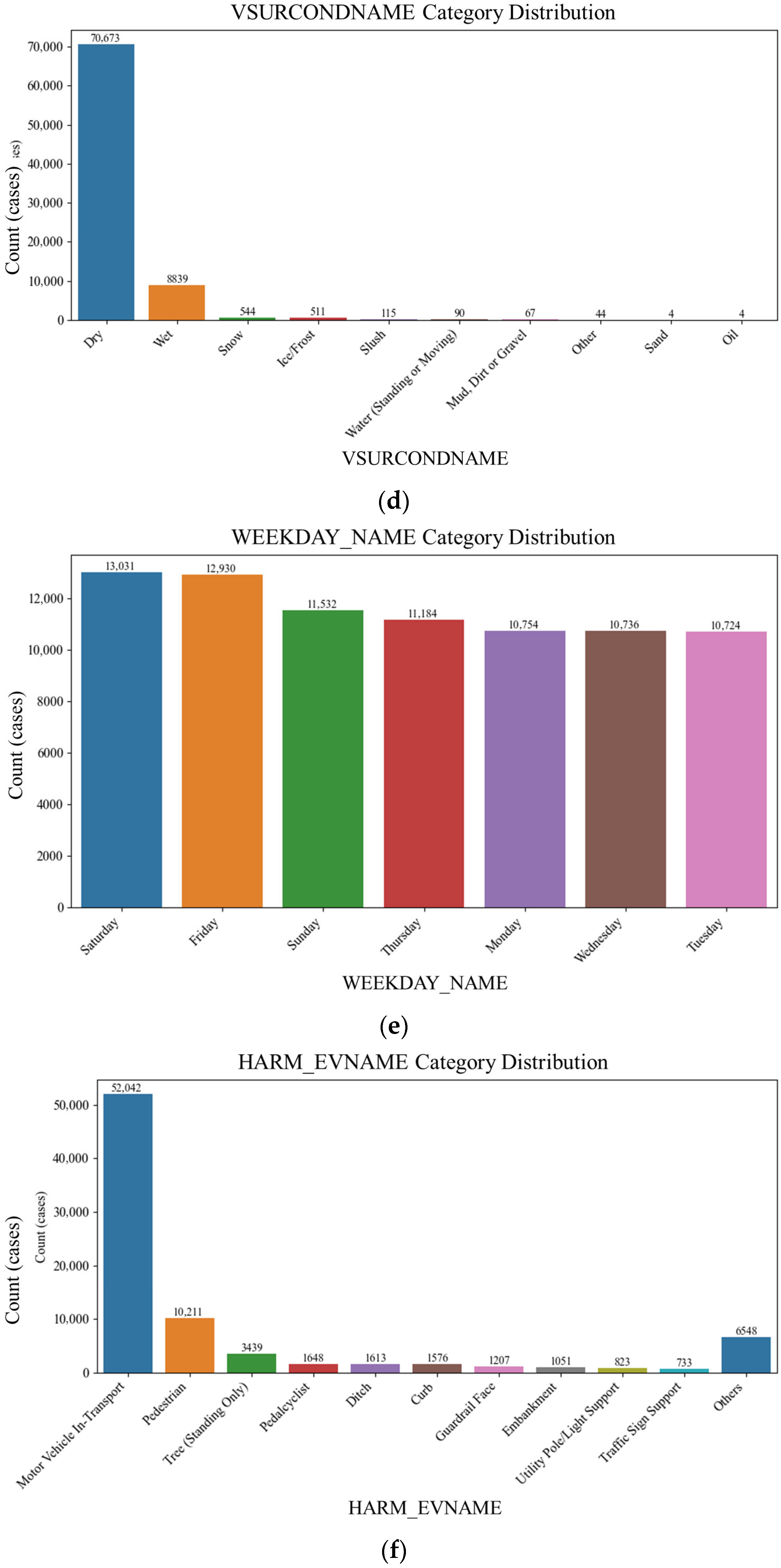
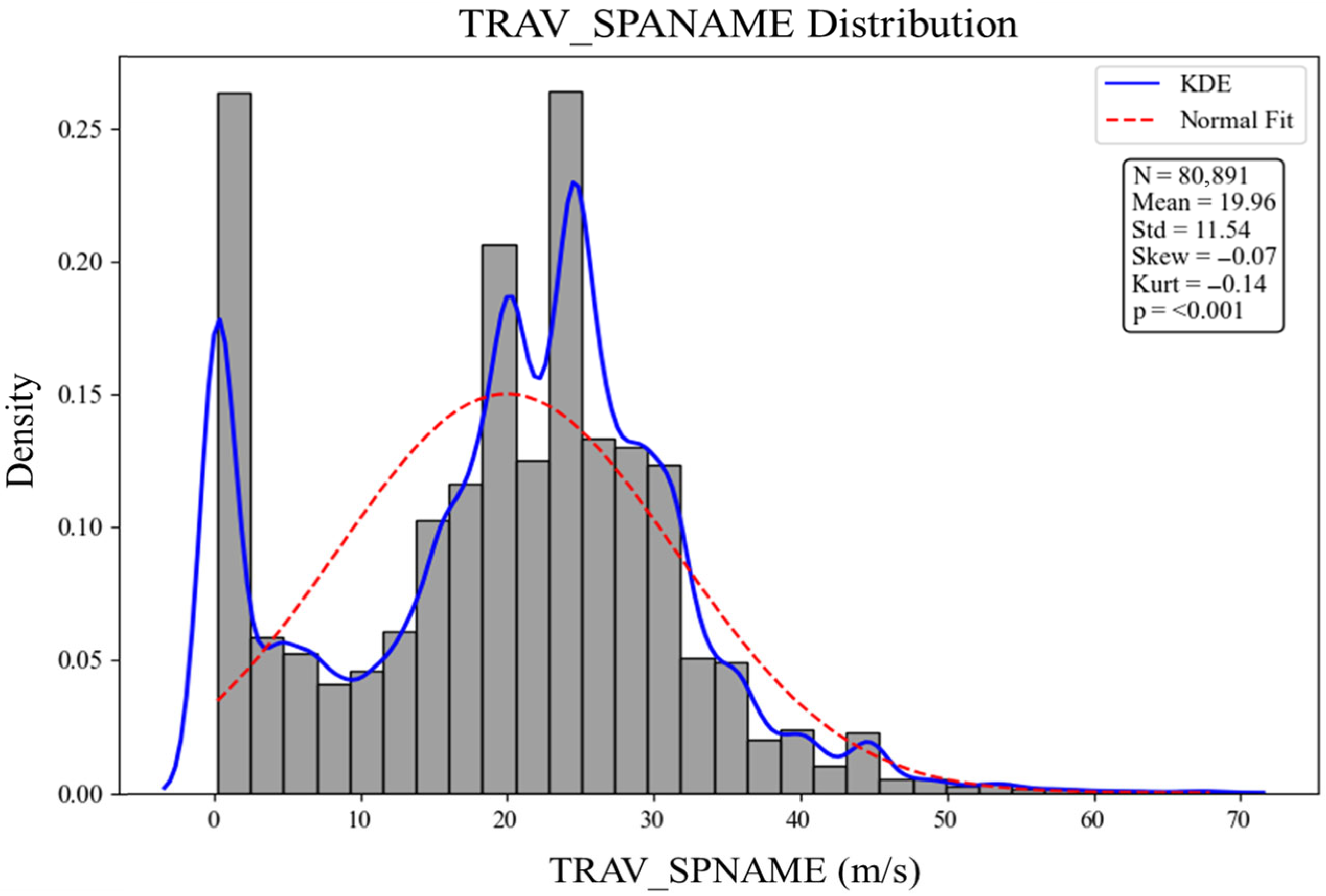



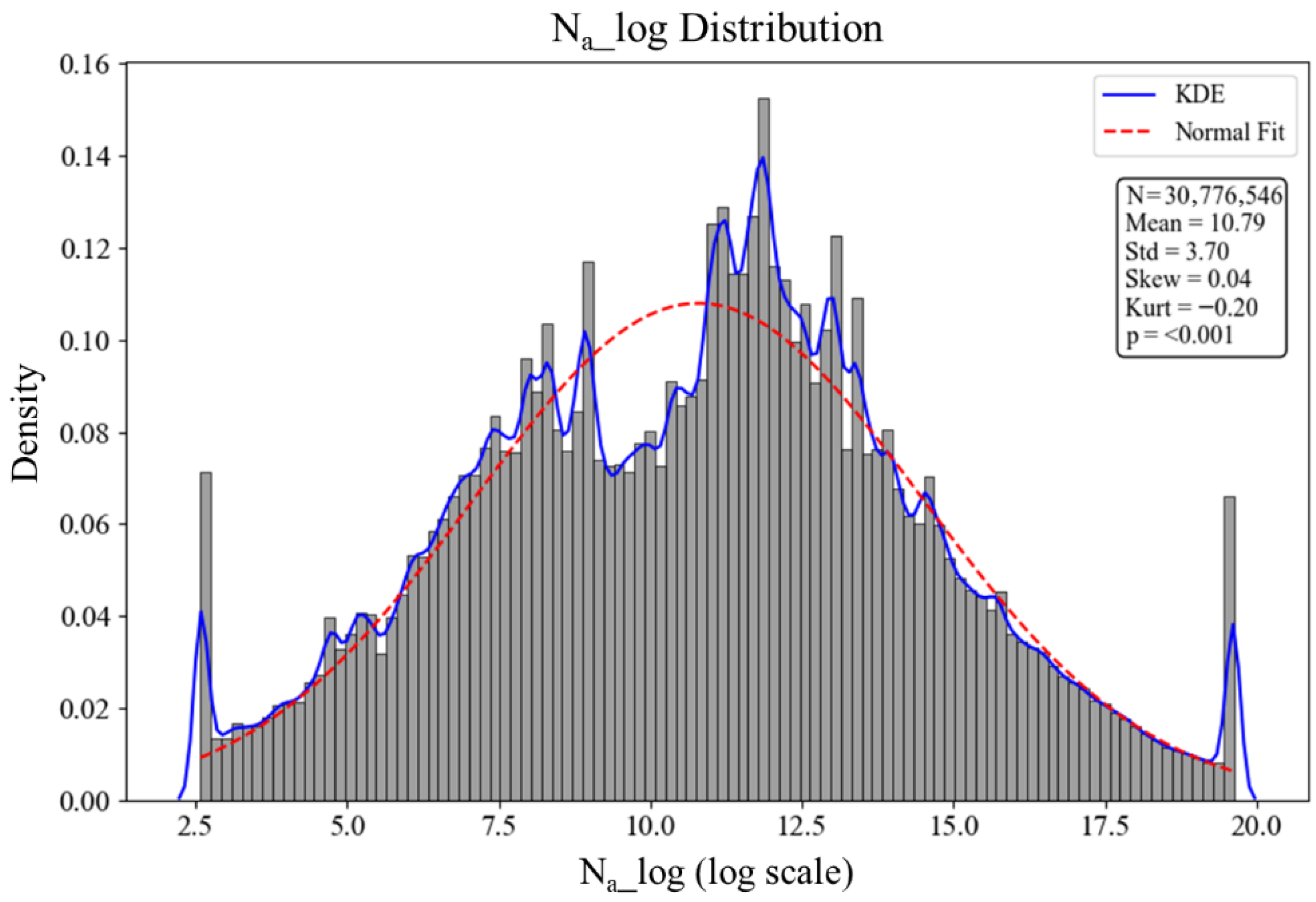
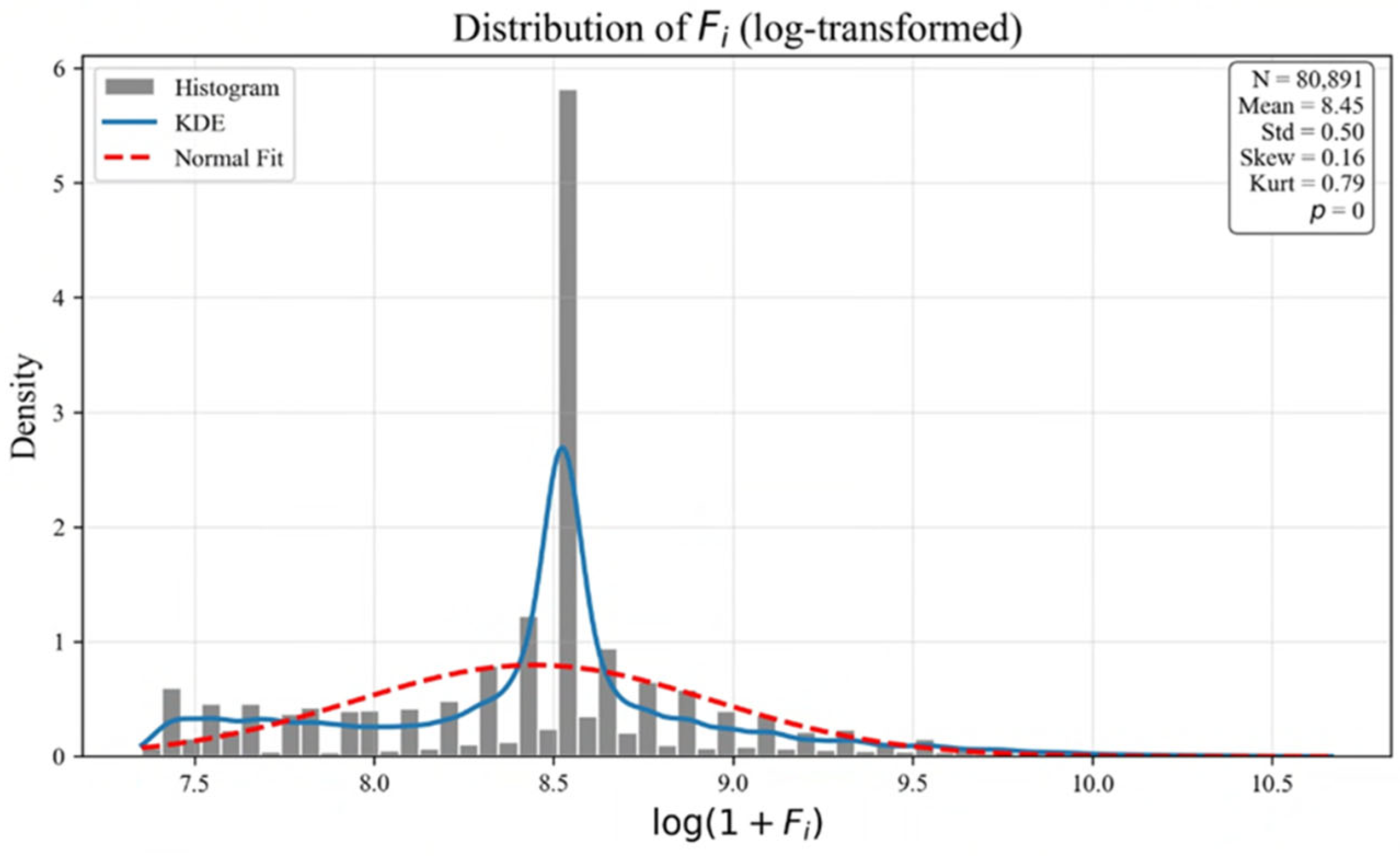
| Variable Name | Data Type | Value Range/Categories | Description |
|---|---|---|---|
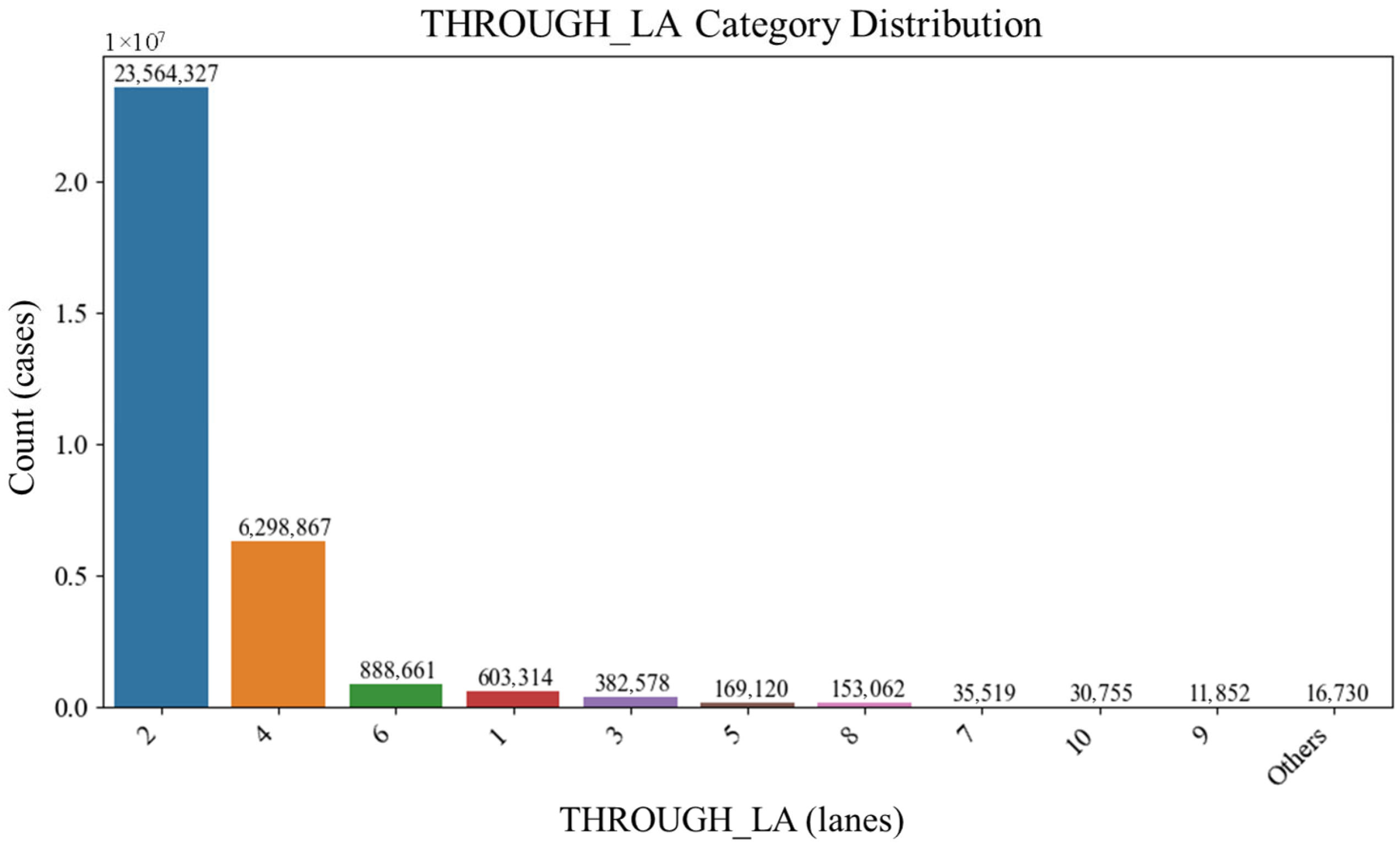
| VNUM_LANNAME | Cat. | 1–9, others | Number of travel lanes |
| VSPD_LIMNAME | Cat. | 25–65, others | Speed limit |
| TRAV_SPNAME (m/s) | Cont. | 0–45 | Actual vehicle travel speed |
| HARM_EVNAME | Cat. | Motor Vehicle, Tree, Rollover, etc. | Type of harm |
| VSURCONDNAME | Cat. | Dry, Wet, Snow, Ice, Others | Road surface condition |
| BODY_TYPNAME | Cat. | Sedan, SUV, Truck, Bus, Others | Vehicle type |
| IMPACT1NAME | Cat. | 1–12 clock directions | Impact position |
| STATENAME | Cat. | U.S. states | Location |
| WEEKDAY_NAME | Cat. | Monday–Sunday | Day of the week |
| Variable Name | Data Type | Value Range/Categories | Description |
|---|---|---|---|
| STATE_CODE | Cat. | U.S. states | Road location |
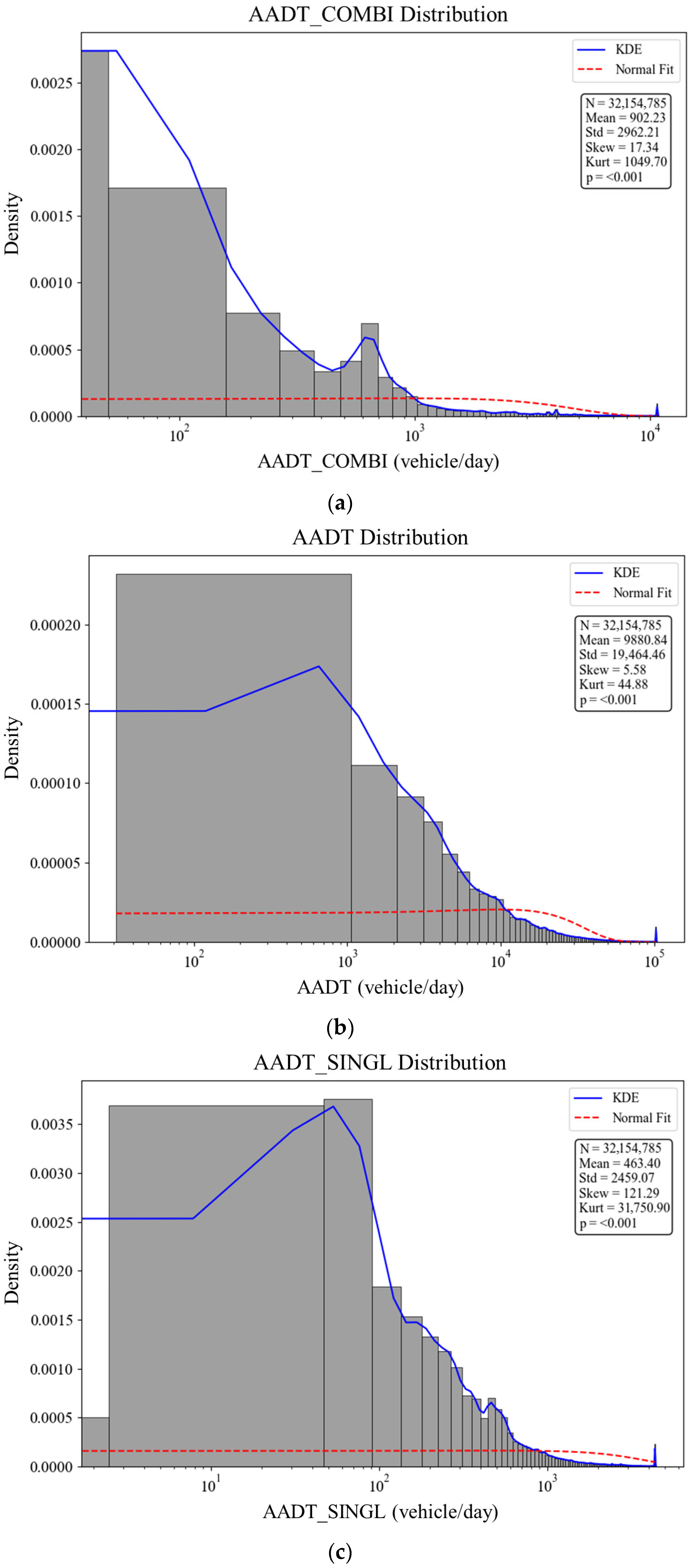
| AADT | Cont. | 1–1,277,520 vehicles/day | Avg. daily traffic (all vehicles) |
| AADT_COMBI | Cont. | 0–522,800 vehicles/day | Daily traffic of large trucks |
| AADT_SINGL | Cont. | 0–1,045,600 vehicles/day | Daily traffic of single-unit trucks |
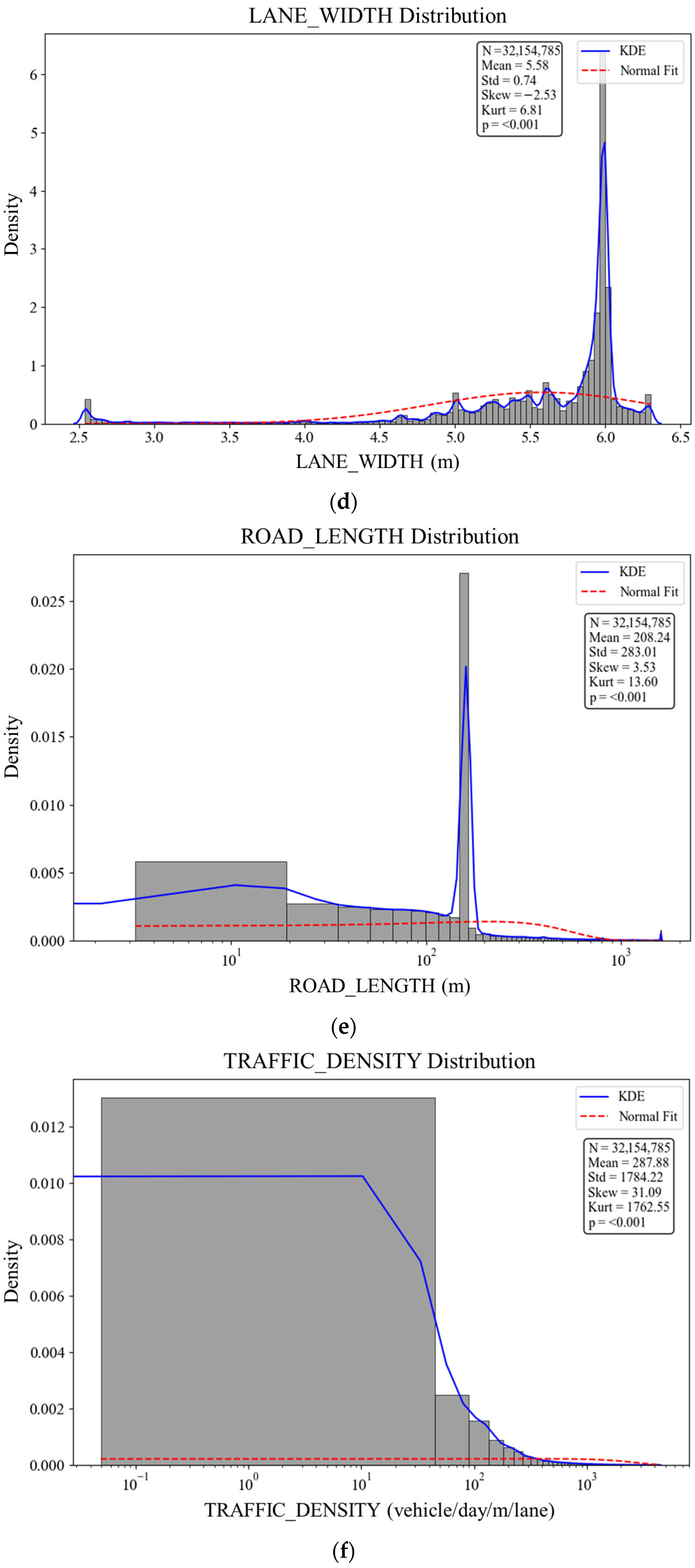
| LANE_WIDTH | Cont. | 2.5–6.5 m | Lane width |
| ROAD_LENGTH | Cont. | 9.8–1998.8 m | Road segment length |
| TRAFFIC_DENSITY | Cont. | 0–1392.5 vehicles/day/m/lane | Density per lane |
| Parameter | Setting | Rationale |
|---|---|---|
| Hidden Layer Structure | [{Dense (128) → BN → Dropout} → Concatenate → Dense (64) → Dropout (0.3) → Dense (32) → Output (1, ReLU)] | Gradual reduction to mitigate overfitting and stabilize learning |
| Activation Function | ReLU | Standard for nonlinear learning in a DNN |
| Dropout Rate | 0.3 | Commonly used value to prevent overfitting [22] |
| Normalization | Batch Normalization | Enhances training stability and convergence |
| Loss Function | Huber Loss/MSE | Balances robustness to outliers with accuracy [23] |
| Optimizer | Adam | Adaptive learning rate, fast convergence |
| Learning Rate | 0.001 | Typical initial value with good convergence |
| Epochs | 200 | Sufficient training with early stopping |
| Early Stopping | Patience = 10 | Prevents overfitting when validation loss stagnates |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, Y.G.; Jo, K.C.; Lee, J.S.; Yu, J.S. Vehicle Collision Frequency Prediction Using Traffic Accident and Traffic Volume Data with a Deep Neural Network. Appl. Sci. 2025, 15, 9884. https://doi.org/10.3390/app15189884
Ko YG, Jo KC, Lee JS, Yu JS. Vehicle Collision Frequency Prediction Using Traffic Accident and Traffic Volume Data with a Deep Neural Network. Applied Sciences. 2025; 15(18):9884. https://doi.org/10.3390/app15189884
Chicago/Turabian StyleKo, Yeong Gook, Kyu Chun Jo, Ji Sun Lee, and Jik Su Yu. 2025. "Vehicle Collision Frequency Prediction Using Traffic Accident and Traffic Volume Data with a Deep Neural Network" Applied Sciences 15, no. 18: 9884. https://doi.org/10.3390/app15189884
APA StyleKo, Y. G., Jo, K. C., Lee, J. S., & Yu, J. S. (2025). Vehicle Collision Frequency Prediction Using Traffic Accident and Traffic Volume Data with a Deep Neural Network. Applied Sciences, 15(18), 9884. https://doi.org/10.3390/app15189884









