A Benchmarking Framework for Hybrid Quantum–Classical Edge-Cloud Computing Systems
Abstract
1. Introduction
- (1)
- It proposes a novel benchmarking framework for evaluating quantum systems within edge-cloud networks using real-world performance metrics.
- (2)
- It leverages established quantum algorithms to assess the performance of quantum platforms under varied conditions and computational loads.
- (3)
- It implements an auxiliary communication model within a virtualized environment to emulate realistic network latencies, enabling comprehensive evaluation of communication performance.
- (4)
- It presents insights from longitudinal experiments, revealing platform-specific trends and integration challenges, particularly in terms of optimizing the integration of quantum technology into practical, real-world tasks.
- (5)
- It offers performance optimization strategies derived from value analysis, facilitating informed tuning of system parameters to enhance efficiency.
2. Background and Conceptual Framework
2.1. Fundamental Mechanisms in Quantum Computing
2.1.1. Dirac Notation, Superposition, Parallelism, and Entanglement
2.1.2. Gate-Based Quantum Computing
2.1.3. Selected Quantum Devices in Hybrid Edge Architectures
- Quantum processing unit (QPU): QPU is the core computational component of a quantum computer, executing quantum circuits on qubits to solve complex problems that are intractable for classical computers. The number of physical qubits in current gate-based quantum computers, particularly superconducting qubits (used by IBM and Google) and trapped-ion qubits (used by Quantinuum), is currently less than 1500. In such a scenario, algorithms that distribute workload over classical and quantum resources are essential to enhance reliability and performance.
- Quantum Switches (QS): quantum switches enable connection of channels between devices in a quantum network for routing quantum information or distributing entanglements. A quantum switch can handle several quantum channels at the same time [23].
- Quantum Repeaters (QR): these devices extend communication distance by overcoming signal loss without violating the no-cloning principle, using techniques such as teleportation, entanglement swapping, and error correction [24]. Quantum relays function similarly but lack entanglement purification and quantum memory, instead improving transmission range by boosting the signal-to-noise ratio at detectors [25].
- Quantum memory: quantum memory stores states of single photons or entangled states for short periods, without destroying their quantum properties. They assist hybrid edge computing by enabling synchronization of operations and storing entangled states until nodes are aligned.
- Quantum sensors: utilize properties like superposition and entanglement to achieve measurement capabilities exceeding those of classical sensors [26]. At the edge, quantum sensors provide ultra-precise measurements and improve the quality of input data. These sensors can operate reliably in constrained environments like battlefields and remote areas.
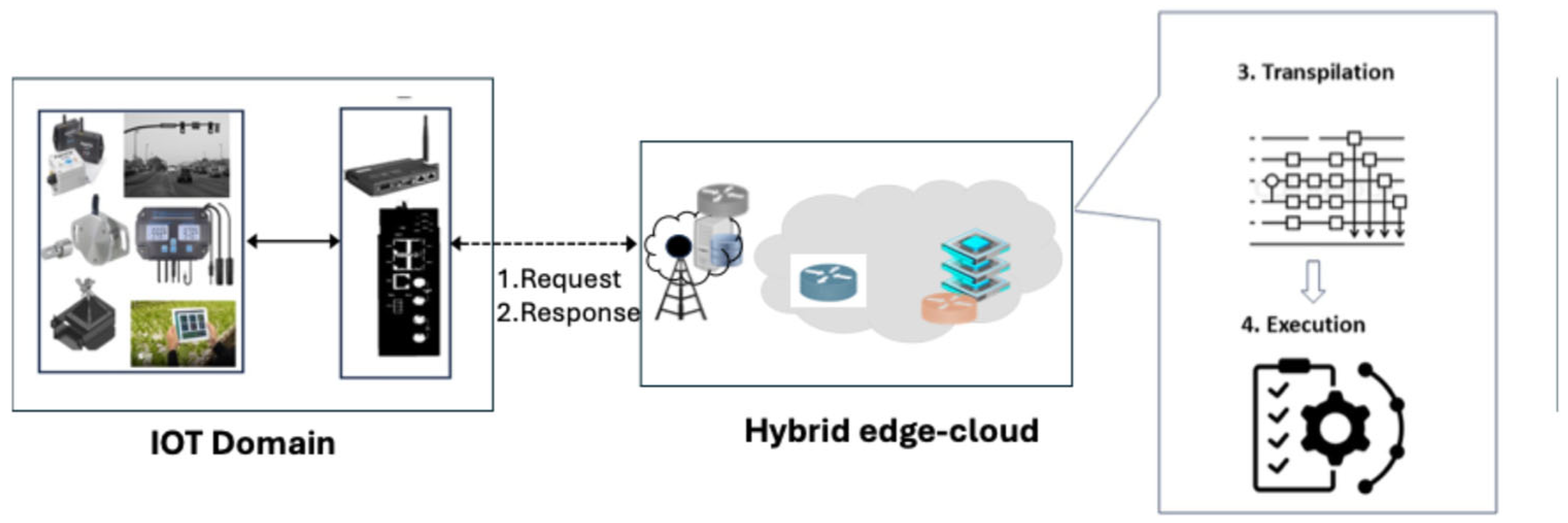
2.1.4. Architectural Aspects of the Hybrid Edge-Cloud Systems
- End-point Layer: this layer comprises sensing, actuating, and measuring devices located near the physical environment. These devices collect high volumes of raw data, which must be processed or forwarded for analysis.
- Edge Layer: the edge layer includes local classical compute nodes with moderate processing and storage capacity. Quantum devices may also be integrated at the edge to support latency-sensitive hybrid computations closer to the data source.
- Main Cloud Layer: this layer provides access to high-capacity classical and quantum computing resources for computationally intensive tasks, such as training large-scale AI models or executing complex quantum circuits. Cloud-based quantum platforms such as Amazon Braket, IBM Quantum, and Quantinuum Nexus allow users to compile, transpile, and optimize quantum programs through cloud APIs.
- Communication layer: this layer provides reliable and secure transmission channels created through classical and quantum communication processors, routers, switches, relays, and repeaters. This layer aims to maintain low latency and high throughput.
- Orchestration layer: this layer is responsible for managing and coordinating cross-layer provisioning of resources from a pool of interacting classical and quantum components. It carries out key functions such as task partitioning, scheduling, and workflow management across the hybrid environment. It helps adapt to system challenges by handling noise and errors, device heterogeneity, and communication across components.
2.2. Background of Quantum Benchmarking
2.2.1. Formal Explanation of Quantum Benchmarking
2.2.2. Types of Quantum Benchmarking
- 1.
- Qubit-Level Benchmarking focuses on the basic building blocks of quantum gates, i.e., qubits. The number of qubits directly relates to the computational capacity of a quantum processor [32]. The key metrics are coherence times, which quantify the duration over which the qubits maintain their quantum states, and frequency response, which characterizes the qubits’ spectrum behavior and interaction with control signals.
- 2.
- Gate-Level Benchmarking looks at how well individual quantum gates perform. It is widely recognized as a critical component of any comprehensive quantum benchmarking framework. Common techniques at this layer include
- Randomized benchmarking (RB): provides an estimate of average gate fidelity while mitigating the influence of SPAM (state preparation and measurement) errors. RB is scalable and is less affected by noise.
- Direct Fidelity Estimation (DFE): estimates gate fidelity under the assumption of negligible SPAM errors. DFE provides a single value between 0 and 1 as a measure of gate implementation, where 1 represents the ideal gate implementation.
- Quantum Set Tomography (QPT): offers complete gate characterization but is resource intensive and does not scale well.
- 3.
- Circuit-Level Benchmarking tests full quantum circuits to see how well they perform under real-world conditions. Benchmarks in this category use some of the following metrics to assess how circuits behave as they scale in depth and complexity:
- Quantum Volume: reflects a system’s ability to reliably execute increasingly complex circuits reliably. It captures a combination of qubit count, gate fidelity, connectivity, and compiler performance.
- Circuit Layer Operations Per Second (CLOPS): measures the execution speed of a quantum processor in executing layers of QV circuits. It is a throughput-oriented performance metric.
- Cross-entropy benchmarking (XEB): a scalable noise characterization and benchmarking scheme that estimates the fidelity of an n-qubit circuit composed of single- and two-qubit gates.
- 4.
- Processor-Level Benchmarking: This layer evaluates the overall performance of quantum processors. It includes system-wide metrics like quantum volume, holistic workload testing, and time-to-solution, which measures how quickly and precisely a device can complete a task.
- 5.
- Platform Level Benchmarking: focuses on the broader quantum ecosystem—cloud access, compilers, SDKs, and APIs. Different providers offer unique environments with their own software stacks, like IBM’s Qiskit, Google’s Cirq, Quantinuum’s TKET, the Berkeley Quantum Synthesis Toolkit (BQSKit), Quantum Tool Suite (QTS), and Duke University’s Staq—all offer varying degrees of abstraction, performance optimization, and hardware integration [33]. Benchmarking at this level helps compare platforms using tools like Open Quantum Assembly Language (QASMBench) or MQT Bench, which provide consistent tests across different hardware technologies (e.g., superconducting, trapped ion, or photonic qubits).
- 6.
- Application-Level Benchmarking is about testing how well the quantum systems handle real-world problems. Frameworks like Quantum computing Application benchmark (QUARK), Munich Quantum Toolkit (MQT), and workload-specific tests examine performance from an application perspective, looking at how algorithms like Variational Quantum Factoring (VQF) behave on different systems.
- 7.
- Full Stack Benchmarking ties everything together, evaluating the entire system—from hardware and circuits up through orchestration, resource management, and latency. This is especially useful in NISQ-era applications involving hybrid quantum–classical systems, where performance at every layer impacts the outcome.
2.2.3. Quantum Benchmarking Metrics
- Benchmarking quantum systems requires a range of performance metrics to assess their reliability, speed, and computational accuracy. Some of the most used metrics across quantum benchmarking frameworks include:
- Qubit coherence: Qubit coherence refers to the duration of time for which a qubit can maintain its quantum state before decoherence occurs. Coherence is essential for preserving superposition and entanglement. Coherence time is a critical performance indicator, as environmental disturbances can cause decoherence, leading to loss of quantum information and rendering computations unreliable [34].
- Average gate fidelity: This metric quantifies the difference between an ideal unitary gate operation and its real-world implementation. High average gate fidelity indicates that a quantum gate behaves closely to its theoretical counterpart, minimizing operational errors [35].
- Circuit fidelity: Circuit fidelity measures how accurately an entire quantum circuit executes its intended operation. It evaluates the similarity between the final state of the physical system and the ideal (noiseless) state, reflecting the circuit’s overall correctness and resilience to noise [36].
- Error rate: quantum computing error rate refers to the probability that a qubit will change state during computation. Current quantum computers typically have error rates in the range of 0.1% to 1%, which is significantly higher than the error rates in classical computer systems [37].
- Quantum Volume: is a metric representing the largest square-shaped quantum circuit (where width, or the number of qubits, equals the depth, or the number of gate layers) that a processor can implement successfully. It captures the interplay of qubit count, gate fidelity, connectivity, and compiler efficiency.
- Qubit readout fidelity: Also known as qubit measurement fidelity, it refers to the error rate associated with qubit readout operations. It reflects the likelihood that the measured output truly represents the actual state of the qubit at the time of measurement.
- Quantum gate execution time: also referred to as quantum gate speed, it indicates the time needed to perform quantum gate operations. Faster execution times generally enable deeper circuits within limited coherence windows.
- SPAM fidelity: State Preparation and Measurement Process (SPAM) fidelity refers to how well a quantum computer can initialize qubits into a desired state and accurately read out the qubit’s state after computations. High SPAM fidelity is essential for reliable quantum input-output operations [38].
2.3. Benchmarking in Hybrid Quantum–Classical Edge-Cloud Systems
3. Related Work and Research Gaps
3.1. Related Work
3.2. Research Gaps in Quantum Computing, Edge-Cloud Computing, and Quantum Benchmark Framework
- Since the integration of quantum computing and the edge-cloud environment is still in its infancy, the focus of most existing research is on gains on the privacy front rather than performance issues like end-to-end latency involving distributed compute and networking over edge, and cloud domains. The existing benchmarking frameworks like SupermarQ and Quark evaluate centralized hybrid algorithms and do not account for quantum and classical resources distributed at the edge and in the main clouds.
- Multi-domain architectures are not focused on. Real life environments are envisaged to have classical and quantum devices communicating with each other in the same and across domains.
- Transpilation and its topology optimization levels are not stressed as important factors. If a quantum computer needs to run high-level circuits, these circuits must be converted (i.e., transpiled) to the corresponding primitive quantum gates of specific QPUs [49]. Unlike traditional compilation, which translates source code into a target language [50], transpilation specifically transforms a quantum circuit to align with the topology and constraints of a given quantum device [50]. For instance, while some compilers provide multiple levels of optimization for classical systems, many quantum platforms also offer varying optimization levels in transpilation. This step is pivotal because the efficient execution of quantum circuits depends on how well the transpilation process adapts the logical qubit connections to the physical architecture of the QPUs.
- Insufficient evaluation of heterogeneous resource allocation. Benchmarks do not evaluate how well systems handle resource-aware dynamic offloading or adaptive load balancing in hybrid edge-cloud scenarios.
4. Materials and Methods
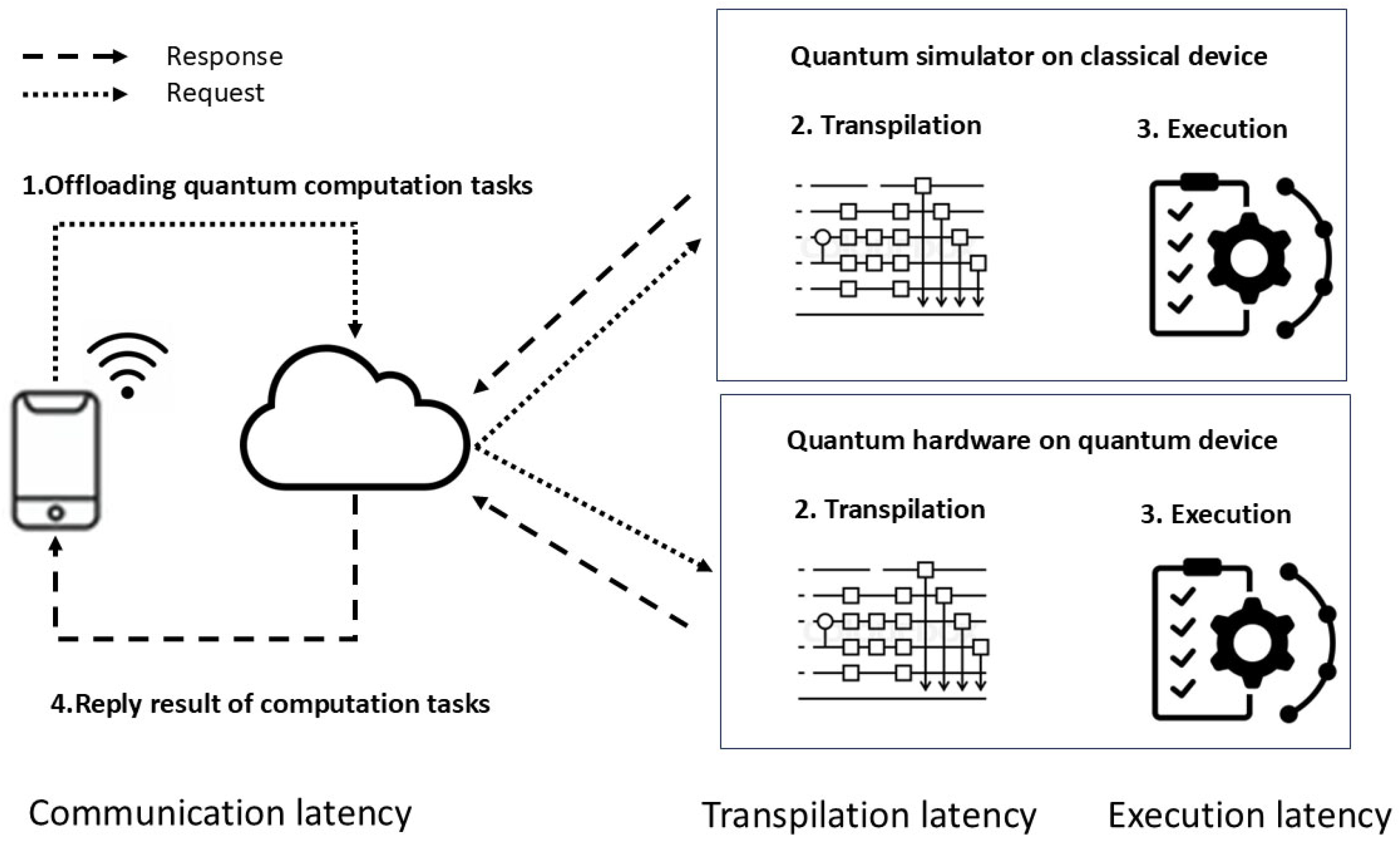
4.1. Description of the Benchmarking Framework
- : Communication Latency
- : Transpilation Latency
- : Execution Latency
4.2. Factors Impacting the Latency Score in Quantum-Edge-Cloud
4.3. The Proposed Benchmarking Framework
4.3.1. Communication Latency
4.3.2. Transpilation Latency—Method A
4.3.3. Transpilation Latency—Method B
4.3.4. Execution Latency—Method A
4.3.5. Execution Latency—Method B
4.4. Experimental Environment and Computational Resources
4.5. Quantum Algorithms Selected for Latency Evaluation
- Shor’s Algorithm is chosen for its ability to solve integer factorization in polynomial time O ((log N)3), which is crucial for assessing the power of quantum systems in breaking encryption.
- Grover’s algorithm is selected for its efficiency in searching unsorted databases by reducing the complexity of unstructured search from O(N) to .
- The quantum walks algorithm is included to evaluate the quantum system’s probabilistic modeling and simulation capabilities relevant in domains such as network routing and predictive maintenance.
4.5.1. Shor’s Algorithm
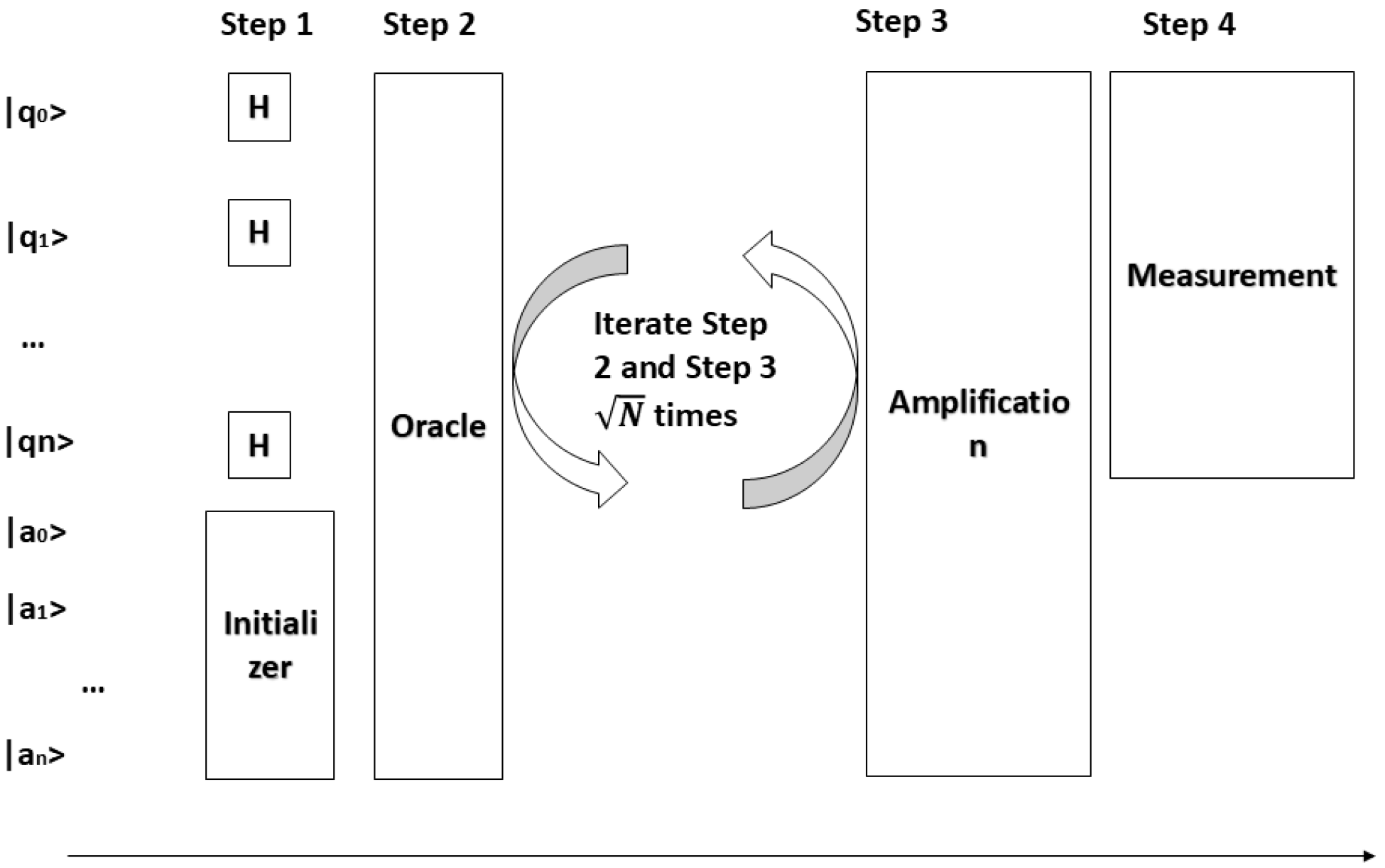
4.5.2. Grover’s Algorithm
- ∣ψ⟩ represents the equal superposition state,
- The symbol I is the identity operator.
4.5.3. Quantum Walks Algorithm
5. Experiments and Results
5.1. Communication Latency Results
5.1.1. Communication Latency: A Case Study with Grover’s Algorithm
- Simulators return output as a histogram of quantum states and their occurrence counts.
- QPUs return measured results in a similar format, though with more variation due to noise.
- Simulator Output (Optimization Level 1):
- QPU Output (Optimization Level 1):
- The output is a probability distribution over all 8 possible 3-qubit states:
5.1.2. Communication Latency: A Case Study with Shor’s Algorithm
5.1.3. Communication Latency: Case Study with Quantum Walks Algorithm
5.2. Transpilation Latency
5.2.1. Transpilation Latency of Grover’s Algorithm
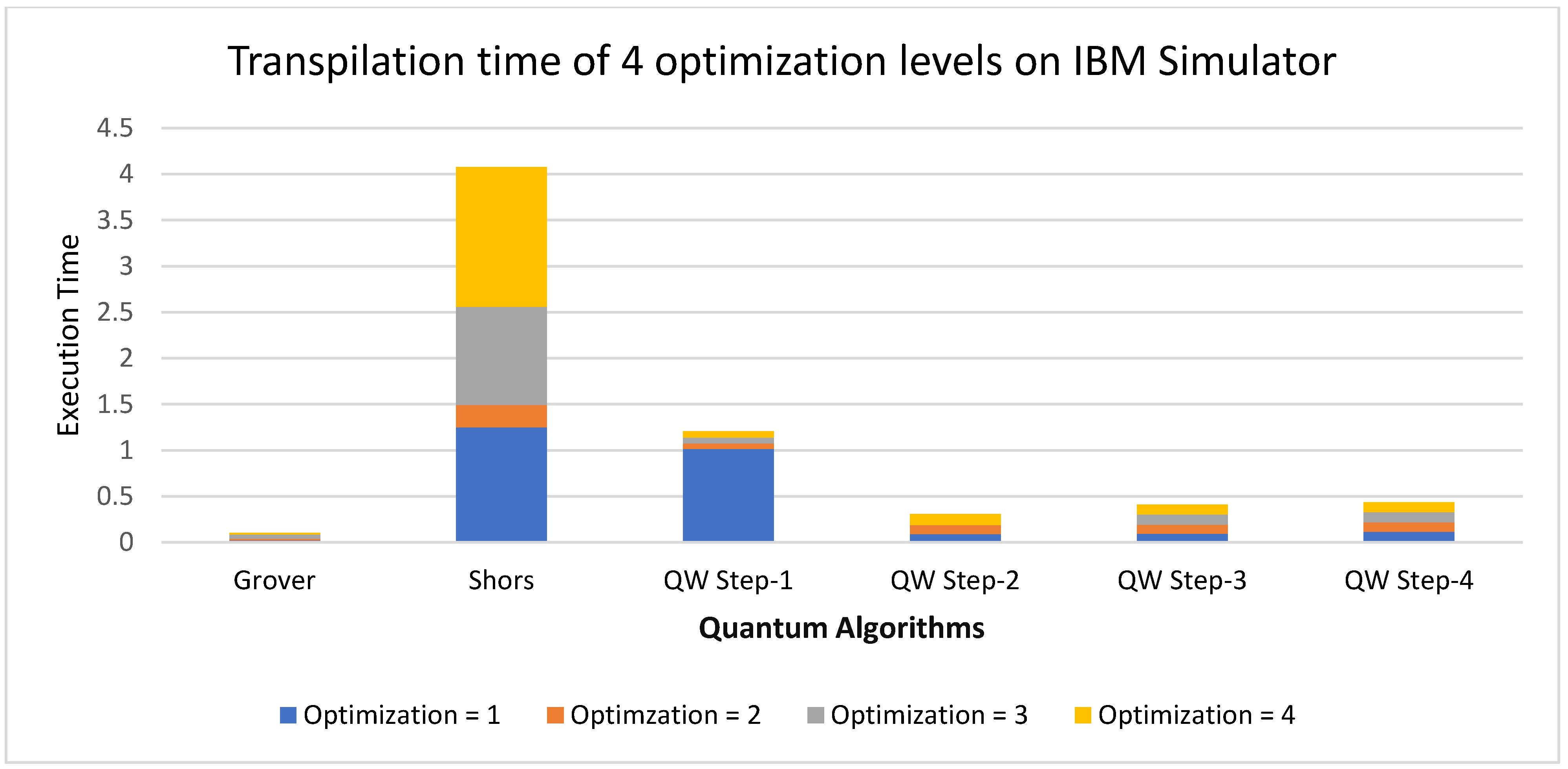
5.2.2. Transpilation Latency of Shor’s Algorithm
5.2.3. Transpilation Latency of Quantum Walks Algorithm
5.3. Execution Latency
5.3.1. Execution Latency of Grover’s Algorithm
5.3.2. Execution Latency of Shor’s Algorithm
5.3.3. Execution Latency of Quantum Walks Algorithm
5.4. The Latency Score—Method A
5.5. Evaluation of Method A
5.6. The Latency Score—Method B
6. Analysis and Discussion of the Experimental Results
6.1. Analysis of Experimental Results
- 1.
- Impact of Optimization Levels on Execution Time
- 2.
- Comparative Performance of Simulators and QPUs
- 3.
- Transpilation Time Analysis
- 4.
- Impact of Fidelity
- 5.
- Overall Platform Performance
6.2. Conclusions
- (a)
- In all experimental scenarios, quantum simulators demonstrated superior latency performance compared to physical quantum processing units. This outcome underscores the current limitations in QPU technological maturity, particularly with respect to scalability, reliability, and noise resilience.
- (b)
- Although IBM offers a higher qubit count, Amazon’s platform achieved better performance for all tested algorithms. This finding highlights that system architecture, compiler efficiency, and optimization methodologies exert greater influence than raw hardware specifications. Thus, qubit count alone is an insufficient measure of platform capability.
- (c)
- The experiments reveal that transpilation introduces considerable overhead, which can adversely affect total execution time. This emphasizes the necessity of striking a balance between optimization strategies during transpilation and practical constraints of execution.
7. Future Research
- (1)
- A deeper investigation of the interaction between transpilation optimization levels and QPU topology will help clarify the trade-offs between aggressive optimization and execution overhead.
- (2)
- Incorporating a wider variety of quantum algorithms will refine benchmarking formulas, update key parameters, and generate broader insights into platform behavior across diverse computational tasks.
- (3)
- Advances in practical QPUs are expected to enable flexible allocation of qubits, allowing tasks to leverage computational power dynamically according to problem complexity.
- (4)
- Extending the framework from classical to quantum communication networks may provide more accurate insights into true end-to-end performance in hybrid quantum–edge-cloud systems.
- (5)
- Incorporating real-time fidelity monitoring, rather than static fidelity values, will improve the accuracy of performance assessments and strengthen benchmarking methodologies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Resch, S.; Karpuzcu, U.R. Benchmarking quantum computers and the impact of quantum noise. ACM Comput. Surv. (CSUR) 2021, 54, 142. [Google Scholar] [CrossRef]
- Grover, L.K. Synthesis of quantum superpositions by quantum computation. Phys. Rev. Lett. 2000, 85, 1334. [Google Scholar] [CrossRef]
- What Is Quantum Computing? Available online: https://scienceexchange.caltech.edu/topics/quantum-science-explained/quantum-computing-computers (accessed on 17 February 2025).
- Gupta, M.; Nene, M.J. Quantum computing: An entanglement measurement. In Proceedings of the 2020 IEEE International Conference on Advent Trends in Multidisciplinary Research and Innovation (ICATMRI), Buldhana, India, 30 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- What Are the Applications of Quantum Entanglement? Consensus. Available online: https://consensus.app/questions/what-applications-quantum-entanglement/ (accessed on 17 July 2025).
- Hossain, M.I.; Sumon, S.A.; Hasan, H.M.; Akter, F.; Badhon, M.B.; Islam, M.N.U. Quantum-Edge Cloud Computing: A Future Paradigm for IoT Applications. arXiv 2024, arXiv:2405.04824. [Google Scholar] [CrossRef]
- Acuaviva, A.; Aguirre, D.; Peña, R.; Sanz, M. Benchmarking Quantum Computers: Towards a Standard Performance Evaluation Approach. arXiv 2024, arXiv:2407.10941. [Google Scholar] [CrossRef]
- Varghese, B.; Wang, N.; Bermbach, D.; Hong, C.H.; Lara, E.D.; Shi, W.; Stewart, C. A survey on edge performance benchmarking. ACM Comput. Surv. (CSUR) 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Hao, T.; Hwang, K.; Zhan, J.; Li, Y.; Cao, Y. Scenario-based AI benchmark evaluation of distributed cloud/edge computing systems. IEEE Trans. Comput. 2023, 72, 719–731. [Google Scholar] [CrossRef]
- Lorenz, J.M.; Monz, T.; Eisert, J.; Reitzner, D.; Schopfer, F.; Barbaresco, F.; Kurowski, K.; Schoot, W.; Strohm, T.; Senellart, J.; et al. Systematic benchmarking of quantum computers: Status and recommendations. arXiv 2025, arXiv:2503.04905. [Google Scholar] [CrossRef]
- Cross, A.W.; Bishop, L.S.; Sheldon, S.; Nation, P.D.; Gambetta, J.M. Validating quantum computers using randomized model circuits. Phys. Rev. A 2019, 100, 032328. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Shenvi, N.; Kempe, J.; Whaley, K.B. Quantum random-walk search algorithm. Phys. Rev. A 2023, 67, 052307. [Google Scholar] [CrossRef]
- Q-CTRL’s Performance Management on 127-Qubit IBM Brisbane Processor. Available online: https://quantumzeitgeist.com/q-ctrls-performance-management-on-127-qubit-ibm-brisbane-processor/ (accessed on 13 September 2024).
- Wille, R.; Van Meter, R.; Naveh, Y. IBM’s Qiskit tool chain: Working with and developing for real quantum computers. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019; pp. 1234–1240. [Google Scholar] [CrossRef]
- Aerts, D. Quantum Mechanics: Structures, Axioms and Paradoxes. In Quantum Structures and the Nature of Reality: The Indigo Book of “Einstein Meets Magritte”; Springer: Dordrecht, The Netherlands, 1999. [Google Scholar] [CrossRef][Green Version]
- Rieffel, E.; Wolfgang, P. An introduction to quantum computing for non-physicists. ACM Comput. Surv. (CSUR) 2020, 32, 300–335. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics; No. 27; Oxford University Press: Oxford, UK, 1981. [Google Scholar]
- Berberich, J.; Daniel, F. Quantum computing through the lens of control: A tutorial introduction. IEEE Control. Syst. 2024, 44, 24–49. [Google Scholar] [CrossRef]
- Dirac, P.A.M. A new notation for quantum mechanics. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1939; Volume 35, pp. 416–418. [Google Scholar] [CrossRef]
- Furutanpey, A. Architectural Vision for Quantum Computing in the Edge-Cloud Continuum. In Proceedings of the 2023 IEEE International Conference on Quantum Software (QSW), Chicago, IL, USA, 2–8 July 2023. [Google Scholar] [CrossRef]
- Rambo, T.M.; McCusker, K.; Huang, Y.P.; Kumar, P. Low-loss all-optical quantum switching. In Proceedings of the 2013 IEEE Photonics Society Summer Topical Meeting Series, Waikoloa, HI, USA, 8–10 July 2013; pp. 179–180. [Google Scholar] [CrossRef]
- Aliro. What are Quantum Repeaters? Available online: https://www.aliroquantum.com/blog/what-are-quantum-repeaters (accessed on 17 July 2025).
- Collins, D.; Nicolas, G.; Hugues, D.R. Quantum relays for long distance quantum cryptography. J. Mod. Opt. 2005, 52, 735–753. [Google Scholar] [CrossRef]
- Awschalom, D.; Berggren, K.K.; Bernien, H.; Bhave, S.; Carr, L.D.; Davids, P.; Economou, S.E.; Englund, D.; Faraon, A.; Fejer, M.; et al. Development of Quantum Interconnects (QuICs) for Next-Generation Information Technologies. PRX Quantum 2021, 2, 017002. [Google Scholar] [CrossRef]
- Swayn, M. Quantum Companies Battle for SPAM Dominance. Quantum Insider. 2024. Available online: https://thequantuminsider.com/2022/03/04/quantum-companies-battle-for-spam-dominance/ (accessed on 18 June 2025).
- Sim, S.E.; Steve, E.; Richard, R.H. Using benchmarking to advance research: A challenge to software engineering. In Proceedings of the 25th International Conference on Software Engineering, Portland, OR, USA, 3–10 May 2003; pp. 74–83. [Google Scholar] [CrossRef]
- Weber, L.M.; Saelens, W.; Cannoodt, R.; Soneson, C.; Hapfelmeier, A.; Gardner, P.P.; Boulesteix, A.L.; Saeys, Y.; Robinson, M.D. Essential guidelines for computational method benchmarking. Genome Biol. 2019, 20, 125. [Google Scholar] [CrossRef] [PubMed]
- Proctor, T.; Young, K.; Baczewski, A.D.; Blume-Kohout, R. Benchmarking quantum computers. Nat. Rev. Phys. 2025, 7, 105–118. [Google Scholar] [CrossRef]
- Quetschlich, N.; Burgholzer, L.; Wille, R. MQT Bench: Benchmarking software and design automation tools for quantum computing. Quantum 2023, 7, 1062. [Google Scholar] [CrossRef]
- Nation, P.D.; Saki, A.A.; Brandhofer, S.; Bello, L.; Garion, S.; Treinish, M.; Javadi-Abhari, A. Benchmarking the performance of quantum computing software for quantum circuit creation, manipulation and compilation. Nat. Comput. Sci. 2025, 5, 427–435. [Google Scholar] [CrossRef]
- Mitchem, S. What is Quantum Coherence. Argonne National Laboratory, 19 February 2025. Available online: https://www.anl.gov/article/what-is-quantum-coherence (accessed on 10 June 2025).
- Wudarski, F.; Marshall, J.; Petukhov, A.; Rieffel, E. Augmented fidelities for single-qubit gates. Phys. Rev. A 2020, 102, 052612. [Google Scholar] [CrossRef]
- Vadali, A.; Kshirsagar, R.; Shyamsundar, P.; Perdue, G.N. Quantum circuit fidelity estimation using machine learning. Quantum Mach. Intell. 2024, 6, 1. [Google Scholar] [CrossRef]
- Microsoft. Explore Quantum. Available online: https://quantum.microsoft.com/en-us/insights/education/concepts/quantum-error-correction (accessed on 18 June 2025).
- Michielsen, K.; Nocon, M.; Willsch, D.; Jin, F.; Lippert, T.; De Raedt, H. Benchmarking gate-based quantum computers. Comput. Phys. Commun. 2017, 220, 44–55. [Google Scholar] [CrossRef]
- Weder, B.; Barzen, J.; Leymann, F.; Zimmermann, M. Hybrid quantum applications need two orchestrations in superposition: A software architecture perspective. In Proceedings of the 2021 IEEE International Conference on Web Services (ICWS), Chicago, IL, USA, 5–10 September 2021; pp. 1–13. [Google Scholar]
- Gupta, L. Collaborative Edge-Cloud AI for IoT Driven Secure Healthcare System. In Proceedings of the 2023 IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 17–20 April 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Tomesh, T.; Gokhale, P.; Omole, V.; Ravi, G.S.; Smith, K.N.; Viszlai, J.; Wu, X.-C.; Hardavellas, N.; Martonosi, M.R.; Chong, F.T. Supermarq: A scalable quantum benchmark suite. In Proceedings of the 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 2–6 April 2022; pp. 587–603. [Google Scholar] [CrossRef]
- Lubinski, T.; Johri, S.; Varosy, P.; Coleman, J.; Zhao, L.; Necaise, J.; Baldwin, C.H.; Mayer, K.; Proctor, T. Application-oriented performance benchmarks for quantum computing. IEEE Trans. Quantum Eng. 2023, 4, 3100332. [Google Scholar] [CrossRef]
- Finžgar, J.R.; Ross, P.; Hölscher, L.; Klepsch, J.; Luckow, A. Quark: A framework for quantum computing application benchmarking. In Proceedings of the 2022 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 18–23 September 2022; pp. 226–237. [Google Scholar] [CrossRef]
- Karalekas, P.J.; Tezak, N.A.; Peterson, E.C.; Ryan, C.A.; Da Silva, M.P.; Smith, R.S. A quantum-classical cloud platform optimized for variational hybrid algorithms. Quantum Sci. Technol. 2020, 5, 024003. [Google Scholar] [CrossRef]
- Natu, S.; Triana, E.; Kim, J.S.; O’Riordan, L.J. Accelerate Hybrid Quantum-Classical Algorithms on Amazon Braket Using Embedded Simulators from Xanadu’s PennyLane Featuring NVIDIA cuQuantum. AWS Quantum Technologies Blog. 2022. Available online: https://aws.amazon.com/blogs/quantum-computing/accelerate-your-simulations-of-hybrid-quantum-algorithms-on-amazon-braket-with-nvidia-cuquantum-and-pennylane/ (accessed on 15 July 2025).
- Ma, L.; Leah, D. Hybrid quantum edge computing network. In Quantum Communications and Quantum Imaging XX; SPIE: Bellingham, WA, USA, 2022; Volume 12238, pp. 83–93. [Google Scholar] [CrossRef]
- Wulff, E.; Garcia Amboage, J.P.; Aach, M.; Gislason, T.E.; Ingolfsson, T.K.; Ingolfsson, T.K.; Pasetto, E.; Delilbasic, A.; Riedel, M.; Sarma, R. Distributed hybrid quantum-classical performance prediction for hyperparameter optimization. Quantum Mach. Intell. 2024, 6, 59. [Google Scholar] [CrossRef]
- Sangle, R.; Khare, T.; Seshadri, P.V.; Simmhan, Y. Comparing the orchestration of quantum applications on hybrid clouds. In Proceedings of the 2023 IEEE/ACM 23rd International Symposium on Cluster, Cloud and Internet Computing Workshops (CCGridW), Bangalore, India, 1–4 May 2023; pp. 313–315. [Google Scholar] [CrossRef]
- Li, A.; Stein, S.; Krishnamoorthy, S.; Ang, J. Qasmbench: A low-level quantum benchmark suite for nisq evaluation and simulation. ACM Trans. Quantum Comput. 2023, 4, 1–26. [Google Scholar] [CrossRef]
- Waite, W.M.; Goos, G. Compiler Construction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; p. 3. [Google Scholar] [CrossRef]
- Transpiler. Available online: https://docs.quantum.ibm.com/api/qiskit/transpiler (accessed on 17 February 2025).
- Level3.py. Available online: https://github.com/Qiskit/qiskit/blob/main/qiskit/transpiler/preset_passmanagers/level3.py (accessed on 17 February 2025).
- Wang, Q. Optimal trace distance and fidelity estimations for pure quantum states. IEEE Trans. Inf. Theory 2024. 70, 8791–8805. [CrossRef]
- Pedersen, L.H.; Møller, N.M.; Mølmer, K. Fidelity of quantum operations. Phys. Lett. A 2007, 367, 47–51. [Google Scholar] [CrossRef]
- Hua, F.; Wang, M.; Li, G.; Peng, B.; Liu, C.; Zheng, M.; Stein, S.; Ding, Y.; Zhang, E.Z.; Humble, T.; et al. QASMTrans: A QASM Quantum Transpiler Framework for NISQ Devices. In Proceedings of the SC’23 Workshops of The International Conference on High Performance Computing, Network, Storage, and Analysis, New York, NY, USA, 12–17 November 2023; pp. 1468–1477. [Google Scholar] [CrossRef]
- Mixed States; Pure States. Available online: https://pages.uoregon.edu/svanenk/solutions/Mixed_states.pdf (accessed on 17 February 2025).
- Soeparno, H.; Anzaludin, S.P. Cloud quantum computing concept and development: A systematic literature review. Procedia Comput. Sci. 2021, 179, 944–954. [Google Scholar] [CrossRef]
- Ferracin, S.; Hashim, A.; Ville, J.L.; Naik, R.; Carignan-Dugas, A.; Qassim, H.; Morvan, A.; Santiago, D.I.; Siddiqi, I.; Wallman, J.J. Efficiently improving the performance of noisy quantum computers. Quantum 2024, 8, 1410. [Google Scholar] [CrossRef]
- Castelvecchi, D. IBM releases first-ever 1,000-qubit quantum chip. Nature 2023, 624, 238. [Google Scholar] [CrossRef]
- Available online: https://aws.amazon.com/braket/ (accessed on 17 September 2024).
- Norimoto, M.; Taku, M.; Naok, I. Quantum speedup for multiuser detection with optimized parameters in Grover adaptive search. IEEE Access 2024, 12, 83810–83821. [Google Scholar] [CrossRef]
- Chappell, J.M.; Iqbal, A.; Lohe, M.A.; von Smekal, L.; Abbott, D. An improved formalism for quantum computation based on geometric algebra—Case study: Grover’s search algorithm. Quantum Inf. Process. 2013, 12, 1719–1735. [Google Scholar] [CrossRef]
- Bogatyrev, V.A.; Moskvin, V.S. Application of grover’s algorithm in route optimization. In Proceedings of the 2023 Intelligent Technologies and Electronic Devices in Vehicle and Road Transport Complex (TIRVED), Moscow, Russia, 15–17 November 2023. [Google Scholar] [CrossRef]
- Khanal, B.; Rivas, P.; Orduz, J.; Zhakubayev, A. Quantum machine learning: A case study of grover’s algorithm. In Proceedings of the 2021 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2021; pp. 79–84. [Google Scholar] [CrossRef]
- Qiang, X.; Ma, S.; Song, H. Quantum walk computing: Theory, implementation, and application. Intell. Comput. 2024, 3, 97. [Google Scholar] [CrossRef]
- Goldsmith, M.; Saarinen, H.; García-Pérez, G.; Malmi, J.; Rossi, M.A.; Maniscalco, S. Link prediction with continuous-time classical and quantum walks. Entropy 2023, 25, 730. [Google Scholar] [CrossRef] [PubMed]
- Razzoli, L.; Cenedese, G.; Bondani, M.; Benenti, G. Efficient Implementation of Discrete-Time Quantum Walks on Quantum Computers. Entropy 2024, 26, 313. [Google Scholar] [CrossRef] [PubMed]
- Samya, M.; Singh, S.S. Quantum-Social Network Analysis for Community Detection: A Comprehensive Review. IEEE Trans. Comput. Soc. Syst. 2024, 11, 6795–6806. [Google Scholar] [CrossRef]
- Daniela, B.; Haeberlein, H.M.; Tim, C. Amazon Braket Launches New Superconducting Quantum Processor from IQM. Available online: https://aws.amazon.com/blogs/quantum-computing/amazon-braket-launches-new-superconducting-quantum-processor-from-iqm/ (accessed on 22 May 2024).







| Optimization Levels | On Simulator | On QPUs |
|---|---|---|
| 1 | [‘110’: 95, ‘000’: 3, ‘101’: 2] | [‘110’: 39, ‘100’: 14, ‘111’: 13, ‘011’: 8, ‘001’: 6, ‘101’: 6, ‘000’: 8, ‘010’: 6] |
| … | … | … |
| Message Length in Bytes | 222 | 340 |
| Platform | On Simulator | On QPUs |
|---|---|---|
| Amazon Braket | [0.03 0.04 0.06 0.02 0.03 0.03 0.76 0.03] | [0.02 0.1 0.09 0.08 0.06 0.02 0.53 0.1] |
| Message Length in Bytes | 48 | 46 |
| Optimization Levels | On Simulator | On QPUs |
|---|---|---|
| Level 1 | [‘10000000’: 27, ‘0000000’: 27, ‘01000000’: 21, ‘11000000’: 25] | [‘10000100’: 1, ‘01101111’: 1, ‘10100010’: 2, … ‘01001110’: 2] |
| … | … | … |
| Total Message Length in Bytes | 264 | 558 |
| Platform | On Simulator | On QPUs |
|---|---|---|
| Amazon Braket | [‘00001110’: 10, ‘00000010’: 8, …, ‘11001011’: 2] | [‘11111111’: 20, ‘11110111’: 7, … ‘11111010’: 1] |
| Total Message Length in Bytes | 256 | 828 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Quantum Walks Steps | 1 | 2 | 3 | 4 |
| 1 | [‘00’: 100] | [‘00’: 100] | [‘00’: 100] | [‘00’: 100] |
| … | … | … | … | … |
| Total Message Length in Bytes | 113 | 122 | 124 | 124 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Steps | 1 | 2 | 3 | 4 |
| 1 | [‘10’: 4, ‘11’: 2, ‘01’: 10, ‘00’: 84] | [‘11’: 1, ‘01’: 6, ‘10’: 6, ‘00’: 87] | [‘00’: 100] | [‘00’: 100] |
| … | … | … | … | … |
| Total Message Length in Bytes | 52 | 102 | 102 | 162 |
| Algorithms | On Simulator | On QPUs |
|---|---|---|
| Quantum Walks | [1: 0.512, 3: 0.488], [0: 0.54, 2: 0.463], [3: 1.0], [2: 1.0] | [1: 0.512, 3: 0.488], [0: 0.537, 2: 0.463], [3: 1.0], [2: 1.0] |
| Total Message Length in Bytes | 90 | 90 |
| Feature | Grover’s Algorithm | Shor’s Algorithm | Quantum Walks Algorithm |
|---|---|---|---|
| Algorithm Type | Amplitude amplification | Period finding/integer factorization | Probabilistic traversal/graph search |
| Use Case | Unstructured search | Cryptographic analysis | Graph-based modeling, optimization |
| Platform(s) Used | IBM Quantum, Amazon Braket | IBM Quantum, Amazon Braket | IBM Quantum, Amazon Braket |
| Request Message Format | {name: ‘grover’, n: 110} | {name: ‘shors’, a: 7, N: 15} | {name: ‘quantumwalk’, n: 4, step: 4} |
| Request Message Size | 27 bytes | 39 bytes | 42 bytes |
| Number of Qubits Used | 3 qubits | 8 qubits | 2–3 qubits (for a 4-node graph) |
| Response Format (IBM) | Frequency counts of quantum states (e.g., {‘110’: 95, ‘000’: 3}) | Frequency counts of 8-bit states (e.g., {‘10000000’: 27}) | Frequency counts of 2-bit states (e.g., {‘00’: 84, ‘01’: 10}) |
| Response Format (Amazon) | Probability vector over 8 states (e.g., [0.76 for ‘110’]) | Similar frequency-based results | Node-indexed probability map (e.g., {1: 0.512, 3: 0.488}) |
| Output Data Size | Small to medium | Medium to large | Small to medium |
| Latency Sensitivity | Low to moderate | High (larger messages, more qubits) | Moderate (repeats per step) |
| Communication Complexity Impact | Minimal message variance | High due to circuit/output size | Varies with number of steps |
| Optimization Levels | ||||
|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 4 | |
| Simulator | 2.3 × 10−2 | 1.5 × 10−2 | 4.7× 10−2 | 2.0 × 10−2 |
| QPUs | 1.29 × 10−1 | 2.1 × 10−2 | 2.2 × 10−2 | 2.1× 10−2 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Transpilation Time | Level 1 | Level 2 | Level 3 | Level 4 |
| On Simulator | 1.25 | 2.45 × 10−1 | 1.06 | 1.52 |
| On QPUs | 2.49 × 10 | 2.47 × 10 | 8.28 × 10 | 1.24 × 102 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Steps | Level 1 | Level 2 | Level 3 | Level 4 |
| 1 | 1.02 | 6.0× 10−2 | 6.3 × 10−2 | 6.6 × 10−2 |
| 2 | 8.9 × 10−2 | 9.8 × 10−2 | 1.09 × 10−1 | 1.22 × 10−1 |
| 3 | 9.6 × 10−2 | 9.5 × 10−2 | 1.12 × 10−1 | 1.08 × 10−1 |
| 4 | 1.18 × 10−1 | 9.9 × 10−2 | 1.11 × 10−1 | 1.1 × 10−1 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Steps | 1 | 2 | 3 | 4 |
| 1 | 5.0 × 10−2 | 2.7 × 10−2 | 3.4 × 10−2 | 4.3 × 10−2 |
| 2 | 6.3 × 10−2 | 6.3 × 10−2 | 1.3 × 10−1 | 1.17 × 10−1 |
| 3 | 1.97 × 10−1 | 6.3 × 10−2 | 8.5 × 10−2 | 1.1 × 10−1 |
| 4 | 8.2 × 10−2 | 1.19 × 10−1 | 2.87 × 10−1 | 1.22 × 10−1 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Execution Time | Level 1 | Level 2 | Level 3 | Level 4 |
| Simulator | 8.7 × 10−2 | 6.4 × 10−2 | 1.8× 10−2 | 3.2× 10−2 |
| QPUs | 2.37 × 10 | 3.66 × 10 | 2.98 × 10 | 2.52 × 10 |
| Amazon Platform | Execution time |
|---|---|
| Simulator | 4.86 × 10−5 |
| QPUs | 1.23 × 102 |
| Optimization Levels | ||||
|---|---|---|---|---|
| Execution Time | Level 1 | Level 2 | Level 3 | Level 4 |
| Simulator | 1.48 × 10−1 | 1.89 × 10−1 | 2.37 × 10−1 | 1.77 × 10−1 |
| QPUs | 9.45 × 10 | 6.17 × 10 | 7.41 × 10 | 8.09 × 10 |
| Platform | Execution Time |
|---|---|
| Simulator | 3.30 × 10−1 |
| QPUs | 1.32 × 10 |
| Execution Time | Optimization Levels | |||
|---|---|---|---|---|
| Steps | Level 1 | Level 2 | Level 3 | Level 4 |
| 1 | 3.1 × 10−3 | 4.0 × 10−3 | 1.7 × 10−3 | 1.8 × 10−3 |
| 2 | 2.87 × 10−2 | 2.1 × 10−3 | 4.5 × 10−3 | 2.7 × 10−3 |
| 3 | 2.5 × 10−3 | 2.1 × 10−3 | 2.5 × 10−3 | 1.29 × 10−2 |
| 4 | 2.1 × 10−3 | 2.29 × 10−2 | 7.8 × 10−3 | 3.0 × 10−3 |
| Execution Time | Optimization Levels | |||
|---|---|---|---|---|
| Steps | 1 | 2 | 3 | 4 |
| 1 | 3.07 × 10 | 3.05 × 10 | 2.59 × 10 | 3.05 × 10 |
| 2 | 3.28 × 10 | 3.65 × 10 | 3.08 × 10 | 3.09 × 10 |
| 3 | 3.00 × 10 | 3.69 × 10 | 3.00 × 10 | 2.46 × 10 |
| 4 | 2.56 × 10 | 3.83 × 10 | 3.07 × 10 | 3.67 × 10 |
| Platform | Execution Time |
|---|---|
| Simulator | 3.18 × 10−1 |
| QPUs | 1.56 × 10 |
| Algorithms | IBM Simulator | IBM QPU | Amazon Simulator | Amazon QPU |
|---|---|---|---|---|
| Grover’s | 1.37 × 10−1 | 1.47 × 10 | 1.08 × 10−2 | 1.23 × 102 |
| Shor’s | 2.89 | 2.47 × 102 | 3.71 × 10−1 | 1.34 × 10 |
| Quantum Walks | 3.81 × 10−1 | 1.66 × 10 | 3.37 × 10−1 | 1.56 × 10 |
| Algorithms | IBM Simulator | IBM QPU | Amazon Simulator | Amazon QPU |
|---|---|---|---|---|
| Grover’s | 1.59 × 10−1 | 2.38 × 10 | 1.08 × 10−2 | 1.23 × 102 |
| Shor’s | 1.20 | 3.29 × 102 | 3.71 × 10−1 | 1.34 × 10 |
| Quantum Walks | 1.32 × 10−1 | 2.71 × 10 | 3.37 × 10−1 | 1.56 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, G.; Gupta, L. A Benchmarking Framework for Hybrid Quantum–Classical Edge-Cloud Computing Systems. Appl. Sci. 2025, 15, 10245. https://doi.org/10.3390/app151810245
Yao G, Gupta L. A Benchmarking Framework for Hybrid Quantum–Classical Edge-Cloud Computing Systems. Applied Sciences. 2025; 15(18):10245. https://doi.org/10.3390/app151810245
Chicago/Turabian StyleYao, Guoxing, and Lav Gupta. 2025. "A Benchmarking Framework for Hybrid Quantum–Classical Edge-Cloud Computing Systems" Applied Sciences 15, no. 18: 10245. https://doi.org/10.3390/app151810245
APA StyleYao, G., & Gupta, L. (2025). A Benchmarking Framework for Hybrid Quantum–Classical Edge-Cloud Computing Systems. Applied Sciences, 15(18), 10245. https://doi.org/10.3390/app151810245






