Application of Supervised Neural Networks to Classify Failure Modes in Reinforced Concrete Columns Using Basic Structural Data

Abstract

Reinforced concrete (RC) columns play a vital role in structural integrity, and accurately predicting their failure modes is essential for enhancing seismic safety and performance. This study explores the use of a supervised machine learning approach—specifically, an artificial neural network (ANN) model—to classify failure modes of RC columns. The model is trained using data from the well-established Pacific Earthquake Engineering Research Center (PEER) structural performance database, which contains results from over 400 cyclic lateral-load tests on RC columns. These tests encompass a wide range of column types, including those with spiral or circular hoop confinement, rectangular ties, and varying configurations of longitudinal reinforcement with or without lap splices at critical sections. The ANNs were evaluated using a randomly selected subset from the PEER database, achieving classification accuracies of 94% for rectangular columns and 95% for circular columns. Notably, in certain cases, the model’s predictions aligned with or exceeded the accuracy of traditional building code-based methods. These findings underscore the strong potential of machine learning—particularly ANNs—for reliably postdicting failure modes (even the brittle ones) in RC columns, signaling a promising advancement in the field of earthquake engineering.

1. Introduction

The failure behavior of structural elements—such as reinforced concrete (RC) columns—is influenced by a variety of factors. These include geometric characteristics, longitudinal reinforcement, the effectiveness of transverse reinforcement in providing confinement, and the loading history. The performance of these columns throughout the loading range is governed by several interacting resistance mechanisms, including flexure, shear, buckling of longitudinal bars under compression, and—in cases with lap splices—the development behavior of the lap-splice itself. Often, a combination of these mechanisms determines the overall response of a column, particularly under cyclic loading. Numerous models have been developed to predict both the strength and deformation capacity of columns. However, comparisons with experimental data show that predictions for deformation capacity carry significantly more uncertainty—by at least an order of magnitude—than those for strength [1,2].

System identification and damage detection form a dual-focused research area that increasingly utilizes machine learning (ML) to simulate structural behavior and forecast seismic responses. Laboratory testing of RC structures has generated valuable data, enabling ML techniques to identify failure modes, predict strength and capacity, and model constitutive behavior [3]. Recently, ML has been applied to risk assessment and predictive modeling within civil engineering [4,5,6,7,8,9,10,11]. Some studies have focused specifically on predicting failure modes and estimating shear strength in beam–column joints. For instance, Mitra et al. (2011) [12] distinguished between non-ductile joint shear failures and ductile beam yielding in interior joints [6,9,12,13]. Similarly, Tang et al. (2022) [14] performed low-cycle reciprocating load tests on 23 recycled aggregate concrete-filled steel tube columns and three conventional counterparts. They used artificial intelligence—specifically, random forests, optimized via the firefly algorithm—to analyze how different parameters affect the seismic performance of concrete columns. Further related research, including multi-objective optimization studies, is discussed in Tang et al. (2023) [15].

Machine learning (ML), a branch of artificial intelligence (AI), has demonstrated significant effectiveness in optimizing and predicting structural behavior [16,17,18,19,20,21,22,23,24]. Unlike traditional approaches to analyzing reinforced concrete (RC) slab–column systems, ML enables engineers to efficiently process large datasets and uncover intricate patterns related to dynamic behavior. Its strength lies in the ability to account for a wide range of input variables and their complex interdependencies, making ML highly valuable for predicting failure modes and enhancing structural optimization [25,26,27,28,29]. The integration of ML into structural engineering has led to notable progress in understanding and modeling the complex behavior of RC structures. For instance, Zhou et al. [30] explored the use of deep learning models—including multi-layer perceptrons and one-dimensional convolutional neural networks—to predict failure modes and structural responses of RC slabs under blast loads. Their findings demonstrate that ML techniques can effectively handle multi-dimensional datasets, providing accurate and interpretable predictions that outperform traditional methods. Similarly, hybrid approaches that combine ML with optimization algorithms have improved the accuracy of punching shear strength (PSS) predictions in RC slabs [31]. The importance of interpretability in ML applications has also been emphasized. Shen et al. [32], for example, applied XGBoost alongside SHAP (Shapley Additive Explanations) to illustrate how key input variables—such as reinforcement ratios—affect structural performance. This level of transparency increases confidence in ML models, particularly for safety-critical engineering applications. In addition to static failure mode prediction, ML has been successfully applied to dynamic analysis. Zhao et al. [33] utilized support vector machines and Gaussian process regression to estimate the maximum displacement of RC slabs under blast loading. Their study highlighted the superior accuracy and efficiency of ML models compared to traditional numerical simulations, making them well-suited for real-time evaluations. Additionally, Albostami et al. [34] investigated the use of artificial neural networks (ANNs) and evolutionary algorithms for optimizing the punching shear strength of steel fiber-reinforced concrete slabs. Collectively, these studies highlight the transformative potential of ML in structural engineering applications [35,36].

Previous research by the authors [36] has highlighted several key findings regarding key features affecting the ductility of RC columns. For example, regarding concrete strength, the following remarks can be made:

(a)

Higher-strength materials exhibit lower ultimate strain,

(b)

Confinement can increase strain capacity;

(c)

Higher concrete strength reduces the compression zone at both yielding and failure.

Overall, greater concrete strength tends to reduce ductility. The presence of compressive axial load further decreases the curvature ductility of a section. Experimental results support this trend, showing increased brittleness, especially when axial load ratios exceed the balanced failure condition. The shear span-to-depth ratio (aspect ratio) plays a critical role in shear behavior. For columns with a small aspect ratio, shear deformations may become significant relative to flexural deformations. When shear response dominates, the hysteresis (force–deformation) curve displays more pronounced pinching and a faster reduction in energy dissipation capacity. Finally, displacement ductility is inversely related to the aspect ratio, which, for a given flexural resistance, is itself inversely related to shear demand (maximum shear force). According to the literature [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36], ANNs and deep learning can capture better the above-described nonlinearity between these features of RC columns and the final failure mode.

This study investigates the effectiveness of a supervised learning algorithm—ANNs—as a predictive tool for postdicting the failure modes of reinforced concrete (RC) columns. The assessment is based on a well-known experimental dataset originally compiled by Berry et al. (2004) [37], widely recognized as the PEER (Pacific Earthquake Engineering Research Center) structural performance database. This comprehensive dataset consolidates results from over 400 cyclic lateral-load tests on RC columns, covering various types, including spiral or circular hoop-confined columns, rectangular tied columns, and those with or without lap splices in the longitudinal reinforcement at critical sections. Where available, the database includes detailed information for each test, such as column geometry, material characteristics, reinforcement specifications, test setup (accounting for P-Delta effects), axial load, digital records of lateral force–displacement at the column top, and associated top displacements corresponding to different levels of observed damage.

In the latter database [37], column failure modes were categorized as follows:

(a)

Flexure-critical;

(b)

Flexure–shear-critical;

(c)

Shear-critical.

These classifications were based on the following criteria:

• If no shear damage was reported, the column was categorized as flexure critical.
• If shear damage (diagonal cracks) was noted, the absolute maximum effective force (F_eff)—the highest measured force in the experimental response—was compared to the calculated “ideal” force (F_0.004), corresponding to a maximum axial compressive strain of 0.004 (the strain at which unconfined concrete spalls). The failure displacement ductility (μ_fail) was defined as the displacement ductility at 80% of the maximum effective force (F_eff). If $F_{eff}<0.95·F_{0.004}$ or if ${\mu }_{fail}\le 2$, the column was classified as shear-critical. Otherwise, the column was categorized as flexure–shear-critical. All columns in the database were further grouped by cross-sectional shape (rectangular or circular).

This paper has the following contributions in the research area of ML methods in earthquake engineering:

• According to the authors’ knowledge, the PEER structural performance database is employed for the first time in order to detect the failure mode of RC columns based on the traditional methods which employ engineering mechanics solutions applied to the whole database.
• The above results are thoroughly compared to the performance of ANNs for the entire database, both for rectangular and circular RC columns.
• Finally, all the performance metrics necessary for the evaluation of the ML methodology in detecting the failure mode of RC columns are provided too.

The structure of this study is as follows: After the Introduction, which describes the initiatives of this research paper, the employed data and the performed traditional methodology are described in Section 2. In the latter section, the performance of traditional methods based on engineering mechanics and building code scrutiny is given in detail. The steps of the supervised ML method carried out in Python programming language (Python 3.12) and its output results are provided in Section 2 and Section 3. Finally, the discussion of the latter results is presented in Section 4, while the conclusions and future work are presented in Section 5.

2. Materials and Methods

Reinforced concrete (RC) columns play a critical role in the structural integrity of buildings, as their failure can result in severe and disproportionate impacts on the entire system. The behavior of RC columns subjected to combined axial load, shear, and flexure has been the focus of extensive research for decades. For flexural behavior, methods such as sectional analysis or fiber modeling in a one-dimensional stress field can effectively estimate ultimate strength, yield deformation, and predict flexural failure modes. However, when shear or combined shear–flexure behavior governs the response, sectional analysis alone becomes insufficient. This is because shear force transfer involves complex stress fields that span the entire member, extending to its supports. Figure 1 shows the shear strength degradation models adopted by EN 1998-3 (2005) [38] and ASCE/SEI 41 (2007) [39], which are used to depict the envelope of resistance curves for RC columns as a function of displacement ductility.

These models are used as the primary basis for determining whether shear failure occurs before or after flexural yielding—identified by the intersection point of the shear strength curve and the flexural capacity curve. To define the shear failure strength and deformation of a reinforced concrete column, the flexural capacity curve must first be established using conventional flexural analysis. This curve is then combined with the shear strength degradation curve provided by design codes. This method is employed in the current section to assess how accurately building code-based provisions can identify the actual failure mode of RC columns, prior to evaluating the same performance using machine learning techniques in the following Section.

2.1. Flexural Capacity

Flexural capacity curves, as shown in Figure 1 for the RC columns in the PEER database [37], are derived from nonlinear static pushover or cyclic analyses performed using the widely recognized MATLAB (2024b) toolbox, FEDEAS Lab Release 3.0 [40,41,42], under the assumption of flexural behavior without shear failure. Numerical simulations were conducted using a nonlinear fiber beam–column element that captures the spread of plasticity along the member. The longitudinal beam element is modeled using a force-based approach with a linear moment distribution, which constructs a flexibility matrix that is updated incrementally as nonlinearity increases. Strain–displacement relationships are implicitly determined by inverting this flexibility matrix to derive stiffness. Assuming strain compatibility among the constituent materials, the model evaluates sectional responses at specific integration points along the member’s length. At the sectional level, the Bernoulli assumption—that plane sections remain plane and perpendicular to the member’s axis—was employed to relate fiber strains to sectional curvature and axial strain. Nonlinear uniaxial material models define the normal stress–strain behavior of individual fibers, while shear effects on principal stress orientations across the section are neglected. Figure 2 illustrates a typical discretization of a column section. Sectional stress resultants, including moment and axial load, were obtained by summing the contributions of the fiber stress resultants.

2.2. Shear Capacity

Shear capacity curves of the RC columns of the PEER database were obtained based on the shear strength degradation model of Figure 1. According to EN 1998-3 (2005) [38], the part of the cyclic shear resistance that depends on concrete and transverse steel contribution (excluding the part owing to axial load contribution), V_R, decreases with the plastic part of ductility demand, expressed in terms of ductility ratio of the transverse deflection of the shear span or of the chord rotation at member end: ${{\mu }_{\Delta }}^{pl}={\mu }_{\Delta }-1.$ For this purpose, ${{\mu }_{\Delta }}^{pl}$ may be calculated as the ratio of the plastic part of the chord rotation, θ_p, normalized to the chord rotation at yielding,${\theta }_y$. Thus, EN 1998-3 (2005) [38] defines shear strength accounting for the above reduction as follows:

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{V}_R=\left[\left(h-x\right)/2L_s\right]·\min \left(N;0.55A_c{f}_c\right)+\left[1-0.05min\left(5;{{\mu }_{\Delta }}^{pl}\right)\right]· \\ \left\{0.16max\left(0.5;100{\rho }_{tot}\right)\left[1-0.16min\left(5;L_V/h\right)\right]\sqrt{f_c}{A}_c+V_w\right\}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

(1)

where $\mathit{h}$ is the depth of the cross-section (equal to the diameter D for circular sections); $\mathit{x}$ is the compressive zone depth; $\mathit{N}$ is the compressive axial force (positive, taken as being zero for tension); ${\mathit{L}}_{\mathit{s}}=$ $M/V$ is the shear span of the member; ${\mathit{A}}_{\mathit{c}}$ is the cross-sectional area, taken as being equal to ${\mathit{b}}_{\mathit{w}}\mathit{d}$ for a cross-section with a rectangular web of width (thickness) ${\mathit{b}}_{\mathit{w}}$ and structural depth $\mathit{d}$ or to $\mathit{\pi }{{\mathit{D}}_{\mathit{c}}}^{\mathbf{2}}/\mathbf{4}$ (where ${\mathit{D}}_{\mathit{c}}$ is the diameter of the concrete core to the inside of the hoops) for circular sections; ${\mathit{f}}_{\mathit{c}}$ is the concrete compressive strength, and ${\mathit{\rho }}_{\mathit{t}\mathit{o}\mathit{t}}$ is the total longitudinal reinforcement ratio. The term ${\mathit{V}}_{\mathit{w}}$ is the contribution of transverse reinforcement to shear resistance, taken as equal to the following:

$$V_w={\displaystyle \frac{\pi }{2}}{\displaystyle \frac{A_{sw}}{S}}{f}_{yw}\left(D-2c\right)$$

(2)

where, ${\mathit{f}}_{\mathit{y}\mathit{w}}$ is the yield stress of the transverse reinforcement, A_sw is the area of the spiral wire, c is the concrete cover, and S is the spiral step (spacing between successive turns of a spiral). Similarly, for rectangular cross-sections with a web having a width of ${\mathit{b}}_{\mathit{w}}$,

$$V_w={\rho }_w{b}_{w}z{f}_{yw}$$

(3)

where ${\mathit{\rho }}_{\mathit{w}}$ is the transverse reinforcement ratio, $\mathit{z}$ is the height of the equivalent truss (internal lever arm between longitudinal tension and compression resultants, i.e., d-d′ in beams and columns). In concrete columns with a shear span ratio of $L_s/h$ less than or equal to 2, the shear strength, $V_R$ cannot exceed the value corresponding to failure by web crushing along the diagonal of the column after flexural yielding, $V_{R,max}$, which, under cyclic loading, may be calculated from the following expression:

$$V_{R,max}=\left(4/7\right)\left[1-0.02min\left(5;{{\mu }_{\Delta }}^{pl}\right)\right]\left[1+1.35\left(N/A_c{f}_c\right)\right]\left[1+0.45\left(100{\rho }_{tot}\right)\right]·\sqrt{min\left(40;f_c\right)}{b}_{w}z·sin2\delta$$

(4)

where $\mathit{\delta }$ is the angle between the diagonal strut that is defined by the centroids of the compression zones at the column ends, and the axis of the column ($\tan \delta =h/2L_s$).

ASCE/SEI 41 [39] represents the most recent update in a series of guidelines developed following the FEMA [43] initiatives from the 1990s and 2000s, which aimed to establish a consistent assessment framework for existing structures. The FEMA/ATC documents were the first to provide an integrated reference for performance-based engineering, where deformation and force demands under various seismic hazards are compared against structural capacities at different performance levels (i.e., damage states). At the start of this significant FEMA project, limited data existed on the performance of existing components, leading to inconsistent application of reliability concepts in developing performance criteria. Estimating the shear strength of an RC element remains a complex challenge because it requires a thorough understanding of multiple interacting behavior mechanisms under reversed cyclic loading. Shear strength is strongly influenced by factors such as loading history, element dimensions (e.g., aspect ratio), concrete strength, longitudinal reinforcement ratio, and particularly the ratio and detailing of transverse reinforcement. To date, it has not been possible to theoretically derive shear strength solely from first principles of mechanics without relying on calibrated empirical constants. Consequently, shear strength estimates based on design expressions are inherently dependent on the experimental datasets used to calibrate them, as well as on researchers’ interpretations regarding the influence of various variables on shear mechanics. The following formula for estimating the shear strength of reinforced concrete columns is recommended by the ASCE/SEI 41 (2007) [39] Code for seismic rehabilitation of existing buildings:

$$V_R=V_c+V_w=k\left({\mu }_{\Delta }\right)\left[\left(0.5\sqrt{f_c}/\left(L_s/d\right)\right)\sqrt{1+N/\left(0.5A_g\sqrt{f_c}\right)}\right]0.8A_g+k\left({\mu }_{\Delta }\right)·\left[A_{sw}{f}_{yw}d/S\right]$$

(5)

where ${\mathit{V}}_{\mathit{c}}$ is the concrete’s contribution to shear resistance; ${\mathit{V}}_{\mathit{w}}$ is the contribution of transverse reinforcement; $\mathit{d}$ is the effective depth; ${\mathit{L}}_{\mathit{s}}$ is the shear span of the column; $\mathit{N}$ is the axial force (compression positive, taken as zero for tension); ${\mathit{A}}_{\mathit{g}}$ is the gross cross-sectional area of the column; ${\mathit{A}}_{\mathit{s}\mathit{w}}$ is the cross-sectional area of one layer of stirrup reinforcement parallel to the shear action; and $\mathit{S}$ is the centerline spacing of stirrups along the length of the member. If S is equal to or greater than half of the effective depth of the column, then the contribution of steel reinforcement ${\mathit{V}}_{\mathit{w}}$ to shear strength is reduced to 50% of its estimated value from the above equation. If S is equal to or greater than the effective depth of the column, then zero shear strength contribution from steel reinforcement ${\mathit{V}}_{\mathit{w}}$ is considered; ${\mathit{f}}_{\mathit{c}}$ is the concrete compressive strength; $\mathit{k}\left({\mathit{\mu }}_{\mathit{\Delta }}\right)$ is the shear strength reduction coefficient that depends on ductility demand. If ductility demand is less than or equal to 2, then the factor is equal to 1 (i.e., no strength reduction). If the ductility is greater than 6, then the reduction factor is equal to 0.6. For ductility between 2 and 6, the reduction factor is linearly interpolated between the proposed values.

2.3. Failure Mode Prediction

The next section will evaluate the effectiveness of machine learning methods—particularly ANNs—in predicting the failure modes of RC columns using test cases from the PEER structural performance database [37]. In this section, the performance evaluation will instead be carried out using the traditional engineering mechanics approach, applied to the same set of column tests. Furthermore, the confusion matrix will be introduced as a performance metric for the traditional method, encompassing both circular and rectangular RC columns from the PEER database.

For a circular column that failed in flexure, a single beam–column element was used to model the entire length of the cantilever column (Figure 2), with five Gauss–Lobatto integration points distributed along the element (FEDEAS Lab [40,41,42]). The effect of confinement on the concrete core was incorporated by adjusting the properties of the uniaxial stress–strain relationship for concrete in compression [44,45]. The P-Delta effect was not considered in this simulation. The resulting lateral force–lateral displacement response is shown in Figure 3, compared against experimental data. Similarly, for a rectangular RC column from the test set that also failed in flexure, a single fiber element represented the entire cantilever height (Figure 2), with five Gauss–Lobatto integration points along its length. The uniaxial stress–strain behavior of concrete was modeled using the relationship proposed by Mander et al. (1988) [45]. However, the differing confinement between the unconfined concrete cover and the confined core was not accounted for in the section discretization (Figure 2). The longitudinal steel reinforcement’s stress–strain behavior was simulated using the Menegotto and Pinto (1973) model [46]. The P-Delta effect was included here. The lateral force–lateral displacement curve obtained from this numerical simulation is compared with experimental results in Figure 4. As with the circular columns, a strong correlation between numerical and experimental results was observed [47]. Consequently, it will be assumed that the traditional engineering mechanics methods and code provisions can predict flexural failure modes of both circular and rectangular columns with 100% accuracy.

Figure 5 shows a comparison between analytical and experimental responses for a rectangular column (ID#140) that failed in shear. The correlation is notably poor, even regarding the initial stiffness predicted by flexural analysis. This discrepancy is due to the exclusion of deformation effects from reinforcement pullout and shear deformation. It is apparent that only the degrading shear strength model from ASCE/SEI 41 (2007) [39] intersects the flexural capacity curve, indicating shear failure caused by shear strength degradation. However, the predicted displacement at which this failure occurs precedes the actual onset of strength degradation observed experimentally. Because not all code provisions correctly predicted the failure mode in this case, the prediction is considered unsuccessful.

Both shear strength degradation models shown in Figure 6 predicted shear failure occurring after yielding, but at displacements considerably smaller than those recorded in the experimental results. Among the two, the EN 1998-3 (2005) [38] model offered a closer estimation of shear failure strength than the ASCE/SEI 41 (2007) [39] model. In this instance, the traditional method successfully predicted the failure mode. Additional comparison cases for the whole PEER database can be found in [47].

The performance metrics for predicting failure modes of circular RC columns using the traditional method are presented below. This approach, grounded in engineering mechanics and building code provisions (also see [47], Figure 2), achieves an accuracy of 81% in identifying the actual failure modes of the tested columns. This accuracy is determined from

Table 1. Confusion matrix in numbers for prediction through engineering mechanics and code provisions of the failure mode of circular RC columns of the PEER structural performance database.

		Confusion Matrix in Numbers
True Values	Flexure	12	0	0
	Flexure–Shear	2	5	0
	Shear	0	2	0
		Flexure	Flexure–Shear	Shear
		Predicted Values

by dividing the sum of the diagonal elements by the total sum of all elements in the table.

Lastly, the performance metrics for predicting failure modes of rectangular RC columns using the traditional method are also presented below. This approach, based on engineering mechanics and code provisions (see also [47]), attains an accuracy of 97% in correctly identifying the actual failure modes of the tested columns. The accuracy is calculated from

Table 2. Confusion matrix in numbers for prediction through engineering mechanics and code provisions of the failure mode of rectangular RC columns of the PEER structural performance database.

		Confusion Matrix in Numbers
True Values	Flexure	57	0	0
	Flexure–Shear	1	3	0
	Shear	1	0	0
		Flexure	Flexure–Shear	Shear
		Predicted Values

by dividing the sum of the diagonal elements by the total sum of all elements in the table.

2.4. Artificial Neural Networks with Python

Following the presentation of failure modes and performance metrics obtained from traditional nonlinear structural analysis methods, this section introduces a methodology for predicting failure modes of reinforced concrete columns using machine learning (ML) techniques. The focus is on supervised ML approaches, particularly ANNs, applied to a randomly selected test set from the PEER database [37].

The typical workflow for any machine learning task includes the following steps:

• Define the problem and determine the necessary data.
• Gather the data in a usable format.
• Identify and address any data gaps or uncertainties.
• Prepare the data for input into the machine learning model.
• Train the model using the training dataset.
• Apply the trained model to make predictions on the test dataset.
• Evaluate the predictions against known test outcomes and calculate performance metrics.
• If results are unsatisfactory, improve the model, collect more data, or investigate alternative modeling methods.

Neural networks are models that attempt to mimic the functioning of the human brain to solve various types of problems, including classification problems, regression, and forecasting the future values of a variable. The specialized branch of machine learning that specializes in training neural networks (especially those with complex structures) is called deep learning in the literature (Burkov A., 2019 [48]). A neuron is the building block of a neural network. In other words, a neural network consists of a set of neurons that are arranged within the network in different layers.

The process of training an ANN on the available data involves determining the optimal values of the parameters that “connect” each neuron in one layer to the neurons in the immediately preceding layer. In this study, there were 500 neurons in the hidden layer. This process, called forward propagation, can be described in the following steps:

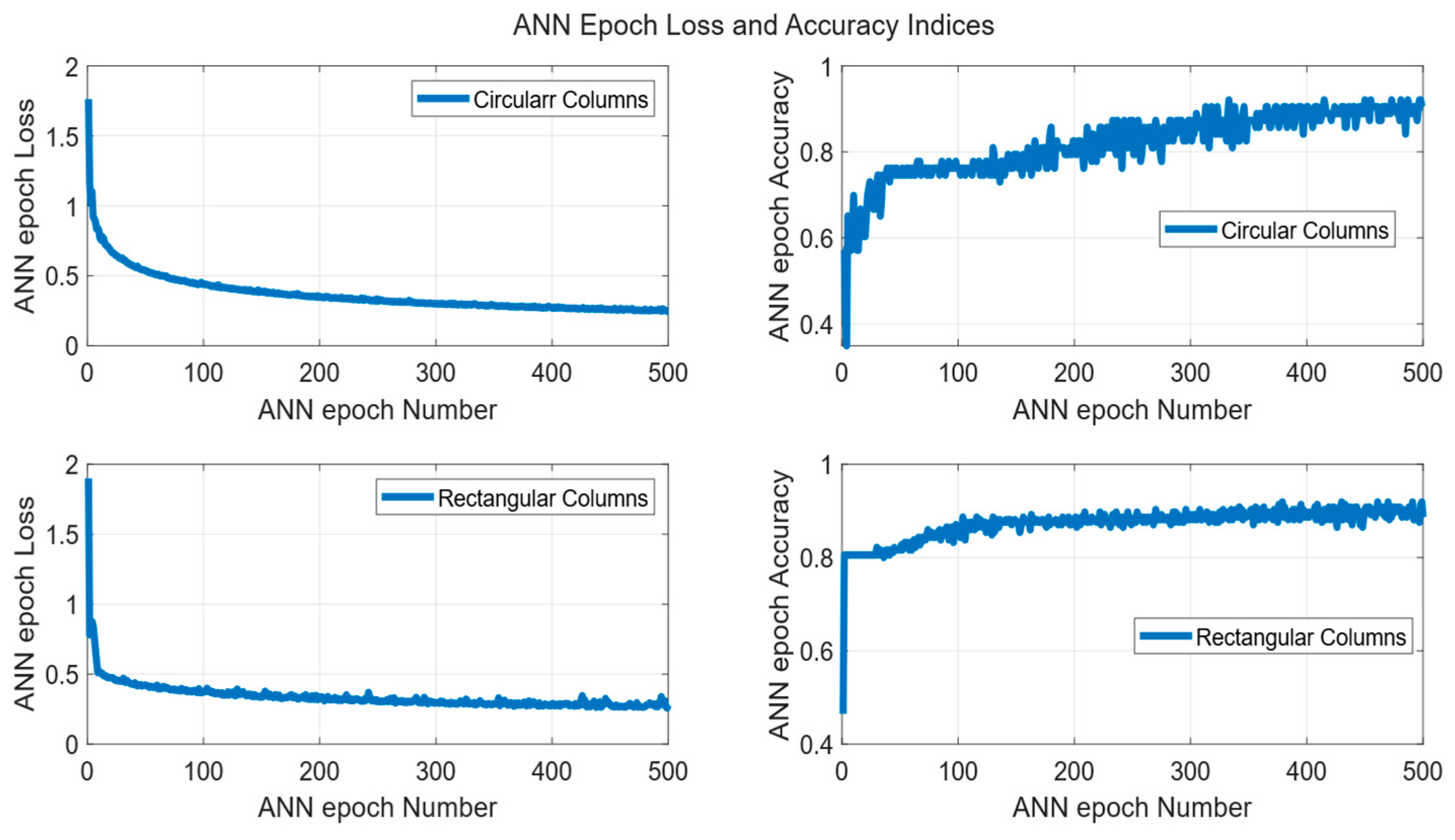
• The records of the entire training set pass through the neural network, and for each one, the network generates a prediction of the variable to be predicted.
• The above predictions are used to calculate the value of the cost function, which quantifies the “error” made by the ANN in attempting to predict the value to be predicted. A very common choice is the mean squared error (MSE) function.
• Forward propagation, described in steps 1 and 2, is followed by backward propagation, during which the parameter values used in the neural network in steps 1 and 2 to generate predictions from the ANN are revised and renewed in such a way as to contribute to reducing the value of the cost function calculated above. This process is called backward propagation because the revision–renewal of the parameter values starts from the output layer and reaches the input layer of the ANN.
• The process described in steps 1 to 3, where the records of the training set are forward propagated to calculate a value of the cost function and then backward propagated with the aim of updating the values of the parameters used in order to reduce the value of the cost function calculated, is referred to in the literature as an epoch.
• The next epoch begins, using the revised values of the parameters determined during the backward propagation of the previous epoch. The training process stops at the last epoch selected, and the ANN parameter values obtained in the backward propagation of the last epoch are the final ones for the ANN.

It is worth noting that the number of epochs (here equal to 500) that will take place during ANN training is selected by the analyst and constitutes a hyperparameter of the ANN model. Usually, the number of epochs to be used is determined by trial and error, and the general rule is that fewer epochs often lead to ANNs that exhibit underfitting, while too many epochs are associated with ANNs that exhibit overfitting, since in one case the model comes into contact with the testing set records a few times, while in the other case it examines the test set records more times.

From a mathematical point of view, training a neural network, like a “classic” supervised learning model, can be described as the problem of minimizing the selected cost function under the values of the model parameters, which in the case of an artificial neural network are the parameters that weight the outputs of the neurons of the immediately preceding layer of the network at the input of the neurons of the immediately following layer of the network. Such a problem is usually too complex to be solved accurately with closed-form solutions. Thus, in practice, this problem is solved using numerical methods. This numerical solution is aided by optimization algorithms, which are algorithmic procedures that “guide” the process of finding the values of the network parameters that correspond to the minimum value of the cost function.

The adaptive moment estimator (Adam) algorithm applied in this study is one of the most widely used solving algorithms today. It maintains a different learning rate for each parameter of the network, unlike other algorithms that use a common learning rate for all parameters. It is considered one of the best options for training neural networks that solve complex problems, as it is quite effective on complex and noisy data and helps to quickly converge on the final solution to the problem.

It is also clear that choosing the appropriate activation function for both the neurons of the hidden layers of a neural network and the neurons of the output layer is a crucial choice in the process of developing a neural network model. The choice varies depending on the problem that the neural network is called upon to solve (regression or classification) and whether the activation function will be used in the hidden layer or in the output layer of the network. The following

Table 3. Activation functions applied to the ANNs in this study.

Activation Function	Equation	Application
ReLu	F(x) = max(0, x)	Classification Problems with many hidden layers
Softmax	$F\left(x^j\right)=e^{x^j}/{\sum }_{k=1}^D{e}^{x^k}$	Non-binary classification problems and applied to the output layer

summarizes the activation functions applied in this study.

A very important hyperparameter in training a neural network is the cost function that will be used. As explained, the entire process of training a model consists of finding the optimal estimates of the model parameters, i.e., those that minimize the selected cost function. Up to this point, reference has been made mainly to the mean square error (MSE) function, which, although widely used and useful, cannot be used in classification problems. It is worth noting that while in the case of binary classification, the output layer of the ANN contains one neuron (producing as output the probability Y = 1), in non-binary classification, the output layer contains as many neurons as there are possible (distinct) values of the variable to be predicted (Figure 7). In

Table 4. Cost Function of the ANN for the non-binary classification problem of this study.

Cost Function	Equation	Application
Multiclass Cross Entropy (MCE)	$MCE=-{\sum }_{j=1}^c{Y}_i^{j}log\left({\widehat{Y}}_i^j\right)$	Non-binary classification problems

, the cost function applied here for non-binary classification is reported.

3. Results

A review of the full PEER database [37] for both circular and rectangular RC columns reveals that not all necessary parameters for defining the key variables influencing failure mode and displacement ductility are available for every column. Therefore, data files containing the required parameters—such as aspect ratio, axial load ratio, concrete strength, transverse reinforcement ratio, and normalized maximum shear stress—were generated and categorized into two groups based on section shape: rectangular and circular RC columns (see Appendix A).

These datasets were then split into training and testing sets for each column type. The test data were set to comprise 25% of the total dataset, with the remaining 75% allocated for training (based on previous research by the authors on the same data as the best choice [36]). During the training phase, the model was provided with both the input features and the corresponding failure modes (flexure, flexure–shear, or shear—hot-encoded in the dataset as 0, 1, and 2, respectively), enabling it to learn the relationships between the features and the target variable. As previously discussed, it is expected that these input features are correlated with the failure mode, and the model’s objective is to discover this underlying relationship.

Once trained, the model is tested using the test dataset, where it is given only the feature data—without the actual failure mode labels—and is asked to predict the failure modes. Since the true failure modes are known to the supervisors, the model’s accuracy can then be evaluated. In general, dividing the dataset into training and testing subsets (hold-out method) ensures that the model is evaluated on data representative of the entire dataset while preventing overfitting.

3.1. Rectangular RC Columns

The performance metrics for rectangular RC columns are presented below. The ANN model achieved an accuracy of 94% in predicting the actual failure modes of the columns in the test dataset. This accuracy is calculated from

Table 5. Confusion matrix in numbers for ML prediction of the failure mode of rectangular RC columns of the PEER structural performance database with ANNs.

		Confusion Matrix in Numbers *
True Values	Flexure	56	1	0
	Flexure–Shear	2	1	1
	Shear	0	0	1
		Flexure	Flexure–Shear	Shear
		Predicted Values

* Also see Figure 8.

by dividing the sum of the diagonal elements by the total sum of all elements in the table. Additional performance metrics are provided in

Table 6. Performance metrics.

Performance Metrics *
	True Positive	True Negative	False Positive	False Negative	Accuracy	Precision	Recall
Flexure	56	1 + 1 + 1 + 0 = 3	2 + 0 = 2	1 + 0 = 1	(56 + 3)/(56 + 3 + 2 + 1) = 59/62 = 95%	(56)/(56 + 2) = 56/58 = 97%	(56)/(56 + 1) = 56/57 = 98%
Flexure–Shear	1	56 + 0 + 0 + 1= 57	1 + 0 =1	2 + 1 = 3	(1 + 57)/(1 + 57 + 1 + 3) = 58/62 = 94%	(1)/(1 + 1) = 1/2 = 50%	(1)/(1 + 3) = 1/4 = 25%
Shear	1	56 +1 + 2 + 1 = 60	1 + 0 = 1	0 + 0 = 0	(1 + 60)/(1 + 60 + 1 + 0) = 61/62 = 98%	(1)/(1 + 1) = 1/2 = 50%	(1)/(1 + 0) = 1/1 = 100%

* Also see Table 5.

. Furthermore, Table 6 indicates that the model performs better at predicting flexural and shear failure modes than flexure–shear failures. This is understandable, as distinguishing flexure–shear failure is often more complex, even in practical engineering assessments, particularly in seismic structural assessment. When each influencing parameter in the feature data is examined individually, the transverse reinforcement ratio emerges as the most significant factor for the model’s success. This outcome verifies that the model has accurately captured the relationship between all features and the target failure mode, which is essential for building a prediction model based on physically meaningful ML methods [36]. It is important to note that Table 5 provides a clear explanation of the data illustrated in Figure 8, while Table 6 further clarifies the interpretation of Table 5.

In addition, the following metrics are applied and depicted in Figure 9:

• The receiver operating characteristic (ROC) curve demonstrates the balance between True acceptance rate (TAR) along the y-axis and false acceptance rate (FAR) along the x-axis. The upper left corner of the contour represents the ideal point where TAR equals one and FAR equals zero.
• The area under the curve (AUC) is used to quantify the quality of the authentication model as an alternative to accuracy. The value of AUC ranges from 0.0 to 1.0.

Finally, the principal component analysis (PCA) model is a model widely used for reducing the dimensionality of data (dimensionality reduction) in order to utilize only features–variables that provide knowledge and significantly improve models during the training phase. The graph below (Figure 10) shows a simple problem for the purposes of the presentation, since the human eye cannot visualize more than three dimensions. Specifically, each record (green dot) is initially described by a set of three variables (X1, X2, and X3) and then, after applying the principal component analysis, the same set can be described by just two variables, the two principal components (PC1 and PC2), thereby reducing the dimensions of the problem without losing important information from the data. In the employed ANN model, the input variables are 5 (see Appendix A). Based on that, in order to identify the decision boundaries or failure surface boundaries of the ANN model and its performance on the test set, the decision surface is plotted in Figure 11 for rectangular RC columns. It can be clearly seen that the model is not successful in predicting the flexure–shear failure mode, as the previous performance metrics imply too.

3.2. Circular RC Columns

The performance metrics for circular RC columns are presented below. The ANN model achieved an accuracy of 95% in predicting the actual failure modes of the columns in the test dataset. This accuracy is calculated from

Table 7. Confusion matrix in numbers for ML prediction of the failure mode of circular RC columns of the PEER structural performance database with ANNs.

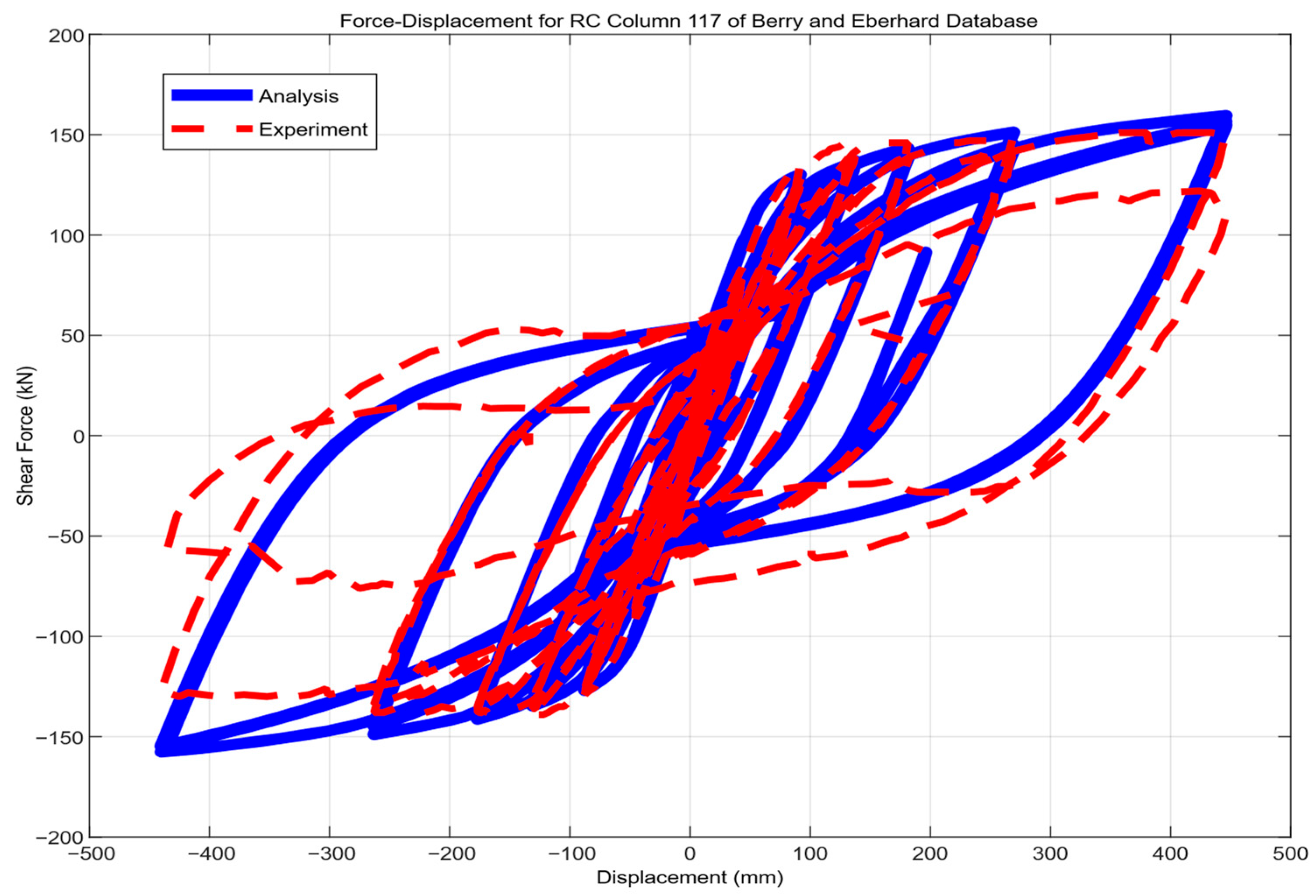
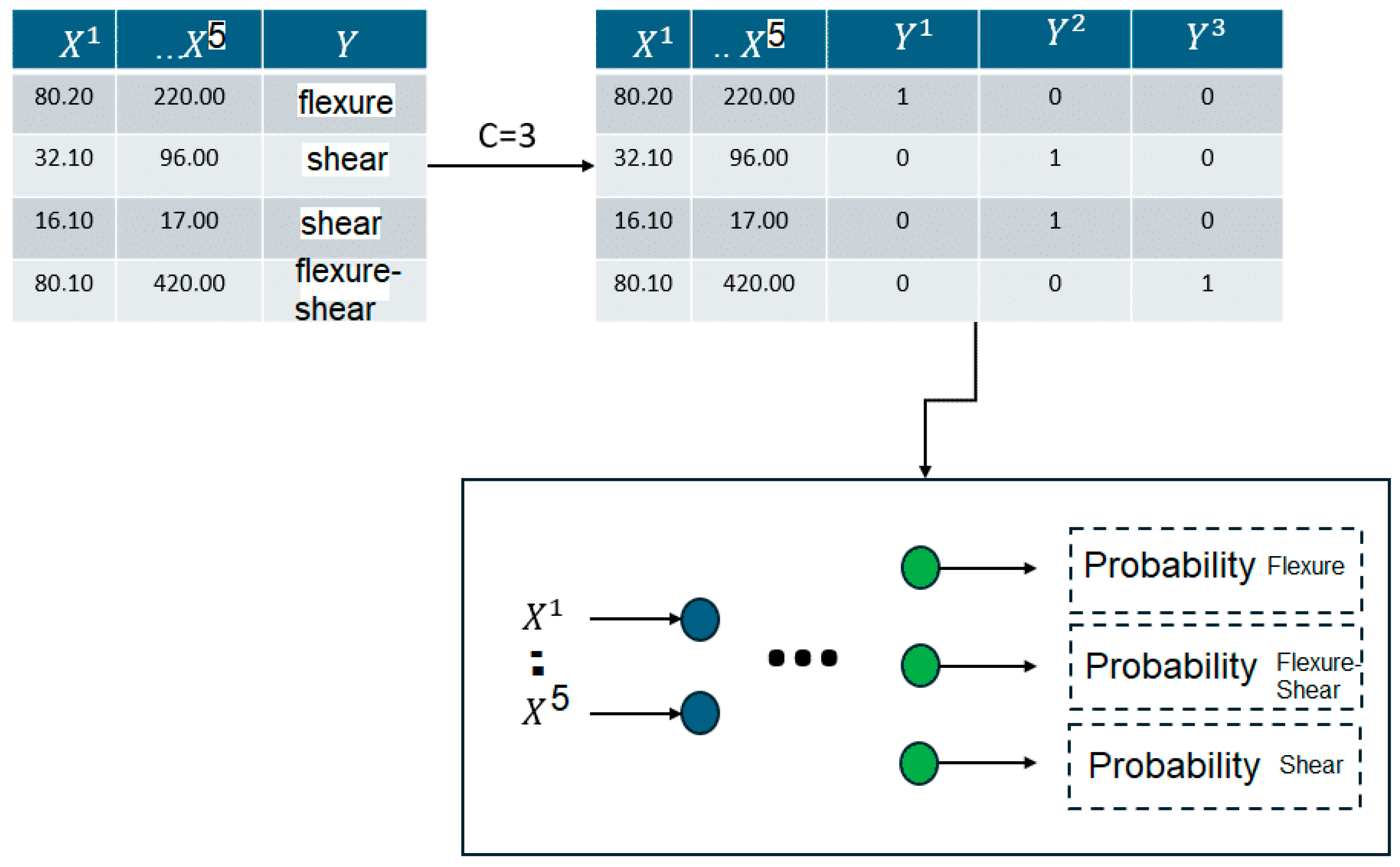
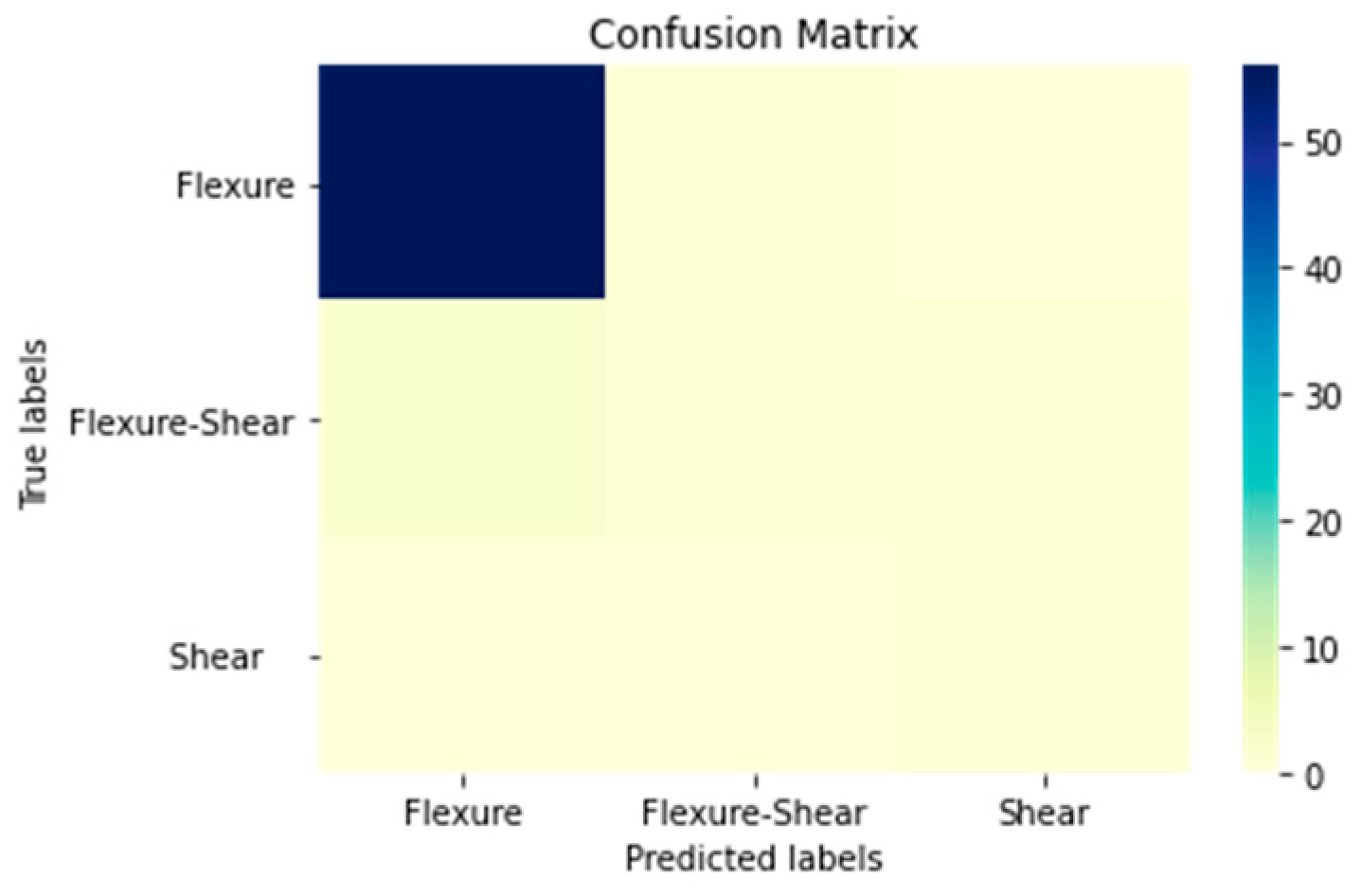
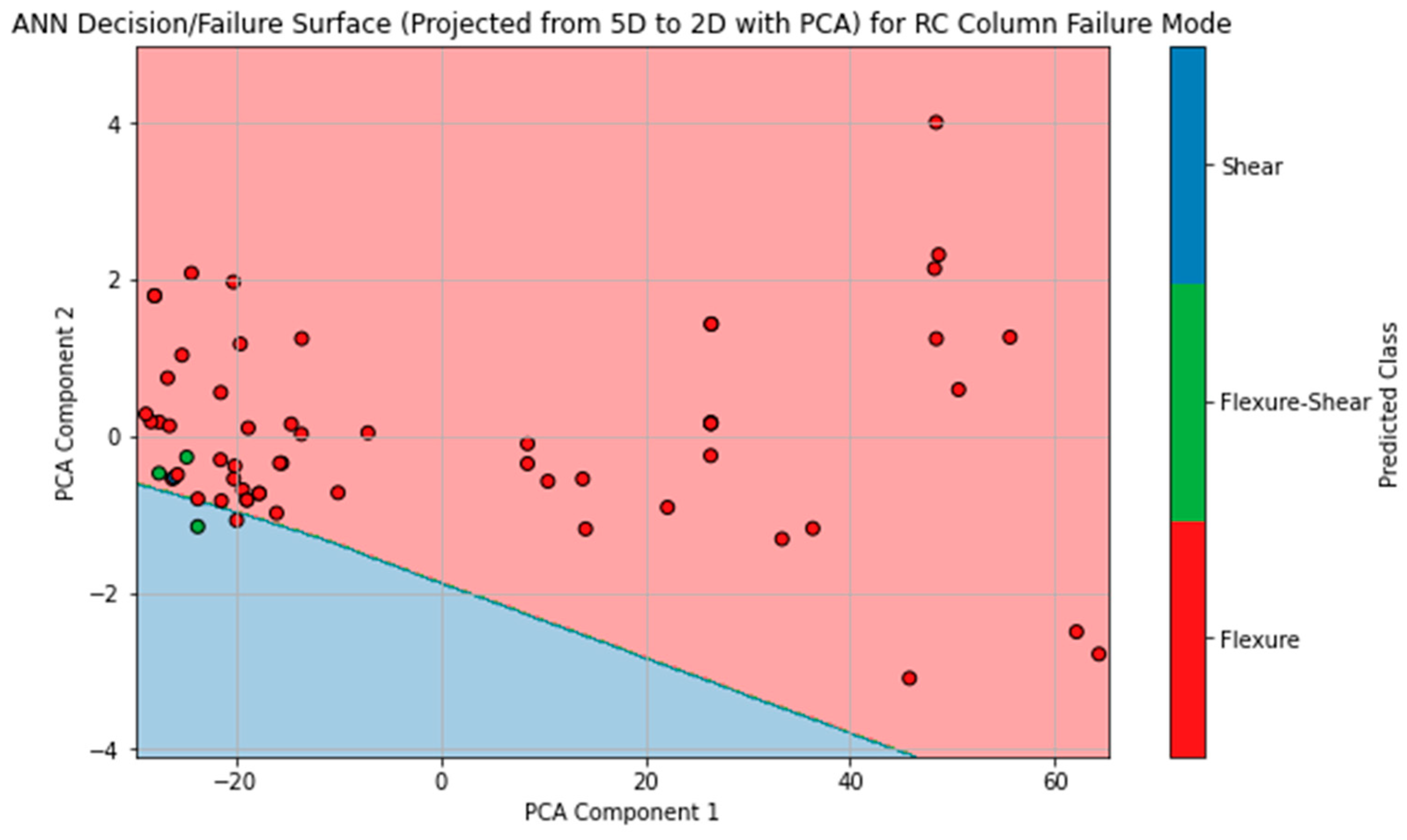
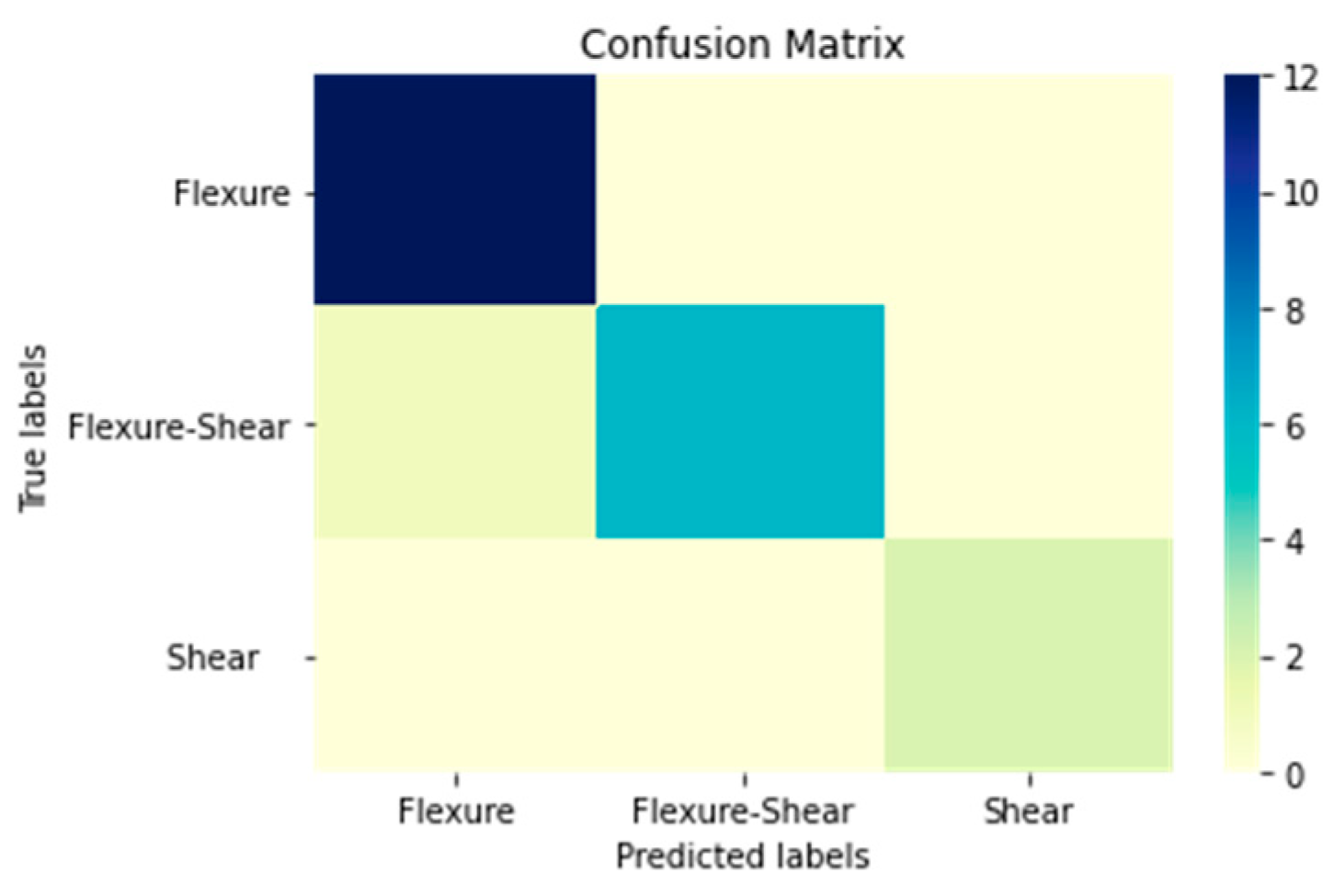
		Confusion Matrix in Numbers *
True Values	Flexure	12	0	0
	Flexure–Shear	1	6	0
	Shear	0	0	2
		Flexure	Flexure–Shear	Shear
		Predicted Values

* Also see Figure 12.

by dividing the sum of the diagonal elements by the total sum of all elements in the table. Additional performance metrics are provided in

Table 8. Performance metrics.

Performance Metrics *
	True Positive	True Negative	False Positive	False Negative	Accuracy	Precision	Recall
Flexure	12	6 + 0 + 0 + 2 = 8	1 + 0 = 1	0 + 0 = 0	(12 + 8)/(12 + 8 + 1 + 0) = 20/21 = 95%	(12)/(12 + 1) = 12/13 = 92%	(12)/(12 + 0) = 12/12 = 100%
Flexure–Shear	6	12 + 0 + 0 + 2 = 14	0 + 0 = 0	1 + 0 = 1	(6 + 14)/(6 + 14 + 0 + 1) = 20/21 = 95%	(6)/(6 + 0) = 6/6 = 100%	(6)/(6 + 1) = 6/7 = 86%
Shear	2	12 +0 + 1 + 6 = 19	0 + 0 = 0	0 + 0 = 0	(2 + 19)/(2 + 19 + 0 + 0) = 21/21 = 100%	(2)/(2 + 0) = 2/2 = 100%	(2)/(2 + 0) = 2/2 = 100%

* Also see Table 7.

. Furthermore, Table 8 indicates that the model performs better at predicting flexural and shear failure modes than flexure–shear failures. This is understandable, as mentioned already, as distinguishing flexure–shear failure is often more complex even in practical engineering assessments, particularly in seismic assessments. By analyzing each influencing parameter in the feature data individually, it becomes evident that the transverse reinforcement ratio is the most critical factor for the model’s success. This finding confirms that the model has correctly captured the relationship between all features and the target failure mode. Such alignment is essential for developing an ML prediction model grounded in physical meaning [36]. It is important to note that Table 5 provides a clear explanation of the data illustrated in Figure 12, while Table 8 further clarifies the interpretation of Table 7.

In addition, the two metrics of ROC and AUC are applied and depicted in Figure 13. Finally, in order to identify the decision boundaries or failure surface boundaries of the ANN model and its performance on the test set, the decision surface is plotted in Figure 14 for circular RC columns. It can be clearly seen that the model is not perfectly successful in predicting the flexure–shear failure mode, as the previous performance metrics imply too.

Finally, for both ANNs for circular and rectangular columns, the loss and accuracy indices during training are depicted in Figure 15 below. The influence of the number of epochs on these indices is evident. This figure compares the training behavior of ANNs for circular and rectangular columns over 500 epochs, showing loss (left) and accuracy (right). For circular columns, the loss decreases smoothly from about 1.6 to ~0.3–0.4, while accuracy starts near 50% and gradually climbs with fluctuations to ~90% by epoch 500, suggesting the task is more complex and requires longer training. In contrast, for rectangular columns, the loss drops sharply from ~2.0 to ~0.2–0.3 within the first 50 epochs, and accuracy starts higher (around 80%), quickly stabilizing near 90% by ~100 epochs with much smoother convergence. Overall, rectangular columns are easier for the ANN to learn, showing faster, more stable performance, while circular columns demand more epochs and display greater variability.

4. Discussion

Based on previous studies by the authors [1,2,36], the current state of modeling the lateral load response of reinforced concrete columns still presents several challenges. Key areas requiring improvement include more accurate estimation of the behavior of columns prone to shear failure after flexural yielding; enhanced methods for predicting shear strength and its degradation with increasing displacement ductility; consideration of reinforcement pullout effects on stiffness; better representation of hysteresis loop shapes; understanding the negative impact of axial loads at large displacements; and accurately determining the deformation levels (e.g., drift ratios) associated with key points along the column’s response curve. These unresolved issues must be addressed before performance-based assessment frameworks can be considered complete and fully reliable [1,2,36]. In addition, the overall accuracy of other machine learning methods, such as random forests, performed by the authors [36] for rectangular RC columns reaches 94%, while for circular RC columns, it is 86%. The performance in the latter case is affected by the size of the training and testing datasets, rather than by the number of decision trees used in the random forest algorithm. Lastly, brittle failures—particularly in circular RC columns—show relatively low precision and recall scores.

Within this context, the present study demonstrates that integrating physical knowledge—via experimental databases—into machine learning (ML) approaches can lead to accurate predictions of RC column failure modes. The results show that the ANN model effectively predicts failure modes for both circular and rectangular RC columns and for ductile and brittle failure mode types. The model achieved an overall accuracy of 94% for rectangular RC columns and 95% for circular ones. In comparison, as shown in Section 2, the traditional code-based method incorporating nonlinear structural analysis attained accuracies of 97% and 81% for rectangular and circular columns, respectively. These results indicate that the ANN approach outperformed the traditional engineering mechanics-based method in predicting the failure modes of circular columns. The latter was also confirmed by the precision and recall scores for brittle failure modes in circular RC columns. These findings suggest neural networks or deep learning may offer better performance in these cases compared to other ML methods such as random forests [36,47,49].

5. Conclusions

Accurately predicting the failure modes of RC columns is critical for developing effective retrofitting strategies for modern buildings and bridges. Traditional methods, which primarily rely on nonlinear structural analysis, are often time-consuming and require substantial effort to achieve reliable results. This study explores the integration of physical knowledge with machine learning (ML) techniques to enhance failure mode prediction for RC columns. Leveraging the PEER structural performance database, the research proved that supervised ML models—specifically ANNs—can effectively classify failure modes when applied to a randomly selected test set from the PEER database, especially when supplemented with physical insights. In several instances, the ML model’s predictions matched or surpassed those obtained using conventional building code-based methods. Importantly, this study is the first to apply its methodology to the whole PEER database, through nonlinear structural analysis using both traditional methods and supervised ML techniques, to predict RC column failure modes. It also addresses the influence of column cross-sectional geometry—a factor often overlooked in previous studies that predominantly focused on circular columns. These outcomes underscore the significant potential of ML to advance the field of earthquake engineering. Future research endeavors of the authors could include a real-world structural case for seismic assessment and retrofit based on ML methods.